Vibration characteristics investigation of a dual rotor-bearing outer ring–pedestal-casing system with clearance fit

Abstract

Due to thermal expansion of the mechanical structure, assembly processes, bearing wear, and long-term vibration during operation, a clearance fit may occur between the bearing outer ring and its pedestal. The clearance fit may result in relative motion between the bearing outer ring and pedestal, thereby altering the support characteristics of the rotor and subsequently impacting the dynamic characteristics of the rotor-bearing system. The stable operation of the system may be at risk in this case. In this paper, the dynamic model of the coupling system of a dual rotor-bearing outer ring-pedestal-casing with clearance fit is established based on the finite element method and lumped parameter method. The dimensionality of the system equation is reduced using the fixed-interface component mode synthesis (CMS) method and solved numerically. The impact of clearance fit on the vibration characteristics of the system is investigated under three operational conditions: imbalance of the inner rotor, imbalance of the outer rotor, and simultaneous imbalance of both two rotors. Furthermore, an analysis is conducted to evaluate the motion state of the system with clearance fit. Lastly, the vibration transmission characteristics between the rotor-bearing outer ring-pedestal-casing are studied. The results indicate that the harmonic components corresponding to the rotational speed frequency of rotors will appear on the spectrum and envelope spectrum of the system with clearance fit. The natural frequency of the system may be excited in the resonance region. Due to the influence of gravity, the dynamic characteristics of the system vary significantly at low and high rotational speeds. Additionally, the vibration transmission characteristics of the system are significantly influenced by both the rotational speeds and clearance fit.

1 Introduction

The dynamic characteristics of the rotor system in rotating machinery play a crucial role in ensuring stable operation. In rotating machinery such as gas turbines, a certain clearance is typically reserved between the bearing outer ring and the pedestal to prevent excessive stress concentration caused by temperature changes in the support system. This allows for structural adjustment during thermal expansion and contraction, while facilitating assembly. The presence of clearance fit can result in collision and friction between the bearing outer ring and the corresponding surface of the pedestal, leading to nonlinear and time-varying contact characteristics that contribute to the dynamic behavior of the rotor-bearing system.

The impact of the radial clearance within the bearing on the dynamic characteristics of the rotor-bearing system has been extensively investigated by numerous scholars. The contact problem between the rolling element and the raceway was simplified by Sunnersjo [1] as a nonlinear spring, and an investigation was conducted on the varying compliance vibration of the bearing. Subsequently, some scholars incorporated the nonlinear bearing force into the rotor system. Tiwari [2,3,4,5] conducted a study on the unbalanced response of a rotor system supported by ball bearings. Harsha and Bai [6,7,8,9,10] investigated the vibration characteristics and stability of the rotor-bearing system, considering nonlinear factors such as radial clearance and bearing waviness. The scholars also initiated the investigation of the nonlinear response exhibited by intricate rotor systems on this foundation. The research conducted by Wang [11] revealed that reducing radial clearance can effectively decrease overall vibration in aero-engines and enhance the stability of rotor operation. Zhang [12] and Jin [13] focused on the impact of radial clearance in a rolling bearing on the varying compliance vibration of a rotor system. Chen [14] analyzed the influence of radial clearance in the intermediate bearing on the nonlinear dynamic characteristics of the dual rotor-bearing-casing system.

Additionally, the dynamics characteristics of a single rotor system under the clearance fit between the bearing outer ring and the pedestal have also attracted attention from some scholars. Mao [15] studied the effect of ring deformation on the dynamic characteristics of cylindrical roller bearings. The introduction of the clearance fit into the rotor system was subsequently proposed by some scholars. Liu [16, 17] proposed a simplified model for the connection between the bearing outer ring and the pedestal, which consists of two linear spring-damping elements. The stiffness of the matching interface was determined by combining the slicing method with integral method, enabling an investigation into the vibration characteristics of the rotor-bearing system during bearing failure. Chen [18] and Wang [19, 20] developed a clearance fit model, which exhibits similarities to the classical stator-rotor rubbing model. The investigation focused on analyzing the impact of tightening torque and rotor unbalance on a system with clearance fit, while also examining the influence of a squeezed oil film damper on system vibration caused by fit loosening. Cao [21,22,23] simplified the contact problem between the bearing outer ring and the pedestal into a series of spring-damping systems that are uniformly distributed. By utilizing rigid body elements, a dynamic model of the rotor-bearing-pedestal system with clearance fit was established, enabling the study of its impact on system vibration. Additionally, the design parameter of fit clearance was taken into consideration, and an optimal scheme for the fit clearance of the machine tool spindles was provided. Wu [24] and Zhang [25] built a rotor-bearing-pedestal model incorporating multiple fit clearances to investigate the impact of fit clearances and rotor unbalance on the dynamic response of the system. Xu [26] presented a three-dimensional clearance fit model that incorporates the 6-DOF model of the bearing outer ring. The vibration and contact characteristics of the rotor-bearing system were investigated under clearance fit. Furthermore, several scholars have also focused their attention on the impact of temperature in the context of clearance fit. The thermal deformation difference between the bearing outer ring and pedestal of the all-ceramic bearing was considered by Shi [27, 28], who investigated the impact of temperature and rotational speed on the dynamic characteristics of the bearing. Bai [29, 30] developed a clearance fit model that incorporates temperature effects to investigate the influence of bearing outer ring spin motion on the local defect frequency offset across various fit clearances. Other than that, the relationship between fit clearance, rotational speed, and acoustic radiation characteristics of bearings was explored. Moreover, the issue of bolt loosening faults in bearing pedestal has attracted attention from some scholars. Lu [31], Jiang [32], and Yang [33] analyzed the vibration and stability of the rotor system under the condition of foundation loosening, and proposed the assessment method of foundation loosening under constant rotational speed.

In addition to the aforementioned studies, a substantial number of scholars have also conducted research on modeling and the dynamic characteristics of dual-rotor systems. Fei [34] established a typical dual rotor model based on the finite element method. Lu [35] modeled a dynamic model for a dual rotor system supported by ball bearings and studied the time-varying stiffness of the bearings as well as the vibration characteristics of the system in relation to radial clearance. Kang [36] investigated the backward whirling characteristics of a counter-rotating dual rotor-bearing system. Wang [37] employed theoretical and experimental methods to obtain the inherent characteristics and unbalanced response of a dual rotor system. Hou [38] used the Lagrange equation to derive the dynamic equation of a dual rotor-bearing system and discussed its combined resonance problem. The study conducted by Jin [39] focused on the dimension reduction method of a complex dual rotor-bearing model. It is worth noting that Hou [40] presented a theoretical solution for the vibration response of the dual rotor system and investigated the influence of parameters such as speed ratio and radial clearance on the system's vibration. The vibration characteristics of dual-rotor systems with coupling misalignment have also been the focus of attention for certain scholars. Lu [41] investigated the dynamic characteristics of the dual rotor bearing system with parallel misalignment. Wang [42] proposed a dynamic model of a dual rotor system with unbalance-misalignment coupling faults. The dual rotor systems with rub-impact fault have also been the subject of research by several scholars. Jin [43] established a model of a dual rotor-coupling misalignment system with blade-casing rubbing. Yang [44] and Wang [45] studied the vibration characteristics of a dual rotor-casing system in the presence of bearing loosening and rub-impact faults. Yu [46, 47] built an ANSYS model for a dual-rotor system in an aero-engine and investigated the dynamic characteristics of the system when subjected to sudden unbalance and rub-impact faults caused by blade shedding. The vibration response and stability of a dual rotor system under rub-impact faults were studied by Yang [48], Sun [49, 50], Fu [51], and Wang [52]. It is worth noting that Yu [53] focused on the dynamic behaviors of the dual rotor system in the presence of rub-impact faults occurring between the low-pressure and high-pressure rotors. Furthermore, Gao [54] investigated the mechanism of sudden shock vibration in the dual rotor system while considering a local defect in the outer ring of the intermediate bearing. Wang [55] and Gao [56] analyzed the vibration characteristics of a dual-rotor system under single point fault and compound fault of the intermediate bearing. Lu [57] simulated the nonlinear dynamic response of a dual rotor system with crack faults. Gao [58,59,60] studied the coupling mechanism between the dynamic behaviors of a dual rotor system and the thermal behaviors of the intermediate bearing under dynamic loads.

In the current research, scholars primarily focus on the modeling method of clearance fit and the issue of nonlinear vibration response in bearing or single-rotor systems under clearance fit. The focus of dual-rotor-bearing systems lies primarily on the modeling and solution methods, while also exploring the impact of various factors such as internal radial clearance of bearings, coupling misalignment, blade-casing rubbing, rub-impact faults occurring between the low-pressure and high-pressure rotor, bolt loosening faults in bearing pedestal, and thermal behaviors of the bearing on the rotor systems. However, nonlinear dynamic problems caused by the clearance fit between the bearing outer ring and the pedestal are of less concern in terms of the dual rotor-bearing-pedestal-casing system. The rolling bearing serves as the core component of the rotor system in rotating machinery, such as gas turbines. The presence of a certain clearance between the bearing outer ring and the pedestal may arise due to factors such as assembly design, machining errors, temperature variations, and wear during operation. This clearance is known as fit clearance. The fit clearance may result in significant vibration and shock response within the rotor-bearing system, thereby inevitably impacting the operational performance of the system. Additionally, the issue of clearance fit is present not only in the single rotor-bearing system but also in the dual rotor-bearing system. Being distinct from a single rotor, the dual-rotor system comprises an inner rotor and an outer rotor that generally operate at distinct rotational speeds. Consequently, the dual rotor system is simultaneously subject to two unbalanced excitations of different frequencies during operation. More importantly, the dual-rotor configurations with intermediate bearings are generally employed in certain gas turbines, thereby enhancing the dynamic coupling effect between the inner and outer rotors. In summary, it is essential to investigate the dynamic characteristics of the dual rotor-bearing outer ring-pedestal-casing system and elucidate the correlation between fit clearance and system vibration, considering both the imbalances of inner and outer rotors, nonlinearity of bearing forces, and clearance fit between bearing outer ring and the pedestal.

In this paper, the clearance fit model between the bearing outer ring and the pedestal is established, and then the dynamic equations of the dual rotor-bearing outer ring-pedestal-casing are derived based on the finite element method and lumped parameter method. The dimensionality of the system equation is reduced through the application of the fixed-interface CMS method. The impact of rotor unbalance, rotational speed, and fit clearance on the vibration characteristics and stability of the system are investigated. Additionally, it delves into the discussion of vibration transfer characteristics among the rotor-bearing outer ring-pedestal-casing. The results presented in this paper offer a comprehensive understanding of the vibration behaviors of the dual rotor system under clearance fit, thereby providing valuable insights into the process of structural design.

2 Model of a dual rotor–bearing outer ring–pedestal-casing system

2.1 Geometric structure

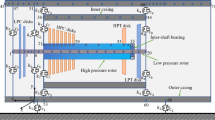
A dual rotor-bearing outer ring–pedestal-casing model is established based on reference [34], as depicted in Fig. 1. The system consists of an inner rotor, an outer rotor, a casing, bearings, and pedestals. The blade disk systems on both rotors have been simplified into rigid disk elements. The inner rotor is supported by bearings 1 and 2, while bearing 3 supports the outer rotor. Bearing 4 serves as an intermediate bearing that connects the inner and outer rotors. The supports 1 and 2 are used to restrict the movement of the casing. The detailed structural parameters can be found in Appendix 1. A Timoshenko beam model incorporating gyroscopic effects is employed for both the inner and outer rotors, while a non-rotating hollow Timoshenko beam model is utilized for the casing. The interference fit is adopted between the bearing inner ring and rotor. The bearing outer ring and the pedestal are treated as concentrated masses and their dynamic models are established using the lumped parameter method. The interaction between the bearing outer ring and pedestal primarily occurs in the radial directions, with limitations imposed on their axial and rotational degrees of freedom.

Fig. 1

The structure diagram of a dual rotor-bearing outer ring-pedestal-casing system

2.2 The force between the inner and outer rings of the bearing

Figure 2 shows a model of an elastic restoring force for a rolling bearing. The contact between the rolling element and the inner and outer rings is simplified as two spring-damping systems, namely k_in-c_in and k_out-c_out. Due to the small mass of the rolling body compared to that of the ring, it can be disregarded, and the force transfer relationship between the inner and outer rings can be obtained by connecting their respective spring-damping systems in series. The inner and outer rings of the bearing are interconnected through numerous a multitude of evenly distributed spring-damping systems. According to Hertz contact theory for rolling bearings, disregarding damping effects, the elastic force generated by the contact between the jth rolling element and the inner and outer rings is

$$ f_{j} = k_{b} \delta_{j}^{1.5} H(\delta_{j} ) $$

(1)

where k_b represents the equivalent contact stiffness, H(·) denotes the Heaviside function, and δ_j is the contact deformation and there is

$$ \delta_{j} = \left( {x_{i} - x_{o} } \right)\cos \theta_{j} + \left( {y_{i} - y_{o} } \right)\sin \theta_{j} - \delta_{0} $$

(2)

where x_i, x_o. y_i, y_o are the displacements of the inner and outer rings in the x and y direction, respectively. δ₀ is the radial clearance, and θ_j is the azimuth of the jth rolling element, as

$$ \theta_{j} = w_{c} t + 2\pi \left( {j - 1} \right)/Z $$

(3)

where w_c is the rotational speed of the cage and Z is the number of rolling elements, then the force between the inner and outer rings of the bearing is

$$ f_{x} = k_{b} \sum\limits_{j = 1}^{Z} {\delta_{j}^{1.5} H(\delta_{j} )\cos \theta_{j} } \begin{array}{*{20}c} , \\ \end{array} f_{y} = k_{b} \sum\limits_{j = 1}^{Z} {\delta_{j}^{1.5} H(\delta_{j} )\sin \theta_{j} } $$

(4)

Fig. 2

The model of an elastic restoring force for a rolling bearing

2.3 Clearance fit model between bearing outer ring and pedestal

The force model between the bearing outer ring and pedestal is considered as a friction collision model between the two stators, similar to the rub-impact model between the blade and the casing [18]. The collision force and friction are derived in this section. Figure 3 illustrates the clearance fit model between the bearing outer ring and the pedestal. The fit clearance δ_c is defined as the difference between the outer radius of the outer ring R_or and the inner radius of the pedestal R_p. The initial center position of the outer ring and the pedestal is denoted as point O, while point p represents the central position of the outer ring with respect to the motion of the pedestal. Additionally, β refers to the angle formed by the contact point of the outer ring and the pedestal relative to the x-axis. The generation of supporting force occurs when the relative displacement between the bearing outer ring and the pedestal exceeds the fit clearance.

Fig. 3

The model of clearance fit between the bearing outer ring and the pedestal

The vibration displacement and velocity of the outer ring in the x and y directions are denoted as x_or, v_xor, y_or, and v_yor, respectively. Similarly, the vibration displacement and velocity of the pedestal in the x and y directions are represented by x_p, v_xp, y_p, and v_yp. The radial displacement R_op and tangential velocity V_op of the outer ring concerning the pedestal are

$$ R_{op} = \sqrt {\left( {x_{or} - x_{p} } \right)^{2} + \left( {y_{or} - y_{p} } \right)^{2} } $$

(5)

$$ V_{op} = \left( {v_{xor} - v_{xp} } \right)\sin \beta - \left( {v_{yor} - v_{yp} } \right)\cos \beta $$

(6)

where the angular position β of the contact point shall satisfy the following equation, as

$$ \sin \beta = \left( {y_{or} - y_{p} } \right)/R_{op} ,\cos \beta = \left( {x{}_{or} - x_{p} } \right)/R_{op} $$

(7)

According to Hertz contact theory and Coulomb law of friction, the collision force F_n and the friction force f_n can be determined as

$$ F_{n} = k_{r} \left( {R_{op} - \delta } \right),f_{n} = f_{r} F_{n} {{V_{op} } \mathord{\left/ {\vphantom {{V_{op} } {\left| {V_{op} } \right|}}} \right. \kern-0pt} {\left| {V_{op} } \right|}} $$

(8)

where f_r is the friction coefficient, the contact stiffness k_r can be calculated using the equation k_r = 0.3553E′l^8/9. The symbol E′ represents the equivalent elastic modulus, while l denotes the effective line contact length. The contact forces in the x and y directions can be as follows:

$$ \begin{aligned} p_{x} & = - F_{n} \cos \beta - \frac{{V_{{op}} }}{{\left| {V_{{op}} } \right|}}f_{r} F_{n} \sin \beta , \\ p_{y} & = - F_{n} \sin \beta + \frac{{V_{{op}} }}{{\left| {V_{{op}} } \right|}}f_{r} F_{n} \cos \beta \\ \end{aligned} $$

(9)

2.4 Model of outer ring and pedestal

The force transfer model of the supporting system is illustrated in Fig. 4. It is mainly divided into four parts: rotor, pedestal, out ring, and casing. The dynamic equations of the bearing outer ring and pedestal are derived under the assumption of a linear connection between each component. However, when considering the nonlinear force (f_x, f_y, p_x, and p_y) between them, the linear stiffness can be set to 0 and this nonlinear force can be introduced into the system as an external force.

Fig. 4

The model of force transfer of supporting system

Assuming that the ith node of the rotor is connected to the outer ring and that the jth node of the casing is connected to the pedestal. The variables x_ri, x_or, x_p, x_cj, y_ri, y_p, and y_cj denote the displacements of the rotor, outer ring, pedestal, and casing in the x and y directions. The stiffness and damping between the rotor and outer ring are denoted as k_ro and c_ro, respectively, while k_op and c_op represent the stiffness and damping between the outer ring and pedestal. Similarly, c_pc and k_pc indicate the stiffness and damping between the pedestal and casing. The differential equation governing the motion of the outer ring and pedestal can be formulated as follows:

$$ \left\{ {\begin{array}{*{20}l} {m_{or} \ddot{x}_{or} + c_{op} \left( {\dot{x}_{or} - \dot{x}_{p} } \right) + k_{op} \left( {x_{or} - x_{p} } \right) = f_{rorx} - m_{or} g} \hfill \\ {m_{or} \ddot{y}_{or} + c_{op} \left( {\dot{y}_{or} - \dot{y}_{p} } \right) + k_{op} \left( {y_{or} - y_{p} } \right) = f_{rory} } \hfill \\ {m_{p} \ddot{x}_{p} + c_{op} \left( {\dot{x}_{p} - \dot{x}_{or} } \right) + k_{op} \left( {x_{p} - x_{or} } \right) = f_{pcx} - m_{p} g} \hfill \\ {m_{p} \ddot{y}_{p} + c_{op} \left( {\dot{y}_{p} - \dot{y}_{or} } \right) + k_{op} \left( {y_{p} - y_{or} } \right) = f_{pcy} } \hfill \\ \end{array} } \right. $$

(10)

where m_or and m_p represent the mass of the outer ring and the pedestal, respectively. The forces exerted by the rotor on the outer ring in the x and y directions are denoted as f_rorx and f_rory, respectively. Similarly, the forces exerted by the casing on the outer ring in the x and y directions are denoted as f_pcx and f_pcy, respectively. There are

$$ \left\{ {\begin{array}{*{20}c} {f_{rorx} = - c_{ro} \left( {\dot{x}_{or} - \dot{x}_{ri} } \right) - k_{ro} \left( {x_{or} - x_{ri} } \right),\begin{array}{*{20}c} {f_{rory} = - c_{ro} \left( {\dot{y}_{or} - \dot{y}_{ri} } \right) - k_{ro} \left( {y_{or} - y_{ri} } \right)} & {} \\ \end{array} } \\ {f_{pcx} = - c_{pc} \left( {\dot{x}_{p} - \dot{x}_{cj} } \right) - k_{pc} \left( {x_{p} - x_{cj} } \right),\begin{array}{*{20}c} {f_{pcy} = - c_{pc} \left( {\dot{y}_{p} - \dot{y}_{cj} } \right) - k_{pc} \left( {y_{p} - y_{cj} } \right)} & {} \\ \end{array} } \\ \end{array} } \right. $$

(11)

Then the dynamic equation of the supporting system at bearing 1, 2, and 3 is expressed as a matrix in the following format:

$$ \left\{ {\begin{array}{*{20}l} {{\mathbf{M}}_{op} {\ddot{\mathbf{X}}}_{op} + {\mathbf{C}}_{op} {\dot{\mathbf{X}}}_{op} + {\mathbf{K}}_{op} {\mathbf{X}} = {\mathbf{F}}_{opx} } \hfill \\ {{\mathbf{M}}_{op} {\ddot{\mathbf{Y}}}_{op} + {\mathbf{C}}_{op} {\dot{\mathbf{Y}}}_{op} + {\mathbf{K}}_{op} {\mathbf{Y}} = {\mathbf{F}}_{opy} } \hfill \\ \end{array} } \right. $$

(12)

where M_op, C_op, and K_op are the mass matrix of the outer ring and the pedestal, respectively. The external force vectors are denoted as F_opx and F_opy. X_op and Y_op are generalized displacement vectors, depicted as

$$ \left\{ {\begin{array}{*{20}l} {{\mathbf{X}}_{op} = \left\{ {\begin{array}{*{20}l} {x_{or1} ,} \hfill & {x_{p1} ,} \hfill & {x_{or2} ,} \hfill & {x_{p2} ,} \hfill & {x_{or3} ,} \hfill & {x_{p3} } \hfill \\ \end{array} } \right\}^{T} } \hfill \\ {{\mathbf{Y}}_{op} = \left\{ {\begin{array}{*{20}l} {y_{or1} ,} \hfill & {y_{p1} ,} \hfill & {y_{or2} ,} \hfill & {y_{p2} ,} \hfill & {y_{or3} ,} \hfill & {y_{p3} } \hfill \\ \end{array} } \right\}^{T} } \hfill \\ \end{array} } \right. $$

(13)

2.5 Dynamic equations of rigid disk and beam elements

The rotor consists of multiple rigid disk elements, uniform section and variable section beam elements, while the casing is divided into several uniform section beam elements. The equations of these elements need to be derived in order to obtain the dynamic equations of the dual rotor and casing. The models of these three types of elements are shown in Fig. 5. The displacement vectors of the rigid disk element in the xos and yos plane are defined as u_rd1 = [x_d,θ_y]^T and u_rd2 = [y_d,-θ_x]^T, respectively. By substituting the kinetic energy of the disk into the Lagrange equation, we obtain

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{rd} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{M}}_{rd} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\ddot{\mathbf{u}}}_{rd1} } \\ {{\ddot{\mathbf{u}}}_{rd2} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {{\mathbf{G}}_{rd} } \\ { - {\mathbf{G}}_{rd} } & {\mathbf{0}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\dot{\mathbf{u}}}_{rd1} } \\ {{\dot{\mathbf{u}}}_{rd2} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {{\mathbf{Q}}_{rd1} } \\ {{\mathbf{Q}}_{rd2} } \\ \end{array} } \right\} $$

(14)

where M_rd and G_rd are the mass matrix and rotation matrix of the disk respectively. Q_rd1 and Q_rd2 represent the external force vectors.

Fig. 5

The models of the three types of elements

The displacement vectors of the beam element in the xos plane and yos plane are denoted as u_b1 = [x_i,θ_yi,x_j,θ_yj]^T and u_b2 = [y_i,-θ_xi,y_j,-θ_xj]^T, respectively. The kinetic energy and potential energy of a beam element with an equal section can be determined by integrating the kinetic energy and potential energy of the microelement ds along the length l of the beam element. Then the translational inertia matrix M_sT, rotational inertia matrix M_sR, gyro matrix J_s, and stiffness matrix K_s can be derived from the Lagrange equation, which can be written as.

$$ {\mathbf{M}}_{sT} = \int_{0}^{l} {\rho A{\mathbf{N}}^{{\varvec{T}}} } {\mathbf{N}}{\varvec{d}}s $$

(15)

$$ {\mathbf{J}}_{s} = 2{\mathbf{M}}_{sR} = 2\int_{0}^{l} {\rho I{\mathbf{D}}^{T} } {\mathbf{D}}{\text{d}}s $$

(16)

$$ {\mathbf{K}}_{s} = \int_{0}^{l} {\left( {EI{\mathbf{N}}^{\prime \prime \prime T} {\mathbf{N}}^{\prime \prime } + \frac{{E^{2} I^{2} }}{\mu AG}{\mathbf{N}}^{\prime \prime \prime T} {\mathbf{N}}^{\prime \prime \prime } } \right){\text{d}}s} $$

(17)

where N and D represent the shape functions [61], ρ denotes material density, A is section area, I stands for the moment of inertia, E and G are the tensile and shear elastic moduli respectively, while μ is the shear coefficient. However, the section area A and the moment of inertia I of the beam element of variable section vary with the axial position and can be represented by a polynomial function along the axial position s [62]. The general equation for the variation in the radius of the section with the highest degree of 2 is derived in this paper. The inner and outer radii are denoted by r_v = a_rs² + b_rs + c_r and R_v = a_Rs² + b_Rs + c_R, respectively. The cross-section shape is linear (conical beam element) when the coefficient a_R = a_r = 0, there are

$$ \begin{gathered} I(s) = \sum\limits_{n = 0}^{{m_{I} }} {I_{n} \left( \frac{s}{l} \right)^{n} } = \frac{\pi }{4}\left( {c_{R}^{4} - c_{r}^{4} } \right) + \pi l\left( {b_{R} c_{R}^{3} - b_{r} c_{r}^{3} } \right)\left( \frac{s}{l} \right) \hfill \\ \begin{array}{*{20}c} {} & {} & { + \frac{\pi }{2}l^{2} \left( {2a_{R} c_{R}^{3} + 3b_{R}^{2} c_{R}^{2} - 2a_{r} c_{r}^{3} - 3b_{r}^{2} c_{r}^{2} } \right)\left( \frac{s}{l} \right)^{2} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {} & {} & { + \pi l^{3} } \\ \end{array} \left( {3a_{R} b_{R} c_{R}^{2} + b_{R}^{3} c_{R} - 3a_{r} b_{r} c_{r}^{2} - b_{r}^{3} c_{r} } \right)\left( \frac{s}{l} \right)^{3} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & { + \frac{\pi }{4}l^{4} \left( {6a_{R}^{2} c_{R}^{2} + 12a_{R} b_{R}^{2} c_{R} + b_{R}^{4} - 6a_{r}^{2} c_{r}^{2} - 12a_{r} b_{r}^{2} c_{r} - b_{r}^{4} } \right)} \\ \end{array} \left( \frac{s}{l} \right)^{4} \hfill \\ \begin{array}{*{20}c} {} & {} & { + \pi l^{5} \left( {4a_{R}^{2} b_{R} c_{R} + a_{R} b_{R}^{3} - 4a_{r}^{2} b_{r} c_{r} - a_{r} b_{r}^{3} } \right)} \\ \end{array} \left( \frac{s}{l} \right)^{5} \hfill \\ \begin{array}{*{20}c} {} & {} & { + \frac{\pi }{2}} \\ \end{array} l^{6} \left( {3a_{R}^{2} b_{R}^{2} + 2a_{R}^{3} c_{R} - 3a_{r}^{2} b_{r}^{2} - 2a_{r}^{3} c_{r} } \right)\left( \frac{s}{l} \right)^{6} \hfill \\ \begin{array}{*{20}c} {} & {} & { + \pi l^{7} \left( {a_{R}^{3} b_{R} - a_{r}^{3} b_{r} } \right)} \\ \end{array} \left( \frac{s}{l} \right)^{7} + \frac{\pi }{4}l^{8} \left( {a_{R}^{4} - a_{r}^{4} } \right)\left( \frac{s}{l} \right)^{8} \hfill \\ \end{gathered} $$

(18)

$$ \begin{gathered} A(s) = \sum\limits_{n = 0}^{{m_{s} }} {A_{n} \left( \frac{s}{l} \right)}^{n} = \pi \left( {c_{R}^{2} - c_{r}^{2} } \right) + 2\pi l\left( {b_{R} c_{R} - b_{r} c_{r} } \right)\left( \frac{s}{l} \right) + \pi l^{2} \left( {2a_{R} c_{R} + b_{R}^{2} - 2a_{r} c_{r} - b_{r}^{2} } \right)\left( \frac{s}{l} \right)^{2} \hfill \\ \begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {} & { + 2\pi l^{3} \left( {a_{R} b_{R} - a_{r} b_{r} } \right)\left( \frac{s}{l} \right)^{3} + \pi l^{4} \left( {a_{R}^{2} - a_{r}^{2} } \right)\left( \frac{s}{l} \right)} \\ \end{array} } \\ \end{array}^{4} \hfill \\ \end{gathered} $$

(19)

The conical shape of the variable section is taken into consideration in this paper, and the deformation coefficient φ_v of the section is assumed to be a constant, which can be determined by calculating the section parameters at both ends of the beam element [39]. The translational inertia matrix M_sTv, rotational inertia matrix M_sRv, gyro matrix J_sv, and stiffness matrix K_sv of conical beam elements can be obtained by substituting Eq. (18–19) into Eq. (15–17), there are

$$ {\mathbf{M}}_{sTv} = \sum\limits_{n = 0}^{{m_{S} }} {\left( {\rho A} \right)_{n} \int_{0}^{l} {\left( \frac{s}{l} \right)^{n} {\mathbf{N}}^{T} {\mathbf{N}}{\text{d}}s} } $$

(20)

$$ {\mathbf{J}}_{sv} = 2M_{sRv} = 2\sum\limits_{n = 0}^{{m_{I} }} {(\rho I)_{n} \int_{0}^{l} {\left( \frac{s}{l} \right)^{n} {\mathbf{D}}^{T} {\mathbf{D}}{\text{d}}s} } $$

(21)

$$ {\mathbf{K}}_{sv} = \sum\limits_{n = 0}^{{m_{I} }} {(EI)_{n} \int_{0}^{l} {\left( \frac{s}{l} \right)^{n} {\mathbf{N}}^{\prime \prime T} {\mathbf{N}}^{\prime \prime } {\text{d}}s} } + \sum\limits_{n = 0}^{{m_{I} }} {\left( {\frac{{EI\varphi_{v} l^{2} }}{12}} \right)_{n} \int_{0}^{l} {\left( \frac{s}{l} \right)^{n} {\mathbf{N}}^{\prime \prime \prime T} {\mathbf{N}}^{\prime \prime \prime } {\text{d}}s} } $$

(22)

Then the dynamic equation of the beam element can be expressed as follows:

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{b} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{M}}_{b} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\ddot{\mathbf{u}}}_{b1} } \\ {{\ddot{\mathbf{u}}}_{b2} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\Omega {\mathbf{J}}_{b} } \\ { - \Omega {\mathbf{J}}_{b} } & {\mathbf{0}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\dot{\mathbf{u}}}_{b1} } \\ {{\dot{\mathbf{u}}}_{b2} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {{\mathbf{K}}_{b} } \\ {{\mathbf{K}}_{b} } & {\mathbf{0}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{u}}_{b1} } \\ {{\mathbf{u}}_{b2} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {{\mathbf{Q}}_{b1} } \\ {{\mathbf{Q}}_{b2} } \\ \end{array} } \right\} $$

(23)

where M_b, J_b, and K_b represent the mass matrix, gyro matrix, and stiffness matrix of the beam element with either uniform or variable cross-sections respectively. Ω denotes the rotational speed, while Q_b1 and Q_b2 are the external force vectors.

2.6 Assembly of dynamic equations

Figure 6 shows the assembly diagram of the dynamic equations for the system. The equation assembly is conducted under the assumption that all boundary conditions are linear. When considering the nonlinearity of the boundary conditions, the treatment remains consistent with Sect. 2.4. The mass matrices M_L, M_H, the rotation matrices G_L, G_H, and the stiffness matrices K_L, K_H of the inner and outer rotors in a plane can be obtained according to the element combination rule of the finite element method. Similarly, the mass matrix M_C and stiffness matrix K_C of the casing can also be derived. K_wbc is the stiffness matrix of the system without considering the boundary condition, while K_RC represents the boundary condition matrix. Then the total stiffness matrix K can be expressed as K = K_wbc + K_RC. Then the equation of the whole system can be formulated as follows:

$$ {\mathbf{M}} \ddot{\mathbf{U}}+\left( {{\mathbf{C}} + {\mathbf{G}}} \right){\dot{\mathbf{U}}}{ + }{\mathbf{KU}} = {\mathbf{Q}} $$

(24)

where the mass matrix and rotation matrix are denoted as M and G, respectively. The Rayleigh damping matrix is represented by C. Q represents the external force vector, while U denotes the displacement vector, as

$$ {\mathbf{U}} = \left\{ {x_{1} ,\theta_{y1} ,x_{2} ,\theta_{y2} , \cdots ,x_{20} ,\theta_{y20} ,x_{or1} ,x_{p1} , \cdots ,x_{or3} ,x_{p3} ,y_{1} , - \theta_{x1} , \cdots ,y_{20} , - \theta_{y20} , \cdots ,y_{or1} , \cdots ,y_{p3} } \right\}^{T} $$

(25)

Fig. 6

Assembly diagram of dynamic equations a without boundary conditions; b stiffness matrix with boundary conditions

3 The reduction of system dimensions and validation of dynamic equations.

3.1 The method of dimensionality reduction.

Given the nonlinearity of the equations and a total of 92 degrees of freedom in the system, the fixed-interface CMS method is employed to effectively reduce the dimension of equations. The displacement vector of the system is partition internal degrees of freedom U_i and interface degrees of freedom U_j. The Eq. (24) of the system is reorganized based on the sequence of internal and interface degrees of freedom.

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{ii} } & {{\mathbf{M}}_{ij} } \\ {{\mathbf{M}}_{ji} } & {{\mathbf{M}}_{jj} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\ddot{\mathbf{U}}}_{i} } \\ {{\ddot{\mathbf{U}}}_{j} } \\ \end{array} } \right\} + \left( {\left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{ii} } & {{\mathbf{C}}_{ij} } \\ {{\mathbf{C}}_{ji} } & {{\mathbf{C}}_{jj} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\mathbf{G}}_{ii} } & {{\mathbf{G}}_{ij} } \\ {{\mathbf{G}}_{ji} } & {{\mathbf{G}}_{jj} } \\ \end{array} } \right]} \right)\left\{ {\begin{array}{*{20}c} {{\dot{\mathbf{U}}}_{i} } \\ {{\dot{\mathbf{U}}}_{j} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{ii} } & {{\mathbf{K}}_{ij} } \\ {{\mathbf{K}}_{ji} } & {{\mathbf{K}}_{jj} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{U}}_{i} } \\ {{\mathbf{U}}_{j} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\mathbf{Q}}_{j} } \\ \end{array} } \right\} $$

(26)

The physical domain equation is transformed into the modal domain, and the system dimension is reduced by incorporating low-order modes that preserve internal degrees of freedom. The Craig-Bampton fixed interface coordinate transformation is

$$ \left\{ {\begin{array}{*{20}c} {{\mathbf{U}}_{i} } \\ {{\mathbf{U}}_{{\varvec{j}}} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {{{\varvec{\uppsi}}}_{k} } & { - {\mathbf{K}}_{ii}^{ - 1} {\mathbf{K}}_{ij} } \\ {\mathbf{0}} & {{\mathbf{I}}_{j} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{P}}_{k} } \\ {{\mathbf{U}}_{j} } \\ \end{array} } \right\} = {\mathbf{T}}\left\{ {\begin{array}{*{20}c} {{\mathbf{P}}_{k} } \\ {{\mathbf{U}}_{j} } \\ \end{array} } \right\} $$

(27)

where ${\uppsi }_{k}$ represents the pre-k primary mode reserved, P_k denotes the displacement vector in the modal domain, I_j stands for the identity matrix, and T is the coordinate transformation matrix. The equation after undergoing dimensionality reduction is as follows:

$$ {\mathbf{T}}^{T} \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{ii} } & {{\mathbf{M}}_{ij} } \\ {{\mathbf{M}}_{ji} } & {{\mathbf{M}}_{jj} } \\ \end{array} } \right]{\mathbf{T}}\left\{ {\begin{array}{*{20}c} {{\ddot{\mathbf{P}}}_{k} } \\ {{\ddot{\mathbf{U}}}_{j} } \\ \end{array} } \right\} + {\mathbf{T}}^{T} \left( {\left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{ii} } & {{\mathbf{C}}_{ij} } \\ {{\mathbf{C}}_{ji} } & {{\mathbf{C}}_{jj} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\mathbf{G}}_{ii} } & {{\mathbf{G}}_{ij} } \\ {{\mathbf{G}}_{ji} } & {{\mathbf{G}}_{jj} } \\ \end{array} } \right]} \right){\mathbf{T}}\left\{ {\begin{array}{*{20}c} {{\dot{\mathbf{P}}}_{k} } \\ {{\dot{\mathbf{U}}}_{j} } \\ \end{array} } \right\} + {\mathbf{T}}^{T} \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{ii} } & {{\mathbf{K}}_{ij} } \\ {{\mathbf{K}}_{ji} } & {{\mathbf{K}}_{jj} } \\ \end{array} } \right]{\mathbf{T}}\left\{ {\begin{array}{*{20}c} {{\mathbf{P}}_{k} } \\ {{\mathbf{U}}_{j} } \\ \end{array} } \right\} = {\mathbf{T}}^{T} \left\{ {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\mathbf{Q}}_{j} } \\ \end{array} } \right\} $$

(28)

3.2 Verification of dynamic equations and analysis of inherent characteristics

The inherent characteristics and unbalanced response of the system are verified using the software ANSYS, as well as the initial model and dimensionality reduction model, in order to validate the accuracy of the dynamic equation and program derived in this paper. The beam element in ANSYS modeling is simulated using the Beam188 element, while the Combi214 element represents a bearing and the lumped mass is modeled as the Mass21 element. The supporting system is linear, with the specific supporting parameters provided in Appendix 1. The two rotors are co-rotation, with the outer rotor rotating at a speed 1.5 times that of the inner rotor. When the rotor is stationary, the first twelve natural frequencies of the system are presented in Table 1. Since the inherent characteristics of plane XOZ and YOZ are identical in the stationary rotor state, the phenomenon of equal second-order natural frequencies is observed in Table 1. The occurrence of this phenomenon is typically absent during rotor rotation. It can be observed that the natural frequencies calculated by the three methods exhibit a high degree of consistency, with a maximum discrepancy of only 0.08%. The Campbell diagram of a dual rotor system is presented in Fig. 7a, where the horizontal axis represents the rotation speed of the inner rotor. The first three critical speeds of the inner rotor's main excitation are denoted as A1, A2, and A3, while the first three critical speeds of the outer rotor's main excitation are represented as B1, B2, and B3. The comparison of unbalance responses among the three models at a rotation speed of 2000 r/min in Fig. 7b, revealing a remarkable similarity in their respective responses. Additionally, the critical speeds of these three models are presented in Table 2. By comparing the three models, it is observed that the error of the third order critical speed (11,117 r/min) for the main excitation of the inner rotor exhibits the highest magnitude, measuring 4.44%. However, comparatively smaller errors are found in estimating critical speeds for other orders. Compared to ANSYS, the high-order critical speed calculated in this paper exhibits a relatively larger error compared to the low-order calculations. However, it is important to note that the investigated speed range of the inner rotor in this study spans from 0 to 10,000 r/min. Besides, the modal shapes corresponding the critical speeds of the inner rotor's and outer rotor's main excitation in XOZ plane are also analyzed in this paper, as depicted in Fig. 8. The mode shapes corresponding to the critical speeds of both the inner and outer rotors exhibit remarkable similarity at the same order, owing to little differences in the natural frequencies excited by these two cases. It can be observed that the mode shapes of the system are primarily manifested as the rotors at this time. In conclusion, based on the aforementioned analysis of inherent characteristics in the system, it can be concluded that the accuracy of both the derived model and program presented in this paper is suitable and effective for the following research.

Table 1 The natural frequency of the system with the rotors at rest

Fig. 7

The verification of model a Campbell diagram; b unbalanced response

Table 2 The result of critical speeds

Fig. 8

The modal shapes corresponding the critical speeds of the inner rotor's and outer rotor's main excitation in XOZ plane a inner rotor-order 1; b outer rotor-order 1; c inner rotor-order 2; d outer rotor-order 2; e inner rotor-order 3; f outer rotor-order 3

4 Result analysis and discussion

4.1 The impact of clearance fit on system vibration under linear bearing force

The support system of both the inner and outer rotors may potentially experience a clearance fit issue. Without loss of generality, the vibration characteristics of the system are exclusively discussed in this paper when there is a clearance fit in the inner rotor. The issue of clearance fit for the outer rotor is similar to that of the inner rotor. The imbalance between the inner and outer rotors in the dual rotor system is inevitable due to factors such as machining, assembly, wear, and other reasons. In this section, the issue of clearance fit at the left bearing of the inner rotor is considered. The fit clearances are assumed to be 0μm, 20μm, and 40μm and all bearing forces are linear. The unbalanced positions of the inner and outer rotors are located at disk 1 and disk 3, respectively. It is assumed that both disk 1 on the inner rotor and disk 3 on the outer rotor have an eccentricity of 10μm. The rotational speed range of the inner rotor under investigation spans from 0 to 10,000 r/min, with the vibration response of node 1 being chosen as the designated output. Furthermore, since the ratio between the rotation speed of the outer rotor and that of the inner rotor remains constant, it is possible to calculate the speed of one rotor based on the speed of the other. In this paper, the rotation speeds of the inner rotor are utilized to depict the operational condition of the system.

4.1.1 Vibration characteristics of the system under unbalance of the inner rotor

In this subsection, the inner rotor is unbalanced, while the outer rotor is balanced. The impact of the imbalance of the inner rotor on system vibration is investigated under clearance fit. Figure 9a shows the variation in the peak-to-peak value of system vibration with speed changes across three different fit clearances. The figure displays two resonance regions (I1 and I2), which primarily correspond to the system's resonance resulting from the first two critical speeds of the primary excitation of the inner rotor. When the fit clearance is 0μm, only two formants are observed. However, when the fit clearance is 20μm and 40μm, there will be a significant leftward shift in the positions of the two main formants, accompanied by the emergence of additional smaller formants within the resonance region. Figure 9b illustrates the time domain curve of acceleration with clearances of 0μm and 20μm at a rotational speed of 2800 r/min. The presence of an impact component in the system signal is clearly observed, and the time interval T of the impact signal is directly related to the frequency f_i of the inner rotor speed, satisfying the equation T·f_i = 1.

Fig. 9

Vibration response under the imbalance of the inner rotor a the amplitude-frequency response; b time domain response at rotational speed 2800 r/min

The three-dimensional spectrums for the three different fit clearances are presented in Fig. 10. The frequency f_i of the inner rotor's speed primarily appears in the spectrum when the clearance is 0μm. However, a distinction arises as the spectrum demonstrates the presence of multiple frequency components nf_i (n $\ge {2}$) of the rotational speed when the fit clearances are 20μm and 40μm. Moreover, a complex frequency band emerges within the resonance region, exhibiting greater prominence when the fit clearance is 40μm. The nonlinearity of the system may be amplified as the clearance increases. Figure 10 also demonstrates that when there is a fit clearance between the bearing outer ring and the pedestal, their collision may induce the first order forward precession mode frequency f_n of the system, resulting in parametric vibration within the system. It is worth noting that the mode of the rotor system is unique compared to the general vibration system, as it undergoes variations with changes in rotational speed. Furthermore, the combined frequencies of f_i and f_n also appear in the spectrum at the same time.

Fig. 10

Three-dimensional spectra of different fit clearances under unbalance of the inner rotor a 0μm; b 20μm; c 40μm

The spectral characteristics of the displacement signal and the envelope spectrum of the acceleration signal are investigated to gain a more comprehensive understanding, under the condition with a fit clearance of 20μm. The envelope spectrum exhibits higher sensitivity towards shock events, and the application of envelope analysis on vibration acceleration signals enables better detection of shock signals. The envelope spectrum and FFT spectrum of rotational speeds 2800 and 6800 r/min are shown in Fig. 11, clearly demonstrating the presence of speed frequency f_i and its harmonic frequency nf_i (n $\ge$ 2) in both the spectrum and envelope spectrum. However, the amplitude of the harmonic frequency component in the FFT spectrum is relatively lower compared to that of the envelope spectrum. Additionally, both the FFT spectrum and envelope spectrum indicate the presence of the first order forward precession mode frequency f_n of the system and the combined frequency nf_i $\pm$ f_n when operating at a rotational speed of 6800 r/min in the resonance region. The reason lies in the significant impact force experienced by the bearing outer ring and pedestal, which can induce resonance at the natural frequency of the system and result in parametric vibration.

Fig. 11

The envelope spectrum and FFT spectrum at fit clearance 20μm a 2800 r/min; b 6800 r/min

4.1.2 Vibration characteristics of the system under unbalance of the outer rotor

In this subsection, the outer rotor is unbalanced, while the inner rotor is balanced. The impact of the imbalance of the outer rotor on system vibration is discussed under clearance fit. The variation curves of the system's vibration peak-peak value with rotational speed are illustrated in Fig. 12 under three distinct fit clearances. The system exhibits three resonance regions, namely O1, O2, and O3, which can be attributed to the resonances induced by the first three critical speeds of the outer rotor's main excitation. The vibration response of the three fit clearances in the resonance region O1 exhibits a consistent pattern, while the vibration peak values differ at the resonance regions O2 and O3 due to variations in fit clearances. The support characteristics between the bearing outer ring and the pedestal vary with changes in the fit clearance, while the vibration of the system is also influenced by the rotational speed and motion state of the rotor, thus resulting in this phenomenon. Figure 12b depicts the time-domain curves of acceleration with clearances of 0μm and 20μm at a rotational speed of 4400 r/min. It has been observed that the system exhibits an impact phenomenon when the fit clearance is 20μm, the time interval T of the impact signal, as well as the rotational speed frequency f_o of the outer rotor satisfies T $\bullet$ f_o = 1.

Fig. 12

Vibration response under the imbalance of the outer rotor a the amplitude-frequency response; b time domain response at a rotational speed 4400 r/min

Similarly, the three-dimensional spectra corresponding to the three fit clearances are shown in Fig. 13. When the fit clearance is 0μm, the nonlinear characteristics are not significant, and only the rotational speed frequency f_o of the outer rotor exists in the three-dimensional spectrum. However, when the clearance is 20μm and 40μm, there are not only frequency f_o but also harmonic frequency components such as 2f_o and 3f_o. The resonance region of the system does not exhibit a natural frequency, which contrasts with the unbalanced condition of the inner rotor. The nonlinearity of the system is manifested in the fit clearance of the inner rotor. The occurrence of this phenomenon may be attributed to the transmission of small vibrations from the unbalanced excitation of the outer rotor to the inner rotor through the casing and intermediate bearing.

Fig. 13

Three-dimensional spectrum of different fit clearances under unbalance of the outer rotor a 0μm; b 20μm; c 40μm

4.1.3 Vibration characteristics under unbalance of both the inner and outer rotors

The vibration characteristics of the system under clearance fit are investigated in this section, considering both the inner and outer rotors with unbalanced conditions. Figure 14a depicts the variation of the system vibration's peak-to-peak value concerning the rotational speed for three different fit clearances. The curve displays four resonance regions, namely IO1, IO2, IO3, and IO4. Among them, the occurrence of IO1 and IO3 can be attributed to the first and second critical speeds, respectively, which arise from the main excitation of the outer rotor. Similarly, the appearance of IO2 is associated with the first critical speed resulting from the main excitation of the inner rotor. Additionally, the formation of IO4 is primarily attributed to the second critical speed of the main excitation of the inner rotor. Indeed, the third critical speed of the main excitation of the outer rotor also contributes to the emergence of IO4, albeit with a smaller magnitude compared to that of the inner rotor. Figure 14b shows the variations in the positions of the four formants across different fit clearances. The formant position gradually shift to the left as the fit clearance increases, which is most pronounced in the resonance region IO4 (large vibration). The alteration of the fit clearance leads to a change in the supporting characteristics of the rotor system, thereby resulting in this phenomenon.

Fig. 14

Vibration response when both inner and outer rotors are unbalanced a the amplitude-frequency response; b resonance position under different fit clearance

The three-dimensional spectrum for varying fit clearances is shown in Fig. 15. When the fit clearance is 0μm, only the frequencies f_i and f_o are present in the spectrum. However, multiple excitation frequencies nf_i and nf_o (n $\ge$ 1) are observed when the fit clearance is 20μm and 40μm. Additionally, combined frequencies nf_i $\pm$ mf_o (where n and m are positive integers) also emerge. Then the acceleration envelope spectrum and time domain curves under three unbalanced working conditions are shown in Fig. 16, with a fit clearance of 20μm as the research condition and a rotational speed of 6800 r/min (IO4 resonance region) as the output. Compared to the unbalanced condition of the inner rotor (as depicted in Fig. 10b), the spectrum exhibits distinct frequencies, including f_o, 2f_o, f_o $\pm$ f_i 2f_i + f_o, and other characteristic components. However, it should be noted that the natural frequency of the system is not excited within the resonance region. The vibration of the system in this case is lower compared to that caused solely by the imbalance of the inner rotor. The reason for this is that the nonlinear system is being stimulated by multiple distinct frequencies. The imbalance of the outer rotor can partially mitigate the vibration resulting from the inner rotor's imbalance. Furthermore, when the rotational speed is in resonance region IO4, the vibration caused by the imbalance of the outer rotor is small.

Fig. 15

The three-dimensional spectrum for varying fit clearances a 0μm; b 20μm; c 40μm

Fig. 16

The envelope spectrum and time domain curves at a rotational speed 6800 r/min a envelope spectrum; b time domain curves

To enhance our understanding of this phenomenon, Fig. 17 presents the relative displacements of the bearing outer ring and the pedestal under three unbalanced working conditions at a rotational speed of 6800 r/min. The red line represents the boundary of the fit clearance, which is 20μm. Meanwhile, the blue line indicates the relative position of the bearing outer ring in relation to the pedestal. The unbalance of the inner rotor will result in periodic lifting of the rotor, leading to a complex relative motion orbit. The bearing outer ring and the pedestal remain in non-contact for a certain period, followed by a subsequent collision impact between them. The distinction lies in the fact that when there is an imbalance in the outer rotor, the bearing outer ring and pedestal are constantly in a state of contact, with varying contact positions, yet without any pronounced impact phenomenon. However, when considering the imbalance between the inner and outer rotors simultaneously, the rotor also undergoes periodic lifting. Nevertheless, during this time, the relative motion trajectory remains relatively stable with only brief periods of non-contact. Consequently, compared to Fig. 17a, the collision impact is significantly reduced and does not induce resonance in the system's natural frequency.

Fig. 17

The relative movement of bearing outer ring and pedestal at a rotational speed 6800 r/min a imbalance of the inner rotor; b imbalance of the outer rotor c imbalance of both the inner and outer rotors

4.1.4 The impact of fit clearance on system vibration response

The inner and outer rotors are both considered to be unbalanced in this subsection, with rotational speeds of 1000 r/min and 5500 r/min selected in the non-resonant region. The vibration response of the system is depicted in Fig. 18 for various fit clearances, while the positional variation of the contact center between the bearing outer ring and the pedestal is shown in Fig. 19. It can be obviously observed that the vibration in the horizontal (Y) direction is evidently more pronounced compared to that in the vertical (X) direction. The inclusion of the vertical direction accounts for the influence of gravity, which effectively dampens the vibrations resulting from the imbalance in that direction. The vibration value in the horizontal direction increases with the increase of the fit clearance at a low rotational speed of 1000 r/min, while there is no significant change in the vibration in the vertical direction with the increase of the fit clearance. The difference lies in the fact that at a higher rotational speed 5500 r/min, the vibration peak values exhibit an increasing trend in both horizontal and vertical directions with the increment of the fit clearance within a small range. However, once the fit clearance reaches a certain extent, the vibration starts to decrease. It is believed that the main factor behind this phenomenon is the imbalance force of the rotor and the operational state of the system. At low rotational speeds, the unbalanced force of the rotor is tiny, preventing periodic lifting of the rotor. The contact center angle range between the bearing outer ring and pedestal is observed to be small in Fig. 19a.

Fig. 18

The vibration response varied with different fit clearances a 1000 r/min; b 5500 r/min

Fig. 19

The angle range of the contact center between the bearing outer ring and pedestal under different fit clearances a 1000 r/min; b 5500 r/min

In terms of vertical direction, gravity exerts a dominant influence, resulting in small impact on system vibration caused by clearance fit. The horizontal vibration is primarily attributed to the imbalance force and the fit clearance force, which impact the supporting characteristics of the rotor system, consequently leading to an increase in vibration along this direction. Additionally, the unbalanced force of the rotor increases at higher rotational speeds, which may potentially make it lift at a certain time. The contact center angle range between the bearing outer ring and pedestal is larger in Fig. 19b compared to low rotational speeds. However, the range of the contact center angle will initially expand and then contract as the fit clearance increases. Similarly, there will be an initial increase followed by a decrease in system vibration. Furthermore, when the fit clearance range is between 30 and 40μm, the angle range of the contact center becomes relatively large, corresponding to the position of the peak-to-peak value in Fig. 18b. The increase in fit clearance may lead to a reduction in system vibration; however, it can also accelerate the wear of the bearing outer ring and pedestal, as well as generate an elevation in mechanical system temperature. Therefore, it is crucial to control the amount of fit clearance within reasonable limits.

4.1.5 The motion state analysis of the system with clearance fit

The support characteristics of the rotor become nonlinear and time-varying when there is a clearance fit between the bearing outer ring and pedestal, which may potentially lead to changes in the system's motion state. The operating conditions 1, 2, and 3 correspond to the imbalance of the inner rotor, the imbalance of the outer rotor, and both imbalances of the inner and outer rotors respectively in this subsection. The bifurcation diagrams of the system are depicted in Figs. 20 and 21, corresponding to the scenarios without a fit clearance and with a fit clearance of 40μm, respectively. The motion states of operating conditions 1 and 2 exhibit single-period motion in the absence of clearance fit, as they are both single-frequency excitation systems. However, condition 3 is a dual-frequency excitation system in which the motion of the system exhibits both single-period and multi-period behavior. Furthermore, the presence of a clearance fit in the system results in the occurrence of quasi-periodic motion in the second resonance region of the main excitation of the inner rotor under operating conditions 1 and 3. The key difference lies in the fact that the system consistently maintains a single-period motion state under operating condition 2. This means that the motion state of the system is less affected by the unbalance of the outer rotor when there is a clearance fit in the inner rotor, and within a specific range of fit clearance, the system exhibits no chaotic motion.

Fig. 20

Bifurcation diagram without clearance fit a imbalance of the inner rotor; b imbalance of the outer rotor c both imbalances of the inner and outer rotors

Fig. 21

Bifurcation diagram with clearance fit a imbalance of the inner rotor; b imbalance of the outer rotor c both imbalances of the inner and outer rotors

4.2 The impact of clearance fit on system vibration under nonlinear bearing force

The vibration characteristics of the system are investigated in this section, taking into account the nonlinear elastic restoring force of the bearings under clearance fit. The presence of both the nonlinear force of the bearing and clearance fit is assumed in system 1, while only the effect of bearing nonlinear force is considered in system 2. In system 3, both the linear force of the bearing and clearance fit are present. The main focus lies in comparing the differences in spectral characteristics among these three systems. Assuming that both the inner and outer rotors exhibit unbalanced forces, a radial clearance of 1μm is maintained for all bearings. The response with a fit clearance of 20μm is selected as the output. Figure 22 shows the three-dimensional spectrum of these three systems. In comparison to system 3, the resonance region spectrum of system 1 exhibits the first order forward precession mode frequency f_n and combination frequency f_i $-$ f_n. This indicates that the resonance region experiences a heightened level of vibration in the system, taking into account both the nonlinearity of radial clearance and clearance fit. Additionally, it is worth noting that when only considering the nonlinear force of the bearing (system 2), frequencies 2f_i, 2f_o, and the combined frequency f_i $\pm$ f_o will also be present in the spectrum; however, the presence of the combined frequency may be less apparent. Therefore, the presence of combined frequencies and harmonic frequencies in the spectrum does not necessarily indicate that it is solely attributed to clearance fit; instead, it could also be attributed to bearing nonlinearity or other factors.

Fig. 22

The three-dimensional spectrum of systems a system 1; b system 2; c system 3

Furthermore, the comparison of envelope spectrum between the three systems at low and high rotational speeds is conducted. When considering the nonlinear forces exerted by the bearings, the system is also subjected to the varying compliance (VC) vibration frequency f_vc of the four bearings. Figures 23 and 24 show the envelope spectrum at the rotational speed of 1000 and 5000 r/min, respectively. In Fig. 23, the spectrum of system 1 not only includes f_i, f_o, and the combined frequency mf_i $\pm$ nf_o as in system 3, but also encompasses the combined frequency of f_i, f_o, and f_vc (f₁, f₂, f₃, f₄). The reason for this is that the small unbalanced force of the rotor at low rotational speed allows for a conspicuous manifestation of VC vibration, resulting in the combination of multiple excitation frequencies. The spectrum of system 2 exhibits the formation of a complex frequency band at low frequencies, while the intermediate bearing VC frequency f₄ and its harmonics nf₄ are observed in the high-frequency range. In Fig. 24, the significant imbalance force of the rotor at this moment mitigates the impact of bearing VC vibration on the system. The spectral characteristics of systems 1 and 3 are similar when considering the clearance fit. In system 2, frequencies f_i, f_o, and f_i $\pm$ f_o only appear in the low-frequency range, while there is no prominent frequency component in the high-frequency range. To summarize, the nonlinear force resulting from the radial clearance of the bearing exerts a more pronounced impact on low-speed operating conditions and a relatively lesser influence on high-speed working conditions. However, the spectrum characteristics of the clearance fit can be observed regardless of whether the nonlinear force of the bearing is taken into account.

Fig. 23

The envelope spectrum of the three systems at a rotational speed 1000 r/min a system 1; b system 2; c system 3

Fig. 24

The envelope spectrum of the three systems at a rotational speed 5000 r/min a system 1; b system 2; c system 3

4.3 The vibration transmission characteristics among the rotor-outer ring-pedestal-casing

The vibration transmission characteristics among the rotor-outer ring-pedestal-casing are investigated in this section, taking into account the imbalance of both the inner and outer rotors. The ratio η is used to characterize the transmission characteristics of the vibration source to the response point of concern by quantifying the root mean square (RMS) of vibration acceleration experienced of both the casing and rotor, that is, vibrational transmissibility is η = RMS(A_Casing)/RMS(A_Rotor). The outputs have been designated as the responses of the rotor (node 1) and casing (node 12) at the location of bearing 1. The linear stiffness values for support conditions 1, 2, 3, 4, and 5 are set as k1 = 5 $\times$ 10⁶N/m, k2 = 1 $\times$ 10⁷N/m, k3 = 1 $\times$ 10⁸N/m, k4 = 2.5 $\times$ 10⁸N/m, and k5 = 1 $\times$ 10⁹N/m respectively between the bearing outer ring and pedestal. Additionally, support conditions 6 and 7 are defined by fit clearances of 20um and 40um, respectively. The variation curves of vibrational transmissibility with rotational speeds across seven distinct support conditions are shown in Fig. 25a. The support conditions 3 and 7 have been selected for the purpose of comparing the magnitude of vibration acceleration in the system with and without clearance fit, as illustrated in Fig. 25b. It can be observed that the vibration transmissivity is relatively lower under support conditions 1 and 2 compared to that under clearance fit across a majority of the speed range; however, it is relatively higher under support conditions 3,4 and 5 compared to the clearance fit across a majority of the speed range. The primary reason for this phenomenon can be attributed to the disparity in stiffness between the bearing outer ring and the pedestal. The observation reveals that in the absence of a clearance fit, the vibrational transmissibility of the system increases proportionally with the stiffness between the bearing outer ring and the pedestal. Moreover, it is evident that there is a peak value of vibration transmissibility in the resonance region. In other words, by reducing the stiffness of the support system between the rotor and the casing and avoiding the operation of the rotor within the resonance region, one can achieve the objective of minimizing casing vibration. The vibration transmissibility of the system exhibits multiple convex small peaks (burrs) overall due to the nonlinearity of the system with clearance fit. It is worth noting that the vibration transmissibility in the resonance region surpasses that in the non-resonance region.

Fig. 25

The vibration responses of seven distinct support conditions a vibrational transmissibility; b comparison of support conditions 3 and 7

Furthermore, the vibration transmissibility remains consistent under various fit clearances at low rotational speeds (0–1500 r/min). The reason for this is that the unbalanced force exerted by the rotor is relatively smaller than the gravity. The rotor cannot be lifted periodically under the clearance fit due to the dominant influence of gravity, resulting in smaller vibration.

Similarly, support conditions 3 and 7 have been selected for investigation. The variation curves in vibration acceleration of the rotor, bearing outer ring, pedestal, and casing with changes in rotational speeds are shown in Fig. 26. When there is no clearance fit, the primary source of system vibration is rotor imbalance, which leads to a gradual reduction in vibration levels across the rotor, outer ring, pedestal, and casing. However, in the case of a clearance fit, the vibration source of the system can be attributed to the rotor imbalance, as well as to the contact force and friction resulting from the clearance fit. The collision and impact between the bearing outer ring and the pedestal may result in significant vibration of the bearing outer ring. The impact energy is transmitted through two paths: from the outer ring to the rotor, and from the pedestal to the casing. However, it can be noted that the vibration of the casing remains very small.

Fig. 26

The variation curve of RMS of vibration acceleration with rotational speeds a without clearance fit; b clearance fit

5 Conclusion

In this paper, a dynamic model of a dual rotor-bearing outer ring-pedestal-casing system is established using both the finite element and lumped parameter methods. The nonlinear force resulting from clearance fit between the bearing outer ring and the pedestal is derived. The fixed-interface CMS method is employed to reduce the dimensionality of the system equation, and the effects of rotor imbalance, fit clearance, and rotational speed on the dynamic characteristics of the system are investigated. Additionally, the vibration transmission characteristics among the rotor-bearing outer ring-pedestal-casing under clearance fit are discussed. The main conclusions are summarized as follows:

• (1) The presence of a clearance fit in the system results in the appearance of the harmonic component of the rotor's rotational speed frequency in the spectrum, considering the linear stiffness of the bearing. The imbalance of the inner rotor will excite the natural frequency of the system within the resonance region, as well as its combined frequency with the speed frequency. Additionally, the imbalance of the outer rotor can partially mitigate the vibration resulting from the inner rotor's imbalance when there is a clearance fit in the inner rotor.

• (2) The vertical vibration is significantly less than the horizontal vibration due to the effect of gravity. The horizontal vibration will exhibit an increase at low rotational speeds as the fit clearance increases, while the vertical vibration will remain relatively unchanged. The vibration in both vertical and horizontal directions will increase as the fit clearance increases within the range of small clearances at higher rotational speeds. Additionally, the system may exhibit quasi-periodic motion under clearance fit, but chaotic motion is not observed.

• (3) When considering the nonlinear forces of bearings and unbalanced forces of the two rotors, harmonic components and combined frequency of the exciting forces still appear in the spectrum; however, their presence may not be apparent. Moreover, the vibration intensity in the resonance region is more pronounced when considering both the radial clearance of the bearing and the clearance fit, as compared to a system that only considers the clearance fit. The influence of bearing internal excitation on system vibration is more pronounced in low rotational speed compared to high rotational speed.

• (4) The vibrational transmissibility of the rotor-outer ring-pedestal-casing system increases proportionally with the stiffness between the bearing outer ring and the pedestal. At low rotational speeds, the vibrational transmissibility remains relatively unchanged for various fit clearances. Furthermore, the vibrational transmissibility is higher in the resonance region compared to the non-resonance region.

Appendix 1: The structural geometric parameters

See Tables

Table 3 Length parameters for dual rotor and casing

3,

Table 4 Diameter parameters for dual rotor and casing

4,

Table 5 Parameters of rigid disks

5,

Table 6 Linear stiffness and damping of bearing and casing supports

6,

Table 7 Linear stiffness and damping of bearing pedestal

7 and

Table 8 The geometric structure parameters of the four bearings

8.