1 Introduction

Nonlinear issue is an interdisciplinary subject which studies nonlinear phenomena. Research activities on solitons theory have attracted more attention with expanded applications in many scientific fields. Therefore, it is very important and meaningful to consider the solution of nonlinear partial differential equations (NLPDEs). Recently, several effective methods have been established, including \(\frac{G'}{G}-\)expansion method [1,2,3,4,5], exp-expansion method [6,7,8,9,10], auxiliary equation method [8, 11, 12], the symmetric transformation [12, 13], Backlund transformation [14], and so on. These methods are used to investigate integrability and different exact solutions. But most solutions are only solitary wave solutions. With the introduction of Hirota bilinear method [15,16,17,18,19, 24, 25], linear superposition principle and perturbation method are applied to extensively solve multi-soliton solutions, rogue wave solutions and others. Hirota bilinear method enriches the solutions of NLPDEs. The discovery of multi-soliton solutions via a direct method was done by Ryogo Hirota [16], but there are no considering rogue wave solutions and others. The author has used bilinear derivative operators to derive Ito equation to bilinear form, and successfully solved multi-soliton and lump solutions [25]. However, research of most scholars is in constant coefficient NLPDEs. For comprehensive understanding the physical phenomena and features, NLPDEs with variable coefficients have been became particularly significant. In the literature [18], rogue wave and lump solutions of variable coefficient B-type Kadomtsev–Petviashvili equation have thus been calculated with Hirota bilinear method. These solutions arouse wide concern of the scientists to the traveling multi-wave and play an important role in nonlinear sciences, such as optical fiber communications, fluid dynamics and plasma physics.

In a large number of literature, the linear superposition principle and its extended have provided a direct way of searching multi-soliton solutions, rogue wave solutions and others from the bilinear equations. But there are few research on NLPDEs with variable coefficients. Therefore, this work analyzes (3+1)-dimensional variable coefficients generalized shallow water equation(GSWE) [15, 20,21,22], which is used to describe traveling wave propagation in ocean, estuary, atmosphere and tsunami prediction.

$$\begin{aligned} \alpha (t)u_{yt}+\beta (t)u_{xxxy}+\gamma (t)u_{xz}+\delta (t)(u_{x}u_{y})_{x}=0,\nonumber \\ \end{aligned}$$
(1)

where \(\alpha (t),\beta (t),\gamma (t),\delta (t)\) are real functions. Additionally, Eq. (1) can easily become \(Jimbo--Miwa\) equation [16, 24]

$$\begin{aligned} 2u_{yt}+u_{xxxy}-3u_{xz}+3u_{xx}u_{y}+3u_{x}u_{xy}=0, \end{aligned}$$
(2)

which is derived by KP equation, and if \(z=y,u_{yt}=u_{xt}\), Eq. (1) can reduce to (2+1) GSWE [21]

$$\begin{aligned} u_{yt}+\alpha u_{y}u_{xx}+2\alpha u_{x}u_{xy}+\beta u_{xy}+\gamma u_{xxxy}=0. \end{aligned}$$
(3)

As we all know, bilinear formulism satisfies linear superposition principle. And many equations can be transformed under the transformation

$$ \begin{aligned} u(x,y,t)=\textrm{log}(f(x,y,t))_{x}\ \& \ \textrm{log}(f(x,y,t))_{xx},\nonumber \end{aligned}$$

where \(f=f(x,y,t)\) is assumed as follows:

$$\begin{aligned} f= & {} 1+e^{a_{1}x+a_{2}y+a_{3}t}+\cdots , \nonumber \\ f= & {} (a_{1}x+a_{2}y+a_{3}t)^{2}+(a_{4}x+a_{5}y+a_{6}t)^{2}, \nonumber \\ f= & {} e^{k_{1}x+k_{2}y+k_{3}t}+\cos (k_{4}x+k_{5}y+k_{6}t)\\{} & {} +\cosh (k_{7}x+k_{8}y+k_{9}t),\nonumber \\ f= & {} (a_{1}x+a_{2}y+a_{3}t)^{2}+(a_{4}x+a_{5}y+a_{6}t)^{2}\\{} & {} +e^{k_{1}x+k_{2}y+k_{3}t}, \nonumber \\&\vdots&\nonumber \\ f= & {} (a_{1}x+a_{2}y+a_{3}t)^{2}+(a_{4}x+a_{5}y+a_{6}t)^{2}\\{} & {} +\sin (k_{1}x+k_{2}y+k_{3}t). \nonumber \end{aligned}$$

where \(a_{i}, k_{j}\) are the complex constants, \(i,j=1,2,3,\cdots \) For instance, f composed for two polynomial functions is used to solve lump solutions, f composed for many exponential functions is used in multi-soliton solutions, f composed for exponential, trigonometric and hyperbolic functions is used in breather solutions, etc. There is a feature that f is composed for kinds of functions.

Thus, the main thought is that these functions in f are tried to generalize as auxiliary equation function

$$\begin{aligned} G''(\zeta )=\lambda G'(\zeta )+\mu G(\zeta ), \end{aligned}$$
(4)

which is introduced by Wang Mingliang [1] in 2008. And its solution is

$$\begin{aligned}{} & {} G(\zeta )= \left\{ \begin{array}{lr} G_{1}(\zeta )=(b_1\sinh (\frac{\sqrt{\varDelta }}{2}\zeta )\\ \qquad +b_2\cosh (\frac{\sqrt{\varDelta }}{2}\zeta ))e^{-\frac{\lambda }{2}\zeta }&{},\varDelta >0\\ G_{2}(\zeta )=(b_1\sin (\frac{\sqrt{-\varDelta }}{2}\zeta )\\ \qquad +b_2\cos (\frac{\sqrt{-\varDelta }}{2}\zeta ))e^{-\frac{\lambda }{2}\zeta }&{},\varDelta <0\\ G_{3}(\zeta )=(b_1+b_2\zeta )e^{-\frac{\lambda }{2}\zeta }&{},\varDelta =0 \end{array} \right. \end{aligned}$$
(5)

where \(\varDelta =\lambda ^2+4\mu \), \(\lambda ,\mu ,b_{1},b_{2}\) are the constants. In Sect. 2, (3+1)-dimensional variable coefficients GSWE is successfully calculated via modified Hirota bilinear method. The solutions will be generated from exponential, polynomial, trigonometric and hyperbolic functions. Finally, some conclusions are given in Sect. 3.

2 Application for (3+1)-D variable coefficients GSWE

For facilitating calculation, via inserting

$$\begin{aligned} u(x,y,z,t)=w_x(x,y,z,t), \end{aligned}$$
(6)

into Eq. (1) and integrating it with respect to x yields, Eq. (1) can be transformed into an equivalent form

$$\begin{aligned} \alpha (t)w_{yt}{} & {} +\beta (t)w_{xxxy}+\gamma (t)w_{xz}\nonumber \\{} & {} +\delta (t)w_{xx}w_{xy}=0. \end{aligned}$$
(7)

Then, substituting the rational transformation

$$\begin{aligned} w(x,y,z,t)=\frac{F(x,y,z,t)}{G(x,y,z,t)}, \end{aligned}$$
(8)

into Eq. (7), and an equation about F(x, y, z, t) and G(x, y, z, t) can be obtained

$$\begin{aligned} P(F,G,F_t,G_t,F_x,G_x,F_{y},G_{y},F_{z},G_{z},\cdots )=0. \nonumber \\ \end{aligned}$$
(9)

Next \(\varPhi \) and \(\varPsi \) selected from Eq. (9) add to zero, and the relation between F(x, y, z, t) and G(x, y, z, t) can be obtained. \(\varPhi \) and \(\varPsi \) meet the following conditions.

  1. 1.

    \(\varPhi \) is obtained by rational transformation of the highest order linear term in Eq. (7); \(\varPsi \) is obtained by rational transformation of the highest power nonlinear term in Eq. (7).

  2. 2.

    \(\varPhi \) and \(\varPsi \) are formed from F(x, y, z, t), G(x, y, z, t) and their first-order differentials.

In short, via equating the coefficients of \(\frac{1}{G^{5}}\) to zero in Eq. (9), the relation can be obtained

$$\begin{aligned} F=\frac{6\beta (t)G_{x}}{\delta (t)}. \end{aligned}$$
(10)

When Eq. (10) is substituted into Eq. (9), the bilinear form of GSWE is calculated

$$\begin{aligned}{} & {} \frac{1}{G^{2}}D_\textrm{GSWE}\nonumber \\{} & {} \quad =\frac{1}{G^{2}}\left\{ -\frac{6\beta (t)}{\delta (t)} \left[ \alpha (t)G_{t}G_{y}+\gamma (t)G_{z}G_{x}\right. \right. \nonumber \\{} & {} \left. \qquad +\beta (t)(-3G_{xy}G_{xx}+3G_{x}G_{xxy}+G_{y}G_{xxx})\right] \nonumber \\{} & {} \qquad +G\left[ \alpha (t)\left( \left( \frac{6\beta (t)}{\delta (t)}\right) 'G_{y} +\frac{6\beta (t)}{\delta (t)}G_{yt}\right) \right. \nonumber \\{} & {} \left. \left. \qquad +\frac{6\beta (t)}{\delta (t)}\left( \gamma (t)G_{xz}+\beta (t)G_{xxxy}\right) \right] \right\} \nonumber \\{} & {} \quad =0. \end{aligned}$$
(11)

According to the above in Sect. 1, auxiliary equation function are used to generalize functions in f and to derive solutions for Eq. (1). So the transformation (12) and auxiliary equation(13) are introduced

$$\begin{aligned}{} & {} G=a_{1}g(\xi )+a_{6}f(\eta ),\nonumber \\{} & {} \xi =a_{2}x+a_{3}y+a_{4}z+a_{5}(t),\nonumber \\{} & {} \eta =a_{7}x+a_{8}y+a_{9}z+a_{10}(t), \end{aligned}$$
(12)
$$\begin{aligned}{} & {} g''(\xi )=\lambda _{g}g'(\xi )+\mu _{g}g(\xi ),f''(\eta )\nonumber \\{} & {} \quad =\lambda _{f}f'(\eta )+\mu _{f}f(\eta ), \end{aligned}$$
(13)

where \(a_{i}(i=1-4,6-9),\lambda _{f},\lambda _{g},\mu _{f},\mu _{g}\) are real constants, \(a_{5}(t),a_{10}(t)\) are real functions. In addition, Eq. (13) is essentially Eq. (4). When the parameters of auxiliary equation is evaluated for different values, \(g(\xi ),f(\eta )\) will present different function forms.

According to Eqs. (6), (8), (10), transformation (12) and introduce auxiliary equation(13), the initial solution is obtained

$$\begin{aligned} u= & {} \frac{6\gamma (t)}{\delta (t)}\left[ \frac{a_{1}a_{2}^{2}\mu _{g}g(\xi )+a_{6}a_{7}^{2}\mu _{f}f(\eta )}{a_{1}g(\xi )+a_{6}f(\eta )}\right. \nonumber \\{} & {} +\frac{a_{1}a_{2}^{2}\lambda _{g}g'(\xi )+a_{6}a_{7}^{2}\lambda _{f}f'(\eta )}{a_{1}g(\xi )+a_{6}f(\eta )}\nonumber \\{} & {} \left. -\left( \frac{a_{1}a_{2}g'(\xi )+a_{6}a_{7}f'(\eta )}{a_{1}g(\xi )+a_{6}f(\eta )}\right) ^2\right] . \end{aligned}$$
(14)

It is obvious from the initial solution that a lot of unknowns for \(a_{i},f(\eta ),g(\xi )\) are considered. So substituting transformation (12) into Eq.(11) and equating all the coefficients of the \(f^{j}g^{k}(f')^{l}(g')^{m}(j,k,l,m=0,1,2\cdots )\) term to zero, we have the following sets of constraints:

Family-1

$$\begin{aligned}{} & {} a_{1}=a_{1},a_{2}=a_{2},a_{3}=a_{3},a_{4}=a_{4},\nonumber \\{} & {} a_{5}(t)=-\int _{0}^{t}\frac{a_{2}a_{4}\gamma (t^{*})+4a_{2}^{3}a_{3}\mu _{g}\beta (t^{*})}{a_{3}\alpha (t^{*})}{{\varvec{d}}}t^{*},\nonumber \\{} & {} a_{6}=a_{6}, a_{7}=a_{7},a_{8}=\frac{a_{3}a_{7}}{a_{2}},a_{9}=a_{9},\nonumber \\{} & {} a_{10}(t)=-\int _{0}^{t}\frac{a_{2}a_{9}\gamma (t^{*})+4a_{2}^{2}a_{3}a_{7}\mu _{g}\beta (t^{*})}{a_{3}\alpha (t^{*})}{{\varvec{d}}}t^{*},\nonumber \\{} & {} \lambda _{g}=0,\mu _{g}=\mu _{g}, \lambda _{f}=0,\mu _{f}\nonumber \\{} & {} \qquad =\frac{a_{2}^{2}}{a_{7}^{2}}\mu _{g},\frac{6\beta (t)}{\delta (t)}=a_{11}. \end{aligned}$$
(15)

where \(a_{11}\) is integration constant. With help of the above solved relationship and translation Eq. (12), we have

$$\begin{aligned} \xi _{1}= & {} a_{2}x+a_{3}y+a_{4}z\nonumber \\{} & {} -\int _{0}^{t}\frac{a_{2}a_{4}\gamma (t^{*})+4a_{2}^{3}a_{3}\mu _{g}\beta (t^{*})}{a_{3}\alpha (t^{*})}{{\varvec{d}}}t^{*},\nonumber \\ \eta _{1}= & {} a_{7}x+\frac{a_{3}a_{7}}{a_{2}}y+a_{9}z\nonumber \\{} & {} - \int _{0}^{t}\frac{a_{2}a_{9}\gamma (t^{*})+4a_{2}^{2}a_{3}a_{7}\mu _{g}\beta (t^{*})}{a_{3}\alpha (t^{*})}{{\varvec{d}}}t^{*}. \end{aligned}$$
(16)

Since the parameters of the auxiliary equation are unknown quantities, the solutions are considered as the following three cases.

Case 1 If the parameters are taken as

$$\begin{aligned} \mu _{g}>0, \mu _{f}>0, \end{aligned}$$
(17)

\(g(\xi _{1})\) and \(f(\eta _{1})\) are identified as hyperbolic function because of solution of the auxiliary equation Eq. (5). According to \(g(\xi _{1})\) and \(f(\eta _{1})\) considered in the previous article, the initial solution Eq. (14) and parameters Eqs. (15), (16), these results give the soliton solution

$$\begin{aligned} u_{1}= & {} a_{11}a_{2}^{2}\mu _{g}\{1-[a_{1}(b_{2g}\sinh (\sqrt{\mu _{g}}\xi _{1})\nonumber \\{} & {} +b_{1g}\cosh (\sqrt{\mu _{g}}\xi _{1}))+a_{6}(b_{2f}\sinh (\sqrt{\mu _{f}}\eta _{1})\nonumber \\{} & {} +b_{1f}\cosh (\sqrt{\mu _{f}}\eta _{1}))]^{2}[a_{1}(b_{1g}\sinh (\sqrt{\mu _{g}}\xi _{1})\nonumber \\{} & {} +b_{2g}\cosh (\sqrt{\mu _{g}}\xi _{1}))+a_{6}(b_{1f}\sinh (\sqrt{\mu _{f}}\eta _{1})\nonumber \\{} & {} +b_{2f}\cosh (\sqrt{\mu _{f}}\eta _{1}))]^{-2}\}. \end{aligned}$$
(18)

Case 2 If the parameters are taken as

$$\begin{aligned} \mu _{g}<0, \mu _{f}<0, \end{aligned}$$
(19)

\(g(\xi _{1})\) and \(f(\eta _{1})\) are identified as trigonometric functions by Eq. (5). According to Eq. (15), Eqs. (16) and (14), the periodic soliton solution is analogized

$$\begin{aligned} u_{2}= & {} a_{11}a_{2}^{2}\mu _{g}\{1+[a_{1}(b_{2g}\sin (\sqrt{-\mu _{g}}\xi _{1})\nonumber \\{} & {} -b_{1g}\cos (\sqrt{-\mu _{g}}\xi _{1}))+a_{6}(b_{2f}\sin (\sqrt{-\mu _{f}}\eta _{1})\nonumber \\{} & {} -b_{1f}\cos (\sqrt{-\mu _{f}}\eta _{1}))]^{2}[a_{1}(b_{1g}\sin (\sqrt{-\mu _{g}}\xi _{1})\nonumber \\{} & {} +b_{2g}\cos (\sqrt{-\mu _{g}}\xi _{1}))+a_{6}(b_{1f}\sin (\sqrt{-\mu _{f}}\eta _{1})\nonumber \\{} & {} +b_{2f}\cos (\sqrt{-\mu _{f}}\eta _{1}))]^{-2}\}. \end{aligned}$$
(20)

Case 3 If the parameters are taken as

$$\begin{aligned} \mu _{g}=\mu _{f}=0, \end{aligned}$$
(21)

\(g(\xi _{1})\) and \(f(\eta _{1})\) are identified as polynomial functions by Eq. (5). According to Eqs. (15), (16) and (14), the rational soliton solution is obtained

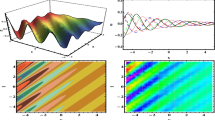
$$\begin{aligned} u_{3} = -a_{11}\left( \frac{a_{1}a_{2}b_{2g}+a_{6}a_{7}b_{2f}}{a_{1}(b_{1g}+b_{2g}\xi _{1})+a_{6}(b_{1f}+b_{2f}\eta _{1})}\right) ^{2}. \nonumber \\ \end{aligned}$$
(22)

From (15), \(\varDelta _{g}\) and \(\varDelta _{f}\) are linearly correlated, and have the same positive and negative properties. Therefore, \(f(\xi _{1})\) and \(g(\eta _{1})\) have the same function form. The localized structures of Eqs. (18), (20) with Eq. (22) for particular values of the parameters are shown in Fig. 1. The 3D graph corresponding to solutions is drawn, wherein we take \(a_{1}=a_{2}=a_{4}=a_{7}=a_{11}=b_{1g}=a_{9}=\mu _{g}=b_{2f}=1,b_{2g}=2,a_{3}=a_{6}=b_{1f}=-1,\alpha (t)=t,\beta (t)=\gamma (t)=1\) for \(u_{1}\), \(a_{1}=a_{2}=a_{4}=a_{7}=a_{11}=b_{1g}=a_{9}=b_{2f}=1,b_{2g}=2,a_{3}=a_{6}=\mu _{g}=b_{1f}=-1,\alpha (t)=t,\beta (t)=\gamma (t)=1\) for \(u_{2}\), and \(a_{1}=a_{2}=a_{4}=a_{7}=a_{11}=b_{1g}=1,a_{6}=a_{9}=b_{2f}=2,a_{3}=b_{1f}=-1,b_{2g}=2,\alpha (t)=t,\beta (t)=\gamma (t)=1\) for \(u_{3}\).

Fig. 1
figure 1

3D graph of \(u_{1}\)(left),\(u_{2}\),\(u_{3}\)(right)

Full size image

Family-2

$$\begin{aligned}{} & {} a_{1}=a_{1},a_{2}=a_{2},a_{3}=a_{3},a_{4}=a_{4},\nonumber \\{} & {} a_{5}(t)=-\int _{0}^{t}\frac{a_{2}a_{4}\gamma (t^{*})+a_{2}^{3}a_{3}\lambda _{g}^{2}\beta (t^{*})}{a_{3}\alpha (t^{*})}{{\varvec{d}}}t^{*},\nonumber \\{} & {} a_{6}=a_{6},a_{7}=0, a_{8}=0,a_{9}=a_{9},\nonumber \\{} & {} a_{10}(t)=-\int _{0}^{t}\frac{a_{2}a_{9}\gamma (t^{*})}{a_{3}\alpha (t^{*})}{{\varvec{d}}}t^{*},\nonumber \\{} & {} \lambda _{f}=\lambda _{f},\mu _{f}=\mu _{f},\lambda _{g}=\lambda _{g},\mu _{g}=0,\frac{6\beta (t)}{\delta (t)}=a_{11}. \nonumber \\ \end{aligned}$$
(23)

And then, we have

$$\begin{aligned} \xi _{2}= & {} a_{2}x+a_{3}y+a_{4}z \nonumber \\{} & {} -\int _{0}^{t}\frac{a_{2}a_{4}\gamma (t^{*})+a_{2}^{3}a_{3}\lambda _{g}^{2}\beta (t^{*})}{a_{3}\alpha (t^{*})}{{\varvec{d}}}t^{*},\nonumber \\ \eta _{2}= & {} a_{9}z-\int _{0}^{t}\frac{a_{2}a_{9}\gamma (t^{*})}{a_{3}\alpha (t^{*})}{{\varvec{d}}}t^{*}. \end{aligned}$$
(24)

Here, the solution is considered as follows.

Case 1 If the parameters is taken as

$$\begin{aligned} \lambda _{g}\ne 0, \lambda _{f}^{2}+4\mu _{f}>0, \end{aligned}$$
(25)

\(g(\xi _{2})\) and \(f(\eta _{2})\) are identified as mixture of hyperbolic and exponential functions through Eq. (5). According to Eqs. (23), (24) and (14), solution is

$$\begin{aligned}{} & {} u_{4}=a_{11}\left\{ \frac{a_{1}a_{2}^{2}\lambda _{g}^{2}( b_{1g}- b_{2g})e^{-\lambda _{g}\xi _{2}}}{a_{1}[b_{2g}\pm b_{1g}+(b_{2g}\mp b_{1g})e^{-\lambda _{g}\xi _{2}}]+2a_{6}f(\eta _{2})}\right. \nonumber \\{} & {} \left. -\left( \frac{a_{1}a_{2}\lambda _{g}( b_{1g}- b_{2g})e^{-\lambda _{g}\xi _{2}}}{a_{1}[b_{2g}\pm b_{1g}+(b_{2g}\mp b_{1g})e^{-\lambda _{g}\xi _{2}}] +2a_{6}f(\eta _{2})}\right) ^{2}\right\} . \nonumber \\ \end{aligned}$$
(26)

where

$$\begin{aligned} f(\eta _{2})= & {} G_{1}|_{\zeta =\eta _{2},\lambda =\lambda _{f},\mu =\mu _{f},b_{1}=b_{1f},b_{2}=b_{2f}}\nonumber \\= & {} [b_{1f}\sinh (\frac{\sqrt{\lambda _{f}^{2}+4\mu _{f}}}{2}\eta _{2})\nonumber \\{} & {} +b_{2f}\cosh (\frac{\sqrt{\lambda _{f}^{2}+4\mu _{f}}}{2}\eta _{2})]e^{-\frac{\lambda _{f}}{2}\eta _{2}}. \end{aligned}$$
(27)

The 3D graph and contour graph corresponding to solutions are drawn in Fig. 2, wherein we take \(a_{1}=a_{2}=a_{9}=a_{11}=1,a_{3}=a_{4}=-1,a_{6}=-2,b_{1g}=2b_{2g}=2b_{1f}=b_{2f}=\lambda _{g}=2,\alpha (t)=1,\beta (t)=\cos (t),\gamma (t)=1.\)

Fig. 2
figure 2

3D graph (up) and contour graph (down) of \(u_{4}\) at \(\varDelta _{f}>0(\lambda _{f}=1,\mu _{f}=\frac{3}{4})\)

Full size image

Case 2 If the parameters are taken as

$$\begin{aligned} \lambda _{g}\ne 0, \lambda _{f}^{2}+4\mu _{f}<0, \end{aligned}$$
(28)

\(g(\xi _{2})\) is mixture of hyperbolic and exponential functions, \(f(\eta _{2})\) is mixture of trigonometric and exponential functions. In particular, form of the solution \(u_{5}\) in this case is analogous to last case. Thus, we can obtain

$$\begin{aligned}{} & {} u_{5}=a_{11}\{\frac{a_{1}a_{2}^{2}\lambda _{g}^{2}( b_{1g}- b_{2g})e^{-\lambda _{g}\xi _{2}}}{a_{1}[b_{2g}\pm b_{1g}+(b_{2g}\mp b_{1g})e^{-\lambda _{g}\xi _{2}}]+2a_{6}f(\eta _{2})}\nonumber \\{} & {} \quad -(\frac{a_{1}a_{2}\lambda _{g}( b_{1g}- b_{2g})e^{-\lambda _{g}\xi _{2}}}{a_{1}[b_{2g}\pm b_{1g}+(b_{2g}\mp b_{1g})e^{-\lambda _{g}\xi _{2}}] +2a_{6}f(\eta _{2})})^{2}\}, \nonumber \\ \end{aligned}$$
(29)

whereas

$$\begin{aligned} f(\eta _{2})={} & {} G_{2}|_{\zeta =\eta _{2},\lambda =\lambda _{f},\mu =\mu _{f},b_{1}=b_{1f},b_{2}=b_{2f}}\nonumber \\ ={} & {} [b_{1f}\sin (\frac{\sqrt{-\lambda _{f}^{2}-4\mu _{f}}}{2}\eta _{2})\nonumber \\{} & {} +b_{2f}\cos (\frac{\sqrt{-\lambda _{f}^{2}-4\mu _{f}}}{2}\eta _{2})]e^{-\frac{\lambda _{f}}{2}\eta _{2}}. \end{aligned}$$
(30)

The 3D graph and contour graph corresponding to solutions are drawn in Fig. 3, wherein we take \(a_{1}=a_{2}=a_{9}=a_{11}=1,a_{3}=a_{4}=-1,a_{6}=-2,b_{1g}=-1,b_{2g}=b_{1f}=1,b_{2f}=0,\lambda _{g}=2,\alpha (t)=\beta (t)=1,\gamma (t)=t.\)

Fig. 3
figure 3

3D graph (up) and contour graph (down) of \(u_{5}\) at \(\varDelta _{f}>0(\lambda _{f}=1,\mu _{f}=\frac{3}{4})\)

Full size image

Case 3 If the parameters are taken as

$$\begin{aligned} \lambda _{g}=0, \lambda _{f}^{2}+4\mu _{f}>0, \end{aligned}$$
(31)

\(g(\xi _{2})\) is polynomial function, \(f(\eta _{2})\) is mixture of hyperbolic and exponential functions. Likewise, solution is obtained

$$\begin{aligned}{} & {} u_{6}=\frac{-a_{11}a_{1}^{2}a_{2}^{2}b_{2g}^{2}}{(a_{1}(b_{1g}+b_{2g}\xi _{2}) +a_{6}f(\eta _{2}))^{2}}, \end{aligned}$$
(32)

where \(f(\eta _{2})=G_{1}|_{\zeta =\eta _{2},\lambda =\lambda _{f},\mu =\mu _{f},b_{1}=b_{1f},b_{2}=b_{2f}}\) Eq. (27). The 3D graph and contour graph corresponding to solutions are drawn in Fig. 4, wherein we take \(a_{1}=a_{3}=a_{6}=1,a_{2}=a_{4}=a_{11}=-1,a_{9}=2,2b_{1g}=b_{2g}=2b_{1f}=b_{2f}=2,\lambda _{g}=0,\alpha (t)=1,\gamma (t)=\cos (t)\).

Fig. 4
figure 4

3D graph (up) and contour graph (down) of \(u_{6}\) at \(\varDelta _{f}>0(\lambda _{f}=1,\mu _{f}=\frac{15}{4})\)

Full size image

Case 4 If the parameters are taken as

$$\begin{aligned} \lambda _{g}=0, \lambda _{f}^{2}+4\mu _{f}<0, \end{aligned}$$
(33)

the solution form in this case is analogous to last case. And then, solution is obtained

$$\begin{aligned}{} & {} u_{7}=\frac{-a_{11}a_{1}^{2}a_{2}^{2}b_{2g}^{2}}{(a_{1}(b_{1g}+b_{2g}\xi _{2}) +a_{6}f(\eta _{2}))^{2}}; \end{aligned}$$
(34)

whereas \(f(\eta _{2})=G_{2}|_{\zeta =\eta _{2},\lambda =\lambda _{f},\mu =\mu _{f},b_{1}=b_{1f},b_{2}=b_{2f}}\) Eq. (30). The 3D graph and contour graph corresponding to solutions are drawn in Fig. 5, wherein we take \(a_{1}=a_{3}=a_{6}=1,a_{2}=a_{4}=a_{11}=-1,a_{9}=2,b_{1g}=b_{2g}=b_{1f}=b_{2f}=1,\lambda _{g}=0,\alpha (t)=1,\gamma (t)=t.\)

Fig. 5
figure 5

3D graph (up) and contour graph (down) of \(u_{7}\) at \(\varDelta _{f}<0(\lambda _{f}=0,\mu _{f}=-1)\)

Full size image

In Family-2, \(\varDelta _{g}\) is non-negative, and is linearly independent with \(\varDelta _{f}\). Therefore, there are 6 cases to consider. But cases for

$$\begin{aligned} (I){} & {} \lambda _{g}\ne 0, \lambda _{f}^{2}+4\mu _{f}=0, \nonumber \\ (II){} & {} \lambda _{g}=0, \lambda _{f}^{2}+4\mu _{f}=0\nonumber \end{aligned}$$

are not shown. \(g(\xi _{2})\) and \(f(\eta _{2})\) are hyperbolic function and mixture of polynomial and exponential functions in (I), but are polynomial function and mixture of hyperbolic and exponential functions in \(u_{6}\), so solutions in case 3 and (I) possess the similar function form. The same is true that solution form in (II) is similar to \(u_{3}\), because \(g(\xi _{2})\) and \(f(\eta _{2})\) are polynomial function and its and exponential functions mixed function. Hence, only four solutions are shown. From the graphs, it is evident that the \(\alpha (t),\beta (t),\gamma (t)\) influences the development of the wave. According to the case 1 and Eq. 23, \(g(\xi _{2})\) and \(f(\eta _{2})\) could be changed from mixture of hyperbolic and exponential functions to exponential functions, so \(u_{4}\) is a kink wave with a height difference in Fig. 2. \(u_{4}\) in influence of variable coefficients \(\beta (t)=\cos (t)\) has a periodic change, but its whole direction with time t has no variation. Figures 3,  4 and  5 are rogue wave. Figures 3 and  5 have tended to be symmetrical under the influence of \(\gamma (t)=t\). In addition, Fig. 4 is also under \(\beta (t)=\cos (t)\) and shows a complete periodic about x, y and time t. It is clearly found that \(u_{6}\) changes dramatically from time 4 to 5.5.

Family-3

$$\begin{aligned}{} & {} a_{1}=a_{1},a_{2}=a_{2},a_{3}=0,a_{4}=0,\nonumber \\{} & {} a_{5}(t)=-\int _{0}^{t}\frac{a_{2}a_{9}\gamma (t^{*})+a_{2}^{3}a_{8}\mu _{g}\beta (t^{*})}{a_{8}\alpha (t^{*})}{{\varvec{d}}}t^{*},\nonumber \\{} & {} a_{6}=a_{6},a_{7}=0,a_{8}=a_{8},a_{9}=a_{9},a_{10}(t)=a_{10},\nonumber \\{} & {} \lambda _{f}=\lambda _{f},\mu _{f}=\mu _{f},\lambda _{g}=0,\mu _{g}\nonumber \\{} & {} =\mu _{g}, \frac{6\beta (t)}{\delta (t)}=a_{11}. \end{aligned}$$
(35)

And then, we have

$$\begin{aligned} \xi _{3}= & {} a_{3}x-\int _{0}^{t}\frac{a_{2}a_{9}\gamma (t^{*})+a_{2}^{3}a_{8}\mu _{g}\beta (t^{*})}{a_{8}\alpha (t^{*})}{{\varvec{d}}}t^{*},\nonumber \\ \eta _{3}= & {} a_{8}y+a_{9}z+a_{10}. \end{aligned}$$
(36)

The solution is considered as follows.

Case 1

If the parameters are taken as

$$\begin{aligned} \mu _{g}>0, \lambda _{f}^{2}+4\mu _{f}>0, \end{aligned}$$
(37)

\(g(\xi _{3})\) is hyperbolic functions, \(f(\eta _{3})\) is mixture of hyperbolic and exponential functions. Solution is obtained

$$\begin{aligned} u_{8}= & {} a_{11}a_{2}^{2}\mu _{g}\{\nonumber \\{} & {} \frac{a_{1}[b_{1g}\sinh (\sqrt{\mu _{g}}\xi _{3}) +b_{2g}\cosh (\sqrt{\mu _{g}}\xi _{3})]}{a_{1}[b_{1g}\sinh (\sqrt{\mu _{g}}\xi _{3})+b_{2g}\cosh (\sqrt{\mu _{g}}\xi _{3})] +a_{6}f(\eta _{3})}\nonumber \\{} & {} -(\frac{a_{1}[b_{2g}\sinh (\sqrt{\mu _{g}}\xi _{3})+b_{1g}\cosh (\sqrt{\mu _{g}}\xi _{3})]}{a_{1}[b_{1g}\sinh (\sqrt{\mu _{g}}\xi _{3}) +b_{2g}\cosh (\sqrt{\mu _{g}}\xi _{3})] +a_{6}f(\eta _{3})})^{2}\}; \nonumber \\ \end{aligned}$$
(38)

where

$$\begin{aligned} f(\eta _{3})={} & {} G_{1}|_{\zeta =\eta _{3},\lambda =\lambda _{f},\mu =\mu _{f},b_{1}=b_{1f},b_{2}=b_{2f}}\nonumber \\ ={} & {} [b_{1f}\sinh (\frac{\sqrt{\lambda _{f}^{2}+4\mu _{f}}}{2}\eta _{3})\nonumber \\{} & {} +b_{2f}\cosh (\frac{\sqrt{\lambda _{f}^{2}+4\mu _{f}}}{2}\eta _{3})]e^{-\frac{\lambda _{f}}{2}\eta _{3}}. \end{aligned}$$
(39)

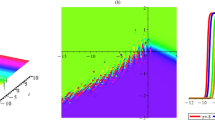
The 3D graph, contour graph and 2D graph corresponding to solutions are drawn in Fig. 6, wherein we take \(a_{1}=a_{2}=a_{8}=a_{10}=a_{11}=1,a_{6}=-1,a_{9}=3,2b_{1g}=b_{2g}=2b_{1f}=b_{2f}=2,\mu _{g}=1,\alpha (t)=1,\beta (t)=\gamma (t)=t\).

Fig. 6
figure 6

\(u_{8}\) at \(\varDelta _{f}>0(\mu _{f}=\frac{3}{4},\lambda _{f}=1)\)

Full size image

Case 2 If the parameters is taken as

$$\begin{aligned} \mu _{g}>0, \lambda _{f}^{2}+4\mu _{f}<0, \end{aligned}$$
(40)

\(g(\xi _{3})\) is hyperbolic functions, \(f(\eta _{3})\) is mixture of trigonometric and exponential functions. Solution is obtained

$$\begin{aligned}{} & {} u_{9}=a_{11}a_{2}^{2}\mu _{g}\nonumber \\{} & {} \left\{ \frac{a_{1}[b_{1g}\sinh (\sqrt{\mu _{g}}\xi _{3}) +b_{2g}\cosh (\sqrt{\mu _{g}}\xi _{3})]}{a_{1}[b_{1g}\sinh (\sqrt{\mu _{g}}\xi _{3})+b_{2g}\cosh (\sqrt{\mu _{g}}\xi _{3})] +a_{6}f(\eta _{3})}\right. \nonumber \\{} & {} \left. -\left( \frac{a_{1}[b_{2g}\sinh (\sqrt{\mu _{g}}\xi _{3})+b_{1g}\cosh (\sqrt{\mu _{g}}\xi _{3})]}{a_{1}[b_{1g}\sinh (\sqrt{\mu _{g}}\xi _{3}) +b_{2g}\cosh (\sqrt{\mu _{g}}\xi _{3})] +a_{6}f(\eta _{3})}\right) ^{2}\right\} , \nonumber \\ \end{aligned}$$
(41)

where

$$\begin{aligned} f(\eta _{3})={} & {} G_{2}|_{\zeta =\eta _{2},\lambda =\lambda _{f},\mu =\mu _{f},b_{1}=b_{1f},b_{2}=b_{2f}}\nonumber \\ ={} & {} [b_{1f}\sin (\frac{\sqrt{-\lambda _{f}^{2}-4\mu _{f}}}{2}\eta _{3})\nonumber \\{} & {} +b_{2f}\cos (\frac{\sqrt{-\lambda _{f}^{2}-4\mu _{f}}}{2}\eta _{3})]e^{-\frac{\lambda _{f}}{2}\eta _{3}}. \end{aligned}$$
(42)

The 3D graph, contour graph and 2D graph corresponding to solutions are drawn in Fig. 7, wherein we take \(a_{1}=a_{2}=a_{8}=a_{10}=a_{11}=\mu _{g}=1,a_{6}=-1,a_{9}=3,2b_{1g}=b_{2g}=2b_{1f}=b_{2f}=2,\alpha (t)=1,\beta (t)=\gamma (t)=t\).

Fig. 7
figure 7

\(u_{9}\) at \(\varDelta _{f}<0(\mu _{f}=-\frac{5}{4},\lambda _{f}=1)\)

Full size image

Case 3 If the parameters are taken as

$$\begin{aligned} \mu _{g}<0, \lambda _{f}^{2}+4\mu _{f}>0, \end{aligned}$$
(43)

solution is obtained

$$\begin{aligned}{} & {} u_{10}=a_{11}a_{2}^{2}\mu _{g}\nonumber \\{} & {} \left\{ \frac{a_{1}(b_{1g}\sin (\sqrt{-\mu _{g}}\xi _{3}) +b_{2g}\cos (\sqrt{-\mu _{g}}\xi _{3}))}{a_{1}(b_{1g}\sin (\sqrt{-\mu _{g}}\xi _{3})+b_{2g}\cos (\sqrt{-\mu _{g}}\xi _{3})) +a_{6}f(\eta _{3})}\right. \nonumber \\{} & {} \left. +\left( \frac{a_{1}(-b_{2g}\sin (\sqrt{-\mu _{g}}\xi _{3})+b_{1g}\cos (\sqrt{-\mu _{g}}\xi _{3}))}{a_{1}(b_{1g}\sin (\sqrt{-\mu _{g}}\xi _{3}) +b_{2g}\cos (\sqrt{-\mu _{g}}\xi _{3})) +a_{6}f(\eta _{3})}\right) ^{2}\right\} ; \nonumber \\ \end{aligned}$$
(44)

where \(f(\eta _{3})=G_{1}|_{\zeta =\eta _{3},\lambda =\lambda _{f},\mu =\mu _{f},b_{1}=b_{1f},b_{2}=b_{2f}}\) Eq. (39). The 3D graph, contour graph and 2D graph corresponding to solutions are drawn in Fig. 8, wherein we take \(a_{1}=a_{2}=a_{8}=a_{11}=1,a_{6}=5,a_{9}=3,a_{10}=0,2b_{1g}=b_{2g}=2b_{1f}=b_{2f}=2,\mu _{g}=-1,\alpha (t)=1,\beta (t)=\gamma (t)=t\).

Fig. 8
figure 8

\(u_{10}\) at \(\varDelta _{f}>0(\mu _{f}=\frac{3}{4},\lambda _{f}=1)\)

Full size image
Fig. 9
figure 9

\(u_{11}\) at \(\varDelta _{f}<0(\mu _{f}=-\frac{5}{4},\lambda _{f}=-1)\)

Full size image
Fig. 10
figure 10

\(u_{12}\) at \(\varDelta _{f}<0(\mu _{f}=-1,\lambda _{f}=2)\)

Full size image

Case 4 If the parameters are taken as

$$\begin{aligned} \mu _{g}<0, \lambda _{f}^{2}+4\mu _{f}<0, \end{aligned}$$
(45)

solution is obtained

$$\begin{aligned}{} & {} u_{11}=a_{11}a_{2}^{2}\mu _{g}\nonumber \\{} & {} \left\{ \frac{a_{1}(b_{1g}\sin (\sqrt{-\mu _{g}}\xi _{3}) +b_{2g}\cos (\sqrt{-\mu _{g}}\xi _{3}))}{a_{1}(b_{1g}\sin (\sqrt{-\mu _{g}}\xi _{3})+b_{2g}\cos (\sqrt{-\mu _{g}}\xi _{3})) +a_{6}f(\eta _{3})}\right. \nonumber \\{} & {} \left. +\left[ \frac{a_{1}(-b_{2g}\sin (\sqrt{-\mu _{g}}\xi _{3})+b_{1g}\cos (\sqrt{-\mu _{g}}\xi _{3}))}{a_{1}(b_{1g}\sin (\sqrt{-\mu _{g}}\xi _{3}) +b_{2g}\cos (\sqrt{-\mu _{g}}\xi _{3})) +a_{6}f(\eta _{3})}\right] ^{2}\right\} ; \nonumber \\ \end{aligned}$$
(46)

where \(f(\eta _{3})=G_{2}|_{\zeta =\eta _{3},\lambda =\lambda _{f},\mu =\mu _{f},b_{1}=b_{1f},b_{2}=b_{2f}}\) Eq. (42). The 3D graph, contour graph and 2D graph corresponding to solutions are drawn in Fig. 9, wherein we take \(a_{1}=a_{2}=a_{8}=a_{11}=1,a_{6}=5,a_{9}=3,a_{10}=0,2b_{1g}=b_{2g}=2b_{1f}=b_{2f}=2,\mu _{g}=-1,\alpha (t)=1,\beta (t)=\gamma (t)=t\).

Case 5 If the parameters are taken as

$$\begin{aligned} \mu _{g}<0, \lambda _{f}^{2}+4\mu _{f}=0, \end{aligned}$$
(47)

solution is obtained

$$\begin{aligned}{} & {} u_{12}=a_{11}a_{2}^{2}\mu _{g}\nonumber \\{} & {} \left\{ \frac{a_{1}[b_{1g}\sin (\sqrt{-\mu _{g}}\xi _{3}) +b_{2g}\cos (\sqrt{-\mu _{g}}\xi _{3})]}{a_{1}[b_{1g}\sin (\sqrt{-\mu _{g}}\xi _{3})+b_{2g}\cos (\sqrt{-\mu _{g}}\xi _{3})] +a_{6}f(\eta _{3})}\right. \nonumber \\{} & {} \left. +\left( \frac{a_{1}[-b_{2g}\sin (\sqrt{-\mu _{g}}\xi _{3})+b_{1g}\cos (\sqrt{-\mu _{g}}\xi _{3})]}{a_{1}[b_{1g}\sin (\sqrt{-\mu _{g}}\xi _{3}) +b_{2g}\cos (\sqrt{-\mu _{g}}\xi _{3})] +a_{6}f(\eta _{3})}\right) ^{2}\right\} ; \nonumber \\ \end{aligned}$$
(48)

where

$$\begin{aligned} f(\eta _{3})={} & {} G_{3}|_{\zeta =\eta _{3},\lambda =\lambda _{f},\mu =\mu _{f},b_{1}=b_{1f},b_{2}=b_{2f}}\nonumber \\ ={} & {} (b_{1f}+b_{2f}\eta _{3})e^{-\frac{\lambda _{f}}{2}\eta _{3}}. \end{aligned}$$
(49)

The 3D graph, contour graph and 2D graph corresponding to solutions are drawn in Fig. 10, wherein we take \(a_{1}=a_{2}=a_{8}=a_{11}=1,a_{6}=5,a_{9}=3,a_{10}=0,2b_{1g}=b_{2g}=2b_{1f}=b_{2f}=2,\mu _{g}=-1,\alpha (t)=\beta (t)=\gamma (t)=t\).

Family-3, \(\varDelta _{g}\) and \(\varDelta _{f}\) is linearly independent. When \(\varDelta _{g}\) takes a certain value, there are three cases for \(\varDelta _{f}\). So there are 9 cases that need to be analyzed. But cases for

$$\begin{aligned} (I){} & {} \mu _{g}>0, \lambda _{f}^{2}+4\mu _{f}=0, \nonumber \\ (II){} & {} \mu _{g}=0, \lambda _{f}^{2}+4\mu _{f}>0, \nonumber \\ (III){} & {} \mu _{g}=0, \lambda _{f}^{2}+4\mu _{f}<0, \nonumber \\ (IV){} & {} \mu _{g}=0, \lambda _{f}^{2}+4\mu _{f}=0 \nonumber \end{aligned}$$

are not shown. Periodic solutions, which are similar to \(u_{6}\), are obtained when some parameters are set to (I) and (II); rogue wave solutions, which are similar to \(u_{7}\) are obtained when some parameters are set to (III); soliton solutions, which are similar to \(u_{3}\) are obtained when some parameters are set to (IV). The analysis is the same as Family-2. Therefore, only five solutions are shown. It is obvious from the image that Fig. 7 is rogue wave solution, and Fig. 8 is breather solution. g and f in \(u_{8}\) are hyperbolic functions and mixture of hyperbolic and exponential functions, so solution \(u_{8}\) is similar to \(u_{4}\) and can be constructed from exponential functions. However, there is no kink in Fig. 6. According to image Fig. 6 display, \(u_{8}\) is interaction solution via exponential form [19]. Through 2D graph, we can obtain the dynamic behavior of solving solution with x, y, z, t. In Figs. 9 and  10, we have the x-periodic and y-periodic soliton structures of solutions. The alternation of light and dark of soliton can be observed in Fig. 9.

3 Conclusions

This work studied (3+1)-dimensional variable coefficients GSWE. Via rational transformation, the bilinear formulism of Eq. (1) is determined. Thereafter, the corresponding system of algebraic equations is constructed by introduced auxiliary equation. The results obtained demonstrate that modified Hirota bilinear method possesses the following advantages: it can deal with the relationship between the highest order linear term and the highest order nonlinear term; it avoids the problems arising from setting the solution and transforming the bilinear formulism; it successfully calculates a large number of solutions included rogue wave solutions, interaction solutions, breather solutions. In order to better understand the physical phenomena, 3D, contour and 2D graph were showed by choosing appropriate values of the parameter. Through the graph analysis of the solution, we clearly find that \(\alpha (t),\beta (t),\gamma (t)\) affects the trend of wave movement. In particular, when variable coefficients \(\beta (t)=\cos (t)\), the travels of \(u_{6}\) is periodic changes. Via calculation result, the variable coefficients \(\beta (t)\) and \(\delta (t)\) need to satisfy certain conditions. This method used in this paper is reliable to search the exact solutions of other nonlinear models. These results provide useful information and new ideas for the study of nonlinear problems with variable coefficients.