Deformation rogue wave to the (2+1)-dimensional KdV equation

Abstract

Deformation rogue wave as exact solution of the (2+1)-dimensional Korteweg–de Vries (KdV) equation is obtained via the bilinear method. It is localized in both time and space and is derived by the interaction between lump soliton and a pair of resonance stripe solitons. In contrast to the general method to get the rogue wave, we mainly combine the positive quadratic function and the hyperbolic cosine function, and then the lump soliton can be evolved rogue wave. Under the small perturbation of parameter, rich dynamic phenomena are depicted both theoretically and graphically so as to understand the property of (2+1)-dimensional KdV equation deeply. In general terms, these deformations mainly have three types: two rogue waves, one rogue wave or no rogue wave.

1 Introduction

In soliton theory, soliton solutions can describe many nonlinear phenomena in nature. Recently, rogue wave or freak wave [1,2,3,4], which has captured imagination of general public, scientists and ocean engineers for a long time, is originally observed to reflect the transient gigantic ocean waves of extreme amplitudes that seem to appear from nowhere in high seas and can lead to disastrous outcomes. In addition to the open ocean, rogue waves have been seen in many other physical systems, including deepwater [5,6,7,8,9], surface ripples [10] and optical fibers [11, 12]. The reasons for appearing such waves are a hot topic of great interest. A significant one is the nonlinear mechanism of the solitons interaction, for instance, the Benjamin–Feir instability [13, 14], resonance interaction by three or more waves. Mathematically, rogue wave is a kind of rational solution that is localized in both time and space. Currently, there is a trend to study the rogue wave with the nonlinear Schr$\ddot{o}$dinger equation [15,16,17,18] by using many methods. In addition, many other nonlinear soliton equations have been proved to have rogue wave solutions, such as the Hirota equation [19], the Sasa–Satsuma equation [20], the Yajima–Oikawa system [21] and KP equation [22, 23].

In this letter, we focus on the basic (2+1)-dimensional KdV equation

$$\begin{aligned} \left\{ \begin{aligned}&u_t-u_{xxx}+3(uv)_x=0,\\&u_x=v_y, \end{aligned} \right. \end{aligned}$$

(1)

which was first derived by Boiti et al. [24] using a weak Lax pair context and can also be considered as a model for an incompressible fluid [25] where u is a component of the velocity. This equation has been discussed from various aspects. Such as, with the variable separation method, its dromion solutions [26], localized stable solutions [27] and the interaction of localized coherent structures [28] are given, and by using the Laurent series expansion method, its period solutions [29] and singularity structure analysis [30] are presented. Moreover, its quasi-periodic waves [31], lump solution [32] and multiple soliton [33] are obtained with the Hirota bilinear operator. It is found that the perturbation parameter of seed solution $u_0$ plays an important role in the obtained solution. Its multi-soliton solution and lump solution will vary as $u_0$ makes a small perturbation in the neighborhood of $u_0=0$. However, the rogue wave has not been presented. In this paper, based on the bilinear operator and symbol calculation, the rogue wave is obtained with the combination of positive quadratic function and a hyperbolic cosine function. It is verified that the deformation rogue waves depend on not only the initial $u_0$, but also the other parameters. We only discuss the impact of the initial value $u_0$ on the basis of other parameters that are constants. It is interesting that due to the different values of $u_0$, the obtained solution will be varied essentially; the deformations among one rogue wave, two rogue waves or no rogue wave are investigated and exhibited mathematically and graphically.

2 Rogue wave aroused by the interaction between lump soliton and a pair of resonance stripe solitons

Through the Painlev$\acute{e}$ analysis, assume

$$\begin{aligned} \left\{ \begin{aligned} u&=u_0-2(\text{ ln }f)_{xy},\\ v&=-2(\text{ ln }f)_{xx}, \end{aligned} \right. \end{aligned}$$

(2)

where $f=f(x,y,t)$ is an unknown function to de determined and $u_0$ is a seed solution. Substituting Eq. (2) to Eq. (1), we can receive its bilinear formula

$$\begin{aligned} \left( D_yD_t+D_yD_x^3-3u_0D_x^2\right) f\cdot f=0. \end{aligned}$$

(3)

Fig. 1

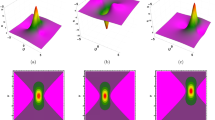
(Color online) Evolution plots of Eq. (7) by choosing $a_4=0, a_5=0.01, a_6=0.5, k=2, k_1=0.5, u_0=0.05,$ at times a $t=-100$, b $t=-40$, c $t=-10$, d $t=0$, e $t=10$, f $t=40$, g $t=100$

Fig. 2

Corresponding density plots of Fig. 1

To search for its rogue wave soliton, take f as a combination of positive quadratic function and a hyperbolic cosine, that is,

$$\begin{aligned} f=m^2+n^2+a_9+l, \end{aligned}$$

(4)

where

$$\begin{aligned} m= & {} a_1x+a_2y+a_3t+a_4,~~n=a_5x+a_6y+a_7t+a_8,l\\= & {} k\text{ cosh }(k_1x+k_2y+k_3t), \end{aligned}$$

and $a_i, (i=1, 2,\ldots 9), k, k_1, k_2, k_3$ are parameters to be determined. A complex calculation with f above can lead to 13 classes of constraining equations for the parameters, and we only choose two classes to analyze: Case I

$$\begin{aligned} \begin{aligned} a_1&=\frac{a_6k_1^2}{2u_0},~~a_2=-\frac{2a_5u_0}{k_1^2},~~a_3=\frac{3k_1^2a_5}{2},~~a_7=-\frac{3a_6k_1^4}{4u_0},\\ a_8&=-\frac{a_4a_6k_1^2}{2a_5u_0}, a_9=\frac{2k_1^2u_0^2k^2}{a_6^2k_1^4+4a_5^2u_0^2},~~k_2=\frac{2u_0}{k_1},~~k_3=\frac{k_1^3}{2}, \end{aligned} \end{aligned}$$

(5)

the parameters should satisfy

$$\begin{aligned} u_0\ne 0, ~~~k_1\ne 0, ~~~a_5\ne 0, ~~~a_6\ne 0, ~~~k>0 \end{aligned}$$

(6)

in order to insure the analytical, positive and rationally localized in all directions in the (x, y)-plane of f.

Substituting Eq. (5) to Eq. (4)and with the transformation Eq. (2), we can give rise to the solution for Eq. (1)

$$\begin{aligned} \left\{ \begin{aligned} u&=2\frac{(2a_1m+2a_5n+kk_1\text{ sinh }(k_1x+k_2y+k_3t))(2a_2m+2a_6n+kk_2\text{ sinh }(k_1x+k_2y+k_3t)}{f^2}\\&\qquad -2\frac{2a_1a_2+2a_5a_6+k_1k_2l}{f}+u_0,\\ v&=-2\frac{2a_1^2+2a_5^2+k_1^2l}{f}+2\frac{(2a_1m+2a_5n+kk_1\text{ sinh }(k_1x+k_2y+k_3t))^2}{f^2}, \end{aligned} \right. \end{aligned}$$

(7)

where f, m, n satisfy Eq. (4) and Eq. (5).

Obviously, this pair of solutions Eq. (7) represents a solitary wave solution in the form of a combination of rational solution and a pair of resonance stripe solitary solutions. This solution includes a family of four waves solutions, two waves with different velocities and a pair of resonance stripe solitary waves. By choosing the suit parameters values, we give four kinds of deformation rogue waves due to the small perturbation to the seed solution $u_0$ on the basis of other parameters that are constants, which are shown in Figs. 1, 2, 3, 4, 5, 6, 7 and 8.

Figure 1a depicts there are two stripe solitons; lump soliton is invisible, as a ghoston. When $t=-40$, there appears one small wave packet, which arises from one stripe soliton as shown in (b); when $t=-10$, it is interesting that one wave packet changes two wave packets and they still attach to the stripe soliton. Moreover, these two wave packets locate into the middle of the stripe soliton, possessing a peak wave profile as shown in Fig. 1d. Whereafter, these two wave packets begin to disappear and out of our horizon. This whole process is the generating mechanism of two rogue waves.

Fig. 3

(Color online) Evolution plots of Eq. (7) by choosing $a_4=0, a_5=0.01, a_6=0.5, k=2, k_1=0.5, u_0=0.15,$ at times a $t=-120$, b $t=-50$, c $t=0$, d $t=50$, e $t=120$

Fig. 4

Corresponding density plots of Fig. 3

Figure 3a depicts a pair of resonance solitons and the lump soliton is in a invisible place, similar to a ghoston, and Fig. 3b shows when $t=-50$, lump soliton appears gradually, from one of the resonance stripe solitons. When $t=0$, there exists a rogue wave, derived from the lump soliton, located in the middle of these two resonance solitons and linked them with each other as shown in Fig. 3c. Then, the lump soliton begins to transfer, until it attaches to the other stripe soliton successfully as shown in Fig. 3d and finally goes out of our vision as shown in Fig. 3(e).

Fig. 5

Compared with Fig. 3 for the perturbation of $u_0$ by choosing $a_4=0, a_5=0.01, a_6=0.5, k=2, k_1=0.5, u_0=0.21,$ at times a $t=-120$, b $t=-50$, c $t=0$, d $t=50$, e $t=120$

Fig. 6

Corresponding density plots of Fig. 5

Fig. 7

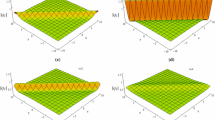
(Color online) Evolution plots of Eq. (7) by choosing $a_4=0, a_5=0.01, a_6=0.5, k=2, k_1=0.5, u_0=0.5,$ at times a $t=-50$, b $t=0$ and c $t=50$. a–c depict there are only two stripe solitons; rogue waves cannot be seen at any time due to the perturbation of $u_0$ by contrasting Fig. 1 which has two rogue waves at $t=0$

Fig. 8

Corresponding density plots of Fig. 7

Case II

$$\begin{aligned}&a_3=\frac{3a_1\left( 4a_1^2u_0^2-k_1^4a_6^2\right) }{2a_6^2k_1^2},~~a_5=\frac{4a_1^2u_0^2-k_1^4a_6^2}{4a_6k_1^2u_0},\nonumber \\&a_7=\frac{3\left( a_6^4k_1^8-24a_1^2a_6^2k_1^4u_0^2+16a_1^4u_0^4\right) }{16u_0a_6^3k_1^4},\nonumber \\&a_9=\frac{a_6^4k_1^8+8a_1^2a_6^2k_1^4u_0^2+16a_1^4u_0^4}{8a_6^2k_1^6u_0^2},\nonumber \\&k=\frac{a_6^4k_1^8+8a_1^2a_6^2k_1^4u_0^2+16a_1^4u_0^4}{8a_6^2k_1^6u_0^2},\nonumber \\&k_2=\frac{4u_0a_6^2k_1^3}{k_1^4a_6^2+4a_1^2u_0^2},\nonumber \\&a_2=0,~~k_3=\frac{12a_1^2u_0^2-k_1^4a_6^2}{4k_1a_6^2}, \end{aligned}$$

(8)

then the solution of Eq. (1) is still the form of Eq. (7) and where f, m, n satisfy Eqs. (4) and (8).

By choosing suit parameters, we show three kinds of deformation rogue waves in Figs. 9, 10, 11 and 12 which are different from case I.

Fig. 9

Another evolution plots of Eq. (1) with the parameters constraint by choosing $a_4=0, a_8=0, a_1=0.1, a_6=0.5, k_1=0.5, u_0=0.6$, at times a $t=-100$, b $t=-30$, c $t=0$, d $t=30$, d $t=100$

Figure 9 shows the generation of deformation rogue wave, which is similar to Fig. 1, but the structures of Figs. 1 and 9 are different at the same time, especially at $t=0$. Meanwhile, compared with Fig. 3, we give the relative one rogue waves in Fig. 10

Fig. 10

(Color online) One rogue wave of Eq. (1) by choosing $a_4=0, a_8=0, a_1=0.1, a_6=0.5, k_1=0.5, u_0=2$ at times a $t=-20$, b $t=-8$, c $t=0$, d $t=8$, e $t=20$

It is found that Figs. 3 and 10 have no difference no matter the structure of rogue or the generation mechanism. However, for the third situation—no rogue waves, it changes greatly, which is shown in Fig. 11,

Fig. 11

(Color online) No rogue wave of Eq. (1) by choosing $a_4=0, a_8=0, a_1=0.1, a_6=0.5, k_1=0.5, u_0=0.1$ at times a $t=-200$, b $t=-50$, c $t=0$, d $t=50$, e $t=200$

There is a pair of resonance stripe solitons at $t=-200$ shown in Fig. 11a; due to the drive of an invisible soliton, the stripe solitons begin to change into semicircle waves with the same velocity and spread direction, until $t=0$; these exist semicircle waves separated by the origin O(0, 0); whereafter, they turn to the stripe solitons in a symmetry shape. Its corresponding density plots can verify the dynamics property (from stripe soliton to semicircle soliton and return to the stripe soliton) more obvious.

Fig. 12

(Color online) Corresponding density plots of Fig. 11

3 The theoretical analysis for the types of rogue wave

Section 2 shows two dynamics properties to Eq. (1); first, we discuss the types of the rogue wave varies with the change in the parameters $u_0$ for case I. After calculation, we know that the $(x, y)=(0, 0)$ is the critical point of $U(x, y) = u(x, y, 0)$ with the initial phase $a_8=a_4=0$. Thus, at the point O(0, 0), the second-order derivative can be calculated

$$\begin{aligned} \nabla _1= & {} \frac{\partial ^2}{\partial x^2}U(x, y, 0)\big |_{O(0, 0)}=\frac{r_1\left( a_6^2k_1^4+4a_5^6u_0^2\right) }{a_6^2k_1^4+2kk_1^2u_0^2+4a_5^2u_0^2},\nonumber \\ \triangle _1= & {} \left| \begin{array}{cc} \frac{\partial ^2}{\partial x^2}U(x, y, 0) &{} \frac{\partial ^2}{\partial x\partial y}U(x, y, 0)\\ \frac{\partial ^2}{\partial x \partial y}U(x, y, 0) &{} \frac{\partial ^2}{\partial y^2}U(x, y, 0) \end{array}\right| _{O(0, 0)}=\frac{512s_1\left( a_6^2k_1^4+4a_5^2u_0^2\right) ^2\left( \frac{a_6^2k_1^4}{4}+a_5^2u_0^2\right) ^2\left( kk_1^2u_0^2-\frac{a_6^2k_1^4}{2}-2a_5^2u_0^2\right) }{u_0^4k^4k_1^8\left( a_6^2k_1^4+2kk_1^2u_0^2+4a_5^2u_0^2\right) ^4},\nonumber \\ \end{aligned}$$

(9)

where

$$\begin{aligned} \begin{aligned} r_1&=\frac{3a_6^2k_1^4-2kk_1^2u_0^2+12a_5^2u_0^2}{u_0k},\\ s_1&=\frac{k_1^{10}a_6^4}{16}\left( k_1^2a_6^2+10ku_0^2\right) +k_1^8\left( k^2a_6^2u_0^4\right. \\&\quad \left. +\frac{3a_5^2a_6^4u_0^2}{4}\right) +ku_0^4k_1^6\left( 5a_5^2a_6^2-k^2u_0^2\right) \\&\quad +k_1^4\left( 3a_5^4a_6^2u_0^4+4a_5^2k^2u_0^6\right) +2a_5^4u_0^6\left( 5kk_1^2+2a_5^2\right) . \end{aligned} \end{aligned}$$

Obviously, the sign of $\nabla _1$ is uniquely determined by the sign of $r_1$ and the sign of $\triangle _1$ is determined by the sign of $s_1(kk_1^2u_0^2-\frac{a_6^2k_1^4}{2}-2a_5^2u_0^2)$; with the extreme value theory of two variables, we can obtain the following several cases:

(1) If $r_1>0, s_1\left( kk_1^2u_0^2-\frac{a_6^2k_1^4}{2}-2a_5^2u_0^2\right) >0$ or $r_1<0, s_1\left( kk_1^2u_0^2-\frac{a_6^2k_1^4}{2}-2a_5^2u_0^2\right) >0$, then the point O(0, 0) is only the minimal value or maximum value.

$$\begin{aligned} U(0, 0, 0)=\frac{u_0\left( 2kk_1^2u_0^2-a_6^2k_1^4-4a_5^2u_0^2\right) }{a_6^2k_1^4+2kk_1^2u_0^2+4a_5^2u_0^2}. \end{aligned}$$

Moreover, U(0, 0, 0) has two extreme points with respect to $u_0^2$ as

$$\begin{aligned} \begin{aligned} u_1&=\frac{\left( 2kk_1^2-2a_5^2+\sqrt{5k^2k_1^4-8a_5^2kk_1^2}\right) k_1^4a_6^2}{2\left( 4a_5^4-k^2k_1^4\right) },\\ u_2&=-\frac{\left( -2kk_1^2+2a_5^2+\sqrt{5k^2k_1^4-8a_5^2kk_1^2}\right) k_1^4a_6^2}{2\left( 4a_5^4-k^2k_1^4\right) }; \end{aligned} \end{aligned}$$

for brevity, we choose $5k^2k_1^4-8a_5^2kk_1^2>0, k^2k_1^4-4a_5^4>0$ for analysis.

When $u_0^2\,{<}\,u_1$ or $u_0^2\,{>}\,u_2, \frac{\partial U(0, 0, 0)}{\partial (u_0^2)}\,{>}\,0$, U(0, 0, 0) increase monotonically; when $u_1<u_0^2<u_2$, $\frac{\partial U(0, 0, 0)}{\partial (u_0^2)}<0$, U(0, 0, 0) decrease monotonically. Therefore, with the perturbation of $u_0$, the structures of rogue waves will vary essentially, which are shown in Figs. 3c and 5c.

(2) If $s_1\left( kk_1^2u_0^2-\frac{a_6^2k_1^4}{2}-2a_5^2u_0^2\right) <0,$ then the point O(0, 0) is not a local extremum point. So the point U(0, 0, 0) is called a saddle point of U(x, y, 0). Furthermore, similar to the (1), with the perturbation of $u_0$, the structures of rogue waves will vary essentially, which are shown in Figs. 1d and 7b; Fig. 1d exhibits two rogue waves and its corresponding density plot is like a four-petaled flower, and Fig. 7b exhibits no rogue waves and its corresponding density plot only has two stripe solitons.

In order to depict the dynamics properties of the perturbation of seed solution $u_0$, we list the possible deformation rogue waves by choosing $a_4=0, a_5=0.01, a_6\,{=}\,0.5, k\,{=}\,2, k_1\,{=}\,0.5$; in this case, U(0, 0, 0) has one extreme points about $u_0^2=0.0036$; when $u_0^2>0.0036, U(0, 0, 0)$ increase monotonically; conversely, it decreases monotonically and $u_0=0.0036$ is the minimum. As to $\triangle _1$, it has two roots about $u_0^2$: One is $u_0^2=0.0156$ and another is $u_0^2=0.0456$; when $u_0^2<0.0156$ or $u_0^2\,{>}\,0.0456, \triangle _1\,{<}\,0$ and there maybe appear two rogue waves or no rogue wave; when $0.0156<u_0^2<0.0456$, $\triangle _1>0$ and there maybe appear one rogue wave or no rogue wave, which depend on the amplitude of U(0, 0, 0).

Next, we discuss the rogue wave varies aroused by the perturbation of $u_0$ in case II; in this case, the $(x, y)=(0, 0)$ is still the critical point of $U(x, y) = u(x, y, 0)$ with the initial phase $a_8=a_4=0$. In the same way, the second-order derivative can be given as

$$\begin{aligned} \begin{aligned} \nabla _2&=\frac{\partial ^2}{\partial x^2}U(x, y, 0)\big |_{O(0, 0)}=\frac{2r_2a_6^2k_1^6}{\left( a_6^2k_1^4+4a_1^2u_0^2\right) ^2},\\ \triangle _2&=\left| \begin{array}{cc} \frac{\partial ^2}{\partial x^2}U(x, y, 0) &{} \frac{\partial ^2}{\partial x\partial y}U(x, y, 0)\\ \frac{\partial ^2}{\partial x \partial y}U(x, y, 0) &{} \frac{\partial ^2}{\partial y^2}U(x, y, 0) \end{array}\right| _{O(0, 0)}\\&\quad =\frac{1024s_2a_1^2k_1^{20}a_6^{10}u_0^6}{\left( a_6^2k_1^4+4a_1^2u_0^2\right) ^8} \end{aligned} \end{aligned}$$

(10)

where

$$\begin{aligned} \begin{aligned} r_2&=u_0\left( 20a_1^2u_0^2-a_6^2k_1^4\right) ,\\ s_2&=80a_1^4u_0^4-8a_1^2a_6^2k_1^4u_0^2-3a_6^4k_1^8. \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} r_2&=u_0\left( 20a_1^2u_0^2-a_6^2k_1^4\right) ,\\ s_2&=80a_1^4u_0^4-8a_1^2a_6^2k_1^4u_0^2-3a_6^4k_1^8. \end{aligned} \end{aligned}$$

It is apparent that the sign of $\nabla _2$ is determined by the sign of $r_2$ and the sign of $\triangle _2$ is determined by the sign of $s_2$. According to the extremum principle of two dimensional function, it can be proved that:

(1) If $s_2>0$, the U(0, 0, 0) is the unique extremum

$$\begin{aligned} U(0, 0, 0)=\frac{u_0\left( a_6^2k_1^4-4a_1^2u_0^2\right) ^2}{\left( a_6^2k_1^4+4a_1^2u_0^2\right) ^2}, \end{aligned}$$

and U(0, 0, 0) has two extreme points with respect to $u_0^2$ as

$$\begin{aligned} \begin{aligned} u_1'&=\frac{a_6^2k_1^4}{4a_1^2},\\ u_2'&=\frac{\left( \sqrt{17}-4\right) a_6^2k_1^4}{4a_1^2}, \end{aligned} \end{aligned}$$

when $0<u_0^2<u_2'$ or $u_0^2>u_1', U(0, 0, 0)$ increase monotonically, and when $u_2'<u_0^2<u_1', U(0, 0, 0)$ decrease monotonically, $u_1'$ is the minimum.

(2) If $s_2<0$, then U(0, 0, 0) is not the local extreme point; a direct calculation gives that $s_2$ has one zero point at $u_0^2=u_1'$, when $u_0^2<u_1', s_2<0$ and conversely $s_2>0$. So we can get a conclusion that the deformation rogue wave maybe appears at the neighbor of $u_0^2=u_1'$, which are shown in Figs. 9, 10, 11 and 12.

4 Conclusion

In this paper, using the combination method of positive quadratic function and hyperbolic cosine function, we discuss the deformation rogue waves to the (2+1)-dimensional KdV equation with a small parameter perturbation in the neighborhood of $u_0=0$. By choosing two different parameter values, we give two kinds of deformation rogue waves. According to the extreme points of U(0, 0, 0) and the zero points of $\triangle _1$ and $\triangle _2$, both of these two cases have three kinds of deformation, which is shown in Figs. 1, 2, 3, 4, 5, 6, 7 and 8 and Figs. 9, 10, 11 and 12, respectively. In Fig. 1, there are two rogue waves with the same velocity, appearing on one of the stripe soliton and disappearing on the other stripe soliton. Figure 3 depicts there is only one rogue wave, whose spread trace and generation mechanism are similar to the rogue waves in Fig. 1. Figures 5 and 7 show there is no rogue wave at $t=0$, let alone at other time. Likewise, Fig. 9 shows two rogue waves, Fig. 10 shows one rogue wave, and Fig. 11 shows no rogue wave. On the basis of different parameters, the generation mechanism of rogue wave is same, but their structures vary greatly. It is hoped that these rich dynamic phenomena can provide some useful information to the nonlinear soliton theory.