MILM hybrid identification method of fractional order neural-fuzzy Hammerstein model

Abstract

Aiming at the difficult identification of fractional order Hammerstein nonlinear systems, including many identification parameters and coupling variables, unmeasurable intermediate variables, difficulty in estimating the fractional order, and low accuracy of identification algorithms, a multiple innovation Levenberg–Marquardt algorithm (MILM) hybrid identification method based on the fractional order neuro-fuzzy Hammerstein model is proposed. First, a fractional order discrete neuro-fuzzy Hammerstein system model is constructed; secondly, the neuro-fuzzy network structure and network parameters are determined based on fuzzy clustering, and the self-learning clustering algorithm is used to determine the antecedent parameters of the neuro-fuzzy network model; then the multiple innovation principle is combined with the Levenberg–Marquardt algorithm, and the MILM hybrid algorithm is used to estimate the linear module parameters and fractional order. Finally, the academic example of the fractional order Hammerstein nonlinear system and the example of a flexible manipulator are identified to prove the effectiveness of the proposed algorithm.

1 Introduction

In recent years, many viscoelastic materials (including viscoelastic solid and fluid substances) [1], “anomalous” diffusion (plasma motion at high temperature and high pressure) [2], thermal conduction of soft substances(also known as complex fluid, a complex state between ideal solids and liquids) [3] have emerged in complex physics, mechanics, chemistry, biology and engineering, which cannot be well described physically by integer order models, and the introduction of fractional order models can better describe the dynamics of the actual above-mentioned systems characteristic. These phenomena involve the memory and inheritance of physical and mechanical processes, paths and dependencies, and global correlations. The use of fractional calculus in the modeling process has different geometric interpretations or physical meanings.

Both the fractional order model and the integer order model can describe actual work such as physics, chemistry, and mechanics. However, the physical meanings of fractional differential equations and integer differential equation models are fundamentally different. In terms of time, the integer order differential equation is characterized by a change or a certain property at a certain moment in a physical, chemical or mechanical process, while the property represented by the fractional order differential equation is related to the entire dynamic development and change process of the system; in terms of space, integer order spatial differential equations describe the local properties of a physical process at a certain position in space, while the physical process described by fractional order spatial differential equations is related to the changes in the entire space [4]. In terms of model generalization ability, the fractional order differential equation model overcomes the shortcomings of the traditional integer order differential equation model that the theoretical model does not match the experimental results when describing some complex physical and mechanical processes, and can better simulate the dynamic characteristics of the actual system, and can achieve better consistency between experimental effects and research models [5].

Based on actual field sampled data, the establishment of a system process model is generally called a system identification method. Practice has proved that some systems in actual engineering, such as viscoelastic systems, electrochemical diffusion, and fractal systems, are often difficult to accurately describe with traditional integer order models. This requires the use of system identification methods to accurately describe the actual systems with fractional order models. In the field of control research, the use of system identification methods to obtain system fractional order model descriptions is a common and effective modeling method.

According to the different forms of fractional order models used, the identification models can be divided into fractional order transfer function models and fractional order state-space models. In terms of fractional order system identification based on transfer function model, Victor S et al. used a fractional Poisson filter to provide a time domain identification method based on equation error and output error [6]; Based on the auxiliary variable model, Fahim SM extended this method to fractional order systems, and gave the optimal algorithm of the improved auxiliary variable method [7]; Karima Hammar et al. studied the modeling problem of Hammerstein–Wiener nonlinear fractional order system on the basis of discrete transfer function. Using the Levenberg–Marquardt identification algorithm, the parameter identification and fractional parameter estimation in the model are given [8]. This paper adopts a gradient descent identification algorithm similar to single innovation, which has the problem of low identification accuracy; In addition, Shalaby R and Malti R proposed identification methods for fractional order continuous systems based on orthogonal basis functions and block impulse functions, respectively [9, 10].

Based on the identification of fractional state-space equations, Jonscher and Westerlund established a fractional order state-space model containing inductance and capacitance based on fractional calculus [11, 12]; Based on the fractional order state space model of the inductor-capacitor and the improved Oustaloup method, Tan Cheng et al. used the fractional order Lyapunov stability theory to design a nonlinear controller to control the boost circuit in pseudo-continuous mode [13]. In addition, there are also references that give short-term memory and frequency domain identification methods for fractional order continuous system state-space models [14,15,16,17].

The Hammerstein model is a model that combines a dynamic linear model with a static nonlinear model. It can describe a large class of industrial nonlinear processes. Therefore, its identification research has attracted widespread attention from researchers. Classic two-stage identification methods such as over-parameterization and iterative methods, random methods, frequency domain methods, and blind identification methods are often used [18,19,20,21,22,23,24], which separate the static nonlinear module from the dynamic linear module, but it has the shortcoming that if the system has process noise, the product term of the identified parameter has a large deviation; and it can separate the original system parameters more accurately only when the rank of the parameter product matrix is 1.

2 Related work and innovations

The fractional order Hammerstein nonlinear model can better describe the dynamic characteristics of the original actual system, but its identification has the following difficulties: (1) There are many identification parameters and coupling variables; (2) the intermediate variables cannot be measured; (3) the fractional order is difficult to estimate; (4) the accuracy of the identification algorithm is low. The methods proposed in the references are all based on polynomial fractional order Hammerstein nonlinear systems. For multivariable functions, this type of system requires a large number of parameters and high-order numbers, and the nonlinearity is difficult to parameterize. However, for the mathematical model description of the nonlinear module of the nonlinear Hammerstein system, data-based neural networks, fuzzy systems, and neuro-fuzzy systems can also be used; these models are very suitable for processing complex nonlinear systems. Since these models have been proven to have the universal ability to approximate nonlinear systems, they are often used to build nonlinear system models. Therefore, this paper proposes a multi-innovation Levenberg–Marquardt (MILM) hybrid identification method based on the fractional order neuro-fuzzy Hammerstein model. The main innovations are as follows:

• (1) Use the neuro-fuzzy network to fit the static nonlinear module of the fractional order Hammerstein nonlinear model;

• (2) A self-learning neuro-fuzzy network method based on fuzzy clustering is proposed to determine the structure and parameters of the neuro-fuzzy network;

• (3) The MILM hybrid identification algorithm is proposed. The L-M identification algorithm is used to estimate the dynamic linear module parameters, and the scalar innovation is expanded into a vector of multiple innovations, and the information vector is expanded to an information matrix, which improves the accuracy of the single innovation L-M identification algorithm.

The algorithm proposed in this paper with these innovative points can improve the convergence and accuracy of the identification algorithm, and it has reference significance for the author and other scholars for the modeling and identification of fractional order Hammerstein models.

The overall structure of this paper is arranged as follows: Sect. 2 expounds the related work and innovations of this paper; Sect. 3 describes the fractional calculus operator and the fractional order linear model, and constructs a fractional order discrete neuro-fuzzy Hammerstein system model; Sect. 4 proposes the self-learning neuro-fuzzy network method and MILM hybrid identification algorithm; Sect. 5 uses the fractional order Hammerstein nonlinear academic example of the discontinuous function and the example of a flexible manipulator for verification, and compares the accuracy of the identification result of the example of the flexible manipulator with the single innovation L-M algorithm in [8].

3 Description of the problem

This section introduces the basic concepts related to fractional calculation and describes the fractional order linear model and the fractional order neuro-fuzzy Hammerstein model. First, the basic principles of fractional calculus used in this paper are given. Secondly, the linear model of the fractional order transfer function is described and defined in detail. Finally, the fractional order neuro-fuzzy Hammerstein model is defined, and the nonlinearity of the fractional order Hammerstein model is fitted with a neuro-fuzzy network.

3.1 Fractional Calculus

The calculation and application of fractional order systems have attracted the attention of many researchers, and they have been applied in the fields of identification, control, filtering, and fault diagnosis. Fractional integral and differential calculations have been mentioned in many references [25,26,27]. Fractional calculus operators have different definitions in different references, mainly including GL fractional calculus operators, RL fractional calculus operators and Caputo fractional calculus operators. The GL calculus operator is defined as follows:

$$ \Delta^{\alpha } x(kh) = \frac{1}{{h^{\alpha } }}\sum\limits_{j = 0}^{k} {( - {1})^{j} \left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right)x((k - j)h} ). $$

(1)

In Eq. (1), $\Delta^{\alpha }$ represents a fractional difference operator with order$\alpha$, the initial value is 0, $x(kh)$ represents a function of $t = kh$, k is the number of samplings, the system sampling time is $h$, and $\left( {\begin{array}{*{20}l} \alpha \hfill \\ j \hfill \\ \end{array} } \right)$ is defined by the following equation:

$$ \left( {\begin{array}{*{20}l} \alpha \hfill \\ j \hfill \\ \end{array} } \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{for}}\;j = 0} \hfill \\ {\frac{\alpha (\alpha - 1) \cdots (\alpha - j + 1)}{{j!}}} \hfill & {{\text{for}}\;j > 0} \hfill \\ \end{array} } \right. $$

(2)

According to Eq. (2), the following recurrence relation can be obtained,

$$ \left\{ {\begin{array}{*{20}l} {\beta (0) = 1} \hfill \\ {\beta (j) = \beta (j - 1)\frac{(j - \alpha - 1)}{j}{\text{ for }}j = 1, \ldots ,k} \hfill \\ \end{array} } \right. $$

(3)

Among them, $\beta (j) = ( - 1)^{j} \left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right)$, combining Eqs. (2) and (3), Eq. (1) can be written as:

$$ \Delta^{\alpha } x(kh) = \frac{1}{{h^{\alpha } }}\sum\limits_{j = 0}^{k} {\beta (j)} x((k - j)h) $$

(4)

Assuming that the system sampling time $h = 1$, Eq. (4) can be sorted into the following equation:

$$ \Delta^{\alpha } x(k) = \sum\limits_{j = 0}^{k} \beta (j)x(k - j) $$

(5)

In the following chapters, Eq. (5) is used as a fractional order operator to study the modeling of fractional order nonlinear systems.

3.2 Description of the fractional order linear model

In this paper, consider the form of the following discrete linear transfer function:

$$ y(k) = G(z)u(k) = \frac{B(z)}{{A(z)}}u(k) $$

(6)

where $u(k)$ and $y(k)$ are the system input and output, respectively. $A(z)$ and $B(z)$ are the denominator and numerator polynomial of the transfer function, $A(z) = 1 + a_{1} z^{{ - \alpha_{1} }} + a_{2} z^{{ - \alpha_{2} }} + \cdots + a_{{n_{a} }} z^{{ - \alpha_{{n_{a} }} }}$, $B(z) = b_{1} z^{{ - \gamma_{1} }} + b_{2} z^{{ - \gamma_{2} }} + \cdots + b_{{n_{b} }} z^{{ - \gamma_{{n_{b} }} }}$; $\alpha_{i}$ and $\gamma_{j}$($i = 1,2,...,n_{a}$, $j = 1,2,...,n_{b}$) are the fractional orders of the corresponding polynomial, $\alpha_{i} \in {\mathbb{R}}^{ + }$, $\gamma_{j} \in {\mathbb{R}}^{ + }$, and $z^{ - 1}$ is the backshift operator, that is, $z^{ - 1} y(k) = y(k - 1)$.

For Eq. (6), when the fractional order is completely different, the fractional order model of Eq. (6) is defined as a general non-identical (disproportionate) fractional order system; otherwise, each fractional order is an integer multiple of the base order $\alpha$ ($\alpha$ is the order factor), that is, $\alpha_{i} = i\alpha ,\gamma_{i} = j\alpha$$(i = 1,2...,n_{a} ;j = 1,2...,n_{b} )$, at this time the model is defined as a homogeneous (proportionate) order system. In this paper, considering the proportional fractional order system, Eq. (6) can be written as:

$$ y(k) = \frac{B(z)}{{A(z)}}u(k) = \frac{{b_{1} z^{ - \alpha } + b_{2} z^{ - 2\alpha } + \cdots + b_{{n_{b} }} z^{{ - n_{b} \alpha }} }}{{1 + a_{1} z^{ - \alpha } + a_{2} z^{ - 2\alpha } + \cdots + a_{{n_{a} }} z^{{ - n_{a} \alpha }} }}u(k) $$

(7)

Using the discrete fractional operator $\Delta$ of Eqs. (5), (7) can be written as the following equation:

$$ \begin{aligned} y(k) = & [1 - A(z)]y(k) + B(z)u(k) \\ = & - a_{1} \Delta^{\alpha } y(k - 1) - a_{2} \Delta^{\alpha } y(k - 2) - \cdots - a_{{n_{a} }} \Delta^{\alpha } y(k - n_{a} ) \\ & \quad + b_{1} \Delta^{\alpha } u(k - 1) + b_{2} \Delta^{\alpha } u(k - 2) + \cdots + b_{{n_{b} }} \Delta^{\alpha } u(k - n_{b} ) \\ { = } & - \sum\limits_{i = 1}^{{n_{a} }} {a_{i} \Delta^{\alpha } } y(k - i)\,{ + }\sum\limits_{i = 1}^{{n_{b} }} {b_{i} \Delta^{\alpha } } u(k - i) \\ \end{aligned} $$

(8)

Equation 8 is used as the model of the fractional order linear module part.

3.3 Description of the fractional order Neural-Fuzzy Hammerstein Model

Consider a Hammerstein model with external noise, which is described as follows:

$$ S_{c} :\left\{ {\begin{array}{*{20}c} {\overline{u}(k) = f(u(k))\;\begin{array}{*{20}c} {\;\;\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} \\ \end{array} {\text{ Static nonlinear module part}}} \\ {A(z)y(k) = B(z)\overline{u}(k) + v(k)\;{\text{Dynamic linear module part}}} \\ \end{array} } \right.{ } $$

(9)

where $u(k)$ and $y(k)$, respectively, represent the input and output of the system at the k-th time; $\overline{u}(k)$ represents the output of the static nonlinear module at the k-th time; $v(k)$ is a white noise sequence with a mean value of 0 and a variance of $\sigma^{{2}}$; $f( \bullet )$ represents a nonlinear function, $A(z)$ and $B(z)$ are fractional polynomials of the same element, and their expressions are given as follows:

$$ \begin{aligned} & A(z) = 1 + a_{1} z^{ - \alpha } + a_{2} z^{ - 2\alpha } + \cdots + a_{{n_{a} }} z^{{ - n_{a} \alpha }} \\ & B(z) = b_{1} z^{ - \alpha } + b_{2} z^{ - 2\alpha } + \cdots + b_{{n_{b} }} z^{{ - n_{b} \alpha }} \\ \end{aligned} $$

(10)

For model (9), its structure can be represented by Fig. 1.

Fig. 1

The structure diagram of the fractional order neuro-fuzzy Hammerstein model

In Fig. 1, the static nonlinear module is fitted with a neural-fuzzy network model, which is specifically the following T-S fuzzy model:

$$ R^{l} :\;{\text{If}}\;u(kT)\;{\text{is}}\;F^{l} ,\;{\text{then}}\;\overline{u}(kT) = w_{l} \;,\;l = 1,2, \ldots c $$

(11)

Among them, $R^{l}$ represents the l-th rule; $u(k)$ is the input of the model; $w_{l}$ is the subsequent parameter of the l-th rule; c is the total number of rules; $F^{l}$ is the fuzzy set, which is described by the Gaussian membership function $\mu_{{F^{l} }}$.

The abovementioned T-S fuzzy model can be described by a neuro-fuzzy network model. Figure 2 shows the specific structure of the network, which has four levels. The specific conditions are as follows:

Fig. 2

The structure of the neuro-fuzzy network

Level 1:

(The input level). This level is directly transferred to the next level by the input signal $u(k)$;

Level 2:

(Membership function level). Receive the signal from the input level and calculate the membership function of the input signal. The degree of membership in this level is taken as a following Gaussian function form:

$$ \mu_{{F^{l} }} {(}u{(}k{\text{)) = exp}}\left( { - \frac{{\left( {u(k) - c_{l} } \right)^{2} }}{{\delta_{l}^{2} }}} \right),\;l = 1,2, \ldots ,c. $$

(12)

Among them, $c_{l}$ and $\delta_{l}^{2}$ are the center and width of the Gaussian membership function, respectively, and they and the rule number c are the antecedent parameters of the neural-fuzzy network.

Level 3:

(Fuzzy rules level). The number of nodes in this level is equal to the number of rules.

Level 4:

(The output level). This level performs de-obfuscation operation, and its output is given as follows:

$$ \overline{u}\left( k \right) = \sum\limits_{l = 1}^{c} {w_{l} \phi_{l} \left( {u\left( k \right)} \right)} $$

(13)

Among them, $\phi_{l} \left( {u\left( k \right)} \right) = \frac{{\mu_{{F^{l} }} \left( {u\left( k \right)} \right)}}{{\sum\limits_{l = 1}^{c} {\mu_{{F^{l} }} \left( {u\left( k \right)} \right)} }}$ and $w_{l}$ is the subsequent parameter of the neuro-fuzzy network.

Specifically, the input–output relationship of the neuro-fuzzy Hammerstein system can be expressed by the following equation,

$$ y(k) = [1 - A(z)]y(k) + B(z)f(u(k)) + v(k) $$

(14)

The static nonlinear function $f( \cdot )$ is a nonlinear function composed of several fuzzy basis functions. They are given as follows:

$$ \begin{aligned} \overline{u}(k) = & f(u(k)) \\ = & w_{1} \phi_{1} (u(k)) + w_{2} \phi_{2} (u(k)) + \cdots + w_{c} \phi_{c} (u(k)) \\ { = } & \sum\limits_{l = 1}^{c} {w_{l} } \phi_{l} (u(k)) \\ \end{aligned} $$

(15)

Among them, $\phi_{1} (u(k)),...,\phi_{c} (u(k))$ is c fuzzy basis functions, $\phi_{l} \left( {u\left( k \right)} \right) = \frac{{\mu_{{F^{l} }} \left( {u\left( k \right)} \right)}}{{\sum\limits_{l = 1}^{c} {\mu_{{F^{l} }} \left( {u\left( k \right)} \right)} }}$, and $\mu_{{F^{l} }}$ is the Gaussian membership function of the l-th rule.

Substituting Eq. (15) into Eq. (14), we have

$$ \begin{gathered} y(k) = - \sum\limits_{i = 1}^{{n_{a} }} {a_{i} z^{ - i\alpha } y(k)} + \sum\limits_{j = 1}^{{n_{b} }} {b_{j} z^{ - j\alpha } f(u(k))} + v(k) \hfill \\ \quad \quad { = } - \sum\limits_{i = 1}^{{n_{a} }} {a_{i} z^{ - i\alpha } y(k)} + \sum\limits_{j = 1}^{{n_{b} }} {b_{j} z^{ - j\alpha } \sum\limits_{l = 1}^{c} {w_{l} } \phi_{l} (u(k))} + v(k) \hfill \\ \end{gathered} $$

Using the discrete fractional operator $\Delta$ of Eqs. (5), (15) can be written as:

$$ \begin{aligned} y(k) = & - \sum\limits_{i = 1}^{{n_{a} }} {a_{i} \Delta^{\alpha } y(k - i)} + \sum\limits_{j = 1}^{{n_{b} }} {b_{j} \sum\limits_{l = 1}^{l} {w_{l} \Delta^{\alpha } \phi_{l} (u(k - j))} } + v(k) \\ { = } & - \sum\limits_{i = 1}^{{n_{a} }} {a_{i} \Delta^{\alpha } y(k - i)} + w_{1} \sum\limits_{j = 1}^{{n_{b} }} {b_{j} \Delta^{\alpha } \phi_{1} (u(k - j)) + \cdots } \\ & \quad { + }w_{c} \sum\limits_{j = 1}^{{n_{b} }} {b_{j} \Delta^{\alpha } \phi_{c} (u(k - j))} + v(k) \\ \end{aligned} $$

(16)

Define the parameter vector as:

$$ {\mathbf{a}} = [a_{1} a_{2} \cdots a_{{n_{a} }} ]^{{\text{T}}} \in {\mathbb{R}}^{{n_{a} }} ,\;{\mathbf{b}} = [b_{1} b_{2} \cdots b_{{n_{b} }} ]^{{\text{T}}} \in {\mathbb{R}}^{{n_{b} }} ,\;{\mathbf{w}} = [w_{1} w_{2} \cdots w_{c} ]^{{\text{T}}} \in {\mathbb{R}}^{c} $$

(17)

In order to obtain the unique parameters of the model, the model parameters are standardized. For this reason, set the first element in the parameter ${\mathbf{w}}$ to be 1, $w_{1} = 1$. On this basis, Eq. (16) can be rewritten as:

$$ \begin{aligned} y(k) = & - \sum\limits_{i = 1}^{{n_{a} }} {a_{i} \Delta^{\alpha } y(k - i) + } \sum\limits_{j = 1}^{{n_{b} }} {b_{j} \Delta^{\alpha } \phi_{{1}} (u(k - j)) + ..._{{}} } \\ & \quad { + }w_{2} \sum\limits_{j = 1}^{{n_{b} }} {b_{j} \Delta^{\alpha } \phi_{{2}} (u(k - j)) + } \cdots \\ & \quad + w_{c} \sum\limits_{j = 1}^{{n_{b} }} {b_{i} \Delta^{\alpha } \phi_{c} (u(k - j)) + v(k)} \\ \end{aligned} $$

(18)

According to the definition of each parameter vector of Eq. (17), Eq. (18) can be written in the form of linear regression,

$$ y(k) = {\mathbf{\varphi }}^{{\text{T}}} (k,\alpha ){{\varvec{\uptheta}}} + v(k) $$

(19)

where ${\mathbf{\varphi }}^{{\text{T}}} (k,\alpha )$ is the information vector, which is

$$ {\mathbf{\varphi }}^{{\text{T}}} (k,\alpha ) = \left[ {\begin{array}{*{20}c} {{{\varvec{\uppsi}}}(k,\alpha )} \\ {{{\varvec{\upzeta}}}(k,\alpha )} \\ \end{array} } \right] \in {\mathbb{R}}^{n} ,n = n_{a} + c \times n_{b} $$

(20)

Among them, ${{\varvec{\uppsi}}}(k,\alpha ) = [\Delta^{\alpha } y(k - 1), \cdots ,\Delta^{\alpha } y(k - n_{a} )]^{{\text{T}}} \in {\mathbb{R}}^{{n_{a} }}$;

$$ \begin{aligned} & {{\varvec{\upzeta}}}(k,\alpha ) = [{{\varvec{\upzeta}}}_{{1}}^{{\text{T}}} (k,\alpha ),{{\varvec{\upzeta}}}_{{2}}^{{\text{T}}} (k,\alpha ), \ldots ,{{\varvec{\upzeta}}}_{c}^{{\text{T}}} (k,\alpha )]^{{\text{T}}} \in {\mathbb{R}}^{{c \times n_{b} }} ; \\ & {{\varvec{\upzeta}}}_{j} (k,\alpha ) = [\Delta^{\alpha } \phi_{j} (u(k - 1)), \cdots ,\Delta^{\alpha } \phi_{j} (u(k - n_{b} ))]^{{\text{T}}} ,j = 1,2, \ldots ,c \\ \end{aligned} $$

${{\varvec{\uptheta}}}$ is an unknown parameter vector, which is ${{\varvec{\uptheta}}}{ = [}{\mathbf{a}}{,}{\mathbf{b}}{,}w_{2} {\mathbf{b}}, \ldots ,w_{c} {\mathbf{b}}{]}^{{\text{T}}} = [{\mathbf{a}},{\mathbf{w}} \otimes {\mathbf{b}}]^{{\text{T}}} \in {\mathbb{R}}^{n}$. In the Eq, $\otimes$ is the Kronecker product or direct product, if ${\mathbf{A}} = [a_{ij} ] \in {\mathbb{R}}^{m \times n} ,\;{\mathbf{B}} = [b_{ij} ] \in {\mathbb{R}}^{p \times q} ,\;{\mathbf{A}} \otimes {\mathbf{B}} = [a_{ij} {\mathbf{B}}] \in {\mathbb{R}}^{(mp) \times (nq)} .$

For the fractional order neural-fuzzy Hammerstein model described in Fig. 1, the purpose of identification is to use sampled data $\left\{ {u(k),y(k)} \right\},\,k = 1,2, \ldots ,$ to determine the neural-fuzzy network parameters $c_{l} ,\;\delta_{l} ,\;w_{l}$ and the number of rules c of the nonlinear module, and the dynamic fractional order linear module parameters, including $a_{i} ,\;b_{i}$ and the fractional order $\alpha$. To this end, this paper divides the identification process into two processes: one process first determines the antecedent parameters of the nonlinear module neuro-fuzzy network; the other process is to identify the parameters of the linear module, the fractional order and the conclusion parameters of the neuro-fuzzy network. In Sect. 4, the two identification processes will be described in detail.

4 Model parameter identification

This section describes the identification method of model parameters in the previous section. First, the antecedent parameters of the neuro-fuzzy network are determined. Secondly, the multi-innovation L-M identification algorithm adopted by the parameters of the dynamic linear module is described. Finally, the process of the entire identification algorithm is summarized.

4.1 Determining the antecedent parameters of the neural-fuzzy network

For the neuro-fuzzy network model, it is necessary to determine $c_{l} ,\;\delta_{l}$ and the number of rules c, which is actually a nonlinear optimization process. In this paper, a self-learning clustering algorithm is used to determine the antecedent parameters $c_{l} ,\;\delta_{l}$ of the neuro-fuzzy network model and the number of rules c. The specific learning process is as follows:

• (1) Collect the input data $u(k),\,k = 1,2, \ldots ,$ take the input data $u({1})$ as the first cluster, and set the cluster center $c_{{1}} { = }u(1)$. At this time, the number of clusters $\overline{N} = 1$, and the number of data pairs belonging to the first category is $\overline{N}_{{1}} { = 1}$.

• (2) For the k-th input data $u(k)$, calculate the similarity between the k-th training data and each cluster center $c_{l} (l = 1,2, \ldots ,c)$ according to the similarity criterion, and find the cluster L with the greatest similarity, that is, find the class to which $u(k)$ belongs (fuzzy rules). Define the similarity criterion as follows:

  $$ S_{L} = \mathop {\max }\limits_{1 \le l \le c} \sqrt {e^{{ - \left\| {u(k) - c_{l} } \right\|_{2}^{2} }} } $$

  (21)

• (3) Determine whether to add new clusters according to the following criteria.

If $S_{L} < S_{0}$ (S₀ represents a preset threshold), it indicates that the k-th input data does not belong to an existing cluster, and a new cluster must be established. Let $c_{{\overline{N} + 1}} = u(k)$, and let $\overline{N} = \overline{N} + 1$, $\overline{N}_{{\overline{N}}} = 1$, ($\overline{N}_{{\overline{N}}}$ represents the number of data pairs belonging to the $\overline{N}$-th cluster).

If $S_{L} \ge S_{0}$, it indicates that the k-th input data belongs to the existing L-th cluster. Let $\overline{N}_{L} = \overline{N}_{L} + 1$ and adjust the center of the L-th cluster as follows:

$$ c_{L} = c_{L} + \frac{\lambda }{{\overline{N}_{L} + 1}}(u(k) - c_{L} ) $$

(22)

In Eq. (22), $\lambda \in [0,1][0,1]$. It can be seen from Eq. (15) that as more and more data points belong to this cluster, the adjustment rate $\frac{\lambda }{{\overline{N}_{L} + 1}}$ of the cluster center decreases. In general, the larger the parameter $\lambda$, the larger the update range of the cluster centers. The parameter $\lambda$ cannot be too large, otherwise it will destroy the existing classification.

(4) Let $k = k + 1$, repeat the above steps (2) and (3) until all the input data are assigned to the corresponding clusters. Thus, the number of clusters (fuzzy rules) is $\overline{N}$, and the number of rules is finally determined to be $c = \overline{N}$. The width of the membership function is given as follows:

$$ \delta_{l} = \mathop {\min }\limits_{\begin{subarray}{l} j = 1,2,...,c \\ j \ne l \end{subarray} } \frac{{\left\| {c_{l} - c_{j} } \right\|_{2} }}{\rho } $$

(23)

In Eq. (23), $\rho$ is the overlap coefficient, generally ${1} \le \rho \le {2}$.

Through the abovementioned self-learning clustering process, the input data can be clustered to obtain the parameters $c_{l} ,\;\delta_{l}$ and the rule number c of the neuro-fuzzy antecedent structure. Through self-learning clustering to determine the centers and widths of various types, the fuzzy basis function $\phi_{1} (u(k)), \ldots ,\phi_{c} (u(k))$ in Eq. (15) can be determined, the parameters $a_{i} ,\;b_{j}$ of the fractional order linear module, the fractional order $\alpha$, and the conclusion parameter $w_{l}$ of the neural-fuzzy network are completed by the multi-innovation L-M identification algorithm.

4.2 Estimation of dynamic linear module parameters

The estimation of the linear dynamic module parameters mainly determines the linear model parameters and the fractional order. This paper uses the L-M gradient descent algorithm to achieve. The L-M gradient descent algorithm is essentially a nonlinear optimization method, which includes Gauss–Newton optimization and gradient descent methods. However, the disadvantage of this method is that the accuracy is not high. For this reason, this paper applies the principle of multiple innovations to the L-M algorithm and proposes a multiple innovation L-M algorithm to solve the parameter identification problem of the dynamic linear module. The principle of multi-innovation identification has been applied in many references. The principle is to expand the scalar innovation into the multi-innovation of the vector and the information vector into the information matrix; therefore, both the previous sampling information and the current information are used in the identification algorithm, thereby improving the identification accuracy.

To this end, consider the following identification objective function,

$$ J = \frac{1}{N}\sum\limits_{k = 1}^{N} {e^{2} (k)} $$

(24)

where $N$ is the total number of samples; $e(k)$ is the prediction error or innovation, which is

$$ e(k) = y(k) - \hat{y}(k) = y(k) - {\mathbf{\varphi }}^{{\text{T}}} (k,\hat{\alpha })\hat{\theta } $$

(25)

Among them, $\hat{y}(k)$, ${\hat{\mathbf{\theta }}}$ and $\hat{\alpha }$ are the output of the estimation model, the estimation of the parameter vector ${{\varvec{\uptheta}}}$ and the estimation of the fractional order $\alpha$, respectively. If the objective function (24) has a minimum value, then there is the following iterative L-M algorithm:

$$ {{\varvec{\uptheta}}}^{(i + 1)} = {{\varvec{\uptheta}}}^{(i)} + \left\{ {\left[ {J^{^{\prime\prime}} + \lambda I} \right]^{ - 1} J^{^{\prime}} } \right\}_{{\hat{\theta } = \theta^{(i)} }} $$

(26)

$$ \alpha^{(i + 1)} = \alpha^{(i)} + \left\{ {\left[ {J^{^{\prime\prime}} + \lambda I} \right]^{ - 1} J^{^{\prime}} } \right\}_{{\hat{\alpha } = \alpha^{(i)} }} $$

(27)

Among them, $\lambda$ is the adjustment operator that guarantees the convergence of the algorithm. Based on the prediction error of Eq. (25), the first derivative $J_{{\hat{\theta }}}^{^{\prime}}$ and the second derivative $J_{{\hat{\theta }}}^{^{\prime\prime}}$ of the objective function with respect to the parameter $\hat{\theta }$ are given as follows:

$$ J_{{\hat{\theta }}}^{{\prime }} = - \frac{2}{N}{\mathbf{\varphi }}(k,\hat{\alpha })\left[ {y(k) - {\mathbf{\varphi }}^{{\text{T}}} (k,\hat{\alpha })\hat{\theta }} \right] $$

(28)

$$ J_{{\hat{\theta }}}^{{\prime \prime }} = \frac{2}{N}{\mathbf{\varphi }}(k,\hat{\alpha }){\mathbf{\varphi }}^{{\text{T}}} (k,\hat{\alpha }) $$

(29)

Based on the prediction error of Eq. (25), the first derivative $J_{{\hat{\alpha }}}^{^{\prime}}$ of the objective function with respect to the fractional order $\hat{\alpha }$ is given as follows:

$$ \begin{aligned} J_{{\hat{\alpha }}}^{^{\prime}} = & - \frac{2}{N}\left[ {\frac{{\partial {\mathbf{\varphi }}^{{\text{T}}} (k,\hat{\alpha }){\hat{\mathbf{\theta }}}}}{{\partial \hat{\alpha }}}} \right]^{{\text{T}}} \;\left[ {y(k) - {\mathbf{\varphi }}^{{\text{T}}} (k,\hat{\alpha }){\hat{\mathbf{\theta }}}} \right] \\ = & - \frac{2}{N}\left[ {\frac{{\partial \hat{y}(k)}}{{\partial \hat{\alpha }}}} \right]^{{\text{T}}} \left[ {y(k) - {\mathbf{\varphi }}^{{\text{T}}} (k,\hat{\alpha }){\hat{\mathbf{\theta }}}} \right] \\ = & - \frac{2}{N}\left[ {\sigma \hat{y}(k)/\hat{\alpha }} \right]^{{\text{T}}} \left[ {y(k) - {\mathbf{\varphi }}^{{\text{T}}} (k,\hat{\alpha }){\hat{\mathbf{\theta }}}} \right] \\ \end{aligned} $$

where $\sigma \hat{y}(k)/\hat{\alpha }$$= \frac{{\partial \hat{y}(k)}}{{\partial \hat{\alpha }}}$ is the sensitivity function with respect to the fractional order. The sensitivity function is calculated as follows:

$$ \sigma \hat{y}(k)/\hat{\alpha } \approx \frac{{\hat{y}(k,\hat{\alpha } + \delta \hat{\alpha }) - \hat{y}(k,\hat{\alpha })}}{{\delta \hat{\alpha }}} $$

(30)

where $\delta \hat{\alpha }$ is the small change of the fractional order $\hat{\alpha }$.

Based on the prediction error of Eq. (25), the second derivative $J_{{\hat{\alpha }}}^{^{\prime\prime}}$ of the objective function with respect to the fractional order $\hat{\alpha }$ is given as follows:

$$ \begin{aligned} J_{{\hat{\alpha }}}^{{\prime \prime }} = & \frac{2}{N}\left( {\frac{{\partial \hat{y}(k)}}{{\partial \hat{\alpha }}}} \right)^{{\text{T}}} \left( {\frac{{\partial \hat{y}(k)}}{{\partial \hat{\alpha }}}} \right) \\ = & \frac{2}{N}\left( {\sigma \hat{y}(k)/\hat{\alpha }} \right)^{{\text{T}}} \left( {\sigma \hat{y}(k)/\hat{\alpha }} \right). \\ \end{aligned} $$

(31)

Therefore, $J_{{\hat{\theta }}}^{{\prime }} ,\;J_{{\hat{\theta }}}^{{\prime \prime }} ,\;J_{{\hat{\alpha }}}^{{\prime }}$ and $J_{{\hat{\alpha }}}^{{\prime \prime }}$ are organized as:

$$ \left[ {\begin{array}{*{20}c} {J_{{\hat{\theta }}}^{{\prime }} } \\ {J_{{\hat{\alpha }}}^{{\prime }} } \\ \end{array} } \right] = - \frac{2}{N}\left[ {\begin{array}{*{20}c} {{\mathbf{\varphi }}(k,\hat{\alpha })\left[ {y(k) - {\mathbf{\varphi }}^{{\text{T}}} (k,\hat{\alpha })\hat{\theta }} \right]} \\ {\left[ {\sigma \hat{y}(k)/\hat{\alpha }} \right]^{{\text{T}}} \left[ {y(k) - {\mathbf{\varphi }}^{{\text{T}}} (k,\hat{\alpha }){\hat{\mathbf{\theta }}}} \right]} \\ \end{array} } \right] $$

(32)

$$ \left[ {\begin{array}{*{20}c} {J_{{\hat{\theta }}}^{{\prime \prime }} } \\ {J_{{\hat{\alpha }}}^{{\prime \prime }} } \\ \end{array} } \right] = \frac{2}{N}\left[ {\begin{array}{*{20}c} {{\mathbf{\varphi }}(k,\hat{\alpha }){\mathbf{\varphi }}^{{\text{T}}} (k,\hat{\alpha })} \\ {\left[ {\sigma \hat{y}(k)/\hat{\alpha }} \right]^{{\text{T}}} \left[ {\sigma \hat{y}(k)/\hat{\alpha }} \right]} \\ \end{array} } \right]. $$

(33)

In the algorithms (26) and (27), the single innovation $y(k) - {\mathbf{\varphi }}^{{\text{T}}} (k,\hat{\alpha }){\hat{\mathbf{\theta }}}$ is mainly used. For the L-M algorithm, its identification accuracy is not high. To this end, this paper proposes a multi-innovation L-M identification algorithm (MILM).

First, define the L-dimensional multi-innovation vector ${\mathbf{E}}(L,k,\hat{\alpha })$, the input and output information matrix ${\hat{\mathbf{\Phi }}}(L,k,\hat{\tilde{\alpha }})$, and the stacked output vector ${\mathbf{Y}}(L,k)$ as follows:

$$ \begin{aligned} {\mathbf{E}}(L,k,\hat{\alpha }) = & [y(k) - {\mathbf{\varphi }}^{{\text{T}}} (k,\hat{\alpha }){\hat{\mathbf{\theta }}},y(k - 1) - {\mathbf{\varphi }}^{{\text{T}}} (k - 1,\hat{\alpha }){\hat{\mathbf{\theta }}}, \ldots , \\ & \quad y(k - L + 1) - {\mathbf{\varphi }}^{{\text{T}}} (k - L + 1,\hat{\alpha }){\hat{\mathbf{\theta }}}]^{{\text{T}}} \in {\mathbb{R}}^{L} \\ \end{aligned} $$

(34)

$$ \begin{aligned} {{\varvec{\Phi}}}(L,k,\hat{\alpha }) = & [{\mathbf{\varphi }}(k,\hat{\alpha }),{\mathbf{\varphi }}(k - 1,\hat{\alpha }),..., \\ & \quad {\mathbf{\varphi }}(k - L + 1,\hat{\alpha })] \in {\mathbb{R}}^{n \times L} \\ \end{aligned} $$

(35)

$$ {\mathbf{Y}}(L,k) = \left[ {y(k),y(k - 1), \ldots ,y(k - L + 1)} \right]^{{\text{T}}} \in {\mathbb{R}}^{L} ,\;n = n_{a} + cn_{b} . $$

(36)

The L-dimensional multi-innovation vector ${\mathbf{E}}(L,k,\hat{\alpha })$ can be expressed as

$$ {\mathbf{E}}(L,k,\hat{\alpha }) = {\mathbf{Y}}(L,k) - {{\varvec{\Phi}}}^{{\text{T}}} (L,k,\hat{\alpha }){\hat{\mathbf{\theta }}}. $$

(37)

Define the stacking sensitivity function vector ${{\varvec{\Xi}}}(L,k,\hat{\alpha })$ as

$$ \begin{aligned} {{\varvec{\Xi}}}(L,k,\hat{\alpha }) = & [\sigma \hat{y}(k)/\hat{\alpha },\sigma \hat{y}(k - 1)/\hat{\alpha }, \ldots , \\ \, & \quad \sigma \hat{y}(k - L + 1)/\hat{\alpha }]^{{\text{T}}} \in {\mathbb{R}}^{L} . \\ \end{aligned} $$

(38)

In this way, Eqs. (32) and (33) can be written as gradients with multiple innovations,

$$ \left[ {\begin{array}{*{20}c} {J_{{\hat{\theta }}}^{{\prime }} } \\ {J_{{\hat{\alpha }}}^{{\prime \prime }} } \\ \end{array} } \right] = - \frac{2}{N}\left[ {\begin{array}{*{20}c} {{{\varvec{\Phi}}}(L,k,\hat{\alpha })\left[ {Y(k) - {{\varvec{\Phi}}}^{{\text{T}}} (L,k,\hat{\alpha })\hat{\theta }} \right]} \\ {\left[ {{{\varvec{\Xi}}}(L,k,\hat{\alpha })} \right]^{{\text{T}}} \left[ {Y(k) - {{\varvec{\Phi}}}^{{\text{T}}} (L,k,\hat{\alpha })\hat{\theta }} \right]} \\ \end{array} } \right] $$

(39)

$$ \left[ {\begin{array}{*{20}c} {J_{{\hat{\theta }}}^{{\prime \prime }} } \\ {J_{{\hat{\alpha }}}^{{\prime \prime }} } \\ \end{array} } \right] = \frac{2}{N}\left[ {\begin{array}{*{20}c} {{{\varvec{\Phi}}}(L,k,\hat{\alpha }){{\varvec{\Phi}}}^{{\text{T}}} (L,k,\hat{\alpha })} \\ {\left[ {{{\varvec{\Xi}}}(L,k,\hat{\alpha })} \right]^{{\text{T}}} \left[ {{{\varvec{\Xi}}}(L,k,\hat{\alpha })} \right]} \\ \end{array} } \right]. $$

(40)

After obtaining the estimated parameter vector ${\hat{\mathbf{\theta }}}$, the first $n_{a}$ element in ${\hat{\mathbf{\theta }}}$ is the estimate of the vector ${\hat{\mathbf{a}}}$, and the element $n_{a} { + 1}$ to the element $n_{a} { + }n_{b}$ in ${\hat{\mathbf{\theta }}}$ is the estimate of the vector ${\hat{\mathbf{b}}}$. By observing the parameter vector ${\hat{\mathbf{\theta }}}$, there are $n_{b}$ valuations of $\hat{w}_{j}$. For this reason, they are calculated by the average method,

$$ \hat{w}_{j} = \frac{1}{{n_{b} }}\sum\limits_{i = 1}^{{n_{b} }} {\frac{{\theta_{{n_{a} + (j - 1)n_{b} + i}} }}{{\hat{b}_{i} }}} ,\;j = 2,3, \ldots ,c. $$

(41)

In this paper, a hybrid method based on fuzzy clustering to determine the structure and network parameters of the neuro-fuzzy network and using multiple innovations to estimate the parameters of the linear module is proposed. The former clustering method is the premise and foundation of the hybrid algorithm, and the latter multi-innovation method is the key to the hybrid identification algorithm. The following summarizes the hybrid algorithm as follows:

Step 1:

Set m = 1, k = 1, c = 1, set the initial parameter values $\hat{\theta }^{0}$, $\hat{\alpha }^{0}$, p and $\delta \hat{\alpha }$;

Step 2:

Collect input data $\left\{ {u(k)} \right\},\;k = 1,2, \ldots ,N$, and determine the neuro-fuzzy antecedent parameters $\hat{c}_{l}$, $\hat{\delta }_{l}$ and the number of rules $\hat{c}$ according to self-learning clustering;

Step 3:

According to the sampled data $\left\{ {u(k),y(k)} \right\},\;k = 1,2, \ldots ,N$, perform the identification of the linear module parameter ${\hat{\mathbf{\theta }}}$ and the identification of the neural-fuzzy network follow-up parameter $\hat{w}_{l}$;

Step 4:

After obtaining the parameters of the neural-fuzzy network and the linear module, perform the identification of the fractional order $\hat{\alpha }$;

Step 5:

Let k = k + 1, if $s \le P$, go to step 3, otherwise go to step 6;

Step 6:

If $\frac{{\left| {J({\hat{\mathbf{\theta }}}^{(m + 1)} ) - J({\hat{\mathbf{\theta }}}^{(m)} )} \right|}}{{\left| {J({\hat{\mathbf{\theta }}}^{(m)} )} \right|}} \le \xi$, then set ${\hat{\mathbf{\theta }}} = {\hat{\mathbf{\theta }}}^{(m)}$, $\hat{\alpha } = \alpha^{(m)}$ and $J({\hat{\mathbf{\theta }}}) = J({\hat{\mathbf{\theta }}}^{(m)} )$, algorithm end. Otherwise $m = m + 1$, $s = 1,$ go to step 3.

5 Simulation examples

This section uses two examples to verify the effectiveness of the proposed method. The first example is an academic example of a discontinuous fractional order Hammerstein nonlinear system, which proves the theoretical feasibility of the method in this paper. Secondly, the method in this paper is applied to an actual system example of a flexible manipulator experiment, and the effect is compared with the results of reference [8], which proves that the method in this paper is more closely fitting with the actual system.

5.1 Academic example

In order to verify the effectiveness of the proposed algorithm, consider the Hammerstein fractional order nonlinear system with discontinuous functions:

$$ \begin{aligned} \overline{u}(k) = & \left\{ {\begin{array}{*{20}c} {2 - \cos (3u(k)) - \exp ( - u(k)),} & {u(k) \le 3.15} \\ {3,} & {u(k) > 3.15} \\ \end{array} } \right. \\ y(k) = & (1 - A(z))y(k) + B(z)\overline{u}(k) + v(k) \\ \end{aligned} $$

where $u(k)$ and $y(k)$ are the system input and the system output, respectively. $A(z)$ and $B(z)$ are the denominator polynomial and the numerator polynomial, respectively,

$$ \begin{aligned} & A(z){ = }a_{1} z^{ - \alpha } + a_{2} z^{ - 2\alpha } , \\ & B(z){ = }b_{1} z^{ - \alpha } + b_{2} z^{ - 2\alpha } , \\ & \overline{u}(k) = \sum\limits_{j = 1}^{c} {w_{j} \phi_{j} (u(k))} . \\ \end{aligned} $$

The entire output of the system is given as follows:

$$ y(k) = \sum\limits_{i = 1}^{2} {a_{i} } \Delta^{\alpha } y(k - i){ + }\sum\limits_{j = 1}^{c} {w_{j} \sum\limits_{i = 1}^{2} {b_{i} } \Delta^{\alpha } \phi_{j} (u(k - i)) + v(k)} $$

Taking the fractional order $\alpha { = 0}{\text{.6}}$, the entire output of the system is given as follows:

$$ \begin{aligned} y(k) = & a_{1} \Delta^{0.6} y(k - 1) + a_{2} \Delta^{0.6} y(k - 2) + b_{1} \Delta^{0.6} \phi (u(k - 1)) + \cdots \\ & \quad { + }b_{2} \Delta^{0.6} \phi (u(k - 2)) + w_{2} b_{1} \Delta^{0.6} \phi (u(k - 1)) + \cdots \\ & \quad { + }w_{2} b_{2} \Delta^{0.6} \phi (u(k - 2)) + \cdots + w_{c} b_{1} \Delta^{0.6} \phi (u(k - 1)) + \cdots \\ & \quad + w_{c} b_{2} \Delta^{0.6} \phi (u(k - 2)) + v(k) \\ \end{aligned} $$

The parameter vector is given as follows:

$$ {\mathbf{a}} = [a_{1} \;a_{2} ]^{{\text{T}}} = [{0}{\text{.1}}\;0.{2}]^{{\text{T}}} ,\;{\mathbf{b}} = [b_{1} \;b_{2} ]^{{\text{T}}} = [ - 0.4\; - {0}{\text{.2}}]^{{\text{T}}} . $$

In the simulation, the input signal is a random signal with zero mean and unit variance, and the number of sampling is 1000, as shown in Fig. 3. The noise signal is an independent random signal with zero mean value and variance $\sigma^{{2}} { = 0}{\text{.01}}$. Figure 4 shows the noise signal with 1000 sampling times. In the research, the length of multi-innovation $L = 1,3,5$ is selected. The neural-fuzzy network is used to approximate the static nonlinear system, and the self-learning fuzzy clustering is used to learn the antecedent structure. The initial value of the rule number is $c = 2$ and each rule adopts an exponential clustering function. In order to verify the effectiveness of the proposed method, the objective function $J$ in Eq. (24) is used to verify.

Fig. 3

System input signal

Fig. 4

System noise signal

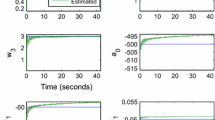
Figure 5 shows the actual output signal of the system; Fig. 6 is the objective functions $J$ of different multiple innovations. Through comparison and analysis, it can be seen that multiple innovations are more advantageous than single innovations. As the information length increases, the objective function $J$ gradually decreases, and the identification accuracy is significantly improved. Using self-organizing learning fuzzy clustering method, the number of system rules is 8, so the parameter vector to be estimated of the system is ${{\varvec{\uptheta}}}{ = [}{\mathbf{a}}{,}{\mathbf{b}}{,}w_{2} {\mathbf{b}}, \cdots ,w_{8} {\mathbf{b}}{]}^{{\text{T}}} \in {\mathbb{R}}^{n}$, and the estimated values of system parameters are shown in Tables 1, 2. (Note: The specific value is calculated by Eq. (41), for example:$\hat{w}_{2} = \left( {\frac{{w_{2} b_{1} }}{{b_{1} }} + \frac{{w_{2} b_{2} }}{{b_{2} }}} \right)/2$). Figure 7 is the comparison result between the output of the identification model and the actual output of the system when the multi-innovation length $L = 5$, and the figure is partially. Fig. 8 is the system fractional order estimation curve, and finally converges to $\alpha { = 0}{\text{.551825}}$; Fig. 9 is the system output estimation error curve. Through analysis and comparison, the output of the system identification model and the actual output of the system have a good fitting effect and basically coincide.

Fig. 5

The actual output signal of the system

Fig. 6

Objective function $J$ under different innovation lengths $(L = 1,3,5)$

Table 1 Estimated value of system parameters and fractional order (L = 5)

Table 2 Partial estimated value of system parameters and fractional order (L = 5)

Fig. 7

The actual output and estimated output of the system $(L = 5)$

Fig. 8

Estimated value of system fractional order

Fig. 9

System output estimation error

5.2 Example of a flexible manipulator

In order to further show the effectiveness of the proposed method, this paper also applies the proposed method to a flexible robotic arm system. The system consists of a flexible arm mounted on a motor. The input is the reaction torque of the structure on the ground, and the output is the acceleration of the flexible arm. The benchmark data set of the flexible manipulator obtained by DAISY database [28] (system identification database) is further verified. The measured data set contains 1024 input and output samples as shown in Figs. 10, 11. The noise signal is an independent random signal with zero mean and variance $\sigma^{{2}} { = 0}{\text{.01}}$, and Fig. 12 shows the noise signal with 1024 sampling times.

Fig. 10

System input signal

Fig. 11

The actual output signal of the system

Fig. 12

System noise signal

In the research, select the multi-innovation length $L = 1,3,5$. Figure 13 is the objective functions of different multiple innovations. Through comparison and analysis, it can be seen that multiple innovations have more advantages than single innovations. Obviously, as the length of multiple innovations increases, the objective function $J$ gradually decreases. The recognition accuracy is significantly improved. Using self-organizing learning fuzzy clustering method, the number of system rules is 5, so the system parameter vector to be estimated is ${{\varvec{\uptheta}}}{ = [}{\mathbf{a}}{,}{\mathbf{b}}{,}w_{2} {\mathbf{b}}, \cdots ,w_{5} {\mathbf{b}}{]}^{{\text{T}}} \in {\mathbb{R}}^{n}$, and the system parameter estimated value is shown in Tables 3, 4. (Note: The specific value is calculated by Eq. (41), for example: $\hat{w}_{2} = (\frac{{w_{2} b_{1} }}{{b_{1} }} + \frac{{w_{2} b_{2} }}{{b_{2} }})/2$). Figure 14 shows the comparison result between the output of the identification model and the actual output of the system when the multi-innovation length $L = 5$, and it is partially enlarged; Fig. 15 is the system fractional order estimation curve, which finally converges to $\alpha { = 0}{\text{.742542}}$; Fig. 16 is the system output estimation error curve. Through analysis and comparison, the output of the system identification model and the actual output of the system have a good fitting effect and basically coincide.

Fig. 13

Objective function $J$ under different innovation lengths $(L = 1,3,5)$

Table 3 Estimated value of system parameters and fractional order $(L = 5)$

Table 4 Partial estimated value of system parameters and fractional order $(L = 5)$

Fig. 14

The actual output and estimated output of the system $(L = 5)$

Fig. 15

Estimated value of system fractional order

Fig. 16

System output estimation error

In order to show the effectiveness of the proposed method, the method in this paper is also compared with the single innovation L-M algorithm proposed in the reference [8]. Figure 17 shows the objective function $J$ curve between the method in this paper (L = 5) and the reference method. Through comparative analysis and comparison, it is obvious that the method in this paper has small errors and high identification accuracy.

Fig. 17

Objective function $J$ under different methods

6 Conclusion

Aiming at the difficulty in identifying fractional order Hammerstein nonlinear systems, a MILM hybrid identification method based on neuro-fuzzy principle is proposed. The static nonlinear module of the Hammerstein model is fitted by neuro-fuzzy, the self-learning clustering algorithm determines the antecedent parameters and the number of rules of the neuro-fuzzy network model, and the multi-innovation Levenberg–Marquardt algorithm is designed to estimate the system parameters and the fractional order of the system. Through simulation verification, proper use of multiple innovations in the algorithm can improve the identification accuracy. But for the self-learning method, the selection of similarity is empirical, and this will also become our research focus in the future. The modeling research of multi-input multi-output fractional order nonlinear systems is still a challenging topic, which is also the research direction of researchers in the future.