Investigation of nonlinear characteristics of the motor-gear transmission system by trajectory-based stability preserving dimension reduction methodology

Abstract

Gear-motor system is a typically nonlinear system because of many nonlinear factors, such as time-varying meshing stiffness, backlash, and the nonlinear relationship between the electric motor torque and speed. At present, the nonlinear analytical methods can only be used for simplified gear dynamic model. Though the numerical methods can be used for the complicated dynamic model, the quantitative analysis of stability is difficult and rarely conducted. Therefore, a kind of trajectory-based stability preserving dimension reduction (TSPDR) methodology is proposed to investigate nonlinear dynamic characteristics of the gear-motor system. In the TSPDR methodology herein, the complementary cluster center of inertia-relative motion (CCCOI-RM) transformation is chosen and the stability margins are specially defined for distinguishing the stable motion modes of the motor-gear system, to make the TSPDR methodology used in the nonlinear analysis of the gear-motor system. Furthermore, the critical values are obtained for alteration of different motion modes and the nonlinear characteristics of each motion modes are analyzed. At last, combined with modal analysis, the relationship between the stability and resonance of the gear-motor system is revealed.

1 Introduction

Gear-motor system is a typically nonlinear system because of many nonlinear factors, such as time-varying meshing stiffness, backlash, and the nonlinear relationship between the electric motor torque and speed. At present, numerous investigations are carried out for the gear systems, but a few for the gear-motor system. Considering time-varying meshing stiffness, viscous damping, and gear errors, Amabili [1] constructed a single degree-of-freedom model of a pair of low contact ratio spur gears, and then obtained a continuous closed-form solution. At last, transition curves which separate stable and unstable regions were computed by Hill infinite determinant to investigate the influences of the damping and contact ratio. Sika [2] proposed a one degree-of-freedom model which considered time-varying mesh stiffness and unsteady input rotations because of engine speed fluctuation. Then, the stability is analyzed by calculating the monodromy matrix. The influences of the mesh stiffness variations and damping on the stability are also discussed. Han [3] carried out a parametric stability research for a spur gear pair system with consideration of the effect of ETC (Extended Tooth Contact, caused by pre-mature and post-mature contact of tooth pairs). The effects of ETC, operating torques, and mesh damping were also discussed on unstable regions. Moradi [4] obtained forced vibration responses of the gear system based on the classical single degree-of-freedom (SDOF) gear dynamic model by multiple scale method, and investigated the jump phenomenon, stability, as well as the effect of gear dynamic and manufacturing parameters on the dynamic transmission error (DTE). Litak [5] simulated the nonlinear vibration of a gear pair including shaft flexibility, observed that the extra degree of freedom, which may represent a flexible shaft or a vibration neutraliser, has a considerable effect on the dynamics. For example, in their paper, there were a number of chaotic and regular attractors in Poincare sections with respect to the shaft stiffness. Considering the contact loss of gears, Eritenel [6] investigates the three-dimensional nonlinear vibration of gear pairs, finding that resonances of twist and mesh deflection modes are shown to be nonlinear because of partial and total contact loss. Zhou [7] proposed an eight-degree-of-freedom (8-DOF) nonlinear gear-rotor-bearing model. Based on the model, the nonlinear vibration characteristics are investigated by the Runge–Kutta method, finding that the nonlinear dynamic characteristics, such as periodic motion, quasi-periodic motion, chaotic behaviors, and impacts, are strongly attributed to the interaction between internal and external excitations. Theodossiades [8] investigated the dynamics of a motor-gear system, demonstrating that the quasi-periodic and chaotic long-time responses existed for selected combinations of the system parameters.

From above literature analysis, some deficiencies can be found for the investigation of nonlinear characteristics of the motor-gear transmission system:

• (1) There is much research on nonlinear characteristics of the gear transmission system, but little on the motor-gear transmission system.

• (2) The analytical methods can only be used for simplified gear dynamic model. Though the numerical methods can be used for the complicated gear dynamic model, the quantitative analysis of stability is difficult and rarely conducted.

• (3) At present, the critical values are usually obtained between the stability and instability. In reality, various modes of motion exist as the system parameters changes when the system is stable, but critical values between these various modes of motion are seldom investigated in present studies of motor-gear nonlinear dynamics.

The main cause of the second deficiency is that it is difficult to obtain the closed-form solution and conduct quantitative stability analysis of complicated dynamic model. Therefore, Xue [9] proposed the trajectory-based stability preserving dimension reduction (TSPDR) methodology to quantitatively investigate the nonlinear stability of complicated dynamic system and applied it to electrical power system successfully. This methodology can be summarized to four steps:

Step 1 :

Obtaining the system motion trajectory by numerical computation method;

Step 2 :

Stability preserving dimension reduction, that is, the number of degrees of freedom of system decreases from n to 1 with the system stability preserving. There are three kinds of dimension reduction methods which are described detailedly by Xue [9]. For the sake of descriptive integrality, these methods are depicted herein by citation and paraphrasing based on Xue’s [9] literature.

(1):

CCCOI-RM (Complementary Cluster Center of Inertia-Relative Motion) transformation. Firstly, CCCOI (Complementary Cluster Center of Inertia) transformation is used. It divides the whole set of disturbed trajectories into complementary subsets in all possible ways. For each pair of complementary clusters, the trajectories within either cluster are aggregated into an equivalent trajectory at the inertia center of the relevant cluster, thus trajectories of the equivalent two-rigid-body system are formed. Then RM (relative motion) transformation is used to obtain the relative displacement between the trajectories of the equivalent two-rigid-body system.

(2):

CAP (coordinate-axis projection) transformation. It uses a unit-matrix transformation to realize the reduction in degree of freedom from n to 1.

(3):

CPP (coordinates-plane projection) transformation. It divides the system into a pair of complementary subsets, namely subset $\mathbf{X}_{1}$ of 2 dimensions and its complementary subset $\mathbf{X}_{2}$ of n-2 dimensions by using a two-block unit-matrix transformation. Independent of the actual trajectory, the nonlinear characteristics of the subsystem $\mathbf{X}_{1}$ are analyzed with $\mathbf{X}_{2}$ acting as parameters.

Step 3 :

Defining the stability margin in the phase plane after transformation. The stability margin can be defined in various ways, such as, definition for distinguishing the stability and instability or distinguishing the stable motion modes.

Step 4 :

Obtaining the critical value by sensitivity analysis.

If the CCCOI-RM combined with the stability margin defined for distinguishing the stability and instability is chosen for stability analysis, it is called CCEBC (Complementary Cluster Energy Barrier Criterion), which has been widely used by power grids in China, France, Canada and USA for system planning, operation, as well as for preventive and emergency controls [9] and also used for nonlinear dynamic analysis of modified Lorenz system [10], Zhou system [11], and Liu chaotic system [12]. The CAP is chosen, combined with the stability margin defined for distinguishing the stable motion modes, for stability analysis of nonlinear rotor systems [13]. The CCEBC just can be used for bounded stability analysis, while, the interaction between motions of each DOF is not considered in the CAP transformation.

In this study, the nonlinear dynamic characteristics of the gear-motor system are investigated by trajectory-based stability preserving dimension reduction (TSPDR) methodology. In the TSPDR methodology herein, the CCCOI-RM is chosen and the stability margins are specially defined for distinguishing the stable motion modes of the motor-gear system, to make the TSPDR methodology be used in the nonlinear analysis of the gear-motor system. At last, combined with modal analysis, the relationship between the stability and resonance of the gear-motor system is revealed.

2 Dynamic model of the motor-gear system

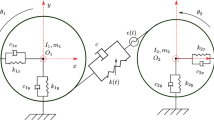
Figure 1 illustrates the dynamic model of the motor-gear system. The symbols $\theta _{\mathrm{m}}$, $\theta _{1}$, $\theta _{2}$, and $\theta _{\mathrm{l}}$ denote the angular displacements of the electric motor rotor, driving gear, driven gear, and load, respectively. The symbols $J_{\mathrm{m}}$, $J_{1}$, $J_{2}$, and $J_{\mathrm{l}}$ denote the rotational inertias of the electric motor, driving gear, driven gear, and load, respectively. The symbols $k_{\mathrm{m1}}$ and $c_{\mathrm{m1}}$ denote the connecting stiffness and damping between electric motor and driving gear, respectively. The symbols $k_{\mathrm{m}}$ and $c_{\mathrm{m}}$ denote the meshing stiffness and damping between the driving gear and driven gear, respectively. The symbols $k_{\mathrm{2l}}$ and $c_{\mathrm{2l}}$ denote the connecting stiffness and damping between the driven gear and load, respectively. The symbols $T_{\mathrm{m}}$ and $T_{\mathrm{l}}$ denote the electromagnetic torque and loading torque, respectively. The mathematical model is given as Eq. (1).

$$\begin{aligned}&\left\{ {\begin{array}{l} {{J_\mathrm{{m}}}{{\ddot{\theta }}_\mathrm{{m}}} + {k_{\mathrm{{m1}}}}({\theta _\mathrm{{m}}} - {\theta _1}) + {c_{\mathrm{{m1}}}}({{\dot{\theta }}_m} - {{\dot{\theta }}_1}) = {T_\mathrm{{m}}}}\\ {{J_1}{{\ddot{\theta }}_1} - {k_{m1}}({\theta _\mathrm{{m}}} - {\theta _1}) - {c_{\mathrm{{m1}}}}({{\dot{\theta }}_\mathrm{{m}}} - {{\dot{\theta }}_1}) + {k_\mathrm{{m}}}{\delta _{12}} + {c_\mathrm{{m}}}{{\dot{\delta }}_{12}} = 0}\\ {{J_2}{{\ddot{\theta }}_2} - {k_m}{{\dot{\delta }}_{12}} - {c_m}{{\dot{\delta }}_{12}} + {k_{\mathrm{{2l}}}}({\theta _2} - {\theta _\mathrm{{l}}})+ {c_{\mathrm{{2l}}}}({{\dot{\theta }}_2} - {{\dot{\theta }}_\mathrm{{l}}}) = 0}\\ {{J_\mathrm{{l}}}{{\ddot{\theta }}_\mathrm{{l}}} - {k_{\mathrm{{2l}}}}({\theta _2} - {\theta _\mathrm{{l}}}) - {c_{\mathrm{{2l}}}}({{\dot{\theta }}_2} - {{\dot{\theta }}_\mathrm{{l}}}) = - {T_\mathrm{{l}}}} \end{array}} \right. \nonumber \\ \end{aligned}$$

(1)

where $\delta _{12}$ is the gear teeth deformation;

$$\begin{aligned} \delta _{12} =\left\{ {\begin{array}{ll} r_{\mathrm{b1}}\theta _1 -r_{\mathrm{b2}} \theta _2 -\mathrm{e}-\mathrm{b}/2 &{} \hbox {if} \quad r_{\mathrm{b1}} \theta _1 -r_{\mathrm{b2}} \theta _2 -\mathrm{e}>\mathrm{b}/2 \\ 0 &{} \hbox {if} \quad - \mathrm{b}/2 \le r_{\mathrm{b1}} \theta _1 -r_{\mathrm{b2}} \theta _2 -\mathrm{e}\le \mathrm{b}/2 \\ r_{\mathrm{b1}} \theta _1 -r_{\mathrm{b2}} \theta _2 -\mathrm{e}+\mathrm{b}/2 &{} \hbox {if} \quad r_{\mathrm{b1}} \theta _1 -r_{\mathrm{b2}} \theta _2 -\mathrm{e}\le -\mathrm{b}/2\\ \end{array}} \right. \end{aligned}$$

(2)

e is the gear error; b is the backlash. If the tooth separation does not appear, the dynamic characteristics will not be affected by the backlash.

Fig. 1

Dynamic model of the motor-gear system

In Eq. (1), the meshing stiffness $k_{\mathrm{m}}$ is the period function of $\theta _{1}$ and the period $T_{\mathrm{km}}$ is $2\pi /c_{1}$, where $\theta _{1}$ and $c_{1}$ is the angular displacement and teeth number of the driving gear. Considering the effect of extended tooth contact (ETC), the mesh stiffness in the pre-mature and post-mature contact regions is gradually rather than abruptly varying with $\theta _{1}$; therefore, the mesh stiffness is approximated linearly by trapezoidal waveforms [3] as shown in Fig. 2. The transition period between the single-pair mesh and double-pair mesh is taken as 0.06 times of the meshing period [14, 15]. The meshing stiffness can be derived as Eq. (3).

$$\begin{aligned} k_\mathrm{m} =\left\{ {\begin{array}{ll} k_{\min } &{} \hbox {if}\quad 0 \le \bmod (\theta _1 ,2\pi /c_1 )/(2\pi /c_1 )<1.88-\varepsilon \\ k_{\min } +\frac{(k_{\max } -k_{\min } )}{0.06}[{\bmod (\theta _1 ,2\pi /c_1 )/(2\pi /c_1 )-(1.88-\varepsilon )}] &{} \hbox {if}\quad 1.88{-}\varepsilon \le \bmod (\theta _1 ,2\pi /c_1 )/(2\pi /c_1 )<1.94-\varepsilon \\ k_{\max } &{} \hbox {if} \quad 1.94-\varepsilon \le \bmod (\theta _1 ,2\pi /c_1 )/(2\pi /c_1 )<0.94 \\ k_{\max } -\frac{(k_{\max } -k_{\min } )}{0.06} [{\bmod (\theta _1,2\pi /c_1 )/(2\pi /c_1 )-0.94} ] &{}\hbox {if} \quad 0.94\le \bmod (\theta _1 ,2\pi /c_1 )/(2\pi /c_1 )<1\\ \end{array}} \right. \quad \, \end{aligned}$$

(3)

where the symbols $k_{\mathrm{min}}$ and $k_{\mathrm{max}}$ denote the meshing stiffness of single-pair and double-pair mesh, respectively; the symbols $\theta _{1}$ and $c_{1}$ is the angular displacement and teeth number of the driving gear; the symbols $\varepsilon$ is the contact ratio; mod(a, m) returns the remainder after division of a by m.

In motor-gear system, except backlash and varying meshing stiffness, which are non-ignorable nonlinear factors [5, 16], the nonlinear electromagnetic torque is also an important nonlinear factor. In Eq. (1), the electromagnetic torque $T_{\mathrm{m}}$ can be obtained by steady-state model of the electric motor [17]. The steady-state model, namely, the mechanical characteristic of the electric motor, reflects the relationship of the torque and the rotating speed of the electric motor. The mechanical characteristic of the electric motor can be derived by steady-state electric circuit analysis of the electric motor as shown in Fig. 3. The mechanical characteristic of the electric motor is derived as Eq. (4). Figure 4 shows the curve of the mechanical characteristic of the asynchronous motor. AC is the stable operation interval of the motor. B is the rated power point.

$$\begin{aligned} {T_\mathrm{m}} = \frac{{{\mathrm{m}_1}}}{{{\omega _\mathrm{s}}}}\frac{{U_{\phi } ^2\frac{{{{R'}_2}}}{s}}}{{{{\left( {{R_1} + \frac{{{{R'}_2}}}{\mathrm{s}}} \right) }^2} + {{({{X_{\sigma 1}} + {{X'}_{\sigma 2}}})}^2}}} \end{aligned}$$

(4)

Fig. 2

Gear meshing stiffness

Fig. 3

Equivalent circuit of the asynchronous electric motor

$T_{\mathrm{m}}$ :

Electromagnetic torque of the electric motor, Nm;

$\mathrm{m}_{1}$ :

Phase number, $m_{1}=3$ here;

$\omega _{\mathrm{s}}$ :

Synchronous angular velocity, $\hbox {rad}\,{\mathrm{s}}^{-1}$;

$U_{\phi }$ :

Phase voltage, v;

$R_{1}$ :

Stator resistance, $\Omega$;

$R'_{2}$ :

Equivalent rotor resistance, $\Omega$;

$X_{\sigma 1}$ :

Stator leakage reactance, $\Omega$;

$X'_{\sigma 2}$ :

Equivalent rotor leakage reactance, $\Omega$;

$X_{\mathrm{m}}$ :

Magnetizing inductance, $\Omega$;

s :

Slip ratio, $\mathrm{s}=(\omega _{\mathrm{s}}-\omega )/\omega _{\mathrm{s}}$;

$\omega$ :

Angular velocity of the motor rotor, $\hbox {rad}\,{\mathrm{s}}^{-1}$.

Fig. 4

Mechanical characteristic of the asynchronous motor

Because the system parameters are varying with the state variables, for example, the electromagnetic torque varies with the angular velocity of motor rotor and the meshing stiffness varies with the angular displacement of the driving gear, obvious nonlinearity is induced in this model, and it is nearly impossible to obtain the closed solution, though the model herein is relatively simple. In addition, the gear teeth deformation will reach 0 if the tooth separation appears, that is, dead zone emerges, which will induce obvious nonlinearity into this model. The parameters of the gear-motor system are shown in Table 1.

Table 1 The parameters of the gear-motor system

3 Procedures to obtain the critical values by TSPDR

It is mentioned that TSPDR includes four steps, so this section is arranged according to the four steps. The first step, obtaining the system motion trajectory by numerical computation method, can be seen in much literature about numerical calculation; therefore, the first step will not introduced herein, and the later three steps will presented in detail.

3.1 Step 2: dimension reduction by CCCOI-RM

The dynamic problems can be expressed as Eq. (5). Where, $\mathbf{X}=[{\varvec{\updelta }}^{\mathrm{T}}$, ${\varvec{\upomega }}^{\mathrm{T}}$] is a vector of motion state variables consisting of generalized position ${\varvec{\updelta }}$ and speed ${\varvec{\upomega }}$; vector Z stands for non-motion state variables; vector Y stands for algebraic variables; $M_{k}$ is generalized inertia; $\tau$ is generalized scenario; $P_{mk}$ is driving force (or torque); $P_{ek}$ is the brake force (or torque); $P_{mk}$, $P_{ek}$, f, and ${\varvec{\Psi }}$ are nonlinear functions; $k=1, 2, {\ldots }, n$ stands for one of the n rigid-body.

$$\begin{aligned} M_k \ddot{\delta }_k= & {} P_{mk} (\mathbf{X},\mathbf{Z},\mathbf{Y},t,\tau ) -P_{ek} (\mathbf{X},\mathbf{Z},\mathbf{Y},t,\tau ) \nonumber \\ \dot{\mathbf{Z}}= & {} \mathbf{f}(\mathbf{X},\mathbf{Z},\mathbf{Y},t,\tau ) \nonumber \\ \mathbf{0}= & {} {\varvec{\Psi }}(\mathbf{X},\mathbf{Z},\mathbf{Y},t,\tau ) \end{aligned}$$

(5)

The trajectories $\delta _{k}$ ($k=1, 2, {\ldots }, n$) can be obtained by numerical calculation method, then these trajectories can be divided in two complementary cluster, S and A, as shown in Fig. 5. The symbols $\delta _{\mathrm{s}}$ and $\delta _{\mathrm{a}}$ denote the equivalent trajectory at the inertia center of the S and A cluster, respectively, which can be obtained by CCCOI transformation as Eq. (6). Then, the relative displacement of $\delta _{\mathrm{s}}$ and $\delta _{\mathrm{a}}$, denoted by $\delta$, can be obtained by RM transformation as Eq. (7). Thus, the CCCOI-RM transformation is finished. The nonlinear characteristics of the dynamic system can be analyzed in phase plane of $\delta$ and $\dot{\delta }$. Emphatically, if the reducer is included in the system, the $\delta$ and M in Eq. (6) must be the transformed displacements and inertias as Eq. (8), where, i, $\delta ^{\prime }$, and $M^{\prime }$ are the transmission ratio, displacement and inertia at low speed stage, respectively.

$$\begin{aligned}&\left\{ {\begin{array}{l} \delta _\mathrm{s} ={\sum _{i\in S} {M_i \delta _i } }/{\sum _{i\in S} {M_i } }\\ \delta _\mathrm{a} ={\sum _{j\in A} {M_j \delta _j } }/{\sum _{j\in A} {M_j } }\\ \end{array}} \right. \end{aligned}$$

(6)

$$\begin{aligned}&\delta =\delta _\mathrm{s} -\delta _\mathrm{a} \end{aligned}$$

(7)

$$\begin{aligned}&\left\{ {\begin{array}{l} \delta = i{\delta }' \\ M={M}'/ i^{2} \\ \end{array}} \right. \end{aligned}$$

(8)

Fig. 5

Trajectories of the nonlinear dynamic system

In this study, the gear meshing is main cause of nonlinearity of the gear-motor system, so the generalized displacements before and after the gear meshing are separated in two cluster, that is, the $\theta _{\mathrm{m}}$ and $\theta _{1}$ are classified in S cluster, while the $\theta _{2}$ and $\theta _{l}$ are classified in A cluster. Therefore, the trajectory after dimension reduction ($\delta$) of the model in Sect. 2 can be obtained by CCCOI-RM transformation.

3.2 Step 3: definition of the stability margin

The phase orbits of the gear-motor system for different load rotational inertias ($J_{\mathrm{l}}$) are shown in Fig. 6. Two focal points ($O_{1}$ and $O_{2}$) emerge in Fig. 6a, which are corresponding to the meshing stiffness zones of single-pair and double-pair mesh, respectively. When the meshing stiffness is single-pair meshing stiffness, the phase orbit attenuates around $O_{1}$. When the meshing stiffness is double-pair meshing stiffness, the phase orbit attenuates around $O_{2}$. The phase orbit changes to attenuates around from one focal point to another focal point when the meshing stiffness alternates.

In Fig. 6a and b, the phase orbit has several intersection points in the right part of the phase diagram. As the load rotational inertia increases, if the alteration of meshing stiffness from single-pair to double-pair mesh emerges in point A ($A^{\prime }$ in Fig. 6c), the phase orbit has only one intersection point in the right part of the phase diagram, as shown in Fig. 6c, which is a critical condition. As the load rotational inertia continues increasing, the phase orbits also have only one intersection point in the right part of the phase diagram, as shown in Fig. 6d and e. If the alteration of meshing stiffness from single-pair to double-pair mesh emerges in point C ($C^{\prime }$ in Fig. 6g), the phase orbit has no intersection point in the right part of the phase diagram, as shown in Fig. 6g, which is a critical condition. As the load rotational inertia continues increasing, the phase orbit has no intersection point in the right part of the phase diagram either, as shown in Fig. 6h.

As the load rotational inertia increases, if the alteration of meshing stiffness from double-pair to single-pair mesh emerges in point B ($B^{\prime }$ in Fig. 6e), the phase orbit has only one intersection point in the left part of the phase diagram, as shown in Fig. 6e, which is a critical condition. As the load rotational inertia continues increasing, the phase orbits also have only one intersection point in the left part of the phase diagram, as shown in Fig. 6f and g. If the alteration of meshing stiffness from double-pair to single-pair mesh emerges in point D ($D^{\prime }$ in Fig. 6i), the phase orbit has no intersection point in the right part of the phase diagram, as shown in Fig. 6i, which is a critical condition. The intersection points in the both left and right parts disappear in Fig. 6i. As the load rotational inertia continues increasing, the phase orbit has no intersection point as shown in Fig. 6j.

Fig. 6

Phase orbits of the gear-motor system at different values of load rotational inertia ($J_{\mathrm{l}}$)

From above analysis, four critical conditions can be found as shown in Fig. 6c, e, g and i. The stability margins need to be defined to search these critical conditions. The phase orbits of the gear-motor system when $J_{\mathrm{l}} =3\times 10^{-4}\ \hbox {kg m}^{2}$ is given in Fig. 7a. In Fig. 7, points 1 – 5 are the extreme value of vibrating velocity, where the system kinetic energy reaches the extreme value, while the potential energy reaches 0, which is similar to spring oscillator. Therefore, the system energy is equal to kinetic energy ($\mathrm{mv}^{2}/2$, $\mathrm{m}$ is mass and $\mathrm{v}$ is speed) at points 1 – 5. Because just the ratio of energy is used in the definition stability in Eq. (9), the $\mathrm{m}/2$ can be ignored in the expression of system energy. Therefore, the system energy can be represents by the square of velocity at points 1 – 5, that is, $E_{1-5}=(\mathrm{v}_{1-5})^{2}$, where, the symbol $E_{1-5}$ and $\mathrm{v}_{1-5}$ are system energy and vibrating speed at point 1 – 5, respectively, $\mathrm{v}_{1-5} =\dot{\delta }_{1-5}$ in Fig. 7.

Fig. 7

The phase orbit of the gear-motor system (a) and fitting curve of the system energy when $J_{\mathrm{l}} =3 \times 10^{-4}\ \hbox {kg m}^{2}$

Fig. 8

The phase orbit of the gear-motor system when $J_{\mathrm{l}}=1.351\times 10^{-2}\ \hbox {kg m}^{2}$

In the damped vibration system, the system energy attenuates as exponential function, which is fitted by points 1 – 5 as Fig. 7b. In Fig. 7b, the time of point 1 is regarded as the starting point of time axis, and time of point 2 – 4 on time axis is the relative time to point 1. The system energy at A, C, and K can be obtained with the fitting formula. K is the point where meshing stiffness alters from single-pair to double-pair mesh. A and C are the points where the velocity is zero. If K coincides with A, the phase orbit has only one intersection point in the right part of the phase diagram, and the stability margin is denoted as $\eta _{A}$ for this critical condition. If K coincides with C, the phase orbit has no intersection point in the right part of the phase diagram, and the stability margin is denoted as $\eta _{C}$ for this critical condition. It can be considered that if the energy of point K is equal to point A or C, the critical conditions appear. Therefore, the stability margins are defined as Eq. (9). Similarly, the stability margins for points B and D.

$$\begin{aligned} \eta _A= & {} 1-\frac{E_K }{E_A}\nonumber \\ \eta _C= & {} 1-\frac{E_K }{E_C} \end{aligned}$$

(9)

where $E_{K}$, $E_{A}$, and $E_{C}$ are the system energy at point K, A, and C, respectively. $\eta _{A}$ or $\eta _{C}$ reflect the difficulty degree of change from K to A or C, respectively, in another words, the amount of energy injected to system to make K move to A or C. The larger $\eta _{A}$ or $\eta _{C}$ is, the more difficult change from K to A or C is, and the more energy need to be injected to system, that is, the more stable the system is.

When the load rotational inertia ($J_{\mathrm{l}}$) is large, for example, $J_{\mathrm{l}}=1.351\times 10^{-2}\ \hbox {kg m}^{2}$, some special conditions will be encountered for calculation of stability margins as shown in Fig. 8. Point O is corresponding to K in Fig. 7, where the meshing stiffness alters of from single-pair to double-pair mesh. Point P is corresponding to L in Fig. 7, where the meshing stiffness alters of from double-pair to single-pair mesh. Point Q is corresponding to D in Fig. 7, where the angular velocity reaches 0. The point P is ahead of Q in time in Fig. 8, while, the point L is behind D in time correspondingly in Fig. 7. The definition of stability margins in Eq. (9) is not suitable herein. Therefore, the absolute value of the angular velocity at point R, where the angular velocity reaches the extreme after passing through zero value, is defined as the stability margin, as shown in Eq. (10). When the stability margin $\eta _{R}$ reaches zero, the critical condition appears.

$$\begin{aligned} \eta _R =|{\dot{\delta }}_{\mathrm{R}}| \end{aligned}$$

(10)

3.3 Step 4: obtaining the critical value

The procedure to obtain the critical value is shown as the flow chart in Fig. 9. Firstly, 2 – 3 initial parameters are chosen to be substitute into the dynamic model for simulation. Then, the dimensions of the simulation results are reduced for calculation of the stability margins. Next, if stability margin is equal to zero, the critical value is output, otherwise, the next parameter value is obtained by the interpolation based on the pre-existing parameter and corresponding stability values, as illustrated in Fig. 10, and substituted into the dynamic model for next dynamic simulation. In Fig. 10, points 1 – 3 are the pre-existing parameter and corresponding stability values, while point 4 is the next parameter value obtained by interpolation under the condition that the corresponding stability margin is zero.

Fig. 9

The flow chart of the procedure to obtain the critical value

Fig. 10

illustration of obtaining the next parameter value by interpolation based on the pre-existing value and the corresponding stability

With the method above, the critical values of load inertia $J_{\mathrm{l}}$, where the stability margins $\eta _{A}$, $\eta _{B}$, $\eta _{C}$, and $\eta _{D}$ are equal to zero, can be obtained, which are $6.605 \times 10 ^{-4}$, $2.653 \times 10^{-3}$, $3.622 \times 10 ^{-3}$, and $1.52 \times 10^{-2}\ \hbox {kg m}^{2}$, respectively. The search process for the critical values is presented in Table 2. The variation trends of stability margins with load rotational inertia are given in Fig. 11. It should be noted that, when the load rotational inertia is larger, especially near the critical value, as the condition shown in Fig. 8, the stability margin should be calculated by Eq. (10). Therefore, the curve is not continuous near the critical value as the dashed line show in Fig. 11d. The parameter of load rotational inertia is divided into several intervals by these critical values, and the representative phase diagrams of each interval are given in Fig. 6.

Table 2 The search process for the critical values

Fig. 11

The variation trends of stability margins with load rotational inertia

4 Nonlinear dynamic analysis of the motor-gear system

As the above analysis, the parameter of load rotational inertia is divided into several intervals by these critical values, that is, $J_{\mathrm{l}}<6.605\times 10^{-4}\ \hbox {kg}\, \hbox {m}^{2}$, $6.605\times 10^{-4}\ \hbox {kg}\,\hbox {m}^{2}<J_{\mathrm{l}}<2.653\times 10^{-3} \ \hbox {kg}\,\hbox {m}^{2}$, $2.653\times 10^{-3} \ \hbox {kg}\,\hbox {m}^{2}<J_{\mathrm{l}}<3.622\times 10^{-3} \ \hbox {kg}\,\hbox {m}^{2}$, $3.622\times 10^{-3} \ \hbox {kg}\,\hbox {m}^{2}<J_{\mathrm{l}}<1.52\times 10^{-2} \ \hbox {kg}\,\hbox {m}^{2}$, and $J_{\mathrm{l}}> 1.52\times 10^{-2} \ \hbox {kg}\,\hbox {m}^{2}$. Therefore, the nonlinear dynamic characteristics will be analyzed in each interval. In the interval of $J_{\mathrm{l}}<6.605\times 10^{-4}\ \hbox {kg}\,\hbox {m}^{2}$, for example, $J_{\mathrm{l}}=5\times 10^{-5}\ \hbox {kg}\,\hbox {m}^{2}$, the dynamic meshing force in time (a) and frequency (b) domain is given in Fig. 12. The frequency spectrum contains the components of the meshing frequency ($f_{\mathrm{m}}$) and its all kinds of multiplication, that is, the vibration energy spread among all the components of meshing frequency and its multiplication.

Fig. 12

The dynamic meshing force in time (a) and frequency (b) domain when $J_{\mathrm{l}}=5\times 10^{-5}\ \hbox {kg}\, \hbox {m}^{2}$

In the interval of $6.605 \times 10^{-4}\ \hbox {kg} \, \hbox {m}^{2}< J_{\mathrm{l}} <2.653 \times 10^{-3} \ \hbox {kg}\,\hbox {m}^{2}$, for example, $J_{\mathrm{l}}=1.443 \times 10 ^{-3}\ \hbox {kg}\,\hbox {m}^{2}$, The dynamic meshing force in time (a) and frequency (b) domain is given in Fig. 13. The frequency spectrum contains the components of the meshing frequency and its multiplications, and the amplitudes of $4f_{\mathrm{m}}$ and its nearby frequency multiplications are relatively higher, that is, the vibration energy spread among all the components of meshing frequency, but mainly concentrates on the frequency components of $4f_{\mathrm{m}}$ and its nearby multiplications. In the interval of $2.653 \times 10 ^{-3}\ \hbox {kg}\,\hbox {m}^{2}<J_{\mathrm{l}}<3.622\times 10^{-3}\ \hbox {kg}\,\hbox {m}^{2}$, for example, $J_{\mathrm{l}}=2.783 \times 10^{-3}\ \hbox {kg}\,\hbox {m}^{2}$, the dynamic meshing force in time (a) and frequency (b) domain is given in Fig. 14. The frequency components and energy distribution is similar with that in Fig. 14.

Fig. 13

The dynamic meshing force in time (a) and frequency (b) domain when $J_{\mathrm{l}}=1.443 \times 10^{-3}\ \hbox {kg}\, \hbox {m}^{2}$

Fig. 14

The dynamic meshing force in time (a) and frequency (b) domain when $J_{\mathrm{l}}=2.738 \times 10^{-3}\ \hbox {kg}\, \hbox {m}^{2}$

In the interval of $3.622\times 10^{-3} \ \hbox {kg}\,\hbox {m}^{2}<J_{\mathrm{l}}<1.52\times 10^{-2} \ \hbox {kg}\,\hbox {m}^{2}$, for example, $J_{\mathrm{l}}=7.499 \times 10^{-3} \ \hbox {kg}\,\hbox {m}^{2}$, the dynamic meshing force in time (a) and frequency (b) domain is given in Fig. 15. The frequency spectrum contains the components of the meshing frequency and multiplications, and the amplitude of $2f_{\mathrm{m}}$ is relatively higher, that is, the vibration energy mainly concentrates on the frequency components of $2f_{\mathrm{m}}$. In the interval of $J_{\mathrm{l}}>1.52 \times 10 ^{-2}\ \hbox {kg} \, \hbox {m}^{2}$, for example, $J_{\mathrm{l}}=3.589 \times 10^{-2}\ \hbox {kg} \, \hbox {m}^{2}$, the dynamic meshing force in time (a) and frequency (b) domain is given in Fig. 16. The frequency spectrum contains the components of the meshing frequency and multiplications, and the amplitude of $f_{\mathrm{m}}$ is relatively higher, that is, the vibration energy mainly concentrates on the frequency components of $f_{\mathrm{m}}$.

Fig. 15

The dynamic meshing force in time (a) and frequency (b) domain when $J_{\mathrm{l}}=7.499 \times 10^{-3}\ \hbox {kg}\,\hbox {m}^{2}$

Fig. 16

The dynamic meshing force in time (a) and frequency (b) domain when $J_{\mathrm{l}}=3.589 \times 10^{-2}\ \hbox {kg}\,\hbox {m}^{2}$

From the above analysis, it is found that the fluctuation of dynamic meshing force is lower and the fluctuation energy is scattered among the frequency components, when $J_{\mathrm{l}}<3.622 \times 10^{-3}\ \hbox {kg}\,\hbox {m}^{2}$, while, the fluctuation of dynamic meshing force is higher and the fluctuation energy are concentrated the frequency components of $2f_{\mathrm{m}}$ and $f_{\mathrm{m}}$, when $3.622 \times 10^{-3}\ \hbox {kg}\, \hbox {m}^{2}<J_{\mathrm{l}}<1.52 \times 10^{-2}\ \hbox {kg}\,\hbox {m}^{2}$ and $J_{\mathrm{l}} >1.52 \times 10^{-2}\ \hbox {kg}\,\hbox {m}^{2}$, respectively. The meshing forces are the main internal excitation sources of motor-gear system, so, the system resonance trends to appear in these two intervals, when the frequency components of meshing forces are low-order meshing frequencies.

In the interval of $3.622 \times 10 ^{-3}\ \hbox {kg}\,\hbox {m}^{2}<J_{\mathrm{l}}<1.52\times 10^{-2}\ \hbox {kg}\,\hbox {m}^{2}$, the phase orbit has only one intersection point, similar to the phase orbit of the double period motion. The dynamic meshing force is excitation source with the main frequency components of $2f_{\mathrm{m}}$ (1240.6 Hz). According to the linear vibration theory, the resonance emerges if the excitation frequency is equal to the natural frequency. However, the motor system is nonlinear dynamic system with time-varying meshing stiffness parameters. Therefore, the natural frequencies are calculated with single-pair meshing stiffness, mean meshing stiffness, and double-pair meshing stiffness, respectively, and then, the corresponding values of $J_{\mathrm{l}}$ leading to the natural frequency of 1240.6 Hz can be obtained as shown in Table 3. The phase orbits and dynamic meshing forces for $J_{\mathrm{l}} =0.00485$, 0.00762, $0.00910\ \hbox {kg}\,\hbox {m}^{2}$ are given in Fig 17. The phase orbits of these three values are similar as shown in Fig. 17a. In Fig. 17b, the amplitude of dynamic meshing force is largest for $0.00910\ \hbox {kg}\, \hbox {m}^{2}$ which is obtained with double-pair meshing stiffness. The tooth separation also appears, that is, the dynamic meshing force reaches zero, which reflects that the system resonance occurs.

Table 3 The values of $J_{\mathrm{l}}$ leading the natural frequency of 1240.6 Hz

Fig. 17

The phase orbits (a) and dynamic meshing forces (b) for different value of $J_{\mathrm{l}}$ leading the natural frequency of 1240.6 Hz

In the interval of $J_{\mathrm{l}}>1.52 \times 10^{-2}\ \hbox {kg}\,\hbox {m}^{2}$, the phase orbit has no intersection point, similar to the phase orbit of the period motion. The dynamic meshing force is excitation source with the main frequency components of $f_{\mathrm{m}}$ (620.3 Hz). The values of $J_{\mathrm{l}}$ leading to the natural frequency of 620.3 Hz are given in Table 4, when single-pair meshing stiffness, mean meshing stiffness, and double-pair meshing stiffness are used, respectively. The phase orbits and dynamic meshing forces for $J_{\mathrm{l}}=0.03835$, 0.1243, $0.3525\ \hbox {kg}\, \hbox {m}^{2}$ are given in Fig 18. The phase orbits of these values are similar as shown in Fig. 18a. In Fig. 17b, the dynamic meshing forces for $J_{\mathrm{l}}=0.03835$, $0.1243\ \hbox {kg}\,\hbox {m}^{2}$ all reached zero, and the amplitude of dynamic meshing force for $0.1243\ \hbox {kg}\, \hbox {m}^{2}$ is larger. Though $J_{\mathrm{l}}=0.03835$, $0.1243\ \hbox {kg}\, \hbox {m}^{2}$ are obtained by setting the natural frequency as 620.3 Hz when the single-pair and mean meshing stiffness are used, respectively, the amplitudes of dynamic meshing force for these two values are smaller than $0.01\ \hbox {kg}\, \hbox {m}^{2}$ which is obtained by simulating trial to get the maximal amplitude of dynamic meshing force.

Table 4 The values of $J_{\mathrm{l}}$ leading the natural frequency of 620.3 Hz

Fig. 18

The phase orbits (a) and dynamic meshing forces (b) for different value of $J_{\mathrm{l}}$ leading the natural frequency of 620.3 Hz

In a summary, when the phase orbit is similar to that of the period doubling motion, the main frequency component of the dynamic meshing force is $2f_{\mathrm{m}}$, where $f_{\mathrm{m}}$ is meshing frequency, while, when the phase orbit is similar to that of the period motion, the main frequency component of the dynamic meshing force is $f_{\mathrm{m}}$. The dynamic meshing force can act as excitation source, causing system resonance. The parameters values obtained with single-pair, mean, and double-pair meshing stiffness should all be paid attention to when the system resonance parameters are searching.

5 Conclusion

• (1) A kind of trajectory-based stability preserving dimension reduction (TSPDR) methodology is proposed to investigate nonlinear dynamic characteristics of the gear-motor system. In the TSPDR methodology herein, the CCCOI-RM is chosen and the stability margins are specially defined for distinguishing the stable motion modes of the motor-gear system, to make the TSPDR methodology be used in the nonlinear analysis of the gear-motor system.

• (2) Based on the proposed TSPDR methodology, the critical values are obtained for alteration of different motion modes, and the nonlinear characteristics of each motion modes are analyzed. When the phase orbit is similar to that of the period doubling motion, the main frequency component of the dynamic meshing force is $2f_{\mathrm{m}}$, where $f_{\mathrm{m}}$ is meshing frequency, while, when the phase orbit is similar to that of the period motion, the main frequency component of the dynamic meshing force is $f_{\mathrm{m}}$. The fluctuation of dynamic meshing force is lower and the fluctuation energy are scattered among the frequency components, if the phase orbits are other shapes in this investigation.

• (3) Combined with modal analysis, the relationship between the stability and resonance of the gear-motor system is revealed. The dynamic meshing force can act as excitation source, causing system resonance. However, the motor-gear system is different from the generic linear system in the aspect that the resonance may happen at the natural frequency calculated with single-pair, mean, and double-pair meshing stiffness and its neighboring frequency. Therefore, all the parameters values obtained with single-pair, mean, and double-pair meshing stiffness should be paid attention to when the system resonance parameters are searched.