Introduction

The high-speed rotating machines are widely used in modern industries such as aero-engines, generators and electric motors. The performance requirement has been highly improved because the rotating machines often operate over the critical speed. The dual-rotor structure for the rotating machines appears due to its higher degree of reliability and the better dynamic characteristics [1]. The inter-shaft bearings are applied to minimize the shaft deformation caused by rotor unbalances and aircraft maneuvers flight in the dual-rotor system [2]. Some nonlinear dynamic phenomena, such as jump phenomenon [3] and resonance hysteresis phenomenon [4], may occur because of the nonlinearity of the inter-shaft bearing. It is very necessary to investigate on the mechanism of these nonlinear phenomena by analytic method.

There are some scholars have researched on the dynamic characteristic of the dual-rotor system in the past few decades. Hibner [5] used a unique transfer-matrix method to predict the vibration response of a dual-rotor aero-engine with nonlinear viscous damping. Based on which, Gupta et al. [6] developed an extended-transfer matrix procedure to acquire the unbalance responses of a dual rotor test rig. Gao et al. [7] presented a dynamic model for the inter-shaft bearing with a local defect and studied the nonlinear dynamic characteristics of a dual-rotor system affected by the local defect. A linear finite element (FE) model was proposed to predict the unbalance responses and compared with the experimental results of a dual rotor rig by Guskov et al. [1]. The FE method [8], as a highly effective method to establish the mathematical model for a complex multi-rotor system, has been widely used in recent years. Yang et al. [9] also established a FE dynamic model for the dual-rotor system considering fixed point rubbing, and carried out an experiment on a dual-rotor test rig to verify the effectiveness of the dynamic model. The blade-casing rubbing of a whole aero-engine was taken into consideration and a FE model of a dual-rotor-blade-casing (DRBC) system was put forward by Wang et al. [10, 11]. Lu et al. [12] set up a FE model of a dual-rotor system with a breathing transverse crack in HP hollow shaft to discuss the effect of the crack depth and location on the nonlinear dynamic response. The researches above all take numerical method to calculate the vibration response of the dynamic model, none of them have investigated on the mechanism of the nonlinear phenomena by analytic method.

There does exist some literatures about the analytic solution for the dual-rotor system. The analytic expressions for critical speeds and mass unbalance responses in a 2DOF simple model for the dual-rotor system with considering the gyroscopic effect was obtained by Ferraris et al. [13]. Sun et al. [14, 15] presented the dynamic equation of a dual-rotor system with rub-impact and applied the method, named as multi-harmonic balance-alternating frequency/time domain, to study the steady-state response characteristics. The inter-shaft bearings in above literatures are simplified as a linear elastic spring, which means none of them consider the nonlinearities of the inter-shaft bearings and the nonlinear phenomena.

The motivation of this paper is to investigate the mechanism of the nonlinear phenomena in a simple dual-rotor system at the case of primary resonance. Different from the numerical method, the analytic method, i.e., multiple scales method, is utilized to obtain the stable solutions and the unstable solutions of the dynamic equations, which enables us to make the mechanism of the nonlinear phenomena clear. It is very difficult to directly solve the 4DOF dynamic equation of the dual-rotor system by analytic method because of the nonlinearity of the inter-shaft bearing. Since the symmetry of the HP and LP rotors in vertical and horizontal directions, the 4DOF dynamic equation could be transformed into a 2DOF equation in complex coordinate, then the multiple scales method can be employed to solve the stable solutions and unstable solutions for the dynamic equations of dual-rotor system. Based on which, the induced mechanism of the jump phenomenon and the resonance hysteresis phenomenon can be revealed. The nonlinear stiffness of the inter-shaft bearing will promote these nonlinear phenomena while the linear stiffness of the inter-shaft bearing and the damping of the system will suppress them. The nonlinear mechanism obtained in this paper help us find out the reason of the nonlinear phenomena, which is beyond the reach of the numerical method.

Governing Equation of Motion

Dual-Rotor System

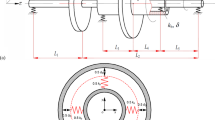
Figure 1 shows a schematic diagram of a simple dual-rotor and an inter-shaft bearing system [7, 14]. The simplified dual-rotor system, obtained through the simplifying process for dynamic model [16], is composed of a higher pressure (HP) rotor, a lower pressure (LP) rotor and an inter-shaft bearing. Each rotor contains a disk and a shaft. Both ends of the LP rotor and the left end of the HP rotor are supported by simple supports in both horizontal and vertical directions, while the right end of the HP rotor is connected with the LP rotor by the inter-shaft bearing, which is seen as a nonlinear elastic spring contains a linear stiffness and a nonlinear stiffness. In which, k1, c1, ω1 are the stiffness, the damping, and the rotation speed of the LP rotor, respectively; k2, c2, ω2 are the stiffness, the damping, and the rotation speed of the HP rotor, respectively; O1, O2 are the geometric centers of LP and HP disks; li (i = 1–4) are the lengths of the shafts; l is the length of the LP shaft.

Fig. 1
figure 1

Schematic diagram of a simplified dual-rotor and an inter-shaft bearing system

Full size image

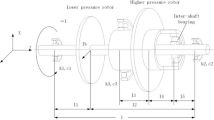
The vibration modal shape of the simplified dual-rotor system is shown in Fig. 2, the LP shaft is more slender than the HP shaft. Base on which, the LP rotor can be assumed as a flexible rotor while the HP rotor can be assumed as a rigid rotor. Where the displacements of the LP disk geometric center (O1) in the vertical and horizontal directions are marked as x1 and y1 respectively; the displacements of the HP disk geometric center (O2) in the vertical and horizontal directions are marked as x2 and y2 respectively. Besides, the rotational angles of LP disk around the x-axis and the y-axis are marked as θx, θy respectively; the rotational angles of HP disk around the x-axis and the y-axis are marked as φx, φy respectively. The rotational angles θx, θy and φx, φy can be represented by the displacements x1, y1 and x2, y2 respectively, if the modal shape functions of the LP and HP shafts are assumed as specific functions with mathematical expressions. Base on which, the 4DOF dynamic equations of the simplified dual-rotor system can be obtained.

Fig. 2
figure 2

The vibration modal shape of the simplified dual-rotor system

Full size image

The LP and HP shafts are regarded as Euler beams, which ignores shear deformation and torsional deformation. Moreover, the assumed mode method (AAM) is applied to attain the governing equation of motion of the dual-rotor system. The LP shaft is a slender one, thus, assume the modal shape of the LP shaft is a sine function as

$$\, f_{1} \left( {z_{1} } \right) = \sin \left( {\pi \frac{{z_{1} }}{l}} \right), \, z_{1} \in \left[ {0,l} \right].$$
(1)

According to Eq. (1), the vertical and horizontal displacements of the LP shaft at z1 can be expressed as

$$u_{1} \left( {z_{1} , \, t} \right) = \frac{{f_{1} \left( {z_{1} } \right)}}{{f_{1} \left( {l_{1} } \right)}}x_{1} \left( t \right) = \frac{{f_{1} \left( {z_{1} } \right)}}{{f_{1} \left( {l_{1} } \right)}}x_{1} ,$$
$$v_{1} \left( {z_{1} , \, t} \right) = \frac{{f_{1} \left( {z_{1} } \right)}}{{f_{1} \left( {l_{1} } \right)}}y_{1} \left( t \right) = \frac{{f_{1} \left( {z_{1} } \right)}}{{f_{1} \left( {l_{1} } \right)}}y_{1} .$$

Then the corresponding rotational angles of LP shaft around x and y axes can be expressed as

$$\theta_{x} \left( {z_{1} , \, t} \right) \approx - \frac{{\partial v_{1} \left( {z_{1} , \, t} \right)}}{{\partial z_{1} }} = - h_{1} \left( {z_{1} } \right)y_{1} ,$$
$$\theta_{y} \left( {z_{1} , \, t} \right) \approx \frac{{\partial u_{1} \left( {z_{1} , \, t} \right)}}{{\partial z_{1} }} = h_{1} \left( {z_{1} } \right)x_{1} .$$

where \(h_{1} \left( {z_{1} } \right) = \frac{{{\text{d}}f_{1} \left( {z_{1} } \right)}}{{f_{1} \left( {l_{1} } \right){\text{d}}z_{1} }}\).

The kinetic energy of the LP shaft can be obtained as

$$\begin{aligned} T_{{{\text{s}}1}} & = \frac{{\rho_{1} \pi r_{1}^{2} }}{2}\int_{0}^{l} {\left( {\dot{u}_{1}^{2} + \dot{v}_{1}^{2} } \right){\text{d}}z_{1} } + \frac{{\rho_{1} I_{1} }}{2}\int_{0}^{l} {\left( {\dot{\theta }_{x}^{2} + \dot{\theta }_{y}^{2} } \right){\text{d}}z_{1} } + \rho_{1} I_{1} \int_{0}^{l} {\left( {\omega_{1}^{2} - 2\omega_{1} \theta_{x} \dot{\theta }_{y} } \right){\text{d}}z_{1} } \\ & = \frac{{\rho_{1} \pi r_{1}^{2} }}{{2f_{1}^{2} \left( {l_{1} } \right)}}\left( {\dot{x}_{1}^{2} + \dot{y}_{1}^{2} } \right)\int_{0}^{l} {f_{1}^{2} {\text{d}}z_{1} } + \frac{{\rho_{1} I_{1} }}{2}\left( {\dot{x}_{1}^{2} + \dot{y}_{1}^{2} } \right)\int_{0}^{l} {h_{1}^{2} {\text{d}}z_{1} } + \rho_{1} I_{1} \left( {\omega_{1}^{2} l + 2\omega_{1} \dot{x}_{1} y_{1} \int_{0}^{l} {h_{1}^{2} {\text{d}}z_{1} } } \right), \\ \end{aligned}$$
(2a)

where r1 and ρ1 are the radius and the density of the LP shaft, the LP shaft’s area moment of inertia is \(I_{1} { = }\frac{{\pi r_{1}^{4} }}{4}\).

The LP disk is fixed with the LP shaft at \(z_{1} = l_{1}\), thus, the kinetic energy of the LP disk can be expressed as

$$\begin{aligned} T_{{{\text{d}}1}} = \frac{1}{2}m_{1} \left[ {\dot{u}_{1}^{2} \left( {l_{1} } \right) + \dot{v}_{1}^{2} \left( {l_{1} } \right)} \right] + \frac{1}{2}J_{{{\text{d}}1}} \left[ {\dot{\theta }_{x}^{2} \left( {l_{1} } \right) + \dot{\theta }_{y}^{2} \left( {l_{1} } \right)} \right] + \frac{1}{2}J_{{{\text{p}}1}} \left[ {\omega_{1}^{2} - 2\omega_{1} \theta_{x} \left( {l_{1} } \right)\dot{\theta }_{y} \left( {l_{1} } \right)} \right] \\ = \frac{1}{2}m_{1} \left( {\dot{x}_{1}^{2} + \dot{y}_{1}^{2} } \right) + \frac{1}{2}J_{{{\text{d}}1}} h_{1}^{2} \left( {l_{1} } \right)\left( {\dot{x}_{1}^{2} + \dot{y}_{1}^{2} } \right) + \frac{1}{2}J_{{{\text{p}}1}} \left( {\omega_{1}^{2} + 2\omega_{1} h_{1}^{2} \left( {l_{1} } \right)\dot{x}_{1} y_{1} } \right), \\ \end{aligned}$$
(2b)

where m1 is the mass of the LP disk, Jp1 and Jd1 are the LP disk’s polar and diameter moment of inertia.

The HP shaft is a stubby shaft, thus, assume the modal shape of the HP shaft is

$$f_{2} \left( {z_{2} } \right) = z_{2} - l_{2} , \, z_{2} \in \left[ {l_{2} ,l_{4} } \right].$$
(3)

According to Eq. (3), the vertical and horizontal displacements of the HP shaft at z2 can be expressed as

$$u_{2} \left( {z_{2} , \, t} \right) = \frac{{f_{2} \left( {z_{2} } \right)}}{{f_{2} \left( {l_{3} } \right)}}x_{2} \left( t \right) = \frac{{f_{2} \left( {z_{2} } \right)}}{{f_{2} \left( {l_{3} } \right)}}x_{2} ,$$
$$v_{2} \left( {z_{2} , \, t} \right) = \frac{{f_{2} \left( {z_{2} } \right)}}{{f_{2} \left( {l_{3} } \right)}}y_{2} \left( t \right) = \frac{{f_{2} \left( {z_{2} } \right)}}{{f_{2} \left( {l_{3} } \right)}}y_{2} .$$

Then the corresponding rotational angles of HP shaft around x and y axes can be expressed as

$$\varphi_{x} \left( {z_{2} , \, t} \right) \approx - \frac{{\partial v_{2} \left( {z_{2} , \, t} \right)}}{{\partial z_{2} }} = - \;h_{2} \left( {z_{2} } \right)y_{2} ,$$
$$\varphi_{y} \left( {z_{2} , \, t} \right) \approx \frac{{\partial u_{2} \left( {z_{2} , \, t} \right)}}{{\partial z_{2} }} = h_{2} \left( {z_{2} } \right)x_{2} .$$

where \(h_{2} \left( {z_{2} } \right) = \frac{{df_{2} \left( {z_{2} } \right)}}{{f_{2} \left( {l_{3} } \right)dz_{2} }} = \frac{1}{{l_{3} - l_{2} }}\).

The kinetic energy of the HP shaft can be obtained as

$$\begin{aligned} T_{\text{s2}} = \frac{{\rho_{2} \pi \left( {r_{3}^{2} - r_{2}^{2} } \right)}}{2}\int_{{l_{2} }}^{{l_{4} }} {\left( {\dot{u}_{2}^{2} + \dot{v}_{2}^{2} } \right){\text{d}}z_{2} } + \frac{{\rho_{2} I_{2} }}{2}\int_{{l_{2} }}^{{l_{4} }} {\left( {\dot{\varphi }_{x}^{2} + \dot{\varphi }_{y}^{2} } \right){\text{d}}z_{2} } + \rho_{2} I_{2} \int_{{l_{2} }}^{{l_{4} }} {\left( {\omega_{2}^{2} - 2\omega_{2} \varphi_{x} \dot{\varphi }_{y} } \right){\text{d}}z_{2} } \\ = \frac{{\rho_{2} \pi \left( {r_{3}^{2} - r_{2}^{2} } \right)}}{{2f_{2}^{2} \left( {l_{3} } \right)}}\left( {\dot{x}_{2}^{2} + \dot{y}_{2}^{2} } \right)\int_{{l_{2} }}^{{l_{4} }} {f_{2}^{2} {\text{d}}z_{2} } + \frac{{\rho_{2} I_{2} }}{2}\left( {\dot{x}_{2}^{2} + \dot{y}_{2}^{2} } \right)\int_{{l_{2} }}^{{l_{4} }} {h_{2}^{2} {\text{d}}z_{2} } + \rho_{2} I_{2} \left[ {\omega_{2}^{2} \left( {l_{4} - l_{2} } \right) + 2\omega_{2} \dot{x}_{2} y_{2} \int_{{l_{2} }}^{{l_{4} }} {h_{2}^{2} {\text{d}}z_{2} } } \right], \\ \end{aligned}$$
(4a)

where r2, r3 and ρ2 are the inner and outer radiuses, and the density of the HP shaft (hollow shaft), the HP shaft’s area moment of inertia is \(I_{2} { = }\frac{{\pi \left( {r_{3}^{4} - r_{2}^{4} } \right)}}{4}\).

The HP disk is fixed with the HP shaft at \(z_{2} = l_{3}\), thus, the kinetic energy of the HP disk can be expressed as

$$\begin{aligned} T_{\text{d2}} = \frac{1}{2}m_{2} \left[ {\dot{u}_{2}^{2} \left( {l_{3} } \right) + \dot{v}_{2}^{2} \left( {l_{3} } \right)} \right] + \frac{1}{2}J_{\text{d2}} \left( {\dot{\varphi }_{x}^{2} \left( {l_{3} } \right) + \dot{\varphi }_{y}^{2} \left( {l_{3} } \right)} \right) + \frac{1}{2}J_{\text{p2}} \left( {\omega_{2}^{2} - 2\omega_{2} \varphi_{x} \left( {l_{3} } \right)\dot{\varphi }_{y} \left( {l_{3} } \right)} \right) \\ = \frac{1}{2}m_{2} \left( {\dot{x}_{2}^{2} + \dot{y}_{2}^{2} } \right) + \frac{1}{2}J_{\text{d2}} h_{2}^{2} \left( {l_{3} } \right)\left( {\dot{x}_{2}^{2} + \dot{y}_{2}^{2} } \right) + \frac{1}{2}J_{\text{p2}} \left( {\omega_{2}^{2} + 2\omega_{2} h_{2}^{2} \left( {l_{3} } \right)\dot{x}_{2} y_{2} } \right), \\ \end{aligned}$$
(4b)

where m2 is the mass of the HP disk, Jp2 and Jd2 are the HP disk’s polar and diameter moment of inertia.

Therefore, the kinetic energy of the dual-rotor system can be expressed as

$$T = T_{\text{d1}} + T_{\text{s1}} + T_{\text{d2}} + T_{\text{s2}} .$$
(5)

The potential energy of the dual-rotor system can be expressed as

$$V = \frac{1}{2}k_{1} \left( {x_{1}^{2} + y_{1}^{2} } \right) + \frac{1}{2}k_{2} \left( {x_{2}^{2} + y_{2}^{2} } \right),$$
(6)

where k1 and k2 represent the stiffness coefficients of LP and HP shafts.

The Rayleigh’s dissipation energy of the dual-rotor system can be expressed as

$$D = \frac{1}{2}c_{1} \left( {\dot{x}_{ 1}^{2} + \dot{y}_{ 1}^{2} } \right) + \frac{1}{2}c_{2} \left( {\dot{x}_{ 2}^{2} + \dot{y}_{ 2}^{2} } \right),$$
(7)

where c1 and c2 represent damping coefficients of LP and HP shafts.

The generalized force virtual work of the dual-rotor system can be expressed as

$$\begin{aligned} \delta W & = m_{1} \omega_{1}^{2} e_{1} \cos \left( {\omega_{1} t} \right)\delta x_{1} + m_{1} \omega_{1}^{2} e_{1} \sin \left( {\omega_{1} t} \right)\delta y_{1} + m_{2} \omega_{2}^{2} e_{2} \cos \left( {\omega_{2} t} \right)\delta x_{2} + m_{2} \omega_{2}^{2} e_{2} \sin \left( {\omega_{2} t} \right)\delta y_{2} \\ & \;\;\;\; - \;F_{x} \left( {F_{1} \delta x_{ 1} - F_{2} \delta x_{ 2} } \right) - F_{y} \left( {F_{1} \delta y_{ 1} - F_{2} \delta y_{ 2} } \right) \\ \end{aligned} ,$$
(8)

where \(F_{1} = \frac{{f_{1} \left( {l_{4} } \right)}}{{f_{1} \left( {l_{1} } \right)}}\), \(F_{2} = \frac{{f_{2} \left( {l_{4} } \right)}}{{f_{2} \left( {l_{3} } \right)}}\); Fx and Fy are vertical and horizontal nonlinear contact forces of the inter-shaft bearing; e1 and e2 are unbalances of the LP and HP rotors; δ∙ (x1, y1, x2, y2) are the virtual displacement.

Nonlinear Contact Force of the Inter-Shaft Bearing

The inner race of the inter-shaft bearing is fixed with the LP shaft at \(z_{1} = l_{4}\), the vertical and horizontal displacements of the inner race can be expressed as

$$x_{\text{i}} = u_{1} \left( {l_{4} , \, t} \right) = F_{1} x_{1} ,\;\;\;y_{\text{i}} = v_{1} \left( {l_{4} , \, t} \right) = F_{1} y_{1} .$$

The outer race of the inter-shaft bearing is fixed with the HP shaft at \(z_{2} = l_{4}\), the vertical and horizontal displacements of the outer race can be expressed as

$$x_{\text{o}} = u_{2} \left( {l_{4} , \, t} \right) = F_{2} x_{2} ,\;\;\;y_{\text{o}} = v_{2} \left( {l_{4} , \, t} \right) = F_{2} y_{2} .$$

The inter-shaft bearing is considered as a nonlinear elastic spring, which contains a linear stiffness and a cubic nonlinear stiffness [17, 18]. The nonlinear restoring force of the inter-shaft bearing can be expressed as

$$\begin{aligned} F_{x} = k_{\text{s}} \left( {x_{\text{i}} - x_{\text{o}} } \right) + k_{\text{n}} \left[ {\left( {x_{\text{i}} - x_{\text{o}} } \right)^{3} - 3\left( {x_{\text{i}} - x_{\text{o}} } \right)\left( {y_{\text{i}} - y_{\text{o}} } \right)^{2} } \right] \\ = k_{\text{s}} \left( {F_{1} x_{ 1} - F_{2} x_{ 2} } \right) + k_{\text{n}} \left[ {\left( {F_{1} x_{ 1} - F_{2} x_{ 2} } \right)^{3} - 3\left( {F_{1} x_{ 1} - F_{2} x_{ 2} } \right)\left( {F_{1} y_{ 1} - F_{2} y_{ 2} } \right)^{2} } \right], \\ \end{aligned}$$
(9a)
$$\begin{aligned} F_{y} = k_{\text{s}} \left( {y_{\text{i}} - y_{\text{o}} } \right) + k_{\text{n}} \left[ {\left( {y_{\text{i}} - y_{\text{o}} } \right)^{3} - 3\left( {y_{\text{i}} - y_{\text{o}} } \right)\left( {x_{\text{i}} - x_{\text{o}} } \right)^{2} } \right] \\ = k_{\text{s}} \left( {F_{1} y_{ 1} - F_{2} y_{ 2} } \right) + k_{\text{n}} \left[ {\left( {F_{1} y_{ 1} - F_{2} y_{ 2} } \right)^{3} - 3\left( {F_{1} y_{ 1} - F_{2} y_{ 2} } \right)\left( {F_{1} x_{ 1} - F_{2} x_{ 2} } \right)^{2} } \right], \\ \end{aligned}$$
(9b)

where ks and kn are the linear and nonlinear stiffness of the inter-shaft bearing.

The Governing Equation of Motion

Substitute Eqs. (5)–(8) into the Lagrange’s equation of the second kind, the governing equation of motion [12, 19] with 4DOF can be derived as

$$M_{1} \ddot{x}_{1} + c_{1} \dot{x}_{1} + \omega_{1} {\text{g}}_{1} \dot{y}_{1} + k_{1} x_{1} = m_{1} \omega_{1}^{2} e_{1} \cos \omega_{1} t - F_{1} F_{x} ,$$
(10a)
$$M_{1} \ddot{y}_{1} + c_{1} \dot{y}_{1} - \omega_{1} g_{1} \dot{x}_{1} + k_{1} y_{1} = m_{1} \omega_{1}^{2} e_{1} \sin \omega_{1} t - F_{1} F_{y} ,$$
(10b)
$$M_{2} \ddot{x}_{2} + c_{2} \dot{x}_{2} + \omega_{2} g_{2} \dot{y}_{2} + k_{2} x_{2} = m_{2} \omega_{2}^{2} e_{2} \cos \omega_{2} t + F_{2} F_{x} ,$$
(10c)
$$M_{2} \ddot{y}_{2} + c_{2} \dot{y}_{2} - \omega_{2} g_{2} \dot{x}_{2} + k_{2} y_{2} = m_{2} \omega_{2}^{2} e_{2} \sin \omega_{2} t + F_{2} F_{y} ,$$
(10d)

where the gyro effect is reflected in the parameters M1, M2, g1, g2, and the calculation formulas are shown as follows

$$M_{1} = m_{1} + H_{1}^{2} J_{{{\text{d}}1}} + \frac{{\rho_{1} \pi r_{1}^{2} }}{{f_{1}^{2} \left( {l_{1} } \right)}}\int_{0}^{l} {f_{1}^{2} {\text{d}}z_{1} } + \rho_{1} I_{1} \int_{0}^{l} {h_{1}^{2} {\text{d}}z_{1} } ,$$
$$M_{2} = m_{2} + H_{2}^{2} J_{{{\text{d}}2}} + \frac{{\rho_{2} \pi \left( {r_{3}^{2} - r_{2}^{2} } \right)}}{{f_{2}^{2} \left( {l_{3} } \right)}}\int_{{l_{2} }}^{{l_{4} }} {f_{2}^{2} {\text{d}}z_{2} } + \rho_{2} I_{2} \int_{{l_{2} }}^{{l_{4} }} {h_{2}^{2} {\text{d}}z_{2} } ,$$
$$g_{1} = H_{1}^{2} J_{{{\text{p}}1}} + 2\rho_{1} I_{1} \int_{0}^{l} {h_{1}^{2} {\text{d}}z_{1} } ,\;\;\;g_{2} = H_{2}^{2} J_{\text{p2}} + 2\rho_{2} I_{2} \int_{{l_{2} }}^{{l_{4} }} {h_{2}^{2} {\text{d}}z_{2} } .$$

where \(H_{1} = \frac{{{\text{d}}f_{1} \left( {l_{1} } \right)}}{{f_{1} \left( {l_{1} } \right){\text{d}}z}}\), \(H_{2} = \frac{1}{{l_{3} - l_{2} }}\).

The values of structure parameters [7, 20] for the simple dual-rotor system are given as follows:

$$\begin{aligned} m_{1} & = 97.37\;\;{\text{kg}},{\text{ }}J_{{p1}} = 3.6907\;\;{\text{kg}}\;{\text{m}}^{{\text{2}}} ,{\text{ }}J_{{d1}} = 1.8454\;\;{\text{kg}}\;{\text{m}}^{{\text{2}}} ,{\text{ }}m_{2} = 108.3\;{\text{kg}},{\text{ }}J_{{p2}} = 4.0114\;\;{\text{kg}}\;\;{\text{m}}^{2} ,{\text{ }}J_{{d2}} = 2.0060\;\;{\text{kg}}\;{\text{m}}^{2} ,{\text{ }} \\ k_{1} & = k_{2} = 8 \times 10^{7} \;\;{\text{N/m}},{\text{ }}c_{1} = c_{2} = 600\;\;{\text{N}}\;{\text{s/m}},{\text{ }}\rho _{1} = \rho _{2} = 7800\;\;{\text{kg/m}}^{3} ,{\text{ }}e_{1} = 1\;\;{{\upmu m}},{\text{ }}e_{2} = 3\;\;{{\upmu m}},{\text{ }} \\ l & = 1.5913\;\;{\text{m}},{\text{ }}l_{1} = 0.2250\;{\text{m}},{\text{ }}l_{2} = 0.3555\;\;{\text{m}},{\text{ }}l_{3} = 0.8675\;{\text{ m}},{\text{ }}l_{4} = 1.4918\;\;{\text{m}},{\text{ }} \\ r_{1} & = 20\;\;{\text{mm}},{\text{ }}r_{2} = 30\;{\text{mm, }}r_{3} = 35\;\;{\text{mm}},{\text{ }}\lambda = 1.2,{\text{ }}k_{{\text{s}}} = 1 \times 10^{9} \;{\text{N/m}},{\text{ }}k_{{\text{n}}} = 1 \times 10^{{23}} \;{\text{N/m}}^{3} . \\ \end{aligned}$$

Multiple Scales Solution

The Governing Equation Transferring

Compare Eqs. (10a) and (10b) carefully, it can be found that the two equations are very similar with each other, in which, the coefficients of the two equations are almost the same because of the symmetry of the LP rotors in horizontal and vertical directions. So it is the same with Eqs. (10c) and (10d) because of the symmetry of the HP rotors in horizontal and vertical directions. Therefore, the 4DOF equation in real coordinate can be transformed into a 2DOF equation in complex coordinate [21].

Let \(\tau = \omega_{ 1} t\), \(r_{1} = \frac{{x_{1} }}{{e_{1} }} + i\frac{{y_{1} }}{{e_{1} }}\), \(r_{2} = \frac{{x_{2} }}{{e_{1} }} + i\frac{{y_{2} }}{{e_{1} }}\), \(F_{\text{b}} = \frac{{F_{x} }}{{e_{1} }} + i\frac{{F_{y} }}{{e_{1} }}\), Eq. (10a–10d) are changed into

$$r^{\prime\prime}_{ 1} + \left( {C_{1} - iG_{1} } \right)r^{\prime}_{ 1} + \frac{{k_{1} }}{{M_{1} \omega_{1}^{2} }}r_{ 1} = E_{1} e^{i\tau } - \frac{{F_{1} }}{{M_{ 1} \omega_{1}^{2} }}F_{\text{b}} ,$$
(11a)
$$r^{\prime\prime}_{ 2} + \left( {C_{2} - iG_{2} } \right)r^{\prime}_{ 2} + \frac{{k_{2} }}{{M_{2} \omega_{1}^{2} }}r_{ 2} = \lambda^{2} E_{2} e^{i\lambda \tau } + \frac{{F_{2} }}{{M_{ 2} \omega_{1}^{2} }}F_{\text{b}} ,$$
(11b)

where \(E_{1} = \frac{{m_{1} }}{{M_{1} }}\), \(E_{2} = \frac{{m_{2} }}{{M_{2} }} \cdot \frac{{e_{2} }}{{e_{1} }}\), \(C_{1} = \frac{{c_{1} }}{{M_{1} \omega_{1} }}\), \(C_{2} = \frac{{c_{2} }}{{M_{2} \omega_{1} }}\),\(G_{1} = \frac{{g_{1} }}{{M_{ 1} }}\), \(G_{2} = \frac{{\lambda g_{2} }}{{M_{ 2} }}\), \(\lambda = \frac{{\omega_{2} }}{{\omega_{1} }}\) (the speed ratio).

The nonlinear contact force of the inter-shaft bearing in the complex coordinate can be expressed as

$$F_{\text{b}} = \frac{{F_{x} }}{{e_{1} }} + i\frac{{F_{y} }}{{e_{1} }} = k_{\text{s}} \left( {r_{\text{i}} - r_{\text{o}} } \right) + e_{1}^{2} k_{\text{n}} \left( {\bar{r}_{\text{i}} - \bar{r}_{\text{o}} } \right)^{3} = k_{\text{s}} \left( {F_{1} r_{ 1} - F_{2} r_{ 2} } \right) + e_{1}^{2} k_{\text{n}} \left( {F_{1} \bar{r}_{ 1} - F_{2} \bar{r}_{ 2} } \right)^{3} ,$$
(12)

the details of the calculation process are shown in “Appendix”.

To solve Eq. (11a, 11b) by multiple scales method, substituting Eq. (12) into Eq. (11a, 11b) and transposing the terms as follows

$$r^{\prime\prime}_{ 1} + \frac{{k_{1} + F_{1}^{2} k_{\text{s}} }}{{M_{ 1} \omega_{1}^{2} }}r_{ 1} - \frac{{F_{1} F_{2} k_{\text{s}} }}{{M_{ 1} \omega_{1}^{2} }}r_{ 2} = E_{1} e^{i\tau } - \left( {C_{1} - iG_{1} } \right)r^{\prime}_{ 1} - \frac{{F_{1} e_{1}^{2} k_{\text{n}} }}{{M_{ 1} \omega_{1}^{2} }}\left( {F_{1} \bar{r}_{ 1} - F_{2} \bar{r}_{ 2} } \right)^{3} ,$$
(13a)
$$r^{\prime\prime}_{ 2} - \frac{{F_{1} F_{2} k_{\text{s}} }}{{M_{ 2} \omega_{1}^{2} }}r_{ 1} + \frac{{k_{2} + F_{2}^{2} k_{\text{s}} }}{{M_{ 2} \omega_{1}^{2} }}r_{ 2} = \lambda^{2} E_{2} e^{i\lambda \tau } - \left( {C_{2} - iG_{2} } \right)r^{\prime}_{ 2} + \frac{{F_{2} e_{1}^{2} k_{\text{n}} }}{{M_{ 2} \omega_{1}^{2} }}\left( {F_{1} \bar{r}_{ 1} - F_{2} \bar{r}_{ 2} } \right)^{3} .$$
(13b)

Equation (13a, 13b) in the matrix form can be noted as

$$\varvec{r^{\prime\prime}} + \varvec{Kr} = \varvec{Q,}$$
(14)

where \(\varvec{r} = \left[ {\begin{array}{*{20}c} {r_{1} } \\ {r_{2} } \\ \end{array} } \right]\), \(\varvec{K} = \frac{1}{{\omega_{1}^{2} }}\left[ {\begin{array}{*{20}c} {\frac{{k_{1} + F_{1}^{2} k_{\text{s}} }}{{M_{ 1} }}} & { - \frac{{F_{1} F_{2} k_{\text{s}} }}{{M_{ 1} }}} \\ { - \frac{{F_{1} F_{2} k_{\text{s}} }}{{M_{ 2} }}} & {\frac{{k_{2} + F_{2}^{2} k_{\text{s}} }}{{M_{ 2} }}} \\ \end{array} } \right]\), \(\varvec{Q} = \left[ {\begin{array}{*{20}c} {Q_{1} } \\ {Q_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {E_{1} e^{i\tau } - \left( {C_{1} - iG_{1} } \right)r^{\prime}_{ 1} - \frac{{F_{1} e_{1}^{2} k_{\text{n}} }}{{M_{ 1} \omega_{1}^{2} }}\left( {F_{1} \bar{r}_{ 1} - F_{2} \bar{r}_{ 2} } \right)^{3} } \\ {\lambda^{2} E_{2} e^{i\lambda \tau } - \left( {C_{2} - iG_{2} } \right)r^{\prime}_{ 2} + \frac{{F_{2} e_{1}^{2} k_{\text{n}} }}{{M_{ 2} \omega_{1}^{2} }}\left( {F_{1} \bar{r}_{ 1} - F_{2} \bar{r}_{ 2} } \right)^{3} } \\ \end{array} } \right]\).

The eigenvalues and the eigenvectors of the system are

$$\left( {\varvec{\varPhi},\varvec{\varOmega}} \right) = {\text{eig}}\left( \varvec{K} \right),$$

where \({\text{eig}}\left( \cdot \right)\) is the function to calculate the eigenvalues and the eigenvectors of the square matrix.

Let the eigenvalues is \(\varvec{\varOmega}= \frac{1}{{\omega_{1}^{2} }}\left[ {\begin{array}{*{20}c} {\varOmega_{1}^{2} } & 0 \\ 0 & {\varOmega_{2}^{2} } \\ \end{array} } \right]\), where \(\varOmega_{1}\), \(\varOmega_{2}\) are the first order and the second order critical speeds of the linearized dual-rotor system respectively. In addition, the eigenvectors is assumed as \(\varvec{\varPhi}= \left[ {\begin{array}{*{20}c} {p_{1} } & {p_{2} } \\ 1 & 1 \\ \end{array} } \right]\), then the inverse matrix of the eigenvectors is \(\varvec{\varPhi}^{ - 1} = \left[ {\begin{array}{*{20}c} {q_{1} } & {1 - q_{2} } \\ { - q_{1} } & {q_{2} } \\ \end{array} } \right]\), where \(q_{1} { = }\frac{1}{{p_{1} - p_{2} }}\), \(q_{2} { = }\frac{{p_{1} }}{{p_{1} - p_{2} }}\).

Let the both sides of Eq. (14) premultiply \(\varvec{\varPhi}^{ - 1}\), and expand into 2DOF equation as follows

$$R^{\prime\prime}_{ 1} + \frac{{\varOmega_{1}^{2} }}{{\omega_{1}^{2} }}R_{ 1} = q_{1} Q_{1} + \left( {1 - q_{2} } \right)Q_{2} ,$$
(15a)
$$R^{\prime\prime}_{ 2} + \frac{{\varOmega_{2}^{2} }}{{\omega_{1}^{2} }}R_{ 2} = - \;q_{1} Q_{1} + q_{2} Q_{2} ,$$
(15b)

where \(R_{ 1} = q_{1} r_{1} + \left( {1 - q_{2} } \right)r_{2}\), \(R_{ 2} = - q_{1} r_{1} + q_{2} r_{2}\).

The dual-rotor system is excited by the double-frequency excitation, that is, the unbalance of the LP rotor and the HP rotor. Thus, the first order critical speed is consisted of two interrelated primary resonances, first of which is induced by the unbalance of the HP rotor and second of which is induced by the unbalance of the LP rotor. The dual-rotor system rotates at a constant rotation speed ratio \(\lambda = \frac{{\omega_{2} }}{{\omega_{1} }}\) (\(\lambda > 1\) in general). Therefore, as the rotation speed increases, first primary resonance will be induced by the unbalance of the HP rotor at \(\omega_{2} = \lambda \omega_{1} \approx \varOmega_{1}\) and second primary resonance will be induced by the unbalance of the LP rotor at \(\omega_{1} \approx \varOmega_{1}\).

According the parameters of the dual-rotor system, the assumptions are as follows:

  1. 1.

    The damping and the nonlinearity of the system are both small;

  2. 2.

    \(\varOmega_{2} > > \varOmega_{1}\) (\(\varOmega_{2} = \eta \varOmega_{1} ,\eta \approx 7.35\)), i.e., the second order critical speed of the dual-rotor system is far greater than the first order critical speed. This research concentrated on the first-order critical speed of the dual-rotor system;

  3. 3.

    The first order critical speed contains two interrelated RPs, i.e. first primary RP induced by the unbalance of the HP rotor when \(\omega_{2} = \lambda \omega_{1} \approx \varOmega_{1}\) and second primary RP induced by the unbalance of the LP rotor when \(\omega_{1} \approx \varOmega_{1}\).

Primary resonance induced by LP rotor at ω 1 ≈ Ω 1

The times scales are \(T_{1} = \tau\), \(T_{2} = \varepsilon \tau\), and assume that the tuning parameter σ1 as follows

$$\frac{{\varOmega_{1}^{2} }}{{\omega_{1}^{2} }} = 1 - \varepsilon \sigma_{1} .$$
(16)

Then the solutions of Eq. (15a, 15b) can be expanded as

$$R_{1} = R_{11} + \varepsilon R_{12} ,$$
(17a)
$$R_{2} = R_{21} + \varepsilon R_{22} .$$
(17b)

Substituting Eqs. (16)–(17a, 17b) into Eq. (15a, 15b) and equating terms of coefficients ε0 and ε1 to zero, we can obtain the equations as follows:

Order of ε0:

$$D_{1}^{2} R_{11} + R_{11} = \left( {1 - q_{2} } \right)\lambda^{2} E_{2} e^{{i\lambda T_{1} }} ,$$
(18a)
$$D_{1}^{2} R_{21} + \eta^{2} R_{21} = q_{2} \lambda^{2} E_{2} e^{{i\lambda T_{1} }} ,$$
(18b)

Order of ε1:

$$\begin{aligned} D_{1}^{2} R_{12} + R_{12} & = - \;2D_{1} D_{2} R_{11} + \sigma_{1} R_{11} + q_{1} E_{1} e^{{iT_{1} }} - q_{1} \left( {C_{1} - iG_{1} } \right)\left( {p_{1} D_{1} R_{11} + p_{2} D_{1} R_{21} } \right) \\ & \;\;\;\; - \left( {1 - q_{2} } \right)\left( {C_{2} - iG_{2} } \right)\left( {D_{1} R_{11} + D_{1} R_{21} } \right) + \gamma_{1} \left[ {\left( {p_{1} F_{1} - F_{2} } \right)\bar{R}_{11} + \left( {p_{2} F_{1} - F_{2} } \right)\bar{R}_{21} } \right]^{3} , \\ \end{aligned}$$
(19a)
$$\begin{aligned} \hfill D_{1}^{2} R_{22} + \eta^{2} R_{22} = - 2D_{1} D_{2} R_{21} + \sigma_{1} \eta^{2} R_{21} - q_{1} E_{1} e^{{iT_{1} }} + q_{1} \left( {C_{1} - iG_{1} } \right)\left( {p_{1} D_{1} R_{11} + p_{2} D_{1} R_{21} } \right) \\ \hfill - q_{2} \left( {C_{2} - iG_{2} } \right)\left( {D_{1} R_{11} + D_{1} R_{21} } \right) + \gamma_{2} \left[ {\left( {p_{1} F_{1} - F_{2} } \right)\bar{R}_{11} + \left( {p_{2} F_{1} - F_{2} } \right)\bar{R}_{21} } \right]^{3} , \\ \end{aligned}$$
(19b)

where \(D_{\text{j}} = \frac{\partial \left( \cdot \right)}{{\partial T_{\text{j}} }} \, \left( {{\text{j}} = 1,2} \right)\), \(\gamma_{1} = \left[ {\frac{{\left( {1 - q_{2} } \right)F_{2} }}{{M_{ 2} \omega_{1}^{2} }} - \frac{{q_{1} F_{1} }}{{M_{ 1} \omega_{1}^{2} }}} \right]e_{1}^{2} k_{\text{n}}\), \(\gamma_{2} = \left[ {\frac{{q_{2} F_{2} }}{{M_{ 2} \omega_{1}^{2} }} + \frac{{q_{1} F_{1} }}{{M_{ 1} \omega_{1}^{2} }}} \right]e_{1}^{2} k_{\text{n}}\), \(\eta = \frac{{\varOmega_{2} }}{{\varOmega_{{_{1} }} }}\).

Then general solutions and special solutions of Eq. (18a, 18b) in the polar form are

$$R_{11} = B_{1} e^{{i\left( {T_{1} + \varphi_{1} } \right)}} + {\text{cc}} + b_{1} e^{{i\lambda T_{1} }} ,$$
(20a)
$$R_{21} = B_{2} e^{{i\left( {\eta T_{1} + \varphi_{2} } \right)}} + {\text{cc}} + b_{2} e^{{i\lambda T_{1} }} ,$$
(20b)

where \(b_{1} { = }\frac{{\left( {1 - q_{2} } \right)\lambda^{2} E_{2} }}{{1 - \lambda^{2} }}\),\(b_{2} { = }\frac{{q_{2} \lambda^{2} E_{2} }}{{\eta^{2} - \lambda^{2} }}\).

Substituting Eq. (20a, 20b) into Eq. (19a, 19b), eliminating the secular terms, and separating real parts and imaginary parts, we can obtain that

$$D_{2} B_{1} = - \frac{1}{2}\left( {\alpha_{4} B_{1} + q_{1} E_{1} \sin \varphi_{1} } \right),$$
(21a)
$$B_{1} D_{2} \varphi_{1} = - \frac{1}{2}\left[ {\alpha_{1} B_{1}^{3} + \alpha_{2} B_{1} B_{2}^{2} + \left( {\alpha_{3} + \sigma_{1} } \right)B_{1} + q_{1} E_{1} \cos \varphi_{1} } \right],$$
(21b)
$$D_{2} B_{2} = - \frac{1}{2}\beta_{4} B_{2} ,$$
(21c)
$$B_{2} D_{2} \varphi_{2} = - \frac{1}{2\eta }B_{2} \left[ {\beta_{1} B_{2}^{2} + \beta_{2} B_{1}^{2} + \left( {\beta_{3} + \eta \sigma_{1} } \right)\eta } \right],$$
(21d)

where \(\alpha_{1} = 3\gamma_{1} \left( {p_{1} F_{1} - F_{2} } \right)^{3}\), \(\alpha_{2} = 6\gamma_{1} \left( {p_{1} F_{1} - F_{2} } \right)\left( {p_{2} F_{1} - F_{2} } \right)^{2}\), \(\alpha_{3} = - \;q_{1} p_{1} G_{1} - \left( {1 - q_{2} } \right)G_{2}\), \(\alpha_{4} = q_{1} p_{1} C_{1} + \left( {1 - q_{2} } \right)C_{2}\), \(\beta_{1} = 3\gamma_{2} \left( {p_{2} F_{1} - F_{2} } \right)^{3}\), \(\beta_{2} = 6\gamma_{2} \left( {p_{1} F_{1} - F_{2} } \right)^{2} \left( {p_{2} F_{1} - F_{2} } \right)\), \(\beta_{3} = q_{1} p_{2} G_{1} - q_{2} G_{2}\), \(\beta_{4} = - q_{1} p_{2} C_{1} + q_{2} C_{2}\).

Letting the right sides of Eq. (21) equal to zero, according to Eq. (21c), it can be obtained that \(B_{2} = 0\). \(B_{2}\) is the amplitude of the second order critical speed’s frequency (Ω2) near the speed region of the first order critical speed (\(\omega_{1} \approx \varOmega_{1}\)). So \(B_{2}\) will always be approximately equal to zero when \(\varOmega_{2} > > \varOmega_{1}\), i.e., \(\eta > > 1\) (satisfy the assumption 2). It is consistent with the facts. Thus, Eq. (21a–21d) are transformed into

$$D_{2} B_{1} = - \frac{1}{2}\left( {\alpha_{4} B_{1} + q_{1} E_{1} \sin \varphi_{1} } \right),$$
(22a)
$$B_{1} D_{2} \varphi_{1} = - \frac{1}{2}\left[ {\alpha_{1} B_{1}^{3} + \left( {\alpha_{3} + \sigma_{1} } \right)B_{1} + q_{1} E_{1} \cos \varphi_{1} } \right].$$
(22b)

Eliminating φ1 in Eq. (22a, 22b), and the amplitude frequency response equation for the primary resonance induced by the unbalance of the LP rotor can be obtained as follows

$$\alpha_{1}^{2} V^{3} + 2\alpha_{1} \left( {\alpha_{3} + \sigma_{1} } \right)V^{2} + \left[ {\left( {\alpha_{3} + \sigma_{1} } \right)^{2} + \alpha_{4}^{2} } \right]V - E_{1}^{2} q_{1}^{2} = 0,$$
(23)

where \(V = B_{1}^{2}\).

Primary resonance induced by HP rotor at ω 2 = λω 1 ≈ Ω 1

The times scales are \(T_{1} = \tau\), \(T_{2} = \varepsilon \tau\), and assume that the tuning parameter σ2 as follows

$$\frac{{\varOmega_{1}^{2} }}{{\omega_{1}^{2} }} = \lambda^{2} - \varepsilon \sigma_{2} .$$
(24)

Then the solutions of Eq. (15a, 15b) can be expanded as

$$R_{1} = R_{11} + \varepsilon R_{12} ,$$
(25a)
$$R_{2} = R_{21} + \varepsilon R_{22} .$$
(25b)

Substituting Eqs. (24)–(25a, 25b) into Eq. (15a, 15b) and equating terms of coefficients of ε0 and ε1 to zero, we can obtain the equations as follows:

Order of ε0:

$$D_{1}^{2} R_{11} + \lambda^{2} R_{11} = q_{1} E_{1} e^{{iT_{1} }} ,$$
(26a)
$$D_{1}^{2} R_{21} + \left( {\lambda \eta } \right)^{2} R_{21} = - q_{1} E_{1} e^{{iT_{1} }} ,$$
(26b)

Order of ε1:

$$\begin{aligned} \hfill D_{1}^{2} R_{12} + \lambda^{2} R_{12} = - 2D_{1} D_{2} R_{11} + \sigma_{2} R_{11} + \left( {1 - q_{2} } \right)\lambda^{2} E_{2} e^{{i\lambda T_{1} }} - q_{1} \left( {C_{1} - iG_{1} } \right)\left( {p_{1} D_{1} R_{11} + p_{2} D_{1} R_{21} } \right) \\ \hfill - \left( {1 - q_{2} } \right)\left( {C_{2} - iG_{2} } \right)\left( {D_{1} R_{11} + D_{1} R_{21} } \right) + \gamma_{1} \left[ {\left( {p_{1} F_{1} - F_{2} } \right)\bar{R}_{11} + \left( {p_{2} F_{1} - F_{2} } \right)\bar{R}_{21} } \right]^{3} , \\ \end{aligned}$$
(27a)
$$\begin{aligned} \hfill D_{1}^{2} R_{22} + \left( {\lambda \eta } \right)^{2} R_{22} = - 2D_{1} D_{2} R_{21} + \sigma_{2} \eta^{2} R_{21} - q_{2} \lambda^{2} E_{2} e^{{i\lambda T_{1} }} + q_{1} \left( {C_{1} - iG_{1} } \right)\left( {p_{1} D_{1} R_{11} + p_{2} D_{1} R_{21} } \right) \\ \hfill - q_{2} \left( {C_{2} - iG_{2} } \right)\left( {D_{1} R_{11} + D_{1} R_{21} } \right) + \gamma_{2} \left[ {\left( {p_{1} F_{1} - F_{2} } \right)\bar{R}_{11} + \left( {p_{2} F_{1} - F_{2} } \right)\bar{R}_{21} } \right]^{3} . \\ \end{aligned}$$
(27b)

Then general solutions and special solutions of Eq. (26a, 26b) in the polar form are

$$R_{11} = A_{1} e^{{i\left( {\lambda T_{1} + \varphi_{1} } \right)}} + {\text{cc}} + a_{1} e^{{iT_{1} }} ,$$
(28a)
$$R_{21} = A_{2} e^{{i\left( {\lambda \eta T_{1} + \varphi_{2} } \right)}} + {\text{cc}} + a_{2} e^{{iT_{1} }} ,$$
(28b)

where \(a_{1} { = }\frac{{q_{1} E_{1} }}{{\lambda^{2} - 1}}\), \(a_{2} { = } - \frac{{q_{1} E_{1} }}{{\left( {\lambda \eta } \right)^{2} - 1}}\).

Substituting Eq. (28a, 28b) into Eq. (27a, 27b), eliminating the secular terms, and separating real parts and imaginary parts, we can obtain that

$$D_{2} A_{1} = - \frac{1}{2\lambda }\left[ {\lambda \alpha_{4} A_{1} + \lambda^{2} \left( {1 - q_{2} } \right)E_{2} \sin \varphi_{1} } \right],$$
(29a)
$$A_{1} D_{2} \varphi_{1} = - \frac{1}{2\lambda }\left[ {\alpha_{1} A_{1}^{3} + \alpha_{2} A_{1} A_{2}^{2} + \left( {\lambda \alpha_{3} + \sigma_{2} } \right)A_{1} + \lambda^{2} \left( {1 - q_{2} } \right)E_{2} \cos \varphi_{1} } \right],$$
(29b)
$$D_{2} A_{2} = - \frac{1}{2}\beta_{4} A_{2} ,$$
(29c)
$$A_{2} D_{2} \varphi_{2} = - \frac{1}{2\lambda \eta }A_{2} \left[ {\beta_{1} A_{2}^{2} + \beta_{2} A_{1}^{2} + \left( {\lambda \beta_{3} + \eta \sigma_{2} } \right)\eta } \right].$$
(29d)

Letting the right sides of Eq. (29a–29d) to zero, according to Eq. (29c), it can be found that \(A_{2} = 0\). \(A_{2}\) is the amplitude of second order critical speed’s frequency (Ω2) near the speed region of the first order critical speed (\(\omega_{2} = \lambda \omega_{1} \approx \varOmega_{1}\)). So \(A_{2}\) will always be approximately equal to zero when \(\varOmega_{2} > > \varOmega_{1}\), i.e. \(\eta > > 1\) (satisfy the assumption 2). It is consistent with the facts. So Eq. (29a–29d) are transformed into

$$D_{2} A_{1} = - \frac{1}{2\lambda }\left[ {\lambda \alpha_{4} A_{1} + \lambda^{2} \left( {1 - q_{2} } \right)E_{2} \sin \varphi_{1} } \right],$$
(30a)
$$A_{1} D_{2} \varphi_{1} = - \frac{1}{2\lambda }\left[ {\alpha_{1} A_{1}^{3} + \left( {\lambda \alpha_{3} + \sigma_{2} } \right)A_{1} + \lambda^{2} \left( {1 - q_{2} } \right)E_{2} \cos \varphi_{1} } \right],$$
(30b)

Eliminating φ1 in Eq. (30a, 30b), and the amplitude frequency response equation for the primary resonance induced by the unbalance of the HP rotor can be obtained as follows

$$\alpha_{1}^{2} U^{3} + 2\alpha_{1} \left( {\lambda \alpha_{3} + \sigma_{2} } \right)U^{2} + \left[ {\left( {\lambda \alpha_{3} + \sigma_{2} } \right)^{2} + \lambda^{2} \alpha_{4}^{2} } \right]U - \lambda^{4} \left( {1 - q_{2} } \right)^{2} E_{2}^{2} = 0 .$$
(31)

where \(U = A_{1}^{2}\).

Results and Discussions

Multiple Scales Results and Numerical Verification

The dynamic responses of the dual-rotor system are comprised of double frequencies at least, i.e. the frequencies of LP and HP rotors’ unbalance excitations [22]. The multiple scales method is applied to solve the 2DOF Eq. (15a, 15b) while the Runge–Kutta method is applied to solve the 4DOF Eq. (10a–10d), the amplitude frequency response curves (AFRCs) solved by both methods are shown in Fig. 3. The initial states of motion for the initial rotation speed \(\omega_{1} = 600\;\;\;{\text{rad/s}}\) are set as \(\left[ {\begin{array}{*{20}c} {x_{1} } & {\dot{x}_{1} } & {y_{1} } & {\dot{y}_{1} } & {x_{2} } & {\dot{x}_{2} } & {y_{2} } & {\dot{y}_{2} } \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]\), but for other rotation speeds, the initial states are set as the final states of the previous rotation speed. The integration duration should be long enough to ensure steady-state responses, for Eq. (10a–10d), the integration duration is set as \(t = \left( {0, \, 10{\text{ s}}} \right)\). The time step should be small enough to ensure the accuracy of the numerical results, for Eq. (10a–10d), the time step is set as 10−4 s. The errors of the numerical results for every rotation speed are less than 10−6. The effective value is used to express the vibration amplitude solved by the Runge–Kutta method, while the multiple scales method can directly calculate the vibration amplitude. It can be seen that the multiple scales results are basically identical with the Runge–Kutta results, while multiple scales method can obtain the unstable solution and save a lot of time during the calculation. In appearance, the AFRC of LP rotor is very similar with the AFRC of HP rotor, while the amplitude of the LP rotor is much greater than the amplitude of the HP rotor. It is because the LP rotor is more slender than the HP rotor, therefore, the LP rotor can be assumed as a flexible rotor while the HP rotor can be assumed as a rigid rotor. It is true that the deformation of a slender shaft (LP shaft) is much greater than a stubby shaft (HP shaft) under the same condition. Moreover, there exist two primary RPs in each AFRC, the frequency of the first one induced by the unbalance of HP rotor is \(\omega_{\text{A}} = 695\;\;{\text{rad/s}}\) and the frequency of the second one induced by the unbalance of LP rotor is \(\omega_{\text{B}} = 879\;\;{\text{rad/s}}\). Compare values of \(\omega_{\text{A}}\), \(\omega_{\text{B}}\) and \(\lambda { = }1.2\), the approximate law shows like \(\frac{{\omega_{\text{B}} }}{{\omega_{\text{A}} }} \approx \lambda\).

Fig. 3
figure 3

AFRCs solved by multiple scales method and Runge–Kutta method. a For LP rotor. b For HP rotor

Full size image

In summary, the 4DOF equation in real coordinate could be simplified into the 2DOF equation in complex coordinate when the 4DOF equation could be divided into two pairs of equations and each pair of equations are very similar with each other. Then the multiple scales method could be applied to solve the responses of the 2DOF dynamic equation, and the multiple scales results are basically identical with the original 4DOF dynamic equation.

Effect of Inter-Shaft Bearing’s Linear Stiffness

The primary RPs affected by the linear stiffness of inter-shaft bearing are discussed during this section. The AFRCs of LP rotor for different linear stiffness, i.e., \(k_{\text{s}} = 2.2k_{\text{s0}}\), \(k_{\text{s}} = 2.5k_{\text{s0}}\), \(k_{\text{s}} = 3k_{\text{s0}}\) and \(k_{\text{s}} = 10k_{\text{s0}}\) (\(k_{{{\text{s}}0}} = 10^{8} \;\;{\text{N/m}}\)), are shown in Fig. 4. When the linear stiffness become smaller enough, the jump phenomenon and the resonance hysteresis phenomenon happen to the primary RPs A and B, both of which show the hardening characteristic, and the unstable solution could also be obtained. With the linear stiffness further increasing, the amplitudes of the jump phenomenon and the resonance hysteresis intervals for both A and B all become smaller or even disappear. It implies increasing the linear stiffness is helpful to reduce the nonlinear phenomena of the primary resonances.

Fig. 4
figure 4

AFRCs of LP rotor for different linear stiffness. (Solid line for stable solution, dotted line for unstable solution)

Full size image

For further detailed analysis of primary RPs affected by the linear stiffness, the enlarged drawings of the primary RPs A and B in Fig. 4 are shown in Fig. 5. With the linear stiffness increasing, the frequencies of both RPs decrease obviously and the amplitudes of both RPs decrease slightly. The nonlinear phenomena of A and B disappear gradually until the linear stiffness increase to \(k_{\text{s}} = 10k_{\text{s0}}\). Both RPs A and B show the hardening characteristic.

Fig. 5
figure 5

The enlarged drawings of the primary RPs in the AFRC of LP rotor for different linear stiffness. a For RP A. b For RP B. (Solid line for stable solution, dotted line for unstable solution)

Full size image

Effect of Inter-Shaft Bearing’s Nonlinear Stiffness

The primary RPs affected by the nonlinear stiffness of inter-shaft bearing is discussed during this section. The AFRCs of LP rotor for different nonlinear stiffness, i.e., \(k_{\text{n}} = 0k_{\text{n0}}\), \(k_{\text{n}} = k_{\text{n0}}\), \(k_{\text{n}} = 2k_{\text{n0}}\) and \(k_{\text{n}} = 4k_{\text{n0}}\) (\(k_{{{\text{n}}0}} = 10^{23} \;\;{\text{N/m}}^{3}\)), are shown in Fig. 6. With the nonlinear stiffness increasing, the jump phenomenon and the resonance hysteresis phenomenon happen to the primary RPs A and B, both of which show the hardening characteristic, the amplitudes of the jump phenomenon and the resonance hysteresis intervals for both A and B all become larger. It implies decreasing the nonlinear stiffness is helpful to reduce the nonlinear phenomena of the primary resonances.

Fig. 6
figure 6

AFRCs of LP rotor for different nonlinear stiffness. (Solid line for stable solution, dotted line for unstable solution)

Full size image

For further detailed analysis of primary RPs affected by the nonlinear stiffness, the enlarged drawings of the primary RPs A and B in Fig. 6 are shown in Fig. 7. A and B start to behave nonlinear phenomena when \(k_{\text{n}} = k_{\text{n0}}\). With the nonlinear stiffness increasing, the frequencies of both RPs increase obviously and the amplitudes of both RPs increase slightly. The nonlinear phenomena happen to RPs A and B gradually until the nonlinear stiffness increase to \(k_{\text{n}} = k_{\text{n0}}\). Both RPs A and B show the hardening characteristic.

Fig. 7
figure 7

The enlarged drawings of the primary RPs in the AFRC of LP rotor for different nonlinear stiffness. a For RP A. b For RP B. (Solid line for stable solution, dotted line for unstable solution)

Full size image

In a word, the effect of inter-shaft bearing’s linear stiffness and nonlinear stiffness on the primary RPs is opposite with each other. The linear stiffness will suppress the nonlinear phenomena while the nonlinear stiffness will promote the nonlinear phenomena. Increasing the linear stiffness and decreasing nonlinear stiffness of the inter-shaft bearing is helpful for preventing the nonlinear phenomena of the dual-rotor system.

Effect of Rotation Speed Ratio

The primary RPs affected by the rotation speed ratio is discussed during this section. The AFRCs of LP rotor for different rotation speed ratios, i.e., \(\lambda = 1.1\), \(\lambda = 1.15\), \(\lambda = 1.2\) and \(\lambda = 1.3\), are shown in Fig. 8. It can be seen that the second RP B is nearly still while the first RP A changes obviously. With λ increasing, the second RP B is almost still while the frequency of the first RP A is decreasing obviously and the amplitude of first RP A is still, but the ratios among them still satisfy the approximate law \(\frac{{\omega_{\text{B}} }}{{\omega_{\text{A}} }} \approx \lambda\). It implies the effect of rotation speed ratio is mainly concentrated on the frequency of the first primary RP A.

Fig. 8
figure 8

AFRCs of LP rotor for different rotation speed ratios. (Solid line for stable solution, dotted line for unstable solution)

Full size image

Conclusion

In this paper, the mechanism of nonlinear phenomena in a simple dual-rotor system at the case of primary resonance has been investigated, based on which, the primary resonances affected by the typical parameters of dual-rotor system has been analyzed thereafter. Some important conclusions are listed as follows:

  1. 1.

    If the system is symmetric in two directions, the dynamic equations can be transformed from the real coordinate into the complex coordinate, which reduces the DOF by half. It is an effective way to reduce calculation time and study the mechanism of nonlinear phenomena.

  2. 2.

    The nonlinear phenomena, including jump phenomenon and resonance hysteresis phenomenon, happen to both primary resonances because of the nonlinearities of the inter-shaft bearing. Thus, the nonlinear stiffness promote the nonlinear phenomena while the linear stiffness suppress them.

  3. 3.

    The rotation speed ratio only affect the frequency of the first primary resonance, it has no effect on the nonlinear phenomena and the amplitudes of both primary resonances. The ratio between the frequencies of two primary resonances is approximately equal to the rotation speed ratio all the time.

The nonlinear mechanism obtained in this paper help us find out the reason of the nonlinear phenomena in a dual-rotor system due to the nonlinearities of the inter-shaft bearing, which are very helpful to prevent the generation of the nonlinear phenomena.