1 Introduction

The dynamical model of a substantial number of practical systems such as power, transportation, robotic, and aerospace systems is affected by unknown uncertainties and external disturbances. In view of these undesirable and unpredictable variations, some studies have been carried out to investigate the stability and robust performance analysis of systems over the past few years. Among them, the concept of sliding mode (SM) control that enforces the system states onto a sliding surface by a discontinuous control law and stays on it during the whole succeeding time is a useful strategy that has been proposed [1, 2]. For instance, a higher-order SM observer-based control scheme was suggested for nonlinear systems with unknown inputs [3]. The method was then developed and combined with interval observer in [4] to analyze linear parameter-varying systems composed of strongly observable subsystems. For bounded and derivative bounded uncertainties and to mitigate chattering phenomena, an adaptive high-order SM control policy has been used in [5]. Moreover, a dynamic SM algorithm, incorporating a disturbance observer, was suggested to investigate a mismatched disturbance in [6]. For linear and Lipschitz nonlinear systems, polytopic type and norm bounded uncertainties have been extensively discussed in the research works [7]. It is worth mentioning that the parametric uncertainty has been addressed recently to overcome the computational burden and conservatism of analyzing uncertain systems subject to Lipschitz nonlinearities [8,9,10].

However, the aforementioned results require exact model information for the control problem. Note that the considered uncertainties are bounded and we have access to the information of the upper bounds or belong to specific intervals. With the restrictions imposed on the robust stability analysis, a great number of physical systems with unknown and complex dynamics or unknown parameter variations cannot be fully addressed. Learning mechanisms and neuro-fuzzy-based controllers were employed to deal with unknown dynamics [11].

For a Takagi-Sugeno (TS) fuzzy model-based system, the boundary/regional information of the membership functions was used and the framework of multidimensional fuzzy summation has been achieved in [12, 13]. Moreover, a distributed compensator and constraints on the membership functions have been considered to reduce the conservativeness of the stabilization conditions for a TS fuzzy control system [14, 15]. The event-triggered scheme for TS fuzzy systems is developed in [16,17,18].

Another learning-based control involves the interval type-2 fuzzy logic system (IT2FLS) which has been implemented via type-2 fuzzy (T2F) sets [19]. Moreover, the Lyapunov stability analysis has been employed as an stability analysis tool for T2F-based control policies [20]. Optimization algorithms such as genetic and ant colony have been extended to design an optimal T2F controller [21]. By selecting the bee colony optimization technique, a T2F control approach was proposed in [22]. This concept with the backtracking search algorithm is implemented for the control traffic signal issues [23]. Moreover, utilizing a non-singleton T2F-based and invasive weed optimization algorithm, unknown dynamics were approximated in [24] to synchronize fractional-order chaotic systems. A T2F PI control method was designed to enhance the robust performance of a system and reduce computational complexities in [25]. Solving an iterative optimization algorithm and employing the SM control approach result in an T2F controller [26]. Moreover, a self-triggered mechanism was developed for applying an T2F control method [27]. A predictive T2F controller was proposed to regulate the glucose level in type-1 diabetes subject to completely unknown dynamics [28]. The tracking control problem was investigated via an IT2 fuzzy [29]. An T2F set was also used for nonlinear networked systems to design a fuzzy filter [30]. An observer-based T2F strategy was employed in [31] to study chaotic systems. For AC-microgrids, the frequency regulation problem was analyzed via a T2FLS with adaptive optimization rules [32]. A T2FLS incorporating a restricted Boltzmann machine has been extended for fractional-order multi-agent systems [33]. Such strategies have been combined with square-root-cubature Kalman filter to reduce the voltage oscillation of active/reactive power regulation problem [34]. Note that T2F-based control law has been developed to reduce the effect of noisy measurement [35].

Recently, the concept of an interval type-3 fuzzy logic system (IT3FLS) has been suggested for the efficiency and accuracy improvement of previous fuzzy control results. From the approximation ability perspective, an IT3FLS is able to approximate more complex nonlinearities and uncertainties of nonlinear systems compared to the other learning approaches. Furthermore, compared to the T1FLS and T2FLS in which the memberships are crisp value and type-1 fuzzy set, in an IT3FLS the membership has been defined as an T2F set [36]. While reducing the approximation and tracking error signals, IT3FLS-based strategies provide more degrees of freedom in designing a robust controller for unknown systems. Inspired by this concept, an accurate approximation of unknown micro-electro-mechanical system gyroscopes models was employed for the control synthesis strategy in [37]. Considering an adaptive IT3FLS, the robust stabilization of the 5G telecom power system has been analyzed [38]. Recently, an adaptive fuzzy kernel size was employed for optimizing rule and antecedent parameters in [39].

In this work, an improved nonlinear observer-based control scheme is designed to study the robust stabilization of nonlinear systems via developing a novel IT3FLS. The suggested learning scheme outperforms conventional robust control policies and neuro-fuzzy control policies demanding the known information about the system models, the structure of uncertainties, and upper bounds of external disturbances. As a consequence, the learning-based control method with fast tuning parameters proposed in this paper enables us to analyze general types of uncertainties, unknown models, and external disturbances while reconstructing unmeasurable states through a novel learning observer. Therefore, the stability and robustness of a wide and general class of complex nonlinear systems can be studied via the method of this paper. In the novel learning IT3FLS, new membership functions and online optimized tuning rules are designed. Furthermore, applying a novel adaptive compensator to the system boosts the robustness of the closed-loop system and weakens the effects of approximation error signals. The stability of the closed-loop system is then ensured via the Lyapunov tool and Barbalat’s lemma. The suggested method is tested on different cases to highlight an excellent robust performance.

The remaining is organized as follows. In Sect. 2, the problem is described. In Sect. 3, the suggested FLS is explained. The observer scheme is designed in Sect. 4. The stability is studied in Sect. 5. The implementation and computer simulations are investigated in Sects. 6–7. Finally, the conclusions are given in Sect. 8.

2 System representation

Consider a nonlinear system as follows:

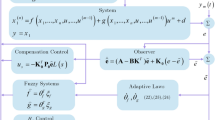
$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{x}}_i = x_{i+1} , i = 1 ,..., n-1 \\ {\dot{x}}_n = a ({\varvec{x}}) + b({\varvec{x}}) u + \delta (t) \\ y = x_1 \end{array}\right. } \end{aligned}$$
(1)

where \( {\varvec{x}} = {\left[ {{x_1},{x_2}, ... ,{x_n}} \right] ^T} = {\left[ {{x_1},{{\dot{x}}_1} ,... ,x_1^{(n - 1)}} \right] ^T}\) expresses state vector. In addition, nonlinear vector-valued functions a(.) and b(.) are unknown but bounded, \(u,y \in \mathbb {{\mathbb {R}}}\) denote the control signal and output of the system. For the unknown exogenous disturbance \( \delta (t) \), it is supposed that there exists an upper bound. The suggested control diagram is depicted in Fig. 1. To study the tracking control problem by defining reference signal, the following tracking errors are considered

$$\begin{aligned} \begin{array}{l} {\varvec{r}}= {\left[ {{r},{\dot{r}}, ... ,r^{(n - 1)}} \right] ^T}\\ {\varvec{e}}= {\varvec{x}} - {\varvec{r}} = {\left[ {{\varvec{e}}_1,\dot{{\varvec{e}}}_1,...,{{\varvec{e}}_1^{(n - 1)}}} \right] ^T}\\ {\hat{\varvec{e}}}= {\hat{\varvec{x}}} - {\varvec{r}}= {\left[ {{\hat{{\varvec{e}}}_1},\dot{\hat{{\varvec{e}}}}_1,...,{{\hat{{\varvec{e}}}_1}^{(n - 1)}}} \right] ^T} \end{array} \end{aligned}$$
(2)

where the estimations of \({\varvec{x}} \) and \( {\varvec{e}} \) are expressed as \( {\hat{\varvec{x}}} \) and \( \hat{{\varvec{e}}}\). Moreover, one can rewrite the system dynamic as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{{\varvec{x}}} = \Xi {\varvec{x}} + \Pi \left[ a ({\varvec{x}}) + b({\varvec{x}}) u + \delta (t) \right] ,\\ y = {\Psi ^T} {\varvec{x}} \end{array}\right. } \end{aligned}$$
(3)

in which

$$\begin{aligned}&\Xi = \left[ {\begin{array}{*{20}{c}} 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad \cdots &{}\quad 0&{}\quad 0\\ \cdots &{}\quad \cdots &{}\quad \cdots \quad &{} \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad 0&{}\quad 1\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad 0&{}\quad 0 \end{array}} \right] ,\,\,\,\nonumber \\&\Pi = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ \vdots \\ 0\\ 1 \end{array}} \right] ,\,\,\Psi = \left[ {\begin{array}{*{20}{c}} 1\\ 0\\ \vdots \\ 0\\ 0 \end{array}} \right] \end{aligned}$$
(4)

Assumption 1

It is supposed that \(0< b({\varvec{x}}) < \infty \); therefore, (3) is controllable in region \({U_c} \subset {{\mathbb {R}}^n}\), designated as certain controllability [40, 41], also \(0< b({\varvec{x}}) < \infty \) represents a fixed control direction.

In the case of known system functions \( a ({\varvec{x}})\) and \(b({\varvec{x}}) \) and when disturbance \(\delta (t) = 0\), the control law \({u^ * }\) is applied as follows to the system:

$$\begin{aligned} {u^ * } = {b^{ - 1}}({\varvec{x}}) \left[ { - a ({\varvec{x}}) + r^{(n)} - {\mathcal {K}}_c^T {\varvec{x}} } \right] \end{aligned}$$
(5)

Note that we design \({{\mathcal {K}}_c} = {\left[ {{k_{c1}},{k_{c2}},...,{k_{cn}}} \right] ^T} \in {{\mathbb {R}}^n}\) such that \({s^n} + {k_{cn}}{s^{n - 1}} + \cdots + {k_{c1}}\) is Hurwitz stable [42]. However, the controller (5) cannot be applied to the system. Based on the following procedure, the improved nonlinear robust control policy is designed.

  • A novel adaptive IT3FLS is utilized for approximating unknown dynamic and nonlinear terms.

  • Based on the approximation information of a novel IT3FLS, an observer is designed to improve the robust stabilization.

  • The adaptive compensator is implemented to diminish the undesirable effects of the approximation error signals.

Fig. 1
figure 1

Diagram of the suggested controller

Full size image

3 Type-3 FLS

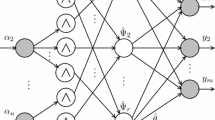
This section is allocated for the structure of IT3FLSs (see Fig. 2) explained as:

Fig. 2
figure 2

Type-3 FLS

Full size image

  • The inputs are \(x _1,...,x _n\).

  • Consider \({{\tilde{\varphi }}_i^j}\) as the \(j-th\) fuzzy set (FS) for \(x _i\), the memberships at secondary levels \({ {{\underline{\sigma }}_i}}\) and \({ {{{\bar{\sigma }} }_i}}\) are obtained as [43]:

    $$\begin{aligned} {{\bar{\xi } }_{{\tilde{\varphi }}_{i\,\,| {{{\bar{\sigma }} }_i}}^j}} = \left\{ {\begin{array}{*{20}{c}} {1 - {{\left( {\frac{{\left| {x _i - {C_{{\tilde{\varphi }}_i^j}}} \right| }}{{{{{\underline{\vartheta }} }_{{\tilde{\varphi }}_i^j}}}}} \right) }^{{{{\bar{\sigma }} }_i}}}\, \hbox {if} \,{C_{{\tilde{\varphi }}_i^j}} - {{{\underline{\vartheta }} }_{{\tilde{\varphi }}_i^j}}< x _i \le {C_{{\tilde{\varphi }}_i^j}}}\\ {1 - {{\left( {\frac{{\left| {x _i - {C_{{\tilde{\varphi }}_i^j}}} \right| }}{{{{{\bar{\vartheta }}}_{{\tilde{\varphi }}_i^j}}}}} \right) }^{{{{\bar{\sigma }} }_i}}}\, \hbox {if} \,{C_{{\tilde{\varphi }}_i^j}} < x _i \le {C_{{\tilde{\varphi }}_i^j}} + {{{\bar{\vartheta }}}_{{\tilde{\varphi }}_i^j}}}\\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hbox {if} \,x _i > {C_{{\tilde{\varphi }}_i^j}} + {{{\bar{\vartheta }}}_{{\tilde{\varphi }}_i^j}}\,or\,x _i \le {C_{{\tilde{\varphi }}_i^j}} - {{{\underline{\vartheta }} }_{{\tilde{\varphi }}_i^j}}} \end{array}} \right. \end{aligned}$$
    (6)
    $$\begin{aligned} {{\bar{\xi } }_{{\tilde{\varphi }}_{i\,\,| {{{\underline{\sigma }} }_i}}^j}} = \left\{ {\begin{array}{*{20}{c}} {1 - {{\left( {\frac{{\left| {x _i - {C_{{\tilde{\varphi }}_i^j}}} \right| }}{{{{{\underline{\vartheta }} }_{{\tilde{\varphi }}_i^j}}}}} \right) }^{{{{\underline{\sigma }} }_i}}}\, \hbox {if} \,{C_{{\tilde{\varphi }}_i^j}} - {{{\underline{\vartheta }} }_{{\tilde{\varphi }}_i^j}}< x _i \le {C_{{\tilde{\varphi }}_i^j}}}\\ {1 - {{\left( {\frac{{\left| {x _i - {C_{{\tilde{\varphi }}_i^j}}} \right| }}{{{{{\bar{\vartheta }}}_{{\tilde{\varphi }}_i^j}}}}} \right) }^{{{{\underline{\sigma }} }_i}}}\, \hbox {if} \,{C_{{\tilde{\varphi }}_i^j}} < x _i \le {C_{{\tilde{\varphi }}_i^j}} + {{{\bar{\vartheta }}}_{{\tilde{\varphi }}_i^j}}}\\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hbox {if} \,x _i > {C_{{\tilde{\varphi }}_i^j}} + {{{\bar{\vartheta }}}_{{\tilde{\varphi }}_i^j}}\,or\,x _i \le {C_{{\tilde{\varphi }}_i^j}} - {{{\underline{\vartheta }} }_{{\tilde{\varphi }}_i^j}}} \end{array}} \right. \end{aligned}$$
    (7)
    $$\begin{aligned} {\underline{\xi } _{{\tilde{\varphi }}_{i\,\,| {{{\bar{\sigma }} }_i}}^j}} = \left\{ {\begin{array}{*{20}{c}} {1 - {{\left( {\frac{{\left| {x _i - {C_{{\tilde{\varphi }}_i^j}}} \right| }}{{{{{\underline{\vartheta }} }_{{\tilde{\varphi }}_i^j}}}}} \right) }^{\frac{1}{{{{{\bar{\sigma }} }_i}}}}}\, \hbox {if} \, {C_{{\tilde{\varphi }}_i^j}} - {{{\underline{\vartheta }} }_{{\tilde{\varphi }}_i^j}}< x _i \le {C_{{\tilde{\varphi }}_i^j}}}\\ {1 - {{\left( {\frac{{\left| {x _i - {C_{{\tilde{\varphi }}_i^j}}} \right| }}{{{{{\bar{\vartheta }}}_{{\tilde{\varphi }}_i^j}}}}} \right) }^{\frac{1}{{{{{\bar{\sigma }} }_i}}}}}\, \hbox {if} \, {C_{{\tilde{\varphi }}_i^j}} < x _i \le {C_{{\tilde{\varphi }}_i^j}} + {{{\bar{\vartheta }}}_{{\tilde{\varphi }}_i^j}}}\\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hbox {if} \,x _i > {C_{{\tilde{\varphi }}_i^j}} + {{{\bar{\vartheta }}}_{{\tilde{\varphi }}_i^j}}\,or\,x _i \le {C_{{\tilde{\varphi }}_i^j}} - {{{\underline{\vartheta }} }_{{\tilde{\varphi }}_i^j}}} \end{array}} \right. \end{aligned}$$
    (8)
    $$\begin{aligned} {\underline{\xi } _{{\tilde{\varphi }}_{i\,\,| {{{\underline{\sigma }} }_i}}^j}} = \left\{ {\begin{array}{*{20}{c}} {1 - {{\left( {\frac{{\left| {x _i - {C_{{\tilde{\varphi }}_i^j}}} \right| }}{{{{{\underline{\vartheta }} }_{{\tilde{\varphi }}_i^j}}}}} \right) }^{\frac{1}{{{{{\underline{\sigma }} }_i}}}}}\, \hbox {if} \,{C_{{\tilde{\varphi }}_i^j}} - {{{\underline{\vartheta }} }_{{\tilde{\varphi }}_i^j}}< x _i \le {C_{{\tilde{\varphi }}_i^j}}}\\ {1 - {{\left( {\frac{{\left| {x _i - {C_{{\tilde{\varphi }}_i^j}}} \right| }}{{{{{\bar{\vartheta }}}_{{\tilde{\varphi }}_i^j}}}}} \right) }^{\frac{1}{{{{{\underline{\sigma }} }_i}}}}}\, \hbox {if} \,{C_{{\tilde{\varphi }}_i^j}} < x _i\le {C_{{\tilde{\varphi }}_i^j}} + {{{\bar{\vartheta }}}_{{\tilde{\varphi }}_i^j}}}\\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hbox {if} \,x _i > {C_{{\tilde{\varphi }}_i^j}} + {{{\bar{\vartheta }}}_{{\tilde{\varphi }}_i^j}}\,\,or\,\,x _i \le {C_{{\tilde{\varphi }}_i^j}} - {{{\underline{\vartheta }} }_{{\tilde{\varphi }}_i^j}}} \end{array}} \right. \end{aligned}$$
    (9)

    where \({{\bar{\xi } }_{{\tilde{\varphi }}_{i\, \, | {{{\bar{\sigma }} }_i}}^j}}\)/\({{\bar{\xi } }_{{\tilde{\varphi }}_{i\, \, | {{\underline{\sigma }}_i}}^j}}\) and \({\underline{\xi } _{{\tilde{\varphi }}_{i\, \, | {{{\bar{\sigma }} }_i}}^j}}\)/\({\underline{\xi } _{\tilde{\varphi }_{i\, \, | {{{\underline{\sigma }} }_i}}^j}}\) denote the upper/lower memberships for \({{\tilde{\varphi }}_i^j}\) at \({ {{{\underline{\sigma }} }_i}}\) and \({ {{{\bar{\sigma }} }_i}}\). \({{C_{{\tilde{\varphi }}_i^j}}}\) denote the center of \({{C_{\tilde{\varphi }_i^j}}}\) and \({{{{\underline{\vartheta }} }_{\tilde{\varphi }_i^j}}}\) and \({{{{\bar{\vartheta }}}_{{\tilde{\varphi }}_i^j}}}\) are the distances of \({{C_{{\tilde{\varphi }}_i^j}}}\) to the start/end points of \({{\tilde{\varphi }}_i^j}\) (see Fig. 3).

  • The rule firings are obtained as:

    $$\begin{aligned} {\bar{\Phi }} _{{{{\bar{\sigma }} }_i}}^l = \prod \nolimits _{j = 1}^n {{{\bar{\xi }}_{{\tilde{\varphi }} _{j\, \, \, \, \, \, \, \, |\, \, {{\bar{\sigma }}_i}}^{{p_j}}}}} \end{aligned}$$
    (10)
    $$\begin{aligned} {\bar{\Phi }} _{{{{\underline{\sigma }} }_i}}^l = \prod \nolimits _{j = 1}^n {{{{\bar{\xi }} }_{{\tilde{\varphi }} _{j\, \, \, \, \, \, \, \, |\, \, {{{\underline{\sigma }} }_i}}^{{p_j}}}}} \end{aligned}$$
    (11)
    $$\begin{aligned} {\underline{\Phi }} _{{{{\bar{\sigma }} }_i}}^l = \prod \nolimits _{j = 1}^n {{{{\underline{\xi }} }_{{\tilde{\varphi }} _{j\, \, \, \, \, \, \, \, |\, \, {{{\bar{\sigma }} }_i}}^{{p_j}}}}} \end{aligned}$$
    (12)
    $$\begin{aligned} {\underline{\Phi }} _{{{{\underline{\sigma }} }_i}}^l = \prod \nolimits _{j = 1}^n {{{{\underline{\xi }} }_{{\tilde{\varphi }} _{j\, \, \, \, \, \, \, \, |\, \, {{{\underline{\sigma }} }_i}}^{{p_j}}}}} \end{aligned}$$
    (13)

    where \(l-th\) rule is:

    $$\begin{aligned} \begin{array}{l} l - th\,Rule:\\ if\,{x _1}\,is\,\,{\tilde{\varphi }}_{1\,\,\,\, }^{{p_1}}\,and\,{x _2}\,is\,\,{\tilde{\varphi }}_2^{{p_2}}\,and\, \cdots \,\,{x _n}\,\,is\,\,{\tilde{\varphi }}_n^{{p_n}}\\ \,\,\,\,Then\,\,\mu \in \left[ {{{{\underline{\theta }} }_l},{{{\bar{\theta }} }_l}} \right] ,l = 1,...,M \end{array} \end{aligned}$$
    (14)

    where \({\tilde{\varphi }}_i^{{p_j}}\) is the \({{p_j}}-th\) FS for \(x _i\) and \({{{\underline{\theta }} }_l}\) and \({{\bar{\theta }} }_l\) are consequent trainable parameters.

  • The output is written as:

    $$\begin{aligned} \mu = \frac{{\sum \nolimits _{i = 1}^{{n_\sigma }} {\left( {{{{\underline{\sigma }} }_i}{{{\underline{\mu }} }_i} + {{{\bar{\sigma }} }_i}{{{\bar{\mu }}}_i}} \right) } }}{{\sum \nolimits _{i = 1}^{{n_\sigma }} {\left( {{{{\underline{\sigma }} }_i} + {{{\bar{\sigma }} }_i}} \right) } }} \end{aligned}$$
    (15)

    where

    $$\begin{aligned} {{{\bar{\mu }}}_i} = \frac{{\sum \nolimits _{l = 1}^{n_r} {\left( {{\bar{\Phi }} _{ {{{\bar{\sigma }} }_i}}^l{{{\bar{\theta }} }_l} + {\underline{\Phi }} _{ {{{\bar{\sigma }} }_i}}^l{{{\underline{\theta }} }_l}} \right) } }}{{\sum \nolimits _{l = 1}^{n_r} {\left( {{\bar{\Phi }} _{{{{\bar{\sigma }} }_i}}^l + {\underline{\Phi }} _{ {{{\bar{\sigma }} }_i}}^l} \right) } }} \end{aligned}$$
    (16)
    $$\begin{aligned} {{\underline{\mu }} _i} = \frac{{\sum \nolimits _{l = 1}^{n_r} {\left( {{\bar{\Phi }} _{ {{{\underline{\sigma }} }_i}}^l{{{\bar{\theta }} }_l} + {\underline{\Phi }} _{ {{{\underline{\sigma }} }_i}}^l{{{\underline{\theta }} }_l}} \right) } }}{{\sum \nolimits _{l = 1}^{n_r} {\left( {{\bar{\Phi }} _{ {{{\underline{\sigma }} }_i}}^l + {\underline{\Phi }} _{{{{\underline{\sigma }} }_i}}^l} \right) } }} \end{aligned}$$
    (17)

    The output (15) is rewritten as:

    $$\begin{aligned} {\hat{y}}\left( {x|\theta } \right) = {\theta ^T}\zeta \end{aligned}$$
    (18)

    where

    $$\begin{aligned} {\zeta ^T} = \left[ {{{{\underline{\zeta }} }_1},...,{{{\underline{\zeta }} }_{{n_r}}},{{{\bar{\zeta }} }_1},...,{{{\bar{\zeta }} }_{{n_r}}}} \right] \end{aligned}$$
    (19)
    $$\begin{aligned} {\theta ^T} = \left[ {{{{\underline{\theta }} }_1},...,{{{\underline{\theta }} }_{{n_r}}},{{{\bar{\theta }} }_1},...,{{{\bar{\theta }} }_{{n_r}}}} \right] \end{aligned}$$
    (20)
    $$\begin{aligned} \begin{array}{l} {{\underline{\zeta }} _l} = \frac{{\sum \nolimits _{i = 1}^{{n_\sigma }} {{{{\underline{\sigma }} }_i}{\underline{\Phi }} _{{{{\underline{\sigma }} }_i}}^l} }}{{\sum \nolimits _{i = 1}^{{n_\sigma }} {\left( {{{{\underline{\sigma }} }_i} + {{{\bar{\sigma }} }_i}} \right) } \sum \nolimits _{l = 1}^{{n_r}} {\left( {{\bar{\Phi }} _{{{{\underline{\sigma }} }_i}}^l + {\underline{\Phi }} _{{{{\underline{\sigma }} }_i}}^l} \right) } }} + \\ \,\,\,\,\,\,\,\frac{{\sum \nolimits _{i = 1}^{{n_\sigma }} {{{{\bar{\sigma }} }_i}{\underline{\Phi }} _{{{{\bar{\sigma }} }_i}}^l} }}{{\sum \nolimits _{i = 1}^{{n_\sigma }} {\left( {{{{\underline{\sigma }} }_i} + {{{\bar{\sigma }} }_i}} \right) } \sum \nolimits _{l = 1}^{{n_r}} {\left( {{\bar{\Phi }} _{{{{\bar{\sigma }} }_i}}^l + {\underline{\Phi }} _{{{{\bar{\sigma }} }_i}}^l} \right) } }} \end{array} \end{aligned}$$
    (21)
    $$\begin{aligned} \begin{array}{l} {{{\bar{\zeta }} }_l} = \frac{{\sum \nolimits _{i = 1}^{{n_\sigma }} {{{{\underline{\sigma }} }_i}{\bar{\Phi }} _{{{{\underline{\sigma }} }_i}}^l} }}{{\sum \limits _{i = 1}^{{n_\sigma }} {\left( {{{{\underline{\sigma }} }_i} + {{{\bar{\sigma }} }_i}} \right) } \sum \nolimits _{l = 1}^{{n_r}} {\left( {{\bar{\Phi }} _{{{{\underline{\sigma }} }_i}}^l + {\underline{\Phi }} _{{{{\underline{\sigma }} }_i}}^l} \right) } }} + \\ \,\,\,\,\,\,\,\frac{{\sum \nolimits _{i = 1}^{{n_\sigma }} {{{{\bar{\sigma }} }_i}{\bar{\Phi }} _{{{{\bar{\sigma }} }_i}}^l} }}{{\sum \nolimits _{i = 1}^{{n_\sigma }} {\left( {{{{\underline{\sigma }} }_i} + {{{\bar{\sigma }} }_i}} \right) } \sum \nolimits _{l = 1}^{{n_r}} {\left( {{\bar{\Phi }} _{{{{\bar{\sigma }} }_i}}^l + {\underline{\Phi }} _{{{{\bar{\sigma }} }_i}}^l} \right) } }} \end{array} \end{aligned}$$
    (22)
Fig. 3
figure 3

Type-3 FS

Full size image

4 Observer-based control policy

To tackle the complexities of the problem, the control signal (5) is modified and rewritten as follows:

$$\begin{aligned} u= & {} {\left( {{\hat{b}} ( {\hat{\varvec{x}}}) + \varepsilon \mathrm{sign}\left( {{\hat{b}} \left( {\hat{\varvec{x}}} \right) } \right) } \right) ^{ - 1}}\nonumber \\&\times \left[ { -{{\hat{a}} ( {\hat{\varvec{x}}})} + r^{(n)} - {\mathcal {K}}_c^T \hat{{\varvec{e}}} + {u_s}} \right] \end{aligned}$$
(23)

where \( {\hat{\varvec{x}}} /{\hat{a}} ( {\hat{\varvec{x}}}) / {\hat{b}} ( {\hat{\varvec{x}}}) / \hat{{\varvec{e}}} \) denote the estimates of \( {{\varvec{x}}} / a ( {{\varvec{x}}}) / b ( {{\varvec{x}}}) / {{\varvec{e}}} \). Furthermore, a small positive constant \(\varepsilon \) in the term \(\varepsilon \mathrm{sign}\left( {{\hat{b}} \left( {\hat{\varvec{x}}} \right) } \right) \) in (23) provides us the ability to solve the singularity of the control signal u and \(\mathrm{sign}\left( {{\hat{b}} \left( {\hat{\varvec{x}}} \right) } \right) \) denotes a signum function described as follows:

$$\begin{aligned} {\mathrm{sign}}\left( {{\hat{b}} \left( {{\hat{\varvec{x}}}} \right) } \right) = \left\{ \begin{array}{*{20}{c}} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\, {{\hat{b}} \left( {\hat{\varvec{x}}} \right) } \ge 0}\\ {0\,\,\,\,\,\,\,\,\,\,\,\,\, {{\hat{b}} \left( {\hat{\varvec{x}}} \right) } < 0} \end{array} \right. \end{aligned}$$
(24)

The adaptation law \({u_s}\) is designed to diminish the undesirable effects of the errors and disturbances preserving the robustness of the suggested control method. Through adding and subtracting the term \(\left( {{\hat{b}} ( {\hat{\varvec{x}}}) + \varepsilon \mathrm{sign}\left( {{\hat{b}} \left( {\hat{\varvec{x}}} \right) } \right) } \right) u \), Eq. (3) will be written as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \mathop {\mathbf{x}}\limits ^{.} = \Xi {\mathbf{x}} + \Pi \left( \begin{array}{l} a({\mathbf{x}}) + \left[ b({\mathbf{x}}) - {\hat{b}}(\widehat{\mathbf{x}}) - \varepsilon \mathrm{sign}\left( {{\hat{b}}\left( {\widehat{\mathbf{x}}} \right) } \right) \right] u\\ + \left[ {{\hat{b}}(\widehat{\mathbf{x}}) + \varepsilon \mathrm{sign}\left( {{\hat{b}}\left( {\widehat{\mathbf{x}}} \right) } \right) } \right] u + \delta (t) \end{array} \right) \\ y = {\Psi ^T}{\mathbf{x}} \end{array} \right. \nonumber \\ \end{aligned}$$
(25)

Moreover, employing (23) for (25) results in

$$\begin{aligned} \dot{{\varvec{e}}}= & {} \Xi {\varvec{e}} - \Pi {\mathcal {K}}_c^T \hat{{\varvec{e}}} + \Pi \left( a ({\varvec{x}}) - {\hat{a}} ( {\hat{\varvec{x}}}) \right. \nonumber \\&+ \left. \left[ b ({\varvec{x}}) - {{\hat{b}} ( {\hat{\varvec{x}}}) - \varepsilon \mathrm{sign}\left( {{\hat{b}} \left( {\hat{\varvec{x}}} \right) } \right) } \right] u \right. \nonumber \\&\left. + \, u_s + \delta (t) \right) \nonumber \\ {{\varvec{e}}_1}= & {} {\Psi ^T} {\varvec{e}} \end{aligned}$$
(26)

where \({{\varvec{e}}_1} = y - r = {x_1} - r\). Regarding (26), to estimate the vector \({\varvec{e}} \), the observer is utilized in the form of the following

$$\begin{aligned} \begin{array}{*{20}{l}} {\dot{{\hat{\varvec{e}}}}} = \left( {\Xi - \Pi {{{\mathcal {K}}}}_c^T} \right) {{\hat{\varvec{e}}}} + {{{{\mathcal {L}}}}_0}{\Psi ^T}{{\varvec{\tilde{e}}}}\\ {{{\varvec{{\hat{e}}}}}_1} = {\Psi ^T}{{{\varvec{\tilde{e}}s}}} \end{array} \end{aligned}$$
(27)

where the gains \( {\mathcal {L}}_0 = {\left[ {{l_{o1}},{l_{o2}},...,{l_{on}}} \right] ^T} \in {{\mathbb {R}}^n}\) is designed to make the characteristic polynomial \(\Xi - {\mathcal {L}}_0 {\Psi ^T} \) Hurwitz. By subtracting Eq. (27) from (26), the estimation error dynamic \(\dot{{\tilde{\varvec{{e}}}}}\) is acquired as follows:

$$\begin{aligned} {\dot{{\tilde{\varvec{e}}}}}= & {} \left( {\Xi - {{{{\mathcal {L}}}}_0}{\Psi ^T}} \right) {{\tilde{\varvec{e}}}} \nonumber \\&+ \Pi \left( {a({\mathbf{x}}) - {\hat{a}}(\widehat{\mathbf{x}}) \left[ {b({\mathbf{x}}) - {\hat{b}}(\widehat{\mathbf{x}}) - \varepsilon \mathrm{sign}\left( {{\hat{b}}\left( {\widehat{\mathbf{x}}} \right) } \right) } \right] u }\right. \nonumber \\&\left. + \, {u_s} + \delta (t) \right) \nonumber \\ {\tilde{\varvec{e}}_1}= & {} {\Psi ^T}{{\tilde{\varvec{e}}}} \end{aligned}$$
(28)

5 Stability analysis

This section deals with the stability analysis and convergence of the error signals via the Lyapunov tools and Barbalat’s approach. To analyze the stability, adding and subtracting \({\hat{a}}^* ( {\hat{\varvec{x}}}) \) and \( {\hat{b}}^* ( {\hat{\varvec{x}}}) u\) in (28) leads to

$$\begin{aligned} \dot{\tilde{{\varvec{e}}}}&= \left( \Xi - {\mathcal {L}}_0 {\Psi ^T} \right) \tilde{{\varvec{e}}} + \Pi \left( a ({\varvec{x}}) - {\hat{a}}^* ( {\hat{\varvec{x}}}) \right. \nonumber \\&\quad \left. + \left[ b ({\varvec{x}}) - {{\hat{b}}^* ( {\hat{\varvec{x}}}) - \varepsilon \mathrm{sign}\left( {{\hat{b}} \left( {\hat{\varvec{x}}} \right) } \right) } \right] u \right. \nonumber \\&\quad \left. + \left[ {\hat{b}}^* ( {\hat{\varvec{x}}}) - {\hat{b}} ( {\hat{\varvec{x}}}) \right] u \right. \nonumber \\&\quad \left. + {\hat{a}}^* ( {\hat{\varvec{x}}}) - {\hat{a}} ( {\hat{\varvec{x}}}) + u_s + \delta (t) \right) \nonumber \\ {\tilde{{\varvec{e}}}_1}&= {\Psi ^T} \tilde{{\varvec{e}}} \end{aligned}$$
(29)

From (18), \(\left[ {\hat{a}}^* ( {\hat{\varvec{x}}}) - {\hat{a}}( {\hat{\varvec{x}}}) \right] \) and \( \left[ {\hat{b}}^* ( {\hat{\varvec{x}}}) - {\hat{b}}( {\hat{\varvec{x}}}) \right] \) are expressed as:

$$\begin{aligned} \begin{array}{l} \left[ {\hat{a}}^* ( {\hat{\varvec{x}}}) - {\hat{a}}( {\hat{\varvec{x}}}) \right] = {\left( {\theta _a^ * - \theta _a^{}} \right) ^T}\zeta _a^{} = {\tilde{\theta }} _a^T\zeta _a^{}\\ \left[ {\hat{b}}^* ( {\hat{\varvec{x}}}) - {\hat{b}}( {\hat{\varvec{x}}}) \right] = {\left( {\theta _b^ * - \theta _b^{}} \right) ^T}\zeta _b^{} = {\tilde{\theta }} _b^T\zeta _b^{} \end{array} \end{aligned}$$
(30)

The approximation errors \({J_a}\) and \({J_b}\) are defined as:

$$\begin{aligned} \begin{array}{l} {J_a} \buildrel \Delta \over = a ( {{\varvec{x}}}) - {\hat{a}}^* ( {\hat{\varvec{x}}}) \\ {J_b} \buildrel \Delta \over = b ( {{\varvec{x}}}) - {\hat{b}}^* ( {\hat{\varvec{x}}}) \end{array} \end{aligned}$$
(31)

Note that \(a ( {{\varvec{x}}}) \) and \(b ( {{\varvec{x}}})\) are bounded which leads to the boundedness of \({J_a} \) and \({J_b}\) in (31) with the upper bounds \({{\bar{J}}_a}\) and \({{\bar{J}}_b}\). Now, regarding (30) and (31), one has

$$\begin{aligned} \dot{\tilde{{\varvec{e}}}}&= \left( \Xi - {\mathcal {L}}_0 {\Psi ^T} \right) \tilde{{\varvec{e}}} \nonumber \\&\quad + \Pi \left( J_a + \left[ { J_b - \varepsilon \mathrm{sign}\left( {{\hat{b}} \left( {\hat{\varvec{x}}} \right) } \right) } \right] u \right. \nonumber \\&\quad \left. + \, {\tilde{\theta }} _b^T\zeta _b u + {\tilde{\theta }} _a^T\zeta _a+ u_s + \delta (t) \right) \nonumber \\ {\tilde{{\varvec{e}}}_1}&= {\Psi ^T} \tilde{{\varvec{e}}} \end{aligned}$$
(32)

Select the Lyapunov function as:

$$\begin{aligned} V(t)= & {} \frac{1}{2} {\hat{{\varvec{e}}}}^T {{\mathcal {P}}_c} {\hat{{\varvec{e}}}} \nonumber \\&+ \frac{1}{2} {\tilde{{\varvec{e}}}}^T {{\mathcal {P}}_o} {\tilde{{\varvec{e}}}}+ \frac{1}{{2{\gamma _a}}}{\tilde{\theta }} _a^T{\tilde{\theta }} _a^{} + \frac{1}{{2{\gamma _b}}}{\tilde{\theta }} _b^T{\tilde{\theta }} _b^{}\nonumber \\&+ \frac{1}{{2{\gamma _{{{\hat{{\bar{J}}}}_a}}}}}{\left( {{{{\bar{J}}}_a} - {{\hat{{\bar{J}}}}_a}} \right) ^2} + \frac{1}{{2{\gamma _{{{\hat{{\bar{J}}}}_b}}}}}{\left( {{{{\bar{J}}}_b} - {{\hat{{\bar{J}}}}_b}} \right) ^2}\nonumber \\&+ \frac{1}{{2{\gamma _{\hat{{\bar{\delta }}}}}}}{\left( {{\bar{\delta }} - {\hat{{\bar{\delta }}}}} \right) ^2} \end{aligned}$$
(33)

where \( \hat{{\bar{J}}}_a/ \hat{{\bar{J}}}_b / \hat{{\bar{\delta }}} \), are estimations of \( {{\bar{J}}}_a/ {{\bar{J}}}_b / {{\bar{\delta }}} \) which are the upper bounds of \( J_a / J_b / \delta \). Moreover, defining \({\tilde{\theta }} _a^{} = \theta _a^ * - \theta _a^{}\,and\,{\tilde{\theta }} _b^{} = \theta _b^ * - \theta _b^{}\), \({\gamma _{{{\hat{{\bar{J}}}}_a}}}\), \({\gamma _{{{\hat{\bar{J}}}_b}}}\), \({\gamma _a}\) and \({\gamma _b}\) are the adaptation rate of \({{\hat{{\bar{J}}}}_a}\), \({{\hat{{\bar{J}}}}_b}\) , \(\theta _a^{}\) and \(\theta _b^{}\), respectively. \({{\mathcal {P}}_c}, {{\mathcal {P}}_o} \in {\mathbb {R}}^{n \times n}\) are positive definite matrices satisfying the following

(34)

where \({\Xi _c} = \Xi - \Pi {\mathcal {K}}_c^T \), \({\Xi _o} = \Xi - {\mathcal {L}}_o^{}{\Psi ^T}\), and \({Q_c}/{Q_o}\) are the arbitrary \(n \times n\) positive definite matrices. Utilizing (32), the time derivative of V is in the form of the following

(35)

Considering the terms \({\tilde{\theta }} _a^T\zeta _a^{}{ {\tilde{{\varvec{e}}}} ^T}{{\mathcal {P}}_o}\Pi - \frac{1}{{{\gamma _a}}}{\tilde{\theta }} _a^T{\dot{\theta }} _a^{}\) and \({\tilde{\theta }} _b^T\zeta _b^{}{ {\tilde{{\varvec{e}}}} ^T}{{\mathcal {P}}_o} \Pi u - \frac{1}{{{\gamma _b}}}{\tilde{\theta }} _b^T{\dot{\theta }} _b^{}\), the adaptation laws of \(\theta _a^{}/ \theta _b^{}\) can be obtained as follows:

$$\begin{aligned} \begin{array}{l} {{{\dot{\theta }} }_a} \buildrel \Delta \over = {\gamma _a}{ \tilde{{\varvec{e}}} ^T}{{\mathcal {P}}_o}\Pi {\zeta _a}\\ {{{\dot{\theta }} }_b} \buildrel \Delta \over = {\gamma _b}{ \tilde{{\varvec{e}}} ^T}{{\mathcal {P}}_o}\Pi {\zeta _b}u \end{array} \end{aligned}$$
(36)

Note that \({\tilde{{\varvec{e}}} ^T }{{\mathcal {P}}_o}\Pi \) is scalar. Regarding (34), (36), and \(\dot{V}(t)\), and after some calculations, it can be deduced that

$$\begin{aligned} \dot{V}(t)&\le - \frac{1}{2} \hat{{\varvec{e}}} ^T {{\mathcal {Q}}_c} \hat{{\varvec{e}}} - \frac{1}{2} \tilde{{\varvec{e}}} ^T {{\mathcal {Q}}_o} \tilde{{\varvec{e}}} + \hat{{\varvec{e}}} ^T {\mathcal {P}}_c {\mathcal {L}}_o \tilde{{\varvec{e}}}_1 \nonumber \\&\quad + \left( {\bar{J}}_a - \hat{{\bar{J}} }_a \right) \left[ \left| \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi \right| - \frac{1}{{{\gamma _{{{\hat{{\bar{J}}}}_a}}}}} \dot{\hat{{\bar{J}}} }_a \right] \nonumber \\&\quad + \left( {\bar{J}}_b - \hat{{\bar{J}} }_b \right) \left[ \left| \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi \right| \left| u \right| - \frac{1}{{{\gamma _{{{\hat{{\bar{J}}}}_b}}}}} \dot{\hat{{\bar{J}}} }_b \right] \nonumber \\&\quad + \left( {\bar{\delta }} - \hat{{\bar{\delta }} } \right) \left[ \left| \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi \right| - \frac{1}{{{\gamma _{{{\hat{{\bar{\delta }}}}}}}}} \dot{\hat{{\bar{\delta }}} } \right] \nonumber \\&\quad + \left| \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi \right| \hat{{{\bar{J}}}}_a + \left| \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi \right| \left| u \right| \hat{ {{\bar{J}}}}_b \nonumber \\&\quad - \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi \varepsilon \mathrm{sign}\left( {{\hat{b}}( {{\hat{\varvec{x}}}} )} \right) u+ \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi u_s \nonumber \\&\quad + \left| \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi \right| \hat{{\bar{\delta }}} \end{aligned}$$
(37)

According to (37), the adaptation laws of \({{\hat{\bar{J}}}_a}\), \({{\hat{{\bar{J}}}}_b}\) and \(\hat{{\bar{\delta }}}\) can be defined as:

$$\begin{aligned} \begin{array}{l} {{\dot{\hat{{\bar{J}}}}}_a} \buildrel \Delta \over = {\gamma _{{{\hat{{\bar{J}}}}_a}}}\left| \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi \right| \\ {{\dot{\hat{{\bar{J}}}}}_b} \buildrel \Delta \over = {\gamma _{{{\hat{{\bar{J}}}}_b}}}\left| \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi \right| \left| u \right| \\ \dot{\hat{{\bar{\delta }}}} \buildrel \Delta \over = {\gamma _{\hat{{\bar{\delta }}}}}\left| \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi \right| \end{array} \end{aligned}$$
(38)

Using adaptation laws (38), Eq. (37) can be rewritten as follows:

$$\begin{aligned} \dot{V}(t)&\le - \frac{1}{2} \hat{{\varvec{e}}} ^T {{\mathcal {Q}}_c} \hat{{\varvec{e}}} - \frac{1}{2} \tilde{{\varvec{e}}} ^T {{\mathcal {Q}}_o} \tilde{{\varvec{e}}} + \hat{{\varvec{e}}} ^T {\mathcal {P}}_c {\mathcal {L}}_o \tilde{{\varvec{e}}}_1 \nonumber \\&\quad + \left| \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi \right| \hat{{{\bar{J}}}}_a + \left| \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi \right| \left| u \right| \hat{ {{\bar{J}}}}_b\nonumber \\&\quad - \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi \varepsilon \mathrm{sign}\left( {{\hat{b}}( {{\hat{\varvec{x}}}} )} \right) u\nonumber \\&\quad + \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi u_s + \left| \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi \right| \hat{{\bar{\delta }}} \end{aligned}$$
(39)

Considering (39), the compensator \(\,{u_s}\) is designed as

(40)

From (39) and (40), and considering:

$$\begin{aligned} \mathrm{sign}\left( {{{{{\tilde{\varvec{e}}}}}^T}{P_o}\Pi } \right) \cdot \left( {{{{{\tilde{\varvec{e}}}}}^T}{P_o}\Pi } \right) = \left| {{{{{\tilde{\varvec{e}}}}}^T}{P_o}\Pi } \right| \end{aligned}$$
(41)

and

$$\begin{aligned} \frac{{\mathrm{sign}\left( {{{{{\tilde{\varvec{e}}}}}^T}{P_o}\Pi } \right) \cdot \left( {{{{{\tilde{\varvec{e}}}}}^T}{P_o}\Pi } \right) }}{{\left| {{{{{\tilde{\varvec{e}}}}}^T}{P_o}\Pi } \right| + \varepsilon }} \approx 1 \end{aligned}$$
(42)

one achieves that

$$\begin{aligned} \dot{V}(t) \le - \frac{1}{2} \hat{{\varvec{e}}} ^T {{\mathcal {Q}}_c} \hat{{\varvec{e}}} - \frac{1}{2} \tilde{{\varvec{e}}} ^T {{\mathcal {Q}}_o} \tilde{{\varvec{e}}} \end{aligned}$$
(43)

To prove \(\mathop {\lim }\limits _{t \rightarrow \infty } \, {\hat{{\varvec{e}}} } = 0\) and \(\mathop {\lim }\limits _{t \rightarrow \infty } \,\tilde{{\varvec{e}}} = 0\), one has to demonstrate \({\hat{{\varvec{e}}} } \in {\ell _2}\, ,{\tilde{{\varvec{e}}} } \in {\ell _2}\) and the boundedness of \( \dot{{\hat{{\varvec{e}}} } } / \dot{{\tilde{{\varvec{e}}} } } \). Moreover, we have

$$\begin{aligned} \int _0^t {\dot{V}(\tau )} d\tau = V(t) - V(0) \end{aligned}$$
(44)

Regarding the properties of the Lyapunov function, it is crystal clear that

$$\begin{aligned} - \int _0^t {\dot{V}(\tau )} d\tau = V(0) - V(t) \le V(0) < \infty \end{aligned}$$
(45)

Moreover, it is evident that

$$\begin{aligned}&- \frac{1}{2} \hat{{\varvec{e}}} ^T {{\mathcal {Q}}_c} \hat{{\varvec{e}}} \le - \frac{1}{2}{\lambda _{\min }}\left( {{\mathcal {Q}}_c} \right) {\left\| \hat{ {{\varvec{e}}} } \right\| ^2}, \,\,\,\,\,\,\ - \frac{1}{2} \tilde{{\varvec{e}}} ^T {{\mathcal {Q}}_o} \tilde{{\varvec{e}}} \le \nonumber \\&\quad - \frac{1}{2}{\lambda _{\min }}\left( {{\mathcal {Q}}_o} \right) {\left\| \tilde{ {{\varvec{e}}} } \right\| ^2}, \end{aligned}$$
(46)

in which \({\lambda _{\min }}\left( {{ {{\mathcal {Q}}_c}}} \right) \) and \({\lambda _{\min }}\left( {{ {{\mathcal {Q}}_o}}} \right) \) denote the minimum eigenvalues of \({ {{\mathcal {Q}}_c}}\) and \({ {{\mathcal {Q}}_o}}\) respectively, then

$$\begin{aligned} \begin{array}{l} \frac{1}{2}\int _0^t {\left[ {{\lambda _{\min }}\left( {{Q_c}} \right) {{\left\| { \hat{ {{\varvec{e}}} } (\tau )} \right\| }^2} + {\lambda _{\min }}\left( {{Q_o}} \right) {{\left\| { \tilde{ {{\varvec{e}}} } (\tau )} \right\| }^2}} \right] } \,d\tau< \infty \\ \quad \Rightarrow \sqrt{\int _0^t {\left[ {{{\left\| { \hat{ {{\varvec{e}}} } (\tau )} \right\| }^2} + {{\left\| { \tilde{ {{\varvec{e}}} } (\tau )} \right\| }^2}} \right] } } \,d\tau< \infty \\ \quad \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\sqrt{\int _0^t {{{\left\| { \hat{ {{\varvec{e}}} } (\tau )} \right\| }^2}} } \,d\tau< \infty }\\ {\sqrt{\int _0^t {{{\left\| { \tilde{ {{\varvec{e}}} } (\tau )} \right\| }^2}} } \,d\tau < \infty } \end{array}} \right. \end{array} \end{aligned}$$
(47)

Therefore, one can get that \( \hat{ {{\varvec{e}}} } \in {\ell _2}\,, \tilde{ {{\varvec{e}}} } \in {\ell _2}\). Moreover, regarding (27), (32), and assuming that the control signal and approximation errors \({J_a/J_b}\) are bounded, one has \( \dot{\hat{ {{\varvec{e}}} } } \in {\ell _\infty }\,, \dot{\tilde{ {{\varvec{e}}} }} \in {\ell _\infty }\). As a sequence, utilizing the Barbalat’s lemma results in

$$\begin{aligned} \begin{array}{l} \mathop {\lim }\limits _{t \rightarrow \infty } \, \hat{ {{\varvec{e}}} } (t) = 0\\ \mathop {\lim }\limits _{t \rightarrow \infty } \, \tilde{ {{\varvec{e}}} } (t) = 0 \end{array} \end{aligned}$$
(48)

Remark 1

The IT3FLSs have a better ability to estimate the uncertainties. So, instead of considering upper bounds for uncertainties in a conservative approach, IT3FLSs by giving a better estimation efficiency, help in the reduction of conservatism.

6 Practical implementation

Example 1

In this section, the capability of the designed control strategy is experimentally scrutinized. The setup is depicted in Fig. 4. The robot has two conventional wheels with a diameter of 7 cm that are coupled to two high-precision motor steppers and two idle pins to keep it balanced. The robot contains eight sharp sensors on each of its four sides, as well as an MPU6050 angle acceleration sensor at its center of gravity. The motors are mounted on a 1.5 mm aluminum chassis that serves as the robot’s bottom plate. Two-phase stepper motors provide a step precision of 1.8 degrees per step. The surface of the chassis is lifted using four 7 cm spacers in order to install the PCB on it. The NRF24L01 radio transmitter module is used to communicate between the robot and the laptop. This module’s communication modulation is GFSK, and the chip’s communication frequency is 2.4 GHz. The objective is to design a control law to ensure that the robot follows the desired path.

Fig. 4
figure 4

Example 1: Experimental setup

Full size image

The desired path is considered to be the first state of following chaotic system:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {D_t^{0.97}{y_{11}} = 35\left( {{y_{12}} - {y_{11}}} \right) + 35{y_{12}}{y_{13}}}\\ {D_t^{0.97}{y_{12}} = 25{y_{11}} - 5{y_{11}}{y_{13}} + {y_{12}} + {y_{14}}}\\ {D_t^{0.97}{y_{13}} = {y_{11}}{y_{12}} - 4{y_{13}}}\\ {D_t^{0.97}{y_{14}} = - 35{y_{12}}} \end{array}} \right. \end{aligned}$$
(49)

The path following performance is depicted in Fig. 5. It is perceptible that the robot tracks the prescribed chaotic path by implementing the suggested controller (23).

Fig. 5
figure 5

Example 1: The path-following response

Full size image

One of the applications of the suggested approach is to design a secure path for patrol robots. As the robots follow the designed chaotic reference signal, the prediction of their path gets harder. In this way, the vertical coordinate represents displacement. In another way, the chaotic reference can be used for the speed of the robot. In other words, the robot moves in a straight line at a chaotic variable speed.

7 Computer simulations

Three computer simulations will be performed in this section to analyze the satisfaction of both observer and control objectives with unknown models/states, uncertainties, and external disturbances. The designing process is illustrated in detail for the first example. For the other examples, the process is similar. In all examples, the range of input space is normalized into − 1 and 1, and for each input, 3 MFs are considered. The centers of MFs are considered to be − 1, 0, and 1, to cover the input range.

Example 2

Based on the Euler-Lagrange equations, the flexible joint robot subject to unknown models is studied (see [44, 45] for more details)

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {I{{\ddot{r}}_1} + \varrho g \aleph \sin ({r_1}) + \rho ({r_1} - {r_2}) = 0}\\ {\mu {{\ddot{r}}_2} - \rho ({r_1} - {r_2}) = u\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \end{array}} \right. \end{aligned}$$
(50)

The system dynamic is converted to the form of:

$$\begin{aligned} \begin{array}{l} {{\dot{x}}_1} = {x_2}\\ {{\dot{x}}_2} = - \frac{{\varrho g \aleph }}{I}\sin ({x_1}) - \frac{\rho }{I}\left( {{x_1} - {x_3}} \right) \\ {{\dot{x}}_3} = {x_4}\\ {{\dot{x}}_4} = \frac{\rho }{\mu }\left( {{x_1} - {x_3}} \right) + \frac{1}{\mu }u \end{array} \end{aligned}$$
(51)

Utilizing a transformation results in

$$\begin{aligned} {{\dot{z}}_1}= & {} {z_2}\nonumber \\ {{\dot{z}}_2}= & {} {z_3}\nonumber \\ {{\dot{z}}_3}= & {} {z_4}\nonumber \\ {{\dot{z}}_4}= & {} - \left( {\frac{{\varrho g \aleph }}{I}\cos ({z_1}) + \frac{\rho }{I} + \frac{\rho }{J}} \right) {z_3}\nonumber \\&+ \frac{{\varrho g \aleph }}{I}\left( {z_2^2 - \frac{\rho }{\mu }} \right) \sin ({z_1}) + \frac{\rho }{{I \mu }}u \end{aligned}$$
(52)

in which,

$$\begin{aligned} \begin{array}{l} {z_1} = {x_1}\\ {z_2} = {x_2}\\ {z_3} = - \frac{{\varrho g \aleph }}{I}\sin ({x_1}) - \frac{\rho }{I}\left( {{x_1} - {x_3}} \right) \\ {z_4} = - \frac{{\varrho g \aleph }}{I}{x_2}\cos ({x_1}) - \frac{\rho }{I}\left( {{x_2} - {x_4}} \right) \end{array} \end{aligned}$$
(53)

Now, (52) is expressed as:

$$\begin{aligned} \begin{array}{l} {{\dot{z}}_i} = {z_{i + 1}}\,,i = 1,2,3\\ {{\dot{z}}_4} = a(z) + u + \delta \\ z = {\left[ {\begin{array}{*{20}{c}} {{z_1}}&{}{{z_2}}&{}{{z_3}}&{}{{z_4}} \end{array}} \right] ^T} \end{array} \end{aligned}$$
(54)

The system parameters are declared as:

\(g = 9.80m/{s^2},\,\varrho = 2kg,\,\rho = 2N/m,\,I = 2Kg{m^2}\) and \(\aleph = 1m\). Moreover, \( \delta \) denotes white noise with the static characteristic (\( N \sim (0,0.1\)), affecting the performance of the system. To implement the suggested observer-based, one has the following

  1. 1.

    The gains \({{\mathcal {K}}_c}\) and \({{\mathcal {L}}_o}\) should adjust the roots of \({s^4} + {k_{c4}}{s^3} + {k_{c3}}{s^2} + {k_{c2}}s + {k_{c1}}\) and \({s^4} + {l_{o1}}{s^3} + {l_{o2}}{s^2} + {l_{o3}}s + {l_{o4}}\) as \(-10\) and \(-20\), respectively.

  2. 2.

    Solving (34), matrices \({{\mathcal {P}}_c}\) and \({{\mathcal {P}}_o}\) are selected as:

    $$\begin{aligned} \begin{array}{l} \,{{\mathcal {Q}}_c} = {{\mathcal {Q}}_o} = {10^{ - 3}}\left[ {\begin{array}{*{20}{c}} 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{array}} \right] \\ \,{{\mathcal {P}}_c} = \left[ {\begin{array}{*{20}{c}} {{\mathrm{1}}{\mathrm{.3881}}}&{}\quad {{\mathrm{0}}{\mathrm{.6549}}}&{}\quad {{\mathrm{0}}{\mathrm{.0955}}}&{}\quad 0\\ {{\mathrm{0}}{\mathrm{.6549}}}&{}\quad {{\mathrm{0}}{\mathrm{.3297}}}&{}\quad {{\mathrm{0}}{\mathrm{.0542}}}&{}\quad {{\mathrm{0}}{\mathrm{.0003}}}\\ {{\mathrm{0}}{\mathrm{.0955}}}&{}\quad {{\mathrm{0}}{\mathrm{.0542}}}&{}\quad {{\mathrm{0}}{\mathrm{.0120}}}&{}\quad {{\mathrm{0}}{\mathrm{.0001}}}\\ 0&{}\quad {{\mathrm{0}}{\mathrm{.0003}}}&{}\quad {{\mathrm{0}}{\mathrm{.0001}}}&{}\quad {\mathrm{0}} \end{array}} \right] \\ {{\mathcal {P}}_o} = \left[ {\begin{array}{*{20}{c}} {{\mathrm{313}}{\mathrm{.5117}}}&{}\quad {{\mathrm{- 0}}{\mathrm{.0005}}}&{}\quad {{\mathrm{- 0}}{\mathrm{.5047}}}&{}\quad {{\mathrm{0}}{\mathrm{.0005}}}\\ {{\mathrm{- 0}}{\mathrm{.0005}}}&{}\quad {{\mathrm{0}}{\mathrm{.5047}}}&{}\quad {{\mathrm{- 0}}{\mathrm{.0005}}}&{}\quad {{\mathrm{- 0}}{\mathrm{.0040}}}\\ {{\mathrm{- 0}}{\mathrm{.5047}}}&{}\quad {{\mathrm{- 0}}{\mathrm{.0005}}}&{}\quad {{\mathrm{0}}{\mathrm{.0040}}}&{}\quad {{\mathrm{- 0}}{\mathrm{.0005}}}\\ {{\mathrm{0}}{\mathrm{.0005}}}&{}\quad {{\mathrm{- 0}}{\mathrm{.0040}}}&{}\quad {{\mathrm{- 0}}{\mathrm{.0005}}}&{}\quad {{\mathrm{0}}{\mathrm{.0001}}} \end{array}} \right] \end{array} \end{aligned}$$
    (55)
  3. 3.

    Given \(y = {z_1} = {x_1}\) and \({r}(s) = \frac{1}{s} \frac{{10}}{{s + 10}}\), solving (27) to obtain \({\hat{z}} = {\left[ {\begin{array}{*{20}{c}} {{{{\hat{z}}}_1}}&{{{{\hat{z}}}_2}}&{{{{\hat{z}}}_3}}&{{{{\hat{z}}}_4}} \end{array}} \right] ^T}\).

  4. 4.

    The proposed IT3FLS \({\hat{a}}({\hat{z}})\) is implemented for the approximation of a(z) in (54). Note that 3 MFs are employed for inputs.

  5. 5.

    The adaptation rates are \({\gamma _{{{\hat{{\bar{J}}}}_a}}} = 0.5,\,{\gamma _{\hat{{\bar{\delta }}}}} = 0.5,\,{\gamma _{{\theta _a}}} = 0.1\)

  6. 6.

    Regarding (23), one can design

    $$\begin{aligned} {u_s}&= - \tanh \left( \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi \right) \left\{ {{\hat{{\bar{J}}}}_a} + {\hat{{\bar{\delta }}}} +{\varepsilon \tanh \left( {{\hat{b}}(\widehat{\mathbf{x}})} \right) u}\right. \nonumber \\&\quad \left. + \frac{ \hat{{\varvec{e}}} ^T {\mathcal {P}}_c {\mathcal {L}}_o \tilde{{\varvec{e}}}_1 }{ \left| \tilde{{\varvec{e}}}^T {\mathcal {P}}_o \Pi \right| + 0.001 \,} \right\} \end{aligned}$$
    (56)
Fig. 6
figure 6

Example 2: The tracking response

Full size image
Fig. 7
figure 7

Example 2: Control signal

Full size image

Simulation results on a flexible joint robot are demonstrated in Figs. 6 and 7, while Fig. 6 portrays the tracking performance/errors. It is obvious that applying the suggested procedure results in stable tracking errors and robust stability of the closed-loop system. Furthermore, Fig. 7 verifies that the variation of the control signal is appropriate.

Example 3

The suggested IT3FLS-based control law is employed to control the two-link robot manipulator. The system dynamic is represented as [46]:

$$\begin{aligned} \begin{array}{l} {H_{11}}{{\ddot{q}}_1} + {H_{12}}{{\ddot{q}}_2} - h{{\dot{q}}_2}{{\dot{q}}_1} - h\left( {{{\dot{q}}_2} + {{\dot{q}}_2}} \right) {{\dot{q}}_2} = {\tau _1}\\ {H_{21}}{{\ddot{q}}_1} + {H_{22}}{{\ddot{q}}_2} + h{{\dot{q}}_1}{{\dot{q}}_1} = {\tau _2} \end{array} \end{aligned}$$
(57)

with

$$\begin{aligned} \begin{array}{l} {H_{11}} = {\alpha _1} + 2{\alpha _3}\cos {q_2} + 2{\alpha _4}\sin {q_2} \varphi \\ {H_{12}} = {H_{21}} = {\alpha _2} + {\alpha _3}\cos {q_2} + {\alpha _4}\sin {q_2}\,\\ {H_{22}} = {\alpha _2}\\ h = {\alpha _3}\sin {q_2} - {\alpha _4}\cos {q_2}\\ {\alpha _1} = {I_1} + {m_1}l_{c1}^2 + {I_e} + {m_e}l_{ce}^2 + {m_e}l_1^2\\ {\alpha _2} = {I_e} + {m_e}l_{ce}^2\,\,\\ {\alpha _3} = {m_e}l_1^{}l_{ce}^{}\cos {\delta _e}\\ {\alpha _4} = {m_e}l_1^{}l_{ce}^{}\sin {\delta _e} \end{array} \end{aligned}$$
(58)

Moreover, it is easy to acquire that

$$\begin{aligned} {{\dot{x}}_{11}}= & {} {x_{12}}\nonumber \\ {{\dot{x}}_{12}}= & {} {a_1}({x_{11}},{x_{12}},{x_{21}},{x_{22}},{u_2})\nonumber \\&+ {b_1}({x_{11}},{x_{12}},{x_{21}},{x_{22}})\,{u_1}\nonumber \\ {{\dot{x}}_{21}}= & {} {x_{22}}\nonumber \\ {{\dot{x}}_{22}}= & {} {a_2}({x_{11}},{x_{12}},{x_{21}},{x_{22}},{u_1})\nonumber \\&+\, {b_2}({x_{11}},{x_{12}},{x_{21}},{x_{22}})\,{u_2}\nonumber \\ {y_1}= & {} {x_{12}}\,\,\,,\,\,\,{y_2} = {x_{22}}\,\, \end{aligned}$$
(59)

where

Fig. 8
figure 8

Example 3: Tracking performance

Full size image
Fig. 9
figure 9

Example 3: Control signals

Full size image
$$\begin{aligned} \begin{array}{l} {x_{11}} = {q_1},\,{x_{12}} = {{\dot{q}}_1},\,{x_{21}} = {q_2},\,{x_{22}} = {{\dot{q}}_2}\,,{u_1} = {\tau _1},\,{u_2} = {\tau _2}\\ \left[ {\begin{array}{*{20}{c}} {{a_1}}\\ {{a_2}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {{H_{11}}}&{}{{H_{12}}}\\ {{H_{21}}}&{}{{H_{22}}} \end{array}} \right] ^{ - 1}}\left[ {\begin{array}{*{20}{c}} { - h{x_{22}}}&{}{ - h\left( {{x_{22}} + {x_{12}}} \right) }\\ {h{x_{12}}}&{}0 \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{x_{12}}}\\ {{x_{22}}} \end{array}} \right] \\ {b_1} = \frac{{{H_{22}}}}{{{H_{22}}{H_{11}} - {H_{12}}{H_{21}}}}\,\,,\,\,{b_2} = \frac{{{H_{11}}}}{{{H_{22}}{H_{11}} - {H_{12}}{H_{21}}}} \end{array} \end{aligned}$$
(60)

Simulation parameters are \({m_1} = 1\,,\,{l_1} = 1,{m_e} = 2,{\delta _e} = {30^ \circ },\,\,{I_1} = 0.12,{l_{c1}} = 0.5,{I_e} = 0.25,{l_{ce}} = 0.6\) and \({r} = \sin (t)\). Utilizing the suggested method of this paper, \({a_1}\), \({a_2}\), \({b_1}\) and \({b_2}\) in (59) are estimated using the proposed IT3FLS \({{\hat{a}}_1}\), \({{\hat{a}}_2}\), \({{\hat{b}}_1}\) and \({{\hat{b}}_2}\). Note that functions \({{\hat{a}}_1}\) and \({{\hat{a}}_2}\) have five inputs. Moreover, one has the following:

$$\begin{aligned}&{{\mathcal {Q}}_c} = \left[ {\begin{array}{*{20}{c}} 1&{}0\\ 0&{}1 \end{array}} \right] ,\,\,{{\mathcal {P}}_c} = \left[ {\begin{array}{*{20}{c}} {{\mathrm{3}}{\mathrm{.3462}}}&{}\quad {{\mathrm{0}}{\mathrm{.003}}}\\ {{\mathrm{0}}{\mathrm{.003}}}&{}\quad {{\mathrm{0}}{\mathrm{.0193}}} \end{array}} \right] \,,\nonumber \\&{{\mathcal {K}}_c} = {\left[ {\begin{array}{*{20}{c}} {169}&{26} \end{array}} \right] ^T}\nonumber \\&{{\mathcal {L}}_o} = \left[ {\begin{array}{*{20}{c}} 1&{}0\\ 0&{}1 \end{array}} \right] ,\,\,{{\mathcal {P}}_o} = \left[ {\begin{array}{*{20}{c}} {{\mathrm{10}}{\mathrm{.0062}}}&{}\quad { - 0.5}\\ { - 0.5}&{}\quad {{\mathrm{0}}{\mathrm{.0313}}} \end{array}} \right] ,\nonumber \\&{{\mathcal {L}}_o} = {\left[ {\begin{array}{*{20}{c}} {80}&\quad {{\mathrm{1600}}} \end{array}} \right] ^T}\nonumber \\&{\gamma _{{{\hat{{\bar{J}}}}_a}}} = 0.1,\,\,{\gamma _{\hat{{\bar{\delta }}}}} = 0.1,\,\,{\gamma _{{\theta _a}}} = 10,{\mathrm{}}{\gamma _{{\theta _b}}}\nonumber \\&\quad = 10,\,\,{\mathrm{}}{\gamma _{{{\hat{{\bar{w}}}}_b}}} = 0.1,\,\,\,\varepsilon = 0.001{\mathrm{}} \end{aligned}$$
(61)

The time evolutions of errors and the controller are sketched in Figs. 8 and 9, respectively. Regarding simulation analysis, it is vividly clear that the suggested IT3FLS control strategy is able to estimate and stabilize the state variables of unknown dynamics with significant performance and without chattering phenomenon.

Fig. 10
figure 10

Example 4: Tracking performance

Full size image
Fig. 11
figure 11

Example 4: Controls signals

Full size image

Example 4

The control law is implemented for the two inverted pendulums. The dynamics are as follows: (see [47] for detailed discussion)

$$\begin{aligned} \begin{array}{l} {{\dot{x}}_{11}} = {x_{12}}\\ {{\dot{x}}_{12}} = {a_1}({x_{11}},{x_{12}},{x_{21}},{x_{22}}) + {b_1}{u_1}\\ {{\dot{x}}_{21}} = {x_{22}}\\ {{\dot{x}}_{22}} = {a_2}({x_{11}},{x_{12}},{x_{21}},{x_{22}}) + {b_2}{u_2}\\ {y_1} = {x_{12}}\,\,\,,\,\,\,{y_2} = {x_{22}}\,\, \end{array} \end{aligned}$$
(62)

with

$$\begin{aligned}&{a_1}({x_{11}},{x_{12}},{x_{21}},{x_{22}})\nonumber \\&\quad = \frac{g}{{cl}}{x_{11}} - \frac{m}{M}x_{12}^2\sin ({x_{11}})+ \frac{{k\left[ {\varphi (t) - cl} \right] }}{{cm{l^2}}} \nonumber \\&\quad \qquad \left( { - \varphi (t){x_{11}} + \varphi (t){x_{21}} - {x_1} + {x_2}} \right) \nonumber \\&{a_2}({x_{11}},{x_{12}},{x_{21}},{x_{22}}) = \frac{g}{{cl}}{x_{21}} - \frac{m}{M}x_{22}^2\sin ({x_{21}}) \nonumber \\&\qquad + \frac{{k\left[ {\varphi (t) - cl} \right] }}{{cm{l^2}}}\nonumber \\&\qquad \times \left( { - \varphi (t){x_{21}} + \varphi (t){x_{11}} + {x_1} - {x_2}} \right) \nonumber \\&{b_1} = {b_2} = \frac{1}{{cm{l^2}}} \nonumber \\&\quad = \sin (wt),\,\,\,\,\,\,\,\,\,{x_1} = \sin ({w_1}t),\,\,\,\,\nonumber \\&{x_2} = \sin ({w_2}t) + L \end{aligned}$$
(63)

For simulations, the parameters are \(M = m = 0.98\,0,\,\,l = 1.1,\,\,c = 0.50,\,\,w = 4,\,\,{w_1} = \,2,\,\,{w_1} = \,3,\,\,L = 2\), and \({r} = 0\).

From the proposed method, \({a_1}\) and \({a_2}\) in (62) are unknown and will be approximated via the proposed IT3FLS. \(\left( {{{{\hat{x}}}_{11}},{{{\hat{x}}}_{12}}} \right) \) and \(\left( {{{{\hat{x}}}_{21}},{{{\hat{x}}}_{22}}} \right) \) are selected for input of membership functions where \(\left[ {\begin{array}{*{20}{c}} { - 1}&0&1 \end{array}} \right] \) denote centers and upper/lower width are selected as 0.8/0.4. To design the control strategy, the parameters are:

$$\begin{aligned}&\,{{\mathcal {Q}}_c} = \left[ {\begin{array}{*{20}{c}} 1&{}0\\ 0&{}1 \end{array}} \right] ,\,\,{{\mathcal {P}}_c} = \left[ {\begin{array}{*{20}{c}} {25.01}&{}\quad 0\\ 0&{}\quad {0.0025} \end{array}} \right] \,,\nonumber \\&\,{{\mathcal {K}}_c} = {\left[ {\begin{array}{*{20}{c}} {10000}&\quad {200} \end{array}} \right] ^T}\nonumber \\&\,{{\mathcal {Q}}_o} = \left[ {\begin{array}{*{20}{c}} 1&{}\quad 0\\ 0&{}\quad 1 \end{array}} \right] ,\,\,{{\mathcal {P}}_o} = \left[ {\begin{array}{*{20}{c}} {137.5}&{}\quad { - 0.5}\\ { - 0.5}&{}\quad {0.0023} \end{array}} \right] ,\nonumber \\&\,{{\mathcal {L}}_o} = {\left[ {\begin{array}{*{20}{c}} {1100}&{{\mathrm{302500}}} \end{array}} \right] ^T}\nonumber \\&{\gamma _{{{\hat{{\bar{J}}}}_{a1}}}} = 0.05,\,\,{\gamma _{{{\hat{{\bar{J}}}}_{a2}}}} = 0.05,\nonumber \\&{\gamma _{{\theta _{a1}}}} = 5,{\mathrm{}}{\gamma _{{\theta _{a2}}}} = 5,\,\,\,\varepsilon = 0.001{\mathrm{}} \end{aligned}$$
(64)

The tracking trajectory is sketched in Fig. 10, while controllers are in Fig. 11. Comparing with the results of [47], the tunable parameters of this paper are less than that of [47] and the tracking errors are considerably less which confirm the superiority of the IT3FLS observer-based control policy of this paper.

Example 5

To have a comparison, Table 1 provides previous results of type-1/type-2 fuzzy-based strategies. In this regard, \(e_i = y_i - r\) \(i = 1,2\) and \({e_{ij}} = {x_{ij}} - {{\hat{x}}_{ij}},\,i,j = 1,2\) stand for the error signals. Note that T represents the final time and the sampling time specified by \(t_s=0.001\). It is obvious that utilizing IT3FLS leads to the better performance compared with employing type-2/type-1. Moreover, the number MFs is decreased which is another advantage of applying IT3FLS of this paper. Therefore, wide ranges of complexities and uncertainties can be studied via the suggested method of this paper.

Table 1 Example 5: The comparison of results
Full size table

8 Conclusion

Based on an online approximation of nonlinear functions via designing novel IT3FLS, an observer-based control law was developed to study uncertain nonlinear systems in this paper. The proposed method removed the restrictions of previous results of model-based control strategies and type-1/type-2 fuzzy-based control approaches and also improved the performance of a system and robustness against unknown dynamics, uncertainties, and unknown disturbances without detailed dynamics model information. Utilizing the proposed adaptive laws, approximation errors converged to zero and the upper bounds of exogenous disturbances were estimated online. Moreover, the stability of all error dynamics was guaranteed via using an appropriate Lyapunov function. Several simulations and a practical implementation have been provided to highlight the capabilities of our method in reducing computational burden, acquiring appropriate transient response, solving the robust tracking control problem, and ensuring robustness against unknown exogenous disturbances and uncertainties.