1 Introduction

The Mecanum-wheel omnidirectional mobile robots can move in any direction on the plane. This omnidirectional movement feature makes the Mecanum-wheel omnidirectional mobile robots widely used in industry and daily life, especially in narrow and restricted working environments, such as warehouse robots, inspection robots, rescue robots, sweeping robots and service robots. Therefore, the Mecanum-wheel omnidirectional mobile robots have aroused extensive research interest.

In order to make the mobile robot move according to the reference trajectory, it is necessary to design accurate tracking controllers for them. In [1], a static friction model is used and a model-predictive controller with friction compensation is applied to trajectory tracking of a three-wheel omnidirectional mobile robot. In [2], a high-order sliding mode observer is implemented for output feedback, and four continuous sliding mode output-feedback controllers are presented to deal with the robust trajectory tracking problem of a four-wheel omnidirectional mobile robot. In [3], a robust controller with the combination of backstepping technique and sliding mode control is designed for a four-wheel omnidirectional mobile robot. In [4], the tracking problem of an omnidirectional mobile robot is solved by considering some suitable modifications of the computed-torque control. In [5], a differential sliding mode controller is designed to move a three-wheel omnidirectional mobile platform. In [6], to solve the tracking problem of an omnidirectional mobile robot for aircraft skin inspection, a robust adaptive terminal sliding mode control scheme is proposed.

In the above several strategies of controlling a mobile robot, all the parameters of the mobile robot need to be known. Indeed, some time-invariant parameters can be obtained by measurement or consulting the manual, for example, the length and width of the robot chassis, the radius of the wheels. However, for some parameters related to the working environment of mobile robots and parameters that change greatly over time, such as the viscous and static friction coefficients, it is unrealistic to obtain their real-time values. Then, there are some studies that focus on trajectory tracking control when there are unknown dynamics or unknown parameters in the mobile robot model. In [7], it is assumed that in the robot dynamics there are unknown terms modeled as an unknown input signal and that a generalized proportional integral observer is used to estimate the unknown input of a three-wheel omnidirectional mobile robot. In [8], one assumes that some parameters, such as mass and the moment of inertia, are unknown and the adaptive backstepping approach is applied to deal with the unknown parameters of a three-wheel omnidirectional mobile robot. In [9], some system parameters are assumed unknown and a switching controller is proposed for a three-wheel omnidirectional mobile robot, which consists of an adaptive linearizing controller, an adaptive sliding-mode controller, a switching algorithm and a standard robust controller.

Advanced control strategies can reduce the negative effects of unknown dynamics or unknown parameters to a certain extent, but such a controller will not have excellent tracking performance. A more direct and effective method is to use learning models with universal approximation capabilities such as fuzzy systems and neural networks to replace the unknown models. The best approximation to the unknown model can be achieved by adaptively adjusting the parameters of the approximator, so that the influence of the unknown model on the control objective can be compensated by the universal approximator. In [10], a neural network is utilized to emulate the uncertain nonlinear function and an adaptive sliding mode controller is designed for a four-Mecanum-wheel mobile robot to track the trajectory. In [11], fuzzy wavelet networks are used to on-line approximate some uncertain nonlinear terms of the controller, and a nonsingular terminal sliding mode controller is presented for trajectory tracking of a four-Mecanum-wheel mobile robot.

In other fields besides omnidirectional mobile robots, it is also very common to use universal approximators to deal with unknown dynamics. The difference between the fuzzy system and the neural network is that the fuzzy system has explicitly rules-based reasoning mechanism and can be combined with human experience and expert knowledge [12]. In [12], fuzzy logic systems are developed to approximate the unknown nonlinear functions in spacecraft proximity systems, which solves the relative pose motion problem of the spacecraft. In [13], to achieve tracking tasks, interval type-2 fuzzy systems are utilized to approximate unknown nonlinear functions in flexible-joint manipulator. In [14], fuzzy systems are constructed to approximate unknown time-varying unmodeled dynamics in a hypersonic flight vehicle for better tracking performance. In addition to being used to approximate unknown models, fuzzy systems are also used to represent known but complex models to reduce the complexity and calculation of the controller. In [15], for rendering outputs track reference signals, the fuzzy systems are applied to handle known complex nonlinear functions in a two cascaded continuous stirred tank reactors. In [16], under the influence of various nonlinearities and uncertainties, fuzzy systems are introduced to approximate known dynamics in bilateral teleoperation manipulators, in order to implement the control design without the prior modeling knowledge. In [17], a new control method is proposed to ensure a Takagi–Sugeno (T-S) fuzzy system to achieve \(H_\infty \) performance. Then in [18], a T-S fuzzy system is used to represent the continuous-time nonlinear system, and by introducing a matrix decoupling technique, the fuzzy resilient filtering error system can meet the prescribed \(H_\infty \) performance. Although the above controllers can guarantee the asymptotical convergence of the tracking error, it cannot guarantee the transient performance and the finite-time convergence of the tracking error.

In terms of transient performance, that is, to constrain the tracking error within a prescribed region, a common approach is to use an error transformation function to transform the tracking error, turning the problem of guaranteeing transient performance into a bounded problem. In [19], the error transformation function is employed to guarantee the transient tracking performance of underactuated unmanned surface vessels. In [20], performance functions are constructed and the error transformation function is used to ensure that the tracking error of air-breathing hypersonic vehicles is confined within the prescribed boundaries. In [21], an error transformation function is introduced to transform the constrained tracking problem into the unconstrained stabilization problem, and then, the prescribed transient tracking performances of a marine surface vessel are guaranteed. In [22], a finite-time performance function is adopted to ensure the tracking errors converge to the given range in the tracking problem of stochastic nonlinear systems with unmodeled dynamics.

In terms of finite-time convergence, the traditional asymptotic stability theory can only guarantee the infinite-time stability of the control object. In order to stabilize the control object in a finite time, that is, the tracking error converges within a finite time, the finite-time stability theory has been developed. The finite-time stability theory is first proposed by reference [23, 24], and then, other forms of finite-time stability theory [25,26,27,28] are proposed for the convenience of application. In [29], a finite-time adaptive neural controller of which the design parameters are optimized is developed to handle the finite-time optimal control problem for a class of nonlinear systems. In [30], for the tracking problem of a class of multi-input and multi-output (MIMO) nonlinear systems, a finite-time adaptive neural controller is constructed . In [31], a finite-time performance-constrained adaptive fuzzy controller is designed to solve the control problem of stochastic high-order nonlinear systems. In [32], by finite-time stability theory, the event-triggered finite-time adaptive fuzzy control design is achieved, for stochastic nonlinear nonstrict feedback systems with unmodeled dynamics. However, the settling time determined by the finite-time stability theory depends on the initial values of the control system. In order to improve this defect, as an evolution of the finite-time stability theory, the fixed-time stability theory has been developed. The fixed-time stability theory is first proposed by reference [33], but when uncertainties exist in the control system, which is more practical and more general case, this theory is not applicable. Therefore, another practical fixed-time stability theory [34, 35], which is more suitable for the general case, was established. In [34], a fixed-time controller is derived to guarantee that the attitude of a rigid spacecraft converges to the equilibrium in a fixed settling time even in the presence of external disturbances and actuator faults. In [36], an adaptive fixed-time controller is designed to guarantee that a stratospheric airship tracks the reference trajectory within a fixed time under external disturbances. In [37], a fixed-time fault-tolerant controller is given to solve the fixed-time tracking problem of a underwater walking robot with external disturbances, error constraints and actuator faults.

The use of universal approximator, error transformation function and fixed-time control can already make the mobile robot have good tracking performance. However, when the mobile robot is faced with external disturbances, new unknown terms appear, which are bound to adversely affect the tracking performance of the mobile robot. If the disturbance is measurable, using a feedforward control strategy to add a compensation term for the disturbance in the controller can eliminate the influence of the disturbance. The actual situation is that the disturbance is often not measurable, and its mathematical model is often unknown, which makes it unrealistic to use a universal approximator to approximate the disturbance. The feasible way is to use the state observer to observe the disturbance with the help of the measurable state, in order to achieve the purpose of measuring and estimating the disturbance. If the universal approximator has been used, the disturbance observer can also estimate the approximation error of the universal approximator, making the tracking performance of the mobile robot even further. In [38], a nonlinear disturbance observer is introduced into the robotic exoskeleton to counteract the lumped disturbance. In [39], an adaptive sliding mode disturbance observer is proposed to compensate the system uncertainty with complex and uncertain dynamics. In [40], the reduced-order extended state observer is proposed to estimate the friction of a three-wheel omnidirectional mobile robot without any explicit friction mode. Some other disturbance observers are summarized in [41]. By means of the mentioned finite-time stability theory and fixed-time stability theory, in [42], a finite-time extended state observer is constructed to estimate the unavailable velocities and external disturbances in the distributed formation control problem of marine surface vehicles. In [43], a fixed-time extended state observer is developed to estimate unmeasured velocities and lumped disturbances for marine surface vessels.

This paper will set out to solve the problems in the four-Mecanum-wheel mobile robot mentioned above: unknown dynamics and unknown disturbances, guaranteeing the transient performance of the tracking error, guaranteeing the convergence time of the tracking error and the observation error. The fuzzy systems are used to approximate the dynamics with unknown friction coefficients in the mobile robot. The error transformation function is used to guarantee the transient performance of the tracking error. A fixed-time extended state observer is introduced to observe external disturbances and ensure the observation error converges in a fixed time. Finally, a fixed-time adaptive tracking controller is designed based on the backstepping technique to complete the trajectory tracking task and guarantee the tracking error converges within a fixed time. Compared with the previous literature, the main contributions of this paper are listed as follows:

  1. 1)

    The friction is not handled directly in [2, 4]. A static friction model is only established in [1, 9, 11] . References [3, 5, 8] assume that the static friction and the viscous friction are known. Reference [40] assumes the viscous friction coefficient known and uses a disturbance observer to observe the static friction. Different from the existing results, this paper uses fuzzy systems to approximate unknown dynamics with unknown viscous friction coefficients in the mobile robot and uses an observer to estimate the static friction. The independence of viscous friction coefficients makes the controller proposed in this paper more robust.

  2. 2)

    By introducing the practice fixed-time stability theory proposed in [34, 35], an adaptive fixed-time tracking controller is designed, which theoretically ensures that the tracking error of the mobile robot converges to the neighborhood of the origin within a fixed time, and the settling time is independent of the initial state. To make the adaptive laws of the fuzzy systems as simple and intuitive as possible and to prove that the system satisfies the practice fixed-time stability theory, Lemma 4 is specially proposed and proved to handle the term of adaptive laws whose exponent is greater than 1.

  3. 3)

    In the presence of unknown dynamics and external disturbances, it is difficult to guarantee the transient performance of the tracking error. The fuzzy systems approximating unknown dynamics, the fixed-time extended state observer estimating external disturbances, the error transformation function ensuring the trajectory tracking errors of the mobile robot have a predetermined performance. Unlike the existing literature, which can only guarantee the asymptotic convergence of the tracking error of the mobile robot, the controller designed in this paper can keep the tracking error within a predetermined region at all times even under unknown dynamics and external disturbances.

This paper is organized as follows: In Sect. 2, the problem preliminaries are given, involving the fixed-time theory, useful scaling inequalities, fuzzy systems, error transformation functions and the mathematical model of a four-Mecanum-wheel omnidirectional robot. In Sect. 3, a fixed-time adaptive fuzzy controller is derived by backstepping technique and a fixed-time extended state observer for observing external disturbances is designed. In Sect. 4, a comparative simulation example is shown. In Sect. 5, the conclusion of this paper is drawn.

2 Preliminaries

2.1 Fixed-time stability

Lemma 1

([34, 35]): Consider the system \({\dot{\varsigma }}=f(\varsigma )\). If there exists a smooth positive-define function \(V(\varsigma )\), and scalars \(\alpha>0,\beta>0,0<p<1,q>1\), and \(\rho >0\) such that

$$\begin{aligned} \dot{V}(\varsigma )\le -\alpha V^p(\varsigma )-\beta V^q(\varsigma )+\rho ,t\ge 0, \end{aligned}$$
(1)

then the nonlinear system \({\dot{\varsigma }}=f(\varsigma )\) is practical fixed-time stable and the settling time \( T_{set} \) can be estimated by

$$\begin{aligned} T_{set} \le \frac{1}{\alpha \phi (1-p)}+\frac{1}{\beta \phi (q-1)}, \end{aligned}$$

where \(0<\phi <1\) is a constant. The residual set of the solution of system \({\dot{\varsigma }}=f(\varsigma )\) is given by:

$$\begin{aligned} \varsigma \in \left\{ V(\varsigma ) \le min \left\{ \left( \frac{\rho }{\alpha (1-\phi )}\right) ^{\frac{1}{p}},\left( \frac{\rho }{\beta (1-\phi )}\right) ^{\frac{1}{q}}\right\} \right\} . \end{aligned}$$

2.2 Inequalities

Lemma 2

([37]): For \( x_i \in R, i=1,2,\cdots ,n \), one has

$$\begin{aligned} \sum \limits _{i=1}^{n} |x_i|^{\lambda } \ge {\left\{ \begin{array}{ll} \left( \sum \limits _{i=1}^{n}|x_i| \right) ^{\lambda }, 0<\lambda \le 1 \\ n^{1-\lambda }\left( \sum \limits _{i=1}^{n}|x_i| \right) ^{\lambda }, \lambda >1 \end{array}\right. } \end{aligned}$$
(2)

Lemma 3

([25]): For real number z and \(\xi \), and any positive constants \(\mu ,\theta ,\iota \), the following relation holds,

$$\begin{aligned} |z|^\mu |\xi |^\theta \le \frac{\mu }{\mu +\theta }\iota |z|^{\mu +\theta }+\frac{\theta }{\mu +\theta }\iota ^{-\frac{\mu }{\theta }}|\xi |^{\mu +\theta }. \end{aligned}$$
(3)

Lemma 4

For real number x, odd numbers \(r_1>r_2\), constant \(c,r=r_1/r_2>1\), there exists a constant \(\Xi >0\) such that

$$\begin{aligned} x(c-x)^r-\frac{1}{1+r}(c^{r+1}-x^{r+1}) \le \Xi . \end{aligned}$$
(4)

Proof

Denote \(g(x)=x(c-x)^r-\frac{1}{1+r}(c^{r+1}-x^{r+1})\). The derivative of g(x) with respect to x is

$$\begin{aligned} g'(x)&=(c-x)^r-rx(c-x)^{r-1}+x^r \\&=x^r\left( \left( \frac{c}{x}-1\right) ^r-r\left( \frac{c}{x}-1\right) ^{r-1}+1\right) . \end{aligned}$$

Let \(c/x=t,f(t)=(t-1)^r-r(t-1)^{r-1}+1\), and the derivative of f(t) with respect to t, \(f'(t)=(t-1)^{r-2}(rt-r^2)\), has two zeros, \( t_1=1,t_2=r \). It can be calculated that \(f(t_1)=1,f(t_2)=1-(r-1)^{r-1},f(0)=-r\). When \(t<1,f'(t)>0\), f(t) increases. When \(1<t<r\), \(f'(t)<0\), f(t) decreases. When \(t>r\), \(f'(t)>0\), f(t) increases.

Case 1: If \(1<r<2,f(t_2)>0\), f(t) has only one zero, \(t_0 \in (0,1)\). When \(t<t_0,f(t)<0\). When \(t>t_0,f(t)>0\). That is, \(g'(x)\) has only one zero, \(x_0=c/t_0\). When \(x>x_0,g'(x)<0\), g(x) decreases. When \(x<x_0,g'(x)>0\), g(x) increases. At \(x_0\), g(x) gets the absolute maximum value \(\Xi =g(x_0)>g(c)=0\). Then, \(g(x)\le \Xi \) holds.

Case 2: If \(r>2,f(t_2)<0\), f(t) has three zeros, \(t_0 \in (0,1), t_1 \in (1,r),t_2 \in (r,\infty )\). When \(t<t_0\), \(f(t)<0\). When \(t_0<t<t_1\), \(f(t)>0\). When \(t_1<t<t_2\), \(f(t)<0\). When \(t>t_2\), \(f(t)>0\). That is, \(g'(x)\) has three zeros, \(x_0=c/t_0,x_1=c/t_1,x_2=c/t_2\).

Case \(c>0\): When \(x<x_2,g'(x)>0\), g(x) increases. When \(x_2<x<x_1,g'(x)<0\), g(x) decreases. When \(x_1<x<x_0,g'(x)>0\), g(x) increases. When \(x>x_0,g'(x)<0\), g(x) decreases. Function g(x) gets the local maximum values at \(x_2\) and \(x_0\). At \(x=x_2\),

$$\begin{aligned} g(x_2)&=x_2(c-x_2)^r-\frac{1}{1+r}(c^{r+1}-x_2^{r+1}),\\ g'(x_2)&=(c-x_2)^r-rx_2(c-x_2)^{r-1}+x_2^r=0. \end{aligned}$$

Substituting \(g'(x_2)=0\) into \(g(x_2)\) produces

$$\begin{aligned} g(x_2)=&x_2(c-x_2)^r \!-\! \frac{1}{1+r}\big (c^{r+1}\!+\!x_2(c-x_2)^r \\&-\! rx_2^2(c-x_2)^{r-1}\big ) \\ =&\frac{r}{1+r}cx_2(c-x_2)^{r-1}-\frac{1}{1+r}c^{r+1} \end{aligned}$$

According to \(x_2=c/t_2\) and \(t_2\in (r,\infty )\), one can know \(0<x_2<c/r\). Then,

$$\begin{aligned}&(c-x_2)^{r-1}<c^{r-1},\\&\quad g(x_2)<c^r\big ( \frac{r}{1+r}x_2-\frac{1}{1+r}c \big )<0=g(c). \end{aligned}$$

According to \(x_0=c/t_0,t_0\in (0,1)\), it can be inferred that \(x_0>c>0\). According to \(x_1=c/t_1,t_1\in (1,r)\), it can be inferred that \(c/r<x_1<c<x_0\). On the basis of g(x) monotonically increasing in \((x_1,x_0)\), \(g(x_0)>g(c)\) is obtained. Therefore, \(g(x_2)<g(x_0)\). So \(\Xi =g(x_0)\) and \(g(x)\le \Xi \) holds.

Case \(c<0\): When \(x<x_0,g'(x)>0\), g(x) increases. When \(x_0<x<x_1,g'(x)<0\), g(x) decreases. When \(x_1<x<x_2,g'(x)>0\), g(x) increases. When \(x>x_2,g'(x)<0\), g(x) decreases. Function g(x) also gets the two local maximum values at \(x_2\) and \(x_0\). According to \(x_2=c/t_2,t_2\in (r,\infty )\), one gets \(0>x_2>c/r\). Similarly, \((c-x_2)^{r-1}<c^{r-1}\) and \(g(x_2)<0=g(c)\) are obvious. According to \(x_0=c/t_0,t_0\in (0,1)\), one has \(x_0<c\). According to \(x_1=c/t_1,t_1\in (1,r)\), one has \(c/r>x_1>c>x_0\). On the basis of g(x) monotonically decreasing in \((x_0,x_1)\), it is easy to know \(g(x_0)>g(c)\). Therefore, \(g(x_0)>g(x_2)\). So \(\Xi =g(x_0)\) and \(g(x) \le \Xi \) holds. \(\square \)

Remark 1

Lemma 4 mainly serves the stability analysis part. Substituting \(x={\tilde{\theta }}, c=\theta ^*, r=2q-1\) into Lemma 4 produces

$$\begin{aligned} {\tilde{\theta }}\left( \theta ^* - {\tilde{\theta }} \right) ^{2q-1}-\frac{1}{2q}\left( \theta ^{*^{2q}}-{\tilde{\theta }}^{2q} \right) \le \Xi . \end{aligned}$$

If \(\theta \) is regarded as the adaptive parameter vector of fuzzy systems, then by substituting \({\hat{\theta }}=\theta ^* - {\tilde{\theta }}\) and slightly making some adjustments, (38) can be obtained.

2.3 Fuzzy system

Fuzzy systems usually consist of the following basic fuzzy rules:

$$\begin{aligned} \begin{aligned} R^i:\ if\ x_1\ is\ A_1^{l_1}\ and&\ x_2\ is\ A_2^{l_2}\ and\ \cdots \ and\ x_n\ is\ A_n^{l_n},\\ {}&then\ y\ is\ Y^{l_1l_2\cdots l_n}, \end{aligned} \end{aligned}$$

where \(A_1^{l_1},A_2^{l_2},\cdots ,A_n^{l_n},Y^{l_1l_2\cdots l_n}\) are fuzzy sets, and \(x_i\) is the input and y is the output. Through singleton function, center average defuzzification, and product inference [25], the output of the fuzzy system can be expressed as:

$$\begin{aligned} y=\frac{\sum \nolimits _{l_1=1}^{p_1} \cdots \sum \nolimits _{l_n=1}^{p_n} y^{l_1\dots l_n}\left( \prod \nolimits _{i=1}^{n} \mu _{A_i}^{l_i}(x_i)\right) }{\sum \nolimits _{l_1=1}^{p_1} \cdots \sum \nolimits _{l_n=1}^{p_n}\left( \prod \nolimits _{i=1}^{n}\mu _{A_i}^{l_i}(x_i)\right) } =\theta ^T\xi (x),\nonumber \\ \end{aligned}$$
(5)

where

$$\begin{aligned} \begin{aligned}&\theta =[y^{1\cdots 1},y^{1\cdots 2},\cdots ,y^{p_1\cdots p_n}],\\&\xi (x) =[\xi ^{1\cdots 1}(x),\xi ^{1\cdots 2}(x),\cdots ,\xi ^{p_1\cdots p_n}(x)]^T,\\&\xi ^{l_1\cdots l_n}(x) =\frac{\left( \prod \nolimits _{i=1}^{n} \mu _{A_i}^{l_i}(x_i)\right) }{\sum \nolimits _{l_1=1}^{p_1} \cdots \sum \nolimits _{l_n=1}^{p_n}\left( \prod \limits _{i=1}^{n}\mu _{A_i}^{l_i}(x_i)\right) }, \end{aligned} \end{aligned}$$

and \(y^{l_1\cdots l_n}\) is the center of the fuzzy set \(Y^{l_1\cdots l_n}\), \(\mu (x)\) the membership function. \(\mu _{A_i}^{l_i}(x_i)\) represents the membership of \(x_i\) belonging to fuzzy set \(A_i^{l_i}\).

Lemma 5 ([25]): Let f(x) be a continuous function defined on a compact set \(\Omega \). Then for any a constant \(\varepsilon >0\), there exists a fuzzy system (5) such that

$$\begin{aligned} sup_{x \in \Omega }|f(x)-\theta ^T \xi (x)| \le \varepsilon . \end{aligned}$$
(6)

2.4 Guaranteed transient performance

Define the error variable \(e=x-x_d\), where x represents the system state, and \(x_d\) represents the reference signal to be tracked by x. Guaranteeing transient performance means constraining the error within the upper and lower boundaries, expressed as

$$\begin{aligned} \underline{\eta }<e<\overline{\eta }, \end{aligned}$$
(7)

where \(\overline{\eta }\) represents the upper boundaries, \(\underline{\eta }\) represents the lower boundaries. Generally, the upper and lower boundaries are taken as exponential decay form:

$$\begin{aligned} \eta =(\eta _0-\eta _\infty )e^{-at}+\eta _\infty , \end{aligned}$$
(8)

where \(\eta _0>\eta _\infty>0, a>0\). Assume that the upper and lower boundaries are symmetrical, written as \(-\eta<e<\eta \) and define \(z=e/\eta \), then (7) becomes \(-1<z<1\). Selecting the error transformation [19, 20]

$$\begin{aligned} v=\frac{1}{2} ln \frac{1+z}{1-z} \end{aligned}$$
(9)

can transform the variable z from \((-1,1)\) to \((-\infty ,\infty )\). As long as it can be proved that v is bounded, it can be guaranteed that \(z \in (-1,1)\), meaning that the error e is constrained within the predetermined upper and lower boundaries. Thanks to the error transformation function, the error constraint problem is transformed into a bounded problem.

2.5 Dynamic model

Fig. 1
figure 1

Robot coordinate system and global coordinate system

Full size image

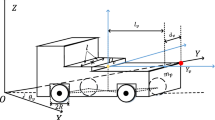
The schematic diagram of the four-Mecanum-wheel omnidirectional mobile robot is shown in Fig. 1. The speed transformation relationship between the robot coordinate \(x_r o_r y_r\) and the global coordinate xoy can be expressed as:

$$\begin{aligned} \dot{q}_r=R(\theta )\dot{q}, \end{aligned}$$
(10)

where

$$\begin{aligned} R(\theta )=\begin{bmatrix} cos\theta &{} -sin\theta &{} 0\\ sin\theta &{} cos\theta &{} 0\\ 0 &{} 0 &{} 1 \end{bmatrix}, \end{aligned}$$

and \(\dot{q}=[\dot{x},\dot{y},\dot{\theta }]^T\) indicates the speed of the robot in the \( x,y,\theta \) direction in the global coordinate system, \(\dot{q}_r=[\dot{x}_r,\dot{y}_r,\dot{\theta }_r]^T\) the speed of the robot in the \(x_r,y_r,\theta _r\) direction in the robot coordinate system.

According to Fig.1, the kinematics model of the mobile robot can be obtained:

$$\begin{aligned} \dot{q}_r=J\dot{\Theta }, \end{aligned}$$
(11)

where

$$\begin{aligned} J=\frac{r}{4}\begin{bmatrix} -1 &{} 1 &{}-1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ \frac{1}{L_1+L_2}&{}\frac{-1}{L_1+L_2}&{}\frac{-1}{L_1+L_2}&{}\frac{1}{L_1+L_2} \end{bmatrix} \end{aligned}$$
(12)

represents the transformation matrix from \(\dot{\Theta }\) to \(\dot{q}_r\), \(\dot{\Theta }=[\dot{\theta }_1,\dot{\theta }_2,\dot{\theta }_3,\dot{\theta }_4]^T\) the angular velocity of each wheel of the robot, r the radius of the wheel, \(L_1\) and \(L_2\) the distance from the center of the robot to the center of the wheel in the \(x_r\) and \(y_r\) directions, respectively. By generalized inverse operation, the right inverse matrix of J can be obtained:

$$\begin{aligned}&J \cdot J^+=I, \nonumber \\&\quad J^+=J^T(J \cdot J^T)^{-1}=\frac{1}{r}\begin{bmatrix} -1 &{} 1 &{} (L_1+L_2) \\ 1 &{} 1 &{} -(L_1+L_2) \\ -1 &{} 1 &{} -(L_1+L_2) \\ 1 &{} 1 &{} (L_1+L_2) \end{bmatrix}. \end{aligned}$$
(13)

Then, the formula using \(\dot{q}_r\) to represent \(\dot{\Theta }\) is obtained:

$$\begin{aligned} \dot{\Theta }=J^+ \dot{q}_r . \end{aligned}$$
(14)

The dynamic model of the robot can be obtained by the Lagrange dynamic equation [10, 44]:

$$\begin{aligned} M\ddot{\Theta }+D\dot{\Theta }=\tau +d, \end{aligned}$$
(15)

where

$$\begin{aligned} M&=\begin{bmatrix} {\begin{matrix} A+B+I_M &{} -A &{} A &{} B-A \\ -A &{} A+B+I_M &{} B-A &{} A\\ A &{} B-A &{} A+B+I_M &{} -A \\ B-A &{} A &{} -A &{} A+B+I_M\\ \end{matrix}} \end{bmatrix},\\ A&=\frac{I_z r^2}{16(L_1+L_2)^2},\\ B&=\frac{mr^2}{8},\\ D&=diag(D_1,D_2,D_3,D_4), \end{aligned}$$

and \(\tau =[\tau _1,\tau _2,\tau _3,\tau _4]^T\) represents the torque inputs of the robot’s four wheels, \(I_z\) moment of inertia of the robot, \(I_M\) moment of inertia of the wheels, m mass of the robot, \(D_i\) unknown viscous friction coefficient of the four wheels, d external disturbances including the static friction.

According to (10) \(\sim \) (14), we can obtain

$$\begin{aligned} MJ^+R(\theta )\ddot{q}+DJ^+R(\theta )\dot{q}+d=\tau . \end{aligned}$$
(16)

Transform the torque input \(\tau \), external disturbances d to the torque input \({\bar{\tau }}=[{\bar{\tau }}_4,{\bar{\tau }}_5,{\bar{\tau }}_6]^T\), external disturbances \(\bar{d}=[\bar{d}_4,\bar{d}_5,\bar{d}_6]^T\)

$$\begin{aligned} \begin{aligned} \tau&=MJ^+ R(\theta ){\bar{\tau }} \\ d&=-MJ^+ R(\theta )\bar{d} \end{aligned} \qquad . \end{aligned}$$
(17)

Remark 2

Imitating the speed transformation relationship (10) and the kinematics model (14) to make such a transformation is to change the four-dimensional torque input \(\tau \) into three-dimensional input \({\bar{\tau }}\), so as to correspond to the three-dimensional output, which facilitates the design of the controller. Multiplying the matrix M is to cancel out the M on the left side of (16). After the three-dimensional controller \({\bar{\tau }}\) is designed, it can be transformed into four-dimensional \(\tau \) by (17), and then, \(\tau \) can be used as the torque inputs of the four wheels of the mobile robot dynamic model (15).

Multiply both sides of (16) by \( R(\theta )^{-1}J M^{-1} \), and then (16) can be rewritten as:

$$\begin{aligned} \ddot{q}=F(\theta )\dot{q}+{\bar{\tau }}+\bar{d}, \end{aligned}$$
(18)

where

$$\begin{aligned} F(\theta )&=-R(\theta )^{-1}J M^{-1}D J^+ R(\theta ). \end{aligned}$$

According to (18), let \(x_1=x,x_2=y,x_3=\theta ,x_4=\dot{x},x_5=\dot{y},x_6=\dot{\theta }\), and state space model can be obtained,

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}_1=\dot{x}_4 \\ \dot{x}_2=\dot{x}_5 \\ \dot{x}_3=\dot{x}_6 \\ \dot{x}_4=f_4(x_3,x_4,x_5,x_6)+{\bar{\tau }}_4+\bar{d}_4 \\ \dot{x}_5=f_5(x_3,x_4,x_5,x_6)+{\bar{\tau }}_5+\bar{d}_5 \\ \dot{x}_6=f_6(x_3,x_4,x_5,x_6)+{\bar{\tau }}_6+\bar{d}_6 \\ \end{array}\right. }. \end{aligned}$$
(19)

3 Fixed-time controller design

3.1 Controller design

Consider the state space model (19). Let \( e_1=x_1-x_{1d},e_2=x_2-x_{2d},e_3=x_3-x_{3d},e_4=x_4-\alpha _1,e_5=x_5-\alpha _2,e_6=x_6-\alpha _3 \), where \(\alpha _1,\alpha _2,\alpha _3\) is the virtual input of Step 1, and \(x_{1d},x_{2d},x_{3d}\) is the reference of \(x_1,x_2,x_3\), respectively. Define the boundary function of \(e_1,e_2,e_3\) as \(\eta _1=(\eta _{1_0}-\eta _{1_\infty })e^{-a_{\eta _1}t}+\eta _{1_\infty },\eta _2=(\eta _{2_0}-\eta _{2_\infty })e^{-a_{\eta _2}t}+\eta _{2_\infty },\eta _3=(\eta _{3_0}-\eta _{3_\infty })e^{-a_{\eta _3}t}+\eta _{3_\infty } \), respectively. In addition, define variables \(z_1=e_1/\eta _1 \in (-1,1),z_2=e_2/\eta _2 \in (-1,1),z_3=e_3/\eta _3 \in (-1,1)\) and error transformation functions

$$\begin{aligned} \begin{aligned} v_1&=\frac{1}{2} ln \frac{1+z_1}{1-z_1} \\ v_2&=\frac{1}{2} ln \frac{1+z_2}{1-z_2} \\ v_3&=\frac{1}{2} ln \frac{1+z_3}{1-z_3} \end{aligned}. \end{aligned}$$
(20)

Differentiating \(e_1,e_2,e_3\) and \(v_1,v_2,v_3\) yields

$$\begin{aligned} \dot{e}_1&=x_4-\dot{x}_{1d}=e_4+\alpha _1-\dot{x}_{1d}\nonumber \\ \dot{e}_2&=x_5-\dot{x}_{2d}=e_5+\alpha _2-\dot{x}_{2d}\nonumber \\ \dot{e}_3&=x_6-\dot{x}_{3d}=e_6+\alpha _3-\dot{x}_{3d}\nonumber \\ \dot{v}_1&=\sigma _1 \left( e_4+\alpha _1-\dot{x}_{1d}-e_1 \frac{\dot{\eta _1}}{\eta _1} \right) \nonumber \\ \dot{v}_2&=\sigma _2 \left( e_5+\alpha _2-\dot{x}_{2d}-e_2 \frac{\dot{\eta _2}}{\eta _2} \right) \nonumber \\ \dot{v}_3&=\sigma _3 \left( e_6+\alpha _3-\dot{x}_{3d}-e_3 \frac{\dot{\eta _3}}{\eta _3} \right) \nonumber \\ \sigma _1&=\frac{1}{1-z_1^2} \frac{1}{\eta _1}\nonumber \\ \sigma _2&=\frac{1}{1-z_2^2} \frac{1}{\eta _2}\nonumber \\ \sigma _3&=\frac{1}{1-z_3^2} \frac{1}{\eta _3} \end{aligned}$$
(21)

Step 1: Choose the following Lyapunov function

$$\begin{aligned} V_1=\frac{1}{2}v_1^2+\frac{1}{2}v_2^2+\frac{1}{2}v_3^2. \end{aligned}$$
(22)

The derivative of \(V_1\) is:

$$\begin{aligned} \dot{V}_1&=v_1 \sigma _1 \left( e_4+\alpha _1-\dot{x}_{1d}-e_1\frac{\dot{\eta _1}}{\eta _1} \right) \nonumber \\&\quad +v_2 \sigma _2 \left( e_5+\alpha _2-\dot{x}_{2d}-e_2\frac{\dot{\eta _2}}{\eta _2} \right) \nonumber \\&\quad +v_3 \sigma _3 \left( e_6+\alpha _3-\dot{x}_{3d}-e_3\frac{\dot{\eta _3}}{\eta _3} \right) . \end{aligned}$$
(23)

Design the virtual input \(\alpha _1\) as

$$\begin{aligned} \begin{aligned} \alpha _1&=\dot{x}_{1d}+e_1\frac{\dot{\eta _1}}{\eta _1}-a_1v_1-b_1v_1^{2q-1}, \\ \alpha _2&=\dot{x}_{2d}+e_2\frac{\dot{\eta _2}}{\eta _2}-a_2v_2-b_2v_2^{2q-1}, \\ \alpha _3&=\dot{x}_{3d}+e_3\frac{\dot{\eta _3}}{\eta _3}-a_3v_3-b_3v_3^{2q-1}, \end{aligned} \end{aligned}$$
(24)

where \(a_1,a_2,a_3,b_1,b_2,b_3,2q-1=q_1/q_2\) are design parameters and \(q_1>q_2\) are odd numbers. Substitute (24) into (23) to get:

$$\begin{aligned} \dot{V}_1&=\sigma _1 (-a_1v_1^2-b_1v_1^{2q})+v_1\sigma _1 e_4\nonumber \\&\quad +\sigma _2 (-a_2v_2^2-b_2v_2^{2q})+v_2\sigma _2 e_5\nonumber \\&\quad +\sigma _3 (-a_3v_3^2-b_3v_3^{2q})+v_3\sigma _3 e_6. \end{aligned}$$
(25)

Step 2:Choose the Lyapunov function

$$\begin{aligned} V_4=V_1+\frac{1}{2}e_4^2+\frac{1}{2}e_5^2+\frac{1}{2}e_6^2. \end{aligned}$$
(26)

The derivative of \(V_4\) is:

$$\begin{aligned} \dot{V}_4&=\sigma _1 (-a_1v_1^2-b_1v_1^{2q})+e_4(v_1\sigma _1+f_4+{\bar{\tau }}_4+\bar{d}_4\nonumber \\&\quad -\dot{\alpha }_1)+\sigma _2 (-a_2v_2^2-b_2v_2^{2q})+e_5(v_2\sigma _2+f_5\nonumber \\&\quad +{\bar{\tau }}_5+\bar{d}_5-\dot{\alpha }_2)+\sigma _3 (-a_3v_3^2-b_3v_3^{2q})\nonumber \\&\quad +e_6(v_3\sigma _3+f_6+{\bar{\tau }}_6+\bar{d}_6-\dot{\alpha }_3). \end{aligned}$$
(27)

The controller can be designed as:

$$\begin{aligned} \begin{aligned} {\bar{\tau }}_4&=-v_1\sigma _1-f_4-\bar{d}_4+\dot{\alpha }_1-a_4 e_4-b_4 e_4^{2q-1}, \\ {\bar{\tau }}_5&=-v_2\sigma _2-f_5-\bar{d}_5+\dot{\alpha }_2-a_5 e_5-b_5 e_5^{2q-1}, \\ {\bar{\tau }}_6&=-v_3\sigma _3-f_6-\bar{d}_6+\dot{\alpha }_3-a_6 e_6-b_6 e_6^{2q-1}, \end{aligned} \end{aligned}$$
(28)

where \(a_4,a_5,a_6,b_4,b_5,b_6,2q-1=q_1/q_2\) are design parameters and \(q_1>q_2\) are odd numbers.

Due to the unknown viscous friction coefficients, the function \(f_4,f_5,f_6\) is unknown. The problem can be solved by approximating \(f_4,f_5,f_6\) with the following fuzzy system,

$$\begin{aligned} \begin{aligned}&f_4(x_3,x_4,x_5,x_6)=\theta ^{*^T}_{f_4}\xi _{f_4}(x_3,x_4,x_5,x_6)+\epsilon _{f_4}, \\&f_5(x_3,x_4,x_5,x_6)=\theta ^{*^T}_{f_5}\xi _{f_5}(x_3,x_4,x_5,x_6)+\epsilon _{f_5}, \\&f_6(x_3,x_4,x_5,x_6)=\theta ^{*^T}_{f_6}\xi _{f_6}(x_3,x_4,x_5,x_6)+\epsilon _{f_6}. \end{aligned} \end{aligned}$$
(29)

\(\theta ^{*}_{f_4},\theta ^{*}_{f_5},\theta ^{*}_{f_6}\) is the best parameter of the fuzzy systems but unknown. Thus, only the estimation \({\hat{\theta }}_{f_4},{\hat{\theta }}_{f_5},{\hat{\theta }}_{f_6}\) of the best parameter \(\theta ^{*}_{f_4},\theta ^{*}_{f_5},\theta ^{*}_{f_6}\) can be used in the controller. Similarly, the controller can only use the estimation \(\hat{\bar{d}}_4,\hat{\bar{d}}_5,\hat{\bar{d}}_6\) of the disturbance \(\bar{d}_4,\bar{d}_5,\bar{d}_6\). \(\hat{\bar{d}}_4,\hat{\bar{d}}_5,\hat{\bar{d}}_6\) will be obtained by the fixed-time extended observer designed in the next subsection. In order to facilitate the calculation of \(\dot{\alpha }_1,\dot{\alpha }_2,\dot{\alpha }_3\), let \(\alpha _1,\alpha _2,\alpha _3\) pass through low-pass filters [45, 46]

$$\begin{aligned} \begin{aligned}&\psi \dot{{\bar{\alpha }}}_1+{\bar{\alpha }}_1=\alpha _1,{\bar{\alpha }}_1(0)=\alpha _1(0), \\&\psi \dot{{\bar{\alpha }}}_2+{\bar{\alpha }}_2=\alpha _2,{\bar{\alpha }}_2(0)=\alpha _2(0), \\&\psi \dot{{\bar{\alpha }}}_3+{\bar{\alpha }}_3=\alpha _3,{\bar{\alpha }}_3(0)=\alpha _3(0), \end{aligned} \end{aligned}$$
(30)

where \(\psi >0\) is a parameter. Consequently, the calculation can be simplified by using: \(\dot{{\bar{\alpha }}}_1,\dot{{\bar{\alpha }}}_2,\dot{{\bar{\alpha }}}_3\) instead of \(\dot{\alpha }_1,\dot{\alpha }_2,\dot{\alpha }_3\). So controller (28) can be modified to

$$\begin{aligned} \begin{aligned}&{\bar{\tau }}_4=-v_1\sigma _1-\hat{{\bar{\theta }}}^T_{f_4}\xi _{f_4}-\hat{\bar{d}}_4+\dot{{\bar{\alpha }}}_1-a_4 e_4-b_4 e_4^{2q-1}, \\&{\bar{\tau }}_5=-v_2\sigma _2-\hat{{\bar{\theta }}}^T_{f_5}\xi _{f_5}-\hat{\bar{d}}_5+\dot{{\bar{\alpha }}}_2-a_5 e_5-b_5 e_5^{2q-1}, \\&{\bar{\tau }}_6=-v_3\sigma _3-\hat{{\bar{\theta }}}^T_{f_6}\xi _{f_6}-\hat{\bar{d}}_6+\dot{{\bar{\alpha }}}_3-a_6 e_6-b_6 e_6^{2q-1}. \end{aligned} \end{aligned}$$
(31)

For the purpose of making \({\hat{\theta }}^T_{f_4}\xi _{f_4},{\hat{\theta }}^T_{f_5}\xi _{f_5},{\hat{\theta }}^T_{f_6}\xi _{f_6}\) approach \(f_4,f_5,f_6\), respectively, the adaptive law of \({\hat{\theta }}^T_{f_4},{\hat{\theta }}^T_{f_5},{\hat{\theta }}^T_{f_6}\) can be designed as:

$$\begin{aligned} \begin{aligned}&\dot{{\hat{\theta }}}_{f_4}=\lambda _{f_4}e_4\xi _{f_4}-\gamma _{f_4}{\hat{\theta }}_{f_4}-\kappa _{f_4}{\hat{\theta }}_{f_4}^{2q-1}, \\&\dot{{\hat{\theta }}}_{f_5}=\lambda _{f_5}e_5\xi _{f_5}-\gamma _{f_5}{\hat{\theta }}_{f_5}-\kappa _{f_5}{\hat{\theta }}_{f_5}^{2q-1}, \\&\dot{{\hat{\theta }}}_{f_6}=\lambda _{f_6}e_6\xi _{f_6}-\gamma _{f_6}{\hat{\theta }}_{f_6}-\kappa _{f_6}{\hat{\theta }}_{f_6}^{2q-1}. \end{aligned} \end{aligned}$$
(32)

\(\lambda _{f_4},\lambda _{f_5},\lambda _{f_6},\gamma _{f_4},\gamma _{f_5},\gamma _{f_6},\kappa _{f_4},\kappa _{f_5},\kappa _{f_6},2q-1=q_1/q_2\) are design parameters and \(q_1>q_2\) are odd numbers.

Remark 3

In fact, the Mecanum-wheel mobile robot is a four-input three-output system, and it is very difficult to design an adaptive fuzzy controller directly. A unique feature of the controller design in this paper is that through transformation (17), the four-dimensional input variable \(\tau \) is transformed into a three-dimensional input \({\bar{\tau }}\), making the mobile robot a three-input three-output system, so the design of the fuzzy controller is carried out smoothly. After getting the controller \({\bar{\tau }}\), bring \({\bar{\tau }}\) into (17) to get \(\tau \), which can be given to the four motors of the robot as control inputs. In addition, by expressing \(f_4,f_5,f_6\) containing the unknown viscous friction coefficients with fuzzy systems, the problem of unknown coefficients of viscous friction can be solved.

Remark 4

Supposing differentiating \(\alpha _1\) directly without using (30), the calculation of \(\dot{\alpha }_1\) will be very complicated and extra variables \(\ddot{x}_1,\ddot{x}_{1d},\ddot{\eta }_1\) are needed. This problem can be easily solved by (30), which simplifies the calculation and does not provide additional variable values. All that needs to be done is to adjust the parameter \(\psi \).

Remark 5

Compared with general controllers, \(v_1^{2q-1},e_4^{2q-1}\) are added to controllers (24) and (28). This is for the \(v_1^{2q},e_4^{2q}\) to appear in \(\dot{V}\) in the subsequent stability analysis of subsection C, so that \(\dot{V}\) can satisfy the determination formula (1). However, the \({\hat{\theta }}_{f_4}^{2q-1}\) term in the adaptive law (32) cannot result in \({\tilde{\theta }}_{f_4}^{2q}\) directly, for which Lemma 4 is specially introduced and proved to make \({\tilde{\theta }}_{f_4}^{2q}\) appear in \(\dot{V}\) of (34).

3.2 Fixed-time extended state observer design

Assumption 1

According to [43], the derivative of the disturbance \(\bar{d}_4,\bar{d}_5,\bar{d}_6\) is bounded, such that \(||\dot{\bar{d}}_4|| \le H_{d4},||\dot{\bar{d}}_5|| \le H_{d5},||\dot{\bar{d}}_6|| \le H_{d6}\) holds.

Remark 6

Observer (33) needs to calculate \(\dot{\hat{\bar{d}}}_4,\dot{\hat{\bar{d}}}_5,\dot{\hat{\bar{d}}}_6\) to represent the estimations of \(\dot{\bar{d}}_4,\dot{\bar{d}}_5,\dot{\bar{d}}_6\), and then, \(\dot{\hat{\bar{d}}}_4,\dot{\hat{\bar{d}}}_5,\dot{\hat{\bar{d}}}_6\) is integrated to obtain the estimations \(\hat{\bar{d}}_4,\hat{\bar{d}}_5,\hat{\bar{d}}_6 \) of the disturbances \(\bar{d_4},\bar{d_5},\bar{d_6}\). Therefore, it is necessary to ensure that the \(\dot{\hat{\bar{d}}}_4,\dot{\hat{\bar{d}}}_5,\dot{\hat{\bar{d}}}_6\) to be calculated is bounded, that is, to ensure that the actual \(\dot{\bar{d}}_4,\dot{\bar{d}}_5,\dot{\bar{d}}_6\) is bounded.

With reference to the fixed-time extended state observer (FXESO) proposed in [43], the FXESO for subsystem (19) can be designed as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\hat{x}}_4={\hat{\theta }}^T_{f_4} \xi _{f_4} + {\bar{\tau }}_4+\hat{\bar{d}}_4 +k_4sig^{\mu _1}(\tilde{x}_4)+h_4sig^{\nu _1}(\tilde{x}_4) \\ \dot{\hat{x}}_5={\hat{\theta }}^T_{f_5} \xi _{f_5} + {\bar{\tau }}_5+\hat{\bar{d}}_5 +k_4sig^{\mu _1}(\tilde{x}_5)+h_4sig^{\nu _1}(\tilde{x}_5) \\ \dot{\hat{x}}_6={\hat{\theta }}^T_{f_6} \xi _{f_6} + {\bar{\tau }}_6+\hat{\bar{d}}_6 +k_4sig^{\mu _1}(\tilde{x}_6)+h_4sig^{\nu _1}(\tilde{x}_6) \\ \dot{\hat{\bar{d}}}_4=k_dsig^{\mu _2}(\tilde{x}_4)+h_dsig^{\nu _2}(\tilde{x}_4)+w_dtanh(\tilde{x}_4) \\ \dot{\hat{\bar{d}}}_5=k_dsig^{\mu _2}(\tilde{x}_5)+h_dsig^{\nu _2}(\tilde{x}_5)+w_dtanh(\tilde{x}_5) \\ \dot{\hat{\bar{d}}}_6=k_dsig^{\mu _2}(\tilde{x}_6)+h_dsig^{\nu _2}(\tilde{x}_6)+w_dtanh(\tilde{x}_6) \end{array}\right. }, \end{aligned}$$
(33)

where \(sig^{\mu }(\cdot )=|\cdot |^{\mu }sign(\cdot ),sig^{\nu }(\cdot )=|\cdot |^{\nu }sign(\cdot ), \tilde{x}_4=x_4-\hat{x}_4,\tilde{x}_5=x_5-\hat{x}_5,\tilde{x}_6=x_6-\hat{x}_6,tanh(x)=(e^x-e^{-x})/(e^x+e^{-x}),H_{d4}<w_d,H_{d5}<w_d,H_{d6}<w_d,0<\mu _i<1,\mu _i=i{\bar{\mu }}-(i-1),\nu _i>1,\nu _i=i{\bar{\nu }}-(i-1),i=1,2,{\bar{\mu }}=1-\delta _1,{\bar{\nu }}=1+\delta _2\). \(\delta _1,\delta _2\) are small enough positive constants. The FXESO gains \(k_4,h_4,k_d,h_d\) should make the following matrices Hurwitz,

$$\begin{aligned} P_1= \begin{bmatrix} -k_4 &{} 1 \\ -k_d &{} 0 \end{bmatrix}, P_2= \begin{bmatrix} -h_4 &{} 1 \\ -h_d &{} 0 \end{bmatrix}. \end{aligned}$$

Lemma 5

([43]): Under Assumption 1, the FXESO (33) can simultaneously estimate \(x_4,\bar{d}_4\) in fixed time bounded by:

$$\begin{aligned} T_b \le \frac{\lambda ^\vartheta _{max}(\Omega _1)}{\gamma _1\vartheta }+\frac{1}{\gamma _2\varsigma \varpi ^\varsigma } \end{aligned}$$

where \(\gamma _1\!=\!\lambda _{min}(Q_1)/\lambda _{max}(\Omega _1), \gamma _2\!=\!\lambda _{min}(Q_2)/\lambda _{max}(\Omega _2), \vartheta =1-{\bar{\mu }},\varsigma ={\bar{\nu }}-1, \varsigma \le \lambda _{min}(\Omega _2)\). \(Q_1,Q_2,\Omega _1,\Omega _2\) are nonsingular, symmetric, positive-definite matrices satisfied \(\Omega _1P_1+P_1\Omega _1^T=-Q_1,\Omega _2P2+P_2^T\Omega _2=-Q2\).

3.3 Stability analysis

Theorem 1

Consider the omnidirectional mobile robot system (19). The virtual controllers (24), the controllers (31) with the adaptive laws (32) and the fixed-time extended state observers (33) can enable the system to have the following properties.

  1. (1)

    All of the signals in the closed-loop system are bounded.

  2. (2)

    The tracking errors are constrained within the predetermined boundaries \(\eta _i\) and converge to the neighborhood of the origin in a fixed time.

Proof

Choose the Lyapunov function as

$$\begin{aligned} V&=\frac{1}{2}v_1^2+\frac{1}{2}v_2^2+\frac{1}{2}v_3^2+\frac{1}{2}e_4^2+\frac{1}{2}e_5^2+\frac{1}{2}e_6^2 \nonumber \\&\quad +\frac{1}{2\lambda _{f_4}}{\tilde{\theta }}_{f_4}^T{\tilde{\theta }}_{f_4}+\frac{1}{2\lambda _{f_5}}{\tilde{\theta }}_{f_5}^T{\tilde{\theta }}_{f_5}+\frac{1}{2\lambda _{f_6}}{\tilde{\theta }}_{f_6}^T{\tilde{\theta }}_{f_6}, \end{aligned}$$
(34)

where \({\tilde{\theta }}_{f_4}=\theta ^*_{f_4}-{\hat{\theta }}_{f_4},{\tilde{\theta }}_{f_5}=\theta ^*_{f_5}-{\hat{\theta }}_{f_5},{\tilde{\theta }}_{f_6}=\theta ^*_{f_6}-{\hat{\theta }}_{f_6}\). The derivative of V is:

$$\begin{aligned} \begin{aligned} \dot{V}&=\sigma _1v_1\left( \alpha _1-\dot{x}_{1d}-e_1\frac{\dot{\eta _1}}{\eta _1}\right) +\sigma _2v_2\Bigg (\alpha _2-\dot{x}_{2d}\\&\quad -e_2\frac{\dot{\eta _2}}{\eta _2}\Bigg )+\sigma _3v_3\left( \alpha _3-\dot{x}_{3d}-e_3\frac{\dot{\eta _3}}{\eta _3}\right) \\&\quad +e_4\big (v_1\sigma _1+f_4+{\bar{\tau }}_4+\bar{d}_4-\dot{\alpha }_1\big )-\frac{1}{\lambda _{f_4}}{\tilde{\theta }}^T_{f_4}\dot{{\hat{\theta }}}_{f_4} \\&\quad +e_5\big (v_2\sigma _2+f_5+{\bar{\tau }}_5+\bar{d}_5-\dot{\alpha }_2\big )-\!\frac{1}{\lambda _{f_5}}{\tilde{\theta }}^T_{f_5}\dot{{\hat{\theta }}}_{f_5}\\&\quad +\!e_6\big (v_3\sigma _3+\!f_6+{\bar{\tau }}_6+\!\bar{d}_6-\dot{\alpha }_3\big )-\!\frac{1}{\lambda _{f_6}}{\tilde{\theta }}^T_{f_6}\dot{{\hat{\theta }}}_{f_6} \end{aligned}. \end{aligned}$$
(35)

Replace \(f_4,f_5,f_6\) with the form of fuzzy systems

$$\begin{aligned}&f_4=\theta ^{*^T}_{f_4}\xi _{f_4}+\epsilon _{f_4},\nonumber \\&f_5=\theta ^{*^T}_{f_5}\xi _{f_5}+\epsilon _{f_5},\nonumber \\&f_6=\theta ^{*^T}_{f_6}\xi _{f_6}+\epsilon _{f_6}, \end{aligned}$$

and substitute the virtual controllers (24), the controllers (31) and the adaptive laws (32) into (35), one can have

$$\begin{aligned} \dot{V}&=\sigma _1\left( -a_1v_1^2-b_1v_1^{2q} \right) +\sigma _2\left( -a_2v_2^2-b_2v_2^{2q} \right) \nonumber \\&\quad +\!\sigma _3\left( -\!a_3v_3^2-\!b_3v_3^{2q} \right) -\!a_4e_4^2-\!b_4e_4^{2q}\nonumber \\&\quad +\!e_4\big (\dot{{\tilde{\alpha }}}_{1}+\!\tilde{\bar{d}}_4 +\!\epsilon _{f_4}\big )+\frac{\gamma _{f_4}}{\lambda _{f_4}}{\tilde{\theta }}^T_{f_4}{\hat{\theta }}_{f_4}+\frac{\kappa _{f_4}}{\lambda _{f_4}}{\tilde{\theta }}^T_{f_4}{\hat{\theta }}_{f_4}^{2q-1}\nonumber \\&\quad -a_5e_5^2-b_5e_5^{2q} +e_5\big (\dot{{\tilde{\alpha }}}_{2} +\tilde{\bar{d}}_5 +\!\epsilon _{f_5}\big ) +\frac{\gamma _{f_5}}{\lambda _{f_5}}{\tilde{\theta }}^T_{f_5}{\hat{\theta }}_{f_5}\nonumber \\&\quad +\frac{\kappa _{f_5}}{\lambda _{f_5}}{\tilde{\theta }}^T_{f_5}{\hat{\theta }}_{f_5}^{2q-1}-a_6e_6^2-b_6e_6^{2q}\nonumber \\&\quad +\!e_6\big (\dot{{\tilde{\alpha }}}_{3}+\!\tilde{\bar{d}}_6 +\epsilon _{f_6}\big ) +\!\frac{\gamma _{f_6}}{\lambda _{f_6}}{\tilde{\theta }}^T_{f_6}{\hat{\theta }}_{f_6}+\!\frac{\kappa _{f_6}}{\lambda _{f_6}}{\tilde{\theta }}^T_{f_6}{\hat{\theta }}_{f_6}^{2q-1}, \end{aligned}$$
(36)

where \({\tilde{\alpha }}_{1}={\bar{\alpha }}_{1}-\alpha _{1},{\tilde{\alpha }}_{2}={\bar{\alpha }}_{2}-\alpha _{2},{\tilde{\alpha }}_{3}={\bar{\alpha }}_{3}-\alpha _{3}\). According to Yang’s inequality,

$$\begin{aligned} \begin{aligned}&{\tilde{\theta }}^T_{f_4}{\hat{\theta }}_{f_4} \le \frac{1}{2}\theta ^{*^T}_{f_4}\theta ^{*}_{f_4}-\frac{1}{2}{\tilde{\theta }}^T_{f_4}{\tilde{\theta }}_{f_4}\\&{\tilde{\theta }}^T_{f_5}{\hat{\theta }}_{f_5} \le \frac{1}{2}\theta ^{*^T}_{f_5}\theta ^{*}_{f_5}-\frac{1}{2}{\tilde{\theta }}^T_{f_5}{\tilde{\theta }}_{f_5}\\&{\tilde{\theta }}^T_{f_6}{\hat{\theta }}_{f_6} \le \frac{1}{2}\theta ^{*^T}_{f_6}\theta ^{*}_{f_6}-\frac{1}{2}{\tilde{\theta }}^T_{f_6}{\tilde{\theta }}_{f_6}\\&e_4(\dot{{\tilde{\alpha }}}_{1}+\tilde{\bar{d}}_4+\epsilon _{f_4}) \le \frac{1}{2}e_4^2+\frac{1}{2}(\dot{{\tilde{\alpha }}}_{1}+\tilde{\bar{d}}_4+\epsilon _{f_4})^2\\&e_5(\dot{{\tilde{\alpha }}}_{2}+\tilde{\bar{d}}_5+\epsilon _{f_5}) \le \frac{1}{2}e_5^2+\frac{1}{2}(\dot{{\tilde{\alpha }}}_{2}+\tilde{\bar{d}}_5+\epsilon _{f_5})^2\\&e_6(\dot{{\tilde{\alpha }}}_{3}+\tilde{\bar{d}}_6+\epsilon _{f_6}) \le \frac{1}{2}e_6^2+\frac{1}{2}(\dot{{\tilde{\alpha }}}_{3}+\tilde{\bar{d}}_6+\epsilon _{f_6})^2 \end{aligned} . \end{aligned}$$
(37)

By Lemma 4

$$\begin{aligned} \begin{aligned} {\tilde{\theta }}^T_{f_4}{\hat{\theta }}^{2q-1}_{f_4}&\le \frac{1}{2q}\left( \theta ^{*^T}_{f_4}\theta ^*_{f_4}\right) ^q-\frac{1}{2q}\left( {\tilde{\theta }}^T_{f_4}{\tilde{\theta }}_{f_4} \right) ^q+\Xi _4\\ {\tilde{\theta }}^T_{f_5}{\hat{\theta }}^{2q-1}_{f_5}&\le \frac{1}{2q}\left( \theta ^{*^T}_{f_5}\theta ^*_{f_5}\right) ^q-\frac{1}{2q}\left( {\tilde{\theta }}^T_{f_5}{\tilde{\theta }}_{f_5} \right) ^q+\Xi _5\\ {\tilde{\theta }}^T_{f_6}{\hat{\theta }}^{2q-1}_{f_6}&\le \frac{1}{2q}\left( \theta ^{*^T}_{f_6}\theta ^*_{f_6}\right) ^q-\frac{1}{2q}\left( {\tilde{\theta }}^T_{f_6}{\tilde{\theta }}_{f_6} \right) ^q+\Xi _6 \end{aligned}. \end{aligned}$$
(38)

Applying (37)(38) to (36),

Table 1 Model data and controller parameters
Full size table
$$\begin{aligned} \dot{V}&\le \sigma _1\left( -a_1v_1^2-b_1v_1^{2q} \right) +\sigma _2\left( -a_2v_2^2-b_2v_2^{2q} \right) \nonumber \\&\quad +\!\sigma _3\left( -\!a_3v_3^2-\!b_3v_3^{2q} \right) -(a_4-\frac{1}{2})e_4^2-b_4e_4^{2q}\nonumber \\&\quad +\frac{\gamma _{f_4}}{2\lambda _{f_4}}\theta ^{*^T}_{f_4}\theta ^{*}_{f_4}- \frac{\gamma _{f_4}}{2\lambda _{f_4}}{\tilde{\theta }}^T_{f_4}{\tilde{\theta }}_{f_4}+\frac{\kappa _{f_4}}{2q\lambda _{f_4}}\left( \theta ^{*^T}_{f_4}\theta ^*_{f_4}\right) ^q\nonumber \\&\quad -\frac{\kappa _{f_4}}{2q\lambda _{f_4}}\left( {\tilde{\theta }}^T_{f_4}{\tilde{\theta }}_{f_4} \right) ^q+\Xi _4+\frac{1}{2}\big (\dot{{\tilde{\alpha }}}_{1}+\tilde{\bar{d}}_4+\epsilon _{f_4}\big )^2\nonumber \\&\quad -(a_5-\frac{1}{2})e_5^2-b_5e_5^{2q}+\frac{\gamma _{f_5}}{2\lambda _{f_5}}\theta ^{*^T}_{f_5}\theta ^{*}_{f_5}- \frac{\gamma _{f_5}}{2\lambda _{f_5}}{\tilde{\theta }}^T_{f_5}{\tilde{\theta }}_{f_5}\nonumber \\&\quad +\frac{\kappa _{f_5}}{2q\lambda _{f_5}}\left( \theta ^{*^T}_{f_5}\theta ^*_{f_5}\right) ^q-\frac{\kappa _{f_5}}{2q\lambda _{f_5}}\left( {\tilde{\theta }}^T_{f_5}{\tilde{\theta }}_{f_5} \right) ^q+\Xi _5\nonumber \\&\quad +\frac{1}{2}\big (\dot{{\tilde{\alpha }}}_{2}+\tilde{\bar{d}}_5+\epsilon _{f_5}\big )^2-(a_6-\frac{1}{2})e_6^2-b_6e_6^{2q}\nonumber \\&\quad +\frac{\gamma _{f_6}}{2\lambda _{f_6}}\theta ^{*^T}_{f_6}\theta ^{*}_{f_6}-\frac{\gamma _{f_6}}{2\lambda _{f_6}}{\tilde{\theta }}^T_{f_6}{\tilde{\theta }}_{f_6}+\frac{\kappa _{f_6}}{2q\lambda _{f_6}}\left( \theta ^{*^T}_{f_6}\theta ^*_{f_6}\right) ^q\nonumber \\&\quad -\frac{\kappa _{f_6}}{2q\lambda _{f_6}}\left( {\tilde{\theta }}^T_{f_6}{\tilde{\theta }}_{f_6} \right) ^q+\Xi _6+\frac{1}{2}\big (\dot{{\tilde{\alpha }}}_{3}+\tilde{\bar{d}}_6+\epsilon _{f_6}\big )^2 \end{aligned}$$
(39)

Denote

$$\begin{aligned} \varrho _4&=\!\frac{\gamma _{f_4}}{2\lambda _{f_4}}\theta ^{*^T}_{f_4}\theta ^{*}_{f_4}+\!\frac{\kappa _{f_4}}{2q\lambda _{f_4}}\left( \theta ^{*^T}_{f_4}\theta ^*_{f_4}\right) ^q+\!\Xi _4\!\\&\quad +\frac{1}{2}\big (\dot{{\tilde{\alpha }}}_{1}+\!\tilde{\bar{d}}_4+\!\epsilon _{f_4}\big )^2 \\ \varrho _5&=\!\frac{\gamma _{f_5}}{2\lambda _{f_5}}\theta ^{*^T}_{f_5}\theta ^{*}_{f_5}+\!\frac{\kappa _{f_5}}{2q\lambda _{f_5}}\left( \theta ^{*^T}_{f_5}\theta ^*_{f_5}\right) ^q+\!\Xi _5\!\\&\quad +\frac{1}{2}\big (\dot{{\tilde{\alpha }}}_{2}+\!\tilde{\bar{d}}_5+\!\epsilon _{f_5}\big )^2 \\ \varrho _6&=\!\frac{\gamma _{f_6}}{2\lambda _{f_6}}\theta ^{*^T}_{f_6}\theta ^{*}_{f_6}+\!\frac{\kappa _{f_6}}{2q\lambda _{f_6}}\left( \theta ^{*^T}_{f_6}\theta ^*_{f_6}\right) ^q+\!\Xi _6\!\\&\quad + \frac{1}{2}\big (\dot{{\tilde{\alpha }}}_{3}+\!\tilde{\bar{d}}_6+\!\epsilon _{f_6}\big )^2 \end{aligned}$$

and sort (39),

$$\begin{aligned} \dot{V}&\le -2\sigma _1a_1\big (\frac{1}{2}v_1^2\big )-2^q\sigma _1b_1\left( \frac{1}{2}v_1^2\right) ^q-2\sigma _2a_2\big (\frac{1}{2}v_2^2\big )\nonumber \\&\quad -2^q\sigma _2b_2\left( \frac{1}{2}v_2^2\right) ^q-2\sigma _3a_3\big (\frac{1}{2}v_3^2\big )-2^q\sigma _3b_3 \nonumber \\&\quad \times \left( \frac{1}{2}v_3^2\right) ^q -\!(2a_4\!-\!1)\left( \frac{1}{2}e_4^2\right) \!-\!2^qb_4\left( \frac{1}{2}e_4^2\right) ^q\!\nonumber \\&\quad -\!\gamma _{f_4}\left( \frac{1}{2\lambda _{f_4}}{\tilde{\theta }}^T_{f_4}{\tilde{\theta }}_{f_4}\right) -\frac{\kappa _{f_4}(2\lambda _{f_4})^{q-1}}{q}\nonumber \\&\quad \times \left( \frac{1}{2\lambda _{f_4}}{\tilde{\theta }}^T_{f_4}{\tilde{\theta }}_{f_4} \right) ^q\!+\!\varrho _4\!-\!(2a_5\!-\!1)\left( \frac{1}{2}e_5^2\right) \nonumber \\&\quad -\!2^qb_5\left( \frac{1}{2}e_5^2\right) ^q\!-\!\gamma _{f_5}\left( \frac{1}{2\lambda _{f_5}}{\tilde{\theta }}^T_{f_5}{\tilde{\theta }}_{f_5}\right) \nonumber \\&\quad -\frac{\kappa _{f_5}(2\lambda _{f_5})^{q-1}}{q}\left( \frac{1}{2\lambda _{f_5}}{\tilde{\theta }}^T_{f_5}{\tilde{\theta }}_{f_5} \right) ^q -\!(2a_6\!-\!1)\nonumber \\&\quad \times \left( \frac{1}{2}e_6^2\right) -\!2^qb_6 \left( \frac{1}{2}e_6^2\right) ^q\!-\!\gamma _{f_6}\left( \frac{1}{2\lambda _{f_6}}{\tilde{\theta }}^T_{f_6}{\tilde{\theta }}_{f_6}\right) \nonumber \\&\quad -\frac{\kappa _{f_6}(2\lambda _{f_6})^{q-1}}{q}\left( \frac{1}{2\lambda _{f_6}}{\tilde{\theta }}^T_{f_6}{\tilde{\theta }}_{f_6} \right) ^q+\varrho _6 \end{aligned}$$
(40)

Let

$$\begin{aligned} \alpha&=min\{ 2\sigma _1a_1,(2a_4-1),\gamma _{f_4},2\sigma _2a_2,(2a_5-1),\\&\quad \gamma _{f_5}, 2\sigma _3a_3,(2a_6-1),\gamma _{f_6} \},\\ \omega&=min\{ 2^q\sigma _1b_1,2^qb_4,\kappa _{f_4}(2\lambda _{f_4})^{q-1}/q,2^q\sigma _2b_2,\\&\quad 2^qb_5, \kappa _{f_5}(2\lambda _{f_5})^{q-1}/q,2^q\sigma _3b_3,2^qb_6,\\&\quad \kappa _{f_6}(2\lambda _{f_6})^{q-1}/q \} \end{aligned}$$

, and then, (40) is scaled to

$$\begin{aligned} \begin{aligned} \dot{V}&\le -\alpha \bigg (\frac{1}{2}v_1^2 +\frac{1}{2}v_2^2+\frac{1}{2}v_3^2+\frac{1}{2}e_4^2+\frac{1}{2}e_5^2+\frac{1}{2}e_6^2\\&\quad +\frac{1}{2\lambda _{f_4}}{\tilde{\theta }}^T_{f_4}{\tilde{\theta }}_{f_4}+\frac{1}{2\lambda _{f_5}}{\tilde{\theta }}^T_{f_5}{\tilde{\theta }}_{f_5}+\frac{1}{2\lambda _{f_6}}{\tilde{\theta }}^T_{f_6}{\tilde{\theta }}_{f_6}\bigg )\\&\quad -\omega \bigg (\Big (\frac{1}{2}v_1^2\Big )^q+\Big (\frac{1}{2}v_2^2\Big )^q+\Big (\frac{1}{2}v_3^2\Big )^q+\Big (\frac{1}{2}e_4^2\Big )^q\\&\quad +\Big (\frac{1}{2}e_5^2\Big )^q+\Big (\frac{1}{2}e_6^2\Big )^q+\Big ( \frac{1}{2\lambda _{f_4}}{\tilde{\theta }}^T_{f_4}{\tilde{\theta }}_{f_4} \Big )^q\\&\quad +\Big ( \frac{1}{2\lambda _{f_5}}{\tilde{\theta }}^T_{f_5}{\tilde{\theta }}_{f_5} \Big )^q+\Big ( \frac{1}{2\lambda _{f_6}}{\tilde{\theta }}^T_{f_6}{\tilde{\theta }}_{f_6} \Big )^q\bigg )\\&\quad +\varrho _4+\varrho _5+\varrho _6 \end{aligned}. \end{aligned}$$
(41)

By Lemma 2,

$$\begin{aligned} \begin{aligned}&\Big (\frac{1}{2}v_1^2\Big )^q+\Big (\frac{1}{2}v_2^2\Big )^q+\Big (\frac{1}{2}v_3^2\Big )^q+\Big (\frac{1}{2}e_4^2\Big )^q+\Big (\frac{1}{2}e_5^2\Big )^q\\&\quad +\Big (\frac{1}{2}e_6^2\Big )^q+\Big ( \frac{1}{2\lambda _{f_4}}{\tilde{\theta }}^T_{f_4}{\tilde{\theta }}_{f_4} \Big )^q+\Big ( \frac{1}{2\lambda _{f_5}}{\tilde{\theta }}^T_{f_5}{\tilde{\theta }}_{f_5} \Big )^q\\&\quad +\Big ( \frac{1}{2\lambda _{f_6}}{\tilde{\theta }}^T_{f_6}{\tilde{\theta }}_{f_6} \Big )^q \ge 9^{1-q}\bigg (\frac{1}{2}v_1^2 +\frac{1}{2}v_2^2+\frac{1}{2}v_3^2\\&\quad +\frac{1}{2}e_4^2+\frac{1}{2}e_5^2\!+\!\frac{1}{2}e_6^2\!+\!\frac{1}{2\lambda _{f_4}}{\tilde{\theta }}^T_{f_4}{\tilde{\theta }}_{f_4}\!+\!\frac{1}{2\lambda _{f_5}}{\tilde{\theta }}^T_{f_5}{\tilde{\theta }}_{f_5}\!\\+\!&\quad \frac{1}{2\lambda _{f_6}}{\tilde{\theta }}^T_{f_6}{\tilde{\theta }}_{f_6}\bigg )^q \end{aligned}. \end{aligned}$$
(42)

Substitute (42) into (41) and define \(9^{1-q}\omega =\beta ,\varrho =\varrho _4+\varrho _5+\varrho _6\),

$$\begin{aligned} \dot{V}\le -\alpha V-\beta V^q+\varrho . \end{aligned}$$
(43)

By Lemma 3,

$$\begin{aligned} V^p=1^{1-p}\cdot V^p \le (1-p)\iota +p\ \iota ^{-\frac{1-p}{p}}\ V, \end{aligned}$$
(44)

where \(0<p<1\). Let \(\iota =p^{\frac{p}{1-p}}\) and (44) becomes

$$\begin{aligned} V \ge V^p-(1-p)p^{\frac{p}{1-p}} . \end{aligned}$$
(45)

Apply (45) to (43) for scaling and let \(\rho =\varrho +\alpha (1-p)p^{\frac{p}{1-p}}\),

$$\begin{aligned} \dot{V}\le -\alpha V^p-\beta V^q+\rho . \end{aligned}$$
(46)

With reference to Lemma 1, it is known that system (19) is practical fixed-time stable and the convergence time T of the tracking error is bounded by:

$$\begin{aligned} T \le \frac{1}{\alpha \phi (1-p)}+\frac{1}{\beta \phi (q-1)}, \end{aligned}$$
(47)

which is independent of the initial states of the system. Then, it can be seen that \(v_i\) is bounded and the tracking error \(e_i\) is confined within the predetermined boundaries. \(\square \)

Fig. 2
figure 2

Trajectory tracking simulation results

Full size image
Fig. 3
figure 3

Tracking results in \( x,y,\theta \) directions

Full size image
Fig. 4
figure 4

Input \( \tau \)

Full size image

4 Simulation

The simulation of fixed-time observer-based adaptive fuzzy controller with guaranteed transient performance (FXAFC-G) proposed in this paper, fixed-time observer-based adaptive fuzzy controller without guaranteed transient performance (FXAFC) and the observer-based super-twisting sliding mode controller (STSMC) proposed in [40] are carried out. The robot parameters [44] and controller parameters used in the simulation are shown in TABLE 1. It should be noted that STSMC needs the values of viscous friction coefficients. In order to reflect the actual situation that the coefficient fluctuates up and down the average value, the viscous friction coefficients D are set to \(D=diag([0.3,0.4,0.35,0.45])+ diag([0.06sin(0.2t),0.08cos(0.1t),0.07sin(0.15t), 0.09cos(0.25t)])\). The viscous friction coefficients used by STSMC are diag([0, 3, 0.4, 0.35, 0, 45]), while FXAFC-G and FXAFC do not need this parameter. The boundary function selected for the tracking error \(e_1,e_2,e_3\) is the same \(\eta _1=\eta _2=\eta _3=(100-0.01)e^{-t}+0.01\). The initial values of the adaptive parameters of the fuzzy systems are all set to 0, and setting initial values of adaptive parameters of fuzzy systems differently does not affect the simulation results.

$$\begin{aligned} {\left\{ \begin{array}{ll} x_d=5cos(0.1t) \\ y_d=2.5sin(0.2t) \\ \theta _d=2sin(0.1t) \end{array}\right. } \end{aligned}$$
(48)
Fig. 5
figure 5

Tracking errors

Full size image
Fig. 6
figure 6

Trajectory tracking under disturbances

Full size image

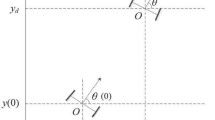
The reference trajectory is (48) of which the shape is like “\(\infty \)”. The initial state of the mobile robot is \( (x_0,y_0,\theta _0)=(0,0,0) \), and the initial state of the reference trajectory is \( (x_{d0},y_{d0},\theta _{d0})=(5,0,0) \), as can be seen in Fig. 2. In reality, the torque input of the mobile robot must be a finite value, so in simulation, the four-dimensional torque input \(\tau \) is limited to \(-12<\tau <12\). Restricting the torque input \(\tau \) to \((-12,12)\) is due to the consideration of the saturation problem of the motors on the actual robot, and it can be clearly pointed out that after the input saturation constraint is added, the stability of the mobile robot will not be affected.

The comparison of simulation results of trajectory tracking is shown in Fig.2. A more detailed tracking comparison of \(x,y,\theta \) is shown in Fig. 3. Figures 2 and 3 show that three controllers can make the mobile robot track the reference trajectory. The input \(\tau \) is shown in Fig. 4a. Figure 4b is an enlarged view of the framed part in Fig. 4a.

In Fig. 4b, it can be seen that the STSMC in [40] still has a relatively large chattering problem, which is the reason for the worse stability in the steady state. The cause of this problem is the switch item sign(s) of the sliding mode surface s existing in the sliding mode controller. Every coin has two sides. The switching characteristic of the sliding mode control makes the system anti-disturbance, but it also brings chattering problem to the system. Therefore, the chattering problem of sliding mode control can only be weakened but not eliminated. Correspondingly, adaptive fuzzy control does not have such a chattering problem.

The overall comparison of the tracking error is shown in Fig. 5b, the comparison of the transient process shown in Fig. 5a, the comparison of the steady-state error shown in Fig. 5c. Figure 5a is an enlarged view of the left frame of Fig. 5b, and Fig. 5c is an enlarged view of the right frame of Fig. 5b.

Figure 5a shows that the FXAFC-G designed in this paper can track the reference signal more quickly and more smoothly, while the FXAFC and the STSMC have a large overshoot and require more time to track the reference trajectory. Figure 5c shows that the FXAFC-G in this paper can achieve smallest steady-state errors and best stationarity, while FXAFC causes huge steady error. By comparing the two cases with guaranteed transient performance and without guaranteed transient performance, it can be seen that the error transformation function plays a huge role in ensuring the transient performance, which can not only improve the rapidity but also reduce the steady-state error.

As for the fixed-time convergence, according to the definition of \(\alpha ,\omega \) and the controller parameters in TABLE 1, it can be obtained that \(\alpha <1,\omega \le 0.95\). Then by \(\beta =9^{1-q}\omega \), \(\beta \le 0.22\). From \(0<\phi<1, 0<p<1\), it can be seen that in (47), \(\frac{1}{\alpha \phi (1-p)}+\frac{1}{\beta \phi (q-1)} >7.8 s\), which indicates that the convergence time \(T < 7.8s\). This can be verified directly from Figs.5 and 6. In Figs. 5a and 6a, the simulation curves of FXAFC and FXAFC-G all converge to the neighbor of 0 before 7.8s.

On the basis of the existing simulation, the external disturbance \(d=[sin(5t),sin(4t),cos(5t),cos(4t)]^T\) is added and the simulation result is shown in Fig. 6. It can be clearly seen from Fig. 6 that the FXESO-based FXAFC-G designed in this paper can greatly suppress disturbances, while the ESO-based STSMC cannot resist the disturbance very well. Even the FXESO-based FXAFC without guaranteed transient performance is better than the ESO-based STSMC in terms of disturbance rejection, which indicates that the effect of FXESO on the disturbance observation is very significant.

In summary of simulation, compared with STSMC, the proposed method FXAFC-G has nearly the same rapidity but smaller steady-state errors, better anti-disturbance performance, and no input chattering problem. Furthermore, FXAFC-G can still achieve the tracking tasks even if the viscous friction coefficients are unknown and can predetermine the bound and the convergence time of the tracking errors.

5 Conclusion

For the tracking problem of the four-Mecanum-wheel mobile robot, this paper uses fuzzy systems to approximate the dynamics with unknown viscous friction coefficients and designs a fixed-time adaptive fuzzy tracking controller to enable the mobile robot to track the reference trajectory within a fixed time. An error transformation function is introduced to guarantee the transient performance of tracking errors, and a fixed-time extended state observer is used to observe external disturbances. The FXESO-based transient performance guaranteed fixed-time adaptive fuzzy controller proposed in this paper, the FXESO-based transient performance not guaranteed fixed-time adaptive fuzzy controller and ESO-based super-twisting sliding mode controller are compared and simulated, and the simulation results verify the superiority of the controller in this paper in trajectory tracking and disturbance resistance. In future work, in addition to the four-Mecanum-wheel omnidirectional mobile robot, it is worth considering the application of the controller designed in this paper on other types of omnidirectional mobile robots.