Abstract
This paper presents a novel multi-variable high-order sliding mode quasi-optimal control method for unmanned helicopters. In order to facilitate the theoretical design and engineering implementation, the control system is divided into attitude and position subsystem, and the latter is further subdivided into two parts, horizontal and vertical position control. Then the multi-variable adaptive high-order continuous sliding mode controllers are designed for attitude and position, respectively, based on integral sliding mode surface. A new quadratic performance index is proposed in the design process, which enables the control system to converge in finite time, and the convergence rate can be adjusted by control parameters. Finally, the effectiveness and robustness of the proposed method are verified and compared with existing literature by simulation and practical experiments. The comparison results show that the proposed method has higher tracking accuracy and better robustness.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Due to their unique flight capabilities such as vertical take-off and landing, hovering and strong maneuverability, unmanned helicopters have received continuous attention and research from scholars in the past decades, and have shown wide application prospects in military and civil fields. A stable and reliable flight control system is an important prerequisite for the application of various unmanned helicopters. With the rapid expansion of the application field, the demand for autonomous flight technology of unmanned helicopter is higher. For example, customers not only need stable and reliable flight control system, but also need unmanned helicopters with higher response speed and stronger anti-interference ability to perform specific missions in harsher environment. Therefore, it is of great academic significance and application value to explore autonomous flight control system of unmanned helicopter with stronger control performance.
In recent years, researchers have devoted a lot of efforts to the autonomous flight control technology of unmanned helicopter, which has provided a great deal of valuable experience. Because small unmanned helicopter is a nonlinear, high-order and highly coupled complex model, it is very difficult to obtain its accurate nonlinear model, lots of researchers use PID control method to design the flight control system. Researchers from Applied Nonlinear Controls Lab (ANCL) of University of Alberta have designed an attitude controller for unmanned helicopter by combining PID control and feedforward control, and verified it in real flight [12]. Then, the researchers further add position control in [29] and conduct detailed stability analysis by using Lyapunov theory. Finally, the effectiveness is verified by actual flight experiment. However, the traditional PID control method has poor robustness to model uncertainties and external disturbances. Therefore, one of the aims of this paper is to improve the robustness of the closed-loop system by combining sliding mode control with optimal control theory [40].
Linear control method plays an important role in the design of flight control system and is widely used in various aircrafts [8, 9, 20]. One of the unavoidable problems in the design of unmanned helicopter control system using \(H\infty \) control technology is the high order of controller, which leads to the difficulty in engineering application. A hierarchical control structure is designed for a small unmanned helicopter in [35]. The inner loop adopts \(H\infty \) control to stabilize the attitude, and the outer loop uses PI controller to track the reference position, reducing the order of the whole system. Of all \(H\infty \) methods, loop shaping is widely favored due to its simple design process. A hover controller is designed using extended loop shaping in [31, 32] and good simulation results are achieved, but the unmanned helicopter can only fly autonomously under flight modes of hovering and low forward speed. In addition, linear control methods such as LQR [19, 27], LQG [25, 36] and LPV [4, 17] are also widely used in autonomous flight of unmanned helicopters. However, linear control method must rely on the model linearized at the equilibrium point, only the autonomous flight near the equilibrium point can be guaranteed theoretically, which limits the large envelope flight of the unmanned helicopter, leading to relatively conservative control performance. On the contrary, the proposed method makes full use of the high maneuverability of the unmanned helicopter, resulting in a larger flight envelope of the control system, which breaks away from the limit of the equilibrium point.
Because of the advantages of simple structure and small amount of calculation, backstepping control is widely used in autonomous flight of unmanned helicopter, and can be combined with other nonlinear control methods [1, 3, 6, 7, 21, 28, 37, 43, 44]. In [37], the attitude control system is designed by combining backstepping control and adaptive technology with unknown system parameters, which is proved to be asymptotically stable by Lyapunov stability theory, and the effectiveness is verified by simulation and actual flight experiments.The authors of [14, 21] regard model uncertainty and external disturbance as lumped unknown disturbance, and design an autonomous flight controller combining backstepping control and nonlinear disturbance observer. The adaptive backstepping controller of unmanned helicopter is also designed by combining backstepping control with adaptive radial basis function neural network (RBFNN) using online parameter updating law with the least parameters in [41]. Although this method significantly reduces the computational burden of the control system, the cost is the loss of partial robustness.
In order to obtain faster dynamic response and more robust control performance, many researchers turn their attention to finite time and sliding mode control methods [5, 13, 16, 26, 30]. In [18], the finite-time stability of the trajectory tracking control system of unmanned helicopter is studied, and the finite-time convergence of the system is guaranteed by combining sliding mode observer and hybrid active disturbance rejection technology. In [34], adaptive finite time control and radial basis function neural network are combined to study the formation reconstruction of unmanned helicopters. The authors of [5] provide a novel second-order sliding mode control strategy worth learning, which can avoid overestimation of sliding mode gain and does not need the boundedness of the derivatives of uncertainties. In the case of constrained state, the application of robust fractional sliding mode control in autonomous flight of unmanned helicopter in uncertain environment is studied in [15]. In [38], a combination of continuous terminal sliding mode control and disturbance observer is adopted to focus on the autonomous landing of an unmanned helicopter on a moving ship. High-order sliding mode observer is used to estimate the concentrated interference in [39], and then a composite controller is designed by combining hybrid dynamic inverse and non-singular terminal sliding mode control. Finally, the asymptotic convergence of tracking error is obtained even in the presence of time-varying interference. Although the above researches can achieve finite time convergence, they cannot constrain or control the convergence speed of the system, and the problem of overestimation of adaptive sliding mode gain has not been effectively solved. In view of these shortcomings, a new solution is proposed in this paper and verified by simulation and practical experiment.
In order to improve the robustness of unmanned helicopter in autonomous flight to parametric and external uncertainties without knowing the boundedness of uncertainties and avoid overestimation of adaptive gain, a multi-variable adaptive high-order sliding mode quasi-optimal control (AHOSMQC) is proposed in this paper. First of all, the main rotor flapping motion of unmanned helicopter is analyzed and simplified, then the position and attitude dynamics are expressed as multi-variable integral chain with additive and multiplicative uncertainties, and the proposed method is applied, respectively. Finally, the feasibility and robustness of the proposed method is verified by digital simulation and actual flight experiments. The main highlights of this paper are summarized as follows.
Firstly, a multi-variable adaptive high-order sliding mode controller is proposed based on redesigned quadratic performance index and multi-variable finite-time control law. Different from previous literature, it is quasi-optimal and the convergence speed can be adjusted by control parameter, resulting in a faster convergence rate. Moreover, the chattering phenomenon can be effectively eliminated by the proposed high-order sliding mode algorithm, which is more conducive to the engineering implementation of the control algorithm.
Secondly, the boundary of uncertainty is not needed in the design process of the proposed adaptive high-order sliding mode controller. At the same time, the possible additive and multiplicative uncertainties of the system are considered, and the problem of overestimation of adaptive sliding mode gain is solved.
Finally, the whole closed-loop system is proved to converge in finite time by Lyapunov stability theory. What’s more, the effectiveness and robustness of the whole unmanned helicopter control system are verified and compared with the method in [41] by challenging and high maneuvering flight experiments. The simulation and practical experimental results show the superiority of the proposed method.
The organization structure of the remaining text is as follows. Section 2 presents the modeling process. The process of model simplification and analysis is described in Sect. 3. Detailed control design and stability analysis are given in Sect. 4. Section 5 presents the actual flight experiment results and some discussion. Section 6 concludes the paper.
2 Problem formulation
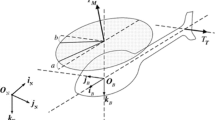
The definition of relevant coordinate system is shown in Fig. 1, where \(O-xyz\) and \(O_b-x_by_bz_b\) represent inertial coordinate system and body coordinate system, respectively. \([u, v, w]^T\) and \([p, q, r]^T\) are, respectively, linear velocity and angular rate vector of the unmanned helicopter in the body coordinate system. a and b are flapping angles of the main rotor in the longitudinal and lateral direction.
According to the Newton–Euler equation [28], the rigid body kinematics and dynamics of a small unmanned helicopter system can be expressed by the following equations
where \(\varvec{P}=[x, y, z]^T\) is the position vector in the inertial coordinate system, \(\varvec{V} = [v_x ,v_y ,v_z ]^T\) represents the linear velocity vector of the center of gravity \(O_b\) in the inertial coordinate system, m is the mass of the whole system, attitude is represented by \(\varvec{\varTheta } = [\phi ,\theta ,\psi ]^T\). \(\varvec{R}(\varvec{\varTheta } )\) is the transformation matrix from body coordinate system to inertial coordinate system, defined as
Abbreviation \(\mathrm {c}(\cdot )\) and \(\mathrm {s}(\cdot )\) represents trigonometric functions \(\cos (\cdot )\) and \(\sin (\cdot )\). \(\mathrm {c}(\phi \theta \psi )=\mathrm {c}(\phi )\mathrm {c}(\theta )\mathrm {c}(\psi )\), \(\mathrm {s}(\phi \theta \psi )=\mathrm {s}(\phi )\mathrm {s}(\theta )\mathrm {s}(\psi )\), and so on. \(\varvec{\omega } =[p,q,r]^T\) is the angular rate vector, \(\varvec{E}_z\) is a unit vector and \(\varvec{E}_z=[0,0,1]^T\), \(\varvec{T}(\varvec{\varTheta })\) is a 3\(\times \)3 matrix, defined as
Besides, \(\varvec{J}=\mathrm {diag}\{ I_{x} ,I_{y} ,I_{z} \}\) is the matrix of rotational inertia.
All external forces except gravity \(\varvec{F}\) and all external torques \(\varvec{M}\) can be expressed in the body coordinate system as follows
where \(X_{\mathrm {mr}}\), \(Y_{\mathrm {mr}}\) and \(Z_{\mathrm {mr}}\) are the components on the \(x_\mathrm {b}\), \(y_\mathrm {b}\) and \(z_\mathrm {b}\) axes of the body coordinate system, respectively, \(X_{\mathrm {fd}}\), \(Y_{\mathrm {fd}}\) and \(Z_{\mathrm {fd}}\) are the components of the airframe resistance on the \(x_\mathrm {b}\), \(y_\mathrm {b}\) and \(z_\mathrm {b}\) axes of the body coordinate system, respectively, \(Z_{\mathrm {ht}}\) and \(M_{\mathrm {ht}}\) are the forces and moments generated by the horizontal tail, respectively, \(Y_{\mathrm {vt}}\), \(L_{\mathrm {vt}}\) and \(N_{\mathrm {vt}}\) are the forces and moments generated by the vertical tail, respectively, \(Y_{\mathrm {tr}}\), \(L_{\mathrm {tr}}\) and \(N{\mathrm {tr}}\) are the forces and moments generated by the tail rotor, \(L_{\mathrm {mr}}\), \(M_{\mathrm {mr}}\) and \(N_{\mathrm {mr}}\) are the components of the main rotor torques on the \(x_\mathrm {b}\), \(y_\mathrm {b}\) and \(z_\mathrm {b}\) axes of the body coordinate system, respectively.
Main rotor flapping dynamics is a unique and important feature of unmanned helicopters, which must be considered, and modeled as follows
where \(\theta _{\mathrm {lon}}\), \(\theta _{\mathrm {lat}}\) indicate the cyclic pitch angles of the main blade in the longitudinal and lateral direction, which are determined by the servos of the pitch and roll channel. \(\gamma _\mathrm {m}\) is the total locke number of two main rotor blades, \(\varOmega \) is the main rotor rotation speed, \(I_\beta \) is the moment of inertia of the main blades.
Interested readers may refer to [42] for more detailed modeling and parameter determination details.
3 Model preprocessing and analysis
Since the dominant force on the helicopter airframe is the component of the main rotor lift along the body frame \(z_\mathrm {b}\) axis, for convenience, \(X_{\mathrm {Mr}}\) and \(Y_{\mathrm {Mr}}\) are ignored here and are regarded as part of the lumped interference in the design process. Generally, both the longitudinal and lateral flapping angles are very small, so it is reasonable to assume \(c(a) \approx 1\) and \(c(b) \approx 1\). Thus, the external force can be written in a form consisting of the following two parts
where \({\varvec{d}_{\mathrm {F}}}\) is lumped interference composed of ignored forces and other external uncertainties, such as ignored fuselage drag, vertical and horizontal tail aerodynamics. Similarly, the torque of the unmanned helicopter mainly comes from the lift force of the main rotor and the pull force of the tail rotor, so other smaller torque components can be treated as interference. According to the hypothetical conditions \(s(a) \approx a\) and \(s(b) \approx b\), the external torque acting on the unmanned helicopter can be expressed as
where \({\varvec{d}_{\mathrm {M}}}\) is the disturbance torque composed of other neglected torques and external uncertainties.
In addition, the flapping dynamics model of the main rotor is an important motion characteristic of the unmanned helicopter, and has a strong coupling effect with the rigid body dynamics model of the fuselage, which is directly related to the dynamic response of the whole system, so it must be taken into consideration in the control design procedure. However, the flapping angle of the main propeller cannot be effectively measured by any sensor. If the flapping motion is completely ignored, the performance of the control system may be degraded. Therefore, this section attempts to adopt a compromise static quasi-stable flapping dynamic model to approximately replace the complete flapping dynamic model, and verifies the feasibility of this method in both frequency domain and time domain.
According to the system parameters finally determined in [42], the flapping dynamics model (8) of the main rotor can be written as the following state space
where \({\delta _{\mathrm {lat}}}\), \({\delta _{\mathrm {lon}}}\) are aileron servo input and elevator servo input.
It can be seen that the two characteristic roots corresponding to the flapping dynamics model of the main rotor are \(-37.7214+3.2200i\) and \(-37.7214-3.2200i \), the undamped natural frequency is 37.8586 rad /s, the corresponding time constant is 0.0264 second, and the damping ratio is 0.9964.
Since the main rotor flapping motion has a much faster response than the rigid body motion of the fuselage, assuming its response speed is fast enough and ignoring its transient response process, the following simplified static flapping motion model can be obtained
where
According to the body rotation dynamics (4), ignoring the nonlinear cross term and considering only the dominant torque component in the external torque \(\varvec{M}\), the following relation can be obtained
Next, taking roll angular rate as an example, the dynamic responses of the simplified and full flapping dynamics model to the roll angular rate are analyzed in the hovering flight mode. When a helicopter is hovering, the lift of the main rotor is approximately equal to its own weight, i.e., \(T_\mathrm {mr} \approx T_\mathrm {hov}=mg\). By inserting equations (13) into equations (12) and (11), respectively, the transfer function of roll angular rate under the input signal \(\delta _{\mathrm {lat}}\) can be obtained. The open-loop bode graph curve and step response curve are shown in Figs. 2 and 3, respectively.
The frequency characteristic curves show that the simplified model can accurately reflect the dynamic response of the complete model at low frequencies, although some errors still exist at high frequencies. The rise time and adjustment time of the step response of the simplified model are 0.042 s and 0.21 s, respectively, while the rise time and adjustment time of the complete model are 0.053 s and 0.0893 s, respectively. It can be found that the rise time of the two is very close, and the adjustment time is also close. Both frequency domain and time domain analysis results show that the simplified flapping dynamics can effectively approximate the complete flapping model of unmanned helicopter. Therefore, it is feasible to design the flight control system based on the simplified flapping model, and the approximate errors will be compensated by adaptive sliding mode control in the subsequent design.
4 Control design and stability analysis
Consider the following nonlinear system with uncertainty
where \(\varvec{x} \in {\mathbb {R}}^{n}\) is the state vector, and \(\varvec{u} \in {\mathbb {R}}^{m}\) indicates the control input. \(\varvec{F}(\varvec{x},t) \in {\mathbb {R}}^{n}\) and \(\varvec{G}(\varvec{x},t) \in {\mathbb {R}}^{n \times m}\) are smooth and unknown functions.
where \(\varvec{F}_0(\varvec{x},t)\) and \(\varvec{G}_0(\varvec{x},t)\) are known parts of \(\varvec{F}(\varvec{x},t)\) and \(\varvec{G}_(\varvec{x},t)\), \(\varvec{F}_\varDelta (\varvec{x},t)\) and \(\varvec{G}_\varDelta (\varvec{x},t)\) are unknown parts of \(\varvec{F}(\varvec{x},t)\) and \(\varvec{G}(\varvec{x},t)\), respectively. \(\varvec{y}\) is a smooth output vector function. Define the sliding mode variable as
where \( \varvec{H}_\mathrm {d}(\varvec{x},t)\) is a smooth reference trajectory.
For the sake of convenience, the state vector is extended to \( \varvec{x}_\mathrm {ext} = \left[ \varvec{x}^\mathrm {T}, t \right] ^\mathrm {T}\). The extended equation of state can be expressed as
where \(\varvec{G}_\mathrm {ext} = \left[ (\varvec{G}_0 +\varvec{G}_\varDelta )^\mathrm {T}, \varvec{G}_\mathrm {ext,0} \right] ^\mathrm {T}\), \( \varvec{G}_\mathrm {ext,0} = \varvec{0} \in {\mathbb {R}}^{m} \), \(\varvec{F}_\mathrm {ext} = \left[ (\varvec{F}_0 +\varvec{F}_\varDelta )^\mathrm {T}, 1 \right] ^\mathrm {T}\). \(\varvec{F}_\mathrm {ext,n} = \left[ \varvec{F}_0^\mathrm {T}, 1 \right] ^\mathrm {T}\) and \(\varvec{G}_\mathrm {ext,n} = \left[ \varvec{G}_0^\mathrm {T}, \varvec{G}_\mathrm {ext,0} \right] ^\mathrm {T}\) are the known nominal parts of \(\varvec{F}_\mathrm {ext}\) and \(\varvec{G}_\mathrm {ext}\), respectively.
Assumption 1
It is assumed that the relative order of the nonlinear system (14) about the sliding mode variable \(\varvec{s}(\varvec{x},t)\) is constant l and the internal dynamics is stable.
Then control signal \( \varvec{u} \) will appear for the first time in the l-th time derivative of the system sliding mode variable, i.e.,
where \(\varvec{\varPhi }={L}_{\varvec{F}_\mathrm {ext}}^{l} \varvec{H}\), \(\varvec{\varUpsilon }={L}_{\varvec{G}_\mathrm {ext}} {L}_{\varvec{F}_\mathrm {ext}}^{l-1} \varvec{H}\). \({L}_{\varvec{G}_\mathrm {ext}}\), \({L}_{\varvec{F}_\mathrm {ext}}^{l}\), and \({L}_{\varvec{F}_\mathrm {ext}}^{l-1}\) are Lie derivatives of \({\varvec{G}_\mathrm {ext}}\) and \({\varvec{F}_\mathrm {ext}}\) with the corresponding orders.
Definition 1
Consider nonlinear system (14) and the sliding mode variable \( \varvec{s}(\varvec{x},t) \), and assume that the time derivatives of \(\varvec{s},\dot{\varvec{s}},...,\varvec{s}^{(l-1)}\) are continuous. Then
is called the sliding mode set of order l. If it is non-empty and is a local integral set in the sense of Filippov [10], the motion over \(\varXi ^{l} \) is called sliding mode of order l with respect to the sliding mode variable \(\varvec{s} \).
Therefore, the l-order sliding mode control problem of the nonlinear system (14) with respect to the sliding mode variable \( \varvec{s}\) is equivalent to the finite time control problem of the following systems
where \(\varvec{z}=\left[ \varvec{z}_{1}, \varvec{z}_{2}, \ldots , \varvec{z}_{l}\right] ^{\mathrm {T}}=\left[ \varvec{s}, \dot{\varvec{s}}, \ldots , \varvec{s}^{(l-1)}\right] ^{\mathrm {T}},\quad i=1,2,...,l-1\).
Assumption 2
Function \( \varvec{\varPhi } \) and \( \varvec{\varUpsilon } \) can be expressed as
where \(\varvec{\varPhi }_\mathrm {n}\) and \(\varvec{\varDelta }_\varPhi \) are the nominal portion and the uncertain one of \(\varvec{\varPhi }\), \(\varvec{\varUpsilon }_\mathrm {n}\) and \(\varvec{\varDelta }_\varUpsilon \) denote the nominal and uncertain parts of \(\varvec{\varUpsilon }\), respectively. \(\varvec{\varPhi }_\mathrm {n}= {L}_{\varvec{F}_\mathrm {ext,n}}^{l} \varvec{H} \), \(\varvec{\varUpsilon }_\mathrm {n}= {L}_{\varvec{G}_\mathrm {ext,n}} {L}_{\varvec{F}_\mathrm {ext,n}}^{l-1} \varvec{H} \), \(\varvec{\varDelta }_{\varPhi }= {L}_{\varvec{F}_\mathrm {ext}}^{l} \varvec{H} -{L}_{\varvec{F}_\mathrm {ext,n}}^{l} \varvec{H} \), \(\varvec{\varDelta }_{\varUpsilon }= {L}_{\varvec{G}_\mathrm {ext}} {L}_{\varvec{F}_\mathrm {ext}}^{l-1} \varvec{H} -{L}_{\varvec{G}_\mathrm {ext,n}} {L}_{\varvec{F}_\mathrm {ext,n}}^{l-1} \varvec{H} \). Suppose the existence of three unknown constants \(\varepsilon _{\varPhi 1} \), \(\varepsilon _{\varPhi 2}\) and \(\varepsilon _{\varUpsilon }\) to make the following constraint relation for the uncertain function valid
Remark 1
For an unmanned helicopter in a typical non-acrobatic flight envelope, both the uncertain portions of \(\varvec{\varPhi }\) and \(\varvec{\varUpsilon }\) are bounded. In addition, after high-precision model identification and verification, it can be assumed that the norm of the uncertain part \(\varvec{\varDelta }_\varPhi \) is less than the norm of the nominal portion \(\varvec{\varPhi }_\mathrm {n}\).
The control objective is to make \(\varvec{s}, \dot{\varvec{s}}, \ldots , \varvec{s}^{(l-1)} \) converge to the origin in finite time under bounded additive and multiplied uncertainties.
Consider the following integral chain system
where \( i=1,2,...,l-1\), \({\varvec{z}_i} =\left[ z_{i1}, \cdots ,z_{ij}, \cdots , z_{in} \right] ^\mathrm {T} \in {{\mathbb {R}} ^n}\), \( j=1,2,...,n\), \({\varvec{v}_\mathrm {n}} \in {{\mathbb {R}} ^n}\). Lemma 1 proves the existence of continuous finite time feedback control for system (22) by giving an explicit structure with small parameters.
Lemma 1
([2]). Assume that \( \varvec{K}_1,\varvec{K}_2,...,\varvec{K}_l \) are real positive definite diagonal matrices and the polynomial \(\lambda ^l + k_{lj}{\lambda ^{l - 1}} + \cdots + k_{2j}\lambda + k_{1j}\) is Hurwitz stable. There is a parameter \(\varepsilon \in \left( {0,1} \right) \), for any \(\alpha \in \left( {1 - \varepsilon ,1} \right) \), so that feedback control (23) exists, which makes states of system (22) converge to origin in finite time
where sign function \(\varvec{Sgn}({\varvec{z}_i})\) and matrix \(\varvec{K}_i\) are defined as
\(\alpha _{ij} \) satisfies the following constraints
Remark 2
In Lemma 1, the following conclusions can be drawn by induction
When \( i=l \), then
When \( i=l-k \), suppose the following inequality is true
When \( i=l-k-1 \), according to (24), it can be obtained
By combining the expression (27) and (28), it can be obtained
So we can generalize
Since \(0<\alpha _{ij}<1,\ i=1,2,\ldots , l, \ j=1,2,\ldots , n\), even a large value of the state variable will not cause the power function in (23) to grow rapidly. Therefore, when the initial value of the system state is large, the convergence rate of the closed loop system will be slow.
Next, based on Lemma 1, a quasi-optimal finite time control method is proposed to improve the transient process.
Theorem 1
Consider system (22) and linear quadratic performance indicator (31)
\(\varvec{z} = {\left( {\varvec{z}_1^\mathrm {T}, \ldots ,\varvec{z}_l^\mathrm {T}} \right) ^\mathrm {T}} \in {{\mathbb {R}}^{ln}}\), \(\varvec{Q} \in {\mathbb {R}}^{ln \times ln}\), \(\varvec{Q}=\varvec{Q}^{\mathrm {T}} =\varvec{D}^{\mathrm {T}}\varvec{D} \ge 0\), \(\varvec{R}\in {\mathbb {R}}^{n \times n}\) is a positive definite matrix, and \(\delta \) is a positive constant. The system state \(\varvec{z}(t)\) will converge to the origin in finite time under feedback control (32), and the convergence rate is not less than \(e^{-\delta t}\).
where
\(\alpha _{i1}, \alpha _{i2}, \cdots , \alpha _{in}\) are the elements on the main diagonal of diagonal matrix \(\varvec{\alpha }_i\), and \(\varvec{P}\) is the positive definite solution of the Riccati equation (33). \(\square \)
where
\( \varvec{0}_{(\bullet )\times (\bullet )} \) and \(\varvec{I}_{(\bullet )\times (\bullet )}\) denote the zero matrix and the identity matrix of corresponding dimension.
Proof
System (22) is re-expressed as follows
By defining the following variable transformation
State space equation (34) can be re-expressed as
The corresponding quadratic performance indicator (31) can be rewritten as
In this way, the problem is transformed into a common linear time-invariant infinite time LQR problem, whose optimal control is
Corresponding to the original system equation (34), the optimal control is
Lemma 2
([40]). Assuming that \(\left( \varvec{A}_\mathrm {n}+ \delta {{{\varvec{I}}_{ln \times ln}}}, \varvec{B}_\mathrm {n}\right) \) can be stabilized and \(\left( \varvec{A}_\mathrm {n}+ \delta {{{\varvec{I}}_{ln \times ln}}}, \varvec{D} \right) \) can be detected, for system (34) and performance index (31), under the action of optimal control (39), the state convergence rate of the closed-loop system is not less than \(e^{-\delta t}\).
Proof
The proof is shown in Appendix. \(\square \)
Remark 3
According to the modal criterion, the controllability of matrix \(\left( \varvec{A}_\mathrm {n}, \varvec{B}_\mathrm {n}\right) \) is equivalent to that of \(\left( \varvec{A}_\mathrm {n}+ \delta {{{\varvec{I}}_{ln \times ln}}}, \varvec{B}_\mathrm {n}\right) \), while the observability of matrix \(\left( \varvec{A}_\mathrm {n}, \varvec{D}\right) \) is equivalent to that of \(\left( \varvec{A}_\mathrm {n}+ \delta {{{\varvec{I}}_{ln \times ln}}}, \varvec{D}\right) \). Thus, when matrices \(\left( \varvec{A}_\mathrm {n}, \varvec{B}_\mathrm {n}\right) \) and \(\left( \varvec{A}_\mathrm {n}, \varvec{D}\right) \) are controllable and observable, \(\left( \varvec{A}_\mathrm {n}+ \delta {{{\varvec{I}}_{ln \times ln}}}, \varvec{B}_\mathrm {n}\right) \) is stabilized and \(\left( \varvec{A}_\mathrm {n}+ \delta {{{\varvec{I}}_{ln \times ln}}}, \varvec{D}\right) \) is detectable.
Assume that the states of system (22) are far from the origin, i.e., \( \mathop {\max }\limits _{1 \le i \le l} \left( {\left\| {{\varvec{z}_i}} \right\| } \right) > 1 \). According to the definition of equation \( \varvec{S}({\varvec{z}_i},{\alpha _i}) \), the control input of system (22) becomes equation (39).
Since matrix \(\varvec{A}_\mathrm {n}\) and matrix \(\varvec{B}_\mathrm {n}\) are the state matrix and input matrix of system (22), respectively, according to their definitions, the rank of controllability discriminant matrix is \( \mathrm {rank}(\left[ \varvec{B}_\mathrm {n},\varvec{A}_\mathrm {n}\varvec{B}_\mathrm {n},\cdots ,\varvec{A}_\mathrm {n}^{ln-1}\varvec{B}_\mathrm {n}\right] ) =ln\), system (22) is completely controllable, and the system states can be completely observable by choosing the appropriate \(\varvec{Q}\) matrix. In addition, since the \(\varvec{P}\) is a positive definite solution of the algebraic Riccati equation (33), the control input (39) is optimal with respect to the performance index (31), and the system state \( \varvec{z}_i\) will converge asymptotically to the origin in an optimal way. It also means that the states of the system (22) will converge to the following region in finite time with a speed of no less than \(e^{-\delta t}\).
When \( \varvec{z} \in O_\mathrm {nei} \), according to \( \varvec{S}({\varvec{z}_i},{\alpha _i}) \), the control input for system (22) takes the following form
By expanding equation (41) using matrix multiplication, we can get
Since the matrix \(\varvec{P}\) is a positive definite solution of the algebraic Riccati equation (33), the polynomial \(\lambda ^l + k_{lj}{\lambda ^{l - 1}} + \cdots + k_{2j}\lambda + k_{1j}\) is Hurwitz stable. According to Lemma 1, the control input (42) can ensure that the system state converges to zero in finite time. Therefore, the closed-loop system formed by equations (22) and (32) is globally finite time stable, that is, the states of system (22) will converge to zero in finite time under the control (32). \(\square \)
4.1 Attitude control
In order to apply the control method proposed in Theorem 1, the attitude kinematics and dynamics of the unmanned helicopter are transformed into the following forms based on equations (3), (4) and (10)
By using the simplified flapping dynamics model (12) and the follow feedback control
where \(\delta _\mathrm {ped}\) is the rudder servo input, and \(k_\mathrm {ped}\), \(k_\mathrm {r}\) are constants, equation (43) can be transformed into
where \(\varvec{\delta }_\mathrm {aer} = [\varvec{\delta }_\mathrm {cyc}^T, {\delta }_\mathrm {ped}]^T\),
\({M} _{\varDelta 1}= \left( {{k_\beta } + {T_\mathrm {mr}}{H_\mathrm {mr}}} \right) \sin (b) - \left( {{k_\beta } + {T_\mathrm {hov}}{H_\mathrm {mr}}} \right) b + {L_\mathrm {vt}} + {L_\mathrm {tr}} - {H_\mathrm {tr}}{T_\mathrm {tr,ctr}}\) and \({M} _{\varDelta 2} =\left( {{k_\beta } + {T_\mathrm {mr}}{H_\mathrm {mr}}} \right) \sin (a) - \left( {{k_\beta } + {T_\mathrm {hov}}{H_\mathrm {mr}}} \right) a + {M_\mathrm {ht}} \). Redefine the state vector of the attitude subsystem as \( \varvec{x}_1 \buildrel \varDelta \over = \left[ \varvec{\varTheta }^\mathrm {T}, \varvec{\omega }^\mathrm {T}\right] ^\mathrm {T}\), and let the known part and the unknown part of the system be
and
where \( \varvec{J} = \varvec{J}_\mathrm {n} +\varvec{J}_\varDelta \), \( \varvec{J}_\mathrm {n}\) is the measured nominal moment of inertia matrix, and \( \varvec{J}_\varDelta \) is the measurement error of moment of inertia. The sliding mode variable is designed as \( \varvec{z}_\mathrm {att,1} = \varvec{s}_\mathrm {att} = \varvec{\varTheta } -\varvec{\varTheta }_\mathrm {d} \), and \( \varvec{z}_\mathrm {att,2} = \dot{\varvec{s}}_\mathrm {att} \), where \( \varvec{\varTheta }_\mathrm {d} \) is the expected attitude angle vector. Then equation (45) can be rewritten as
Assumption 3
The roll and pitch angle of small unmanned helicopter in the whole autonomous flight process always meet the following constraints
Remark 4
Since the Euler angle is used to represent the attitude of the unmanned helicopter in this paper, the pitch angle needs to be limited to \((-90^{\circ },90^{\circ })\) to avoid suffering from gimbal lock. In addition, in order to limit the maneuvering range of the unmanned helicopter to the typical flight envelope so that Assumption 2 can be reasonably established, the roll angle is also limited to \((-90^{\circ },90^{\circ })\).
On the basis of Assumption 2 and 3, assume that there are three positive real numbers \(\varepsilon _\mathrm {\varPhi 1} \), \(\varepsilon _\mathrm {\varPhi 2}\) and \(\varepsilon _\mathrm {\varUpsilon 1}\), such that the following inequality holds
Let’s define \(\varvec{\alpha }_1 \buildrel \varDelta \over = \text {diag}(\alpha _{11},\alpha _{12},\alpha _{13})\), and \(\varvec{\alpha }_2 \buildrel \varDelta \over = \text {diag}(\alpha _{21},\alpha _{22},\alpha _{23})\), and design functions \(\varvec{S}(\varvec{z}_\mathrm {att,1},\varvec{\alpha }_1)\) and \(\varvec{S}(\varvec{z}_\mathrm {att,2},\varvec{\alpha }_2)\) as follows
where \( \phi _\mathrm {e} = \phi -\phi _\mathrm {d}\), \(\theta _\mathrm {e} =\theta -\theta _\mathrm {d}\), \(\psi _\mathrm {e} = \psi -\psi _\mathrm {d}\), \( \phi _\mathrm {d} \), \( \theta _\mathrm {d}\) and \( \psi _{\mathrm {d}} \) are the desired roll, pitch and yaw angle, respectively. According to equation (32), the virtual control is designed as follows
where \(\varvec{R}_1 \in {\mathbb {R}}^{3\times 3}\) is a positive definite matrix, \( \varvec{P}_1\) is the positive definite solution of the Riccati equation of the following algebraic matrix
where \(\delta _1\) is a positive real number by design, \(\varvec{A}_\mathrm {n1}=\left[ \begin{array}{cc} \varvec{0}_{3\times 3} &{} \varvec{I}_{3\times 3} \\ \varvec{0}_{3\times 3} &{} \varvec{0}_{3\times 3} \end{array} \right] \), \(\varvec{B}_\mathrm {n1}=\left[ \begin{array}{c} \varvec{0}_{3\times 3} \\ \varvec{I}_{3\times 3} \end{array} \right] \), and \(\varvec{Q}_\mathrm {1}=\left[ \begin{array}{cc} \varvec{I}_{3\times 3} &{} \varvec{0}_{3\times 3} \\ \varvec{0}_{3\times 3} &{} \varvec{0}_{3\times 3} \end{array} \right] \).
The first integral sliding mode surface is designed as
where
It is assumed that the final input signal consists of nominal control and adaptive control, i.e.,
Since matrix \( \left( {{k_\mathrm {ped,ctr}}{{\varvec{M}}_2} - {{\varvec{M}}_1}{\varvec{B}}} \right) \) is invertible, \( \varvec{\varUpsilon }_\mathrm {1n} \) is also invertible under Assumption 3, then the nominal control \( \varvec{u}_\mathrm {att,n}\) can be designed as
where \( \begin{aligned} \varvec{S}(\varvec{\sigma }_1) =\left[ \begin{array}{c} {\text {sign}(\sigma _{11})|\sigma _{11}|^{\frac{1}{2}}} \\ {\text {sign}(\sigma _{12})|\sigma _{12}|^{\frac{1}{2}}}\\ {\text {sign}(\sigma _{13})|\sigma _{13}|^{\frac{1}{2}}} \end{array}\right] \end{aligned} \), \(\varvec{K}_\mathrm {\tau 1}\) and \(\varvec{K}_\mathrm {\eta 1}\) are positive definite diagonal matrices.
The adaptive control \( \varvec{u}_\mathrm {att,a}\) is designed as
where \(k_\mathrm {a1}\) is a constant to be designed, and control parameters \({\hat{c}}_1\), \({\hat{c}}_2\) and \({\hat{c}}_3\) are estimated values of the unknown parameters \({c}_1\), \({c}_2\) and \({c}_3\), respectively. \({c}_1\), \({c}_2\) and \({c}_3\) are defined as follows
Next, the adaptive laws are designed as
where \( o_i>0\) and \(p_i>0\), \( i=1,2,3 \) are control parameters to be designed.
4.2 Vertical position control
Using a similar method to the tail rotor force, the main rotor lift \(T_\mathrm {mr}\) in equation (9) can be rewritten as follows
where \(k_\mathrm {int1}\) and \( k_\mathrm {int2} \) are model parameters, \( {\overline{d}}_\mathrm {T} ={d}_\mathrm {T} -k_\mathrm {int1}(v_\mathrm {im}-v_\mathrm {im,hov})\), \({d}_\mathrm {T}\) is the approximation error in the calculation model of the main rotor force. \(\delta _\mathrm {col}\) is the collective pitch servo input of the unmanned helicopter. \(v_\mathrm {im}\) indicates the induced velocity of the main rotor, while \(v_\mathrm {im,hov}\) denotes the induced velocity in hover.
Define the sliding mode variable about the altitude as \( {z}_\mathrm {ver,1} ={s}_\mathrm {ver} = {z} -{z}_\mathrm {d}\), \( {z}_\mathrm {ver,2} = \dot{{s}}_\mathrm {ver} \). Combining equations (62), (1) and (2), the vertical position dynamics of the small unmanned helicopter can be described as
where \( {\varUpsilon }_\mathrm {2n}= \dfrac{k_\mathrm {int1} k_\mathrm {int2} k_\mathrm {col} \mathrm {c}(\phi ) \mathrm {c}(\theta )}{m_\mathrm {n}} \), \({\varPhi }_\mathrm {2n} = \dfrac{k_\mathrm {int1} (w-v_\mathrm {im,hov}) \mathrm {c}(\phi ) \mathrm {c}(\theta )}{m_\mathrm {n}} +g \), \({\varDelta }_{\varUpsilon _2} = \dfrac{k_\mathrm {int1} k_\mathrm {int2} k_\mathrm {col} \mathrm {c}(\phi )\mathrm {c}(\theta )(m_\mathrm {n}-m)}{mm_\mathrm {n}}\), \( {\varDelta }_{\varPhi _2} = ({\bar{d}}_\mathrm {T} + {d}_\mathrm {F})\mathrm {c}(\phi ) \mathrm {c}(\theta )\), \( \ddot{z}_\mathrm {d} \) is the desired acceleration in the vertical direction of the inertial coordinate system, and \( m_\mathrm {n} \) is the measured mass of the aircraft.
Define \(\varvec{x}_2 \buildrel \varDelta \over = \left[ z , v_z \right] ^\mathrm {T}\), and suppose that positive real numbers \(\varepsilon _\mathrm {\varPhi 3} \), \(\varepsilon _\mathrm {\varPhi 4}\) and \(\varepsilon _\mathrm {\varUpsilon 2}\) exist so that the following inequality holds
Select functions \({S}({z}_\mathrm {ver,1},\bar{{\alpha }}_1)\) and \({S}({z}_\mathrm {ver,2},\bar{{\alpha }}_2)\) as
where \(z_\mathrm {e} =z -z_\mathrm {d}\), \(z_{\mathrm {d}} \) is the expected altitude in inertial coordinates. Similar to equation (53), the designed vertical position virtual control is
where \({R}_2 \in {\mathbb {R}}\) is a real number greater than zero, \( \varvec{P}_2\) is the positive definite solution of the following algebraic matrix Riccati equation
where \(\delta _2\) a positive control parameter, \(\varvec{A}_\mathrm {n2}=\left[ \begin{array}{cc} {0} &{} 1 \\ {0} &{} 0 \end{array} \right] \), \(\varvec{B}_\mathrm {n2}=\left[ \begin{array}{c} 0 \\ 1 \end{array} \right] \), and \(\varvec{Q}_\mathrm {2}=\left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 0 \end{array} \right] \).
Select the second integral sliding mode surface as
where \({\mu }_\mathrm {ns} = \int _0^t {\mu _\mathrm {n}} d\tau \). The control input of the altitude servo is divided into nominal control and adaptive control, as follows
obviously, \({\varUpsilon }_\mathrm {2n} \ne 0\). Design the nominal control as
where \({S}({\sigma }_2)= \text {sign}(\sigma _{2})|\sigma _{2}|^{\frac{1}{2}}\), \({K}_\mathrm {\tau 2}\) and \({K}_\mathrm {\eta 2}\) are positive design parameters.
Then design the adaptive control \({u}_\mathrm {ver,a}\) as
where \(k_\mathrm {a2}\) is a constant, \({c}_4\), \({c}_5\) and \({c}_6\) are unknown parameters, whose estimated values are \({\hat{c}}_4\), \({\hat{c}}_5\) and \({\hat{c}}_6\), defined as follows
In order to obtain the estimated values, the three adaptive laws are designed as
where \( o_i>0\), \(p_i>0\), \( i=4,5,6 \).
4.3 Horizontal position control
Compared with attitude, the dynamic response of position of small unmanned helicopters is slower. They can be divided into inner and outer loops to carry out the control design. The dynamic model of the horizontal position can be approximately equivalent to a typical second order integral chain model, which is especially suitable for the control method proposed in this paper.
To facilitate the design, the horizontal position model is extracted from equations (1) and (2), and rewritten as follows
where \({\varvec{P}}_{\mathrm {h}}=[x,y]^\mathrm {T}\) and \({\varvec{V}}_{\mathrm {h}}=[v_x,v_y]^\mathrm {T}\) are the horizontal position and velocity vector in the inertial coordinate system, respectively, \({\varvec{a}}_{\mathrm {hd}}=[a_\mathrm {hd,x},a_\mathrm {hd,y}]^\mathrm {T}\) is the horizontal position virtual control. Similar to 4.1 and 4.2, let \( \varvec{z}_\mathrm {hon,1} = \varvec{s}_\mathrm {hon} = \varvec{P}_\mathrm {h} -\varvec{P}_\mathrm {hd} \) be the sliding mode variable, and \( \varvec{z}_\mathrm {hon,2} = \dot{\varvec{s}}_\mathrm {hon} \). \( \varvec{P}_\mathrm {hd} \) is the expected horizontal position vector. Then equation (75) can be rewritten as
where \(\varvec{\varUpsilon }_\mathrm {3n}= \left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \end{array} \right] \), \(\varvec{\varPhi }_\mathrm {3n}= \left[ \begin{array}{c} 0 \\ 0 \end{array} \right] \), \(\varvec{\varDelta }_{\varPhi _3}\) and \(\varvec{\varDelta }_{\varUpsilon _3}\) can be obtained from equation (2). Based on Assumptions 2 and 3, assume that there exist three positive real numbers \(\varepsilon _\mathrm {\varPhi 5} \) \(\varepsilon _\mathrm {\varPhi 6}\) and \(\varepsilon _\mathrm {\varUpsilon 3}\) such that the following inequality is always true
where \( \varvec{x}_3\) is defined as \( \varvec{x}_3 \buildrel \varDelta \over = \left[ \varvec{P}_\mathrm {h}^\mathrm {T}, \varvec{V}_\mathrm {h}^\mathrm {T}\right] ^\mathrm {T}\).
Define \(\underline{\varvec{\alpha }}_1=\text {diag}({\underline{\alpha }}_{11},{\underline{\alpha }}_{12})\), \(\underline{\varvec{\alpha }}_2=\text {diag}({\underline{\alpha }}_{21},{\underline{\alpha }}_{22})\), and design functions \(\varvec{S}(\varvec{z}_\mathrm {hon,1},\underline{\varvec{\alpha }}_1)\), \(\varvec{S}(\varvec{z}_\mathrm {hon,2},\underline{\varvec{\alpha }}_2)\) as
where \(x_\mathrm {e} = x -x_\mathrm {d}\), \(y_\mathrm {e} =y -y_\mathrm {d}\), \( x_\mathrm {d} \) and \( y_\mathrm {d}\) are the desired longitudinal and lateral horizontal positions, respectively. According to (32), design virtual control
where \(\varvec{R}_3 \in {\mathbb {R}}^{2\times 2}\) is a positive definite matrix, \( \varvec{P}_3\) is the positive definite solution of the following algebraic Riccati equation
where \(\delta _3\) is a designed constant greater than zero, \(\varvec{A}_\mathrm {n3}=\left[ \begin{array}{cc} \varvec{0}_{2\times 2} &{} \varvec{I}_{2\times 2} \\ \varvec{0}_{2\times 2} &{} \varvec{0}_{2\times 2} \end{array} \right] \), \(\varvec{B}_\mathrm {n3}=\left[ \begin{array}{c} \varvec{0}_{2\times 2} \\ \varvec{I}_{2\times 2} \end{array} \right] \), and \(\varvec{Q}_\mathrm {3}=\left[ \begin{array}{cc} \varvec{I}_{2\times 2} &{} \varvec{0}_{2\times 2} \\ \varvec{0}_{2\times 2} &{} \varvec{0}_{2\times 2} \end{array} \right] \).
The third integral sliding surface \( \varvec{\sigma }_3\) is designed as
where \(\varvec{\nu }_\mathrm {hons} =\left[ \int _0^t {\nu _\mathrm {hon,1}} d\tau ,\int _0^t \nu _\mathrm {hon,2} d\tau \right] ^\mathrm {T} \). Similarly, the virtual control of horizontal position consists of nominal control and adaptive control
Design the nominal control \( \varvec{u}_\mathrm {hon,n}\) as follows
where \(\varvec{S}(\varvec{\sigma }_3)=\left[ \text {sign}(\sigma _{31})|\sigma _{31}|^{\frac{1}{2}}, \text {sign}(\sigma _{32})|\sigma _{32}|^{\frac{1}{2}} \right] ^\mathrm {T}\), \(\varvec{K}_\mathrm {\tau 3}\) and \(\varvec{K}_\mathrm {\eta 3}\) are positive definite diagonal matrices.
In addition, the adaptive control \(\varvec{u}_\mathrm {hon,a}\) is designed as follows
where \(k_\mathrm {a3}\) is a design parameter that needs to be selected appropriately, \({\hat{c}}_7\), \({\hat{c}}_8\) and \({\hat{c}}_9\) are, respectively, estimated values of unknown parameters \({c}_7\), \({c}_8\) and \({c}_9\), which are defined as
In order to stabilize the closed-loop system, the three adaptive laws are designed as
where \( o_i>0\), \(p_i>0\), \( i=7,8,9 \).
Next, the desired longitudinal and lateral acceleration in the inertial coordinate system needs to be converted into the desired pitch Angle and roll Angle in the body coordinate system. Taking the expected longitudinal acceleration and the desired pitch angle as an example, the conversion relationship between them is shown in Fig. 4.
where \(x_\mathrm {b0}\) and \(z_\mathrm {b0}\) are the \(x-\) and \(z-\)axis of the initial body coordinate system of the small unmanned helicopter. For the convenience of description, it is assumed that they are recombined with the \(x-\) and \(z-\)-axis of the inertial coordinate system, respectively. \(O_\mathrm {b}-x_\mathrm {b1}y_\mathrm {b1}z_\mathrm {b1}\) is the desired body coordinate system, where the \(y_\mathrm {b1}\)-axis is recombined with its \(y_\mathrm {b0}\) axis in \(O_\mathrm {b}-x_\mathrm {b0}y_\mathrm {b0}z_\mathrm {b0}\), both represented by the black solid points in Fig. 4, and their direction is vertical to paper and pointing outward.
Firstly, it is assumed that the unmanned helicopter is stable on the \(z-\)axis of the inertial coordinate system and the yaw angle is zero. According to the definition of the coordinate system in Fig. 1, the desired pitch \(\theta _\mathrm {d}\) is opposite to the expected longitudinal acceleration \(a_{\mathrm {hd},x}\), then
So similarly,
Assuming that the force of the unmanned helicopter is balanced on \( z-\)axis in the inertial coordinate system, but the yaw angle is not zero, the following equation is established
which indicates that
Combining the three equations of (91), one can get
4.4 Stability analysis
Lemma 3
According to the adaptive laws given in equations (61), (74) and (87), the adaptive parameters \({\hat{c}}_i \ (i=1,2,\ldots ,9)\) have upper bounds. That is, there ar positive real numbers \({\bar{c}}_i\), such that the inequalities \( 0<{\hat{c}}_i \le {\bar{c}}_i \) and \(0<c_i \le {\bar{c}}_i \) are always true for all \(t>0\).
Theorem 2
Under Assumptions 1, 2 and 3, the nonlinear dynamics model of the small unmanned helicopter described in equation (1), (2), (3), (4) and (8) is considered. By defining the integral sliding mode surface as shown in formulas (55), (69) and (82), and the virtual control as shown in formulas (53), (67) and (80), and then designing an adaptive high-order continuous sliding mode quasi-optimal controller composed of equations (57), (58), (59), (61), (70), (71), (72), (74), (83), (84), (85) and (87), the attitude and position tracking errors of the system can converge to the vicinity of the origin in finite time. Moreover, the convergence rate of attitude, vertical position and horizontal position tracking errors can be guaranteed to be no less than \(e^{-\delta _1 t}\), \(e^{-\delta _2 t}\) and \(e^{-\delta _3 t}\), respectively. \(\square \)
Proof
Design the first Lyapunov function as
The following two cases are analyzed.
Case 1: when
Let \( {{\bar{c}}} = {\hat{c}}_1 +{\hat{c}}_2 \Vert \varvec{\chi }_1\Vert +{\hat{c}}_3 \Vert \varvec{\varPhi }_\mathrm {1n} -\varvec{\nu }_\mathrm {n} -\ddot{\varvec{\varTheta }}_\mathrm {d}\Vert \). By substituting equation (57), (58) and (59) into the time derivative of equation (93), and considering equation (50), it can be obtained
According to (61) and using the definition of \(c_1\), \(c_2\) and \(c_3\), one can obtain
Then, substituting equation (95) into inequality (94), we get
Based on the \( C_p\) inequality, one knows that
Therefore, equation (96) can be further deduced as
In addition, it is obvious that the following inequality always holds
According to the inequality (99), equation (98) can be changed into
Based on Lemma 3, it can be known that
By substituting inequality (101) into equation (100), and using the \( C_p \) inequality again, (100) can be further transformed into
where
Case 2: when
the time derivative of equation (93) can be expressed as
Considering that the following inequality is always true
then equation (103) can be further written as
By comparing equations (105) with (98), it is not difficult to see that
where \(\eta _2 =(1 -\varepsilon _\mathrm {\varUpsilon 1}) \sum \limits _{i = 1}^3 \left( \left( \dfrac{o_i}{4p_i} + 1\right) {\bar{c}}_i^2 + {\bar{c}}_i^\frac{3}{2} \right) +(1 -\varepsilon _\mathrm {\varUpsilon 1})\dfrac{k_\mathrm {a1}}{4} \).
Combining case 1 and case 2, one can get
where \( \eta _\mathrm {max} = \max \left( \eta _1,\eta _2 \right) = \eta _2\).
Similarly, the second and third Lyapunov functions are defined as
By using a proof process similar to \({\dot{V}}_1\), it can be obtained
where
Now, the Lyapunov function of the whole closed-loop control system can be defined as
According to equation (107), (109) and the \( C_p \) inequality, the time derivative of equation (110) can be expressed as
Therefore, the attitude and position tracking errors of the closed-loop system are limited in a small set containing the origin in finite time, i.e., the following inequality holds
where \( \varvec{\sigma } = \left[ \varvec{\sigma }_1^\mathrm {T}, {\sigma }_2, \varvec{\sigma }_3^\mathrm {T} \right] ^\mathrm {T} \). By synthesizing case 1 and case 2, it can be found that the system state trajectory converges to the neighborhood of the integral sliding mode \( \varvec{\sigma }_1=\varvec{0} \), \( {\sigma }_2= {0} \) and \( \varvec{\sigma }_3=\varvec{0} \) in finite time. In addition, when the integral sliding mode is reached, it can be obtained
where \( \varvec{\vartheta }_1(t) \), \({\vartheta }_2(t) \) and \( \varvec{\vartheta }_3(t) \) are time-varying functions generated by \( \dot{\varvec{\sigma }}_1 \), \( \dot{{\sigma }}_2\) and \( \dot{\varvec{\sigma }}_3\), respectively. According to Theorem 1, both the first-order sliding mode variable \({\varvec{z}}_\mathrm {att,1}\), \({{z}}_\mathrm {ver,1}\), \({\varvec{z}}_\mathrm {hon,1}\) and the second-order sliding mode variable \({\varvec{z}}_\mathrm {att,2}\), \({{z}}_\mathrm {ver,2}\), \({\varvec{z}}_\mathrm {hon,2}\) can converge to the origin in finite time, that is, they can reach the second-order sliding mode relative to \(\varvec{s}_\mathrm {att}\), \({s}_\mathrm {ver}\) and \(\varvec{s}_\mathrm {hon}\) in finite time, and the tracking error convergence rate of attitude, vertical position and horizontal position is no less than \(e^{-\delta _1 t}\), \(e^{-\delta _2 t}\) and \(e^{-\delta _3 t}\), respectively. \(\square \)
5 Simulation and practical experiment
5.1 Simulation results
In this section, simulation and physical experiment are, respectively, used to verify the performance of the control system designed in this paper, and it is compared with the adaptive radial basis function neural network control (ARBFNNC) in [41]. In order to show the comparative effect clearly, we separate the simulation results from the actual experiment results. The effectiveness of the proposed control method is tested using a typical flight action that reflects all coupling effects of unmanned helicopter. The reference trajectory is given by
The above-mentioned reference flight trajectory expects the small unmanned helicopter to maneuver simultaneously in all directions, which requires high dynamic performance of the control system. For the first 5 seconds, the helicopter is hovering at its original position. From the 5th second on, the helicopter makes a horizontal circular maneuver with the nose pointing at the center of the circle. At the same time, the helicopter makes a upward movement in the vertical direction. In the actual flight process, the unmanned helicopter is mainly disturbed by the longitudinal and lateral gusts in the body coordinate system, especially the lateral gusts seriously affects the stability of the yaw control. Therefore, the gust model adopts the cosine form with a period of 20 seconds as suggested in [11]. Gust interference is shown in Fig. 5.
The main control parameters are selected as follows. \( \varvec{K}_\mathrm {\tau 1}= diag([15,15,15]),\ k_\mathrm {\tau 2} =10,\ \varvec{K}_\mathrm {\tau 3}= diag([5,3]),\ \varvec{K}_\mathrm {\eta 1}= diag([15,15,15]),\ k_\mathrm {\eta _2}=10,\ \varvec{K}_\mathrm {\eta 3}= diag([5,3]), \ \varvec{R}_\mathrm {1}= diag([3,3,3]),\quad R_2 =1,\quad \varvec{R}_\mathrm {3}= diag([5,5]),\ k_\mathrm {a1} = 80,\ k_\mathrm {a2} =60,\ k_\mathrm {a3} = 80,\ \delta _1 =1.5,\; \delta _2 =0.1,\; \delta _3 =0.1 \).
Under the same reference trajectory and interference environment, the control method (AHOSMQC) designed in this paper is compared with the method (ARBFNNC) in [41], and the simulation results are shown in Fig. 6, 7, 8 and 9. The results show that the controller designed in this paper has better control precision and stronger anti-interference ability, and the overall performance is more satisfactory. Figures 6 and 7 show that AHOSMQC can track the desired trajectory more quickly, showing a faster response speed. In addition, it can be seen from Fig. 9 that the dynamic and static tracking errors of the method designed in this paper are smaller than those of the method in [41] in the same interference environment, which is especially true in horizontal positions.
5.2 Practical experiment results
This section first introduces the hardware system of the small unmanned helicopter, whose framework is depicted in Fig. 10, and then shows the test results of the autonomous flight experiment.
The unmanned helicopter system (Heli800E) is reconstructed based on the TREX 800E F3C electric model helicopter, as shown in Fig. 11 and Fig. 12, whose length is 1.478 m, and the main rotor diameter is 1.74 m. The airborne electronic system is the brain of the unmanned helicopter, responsible for collecting control input signals and necessary state information, performing state estimation, filtering algorithm and control algorithm, which requires strong real-time processing ability. In addition, high reliability and security are required. After comprehensive consideration, this paper adopts the open-source hardware and software scheme based on Pixhawk and APM. Pixhawk is selected as the hardware circuit foundation of the unmanned helicopter system platform, and APM is selected as the software foundation of the platform. Selecting the existing open-source project as the basis of the research can greatly simplify the platform construction process, so that we can focus on the flight control algorithm of unmanned helicopter.
The ground station is responsible for the communication between the airborne avionics system and the ground operators. It is mainly used to display and monitor the flight status of the helicopter in real time. At the same time, it is used to adjust the control parameters online, which significantly improves the efficiency of parameter adjustment and makes the flight experiment more convenient. A pair of 915 MHz wireless modems are responsible for real-time information transmission between the ground station and the airborne avionics system. Flight data can be downloaded from the ground station after the flight.
The effectiveness of the proposed control method was tested using a typical flight action that reflects all coupling effects of unmanned helicopter. The unmanned helicopter starts from the hovering state and flies around the circle with a radius of 6 m, always pointing at the center of the circle, while rising at a constant speed of 0.6 meters per second. When \(t \le 5\), the reference trajectory is set as \(x_\mathrm {d}=0, y_\mathrm {d}=0, z_\mathrm {d}=0.8\) and \(\psi _\mathrm {d}=5.24\) rad(300 degree). The initial altitude of the automatic flight is 0.8 meters, and the initial yaw is 300 degree, mainly to ensure the safety of the experiment. For \(t \ge 5\), the reference trajectory is given by
The actual flight experiments are carried out in a windy environment, and the average gust wind speed was about 3.5 m/s.
As with the simulation experiment, the control performance of the method designed in this paper is compared with that designed in [41] under the same environment and input conditions.
The practical experimental results are shown in Fig. 13, 14, 15, 16, 17, 18 and 19. The three dimensional position and horizontal position tracking curves are given in Fig. 13 and Fig. 14, respectively, from which it can be seen that the proposed control method can obtain better control performance even in a windy environment compared with the method in [41].
The single tracking curves of the positions and yaw angle are shown in Fig. 15.
It is obvious from the figure that the unmanned helicopter moves in four channels at the same time. In order to achieve the goal, the proposed control system needs to overcome the inherent coupling effect and uncertainty of the model as well as external gust interference, showing strong maneuverability and robustness. The linear velocity, attitude, angular rate and control input signals in the autonomous flight of the unmanned helicopter are shown in Fig. 16, 17, 18 and 19, respectively. The mean absolute values of the control inputs \(\delta _{lat}\), \(\delta _{lon}\), \(\delta _{col}\) and \(\delta _{ped}\) are 0.0205, 0.0399, 0.5855 and 0.7381, respectively, which are all kept within a reasonable range.
Remark 5
While the main rotor of the unmanned helicopter rotates to generate lift, it exerts a counter-torque on the fuselage. There are many ways to counteract the anti-torque force in a helicopter, the most common is to use the tail rotor. For example, if the main rotor turns clockwise, it exerts a counterclockwise torque on the fuselage, and the tail rotor must be pushed or pulled to generate a clockwise push to counteract the countertorque of the main rotor. Meanwhile, the tail rotor pushing or pulling force has a side force on the fuselage, and this force is usually offset by the roll angle of helicopter fuselage. Combined with the specific tracking route, the nonzero roll angle is finally generated, as seen in Fig. 17.
6 Conclusion
In this paper, a multi-variable adaptive high-order sliding mode quasi-optimal controller is designed. The control structure is based on a redesigned quadratic performance index, leading a quasi-optimal property with variable convergence rate. It is proved theoretically that the position and yaw tracking errors can converge in finite time and the convergence speed is not lower than the design value. In addition, the uncertainty bound required in general sliding mode control is not needed in this paper. Finally, a challenging high-mobility experiment is used to test the theoretical design method. The simulation and practical experiment results show that the proposed control system has better tracking effect on position and yaw, and better robustness to internal uncertain system parameters and external gust.
The research focus of this paper is the control of a single unmanned helicopter. However, multi-agent systems have shown more and more potential applications in various fields [22,23,24]. Our subsequent research will focus on related control problems of multi-agent systems. In addition, due to structural differences, fixed-wing UAV may land safely even in the case of power loss or sensor faults, while traditional unmanned helicopter or quadrotor is often difficult to do so [33]. Therefore, the safety control of unmanned helicopter is also a research direction we will focus on in the future.
Data Availibility Statement
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Ahmed, B., Pota, H.R., Garratt, M.: Flight control of a rotary wing uav–a practical approach. In: IEEE Conference on Decision and Control (2008)
Bhat, S.P., Bernstein, D.S.: Geometric homogeneity with applications to finite-time stability. Math. Control Signals Syst. 17(2), 101–127 (2005)
Bin, X., Jianchuan, G., Yao, Z.: Adaptive backstepping tracking control of a 6-dof unmanned helicopter. IEEE/CAA J. Autom. Sinica 2(1), 19–24 (2015)
Cisneros, P.S.G., Hoffmann, C., Bartels, M., Werner, H.: Linear parameter-varying controller design for a nonlinear quad-rotor helicopter model for high speed trajectory tracking. In: 2016 American Control Conference (ACC), pp. 486–491 (2016)
Ding, S., Mei, K., Yu, X.: Adaptive second-order sliding mode control: a lyapunov approach. IEEE Trans. Autom. Control (2021). https://doi.org/10.1109/TAC.2021.3115447
El-Ferik, S., Syed, A.H., Omar, H.M., Deriche, M.A.: Nonlinear forward path tracking controller for helicopter with slung load. Aerosp. Sci. Technol. 69, 602–608 (2017)
Fang, X., Wu, A., Shang, Y., Dong, N.: A novel sliding mode controller for small-scale unmanned helicopters with mismatched disturbance. Nonlinear Dyn 83(1), 1053–1068 (2016)
Fang, X., Wu, A., Shang, Y., Dong, N.: Robust control of small-scale unmanned helicopter with matched and mismatched disturbances. J. Franklin Inst. 353(18), 4803–4820 (2016)
Fang, Z., Tian, H., Li, P.: Probabilistic robust linear parameter-varying control of a small helicopter using iterative scenario approach. IEEE/CAA J. Autom. Sinica 2(1), 85–93 (2015)
Filippov, A.F.: Differential Equations with Discontinuous Right-hand Side. Kluwer, Dordrecht, The Netherlands (1998)
Frost, W., Turner, R.E.: A discrete gust model for use in the design of wind energy conversion systems. J. Appl. Meteorol. 21(6), 770–776 (1982)
Godbolt, B., Vitzilaios, N.I., Lynch, A.F.: Experimental validation of a helicopter autopilot design using model-based pid control. Journal of Intelligent and Robotic Systems 70(1), 385–399 (2013)
Halbe, O., Hajek, M.: Robust helicopter sliding mode control for enhanced handling and trajectory following. Journal of Guidance, Control, and Dynamics 43(10), 1805–1821 (2020)
He, Y., Pei, H., Sun, T.: Robust tracking control of helicopters using backstepping with disturbance observers. Asian Journal of Control 16(5), 1387–1402 (2015)
Hua, C., Chen, J., Guan, X.: Fractional-order sliding mode control of uncertain quavs with time-varying state constraints. Nonlinear Dynamics 95(2), 1347–1360 (2019)
Huang, Y., Zhu, M., Zheng, Z., Feroskhan, M.: Fixed-time autonomous shipboard landing control of a helicopter with external disturbances. Aerospace Science and Technology 84, 18–30 (2019)
Jafar, A., Bhatti, A.I., Ahmad, S., Ahmed, N.: Robust gain-scheduled linear parameter-varying control algorithm for a lab helicopter: A linear matrix inequality-based approach. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering 232(5), 558–571 (2018)
Jiang, T., Lin, D., Song, T.: Finite-time control for small-scale unmanned helicopter with disturbances. Nonlinear Dynamics 96(3), 1747–1763 (2019)
Kumar, M.V., Omkar, S.N., Suresh, S., Sampath, P., Ganguli, R.: Design of a stability augmentation system for a helicopter using lqr control and ads-33 handling qualities specifications. Aircraft Engineering and Aerospace Technology 80(2), 111–123 (2008)
Liu, H., Derawi, D., Kim, J., Zhong, Y.: Robust optimal attitude control of hexarotor robotic vehicles. Nonlinear Dynamics 74(4), 1155–1168 (2013)
Lu, H., Liu, C., Guo, L., Chen, W.H.: Flight control design for small-scale helicopter using disturbance-observer-based backstepping. Journal of Guidance, Control, and Dynamics 38(11), 2235–2240 (2015)
Lv, M., De Schutter, B., Shi, C., Baldi, S.: Logic-based distributed switching control for agents in power-chained form with multiple unknown control directions. Automatica 137, 110,143 (2022). https://doi.org/10.1016/j.automatica.2021.110143
Lv, M., Yu, W., Cao, J., Baldi, S.: Consensus in high-power multiagent systems with mixed unknown control directions via hybrid nussbaum-based control. IEEE Transactions on Cybernetics (2020). https://doi.org/10.1109/TCYB.2020.3028171
Lv, M., Yu, W., Cao, J., Baldi, S.: A separation-based methodology to consensus tracking of switched high-order nonlinear multiagent systems. IEEE transactions on neural networks and learning systems (2021). https://doi.org/10.1109/TNNLS.2021.3070824
Mahmoud, M.S., Koesdwiady, A.B.: Improved digital tracking controller design for pilot-scale unmanned helicopter. Journal of the Franklin Institute 349(1), 42–58 (2012)
Maqsood, H., Qu, Y.: Nonlinear disturbance observer based sliding mode control of quadrotor helicopter. Journal of Electrical Engineering & Technology 15(3), 1453–1461 (2020)
Masajedi, P., Ghanbarzadeh, A.: Optimal controller designing based on linear quadratic regulator technique for an unmanned helicopter at hover with the presence of wind disturbance. International Journal of Dynamics and Control 1(3), 214–222 (2013)
Raptis, I.A., Valavanis, K.P., Moreno, W.A.: A novel nonlinear backstepping controller design for helicopters using the rotation matrix. IEEE Transactions on Control Systems Technology 19(2), 465–473 (2011)
Sandino, L.A., Bejar, M., Kondak, K., Ollero, A.: Advances in modeling and control of tethered unmanned helicopters to enhance hovering performance. Journal of Intelligent & Robotic Systems 73(1–4), 3–18 (2014)
Thomas, F., Thottungal, A.V., Johnson, M.S.: Composite control of a hovering helicopter based on optimized sliding mode control. Journal of Optimization Theory and Applications pp. 1–20 (2021)
Tijani, I.B., Akmeliawati, R., Legowo, A., Budiyono, A.: robust controller for autonomous helicopter hovering control. Aircraft Engineering & Aerospace Technology 87(4), 330–344 (2015)
Tijani, I.B., Akmeliawati, R., Legowo, A., Budiyono, A., Muthalif, A.A.: robust controller for autonomous helicopter hovering control. Aircraft Engineering & Aerospace Technology 83(6), 363–374 (2011)
Wang, B., Shen, Y., Zhang, Y.: Active fault-tolerant control for a quadrotor helicopter against actuator faults and model uncertainties. Aerospace Science and Technology 99, 105,745 (2020)
Wang, D., Zong, Q., Tian, B., Lu, H., Wang, J.: Adaptive finite-time reconfiguration control of unmanned aerial vehicles with a moving leader. Nonlinear Dynamics 95(2), 1099–1116 (2019)
Wang, H.Q., Mian, A.A., Wang, D.B., Duan, H.B.: Robust multi-mode flight control design for an unmanned helicopter based on multi-loop structure. International Journal of Control Automation & Systems 7(5), 723–730 (2009)
Wang, T., Yang, C., Liang, J., Wu, Y., Wang, C., Zhang, Y.: Chaos-genetic algorithm for the system identification of a small unmanned helicopter. Journal of Intelligent & Robotic Systems 67(3–4), 323–338 (2012)
Yang, J.H., Hsu, W.C.: Adaptive backstepping control for electrically driven unmanned helicopter. Control Engineering Practice 17(8), 903–913 (2009)
Yu, X., Yang, J., Li, S.: Disturbance observer-based autonomous landing control of unmanned helicopters on moving shipboard. Nonlinear Dynamics 102(1), 131–150 (2020)
Zhao, Z., Cao, D., Yang, J., Wang, H.: High-order sliding mode observer-based trajectory tracking control for a quadrotor uav with uncertain dynamics. Nonlinear Dynamics 102(4), 2583–2596 (2020)
Zhong, Y.: Optimal Control. Tsinghua University Press, Beijing (2015)
Zhou, B., Li, Z., Zheng, Z., Tang, S.: Nonlinear adaptive tracking control for a small-scale unmanned helicopter using a learning algorithm with the least parameters. Nonlinear Dynamics 89(2), 1289–1308 (2017)
Zhou, B., Lu, X., Tang, S., Zheng, Z.: Nonlinear system identification and trajectory tracking control for a flybarless unmanned helicopter: theory and experiment. Nonlinear Dynamics 96(4), 2307–2326 (2019)
Zhu, B., Huo, W.: 3-d path-following control for a model-scaled autonomous helicopter. IEEE Transactions on Control Systems Technology 22(5), 1927–1934 (2014)
Zou, Y., Zheng, Z.: A robust adaptive rbfnn augmenting backstepping control approach for a model-scaled helicopter. IEEE Transactions on Control Systems Technology 23(6), 2344–2352 (2015)
Acknowledgements
The author of this paper owes great thanks to Mr. Xuanying Li for his disinterested assistance in outdoor flight experiments. Moreover, the author would like to express sincere gratitude to the Editor and the anonymous reviewers whose insightful comments have helped to improve the quality of this paper considerably.
Funding
The authors have no relevant financial or non-financial interests to disclose. All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.The authors have no financial or proprietary interests in any material discussed in this article. The authors have no financial or proprietary interests in any material discussed in this article.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Informed consent
Informed consent was obtained from all individual participants included in the study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Lemma 4
([40]). Assuming that \(\left( \varvec{A}_\mathrm {n} , \varvec{B}_\mathrm {n}\right) \) is stabilized and \(\left( \varvec{A}_\mathrm {n} , \varvec{D}\right) \) is detectable, then the linear time-invariant infinite time LQR optimal control is asymptotically stable. If \(\left( \varvec{A}_\mathrm {n} , \varvec{D}\right) \) is observable, then the solution \( \bar{\varvec{P}} \) of the Riccati matrix algebraic equation (117) is positive definite.
\(\square \)
Proof of Lemma 2
Since matrix \(\left( \varvec{A}_\mathrm {n}+ \delta {{{\varvec{I}}_{ln \times ln}}}, \varvec{B}_\mathrm {n}\right) \) is stabilized and \(\left( \varvec{A}_\mathrm {n}+ \delta {{{\varvec{I}}_{ln \times ln}}}, \varvec{D} \right) \) is detectable, according to Lemma 4, for the linear time-invariant infinite time LQR problem described by system (36) and performance index (37), the optimal control is given by equation (38), then the system (36) is asymptotically stable. In other words, \({\bar{\varvec{z}}}(t)\) is bounded and asymptotically approaches zero. Thus,
That’s to say, the state \( {{\varvec{z}}}(t) \) converges to the origin at a rate no less than the exponential function \(e^{-\delta t} \). \(\square \)
Rights and permissions
About this article
Cite this article
Zhou, B. Multi-variable adaptive high-order sliding mode quasi-optimal control with adjustable convergence rate for unmanned helicopters subject to parametric and external uncertainties. Nonlinear Dyn 108, 3671–3692 (2022). https://doi.org/10.1007/s11071-022-07433-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-022-07433-3