Finite-time control for small-scale unmanned helicopter with disturbances

Abstract

This work aims to develop finite-time stability property for trajectory tracking control system of small-scale unmanned helicopter subjected to uncertainties and external disturbances. The added power integrator method is applied to construct the nominal feedback control part, such that helicopters’ closed-loop system possesses highly tracking performance due to finite-time convergence property. In view of the existence of strong couplings, approximate feedback linearization is initially conducted to simplify and decouple helicopters’ input–output dynamics. Additionally, to guarantee robustness, the composite active disturbance rejection control idea is employed. These unknown perturbations are estimated using high-order sliding mode disturbance observers and compensated for directly in every virtual control law. Finite-time convergence property of the closed-loop system with disturbances is proven through Lyapunov stability theory. Finally, several comparison simulations illustrate the effectiveness and superiority of our proposed methods.

1 Introduction

Unmanned helicopters have received wide interest in recent decades because of their capabilities, including highly agile maneuvering, vertical taking off and landing, and broad envelope of flight [1, 2]. Helicopters have been widely applied into rescue, surveillance, supervision, defense, and other areas. In most of the practical application scenes, helicopters are required to quickly and accurately track a prescribed trajectory. However, controlling unmanned helicopters, especially small-scale ones, is not an easy task due to their complex aerodynamics, strong nonlinearities and dynamic couplings, and significant parameter and model uncertainties [1,2,3,4]. To date, designing a high-performance controller for helicopters is still an attractive focus.

In the last decades, many meaningful results for helicopter controls have been proposed. Tradition linear control method, such as PID [1], linear quadratic regulation [5], $H_{\infty }$ control theory [4,5,6], and gain-scheduling controllers [7], is based on the model linearized around the trim points that may utilize synthesis techniques. These techniques are convenient for engineering application. However, guaranteeing satisfying performances of the whole system in full envelope is difficult. Nonlinear control technique, including backstepping [8,9,10,11,12], nonlinear dynamic inversion [13], sliding mode (SM) [14], nonlinear model predictive control [15], and output regulation [16], is applied to conquer this main defect.

Robustness becomes one of the main performance indexes of helicopter given the presence of model uncertainties and external perturbations in its operational environment [1, 4]. Traditional robust control strategies, including $H_{\infty }$ control, SM, and adaptive control, are applied to “inactively” attenuate the effect of disturbance at the cost of sacrificing their nominal performance [17]. Recently, an alternative approach called “active” disturbance reject control (ADRC), which provides a compound controller composed of a nominal feedback control part and a disturbance compensation part, is proposed [17, 18]. The nominal feedback control part guarantees basic stability and closed-loop performance, and the other part provides strong robustness in large-range operation. The compensation part is often designed based on disturbance observer (DO) idea, where the lumped unknown disturbances are estimated by a DO and counteracted online. The disturbances in helicopter dynamics satisfy the mismatched condition, which increases the difficulties in designing a robust controller. Recently, some literatures have applied the ADRC technique to deal with helicopters’ control problem. In [10], the composite backstepping controller combined with nonlinear DO is applied to ensure robust and highly trajectory tracking. [12] adopts extend DO to estimate and compensate for the unknown disturbances, as well as dynamic surface control to guarantee the nominal performance. Nonlinear MPC is combined with DO in [15] to realize highly tracking performance subjected to the perturbations.

To further improve tracking performance, our work aims to develop finite-time (FT) convergence property to helicopter control system. The FT system provides rapid convergent speed around the equilibrium point remarkable disturbance rejection performance, which is an attractive property of a controller design [19, 20]. There are two main theory frameworks to complete finite-time stability analysis, including homogenous method and Lyapunov-based method [20]. Our work adopts homogeneous domination framework to achieve FT convergence of tracking errors. The added power integrator method [21,22,23] is applied to design the nominal feedback control part, which ensures nominal control performance and possesses FT convergence property of the closed-loop system. Additionally, in the recursive design procedure, disturbances are estimated via high-order SM DO (HOSMDO) [24,25,26] and then feed-forwardly counteracted in virtual control law design of every step. HOSMDO has many excellent properties, such as insensitivity to disturbances and FT convergence. This novel ADRC design guarantees that the tracking error of the closed-loop system converges to zero in FT under disturbances.

The helicopter is a typical multi-input multi-output (MIMO) system, where strong dynamic couplings exist. By approximate feedback linearization, the helicopters’ input–output dynamics enable to be decoupled and simplified [27]. Due to the properties of helicopter model, there exist two subsystems to consist of the decoupled helicopter dynamics, including position system and yaw angle system. Then, the composite FT control strategy is applied to force helicopter’s trajectory to track reference trajectory under internal and external perturbations. The main contributions of our work are summarized as follows:

• (a) FT control strategy based on added power integrator method is applied to deal with trajectory tracking problem of small-scale unmanned helicopters subjected to unknown perturbations. Our proposed FT controller enjoys speed and improved robustness.

• (b) The composite FT control law based on HOSMDO and added power integrator method, which guarantees FT convergence under disturbances, is proposed. Our work develops FT output regulation technique on MIMO system by combining with the approximate input–output linearization technique.

• (c) FT convergence property of tracking errors in the closed-loop system is proven through Lyapunov theory. Comparison simulation results show that the proposed controller features superior performance in trajectory tracking and disturbance rejection.

Fig. 1

Simple illustration of a small-scale helicopter model

The configuration of this paper is arranged as follows. Section 2 presents the dynamics of a small-scale helicopter and its linearized model that is obtained by approximated feedback linearization. Section 3 proposes the composite control method, provides the FT stability analysis, and produces practical helicopter control signals. Section 4 discusses the simulations conducted in this work. Section 5 draws the conclusions.

2 Small-scale helicopter model

2.1 Small-scale helicopter dynamics

The helicopter is considered a six-degree-of-freedom rigid body model with simplified force and moment generation process. Firstly, two reference frames are defined: the earth reference frame (ERF) $\mathbb {I}=\left\{ {Oxyz} \right\}$, which is fixed to the earth, and the body reference frame (BRF) $\mathbb {B}=\left\{ {O_b x_b y_b z_b } \right\}$ whose origin is located at the helicopter’s center of gravity (c.g.) [3, 4]. Figure 1 shows the definition of the two reference frames.

The dynamics of small-scale unmanned helicopter can be described as follows [3, 4]:

$$\begin{aligned}&{\dot{P}} = V, \end{aligned}$$

(1)

$$\begin{aligned}&{\dot{V}} = g{e_3} + \frac{1}{m}R\left( \Theta \right) F, \end{aligned}$$

(2)

$$\begin{aligned}&{\dot{R}}\left( \Theta \right) = R\left( \Theta \right) S\left( \upomega \right) , \end{aligned}$$

(3)

$$\begin{aligned}&J{\dot{\omega }} = - \omega \times J\omega + M, \end{aligned}$$

(4)

where $P=\left[ {{\begin{array}{ccc} x&{} y&{} z \\ \end{array} }} \right] ^{T}$ and $V=\left[ {{\begin{array}{ccc} u&{} v&{} w \\ \end{array} }} \right] ^{T}$ refer to helicopter’s position and velocity vector in the ERF, respectively; m is helicopter’s mass, and g is the gravitational acceleration; $e_3 =\left[ {{\begin{array}{ccc} 0&{} 0&{} 1 \\ \end{array} }} \right] ^{T}$; $S\left( \cdot \right)$ is a skew-symmetric matrix that corresponds to the vector $\left( \cdot \right)$ [8, 9]; and J represents the approximate inertia matrix given as follows:

$$\begin{aligned} J=\left[ {{\begin{array}{ccc} {J_{xx} }&{} 0&{} {-J_{xz} } \\ 0&{} {J_{yy} }&{} 0 \\ {-J_{xz} }&{} 0&{} {J_{zz} } \\ \end{array} }} \right] . \end{aligned}$$

(5)

The rotation matrix from BRF to ERF is

$$\begin{aligned}&R\left( \Theta \right) \nonumber \\&\quad =\left[ {{\begin{array}{ccc} {C_\theta C_\psi }&{}\quad {S_\phi S_\theta C_\psi -C_\phi S_\psi }&{}\quad {C_\phi S_\theta C_\psi +S_\phi S_\psi } \\ {C_\theta S_\psi }&{}\quad {S_\phi S_\theta S_\psi +C_\phi C_\psi }&{}\quad {C_\phi S_\theta S_\psi -S_\phi C_\psi } \\ {-S_\theta }&{}\quad {S_\phi C_\theta }&{}\quad {C_\phi C_\theta } \\ \end{array} }} \right] ,\nonumber \\ \end{aligned}$$

(6)

where $S_{\left( \cdot \right) }$ and $C_{\left( \cdot \right) }$ denote $\sin \left( \cdot \right)$ and $\cos \left( \cdot \right)$, respectively. $\Theta =\left[ {{\begin{array}{ccc} \phi &{} \theta &{} \psi \\ \end{array} }} \right] ^{T}$ are the Euler angles, which include roll, pitch, and yaw angles. $\omega =\left[ {{\begin{array}{ccc} p&{} q&{} r \\ \end{array} }} \right] ^{T}$ denote the angular rates in the BRF. Attitude kinematics are expressed as follows:

$$\begin{aligned}&{\dot{\Theta }} = \Psi \left( {\Theta } \right) \omega \nonumber \\&\Psi \left( \varTheta \right) = \left[ {\begin{array}{ccc} 1&{}{{S_\phi }{C_\theta }}&{}{{C_\phi }{S_\theta }/{C_\theta }}\\ 0&{}{{C_\phi }}&{}{ - {S_\phi }}\\ 0&{}{{S_\phi }/{C_\theta }}&{}{{C_\phi }/{C_\theta }} \end{array}} \right] . \end{aligned}$$

(7)

In Eqs. (2)–(4), F and M denote the external forces and torque exerted on helicopter’s fuselage in BRF, respectively.

$$\begin{aligned}&F = {F_b} + {F_{\Delta }}, \end{aligned}$$

(8)

$$\begin{aligned}&M = {M_b} + {M_{\Delta }},\nonumber \\&{F_b} = m\left[ {\begin{array}{c} 0\\ 0\\ { - g + {Z_w}w + {Z_\mathrm{col}}{\delta _\mathrm{col}}} \end{array}} \right] ,\nonumber \\&{M_b} = J\left( {A\omega + B{u_c}} \right) , \end{aligned}$$

(9)

where ${u_c} = {\left[ {\begin{array}{cccc} {{\delta _\mathrm{col}}}&{{\delta _\mathrm{lon}}}&{{\delta _\mathrm{lat}}}&\delta _\mathrm{ped} \end{array}} \right] ^\mathrm{T}}$ is helicopter’s control input vector, whose elements denote the main rotor’s collective, longitudinal cyclic, lateral cyclic, and the tail rotor’s collective pitch, respectively. $F_\Delta$ and $M_\Delta$ represent lumped force and torque disturbance in BRF, respectively, that involve external perturbations, parameter variations, and model uncertainties. Constant matrices A and B are expressed as follows [10]:

$$\begin{aligned} A= & {} \left[ {{\begin{array}{ccc} {-\tau L_b }&{} {-\tau L_a }&{} 0 \\ {-\tau M_b }&{} {-\tau M_a }&{} 0 \\ 0&{} 0&{} {N_r } \\ \end{array} }} \right] , \\ B= & {} \left[ \begin{array}{cccc} 0&{} {L_\mathrm{lon} }&{} {L_\mathrm{lat} } &{} 0 \\ 0&{} {M_\mathrm{lon} }&{} {M_\mathrm{lat} } &{} 0 \\ {N_\mathrm{col} }&{} 0&{} 0 &{} {N_\mathrm{ped}} \\ \end{array} \right] , \end{aligned}$$

where the coefficients $L_b$, $L_a$, $M_b$, $M_a$, $L_\mathrm{lon}$, $L_\mathrm{lat}$, $M_\mathrm{lon}$, $M_\mathrm{lat}$, $N_\mathrm{col}$, $N_r$, $N_\mathrm{ped}$, $Z_w$, and $Z_\mathrm{col}$ depend on the helicopter structure, which can be obtained via system identification technique. Along (8) to (9), helicopter dynamics (2) and (4) can be reexpressed as follows:

$$\begin{aligned} {\dot{V}}= & {} g{e_3} + R\left( {\Theta } \right) {e_3}\left( { - g + {Z_w}w + {Z_\mathrm{col}}{\delta _\mathrm{col}}} \right) + {\Delta }F, \nonumber \\\end{aligned}$$

(10)

$$\begin{aligned} {\dot{\omega }}= & {} - {J^{ - 1}}\left( {\omega \times J\omega } \right) + \left( {A\omega + B{u_c}} \right) + \Delta M \end{aligned}$$

(11)

where $\Delta F=\frac{1}{m}R\left( \Theta \right) F_\Delta$, and $\Delta M=J^{-1}M_{\Delta }$.

Given the desired smooth trajectory $P_d \mathop {=}\limits ^{\Delta } \left[ \begin{array}{ccc} {x_d }&{} {y_d }&{} {z_d } \\ \end{array} \right] ^{T}$ and yaw angle $\psi _d$, this work aims to develop control signals $\left[ \begin{array}{cccc}{\delta _\mathrm{col} }&{\delta _\mathrm{lon} }&{\delta _\mathrm{lat}}&{\delta _\mathrm{ped} } \end{array} \right] ^{T}$ for a helicopter model with uncertainties and external disturbances, such that its practical trajectory P and yaw angle $\psi$ converge to $P_d$ and $\psi _d$.

2.2 Approximate feedback linearization

To facilitate controller design and performance analysis, feedback linearization is initially carried out. Traditional exact input–output linearization fails to feedback linearize the whole helicopter system and produces unstable zero dynamics [14, 27]. Thus, approximate feedback linearization is developed to simplify and decouple helicopters’ dynamics. This method requires the second-time derivative of the main rotor thrust $\ddot{T}_{m}$ as the new input, where $T_m =m\left( {g-Z_w w-Z_\mathrm{col} \delta _\mathrm{col} } \right)$. The approximated input–output feedback linearization procedure is performed as follows:

First, $e_{P1} =P-P_d$ is obtained. The derivative of $e_{p1}$ from (1) is given as follows:

$$\begin{aligned} {{\dot{e}}_{P1}} = V - {{\dot{P}}_d}. \end{aligned}$$

(12)

Next, let $e_{P2} =V-\dot{P}_{d}$. Along (10), its derivative is expressed as follows

$$\begin{aligned} {{\dot{e}}_{P2}} = g{e_3} - \frac{1}{m}R\left( {\Theta } \right) {e_3}{T_m} + {\Delta }F - {\ddot{P}_d}. \end{aligned}$$

(13)

Selecting $e_{P3} =ge_3 +\frac{1}{m}R\left( \Theta \right) T_m -\ddot{P}_{d}$, the derivative of $e_{P3}$ is derived from (3) as

$$\begin{aligned} {{\dot{e}}_{P3}} = - \frac{1}{m}R\left( {\Theta } \right) S\left( {\upomega } \right) {e_3}{T_m} - \frac{1}{m}R\left( {\Theta } \right) {e_3}{{\dot{T}}_m} - {\ddot{P}_d}.\nonumber \\ \end{aligned}$$

(14)

Define the transition control variables $\left[ {{\begin{array}{ccc} {M_\phi }&{} {M_\theta }&{} {M_\psi } \\ \end{array} }} \right] ^{T}=-J^{-1}\left( {\omega \times J\omega } \right) +\left( {A\omega +Bu_c } \right)$. Let $e_{P4} =-\frac{1}{m}R\left( \Theta \right) S\left( \upomega \right) T_m -\frac{1}{m}R\left( \Theta \right) \dot{T}_m-\dddot{P}_{d}$, along (11), its time derivative is obtained as

$$\begin{aligned} {{\dot{e}}_{P4}} = {f_{Pe}}\left( t \right) + {u_P} + {\Delta }{M_p}, \end{aligned}$$

(15)

where

$$\begin{aligned} {f_{Pe}}\left( t \right)= & {} - \frac{1}{m}R\left( {\Theta } \right) {S^2}\left( {\upomega } \right) {e_3}{T_m} \\&-\frac{2}{m}R\left( {\Theta } \right) S\left( {\upomega } \right) {e_3}{{\dot{T}}_m} - P_d^{\left( 4 \right) }, \\ {u_P}= & {} - \frac{1}{m}R\left( {\Theta } \right) \left[ {\begin{array}{c} {{T_m}{M_\theta }}\\ { - {T_m}{M_\phi }}\\ {{{\ddot{T}}_m}} \end{array}} \right] ,\hbox { and } \\ {\Delta }{M_p}= & {} - \frac{1}{m}R\left( {\Theta } \right) \left[ {\begin{array}{c} {{T_m}{\Delta }M\left( 2 \right) }\\ { - {T_m}{\Delta }M\left( 1 \right) }\\ 0 \end{array}} \right] . \end{aligned}$$

The position error subsystem is approximately feedback-linearized by applying $\ddot{T}_{M}$ as input. The dynamics of yaw angle errors $e_{\psi 1} =\psi -\psi _d$ is described in Eq. (7) as follows:

$$\begin{aligned} {{\dot{e}}_{\psi 1}} = \frac{{{S_\phi }}}{{{C_\theta }}}q + \frac{{{C_\phi }}}{{{C_\theta }}}r - {{\dot{\psi }} _d}. \end{aligned}$$

(16)

Selecting $e_{\psi 2} =\frac{S_\phi }{C_\theta }q+\frac{C_\phi }{C_\theta }r-\dot{\psi }_{d}$, its derivative yielded along (11) is as follows:

$$\begin{aligned} {{\dot{e}}_{\psi 2}} = {f_{\psi e}}\left( t \right) + {u_\psi } + {\Delta }{M_\psi }, \end{aligned}$$

(17)

where

$$\begin{aligned} {f_{\psi e}}\left( t \right)= & {} \frac{{\left( {{C_\phi }{\dot{\phi }} q + {S_\phi }{M_\theta }} \right) {C_\theta } + \left( { - {S_\phi }{\dot{\phi }} r + {C_\phi }{M_\psi }} \right) {C_\theta } + {S_\phi }q{S_\theta }{\dot{\theta }} ++ {C_\phi }r{S_\theta }{\dot{\theta }} }}{{C_\theta ^2}} \\&- {\ddot{\psi }_d}, \\ {u_\psi }= & {} \frac{{{C_\phi }}}{{{C_\theta }}}{M_\psi },\mathrm{and}~~\Delta {M_\psi } = \frac{{{S_\phi }}}{{{C_\theta }}}{\Delta }M\left( 2 \right) + \frac{{{C_\phi }}}{{{C_\theta }}}{\Delta }M\left( 3 \right) .\\ \end{aligned}$$

Combining (12)–(17), the complete input–output feedback linearization of helicopter dynamics is given as follows:

$$\begin{aligned} {{\dot{e}}_{P1}}= & {} {e_{P2}} \nonumber \\ {{\dot{e}}_{P2}}= & {} {e_{P3}} + {\Delta }F \nonumber \\ {{\dot{e}}_{P3}}= & {} {e_{P4}} \nonumber \\ {{\dot{e}}_{P4}}= & {} {f_{Pe}}\left( t \right) + {u_P} + {\Delta }{M_p} \nonumber \\ {{\dot{e}}_{\psi 1}}= & {} {e_{\psi 2}} \nonumber \\ {{\dot{e}}_{\psi 2}}= & {} {f_{\psi e}}\left( t \right) + {u_\psi } + {\Delta }{M_\psi }. \end{aligned}$$

(18)

where $u_P$ and $u_\psi$ are regarded as new inputs. The input–output dynamics of helicopters have been decoupled via approximate feedback linearization. Our objective is changed to design the input $\left[ {{\begin{array}{cc} {u_P^\mathrm{T} }&{} {u_\psi } \\ \end{array} }} \right] ^{T}$ to ensure that tracking errors of the position and yaw angle will converge to zeros.

In addition, the following assumptions are considered to implement the robust controller for helicopter.

Assumption 1

Disturbances $\Delta F$, $\Delta M_p$, and $\Delta M_\psi$ in (18) satisfy the following condition

$$\begin{aligned}&\left\| \Delta F^{\left( 3 \right) }\right\|<\Lambda _F ,\,\,\left\| \Delta M_p^{\left( 3 \right) }\right\|<\Lambda _{M_p },\\&\quad \left\| \Delta M_\psi ^{\left( 3 \right) }\right\| <\Lambda _{M_\psi } , \end{aligned}$$

where $\Lambda _F$, $\Lambda _{M_p }$, and $\Lambda _{M_\psi }$ are the known constant bound of the third-order time derivative of the disturbances.

Assumption 2

Attitude of the helicopter always lies inside region $\left| \phi \right| <\frac{\pi }{2}$ and $\left| {\theta \left( t \right) } \right| <\frac{\pi }{2}$.

Remark 1

In (18), $\Delta F$, $\Delta M_p$, and $\Delta M_\psi$ are lumped disturbances that act on the helicopter model. $\Delta M_p$ and $\Delta M_\psi$ are matched disturbances, whereas $\Delta F$ is an unmatched disturbance. The unmatched disturbance $\Delta F$ significantly affects tracking precision. Given the existence of unmatched disturbances, various techniques, such as the classic SMC and adaptive control, are restricted.

Remark 2

Assumption 1 ensures the attitude kinematic matrix $\Psi \left( \varTheta \right)$ in (7) is not singular. This assumption is valid in that the helicopter is considered to operate in hovering or low-velocity flight condition.

2.3 Preliminaries

Preliminary lemmas, which will be used to obtain a FT composite controller later, are illustrated as follows.

Lemma 1

[21]. Let m be a ratio of positive odd integers. If $0<m\le 1$, the following inequalities hold

$$\begin{aligned}&\left| {x^{m}-y^{m}} \right| \le 2^{1-m}\left| {x-y} \right| ^{m},\\&\quad \left( {\left| x \right| +\left| y \right| } \right) ^{m}\le \left| x \right| ^{m}+\left| y \right| ^{m}. \end{aligned}$$

$\square$

Lemma 2

[21]. Let $c_1$, $c_2$ be positive real numbers, and $\gamma \left( {x,y} \right) >0$ be a real-valued function. Then,

$$\begin{aligned} \left| x \right| ^{c_1 }\left| y \right| ^{c_2 }\le & {} \frac{c_1 }{c_1 +c_2 }\gamma \left( {x,y} \right) \left| x \right| ^{c_1 +c_2 }\\&+\frac{c_2 }{c_1 +c_2 }\gamma ^{-c_1 /c_2 }\left( {x,y} \right) \left| y \right| ^{c_1 +c_2 }. \end{aligned}$$

$\square$

Lemma 3

[22]. For $x_i \in R$, $i=1,\ldots ,n$, the inequality $\left( {\left| {x_1 } \right| +\cdots +\left| {x_n } \right| } \right) ^{c_p }\le \left| {x_1 } \right| ^{c_p }+\cdots +\left| {x_n } \right| ^{c_p }$ holds where $c_p$ is a real number that satisfies $0<c_p \le 1$. $\square$

Theorem 1

[20]. Considering $\dot{x}=f(x)$, $x\in {\mathcal {N}}$. Suppose a continuous function $V\left( x \right)$ exists such that the following conditions hold:

• (a) $V\left( x \right)$ is positive definite.

• (b) Real number $c_v >0$ and $\alpha \in \left( {0,\,1} \right)$ exist such that

  $$\begin{aligned} V\left( x \right) +c_v \left( {V\left( x \right) } \right) ^{\alpha }<0,\,\,x\in {\mathcal {N}}\backslash \left\{ 0 \right\} . \end{aligned}$$

  Then, the origin is a FT stable equilibrium. $\square$

3 Helicopter controller design

This section expresses the design of the proposed helicopter’s FT control. First, HOSMDO is applied to estimate lumped force and moment disturbances. Second, composite control strategy based on DO and FT control is proposed. At the same time, the FT stability analysis is provided in detail. Finally, the practical control signals for helicopter are produced directly. Figure 2 depicts the control system structure.

Fig. 2

FT controller structure diagram

3.1 HOSMDO

Considering the dynamic system

$$\begin{aligned} {{\dot{x}}_j} = {f_j}\left( t \right) + {d_j}\left( t \right) , \end{aligned}$$

(19)

where $x_j \in \mathbb {R}^{n}$ denotes the system state; $f_j \left( t \right)$ is the known nonlinear smooth function; $d_j \left( t \right) \in \mathbb {R}^{n}$ are unknown bounded perturbation terms due to model uncertainty and external disturbances. Assume that the disturbance $d_j \left( t \right)$ owns the bounded rth-order time derivative, i.e., $\left\| d_j^{\left( r \right) } \left( t \right) \right\| <L_j$. To obtain the estimation of disturbance and its high-order derivatives, a HOSMDO of $d_j \left( t \right)$ is designed as follows [24].

$$\begin{aligned}&{{\dot{z}}_{0,j}} = {f_j}\left( t \right) + {v_0},~{v_0} = {z_1} \nonumber \\&\qquad \qquad - {\lambda _0}L_j^{\frac{1}{{r + 1}}}{\left| {{z_{0,j}} - {x_j}} \right| ^{\frac{r}{{r + 1}}}}\hbox {sign}\left( {{z_{0,j}} - {x_j}} \right) \nonumber \\&{{\dot{z}}_{1,j}} = {v_{1,j}},~{v_{1,j}} = {z_{2,j}} \nonumber \\&\qquad \qquad - {\lambda _1}L_j^{\frac{1}{r}}{\left| {{z_{1,j}} - {v_{0,j}}} \right| ^{\frac{{r - 1}}{r}}}\hbox {sign}\left( {{z_{1,j}} - {v_{0,j}}} \right) \nonumber \\&\vdots \nonumber \\&{{\dot{z}}_{r - 1,j}} = {v_{r - 1,j}},~{v_{r - 1,j}} = {z_{r,j}} \nonumber \\&\qquad ~~\qquad - {\lambda _{r - 1}}L_j^{\frac{1}{2}}{\left| {{z_{r - 1,j}} - {v_{r - 2,j}}} \right| ^{\frac{1}{2}}}\\&\quad \hbox {sign}\left( {{z_{r - 1,j}} - {v_{r - 2,j}}} \right) \nonumber \\&{{\dot{z}}_{r,j}} = {v_{r,j}},~{v_{r,j}} = - {\lambda _r}{L_j}\hbox {sign}\left( {{z_{r,j}} - {v_{r - 1,j}}} \right) \nonumber \end{aligned}$$

(20)

where $\lambda _0 ,\,\lambda _1 ,\ldots ,\lambda _{r-1} ,\lambda _r$ are the observer parameters. $z_{0,j} ,z_{1,j} ,\ldots ,z_{r-1,j} ,z_{r,j}$, $j=1,\,2,\,3$, are the estimates of $x_j ,d_j ,\ldots ,\,d_j^{\left( {r-2} \right) } ,d_j^{\left( {r-1} \right) }$.

Considering that the estimated variables are vector, the multivariable calculation form is adopted, such as $\hbox {sign}\left( {\varvec{X}} \right) =\left[ {\frac{x_1 }{\left| {x_1 } \right| },\,\,\ldots ,\,\frac{x_n }{\left| {x_n } \right| }} \right]$, where $X=\left[ {x_1 ,\,\ldots ,x_n } \right]$, and $\left| X \right| ^{l}=\left[ {\left| {x_1 } \right| ^{l},\ldots ,\left| {x_n } \right| ^{l}} \right]$. Due to no existence of coupling in (19), the system’s properties and analysis process is the same as the scalar system. Followed from (19)–(20), the observer error dynamics are then governed by:

$$\begin{aligned}&{{{\dot{\sigma }} }_{0,j}} = - {\lambda _0}L_j^{\frac{1}{{r + 1}}}{\left| {{\sigma _{0,j}}} \right| ^{\frac{r}{{r + 1}}}}\hbox {sign}\left( {{\sigma _{0,j}}} \right) + {\sigma _{1,j}}\nonumber \\&{{{\dot{\sigma }} }_{i,j}} = -\, {\lambda _1}L_j^{\frac{1}{r}}{\left| {{\sigma _{i,j}} - {{{\dot{\sigma }} }_{i - 1,j}}} \right| ^{\frac{{r - 1}}{r}}}\hbox {sign}\left( {{\sigma _{i,j}} - {{{\dot{\sigma }} }_{i - 1,j}}} \right) \nonumber \\&~~~\qquad +\, {\sigma _{i + 1,j}}\nonumber \\&\vdots \nonumber \\&{{{\dot{\sigma }} }_{r,j}} = - {\lambda _r}{L_j}\hbox {sign}\left( {{\sigma _{r,j}} - {{{\dot{\sigma }} }_{r - 1,j}}} \right) \end{aligned}$$

(21)

where the observer errors are denoted as $\sigma _{0,j} =z_{0,j} -x_j$, $\sigma _{i,j} =z_{i,j} -d_j^{\left( {i-1} \right) }$, and $\sigma _{r,j} =z_{r,j} -d_j^{\left( {r-1} \right) }$. The FT convergence of estimation error is given by the following theory.

Theorem 2

[24]. The parameters in (20) are properly selected, and the following equalities are true after a FT transient process

$$\begin{aligned} \sigma _{0,j} =\cdots =\sigma _{r,j} =0,\,\,\,\hbox {when}\,t>t_j \end{aligned}$$

i.e.,

$$\begin{aligned}&z_{0,j} =x_j ,\,\,z_{1,j} =v_{0,j} =d_j ,\ldots ,\,\,z_{r,j} =d_j^{\left( {r-1} \right) } ,\nonumber \\&\quad \hbox {when}\,\,t>t_j . \end{aligned}$$

(22)

$\square$

Remark 3

The selection of $L_j$ is a trade-off process. Large parameters $L_j$ mean fast convergence rate of HOSMDO. However, the parameters $L_j$ with large values cannot be selected to avoid excessive transient peaking in system responses.

Given $\Delta F$ in Eq. (18), applying HOSMDO its value and high derivatives can be estimated by explicitly defining $x_1 =e_{P2}$, $f_1 \left( t \right) =e_{P3}$, and $d_1 \left( t \right) =\Delta F$. After FT $t_1$, we have $z_{1,\,1} =\Delta F,z_{2,1}=\Delta \dot{F},z_{3,1} =\Delta \ddot{F}$. Similarly, the disturbances $\Delta M_p \quad \Delta M_\psi$ can be observed by selecting $x_2 =e_{P4} ,f_2 \left( t \right) =f_{Pe} \left( t \right) ,$$d_2 \left( t \right) =\Delta M_p$, and $x_3 =e_{\psi 2} ,\,f_3 \left( t \right) =f_{\psi e} \left( t \right) ,),$$d_3 \left( t \right) =\Delta M_\psi$. After time $\hbox {max}\left\{ {t_2 ,\,t_3 } \right\}$, $z_{1,2} =\Delta M_p ,z_{2,2} =\Delta \dot{M}_p ,z_{3,2} =\Delta \ddot{M}_{p}$, and $z_{1,3} =\Delta M_{\psi } ,z_{2,3} =\Delta \dot{M}_{\psi } ,z_{3,3} =\Delta \ddot{M}_{\psi }$.

3.2 FT controller design

Consider the properties of FT convergence of HOSMDO. After time $t_{\max } =\max \left\{ {t_1 ,\,t_2 ,t_3 } \right\}$, the dynamics in (18) can be rewritten as

$$\begin{aligned} {{{\dot{e}}}_{P1}}= & {} {e_{P2}}\nonumber \\ {{{\dot{e}}}_{P2}}= & {} {e_{P3}} + {z_{1,~1}}\nonumber \\ {{{\dot{e}}}_{P3}}= & {} {e_{P4}}\nonumber \\ {{{\dot{e}}}_{P4}}= & {} {f_{Pe}}\left( t \right) + {u_P} + {z_{1,~2}}\nonumber \\ {{{\dot{e}}}_{\psi 1}}= & {} {e_{\psi 2}}\nonumber \\ {{{\dot{e}}}_{\psi 2}}= & {} {f_{\psi e}}\left( t \right) + {u_\psi } + {z_{1,~3}} \end{aligned}$$

(23)

In this subsection, the compound control strategy is proposed based on (23) to simplify the control design. The position error loop in (23) is the vector form with three components, namely, $e_{Pi} =\left[ {{\begin{array}{ccc} {e_{Pi,1} }&{} {e_{Pi,2} }&{} {e_{Pi,3} } \\ \end{array} }} \right] ^{T},\,z_{1,\,j} =\left[ {{\begin{array}{ccc} {z_{1,\,j,1} }&{} {z_{1,\,j,2} }&{} {z_{1,\,j,3} } \\ \end{array} }} \right] ^{T},$$u_P =\left[ {{\begin{array}{ccc} {u_{P,1} }&{} {u_{P,2} }&{} {u_{P,3} } \\ \end{array} }} \right] ^{T},\hbox {and}\,i=1,\ldots ,4,\,\,j=1,2,3$. At the same time, mismatched disturbance exists in the position loop.

Position loop controller design

Step 1 Considering dynamics (23), let a Lyapunov function be

$$\begin{aligned} V_1 =\mathop {\sum }\limits _{i=1}^3 \int _0^{e_{P1,i} } \left( {s^{1/r_1 }} \right) ^{2-r_2 }ds, \end{aligned}$$

(24)

where $r_1 =1$, $r_i =r_{i-1} +\tau$, $-1/5<\tau <0$. $V_1$ is positive by selecting the parameter $\tau$ as a ratio of even and odd integers.

The derivative of (24) along (23) is given as

$$\begin{aligned} {{\dot{V}}_1} \le \mathop {\sum }\limits _{i = 1}^3 e_{P1,i}^{\left( {2 - {r_2}} \right) /{r_1}}\cdot {e_{P2,i}}. \end{aligned}$$

(25)

Applying the concept of backstepping, the virtual control law is arranged as

$$\begin{aligned} e_{P2,i}^*=-\beta _1 e_{P1,i}^{\frac{r_2 }{r_1 }} ,\quad \,i=1,2,3, \end{aligned}$$

(26)

where $\beta _1>3c+\tilde{\beta }_1 >0$, $\tilde{\beta }_1 >0$ are the designed controller constant. Introducing (26) into (25)

$$\begin{aligned}&{{\dot{V}}_1} \le \mathop {\sum }\limits _{i = 1}^3 \left( - \left( {{\beta _1} + 3c} \right) e_{P1,i}^{2/{r_1}} + e_{P1,i}^{\left( {2 - {r_2}} \right) /{r_1}}\right. \nonumber \\&\qquad \quad \left. \cdot \,({e_{P2,i}} - e_{P2,i}^*) \right) . \end{aligned}$$

(27)

Step 2 In this step, the Lyapunov function is selected as

$$\begin{aligned} V_2 =V_1 +\mathop {\sum }\limits _{i=1}^3 \left( {\int _{e_{P2,i}^*}^{e_{P2,i} } \!\left( {s^{\frac{1}{r_2 }}-(e_{P2,i}^*)^{\frac{1}{r_2 }}} \right) ^{2-r_3 }ds} \right) . \end{aligned}$$

(28)

Computing its time derivative along (23), (27), and (28) yields

$$\begin{aligned}&{{{\dot{V}}}_2} \le - \mathop {\sum }\limits _{i = 1}^3 \left( { - {\beta _1}e_{P1,i}^{\frac{2}{{{r_1}}}} + e_{P1,i}^{\frac{{2 - {r_2}}}{{{r_1}}}}({e_{P2,i}} - e_{P2,i}^*)} \right) \nonumber \\&\quad + \mathop {\sum }\limits _{i = 1}^3 \left( {{\left( {{\xi _{2,i}}} \right) }^{2 - {r_3}}}\left( {{e_{P3,i}} + {z_{1,~1,i}}} \right) + ( 2 - {r_3})\right. \nonumber \\&\quad \times \left. \int _{e_{P2,i}^*}^{{e_{P2,i}}} {{\left( {{s^{\frac{1}{{{r_2}}}}} - {{(e_{P2,i}^*)}^{\frac{1}{{{r_2}}}}}} \right) }^{1 - {r_3}}}ds\frac{{\partial {{(e_{P2,i}^*)}^{\frac{1}{{{r_2}}}}}}}{{\partial {e_{P1,i}}}}{{\dot{e}}_{P1,i}} \right) \nonumber \\ \end{aligned}$$

(29)

where $\xi _{2,i} =(e_{P2,i} )^{\frac{1}{r_2 }}-(e_{P2,i}^*)^{\frac{1}{r_2 }}$, $i=1,2,3$. The following relationships are established by applying Lemmas 1–2 directly.

$$\begin{aligned}&e_{P1,i}^{\frac{2-r_2 }{r_1 }} \cdot (e_{P2,i} -e_{P2,i}^*)\le 2^{1-r_2 }\left| {e_{P1,i} } \right| ^{\frac{2-r_2 }{r_1 }}\left| {\xi _{2,i} } \right| ^{r_2 }\\&\qquad \qquad \qquad \qquad \qquad \qquad \le \frac{c}{2}\left| {e_{P1,i} } \right| ^{2}+C_{11} \left| {\xi _{2,i} } \right| ^{2} \\&\quad \left( {2-r_3 } \right) \int _{e_{P2,i}^*}^{e_{P2,i} } \left( {s^{\frac{1}{r_2 }}-(e_{P2,i}^*)^{\frac{1}{r_2 }}} \right) ^{1-r_3 }ds\frac{\partial (e_{P2,i}^*)^{\frac{1}{r_2 }}}{\partial e_{P1,i} }\dot{e}_{p1,i} \\&\quad \le \left( {2-r_3 } \right) \left( {\xi _{2,i} } \right) ^{1-r_3 }\left( {e_{P2,i} -e_{P2,i}^*} \right) \frac{\partial \left( -\beta _1 e_{P1,i}^{\frac{r_2 }{r_1 }} \right) ^{\frac{1}{r_2 }}}{\partial e_{P1,i} }e_{P2,i} \\&\quad \le \left( {-\beta _1 } \right) ^{1/r_2 }\left( {2-r_3 } \right) 2^{1-r_2 }\left( {\xi _{2,i} } \right) ^{1-r_3 }\left| {\xi _{2,i} } \right| ^{r_2 }\\&\quad \times \left( {\left| {e_{P2,i} -e_{P2,i}^*} \right| +\left| {\beta _1 e_{P1,i}^{r_2 } } \right| } \right) \\&\quad \le \left( {-\beta _1 } \right) ^{1/r_2 }\left( {2-r_3 } \right) 2^{1-r_2 }\left| {\xi _{2,i} } \right| ^{1-\tau }\\&\quad \times \left( {2^{1-r_2 }\left| {\xi _{2,i} } \right| ^{r_2 }+\left| {\beta _1 e_{P1,i}^{r_2 } } \right| } \right) \\&\quad \le \frac{c}{2}\left| {e_{P1,i} } \right| ^{2}+C_{12} \left| {\xi _{2,i} } \right| ^{2} \end{aligned}$$

where the constants $C_{11} >0$ and $C_{12} >0$. Substituting the following results into (29), we arrive at

$$\begin{aligned}&{{\dot{V}}_2} \le \mathop {\sum }\limits _{i = 1}^3 \left( - \left( {{\beta _1} - c} \right) e_{P1,i}^2 + \left( {{C_{11}} + {C_{12}}} \right) {{\left| {{\xi _{2,i}}} \right| }^2} \right. \nonumber \\&\quad \left. +\, {{\left( {{\xi _{2,i}}} \right) }^{2 - {r_3}}}\left( {{e_{P3,i}} + {z_{1,~1,i}}} \right) \right) . \end{aligned}$$

(30)

The virtual controller is designed as

$$\begin{aligned} e_{P3,i}^*=-\beta _2 \left( {\xi _{2,i} } \right) ^{r_3 }-z_{1,\,1,i} , \quad i=1,2,3, \end{aligned}$$

(31)

where $\beta _2 >C_{11} +C_{12} +\tilde{\beta }_2 +2c$, $\tilde{\beta }_2 >0$ are selected. Combining (30) and (31) renders

$$\begin{aligned}&{{\dot{V}}_2} \le \mathop {\sum }\limits _{i = 1}^3 \left( - \left( {{\tilde{\beta }_1} + 2c} \right) e_{P1,i}^2 - \left( {{\tilde{\beta }_2} + 2c} \right) {{\left| {{\xi _{2,i}}} \right| }^2}\right. \nonumber \\&\quad \left. +\, {{\left( {{\xi _{2,i}}} \right) }^{2 - {r_3}}}\left( {{e_{P3,i}} - e_{P3,i}^*} \right) \right) . \end{aligned}$$

(32)

Step 3 Lyapunov function is defined as

$$\begin{aligned} V_3 =V_2 +\mathop {\sum }\limits _{i=1}^3 \left( {\int _{\bar{e}_{P3,i}^*}^{\bar{e}_{P3,i} }\! \left( {s^{\frac{1}{r_3 }}-(\bar{e}_{P3,i}^*)^{\frac{1}{r_3 }}} \right) ^{2-r_4 }ds} \right) , \end{aligned}$$

(33)

where $\bar{e}_{P3,i}^*=e_{P3,i}^*+z_{1,\,1,i} =-\beta _2 \left( {\xi _{2,i} } \right) ^{r_3 }$, $\bar{e}_{P3,i} =e_{P3,i} +z_{1,\,1,i}$, and $i=1,2,3$. The derivative is obtained along (23) and (32)

$$\begin{aligned}&{{\dot{V}}_3} \le \mathop {\sum }\limits _{i = 1}^3 \left( - \left( {{\beta _1} - c} \right) e_{P1,i}^2 - {\beta _2}{{\left| {{\xi _{2,i}}} \right| }^2} \right. \nonumber \\&\quad \left. +\, {{\left( {{\xi _{2,i}}} \right) }^{2 - {r_3}}}\left( {{e_{P3,i}} - e_{P3,i}^*} \right) \right) \nonumber \\&\quad +\, \mathop {\sum }\limits _{i = 1}^3 \left( {\begin{array}{c} {{{\left( {{\xi _{3,i}}} \right) }^{2 - {r_4}}}\left( {{e_{P4,i}} + {z_{2,1,i}}} \right) }\\ + \left( {2 - {r_4}} \right) \int _{\bar{e}_{P3,i}^*}^{{{\bar{e}}_{P3,i}}} {{\left( {{s^{\frac{1}{{{r_3}}}}} - {{(\bar{e}_{P3,i}^*)}^{\frac{1}{{{r_3}}}}}} \right) }^{1 - {r_4}}}ds(\frac{{\partial {{(\bar{e}_{P3,i}^*)}^{\frac{1}{{{r_3}}}}}}}{{\partial {e_{P1,i}}}}{{{\dot{e}}}_{P1,i}}\\ + \frac{{\partial {{(\bar{e}_{P3,i}^*)}^{\frac{1}{{{r_3}}}}}}}{{\partial {e_{P2,i}}}}{{{\dot{e}}}_{P2,i}}) \end{array}} \right) \end{aligned}$$

(34)

where $\xi _{3,i} =\left( {\bar{e}_{P3,i} } \right) ^{\frac{1}{r_3 }}-(\bar{e}_{P3,i}^*)^{\frac{1}{r_3 }}$. To construct a FT stabilizer, the inequalities are introduced as follows

$$\begin{aligned}&\left( {\xi _{2,i} } \right) ^{2-r_3 }\left( {e_{P3,i} -e_{P3,i}^*} \right) \le 2^{1-r_3 }\left| {\xi _{2,i} } \right| ^{2-r_3 }\left| {\xi _{3,i} } \right| ^{r_3 }\\&\quad \le \frac{c}{2}\left| {\xi _{2,i} } \right| ^{2}+C_{21} \left| {\xi _{3,i} } \right| ^{2} \\&\quad \left( {2 - {r_4}} \right) \int _{\bar{e}_{P3,i}^*}^{{{\bar{e}}_{P3,i}}} {\left( {{s^{\frac{1}{{{r_3}}}}} - {{(\bar{e}_{P3,i}^*)}^{\frac{1}{{{r_3}}}}}} \right) ^{1 - {r_4}}}ds\\&\quad \times \left( {\frac{{\partial {{(\bar{e}_{P3,i}^*)}^{\frac{1}{{{r_3}}}}}}}{{\partial {e_{P1,i}}}}{{{\dot{e}}}_{P1,i}} + \frac{{\partial {{(\bar{e}_{P3,i}^*)}^{\frac{1}{{{r_3}}}}}}}{{\partial {e_{P2,i}}}}{{{\dot{e}}}_{P2,i}}} \right) \\&\quad \le \left( {2-r_4 } \right) 2^{1-r_3 }\left| {\xi _{3,i} } \right| ^{1-r_4 }\left| {\xi _{3,i} } \right| ^{r_3 }\\&\quad \left( {\frac{\partial (\bar{e}_{P3,i}^*)^{\frac{1}{r_3 }}}{\partial e_{P1,i} }e_{P2,i} +\frac{\partial (\bar{e}_{P3,i}^*)^{\frac{1}{r_3 }}}{\partial e_{P2,i} }\bar{e}_{P3,i} } \right) \end{aligned}$$

where

$$\begin{aligned}&\frac{\partial (\bar{e}_{P3,i}^*)^{\frac{1}{r_3 }}}{\partial e_{P1,i} }e_{P2,i} \le \frac{\partial (\bar{e}_{P3,i}^*)^{\frac{1}{r_3 }}}{\partial e_{P1,i} }\\&\qquad \times \left( {\left( {2^{1-r_2 }\left| {\xi _{2,i} } \right| ^{r_2 }+\left| {\beta _1 e_{P1,i}^{r_2 } } \right| } \right) } \right) \\&\quad \le \tilde{c}_{3,1} \frac{\partial \left( {e_{P1,i} } \right) ^{\frac{1}{r_1 }}}{\partial e_{P1,i} }\left( {2^{1-r_2 }\left| {\xi _{2,i} } \right| ^{r_2 }+\left| {\beta _1 e_{P1,i}^{r_2 } } \right| } \right) \\&\quad =\tilde{c}_{3,1} \left( {2^{1-r_2 }\left| {\xi _{2,i} } \right| ^{r_2 }+\left| {\beta _1 e_{P1,i}^{r_2 } } \right| } \right) \\&\frac{\partial (\bar{e}_{P3,i}^*)^{\frac{1}{r_3 }}}{\partial e_{P2,i} }\bar{e}_{P3,i} \le \frac{\partial (\bar{e}_{P3,i}^*)^{\frac{1}{r_3 }}}{\partial e_{P2,i} }\\&\qquad \times \left( {2^{1-r_3 }\left| {\xi _{3,i} } \right| ^{r_3 }+\left( {C_{11} +C_{12} +\beta _2 } \right) \left| {\xi _{2,i} } \right| ^{r_3 }} \right) \\&\quad \le \frac{\tilde{c}_{3,2} }{r_2 }\left( {\left| {\xi _{2,i} } \right| +(e_{P2,i}^*)^{\frac{1}{r_2 }}} \right) ^{1-r_2 }\\&\qquad \times \left( {2^{1-r_3 }\left| {\xi _{3,i} } \right| ^{r_3 }+\beta _2 \left| {\xi _{2,i} } \right| ^{r_3 }} \right) \end{aligned}$$

Combining the aforementioned analysis by applying Lemma 2 yields

$$\begin{aligned}&\left( {2 - {r_4}} \right) \int _{\bar{e}_{P3,i}^*}^{{{\bar{e}}_{P3,i}}} {\left( {{s^{\frac{1}{{{r_3}}}}} - {{(\bar{e}_{P3,i}^*)}^{\frac{1}{{{r_3}}}}}} \right) ^{1 - {r_4}}}ds\\&\quad \times \left( {\frac{{\partial {{(\bar{e}_{P3,i}^*)}^{\frac{1}{{{r_3}}}}}}}{{\partial {e_{P1,i}}}}{{{\dot{e}}}_{P1,i}} + \frac{{\partial {{(\bar{e}_{P3,i}^*)}^{\frac{1}{{{r_3}}}}}}}{{\partial {e_{P2,i}}}}{{{\dot{e}}}_{P2,i}}} \right) \\&\quad \le c{\left| {{e_{P1,i}}} \right| ^2} + \frac{c}{2}{\left| {{\xi _{2,i}}} \right| ^2} + {C_{22}}{\left| {{\xi _{3,i}}} \right| ^2} \end{aligned}$$

Then, substituting the aforementioned results into (34) renders

$$\begin{aligned}&{{\dot{V}}_3} \le \mathop {\sum }\limits _{i = 1}^3 \left( - \left( {{\beta _1} - 2c} \right) e_{P1,i}^2 - \left( {{\beta _2} - c} \right) {{\left| {{\xi _{2,i}}} \right| }^2} \right. \nonumber \\&\quad +\, {{\left( {{\xi _{3,i}}} \right) }^{2 - {r_4}}}\left( {{e_{P4,i}} + {z_{2,1,i}}} \right) \nonumber \\&\quad \left. +\, {C_{21}}{{\left| {{\xi _{3,i}}} \right| }^2} + {C_{22}}{{\left| {{\xi _{3,i}}} \right| }^2} \right) . \end{aligned}$$

(35)

The virtual control is given as

$$\begin{aligned} e_{P4,i}^*=-\beta _3 \left( {\xi _{3,i} } \right) ^{r_4 }-z_{2,1,i} ,\,i=1,2,3, \end{aligned}$$

(36)

where $\beta _3 >C_{21} +C_{22} +\tilde{\beta }_3 +c$, $\tilde{\beta }_3 >0$. Thus, the corresponding Lyapunov function satisfies

$$\begin{aligned}&{{\dot{V}}_3} \le \mathop {\sum }\limits _{i = 1}^3 \left( - \left( {{{\tilde{\beta }}_1} + c} \right) e_{P1,i}^2 - \left( {{{\tilde{\beta }}_2} + c} \right) {{\left| {{\xi _{2,i}}} \right| }^2}\right. \nonumber \\&\qquad \left. - \left( {{{\tilde{\beta }}_3} + c} \right) {{\left| {{\xi _{3,i}}} \right| }^2} + {{\left( {{\xi _{3,i}}} \right) }^{2 - {r_4}}}\left( {{e_{P4,i}} - e_{P4,i}^*} \right) \right) \nonumber \\ \end{aligned}$$

(37)

Step 4 Lyapunov function is selected as

$$\begin{aligned} V_4 =V_3 +\mathop {\sum }\limits _{i=1}^3 \left( {\int _{\bar{e}_{P4,i}^*}^{\bar{e}_{P4,i} } \left( {s^{\frac{1}{r_4 }}-(\bar{e}_{P4,i}^*)^{\frac{1}{r_4 }}} \right) ^{2-r_5 }ds} \right) , \end{aligned}$$

(38)

where $\bar{e}_{P4,i}^*=e_{P4,i}^*+z_{2,1,i} =-\beta _3 \left( {\xi _{3,i} } \right) ^{r_4 }$, and $\bar{e}_{P4,i} =e_{P4,i} +z_{2,1,i}$. Similarly, computing the time derivative of (38) yields

$$\begin{aligned}&{{\dot{V}}_4} \le \mathop {\sum }\limits _{i = 1}^3 \left( - \left( {{\beta _1} - 2c} \right) e_{P1,i}^2 - \left( {{\beta _2} - c} \right) {{\left| {{\xi _{2,i}}} \right| }^2} \right. \nonumber \\&\qquad \left. -\, {\beta _3}{{\left| {{\xi _{3,i}}} \right| }^2} + {{\left| {{\xi _{3,i}}} \right| }^{2 - {r_4}}}\left( {{e_{P4,i}} - e_{P4,i}^*} \right) \right) \nonumber \\&\qquad +\mathop {\sum }\limits _{i=1}^3 \left( \left| {\xi _{4,i} } \right| ^{2-r_5 }\left( f_{Pe,i} \left( t \right) +u_{P,i} +z_{1,\,2,i} \right. \right. \nonumber \\&\qquad \left. +\,z_{3,\,1,i} \right) +\left( {2-r_5 } \right) \zeta _4\nonumber \\&\qquad \times \left. \int _{\bar{e}_{P4,i}^*}^{\bar{e}_{P4,i} } \left( {s^{\frac{1}{r_4 }}-(\bar{e}_{P4,i}^*)^{\frac{1}{r_4 }}} \right) ^{1-r_5 }ds \right) \nonumber \\&\quad \le \mathop {\sum }\limits _{i=1}^3 \left( -\left( {\beta _1 -3} \right) e_{P1,i}^2 -\left( {\beta _2 -2} \right) \left| {\xi _{2,i} } \right| ^{2}\right. \nonumber \\&\quad -\,(\beta _3 -1)\left| {\xi _{3,i} } \right| ^{2}+\left| {\xi _{4,i} } \right| ^{2-r_5 }\left( f_{Pe,i} \left( t \right) +u_{P,i} \right. \nonumber \\&\quad \left. \left. +\,z_{1,\,2,i} +z_{3,\,1,i} \right) +C_{31} \left| {\xi _{4,i} } \right| ^{2}+C_{32} \left| {\xi _{4,i} } \right| ^{2} \right) \nonumber \\ \end{aligned}$$

(39)

where $\zeta _4 =\frac{\partial (\bar{e}_{P4,i}^*)^{\frac{1}{r_4 }}}{\partial e_{P1,i} }\dot{e}_{P1,i}+\frac{\partial (\bar{e}_{P4,i}^*)^{\frac{1}{r_4 }}}{\partial e_{P2,i} }\dot{e}_{P2,i}+\frac{\partial (\bar{e}_{P4,i}^*)^{\frac{1}{r_4 }}}{\partial e_{P3,i} }\dot{e}_{P3,i}$, $\xi _{4,i} =\left( {\bar{e}_{P4,i} } \right) ^{\frac{1}{r_4 }}-(\bar{e}_{P4,i}^*)^{\frac{1}{r_4 }}$.

The position controller is designed as

$$\begin{aligned}&u_{P,i} =-\beta _4 \left( {\xi _{4,i} } \right) ^{r_5 }-f_{Pe,i} \left( t \right) -z_{1,\,2,i} -z_{3,\,1,i} ,\,\nonumber \\&\quad i=1,2,3, \end{aligned}$$

(40)

where $\beta _4>C_{31} +C_{32} +\tilde{\beta }_4 >0$. Substituting (40) into (39) introduces

$$\begin{aligned}&{{\dot{V}}_4} \le \mathop {\sum }\limits _{i = 1}^3 \left( - {{\tilde{\beta }}_1}e_{P1,i}^2 - {{\tilde{\beta }}_2}{{\left| {{\xi _{2,i}}} \right| }^2} \right. \nonumber \\&\qquad \left. - {{\tilde{\beta }}_3}{{\left| {{\xi _{3,i}}} \right| }^2} - {{\tilde{\beta }}_4}{{\left| {{\xi _{4,i}}} \right| }^2} \right) . \end{aligned}$$

(41)

Yaw angle loop controller design

Step 1 Define a Lyapunov function

$$\begin{aligned} V_{1\psi } =\int _0^{e_{\psi 1} } \left( {s^{1/r_1 }} \right) ^{2-r_2 }ds. \end{aligned}$$

(42)

Considering (23), the first time derivative is given as

$$\begin{aligned} {{\dot{V}}_{1\psi }} = e_{\psi 1}^{\left( {2 - {r_2}} \right) /{r_1}}\cdot {e_{\psi 2}}. \end{aligned}$$

(43)

Design the virtual control as

$$\begin{aligned} e_{\psi 2}^*=-\beta _{1\psi } e_{\psi 1}^{r_2 /r_1 } , \end{aligned}$$

(44)

thus

$$\begin{aligned} {{\dot{V}}_{1\psi }} = - {\beta _{1\psi }}e_{\psi 1}^2 + e_{\psi 1}^{2 - {r_2}}\cdot ({e_{\psi 2}} - e_{\psi 2}^*), \end{aligned}$$

(45)

where the constant $\beta _{1\psi }>c_\psi +\tilde{\beta }_{1\psi } >0$, $\tilde{\beta }_{1\psi } >0$.

Step 2 The Lyapunov function is selected as

$$\begin{aligned} V_{2\psi } =V_{1\psi } +\int _{e_{\psi 2}^*}^{e_{\psi 2} } \left( {s^{\frac{1}{r_2 }}-(e_{\psi 2}^*)^{\frac{1}{r_2 }}} \right) ^{2-r_3 }ds. \end{aligned}$$

(46)

Calculating its derivative yields

Table 1 Parameters of the helicopter

$$\begin{aligned}&{{{\dot{V}}}_{2\psi }} = -\, {\beta _{1\psi }}e_{\psi 1}^2 + e_{\psi 1}^{2 - {r_2}}\cdot ({e_{\psi 2}} - e_{\psi 2}^*) \nonumber \\&\qquad \qquad +\, {\left( {{\xi _{2\psi }}} \right) ^{2 - {r_3}}}\left( {{f_{\psi e}}\left( t \right) + {u_\psi } + {z_{1,~3}}} \right) \nonumber \\&\qquad \qquad + \left( {2 - {r_3}} \right) \int _{e_{\psi 2}^*}^{{e_{\psi 2}}} {\left( {{s^{\frac{1}{{{r_2}}}}} - {{(e_{\psi 2}^*)}^{\frac{1}{{{r_2}}}}}} \right) ^{1 - {r_3}}}ds\frac{{\partial {{(e_{\psi 2}^*)}^{\frac{1}{{{r_2}}}}}}}{{\partial {e_{\psi 1}}}}{{\dot{e}}_{\psi 1}}\nonumber \\&\qquad \le - \left( {{\beta _{1\psi }} - 1} \right) e_{\psi 1}^2 + \left( {{C_{1\psi }} + {C_{2\psi }}} \right) {\left| {{\xi _{2\psi }}} \right| ^2} \nonumber \\&\qquad \quad +\, {\left( {{\xi _{2\psi }}} \right) ^{2 - {r_3}}}\left( {{f_{\psi e}}\left( t \right) + {u_\psi } + {z_{1,~3}}} \right) \end{aligned}$$

(47)

where $\xi _{2\psi } =\left( {e_{\psi 2} } \right) ^{\frac{1}{r_2 }}-(e_{\psi 2}^*)^{\frac{1}{r_2 }}$. Selecting

$$\begin{aligned} u_\psi =-\beta _{2\psi } \left( {\xi _{2\psi } } \right) ^{r_3 }-f_{\psi e} \left( t \right) -z_{1,\,3} , \end{aligned}$$

(48)

where the control constant $\beta _{2\psi }>C_{1\psi } +C_{2\psi } +\tilde{\beta }_{2\psi } >0$, $\tilde{\beta }_{2\psi } >0$ yields

$$\begin{aligned} {{\dot{V}}_{2\psi }} \le - {\tilde{\beta }_{1\psi }}e_{\psi 1}^2 - {\tilde{\beta }_{2\psi }}{\left| {{\xi _{2\psi }}} \right| ^2}. \end{aligned}$$

(49)

3.3 Proof of FT stability

Based on the FT Lyapunov theory, FT stability of the whole system is proven. The detailed proof is given in appendix.

Theorem 3

Consider that the simplified helicopter dynamic system satisfies Assumptions 1 and 2. Proposed controller (40) and (48) can guarantee that the closed-loop system is FT stable. $\square$

Remark 4

In the position controller $u_P$ and yaw angle controller $u_\psi$, the control design parameters include $\tau$, $\beta _1$, $\beta _2$, $\beta _3$, $\beta _4$, $\beta _{1\psi }$, and $\beta _{2\psi }$. Deciding the value of these parameter is a trade-off process. Larger values mean faster closed-loop system state convergence. However, large values cause excessive inputs and overshoot. For our problem, the principle for selecting parameters depends on the dynamic characteristic of small-scale helicopters.

3.4 Practical helicopter control signal

The practical control signals for helicopter can be calculated from $u_P$ in (40) and $u_\psi$ in (48). According to their definitions, one has

$$\begin{aligned}&\left[ {\begin{array}{c} {{M_\phi }}\\ {{M_\theta }}\\ {{{\ddot{T}}_m}} \end{array}} \right] = - m\cdot \left[ {\begin{array}{ccc} 0&{}{{T_m}}&{}0\\ { - {T_m}}&{}0&{}0\\ 0&{}0&{}1 \end{array}} \right] \cdot {R^{ - 1}}\left( {\Theta } \right) \cdot {u_P}, \end{aligned}$$

(50)

$$\begin{aligned}&M_\psi =\frac{C_\theta }{C_\phi }u_\psi . \end{aligned}$$

(51)

Following that, the control commands $\left[ \begin{array}{cccc} {\delta _\mathrm{col} }&{\delta _\mathrm{lon} }&{\delta _\mathrm{lat} }&{\delta _\mathrm{ped} }\end{array} \right] ^{T}$ can be obtained according to the definition of $\left[ {{\begin{array}{ccc} {M_\phi }&{} {M_\theta }&{} {M_\psi } \\ \end{array} }} \right] ^{T}$ and $T_M =\int \int _0^t \ddot{T}_m \hbox {d}t$.

$$\begin{aligned}&\delta _\mathrm{col} =-\left( {\frac{T_m }{m}-g+Z_w w} \right) /Z_\mathrm{col} , \end{aligned}$$

(52)

$$\begin{aligned}&\left[ {{\begin{array}{c} {\delta _\mathrm{lon} } \\ {\delta _\mathrm{lat} } \\ {\delta _\mathrm{ped} } \\ \end{array} }} \right] =\left[ {{\begin{array}{c} {M_\phi } \\ {M_\theta } \\ {M_\psi } \\ \end{array} }} \right] +J^{-1}\left( {\omega \times J\omega } \right) -A\omega -B\left( 1 \right) \delta _\mathrm{col},\nonumber \\ \end{aligned}$$

(53)

where $B\left( 1 \right)$ is the first column of matrix B.

The following result is given directly by applying Theorem 3.

Theorem 4

Consider helicopter dynamic models (1)–(4) under Assumptions 1 and 2. If the controller is designed as (52)–(53), then tracking errors of the position and yaw angle FT converge to zero with disturbances. $\square$

4 Simulation analysis

Numerical simulations are shown to demonstrate the effectiveness of our proposed FT controller. Table 1 summarizes the corresponding helicopter model parameters [10, 28].

Following [10], the lumped disturbances in (10)–(11) are introduced in the simulation. These disturbances include model uncertainties and external disturbances.

$$\begin{aligned} \left[ {{\begin{array}{c} {\Delta F} \\ {\Delta M} \\ \end{array} }} \right] =\Delta \cdot \left[ {{\begin{array}{c} V \\ \Theta \\ \omega \\ \end{array} }} \right] +B_\mathrm{wind} d_\mathrm{wind}, \end{aligned}$$

(54)

where constant matrix $\Delta \in R^{6\times 9}$ represents model uncertainty, and $B_\mathrm{wind}$ denotes the transformation matrix from airspeed to force and moment. All elements of $\Delta$ are pseudorandomly generated within the open interval $\left( {-0.5\,0.5} \right)$. Matrices $\Delta$ and $B_\mathrm{wind}$ are given as follows:

$$\begin{aligned} \Delta= & {} \left[ \begin{array}{ccccccccc} {-0.239}&{}{0.164}&{} {-0.055}&{} {0.456} &{} {0.013} &{} {-0.362}&{} {-0.096}&{} {0.071} &{} {-0.185} \\ {0.203} &{}{0.351}&{} {0.419} &{} {0.351} &{} {-0.135}&{} {0.342} &{} {0.491} &{} {-0.359}&{} {-0.387} \\ {0.035} &{}{0165} &{} {0.232} &{} {0.265} &{} {-0.384}&{} {0.254} &{} {-0.044}&{} {0.357} &{} {0.031} \\ {0.311} &{}{0.045} &{} {0.369} &{} {-0.250}&{} {-0.303}&{} {-0.368} &{} {-0.352}&{} {0.012} &{} {-0.011} \\ {-0.055}&{}{-0.465} &{} {0.062} &{} {0.290} &{} {0.048} &{} {-0.451} &{} {0.426} &{} {-0.454}&{} {0.209} \\ {0.267} &{}{-0.409} &{} {-0.088}&{} {-0.482}&{} {0.057} &{} {0.459} &{} {0.138} &{} {-0.028}&{} {0.343} \\ \end{array} \right] \\ B_\mathrm{wind}= & {} m\cdot \left[ \begin{array}{cc} {-0.0505} &{} 0 \\ 0 &{} {-0.151} \\ 0 &{} 0 \\ {-0.144} &{} {0.143} \\ {-0.0561}&{} {-0.0585} \\ 0 &{} {0.0301} \end{array}\right] \end{aligned}$$

Wind disturbance $d_w$ is assumed to possess wind components along $\left[ {{\begin{array}{cc} {x_b }&{} {y_b } \\ \end{array} }} \right]$ in BRF. This variable is composed of constant and random components, i.e., $d_w =d_c +d_r$. The constant component is set as $\left[ {{\begin{array}{cc} 5&{} 5 \\ \end{array} }} \right] ^{T}$ (m/s). Stochastic wind disturbance is modeled as follows [6]:

$$\begin{aligned} {{\dot{d}}_r} = \left[ {\begin{array}{c} {{{{\dot{d}}}_u}}\\ {{{{\dot{d}}}_v}} \end{array}} \right] = \left[ {\begin{array}{cc} { - 1/{\tau _c}}&{}0\\ 0&{}{ - 1/{\tau _c}} \end{array}} \right] \left[ {\begin{array}{c} {{d_u}}\\ {{d_v}} \end{array}} \right] + \rho \left[ {\begin{array}{c} {{q_u}}\\ {{q_v}} \end{array}} \right] , \end{aligned}$$

where $\tau _c =3.2\,\hbox {s}$ is the time constant; $q_u$ and $q_v$$(\sigma _{q_u } =\sigma _{q_v } =3.6576\,\hbox {m}/\hbox {s})$ are independent with zero mean; $\rho =1/2$. Figure 3 shows the wind disturbance $d_w$ used in the helicopter’ simulation.

Fig. 3

Wind disturbance

Additionally, the flapping dynamics model is considered to provide sufficient fidelity for the simulation process. Flapping dynamics are equivalent to the additional dynamics in the servo loop [28]:

$$\begin{aligned} \tau _f \dot{\bar{\delta }}_\mathrm{lon}= & {} -\tau _f q-\bar{\delta }_\mathrm{lon} +\delta _\mathrm{lon} \nonumber \\ \tau _f \dot{\bar{\delta }}_\mathrm{lat}= & {} -\tau _f p-\bar{\delta }_\mathrm{lat} +\delta _\mathrm{lat} , \end{aligned}$$

(55)

where $\bar{\delta }_\mathrm{lon}$ and $\bar{\delta }_\mathrm{lat}$ are longitudinal and lateral applied control signals, respectively, and $\tau _f =0.1$ is the main rotor’s dynamics time constant.

According to the flight characteristic of small-scale helicopters, the parameters of FT controller combined with DO (FT+DO) are selected properly, where $\tau = -2/31$, $\beta _1 =2$, $\beta _2 =5$, $\beta _3 =20$, $\beta _4 =50$, $\beta _{1\psi } =20$, and $\beta _{2\psi } =50$. The fourth-order SM DO is adopted, and the corresponding parameters are given as $L_1 =L_2 =10$ and $L_3 =20$.

Fig. 4

Trajectory tracking responses of the helicopter

Fig. 5

Velocity response of the helicopter

Fig. 6

Angular response of the helicopter

Fig. 7

Angular rate response of the helicopter

Fig. 8

Control commands of the helicopter

To verify our controller’s superiority, the proposed controller is compared with BS and FT controller without DO. All the parameters of the FT controller are the same as that of FT+DO. BS controller has the following form

$$\begin{aligned}&e_{P2d,bs} =-k_{1,bs} e_{P1} \\&e_{P3d,bs} =-k_{2,bs} \left( {e_{P2} -e_{P2d,bs} } \right) \\&e_{P4d,bs} =-k_{3,bs} \left( {e_{P3} -e_{p3d,bs} } \right) \\&u_p =-f_{Pe} \left( t \right) -k_{4,bs} \left( {e_{p4} -e_{p4d,bs} } \right) \\&e_{\psi 2d,bs} =-k_{1\psi ,bs} e_{\psi 1} \\&u_\psi =-f_{\psi e} \left( t \right) -k_{2\psi ,bs} \left( {e_{\psi 2} -e_{\psi 2d,bs} } \right) \end{aligned}$$

where $k_{1,bs} =2$, $k_{2,bs} =5$, $k_{3,bs} =k_{1\psi ,bs} =20$, and $k_{4,bs} =k_{2\psi ,bs} =50$. The comparison of BS controller highlights the benefits of FT method, which provides rapid convergent speed and improved disturbance rejection performance.

The desired “8-shape” reference trajectory is described as:

$$\begin{aligned} P_d \left( t \right)= & {} \left[ {{\begin{array}{ccc} 0&{} 0&{} {-7\left( {1-e^{-0.3t}} \right) } \\ \end{array} }} \right] ^{T}\hbox { for }t\le 7s \nonumber \\ P_d \left( t \right)= & {} \left[ {{\begin{array}{c} {20\left( {1-\cos \left( {\frac{2\pi }{23}\left( {t-7} \right) } \right) } \right) } \\ {10\sin \left( {\frac{4\pi }{23}\left( {t-7} \right) } \right) } \\ {-7\left( {1-e^{-0.3t}} \right) } \\ \end{array} }} \right] \hbox { for }t>7s \nonumber \\ \psi _d =0 \end{aligned}$$

(56)

Firstly, the helicopter vertically climbs for 7s to simulate the takeoff stage. Then, it follows an “8-shaped” path while continuing to lift. Helicopter’s lift, sideslip, and forward performances are evaluated comprehensively through the moderately aggressive maneuver.

The simulation results are illustrated in Figs. 4, 5, 6, 7, and 8. Figure 4 gives the position response curves of helicopter’s closed-loop system based on the three methods. To quantitatively analyze the tracking performance, the integrated time absolute error (ITAE defined as $\int _0^t t\Vert e\Vert \hbox {d}t$) of three methods is listed in Table 2. Our proposed FT+DO controller tracks the reference trajectory more accurately under model uncertainties and external disturbances than other controllers. Moreover, the comparison of BS and FT control shows that FT stability property not only enjoys convergence speed but also improves robustness of the closed-loop system. Figure 4 also gives the 3D position trajectory intuitively, and the results agree with this analysis. DO plays a significantly important role in the tracking accuracy of the closed-loop system. It attenuates the effect of perturbations and recurve nominal performance of the control system.

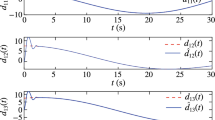
The velocity, angle, and angular rate responses are shown in Figs. 5, 6, and 7. The state responses are a little chattering due to the existence of perturbations and fast tracking the maneuver trajectory. The responses of FT+DO fluctuate heavily to eliminate disturbances rapidly. Violent chattering exists at $t=7\,\hbox {s}$ due to the switching of reference trajectory. Additionally, Fig. 8 displays the curves of controller commands. One can find that the control signals of FT+DO method have smaller vibration than the other at the time of switching of the desired trajectory.

Table 2 Average error of position tracking

5 Conclusion

We design a composite FT control law for helicopter. The helicopter dynamics are simplified and decoupled by approximate feedback linearization. ADRC technique is utilized to realize the accurate trajectory tracking under matched and mismatched disturbances. The disturbances are estimated by HOSMDO and then feed-forwardly compensated for. The FT feedback part is designed via added power integrator method. The compound control law guarantees FT convergence of the tracking errors. Numerical simulation demonstrates that with this obtained FT controller in our work, a small-scale unmanned helicopter exhibits excellent tracking performance with disturbances.

Appendix

1.1 Proof of Theorem 3

The proving course of finite-time (FT) stability is divided into two stages. First, FT stability is established when $t>t_{\max }$. Second, the states of the whole system are proven to not escape in any FT interval.

a) According to (41) and (49), ${{\dot{V}}_4} + {\dot{V}_{2\psi }} \le$$- {\beta _{\max }}\bigg [ \mathop {\sum }\limits _{i = 1}^3 \left( {e_{P1,i}^2 + {{\left( {{\xi _{2,i}}} \right) }^2} + {{\left( {{\xi _{3,i}}} \right) }^2} + {{\left( {{\xi _{4,i}}} \right) }^2}} \right) +{e_{\psi 1}^2} + {{\left( {{\xi _{2\psi }}} \right) }^2} \bigg ] \le 0$

where $\beta _{\max } =\hbox {max}\left\{ {{\begin{array}{cccccc} {\tilde{\beta }_1 }&{\tilde{\beta }_2 }&{\tilde{\beta }_3 }&{\tilde{\beta }_4 }&{\tilde{\beta }_{1\psi } }&{\tilde{\beta }_{2\psi } } \end{array} }} \right\}$. In addition, considering the definition of the Lyapunov function, constant $L>0$ exists such that

$$\begin{aligned}&0\le V_4 +V_{2\psi } \le L\left[ \mathop {\sum }\limits _{i=1}^3 \left( e_{P1,i}^{2-\tau } \right. \right. \\&\quad \left. +\left( {\xi _{2,i} } \right) ^{2-\tau }+\left( {\xi _{3,i} } \right) ^{2-\tau }+\left( {\xi _{4,i} } \right) ^{2-\tau } \right) \nonumber \\&\quad \left. +e_{\psi 1}^{2-\tau } +\left( {\xi _{2\psi } } \right) ^{2-\tau } \right] \end{aligned}$$

Select $\lambda =\beta _{\max } /2L^{\frac{2}{2-\tau }}$. The use of Lemma 3 produces

$$\begin{aligned}&\left( {V_4 +V_{2\psi } } \right) ^{{\prime }}+\lambda \left( {V_4 +V_{2\psi } } \right) ^{\frac{2}{2-\tau }} \\&\quad \le -\beta _{\max } \left[ \mathop {\sum }\limits _{i=1}^3 \left( e_{P1,i}^2 +\left( {\xi _{2,i} } \right) ^{2}+\left( {\xi _{3,i} } \right) ^{2}\right. \right. \\&\quad \left. \left. +\left( {\xi _{4,i} } \right) ^{2} \right) +e_{\psi 1}^2 +\left( {\xi _{2\psi } } \right) ^{2} \right] \\&\qquad +\,\lambda L^{\frac{2}{2-\tau }}\left[ \mathop {\sum }\limits _{i=1}^3 \left( e_{P1,i}^2 +\left( {\xi _{2,i} } \right) ^{2}+\left( {\xi _{3,i} } \right) ^{2}\right. \right. \\&\qquad \left. \left. +\left( {\xi _{4,i} } \right) ^{2} \right) +e_{\psi 1}^2 +\left( {\xi _{2\psi } } \right) ^{2} \right] \\&\quad \le 0 \end{aligned}$$

By applying Theorem 1, we conclude that the state vector will converge on zero in FT.

b) In this step, proof that the helicopter’s state does not escape to infinite in any FT interval is provided. Combining simplified helicopter dynamic system (18), DO (20), and controllers (40) and (48), the following closed-loop dynamics are introduced

$$\begin{aligned} {{{\dot{e}}}_{P1}}= & {} {e_{P2}}\nonumber \\ {{{\dot{\xi }} }_{2,i}}= & {} \frac{1}{{{r_2}}}{({e_{P2,i}})^{\frac{1}{{{r_2}}} - 1}}\left( {{{\bar{e}}_{P3,i}} - {\sigma _{1,1,i}}} \right) + {\left( {{\beta _1}} \right) ^{\frac{1}{{{r_2}}}}}{e_{P2,i}}\nonumber \\ {{{\dot{\xi }} }_{3,i}}= & {} \frac{1}{{{r_3}}}{\left( {{{\bar{e}}_{P3,i}}} \right) ^{\frac{1}{{{r_3}}} - 1}}\left( {{{\bar{e}}_{P4,i}} - {\sigma _{2,1,i}}} \right) + {\left( {{\beta _2}} \right) ^{\frac{1}{{{r_3}}}}}{{{\dot{\xi }} }_2}\nonumber \\ {{{\dot{\xi }} }_{4,i}}= & {} \frac{1}{{{r_4}}}{\left( {{{\bar{e}}_{P4,i}}} \right) ^{\frac{1}{{{r_4}}} - 1}}\left( { - {\beta _4}{{\left( {{\xi _{4,i}}} \right) }^{{r_5}}} - {\sigma _{3,1,i}} - {\sigma _{1,2,i}}} \right) \nonumber \\&\quad + {\left( {{\beta _3}} \right) ^{\frac{1}{{{r_4}}}}}{{\dot{\xi }}_3}\nonumber \\ {{{\dot{e}}}_{\psi 1}}= & {} {e_{\psi 2}}\nonumber \\ {{{\dot{\xi }} }_{2\psi }}= & {} \frac{1}{{{r_2}}}{\left( {{e_{\psi 2}}} \right) ^{\frac{1}{{{r_2}}} - 1}}\left( { - {\beta _{2\psi }}{{\left( {{\xi _{2\psi }}} \right) }^{{r_3}}} - {\sigma _{3,1}}} \right) \nonumber \\&\quad +{\left( {{\beta _1}} \right) ^{\frac{1}{{{r_2}}}}}{e_{\psi 2}} \end{aligned}$$

(a1)

A Lyapunov function is selected as follows:

$$\begin{aligned}&L=\frac{1}{2}\mathop {\sum }\limits _{i=1}^3 \left[ {\left( {e_{P1} } \right) ^{2}+\left( {\xi _{2,i} } \right) ^{2}+\left( {\xi _{3,i} } \right) ^{2}+\left( {\xi _{4,i} } \right) ^{2}} \right] \nonumber \\&\qquad \quad +\frac{1}{2}\left[ {\left( {e_{\psi 1} } \right) ^{2}+\left( {\xi _{2\psi } } \right) ^{2}} \right] \end{aligned}$$

(a2)

Its derivative is expressed as follows:

$$\begin{aligned}&{\dot{L}} = {e_{P1}}{{\dot{e}}_{P1}} + {\xi _2}{{\dot{\xi }} _2} + {\xi _3}{{\dot{\xi }} _3} + {\xi _4}{{\dot{\xi }} _4} \\&\quad =\mathop {\sum }\limits _{i=1}^3 \left[ {e_{P1,i} e_{P2,i} } \right] \\&\qquad +\mathop {\sum }\limits _{i=1}^3 \left[ \xi _{2,i} \left( \frac{1}{r_2 }(e_{P2,i} )^{\frac{1}{r_2 }-1}\left( {\bar{e}_{P3,i} -\sigma _{1,1,i} } \right) \right. \right. \nonumber \\&\qquad \qquad \qquad \left. \left. +\left( {\beta _1 } \right) ^{\frac{1}{r_2 }}e_{P2,i} \right) \right] \\&\qquad +\mathop {\sum }\limits _{i=1}^3 \left[ \xi _{3,i} \left( \frac{1}{r_3 }\left( {\bar{e}_{P3,i} } \right) ^{\frac{1}{r_3 }-1}\left( {\bar{e}_{P4,i} -\sigma _{2,1,i} } \right) \right. \right. \\&\qquad \qquad \qquad \left. \left. +\left( {\beta _2 } \right) ^{\frac{1}{r_3 }}\dot{\xi }_{2} \right) \right] \\&\qquad +\mathop {\sum }\limits _{i=1}^3 \left[ \xi _{4,i} \left( \frac{1}{r_4 }\left( {\bar{e}_{P4,i} } \right) ^{\frac{1}{r_4 }-1}\left( -\beta _4 \left( {\xi _{4,i} } \right) ^{r_5 }\right. \right. \right. \\&\qquad \qquad \qquad \left. \left. \left. -\,\sigma _{3,1,i} -\sigma _{1,2,i} \right) +\left( {\beta _3 } \right) ^{\frac{1}{r_4 }}\left( {\dot{\xi }_{3}} \right) \right) \right] \\&\qquad +\,e_{\psi 2} e_{\psi 2} +\xi _{2\psi } \left( \frac{1}{r_2 }\left( {e_{\psi 2} } \right) ^{\frac{1}{r_2 }-1}\left( -\beta _{2\psi } \left( {\xi _{2\psi } } \right) ^{r_3 }\right. \right. \\&\qquad \left. \left. -\,\sigma _{3,1} \right) +\left( {\beta _1 } \right) ^{\frac{1}{r_2 }}e_{\psi 2} \right) \end{aligned}$$

To simplify the analysis, the following inequalities are obtained using Lemmas 1–2.

$$\begin{aligned}&e_{P1,i} e_{P2,i} \le e_{P1,i} \left( {\left| {e_{P2,i} -e_{P2,i}^*} \right| +\left| {\beta _1 e_{P1,i}^{r_2 } } \right| } \right) \\&\quad \le \left| {e_{P1,i} } \right| ^{2+\tau }+l_1 \left| {\xi _{2,i} } \right| ^{2+\tau } \\&\xi _{2,i} \left( {\frac{1}{r_2 }(e_{P2,i} )^{\frac{1}{r_2 }-1}\left( {\bar{e}_{P3,i} -\sigma _{1,1,i} } \right) } \right) \\&\quad \le \frac{1}{r_2 }\xi _{2,i} \left( {\left| {e_{P2,i} -e_{P2,i}^*} \right| +\left| {\beta _1 e_{P1,i}^{r_2 } } \right| } \right) ^{\frac{1}{r_2 }-1}\\&\quad \left( {\left| {e_{P3,i} -e_{P3,i}^*} \right| +\left| {\beta _2 \left( {\xi _{2,i} } \right) ^{r_3 }} \right| -\sigma _{1,1,i} } \right) \\&\quad \le \left| {e_{P1,i} } \right| ^{2+\tau }+l_{21} \left| {\xi _{2,i} } \right| ^{2+\tau }+l_{22} \left| {\xi _{3,i} } \right| ^{2+\tau }\\&\qquad +\,l_{23} \left| {\sigma _{1,1,i} } \right| \left( {\left| {e_{P1} } \right| ^{2-r_2 }+\left| {\xi _{2,i} } \right| ^{2-r_2 }} \right) \\&\quad \xi _{2,i} \left( {\beta _1 } \right) ^{\frac{1}{r_2 }}e_{P2,i} \le l_{24} \left| {e_{P1} } \right| ^{2+\tau }+l_{25} \left| {\xi _{2,i} } \right| ^{2+\tau } \end{aligned}$$

Similarly,

$$\begin{aligned}&\xi _{3,i} \left( {\frac{1}{r_3 }\left( {\bar{e}_{P3,i} } \right) ^{\frac{1}{r_3 }-1}\left( {\bar{e}_{P4,i} -\sigma _{2,1,i} } \right) +\left( {\beta _2 } \right) ^{\frac{1}{r_3 }}\dot{\xi }_{2}} \right) \\&\quad \le \xi _{3,i} \left( \frac{1}{r_3 }\left( {\left| {e_{P3,i} -e_{P3,i}^*} \right| +\left| {\beta _2 \left( {\xi _{2,i} } \right) ^{r_3 }} \right| } \right) ^{\frac{1}{r_3 }-1}\right. \\&\quad \left. \left( {\bar{e}_{P4,i} -\sigma _{2,1,i} } \right) +\left( {\beta _2 } \right) ^{\frac{1}{r_3 }}\dot{\xi }_{2} \right) \\&\quad \le \left| {e_{P1,i} } \right| ^{2+\tau }+l_{31} \left| {\xi _{2,i} } \right| ^{2+\tau }+l_{32} \left| {\xi _{3,i} } \right| ^{2+\tau }\\&\qquad +\,l_{33} \left| {\xi _{3,i} } \right| ^{2+\tau }+l_{34} \left| {\xi _{4,i} } \right| ^{2+\tau }\\&\qquad +\,l_{35} \left| {\sigma _{2,1,i} } \right| \left( {\left| {\xi _{2,i} } \right| ^{2-r_3 }+\left| {\xi _{3,i} } \right| ^{2-r_3 }} \right) \\&\qquad +\,l_{36} \left| {\sigma _{1,1,i} } \right| \left( {\left| {e_{P1,i} } \right| ^{2-r_2 }+\left| {\xi _{2,i} } \right| ^{2-r_2 }+\left| {\xi _{3,i} } \right| ^{2-r_2 }} \right) \\&\xi _{4,i} \left( \frac{1}{r_4 }\left( {\bar{e}_{P4,i} } \right) ^{\frac{1}{r_4 }-1}\left( {-\beta _4 \left( {\xi _{4,i} } \right) ^{r_5 }-\sigma _{3,1,i} -\sigma _{1,2,i} } \right) \right. \\&\qquad \left. +\left( {\beta _3 } \right) ^{\frac{1}{r_4 }}\left( {\dot{\xi }_{3}} \right) \right) \\&\quad \le {\left| {{e_{P1,i}}} \right| ^{2 + \tau }} + {l_{41}}{\left| {{\xi _{2,i}}} \right| ^{2 + \tau }} + {l_{42}}{\left| {{\xi _{3,i}}} \right| ^{2 + \tau }} \\&\qquad +\, {l_{43}}{\left| {{\xi _{3,i}}} \right| ^{2 + \tau }} + {l_{44}}{\left| {{\xi _{4,i}}} \right| ^{2 + \tau }}\\&\qquad +\, {l_{45}}\left| {{\sigma _{2,1,i}} + {\sigma _{1,2,i}}} \right| \left( {{{\left| {{\xi _{3,i}}} \right| }^{2 - {r_4}}} + {{\left| {{\xi _{4,i}}} \right| }^{2 - {r_4}}}} \right) \\&\qquad +\, {l_{46}}\left| {{\sigma _{2,1,i}}} \right| \left( {{{\left| {{\xi _{2,i}}} \right| }^{2 - {r_3}}} + {{\left| {{\xi _{3,i}}} \right| }^{2 - {r_3}}} + {{\left| {{\xi _{4,i}}} \right| }^{2 + \tau }}} \right) \\&\qquad +\, {l_{47}}\left| {{\sigma _{1,1,i}}} \right| \left( {{\left| {{e_{P1,i}}} \right| }^{2 - {r_2}}} + {{\left| {{\xi _{2,i}}} \right| }^{2 - {r_2}}} \right. \\&\qquad \left. +\, {{\left| {{\xi _{3,i}}} \right| }^{2 - {r_2}}} + {{\left| {{\xi _{4,i}}} \right| }^{2 - {r_2}}} \right) \\&e_{\psi 2} e_{\psi 2} +\xi _{2\psi } \left( \frac{1}{r_2 }\left( {e_{\psi 2} } \right) ^{\frac{1}{r_2 }-1}\left( {-\beta _{2\psi } \left( {\xi _{2\psi } } \right) ^{r_3 }-\sigma _{3,1} } \right) \right. \\&\qquad \left. +\,\left( {\beta _1 } \right) ^{\frac{1}{r_2 }}e_{\psi 2} \right) \\&\quad \le \, l_{1\psi } \left| {e_{\psi 2} } \right| ^{2+\tau }+l_{2\psi } \left| {\xi _{2\psi } } \right| ^{2+\tau }+l_{3\psi } \left| {\sigma _{1,3} } \right| \\&\qquad \left( {\left| {e_{\psi 2} } \right| ^{2-r_2 }+\left| {\xi _{2\psi } } \right| ^{2-r_2 }} \right) \\ \end{aligned}$$

where $l_{i,\,j} >0$ is the bounded constant.

The control loop has no effects on the DO loop. When $t>t_{\max }$, the estimation errors of disturbances converge to zero. Therefore, the errors $\sigma _{i,\,j}$ are bounded. If $\max \left\{ \left| {e_{P1,i} } \right| ,\,\left| {\xi _{2,i} } \right| ,\left| {\xi _{3,i} } \right| ,\left| {\xi _{4,i} } \right| ,\left| {e_{\psi 2} } \right| ,\left| {\xi _{2\psi } } \right| \right\} \le 1$, then $\dot{L}\le B$, where B is a bounded constant. If $\max \left\{ \left| {e_{P1,i} } \right| ,\left| {\xi _{2,i} } \right| ,\left| {\xi _{3,i} } \right| ,\left| {\xi _{4,i} } \right| ,\left| {e_{\psi 2} } \right| ,\left| {\xi _{2\psi } } \right| \right\} >1$ because $2+\tau <2$ and $2-r_2 <2$, then $\dot{L}\le KL+B$, where K is a bounded constant. Thus,

$$\begin{aligned} \dot{L}\le KL+B. \end{aligned}$$

(a3)

Reference [29] proves that the system state in (a2) will not escape to infinite in any FT.

According to the two stages of analysis, the proof of the FT stability is completed. $\square$