1 Introduction

With the developments of integrated circuits and the advances in the computing ability of processors promoting the development of the unmanned helicopter airborne hardware system significantly, the autonomous flight technology of the unmanned helicopter has attracted more and more attention [1, 9, 11, 14, 19, 28, 36]. Compared with full-size manned helicopters, unmanned helicopters can be made much smaller in size, which can greatly reduce the cost of industrial production. Moreover, small-scale unmanned helicopters can replace full-size manned helicopters in carrying out potentially life-threatening tasks, such as monitoring of active volcanoes, forest fire-fighting, and topographic surveys of remote areas, completely eliminating the potential risks borne by human pilots. In addition, compared with fixed-wing unmanned aerial vehicles (UAVs), an unmanned helicopter has unique advantages. For example, it does not need any runways used to take off or land, because it has the maneuver ability of vertical takeoff and landing. Besides, it can hover in the air and move in all directions in the Cartesian space. In spite of the above-described advantages of small-scale unmanned helicopters, they are much more difficult to be controlled for autonomous flight, because they are more vulnerable to aerodynamic interferences [26].

Although the autonomous flight of a small-scale unmanned helicopter has been basically achieved [11, 29, 32, 35, 38], the performances of those controllers are relatively conservative compared to a skilled pilot. For instance, basic attitude control has been achieved by [32] and [38], but the position control is not considered in both two literatures. In addition, the controller in [32] is designed based on a linear model, which is only effective in the vicinity of the equilibrium point, and the control performance is relatively conservative in [38] because the experiment is implemented on a test bed and the effect of the test bed is disregarded without any serious analysis. Thus, it is still a challenging problem to design a nonlinear controller with high tracking accuracy and strong robustness, which should fully consider the nonlinear characteristics of the unmanned helicopter and is supposed to be comparable with skilled pilots. The small-scale unmanned helicopter is a high-order complicated model with high nonlinearity and strong coupling among different channels. How to deal with the nonlinearity and the coupling is a very critical issue in the process of controller design. Since obtaining its exact nonlinear model is very difficult, many researchers use PID control method to design flight control system for an autonomous helicopter [11, 29, 36]. However, the selection of control parameters mainly relies on the designers’ experiences, resulting in a relatively cumbersome adjustment process. And what is worse, the robustness of the PID controller is quite weak in flight environments with external interferences, e.g., wind gusts. In addition, many controllers are designed based on the linearized model around the equilibrium point in which dozens of nonlinear characteristics are ignored to obtain simple linearization controllers [9, 10, 19, 20]. But the linear controllers are effective only when the unmanned helicopter flies near the balanced point. The control performance may be severely degraded, even leading to the instability of the closed-loop system, when the helicopter states deviate from the equilibrium point. As a result, linearization has brought about the application conditions of the controller, and the flight envelope of the unmanned helicopter is restricted. Although combining gain scheduling technique and the linearization method based on multi operating points can expand the flight envelope of the unmanned helicopter [10] to a certain degree, it needs a number of tedious calculations and extra experiments.

In contrast, nonlinear control techniques are more suitable for control systems with large flight envelope, and plentiful research achievements have been brought out in recent years [6, 7, 17, 24, 28, 33, 34, 37, 41]. Second-order sliding mode control is adopted to alleviate the chattering phenomena of the traditional sliding model method in both [7] and [34]. In [7], the multivariable super twisting control is combined with backstepping control based on a sliding mode observer to control an unmanned helicopter. While in [34], the second-order sliding mode control method is combined with an extended state observer to tackle the tracking problem of small-scale helicopters. Unfortunately, like the most of the previous nonlinear controllers [13, 24, 28, 33, 41], the second-order sliding mode flight controller in [34] is constructed under the hypothesis of two-timescale separation, which assumes that the response of the outer-loop is much slower than that of the inner-loop. But this assumption is probably not established when the maneuver of the unmanned helicopter is large. A novel attitude kinematics representation using a rotation matrix is proposed in [31] to transform the nonlinear model into a strict feedback form for applying backstepping control without the assumption of two-timescale separation. However, neither internal uncertainties nor external uncertainties are taken into account. Considering the advantages of the NNs with the ability of online learning over the NNs trained offline [30], the researches in [4] use NNs to learn the dynamics of an UAV online while assuming full state feedback. To further remove the assumption, Dierks [5] proposes a novel virtual control scheme with a NN observer. The authors in [5, 16, 27, 39] all adopt NNs with online learning algorithms to compensate small coupling forces and aerodynamic uncertainties under backstepping control framework. Unfortunately, so many updating laws of weight matrices may lead to the calculation explosion of the airborne computer, making the control system hard to be applied in real flights. Calvo-Rolle [3] proposes an adaptive inverse control using an online learning algorithm for system identification, and the advantage of the method is that it has the ability to deal with non-stationary environments. Unfortunately, it needs \(K\times (K+J)\) (K is the number of hidden neurons and J is the number of outputs) times of iterative calculation at each sampling point to obtain the optimal weights, and the calculation is obviously not small. In [15], the researchers combine backstepping control and NNs to design a flight control system and propose a new identifier which can identify the inertial matrix asymptotically. However, the flapping dynamics of the main rotor is totally neglected, which may lead to the deterioration of control performance. Besides, the inertial matrix identifier has nine adaptive laws, which results in huge computation workload despite using an optimized updating law. Zou [42] also investigates the tracking problem of an unmanned helicopter by combining backstepping control approach with an adaptive RBFNN. Simulations show the effectiveness of the method, nevertheless, the fact that the weights of the adaptive RBFNN are directly estimated increases the computational burden greatly and hinders the implementation of the approach. To surmount this difficulty, an efficient learning algorithm with less learning parameters is introduced in [18, 22, 23] where not only the computation amount is reduced but also good control performances are obtained.

The purpose of this paper is to propose a robust and nonlinear adaptive backstepping controller which needs no assumptions about multi-timescale separation and has a low computational complexity so as to facilitate the practical implementation. Inspired by [18, 21,22,23], new adaptive RBFNNs with online learning algorithms of the least parameters are designed in this paper to enhance the robustness of the flight control system of an unmanned helicopter. In order to complete the backstepping control design smoothly, the attitude kinematics representation proposed in [31] is used. And to avoid complex analytical solutions, the time derivatives of some virtual controls in this paper are calculated through command filters [8]. The main highlights of this paper are summarized as follows: First, a novel identifier is designed to estimate the mass of the unmanned helicopter, which is considered as a constant by many previous researches [31, 35, 37, 39]. However, the mass of an unmanned helicopter decreases with the reduction of fuel in real flights. Furthermore, when an unmanned helicopter performs transport tasks, the mass changes with loading or unloading of goods in the air. The mass is a very important model parameter for the control method based on model and a good adaptive law for the mass can effectively improve the robustness of the controller. Second, unlike the prior literatures [5, 16, 27, 39], an improved neural network learning algorithm with the least parameters is proposed to reduce computation load [21]. With the increase in the neurons in the hidden layer, the number of the updating laws proposed in [5, 16, 27, 39] increases exponentially, resulting in a heavy computational load. For the learning algorithm of the least parameters introduced in this paper, it only needs to estimate one parameter, i.e., the square of the induced Euclidean norm of an ideal weight matrix.

The remaining parts of this paper are arranged as follows: Some preliminaries are introduced in Sect. 2. Section 3 describes the complete nonlinear model of a small-scale unmanned helicopter. The detailed design process of the nonlinear adaptive controller including the stability analysis is elaborated in Sect. 4. Two simulations and some discussions are carried out in Sect. 5. At last, Sect. 6 concludes the paper.

2 Preliminaries

2.1 Mathematical notation

In this paper, the operands \(\left\| \cdot \right\| \) and \(\left\| \cdot \right\| _2\) denote Euclidean norm of column vectors and induced Euclidean norm of matrices, respectively; the notation \(\left| \cdot \right| \) represents absolute value for real numbers; the abbreviations \(c(\cdot )\) and \(s(\cdot )\) indicate the trigonometric function \(\cos (\cdot )\) and \(\sin (\cdot )\), respectively; \({\lambda _{\min } (\cdot )}\) is the minimum eigenvalue of a matrix; \(\hbox {exp}(\cdot )\) means an exponential function.

Fig. 1
figure 1

Modified RBFNN structure adopted in this paper

Full size image

2.2 Modified RBFNNs

RBFNNs can approximate any nonlinear function with an arbitrary precision and have a fast learning convergence speed. A three-layered architecture of a modified RBFNN is illustrated in Fig. 1, whose output is different from the traditional RBFNN, where \(\hat{\varGamma }\) is the estimation of \(\varGamma \) which is defined by \(\varGamma =\Vert W\Vert _2^2\) and the output is \(\hat{f} \left( x \right) = \hat{\varGamma } \left\| H \right\| _2^2\). There are N, K, and M nodes in the input layer, the hidden layer, and the output layer, respectively, where N, K, and M are positive integers. And \(W \in R^{K \times M}\) is the idealized weight matrix between the hidden layer and the output layer; \(H\left( x \right) = \left[ {h_1 \left( x \right) ,h_2 \left( x \right) ,\ldots ,h_K \left( x \right) } \right] ^T \in R^K\). \(h_j \left( x \right) \) is the Gaussian basis function as the following form

$$\begin{aligned} h_j \left( x \right) = \exp \left( { - \dfrac{1}{{2b_j }}\left\| {x - c_j } \right\| ^2 } \right) ,\begin{array}{*{20}c} {} &{} {j = 1,2,\ldots , K}, \\ \end{array} \end{aligned}$$
(1)

where \(c_j = [c_{1j} ,c_{2j} ,\ldots ,c_{Nj} ]^T \in R^N\) and \(b_j \in R\) are the center and the width of the radial basis function \(h_j \left( x \right) \).

The advantage of this modified RBFNN is that there is only one parameter, \(\hat{\varGamma }\), which needs to be updated, lessening the calculation burden dramatically. More details about the modified RBFNN learning algorithm are presented in Remarks 2 and 3.

3 Helicopter model

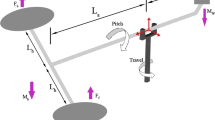
A nonlinear small-scale unmanned helicopter dynamics model has been developed using the first principles modeling approach, including twenty states and four inputs. The system states and the control inputs are summarized in Table 1. Two reference frames, i.e., the body frame and the inertial frame, are depicted in Fig. 2. The small-scale unmanned helicopter can be described by a hybrid nonlinear model, which is mainly composed of the following three parts: fuselage rigid body kinematics and dynamics, main rotor dynamics, and simplified yaw dynamics.

Table 1 Physical descriptions of states and inputs
Full size table

3.1 Fuselage rigid body kinematics and dynamics

The nonlinear fuselage rigid body kinematics and dynamics can be derived by Newton–Euler equation [31] as follows

$$\begin{aligned}&\dot{P}= V, \end{aligned}$$
(2)
$$\begin{aligned}&m\dot{V}= R(\varTheta )F + mgE_z, \end{aligned}$$
(3)
$$\begin{aligned}&\dot{R}(\varTheta )= R(\varTheta )Sk(\omega ), \end{aligned}$$
(4)
$$\begin{aligned}&I\dot{\omega }= - \omega \times I\omega + M, \end{aligned}$$
(5)

where \(P=[x, y, z]^T\) and \(V = [v_x ,v_y ,v_z ]^T\) are the position vector and the linear velocity vector of the centre of gravity of the unmanned helicopter in the inertial frame, respectively; m is the mass of the helicopter; \(\varTheta = [\phi ,\theta ,\psi ]^T\) denotes the attitude angle vector of the fuselage; \(R(\varTheta )\) indicates the transform matrix from the body frame to the inertial frame, specified by

$$\begin{aligned} \begin{array}{l} R(\varTheta )\\ \quad = \left[ {\begin{array}{*{20}c} {c(\theta \psi ) } &{} {s (\phi \theta ) c(\psi ) - c(\phi ) s(\psi ) } &{} {c(\phi \psi ) s(\theta ) + s(\phi \psi ) } \\ {c(\theta ) s(\psi ) } &{} {s (\phi \theta \psi ) + c(\phi \psi ) } &{} {c(\phi ) s(\theta \psi ) -s(\phi ) c(\psi ) } \\ { - s(\theta ) } &{} {s( \phi ) c(\theta ) } &{} {c( \phi \theta ) } \\ \end{array}} \right] \end{array}, \end{aligned}$$
Fig. 2
figure 2

Sketch of the body frame and the inertial frame

Full size image

where \(c(\phi \theta \psi )=c(\phi )c(\theta )c(\psi )\), \(s(\phi \theta \psi )=s(\phi )s(\theta )s(\psi )\), and so on; \(E_z\) is a unit vector along the z axis of the inertial frame, i.e., \(E_z=[0,0,1]^T\); \(\omega =[p,q,r]^T\) denotes the angular velocity vector of the unmanned helicopter represented in the body frame; \(Sk(\omega )\) is the skew-symmetric matrix defined as

$$\begin{aligned} Sk(\omega ) = \left[ {\begin{array}{*{20}c} 0 &{} { - r} &{} q \\ r &{} 0 &{} { - p} \\ { - q} &{} p &{} 0 \\ \end{array}} \right] ; \end{aligned}$$
(6)

\(I=diag\{ I_{x} ,I_{y} ,I_{z} \}\) is the inertial matrix; F and M denote all the external forces except the gravity and all the external moments expressed in the body frame, respectively.

To be more exact, F and M can be, respectively, specified by

$$\begin{aligned} F = \left[ {\begin{array}{*{20}c} {F_x } \\ {F_y } \\ {F_z } \\ \end{array}} \right] = \left[ {\begin{array}{*{20}c} {X_{mr} + X_{fd} } \\ {Y_{mr} + Y_{fd} + Y_{vt} } \\ {Z_{mr} + Z_{fd} } \\ \end{array}} \right] \end{aligned}$$
(7)

and

$$\begin{aligned} M = \left[ {\begin{array}{*{20}c} {M_x } \\ {M_y } \\ {M_z } \\ \end{array}} \right] = \left[ {\begin{array}{*{20}c} {L_{mr} + L_{vt} } \\ {M_{mr} } \\ N_{mr} \\ \end{array}} \right] , \end{aligned}$$
(8)

where \(X_{mr}, Y_{mr}, Z_{mr}\) and \(X_{fd}, Y_{fd}, Z_{fd}\) are, respectively, the components of the main rotor force and the fuselage drag force along the body frame x-, y-, and z-axes; \(Y_{vt}\) and \(L_{vt}\) are the vertical tail force and moment; \(L_{mr}, M_{mr}\), and \(N_{mr}\) are the components of the main rotor moment along the body frame x-, y-, and z-axes. Because the yaw control in manual flight of a small-scale helicopter is very challenging due to the high sensitivity to the control input and the strong coupling effect between the main rotor and the tail rotor, an angular vector control system (AVCS) is usually equipped to facilitate the pilot for heading hold. Thus, the forces and moments of the tail rotor can be disregarded.

It is known that the dominant forces and moments are mainly produced by the main rotor. According to [2], disregarding the effect of the flapping angles and assuming there exist no twists at the blades of the main rotor, the thrust of the main rotor can be expressed as follows

$$\begin{aligned} \left\{ \begin{array}{l} T = (w_b - v_{im} )\dfrac{{\rho \varOmega R^2 C_{l\alpha } b_m c_m }}{4}, \\ v_{im} ^2 = \sqrt{(\dfrac{{v_{int}^2 }}{2})^2 + (\dfrac{T}{{2\rho \pi R^2 }})^2 } - \dfrac{{v_{int}^2 }}{2}, \\ v_{int}^2 = \bar{u}^2 + \bar{v}^2 + {\bar{w}}({\bar{w}} - 2v_{im} ), \\ \end{array} \right. \end{aligned}$$
(9)

with \(w_b = {\bar{w}} +a \bar{u}-b \bar{v} +\dfrac{2}{3}\varOmega R\theta _{col}, \theta _{col} = K_{col} K_a \delta _{col}\), where \(v_{int}\) is an intermediate variable in the calculation process of the main rotor thrust; \(v_{im}\) indicates the induced velocity of the main rotor; \(w_b\) is the resultant velocity at the main rotor in vertical direction; \(b_m\) denotes the number of the main blades; \(c_m\) is the chord length of the main blade; \(\theta _{col}\) is the collective pitch angle controlled by the collective actuator; \(V_{w}=[u_{w}, v_{w}, w_{w}]^T\) denotes the wind velocity vector in the body frame; \(\bar{u} = u - u_{w}\), \(\bar{v} = v - v_{w}\), \({\bar{w}} = w - w_{w}\); \(K_{col}\) is the linkage gain from the collective actuator to the main blade; \(\delta _{col}\) indicates the control signal of the collective actuator. Subsequently, the force components and the moment components generated by the main rotor can be written as follows

$$\begin{aligned} \left\{ \begin{array}{ll} X_{mr} &{}= - T\sin (a), \\ Y_{mr} &{}= T\sin (b), \\ Z_{mr} &{}= - T\cos (a) \cos (b), \\ L_{mr} &{}= (k_\beta + TH_{mr} )\sin (b), \\ M_{mr} &{}= (k_\beta + TH_{mr} )\sin (a), \\ \end{array} \right. \end{aligned}$$
(10)

where \(k_\beta \) and \(H_{mr}\) denote the main rotor spring constant and the vertical distance between the main rotor hub and the centre of gravity, respectively.

The fuselage drag forces are calculated [1, 12] as follows

$$\begin{aligned}&X_{fd} = \left\{ {\begin{array}{ll} { - 0.5\rho S_{fux} \bar{u}v_{im} }, &{}\quad \ \text {if}\quad {\left| {\bar{u}} \right| \le v_{im} }; \\ { - 0.5\rho S_{fux} \bar{u}\left| {\bar{u}} \right| }, &{}\quad \ \text {if}\quad {\left| {\bar{u}} \right| > v_{im} }. \end{array}} \right. \end{aligned}$$
(11)
$$\begin{aligned}&Y_{fd} = \left\{ {\begin{array}{ll} { - 0.5\rho S_{fuy} \bar{v}v_{im} }, &{}\quad \ \text {if}\quad {\left| {\bar{v}} \right| \le v_{im} }; \\ { - 0.5\rho S_{fuy} \bar{v}\left| {\bar{v}} \right| }, &{}\quad \ \text {if}\quad {\left| {\bar{v}} \right| > v_{im} }. \end{array}} \right. \end{aligned}$$
(12)
$$\begin{aligned}&Z_{fd} = - 0.5\rho S_{fuz} \left( {{\bar{w}} - v_{im} } \right) \left| {{\bar{w}} - v_{im} } \right| , \end{aligned}$$
(13)

where \(S_{fux}\), \(S_{fuy}\), and \(S_{fuz}\) are longitudinal, lateral, and vertical effective fuselage areas, respectively.

The vertical tail force is defined by

$$\begin{aligned} Y_{vt} = \left\{ {\begin{array}{ll} { - 0.5\rho C_{l\alpha ,vt} S_{vt} v_{vt} \left| {\bar{u}} \right| }, &{}\quad \text {if}\quad {\left| {v_{vt} } \right| \le 0.3\left| {\bar{u}} \right| }; \\ { - 0.5\rho S_{vt} v_{vt} \left| {v_{vt} } \right| }, &{}\quad \text {if}\quad {\left| {v_{vt} } \right| > 0.3\left| {\bar{u}} \right| }. \\ \end{array}} \right. \end{aligned}$$
(14)

Here \(v_{vt} = \bar{v} - v_{it} - rD_{vt}\), and \(v_{it}\) denotes the induced velocity of the tail rotor. Then the vertical tail moment is given by \(L_{vt}=Y_{vt}H_{vt}\), where \(H_{vt}\) means the vertical distance between the vertical tail and the centre of gravity.

Remark 1

In spite of the fact that the fuselage drag forces and the vertical tail force and moment are taken into account in the modeling process of the small-scale unmanned helicopter to improve the precision of the model, they are omitted in the design procedure of the flight control system for simplicity, testing the robustness of the controller to some extent.

3.2 Main rotor dynamics

Rotor flapping dynamics is a unique feature of a small-scale unmanned helicopter. The dynamics of the stabilizer mounted on the main rotor to facilitate manual operation should also be considered. Then the main rotor flapping dynamics and the stabilizer flapping dynamics are modeled, respectively, as follows

$$\begin{aligned}&\begin{array}{ll} \left[ \begin{array}{l} {\dot{a}} \\ {\dot{b}} \\ \end{array} \right] &{}= \dfrac{{\gamma ^m \varOmega }}{{(\gamma ^m )^2 + 64}} \left[ {\begin{array}{*{20}l} { - \dfrac{{4k_\beta }}{{I_\beta \varOmega ^2 }} - 8} &{} {\gamma ^m - \dfrac{{32k_\beta }}{{\gamma ^m I_\beta \varOmega ^2 }}}\\ {\dfrac{{32k_\beta }}{{\gamma ^m I_\beta \varOmega ^2 }}-\gamma ^m}&{}{ - \dfrac{{4k_\beta }}{{I_\beta \varOmega ^2 }} - 8}\\ \end{array}} \right] \left[ {\begin{array}{*{20}l} a\\ b\\ \end{array}} \right] \\ &{}\quad - \left[ \begin{array}{l} q \\ p \\ \end{array} \right] + \dfrac{{\gamma ^m \varOmega }}{{(\gamma ^m )^2 + 64} } \left[ {\begin{array}{*{20}c} { - \gamma ^m } &{} 8 \\ 8 &{} {\gamma ^m } \\ \end{array}} \right] \left[ \begin{array}{l} B_1^m + K_{mix} d \\ A_1^m + K_{mix} c \\ \end{array} \right] , \\ \end{array} \nonumber \\\end{aligned}$$
(15)
$$\begin{aligned}&\begin{array}{ll} \left[ \begin{array}{l} \dot{c} \\ \dot{d} \\ \end{array} \right] &{}= \dfrac{{\gamma ^s \varOmega }}{{(\gamma ^s )^2 + 64}} \left[ {\begin{array}{*{20}c} { - 8} &{} {\gamma ^s } \\ {-\gamma ^s } &{} { - 8} \\ \end{array}} \right] \left[ {\begin{array}{*{20}c} c \\ d \\ \end{array}} \right] \\ &{}\quad - \left[ \begin{array}{l} q \\ p \\ \end{array} \right] + \dfrac{{\gamma ^s \varOmega }}{{(\gamma ^s )^2 + 64}} \left[ {\begin{array}{*{20}c} { - \gamma ^s } &{} 8 \\ 8 &{} {\gamma ^s } \\ \end{array}} \right] \left[ \begin{array}{l} B_1^s \\ A_1^s \\ \end{array} \right] , \\ \end{array} \end{aligned}$$
(16)

where (a, b) and (c, d) are the flapping angles of the main rotor and the stabilizer in the longitudinal direction and the lateral direction, respectively; \((A_1^m ,B_1^m )\) and \((A_1^s ,B_1^s )\) indicate the cyclic pitch angles of the main blade and the stabilizer, determined by pitch angles of swash plate as follows

$$\begin{aligned} \left\{ \begin{array}{l} A_1^m = K_{bel} A_1, \\ B_1^m = K_{bel} B_1, \\ A_1^s = K_{sb} A_1, \\ B_1^s = K_{sb} B_1, \end{array} \right. \end{aligned}$$
(17)

where \(K_{bel}\) and \(K_{sb}\) are the mechanical gains from the swash plate to the main blade and the stabilizer, respectively; \(A_1 \) and \(B_1\) denote the pitch angles of the swash plate in longitudinal and lateral directions, respectively, which can be calculated from

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {A_1 = K_{lon} K_a \delta _{lon} + \theta _{lon0} }, \\ {B_1 = K_{lat} K_a \delta _{lat} + \theta _{lat0} }, \\ \end{array}} \right. \end{aligned}$$
(18)

\(\theta _{lon0}\) is the initial tilting angle in the longitudinal direction and \(\theta _{lat0}\) is the initial tilting angle in the lateral direction; \(K_a\) denotes the gain of the actuators; \(K_{lon}\) and \(K_{lat}\) are the linkage gains from the elevator actuator and the aileron actuator to the swash plate, respectively.

Fig. 3
figure 3

Diagram of the nonlinear adaptive backstepping control system based on RBF neural networks

Full size image

3.3 Yaw dynamics

The fundamental yaw dynamics can be written as follows

$$\begin{aligned} \dot{r} = N_r r + N_{ped} \bar{\delta } _{ped}, \end{aligned}$$
(19)

where \(N_r\) and \(N_{ped}\) are model parameters; \(\bar{\delta } _{ped}\) is the output of the AVCS mentioned in Sect. 3.1, which is composed of a low-cost rate gyro and an embedded PI controller. Therefore, \(\bar{\delta } _{ped}\) can be further expressed as follows

$$\begin{aligned} \bar{\delta } _{ped} = k_P\left( K_c\delta _{ped}-r \right) +k_I\int \left( K_c\delta _{ped}-r \right) \,dt, \end{aligned}$$
(20)

where \(k_P\) and \(k_I\) are the proportional coefficient and the integral coefficient of the embedded PI controller, respectively.

Then, the integrated yaw dynamics including the dynamics of the AVCS can be modeled as follows

$$\begin{aligned} \left\{ {\begin{array}{*{20}l} {\dot{\delta } _{ped,{\mathop {\mathrm{int}}} } = K_c \delta _{ped} - r}, \\ {\dot{r} = \left( {N_r - N_1 } \right) r + N_2 \delta _{ped,{\mathop {\mathrm{int}}} } + N_1 K_c \delta _{ped} }, \\ \end{array}} \right. \end{aligned}$$
(21)

where \(N_1=N_{ped}k_P\); \(N_2=N_{ped}k_I\).

4 RBF neural networks-based nonlinear adaptive backstepping control design

The design of a robust and nonlinear adaptive flight controller is conducted in this section. The flight control system is divided into three parts: longitudinal–lateral subsystem, heave subsystem, and heading subsystem. Its structure diagram is portrayed in Fig. 3. The control design for longitudinal–lateral subsystem is described in Sect. 4.1; the design procedures for heave subsystem and heading subsystem are presented in Sects. 4.2 and 4.3, respectively; the stability analysis of the closed-loop system is revealed in Sect. 4.4, in which the relative updating laws are also derived by means of the Lyapunov stability theory.

4.1 Longitudinal–lateral subsystem

Since the dominating force is the thrust component along the z axis of the body frame, for simplicity, \(X_{mr}\) and \(Y_{mr}\) are disregarded and included in the lumped disturbance, which also contains other neglected forces in the design procedure. Generally, it can be assumed that \(c(a) \approx 1\) and \(c(b) \approx 1\) because the flapping angles are ordinarily very small. Then the external force F is divided into the following two parts

$$\begin{aligned} F = \underbrace{\left[ {0,0, - T } \right] ^T }_{F_0 } + \underbrace{\left[ {d_x ,d_y ,d_z } \right] ^T }_{d_F }, \end{aligned}$$
(22)

where \(d_F\) is the lumped disturbance resulting from other neglected forces, such as the fuselage drag force and the vertical tail force. Similarly, assuming \(s(a) \approx a\) and \(s(b) \approx b\), the external torque exerted on the unmanned helicopter can be written as

$$\begin{aligned} M= & {} \underbrace{\left[ {\left( {k_\beta + T H_{mr} } \right) b,\left( {k_\beta + T H_{mr} } \right) a,0} \right] ^T }_{M_0}\nonumber \\&+\, \underbrace{\left[ {d_p ,d_q ,d_r } \right] ^T}_{d_M }, \end{aligned}$$
(23)

where \(d_M\) is the lumped disturbance produced by other neglected torques. The flapping dynamics composed of Eqs. (15) and (16) is too complicated for control design. For convenience, under the assumption of \(\dot{c} \approx 0\) and \(\dot{d} \approx 0\), the flapping dynamics is reduced to the following lumped form

$$\begin{aligned} {\dot{\beta } _m = A_m \beta _m + A_\omega \omega _2 + B\delta _{cyc} }, \end{aligned}$$
(24)

where \(\beta _m=[a, b]^T\); \(\omega _2=[p, q]^T\); \(\delta _{cyc}=[\delta _{lat}, \delta _{lon}]^T\); \(A_m\) and \(A_\omega \) are the coefficient matrices calculated from Eqs. (15) and (16).

Input formulas (22) and (23) into the fuselage rigid body kinematics and dynamics (2)–(5), one can extract the longitudinal–lateral subsystem as follows

$$\begin{aligned}&{\dot{P}_2 = V_2 } , \end{aligned}$$
(25)
$$\begin{aligned}&{\dot{V}_2 = \dfrac{1}{m}R_2 (d_z - T) + \dfrac{1}{m}R_N d_{\bar{F}} } , \end{aligned}$$
(26)
$$\begin{aligned}&{\dot{R}_2 = R_M \omega _2 } \end{aligned}$$
(27)
$$\begin{aligned}&{\dot{\omega } _2 = R_\omega \omega _2 + R_\beta \beta _m + d_{\bar{M}} } , \end{aligned}$$
(28)
$$\begin{aligned}&{\dot{\beta } _m = A_m \beta _m + A_\omega \omega _2 + B\delta _{cyc} } , \end{aligned}$$
(29)

where \(P_2 = [x,y]^T \); \(V_2 = [v_x ,v_y ]^T \); \(R_2 = [R_{13} ,R_{23} ]^T \);

\(d_{\bar{F}} = [d_x ,d_y ]^T \); \(R_N = \left[ {\begin{array}{*{20}c} {R_{11} } &{} {R_{12} } \\ {R_{21} } &{} {R_{22} } \\ \end{array}} \right] \); \(R_M = \left[ {\begin{array}{*{20}c} { - R_{12} } &{} {R_{11} } \\ { - R_{22} } &{} {R_{21} } \\ \end{array}} \right] \);

\(d_{\bar{M}} = [d_p ,d_q ]^T + \bar{d}_T H_{mr} \left[ {\begin{array}{*{20}c} 0 &{} 1 /I_x \\ 1 /I_y&{} 0 \\ \end{array}} \right] \beta _m \);

\(R_\omega = \left[ {\begin{array}{*{20}c} 0 &{} r(I_y - I_z ) /I_x\\ r(I_z - I_x ) /I_y&{} 0 \\ \end{array}} \right] \);

\(R_\beta = (k_\beta + T_{int} H_{mr} )\left[ {\begin{array}{*{20}c} 0 &{} 1 /I_x\\ 1 / I_y&{} 0 \\ \end{array}} \right] \); \(R_{ij}\) indicates the element in the \(i\hbox {th}\) row and the \(j\hbox {th}\) column of the transformation matrix \(R(\varTheta )\); T is expressed as

$$\begin{aligned} T = {T_{int} } + \bar{d}_T, \end{aligned}$$
(30)

where \(T_{int}\) is the intermediate control in the heave subsystem and \(\bar{d}_T\) is the lumped disturbance.

Step 1 Define \(P_e = P_2 - P_{2r} \), and differentiate \(P_e\) with respect to the time variable to get

$$\begin{aligned} \dot{P}_e = V_2 - \dot{P}_{2r}. \end{aligned}$$
(31)

By defining the horizontal velocity error as \(V_e = V_2 - \alpha _P \), and substituting it into Eq. (31), one can obtain

$$\begin{aligned} \dot{P}_e = V_2 - \dot{P}_{2r} = V_e + \alpha _P - \dot{P}_{2r}, \end{aligned}$$
(32)

where \(\alpha _P\) is the pseudocontrol. To stabilize the horizontal position error dynamics (32), the pseudocontrol is chosen as

$$\begin{aligned} \alpha _P = - K_P P_e + \dot{P}_{2r}, \end{aligned}$$
(33)

where \(K_P\) is a positive definite diagonal matrix. Applying the pseudocontrol (33) into equation (32), the horizontal position error dynamics becomes

$$\begin{aligned} \dot{P}_e = V_e - K_P P_e. \end{aligned}$$
(34)

Now, define the Lyapunov function candidate for \(P_e\) as follows

$$\begin{aligned} L_P = \dfrac{1}{2}P_e ^T P_e. \end{aligned}$$
(35)

Differentiating (35) and substituting (34) into the differential equation of (35) yield

$$\begin{aligned} \dot{L}_P \le - \lambda _{\min } \left( {K_P } \right) \left\| {P_e } \right\| ^2 + P_e ^T V_e. \end{aligned}$$
(36)

Step 2 For convenience, the horizontal translational dynamics (26) can be rewritten as

$$\begin{aligned} \begin{array}{ll} \dot{V}_2= &{} - \dfrac{1}{{\hat{m}}}R_2 T_{int} \\ &{}+ \underbrace{\dfrac{1}{{\hat{m}}}R_2 \left( {T - \bar{d}_T } \right) + \dfrac{1}{m}(R_2 d_z + R_N d_{\bar{F}} - R_2 T)}_{\Delta _F }, \end{array} \end{aligned}$$
(37)

where \(\hat{m}\) is the estimation of the unmanned helicopter’s mass, which is derived by the adaptive law (69e) presented in Sect. 4.4. \(\Delta _F\) denotes the lumped disturbance. Then, the time derivative of \(V_e\) can be denoted as follows

$$\begin{aligned} \dot{V}_e = - \dfrac{1}{{\hat{m}}}(R_e + \alpha _V )T_{int} + K_P \dot{P}_e - \ddot{P}_{2r} + \Delta _F, \end{aligned}$$
(38)

where \(\Delta _F = W_1 ^T H_1 (V_2 ) + \sigma _1 (V_2 )\); \(W_1\in R^{K_1\times 2 }\) is the ideal neural network weight matrix; \(K_1\) is the number of the nodes in the hidden layer; \(\sigma _1(V_2 ) \in R^{2} \) is the bounded neural network approximation error, and \(H_1 (V_2 )\in R^{ K_1}\) is the Gaussian basis function of \(V_2\); \(R_e\) is specified by \(R_e = R_2 - \alpha _V \).

Subsequently, to stabilize the horizontal velocity error dynamics (38), the pseudocontrol \(\alpha _V\) is designed as

$$\begin{aligned} \begin{array}{ll} \alpha _V =&{} \dfrac{{\hat{m}}}{{T_{int} }}\left( { K_V V_e + P_e + K_P \dot{P}_e -\ddot{P}_{2r}}\right) \\ &{} + \dfrac{{\hat{m}}}{{2T_{int} \varepsilon _1 ^2 }}V_e \hat{\varGamma } _1 H_1 ^T (V_2 )H_1 (V_2 ), \end{array} \end{aligned}$$
(39)

where \(K_V\) is a positive definite diagonal matrix and \(\varepsilon _1\) is a designed positive constant; \(\hat{\varGamma } _1\) is the estimation of \(\varGamma _1\), which is the square of the induced Euclidean norm about \(W_1\), defined as \(\varGamma _1 = \left\| {W_1 } \right\| _2 ^2 \).

Remark 2

A point worth emphasizing is that in some previous literatures [16, 27, 39] the ideal neural network weight matrix \(W_1\) is directly estimated without any optimization, leading to as many as \(K_1\times 2 \) adaptive laws. With the increase in the nodes in the hidden layer or the output layer, the number of the updating laws grows exponentially, resulting in the calculation explosion of the online embedded computer system. Differently from the foregoing documents, this paper adopts an improved learning algorithm of the least parameters, which compensates the uncertainties utilizing only one parameter to estimate the square of the induced Euclidean norm regarding \(W_1\) indirectly, bringing about a more efficient control system in practical applications. In addition, a sequential flowchart illustrated in Fig. 4 is provided to further explain this algorithm.

Fig. 4
figure 4

Sequential flowchart of the learning algorithm

Full size image

Remark 3

In [18] the dynamic surface control approach is combined with “minimal learning parameters” algorithm for MIMO systems. While in [23] and [22] a reinforcement learning algorithm with less learning parameters is put forward to tackle the adaptive tracking control and fault-tolerant control issue for MIMO discrete-time systems. Although the similar RBFNN is used in [18, 23] and [22], the focus of this paper is to propose an adaptive backstepping controller with a learning algorithm of the least parameters for unmanned helicopters, which is different from the works in the above papers. Moreover, the learning algorithms used here are very different from those in [18, 23] and [22]. What they estimated indirectly in the RBF neural network is the Euclidean norm of unknown weights, which is actually different from the modified adaptive neural network designed in this paper. In order to combine the modified RBFNN and the backstepping control technique, and ensure the asymptotic stability of the whole closed-loop system, it is necessary to estimate the square of the norm of the weights rather than the norm itself and this is the difference in dealing with adaptive neural networks between this paper and the literatures mentioned above.

Then, the Lyapunov function candidate for \(V_e\) is defined by

$$\begin{aligned} L_V = \dfrac{1}{2}V_e ^T V_e. \end{aligned}$$
(40)

Combining Eqs. (38) and (39), one obtains the time derivative of \(L_V\)

$$\begin{aligned} \dot{L}_V= & {} - V_e ^T K_V {V_e } - V_e ^T P_e - \dfrac{1}{{\hat{m}}}T_{int} V_e ^TR_e \nonumber \\&+V_e ^T \sigma _1 (V_2 )+ V_e ^T W_1 ^T H_1 (V_2 ) \nonumber \\&- \dfrac{1}{{2\varepsilon _1 ^2 }} V_e ^T V_e \hat{\varGamma } _1 H_1 ^T (V_2 )H_1 (V_2 ) \nonumber \\\le & {} - \left( {\lambda _{\min } \left( {K_V } \right) - \varsigma _V } \right) \left\| {V_e } \right\| ^2 + V_e ^T \sigma _1 (V_2 ) \nonumber \\&- \left\| {V_e } \right\| \left\| {\sigma _1 (V_2 )} \right\| - \left( {\sqrt{\varsigma _V } \left\| {V_e } \right\| -\dfrac{{\left\| {\sigma _1 (V_2 )} \right\| }}{{2\sqrt{\varsigma _V } }}} \right) ^2\nonumber \\&- V_e ^T P_e - \dfrac{1}{{\hat{m}}}T_{int} V_e ^TR_e + V_e ^T W_1 ^T H_1 (V_2 ) \nonumber \\&- \dfrac{1}{{2\varepsilon _1 ^2 }} V_e ^TV_e \hat{\varGamma } _1 H_1 ^T (V_2 )H_1 (V_2 )+ \dfrac{{\left\| {\sigma _1 (V_2 )} \right\| ^2 }}{{4\varsigma _V }} \nonumber \\\le & {} - \left( {\lambda _{\min } \left( {K_V } \right) - \varsigma _V } \right) \left\| {V_e } \right\| ^2 - V_e ^T P_e \nonumber \\&- \dfrac{1}{{\hat{m}}}T_{int} V_e ^TR_e + V_e ^T W_1 ^T H_1 (V_2 )\nonumber \\&- \dfrac{1}{{2\varepsilon _1 ^2 }} V_e ^T V_e \hat{\varGamma } _1 H_1 ^T (V_2 )H_1 (V_2 )+ \dfrac{{\left\| {\sigma _1 (V_2 )} \right\| ^2 }}{{4\varsigma _V }},\nonumber \\ \end{aligned}$$
(41)

where \(\varsigma _V\) is a constant and \(0< \varsigma _V < \lambda _{\min } \left( {K_V } \right) \).

Step 3 Taking the time derivative of \(R_e\) and combining (27) bring about

$$\begin{aligned} \dot{R}_e = R_M \left( {\omega _e + \alpha _R } \right) - \hat{\dot{\alpha }} _V + \tilde{\dot{\alpha }} _V, \end{aligned}$$
(42)

where \(\omega _e = \omega _2 - \alpha _R \) is the roll-pitch angular velocity error, \(\alpha _R\) is the pseudocontrol. A second-order command filter [8] is used here to estimate the time derivative of \(\alpha _V\) due to the extremely tedious solving process of analytic solution for the time derivative of \(\alpha _V\). \(\hat{\dot{\alpha }} _V\) is the estimation of \(\dot{\alpha } _V \), and \(\tilde{\dot{\alpha }} _V = \hat{\dot{\alpha }} _V - \dot{\alpha } _V \) is the estimation error of the second-order command filter.

Then, design the pseudocontrol \(\alpha _R\) as

$$\begin{aligned} \alpha _R = R_M ^{ - 1} \left( { - K_R R_e + \dfrac{1}{{\hat{m}}}T_{int} V_e + \hat{\dot{\alpha }} _V } \right) , \end{aligned}$$
(43)

where \(K_R\) is a positive definite diagonal matrix.

The Lyapunov function candidate including \(R_e\) is specified by

$$\begin{aligned} L_R = \dfrac{1}{2}R_e ^T R_e. \end{aligned}$$
(44)

Taking the time derivative of \(L_R\) and utilizing Eqs. (42) and (43), it generates

$$\begin{aligned} \dot{L}_R= & {} - R_e ^TK_R R_e + \dfrac{1}{{\hat{m}}}T_{int} R_e ^T V_e \nonumber \\&+ R_e ^TR_M \omega _e + R_e ^T\tilde{\dot{\alpha }} _V \nonumber \\\le & {} - \lambda _{\min } \left( {K_R } \right) \left\| {R_e } \right\| ^2 + \dfrac{1}{{\hat{m}}}T_{int} R_e ^T V_e \nonumber \\&+ R_e ^T R_M \omega _e + R_e ^T \tilde{\dot{\alpha }} _V \nonumber \\\le & {} - \left( {\lambda _{\min } \left( {K_R } \right) - \varsigma _R } \right) \left\| {R_e } \right\| ^2 \nonumber \\&+ \dfrac{1}{{\hat{m}}}T_{int} R_e ^T V_e + R_e ^T R_M \omega _e + \dfrac{{\left\| {\tilde{\dot{\alpha }} _V } \right\| ^2 }}{{4\varsigma _R }}, \end{aligned}$$
(45)

where \(\varsigma _R\) is a constant that satisfies the following constraints: \(0< \varsigma _R < \lambda _{\min } \left( {K_R } \right) \).

Step 4 Because of the much faster response of the main rotor compared with the fuselage, the flapping dynamics is approximated by a steady state equation, which is proved to be acceptable and effective for control design in [40]. Then, the simplified flapping dynamics is denoted by

$$\begin{aligned} \beta _m = - A_m ^{ - 1} \left( {A_\omega \omega _2 + B\delta _{cyc} } \right) . \end{aligned}$$
(46)

With Eq. (46) substituted into (28), the roll-pitch angular velocity dynamics becomes

$$\begin{aligned} \dot{\omega } _2 = \left( {R_\omega - R_\beta A_m ^{ - 1} A_\omega } \right) \omega _2 - R_\beta A_m ^{ - 1} B\delta _{cyc} + d_{\bar{M}}. \end{aligned}$$
(47)

Subsequently, the time derivative of \(\omega _e\) can be rewritten as follows

$$\begin{aligned} \dot{\omega } _e= & {} \left( {R_\omega - R_\beta A_m ^{ - 1} A_\omega } \right) \omega _2 \nonumber \\&- R_\beta A_m ^{ - 1} B\delta _{cyc}+ d_{\bar{M}} - \dot{\alpha } _R, \end{aligned}$$
(48)

where \(d_{\bar{M}} = W_2 ^T H_2 \left( {\omega _2 } \right) + \sigma _2 \left( {\omega _2 } \right) \) is the total torture disturbance, which will be estimated by the RBF neural network learning algorithm of the least parameters indirectly; \(\sigma _2 \left( {\omega _2 } \right) \) is the bounded approximation error. Thus, the actual longitudinal–lateral control is designed as follows

$$\begin{aligned} \delta _{cyc}= & {} - \left( {R_\beta A_m ^{ - 1} B} \right) ^{ - 1} \bigg ( - K_\omega \omega _e - R_M ^T R_e \nonumber \\&- R_\omega \omega _2+ R_\beta A_m ^{ - 1} A_\omega \omega _2+ \hat{ \dot{\alpha }} _R \nonumber \\&- \dfrac{1}{{2\varepsilon _2 ^2 }}\omega _e \hat{\varGamma } _2 H_2 ^T (\omega _2 )H_2 (\omega _2 )\bigg ), \end{aligned}$$
(49)

where \(K_\omega \) is a positive definite diagonal matrix; \(\varepsilon _2\) is a positive number; \(\hat{\varGamma } _2\) is the estimation of \(\varGamma _2\), which is specified by \(\varGamma _2 = \left\| {W_2 } \right\| _2 ^2 \); \(\hat{\dot{\alpha }} _R\) is the estimation of \(\dot{\alpha } _R \) through the command filter.

Then the Lyapunov function candidate containing \(\omega _e\) is selected as

$$\begin{aligned} L_\omega = \dfrac{1}{2}\omega _e ^T \omega _e, \end{aligned}$$
(50)

which gives the time derivative of \(L_\omega \)

$$\begin{aligned} \dot{L}_\omega= & {} -\omega _e ^T K_\omega \omega _e -\omega _e ^T R_M ^T R_e + \omega _e ^T W_2 ^T H_2 \left( {\omega _2 } \right) \nonumber \\&- \dfrac{1}{{2\varepsilon _2 ^2 }}\omega _e ^T \omega _e \hat{\varGamma } _2 H_2 ^T (\omega _2 )H_2 (\omega _2 ) + \omega _e ^Td_\omega \nonumber \\\le & {} - \left( {\lambda _{\min } \left( {K_\omega } \right) - \varsigma _\omega } \right) \left\| {\omega _e } \right\| ^2 \nonumber \\&- \omega _e ^T R_M ^T R_e + \omega _e ^T W_2 ^T H_2 \left( {\omega _2 } \right) \nonumber \\&- \dfrac{1}{{2\varepsilon _2 ^2 }}\omega _e ^T \omega _e \hat{\varGamma } _2 H_2 ^T (\omega _2 )H_2 (\omega _2 )+ \dfrac{{\left\| {d_\omega } \right\| ^2 }}{{4\varsigma _\omega }}, \end{aligned}$$
(51)

where \(0< \varsigma _{\omega } < \lambda _{\min } \left( {K_{\omega } } \right) \); \(d_\omega =\sigma _2 \left( {\omega _2 } \right) + \tilde{\dot{\alpha }} _R\), and \(\tilde{\dot{\alpha }} _R\) is the approximation error of the command filter.

4.2 Heave subsystem

As mentioned in Sect. (4.1), the thrust T in (30) can be rewritten as follows

$$\begin{aligned} T = \underbrace{k_1 w + k_1 k_2 K_a \delta _{col} - k_1 \nu _{i0} }_{T_{int} } + \bar{d}_T, \end{aligned}$$
(52)

where \(k_1 = \dfrac{{\rho \varOmega R^2 C_{l\alpha } b_m c_m }}{4}\); \(k_2 = \dfrac{2}{3}\varOmega R\); \(\bar{d}_T = d_T - k_1 (\nu _{im} - \nu _{i0} )\); \(d_T\) is the disturbance including system uncertainty and external disturbance. Moreover, \(\bar{d}_T\) is given by \( \bar{d}_T = -W_3 ^T H_3(w) \left( w \right) - \sigma _3 \left( w \right) \), where \(W_3 \in R^{K_3}\) and \(\sigma _3(w )\in R \) are the ideal neural network weight matrix and the bounded approximation error.

According to Eqs. (2) and (3), the heave subsystem can be specified by the following form

$$\begin{aligned} \left\{ {\begin{array}{l} {\dot{z} = v_z }, \\ {m\dot{v}_z = - T c(\theta ) c(\phi ) + mg}. \end{array}} \right. \end{aligned}$$
(53)

Substituting Eq. (52) into (53), the heave dynamics can be rewritten as follows

$$\begin{aligned} m\ddot{z} = - c(\theta )c(\phi ) \left( {T_{int} + \bar{d}_T } \right) + mg. \end{aligned}$$
(54)

Then the intermediate control \(T_{int}\) is designed as

$$\begin{aligned} T_{int}= & {} - \dfrac{1}{{c(\theta )c(\phi ) }} \hat{m}\left( {\nu - g} \right) + \dfrac{1}{{2\varepsilon _3 ^2 }}\delta _z\hat{\varGamma } _3 H_3(w) ^T H_3(w),\nonumber \\ \end{aligned}$$
(55)

where \(\hat{m}\) is the estimation of the actual mass; \(\hat{\varGamma } _3\) is the estimation of \(\varGamma _3\), which is specified by \(\varGamma _3 = \left\| {W_3 } \right\| ^2 \); \(\nu \) is specified by \(\nu = \ddot{z}_r - 2k_z \dot{z}_e - k_z ^2 z_e \) and \(\delta _z\) is defined as \(\delta _z = \dot{z}_e + k_z z_e \), with \(z_e=z-z_r\).

Presently the actual heave control can be derived as follows by combining Eqs. (52) and (55)

$$\begin{aligned} \delta _{col}= & {} -\dfrac{{\hat{m}(\nu - g)}}{{k_1 k_2 K_a c(\theta )c(\phi )}} +\, \dfrac{{\nu _{i0} - w}}{{k_2 K_a }} \nonumber \\&-\, \dfrac{1}{{2k_1 k_2 K_a \varepsilon _3 ^2 }}\delta _z \hat{\varGamma } _3 H_3 (w)^T H_3 (w). \end{aligned}$$
(56)

With Eq. (55) substituted into (54), it yields

$$\begin{aligned} m\left( {\ddot{z} - \nu } \right)= & {} \tilde{m}\left( {\nu - g} \right) + \sigma _3(w)c(\theta )c(\phi ) \nonumber \\&+W_3 ^T H_3(w)c(\theta )c(\phi ) \nonumber \\&- \dfrac{1}{{2\varepsilon _3 ^2 }}\delta _z\hat{\varGamma } _3 H_3(w) ^T H_3(w)c(\theta )c(\phi ). \end{aligned}$$
(57)

Through the attentive analysis of \(\nu \) and \(\delta _z\), the following expression can be found

$$\begin{aligned} \left( {\ddot{z} - \nu } \right)= & {} \ddot{z}-\ddot{z}_r + 2k_z \dot{z}_e+k_z ^2 z_e \nonumber \\= & {} \dot{\delta }_z+k_z \delta _z. \end{aligned}$$
(58)

Then, define the Lyapunov function candidate for \(\delta _z\) as follows

$$\begin{aligned} L_z = \dfrac{1}{2}m \delta _z^2. \end{aligned}$$
(59)

With Eqs. (57) and (58) substituted into the time derivative equation of (59), the time derivative of \(L_z\) can be calculated as follows

$$\begin{aligned} \dot{L}_z= & {} - mk_z \delta _z^2 + \tilde{m}\delta _z\left( {\nu - g} \right) \nonumber \\&+ W_3 ^T H_3(w)c(\theta )c(\phi ) \delta _z+ \sigma _3(w)c(\theta )c(\phi ) \nonumber \\&- \dfrac{1}{{2\varepsilon _3 ^2 }}\delta _z^2\hat{\varGamma } _3 H_3(w) ^T H_3(w)c(\theta )c(\phi ) \nonumber \\\le & {} - \left( {mk_z - \varsigma _z } \right) \delta _z^2 + \tilde{m}\delta _z \left( {\nu - g} \right) \nonumber \\&+ W_3 ^T H_3(w) \delta _z c(\theta )c(\phi ) \nonumber \\&- \dfrac{1}{{2\varepsilon _3 ^2 }}\delta _z^2\hat{\varGamma } _3 H_3(w) ^T H_3(w) c(\theta )c(\phi ) \nonumber \\&+ \dfrac{{\left( {\sigma _3(w)c(\theta )c(\phi ) } \right) ^2 }}{{4\varsigma _z }}, \end{aligned}$$
(60)

where \(\varsigma _z\) is a positive number which satisfies the following constraints: \(0< \varsigma _z < k_z \).

4.3 Heading subsystem

In this section, the design of the heading control subsystem is carried out. First, the yaw kinematics can be extracted from the attitude kinematics representation (4) as follows

$$\begin{aligned} \dot{\psi } = \dfrac{{s(\phi )}}{{c(\theta )}}q + \dfrac{{c(\phi )}}{{c(\theta )}}r. \end{aligned}$$
(61)

By defining \(\psi _e = \psi - \psi _r \) and \(r_e = r - \alpha _\psi \), the time derivative of \(\psi _e\) can be expressed by

$$\begin{aligned} \dot{\psi } _e = \dfrac{{s(\phi )}}{{c(\theta )}}q + \dfrac{{c(\phi )}}{{c(\theta )}}\left( {r_e + \alpha _\psi } \right) - \dot{\psi } _r. \end{aligned}$$
(62)

Choose the virtual control \(\alpha _\psi \) as

$$\begin{aligned} \alpha _\psi = \dfrac{{c(\theta )}}{{c(\phi )}}\left( { - k_\psi \psi _e + \dot{\psi } _r - \dfrac{{s(\phi )}}{{c(\theta )}}q} \right) , \end{aligned}$$
(63)

where \(k_\psi \) is a positive number.

Take the time derivative of \(r _e\) and combine Eq. (21) to get

$$\begin{aligned} \dot{r}_e = (N_r - N_1 )r + N_1 K_c \delta _{ped} - \dot{\alpha } _\psi + d_r, \end{aligned}$$
(64)

where \(d_r = N_2 \delta _{ped,{\mathop {\mathrm{int}}}}\), which is to be estimated by the RBFNN through \(d_r = W_4 ^T H_4 (r) + \sigma _4 (r)\); \(\sigma _4 (r)\in R\) indicates the bounded approximation error; \(W_4 \in R^{K_4}\) denotes the ideal weight matrix, and \(K_4\) is the number of the nodes in the hidden layer.

Finally, the actual control is chosen as

$$\begin{aligned} \delta _{ped}= & {} \dfrac{1}{{N_1 K_c }} \bigg ( - k_r r_e - (N_r - N_1 )r - \dfrac{{c(\phi )}}{{c(\theta )}}\psi _e \nonumber \\&- \dfrac{1}{{2\varepsilon _4 ^2 }}r_e \hat{\varGamma } _4 H_4 ^T (r)H_4 (r) + \hat{ \dot{\alpha } }_\psi \bigg ), \end{aligned}$$
(65)

where \(k_r\) and \(\varepsilon _4\) are both positive numbers; \(\hat{\varGamma } _4\) is the estimation of \(\varGamma _4\), while \(\varGamma _4\) is given by \(\varGamma _4 = \left\| {W_4 } \right\| ^2 \).

The Lyapunov function candidate including \(\psi _e\) and \(r_e\) is selected as

$$\begin{aligned} L_\psi = \dfrac{1}{2}\psi _e ^2 + \dfrac{1}{2}r_e ^2. \end{aligned}$$
(66)

Substituting Eq. (63) into (62), (65) into (64), and differentiating (66) yield

$$\begin{aligned} \dot{L}_\psi= & {} - k_\psi \psi _e ^2 - k_r r_e ^2 + r_e \left( {\tilde{ \dot{\alpha } }_\psi + \sigma _4 (r)} \right) \nonumber \\&+\, r_e W_4 ^T H_4 (r) - \dfrac{1}{{2\varepsilon _4 ^2 }}r_e^2 \hat{\varGamma } _4 H_4 ^T (r)H_4 (r) \nonumber \\\le & {} - k_\psi \psi _e ^2 - \left( {k_r - \varsigma _r } \right) r_e ^2 \nonumber \\&+\, r_e W_4 ^T H_4 (r) - \dfrac{1}{{2\varepsilon _4 ^2 }}r_e^2 \hat{\varGamma } _4 H_4 ^T (r)H_4 (r) \nonumber \\&+\, \dfrac{{\left( {\tilde{\dot{\alpha }} _\psi + \sigma _4 (r)} \right) ^2 }}{{4\varsigma _r }}, \end{aligned}$$
(67)

where \(\varsigma _r\) is a constant and \(0< \varsigma _r < k_r \); \(\tilde{\dot{\alpha }} _\psi \) is the estimation error of the command filter.

4.4 Stability analysis

Assumption 1

During the whole process of the autonomous flight, the roll angle and the pitch angle of the unmanned helicopter’s fuselage always satisfy the following constraints

$$\begin{aligned} -\pi /2<\phi<\pi /2,\quad -\pi /2<\theta <\pi /2. \end{aligned}$$
(68)

Assumption 2

The desired trajectories \(P_{2r}(t)\), \(z_{r}(t)\), \(\psi _{r}(t)\), and their second-order time derivatives \(\ddot{P}_{2r}(t)\) and \(\ddot{z}_{r}(t)\) are bounded and continuous.

The relative adaptive laws are designed as the following forms

$$\begin{aligned} \dot{\hat{\varGamma }} _1&= \dfrac{{\zeta _1 }}{{2\varepsilon _1 ^2 }}V_e ^T V_e H_1 ^T (V_2 )H_1 (V_2 ) - \xi _1 \hat{\varGamma } _1 , \end{aligned}$$
(69a)
$$\begin{aligned} \dot{\hat{\varGamma }} _2&=\dfrac{{\zeta _2 }}{{2\varepsilon _2 ^2 }}\omega _e ^T \omega _e H_2 ^T (\omega _2 )H_2 (\omega _2 ) - \xi _2 \hat{\varGamma } _2 , \end{aligned}$$
(69b)
$$\begin{aligned} \dot{\hat{\varGamma }} _3&= \dfrac{{\zeta _3 }}{{2\varepsilon _3 ^2 }}\delta _z^2 H_3 ^T (w)H_3 (w)c(\theta )c(\phi ) - \xi _3 \hat{\varGamma } _3 , \end{aligned}$$
(69c)
$$\begin{aligned} \dot{\hat{\varGamma }} _4&= \dfrac{{\zeta _4 }}{{2\varepsilon _4 ^2 }}r_e ^2 H_4 ^T (r)H_4 (r) - \xi _4 \hat{\varGamma } _4 , \end{aligned}$$
(69d)
$$\begin{aligned} \dot{\hat{m}}&= \gamma \left( {g\delta _z - \nu \delta _z - \eta \hat{m}} \right) , \end{aligned}$$
(69e)

where \(\zeta _i\), \(\varepsilon _i\) and \(\gamma \) are designed positive parameters; \(\xi _i\) and \(\eta \) are small correction parameters which are greater than zero. With the appropriate parameters selected for Eq. (69), the estimation errors \(\tilde{m} = \hat{m} - m\) and \(\tilde{\varGamma } _i = \varGamma _i - \hat{\varGamma } _i\) are bounded (\(i=1,2,3,4\)).

Theorem 1

Under Assumption 1 and Assumption 2, considering a small-scale unmanned helicopter specified by Eqs. (2), (3), (4), (5), (15), (16) and (21), the control inputs (49), (56) and (65) can drive the position and yaw tracking errors to converge to an arbitrarily small compact of the origin asymptotically with the supporting of the updating laws (69a), (69b), (69c), (69d) and (69e). And all the error variables \(P_e\), \(V_e\), \(R_e\), \(\psi _e\), \(\omega _e\), \(z_e\), \(\delta _z\), \(r_e\), \(\tilde{m}\), and \(\tilde{\varGamma } _i\) are guaranteed to be semi-globally uniformly ultimately bounded.

Proof

To prove the stability of the overall closed-loop system, the composite Lyapunov function candidate is defined as follows

$$\begin{aligned} L = L_1 + L_2, \end{aligned}$$
(70)

where \(L_1=L_P + L_V + L_R + L_\omega + L_z + L_\psi \) and \(L_2= \sum \nolimits _{i = 1}^4 {\dfrac{1}{{2\zeta _i }}\tilde{\varGamma } _i ^2 } + \dfrac{1}{{2\gamma }}\tilde{m}^2\). Combining Eqs. (36), (41), (45), (51), (60), and (67), the time derivative of L becomes

$$\begin{aligned} \dot{L}\le & {} - \lambda _{\min } \left( {K_P } \right) \left\| {P_e } \right\| ^2 - \left( {\lambda _{\min } \left( {K_V } \right) - \varsigma _V } \right) \left\| {V_e } \right\| ^2 \nonumber \\&-\, \left( {\lambda _{\min } \left( {K_R } \right) - \varsigma _R } \right) \left\| {R_e } \right\| ^2 \nonumber \\&-\, \left( {\lambda _{\min } \left( {K_\omega } \right) - \varsigma _\omega } \right) \left\| {\omega _e } \right\| ^2 \nonumber \\&-\, \left( {mk_z - \varsigma _z } \right) \delta _z^2 - k_\psi \psi _e ^2 \nonumber \\&-\, \left( {k_r - \varsigma _r } \right) r_e ^2+V_e ^T W_1 ^T H_1 (V_2 ) \nonumber \\&-\, \dfrac{1}{{2\varepsilon _1 ^2 }}V_e ^TV_e \hat{\varGamma } _1 H_1 ^T (V_2 )H_1 (V_2 ) \nonumber \\&+\,\omega _e ^T W_2 ^T H_2 (\omega _2 )+ \tilde{m}\delta _z\left( {\nu - g} \right) \nonumber \\&-\,\dfrac{1}{{2\varepsilon _2 ^2 }}\omega _e ^T\omega _e \hat{\varGamma } _2 H_2 ^T (\omega _2 )H_2 (\omega _2 ) \nonumber \\&+\, W_3 ^T H_3 (w)\delta _zc(\theta )c (\phi )\nonumber \\&-\, \dfrac{1}{{2\varepsilon _3 ^2 }}\delta _z^2\hat{\varGamma } _3 H_3 ^T (w)H_3 (w)c(\theta )c (\phi ) \nonumber \\&+\, r_e W_4 ^T H_4 (r) - \dfrac{1}{{2\varepsilon _4 ^2 }}r_e^2 \hat{\varGamma } _4 H_4 ^T (r)H_4 (r) \nonumber \\&+\, \dfrac{{\left\| {\sigma _1 (V_2 )} \right\| ^2 }}{{4\varsigma _V }} +\, \dfrac{{\left\| {\tilde{\dot{\alpha }} _V } \right\| ^2 }}{{4\varsigma _R }}+ \dfrac{{\left\| {d_\omega } \right\| ^2 }}{{4\varsigma _\omega }} \nonumber \\&+\, \dfrac{{\left( {\sigma _3 (w)c(\theta )c(\phi )} \right) ^2 }}{{4\varsigma _z }}+ \dfrac{{\left( {\tilde{\dot{\alpha }} _\psi + \sigma _4 (r)} \right) ^2 }}{{4\varsigma _r }} \nonumber \\&-\, \sum \limits _{i = 1}^4 {\dfrac{1}{{\zeta _i }}} \tilde{\varGamma } _i \dot{\hat{\varGamma }} _i + \dfrac{1}{\gamma }\tilde{m} \dot{ \hat{m}}. \end{aligned}$$
(71)

According to the Cauchy–Schwarz inequality and Assumption 1, Eq. (71) can be rewritten as follows

$$\begin{aligned} \dot{L}\le & {} - \lambda _{\min } \left( {K_P } \right) \left\| {P_e } \right\| ^2 - \left( {\lambda _{\min } \left( {K_V } \right) - \varsigma _V } \right) \left\| {V_e } \right\| ^2 \nonumber \\&- \left( {\lambda _{\min } \left( {K_R } \right) - \varsigma _R } \right) \left\| {R_e } \right\| ^2 \nonumber \\&- \left( {\lambda _{\min } \left( {K_\omega } \right) - \varsigma _\omega } \right) \left\| {\omega _e } \right\| ^2 \nonumber \\&- \left( {mk_z - \varsigma _z } \right) \delta _z^2 - k_\psi \psi _e ^2 - \left( {k_r - \varsigma _r } \right) r_e ^2 \nonumber \\&+ \left\| {V_e } \right\| \left\| {W_1 } \right\| _2 \left\| {H_1 (V_2 )} \right\| \nonumber \\&- \dfrac{1}{{2\varepsilon _1 ^2 }}V_e ^T V_e \hat{\varGamma } _1 H_1 ^T (V_2 )H_1 (V_2 ) \nonumber \\&+ \left\| {\omega _e } \right\| \left\| {W_2 } \right\| _2 \left\| {H_2 (\omega _2 )} \right\| \nonumber \\&- \dfrac{1}{{2\varepsilon _2 ^2 }}\omega _e ^T \omega _e \hat{\varGamma } _2 H_2 ^T (\omega _2 )H_2 (\omega _2 ) \nonumber \\&+ \left| \delta _z \right| \left\| {W_3 } \right\| \left\| {H_3 (w)} \right\| c(\theta )c (\phi ) \nonumber \\&- \dfrac{1}{{2\varepsilon _3 ^2 }}\delta _z^2 \hat{\varGamma } _3 H_3 ^T (w)H_3 (w)c(\theta )c (\phi ) \nonumber \\&+ \tilde{m}\delta _z\left( {\nu - g} \right) + \left| {r_e } \right| \left\| {W_4 } \right\| \left\| {H_4 (r)} \right\| \nonumber \\&- \dfrac{1}{{2\varepsilon _4 ^2 }}r_e ^2 \hat{\varGamma } _4 H_4 ^T (r)H_4 (r)+ \dfrac{{\left\| {\sigma _1 (V_2 )} \right\| ^2 }}{{4\varsigma _V }} \nonumber \\&+ \dfrac{{\left\| {\tilde{\dot{\alpha }} _V } \right\| ^2 }}{{4\varsigma _R }} + \dfrac{{\left\| {d_\omega } \right\| ^2 }}{{4\varsigma _\omega }}+ \dfrac{{\left( {\sigma _3 (w)c(\theta )c(\phi )} \right) ^2 }}{{4\varsigma _z }} \nonumber \\&+ \dfrac{{\left( {\tilde{\dot{\alpha }} _\psi + \sigma _4 (r)} \right) ^2 }}{{4\varsigma _r }} - \sum \limits _{i = 1}^4 {\dfrac{1}{{\zeta _i }}} \tilde{\varGamma } _i \dot{\hat{\varGamma } }_i + \dfrac{1}{\gamma }\tilde{m}\dot{\hat{m}}. \end{aligned}$$
(72)

Then, using the Young’s inequality, Eq. (72) can be further expressed by

$$\begin{aligned} \dot{L}\le & {} - \lambda _{\min } \left( {K_P } \right) \left\| {P_e } \right\| ^2 - \left( {\lambda _{\min } \left( {K_V } \right) - \varsigma _V } \right) \left\| {V_e } \right\| ^2 \\&- \left( {\lambda _{\min } \left( {K_R } \right) - \varsigma _R } \right) \left\| {R_e } \right\| ^2 \\&- \left( {\lambda _{\min } \left( {K_\omega } \right) - \varsigma _\omega } \right) \left\| {\omega _e } \right\| ^2 \\&- \left( {mk_z - \varsigma _z } \right) \delta _z^2 - k_\psi \psi _e ^2 - \left( {k_r - \varsigma _r } \right) r_e ^2\\&+ \dfrac{{\left\| {W_1 } \right\| _2 ^2 \left\| {V_e } \right\| ^2 \left\| {H_1 (V_2 )} \right\| ^2 }}{{2\varepsilon _1 ^2 }} \\&- \dfrac{1}{{2\varepsilon _1 ^2 }}V_e ^T V_e \hat{\varGamma } _1 H_1 ^T (V_2 )H_1 (V_2 ) \\&+ \dfrac{{\left\| {W_2 } \right\| _2 ^2 \left\| {\omega _e } \right\| ^2 \left\| {H_2 (\omega _2 )} \right\| ^2 }}{{2\varepsilon _2 ^2 }} \\&- \dfrac{1}{{2\varepsilon _2 ^2 }}\omega _e ^T \omega _e \hat{\varGamma } _2 H_2 ^T (\omega _2 )H_2 (\omega _2 )\\&+ \dfrac{{\left\| {W_3 } \right\| ^2 \left| \delta _z \right| ^2 \left\| {H_3 (w)} \right\| ^2 }}{{2\varepsilon _3 ^2 }}c(\theta )c(\phi )\\&- \dfrac{1}{{2\varepsilon _3 ^2 }}\delta _z^2 \hat{\varGamma } _3 H_3 ^T (w)H_3 (w)c(\theta )c(\phi ) \\&+ \dfrac{{\left\| {W_4 } \right\| ^2 \left| {r_e } \right| ^2 \left\| {H_4 (r)} \right\| ^2 }}{{2\varepsilon _4 ^2 }} \\&- \dfrac{1}{{2\varepsilon _4 ^2 }}r_e ^2 \hat{\varGamma } _4 H_4 ^T (r)H_4 (r)+ \tilde{m}\delta _z\left( {\nu - g} \right) \\&+ \dfrac{{\left\| {\sigma _1 (V_2 )} \right\| ^2 }}{{4\varsigma _V }} + \dfrac{{\left\| {\tilde{\dot{\alpha }} _V } \right\| ^2 }}{{4\varsigma _R }} + \dfrac{{\left\| {d_\omega } \right\| ^2 }}{{4\varsigma _\omega }}\\&+ \dfrac{{\left( {\sigma _3 (w)c(\theta )c(\phi )} \right) ^2 }}{{4\varsigma _z }}+\dfrac{{\left( {\tilde{\dot{\alpha }}_\psi + \sigma _4 (r)} \right) ^2 }}{{4\varsigma _r }}\\&+ \dfrac{1}{2}\sum \limits _{i = 1}^4 {\varepsilon _i ^2 s_i } - \sum \limits _{i = 1}^4 {\dfrac{1}{{\zeta _i }}} \tilde{\varGamma } _i \dot{\hat{\varGamma } }_i + \dfrac{1}{\gamma }\tilde{m}\dot{\hat{m}} \\\le & {} - \lambda _{\min } \left( {K_P } \right) \left\| {P_e } \right\| ^2- \left( {\lambda _{\min } \left( {K_V } \right) - \varsigma _V } \right) \left\| {V_e } \right\| ^2\\&- \left( {\lambda _{\min } \left( {K_R } \right) - \varsigma _R } \right) \left\| {R_e } \right\| ^2\\&- \left( {\lambda _{\min } \left( {K_\omega } \right) - \varsigma _\omega } \right) \left\| {\omega _e } \right\| ^2\\&- \left( {mk_z - \varsigma _z } \right) \delta _z^2 - k_\psi \psi _e ^2 - \left( {k_r - \varsigma _r } \right) r_e ^2 \\&+ \tilde{\varGamma } _1 \left( {\dfrac{1}{{2\varepsilon _1 ^2 }}V_e ^T V_e H_1 ^T (V_2 )H_1 (V_2 ) - \dfrac{1}{{\zeta _1 }}\dot{\hat{\varGamma }} _1 } \right) \\&+ \tilde{\varGamma } _2 \left( {\dfrac{1}{{2\varepsilon _2 ^2 }}\omega _e ^T \omega _e H_2 ^T (\omega _2 )H_2 (\omega _2 ) - \dfrac{1}{{\zeta _2 }}\dot{\hat{\varGamma } }_2 } \right) \end{aligned}$$
$$\begin{aligned}&\qquad + \tilde{\varGamma } _3 \left( {\dfrac{1}{{2\varepsilon _3 ^2 }}\delta _z^2 H_3 ^T (w)H_3 (w)c(\theta )c(\phi ) - \dfrac{1}{{\zeta _3 }}\dot{\hat{\varGamma }} _3 } \right) \nonumber \\&\qquad + \tilde{\varGamma } _4 \left( {\dfrac{1}{{2\varepsilon _4 ^2 }}r_e ^2 H_4 ^T (r)H_4 (r) - \dfrac{1}{{\zeta _4 }}\dot{\hat{\varGamma }} _4 } \right) \nonumber \\&\qquad - \tilde{m}\left( {g\delta _z - \nu \delta _z - \dfrac{1}{\gamma }\dot{\hat{m}}} \right) + \dfrac{1}{2}\sum \limits _{i = 1}^4 {\varepsilon _i ^2 s_i }\nonumber \\&\qquad + \dfrac{{\left\| {\sigma _1 (V_2 )} \right\| ^2 }}{{4\varsigma _V }} + \dfrac{{\left\| {\tilde{\dot{\alpha }} _V } \right\| ^2 }}{{4\varsigma _R }}+ \dfrac{{\left\| {d_\omega } \right\| ^2 }}{{4\varsigma _\omega }}\nonumber \\&\qquad + \dfrac{{\left( {\sigma _3 (w)c(\theta )c(\phi )} \right) ^2 }}{{4\varsigma _z }} + \dfrac{{\left( {\tilde{\dot{\alpha }} _\psi + \sigma _4 (r)} \right) ^2 }}{{4\varsigma _r }}, \end{aligned}$$
(73)

where \(i=1,2,3,4 \); \(s_i = \left\{ {\begin{array}{ll} 1, &{}\quad \text {if}\ i=1,2,4; \\ {c(\theta )c(\phi )}, &{}\quad \text {if}\ i=3. \end{array}} \right. \)

Input the adaptive laws (69a), (69b), (69c), (69d) and (69e) into (73) and combine the following inequalities

$$\begin{aligned} \left\{ {\begin{array}{l} {\sum \limits _{i = 1}^4 {\dfrac{{\xi _i }}{{\zeta _i }}\tilde{\varGamma } _i \hat{\varGamma } _i \le - \sum \limits _{i = 1}^4 {\dfrac{{\xi _i }}{{2\zeta _i }}\tilde{\varGamma } _i ^2 } + \sum \limits _{i = 1}^4 {\dfrac{{\xi _i }}{{2\zeta _i }}\varGamma _i ^2 } } },\\ {\eta \tilde{m}\hat{m} \le - \dfrac{\eta }{2}\tilde{m}^2 + \dfrac{\eta }{2}m^2 }, \end{array}} \right. \end{aligned}$$
(74)

to get

$$\begin{aligned} \dot{L}\le & {} - \lambda _{\min } \left( {K_P } \right) \left\| {P_e } \right\| ^2 \nonumber \\&- \left( {\lambda _{\min } \left( {K_V } \right) - \varsigma _V } \right) \left\| {V_e } \right\| ^2\nonumber \\&- \left( {\lambda _{\min } \left( {K_R } \right) - \varsigma _R } \right) \left\| {R_e } \right\| ^2 \nonumber \\&- \left( {\lambda _{\min } \left( {K_\omega } \right) - \varsigma _\omega } \right) \left\| {\omega _e } \right\| ^2\nonumber \\&- \left( {mk_z - \varsigma _z } \right) \delta _z^2 - k_\psi \psi _e ^2 - \left( {k_r - \varsigma _r } \right) r_e ^2 \nonumber \\&- \sum \limits _{i = 1}^4 {\dfrac{{\xi _i }}{{2\zeta _i }}\tilde{\varGamma } _i ^2 } + \sum \limits _{i = 1}^4 {\dfrac{{\xi _i }}{{2\zeta _i }}\varGamma _i ^2 } - \dfrac{\eta }{2}\tilde{m}^2 + \dfrac{\eta }{2}m^2\nonumber \\&+ \dfrac{{\left\| {\sigma _1 (V_2 )} \right\| ^2 }}{{4\varsigma _V }} + \dfrac{{\left\| {\tilde{\dot{\alpha }} _V} \right\| ^2 }}{{4\varsigma _R }}\nonumber \\&+ \dfrac{{\left\| {d_\omega } \right\| ^2 }}{{4\varsigma _\omega }} + \dfrac{{\left( {\sigma _3 (w)c(\theta )c(\phi )} \right) ^2 }}{{4\varsigma _z }} \nonumber \\&+ \dfrac{{\left( {\tilde{\dot{\alpha }} _\psi + \sigma _4 (r)} \right) ^2 }}{{4\varsigma _r }} + \dfrac{1}{2}\sum \limits _{i = 1}^4 {\varepsilon _i ^2 s_i } \nonumber \\\le & {} - 2\varSigma L + \Delta , \end{aligned}$$
(75)

where

$$\begin{aligned} \begin{array}{ll} \varSigma = \min \bigg (&{} \lambda _{\min } \left( {K_P } \right) ,\left( {\lambda _{\min } \left( {K_V } \right) - \varsigma _V } \right) , \\ &{}\left( {\lambda _{\min } \left( {K_R } \right) - \varsigma _R } \right) ,\left( {\lambda _{\min } \left( {K_\omega } \right) - \varsigma _\omega } \right) ,\\ &{}\dfrac{{\left( {mk_z - \varsigma _z } \right) }}{m},k_\psi ,\left( {k_r - \varsigma _r } \right) ,\dfrac{{\xi _i }}{2},\dfrac{{\eta \gamma }}{2}\bigg ), \end{array} \end{aligned}$$
(76)

and

$$\begin{aligned} \Delta= & {} \sum \limits _{i = 1}^4 {\dfrac{{\xi _i }}{{2\zeta _i }}\varGamma _i ^2 } + \dfrac{\eta }{2}m^2 + \dfrac{{\left\| {\sigma _1 (V_2 )} \right\| ^2 }}{{4\varsigma _V }} \nonumber \\&+ \dfrac{{\left\| {\tilde{\dot{\alpha }} _V } \right\| ^2 }}{{4\varsigma _R }} + \dfrac{{\left\| {d_\omega } \right\| ^2 }}{{4\varsigma _\omega }} + \dfrac{{\left( {\sigma _3 (w)c(\theta )c(\phi )} \right) ^2 }}{{4\varsigma _z }}\nonumber \\&+ \dfrac{{\left( {\tilde{\dot{\alpha }} _\psi + \sigma _4 (r)} \right) ^2 }}{{4\varsigma _r }} + \dfrac{1}{2}\sum \limits _{i = 1}^4 {\varepsilon _i ^2 s_i }. \end{aligned}$$
(77)

Thus, solving the differential inequality (75) yields

$$\begin{aligned} L(t) \le L(t_0 )e^{ - 2\varSigma (t - t_0 )} + \dfrac{\Delta }{{2\varSigma }}\left( {1 - e^{ - 2\varSigma (t - t_0 )} } \right) , \end{aligned}$$
(78)

where \(t_0\) is the initial time. And inequality (78) means that

$$\begin{aligned} L(t) \rightarrow \dfrac{\Delta }{{2\varSigma }}, \quad \text {as}\ t \rightarrow \infty . \end{aligned}$$
(79)

Defining \(\varPi (t)=L(t_0 )e^{ - 2\varSigma (t - t_0 )} + \frac{\Delta }{{2\varSigma }}\left( {1 - e^{ - 2\varSigma (t - t_0 )} } \right) \), then one can get

$$\begin{aligned}&{\left\| {P_e } \right\| \le \sqrt{2\varPi (t)} } , \end{aligned}$$
(80)
$$\begin{aligned}&{\delta _z \le \sqrt{\dfrac{2}{m}\varPi (t)}} , \end{aligned}$$
(81)
$$\begin{aligned}&{\psi _e \le \sqrt{2\varPi (t)}} . \end{aligned}$$
(82)

Since \(\delta _z = \dot{z}_e + k_z z_e \), the following inequality can be obtained

$$\begin{aligned} z_e \le z_e \left( {t_0 } \right) e^{ - k_z \left( {t - t_0 } \right) } + \frac{{\sqrt{\frac{2}{m}\varPi (t)} }}{{k_z }}\left( {1 - e^{ - k_z \left( {t - t_0 } \right) } } \right) , \end{aligned}$$
(83)

which implies that \(z_e \rightarrow \dfrac{{\sqrt{\frac{2}{m}\varPi (t)} }}{{k_z }}, \quad \text {as}\ t \rightarrow \infty \).

Therefore, the position and the yaw angle tracking errors of the overall closed-loop system are semi-globally uniformly ultimately bounded and can converge to an arbitrarily small neighborhood of the original point by selecting the proper parameters. \(\square \)

Remark 4

As shown in inequality (80), (82), and (83), the size of the neighborhood is adjustable by choosing the parameters \(\varSigma \) and \(k_z\). Since \(c(\phi )\) and \(c(\theta )\) are used in the denominator of the formula (56), Assumption 1 is necessary to guarantee the validity of the formula and the analysis on the stability of the closed-loop system.

Remark 5

Since the autonomous flight of the small-scale helicopter is under the Assumption 1 and the transient response of the dynamics of sensing and actuation systems is much faster than that of the helicopter dynamics [25], the sensing and actuation systems are assumed to be ideal and the dynamics of which can be disregarded during developing a controller.

5 Simulation results and discussion

In this section, the effectiveness and the robustness of the proposed nonlinear adaptive controller augmented by the RBFNNs are evaluated through two simulation experiments. For convenience, the numerical values of the main physical parameters of the small-scale unmanned helicopter are provided in Table 2. Readers interested can refer to the literature [35] for more detailed information. The main controller parameters are the same in the two simulations, which are summarized in Tabel 3. Since the PID controller needs no knowledge of the helicopter model, it is widely used in practical applications in spite of the fact that the controller gains can only be tuned by experience. Thus, in order to be more persuasive, the proposed controller is compared with the PID controller proposed in [25] in both two simulations, which is consist of four single-input single-output PID control loops.

Some model parameter variations and external disturbances are considered in the simulations to verify the robustness of the proposed controller. More specifically, a heavy object is dropped during the flight to test the robustness to the internal disturbances in the first simulation, and the wind gusts of 9 m/s along the body frame x-, y-, and z-axes are added to test the robustness to the external disturbances in the second simulation. Besides, other simulation conditions (e.g., a fixed step size of 0.01 s) are the same for both two simulations.

Table 2 Physical parameters of the unmanned helicopter
Full size table
Table 3 Control parameters of the proposed controller
Full size table
Fig. 5
figure 5

First simulation: the reference trajectory (blue dashed line) and the actual trajectory of the proposed nonlinear adaptive controller (red solid line), and the PID controller (green dashed-dotted line). (Color figure online)

Full size image

5.1 Simulation 1: trajectory tracking with airdrop

The reference trajectory in the first simulation is denoted by the following square curve

$$\begin{aligned} P_r = \left\{ {\begin{array}{ll} {\left( {0.5t} ,\ 0 ,\ 10 \right) ^T }, &{} \quad \text {if}\quad t \le 15 ; \\ {\left( {7.5} ,\ {0.5\left( {t - 15} \right) } ,\ 10 \right) ^T }, &{} \quad \text {if}\quad 15< t \le 30 ; \\ {\left( {0.5\left( {45 - t} \right) } ,\ {7.5} ,\ 10 \right) ^T }, &{} \quad \text {if}\quad 30< t \le 45 ; \\ {\left( 0 ,\ {0.5\left( {60 - t} \right) } ,\ 10 \right) ^T }, &{} \quad \text {if}\quad 45 < t \le 60. \\ \end{array}} \right. \end{aligned}$$
(84)

The purpose of the first simulation is mainly to evaluate the tracking accuracy and the robustness to the internal parameter variation considering the intrinsic coupling among different control channels. To enhance the coupling effect, the nose of the small-scale unmanned helicopter is kept forward during the whole flight, producing the following reference trajectory for \(\psi \)

$$\begin{aligned} \psi _r = \left\{ {\begin{array}{ll} 0, &{} \quad \text {if}\quad t \le 15 ; \\ \dfrac{1}{2}\pi ,&{} \quad \text {if}\quad 15< t \le 30 ;\\ \pi ,&{} \quad \text {if}\quad 30< t \le 45 ;\\ \dfrac{3}{2}\pi ,&{} \quad \text {if}\quad 45 < t \le 60.\\ \end{array}} \right. \end{aligned}$$
(85)

Since the mass is used as a denominator in the control design process, the initial mass cannot be zero or too small. For the sake of fairness, the initial mass is set as 0.5 kg. The actual total mass of the unmanned helicopter is assumed to be 7.495 kg, including an object of 1.495 kg, which is to be dropped off during the flight to trigger an abrupt mass variation. The adaptive parameters are selected as: \(\epsilon _1=0.75\), \(\epsilon _2=\epsilon _3=1\), \(\epsilon _4=5\), \(\zeta _1=\zeta _2=200\), \(\zeta _3=\zeta _4=100\), \(\xi _1=0.005\), \(\xi _2=\xi _4=0.5\), \(\xi _3=0.0001\), and \(\eta =0.005\). The simulation results are shown in Fig. 5.

As shown in Fig. 5a–d, the red solid lines of the proposed controller obviously have higher tracking accuracy than those green dashed-dotted lines of the PID controller despite the airdrop at the 25th second. It is observed from Fig. 5e, f, the roll angle and the pitch angle both deviate from their equilibrium values when the yaw angle changes, resulting from the coupling effect with the yaw channel. However, the roll angle and the pitch angle of the proposed strategy are both stabler than those of the PID method. In addition, Fig. 5g shows the adaptive parameters and Fig. 5h demonstrates that the estimated mass can keep up with the actual value well. The mass estimation is quite valid although there exists a bounded estimation error. Figure 5i depicts the tracking result including the airdrop at the 25th second and the wind gusts of 9 m/s along the body frame x-, y-, and z-axes rising up at the 30th second to further reveal the gap between the two methods more clearly.

Fig. 6
figure 6

Second simulation: the reference trajectory (blue dashed line) and the actual trajectory of the proposed nonlinear adaptive controller (red solid line), and the PID controller (green dashed-dotted line). (Color figure online)

Full size image

Remark 6

As shown in Fig. 5c, when the airdrop happens, the altitude variation of the PID controller is relatively smaller than that of the proposed controller. The result emerges mainly due to the common structure characteristics of the PID controllers which do not need precise model information, while the mass is quite an important model parameter in the proposed controller. However, the proposed strategy makes a rapid recovery from the abrupt height variation and gets a better tracking accuracy than the PID method. This just validates the effectiveness of the mass adaption (69e) and the robustness of the proposed controller.

Remark 7

Fig. 5d depicts that the yaw angle of the nonlinear adaptive controller has a quicker response and a higher tracking precision. It is worth mentioning that the yaw angle changes from \(\pi \) to \(-\pi \) at the 45th second in the simulation although the desired yaw angle is \(3\pi /2\). This is because that the actual yaw angle range of the small-scale unmanned helicopter is between \(-\pi \) and \(\pi \), and the heading control loop takes it into account, making the simulation closer to a real flight.

Remark 8

As observed in Fig. 5g, h, the adaptive parameter \(\hat{\varGamma }_3\) changes most fiercely when the abrupt mass variation happens. This is owing to the fact that the heave subsystem is most seriously affected by the mass variation among all the control channels. Then the adaptive law (69c) reacts fleetly to hold the height of the unmanned helicopter, leading to an abrupt increase in \(\hat{\varGamma }_3\) and maintaining the altitude stable again very quickly, which is consistent with the situation in Fig. 5c.

5.2 Simulation 2: trajectory tracking with wind gusts

In this simulation, the desired position trajectory is selected as a spiral path descending along the inertial frame z-axis, which is more aggressive than what is used in the first simulation, defined as follows:

$$\begin{aligned} P_r = \left\{ {\begin{array}{ll} {\left( {0} ,\ 0 ,\ -3 \right) ^T }, &{} \quad \text {if}\ t \le 5 ;\\ {\left[ {\begin{array}{l} {5(1-cos(\dfrac{\pi }{5}(t-5)))} \\ -5sin(\dfrac{\pi }{5}(t-5)) \\ -23+20 e^{(-0.06(t-5))} \\ \end{array}} \right] }, &{} \quad \text {if}\ t \ge 5. \\ \end{array}} \right. \end{aligned}$$
(86)

And the reference trajectory of the yaw angle is set as \(\psi _r=0\). Moreover, the wind gusts of 9 m/s are exerted along the body frame x-, y-, and z-axes of the unmanned helicopter at the 30th second for both two methods. With the adaptive parameters chosen as: \(\epsilon _1=0.5\), \(\epsilon _2=1.5\), \(\epsilon _3=1\), \(\epsilon _4=5\), \(\zeta _1=300\), \(\zeta _2=200\), \(\zeta _3=\zeta _4=100\), \(\xi _1=0.1\), \(\xi _2=\xi _4=0.5\), \(\xi _3=0.001\), \(\eta =0.001\), and other parameters selected as the same with Simulation 1, the performance results of Simulation 2 are depicted in Fig. 6.

Figure 6a–f illustrates that the tracking errors of the PID method are bigger than those of the proposed strategy in the absence of wind gusts before the 30th second in the simulation. Once the wind gusts are exerted at the 30th second, the PID controller suffers much larger tracking errors and trajectory deviations, while the proposed controller withstands the test of the wind gusts and keeps highly accurate tracking trajectories throughout the total flight process. In addition, as depicted in Fig. 6g, h, the PID controller needs more aggressive roll and pitch angles than the proposed method to track the same reference trajectory, which means that the proposed controller can obtain more efficient and robust tracking results with less aggressive controls. Furthermore, the adaptive parameters are illustrated in Fig. 6i.

Remark 9

It should be stressed that in Fig. 6d 1 radian is about equal to \(57.3^ \circ \). The yaw angle tracking error of the PID method is more than \(5.73^ \circ \) when there are no wind gusts. Once the wind gusts are exerted, the error increases to about \(10^\circ \), which is quite a large tracking error for a small-scale unmanned helicopter.

Remark 10

From Eq. (86), it can be derived that the time required for a cycle is 10 seconds, which is much faster than the reference trajectory used in [16]. Consequently, the proposed control system certainly needs bigger roll and pitch angles than those in [16] to maintain a circular motion of such a high frequency.

Remark 11

Fig. 6i shows that the updating law in the heave subsystem experiences the intensest transition, followed by the adaptive laws in the longitudinal–lateral subsystem, and the adaption in the heading subsystem undergoes the slightest change. That is because the area of the rotating main rotor at high speed is much larger than that of the fuselage, while the area of the rotating tail rotor is the smallest, almost negligible. Correspondingly, the larger the area is, the bigger effect the wind gusts produce, then the intenser change the adaption has.

Remark 12

It is worth mentioning that, in an ideal simulation environment, the PID controller can only withstand up to 9 m/s wind gusts along the body frame x-, y-, and z-axes with terrible tracking errors, while the proposed nonlinear adaptive controller can withstand up to 13 m/s wind gusts with perfectly acceptable tracking errors. Moreover, it has to be pointed out that the approximation ability of the RBFNN learning algorithm with the least parameters is limited, and it is the price that must be paid to reduce the number of the updating laws and the amount of computation.

6 Conclusion

This paper addresses the position and yaw tracking problem of a small-scale unmanned helicopter with unknown mass. To estimate the unknown mass, internal uncertainties, and external uncertainties, a novel nonlinear adaptive controller augmented by the RBFNNs is proposed, including a novel mass adaption and four improved adaptive neural network learning algorithms of the least parameters. All the adaptive laws are derived in the process of the Lyapunov stability analysis, by which the position and yaw tracking errors of the overall closed-loop system are proved to converge to an arbitrarily small compact of the origin asymptotically. Moreover, two simulations confirm that the proposed method is not only effective but also robust to the internal and external uncertainties and is suitable for practical implementation. And the future work is to implement the proposed controller on a specific unmanned helicopter experimental system.