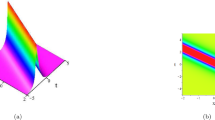1 Introduction

There are extremely complex dynamical processes in nature all the time, and many physical phenomena are nonlinear in our daily life. Research on modulation instability (MI) and dynamical behavior of the localized wave solutions for the nonlinear systems is a fascinating subject in the field of contemporary nonlinear science, which has attracted widespread attention from many experts and scholars. MI [1] is the instability of a monochromatic wave or constant background for disturbances. In experiments, MI is usually used to generate typical nonlinear waves such as soliton, rogue wave, and breather. Theoretically, MI is divided into two stages. The first stage can be described by linear theory, and the second stage is called nonlinear stage. Linear MI analysis can only give the instability criterion of small perturbation and the rate of change of linear instability. The linear phase disturbance grows exponentially with time and quickly reaches a scale comparable to the background wave, thus entering the nonlinear phase. As early as the 1960s, MI, known as Benjamin–Feir instability [2], was discovered in deep water wave theory. As is known to all, MI is a natural phenomenon that can be discovered in many fields, such as nonlinear optics [3], fluid mechanics [4], Bose–Einstein condensation [5], plasma [6], and so on.

Localized wave is one of the main research hotspots in contemporary nonlinear mathematical physics. Soliton, breather, and rogue wave are localized waves with obvious dynamical and physical characteristics in the nonlinear systems. Soliton [7,8,9] has both locality and particle properties, and all integrable equations have soliton solutions that reflect the universal nonlinear phenomena in nature. Breather and rogue wave are two typical localized structures with obvious instability on the plane-wave backgrounds. Breather [10] not only has a periodic structure in a particular direction, but also can be used to explain the phenomenon of rogue wave. Rogue wave [11,12,13,14] is double localized structures in both time evolution and spatial distribution directions, which comes nowhere and disappears without a trace [15]. The mechanism of rogue wave can be regarded as the high amplitude wave, which is generated by the collision of soliton and breather [16]. The occurrence of ocean rogue waves is related to the concentration of energy caused by one or more factors: the effect of wave countercurrent, the influence of terrain, wave instability, wave frequency focus or direction focus, etc. The study of rogue waves is of great significance to the detection of large-wave events near the ocean or coast, experimental observations, theoretical mechanisms, and early warning. Since many optical systems contain interacting wave components of different modes, frequencies, or polarizations, studying localized wave solutions and interaction solutions in the coupled systems has potential practical application value, which would be useful for understanding the corresponding dynamical phenomena in many other relevant fields.

Among various nonlinear systems, one of the most prominent integrable examples, which is widely used to model the propagation of nonlinear wave in monomode optical fibers, is the Fokas–Lenells (FL) equation

$$\begin{aligned}&iu_t-\nu u_{xt}+\gamma u_{xx}+\rho |u|^2(u+ivu_x)=0,\nonumber \\&\rho =\pm 1, ~~x\in {\mathbb {R}}. \end{aligned}$$
(1)

It was proposed by Fokas [17] and Lenells [18], is a completely integrable equation. In [17], Eq. (1) was derived by means of the bi-Hamiltonian method. In [18], the physical derivation of Eq. (1) was presented. Eq. (1) is an integrable generalization of the nonlinear Schrödinger (NLS) equation and relates to the first negative flow of the derivative NLS equation hierarchy, which is similar with the relationship between the Camassa–Holm equation and the first negative flow of KdV hierarchy [19]. When \(\nu =0\), Eq. (1) can be reduced to the NLS equation [20], which is used to describe the nonlinear deep water model, and it occupies a particularly prominent position in nonlinear physics. In [21], Lenells and Fokas not only derived the conservation laws and Lax pair of Eq. (1) via its bi-Hamiltonian structure, but also solved the initial value problem via the inverse scattering transform. Subsequently, there are many results on the localized wave solutions of the FL equation, such as soliton, breather, and rogue wave have been constructed by the Darboux transformation (DT) method [22, 23], the dressing method [24], the Hirota direct method [25], and the complex envelope function method [26]. In [27], long-time asymptotic behavior for the Cauchy problem of the FL equation has been discussed by the Deift–Zhou method [28]. General rogue waves and some new rogue wave patterns for the generalized derivative NLS equations [29] have been constructed by the bilinear KP reduction method. For some other models about the extended forms of the NLS equation, we refer the reader to recent work in [30,31,32,33].

Similar to the various extended forms of the NLS equation, the FL equation also has some generalized forms. Due to the mutual influence of relative velocities between different component fields and the common coupling effect of cross-phase modulation, multi-component coupled nonlinear systems can produce more abundant dynamic phenomena than single-component systems. Therefore, it is necessary to consider the two-component or multi-component FL equation for describing the effects of polarization or anisotropy, which can contribute to better understanding the nonlinear localized wave and its dynamic phenomena. The coupled FL equation [34] can be written as

$$\begin{aligned} \begin{aligned}&p_{xt}+p+i(|p|^2+\frac{1}{2}\sigma |q|^2)p_x+\frac{1}{2}i\sigma pq^*q_x=0,\\&q_{xt}+q+i(\sigma |q|^2+\frac{1}{2}|p|^2)q_x+\frac{1}{2}i\sigma qp^*p_x=0, \end{aligned} \end{aligned}$$
(2)

here \(\sigma =\pm 1\). The coupled FL equation shares the same spatial part of the spectral problem with the coupled derivative NLS equation [35], which is the first nontrivial negative flow of the vector Kaup–Newell hierarchy and relevant in the theory of polarized Alfvén waves and the propagation of the ultra-short pulse. Many effective methods, such as Riemann–Hilbert method [36], DT [37], non-recursive DT [38], and generalized DT [39], have been developed to study on the coupled FL equation. As is known to all, the coupled FL equation is one of the integrable systems as shown in [40] and certainly admits other interesting integrable properties including multi-Hamiltonian structure, infinitely many conservation laws, the general soliton solutions [41], and optical soliton solution [42]. In addition, the baseband MI, rogue wave solutions, and state transitions for a deformed FL equation [43] and semi-rational solutions for the coupled derivative NLS equation [44] have been studied by the generalized DT method. Fundamental Peregrine solitons with unprecedentedly ultrahigh peak amplitude have been discovered for the vector derivative NLS equation [45]. In [46], the coupled FL equation (2) has been extended to three-component coupled system, whose corresponding dynamical behaviors of localized solutions have been studied. In [47], some analytical fractional solitons of the space-time fractional FL equation were studied by the improved Riemann–Liouville fractional derivative rule and two different fractional dual-function methods with Mittag–Leffler function.

In this paper, we will use the following generalized coupled Fokas–Lenells (gc-FL) equation [48]

$$\begin{aligned} \begin{aligned}&iu_{xt}-i\alpha u_{xx}+2\gamma u_x-2\beta (2|u|^2+|v|^2)u_x\\&\quad -2\beta uv^*v_x+4i\beta u=0,\\&iv_{xt}-i\alpha v_{xx}+2\gamma v_x-2\beta (2|v|^2+|u|^2)v_x\\&\quad -2\beta vu^*u_x+4i\beta v=0, \end{aligned} \end{aligned}$$
(3)

as the reference system, where \(\alpha ,\beta \), and \(\gamma \) are real parameters, and u, v are all complex functions with respect to delay time x and propagation distance t. It associates with two conserved quantities

$$\begin{aligned} \begin{aligned} I_1[u,v]&=\int _{-\infty }^{\infty }(u_xu_x^*+v_xv_x^*){\mathrm {d}}x,\\ I_2[u,v]&=\int _{-\infty }^{\infty }\left( -(u_xu_x^*+v_xv_x^*)^2\right. \\&\quad \left. +2i(u_xu_{xx}^*+v_xv_{xx}^*)\right) {\mathrm {d}}x. \end{aligned} \end{aligned}$$
(4)

When \(\alpha =0\),  \(\beta =\frac{1}{4}\), and \(\gamma =0\), Eq. (3) degenerates to the coupled FL equation (2). When \(\alpha =2,~~\gamma =2\), and \(\beta =\frac{1}{2}\), the coupled FL equation studied in [37] is equivalent to the coupled FL equation (2) by a gauge transformation, in which particular case, soliton, first-order breather, and rogue wave solutions have been derived. In fact, Eq. (2) is the two-component integrable generalization of the FL equation (1). As pointed out by Lenells, the FL equation is the generalization of the NLS equation, and describes the propagation of femtosecond pulse in single mode optical silica fiber when higher-order nonlinear optical effects are considered. Due to the inherent stability of solitons, which can propagate over long distances without changing and are ideal information carriers, the NLS equation is a basic model to describe the propagation of light pulses in nonlinear optical fibers. Owing to the practical significance of the FL equation, further study the gc-FL equation (3), one of the generalized forms of the FL equation, must have abundant research significance, which will help us better understand the propagation mechanism of nonlinear pluses in certain fibers.

Recently, the higher-order rogue waves of the gc-FL equation (3) have been constructed in [48]. However, there are still some topics worth studying, such as: (1) Can the expression of its infinitely many conservation laws be derived? (2) Does the semi-rational solutions of gc-FL exist and what are its dynamic characteristics? (3) Whether the conditions for the existence of rogue waves obtained from the analysis of MI and characteristic polynomials are consistent? In the present paper, we will mainly focus on these aspects to study the gc-FL equation (3). Based on the theory of linear stability analysis, we depict the distribution pattern of the MI gain G on the frequency plane (K, k) and derive the constraint condition for the existence of rogue waves, namely \(0<k<\frac{2}{C}\), which is consistent with the constraint obtained from the analysis of the spectrum parameters. According to Riccati-type formulas of the spectral problem, infinitely many conservation laws, and recursion relations for the conserved density and associated flux of the gc-FL equation (3) are derived, respectively. Furthermore, the concrete formula of the higher-order localized wave solution is obtained by the generalized DT method. By selecting different parameters, three kinds of localized wave solutions are discussed, including the first- to third-order rogue wave solutions, and the interaction solutions between higher-order rogue wave and multi-solitons or multi-breathers. Moreover, the dynamical behaviors and the effects of arbitrary parameters on the structure of the localized wave solutions, including higher-order rogue waves, are discussed in detail.

The remainder of our paper is organized as follows. In Sect. 2, we discuss MI distribution features of the gc-FL equation according to the theory of MI analysis. In Sect. 3, we construct infinitely many conservation laws and the generalized DT of the gc-FL equation, and give a concrete formula of the N-order localized wave solution. Interactional localized waves are presented and their dynamical behavior is analyzed in Sect. 4. In the final section, some conclusions are given.

2 Modulation instability of continuous waves

The stability of the solution is modulated by both the nonlinear term and dispersive term in the nonlinear systems. In general, the nonlinear partial differential equation satisfying the fiber communication model, for the stable solution, under the interaction of the nonlinear term and the dispersive term, there will be instability, which is called MI. In nonlinear dispersive media, MI is a nonlinear process, in which a continuous plane wave generates amplitude and frequency self-modulation through a nonlinear dispersive medium, resulting in exponential growth of small perturbations superimposed on a plane wave [20]. The study of MI regions is crucial in many fields and is the basis for interpreting or regulating various models or phenomena in different fields.

In this section, we focus on the MI of continuous waves in the gc-FL equation. The plane-wave solution of Eq. (3) has the following form

$$\begin{aligned} \begin{aligned} u_{\texttt {cw}}=c_1e^{i\theta }=c_1e^{i(kx+\omega t)},\\ v_{\texttt {cw}}=c_2e^{i\theta }=c_2e^{i(kx+\omega t)},\\ \end{aligned} \end{aligned}$$
(5)

where \(c_i(i=1,2)\), k, and \(\omega \) represent the amplitude, frequency, and wavenumber of background, respectively. Substituting Eq. (5) into Eq. (3), it yields the dispersion relation

$$\begin{aligned} \omega =-\frac{4c_1^2\beta k+4c_2^2\beta k-\alpha k^2-2\gamma k-4\beta }{k}. \end{aligned}$$

According to the MI theory, adding small perturbations (\(p,q\ll 1\)) to the plane-wave solution, then a perturbation solution can be given as

$$\begin{aligned} \begin{aligned} u_{\texttt {pert}}=\left( c_1+\epsilon p(x,t)\right) e^{i(kx+\omega t)},\\ v_{\texttt {pert}}=\left( c_2+\epsilon q(x,t)\right) e^{i(kx+\omega t)},\\ \end{aligned} \end{aligned}$$
(6)

with

$$\begin{aligned} \begin{aligned} p(z,t)=m_1e^{i(Kx+\varOmega t)}+n_1e^{-i(Kx+\varOmega t)},\\ q(z,t)=m_2e^{i(Kx+\varOmega t)}+n_2e^{-i(Kx+\varOmega t)},\\ \end{aligned} \end{aligned}$$

where \(m_i\) and \(n_i(i=1,2)\) are small real parameters, K and \(\varOmega \) represent the perturbed frequency and wavenumber, respectively. Substituting the perturbation solution (6) into system (3) generates a system of linear homogeneous equations for \(m_i\) and \(n_i\), that is

$$\begin{aligned} \begin{pmatrix} D_{1,1}&{} D_{1,2} &{} D_{1,3} &{} D_{1,4} \\ D_{2,1}&{} D_{2,2} &{} D_{2,3} &{} D_{2,4} \\ D_{3,1}&{} D_{3,2} &{} D_{3,3} &{} D_{3,4} \\ D_{4,1}&{} D_{4,2} &{} D_{4,3} &{} D_{4,4} \end{pmatrix} \begin{pmatrix} m_1 \\ m_2 \\ n_1 \\ n_2 \end{pmatrix}=0. \end{aligned}$$
(7)

with

$$\begin{aligned} \begin{aligned} D_{1,1}&=(-4\beta c_1^2+K\alpha -\varOmega )k^2\\&\quad +Kk(2\beta c_2^2+K\alpha -\varOmega )-4K\beta ,\\ D_{2,2}&=(-4\beta c_2^2+K\alpha -\varOmega )k^2\\&\quad +Kk(2\beta c_1^2+K\alpha -\varOmega )-4K\beta ,\\ D_{3,3}&=(-4\beta c_1^2-K\alpha +\varOmega )k^2\\&\quad +Kk(-2\beta c_2^2+K\alpha -\varOmega )+4K\beta ,\\ D_{4,4}&=(-4\beta c_2^2-K\alpha +\varOmega )k^2\\&\quad +Kk(-2\beta c_1^2+K\alpha -\varOmega )+4K\beta ,\\ D_{1,3}&=D_{3,1}=-4k^2c_1^2\beta ,\\ D_{2,4}&=D_{4,2}=-4k^2c_2^2\beta ,\\ D_{1,2}&=D_{2,1}=-2\beta c_1c_2k(K+2k),\\ D_{3,4}&=D_{4,3}=2\beta c_1c_2k(K-2k),\\ D_{1,4}&=D_{4,1}=D_{2,3}=D_{3,2}=-4c_1c_2\beta k^2.\\ \end{aligned} \end{aligned}$$

Based on the existence condition for solutions of linear homogeneous equations, and \(m_i\), \(n_i(i=1,2)\) are all nonzero real parameters, then the determinant of coefficient matrix D for \(m_i\) and \(n_i\) is equal to 0, namely

$$\begin{aligned} \texttt {det}(D)=\begin{vmatrix} D_{1,1}&D_{1,2}&D_{1,3}&D_{1,4} \\ D_{2,1}&D_{2,2}&D_{2,3}&D_{2,4} \\ D_{3,1}&D_{3,2}&D_{3,3}&D_{3,4} \\ D_{4,1}&D_{4,2}&D_{4,3}&D_{4,4} \end{vmatrix}=0, \end{aligned}$$
(8)

here \(D=(d_{ij})_{4\times 4}\) with \(d_{ij}\) being the polynomials about \(c_i, \alpha , \beta , \gamma , k, K, \varOmega \), which gives rise to a dispersion relation equation. By solving this equation, MI gain can be obtained

$$\begin{aligned} G&= |\texttt {Im}(\varOmega )|=\Big |\texttt {Im}\Big (\frac{K|\beta |\sqrt{(C^2k^4-2Ck^3+K^2)}}{(K^2-k^2)k}\Big )\Big |,\nonumber \\ C&= c_1^2+c_2^2. \end{aligned}$$
(9)

Below we analyze the above expressions of Eq. (9) and discuss the MI distribution characteristics of the gc-FL equation (3). Obviously, MI region occurs if and only if the perturbed frequency K satisfies the following inequality

$$\begin{aligned} |K|<|k|\sqrt{2Ck-C^2k^2}. \end{aligned}$$

Moreover, based on the MI theory, when perturbed frequency \(K=0\), we can obtain inequations

$$\begin{aligned} {\left\{ \begin{array}{ll} 2Ck-C^2k^2>0,\\ C\ne 0,k\ne 0, \end{array}\right. } \end{aligned}$$

namely

$$\begin{aligned} 0<k<\frac{2}{C}, \end{aligned}$$

this parameter condition can give rise to rogue wave solution, which is described as the left panel of Fig. 1. Obviously, the gain G is only related to four parameters \(\beta ,C,K\), and k, and has nothing to do with parameters \(\alpha \) and \(\gamma \). When setting \(\beta =0\), Eq. (9) is reduced to \(G=0\), which is MI. Since \(\beta \ne 0\) is mentioned in the previous section, then setting \(C=1\) and \(\beta =1\), as shown in Fig. 1, all the areas inside the red line are MI region except \(K=0\). The red dashed line in MI region is a stability region, namely, MI gain rate \(G=0\). In addition, the red line is also stability. With the increase in amplitude C, the area of MI region also decreases gradually. According to the gain expression, it can be seen that it is an even function with respect to K, so its MI distribution pattern is symmetrical with respect to \(K=0\), as shown in the right panel of Fig. 1.

Fig. 1
figure 1

Left panel: condition for the existence of rogue wave at the plane (k, C); Right panel: MI distribution of gain G on the background frequency k and perturbation frequency K plane, choosing free parameters \(C=1\) and \(\beta =1\)

Full size image

3 Infinitely many conservation laws and Darboux transformation for the gc-FL equation

In this section, our main aim is to construct infinitely many conservation laws and N-fold Darboux transformation of the gc-FL equation (3) with the following \(3\times 3\) matrix spectral problem:

$$\begin{aligned} \begin{aligned} \varPsi _x&= U(\lambda ;x,t)\varPsi ,\\ \varPsi _t&= V(\lambda ;x,t)\varPsi ,\\ \end{aligned} \end{aligned}$$
(10)

where

$$\begin{aligned} \begin{aligned} U(\lambda ;x,t)&=i\lambda ^{-2}J+\lambda ^{-1}Q_x, \\ V(\lambda ;x,t)&=\alpha i\lambda ^{-2}J+\alpha \lambda ^{-1}Q_x+2\beta iJQ^2\\&\quad -\gamma iJ-2i\beta \lambda JQ+i\beta \lambda ^{2}J, \\ \end{aligned} \end{aligned}$$
(11)

and

$$\begin{aligned} J= \begin{pmatrix} -1 &{} 0 &{}0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{pmatrix},~~~~ Q=\begin{pmatrix} 0 &{} u &{} v \\ u^*&{} 0 &{} 0 \\ v^*&{} 0 &{} 0 \end{pmatrix}.\\ \end{aligned}$$

Here, \(\varPsi =(\phi (x,t),\psi (x,t),\chi (x,t))^T\) is the vector eigenfunction, u and v are potential functions, i is the imaginary unit, \(\lambda \) is the spectral parameter, \(\alpha \), \(\beta \), \(\gamma \) are real parameters. The upper corner symbols T and \(*\) denote transposition and conjugation, respectively. According to compatibility condition, Eq. (3) can be easily deduced from the zero-curvature equation: \(U_t-V_x+[U,V]=0\).

3.1 Infinitely many conservation laws

For the gc-FL equation (3), \(u=u(t,x)\) and \(v=v(t,x)\) are the solutions. If there exists a pair of continuously differentiable functions \(\omega (t,x,u,v)\) and J(t, x, u, v), such that

$$\begin{aligned} \partial _t\omega (t,x,u,v)=\partial _xJ(t,x,u,v), \end{aligned}$$
(12)

the relationship is said to be a conservation law of Eq. (3), \(\omega (t,x,u,v)\) is called conserved density and J(t, x, u, v) is called associated flux. If the conserved density and associated flux approach zero sufficiently fast as |x| goes to infinity, then by integrating the conservation law (12) with respect to the independent variable x in the whole real domain, we can deduce that

$$\begin{aligned} I[u,v]=\frac{{\mathrm {d}}}{{\mathrm {d}}t}\int _{-\infty }^{\infty }\omega (t,x,u,v){\mathrm {d}}x=0, \end{aligned}$$
(13)

which is a constant of motion.

So far, many classical equations, such as KdV equation [49], mKdV equation [50], and Sine-Gordon equation [51], have been proved to possess infinitely many conservation laws. In 1975, Wadati, Sanuki, and Konno [52] proved that the AKNS equation also has infinitely many conservation laws from the linear problems corresponding to this family of equations. In 2018, Ling, Feng, and Zhu [41] established infinitely many conservation laws for the vector positive and negative orders Kaup–Newell hierarchy, and pointed out that the first nontrivial negative flow was corresponding to the coupled Fokas–Lenells equation.

Based on the Lax pair (10), now we will investigate the infinitely many conservation laws of the gc-FL equation (3). First, we introduce two quantities \(\varGamma _1=\varGamma _1(t,x)=\psi /\phi \) and \(\varGamma _2=\varGamma _2(t,x)=\chi /\phi \). Then, substituting them into the spectral problems (10), two Riccati-type equations can be generated

$$\begin{aligned} \begin{aligned} \varGamma _{1x}&=2i\lambda ^{-2}\varGamma _1+\lambda ^{-1}(u_x^*-u_x\varGamma _1^2-v_x\varGamma _1\varGamma _2),\\ \varGamma _{2x}&=2i\lambda ^{-2}\varGamma _2+\lambda ^{-1}(v_x^*-v_x\varGamma _2^2-u_x\varGamma _1\varGamma _2). \end{aligned} \end{aligned}$$
(14)

Substituting the following suitable expansions

$$\begin{aligned} \begin{aligned} u_x\varGamma _1&=\sum _{n=1}^{\infty }\left( \frac{i}{2}\lambda \right) ^{2n-1}\varGamma _1^{(n)},\\ v_x\varGamma _2&=\sum _{n=1}^{\infty }\left( \frac{i}{2}\lambda \right) ^{2n-1}\varGamma _2^{(n)}, \end{aligned} \end{aligned}$$
(15)

into the Riccati-type equations (14), we can obtain the recursion formulas for \(\varGamma _1^{(n)}\) and \(\varGamma _2^{(n)}\), \((n=1,2,3,\cdots )\), which means all the coefficients of the orders \(O(\lambda ^{-1}),O(\lambda ^{1}),O(\lambda ^{3}),\cdots ,O(\lambda ^{2k-1}), (k=0,1,2,\cdots )\) will be computed, respectively. It then follows

$$\begin{aligned}&\varGamma _1^{(1)}=u_xu_x^*, \end{aligned}$$
(16)
$$\begin{aligned}&\varGamma _1^{(2)}=-\varGamma _1^{(1)}\varGamma _2^{(1)}-\varGamma _1^{(1)2} +2i(\varGamma _{1x}^{(1)}-\frac{u_{xx}}{u_x}\varGamma _1^{(1)})\nonumber \\&\qquad =-u_xu_x^*v_xv_x^*-(u_xu_x^*)^2+2iu_xu_{xx}^*, \end{aligned}$$
(17)
$$\begin{aligned}&\varGamma _1^{(3)}=-\sum _{j=1}^{2}\varGamma _1^{(j)}(\varGamma _1^{(3-j)}+\varGamma _2^{(3-j)})\nonumber \\&\qquad +2i(\varGamma _{1x}^{(2)}-\frac{u_{xx}}{u_x}\varGamma _1^{(2)})\nonumber \\&\quad =2u_xu_x^*(u_xu_x^*+v_xv_x^*)^2-4u_xu_{xxx}^*\nonumber \\&\qquad -2iu_x[2u_{xx}^*(2u_xu_x^*+v_xv_x^*)\nonumber \\&\qquad +u_x^*(u_{xx}u_x^*+2v_xv_{xx}^*+v_{xx}v_x^*)], \end{aligned}$$
(18)
$$\begin{aligned}&\vdots \nonumber \\&\varGamma _1^{(k+1)}=-\sum _{j=1}^{k}\varGamma _1^{(j)}(\varGamma _1^{(k+1-j)}+\varGamma _2^{(k+1-j)})\nonumber \\&\qquad +2i(\varGamma _{1x}^{(k)}-\frac{u_{xx}}{u_x}\varGamma _1^{(k)})~ (k=3,4,5,\cdots ), \end{aligned}$$
(19)

and

$$\begin{aligned}&\varGamma _2^{(1)}=v_xv_x^*, \end{aligned}$$
(20)
$$\begin{aligned}&\varGamma _2^{(2)}=-\varGamma _1^{(1)}\varGamma _2^{(1)}-\varGamma _2^{(1)2} +2i(\varGamma _{2x}^{(1)}-\frac{v_{xx}}{v_x}\varGamma _2^{(1)})\nonumber \\&\quad =-u_xu_x^*v_xv_x^*-(v_xv_x^*)^2+2iv_xv_{xx}^*, \end{aligned}$$
(21)
$$\begin{aligned}&\varGamma _2^{(3)}=-\sum _{j=1}^{2}\varGamma _2^{(j)}(\varGamma _1^{(3-j)}+\varGamma _2^{(3-j)})\nonumber \\&\qquad +2i(\varGamma _{2x}^{(2)}-\frac{u_{xx}}{u_x}\varGamma _2^{(2)})\nonumber \\&\quad =2v_xv_x^*(u_xu_x^*+v_xv_x^*)^2-4v_xv_{xxx}^*\nonumber \\&\qquad -2iv_x[2v_{xx}^*(u_xu_x^*+2v_xv_x^*)\nonumber \\&\qquad +v_x^*(2u_xu_{xx}^*+u_{xx}u_x^*+v_{xx}v_x^*)], \end{aligned}$$
(22)
$$\begin{aligned}&\vdots \nonumber \\&\varGamma _2^{(k+1)}=-\sum _{j=1}^{k}\varGamma _2^{(j)}(\varGamma _1^{(k+1-j)}+\varGamma _2^{(k+1-j)})\nonumber \\&\qquad +2i(\varGamma _{2x}^{(k)}-\frac{v_{xx}}{v_x}\varGamma _2^{(k)})~ (k=3,4,5,\cdots ). \end{aligned}$$
(23)

From the first equation of the \(3\times 3\) matrix spectral problem (10), we have

$$\begin{aligned} \begin{aligned} (\ln \phi )_x&=-i\lambda ^{-2}+\lambda ^{-1}(u_x\varGamma _1+v_x\varGamma _2),\\ (\ln \phi )_t&=-i\alpha \lambda ^{-2}+i\gamma -i\beta \lambda ^2-2i\beta (uu^*+vv^*)\\&\quad +\alpha \lambda ^{-1}(u_x\varGamma _1+v_x\varGamma _2)+2i\beta \lambda (u\varGamma _1+v\varGamma _2). \end{aligned} \end{aligned}$$
(24)

Through the compatibility condition of (24), it yields

$$\begin{aligned}&\lambda ^{-1}(u_x\varGamma _1+v_x\varGamma _2)_t=-2i\beta (uu^*+vv^*)_x\nonumber \\&\quad +\alpha \lambda ^{-1}(u_x\varGamma _1+v_x\varGamma _2)_x+2i\beta \lambda (u\varGamma _1+v\varGamma _2)_x. \end{aligned}$$
(25)

Let \(\omega (t,x,u,v)=\sum _{k=1}^{\infty }\lambda ^{2k-1}\omega _k\) and \(J(t,x,u,v)=\sum _{k=1}^{\infty }\lambda ^{2k-1}J_k\). With the relations (16)–(23), it is natural to obtain the infinitely many conservation laws of the gc-FL equation (3) as follows

$$\begin{aligned} \frac{\partial \omega _k}{\partial t}=\frac{\partial J_k}{\partial x} ~(k=1,2,3,\cdots ), \end{aligned}$$
(26)

here \(\omega _k\) and \(J_k\) represent conserved density and associated flux, respectively. So the first two conserved densities and associated fluxes are

$$\begin{aligned} \begin{aligned} \omega _1&=u_xu_x^*+v_xv_x^*,\\ J_1&=-4\beta (uu^*+vv^*)+\alpha (u_xu_x^*+v_xv_x^*), \end{aligned} \end{aligned}$$
(27)

and

$$\begin{aligned} \begin{aligned} \omega _2&=-(u_xu_x^*+v_xv_x^*)^2+2i(u_xu_{xx}^*+v_xv_{xx}^*),\\ J_2&=-\alpha (u_xu_x^*+v_xv_x^*)^2+2i\alpha (u_xu_{xx}^*+v_xv_{xx}^*)\\&\quad -8i\beta (uu_x^*+vv_x^*). \end{aligned} \end{aligned}$$
(28)

Finally, we can obtain the recursion relations for the conserved density \(\omega _k\) and associated flux \(J_k\) with \(k\ge 3\),

$$\begin{aligned} \begin{aligned} \omega _k&=\varGamma _1^{(k)}+\varGamma _2^{(k)},\\ J_k&=\alpha (\varGamma _1^{(k)}+\varGamma _2^{(k)})-8i\beta (\varGamma _1^{(k-1)}+\varGamma _2^{(k-1)}), \end{aligned} \end{aligned}$$
(29)

here \(\varGamma _{1,2}^{(k)}\) and \(\varGamma _{1,2}^{(k-1)}\) are provided in the relations (16)–(23).

3.2 Darboux transformation for the gc-FL equation

Here, we derive the N-fold Darboux transformation of the gc-FL equation (3). Motivated by the results mentioned in [41], we can get the following symmetric relations

  • \(U(\lambda )=JU(-\lambda )J,~~V(\lambda )=JV(-\lambda )J\), \(U(\lambda )=-JU(\lambda ^*)^\dagger J,~~V(\lambda )=-JV(\lambda ^*)^\dagger J\),

  • \(\varPsi (-\lambda ;x,t)=J\varPsi (\lambda ;x,t)J\),  \(J[\varPsi (\lambda ;x,t)]^\dagger J=[\varPsi (\lambda ^*;x,t)]^{-1}\),

  • \(T(\lambda )=JT(-\lambda )J,~~[T(\lambda )]^{-1}=J[T(\lambda ^*)]^\dagger J\).

The above relationship equations can be deduced by direct calculation, and the upper corner symbol \(\dagger \) indicates the Hermitian adjoint. Due to above symmetric relations between {\(U(\lambda ),V(\lambda )\)} and {\(U(\lambda ^*),V(\lambda ^*)\)}, it is easy to find that if \(\varPsi _i\) is a nonzero solution of the spectral problems (10) at spectral parameter \(\lambda =\lambda _i\), then \(\varPsi _i^\dagger J\) is a nonzero solution of the conjugate form of system (10)

$$\begin{aligned} \varPhi _x=-\varPhi U, ~~\varPhi _t=-\varPhi V \end{aligned}$$

at spectral parameter \(\lambda =\lambda _i^*\), and here U, V have the same forms as in system (10). Through Darboux matrix T[1] (under above symmetric relations), we obtain a new system in the same form as Eq. (10), which can be written as follows

$$\begin{aligned} \varPsi [1]_x= & {} U[1](\lambda ;x,t)\varPsi [1],\nonumber \\ U[1](\lambda ;x,t)= & {} i\lambda ^{-2}J+\lambda ^{-1}Q[1]_x, \nonumber \\ \varPsi [1]_t= & {} V[1](\lambda ;x,t)\varPsi [1],\nonumber \\ V[1](\lambda ;x,t)= & {} \alpha i\lambda ^{-2}J+\alpha \lambda ^{-1}Q[1]_x +2\beta iJQ[1]^2\nonumber \\&-\gamma iJ -2i\beta \lambda JQ[1]+i\beta \lambda ^{2}J, \nonumber \\ \end{aligned}$$
(30)

where

$$\begin{aligned} \begin{aligned} U[1]&=T[1]_xT[1]^{-1}+T[1]UT[1]^{-1}, \\ V[1]&=T[1]_tT[1]^{-1}+T[1]VT[1]^{-1}. \\ \end{aligned} \end{aligned}$$
(31)

Based on the above Darboux matrix symmetric relations and the loop method, T[1], \(T[1]^{-1}\) can be constructed as

$$\begin{aligned} \begin{aligned} T[1]&=E+\frac{A_1}{\lambda -\lambda _1^*}-\frac{JA_1J}{\lambda +\lambda _1^*}, \\ T[1]^{-1}&=E+\frac{JA_1^\dagger J}{\lambda -\lambda _1}-\frac{A_1^\dagger }{\lambda +\lambda _1}, \\ \end{aligned} \end{aligned}$$
(32)

with

$$\begin{aligned} \begin{aligned} A_1=&|x_1> <y_1|J,~~|x_1>=K_1|y_1>,\\ K_1=&{\mathrm {diag}}(-\varTheta _1^{*-1},\varTheta _1^{-1},\varTheta _1^{-1}),\\ \varTheta _1=&\frac{2[\lambda _1^*(|\psi _1|^2+|\chi _1|^2)-\lambda _1|\phi _1|^2]}{\lambda _1^{*2}-\lambda _1^2},\\ \end{aligned} \end{aligned}$$
(33)

where E is the identify matrix, \(|y_1>=\varPsi _1=(\phi _1,\psi _1,\chi _1)^T\) is a special solution with \(u=u[0],~v=v[0]\), which satisfies system (10) at spectral parameter \(\lambda =\lambda _1\), and \(<y_1|=(|y_1>)^\dagger \). Substituting Eq. (32) into Eq. (31) and collecting all the coefficients, the relationship between \(Q_1\) and Q can be deduced as

$$\begin{aligned} Q[1]=Q+A_1-JA_1J. \end{aligned}$$
(34)

Furthermore, the concrete expressions of the relationship between the old and the new solutions for the gc-FL equation (3) can be rewritten as

$$\begin{aligned} \begin{aligned} u[1]=u[0]-\frac{2\phi _1\psi _1^*}{\varTheta _1^*},~~ v[1]=v[0]-\frac{2\phi _1\chi _1^*}{\varTheta _1^*}. \end{aligned} \end{aligned}$$
(35)

Proposition 1

The N-fold DT for the gc-FL equation (3) has the following form

$$\begin{aligned} T_N= & {} T[N]T[N-1]\cdots T[1]\nonumber \\= & {} E+\sum _{i=1}^N \left( \frac{C_i}{\lambda -\lambda _i^*} -\frac{JC_iJ}{\lambda +\lambda _i^*}\right) , \end{aligned}$$
(36)

and

$$\begin{aligned} T_N^{-1}= & {} T[1]^{-1}T[2]^{-1}\cdots T[N]^{-1}\nonumber \\= & {} E+\sum _{i=1}^N \left( \frac{JD_i^\dagger J}{\lambda -\lambda _i}-\frac{D_i^\dagger }{\lambda +\lambda _i}\right) , \end{aligned}$$
(37)

where

$$\begin{aligned} C_i= & {} \mathrm{Res}|_{\lambda =\lambda _i^*}(T_N), ~~D_i=\mathrm{Res}|_{\lambda =\lambda _i}(T_N^{-1}),\\ A_i= & {} |x_i> <y_i|J,~~|x_i>=K_i|y_i>,\\ K_i= & {} {\mathrm {diag}}(-\varTheta _i^{*-1},\varTheta _i^{-1},\varTheta _i^{-1}),\\ |y_i>= & {} \varPsi _i=(\phi _i,\psi _i,\chi _i)^T,\\ \varTheta _i= & {} \frac{2[\lambda _i^*(|\psi _i|^2+|\chi _i|^2)-\lambda _i|\phi _i|^2]}{\lambda _i^{*2}-\lambda _i^2},\\&(i=1,2,\ldots ,N). \end{aligned}$$

Proof

Taking the residue on both sides of Eq. (36), it yields

$$\begin{aligned} \begin{aligned} \mathrm{Res}|_{\lambda =\lambda _i^*}(T_N)&=\left( E+\frac{A_N}{\lambda _i^*-\lambda _N^*}-\frac{JA_NJ}{\lambda _i^*+\lambda _N^*}\right) \\&\quad \cdots A_i\cdots \left( E+\frac{A_1}{\lambda _i^*-\lambda _N^*}\right. \\&\quad \left. -\frac{JA_1J}{\lambda _i^*+\lambda _N^*}\right) =C_i,\\ \mathrm{Res}|_{\lambda =-\lambda _i^*}(T_N)&=-\left( E+\frac{A_N}{-\lambda _i^*-\lambda _N^*}-\frac{JA_NJ}{-\lambda _i^*+\lambda _N^*}\right) \\&\quad \cdots JA_iJ\cdots \left( E+\frac{A_1}{-\lambda _i^*-\lambda _N^*}\right. \\&\quad \left. -\frac{JA_1J}{-\lambda _i^*+\lambda _N^*}\right) .\\ \end{aligned} \end{aligned}$$
(38)

Because of \(\mathrm{Res}|_{\lambda =\lambda _i^*}(T_N)=-J\mathrm{Res}|_{\lambda =-\lambda _i^*}(T_N)J\), Eq. (36) is valid. Similarly, Eq. (37) can also be proved.

This completes the proof of Proposition 1. \(\square \)

Fig. 2
figure 2

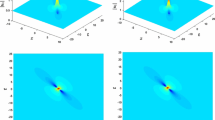
The first- to third-order rogue waves of the gc-FL equation (3) with parameters:\((\alpha ,\beta ,\gamma ,c_1,c_2)=(3,1,2,\frac{\sqrt{3}}{3},\frac{\sqrt{6}}{3})\); and \((m_i,n_i)=(0,0)\) in the first column, \((m_1,n_1)=(100,0)\) and \((m_1,m_2,n_1,n_2)=(100,0,100,0)\) in the second column, \((m_1,m_2,n_1,n_2)=(10,10000,0,0)\) in the third column

Full size image
Fig. 3
figure 3

The first-order interaction solution between a soliton and a rogue wave of the gc-FL equation (3) with parameters: \((\alpha ,\beta ,\gamma ,c_1,c_2)=(3,1,2,1,0)\). The first and second columns show 3D separate structure and the corresponding contour map with \(d=\frac{1}{10}\), respectively; the third column shows collision process over time with \(d=1\)

Full size image
Fig. 4
figure 4

The second-order interaction solution between two solitons and second-order rogue wave of the gc-FL equation with parameters:\((\alpha ,\beta ,\gamma ,c_1,c_2)=(3,1,2,1,0)\); From the left column to the right column the parameters \((d,m_1,n_1)\) are (1,0,0), \((\frac{1}{1000},0,0)\), (1,1000,0), and \((\frac{1}{10000000},1000,0)\), respectively. The odd columns show merge structure; the even columns show separate structure

Full size image

According to the Darboux matrix T[N], we can get the transformations between seed solutions u[0], v[0] and new potential functions u[N], v[N], which is described as Theorem 1.

Theorem 1

The N-fold Darboux transformation of the spectral problems (10) gives rise to the following compact recurrence formulas

$$\begin{aligned} \begin{aligned} u[N]=&u[0]-\frac{2 }{|P|}\left| \begin{array}{cc} P &{} \eta _2^\dagger \\ \eta _1 &{} 0 \\ \end{array} \right| ,\\ v[N]=&v[0]-\frac{2 }{|P|}\left| \begin{array}{cc} P &{} \eta _3^\dagger \\ \eta _1 &{} 0 \\ \end{array} \right| ,\\ \end{aligned} \end{aligned}$$
(39)

where

$$\begin{aligned} \begin{aligned}&P=(p_{ij})_{N\times N},~~p_{ij}=\frac{\varPsi _i^\dagger J\varPsi _j}{\lambda _i^*-\lambda _j}+\frac{\varPsi _i^\dagger \varPsi _j}{\lambda _i^*+\lambda _j},\\&\varPsi _i=(\phi _i^*,\psi _i^*,\chi _i^*),\\&\varPsi _j=(\phi _j^*,\psi _j^*,\chi _j^*)~(1\le i,j\le N),\\&\eta _1=(\phi _1,\phi 2,...,\phi _N), ~~\eta _2=(\psi _1,\psi _2,...,\psi _N),\\&\eta _3=(\chi _1,\chi _2,...,\chi _N). \end{aligned} \end{aligned}$$

Proof

According to the derivation process of one-fold Darboux transformation, there has the following relation after N-fold Darboux transformation, that is

$$\begin{aligned} T_{N,x}+T_{N}U=U[N]T_{N}. \end{aligned}$$
(40)

Substituting Eq. (36) into above equation, which results into the following potential function relation

$$\begin{aligned} Q[N]=Q+\sum _{i=1}^N(C_i-JC_iJ). \end{aligned}$$
(41)

Then, according to the relative properties of matrix rank, it is not difficult to deduce Rank(\(C_i\))=1. So it can be assumed that \(C_i=|x_i> <y_i|\) and \(|y_i>=\varPsi _i=(\phi _i,\psi _i,\chi _i)^T\). Since \(T_NT_N^{-1}=E\) and \(\varPsi _i^\dagger J\) is a nonzero solution of the conjugate form of system (10) at \(\lambda =\lambda _i^*\), thus

$$\begin{aligned} <y_i|T_N^{-1}\mid _{\lambda =\lambda _i^*}=0,~~\varPsi _i^\dagger JT_N^{-1}\mid _{\lambda =\lambda _i^*}=0. \end{aligned}$$

Comparing the above two expressions, without loss of generality, we can choose \(<y_i|=\varPsi _i^\dagger J\). Furthermore, according to \(T_N\mid _{\lambda =\lambda _j}\varPsi _j=0\) and Eq. (36), it holds

$$\begin{aligned}&\varPsi _j+\sum _{i=1}^N\big (\frac{|x_i>\varPsi _i^\dagger J\varPsi _j}{\lambda _j-\lambda _i^*}\nonumber \\&\quad -\frac{J|x_i>\varPsi _i^\dagger \varPsi _j}{\lambda _j+\lambda _i^*}\big )=0,~~(i=1,2,\ldots N). \end{aligned}$$
(42)

Solving Eq. (42), it yields

$$\begin{aligned}&\mathrm{First~~row:}~~(|x_{1,1}>,|x_{2,1}>,...,|x_{N,1}>)\nonumber \\&\quad =(|y_{1,1}>,|y_{2,1}>,...,|y_{N,1}>)P^{-1}\nonumber \\&\quad =(\phi _1,\phi _2,...,\phi _N)P^{-1},\nonumber \\&\mathrm{Other~~rows:}~~(|x_{1,i}>,|x_{2,i}>,...,|x_{N,i}>)\nonumber \\&\quad =(|y_{1,i}>,|y_{2,i}>,...,|y_{N,i}>)S^{-1}\nonumber \\&\quad =(\phi _1,\phi _2,...,\phi _N)S^{-1}~~(i=2,3), \end{aligned}$$
(43)

with

$$\begin{aligned} \begin{aligned}&P=(p_{ij})_{N\times N},~~p_{ij}=\frac{\varPsi _i^\dagger J\varPsi _j}{\lambda _i^*-\lambda _j}+\frac{\varPsi _i^\dagger \varPsi _j}{\lambda _i^*+\lambda _j},\\&S=(s_{ij})_{N\times N},~~s_{ij}=\frac{\varPsi _i^\dagger J\varPsi _j}{\lambda _i^*-\lambda _j}-\frac{\varPsi _i^\dagger \varPsi _j}{\lambda _i^*+\lambda _j}~(1\le i,j\le N). \end{aligned} \end{aligned}$$
(44)

Finally, substituting Eqs. (43)–(44), one gets {\(u[N],v[N]\)} and {u[0],   v[0]} has the following relations

$$\begin{aligned} \begin{aligned} u[N]=&u[0]+\left( \sum _{i=1}^NC_i-JC_iJ\right) _{12}\\ =&u[0]+2\sum _{i=1}^{N}\left( |x_{i,1}>\psi _i^*\right) =u[0]-\frac{2 }{|P|}\left| \begin{array}{cc} P &{} \eta _2^\dagger \\ \eta _1 &{} 0 \\ \end{array} \right| ,\\ v[N]=&v[0]+\left( \sum _{i=1}^NC_i-JC_iJ\right) _{13}\\ =&v[0]+2\sum _{i=1}^{N}(|x_{i,1}>\chi _i^*) =v[0]-\frac{2 }{|P|}\left| \begin{array}{cc} P &{} \eta _3^\dagger \\ \eta _1 &{} 0 \\ \end{array} \right| . \end{aligned} \end{aligned}$$
(45)

This completes the proof of Theorem 1. \(\square \)

4 Interaction solutions between localized waves for the gc-FL equation

In this section, we turn our attention to the construction of higher-order localized waves and their interaction solutions for the gc-FL equation (3). On account of a seed solution under the same spectral parameter \(\lambda \) cannot realize the iterative process of classical DT, it is necessary to introduce a limit process to avoid this deficiency and obtain higher-order localized wave solutions of Eq. (3). To this end, assuming the seed solutions as follows

$$\begin{aligned}&u[0]=c_1\exp (i\theta ),~~v[0]=c_2\exp (i\theta ),~~\theta =ax+bt,\nonumber \\&b=-4\beta (c_1^2+c_2^2)+(a\alpha +2\gamma )+\frac{4\beta }{a},~~(a, c_1, c_2\in {\mathbb {R}}).\nonumber \\ \end{aligned}$$
(46)

By substituting the seed solutions (46) into the Lax pair (10) of the gc-FL equation (11), there appears a variable coefficient differential system. Then, we can convert this variable coefficient differential equations to constant coefficient differential equations through a gauge transformation L=diag(\(e^{-\frac{2i}{3}\theta },e^{\frac{i}{3}\theta },e^{\frac{i}{3}\theta }\)). Finally, the corresponding fundamental vector solution of the gc-FL equation (3) is derived, that is

$$\begin{aligned} \varPsi = \begin{pmatrix} \phi \\ \psi \\ \chi \\ \end{pmatrix} = \begin{pmatrix} (C_1e^{A}-C_2e^{-A})e^{\frac{i}{2}\theta } \\ \rho _1(C_2e^{A}-C_1e^{-A})e^{-\frac{i}{2}\theta }-dc_2e^B\\ \rho _2(C_2e^{A}-C_1e^{-A})e^{-\frac{i}{2}\theta }+dc_1e^B \end{pmatrix}, \end{aligned}$$
(47)

with

$$\begin{aligned}&C_1 = \frac{\Big (a\lambda ^2+2-\sqrt{(a\lambda ^2+2)^2-4a^2\lambda ^2(c_1^2+c_2^2)}\Big )^{\frac{1}{2}}}{\sqrt{(a\lambda ^2+2)^2-4a^2\lambda ^2(c_1^2+c_2^2)}},\nonumber \\&C_2 =\frac{\Big (a\lambda ^2+2+\sqrt{(a\lambda ^2+2)^2-4a^2\lambda ^2(c_1^2+c_2^2)}\Big )^{\frac{1}{2}}}{\sqrt{(a\lambda ^2+2)^2-4a^2\lambda ^2(c_1^2+c_2^2)}},\nonumber \\&A=\frac{i\sqrt{(a\lambda ^2+2)^2-4a^2\lambda ^2(c_1^2+c_2^2)}}{2a\lambda ^2}\nonumber \\&\quad \Big [ax+(a\alpha +2\beta \lambda ^2)t+\sum _{i=1}^{N}\kappa _i\xi ^{2i}\Big ],\nonumber \\&B=\frac{i(x+(\alpha -\gamma \lambda ^2+\beta \lambda ^4)t)}{\lambda ^2},\nonumber \\&\rho _1=\frac{c_1}{\sqrt{c_1^2+c_2^2}},~~\rho _2=\frac{c_2}{\sqrt{c_1^2+c_2^2}},\nonumber \\&\kappa _i=m_i+in_i,~~(d,m_i,n_i\in {\mathbb {R}}), \end{aligned}$$

where \(\xi \) represents a small disturbance parameter. Next, we consider the double roots of the characteristic polynomial of the time partial matrix \(U_0\), and then we can get a constraint condition satisfied by the spectral parameter as follows

$$\begin{aligned} (a\lambda ^2+2)^2-4a^2C\lambda ^2=0, \end{aligned}$$

where

$$\begin{aligned} C=c_1^2+c_2^2. \end{aligned}$$

By solving the above constraint condition, it follows spectral parameter \(\lambda =\pm (\sqrt{C}\pm \sqrt{\frac{aC-2}{a}})\). It is not difficult to find that whether there is an imaginary part of the spectral parameter \(\lambda \) depends on the frequency a and the amplitude C, while the real part completely depends on the amplitude C. However, when the spectral parameter \(\lambda \) contains the imaginary part, namely \(0<a<\frac{2}{C}\), then there are rogue wave solutions of the gc-FL equation (3), which is consistent with the constraint condition for the existence of rogue waves obtained from the MI analysis in Sect. 2 of this article. To obtain the rogue wave solutions, for convenience of calculation, we choose \(a=1\) and \(C=1\), it thus transpires that the corresponding spectral parameter \(\lambda =\lambda _0=1+i\). Applying limitation approach to construct the N-fold generalized Darboux transformation of the gc-FL equation, we can get the relations between the new solutions u[N],  v[N] and the seed solutions u[0],  v[0], whose detailed process is shown in Theorem 2.

Theorem 2

The N-fold generalized Darboux transformation of the spectral problems (10) gives rise to the following compact recurrence formulas

$$\begin{aligned} \begin{aligned} u[N]=&u[0]-\frac{2 }{|{\hat{P}}|}\left| \begin{array}{cc} {\hat{P}} &{} {\hat{\eta }}_2^\dagger \\ {\hat{\eta }}_1 &{} 0 \\ \end{array} \right| ,\\ v[N]=&v[0]-\frac{2 }{|{\hat{P}}|}\left| \begin{array}{cc} {\hat{P}} &{} {\hat{\eta }}_3^\dagger \\ {\hat{\eta }}_1 &{} 0 \\ \end{array} \right| , \end{aligned} \end{aligned}$$
(48)

where

$$\begin{aligned} \begin{aligned}&{\hat{P}}=({\hat{p}}_{kl})_{N\times N},~~1\le k,l\le N,\\&{\hat{\eta }}_1=(\phi _1^{[0]},\phi _1^{[1]},\ldots ,\phi _1^{[N-1]}),\\&{\hat{\eta }}_2=(\psi _1^{[0]},\psi _1^{[1]},\ldots ,\psi _1^{[N-1]}),\\&{\hat{\eta }}_3=(\chi _1^{[0]},\chi _1^{[1]},\ldots ,\chi _1^{[N-1]}). \end{aligned} \end{aligned}$$
(49)

Proof

Let the spectral parameter \(\lambda =\lambda _1=1+i+\xi ^2\) and put it into Eq. (46). By expanding \(\varPsi _1\) at \(\xi =0\), it arrives at

$$\begin{aligned} \varPsi _1(\xi )=\varPsi |_{\lambda =\lambda _1}=\sum _{k=0}^{N-1}\varPsi _1^{[k]}\xi ^{2k}+O(\xi ^{2N}), \end{aligned}$$
(50)

with

$$\begin{aligned} \varPsi _1^{[k]}=\left( \begin{array}{c} \phi _1^{[k]} \\ \psi _1^{[k]} \\ \chi _1^{[k]} \\ \end{array} \right) =\frac{1}{(2k)!}\frac{\partial ^k\varPsi _1}{\partial \xi ^k}|_{\xi =0}. \end{aligned}$$
(51)

Additionally, when \(\lambda _i=\lambda _j=\lambda _1\), through the same limit processing technique, \(p_{ij}\) in Eq. (44) can be rewritten as

$$\begin{aligned} \begin{aligned} p_{ij}=&-\frac{2[(1+\xi ^2+i)(|\psi _1|^2+|\chi _1|^2)-(1+\xi ^{*2}-i)|\phi _1|^2]}{(2+\xi ^2+\xi ^{*2})(2i+\xi ^2-\xi ^{*2})}\\ =&\sum _{k,l=1}^{N}{\hat{p}}_{kl}\xi ^{2(k-1)}\xi ^{2(l-1)}+O(|\xi |^{4N}), \end{aligned} \end{aligned}$$
(52)

with

$$\begin{aligned}&{\hat{p}}_{kl}= \lim _{\xi ,\xi ^*\rightarrow 0}\frac{1}{(2(k-1))!(2(l-1))!} \frac{\partial ^{2(k+l-2)}p_{ij}}{\partial \xi ^{2(k-1)}\xi ^{*2(l-1)}}\\&\quad |_{(\lambda _i=\lambda _1,\lambda _j=\lambda _1)}. \end{aligned}$$

So N-order localized wave solutions of the gc-FL equation (3), namely, the formulas (48) can be deduced.

This completes the proof of Theorem 2. \(\square \)

Fig. 5
figure 5

The third-order interaction solution between three solitons and third-order rogue wave of the gc-FL equation (3) with the parameters \((\alpha ,\beta ,\gamma ,c_1,c_2,d,m1,m2,n1,n2)\) from the left column to the right column are \((3,1,2,1,0,\frac{1}{1000},0,0,0,0)\), \((3,1,2,1,0,\frac{1}{10000000},100,0,100,0)\), and \((3,1,2,1,0,\frac{1}{10000000},10,10000,0,0)\), respectively. Top line: dark solitons interact with different structures of the third-order rogue waves; Bottom line: bright solitons interact with different structures of the third-order rogue waves

Full size image
Fig. 6
figure 6

The first-order interaction solution between a breather and a rogue wave of the gc-FL equation (3) with parameters: \((\alpha ,\beta ,\gamma ,c_1,c_2)=(3,1,2,\frac{\sqrt{3}}{3},\frac{\sqrt{6}}{3})\). Top line: 3D separate structure and corresponding contour pattern with \(d=\frac{1}{100}\); Bottom line: 3D merge structure and corresponding contour pattern with \(d=1\)

Full size image
Fig. 7
figure 7

The second-order interaction solution between two breathers and second-order rogue wave of the gc-FL equation (3) with parameters: \((\alpha ,\beta ,\gamma ,c_1,c_2)=(3,1,2,\frac{\sqrt{3}}{3},\frac{\sqrt{6}}{3})\); From the left column to the right column the parameters \((d,m_1,n_1)\) are (1,0,0), \((\frac{1}{1000},0,0)\), (1,1000,0), and \((\frac{1}{10000000},1000,0)\), respectively. The odd columns show merge structure; the even columns show separate structure

Full size image
Fig. 8
figure 8

The corresponding contour patterns of Fig. 7

Full size image

As k increases, the expression of vector function \(\varPsi _1^{[k]}\) in Eq. (51) will be more complicated. Here, we only give the explicit expressions for \(k=0,1\), that is

$$\begin{aligned} \begin{aligned} \varPsi _1^{[0]}=&\left( \begin{array}{c} \phi _1^{[0]} \\ \psi _1^{[0]} \\ \chi _1^{[0]} \\ \end{array} \right) =\left( \begin{array}{c} \frac{1}{4}[(8i\beta +2\alpha )t+2x+i-1]\sqrt{2+2i} e^{\frac{i}{2}\theta } \\ \frac{1}{4}c_1[(8i\beta +2\alpha )t+2x-i+1]\sqrt{2+2i}e^{-\frac{i}{2}\theta }-dc_2e^{\frac{1}{2}\theta _0} \\ \frac{1}{4}c_2[(8i\beta +2\alpha )t+2x-i+1]\sqrt{2+2i}e^{-\frac{i}{2}\theta }+dc_1e^{\frac{1}{2}\theta _0} \\ \end{array} \right) ,\\ \varPsi _1^{[1]}=&\left( \begin{array}{c} \phi _1^{[1]} \\ \psi _1^{[1]} \\ \chi _1^{[1]} \\ \end{array} \right) =\left( \begin{array}{c} \frac{1}{48}\varOmega _1\sqrt{2+2i}e^{\frac{i}{2}\theta } \\ \frac{1}{48}c_1\varOmega _2\sqrt{2+2i}e^{-\frac{i}{2}\theta }+\frac{1}{2}dc_2[\left( 1-i \right) \left( \alpha +4\,\beta \right) t+ \left( 1-i \right) x]e^{\frac{1}{2}\theta _0} \\ \frac{1}{48}c_2\varOmega _2\sqrt{2+2i}e^{-\frac{i}{2}\theta }-\frac{1}{2}dc_1[\left( 1-i \right) \left( \alpha +4\,\beta \right) t+ \left( 1-i \right) x]e^{\frac{1}{2}\theta _0} \\ \end{array} \right) , \end{aligned} \end{aligned}$$
(53)

with

$$\begin{aligned} \theta _0= & {} (-2i\gamma -4\beta +\alpha )t+x, \nonumber \\ \varOmega _1= & {} (2i\alpha ^3-24i\alpha ^2\beta -96i\alpha \beta ^2\nonumber \\&+128i\beta ^3-2\alpha ^3-24\beta \alpha ^2+96\beta ^2\alpha +128\beta ^3)t^3\nonumber \\&+(6i\alpha ^2-48i\alpha \beta -96i\beta ^2-6\alpha ^2-48\beta \alpha \nonumber \\&+96\beta ^2)t^2x+(-6i\alpha ^2+96i\beta ^2+48\beta \alpha )t^2\nonumber \\&+(6i\alpha -24i\beta -6\alpha -24\beta )tx^2\nonumber \\&+(-12i\alpha +48\beta )tx\nonumber \\&+(21i\alpha +36i\beta -15\alpha +12\beta )t\nonumber \\&+(-2+2i)x^3-6ix^2+(-15+21i)x\nonumber \\&+24in_1+24m_1+3-6i,\nonumber \\ \varOmega _2= & {} (2i\alpha ^3-24i\alpha ^2\beta -96i\alpha \beta ^2+128i\beta ^3\nonumber \\&-2\alpha ^3-24\beta \alpha ^2+96\beta ^2\alpha +128\beta ^3)t^3\nonumber \\&+(6i\alpha ^2-48i\alpha \beta -96i\beta ^2-6\alpha ^2\nonumber \\&-48\beta \alpha +96\beta ^2)t^2x\nonumber \\&-(-6i\alpha ^2+96i\beta ^2+48\beta \alpha )t^2\nonumber \\&+(6i\alpha -24i\beta -6\alpha -24\beta )tx^2\nonumber \\&-(-12i\alpha +48\beta )tx\nonumber \\&+(21i\alpha +36i\beta -15\alpha +12\beta )t\nonumber \\&+(-2+2i)x^3+6ix^2+(-15+21i)x\nonumber \\&+24in_1+24m_1-3+6i. \end{aligned}$$
(54)

Therefore, utilizing the above formulas with different parameters \(N=1,2,3\) in Theorem 2, the first-order, second-order, and third-order semi-rational solutions of the gc-FL equation (3) can be obtained. As N becomes larger, the expression of the solution becomes more complicated. For simplicity, here only the specific expression for the first-order semi-rational solution is given

$$\begin{aligned} \begin{aligned} u[1]=&c_1e^{i\theta }+\frac{2ic_1\varXi _1e^{i\theta }+2i\sqrt{1+i}dc_2\varXi _2e^{\frac{\theta _0^*+i\theta }{2}}}{\sqrt{(}2)(1+i)d^2e^{\frac{\theta _0+\theta _0^*}{2}}+\varXi _3},\\ v[1]=&c_2e^{i\theta }+\frac{2ic_2\varXi _1e^{i\theta }-2i\sqrt{1+i}dc_1\varXi _2e^{\frac{\theta _0^*+i\theta }{2}}}{\sqrt{2}(1+i)d^2e^{\frac{\theta _0+\theta _0^*}{2}}+\varXi _3}, \end{aligned}\nonumber \\ \end{aligned}$$
(55)

with

$$\begin{aligned} \begin{aligned} \theta =&x+(\alpha +2\gamma )t, ~~\theta _0=(\alpha -2i\gamma -4\beta )t+x,\\ \varXi _1=&(2\alpha ^2+32\beta ^2)t^2+2x^2+4\alpha xt\\&+2i(1+4\beta )t+2ix-1,\\ \varXi _2=&(8i\beta +2\alpha )t+2x-1+i,\\ \varXi _3=&2i(16\beta ^2+\alpha ^2)t^2+2ix^2+4i\alpha xt\\&+2(\alpha -4\beta )t+2x+i. \end{aligned} \end{aligned}$$
Fig. 9
figure 9

The third-order interaction solution between three breathers and third-order rogue wave of the gc-FL equation (3) with parameters: \((\alpha ,\beta ,\gamma ,c_1,c_2,d,m1,m2,n1,n2)\) from the left column to the right column are \((3,1,2,1,0,\frac{1}{1000},0,0,0,0)\), \((3,1,2,1,0,\frac{1}{10000000},100,0,100,0)\), and \((3,1,2,1,0,\frac{1}{10000000},10,10000,0,0)\), respectively

Full size image
Fig. 10
figure 10

The corresponding contour maps of Fig. 9

Full size image

Next, we will analyze the dynamical behavior characteristics of the above-mentioned first- to third-order solutions of the gc-FL equation (3). It is not difficult to see that u[1] and v[1] in Eqs. (55) are controllable with parameters \(\alpha \), \(\beta \), \(\gamma \), d, and \(c_i~(i=1..2)\), the latter two parameters play a leading role. According to the selection of parameters d and \(c_i\), there are usually the following three structural solutions.

Case 1. Rogue waves

Choosing the parameters \(d=0\) and \(c_i\ne 0~(i=1..2)\), then Eq. (55) can be rewritten as

$$\begin{aligned} \begin{aligned} u[1]=&c_1e^{i\theta }\Big (1-\frac{2i\varXi _1}{\varXi _3}\Big ),\\ v[1]=&c_2e^{i\theta }\Big (1-\frac{2i\varXi _1}{\varXi _3}\Big ), \end{aligned} \end{aligned}$$
(56)

which are all first-order rogue wave solution of the gc-FL equation (3). From the above expression, it is obvious that these two components u[1], v[1] are proportional, the ratio is \(\frac{c_1}{c_2}\) and these maximum amplitudes have nearly three times the amplitudes of the background wave. As N increases, there are two additional parameters \((m_i,n_i)\), which can control the structure of the higher-order rogue waves solution.

For \(N=2\), there are two structure patterns: a second-order fundamental rogue wave and a second-order triangular rogue wave composed of three standard first-order rogue waves (also known as the triplet structure). When \(N=3\), in addition to above two structures: the third-order fundamental rogue wave and the third-order triangle rogue waves, there is also an additional pentagon rogue waves pattern. The so-called triangle and pentagon are both composed of six standard first-order rogue waves, but they are distributed differently. According to the above analysis, the number of corresponding parameters \(m_i,~n_i\) increase with N increases, and then there are a variety of combination forms about parameters \(m_i,~n_i\), which give rise to more abundant structures of higher-order rogue wave solutions. In short, higher-order rogue wave solutions can be roughly divided into three types: the N-order fundamental structure, the combination of N-triplet of the standard first-order rogue wave, and the combination structure of different order rogue waves, whose order less than \(\frac{N(N+1)}{2}\). Since u and v components are similar in structure, only the density distribution of rogue waves for the u component is given here, as presented in Fig. 2. From top to bottom, the first- to third-order rogue waves are depicted, respectively. And from left to right, the different structures of the same order rogue waves are represented.

Case 2. Soliton+Rogue waves

When parameters \((d,c_1)\ne (0,0)\) and \(c_2=0\) in Eqs. (55), the first-order semi-rational solution of the gc-FL equation can be obtained. At this time, there are two kinds of semi-rational solutions with different structures: bright soliton interacts with rogue wave and dark soliton interacts with rogue wave. The 3D diagrams and contour maps of u and v components are depicted in the first two columns in Fig. 3. The soliton propagates below the background wave in the u component, while the soliton in the v component propagates above the background wave. Obviously, the background amplitude of the u component is 1, and the background amplitude of the v component is 0, which depends entirely on their corresponding seed solutions. In addition, by changing the value of |d| to adjust the strength of the interactional structure of the solution, it results in the variation of the distance between the soliton (dark or bright) and the rogue wave, that is, merge or separation.

The last column of Fig. 3 depicts the collision and interaction process of the dark soliton in the u component and the bright soliton in the v component with rogue wave at different times, respectively. Obviously, both u and v components propagate along the positive direction of the x-axis with time, and at the beginning, only bright and dark soliton solutions located on the negative half of the x-axis exist at \(t=-50\). At \(t=0\), a rogue wave suddenly appears and interacts with the soliton, and causes the energy transfer between them, which results in an increase in the amplitude of the rogue wave and a decrease in the amplitude of the soliton. Then, at \(t=50\), the rogue wave disappears, and the soliton continues to propagate along the positive direction of the x-axis without changing its shape, wave width, and amplitude. Since the background wave height of the rogue wave in the v component is 0, the amplitude of the rogue wave relative to the bright soliton is not obvious when it is close to the bright soliton, but the amplitude of the rogue wave will increase sharply when the complete collision occurs.

According to the formula (48) for N-order localized wave solution of the gc-FL equation given in Theorem 2, the second-order localized wave solution can be obtained by setting the parameter \(N=2\). There are two structures with parameters \((\alpha ,\beta ,\gamma ,c_1,c_2)=(3,1,2,1,0)\): a second-order fundamental rogue wave interacts with two solitons and triplet rogue wave interacts with two solitons. When \(d=1\), the two components \(u_2\) and \(v_2\) show strong interaction as odd columns (merge structure) in Fig. 4; while \(d=\frac{1}{1000}\) or \(\frac{1}{10000000}\), the two components \(u_2\) and \(v_2\) show weak interaction as even columns (separate structure) in Fig. 4. For the v component, it is not difficult to find that the rogue wave can be clearly seen in the case of strong interaction, while the rogue wave is not obvious in the case of weak interaction. The main reason is that the energy surge of the rogue wave driven by soliton under the strong interaction. However, during the weak interaction, the soliton does not completely collide with the rogue wave, so the soliton has more energy relative to the background wave than the rogue wave relative to the background wave, which is demonstrated as the even columns in the last row of Fig. 4.

For \(N=3\) in Eq. (48), the third-order localized wave solution of the gc-FL equation (3) can be naturally deduced. In the case 1, we already know that the third-order rogue wave solution has three kinds of structures, just see bottom patterns in Fig. 2. Similarly, when parameters \((d,c_1)\ne (0,0)\) and \(c_2=0\), three types of interaction solutions can be obtained, which are exhibited in Fig. 5. Here, parameters \((m_i,n_i)\) control the merging and splitting of higher-order rogue waves. The parameter d can regulate the distance between the soliton and the rogue wave to regulate the strength of the interaction. These above interaction structures can be degenerated into higher-order rogue wave solutions at \(d=0\), namely, fundamental structure, triplet triangle structure, and pentagon structure.

Case 3. Breather + Rogue waves

When parameters \((d,c_i)\ne (0,0)(i=1,2)\) in Eq. (55), it gives rise to the semi-rational solution of the interaction between a breather and a rogue wave for the gc-FL equation. Here, the parameter |d| plays the same role as in Case 2, namely, merge or separation between the breather and rogue wave during their interaction. The above dynamical behavior of the two components is shown in Fig. 6. Obviously, it can be seen from their contour patterns that the breather in the u is different from one in v component. The breather in the u component has one peak and two valleys, while the v component has two peaks and two valleys. When rogue wave and the breather are close to each other during the propagation process, it not only causes change in the amplitude, but also causes a certain phase deflection of the breather. When the interaction occurs, the energy of the rogue wave and breather solution will change. When variables x and t tend to infinity, it is not difficult to calculate the background amplitude ratio of the two components u and v, which is \(\frac{c_1}{c_2}\).

In what follows, we consider the higher-order case of Eq. (48) with \(N=2,3,\) and their separate structure forms. When \(N=2\), the interaction between the second-order breather and the second-order fundamental rogue wave can be obtained, which are depicted in the first two columns of Figs. 7 and 8. These two structures are controllable by parameters \(m_1\) and \(n_1\). When \(d=1\), they interact with each other strongly, i.e., the merge structure, as shown in the odd columns of Figs. 7 and 8. On the contrary, when \(d=\frac{1}{10000000}\), they are in a separate state, as shown in the even columns of Figs. 7 and 8. Whether it is merge structure or separate structure, the phase transition of the breather farther away from the rogue wave changes seriously, while breather closer to the rogue wave does not undergo obvious phase transition. In addition, the phase change caused by the fundamental structure is greater than that caused by the triplet structure. When \(N=3\), the interaction between the third-order breather and third-order rogue wave can be obtained. Only parameters \(d,m_i,n_i (i=1,2)\) are adjusted here, and other parameters are consistent with the above case. Similar with case 1, there are also three different interaction solutions, whose dynamical characteristics are demonstrated in Figs. 9 and 10. With the increase in N, the selection of parameters \(m_i\) and \(n_i\) has more combination forms, so more abundant higher-order rogue waves and semi-rational solutions can be obtained.

5 Summary and discussion

This paper mainly studies three aspects of the generalized coupled Fokas–Lenells equation: modulation instability analysis, infinitely many conservation laws, and interaction solutions.

Based on the linear analysis theory, we obtain the concrete expression of MI gain for the generalized coupled Fokas–Lenells equation. Through further analysis of the expression, the MI and MS distribution regions on frequency surface are depicted. Moreover, the constraint condition for the existence of rogue waves is obtained, namely \(0<k<\frac{2}{C}\), which is consistent with the constraint condition obtained in the process of constructing the localized wave solution through the generalized Darboux transformation.

According to the Riccati-type formulas of the spectral problem, infinitely many conservation laws are constructed to investigate the integrability of the generalized coupled Fokas–Lenells equation. In addition, we construct the generalized Darboux transformation and give the compact determinant expression of the N-order localized wave solution. Under the MI analysis, there are mainly three structures:

  • \(\Big \{d=0,~~c_i\ne 0~~(i=1,2)\Big \}\) \(\Longrightarrow \) rogue wave (fundamental, triangular, pentagon)

  • \(\Big \{d\ne 0,~~c_i=0,~~c_j\ne 0~~(i\ne j)\Big \}\) \(\Longrightarrow \) rogue wave + bright-dark soliton

  • \(\Big \{d\ne 0,~~c_i\ne 0~~(i=1,2)\Big \}\) \(\Longrightarrow \) rogue wave + breather.

Here, parameters \((m_i,n_i)\) control the structure of the rogue wave: separation or merge, which leads to the generation of the triangular and pentagon structure, while parameters \((\alpha ,\beta )\) affect the phase deflection of the rogue wave. Owing to above diversity of rogue wave structures, the last two items can lead to the interaction between rogue wave with different structures and bright-dark solitons or breathers, where the value of |d| controls the collision distance, which results in strong or weak interactions to realize their energy exchange.