Rich dynamics in a stochastic predator-prey model with protection zone for the prey and multiplicative noise applied on both species

Abstract

In this manuscript, a new approach of a stochastic predator-prey interaction with protection zone for the prey is developed and studied. The considered mathematical model consists of a system of two stochastic differential equations, SDEs, describing the interaction between the prey and predator populations where the prey exhibits a social behavior called also by “herd behavior.” First, according to the theory of the SDEs, some properties of the solution are obtained, including: the existence and uniqueness of the global positive solution and the stochastic boundedness of the solutions. Then, the sufficient conditions for the persistence in the mean and the extinction of the species are established, where the extinction criteria are discussed in two different cases, namely, the first case is the survival of the prey population, while the predator population goes extinct; the second case is the extinction of all prey and predator populations. Next, by constructing a suitable stochastic Lyapunov function and under certain parametric restrictions, it has been proved that the system has a unique stationary distribution which is ergodic. Finally, some numerical simulations based on the Milstein’s higher-order scheme are performed to illustrate the theoretical predictions.

1 Introduction

In natural ecosystems, the dynamic interaction between the predator and the prey has long been and will continue to be one of the most attractive field in mathematics due to its existence and importance in mathematical ecology. The preservation of the balance in an ecosystem is necessary for the ecologists. It depends on different relationships between organisms in nature, which can be divided into several forms such as competition, symbiosis, predator-prey interactions and so on. One of the first models describing the interaction between species was developed in the 1920s, independently by the American Alfred Lotka [31] (1880–1949) and the Italian Vito Volterra [44] (1860–1940), and is known as Lotka–Volterra or predator-prey model. Throughout the last century, several researchers are interested in the mathematical ecology area [1, 2, 39, 40, 42, 43]. They have proposed and studied several ecological phenomena between species through models of ordinary or partial differential equations which describe the interactions between these species in nature. The results of these studies can determine and predict the behavior of the living beings in nature which provides enough time to ecologists to give an appropriate control strategy that yields to avoid extinction of the living beings.

In terms of mathematical modeling, the global dynamics of predator-prey systems can be affected by many factors such as death rate, birth rate, time delay and so on. One crucial component to describe the relationship between the prey and predator populations is the predator-prey interaction (also called functional response). This latter one can be classified into many different types such as Holling I–IV types, Hassell–Varley type, Crowley–Martin type, and Beddington–DeAngelis type and so on. In savanna forests, most domestic species live in huge groups permanently and establish stable social relationships, such as elephants, zebras, buffaloes, bees, deers and others. This behavior gives them various advantages, where the weakest preys will be inserted in the interior of the herd and the strongest ones take the position in the exterior corridor of the herd. This strategy may reduce the predation rate thanks to the protection zone formed by the prey. In addition, it increases the vigilance for the prey against the predator, which causes confusion for the predator and distracts the predator from his target. Furthermore, the social behavior improves the method of locating food, and also it contributes to the process of promoting feeding to different herds through the exchange of information regarding the location of food or how to get it. The first mathematical approach of the social behavior has been offered by Venturino et al. [1], where they have supposed that the interaction between the prey population and the predator population is done only on the outermost of the herd formed by the prey. It is equivalent to say that the number of the captured prey by a successful predator attack will be proportional to the density which is on the boundary of the herd. This latter leads to a new functional response in terms of square root of the prey density. Later, Braza [2] takes in the account the average time for the predator to process the hunted prey, where he investigate with a new interaction functional with a square root by using an approximation of a classical Holling II functional response. The phenomenon of the herds for the animals tempted many researchers, which enriched the environmental and ecological field. We refer the readers to papers [3, 4, 39,40,41,42,43, 47].

Besides, the prey herd’s shape changes from one species to another depending on the physiological and sociological characteristics that control the behaviors of living beings. However, the way at which the animals interact with their environment, the number of their individuals as well as their individual efficiency, all of these factors and more will determine how the prey form their herd. The concept of herd shape for animals was modeled and introduced for the first time by Venturino et al. [43], where they generalized the interaction between the prey and the predator in both cases 2D and 3D of herd’s forms with a new functional response in terms of a new parameter which models the shape of the herd. For better explanation, we consider the following deterministic model that has been introduced in [43]

$$\begin{aligned} \left\{ \begin{array}{lccc} \dfrac{{\mathrm {d}}}{{\mathrm {d}}t}u(t)=\rho u(t)\left( 1-\dfrac{u(t)}{k}\right) -\delta u^{\alpha }(t)v(t),\\ \dfrac{{\mathrm {d}}}{{\mathrm {d}}t}v(t)=-\eta v(t)+e\delta u^{\alpha }(t)v(t), \end{array} \right. \end{aligned}$$

(1.1)

where u(t) and v(t) stand for prey and predator density at time t, respectively. $\rho$ is the intrinsic growth rate. k is the environment carrying capacity for the prey. $\eta$ represents the natural mortality rate for the predators. $\delta$ stands for the predation rate of the prey population. e is the conversion rate of the prey density to a predator density, and $0<\alpha <1$ represents the rate of the prey herd’s shape. For the biological relevance of the parameter $\alpha$, we consider a simple example for the case of 2D herd shape. We assume that the prey form a group in ${\mathbb {R}}^{2}$ with some regular shape such as the circles or the squares, and we find that the number of the captured preys by the predator will be proportional to the square root of the prey population density (i.e., $\alpha =1/2$). We consider of course the interaction between the two species that affects mainly the prey individuals which are in the boundary of the herd. Clearly, the regular forms do not only exist in the case of 2D, however, in the case of 3D such as birds or sardines, where the prey forms a regular form (cube, sphere and so on). Then, the consumed prey by a predator will be proportional to $u^{2/3}$. Obviously, for $\alpha =1$, model (1.1) turns into the classical predator-prey model of Lotka and Volterra [31, 44]. In these last years, model (1.1) is widely studied by several researchers. In [47], the authors obtained the global dynamics of model (1.1). They discussed the singularity near the original equilibrium point. Further, the dynamical behavior of model (1.1) has been investigated in the presence of spatial diffusion in [14]. More recently, the author in [13] has proposed a new approach of system (1.1) with Holling II functional response as follows

$$\begin{aligned} \left\{ \begin{array}{lccc} \dfrac{{\mathrm {d}}}{{\mathrm {d}}t}u(t)=\rho u(t)\left( 1-\dfrac{u(t)}{k}\right) -\dfrac{\delta u^{\alpha }(t)v(t)}{1+\delta t_{h}u^{\alpha }(t)},\\ \dfrac{{\mathrm {d}}}{{\mathrm {d}}t}v(t)=-\eta v(t)+\dfrac{e\delta u^{\alpha }(t)v(t)}{1+\delta t_{h}u^{\alpha }(t)}, \end{array} \right. \end{aligned}$$

(1.2)

We mention that the parameters of model (1.1) remain the same for model (1.2) and the new parameter $t_{h}$ represents the time spent by predator in handling with the prey (please see [2, 13]). The main interest in [13] is to study the impact of the herd shape rate $\alpha$ on the global dynamics of model (1.2) with the presence of the time delay. In addition, the author has proved that the time delay plays an important role on the stability of the equilibria which gives a rich dynamics such as Hopf bifurcation and transcritical bifurcation (Fig. 1).

Fig. 1

Impact of the prey herd’s shape rate $\alpha$ on the quantity of the captured prey by one predator for different values of $\alpha$ where $\delta =0.5, \ t_{h}=1$

In the real-life situations, all ecological processes are inevitably affected by environmental noise which represents an important parameter in an ecosystem; however, the mathematical modeling of ecological phenomena by a deterministic approach gives limitations in terms of results, which leads to difficulties in fitting of data and predicting the future dynamics of the system precisely. Up to now, a large number of researchers have introduced a stochastic environmental variation using the Brownian motion into parameters in the deterministic model to construct a stochastic predator-prey models, which has been considered as a stochastic fluctuations. For more details on the stochastic predator-prey models, May [34] emphasizes out that due to continuous environmental fluctuation, the parameters in a systems such as the birth rates, carrying capacity, death rates and so on exhibited random fluctuations to a great or lesser extent. Zhang et al. [49] considered a stochastic predator-prey model with hyperbolic mortality and Holling type II functional response in which they founded sufficient conditions for the existence and uniqueness of an ergodic stationary distribution and derived sufficient conditions for extinction of the predator populations. Jingliang and Wang [20] have deeply discussed the persistence, permanent and extinction of a stochastic model of a predator-prey system with Holling-type II functional response. Sengupta et al. [38] examined a stochastic nonautonomous predator-prey system with Holling-type III functional response and predator’s intra-specific competition where they obtained the stochastic permanence. Liu and Bai [25] established the sufficient and necessary criteria for the existence of optimal harvesting strategy for a stochastic predator-prey model. In the literature, the kind of stochastic predator-prey interaction was widely used, and we refer the readers to [5, 8, 9, 11, 12, 17,18,19, 26,27,28,29,30, 33, 45, 46, 48,49,50].

Motivated by the above-referred works and inspired by the work in [13], we introduce a random fluctuation to system (1.2). Our principal topic is to prove that the random fluctuations can completely change the dynamics generated by model (1.2), where in this case the extinction of both species occurs. There are many methods to establish the stochastic fluctuations into dynamical systems. One of the most used approach was adopted in [20, 28, 30, 37]. We suppose that the intrinsic growth rate of prey and the death rate of predator are mainly affected by environmental noise such that

$$\begin{aligned} \rho \longrightarrow \rho +\beta {\mathrm {d}}W_{1}(t),\quad -\eta \longrightarrow -\eta +\gamma {\mathrm {d}}W_{2}(t), \end{aligned}$$

where $W_{i}(t)(i=1,2)$ are the mutually independent standard Brownian motions with $W_{i}(0)=0$. $\beta$ and $\gamma$ are positive and represent the intensities of the white noise. The stochastic predator-prey version corresponding to model (1.2) takes the following form

$$\begin{aligned} \left\{ \begin{array}{lccc} {\mathrm {d}}u(t)=\left[ \rho u(t)\left( 1-\dfrac{u(t)}{k}\right) -\dfrac{\delta u^{\alpha }(t)v(t)}{1+\delta t_{h}u^{\alpha }(t)}\right] {\mathrm {d}}t+\beta u(t){\mathrm {d}}W_{1}(t),\\ {\mathrm {d}}v(t)=\left[ -\eta v(t) +\dfrac{e\delta u^{\alpha }(t)v(t)}{1+\delta t_{h}u^{\alpha }(t)}\right] {\mathrm {d}}t+\gamma v(t){\mathrm {d}}W_{2}(t). \end{array} \right. \nonumber \\ \end{aligned}$$

(1.3)

For our best of knowledge, the dynamics of stochastic predator-prey model (1.3) has never been studied. The present paper is organized as follows. In Sect. 2, some results on the stochastic differential equations have devoted which have been used in the rest of sections. In Sect. 3, the properties of stochastic predator-prey model (1.3) have been established including: the global existence and uniqueness for stochastic boundedness of positive solution by using the Itô’s formula and the comparison theorem of stochastic equations. The persistence and extinction criteria of the species are discussed in Sect. 4, where the sufficient conditions for extinction in two case as well as the persistence of the species have been obtained. In Sect. 5, the existence and uniqueness of an ergodic stationary distribution of the positive solutions for system (1.3) have been proved under certain parametric restrictions. Several numerical simulations are offered in Sect. 6 to support the theoretical results. Finally, conclusions and discussions ended this paper in Sect. 7.

2 Preliminaries

For the purpose of simplicity, it is necessary to give some concepts and basic theory on the stochastic differential equations which are inspired from [32] and then used in the rest of this paper. Let $(\Omega ,{\mathcal {F}},\{{\mathcal {F}}_{t}\}_{t>0},{\mathbb {P}})$ be a complete probability space with a filtration $\{{\mathcal {F}}_{t}\}_{t>0}$ satisfying the usual conditions (i.e., it is increasing and right continuous, while ${\mathcal {F}}_{0}$ contains all ${\mathbb {P}}-$null sets). Also we let $W_{i}(t)$ be a mutually independent standard Brownian motions defined on the complete probability space $(\Omega ,{\mathcal {F}},\{{\mathcal {F}}_{t}\}_{t>0},{\mathbb {P}})$ for $i=1,2$. Define the following n-dimensional Euclidean space

$$\begin{aligned} {\mathbb {R}}_{+}^{n}=\{U=(u_{1},\ldots ,u_{n})\in {\mathbb {R}}^{n} : u_{j}>0,\quad 1\le j\le n\}, \end{aligned}$$

and

$$\begin{aligned} \overline{{\mathbb {R}}}_{+}^{n}=\{U=(u_{1},\ldots ,u_{n})\in {\mathbb {R}}^{n} : u_{j}\ge 0,\quad 1\le j\le n\}. \end{aligned}$$

Lemma 2.1

(Itô’s formula [32])

Consider the n-dimensional Markov process take the following stochastic differential equation

$$\begin{aligned} {\mathrm {d}}U(t)=f(U(t)){\mathrm {d}}t+g(U(t)){\mathrm {d}}W(t),\quad \text {for}\quad t>t_{0},\nonumber \\ \end{aligned}$$

(2.1)

where $U(0)=U_{0}\in {\mathbb {R}}^{n}$ is the initial value and W(t) represents the n-dimensional standard Brownian motion defined on the complete probability space $(\Omega ,{\mathcal {F}},\{{\mathcal {F}}_{t}\}_{t>0},{\mathbb {P}})$. $f\in L^{2}({\mathbb {R}}_{+};{\mathbb {R}}^{n}), \ g\in L^{2}({\mathbb {R}}_{+};{\mathbb {R}}^{n\times m})$ are measurable functions. Denote by $C^{2}({\mathbb {R}}^{n};\overline{{\mathbb {R}}}_{+})$ the family of all nonnegative functions V(U(t), t) defined on ${\mathbb {R}}^{n}$ such that they are continuously twice differentiable in U. Then V(U(t), t) is again an Itô’s process with the stochastic differential equation given as

$$\begin{aligned}&{\mathrm {d}}V(U(t),t)=LV(U(t),t){\mathrm {d}}t\nonumber \\&\quad +V_{U}(U(t),t)g(U(t){\mathrm {d}}W(t),\quad \text {for}\quad t>t_{0}, \end{aligned}$$

(2.2)

where L is the differential operator of Eq. (2.1) defined in [32] as

$$\begin{aligned} L= & {} \sum _{i=1}^{n}f_{i}(U,t)\frac{\partial }{\partial U_{i}}\nonumber \\&+\frac{1}{2}\sum _{i,j=1}^{n}\left[ g^{T}(U,t)g(U,t)\right] _{i,j}\frac{\partial ^{2}}{\partial U_{i}\partial u_{j}}. \end{aligned}$$

(2.3)

Then, we have

$$\begin{aligned} LV(U(t),t)= & {} V_{t}(U(t),t)+V_{U}(U(t),t)f(U)\nonumber \\&\quad +\frac{1}{2}trace\left[ g^{T}(U)V_{UU}(U(t),t)g(U)\right] ,\nonumber \\ \end{aligned}$$

(2.4)

where

$$\begin{aligned} V_{t}(U,t)= & {} \frac{\partial V(U,t)}{\partial t},\quad V_{U}(U,t)\\= & {} \left( \frac{\partial V(U,t)}{\partial U_{1}},\ldots ,\frac{\partial V(U,t)}{\partial U_{n}}\right) ,\quad V_{UU}(U,t)\\= & {} \left( \frac{\partial ^{2}V(U,t)}{\partial U_{i}\partial U_{j}}\right) _{n\times n}. \end{aligned}$$

Definition 2.2

[15] The transition probability function ${\mathbb {P}}(\upsilon ,y,t,N))$ is said to be time-homogeneous (and the corresponding Markov process is called time-homogeneous) if the function ${\mathbb {P}}(\upsilon ,y,t+\upsilon ,N)$ is independent of the variable $\upsilon$, where $0\le \upsilon \le t, \ y\in {\mathbb {R}}^{n}$ and $N\in {\mathfrak {B}}$ with ${\mathfrak {B}}$ is the $\sigma$-algebra of Borel sets in ${\mathbb {R}}^{n}$.

Putting

$$\begin{aligned} {\mathrm {d}}Z(t)=f(Z(t),t){\mathrm {d}}t+\sum _{\varsigma =1}^{k}g_{\varsigma }(Z(t),t){\mathrm {d}}W_{\varsigma }(t){\mathrm {d}}W(t),\nonumber \\ \end{aligned}$$

(2.5)

where Z(t) is a regular time-homogeneous Markov process in ${\mathbb {R}}^{n}$.

The diffusion matrix associated with the process Z(t) is given as

$$\begin{aligned} A(z)=(b_{i,j}(z)),b_{i,j}(z)=\sum _{\varsigma =1}^{k}g_{\varsigma }^{i}g_{\varsigma }^{j}. \end{aligned}$$

(2.6)

Lemma 2.3

[15] We said that the Markov process Z(t) has a unique ergodic stationary distribution $\chi (.)$ if there is a bounded domain $E\subset {\mathbb {R}}^{n}$ with regular boundary $\Gamma$ and the following properties hold:

$\mathbf {(P_{1})}:$ There exists a positive number ${\tilde{c}}$ such that

$$\begin{aligned}&\sum _{i,j=1}^{n}b_{i,j}(z)\xi _{i}\xi _{j}\\&\qquad \qquad \ge {\tilde{c}}\vert \xi \vert ^{2}, \ z\in E, \ \xi \in {\mathbb {R}}^{n}. \end{aligned}$$

$\mathbf {(P_{2})}:$ There is a nonnegative $C^{2}-$function denoted by V such that LV is negative for any ${\mathbb {R}}^{n}_{+}\setminus E$.

3 Properties of the solution

In this section, according to the best result in [18], we prove that model (1.3) is well-posed in the sense that for any pair of positive initial value (u(0), v(0)), system (1.3) has a unique global solution which remains positive and bounded. By using the Lyapunov analysis method [6,7,8, 26], we show that the solution is global. Next, we analyze the boundedness of the state variables u and v.

3.1 Existence and uniqueness of the global positive solution

Since u(t) and v(t) denote the population densities of the prey and the predator, respectively, then, we are only interested in the positive solutions. Thus, we have the following theorem.

Theorem 3.1

For each initial values $(u(0),v(0))\in {\mathbb {R}}_{+}^{2}$, there exists a unique positive local solution (u(t), v(t)) of system (1.3) for all $t\in [0;\tau _{e})$ almost surely (a.s.), and the solution remains in ${\mathbb {R}}_{+}^{2}$ with probability 1 where $\tau _{e}$ is the explosion time.

Proof

Putting

$X(t)=\ln u(t),\quad Y(t)=\ln v(t),$

then from the Itô’s formula [32], system (1.3) can be written as

$$\begin{aligned} \left\{ \begin{array}{lccc} {\mathrm {d}}X(t)=\left[ X(t)\left( \rho -\frac{\beta ^{2}}{2}-\frac{e^{X(t)}}{k}\right) -\frac{\delta e^{\alpha X(t)}}{1+\delta t_{h} e^{\alpha X(t)}}e^{Y(t)}\right] {\mathrm {d}}t+\beta {\mathrm {d}}W_{1}(t),\\ \\ {\mathrm {d}}Y(t)=\left[ -\eta e^{Y(t)}-\frac{\gamma ^{2}}{2}+\frac{e\delta e^{\alpha X(t)}}{1+\delta t_{h} e^{\alpha X(t)}}\right] {\mathrm {d}}t+\gamma {\mathrm {d}}W_{2}(t), \end{array} \right. \end{aligned}$$

(3.1)

with the initial values $X(0)=\ln u(0),\ Y(0)=\ln v(0)$. It is easy to see that the right-hand side of the above system satisfies the local Lipschitz condition; then, for any given initial values $X(0)>0, Y(0)>0$ there is a unique maximal local solution (X(t), Y(t)) for all $t\in [0;\tau _{e})$ where $\tau _{e}$ is the explosion time of the solution. Now, using the Itô’s formula [32], we obtain $u(t)=e^{X(t)}$ and $v(t)=e^{Y(t)}$ as the positive local solution of system (1.3) with the initial value $u(0)>0, \ v(0)>0$. The proof is completed. $\square$

Now, we focus on proving the global existence of the solution for our proposed model (1.3). For this task, we only need to prove that $\tau _{e}$ goes to the infinity (i.e., $\tau _{e}=\infty$); then, we have the following theorem

Theorem 3.2

For each $(u(0),v(0))\in {\mathbb {R}}_{+}^{2}$, there exists a unique positive global solution (u(t), v(t)) of system (1.3) for all $t>0$ almost surely (a.s.), and the solution remains in ${\mathbb {R}}_{+}^{2}$ with probability 1.

Proof

Let $m_{0}$ be a sufficiently large nonnegative integer number, such that u(0) and v(0) lie inside in the interval $[\dfrac{1}{m_{0}},m_{0}]$. For any integer $m>m_{0}$, we can define the following stopping times as [32]

$$\begin{aligned}&\tau _{m}=\inf \left\{ t\in [0;\tau _{e}) : u(t)\notin \left( \dfrac{1}{m},m\right) \quad \text {or}\right. \nonumber \\&\left. \quad v(t)\notin \left( \dfrac{1}{m},m\right) \right\} . \end{aligned}$$

(3.2)

Obviously, $\tau _{m}$ increases when $m\longrightarrow \infty$. Set $\tau _{\infty }=\lim \limits _{m \rightarrow +\infty }\tau _{m}$, with $\tau _{\infty }<\tau _{e}$ a.s.. Next, we only need to prove that $\tau _{\infty }=\infty$, then $\tau _{e}=\infty$ for which we obtain $(u(t),v(t))\in {\mathbb {R}}_{+}^{2}$ a.s. for all $t\ge 0$. If this statement is not verified, then there exist $T>0$ and $\epsilon \in (0,1)$ such that

$$\begin{aligned} {\mathbb {P}}(\tau _{\infty }\le T)>\epsilon . \end{aligned}$$

(3.3)

Consequently, there is an integer $m_{1}>m_{0}$ such that

$$\begin{aligned} {\mathbb {P}}(\tau _{m}\le T)>\epsilon ,\quad \text {for all}\quad m\ge m_{1}. \end{aligned}$$

(3.4)

Now, let

$$\begin{aligned} V(u,v)=u-1-\ln u+\frac{1}{e}(v-1-\ln v) \end{aligned}$$

(3.5)

be a $C^{2}$ function. It is not difficult to prove that $V(u,v)\ge 0$ for all $(u,v)\in {\mathbb {R}}_{+}^{2}$. This statement comes from the following inequality

$$\begin{aligned} u-1-\ln u\ge 0,\ \forall u>0. \end{aligned}$$

(3.6)

Using the Itô’s formula [32] yields

$$\begin{aligned} {\mathrm {d}}V(u,v)= & {} LV(u,v){\mathrm {d}}t+\beta (u-1){\mathrm {d}}W_{1}(t)\nonumber \\&+\gamma \dfrac{1}{e}(v-1){\mathrm {d}}W_{2}(t), \end{aligned}$$

(3.7)

from the definition of the operator L given in Sect. 2, a straightforward calculation gives

$$\begin{aligned} LV= & {} \rho u-\frac{\rho }{k}u^{2}-\rho +\frac{\rho }{k}u+\frac{\delta u^{\alpha }v}{1+\delta t_{h}u^{\alpha }}\\&-\frac{\delta v}{u^{1-\alpha }(1+\delta t_{h}u^{\alpha })}-\frac{\eta }{e}v+\frac{\eta }{e} \\&-\frac{\delta u^{\alpha }v}{1+\delta t_{h}u^{\alpha }}+\frac{\delta u^{\alpha }}{1+\delta t_{h}u^{\alpha }}\\&+\frac{1}{2}\beta ^{2}+\frac{1}{2e}\gamma ^{2},\\\le & {} \frac{\rho _(k+1)}{k}u-\frac{\rho }{k}u^{2}+\frac{\delta u^{\alpha }}{1+\delta t_{h}u^{\alpha }}\\&+\frac{\eta }{e}+\frac{1}{2}\beta ^{2}+\frac{1}{2e}\gamma ^{2},\\\le & {} \frac{\rho (k+1)}{k}u-\frac{\rho }{k}u^{2}+\frac{1}{t_{h}}\\&+\frac{\eta }{e}+\frac{1}{2}\beta ^{2}+\frac{1}{2e}\gamma ^{2},\\\le & {} \frac{\rho (k+1)^{2}}{4k}+\frac{1}{t_{h}}\\&+\frac{\eta }{e}+\frac{1}{2}\beta ^{2}+\frac{1}{2e}\gamma ^{2},\\\le & {} M, \end{aligned}$$

where

$$\begin{aligned}&\frac{\rho (k+1)^{2}}{4k}=\sup _{u\in {\mathbb {R}}_{+}}\\&\left\{ \frac{\rho (k+1)}{k}u-\frac{\rho }{k}u^{2}\right\} , \end{aligned}$$

and M is a positive constant. Then we have

$$\begin{aligned}&{\mathrm {d}}V(u,v)\le M{\mathrm {d}}t+\beta (u-1){\mathrm {d}}W_{1}(t)\nonumber \\&\quad +\gamma (v-1){\mathrm {d}}W_{2}(t). \end{aligned}$$

(3.8)

Now, integrating both sides of the above inequality from 0 to $\tau _{m}\wedge T$ and take the expectation on both sides leads to

$$\begin{aligned}&{\mathbb {E}}V(u(\tau _{m}\wedge T),V(\tau _{m}\wedge T))\nonumber \\&\quad \le V(u(0),v(0))+M{\mathbb {E}}(\tau _{m}\wedge T), \end{aligned}$$

(3.9)

which gives

$$\begin{aligned} {\mathbb {E}}V(u(\tau _{m}\wedge T),V(\tau _{m}\wedge T))\!\le \! V(u(0),v(0))+MT,\nonumber \\ \end{aligned}$$

(3.10)

where $\tau _{m}\wedge T=\min \{\tau _{m},T\}$. Taking $\Omega _{m}=\{\tau _{m}\le T\}$ for $m\ge m_{1}$ and from (3.4) we obtain ${\mathbb {P}}(\Omega _{m})\ge \epsilon$. Note that for any $\omega \in \Omega _{m}$ there exists $u(\tau _{m},\omega )$ or $v(\tau _{m},\omega )$ equals either m or $\frac{1}{m}$. Hence $V(u(\tau _{m},\omega ),v(\tau _{m},\omega ))$ is no less than

$$\begin{aligned} \min \left\{ m-1-\ln m \ ,\ \frac{1}{m}-1-\ln \frac{1}{m}\right\} . \end{aligned}$$

(3.11)

Therefore

$$\begin{aligned}&V(u(\tau _{m},\omega ),v(\tau _{m},\omega ))\nonumber \\&\quad \ge (m-1-\ln m)\wedge \left( \frac{1}{m}-1-\ln \frac{1}{m}\right) . \end{aligned}$$

(3.12)

So, using inequality (3.2), we obtain

$$\begin{aligned}&V(u(0),v(0))+MT\ge {\mathbb {E}}[I_{\Omega _{m}(\omega )}V(u(\tau _{m},\omega ),v(\tau _{m},\omega ))]\nonumber \\&\quad \ge \epsilon (m-1-\ln m)\wedge \left( \frac{1}{m}-1-\ln \frac{1}{m}\right) , \end{aligned}$$

(3.13)

where $I_{\Omega _{m}}$ represents the indicator function of $\Omega _{m}$. Taking $m\longrightarrow \infty$, we get

$$\begin{aligned} \infty >V(u(0),v(0))+MT=\infty , \end{aligned}$$

(3.14)

which gives a contradiction. Hence, we must have $\tau _{\infty }=\infty$ and consequently the solution of system (1.3) exists for all $t\ge 0$. This completes the proof of Theorem 3.2. $\square$

3.2 Stochastic boundedness

Biological validity of a mathematical model is decided by its boundedness. The nonexplosion property in a population dynamical system is often not sufficient. However, the ultimate boundedness property is more desired. Now, we establish the theorem which gives us almost sure eventual boundedness of the solutions. To this end, we first give the definition of stochastic ultimate boundedness which is one of the most important topics in population dynamics

Definition 3.3

(see [23]) The solution $U(t)=(u(t),v(t))$ of system (1.3) is said to be stochastically ultimately bounded, if for all $a\in (0;1)$, there exists a positive constant $\lambda =\lambda (a)$, such that for each initial value $U(0)\in {\mathbb {R}}_+^2$, the solution U(t) satisfying the following property

$$\begin{aligned} \lim \limits _{t \rightarrow \infty }\sup {\mathbb {P}}\{\vert U(t)\vert \ >\lambda \}<a. \end{aligned}$$

(3.15)

Theorem 3.4

For all initial value $(u(0),v(0))\in {\mathbb {R}}_{+}^{2}$, the solutions of system (1.3) are stochastically ultimately bounded.

Proof

Let (u(t), v(t)) be any solution of system (1.3). From Theorem 3.2, we know that the solution (u(t), v(t)) will remain in ${\mathbb {R}}_{+}^{2}$ for all $t\ge 0, a.s.$. Now define the two Lyapunov functions

$$\begin{aligned}&F(u,v)=e^{t}u^{p},\quad G(u,v)=e^{t}v^{p}, \ \text {with} \nonumber \\&\quad (u,v)\in {\mathbb {R}}_{+}^{2} \ \text {and} \ p>0. \end{aligned}$$

(3.16)

From the Itô’s formula [32] and system (1.3), one can obtain

$$\begin{aligned} {\mathrm {d}}(e^{t}u^{p})= & {} e^{t}u^{p}{\mathrm {d}}t+pe^{t}u^{p-1}{\mathrm {d}}u\\&+\dfrac{p(1-p)e^{t}u^{p-1}}{2}({\mathrm {d}}u)^{2},\\= & {} e^{t}u^{p}{\mathrm {d}}t+pe^{t}u^{p-1}\left[ \rho -\frac{\rho u}{k}-\frac{\delta u^{\alpha -1}v}{1+\delta t_{h}u^{\alpha }}\right] {\mathrm {d}}t\\&+\dfrac{1}{2}p(p-1)e^{t}u^{p}\beta ^{2}{\mathrm {d}}t+pe^{t}u^{p}\beta {\mathrm {d}}W_{1}(t),\\= & {} e^{t}u^{p}\left\{ 1+p\left[ \rho -\frac{\rho u}{k}\right. \right. \\&\left. -\frac{\delta u^{\alpha -1}v}{1+\delta t_{h}u^{\alpha }}\right] \\&\left. +\dfrac{p(p-1)}{2}\beta ^{2}\right\} {\mathrm {d}}t+pe^{t}u^{p}\beta {\mathrm {d}}W_{1}(t), \end{aligned}$$

with a similarly calculation, we get

$$\begin{aligned} {\mathrm {d}}(e^{t}v^{p})= & {} e^{t}v^{p}\left\{ 1+p\left[ -\eta +\frac{e\delta u^{\alpha }v}{1+\delta t_{h}u^{\alpha }}\right] \right. \\&\left. +\dfrac{p(p-1)}{2}\gamma ^{2}\right\} {\mathrm {d}}t+pe^{t}v^{p}\gamma {\mathrm {d}}W_{2}(t). \end{aligned}$$

Then, we have

$$\begin{aligned} LF= & {} e^{t}u^{q}\left\{ 1+p\left[ \rho -\frac{\rho u}{k}-\frac{\delta u^{\alpha -1}v}{1+\delta t_{h}u^{\alpha }}\right] \right. \\&\left. +\dfrac{p(p-1)}{2}\beta ^{2}\right\} \le M_{1}e^{t}, \end{aligned}$$

and

$$\begin{aligned} LG= & {} e^{t}v^{q}\left\{ 1+p\left[ -\eta +\frac{e\delta u^{\alpha }v}{1+\delta t_{h}u^{\alpha }}\right] \right. \\&\left. +\dfrac{p(p-1)}{2}\gamma ^{2}\right\} \le M_{2}e^{t}, \end{aligned}$$

where

$$\begin{aligned} M_{1}= & {} \left( \dfrac{k}{\rho }\right) ^{p}\left( \dfrac{1+\rho p+t_{h}^{-\alpha }+\dfrac{1}{2}p(p-1)\beta ^{2}}{p+1}\right) ^{p+1}, \\ M_{2}= & {} \left( \dfrac{1}{m}\right) ^{p}\left( \dfrac{1+\rho p+\left( \dfrac{e}{t_{h}}\right) ^{\alpha }+\dfrac{1}{2}p(p-1)\beta ^{2}}{p+1}\right) ^{p+1}. \end{aligned}$$

Hence, we have

$$\begin{aligned}&e^{t}{\mathbb {E}}[u^{p}]-{\mathbb {E}}[u^{p}(0)]\le M_{1}e^{t} \ \text {and} \ e^{t}{\mathbb {E}}[v^{p}]\\&\quad -{\mathbb {E}}[v^{p}(0)]\le M_{2}e^{t}. \end{aligned}$$

This leads to

$$\begin{aligned}&\lim \limits _{t \rightarrow \infty }\sup {\mathbb {E}}[u^{p}]\le M_{1}<\infty , \\&\lim \limits _{t \rightarrow \infty }\sup {\mathbb {E}}[v^{p}]\le M_{2}<\infty . \end{aligned}$$

Now, for $U(t)=(u(t),v(t))\in {\mathbb {R}}_{+}^{2}$, we have $\vert U(t)\vert ^{p}\le 2^{p/2}(u^{p}+v^{p})$ which gives

$$\begin{aligned} \lim \limits _{t \rightarrow \infty }\sup {\mathbb {E}}[\vert U(t)\vert ^{p}]\le M_{3}<\infty , \end{aligned}$$

where $M_{3}=2^{p/2}(M_{1}+M_{2}).$

For any $a>0$, taking $\lambda (a)=\left( \frac{M_{3}}{a}\right) ^{1/p}$ and applying the Chebyshev inequality yield

$$\begin{aligned}&{\mathbb {P}}\{\vert U(t)\vert \ >\lambda \}\\&\quad \le \frac{{\mathbb {E}}[\vert U(t)\vert ^{q}]}{\lambda ^{p}(a)}. \end{aligned}$$

Thus

$$\begin{aligned}&\lim \limits _{t \rightarrow \infty }{\mathbb {P}}\{\vert U(t)\vert \ >\lambda \}\\&\qquad \le \frac{M_{3}}{\lambda ^{p}(a)}=a. \end{aligned}$$

This leads to required assertion (3.15). The proof of Theorem 3.4 is completed. $\square$

4 Discussion on the persistence and extinction criteria

In this section, we shall discuss the case of the persistence and the extinction of the two population (the prey and the predator) for our proposed model (1.3), where we shall try to give the sufficient conditions which determines the extinction and the persistence of stochastic predator-prey model (1.3). Firstly, we study the extinction scenario in two situations, the first case is the prey population survival where the predator population goes to extinction, the second case is all the two species will die out. Before proceeding with the analysis, we give the following definitions.

Definition 4.1

[49]

(i):

If $\lim \limits _{t \rightarrow \infty }u(t)=0, a.s.$, then the prey density u(t) is said to be extinctive almost surely.

(ii):

If $\lim \limits _{t \rightarrow \infty }v(t)=0, a.s.$, then the predator density v(t) is said to be extinctive almost surely.

Now, we give the fundamental lemma which will be used in the following

Lemma 4.2

[17, 18] Define the following one-dimensional stochastic differential equation

$$\begin{aligned} {\mathrm {d}}U(t)=\rho U(t)\left( 1-\frac{U(t)}{k}\right) {\mathrm {d}}t+\beta U(t){\mathrm {d}}W_{1}(t), \end{aligned}$$

(4.1)

where $\rho ,k$ and $\beta$ are positive, and $W_{1}(t)$ is standard Brownian motion. Then we have the following assertions

• if $\rho <\dfrac{\beta ^{2}}{2}$, then we have $\lim \limits _{t \rightarrow \infty }U(t)=0$.

• if $\rho >\frac{\beta ^{2}}{2}$, then we have

  $$\begin{aligned}&\lim \limits _{t \rightarrow \infty }\frac{\ln U(t)}{t}=0, a.s., \\&\lim \limits _{t \rightarrow \infty } \frac{1}{t}\displaystyle \int _{0}^{t} U(s) \, \mathrm {d}s=k-\frac{k\beta ^{2}}{2\rho }. \end{aligned}$$

Theorem 4.3

Assuming that

$$\begin{aligned} \mathbf {(H):} \ \rho >\frac{\beta ^{2}}{2}, \end{aligned}$$

and let (u(t), v(t)) be a positive solution of system (1.3) with the initial condition $(u(0),v(0))\in {\mathbb {R}}_{+}^{2}$.

Putting

$$\begin{aligned}&A=-\eta -\frac{\gamma ^{2}}{2}+e\delta \displaystyle \int _{0}^{\infty }\\&\frac{u^{\alpha }}{1+\delta t_{h}u^{\alpha }}\chi (u) \, \mathrm {d}u. \end{aligned}$$

If $A<0$, then we have

$$\begin{aligned} \lim \limits _{t \rightarrow \infty }v(t)=0, \ a.s., \end{aligned}$$

which means that the predator density goes to extinction with probability one. In addition, the distribution of u(t) converges weakly a.s. to the measure which has the density

$$\begin{aligned} \chi (u)=\frac{\Theta }{\beta ^{2}}u^{-2+\frac{2\rho }{\beta ^{2}}}e^{-\frac{2\rho }{k\beta ^{2}}}, \ u\in (0;\infty ), \end{aligned}$$

where

$$\begin{aligned}&\Theta =\left[ \frac{1}{\beta ^{2}}\left( \frac{k\beta ^{2}}{2\rho }\right) ^{\frac{2\rho }{\beta ^{2}}-1}\Gamma \right. \\&\left. \left( \frac{2\rho }{\beta ^{2}}-1\right) \right] ^{-1}, \end{aligned}$$

is a constant satisfying $\displaystyle \int _{0}^{\infty } \chi (u) \, \mathrm {d}u=1$ and $\Gamma$ is the gamma function.

Proof

Consider the following 1-dimensional stochastic differential equation

$$\begin{aligned} \left\{ \begin{array}{lc} {\mathrm {d}}U(t)=\rho U(t)\left( 1-\frac{U(t)}{k}\right) {\mathrm {d}}t+\beta U(t){\mathrm {d}}W_{1}(t),\\ U(0)=u(0). \end{array} \right. \nonumber \\ \end{aligned}$$

(4.2)

Putting

$$\begin{aligned} g(u)=\rho u\left( 1-\frac{u}{k}\right) , \ \beta (u)=\beta u, \ u\in (0;\infty ). \end{aligned}$$

By a straightforward calculation we get:

$$\begin{aligned}&\displaystyle \int \frac{g(s)}{\beta (s)^{2}} \, \mathrm {d}s=\displaystyle \\&\int \left( \frac{\rho }{s\beta ^{2}}-\frac{\rho }{k\beta ^{2}}\right) \mathrm {d}s\\&\quad =\frac{\rho }{\beta ^{2}}\ln s-\frac{\rho }{k\beta ^{2}}+\Theta . \end{aligned}$$

Therefore,

$$\begin{aligned}&e^{\displaystyle \int \tfrac{g(s)}{\beta (s)^{2}} \, \mathrm {d}s}\\&\quad =e^{\left( \Theta _{s}\tfrac{\rho }{\beta ^{2}}\right) }e^{\left( -\tfrac{\rho }{k\beta ^{2}}s\right) }. \end{aligned}$$

Then, from Theorem 1.16 in [22] it follows that Eq. (4.2) has the ergodic property and the invariant density is given as

$$\begin{aligned}&\chi (u)=\frac{\Theta }{\beta ^{2}}u^{-2+\tfrac{2\rho }{\beta ^{2}}}\nonumber \\&e^{\left( -\tfrac{2\rho }{k\beta ^{2}}\right) }, \ u\in (0;\infty ), \end{aligned}$$

(4.3)

where

$$\begin{aligned}&\Theta =\left[ \frac{1}{\beta ^{2}}\left( \frac{k\beta ^{2}}{2\rho }\right) ^{\frac{2\rho }{\beta ^{2}}-1}\Gamma \right. \\&\left. \left( \frac{2\rho }{\beta ^{2}}-1\right) \right] ^{-1}, \end{aligned}$$

satisfying

$$\begin{aligned} \displaystyle \int _{0}^{\infty } \chi (x) \, \mathrm {d}x=1, \end{aligned}$$

with

$$\begin{aligned}&\frac{1}{t}\displaystyle \int _{0}^{t} u(s) \, \mathrm {d}s\nonumber \\&\quad =\displaystyle \int _{0}^{\infty } u\chi (u) \, \mathrm {d}u, \ a.s. \end{aligned}$$

(4.4)

Using the comparison theorem of 1-dimensional stochastic differential equation [36], we obtain

$$\begin{aligned} u(t)\le U(t), \ \forall t>0, \ a.s. \end{aligned}$$

(4.5)

Now, applying the Itô’s formula [32] to $\ln v(t)$ for the second equation of system (1.3) and using (4.5), then we obtain

$$\begin{aligned} {\mathrm {d}}\ln v(t)= & {} \left( -\eta -\frac{\gamma ^{2}}{2}+\frac{e\delta u^{\alpha }(t)}{1+\delta t_{h}u^{\alpha }(t)}\right) {\mathrm {d}}t\\&+\gamma {\mathrm {d}}W_{2}(t) \\\le & {} \left( -\eta -\frac{\gamma ^{2}}{2}+\frac{e\delta U^{\alpha }(t)}{1+\delta t_{h}U^{\alpha }(t)}\right) {\mathrm {d}}t\\&+\gamma {\mathrm {d}}W_{2}(t). \end{aligned}$$

For both sides, integrating the above equation from 0 to t and dividing by t gives

$$\begin{aligned}&\frac{\ln v(t)-\ln v(0)}{t}\le -\eta \nonumber \\&\quad -\frac{\gamma ^{2}}{2}\nonumber \\&\quad +e\delta \frac{1}{t}\displaystyle \int _{0}^{t}\nonumber \\&\dfrac{U^{\alpha }(s)}{1+\delta t_{h}U^{\alpha }(s)} \, \mathrm {d}s+\frac{N_{2}(t)}{t}, \end{aligned}$$

(4.6)

where $N_{2}(t)=\displaystyle \int _{0}^{t} \gamma {\mathrm {d}}W_{2}(s) \, \mathrm {d}s$ is a real-valued continuous local martingales. According to [24], we have $\lim \limits _{t \rightarrow \infty }\frac{N_{2}(t)}{t}=0, a.s.$. Next, taking the superior limit on both sides of (4.6) and using Lemma 4.2 together with (4.4), we obtain

$$\begin{aligned}&\lim \limits _{t \rightarrow \infty }\sup \frac{\ln v(t)}{t}\\&\le -\eta -\frac{\gamma ^{2}}{2}+\lim \limits _{t \rightarrow \infty }\sup e\delta \\&\frac{1}{t}\displaystyle \int _{0}^{t} \frac{U^{\alpha }(s)}{1+\delta t_{h}U^{\alpha }(s)} \, \mathrm {d}s, \\&\le -\eta -\frac{\gamma ^{2}}{2}+e\delta \displaystyle \int _{0}^{\infty } \\&\frac{u^{\alpha }}{1+\delta t_{h}u^{\alpha }}\chi (u)\ \mathrm {d}u, \\&=A<0,\ \ a.s., \end{aligned}$$

which leads to the extinction of the predator species, i.e., $\ \lim \limits _{t \rightarrow \infty }v(t)=0, a.s..$

Now, for a sufficiently small $\epsilon _{1}>0$ there exists ${\tilde{t}}$ and a set $\Omega _{\epsilon _{1}}\subset \Omega$ such that ${\mathbb {P}}(\Omega _{\epsilon _{1}})>1-\epsilon$ and

$$\begin{aligned}&\frac{\delta u^{\alpha }v}{1+\delta t_{h}u^{\alpha }}\le \delta u^{\alpha }v\\&\le \delta \epsilon _{1} u^{\alpha }, \ \text {for} \ t\\&\ge {\tilde{t}} \ \text {and} \ \omega \in \Omega _{\epsilon _{1}}. \end{aligned}$$

From

$$\begin{aligned}&\left[ \rho u\left( 1-\frac{u}{k}\right) -\delta \epsilon _{1} u^{\alpha }\right] {\mathrm {d}}t\\&\quad +\beta u{\mathrm {d}}W_{1}(t)\le {\mathrm {d}}u\le \rho u\left( 1-\frac{u}{k}\right) {\mathrm {d}}t+\beta u{\mathrm {d}}W_{1}(t), \end{aligned}$$

we obtain that the distribution of the process u(t) converges weakly to the measure with the density $\mu$. The proof is complete. $\square$

Theorem 4.4

Assume that $\rho <\frac{\beta ^{2}}{2}$ and $e\delta <\frac{\gamma ^{2}}{2}$ hold. Then for any initial condition $(u(0),v(0))\in {\mathbb {R}}_{+}^{2}$ the two species die out, where the solution (u(t), v(t)) of system (1.3) will be extinct exponentially with probability one.

Proof

Applying the Itô’s formula [32] to the first equation of system (1.3), implies that

$$\begin{aligned} {\mathrm {d}}\ln u(t)= & {} \left[ -\frac{\beta ^{2}}{2}+\rho \left( 1-\frac{u(t)}{k}\right) \right. \nonumber \\&\left. -\frac{\delta u^{\alpha -1}(t)v(t)}{1+\delta t_{h}u^{\alpha }(t)}\right] {\mathrm {d}}t+\beta {\mathrm {d}}W_{1}(t). \end{aligned}$$

(4.7)

Integrating the above equation from 0 to t and dividing by t on both sides of (4.7), we obtain

$$\begin{aligned}&\frac{\ln u(t)-\ln u(0)}{t}=\rho \nonumber \\&\quad -\frac{\beta ^{2}}{2}-\frac{\rho }{k}\frac{1}{t}\displaystyle \int _{0}^{t} u(s)\, \mathrm {d}s\nonumber \\&\quad -\delta \frac{1}{t}\displaystyle \int _{0}^{t} \nonumber \\&\frac{u^{\alpha -1}(s)v(s)}{1+\delta t_{h}u^{\alpha }(s)}\, \mathrm {d}s +\beta \frac{ W_{1}(t)}{t}. \end{aligned}$$

(4.8)

Using the strong law of large numbers for local martingales [24], we get

$$\begin{aligned} \lim \limits _{t \rightarrow \infty }\frac{W_{1}(t)}{t}=0, a.s.. \end{aligned}$$

Taking the superior limit on both sides of equation (4.9) gives

$$\begin{aligned}&\lim \limits _{t \rightarrow \infty }\sup \\&\frac{\ln u(t)}{t}\le \rho -\frac{\beta ^{2}}{2}<0, a.s., \end{aligned}$$

which leads to

$$\begin{aligned} \lim \limits _{t \rightarrow \infty }u(t)=0,\ a.s. \end{aligned}$$

Application of Itô’s formula [32] to $\ln v(t)$ yields

$$\begin{aligned} {\mathrm {d}}\ln v(t)= & {} \left[ -\eta -\frac{\gamma ^{2}}{2}\right. \nonumber \\&\left. +\frac{e\delta u^{\alpha }(t)}{1+\delta t_{h}u^{\alpha }(t)}\right] {\mathrm {d}}t\nonumber \\&+\gamma {\mathrm {d}}W_{2}(t). \end{aligned}$$

(4.9)

From $\lim \limits _{t \rightarrow \infty }u(t)=0,\ a.s.$, there exists $T_{0}>0$ such that $u(t)<\epsilon$ for $t>T_{0}$. Hence, we get

$$\begin{aligned}&d\ln v(t)\le \left[ -\frac{\gamma ^{2}}{2}\right. \\&\quad \left. +\frac{e\delta \epsilon ^{\alpha }}{1+\delta t_{h}\epsilon ^{\alpha }}\right] {\mathrm {d}}t\\&\quad +\gamma {\mathrm {d}}W_{2}(t), \\&\le \left( -\frac{\gamma ^{2}}{2}+e\delta \right) {\mathrm {d}}t+\gamma {\mathrm {d}}W_{2}(t). \end{aligned}$$

Integrating the above inequality from 0 to t and dividing by t on both sides, we obtain

$$\begin{aligned}&\frac{\ln v(t)-\ln v(0)}{t}=-\frac{\gamma ^{2}}{2}\nonumber \\&\quad +e\delta +\gamma \frac{W_{2}(t)}{t}. \end{aligned}$$

(4.10)

Applying the strong law of large numbers for local martingales [24], we obtain

$$\begin{aligned} \lim \limits _{t \rightarrow \infty }\frac{W_{2}(t)}{t}=0, a.s. \end{aligned}$$

Taking the superior limit on both sides of (4.10), then we have

$$\begin{aligned}&\lim \limits _{t \rightarrow \infty }\sup \frac{\ln v(t)}{t}\\&\quad \le -\frac{\gamma ^{2}}{2}+e\delta <0,\ a.s., \end{aligned}$$

which gives

$$\begin{aligned} \lim \limits _{t \rightarrow \infty }v(t)=0,\ a.s. \end{aligned}$$

This completes the proof of Theorem 4.4. $\square$

Remark 4.5

(i) :

According to Theorem 4.3, one can easily show that A is the critical value between the extinction and the persistence in the mean for the predator specie. Moreover, from Lemme 4.2, if $A<0$, we obtain

$$\begin{aligned}&\lim \limits _{t \rightarrow \infty }v(t)=0, a.s., \quad \lim \limits _{t \rightarrow \infty } \\&\quad \frac{1}{t}\displaystyle \int _{0}^{t} u(s) \, \mathrm {d}s=k-\frac{k\beta ^{2}}{2\rho }, a.s.. \end{aligned}$$

(ii) :

Theorem 4.4 shows that if the white noise intensities take a big values, then all both species are die out. On the other hand, stochastic predator-prey model (1.3) will be persistent if the white noise disturbances are small enough. This assertion can easily be seen from Theorems 4.3 to 4.3.

5 Existence of ergodic stationary distribution

In this part, according to the theory of Has’minskii [15] and using the Lyapunov function method we try to prove that under certain sufficient conditions, stochastic predator-prey model (1.3) has a unique stationary distribution which is ergodic

Theorem 5.1

Suppose that

$$\begin{aligned} \frac{\beta ^{2}}{2}+\frac{\gamma ^{2}}{2}< \rho -\eta , \ \text {and} \ \rho >\eta , \end{aligned}$$

then for any initial condition $(u(0),v(0))\in {\mathbb {R}}_{+}^{2}$, system (1.3) has a unique stationary distribution $\chi (.)$ which has the ergodic property.

Proof

In order to prove Theorem 5.1, we only need to verify the two assumption $\mathbf {(P_{1})}$ and $\mathbf {(P_{2})}$ in Lemma 2.3. We first begin by proving the validation of the first condition; then, the diffusion matrix of system (1.3) is

$$\begin{aligned} B=\left( \begin{array}{cc} \beta ^{2}u^{2} &{} 0 \\ 0 &{} \gamma ^{2}v^{2} \end{array} \right) . \end{aligned}$$

It is not difficult to see that there exists a positive constant ${\tilde{b}}, \ {\tilde{c}}$ such that

$$\begin{aligned}&\sum _{i,j=1}^{2}{\tilde{b}}_{i,j}(z)\xi _{i}\xi _{j}\\&=\beta ^{2}u^{2}\xi _{1}^{2}+\gamma ^{2}v^{2}\xi _{2}^{2}\\&\ge {\tilde{c}}\vert \xi \vert ^{2}, \ (u,v)\in {\overline{D}}, \ \xi =(\xi _{1},\xi _{2}) \in {\mathbb {R}}^{2}_{+}, \end{aligned}$$

that is to say that B is a positive definite matrix for any compact subset of ${\mathbb {R}}^{2}_{+}$. Thus the assertion $\mathbf {(P_{1})}$ of Lemma 2.3 holds. Now, focusing on proving the second assertion in Lemma 2.3. From system (1.3), we get

$$\begin{aligned} L\left( -\ln u\right)= & {} -\frac{1}{u}\left( \rho u\left( 1-\frac{u}{k}\right) \right. \nonumber \\&\quad \left. -\frac{\delta u^{\alpha }v}{1+\delta t_{h}u^{\alpha }}\right) +\frac{\beta ^{2}}{2}\nonumber \\&=-\left( \rho -\frac{\beta ^{2}}{2}\right) +\rho \frac{u}{k}\nonumber \\&\quad +\frac{\delta u^{\alpha -1}v}{1+\delta t_{h}u^{\alpha }} \end{aligned}$$

(5.1)

and

$$\begin{aligned} L\left( -\ln v\right)= & {} \eta -\frac{e\delta u^{\alpha }}{1+\delta t_{h}u^{\alpha }}\nonumber \\&+\frac{\gamma ^{2}}{2}\le \eta +\frac{\gamma ^{2}}{2}. \end{aligned}$$

(5.2)

Define

$$\begin{aligned} V_{1}(u,v)=-\ln u-\ln v, \end{aligned}$$

then, from (5.1) and (5.2), we have

$$\begin{aligned} LV_{1}= & {} -\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \nonumber \\&\quad +\rho \frac{u}{k}+\frac{\delta u^{\alpha -1}v}{1+\delta t_{h}u^{\alpha }}. \end{aligned}$$

(5.3)

Now, we denote

$$\begin{aligned} V^{*}(u,v)=\Pi V_{1}(u,v)+v^{-\tau }+u+\frac{v}{e}, \end{aligned}$$

where $0<\tau <1$ is a sufficiently small constant satisfying the following assertion

$$\begin{aligned} \rho -\eta >\frac{\tau +1}{2}(\beta ^{2}+\gamma ^{2}), \end{aligned}$$

with

$$\begin{aligned} \Pi= & {} \frac{2}{\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) }\max _{(u,v)\in {\mathbb {R}}_{+}^{2}}\\&\quad \left\{ 2,-\frac{\rho }{2k}u^{2}-\tau v^{-\tau }\right. \\&\left. \left( -\eta -\frac{1+\tau }{2}\gamma ^{2}\right) +\rho u+\tau v^{-\tau -1}-\frac{\eta }{e}v\right\} . \end{aligned}$$

We claim that $V^{*}(u,v)$ is not only continuous, but also tends to $\infty$ as (u, v) approaches the boundary of ${\mathbb {R}}_{+}^{2}$ and as $\vert \vert (u,v)\vert \vert \rightarrow \infty$, where $\vert \vert .\vert \vert$ is the Euclidean norm of a point in ${\mathbb {R}}_{+}^{2}$. Therefore, it must be lower bounded and achieve this lower bound at a point (u(0), v(0)) in the interior of ${\mathbb {R}}_{+}^{2}$. Thus, we can define a nonnegative $C^{2}$-function $V : {\mathbb {R}}_{+}^{2}\rightarrow {\mathbb {R}}_{+}\cup \{0\}$ as

$$\begin{aligned} V(u,v)=\Pi V_{1}(u,v)+V_{2}(v)+V_{3}(u,v), \end{aligned}$$

where

$$\begin{aligned} V_{2}(v)=v^{-\tau }, \quad V_{3}(u,v)=u+\frac{v}{e}-V^{*}(u(0),v(0)). \end{aligned}$$

By applying the Itô’s formula [32] to $V_{2}(v)$ and $V_{3}(u,v)$, we obtain

$$\begin{aligned} LV_{2}= & {} -\tau v^{-\tau -1}\left( -\eta v+\frac{e\delta u^{\alpha }v}{1+\delta t_{h}u^{\alpha }}\right) \nonumber \\&\quad +\frac{\tau (1+\tau )}{2}\gamma ^{2}v^{-\tau }\le \nonumber \\&\quad -\tau v^{-\tau }\left( -\eta -\frac{1+\tau }{2}\gamma ^{2}\right) +\tau v^{-\tau -1}, \end{aligned}$$

(5.4)

and

$$\begin{aligned} LV_{3}= & {} \rho u\left( 1-\frac{u}{k}\right) \nonumber \\&\quad -\frac{\eta }{e}v=-\frac{\rho }{k}u^{2}+\rho u-\frac{\eta }{e}v. \end{aligned}$$

(5.5)

Then, according to (5.4) and (5.5), we get

$$\begin{aligned} LV\le & {} \Pi \left\{ -\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \right. \nonumber \\&\left. +\rho \frac{u}{k}+\frac{\delta u^{\alpha -1}v}{1+\delta t_{h}u^{\alpha }}\right\} \nonumber \\&-\tau v^{-\tau }\left( -\eta -\frac{1+\tau }{2}\gamma ^{2}\right) \nonumber \\&+\tau v^{-\tau -1}-\frac{\rho }{k}u^{2}+\rho u-\frac{\eta }{e}v. \end{aligned}$$

(5.6)

To complete the prove, we need to construct a bounded open domain $E_{\epsilon }$ for which the assumption $p_{2}$ of Lemma 2.3 holds. Let us define the following bounded open set

$$\begin{aligned} E_{\epsilon }= & {} \left\{ (u,v)\in {\mathbb {R}}_{+}^{2} : \epsilon<u< \right. \\&\left. \frac{1}{\epsilon }, \ \epsilon<v< \frac{1}{\epsilon }\right\} , \end{aligned}$$

where $0<\epsilon <1$ is a sufficiently small number which satisfies the following conditions in ${\mathbb {R}}_{+}^{2}\setminus E_{\epsilon }$

$$\begin{aligned}&\epsilon \le \left( \frac{\Pi \left( \rho -\eta -\frac{\beta ^{2}}{2} -\frac{\gamma ^{2}}{2}\right) }{4\delta }\right) ^{\frac{1}{1-\alpha }}, \end{aligned}$$

(5.7)

$$\begin{aligned}&\epsilon \le \frac{\rho }{2k\Pi \delta }, \end{aligned}$$

(5.8)

$$\begin{aligned}&\epsilon \le \frac{1}{4\delta }\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) , \end{aligned}$$

(5.9)

$$\begin{aligned}&\quad -\Pi \left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \nonumber \\&\quad +\frac{\rho }{2k\epsilon ^{2}}+\Pi _{1}\le -1, \end{aligned}$$

(5.10)

$$\begin{aligned}&\quad -\Pi \left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) +\Pi _{2}. \end{aligned}$$

(5.11)

Now, we divide the set ${\mathbb {R}}_{+}^{2}\setminus E_{\epsilon }$ into four subsets defined as

$$\begin{aligned}&E_{\epsilon }^{1}=\left\{ (u,v)\in {\mathbb {R}}_{+}^{2} : u\le \epsilon \right\} ,\quad E_{\epsilon }^{2}\\&\quad =\left\{ (u,v)\in {\mathbb {R}}_{+}^{2} : v\le \epsilon \right\} \\&E_{\epsilon }^{3}=\left\{ (u,v)\in {\mathbb {R}}_{+}^{2} : u\ge \frac{1}{\epsilon }\right\} ,\quad E_{\epsilon }^{4}\\&\quad =\left\{ (u,v)\in {\mathbb {R}}_{+}^{2} : v\ge \frac{1}{\epsilon }\right\} . \end{aligned}$$

clearly, $E_{\epsilon }=E_{\epsilon }^{1}\cup E_{\epsilon }^{2}\cup E_{\epsilon }^{3}\cup E_{\epsilon }^{4}$. Our objective in the next is to prove that $LV(u,v)\le -1$ for any $(u,v)\in E_{\epsilon }^{i}, \ i\in \{1,2,3,4\}$.

Case 1 : If $(u,v)\in E_{\epsilon }^{1}$ and from $u^{1-\alpha }\le \epsilon ^{1-\alpha }$, we have

$$\begin{aligned} u^{1-\alpha }v\le \epsilon ^{1-\alpha }(1+v^{2}). \end{aligned}$$

Then, it follows that

$$\begin{aligned} LV(u,v)\le & {} -\frac{\Pi }{4}\left( \rho -\eta -\frac{\beta ^{2}}{2}\right. \\&\left. -\frac{\gamma ^{2}}{2}\right) +\left[ -\frac{\Pi }{4}\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \right. \\&\left. +\delta \Pi \epsilon ^{1-\alpha }\right] -\frac{\rho }{2k}u^{2}-\delta \Pi \epsilon ^{1-\alpha } v^{2}\\&+\left[ -\frac{\Pi }{2}\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \right. \\&-\frac{\rho }{2k}u^{2}-\delta \epsilon ^{1-\alpha } v^{2}-\tau v^{-\tau }\left( -\eta -\frac{1+\tau }{2}\gamma ^{2}\right) \\&\left. +\rho u+\tau v^{-\tau -1}-\frac{\eta }{e}v\right] ,\\\le & {} -\frac{\Pi }{4}\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \\&+\left[ -\frac{\Pi }{4}\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \right. \\&\left. +\epsilon ^{1-\alpha }\delta \right] -\frac{\rho }{2k}u^{2}-\delta \Pi \epsilon ^{1-\alpha } v^{2}\\&+ \left[ -\frac{\Pi }{2}\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \right. \\&+ \sup _{(u,v)\in {\mathbb {R}}_{+}^{2}} \left\{ -\frac{\rho }{2k}u^{2}-\tau v^{-\tau }\left( -\eta -\frac{1+\tau }{2}\gamma ^{2}\right) \right. \\&\left. \left. +\rho u+\tau v^{-\tau -1}-\frac{\eta }{e}v\right\} \right] . \end{aligned}$$

Since

$$\begin{aligned}&\Pi =\frac{2}{\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) }\max _{(u,v)\in {\mathbb {R}}_{+}^{2}}\\&\left\{ 2,-\frac{\rho }{2k}u^{2}-\tau v^{-\tau }\right. \\&\left. \left( -\eta -\frac{1+\tau }{2}\gamma ^{2}\right) +\rho u+\tau v^{-\tau -1}-\frac{\eta }{e}v\right\} , \end{aligned}$$

we obtain that

$$\begin{aligned}&\Pi \left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \nonumber \\&\quad \le -\frac{\Pi }{4}\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \le -1. \end{aligned}$$

(5.12)

Hence

$$\begin{aligned}&LV(u,v)\le -\frac{\Pi }{4}\left( \rho -\eta -\frac{\beta ^{2}}{2}\right. \\&\quad \left. -\frac{\gamma ^{2}}{2}\right) -\frac{\rho }{2k}u^{2}-\delta \Pi \epsilon ^{1-\alpha } v^{2} \\&\le -\frac{\Pi }{4}\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \le -1. \end{aligned}$$

From (5.7), we have

$$\begin{aligned} LV(u,v)\le -1, \ \forall (u,v)\in E_{\varepsilon }^{1}. \end{aligned}$$

(5.13)

Case 2 : If $(u,v)\in E_{\epsilon }^{2}$, we have $v\le \epsilon$. Since

$$\begin{aligned} u^{1-\alpha }v\le \epsilon (1+u^{2}), \end{aligned}$$

we obtain

$$\begin{aligned} LV(u,v)\le & {} -\frac{\Pi }{4}\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \\&+\left[ -\frac{\Pi }{4}\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \right. \\&\left. +\Pi \delta \epsilon \right] +\left( \Pi \delta \epsilon -\frac{\rho }{2k}\right) u^{2}\\&+ \left[ -\frac{\Pi }{2}\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \right. \\&-\frac{\rho }{2k}u^{2}-\tau v^{-\tau }\left( -\eta -\frac{1+\tau }{2}\gamma ^{2}\right) \\&\left. +\rho u+\tau v^{-\tau -1}-\frac{\eta }{e}v\right] ,\\\le & {} -\frac{\Pi }{4}\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \\&+\left[ -\frac{\Pi }{4}\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) +\Pi \delta \epsilon \right] \\&-\left( \Pi \delta \epsilon -\frac{\rho }{2k}\right) u^{2} \\&+ \left[ -\frac{\Pi }{2}\left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \right. \\&+ \sup _{(u,v)\in {\mathbb {R}}_{+}^{2}} \left\{ -\frac{\rho }{2k}u^{2}-\tau v^{-\tau }\left( -\eta -\frac{1+\tau }{2}\gamma ^{2}\right) \right. \\&\left. \left. +\rho u+\tau v^{-\tau -1}-\frac{\eta }{e}v\right\} \right] . \end{aligned}$$

According to (5.8) and (5.9), it follows that

$$\begin{aligned}&LV(u,v)\le -\frac{\Pi }{4}\left( \rho -\eta -\frac{\beta ^{2}}{2}-\dfrac{\gamma ^{2}}{2}\right) \nonumber \\&\quad \le -1, \ \text {for any} \ (u,v)\in E_{\epsilon }^{2}. \end{aligned}$$

(5.14)

Case 3 : If $(u,v)\in E_{\epsilon }^{3}$, we get $u\le \frac{1}{\epsilon }$. Then we have

$$\begin{aligned} LV(u,v)\le & {} -\Pi \left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \\&-\frac{\rho }{2k}u^{2}+\left\{ -\tau v^{-\tau }\left( -\eta -\frac{1+\tau }{2}\gamma ^{2}\right) \right. \\&+\tau v^{-\tau -1}-\frac{\rho }{2k}u^{2}+\rho u-\frac{\eta }{e}v+\Pi \left( \rho \frac{u}{k}\right. \\&\left. \left. +\frac{\delta u^{\alpha -1}v}{1+\delta t_{h}u^{\alpha }}\right) \right\} ,\\\le & {} -\Pi \left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \\&-\frac{\rho }{2k}u^{2}+\Pi _{1},\\\le & {} -\Pi \left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \\&-\frac{\rho }{2k\epsilon ^{2}}+\Pi _{1}. \end{aligned}$$

Using (5.10) and (5.12), then we obtain

$$\begin{aligned} LV(u,v)\le -1, \ \text {for any} \ (u,v)\in E_{\epsilon }^{3}, \end{aligned}$$

(5.15)

where

$$\begin{aligned}&\Pi _{1}=\sup _{(u,v)\in {\mathbb {R}}_{+}^{2}}\left\{ -\tau v^{-\tau }\left( -\eta -\frac{1+\tau }{2}\gamma ^{2}\right) \right. \\&\quad +\tau v^{-\tau -1}-\frac{\rho }{2k}u^{2}+\rho u-\frac{\eta }{e}v\\&\quad \left. +\Pi \left( \rho \frac{u}{k}+\frac{\delta u^{\alpha -1}v}{1+\delta t_{h}u^{\alpha }}\right) \right\} . \end{aligned}$$

Case 4 : If $(u,v)\in E_{\epsilon }^{4}$, we have $v\le \frac{1}{\epsilon }$. Which gives

$$\begin{aligned} LV(u,v)\le & {} -\Pi \left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) \\&+\left\{ -\tau v^{-\tau }\left( -\eta -\frac{1+\tau }{2}\gamma ^{2}\right) +\tau v^{-\tau -1}-\frac{\rho }{k}u^{2}\right. \\&\left. +\rho u-\frac{\eta }{e}v+\Pi \left( \rho \frac{u}{k}+\frac{\delta u^{\alpha -1}v}{1+\delta t_{h}u^{\alpha }}\right) \right\} ,\\\le & {} -\Pi \left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) +\Pi _{2},\\\le & {} -\Pi \left( \rho -\eta -\frac{\beta ^{2}}{2}-\frac{\gamma ^{2}}{2}\right) +\Pi _{2}. \end{aligned}$$

Therefore, from (5.11) and (5.12) we get

$$\begin{aligned} LV(u,v)\le -1, \ \text {for any} \ (u,v)\in E_{\epsilon }^{4}, \end{aligned}$$

(5.16)

with

$$\begin{aligned} \Pi _{2}= & {} \sup _{(u,v)\in {\mathbb {R}}_{+}^{2}}\left\{ -\tau v^{-\tau }\left( -\eta -\frac{1+\tau }{2}\gamma ^{2}\right) \right. \\&\quad +\tau v^{-\tau -1}-\frac{\rho }{k}u^{2}\\&\quad \left. +\rho u-\frac{\eta }{e}v+\Pi \left( \rho \frac{u}{k}+\frac{\delta u^{\alpha -1}v}{1+\delta t_{h}u^{\alpha }}\right) \right\} . \end{aligned}$$

Thus, if we combine results (5.13), (5.14), (5.15) and (5.16), we can deduce that for a sufficiently small $\epsilon$ we have

$$\begin{aligned} LV(u,v)\le -1, \ \text {for any} \ (u,v)\in {\mathbb {R}}_{+}^{2}\setminus E_{\epsilon }. \end{aligned}$$

(5.17)

Hence, the assertion $\mathbf {(P_{2})}$ of Lemma 2.3 holds. Consequently, stochastic predator-prey model (1.3) has a unique stationary distribution. The proof is completed. $\square$

Fig. 2

Numerical simulation of deterministic system (1.2) with the parameter values $\rho =0.5, \ k=1, \ \delta =0.5, \ t_{h}=2, \ e=0.4, \ \alpha =0.8$ and different value of the parameter $\eta$. In a, we take $\eta =0.9$. In b, we have $\eta =0.1$ and for c, we put $\eta =0.04$

Remark 5.2

Theorem 5.1 shows that when the noises are small enough, then model (1.3) has a unique stationary distribution which is ergodic. The presence of the fractal term “$u^{\alpha }$” in our proposed model (1.3) makes the difficulties when we prove Theorem 5.1. Here we construct a new Lyapunov function and a rectangular set which do not depend on the equilibrium point $(u^{*},v^{*})$ of deterministic model (1.2). The ergodic property in Theorem 5.1 means that the solution of stochastic predator-prey model (1.3) tends to a fixed positive point in the sense of time average with probability one, which implies that system (1.3) is permanent.

6 Numerical simulations

In order to substantiate the analytical findings, we give some numerical examples. Using the semi-implicit Milstein’s higher-order method described in [16], then we obtain the following discretization system as

$$\begin{aligned} \left\{ \begin{array}{lccc} u_{i+1}=u_{i}+\left[ \rho u_{i}\left( 1-\frac{u_{i}}{k}\right) -\frac{\delta u_{i}^{\alpha }v_{i}}{1+\delta t_{h}u_{i}^{\alpha }}\right] \Delta t+\beta u_{i}a_{i}\sqrt{\Delta t}+\frac{\beta ^{2}}{2} u_{i}(a_{i}^{2}-1)\Delta t,\\ \\ v_{i+1}=\left[ -\eta v_{i} +\frac{e\delta u_{i}^{\alpha }v_{i}}{1+\delta t_{h}u_{i}^{\alpha }}\right] \Delta t+\gamma v_{i}b_{i}\sqrt{\Delta t}+\frac{\gamma ^{2}}{2} v_{i}(b_{i}^{2}-1)\Delta t. \end{array} \right. \end{aligned}$$

(6.1)

where the time increments $\Delta t>0$, $a_{i}$ and $b_{i}$ are N(0, 1) independent Gaussian random variables.

Fig. 3

Numerical simulation of deterministic system (1.2) with the parameter values $\delta =0.5, \ k=1, \ t_{h}=2, \ e=0.4, \ \alpha =0.8, \ \eta =0.1$ and multivalues of $\rho$. In a, we take $\rho =0.09$. In b, we have $\rho =0.4$ and for c, we put $\rho =0.9$

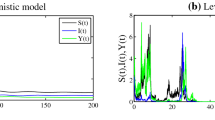
In Fig. 2, we show the numerical simulation of deterministic system (1.2) with the parameter values $\rho =0.5, \ k=1, \ \delta =0.5, \ t_{h}=2, \ e=0.4, \ \alpha =0.8$ and different value of the parameter $\eta$. For (A), we choose $\eta =0.9$; then, we obtain the extinction of the predator specie. In (B), we put $\eta =0.1$, which gives the coexistence of all both species. Next, we fix $\eta =0.04$; then, the system transits to an oscillatory regime where a limit cycle appears.

In Fig. 3, we display the graphical representation of the impact of the intrinsic growth rate $\rho$ on both prey and predator densities equilibrium for the same values of the fixed parameters in Fig. 2 and multivalues of $\rho$. In (A), we choose $\rho =0.09$ which gives $(u^{*},v^{*})=(0.343,0.221)$. In (B), we take $\rho =0.4$ implies that $(u^{*},v^{*})=(0.233,1.621)$. Finally, in (C) we set $\rho =0.9$, yielding $(u^{*},v^{*})=(0.389,4.489)$. Here, we denote that $(u^{*},v^{*})$ represents the positive equilibrium associated with deterministic system (1.2) such that

$$\begin{aligned} u^{*}= & {} \left[ \dfrac{\eta }{\delta (e-t_{h}\eta )}\right] ^{\frac{1}{\alpha }}, \ v^{*}\\&\quad =\dfrac{e\rho }{\eta }\left( 1-\dfrac{u^{*}}{k}\right) , \ e>t_{h}\eta \ \text {and} \ 0<u^{*}<k. \end{aligned}$$

Clearly, one can see the massive impact of the parameters $\eta$ and $\rho$ on the dynamical behavior of deterministic system (1.2), especially on the predator density equilibrium. The large value of the death rate of the predator population $\eta$ may result in the extinction of the predator specie. On the other hand, as the parameter $\rho$ increases, the predator density increases with a considerable values. This means that $\rho$ has a positive and significant impact on the predator density. Biologically speaking, the increase in the number of prey individuals within the herd may result a high rate of infection with various diseases, as well as conflicts between males for mating; all of this leads to herd destabilization, which reduces the defensive effectiveness of the pack and thus facilitates the predator’s task during the hunting process.

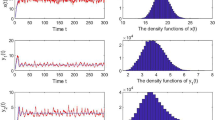
In order to verify the result obtained in Theorem 5.1, we choose the parameter values $\beta ^{2}/2=0.2, \ \gamma ^{2}/2=0.168$ and the other parameter values are pointed out in Table 1. Then we obtain $\beta ^{2}/2+\gamma ^{2}/2=0.368<\rho -\eta =0.46$, and according to Theorem 5.1, we can conclude that stochastic predator-prey system (1.3) has a unique ergodic stationary distribution $\chi (.)$ and ergodic property which means that both prey and predator are persistent a.s. This result is depicted in Fig. 4.

In Fig. 5 our aim is to examine the case of the extinction of the predator population. To this end, we take $\beta ^{2}/2=0.14<\rho =0.55$ which means that the condition $\mathbf {(H)}$ of Theorem 4.3 is satisfied. Recall that the second condition of Theorem 4.3 is that $A<0$ where

$$\begin{aligned} A= & {} -\eta -\frac{\gamma ^{2}}{2}+e\delta \displaystyle \int _{0}^{\infty }\\&\quad \frac{u^{\alpha }}{1+\delta t_{h}u^{\alpha }}\chi (u) \, \mathrm {d}u. \end{aligned}$$

Using the parameters given in Table 1 and a simple integral, we obtain

$$\begin{aligned}&e\delta \displaystyle \int _{0}^{\infty } \\&\dfrac{u^{\alpha }}{1+\delta t_{h}u^{\alpha }}\chi (u) \, \mathrm {d}u\approx 0 .312. \end{aligned}$$

Now, from Fig. 5 we have tree cases. In (A), we choose $\gamma ^{2}/2=0.223$; then, we obtain immediately $A=-0.001<0$. Next, in (B) we put $\gamma ^{2}/2=0.322$ which gives $A=-0.1<0$. In the last case (C), we take $\gamma ^{2}/2=0.655$, and it follows that $A=-0.433<0$. By comparing the three cases in Fig. 5, one can easily observe that the predator population goes more and more toward extinction, while the prey population persist, which means that the noise associated with the predator population can change the properties of the model greatly. More precisely, comparing Fig. 5a, c, we can easily see that with the increase of $\gamma ^{2}$ the density of the predator population v(t) tends to the extinction, while the prey population u(t) persist in mean.

Fig. 4

Numerical simulation of stochastic predator-prey system (1.3) for the parameter values $\rho =0.55, \ k=1, \ \delta =0.26, \ t_{h}=0.71, \ \eta =0.09, \ e=0.39, \ \alpha =1/3$ and the noise intensities $\beta ^{2}/2=0.2, \ \gamma ^{2}/2=0.168$. Here the initial data are $u(0)=0.1, \ v(0)=0.25$

Fig. 5

Numerical simulation of stochastic predator-prey system (1.3) for the parameter values $\rho =0.55, \ k=1, \ \delta =0.26, \ t_{h}=0.71, \ \eta =0.09, \ e=0.39, \ \alpha =1/3$. In a, we choose $\beta ^{2}/=0.14, \ \gamma ^{2}/2=0.223$. In b, we have $\beta ^{2}/2=0.14, \ \gamma ^{2}/2=0.322$ and for the last case c, we put $\beta ^{2}/2=0.14, \ \gamma ^{2}/2=0.655$. The initial data are $u(0)=0.2, \ v(0)=0.25$

Fig. 6

Numerical simulation of stochastic predator-prey system (1.3) for the parameter values $\rho =0.55, \ k=1, \ \delta =0.26, \ t_{h}=0.71, \ \eta =0.09, \ e=0.39, \ \alpha =1/3$. In a, we choose $\beta ^{2}/2=0.54, \ \gamma ^{2}/2=0.09$. In b, we take $\beta ^{2}/2=0.551, \ \gamma ^{2}/2=0.11$ and for the last case c, we put $\beta ^{2}/2=0.81, \ \gamma ^{2}/2=0.52$. Here the initial value $u(0)=0.2, \ v(0)=0.25$

Table 1 Lists of parameters used in the simulations of Figs. 4, 5, 6 and 7

Fig. 7

Impact of the herd shape rate $\alpha$ on the numerical ergodic stationary distribution associated with system (1.3) for the parameter values $\rho =0.55, \ k=1, \ \delta =0.26, \ t_{h}=0.71, \ \eta =0.09, \ e=0.39, \ \beta ^{2}=0.3, \ \gamma ^{2}=0.2$ and different values of the parameter $\alpha$

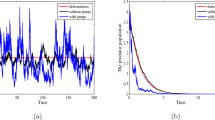
In Fig. 6, we examine numerically the result obtained in Theorem 4.4. For the first case (A) in Fig. 6, we choose $\beta ^{2}/2=0.54$ and $\gamma ^{2}/2=0.09$, then $\rho =0.55>\beta ^{2}/2=0.54$ and $e\delta =0.10>\gamma ^{2}/2=0.09$. Next, in (B) we choose $\beta ^{2}/2=0.551$ and $\gamma ^{2}/2=0.11$, and we obtain $\rho =0.55<\beta ^{2}/2=0.551$ and $e\delta =0.10<\gamma ^{2}/2=0.11$. In the last case (C), we take $\beta ^{2}/2=0.81$ and $\gamma ^{2}/2=0.52$; then, we have $\rho =0.55<\beta ^{2}/2=0.81$ and $e\delta =0.10<\gamma ^{2}/2=0.52$. Other values of the system parameters can be seen from Table 1. For the two last cases, we can easily see that the conditions of Theorem 4.4 hold, which explains the extinction of both populations u and v (please see Fig. 6b, c). In other words, if the noise intensities $\beta ^{2}$ and $\gamma ^{2}$ increase, the prey and the predator populations die out exponentially with probability one.

Figure 7 represents the impact of the prey herd’s shape rate $\alpha$ on the ergodic stationary distribution associated with stochastic predator-prey model (1.3). We choose $\beta ^{2}/2=0.3$ and $\gamma ^{2}/2=0.2$; then, we obtain $\beta ^{2}/2+\gamma ^{2}/2=0.4<\rho -\eta =0.46$. The other parameter values are given in detail in Table 1.

7 Discussion

In order to understand the dynamics induced by environmental driving forces, we explain the effect of the environmental noises on the predator-prey interaction in the presence of social behavior for the prey and multiplicative noise. A new approach of a stochastic predator-prey model is obtained. In the great savanna, many living beings gather to together in huge herds. This provides a protection zone and a useful strategy for defending against predators. On the other hand, as it has been mentioned in introduction section, the prey population can form several shape of herd, and this kind of phenomena has been modeled in [43] and widely studied in the literature. Consequently, a new functional response has been introduced into the interface which are modeled by using a new parameter $\alpha$ representing the prey’s herd shape rate. Further, the real-life situations are often subject to environmental noises. This gives the necessary and the importance of studying the environmental fluctuations impact on the population systems in ecology. In this work, we consider predator-prey model (1.2) of [13] subject to environmental noises. Our aim is to study how the intensities of environmental noises affect stochastic predator-prey model (1.3) by revealing the relationships between the coefficients of the population model and the intensities of environmental noise. From the stochastic model analysis, a rich properties have been deduced. First, the existence of the global positive solution as well as the stochastic uniform boundedness of the solution has been successfully confirmed by using conventional methods. Next, the sufficient conditions for the extinction and persistence of the predator and the prey populations have been established where the extinction criteria are discussed in two cases: the first case is the prey population survival where the predator population die out; the second case is both the prey and predator populations extinction. Moreover, by constructing a suitable stochastic Lyapunov function, it has been proved that stochastic predator-prey model (1.3) has a unique stationary distribution which is ergodic. Theorem 5.1 shows that the stationary distribution exists if the white noise is small. But the large-amplitude environmental fluctuations may destabilize the stochastic system and consequently no stationary distribution can exist. Mathematically speaking, the ergodic stationary distribution can be considered as a stability of system in weak sense that appears as a solution fluctuating near the positive equilibrium of corresponding deterministic system (1.2). From an biological point of view, this means that both prey and predator populations coexist in the long run, which leads to said that the system is permanent.

By comparing the stochastic predator-prey system with corresponding deterministic system (1.2) which has been studied in [13], two interesting facts have been revealed, and the first one is the high environmental noise intensity could drive two species to extinct. In our model, this can be seen in two different cases; the first case is the prey population persist, while the predator extinct. This situation is graphically represented in Fig. 5. The second case is both the two species die out (please see Fig. 6). Here, it has been remarked that A which defined in Theorem 4.3 is the crucial parameter for the persistence in the mean and extinction of model (1.3). The second fact is that the term of herd behavior cannot avoid the extinction of the prey population when the nature presents significant environmental fluctuations although the prey herd’s shape has a significant impact on the solution of stochastic system (1.3) (please see Fig. 7). In deterministic model (1.2), the situation of the extinction of both species is absolutely impossible Fig. 2). Consequently, we can conclude that the survival of living beings is related to the environmental fluctuations more than the nature of their behaviors.

Finally, we would like to mention that some meaningful problems deserve further investigation. For one side, one can propose some more realistic models, such as considering the effects of the prey herd aggressiveness on the predator population, nonlocal prey competition or the harvesting on the populations and so on. On the other side, it is interesting to introduce the telegraph noise in our model, such as continuous-time Markov chain. The motivation for investigating this is that the living beings suffer from unexpected environmental changes such as global warming, temperature increase, humidity, precipitation changes and so on. It has been confirmed that animals have specific responses to climate changes. All living beings respond to climate change either through migration or adaptation. But they extinct if they do not reach one of the two options. So, it is interesting to study the impact of all these factors on the predator-prey interaction in order to improve the condition of living beings and avoid the extinction of species to keep the ecosystem balanced. In the next works, we will try to consider more realistic situations in terms of mathematical modeling.