1 Introduction

Interaction between predator and prey is one of the cornerstones in bio and ecosystems. Understanding the mechanism behind is of great significance for maintaining species diversity, and therefore it remains high attention in many fields of science [26,27,28, 31, 35]. Mathematically, the basic frameworks of this kind of interaction can be described as

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dS}{dt}=\mu (S)-f(S,Y),\\ \frac{dY}{dt}=\delta f(S,Y)-M_Y(Y). \end{array}\right. } \end{aligned}$$
(1)

The biological meanings of parameters and functions appeared are listed in Table 1. System (1) and its variants have extensively studied with attempts to understand the predator–prey interactions [19, 20, 22, 23]. However, the system (1) does not include the effect of infectious diseases on predator–prey interactions explicitly. Recently, Hethcote et al. [14] reported that the prevalence of infectious diseases is one of the main factors that is troubling the development of the population community. The spread of diseases in populations can lead to an increase in mortality, and predators can catch more infected prey. Thus, it has practical significance to gain deep insights into understanding the transmission dynamics of diseases in predator–prey interactions, but there are limited literature in this regards [5, 13, 16, 17, 25].

Table 1 The biological meanings of parameters and functions in (1)
Full size table

May [24] pointed out that birth rate, mortality rate and some other parameters related to population interactions could be affected by environmental noise. The biosphere environment is often changeable, and stochastic noise is also the cause leading to the extinction of individuals. By running a stochastic system several times, we can obtain the distribution of the predicted number of individuals, while a deterministic system will give a single predicted value. Traditionally, there are two common ways to introduce stochastic factors into deterministic population models. One is to assume that the predator–prey interactions are subject to some small random fluctuations. Physically, these small random fluctuations can be described by white noise [4, 6, 9, 11]. Another is to assume that the predator–prey interactions are subject to sudden catastrophic shocks including earthquake, flood, and drought. These catastrophic shocks can be described mathematically by the Lévy process [2, 21]. Several recent studies on predator–prey interactions have focused on the effects of environmental noise [1, 7, 10]. They played an irreplaceable role in studying the effects of diseases on predator–prey interactions. However, most of these models have considered either white noise or Lévy noise alone. Based on the work of [32], here we shall propose a new model, which allows us to examine the effects of white noise, Lévy noise as well as the diseases on the predator–prey interactions.

The paper is arranged as follows. We will, in Sect. 2, formulate the system and then prove some preliminary results. It is then followed by exploring the asymptotic dynamics of the model. Numerical simulations will be conducted in Sect. 4, to illustrate the dynamics of the stochastic system. Finally, we conclude our study with a brief discussion in Sect. 5.

2 Model Formulation and Preliminaries

Let I(t) be the abundance of the infected prey, function g(S, I) the infection rate of I(t), b(I, Y) the attack rate of Y(t) on I(t), \(mb(I,Y),~0\le m\le 1\) the conversion rate from the infected prey to the predator, and \(M_I(I)\) the mortality rate of the infected prey. Supposing that the diseases spread only among the prey yields

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dS}{dt}=\mu (S)-f(S,Y)-g(S,I),\\ \frac{dI}{dt}=g(S,I)-b(I,Y)-M_I(I)\\ \frac{dY}{dt}=\delta f(S,Y)+mb(I,Y)-M_Y(Y),\\ \end{array}\right. } \end{aligned}$$
(2)

where we take

$$\begin{aligned} \mu (S)=rS(t)\left( 1-\frac{S(t)}{K}\right) , \end{aligned}$$

as in [32], \(f(S,Y)=0\) and \(b(I,Y)=pIY,~p>0\), indicating that healthy prey has an absolute escape advantage over infected prey, and \(g(S,I)=\beta SI\). In general, depending on the case in question, \(M_I(I)\) and \(M_Y(Y)\) may take different forms, such as the linear mortality [37], the quadratic mortality [3, 12] and the hyperbolic mortality [36]. In this paper, the mortality rates take forms of

$$\begin{aligned} M_I(t)=cI(t)+wI^2(t), M_Y(t)=dY(t)+hY^2(t), \end{aligned}$$
(3)

where c denotes the disease-related death rate of the infected prey. w is the density dependence of the infected prey, d is the death rate of Y(t), h is the density dependence of the predator. Please note that when \(w=h=0,\) Eq. (3) are linear mortality rates; however, when \(c=d=0\) they quadratic mortality rates. The mortality rate of Eq. (3) has been used in modeling ecosystems of marine bays in [12]. With these specifics, we reach

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dS}{dt}=rS(t)\left( 1-\frac{S(t)}{K}\right) -\beta S(t)I(t),\\ \frac{dI}{dt}=\beta S(t)I(t)-pI(t)Y(t)-cI(t)-wI^2(t),\\ \frac{dY}{dt}=mpI(t)Y(t)-dY(t)-hY^2(t).\\ \end{array}\right. } \end{aligned}$$
(4)

Using the similar argument as [8], we can prove

Proposition 2.1

Let \(R_0=\frac{K\beta }{c}\) and \(R_1=\frac{mp}{d}\frac{r(K\beta -c)}{K\beta ^2+wr}\). Then, for system (4), we know that

  1. (1)

    if \(R_0<1\), the disease-free equilibrium \(E_1(K,0,0)\) is globally asymptotically stable (GAS);

  2. (2)

    if \(R_0>1\) and \(R_1<1\), there exists a unique boundary equilibrium \(E_2(\overline{S},\overline{I},0)=\left( \frac{K(wr+\beta c)}{K\beta ^2+wr},\frac{r(K\beta -c)}{K\beta ^2+wr},0\right) ,\) which is GAS, while \(E_1\) is unstable;

  3. (3)

    if \(R_1>1\), there exists a unique positive equilibrium

    $$\begin{aligned} E_3(S^*,I^*,Y^*)=\left( \frac{K\left( r-\beta I^*\right) }{r},\frac{K\beta rh+dpr-crh}{Kh\beta ^2+mp^2r+wrh},\frac{mpI^*-d}{h}\right) , \end{aligned}$$

    which is GAS, while both \(E_1\) and \(E_2\) are unstable.

To incorporate small stochastic noise into the deterministic system (4), for any initial value \(X_0\) and and \(0\le \varDelta t\ll 1\) we assume that the solution \(X_t=(S_t,I_t,Y_t)'\) is a Markov process with the conditional mean

$$\begin{aligned} \begin{aligned} {{\mathbb {E}}}[X_{t+\varDelta t}-X_t|X=X_0]\approx \left[ \begin{matrix} rS(1-\frac{S}{K})-\beta SI\\ \beta SI-pIY-cI-wI^2\\ mpIY-dY-hY^2\\ \end{matrix}\right] \varDelta t\\ \end{aligned} \end{aligned}$$

and the conditional variance

$$\begin{aligned} \begin{aligned} \text {Var}[X_{t+\varDelta t}-X_t|X=X_0]\approx \left[ \begin{matrix} \sigma _1^2S^2\\ \sigma _2^2I^2\\ \sigma _3^2Y^2\\ \end{matrix}\right] \varDelta t.\\ \end{aligned} \end{aligned}$$

With these considerations, we obtain the stochastic version of the system (4) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} dS=\left( rS(t)\Big (1-\frac{S(t)}{K}\Big )-\beta S(t)I(t)\right) dt+\sigma _1S(t)dB_1(t),\\ dI=\left( \beta S(t)I(t)-cI(t)-pI(t)Y(t)-wI^2(t)\right) dt+\sigma _2I(t)dB_2(t),\\ dY=\left( mpI(t)Y(t)-dY(t)-h Y^2(t)\right) dt+\sigma _3Y(t)dB_3(t),\\ \end{array}\right. } \end{aligned}$$
(5)

where \(B_i(t)~(i=1,2,3)\) present the standard Brownian motions with intensities \(\sigma _i^2\). Similarly, we can obtain the stochastic Lévy predator–prey system as follows accounted for the sudden catastrophic shocks

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} dS=\left( rS(t)\left( 1-\frac{S(t)}{K}\right) -\beta S(t)I(t)\right) dt+\sigma _1S(t)dB_1(t)\\ \qquad \quad + \int _{\mathbb {Z}}S(t^-)\gamma _1(u)\widetilde{\varGamma }(dt,du),\\ dI=(\beta S(t)I(t)-cI(t)-pI(t)Y(t)-wI^2(t))dt+\sigma _2I(t)dB_2(t)\\ \qquad \quad + \int _{\mathbb {Z}}I(t^-)\gamma _2(u)\widetilde{\varGamma }(dt,du),\\ dY=(mpI(t)Y(t)-dY(t)-h Y^2(t))dt+\sigma _3Y(t)dB_3(t)\\ \qquad \quad + \int _{\mathbb {Z}}Y(t^-)\gamma _3(u)\widetilde{\varGamma }(dt,du),\\ \end{array}\right. } \end{aligned} \end{aligned}$$
(6)

where \(\widetilde{\varGamma }(dt,du)=\varGamma (dt,du)-\lambda (du)dt\), \(\varGamma \) is a Poisson counting measure on a measureable subset \({\mathbb {Z}}\) of \((0, \infty )\), and \(\lambda \) is the characteristic measure of the Poisson counting measure \(\varGamma \) with \(\lambda ({\mathbb {Z}})<\infty .\)

Next, we will investigate model (6). For the sake of following discussion, we define

$$\begin{aligned} b_i= & {} \frac{1}{2}\sigma _i+\int _{\mathbb {Z}}\left[ \gamma _i-\ln (1+\gamma _i)\right] ,\\ \langle X(t)\rangle= & {} \frac{1}{t}\int ^t_0X(s)ds,~~\langle X(t)\rangle _*=\liminf _{t\rightarrow +\infty }\langle X(t)\rangle ,~~\langle X(t)\rangle ^*=\limsup _{t\rightarrow +\infty }\langle X(t)\rangle , \end{aligned}$$

and introduce

Definition 2.1

System (6) is called stochastically ultimately bounded if for any \(\varepsilon \in (0,1)\) there exists a \(\chi (=\chi (\omega ))>0\) such that

$$\begin{aligned} \limsup _{t\rightarrow \infty }{\mathbb {P}}\left\{ \left| (S(t),I(t),Y(t))\right| >\chi \right\} <\varepsilon . \end{aligned}$$

3 Main Results

Define

$$\begin{aligned} \begin{aligned} \displaystyle {V(S,I,Y)=S-1-\ln S+I-1-\ln I+\frac{1}{m}(Y-1-\ln {Y}).} \end{aligned} \end{aligned}$$

Applying the same argument as in [33], we have the following result, which suggests the solution of (6) is always biological meaningful.

Theorem 3.1

Given \((S(0),I(0),Y(0))\in {\mathbb {R}}^3_+\). System (6) has a unique positive solution on \(t\ge 0\) with probability one.

Theorem 3.2

The solution of (6) determined by Theorem 3.1 is stochastically ultimately bounded, i.e.,

$$\begin{aligned} \limsup _{t\rightarrow \infty }\ {\mathbb {P}}\left\{ \left| (S(t),I(t),Y(t))\right| >\chi \right\} \le \varepsilon \end{aligned}$$

provided \(\frac{r}{K}>\frac{2\beta }{3}, w>\frac{\beta +2mp}{3}\) and \(h>\frac{mp}{3}\).

Proof

Define \(V(S,I,Y)=S^{\frac{1}{2}}+I^{\frac{1}{2}}+Y^{\frac{1}{2}}.\) By Itô’s formula, we obtain

$$\begin{aligned} \begin{aligned} dV=&\,LVdt+{\frac{1}{2}}\sigma _1S^{\frac{1}{2}}dB_1(t)+\frac{1}{2}\sigma _2I^{\frac{1}{2}}dB_2(t)+\frac{1}{2}\sigma _3Y^{\frac{1}{2}}dB_3(t)\\&+S^{\frac{1}{2}}\int _{\mathbb {Z}}[(1+\gamma _1(u))^{\frac{1}{2}}-1]\widetilde{\varGamma }(dt,du)+I^{\frac{1}{2}}\int _{\mathbb {Z}}[(1+\gamma _2(u))^{\frac{1}{2}}-1]\widetilde{\varGamma }(dt,du)\\&+Y^{\frac{1}{2}}\int _{\mathbb {Z}}[(1+\gamma _3(u))^{\frac{1}{2}}-1]\widetilde{\varGamma }(dt,du), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} LV=&{\frac{1}{2}}S^{\frac{1}{2}}\left( r(1-\frac{S}{K})-\beta I\right) {+}{\frac{1}{2}}I^{\frac{1}{2}}\left( \beta S-c-pY{-}wI\right) {+}{\frac{1}{2}}Y^{\frac{1}{2}}\left( mpI-d-hY\right) \\&-\frac{1}{8}\sigma _1^2S^{\frac{1}{2}}+S^{\frac{1}{2}}\int _{\mathbb {Z}}[(1+\gamma _1(u))^{\frac{1}{2}}-1-{\frac{1}{2}}\gamma _1(u)]\lambda (du)\\&-\frac{1}{8}\sigma _2^2I^{\frac{1}{2}}+I^{\frac{1}{2}}\int _{\mathbb {Z}}[(1+\gamma _2(u))^{\frac{1}{2}}-1-{\frac{1}{2}}\gamma _2(u)]\lambda (du)\\&-\frac{1}{8}\sigma _3^2Y^{\frac{1}{2}}+Y^{\frac{1}{2}}\int _{\mathbb {Z}}[(1+\gamma _3(u))^{\frac{1}{2}}-1-{\frac{1}{2}}\gamma _3(u)]\lambda (du)\\ \le&-\frac{r}{2K}S^{\frac{3}{2}}+S^{\frac{1}{2}}\left( {\frac{1}{2}} r-\frac{1}{8}\sigma _1^2+\int _{\mathbb {Z}}[(1+\gamma _1(u))^{\frac{1}{2}}-1-{\frac{1}{2}}\gamma _1(u)]\lambda (du)\right) \\&-{\frac{1}{2}}wI^{\frac{3}{2}}+ I^{\frac{1}{2}}\left( {\frac{1}{2}}c-\frac{1}{8}\sigma _2^2+\int _{\mathbb {Z}}[(1+\gamma _2(u))^{\frac{1}{2}}-1-{\frac{1}{2}}\gamma _2(u)]\lambda (du)\right) \\&-{\frac{1}{2}}hY^{\frac{3}{2}}+Y^{\frac{1}{2}}\left( -{\frac{1}{2}}d-\frac{1}{8}\sigma _3^2+\int _{\mathbb {Z}}[(1+\gamma _3(u))^{\frac{1}{2}}-1-{\frac{1}{2}}\gamma _3(u)]\lambda (du)\right) \\&+{\frac{1}{2}}\beta I^{{\frac{1}{2}}}S+{\frac{1}{2}}mpY^{\frac{1}{2}}I. \end{aligned} \end{aligned}$$

By the Hölder inequation \(ab\le \frac{a^p}{p}+\frac{b^q}{q},\frac{1}{p}+\frac{1}{q}=1 (p,q>1)\), we have

$$\begin{aligned} I^{\frac{1}{2}} S\le {\frac{1}{3}}I^{\frac{3}{2}}+{\frac{2}{3}}S^{\frac{3}{2}},~Y^{\frac{1}{2}}I\le {\frac{1}{3}}Y^{\frac{3}{2}}+{\frac{2}{3}}I^{\frac{3}{2}}. \end{aligned}$$

Thus

$$\begin{aligned} LV\le & {} -{\frac{1}{2}}\left( \frac{r}{K}-\frac{2\beta }{3}\right) S^{\frac{3}{2}}-{\frac{1}{2}}\left( w-\frac{\beta +2mp}{3}\right) I^{\frac{3}{2}}-{\frac{1}{2}}\left( h-\frac{mp}{3}\right) Y^{\frac{3}{2}}\\&+S^{\frac{1}{2}}\left( {\frac{1}{2}}r+1-\frac{1}{8}\sigma _1^2+\int _{\mathbb {Z}}[(1+\gamma _1(u))^{\frac{1}{2}}-1-{\frac{1}{2}}\gamma _1(u)]\lambda (du)\right) \\&+I^{\frac{1}{2}}\left( {\frac{1}{2}}c+1-\frac{1}{8}\sigma _2^2+\int _{\mathbb {Z}}[(1+\gamma _2(u))^{\frac{1}{2}}-1-{\frac{1}{2}}\gamma _2(u)]\lambda (du)\right) \\&+Y^{\frac{1}{2}}\left( -{\frac{1}{2}}d+1-\frac{1}{8}\sigma _3^2+\int _{\mathbb {Z}}[(1+\gamma _3(u))^{\frac{1}{2}}-1-{\frac{1}{2}}\gamma _3(u)]\lambda (du)\right) \\&-V(S,I,Y)\\\le & {} H-V(S,I,Y),~~H>0~~\text {is~a~constant}. \end{aligned}$$

Applying Itô’s formula to \(e^tV(S,I,Y)\) yields

$$\begin{aligned}&d(e^tV(S,I,Y))\\&\quad =e^t[V(S,I,Y)dt+dV(S,I,Y)]\\&\quad \le e^{t}Hdt+e^t\bigg [{\frac{1}{2}}\left( \sigma _1S^{{\frac{1}{2}}}dB_1(t)+\sigma _2I^{\frac{1}{2}}dB_2(t)+\sigma _3Y^{\frac{1}{2}}dB_3(t)\right) \\&\quad +S^{\frac{1}{2}}\int _{\mathbb {Z}}[(1+\gamma _1(u))^{\frac{1}{2}}-1]\widetilde{\varGamma }(dt,du)+I^{\frac{1}{2}}\int _{\mathbb {Z}}[(1+\gamma _2(u))^{\frac{1}{2}}-1]\widetilde{\varGamma }(dt,du)\\&\quad +Y^{\frac{1}{2}}\int _{\mathbb {Z}}[(1+\gamma _3(u))^{\frac{1}{2}}-1]\widetilde{\varGamma }(dt,du)\bigg ]. \end{aligned}$$

Therefore we have

$$\begin{aligned} e^t{\mathbb {E}}V(S,I,Y)\le V(S(0),I(0),Y(0))+He^t \end{aligned}$$

and

$$\begin{aligned} \limsup _{t\rightarrow +\infty }{\mathbb {E}}V(S,I,Y)\le H. \end{aligned}$$

By elementary inequality

$$\begin{aligned} n^{(1-p/2)\wedge 0}|x|^p\le \sum _{i=1}^nx_i^p\le n^{(1-p/2)\vee 0}|x|^p,~~{\mathbb {R}}_+^n:=\{x\in {\mathbb {R}}^n:x_i>0,1\le i\le n\}, \end{aligned}$$

we have

$$\begin{aligned} \limsup _{t\rightarrow +\infty }{\mathbb {E}}|(S(t),I(t),Y(t))|^{\frac{1}{2}}\le H. \end{aligned}$$

For any \(\varepsilon >0\), set \(\chi =\frac{H^2}{\varepsilon ^2}\), the Chebyshev inequality implies

$$\begin{aligned} {\mathbb {P}}\left\{ \left| (S(t),I(t),Y(t))\right| >\chi \right\} \le \frac{{\mathbb {E}}\left| (S(t),I(t),Y(t))\right| ^{\frac{1}{2}}}{\sqrt{\chi }}, \end{aligned}$$

namely,

$$\begin{aligned} \limsup _{t\rightarrow \infty }\ {\mathbb {P}}\left\{ \left| (S(t),I(t),Y(t))\right| >\chi \right\} \le \varepsilon . \end{aligned}$$

The proof is complete. \(\square \)

To study the persistence and extinction of Eq. (6), we define:

$$\begin{aligned} R_{11}=\frac{mpK\beta (r-b_1)}{rmp(c+b_2)+wr(d+b_3)} \end{aligned}$$

and

$$\begin{aligned} R_{12}=\frac{mpK\beta h\left[ wr(r-b_1)-K\beta ^2(r-b_1)+\beta r(c+b_2)\right] -w^2r^2h(d+b_3)}{mp[wr^2h(c+b_2)+pr\left( mpK\beta (r-b_1)-mpr(c+b_2)-wr(d+b_3)\right) ]}. \end{aligned}$$

Theorem 3.3

For the solution of (6) determined by Theorem 3.1, we have

  1. (i)

    If \(r<\frac{\sigma _1^2}{2}+\int _{\mathbb {Z}}[\gamma _1(u)-\ln (1+\gamma _1(u))]\lambda (du),\) then we have

    $$\begin{aligned} \lim _{t\rightarrow +\infty }S(t)=0, \lim _{t\rightarrow +\infty }I(t)=0,~\lim _{t\rightarrow +\infty }Y(t)=0~~\text {a.s.(almost surely)}, \end{aligned}$$

    i.e., the predator and prey populations are die out.

  2. (ii)

    If \(R_{11}>1\) and \(R_{12}>1\), then we have

    $$\begin{aligned} S(t)\rangle _*>0,~~\langle I(t)\rangle _*>0,~~\langle Y(t)\rangle _*>0~~a.s., \end{aligned}$$

    i.e., the predator and prey populations are persistence in the mean.

Proof

Case (i). For the first equation of system (6), we apply the Itô’s formula, resulting

$$\begin{aligned} \begin{aligned} d\ln S(t)=&\left( r-\frac{r}{K}S(t)-\beta I(t)-\frac{1}{2}\sigma _1^2-\int _{\mathbb {Z}}\left[ \gamma _1(u)-\ln (1+\gamma _1(u))\right] \lambda (du)\right) dt\\&+\sigma _1dB_1(t)+\int _{\mathbb {Z}}\ln (1+\gamma _1(u)\widetilde{\varGamma }(dt,du), \end{aligned} \end{aligned}$$

integrating both sides of which gives

$$\begin{aligned} \begin{aligned} \frac{1}{t}\ln \frac{S(t)}{S(0)} =&\,r-\frac{1}{2}\sigma _1^2-\int _{\mathbb {Z}}\left[ \gamma _1(u)-\ln (1+\gamma _1(u))\right] \lambda (du)-\frac{r}{K}\langle S(t)\rangle -\beta \langle I(t)\rangle \\&+\frac{1}{t}\sigma _1B_1(t)+\frac{1}{t}\int _0^t\int _{\mathbb {Z}}\ln (1+\gamma _1(u))\widetilde{\varGamma }(dt,du)\\ \le&\,r-\frac{1}{2}\sigma _1^2-\int _{\mathbb {Z}}\left[ \gamma _1(u)-\ln (1+\gamma _1(u))\right] \lambda (du)-\frac{r}{K}\langle S(t)\rangle +\frac{1}{t}\sigma _1B_1(t)\\&+\frac{1}{t}\int _0^t\int _{\mathbb {Z}}\ln (1+\gamma _1(u))\widetilde{\varGamma }(dt,du).\\ \end{aligned} \end{aligned}$$
(7)

By using [21], we obtain \( \lim _{t\rightarrow +\infty }S(t)=0~~a.s. \) Similarly, we have

$$\begin{aligned} \begin{aligned} \frac{1}{t}\ln \frac{I(t)}{I(0)} =&-c-\frac{1}{2}\sigma _2^2-\int _{\mathbb {Z}}\left[ \gamma _2(u)-\ln (1+\gamma _2(u))\right] \lambda (du)+\beta \langle S(t)\rangle -p\langle Y(t)\rangle \\&-w\langle I(t)\rangle +\frac{1}{t}\sigma _2B_2(t)+\frac{1}{t}\int _0^t\int _{\mathbb {Z}}\ln (1+\gamma _2(u))\widetilde{\varGamma }(dt,du)\\ \le&-c-\frac{1}{2}\sigma _2^2-\int _{\mathbb {Z}}\left[ \gamma _2(u)-\ln (1+\gamma _2(u))\right] \lambda (du)+\beta \langle S(t)\rangle -w\langle I(t)\rangle \\&+\frac{1}{t}\sigma _2B_2(t)+\frac{1}{t}\int _0^t\int _{\mathbb {Z}}\ln (1+\gamma _2(u))\widetilde{\varGamma }(dt,du).\\ \end{aligned} \end{aligned}$$
(8)

Since \(\lim _{t\rightarrow +\infty }S(t)=0\), for sufficiently large T, there is a constant \(\varepsilon >0\) such that

$$\begin{aligned} -c-\frac{1}{2}\sigma _2^2-\int _{\mathbb {Z}}\left[ \gamma _2(u)-\ln (1+\gamma _2(u))\right] \lambda (du)+\varepsilon <0 \text { for } t>T \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow +\infty }I(t)=0~~\text { almost surely}. \end{aligned} \end{aligned}$$

Note that

$$\begin{aligned} \begin{aligned} \frac{1}{t}\ln \frac{Y(t)}{Y(0)}=&-d-\frac{1}{2}\sigma _3^2-\int _{\mathbb {Z}}\left[ \gamma _3(u)-\ln (1+\gamma _3(u))\right] \lambda (du)+mp\langle I(t)\rangle -h\langle Y(t)\rangle \\&+\frac{1}{t}\sigma _3B_3(t)+\int _0^t\int _{\mathbb {Z}}\ln (1+\gamma _3(u))\widetilde{\varGamma }(dt,du). \end{aligned} \end{aligned}$$
(9)

We conclude by \(\lim _{t\rightarrow +\infty }I(t)=0\) that

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow +\infty }Y(t)=0~~a.s. \end{aligned} \end{aligned}$$

Case (ii). From (7) and [21], we have

$$\begin{aligned} \begin{aligned} \langle S(t)\rangle ^*\le \frac{K\left( r-b_1\right) }{r}, \end{aligned} \end{aligned}$$
(10)

substituting which into (8) gives

$$\begin{aligned} \begin{aligned} \frac{1}{t}\ln \frac{I(t)}{I(0)}\le&-c-b_2+\beta \langle S(t)\rangle ^*-w\langle I(t)\rangle +\frac{1}{t}\sigma _2B_2(t)\\&+\frac{1}{t}\int _0^t\int _{\mathbb {Z}}\ln (1+\gamma _2(u))\widetilde{\varGamma }(dt,du)\\ \le&-c-b_2+\frac{K\beta \left( r-b_1\right) }{r}-w\langle I(t)\rangle +\frac{1}{t}\sigma _2B_2(t)\\&+\frac{1}{t}\int _0^t\int _{\mathbb {Z}}\ln (1+\gamma _2(u))\widetilde{\varGamma }(dt,du).\\ \end{aligned} \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned} \langle I(t)\rangle ^*\le \frac{K\beta (r-b_1)-r(c+b_2)}{wr}. \end{aligned} \end{aligned}$$
(11)

Then (11) and (7) yield

$$\begin{aligned} \begin{aligned} \frac{1}{t}\ln \frac{S(t)}{S(0)}\ge&\,r-b_1-\frac{r}{K}\langle S(t)\rangle -\beta \langle I(t)\rangle ^*+\frac{1}{t}\sigma _1B_1(t)\\&+\frac{1}{t}\int _0^t\int _{\mathbb {Z}}\ln (1+\gamma _1(u))\widetilde{\varGamma }(dt,du)\\ \ge&\,r-b_1-\frac{K\beta ^2(r-b_1)-\beta r(c+b_2)}{wr}-\frac{r}{K}\langle S(t)\rangle +\frac{1}{t}\sigma _1B_1(t)\\&+\frac{1}{t}\int _0^t\int _{\mathbb {Z}}\ln (1+\gamma _1(u))\widetilde{\varGamma }(dt,du).\\ \end{aligned} \end{aligned}$$

Using a result from [21],

$$\begin{aligned} \begin{aligned} \langle S(t)\rangle _*\ge \frac{Kwr(r-b_1)-K^2\beta ^2(r-b_1)+K\beta r(c+b_2)}{wr^2}>0. \end{aligned} \end{aligned}$$
(12)

Similarly, by (11) and (9) one can obtain

$$\begin{aligned} \begin{aligned} \frac{1}{t}\ln \frac{Y(t)}{Y(0)}\le&-d-b_3+mp\langle I(t)\rangle ^*-h\langle Y(t)\rangle +\frac{1}{t}\sigma _3B_3(t)\\&+\frac{1}{t}\int _0^t\int _{\mathbb {Z}}\ln (1+\gamma _3(u))\widetilde{\varGamma }(dt,du)\\ \le&-d-b_3+\frac{mpK\beta (r-b_1)-rmp(c+b_2)}{wr}-h\langle Y(t)\rangle +\frac{1}{t}\sigma _3B_3(t)\\&+\frac{1}{t}\int _0^t\int _{\mathbb {Z}}\ln (1+\gamma _3(u))\widetilde{\varGamma }(dt,du).\\ \end{aligned} \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned} \langle Y(t)\rangle ^*\le \frac{mpK\beta (r-b_1)-rmp(c+b_2)-wr(d+b_3)}{wrh}. \end{aligned} \end{aligned}$$
(13)

Equations (12), (13) and (8) yield

$$\begin{aligned} \frac{1}{t}\ln \frac{I(t)}{I(0)}\ge & {} -c-b_2+\beta \langle S(t)\rangle _*-p\langle Y(t)\rangle ^*-w\langle I(t)\rangle +\frac{1}{t}\sigma _2B_2(t)\\&+\frac{1}{t}\int _0^t\int _{\mathbb {Z}}\ln (1+\gamma _2(u))\widetilde{\varGamma }(dt,du)\\\ge & {} -c-b_2{+}{-}w\langle I(t)\rangle +\frac{K\beta wr(r{-}b_1)-K^2\beta ^3(r-b_1){+}K\beta ^2 r(c+b_2)}{wr^2}\\&-\frac{mp^2K\beta (r-b_1)-rmp^2(c+b_2)-wrp(d+b_3)}{wrh}+\frac{1}{t}\sigma _2B_2(t)\\&+\frac{1}{t}\int _0^t\int _{\mathbb {Z}}\ln (1+\gamma _2(u))\widetilde{\varGamma }(dt,du).\\ \end{aligned}$$

Note that

$$\begin{aligned} \frac{K\beta h\left[ wr(r-b_1)-K\beta ^2(r-b_1)+\beta r(c+b_2)\right] }{wr^2h(c+b_2)+pr\left( mpK\beta (r-b_1)-mpr(c+b_2)-wr(d+b_3)\right) }>1. \end{aligned}$$

We have

$$\begin{aligned} \begin{aligned} \langle I(t)\rangle _*\ge&\frac{1}{w^2r^2h}\big [K\beta h\left( wr(r-b_1)-K\beta ^2(r-b_1)+\beta r(c+b_2)\right) -wr^2h(c+b_2)\\&-pr\left( mpK\beta (r-b_1)-mpr(c+b_2)-wr(d+b_3)\right) \big ]>0. \end{aligned} \end{aligned}$$
(14)

Substituting Eq. (14) into Eq. (9), we have

$$\begin{aligned} \begin{aligned} \frac{1}{t}\ln \frac{Y(t)}{Y(0)}\ge&-d-b_3+mp\langle I(t)\rangle _*-h\langle Y(t)\rangle +\frac{1}{t}\sigma _3B_3(t)\\&+\frac{1}{t}\int _0^t\int _{\mathbb {Z}}\ln (1+\gamma _3(u))\widetilde{\varGamma }(dt,du)\\ \ge&-d-b_3+\frac{mp}{w^2r^2h}\big [K\beta h(wr(r-b_1)-K\beta ^2(r-b_1)+\beta r(c+b_2))\\&-wr^2h(c+b_2)-pr(mpK\beta (r-b_1)-mpr(c+b_2)-wr(d+b_3))\big ]\\&-h\langle Y(t)\rangle +\frac{1}{t}\sigma _3B_3(t)+\frac{1}{t}\int _0^t\int _{\mathbb {Z}}\ln (1+\gamma _3(u))\widetilde{\varGamma }(dt,du).\\ \end{aligned} \end{aligned}$$

Since \(R_{12}>1\), we obtain

$$\begin{aligned} \begin{aligned} \langle Y(t)\rangle _*\ge&\frac{1}{w^2r^2h^2}\Big [mp\big [K\beta h\left( wr(r-b_1)-K\beta ^2(r-b_1)+\beta r(c+b_2)\right) \\&-wr^2h(c+b_2)-pr\left( mpK\beta (r-b_1)-mpr(c+b_2)-wr(d+b_3)\right) \big ]\\&-w^2r^2h(d+b_3)\Big ]>0. \end{aligned} \end{aligned}$$

The proof is complete. \(\square \)

Notes. Theorem 3.3 shows us the dynamics of birth and death of the prey-predator system. By Theorem 3.3, if \(r<\frac{\sigma _1^2}{2}+\int _{\mathbb {Z}}[\gamma _1(u)-\ln (1+\gamma _1(u))]\lambda (du)\), then the predator and prey are die out; while if \(R_{11}>1\) and \(R_{12}>1\), then the predator and prey are persistence in mean. Note that the right end of inequality \(r<\frac{\sigma _1^2}{2}+\int _{\mathbb {Z}}[\gamma _1(u)-\ln (1+\gamma _1(u))]\lambda (du)\) is a function of the intensity of noise and is positively correlated with the intensity of noise. This shows that as long as the intensity of the stochastic noise is large enough, we have \(r<\frac{\sigma _1^2}{2}+\int _{\mathbb {Z}}[\gamma _1(u)-\ln (1+\gamma _1(u))]\lambda (du)\), which means that large environmental disturbances can lead to the extinction of the population.

Theorem 3.4

For the solution of (6), we have

  1. (i)

    if \(R_0<1\), then

    $$\begin{aligned} \begin{aligned} F_1(S,I,V):=&\limsup _{t\rightarrow \infty }\frac{1}{t}{\mathbb {E}}\int _0^t\left[ (S(s)-K)^2+I^2(s)+Y^2(s)\right] ds\le \frac{\delta _1}{\varTheta }; \end{aligned} \end{aligned}$$
  2. (ii)

    if \(R_0>1\) and \(R_1<1,\) then

    $$\begin{aligned} \begin{aligned} F_2(S,I,V):= \limsup _{t\rightarrow \infty }\frac{1}{t}{\mathbb {E}}\int _0^t\left[ (S(s)-\overline{S})^2+(I(s)-\overline{I})^2+Y^2(s)\right] ds\le \frac{\delta _2}{\varTheta }; \end{aligned} \end{aligned}$$
  3. (iii)

    if \(R_1>1,\) then

    $$\begin{aligned} \begin{aligned} F_3(S,I,V):=&\limsup _{t\rightarrow \infty }\frac{1}{t}{\mathbb {E}}\int _0^t\left[ (S(s){-}S^*)^2{+}(I(s){-}I^*)^2{+}(Y(s){-}Y^*)^2\right] ds \\ \le&\frac{\delta _3}{\varTheta }, \end{aligned} \end{aligned}$$

    where \(\varTheta =\min \bigg \{\frac{r}{K},w,\frac{h}{m}\bigg \}\) and

    $$\begin{aligned} \begin{aligned} \delta _1=&\frac{1}{2}\sigma _1^2K+K\int _{\mathbb {Z}}[\gamma _1(u)-\ln (1+\gamma _1(u))]\lambda (du),\\ \delta _2=&\frac{\sigma _1^2\overline{S}}{2}+\frac{\sigma _2^2\overline{I}}{2}+\overline{S}\int _{\mathbb {Z}}[\gamma _1(u)-\ln (1+\gamma _1(u))]\lambda (du)\\&+\overline{I}\int _{\mathbb {Z}}[\gamma _2(u)-\ln (1+\gamma _2(u))]\lambda (du),\\ \delta _3=&\frac{1}{2}\sigma _1^2S^*+\frac{1}{2}\sigma _2^2I^*+\frac{1}{2m}\sigma _3^2Y^*+S^*\int _{\mathbb {Z}}[\gamma _1(u)-\ln (1+\gamma _1(u))]\lambda (du)\\&+I^*\int _{\mathbb {Z}}[\gamma _2(u)-\ln (1+\gamma _2(u))]\lambda (du)\\&+\frac{1}{m}Y^*\int _{\mathbb {Z}}[\gamma _3(u)-\ln (1+\gamma _3(u))]\lambda (du).\\ \end{aligned} \end{aligned}$$

Proof

Case (iii). Since \((S^*,I^*,Y^*)\) is the positive equilibrium point of the system (4), we have

$$\begin{aligned} r\left( 1-\frac{S^*}{K}\right) =\beta I^*,~~\beta S^*-c-pY^*-wI^*=0,~~mpI^*-d-hY^*=0. \end{aligned}$$

Define the Lyapunov function:

$$\begin{aligned} \begin{aligned} V(S,I,Y)&=\displaystyle {S-S^*-S^*\ln \frac{S}{S^*}+I-I^*-I^*\ln \frac{I}{I^*}+\frac{1}{m}\left( Y-Y^*-Y^*\ln \frac{Y}{Y^*}\right) .} \end{aligned} \end{aligned}$$

Applying Itô’s formula to the system (6), we have

$$\begin{aligned} \begin{aligned} dV=&\,LVdt+\sigma _1(S-S^*)dB_1(t)+\int _{\mathbb {Z}}[\gamma _1(u)S-S^*\ln (1+\gamma _1(u))]\widetilde{\varGamma }(dt,du)\\&+\sigma _2(I-I^*)dB_2(t) +\int _{\mathbb {Z}}[\gamma _2(u)I-I^*\ln (1+\gamma _2(u))]\widetilde{\varGamma }(dt,du)\\&+\frac{1}{m}\sigma _3(Y-Y^*)dB_3(t)+\frac{1}{m}\int _{\mathbb {Z}}[\gamma _3(u)Y-Y^*\ln (1+\gamma _3(u))]\widetilde{\varGamma }(dt,du), \end{aligned} \end{aligned}$$
(15)

where

$$\begin{aligned} \begin{aligned} LV=&\,(S-S^*)\left( r(1-\frac{S}{K})-\beta I\right) +\frac{\sigma _1^2S^*}{2}+S^*\int _{\mathbb {Z}}[\gamma _1(u)-\ln (1+\gamma _1(u))]\lambda (du)\\&+(I-I^*)\left( \beta S-c-pY-wI\right) +\frac{\sigma _2^2I^*}{2}+I^*\int _{\mathbb {Z}}[\gamma _2(u)-\ln (1+\gamma _2(u))]\lambda (du)\\&+(Y-Y^*)(pI-\frac{d}{m}-\frac{h}{m}Y)+\frac{\sigma _3^2Y^*}{2m} +\frac{Y^*}{m}\int _{\mathbb {Z}}[\gamma _3(u)-\ln (1+\gamma _3(u))]\lambda (du)\\ =&\,r(S-S^*)-\frac{r}{K}(S-S^*)S-\beta (S-S^*)I+\beta (I-I^*)S-c(I-I^*)\\&-p(I-I^*)Y-w(I-I^*)I+p(Y-Y^*)I-\frac{d}{m}(Y-Y^*)-\frac{h}{m}(Y-Y^*)Y\\&+\frac{1}{2}\left( \sigma _1^2S^*+\sigma _2^2I^*+\frac{1}{m}\sigma _3^2 Y^*\right) +S^*\int _{\mathbb {Z}}[\gamma _1(u)-\ln (1+\gamma _1(u))]\lambda (du)\\&+I^*\int _{\mathbb {Z}}[\gamma _2(u)-\ln (1+\gamma _2(u))]\lambda (du)+\frac{1}{m}Y^*\int _{\mathbb {Z}}[\gamma _3(u)-\ln (1+\gamma _3(u))]\lambda (du)\\ =&-\frac{r}{K}(S-S^*)^2-w(I-I^*)^2-\frac{h}{m}(Y-Y^*)^2+\frac{1}{2}\left( \sigma _1^2S^*+\sigma _2^2I^*+\frac{1}{m}\sigma _3^2 Y^*\right) \\&+S^*\int _{\mathbb {Z}}[\gamma _1(u)-\ln (1+\gamma _1(u))]\lambda (du)+I^*\int _{\mathbb {Z}}[\gamma _2(u)-\ln (1+\gamma _2(u))]\lambda (du)\\&+\frac{1}{m}Y^*\int _{\mathbb {Z}}\left[ \gamma _3(u)-\ln (1+\gamma _3(u))\right] \lambda (du).\\ \end{aligned} \end{aligned}$$

Integrating on both sides of Eq. (15) and then taking expectation result in

$$\begin{aligned} \begin{aligned}&{\mathbb {E}}\int _0^t\bigg \{\frac{r}{K}(S(\theta )-S^*)^2+w(I(\theta )-I^*)^2+\frac{h}{m}(Y(\theta )-Y^*)^2\bigg \}d\theta \\&\quad \le {\mathbb {E}}V(0)+\bigg [\frac{1}{2}\left( \sigma _1^2S^*+\sigma _2^2I^*+\frac{1}{m}\sigma _3^2 Y^*\right) +S^*\int _{\mathbb {Z}}[\gamma _1(u)-\ln (1+\gamma _1(u))]\lambda (du)\\&\qquad +I^*\int _{\mathbb {Z}}[\gamma _2(u)-\ln (1+\gamma _2(u))]\lambda (du)+\frac{1}{m}Y^*\int _{\mathbb {Z}}[\gamma _3(u)-\ln (1+\gamma _3(u))]\lambda (du)\bigg ]t.\\ \end{aligned} \end{aligned}$$
(16)

Dividing Eq. (16) by t and letting \(t\rightarrow \infty \), we have

$$\begin{aligned} \displaystyle {\limsup _{t\rightarrow \infty }}\frac{1}{t}{\mathbb {E}}\int _0^t\left[ (S(s)-S^*)^2+(I(s)-I^*)^2+(Y(s)-Y^*)^2\right] ds\le \frac{\delta _3}{\varTheta }. \end{aligned}$$

The proof of case (iii) is complete. By defining the Lyapunov functions \(V(S,I,Y)=S-K-K\ln \frac{S}{K}+I+\frac{1}{m}Y\) and \(V(S,I,Y)=S-\overline{S}-\overline{S}\ln \frac{S}{\overline{S}}+I-\overline{I}-\overline{I}\ln \frac{I}{\overline{I}}+\frac{1}{m}Y\), respectively, the proofs of cases (i) and (ii) are similar to case (iii), so we omit them here. \(\square \)

Notes. Theorem 3.4 shows that under different conditions, the solution of the stochastic predator–prey system can fluctuate (around the equilibrium of the ODEs system (4)) in different states, and the amplitude of the fluctuation is positively correlated with the intensity of stochastic noise. In particular, when the intensity of the noise is zero, i.e., \(\sigma _i=\gamma _i(u)=0~(i=1,2,3)\), we have

$$\begin{aligned} LV\le -\frac{r}{K}(S-S^*)^2-w(I-I^*)^2-\frac{h}{m}(Y-Y^*)^2\le 0, \end{aligned}$$

which indicates that the interior solution \(E_3(S^*,I^*,Y^*)\) of the ODEs model (4) is GAS provided that \(R_1>1\). Similarly, we can obtain that the boundary equilibrium \(E_1(K,0,0)\) is GAS provided that \(R_0=\frac{K\beta }{c}<1\), and the disease-free equilibrium \(E_2(\overline{S},\overline{I},0)\) is GAS provided that \(R_0>1\) and \(R_1<1\). Therefore, we generalised the global stability of the ODEs system (4).

4 Numerical Simulation

In this section, all simulations are carried out with ©Matlab2013b, the initial value is (2, 2, 3) and the numerical method is based on [15].

We show the extinction and persistence of the system (6). The simulations of the ODEs system (4) were also studied as a comparison. To proceed, we set \(\sigma _i=0.5,\gamma _i(u)=0.1,~i=1,2,3\), \( r=0.12, K=4, \beta =0.5, m=1, p=0.5, d=0.1, h=0.1, c=0.1,w=0.1.\) By straightforward calculation we obtain that:

$$\begin{aligned} R_1=\frac{mp}{d}\frac{r(K\beta -c)}{K\beta ^2+wr}=1.126>1 \end{aligned}$$

and

$$\begin{aligned} r=0.12<\frac{\sigma _1^2}{2}+\int _{\mathbb {Z}}[\gamma _1(u)-\ln (1+\gamma _1(u))]\lambda (du)=0.142. \end{aligned}$$

By Theorem 3.3 (i), one can see that equilibrium \(E_3(0.3415,0.2195,0.0976)\) of system (4) is GAS, and the populations in the stochastic system (6) are die out. Figure 1a shows that the ODE system (4) admits a positive equilibrium, while Fig. 1b shows that stochastic solution of the predator and prey populations go to zero with probability one.

Fig. 1
figure 1

The trajectories of (6) and (4) under the conditions of Theorem 3.3 (i). a The persistence of the ODE system (4); b the predator and prey populations predicted by (6) go extinct with probability 1

Full size image

Next, we set \(\sigma _i=0.02,\gamma _i(u)=0.01,~i=1,2,3\), \(r=22, K=5, \beta =0.1, m=1, p=0.1, d=0.1, h=0.1, c=0.01,w=0.182.\) It follows that:

$$\begin{aligned} R_1=2.6591>1,~~R_{11}=1.0637>1,~~R_{12}=1.7401>.1 \end{aligned}$$

By Theorem 3.3 (ii), we know that the unique positive equilibrium \(E_3(4.9528,2.0755,1.0755)\) of (4) is GAS, and the populations in (6) are persistence in mean. Figure 2a shows that the ODE system (4) admits a positive equilibrium, while Fig. 2b shows that stochastic solution of the predator and prey populations fluctuates around the deterministic equilibrium point \(E_3\).

Fig. 2
figure 2

The trajectories of the stochastic system (6) and the ODEs system (4) under the conditions of Theorem 3.3 (ii). a The persistence of the ODE system (4); b the persistence in mean of the stochastic system (6)

Full size image

We now numerically illustrate the asymptotic dynamics of (6) with \(\sigma _i=0.3,~i=1,2,3, r=1,w=0.2.\) The other parameters are given by:

  1. (1)

    \(K=1,\beta =0.2,m=0.2,p=0.3,d=0.1,h=0.2,c=0.3,w=0.2\);

  2. (2)

    \(K=3,\beta =0.4,m=0.2,p=0.5,d=0.6,h=0.1,c=0.3,w=0.2\);

  3. (3)

    \(K=4,\beta =0.3,m=0.8,p=0.6,d=0.3,h=0.2,c=0.1,w=0.2\).

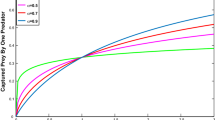
In case (1), by direct calculation we obtain that \(R_0=0.6667<1\), it follows that the ODEs model (4) admits a disease-free equilibrium \(E_1(K,0,0)=(1,0,0)\). To see the effects of noise on the stochastic system (6), we choose \(\gamma _i=0,0.2\) and 0.3 respectively, \(i=1,2,3\). By straightforward calculations we obtain that \(F_1(S,I,V)\le \frac{\delta _1}{\varTheta }=0.225,0.3134\) and 0.4132, respectively. Figure 3a shows that the ODEs system (4) admits a disease-free equilibrium \(E_1(K,0,0)=(1,0,0)\). Figure 3b, d describe that the level of the susceptible prey in the stochastic model vibrates around the solution of the ODEs model, while the infected prey and predator go to zero with probability one.

Fig. 3
figure 3

The trajectories of the stochastic system (6) and the ODEs system (4) under the conditions of Theorem 3.4 (i). a The deterministic model; b the Brownian motion model; c the Lévy jump model with \(\gamma _i=0.2\); d the Lévy jump model with \(\gamma _i=0.3,~i=1,2,3\)

Full size image

In case (2), by direct calculation we obtain that \(R_0=4>1,~R_1=0.2206<1\), it follows that the ODEs model (4) admits a boundary equilibrium \(E_2(\overline{S},\overline{I},0)=(1.4118,1.3235,0)\). To see the effects of noise on the stochastic system (6), we choose \(\gamma _i=0,0.1\) and 0.2 respectively, \(i=1,2,3\). By straightforward calculations we obtain that \(F_2(S,I,V)\le \frac{\delta _2}{\varTheta }=0.6154,0.6796\) and 0.8572, respectively. Figure 4a shows that the ODEs system (4) admits a boundary equilibrium \(E_2(\overline{S},\overline{I},0)=(1.4118,1.3235,0)\). Figure 4b–d show that stochastic solutions of the susceptible prey and infected prey fluctuate around the solution of the ODEs model, while the predator go to zero with probability one.

Fig. 4
figure 4

The trajectories of the stochastic system (6) and the ODEs system (4) under the conditions of Theorem 3.4 (ii). a The deterministic model; b the Brownian motion model; and the Lévy jump model, c for \(\gamma _i=0.1\) and d for \(\gamma _i=0.2,~i=1,2,3\)

Full size image
Fig. 5
figure 5

The trajectories of the stochastic system (6) and the ODEs system (4) under the conditions of Theorem 3.4 (iii). a The deterministic model; b the Brownian motion model; c the Lévy jump model with \(\gamma _i=0.1\); d the Lévy jump model with \(\gamma _i=0.2,~i=1,2,3\)

Full size image

In case (3), by direct calculation we obtain that \(R_1=3.1429>1\), it follows that the ODEs model (4) admits a positive equilibrium \(E_3(S^*,I^*,Y^*)=(2.8,1,0.9)\). To see the effects of noise on the stochastic system (6), we choose \(\gamma _i=0,0.1\) and 0.2 respectively, \(i=1,2,3\). By straightforward calculations we obtain that \(F_3(S,I,V)\le \frac{\delta _3}{\varTheta }=0.7852,0.8671\) and 1.0937, respectively. Figure 5a shows that the ODEs system (4) admits a positive equilibrium \(E_3(S^*,I^*,Y^*)=(2.8,1,0.9)\). Figure 5b–d show that stochastic solutions of the predator and prey fluctuate around the deterministic equilibrium point.

Note that in Fig. 1a, b, all parameters are the same except for the intensity of stochastic noise. This indicates that high-intensity environmental disturbances can lead to the extinction of the population. In addition, Figs. 2, 3, 4 and 5 show that when the stochastic noise is sufficiently small, the environmental disturbance does not cause the extinction of the population, but causes the density of the population to oscillate within a certain small range. In summary, our results that: (i) High-intensity environmental disturbances may lead to population extinction; (ii) Small-intensity environmental disturbances may not cause population extinction, but will cause population size to fluctuate within a certain interval. And the amplitude of the fluctuation is positively correlated with the intensity of the environmental disturbance.

5 Discussion

This paper formulates a stochastic system to study the interactions between predator and prey populations. The model is incorporating the disease invasion and sudden catastrophic shocks. The globally unique positive solution is confirmed by using conventional methods. The stochastic uniform boundedness of the solution is obtained under certain conditions. Sufficient conditions for the persistence and extinction are given to measure the level of population size. Asymptotic dynamics of the solutions are carried out by two criteria parameters. The long-term dynamics of the solutions are demonstrated by numerical simulations. By comparing the stochastic system with the corresponding ODE system, we find that: (i) when the intensity of environmental disturbance is large enough, environmental disturbance may lead to the extinction of the population; (ii) when the intensity of environmental disturbances is small enough, environmental disturbances do not cause extinction of the population but cause the population to fluctuate around a certain level, and the amplitude of the fluctuations is proportional to the intensity of environmental disturbances. Our findings indicate that: (i) when the intensity of environmental disturbances is small, the impact of environmental disturbances on the population can be ignored, and the deterministic model can be used to estimate the dynamics of the population. However, when the intensity of environmental disturbance is large, the impact of environmental disturbance on the dynamics of the population cannot be ignored. Otherwise, the estimation result may be inaccurate.

Many researchers have made great efforts in studying the dynamics of population and infectious diseases [29, 30]. Notably, Lipsitch et al. [18] studied the transmission mechanism of a SIRS infectious disease, but the results they have obtained were somewhat different from the actual situation. One persuasive reason is that they ignored the effects of noise (such as earthquake, flood, drought, typhoon, tsunami). May [24] indicated that the predation rate, environmental accommodation, and other factors could be affected by environmental noise. The biosphere environment in which the population located is often highly stochastic, and stochastic noise is also the cause leading to the extinction of individuals. Hence the effects of noise cannot be ignored. Accordingly, we introduced the Lévy jump into the proposed model and studied the dynamics of the model where noise plays a crucial rule. Compared to the stochastic system driven by Brownian motion in Ref. [34], our system is driven simultaneously by Brownian motion and Poisson motion. Therefore, the model in Ref. [34] can be used to study the effects of small environmental disturbances (such as wind and rain) on population dynamics, and our model can be used to study the effects of small environmental disturbances on population dynamics, as well as to study large environmental disturbances (such as sudden volcanoes and floods) on population dynamics. Therefore, our theoretical analysis is much more complicated than the theoretical analysis in Ref. [34].

The system developed in this paper unifies much of the previous work. It encompasses the influential work of Xiao et al. [32] in understanding the asymptotic stability of the model with the disease in prey and the more recent work on the random disturbance in a predator–prey model [34]. The results may help for the further study of such systems with singular diffusion, indicating that the variables or parameters are subject to the same environmental noise.