1 Introduction

The history of the study to gain knowledge about the interactions among the individuals of the prey–predator species dates back long. Many ecologists and mathematicians [6, 8, 14, 38] have made a significant contributions to analyze prey–predator interactions over the years. Analysis of the persistence and extinction scenario has been one of the most important objectives, though there are several thematic areas of interest. Analyzing these models in rapidly fluctuating environment make these findings more meaningful and interesting.

From field experiments, some theoretical ecologists and biologists have realised that a prey–predator model should involve not only direct killing but also the fear (felt by prey)-factor as they have observed a change in the behaviour and psychology of the prey population in presence of the predator, sometimes more powerful than direct killing [4, 5]. However, the intensity of the impact left by fear factor on the ecosystem is not totally clear till now. There are some controversies and some believe that the physiological impacts of fear on young populations may lead to a lower survival rate of adults, although so far such an impact has not yet been shown by any direct experimental results.

Fear makes different animals respond differently [5, 31, 33, 34]: some find a different place to live, some change their foraging behaviour, some become circumspect, whereas others go through psychological changes. Under fear, a prey species may find a comparatively low risk (with respect to fear) area to live but this effort may get nullified in case the new habitat is not suitable for the prey to live as well - the prey may starve out of fear rather than searching for food [4, 5, 43]. In an experiment made on the snowshoe hare, it has been found that high fear factor played a bigger role in decreasing their reproduction rate than high hare density or poor food level [2]. Therefore, it would not be appropriate to neglect the fear factor prevailing in the minds of the prey species particularly when the reproduction rate is reduced by it [2, 3, 32]. The estimation of Pangle et al. [30] upon direct killings and fear effects on three species of zoo-plankton on Lake Michigan and Lake Erie by the predation of water fleas (Bythotrephes longimanus) over six combinations of location and depth is that the effect of the fear factor on the growth rates were seven times more than the effect of direct killing of them. Altendorf et al. [1] found that mule deer, under the fear of mountain lions, refrained themselves from searching for food to a large extent. Creel et al. [3] found that elk (one of the largest species of the deer family) faces changes in reproductive physiology due to the predation fear of wolves. It has also been found that birds flee from their nests as an anti-predator behaviour when they discover the sound of predator (first sign of danger) [5]. A recent experiment, performed by Zanette et al. [45], on song sparrows during an entire breeding season, found their reproduction rate to have fallen down by 40% only by the fear of predator (sound of predator). A study of Krapivsky et al. [22] shows that different positions and different numbers of the predator (lion) compel lambs to behave differently.

Recently, an observation has brought it into notice that prey population is reduced by the fear of large carnivores and thereby the number of species that the prey population feeds on or competes with has increased. Das and Samanta [7] has found that predator population dominates prey population because of high cost of fear. It emerged out in a field experiment along the shoreline of British Columbia that the racoon’s predation rate and its hunting of intertidal crabs, subtidal red rock crabs and intertidal fish decreased for fear of carnivorous animals and the abundance of intertidal crabs, subtidal red rock crabs and intertidal fish went up by 97%, 61% and 81% respectively [40]. Again, the findings in the cases of Siberian Jay by Eggers et al. [12], dugongs by Wirsing et al. [44] and birds by Ghalambor et al. [13] and Hua et al. [18, 19] have led mathematicians to believe that fear factor plays a key role in population dynamics. Many researchers have studied prey–predator models, but mathematical models considering fear factor have only been successfully developed by Wang et al. [41, 42]. Despite having a lot of field experimental results, there is little evidence which upholds the fact that population dynamics is affected by fear [9, 10, 27,28,29].

Existence of toxic substance in environment is a major concern for bioeconomic modeling. Involving toxic substance in mathematical model is started with the studies of Hallam and Clark [15], Hallam and De Luna [16], Dubey and Hussain [11], Kar and Chaudhuri [21], Samanta [36], etc. General single species or two species communities without any special emphasis on aquatic environments are considered in most of the models. The toxin released by one species or by environment not only affects that species but may affect the growth of the other species also (such as predator of that species). Day by day industries are producing a huge amount of toxicants in to the environment because of growing human needs. These toxicants mostly affect the species which are living there. Maynard Smith [39] incorporated the effects of toxic substances in a two species Lotka–Volterra competitive system by considering that in presence of other species each species produces a toxic substance.

To evaluate the effect of environmental noises on dynamical systems some researches [23, 26, 35] have introduced Gaussian white noise as a model of environmental variations. May in 1973 [26] pointed out that all the parameters such as birth rates, death rates, competition coefficient, carrying capacity etc. involved in a dynamical system can be randomly fluctuated to a great lesser extent for the cause of continuous fluctuation in the environment. Das and Samanta [6] have shown that the environmental noise effects on extinction and persistence of the system.

In the present work, we have considered a prey–predator system in a randomly fluctuating environment incorporating fear of predator (felt by prey) and prey is directly affected by toxic substance and predator gets affected by consuming infected prey.

We have divided the rest of this work into some sections and subsections. Section 2 contains formulation of the model which is divided into four subsections. In Sect. 2.1 functional response is described and Sect. 2.2 deals with fear function. Deterministic model is formulated in Sect. 2.3 followed by stochastic model in Sect. 2.4. Positivity of solutions of both the deterministic and stochastic model is analyzed in Sect. 3 followed by boundedness of solutions in Sect. 4. Section 5 contains uniform continuity criterion of solutions of the stochastic system. In Sect. 6 extinction scenario in presence of environmental noise is discussed. Most important theorem of persistence of the system is discussed in Sect. 7. In Sect. 8 numerical simulation justify the mathematical findings numerically using MATLAB. In Sect. 9, we have given some conclusion of our findings.

2 Model formulation

We shall discuss a predator prey model with the effect of anti-predator defense because of fear (felt by prey) in presence of predator and effect of toxic substance present in the environment (released by some other external sources). It is assumed that the infection among the individuals of the prey species is caused directly by some external toxic substance and the predator gets affected by consuming infected prey.

Let us consider x(t) and y(t) to represent the biomass of prey and predator respectively at any time \(t>0.\) Let us model the effect of fear (felt by prey) through a function \(f(\zeta , \beta , y)\) called fear function that accounts for the cost of anti-predator defence. Here \(\zeta\) represents the cost of minimum fear and \(\displaystyle \frac{1}{\beta }\) stands for the level of fear which causes the anti-predator behavior of the prey. We consider the following system:

$$\begin{aligned} \begin{aligned} \frac{dx}{dt}&= gx f(\zeta , \beta , y) - d_{1}x - r x^{2} - h(x)y \\ \frac{dy}{dt}&= a_{1}h(x)y - d_{2}y \end{aligned} \end{aligned}$$
(2.1)

The term h(x) is the prey density dependent function which defines the intake rate for predator. Here, g is the coefficient of birth rate of the prey, r is the coefficient of the rate of intraspecific competition among the individuals of the prey species, \(d_{1}\) and \(d_{2}\) are the natural mortality rates of prey and predator respectively, \(a_{1}\in (0,1]\) is the conversion rate.

Now we introduce the term \(c_{1}x^{3}\) that accounts for direct transmission of the infection among the individuals of the prey species by external toxic substances and the term \(c_{2}y^{2}\) which comes indirectly through the infection of the predator by consuming infected prey. So, system (2.1) becomes:

$$\begin{aligned} \begin{aligned} \frac{dx}{dt}&= gx f(\zeta , \beta , y) - d_{1}x - r x^{2} - h(x)y - c_{1}x^{3} \\ \frac{dy}{dt}&= a_{1}h(x)y - d_{2}y - c_{2}y^{2} \end{aligned} \end{aligned}$$
(2.2)

2.1 Functional response

The consuming rate per predator towards prey is called functional response in ecology. Ecologist C.S. Holling [17] described functional response into three types: Holling type I, II and III. Holling type II is the mostly used functional response among them and we also consider Holling type II as the functional response in our model. We have considered the following particular form of h(x) in our proposed model:

$$\begin{aligned} h(x)= \frac{\alpha x}{1+ \eta x} \end{aligned}$$
(2.3)

Here, \(\displaystyle \frac{\alpha }{\eta }\) is the maximum consumption rate and \(\displaystyle \frac{1}{\eta }\) is the half saturation constant which are non negative.

2.2 Fear function

As per the experimental evidences, the prey population will be diminished due to the fear effect, so it is reasonable to assume that \(f(\zeta ,\beta ,y)\) has the following properties, where \(\zeta \in [0,1]\) represents the cost of minimum fear and \(\displaystyle \frac{1}{\beta }\) stands for the level of fear:

$$\begin{aligned} \begin{aligned}&(i) \lim _{\frac{1}{\beta }\rightarrow 0} f(\zeta ,\beta ,y) = 1 \ \ \ (ii) f(\zeta ,\beta ,0) = 1 \ \ \ (iii) \lim _{\frac{1}{\beta }\rightarrow \infty } f(\zeta ,\beta ,y) = \zeta \ \\&(iv) \lim _{y \rightarrow \infty } f(\zeta ,\beta ,y) = \zeta \ \ (v) \frac{\partial f(\zeta ,\beta ,y)}{\partial \frac{1}{\beta }}< 0 \ \ \ (vi) \frac{\partial f(\zeta ,\beta ,y)}{\partial y} < 0 \end{aligned} \end{aligned}$$
(2.4)

Now we consider the following function as the fear function for our model:

$$\begin{aligned} f(\zeta ,\beta ,x)= \zeta +\frac{1-\zeta }{1+\frac{y}{\beta }} \end{aligned}$$
(2.5)

which satisfies all the conditions stated in (2.4). We can consider the fear function in many ways satisfying the conditions described in (2.4) and \(0\le \zeta \le 1.\)

2.3 Deterministic model

We take the functions \(f(\zeta , \beta , y)\) and h(x) as described in (2.5) and (2.3) respectively in system (2.2) and obtain the following system:

$$\begin{aligned} \begin{aligned} \frac{dx}{dt}&= gx \left[ \zeta +\frac{\beta (1-\zeta )}{\beta +y} \right] - d_{1}x - r x^{2} - \frac{\alpha x y}{1+ \eta x} - c_{1}x^{3} \\ \frac{dy}{dt}&= a_{1}\frac{\alpha x y}{1+ \eta x} - d_{2}y - c_{2}y^{2} \end{aligned} \end{aligned}$$
(2.6)

Let us consider \(\beta _{1} = g \beta\) and \(\theta = a_{1} \alpha\), then system (2.6) becomes:

$$\begin{aligned} \begin{aligned} \frac{dx}{dt}&= x \left[ g \zeta + \frac{\beta _{1}(1-\zeta )}{\beta + y} \right] - d_{1}x - r x^{2} - \frac{\alpha xy}{1+ \eta x} - c_{1} x^{3} \\ \frac{dy}{dt}&= \frac{\theta xy}{1+ \eta x} - d_{2}y - c_{2}y^{2} \end{aligned} \end{aligned}$$
(2.7)

with initial conditions \(x_0 > 0\) and \(y_0 > 0\).

2.4 Stochastic model

Introducing Gaussian white noise on birth rate and death rate of prey and predator respectively, the following stochastic system arises:

$$\begin{aligned} \begin{aligned} dx&= \left[ (g+ \gamma _{1}) \zeta x + \frac{\beta _{1}(1-\zeta ) x }{\beta + y} - d_{1}x - r x^{2} - \frac{\alpha xy}{1+ \eta x} - c_{1} x^{3} \right] dt \\ dy&= \left[ \frac{\theta xy}{1+ \eta x} - (d_{2}+\gamma _{2})y - c_{2}y^{2} \right] dt \end{aligned} \end{aligned}$$

The parameters g and \(d_{2}\) have been perturbed by independent Gaussian white noise terms \(\gamma _{1}\) and \(\gamma _{2}\) in system (2.7) because these are the vital parameters subject to coupling the environment where the species live [37]. The terms \(\gamma _{1}\) and \(\gamma _{2}\) are independent Gaussian white noises characterised by:

\(\langle \gamma _{j}(t)\rangle = 0\) and \(\langle \gamma _{j}(t_{1})\gamma _{j}(t_{2})\rangle = \sigma ^{2}_{j}\delta _{j}(t_{1}-t_{2}),\) for \(j= 1,2.\)

having the respective intensities \(\sigma _{1}> 0 , \sigma _2 > 0\). The functions \(\delta _{j}(x)\) are the Dirac delta function defined as follows:

$$\begin{aligned} \left\{ \begin{array}{ll}\displaystyle {\delta _{j}(x)=0},\ \text {for}\ x\ne 0,\\ \displaystyle \int _{-\infty }^{\infty }\delta _{j}(x)dx= \lim _{\epsilon \rightarrow 0^{+}} \int _{-\epsilon }^{\epsilon }\delta _{j}(x)dx = 1, \end{array}\right. \end{aligned}$$

and \(\langle \cdot \rangle\) represents the ensemble average. System (2.7) becomes:

$$\begin{aligned} \begin{aligned} dx&= x \left[ (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta + y} - r x - \frac{\alpha y}{1+ \eta x} - c_{1} x^{2} \right] dt + \zeta \sigma _{1} x dw_{1} \\ dy&= y \left[ \frac{\theta x}{1+ \eta x} - d_{2} - c_{2}y \right] dt - \sigma _{2} y dw_{2} \end{aligned} \end{aligned}$$
(2.8)

with initial conditions \(x_0 > 0\) and \(y_0 > 0\), where \(\displaystyle \gamma _{1} = \sigma _1 \frac{dw_1}{dt}\), \(\displaystyle \gamma _{2} = \sigma _2 \frac{dw_2}{dt}\) and two-dimensional standard Brownian motion is expressed as \(w = \left\{ w_1 , w_2 , t \ge 0\right\}\).

3 Positivity

Theorem 3.1

If \((x_0, y_0) \in {\mathbb {R}}_{+}^{2}\) be any initial value, then system (2.7) has global positive solution (x(t), y(t)) which is unique for all \(t \ge 0.\)

Proof

The right hand side of system (2.7) is continuous and locally Lipschitz on \({\mathbb {R}}_{+}^{2}\), the solution (x(t), y(t)) of system (2.7) exists and unique on \([0, \tau ]\), \(\tau \in (0,\infty )\). From (2.7):

$$\begin{aligned} \begin{aligned} x(t)&= x_{0} \exp \int _{0}^{t} \left[ g \zeta + \frac{\beta _{1}(1-\zeta )}{\beta + y} - d_{1} - r x - \frac{\alpha y}{1+ \eta x} - c_{1} x^{2} \right] ds> 0, \ \forall t \ge 0 \\ y(t)&= y_{0} \exp \int _{0}^{t}\left[ \frac{\theta x}{1+ \eta x} - d_{2} - c_{2}y \right] ds > 0, \ \forall t \ge 0 . \end{aligned} \end{aligned}$$

Hence the theorem. \(\square\)

Lemma 3.1

[8] \(z \le 2(z + 1 - \log _{e} (z)) - 2(2 - \log _{e} (2)),\ \forall z> 0.\)

Theorem 3.2

For system (2.8): \((x(t), y(t)) \in {\mathbb {R}}_{+}^{2},\ \forall t> 0\), almost surely.

Proof

Since coefficients of system (2.8) satisfy local Lipschitz condition, for any \((x_0, y_0) \in {\mathbb {R}}_{+}^{2}\) there exists a unique local solution \(x(t), y(t) \in [0, \tau _{e})\), where \(\tau _e\) is the explosion time. To prove that it is a global positive solution, we have to show that \(\tau _{e} = \infty\). Let \(s_0 \ge 0\) be sufficiently large so that both \(x_0\) and \(y_0\) lie in the interval \(\displaystyle \left[ \frac{1}{s_0} , s_0 \right]\). We define stopping time \((\tau _s)\) for each integer \(s \ge s_0\) such that

$$\begin{aligned} \tau _s = \inf \left\{ t \in [0, \tau _e) : x(t) \notin \left( \frac{1}{s} ,s \right) \ \text {or} \ y(t) \notin \left( \frac{1}{s} ,s \right) \right\} , \end{aligned}$$

with \(\inf \phi = \infty\) ( \(\phi\) denotes the empty set). It is easy to observe that \(\tau _s\) increases as \(t \rightarrow \infty\). Here we set \(\displaystyle \tau _{\infty } = \lim _{r \rightarrow \infty } \tau _s\), whence \(\tau _\infty \le \tau _e\) a.s. If it can be proved that \(\tau _\infty = \infty ,\) then it is easy to conclude that \(\tau _e = \infty\) and \((x(t), y(t)) \in {\mathbb {R}}^{2}_{+}\) for all \(t \ge 0\) almost surely. So, to complete the proof, we need to show that \(\tau _\infty = \infty\). It can be proved by contradiction. If possible, suppose the statement is false, then there exists a pair of constants \(T > 0\) and \(\epsilon \in (0, 1)\) such that

$$\begin{aligned} P \left\{ \tau _\infty \le T \right\} > \epsilon . \end{aligned}$$

So, there exists an integer \(s_1 \ge s_0\) such that

$$\begin{aligned} P \left\{ \tau _\infty \le T \right\} > \epsilon , \ \ \forall s\ge s_1 . \end{aligned}$$
(3.1)

Now we define a \({\mathcal {C}}^2\)-function \(G : {\mathbb {R}}^{2}_{+} \longrightarrow \mathbb {R_{+}}\) by

$$\begin{aligned} G(x,y) = (x + 1 - \log _{e}(x)) + (y + 1 - \log _{e}(y)) \end{aligned}$$

Since \((z + 1 - \log _{e}(z)) \ge 0 , \ \forall z >0\), so G(x, y) is positive.

Using Itô formula:

$$\begin{aligned} \begin{aligned} d(G(x,y)) =&\left[ \left( 1-\frac{1}{x} \right) x \left\{ (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta + y} - r x - \frac{\alpha y}{1+ \eta x} - c_{1} x^{2} \right\} \right. \\&\left. + \left( 1-\frac{1}{y} \right) y \left\{ \frac{\theta x}{1+ \eta x} - d_{2} - c_{2}y \right\} +\frac{\sigma _{1}^{2} \zeta ^{2}}{2} +\frac{\sigma _{2}^{2}}{2} \right] dt \\&+ \left[ \left( 1-\frac{1}{x} \right) \zeta \sigma _{1} x dw_{1} - \left( 1-\frac{1}{y} \right) \sigma _{y} y dw_{2} \right] \\ =&\left[ (x-1) \left\{ (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta + y} - r x - \frac{\alpha y}{1+ \eta x} - c_{1} x^{2} \right\} + (y-1) \right. \\&\left. \left\{ \frac{\theta x}{1+ \eta x} - d_{2} - c_{2}y \right\} +\frac{\sigma _{1}^{2} \zeta ^{2} + \sigma _{2}^{2}}{2} \right] dt + \left[ (x-1) \zeta \sigma _{1} dw_{1} - (y-1) \sigma _{y} dw_{2} \right] \\ \le&\left[ (x-1) \left\{ (g \zeta -d_{1}) + \frac{\beta _{1}(1- \zeta ) }{\beta } - r x - \frac{\alpha y}{1+ \eta x} - c_{1} x^{2} \right\} + (y-1) \right. \\&\left. \left\{ \frac{\theta }{\eta } - d_{2} - c_{2}y \right\} +\frac{\sigma _{1}^{2} \zeta ^{2} + \sigma _{2}^{2}}{2} \right] dt + \left[ (x-1) \zeta \sigma _{1} dw_{1} - (y-1) \sigma _{y} dw_{2} \right] \\ \le&\left[ (g \zeta - d_{1})x + \frac{\beta _{1}(1- \zeta )}{\beta } - (g \zeta - d_{1}) - \frac{\beta _{1}(1- \zeta )}{\beta } + rx + \left( \frac{\theta }{\eta } - d_{2} + c_{2} \right) y \right. \\&\left. - \frac{\theta }{\eta } + d_{2} \right] dt + \left[ (x-1) \zeta \sigma _{1} dw_{1} - (y-1) \sigma _{y} dw_{2} \right] \\ \le&\left[ \left\{ g \zeta - d_{1} + \frac{\beta _{1} (1-\zeta )}{\beta } + r \right\} x + \left\{ \frac{\theta }{\eta } - d_{2} + c_{2} \right\} y - \left\{ g \zeta - d_{1} + \frac{\beta _{1} (1-\zeta )}{\beta } \right. \right. \\&\left. \left. + \frac{\theta }{\eta } - d_{2} - \frac{\sigma _{1}^{2} \zeta ^{2} + \sigma _{2}^{2}}{2} \right\} \right] dt + \left[ (x-1) \zeta \sigma _{1} dw_{1} - (y-1) \sigma _{y} dw_{2} \right] \\ =&(b_{1}x + b_{2}y + b_{3})dt + \left[ (x-1) \zeta \sigma _{1} dw_{1} - (y-1) \sigma _{y} dw_{2} \right] \end{aligned} \end{aligned}$$

where, \(b_{1} = \left( g \zeta - d_{1} + \frac{\beta _{1} (1-\zeta )}{\beta } + r \right) , b_{2}= \left( \frac{\theta }{\eta } - d_{2} + c_{2} \right) \ \mathrm {and}\) \(b_{3}= - \left( g \zeta - d_{1} + \frac{\beta _{1} (1-\zeta )}{\beta } + \frac{\theta }{\eta } - d_{2} - \frac{\sigma _{1}^{2} \zeta ^{2} + \sigma _{2}^{2}}{2} \right)\)

Lemma 3.1 leads to the following result:

$$\begin{aligned} \begin{aligned} d(G(x(t),y(t)))&< \left[ 2b_{1} ( x + 1 - \log _{e} (x)) + 2b_{2} ( y + 1 - \log _{e} (y)) + b_{3} \right] dt + (x-1) \zeta \sigma _{1} dw_{1}\\&- (y-1) \sigma _{2} dw_{2}. \end{aligned} \end{aligned}$$

Let \(b_{4} = \max \left\{ 2b_{1}, 2b_{2}, b_{3} \right\}\). We define \(v_{1} \bigwedge v_{2} = \min \{ v_{1}, v_{2} \}\). Hence for \(t_1 \le T\),

$$\begin{aligned} \begin{aligned} \int _{0}^{\tau _{s}\bigwedge t_{1}} d(G(x(t),y(t)))&< \int _{0}^{\tau _{s}\bigwedge t_{1}} b_{4} ( 1+ G(x(t),y(t))) dt \\&\quad + \int _{0}^{\tau _{s}\bigwedge t_{1}} (x-1) \zeta \sigma _{1} dw_{1} - \int _{0}^{\tau _{s}\bigwedge t_{1}} (y-1) \sigma _{2} dw_{2} \end{aligned} \end{aligned}$$

Taking expectation on both sides, we get

$$\begin{aligned} \begin{aligned} E \left( G \left( x \left( \tau _{s}\bigwedge t_{1} \right) ,y \left( \tau _{s}\bigwedge t_{1} \right) \right) \right)&\le G(x_0, y_0) + E \int _{0}^{\tau _{s}\bigwedge t_{1}} b_{4} ( 1+ G(x(t),y(t))) dt \\&\le G(x_0, y_0) + b_{4} t_1 + b_{4} E \int _{0}^{\tau _{s}\bigwedge t_{1}} G(x(t),y(t)) dt \\&\le G(x_0, y_0) + b_{4} T \\&\quad + b_{4} \int _{0}^{t_1} E \left[ G \left( x \left( \tau _{s}\bigwedge t_{1} \right) ,y \left( \tau _{s}\bigwedge t_{1} \right) \right) \right] dt \end{aligned} \end{aligned}$$

By Gronwall inequality [24]:

$$\begin{aligned} E(G( x(\tau _{s}\bigwedge t_{1}),y(\tau _{s}\bigwedge t_{1}))) \le b_{5}, \end{aligned}$$
(3.2)

where \(\displaystyle b_{5} = \left( G(x_0, y_0) + b_{4} T \right) e ^{b_{4}T}.\)

Define \(\displaystyle \Omega _{s} = \left\{ \tau _s \le T \right\}\) for \(\displaystyle s \ge s_{1}\) and by (3.1), \(P(\Omega _{s}) \ge \epsilon .\) Note that for each \(\tau ^{\prime } \in \Omega _{s}\), there exists at least one of \(x(\tau _s,\tau ^{\prime }), y(\tau _s, \tau ^{\prime } )\) which is equal either s or \(\displaystyle \frac{1}{s}\). So \(F\left( x\left( \tau _s, \tau ^{\prime }\right) , y\left( \tau _s, \tau ^{\prime }\right) \right)\) is not less than the smallest of

$$\begin{aligned} \displaystyle s + 1 - \log _{e}(s) \ \text {and} \ \frac{1}{s} +1 - \log _{e}\left( \frac{1}{s}\right) = \frac{1}{s} + 1 + \log _{e}(s). \end{aligned}$$

Consequently,

$$\begin{aligned} G(x(\tau _s, \tau ^{\prime }), y(\tau _s, \tau ^{\prime })) \ge \left( s + 1 - \log _{e}(s) \right) \bigwedge \left( \frac{1}{s} + 1 + \log _{e}(s) \right) . \end{aligned}$$

From (3.1) and (3.2):

$$\begin{aligned} \begin{aligned} b_5&\ge E [ 1_{\Omega _{s}} G (x(\tau _{s} , \tau ^{\prime }), y(\tau _{s} , \tau ^{\prime }))] \\&\ge \epsilon \left[ \left( s + 1 - \log _{e}(s) \right) \bigwedge \left( \frac{1}{s} + 1 + \log _{e}(s) \right) \right] , \end{aligned} \end{aligned}$$

where \(1_{\Omega _{s}}\) is the indicator function of \(\Omega _{s}\). Therefore, \(s \rightarrow \infty\) leads to the contradiction \(\infty > b_{5} = \infty\). Hence \(\tau _{\infty } = \infty\).

\(\square\)

4 Boundedness

Let us discuss about boundedness of solutions of (2.8) and derive the conditions under which the solutions are bounded.

We define \(\displaystyle M_{1}(t) = \int _{0}^{t} \sigma _{1} dw_{1}, \ M_{2}(t) = \int _{0}^{t} \sigma _{2} dw_{2}\) are real valued continuous local martingales. Applying strong law of large numbers: \(\displaystyle \lim _{t \rightarrow \infty } \frac{M_{1}(t)}{t} = \lim _{t \rightarrow \infty } \frac{M_{2}(t)}{t} = 0.\)

Theorem 4.1

Let (x(t), y(t)) be a solution of system (2.8) with \((x_{0}, y_{0}) \in {\mathbb {R}}_{+}^{2}\), then \(E(x^{p}(t)) \le M(p), \forall p \ge 1\), where

$$\begin{aligned} M(p)= \max \left\{ x_{0}^{p}, p\left( \frac{p}{r}\right) ^{p} \left[ \frac{\frac{1}{p}+g\zeta + \frac{\beta _{1}(1-\zeta )}{\beta }+\frac{p-1}{2}\zeta ^{2}\sigma _{1}^{2}}{p+1} \right] ^{p+1} \right\} , \end{aligned}$$

and for \(\displaystyle \frac{\theta }{\eta } + \frac{p-1}{2}\sigma _{2}^{2} \le d_{2}\), \(\displaystyle E\left( y^{p}(t) \right) \le y_{0}^{p}.\)

Proof

From system (2.8), we have

$$\begin{aligned} dx = x \left[ (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta + y} - r x - \frac{\alpha y}{1+ \eta x} - c_{1} x^{2} \right] dt + \zeta \sigma _{1} x dw_{1} \end{aligned}$$

We take \(V(x,t) = e^{t}x^{p}\) and apply Itô formula:

$$\begin{aligned} \begin{aligned} dV(t) =&\left[ e^{t}x^{p} + p e^{t}x^{p-1}x \left\{ (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta + y} - r x - \frac{\alpha y}{1+ \eta x}- c_{1} x^{2} \right\} \right. \\&\left. + \frac{p(p-1)}{2} e^{t}x^{p-2} \zeta ^{2} \sigma _{1}^{2} x^{2} \right] dt + p e^{t}x^{p} \zeta \sigma _{1} x dw_{1} \\ =&p e^{t}x^{p} \left[ \frac{1}{p} + (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta + y} - r x - \frac{\alpha y}{1+ \eta x}- c_{1} x^{2} \right. \\&\left. + \frac{(p-1)}{2} \zeta ^{2} \sigma _{1}^{2} \right] dt + p e^{t}x^{p} \zeta \sigma _{1} x dw_{1} \end{aligned} \end{aligned}$$
$$\begin{aligned} \begin{aligned} \therefore E(V(t)) \le&x_{0}^{p} + p \int _{0}^{t} e^{s} E\left[ x^{p} \left( \frac{1}{p} + (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta } - r x \right. \right. \\&\left. \left. + \frac{(p-1)}{2} \zeta ^{2} \sigma _{1}^{2} \right) \right] ds \end{aligned} \end{aligned}$$

Let \(\displaystyle h(x) = x^{p} \left( \frac{1}{p} + (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta } - r x + \frac{(p-1)}{2} \zeta ^{2} \sigma _{1}^{2} \right)\)

$$\begin{aligned} \begin{aligned} \therefore&h^{\prime }(x) = px^{p-1} \left( \frac{1}{p} + (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta } + \frac{(p-1)}{2} \zeta ^{2} \sigma _{1}^{2} \right) - r (p+1)x^{p} = 0 \\ \implies&x = \frac{1 + p(g \zeta -d_{1}) + \frac{p\beta _{1}(1-\zeta ) }{\beta } + \frac{p(p-1)}{2} \zeta ^{2} \sigma _{1}^{2}}{r(p+1)} \end{aligned} \end{aligned}$$

Hence, \(\displaystyle h_{max} = \left( \frac{p}{r}\right) ^{p} \left[ \frac{ \frac{1}{p} + (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta } + \frac{(p-1)}{2} \zeta ^{2} \sigma _{1}^{2} }{p+1}\right] ^{p+1}\)

\(\therefore\) \(\displaystyle E(v(t)) \le x_{0}^{p} + p \left( \frac{p}{r}\right) ^{p} \left[ \frac{ \frac{1}{p} + (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta } + \frac{(p-1)}{2} \zeta ^{2} \sigma _{1}^{2} }{p+1}\right] ^{p+1} (e^{t} - 1)\)

$$\begin{aligned} \begin{aligned} \text {So},\ E(x^{p}) \le&\left[ x_{0}^{p} - p \left( \frac{p}{r}\right) ^{p} \left( \frac{ \frac{1}{p} + (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta } + \frac{(p-1)}{2} \zeta ^{2} \sigma _{1}^{2} }{p+1}\right) ^{p+1} \right] e^{-t} \\&+ p \left( \frac{p}{r}\right) ^{p} \left( \frac{ \frac{1}{p} + (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta } + \frac{(p-1)}{2} \zeta ^{2} \sigma _{1}^{2} }{p+1}\right) ^{p+1} \end{aligned} \end{aligned}$$

So, for \(t=0\), \(E(x^{p}) \le x_{0}^{p}\) and for \(\displaystyle t \rightarrow \infty\)

\(E(x^{p}) \le p \left( \frac{p}{r}\right) ^{p} \left( \frac{ \frac{1}{p} + (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta } + \frac{(p-1)}{2} \zeta ^{2} \sigma _{1}^{2} }{p+1}\right) ^{p+1}\).

Now let

$$\begin{aligned} M(p)= \max \left\{ x_{0}^{p}, p\left( \frac{p}{r}\right) ^{p} \left[ \frac{\frac{1}{p}+(g\zeta - d_{1}) + \frac{\beta _{1}(1-\zeta )}{\beta }+\frac{p-1}{2}\zeta ^{2}\sigma _{1}^{2}}{p+1} \right] ^{p+1} \right\} . \end{aligned}$$

Hence, \(E(x^{p}) \le M(p).\)

From second equation of (2.8), we have

$$\begin{aligned} \begin{aligned} dy&= y \left[ \frac{\theta x}{1+ \eta x} - d_{2} - c_{2}y \right] dt - \sigma _{2} y dw_{2} \\&\le \left[ \frac{\theta }{\eta }y - d_{2}y \right] dt - \sigma _{2}y dw_{2} \end{aligned} \end{aligned}$$

Let \(G(y)= \log _{e} (y)\) and applying Itô formula:

$$\begin{aligned} \begin{aligned}&d(\log (y)) \le \left[ \frac{\theta }{\eta } - d_{2} - \frac{\sigma _{2}^{2}}{2} \right] dt - \sigma _{2}^{2} dw_{2} \\ \implies&\log (y) \le \log y_{0} + \left[ \frac{\theta }{\eta } - d_{2} - \frac{\sigma _{2}^{2}}{2} \right] t - M_{2} \\ \implies&y(t) \le y_{0} e^{\left( \frac{\theta }{\eta } - d_{2} - \frac{\sigma _{2}^{2}}{2} \right) t - M_{2}} \\ \implies&y^{p}(t) \le y_{0}^{p} e^{p \left( \frac{\theta }{\eta } - d_{2} - \frac{\sigma _{2}^{2}}{2} \right) t - p M_{2}} \end{aligned} \end{aligned}$$
$$\begin{aligned} \therefore E(y^{p}(t)) \le y_{0}^{p} e^{p \left( \frac{\theta }{\eta } - d_{2} + \frac{(p-1)\sigma _{2}^{2}}{2} \right) t }. \end{aligned}$$

Now for \(\displaystyle \frac{\theta }{\eta } + \frac{p-1}{2}\sigma _{2}^{2} \le d_{2}\), \(\displaystyle E\left( y^{p}(t) \right) \le y_{0}^{p}.\)

Hence the theorem.

\(\square\)

5 Some groundworks

Theorem 5.1

Let (x(t), y(t)) be the solution of (2.8) with \((x_0, y_0) \in {\mathbb {R}}_{+}^{2},\) then

  1. (i)

    \(\ \phi (t) \le x(t) \le \Phi (t)\)

  2. (ii)

    \(\ \psi (t) \le y(t) \le \Psi (t)\),

where

$$\begin{aligned} \begin{aligned} \phi (t)&= \frac{1}{\frac{r+c_{1}\int _{0}^{t}\Phi (s)ds}{g\zeta -\alpha \int _{0}^{t}\psi (s)ds-d_{1}-\zeta ^{2} \sigma _{1}^{2}} + \left[ \frac{1}{x_{0}} - \frac{r+c_{1}\int _{0}^{t}\Phi (s)ds}{g\zeta -\alpha \int _{0}^{t}\psi (s)ds-d_{1}-\zeta ^{2}\sigma _{1}^{2}} \right] e^{\left( \alpha \int _{0}^{t}\psi (s)ds-g\zeta + d_{1}+\zeta ^{2}\sigma _{1}^{2} \right) t- \zeta M_{1}(t)}} \\ \Phi (t)&=\frac{1}{\frac{r}{g\zeta - d_{1} - \zeta ^{2} \sigma _{1}^{2}+ \frac{\beta _{1} (1-\zeta )}{\beta }} + \left[ \frac{1}{x_{0}}- \frac{r}{g\zeta - d_{1} - \zeta ^{2} \sigma _{1}^{2}+ \frac{\beta _{1} (1-\zeta )}{\beta }} \right] e^{\left( \zeta ^{2} \sigma _{1}^{2} -g\zeta + d_{1} - \frac{\beta _{1}(1-\zeta )}{\beta }\right) t - \zeta M_{1}(t)}} \\ \psi (t)&=\frac{1}{-\frac{c_{2}}{\left( d_{2}+\sigma _{2}^{2}\right) }+ \left[ \frac{1}{y_{0}}+ \frac{c_{2}}{\left( d_{2}+\sigma _{2}^{2}\right) } \right] e^{\left( d_{2}+\sigma _{2}^{2}\right) t + M_{2}(t)} } \\ \Psi (t)&=\frac{1}{\frac{c_{2}}{\frac{\theta }{\eta }-\sigma _{2}^{2}-d_{2}} + \left[ \frac{1}{y_{0}} - \frac{c_{2}}{\frac{\theta }{\eta }-\sigma _{2}^{2}-d_{2}} \right] e^{\left( \sigma _{2}^{2} -\frac{\theta }{\eta }+d_{2} \right) t + M_{2}(t)}}. \end{aligned} \end{aligned}$$

Proof

From system (2.8), we have

$$\begin{aligned} \begin{aligned} dx&= x \left[ (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta + y} - r x - \frac{\alpha y}{1+ \eta x} - c_{1} x^{2} \right] dt + \zeta \sigma _{1} x dw_{1} \\&\le \left[ \left( g \zeta -d_{1} + \frac{\beta _{1}(1-\zeta ) }{\beta } \right) x - r x^{2} \right] dt + \zeta \sigma _{1} x dw_{1} \end{aligned} \end{aligned}$$

Let us consider \(\Phi (t)\) be the unique solution of the following equation:

$$\begin{aligned} d\Phi (t) = \left[ \left( g \zeta -d_{1} + \frac{\beta _{1}(1-\zeta ) }{\beta } \right) \Phi (t) - r \Phi (t)^{2} \right] dt + \zeta \sigma _{1} \Phi (t) dw_{1} \ \mathrm {with} \ \Phi (0) = x_{0} \end{aligned}$$

Considering \(\displaystyle H_{1}(t) = \frac{1}{\Phi (t)} \ \mathrm {with} \ H_{1}(0) = \frac{1}{x_{0}}\) and applying Itô formula, we get

$$\begin{aligned} \begin{aligned} dH_{1}(t)&= \left[ - \frac{g \zeta -d_{1} + \frac{\beta _{1}(1-\zeta ) }{\beta }}{\Phi } + r + \frac{\zeta ^{2}\sigma _{1}^{2}}{\Phi } \right] dt - \frac{\zeta \sigma _{1}}{\Phi } dw_{1} \\&= \left[ r - \left( g \zeta -d_{1} + \frac{\beta _{1}(1-\zeta ) }{\beta } \right) H_{1} + \zeta ^{2}\sigma _{1}^{2} H_{1} \right] dt - \zeta \sigma _{1} H_{1} dw_{1} \end{aligned} \end{aligned}$$

After solving this stochastic differential equation, we get

$$\begin{aligned} H_{1}(t) = \frac{r}{g\zeta - d_{1} - \zeta ^{2} \sigma _{1}^{2}+ \frac{\beta _{1} (1-\zeta )}{\beta }} + \left[ \frac{1}{x_{0}}- \frac{r}{g\zeta - d_{1} - \zeta ^{2} \sigma _{1}^{2}+ \frac{\beta _{1} (1-\zeta )}{\beta }} \right] e^{\left( \zeta ^{2} \sigma _{1}^{2} -g\zeta + d_{1} - \frac{\beta _{1}(1-\zeta )}{\beta }\right) t - \zeta M_{1}(t)} \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} \Phi (t)&=\frac{1}{\frac{r}{g\zeta - d_{1} - \zeta ^{2} \sigma _{1}^{2}+ \frac{\beta _{1} (1-\zeta )}{\beta }} + \left[ \frac{1}{x_{0}}- \frac{r}{g\zeta - d_{1} - \zeta ^{2} \sigma _{1}^{2}+ \frac{\beta _{1} (1-\zeta )}{\beta }} \right] e^{\left( \zeta ^{2} \sigma _{1}^{2} -g\zeta + d_{1} - \frac{\beta _{1}(1-\zeta )}{\beta }\right) t - \zeta M_{1}(t)}} \\ \text {and} \ x(t) \le \Phi (t) \end{aligned} \end{aligned}$$
(5.1)

From system (2.8) we also have

$$\begin{aligned} \begin{aligned} dy&= y \left[ \frac{\theta x}{1+ \eta x} - d_{2} - c_{2}y \right] dt - \sigma _{2} y dw_{2} \\&\le y \left[ \frac{\theta }{\eta } - d_{2} - c_{2}y \right] dt - \sigma _{2} y dw_{2} \end{aligned} \end{aligned}$$

Let us consider \(\Psi (t)\) be the unique solution of the following equation:

$$\begin{aligned} d\Psi (t) = \left[ \frac{\theta }{\eta } - d_{2} - c_{2}\Psi \right] \Psi dt - \sigma _{2} \Psi dw_{2} \ \mathrm {with} \ \Psi (0) = y_{0} \end{aligned}$$

Considering \(\displaystyle H_{2}(t) = \frac{1}{\Psi (t)} \ \mathrm {with} \ H_{2}(0) = \frac{1}{y_{0}}\) and applying Itô formula, we get

$$\begin{aligned} \begin{aligned} dH_{2}(t)&= \left[ c_{2} - \frac{\frac{\theta }{\eta } - d_{2}}{\Psi } + \frac{\sigma _{2}^{2}}{\Psi } \right] dt + \frac{\sigma _{2}}{\Phi } dw_{2} \\&= \left[ c_{2} + \left( \sigma _{2}^{2} -\frac{\theta }{\eta }+ d_{2} \right) H_{2} \right] dt + \sigma _{2}H_{2} dw_{2} \end{aligned} \end{aligned}$$

After solving this stochastic differential equation, we get

$$\begin{aligned} H_{2}(t) =\frac{c_{2}}{\frac{\theta }{\eta }-\sigma _{2}^{2}-d_{2}} + \left[ \frac{1}{y_{0}} - \frac{c_{2}}{\frac{\theta }{\eta }-\sigma _{2}^{2}-d_{2}} \right] e^{\left( \sigma _{2}^{2} -\frac{\theta }{\eta }+d_{2} \right) t + M_{2}(t)} \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} \Psi (t)&=\frac{1}{\frac{c_{2}}{\frac{\theta }{\eta }-\sigma _{2}^{2}-d_{2}} + \left[ \frac{1}{y_{0}} - \frac{c_{2}}{\frac{\theta }{\eta }-\sigma _{2}^{2}-d_{2}} \right] e^{\left( \sigma _{2}^{2} -\frac{\theta }{\eta }+d_{2} \right) t + M_{2}(t)}} \\ \text {and} \ y(t) \le \Psi (t) \end{aligned} \end{aligned}$$
(5.2)

Again from (2.8), we have

$$\begin{aligned} dy \ge y \left( - d_{2} - c_{2}y \right) dt - \sigma _{2} y dw_{2} \end{aligned}$$

Let us consider \(\psi (t)\) be the unique solution of the following equation:

$$\begin{aligned} d\psi (t) = \psi \left( - d_{2} - c_{2}\psi \right) dt - \sigma _{2} \psi dw_{2} \ \mathrm {with} \ \psi (0) = y_{0} \end{aligned}$$

Considering \(\displaystyle H_{3}(t) = \frac{1}{\psi (t)} \ \mathrm {with} \ H_{3}(0) = \frac{1}{y_{0}}\) and applying Itô formula, we get

$$\begin{aligned} \begin{aligned} dH_{3}(t)&= \left( c_{2} + \frac{d_{2} + \sigma _{2}^{2}}{\psi } \right) dt + \frac{\sigma _{2}}{\psi } dw_{2} \\&= \left[ c_{2} + (d_{2} + \sigma _{2}^{2})H_{3} \right] dt + \sigma _{2}H_{3} dw_{2} \end{aligned} \end{aligned}$$

After solving this stochastic differential equation, we get

$$\begin{aligned} H_{3}(t) = -\frac{c_{2}}{\left( d_{2}+\sigma _{2}^{2}\right) }+ \left[ \frac{1}{y_{0}}+ \frac{c_{2}}{\left( d_{2}+\sigma _{2}^{2}\right) } \right] e^{\left( d_{2}+\sigma _{2}^{2}\right) t + M_{2}(t)} \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} \psi (t)&=\frac{1}{-\frac{c_{2}}{\left( d_{2}+\sigma _{2}^{2}\right) }+ \left[ \frac{1}{y_{0}}+ \frac{c_{2}}{\left( d_{2}+\sigma _{2}^{2}\right) } \right] e^{\left( d_{2}+\sigma _{2}^{2}\right) t + M_{2}(t)}} \\ \text {and} \ y(t) \ge \psi (t) \end{aligned} \end{aligned}$$
(5.3)

From first equation of system (2.8) and using (5.1), we also get

$$\begin{aligned} dx \ge x \left[ (g \zeta -d_{1}) - r x - \alpha \Psi - c_{1} \Phi x \right] dt + \zeta \sigma _{1} x dw_{1} \end{aligned}$$

Let us consider \(\phi (t)\) be the unique solution of the following equation:

$$\begin{aligned} d\phi (t) = \phi \left[ (g \zeta -d_{1}) - r \phi - \alpha \Psi - c_{1} \Phi \phi \right] dt + \zeta \sigma _{1} \phi dw_{1} \ \mathrm {with} \ \phi (0) = x_{0} \end{aligned}$$

Considering \(\displaystyle H_{4}(t) = \frac{1}{\phi (t)} \ \mathrm {with} \ H_{4}(0) = \frac{1}{x_{0}}\) and applying Itô formula, we get

$$\begin{aligned} \begin{aligned} dH_{4}(t)&= \left[ \frac{\alpha \Psi }{\phi } - \frac{(g \zeta -d_{1})}{\phi } + r + c_{1} \Phi + \frac{\zeta ^{2} \sigma _{1}^{2}}{\phi } \right] dt - \frac{\zeta \sigma _{1}}{\phi } dw_{1} \\&= \left[ r + c_{1} \Phi (\alpha \Psi +g \zeta + d_{1} + \zeta ^{2} \sigma _{1}^{2})H_{4} \right] dt - \zeta \sigma _{1}H_{4} dw_{1} \end{aligned} \end{aligned}$$

After solving this stochastic differential equation, we get

$$\begin{aligned} \begin{aligned}H_{4}(t) =&\frac{r+c_{1}\int _{0}^{t}\Phi (s)ds}{g\zeta -\alpha \int _{0}^{t}\psi (s)ds-d_{1}-\zeta ^{2} \sigma _{1}^{2}} + \\&\left[ \frac{1}{x_{0}} - \frac{r+c_{1}\int _{0}^{t}\Phi (s)ds}{g\zeta -\alpha \int _{0}^{t}\psi (s)ds-d_{1}-\zeta ^{2}\sigma _{1}^{2}} \right] e^{\left( \alpha \int _{0}^{t}\psi (s)ds-g\zeta + d_{1}+\zeta ^{2}\sigma _{1}^{2} \right) t- \zeta M_{1}(t)} \end{aligned} \end{aligned}$$
$$\begin{aligned} \begin{aligned} \phi (t)&=\frac{1}{\frac{r+c_{1}\int _{0}^{t}\Phi (s)ds}{g\zeta -\alpha \int _{0}^{t}\psi (s)ds-d_{1}-\zeta ^{2} \sigma _{1}^{2}} + \left[ \frac{1}{x_{0}} - \frac{r+c_{1}\int _{0}^{t}\Phi (s)ds}{g\zeta -\alpha \int _{0}^{t}\psi (s)ds-d_{1}-\zeta ^{2}\sigma _{1}^{2}} \right] e^{\left( \alpha \int _{0}^{t}\psi (s)ds-g\zeta + d_{1}+\zeta ^{2}\sigma _{1}^{2} \right) t- \zeta M_{1}(t)}} \\ \text {and} \ y(t) \ge \psi (t) \end{aligned} \end{aligned}$$
(5.4)

Now, from (5.1), (5.2), (5.3) and (5.4) we can conclude that

\(\ \phi (t) \le x(t) \le \Phi (t)\) and \(\ \psi (t) \le y(t) \le \Psi (t)\) Hence the theorem.

\(\square\)

Theorem 5.2

Let (x(t), y(t)) be a solution of system (2.8), then almost every sample path of (x(t), y(t)) is uniformly continuous on \(t\ge 0\) for any initial value \((x_0, y_0) \in {\mathbb {R}}_{+}^{2}\)if \(\displaystyle \frac{\theta }{\eta } + \frac{p-1}{2}\sigma _{2}^{2} \le d_{2}.\)

Proof

From system (2.8) we have:

$$\begin{aligned} dx = x \left[ (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta + y} - r x - \frac{\alpha y}{1+ \eta x} - c_{1} x^{2} \right] dt + \zeta \sigma _{1} x dw_{1} \end{aligned}$$

We take \(\displaystyle \Gamma _{1}(x(t),y(t)) := x \left[ (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta + y} - r x - \frac{\alpha y}{1+ \eta x} - c_{1} x^{2} \right]\) and \(\displaystyle \Gamma _{2}(x(t),y(t)) := \zeta \sigma _{1} x.\)

Hence, \(\displaystyle dx = \Gamma _{1}(x(t),y(t)) dt + \Gamma _{2}(x(t),y(t)) dw_{1}.\)

Using Theorem 5.1 and \(A.M \ge G.M.\):

$$\begin{aligned} \begin{aligned} E\left| \Gamma _{1}(x(t),y(t))\right| ^{p}&\le \frac{1}{2} E |x|^{2p} + \frac{1}{2} E \left| (g \zeta -d_{1}) + \frac{\beta _{1}(1-\zeta ) }{\beta + y} - r x - \frac{\alpha y}{1+ \eta x} - c_{1} x^{2} \right| ^{2p} \\&\le \frac{1}{2} E (x^{2p}) + \frac{4^{2p-1}}{2} \left[ \left( g \zeta -d_{1}+ \frac{\beta _{1}(1-\zeta ) }{\beta } \right) ^{2p} + r^{2p} E(x^{2p}) + \alpha ^{2p} E(y^{2p}) \right] \\&\le \left( \frac{1}{2} + \frac{4^{2p-1}}{2} r^{2p} \right) E(x^{2p}) + \frac{4^{2p-1}}{2} \left( g \zeta -d_{1}+ \frac{\beta _{1}(1-\zeta ) }{\beta } \right) ^{2p} + \frac{4^{2p-1}}{2} \alpha ^{2p} E(y^{2p}) \\&\le \left( \frac{1}{2} + \frac{4^{2p-1}}{2} r^{2p} \right) M(2p) + \frac{4^{2p-1}}{2} \left( g \zeta -d_{1}+ \frac{\beta _{1}(1-\zeta ) }{\beta } \right) ^{2p} \\&\quad + \frac{4^{2p-1}}{2} \alpha ^{2p} E(y_{0}^{2p}) = H_{1}(p) \ (\mathrm {say}) \end{aligned} \end{aligned}$$

Also we have, \(\displaystyle E\left| \Gamma _{2}(x(t),y(t))\right| ^{p} \le \zeta ^{P} \sigma _{1}^{p} M(p) = H_{2}(p) \ (\mathrm {say})\)

Let us write the SDE in it’s stochastic integration form as follows:

$$\begin{aligned} x(t) = x_{0} + \int _{0}^{t} \Gamma _{1}(x(s),y(s)) ds + \int _{0}^{t} \Gamma _{2}(x(s),y(s)) dw_{1}(s) \end{aligned}$$

From moment inequality [25] of Itô for \(0 \le t_1< t_2 < \infty\) and \(p \ge 2\), we have

$$\begin{aligned} E \left| \int _{t_{1}}^{t_{2}} \Gamma _{2}(x(s),y(s)) dw_{1}(s) \right| ^{p} \le \left[ \frac{p(p-1)}{2} \right] ^{\frac{p}{2}} (t_2 - t_1)^{\frac{p-2}{2}} \int _{t_{1}}^{t_{2}} \left| \Gamma _{2}(x(s),y(s)) \right| ^{p} ds \end{aligned}$$
(5.5)

Now we apply Hölder’s inequality for \(t_{2} - t_{1} \le 1\) and (5.5),

$$\begin{aligned} \begin{aligned} E|x(t_2)-x(t_{1})|^{p}&\le 2^{p-1}E \left[ \int _{t_1}^{t_2} \Gamma _{1}(x(s),y(s)) ds \right] ^{p} + 2^{p-1}E \left[ \int _{t_1}^{t_2} \Gamma _{2}(x(s),y(s)) dw_{1}(s) \right] ^{p} \\&\le 2^{p-1} (t_{2}-t_{1})^{(p-1)} \int _{t_1}^{t_2} H_{1}(p) ds \\&\quad + 2^{(p-1)}\left[ \frac{p(p-1)}{2} \right] ^{\frac{p}{2}} (t_2 - t_1)^{\frac{p-2}{2}} \int _{t_{1}}^{t_{2}} H_{2}(p) ds\\&= 2^{p-1} (t_{2}-t_{1})^{p} H_{1}(p) + 2^{p-1}\left[ \frac{p(p-1)}{2} \right] ^{\frac{p}{2}} (t_{2}-t_{1})^{\frac{p}{2}} H_{2}(p) \\&\le 2^{(p-1)} (t_{2}-t_{1})^{\frac{p}{2}} \left[ 1+ \frac{p(p-1)}{2} \right] \left( H_{1} + H_{2} \right) \end{aligned} \end{aligned}$$

Hence it can be concluded that every sample path of x(t) is locally but uniformly Hölder continuous with exponent \(\gamma \in \left( 0 , \frac{p-2}{2p} \right)\). So, it can be concluded that every sample path of x(t) is uniformly continuous on \(t\ge 0\). Similarly, it can be shown that every sample path of y(t) is uniformly continuous on \(t\ge 0\).

\(\square\)

6 Extinction

A species is said to be extinct if there exists no member which can reproduce or create a new generation in the habitat in long run. That can happen for various environmental and artificial reasons. In the next theorem we shall show that extinction of prey population propel predator population towards extinction.

Definition 6.1

Population x(t) is said to be going extinct with probability one if

$$\begin{aligned} \lim _{t\rightarrow \infty } x(t) = 0 \ \mathrm {a.s.} \end{aligned}$$

Theorem 6.1

Let (x(t), y(t)) be the solution of system (2.8). Then the prey and predator both population go extinct in long run if \(\displaystyle g\zeta + \beta _{1}(1-\zeta ) < d_{1} + \frac{\sigma _{1}^{2} \zeta ^{2}}{2}\), that is,

$$\begin{aligned} \lim _{t\rightarrow \infty } x(t) = \lim _{t\rightarrow \infty } y(t) = 0 \ a.s. \ if \ g\zeta + \beta _{1}(1-\zeta ) < d_{1} + \frac{\sigma _{1}^{2} \zeta ^{2}}{2}. \end{aligned}$$

Proof

We take \(u(x) = \log (x)\) and apply Itô formula on the first equation of system (2.8):

$$\begin{aligned} \begin{aligned} d(\log (x))&= \left[ (g \zeta -d_{1}) + \frac{b_{1}(1-\zeta )}{\beta +y} - rx - \frac{\alpha y}{1+\eta x} - c_{1}x^{2} - \frac{\zeta ^{2}\sigma _{1}^{2}}{2}\right] dt + \zeta \sigma _{1} dw_{1} \\&\le \left[ (g \zeta -d_{1}) + b_{1}(1-\zeta ) - rx - c_{1}x^{2} - \frac{\zeta ^{2}\sigma _{1}^{2}}{2}\right] dt + \zeta \sigma _{1} dw_{1} \end{aligned} \end{aligned}$$

Let \(\displaystyle h(x) = (g \zeta -d_{1}) + b_{1}(1-\zeta ) - rx - c_{1}x^{2} - \frac{\zeta ^{2}\sigma _{1}^{2}}{2}\)

So, \(\displaystyle h^\prime (x) = -r - 2c_{1} x < 0 .\) i.e., h(x) is a deceasing function. Hence, the supremum occurs at \(x=0\).

\(\displaystyle \sup _{x\ge 0} h(x) = (g \zeta -d_{1}) + b_{1}(1-\zeta ) - \frac{\zeta ^{2}\sigma _{1}^{2}}{2}.\)

Hence,

$$\begin{aligned} \begin{aligned} d(\log (x))&\le \left[ (g \zeta -d_{1}) + b_{1}(1-\zeta ) - \frac{\zeta ^{2}\sigma _{1}^{2}}{2} \right] dt + \zeta \sigma _{1} dw_{1} \\ \implies \log (x)&\le \log (x_{0}) + \left[ (g \zeta -d_{1}) + b_{1}(1-\zeta ) - \frac{\zeta ^{2}\sigma _{1}^{2}}{2} \right] t + \zeta M_{1} \\ \therefore \limsup _{t \rightarrow \infty } \frac{\log (x)}{t}&\le (g \zeta -d_{1}) + b_{1}(1-\zeta ) - \frac{\zeta ^{2}\sigma _{1}^{2}}{2}< 0 \left[ \because g\zeta + \beta _{1}(1-\zeta ) < d_{1} + \frac{\sigma _{1}^{2} \zeta ^{2}}{2} \right] \end{aligned} \end{aligned}$$

Therefore, for every \(\epsilon > 0\) there exists \(t_{0} ( > 0 )\) and set \(\Omega _{\epsilon }\) such that \(P(\Omega _{\epsilon }) \ge 1- \epsilon\) and \(x < \epsilon\) for every \(t \ge t_{0}\) and \(x \in \Omega _{\epsilon }.\)

Hence \(\displaystyle \lim _{t\rightarrow \infty } x(t) = 0 \ \mathrm {a.s.}\)

From the second equation of (2.8):

$$\begin{aligned} dy = y \left[ \frac{\theta x}{1+ \eta x} - d_{2} - c_{2}y \right] dt - \sigma _{2} y dw_{2}. \end{aligned}$$

Consider \(v(x) = \log _{e}(y)\) and use Itô formula:

$$\begin{aligned} \begin{aligned} d(\log _{e} y)&= \left[ \frac{\theta x}{1+ \eta x} - d_{2} - c_{2}y - \frac{\sigma _{2}^{2}}{2} \right] dt - \sigma _{2} dw_{2} \\&\le \left[ \theta x - d_{2} - c_{2} y \frac{\sigma _{2}^{2}}{2} \right] dt - \sigma _{2} dw_{2}\\&\le \left[ \theta \epsilon - d_{2} - \frac{\sigma _{2}^{2}}{2} \right] dt - \sigma _{2} dw_{2}\\ \implies \frac{\log _{e} y}{t}&< \frac{\log _{e} y_{0}}{t} + \left( \theta \epsilon - d_{2} - \frac{\sigma _{2}^{2}}{2} \right) - \frac{M_{2}}{t} \\ \implies \limsup _{t \rightarrow \infty } \frac{\log _{e} y}{t}&< \theta \epsilon - d_{2} - \frac{\sigma _{2}^{2}}{2} \end{aligned} \end{aligned}$$

Since, \(\epsilon (>0)\) is arbitrarily small, therefore \(\displaystyle \limsup _{t \rightarrow \infty } \frac{\log _{e} y(t)}{t} < 0 .\) So, we can conclude that \(\displaystyle \lim _{t\rightarrow \infty } y(t) = 0 \ \mathrm {a.s.}\) \(\square\)

7 Persistent

In this section the persistence of system (2.8) will be discussed. First we shall define persistence in mathematical terms.

Definition 7.1

System (2.8) is said to be persistent in mean if \(\ \displaystyle \liminf _{ t \rightarrow \infty } \left\langle y \right\rangle _{t} > 0\), where \(\displaystyle \left\langle y \right\rangle _{t} = \frac{1}{t} \int _{0}^{t} y(s) ds.\)

Lemma 7.1

[7] Suppose \(Z(t) \in {\mathbb {C}} ( \Omega \times [0,\infty ), {\mathbb {R}}_{+}).\)

(a):

If there exist \(T, \delta , \delta _{0} \in {\mathbb {R}}_{+}\) such that \(\displaystyle \log _{e} Z(t) \le \delta t - \delta _{0} \int _{0}^{t} Z(s) ds + \sum \limits _{i=1}^{n} \alpha _{i} W(t) \ \ \mathrm {a.s.} \ \forall t \ge T,\) where \(\alpha _{i}\) are constants for \(i = 1,2, ... ,n,\) then

$$\begin{aligned} \left\{ \begin{array}{ll}\displaystyle {\limsup _{t\rightarrow \infty } \left\langle Z \right\rangle _{t} \le \frac{\delta }{\delta _{0}} },\ \mathrm {a.s.}\ \ \ \ \ \mathrm {if} \ \ \delta > 0,\\ \displaystyle \lim _{t\rightarrow \infty } \left\langle Z \right\rangle _{t} = 0, \ \mathrm {a.s.}\ \ \ \ \ \ \ \ \ \ \mathrm {if} \ \ \delta < 0. \end{array}\right. \end{aligned}$$
(b):

If there exist \(T, \delta , \delta _{0} \in {\mathbb {R}}_{+}\) such that

$$\begin{aligned} \displaystyle \log _{e} Z(t) \ge \delta t- \delta _{0} \int _{0}^{t} Z(s) ds+ \sum \limits _{i=1}^{n} \alpha _{i} W_{i}(t) \ \ \ \ a.s. \ \ \forall \ t \ge T, \end{aligned}$$

where \(\alpha _{i}\) are constants for \(i = 1,2,...,n,\) then

$$\begin{aligned} \liminf _{t\rightarrow \infty }\left\langle Z \right\rangle _{t} \ge \frac{\delta }{\delta _{0}} \ \ \ \mathrm {a.s.} \end{aligned}$$

Lemma 7.2

[20] Consider the following one dimensional stochastic system:

$$\begin{aligned} dz(t) = z(t) \left( g\zeta + \frac{\beta _{1}(1-\zeta )}{\beta }- d_{1} - r z(t) \right) dt + \sigma _{1} \zeta z(t) dw_{1}, \ \mathrm {with} \ z(0) = x(0). \end{aligned}$$
(7.1)
(a):

If \(\displaystyle \left( g\zeta + \frac{\beta _{1}(1-\zeta )}{\beta }- d_{1} - \frac{\zeta ^{2}\sigma _{1}^{2}}{2} \right) < 0,\) then \(\displaystyle \lim _{ t \rightarrow \infty } z(t) = 0\) a.s.

(b):

If \(\displaystyle \left( g\zeta + \frac{\beta _{1}(1-\zeta )}{\beta }- d_{1} - \frac{\zeta ^{2}\sigma _{1}^{2}}{2} \right) > 0,\) then \(\displaystyle \lim _{ t \rightarrow \infty } \frac{1}{t} \int _{0}^{t} z(s) ds = g\zeta + \frac{\beta _{1}(1-\zeta )}{\beta }- d_{1} - \frac{\zeta ^{2}\sigma _{1}^{2}}{2}\) and \(\displaystyle {\mathbb {P}} \left\{ \lim _{t\rightarrow \infty }\frac{1}{t} \int _{0}^{t} f(z(s))ds = \int _{{\mathbb {R}}_{+}} f(x) \mu (x) dx \right\} = 1\), where \(\mu (x)\) is the stationary density.

Theorem 7.1

Let us consider \(\displaystyle \left( g\zeta + \frac{\beta _{1}(1-\zeta )}{\beta }- d_{1} - \frac{\zeta ^{2}\sigma _{1}^{2}}{2} \right) > 0\) and \(\displaystyle \Lambda = \theta \int _{0}^{\infty } \frac{z}{1+ \eta z}\mu (x) dx - d_{2} - \frac{\sigma _{2}^{2}}{2}.\) If (x(t), y(t))be a solution of system (2.8) for any \((x_0, y_0) \in {\mathbb {R}}_{+}^{2},\) then system (2.8) is persistent in mean provided \(\Lambda > 0\).

Proof

From the first equation of system (2.8), applying Itô formula, we have

$$\begin{aligned} d(\log _{e} x(t)) = \left[ (g-d_{1})+ \frac{\beta _{1}(1-\zeta )}{\beta } - r x - \frac{\alpha y}{1+ \eta x} - c_{1}x^{2} - \frac{\sigma _{1}^{2}}{2} \right] dt + \zeta \sigma _{1} dw_{1} \end{aligned}$$

Now integrating both sides and dividing by t, we get

$$\begin{aligned} \begin{aligned} \frac{\log _{e} x(t) - \log _{e} x_0}{t}&= \left( g\zeta - d_{1} - \frac{\zeta ^{2}\sigma _{1}^{2}}{2} + \frac{\beta _{1}(1-\zeta )}{\beta } \right) - \frac{r}{t}\int _{0}^{t} x(s)ds \\&- \frac{\alpha }{t} \int _{0}^{t} \frac{y(s)}{1+\eta x(s)} ds + \frac{\zeta M_{1}(t)}{t} = F_{1}(t) (\mathrm {say}) \end{aligned} \end{aligned}$$
(7.2)

Applying Itô formula on (7.1), we have

$$\begin{aligned} d(\log _{e} z(t)) = \left[ g\zeta + \frac{\beta _{1}(1-\zeta )}{\beta }- d_{1} -rz - \frac{\zeta ^{2}\sigma _{1}^{2}}{2} \right] dt + \zeta \sigma _{1} dw_{1}. \end{aligned}$$

Now integrating both sides and dividing by t, we get

$$\begin{aligned} \begin{aligned} \frac{\log _{e} z(t) - \log _{e} z_0}{t}&= \left( g\zeta + \frac{\beta _{1}(1-\zeta )}{\beta }- d_{1} - \frac{\zeta ^{2}\sigma _{1}^{2}}{2} \right) - \frac{r}{t}\int _{0}^{t} z(s)ds + \frac{\zeta M_1}{t} \\&= F_2(t) \ (\mathrm {say)} \end{aligned} \end{aligned}$$
(7.3)

From, (7.2) and (7.3) it can be easily observed that \(F_{1}(t) \le F_{2}(t)\)

$$\begin{aligned} \begin{aligned} \Rightarrow \frac{r}{t}\int _{0}^{t}(z(s)-x(s))ds&\le \frac{\alpha }{t} \int _{0}^{t} \frac{y(s)}{1+\eta x(s)}ds \\ \Rightarrow \frac{1}{t}\int _{0}^{t}(z(s)-x(s))ds&\le \frac{\alpha }{rt} \int _{0}^{t} \frac{y(s)}{1+\eta x(s)}ds \\&\le \frac{\alpha }{rt} \int _{0}^{t} y(s)ds \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \frac{1}{t}\int _{0}^{t}(z(s)-x(s))ds \le \frac{\alpha }{rt} \int _{0}^{t} y(s)ds \end{aligned}$$
(7.4)

From second equation of system (2.8), applying Itô formula, we have

$$\begin{aligned} \begin{aligned} d(\log _{e} y(t))&= \left[ \frac{\theta x}{1+\eta x} - d_{2} - c_{2}y - \frac{\sigma _{2}^{2}}{2} \right] dt - \sigma _{2} dw_{2} \\&= \left[ \frac{\theta z}{1+\eta z} - \left( \frac{\theta z}{1+\eta z} - \frac{\theta x}{1+\eta x} \right) - d_{2} - c_{2}y - \frac{\sigma _{2}^{2}}{2} \right] dt - \sigma _{2} dw_{2} \\&\ge \left[ \frac{\theta z}{1+\eta z} - \theta \left( z(t) - x(t) \right) - d_{2} - c_{2}y - \frac{\sigma _{2}^{2}}{2} \right] dt - \sigma _{2} dw_{2} \end{aligned} \end{aligned}$$

Integrating both side and dividing by t, we get

$$\begin{aligned} \begin{aligned} \frac{\log _{e} y(t) - \log _{e} y_{0}}{t} \ge&\left( -d_{2} - \frac{\sigma _{2}^{2}}{2} \right) + \frac{\theta }{t} \int _{0}^{t} \frac{z(s)}{1+\eta z(s)}ds - \frac{\theta \alpha }{r} \int _{0}^{t} y(s)ds \\&- c_{2} \int _{0}^{t} y(s)ds - \frac{M_{2}(t)}{t} \\ =&\left( -d_{2} - \frac{\sigma _{2}^{2}}{2} \right) - \epsilon + \theta \int _{0}^{\infty } \frac{z}{1+\eta z}\mu (x)dx - \left( c_{2} + \frac{\theta \alpha }{r} \right) \left\langle y \right\rangle _{t} \\&- \frac{M_{2}(t)}{t} \\ =&\Lambda - \epsilon - \left( c_{2} + \frac{\theta \alpha }{r} \right) \left\langle y \right\rangle _{t} - \frac{M_{2}(t)}{t} \end{aligned} \end{aligned}$$

For sufficiently large t, using Lemma 7.1(b) and arbitrariness of \(\epsilon\):

$$\begin{aligned} \liminf _{t\rightarrow \infty } \left\langle y \right\rangle _{t} \ge \frac{r \Lambda }{r c_{2} + \theta \alpha } \ \mathrm {a.s.} \end{aligned}$$

Therefore, from the definition of persistence of a system, it can be concluded that system (2.8) is persistence if \(\Lambda > 0\). Hence the theorem.

\(\square\)

8 Numerical simulations

This section deals with numerical findings to validate theoretical outcomes that the previous sections offered. We approximate the solution of stochastic system (2.8) by numerical simulation using Euler Maruyama method in MATLAB.

To simulate the system, we set the values of biological and environmental parameters as follows:

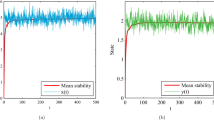
Table 1 Values of parameters for numerical simulations
Full size table

We have started the simulating system (2.8) from the initial point (1.7, 0.72). It is found the effects of environmental noise on prey and predator population and observed that after some initial transients the biomass of prey population varies around 0.6 and predator population varies around 0.3 which are depicted in (1.a) and (1.b) of Fig. 1 respectively.

Fig. 1
figure 1

Trajectories of prey population varies around 0.6 and predator population varies around 0.3 described in system (2.8) for the parametric values in Table 1

Full size image
Fig. 2
figure 2

Extinction of prey and predator population under the stated condition in Theorem 6.1

Full size image

In theoretical study, it is found that prey extincts if \(\displaystyle g\zeta + \beta _{1}(1-\zeta ) < d_{1} + \frac{\sigma _{1}^{2} \zeta ^{2}}{2}\) and extinction of prey propels predator population towards extinction. To satisfy the condition we take \(g = 0.5\) and \(d_{1} = 0.55\) i.e., \(\beta _{1} = g \beta = 0.5\) and simulate system (2.8) in MATLAB. It is found in numerical simulation also that extinction of prey causes immediate extinction of predator population which is depicted in Fig. 2.

Fig. 3
figure 3

System (2.8) persists for the set of values in Table 1 which satisfy the conditions in Theorem 7.1

Full size image
Fig. 4
figure 4

High fear affect negatively on predator population

Full size image

Theorem 7.1 affirms the persistence of system (2.8) under some conditions which are satisfied by the given set of values in Table 1. Figure 3 validates the mathematical result.

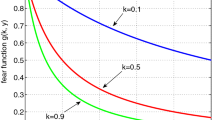
In this work, the fear function has been considered as \(\displaystyle f(\zeta ,\beta ,x)= \zeta +\frac{1-\zeta }{1+\frac{y}{\beta }}\) where \(\zeta\) represents the minimum fear level and \(\frac{1}{\beta }\) is the cost of fear. We have tested the system for high fear level, i.e., for a low value of \(\beta\). Value of \(\beta\) is considered as 0.1, i.e., \(\frac{1}{\beta } =10\) and \(\beta _{1}=g\beta =0.1\) and it can be observed in Fig. 4 that fear affects negatively on predator population.

Fig. 5
figure 5

Very high cost of fear propel predator population toward extinction

Full size image

To test if the cost of fear is very high we have taken \(\frac{1}{\beta } = 100\), i.e., \(\beta =0.01\) and \(\beta _{1}=0.01\). In Fig. 5 we observe that prey population persists but predator population extincts after a certain period of time.

Only for a lower fear level, say, for \(\frac{1}{\beta }=0.0001\) and \(\zeta =0.1\), it is observed that the system persists which is a very normal situation in reality. This behavior is shown in Fig. 6.

Fig. 6
figure 6

System (2.8) persists in presence of minimum fear only

Full size image

We have tested the effects of toxicity numerically. In all the figures from Figs. 1, 2, 3, 4, 5 and 6, values of \(c_{1}\) and \(c_{2}\) have been considered as 0.2 and 0.15 respectively. Now we consider values of \(c_{1}\) and \(c_{2}\) as 1.5 and 0.8 in Fig. 7 and 3.5 and 2.8 in Fig. 8 respectively. Here it is observed that both prey and predator population decrease but mostly predator population gets affected.

Fig. 7
figure 7

Predator population decreases for high toxic \(c_{1} = 1.5\) and \(c_{2}=0.8\)

Full size image

In Fig. 8, it is observed that prey population decreases and predator population is going to extinct after a certain period of time.

Fig. 8
figure 8

Predator population extinct for \(c_{1} = 3.5\) and \(c_{2}=2.8\)

Full size image

If we consider the system in a toxic free environment, i.e., \(c_{1}=0\) and \(c_{2}=0\), then it is observed that prey–predator population persists together which is depicted in Fig. 9.

Fig. 9
figure 9

System (2.8) persists for \(c_{1} = 0\) and \(c_{2}=0\)

Full size image

9 Conclusion

In this work we have considered a Lotka–Volterra predator–prey model where prey species is directly infected by some external toxic substances while the predator is indirectly affected for feeding on these infected prey. This model also involves fear of predator felt by prey. Birth rate of prey and death rate of predator are considered as stochastic parameters and they are perturbed by introducing Gaussian white noise. Existence of unique global positive solutions are established for both deterministic and stochastic systems. It is found analytically that environmental noise plays an important role in the extinction of both the species. In numerical simulation through Fig. 2 this analytical finding is justified. Boundedness and uniform continuity criteria of the solution of the underlying system (2.8) are also derived. We have also established most useful criteria of persistence of this system under some conditions.

In numerical simulations, it is observed how fear factor affects the system. It is also found that fear factor affects negatively on predator population (see Figs. 4, 5). It is observed in Fig. 5 that predator population is going to extinct for a very high cost of fear. It is shown in Fig. 6 that existence of only a lower fear level makes the system persistent.

Numerically, we have also observed the effects of toxicity. High toxicity affects both the species (see Figs. 7, 8). In Fig. 8 it is found that extremely high toxicity can be a cause of extinction of predator. In Fig. 9 we have found that the system persists if it is free from toxicity.