Extended state observer-based adaptive prescribed performance control for a class of nonlinear systems with full-state constraints and uncertainties

Abstract

In this paper, an extended state observer-based adaptive prescribed performance control technique is proposed for a class of nonlinear systems with full-state constraints and uncertainties. An extraordinary feature is that not only the control problem of prescribed performance tracking and full-state constraints are solved simultaneously, but also the parametric uncertainties and disturbances are considered, which will make it difficult to design a stable controller. For this purpose, the extended state observer and adaptive technique are integrated to obtain estimations of disturbances and parameters. Then, based on the combination of prescribed performance and barrier Lyapunov function, a novel backstepping control scheme is developed with feedforward compensation of parameters and disturbances to ensure that the tracking error is kept within a specified prescribed performance bound without violation of full states at all times. Moreover, the boundedness of all signals in the closed-loop system is proved and asymptotic tracking can be realized if the disturbances are time-invariant. Finally, two simulation examples are performed to highlight the efficiency of the proposed approach.

1 Introduction

For practical control systems, high-performance control of nonlinear systems has always attracted much attention due to uncertainties (including parametric uncertainties and disturbances), which exist in most physical systems and may reduce the tracking accuracy and even lead to system instability. Many nonlinear control approaches are designed for nonlinear systems to improve their performance, such as adaptive control [1], adaptive robust control [2], robust adaptive control [3], sliding mode control (SMC) [4] and H∞ control [5]. However, when the disturbance becomes the main obstacle for high-performance control of the system, the above approaches always employ high-gain feedback to suppress the influence of disturbance on the system. As we know, high-gain feedback should be avoided in practical control systems due to high-frequency dynamics and measurement noise, which can deteriorate the control performance of the system and even destabilize system. If disturbances are known, they can be simply compensated by feedforward to eliminate their influence on the control performance. But in fact, the disturbances are unknown and generally immeasurable. Thus, based on disturbance observer, which is employed to get the estimated value of the disturbance, disturbance compensation control approaches are developed to eliminate its adverse effect on the control performance and enhance the anti-disturbance capability of the system. In recent years, nonlinear control strategies based on disturbance observers for total uncertainties were developed [6,7,8,9,10,11,12]. However, due to the bandwidth limitation of the observer caused by noise, the performance of the disturbance observer is limited, so it is difficult to achieve the perfect compensation of the total uncertainties. Putting system parametric uncertainties into system total interference will increase observer burden and reduce observation accuracy. When the uncertainties of the system mainly come from the strong parametric uncertainties, the control performance of disturbance compensation approach is often inferior to the nonlinear adaptive control with strong learning ability for parametric uncertainties [13]. Thus, adaptive control for parametric uncertainties was integrated into the disturbance compensation control, and better control effect was obtained [14,15,16].

However, transient control performance of tracking error is not considered emphatically in the above control strategies, and the performance indexes such as overshoot, convergence speed and steady-state tracking error should be guaranteed by the proposed control scheme in practical engineering. Recently, because of the ability to constrain the tracking performance of the system, prescribed performance control (PPC) attracts a lot of attention [17,18,19]. In order to suppress uncertainties, an adaptive dynamic surface controller with prescribed tracking performance was proposed for MIMO nonlinear systems in [17]. Based on a new formulation of performance, an improved prescribed performance controller was designed for nonaffine pure-feedback systems in [18]. When the system suffers from strong disturbance, these disturbance suppression control strategies still rely on high gain feedback to achieve good control accuracy, which are conservative. Furthermore, some compensation strategies for uncertainties are designed [20,21,22,23]. An adaptive prescribed performance motion controller and a RISE-based asymptotic prescribed performance tracking controller were proposed for nonlinear servo mechanisms [20, 21], where neural network was applied to approximate the system unknown dynamics. A composite controller with sliding mode disturbance observer is designed for space manipulators with prescribed performance [23].

On the other hand, as many practical systems are subject to the effect of the constraints, state constraint control also attracts many researchers. However, the existing PPC studies rarely take into account the system state constraints except [24,25,26,27,28]. In [26], an improved prescribed performance constraint control method was proposed for a strict-feedback nonlinear dynamic system. However, this control strategy only estimates the upper bound of the disturbance to suppress the influence of the disturbance on the control performance, which will cause the control strategy to be conservative. In [27], based on barrier Lyapunov function (BLF), a PPC method with neural network was proposed for Euler–Lagrange systems to constrain full states and achieve prescribed performance tracking, where the adaptive neural network was designed to approximate system uncertainties. In [28], a prescribed performance output feedback dynamic surface control is proposed for a class of strict-feedback uncertain nonlinear systems, full-state constraints is guaranteed by BLF, and neural network is also applied to approximate the system unknown dynamics. As we all know, neural network needs a lot of data for training, which may lead to the accurate estimation convergence time is too long.

Inspired by the above studies, drawn on the experience of the controller design idea in [29, 30], an extended state observer-based adaptive prescribed performance control is studied for a class of nonlinear systems with full-state constraints and uncertainties. The main contributions of the proposed controller are as follows:

• (1) This paper studies a more general class of nonlinear systems with parametric uncertainties and disturbances; the disturbance observer and adaptive control are first integrated into area of prescribed performance-full-state constraints control of nonlinear systems. Compensation strategy for uncertainties is designed. Hence, the control performance is expected to be improved without high gain feedback and the conservatism of controller can be reduced in this study. More importantly, the elimination of uncertainties can improve the feasibility of prescribed performance and state constraints.

• (2) In order to solve synthetically the control problem of prescribed performance tracking and full-state constraints, a backstepping design with uncertainties compensation is proposed by integrating prescribed performance function (PPF) and full-state constraint function, which can guarantee that the constraints of all the state are not violated and the tracking error is kept within a specified bound at all times, simultaneously.

2 Problem formulation and preliminaries

Consider a class of full-state constrained single-input single-output (SISO) nonlinear systems with uncertainties:

$$ \left\{ {\begin{array}{*{20}l} \dot{x}_{i} = x_{i + 1} + \theta^{T} \varphi_{i} \left( {\overline{x}_{i} } \right) + d_{i} \left( t \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} 1 \le i \le n - 1 \hfill \\ \dot{x}_{n} = u + \theta^{T} \varphi_{n} \left( x \right) + d_{n} \left( t \right) \hfill \\ y = x_{1} \hfill \\ \end{array}} \right. $$

(1)

where $\overline{x}_{i}$ = [x₁, x₂, …, x_i]^T ∈ Rⁱ with i = 1, 2, …, n.$\overline{x}_{n}$ = x = [x₁, x₂, …, x_n]^T ∈ Rⁿ is the state vector, u ∈ R is control input, y ∈ R is system output, $\varphi_{i} \in R^{\rho } ,{\kern 1pt} {\kern 1pt} i = 1, \ldots ,n,$ are known shape functions, which are also assumed to satisfy the Lipchitz condition, $\theta { = [}\theta_{1} {,} \ldots {,}\theta_{\rho } {]}^{T} \in R^{\rho }$ is unknown constant parameters vector, $d_{i} \left( t \right)$ ∈ R, i = 1, …, n, are disturbances.

In order to ensure that: (1) All signals in the closed-loop system are bounded; (2) all system states x_i, i = 1, …, n, are constrained in $\Omega_{{x_{i} }} = \left\{ {x_{i} :\left| {x_{i} } \right| \le c_{i} ,i = 1,...,n} \right\}$ for all t ≥ 0 when $x\left( 0 \right) \in \Omega_{{x_{i} }}$,$c_{i} > 0$ are constants; (3) the high control performance with prescribed tracking precision is also achieved. Then, the following assumptions are given and the proposed controller is designed in next section.

Assumption 1

The time derivative $\dot{d}_{i}$ is as follows [31], i.e.,

$$ \left| {\dot{d}_{i} } \right| \le \overline{d}_{id} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,...,n. $$

(2)

where $\overline{d}_{id} > 0$ are constants.

Assumption 2

[32] The desired trajectory x_1d(t) and its ith-order derivatives $x_{1d}^{\left( i \right)} \left( t \right)$, i = 1,..., n satisfy $x_{1d} \left( t \right) \le \upsilon_{0} \le c_{1} - \rho_{0}$ and $\left| {x_{1d}^{\left( i \right)} \left( t \right)} \right| \le \upsilon_{i}$, $\upsilon_{i} > 0$ are constants.

Remark 1

Assumption 1 is a basic premise for extended state observer (ESO)-based control and has been given in [33,34,35], and these studies show that this assumption is applicable to physical applications.

The following lemmas will be used in our design.

Lemma 1

[36] There exist positive definite continuous functions V_i:(−c_i, c_i) → R+ , i = 1, 2,…, n, which are also differentiable on $\Omega_{{x_{i} }}$. V_i(x_i) → ∞ when x_i →  ± c_i, i = 1,2,…,n. If dV_i(x_i)/dt ≤ 0 in set $\Omega_{{x_{i} }}$, then for all t ∈ [0, + ∞], x(t) ∈ $\Omega_{{x_{i} }}$.

Lemma 2

[37] Consider error e(t) and transformed errors z₁(t). If z₁(t) is bounded, prescribed performance of e(t) is satisfied for all t ≥ 0.

3 The controller design and stability analysis

3.1 Extended state observer

In order to estimate all uncertainties, we extend the uncertainties as additional states x_e1, x_e2,…, x_en, respectively, and let h_i(t), i = 1, 2, …, n represent their time derivatives. Different from Cheng et al. [38], this structure cannot be used to estimate the state of the system. Throughout this paper, $\hat{ \bullet }$ represents the estimation of $\bullet$ and $\tilde{ \bullet } = \bullet - \hat{ \bullet }$ denotes the estimation error. ESOs are constructed for each equation of the system model (1) as:

$$ \begin{aligned} \left\{ {\begin{array}{*{20}l} \dot{\hat{x}}_{i} = x_{i + 1} + \hat{\theta }^{T} \varphi_{i} \left( {\overline{x}_{i} } \right) + \hat{x}_{ei} \left( {\overline{x}_{i} ,t} \right) + l_{1} \omega_{i} \left( {x_{i} - \hat{x}_{i} } \right) \hfill \\ \dot{\hat{x}}_{ei} = l_{2} \omega_{i}^{2} \left( {x_{i} - \hat{x}_{i} } \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,...,n - 1 \hfill \\ \end{array}} \right. \hfill \\ \left\{ {\begin{array}{*{20}l} \dot{\hat{x}}_{n} = u + \hat{\theta }^{T} \varphi_{n} \left( x \right) + \hat{x}_{en} \left( {x,t} \right) + l_{1} \omega_{n} \left( {x_{n} - \hat{x}_{n} } \right) \hfill \\ \dot{\hat{x}}_{en} = l_{2} \omega_{n}^{2} \left( {x_{n} - \hat{x}_{n} } \right) \hfill \\ \end{array}} \right. \hfill \\ \end{aligned} $$

(3)

where ω_i > 0, i = 1, …, n are design parameters of observers, l₁ and l₂ are factors of the Hurwitz polynomial s² + l₁s + l₂. Since the uncertainties of each equation in (1) consist of both disturbances $d_{i} \left( {\overline{x}_{i} ,t} \right)$ and parametric uncertainties $\tilde{\theta }$, two definitions of the extended states are given.

Case 1

We extend x_ei = d_i, i = 1,…,n., let h_i(t) be the time derivatives of x_ei. Then, we have

$$ \begin{aligned} \left\{ {\begin{array}{*{20}l} \dot{x}_{i} = x_{i + 1} + \hat{\theta }^{T} \varphi_{i} \left( {\overline{x}_{i} } \right) + x_{ei} \left( {\overline{x}_{i} ,t} \right) + \tilde{\theta }^{T} \varphi_{i} \left( {\overline{x}_{i} } \right) \hfill \\ \dot{x}_{ei} = h_{i} \left( t \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,...,n - 1 \hfill \\ \end{array}} \right. \hfill \\ \left\{ {\begin{array}{*{20}l} \dot{x}_{n} = u + \hat{\theta }^{T} \varphi_{n} \left( x \right) + x_{en} \left( {x,t} \right) + \tilde{\theta }^{T} \varphi_{n} \left( x \right) \hfill \\ \dot{x}_{en} = h_{n} \left( t \right) \hfill \\ \end{array}} \right. \hfill \\ \end{aligned} $$

(4)

Define $\varepsilon_{i} = \left[ {\varepsilon_{i1} ,\varepsilon_{i2} } \right]^{{\text{T}}} = \left[ {\tilde{x}_{i} ,\tilde{x}_{ei} /\omega_{i} } \right]^{{\text{T}}} ,\quad i = 1,...,n$, the estimation error dynamics are obtained as follows:

$$ L_{1} = k_{{c_{1} }} - A_{0} $$

(5)

where $A = \left[ {\begin{array}{*{20}c} { - l_{1} } & 1 \\ { - l_{2} } & 0 \\ \end{array} } \right]$, $B_{1} = \left[ {1,0} \right]^{{\text{T}}}$, $B_{2} = \left[ {0,1} \right]^{{\text{T}}}$.

Case 2

We extend $x_{ei} = d_{i} + \tilde{\theta }^{T} \varphi_{i}$, i = 1, …, n. Then, the dynamic of estimation errors can be obtained by

$$ \dot{\varepsilon }_{i} = \omega_{i} A\varepsilon_{i} + B_{2} \frac{{h_{i} \left( t \right)}}{{\omega_{i} }} $$

(6)

As the matrix A is Hurwitz, $A^{T} P + PA = - 2I$ is established with a positive definite matrix P, the matrix I is an identity matrix.

Remark 2

In the above two cases, the structures of ESOs are the same, according to the different definitions of extended states; we have different dynamic state estimation errors. Based on the BLF with this property, two different results can be obtained by two stability analyses discussed later.

3.2 Controller design

Let the tracking error e(t) = x₁ − x_1d satisfy strictly the following inequality to realize the prescribed performance.

$$ - \rho (t) < e\left( t \right) < \rho (t),\quad \forall t > 0 $$

(7)

where δ_l > 0 and δ_u > 0 are design parameters. The performance function ρ(t) is given in (8), which is strictly positive decreasing smooth and bounded:

$$ \begin{gathered} \rho (t) = (\rho_{0} - \rho_{\infty } ){\text{e}}^{ - kt} + \rho_{\infty } \hfill \\ \mathop {\lim }\limits_{t \to \infty } \rho (t) = \rho_{\infty } > 0 \hfill \\ \end{gathered} $$

(8)

where ρ₀, ρ_∞ and k are positive constants. The approximate curve of prescribed performance index inequality (7) is shown in Fig. 1.

Fig. 1

The prescribed performance diagram

Obviously, in (7), $- \rho_{0}$ and $\rho_{0}$ constrain the lower bound of the undershoot and the upper bound of the overshoot of the output control error e(t), respectively. k is the convergence rate, and ρ_∞ constrains the steady-state bound of e(t). By selecting appropriate parameters such as ρ₀, ρ_∞ and k, the transient and stability performance of output control error can be planned in advance, and the improvement of transient performance can be completed according to the actual demand of the system.

Define z_i = x_i − α_i − 1, i = 2, …, n, α_i − 1 are virtual controllers. The controller design process is given as follows:

Step 1: Define the positive definite BLF as follows:

$$ V_{1} = \frac{1}{2}\log \frac{{\rho^{2} (t)}}{{\rho^{2} (t) - e^{2} \left( t \right)}} = \frac{1}{2}\log \frac{1}{{1 - z_{1}^{2} }} $$

(9)

where log(χ) is the natural logarithm of χ,$z_{1} = e\left( t \right)/\rho \left( t \right)$.

Differentiating V₁, substituting (1) into it yields

$$ \begin{aligned} \dot{V}_{1} & = \frac{{z_{1} \rho^{ - 1} }}{{1 - z_{1}^{2} }}\left( {\dot{e} - \dot{\rho }z_{1} } \right) \\ &= \frac{{z_{1} \rho^{ - 1} }}{{1 - z_{1}^{2} }}\left( {z_{2} { + }\alpha_{1} + \theta^{T} \varphi_{1} \left( {x_{1} } \right) + d_{1} \left( {x_{1} ,t} \right) - \dot{x}_{1d} - \dot{\rho }z_{1} } \right) \\ \end{aligned} $$

(10)

The virtual controller α₁ is designed to be

$$ \alpha_{1} = - \hat{\theta }^{T} \varphi_{1} \left( {x_{1} } \right) - \hat{x}_{e1} + \dot{x}_{1d} + \dot{\rho }z_{1} - k_{1} z_{1} - \frac{{\omega_{1}^{2} \rho^{ - 1} z_{1} }}{{2\left( {1 - z_{1}^{2} } \right)}} $$

(11)

where k₁ > 0 is a design parameter.

Then, the dynamic $\dot{z}_{1}$ becomes

$$ \dot{V}_{1} = \frac{{z_{1} \rho^{ - 1} }}{{1 - z_{1}^{2} }}\left( {z_{2} - k_{1} z_{1} } \right) + \frac{{z_{1} \rho^{ - 1} }}{{1 - z_{1}^{2} }}\left( {\tilde{\theta }^{T} \varphi_{1} \left( {x_{1} } \right) - \hat{x}_{e1} + d_{1} \left( {x_{1} ,t} \right)} \right) - \frac{{\omega_{1}^{2} \rho^{ - 2} z_{1}^{2} }}{{2\left( {1 - z_{1}^{2} } \right)^{2} }} $$

(12)

Step 2: Define the following positive definite BLF

$$ V_{2} = \frac{1}{2}\log \frac{{L_{2}^{2} }}{{L_{2}^{2} - z_{2}^{2} }} + V_{1} $$

(13)

where L₂ > 0 is a design parameter.

Differentiating (13) and noting (1), we have

$$ \begin{aligned} \dot{V}_{2} & = \frac{{z_{2} \dot{z}_{2} }}{{L_{2}^{2} - z_{2}^{2} }} + \dot{V}_{1} \\ &= \frac{{z_{2} }}{{L_{2}^{2} - z_{2}^{2} }}\left( {z_{3} + \alpha_{2} + \theta^{T} \varphi_{2} \left( {\overline{x}_{2} } \right) + d_{2} \left( {\overline{x}_{2} ,t} \right) - \dot{\alpha }_{1} } \right)\\ &\quad +\, \dot{V}_{1} \\ \end{aligned} $$

(14)

The virtual controller α₂ is designed to be

$$ \alpha_{2} = - \hat{\theta }^{T} \varphi_{2} \left( {\overline{x}_{2} } \right) - \hat{x}_{e2} + \dot{\alpha }_{1c} - k_{2} z_{2} - \frac{{\rho^{ - 1} z_{1} \left( {L_{2}^{2} - z_{2}^{2} } \right)}}{{1 - z_{1}^{2} }} - \frac{{\omega_{2}^{2} z_{2} }}{{2\left( {L_{2}^{2} - z_{2}^{2} } \right)}} - \frac{{\left( {\omega_{1} \frac{{\partial \alpha_{1} }}{{\partial x_{1} }}} \right)^{2} z_{2} }}{{2\left( {L_{2}^{2} - z_{2}^{2} } \right)}} $$

(15)

where k₂ > 0 is design parameter,$\dot{\alpha }_{1} = \dot{\alpha }_{1c} + \dot{\alpha }_{1u}$, $\dot{\alpha }_{1c}$ and $\dot{\alpha }_{1u}$ are the calculable part and incalculable part, respectively.

$$ \begin{aligned} \dot{\alpha }_{1c} &= \frac{{\partial \alpha_{1} }}{\partial t} + \frac{{\partial \alpha_{1} }}{{\partial x_{1} }}\hat{\dot{x}}_{1} + \frac{{\partial \alpha_{1} }}{{\partial \hat{x}_{e1} }}\dot{\hat{x}}_{e1} + \frac{{\partial \alpha_{1} }}{{\partial \hat{\theta }}}\dot{\hat{\theta }} \hfill \\ \dot{\alpha }_{1u} &= \frac{{\partial \alpha_{1} }}{{\partial x_{1} }}\tilde{\dot{x}}_{1} \hfill \\ \end{aligned} $$

(16)

Then, we have

$$ \begin{aligned} \dot{V}_{2} & = \frac{{z_{2} }}{{L_{2}^{2} - z_{2}^{2} }}\left( {\tilde{\theta }^{T} \varphi_{2} \left( {\overline{x}_{2} } \right) - \hat{x}_{e2} - \dot{\alpha }_{1u} + d_{2} \left( {\overline{x}_{2} ,t} \right)} \right) - \frac{{k_{2} z_{2}^{2} }}{{L_{2}^{2} - z_{2}^{2} }}{ + }\frac{{z_{2} z_{3} }}{{L_{2}^{2} - z_{2}^{2} }} - \frac{{\omega_{2}^{2} z_{2}^{2} }}{{2\left( {L_{2}^{2} - z_{2}^{2} } \right)^{2} }} \\ & \quad -\, \frac{{\left( {\omega_{1} \frac{{\partial \alpha_{1} }}{{\partial x_{1} }}} \right)^{2} z_{2}^{2} }}{{2\left( {L_{2}^{2} - z_{2}^{2} } \right)^{2} }} + \frac{{ - \rho^{ - 1} k_{1} z_{1}^{2} }}{{1 - z_{1}^{2} }} + \frac{{z_{1} }}{{1 - z_{1}^{2} }}\rho^{ - 1} \left( {\tilde{\theta }^{T} \varphi_{1} \left( {x_{1} } \right) - \hat{x}_{e1} + d_{1} \left( {x_{1} ,t} \right)} \right) - \frac{{\omega_{1}^{2} \rho^{ - 2} z_{1}^{2} }}{{2\left( {1 - z_{1}^{2} } \right)^{2} }} \\ \end{aligned} $$

(17)

Step i: (3 ≤ i ≤ n − 1): Define the following positive definite functions

$$ V_{i} = \frac{1}{2}\log \frac{{L_{i}^{2} }}{{L_{i}^{2} - z_{i}^{2} }} + V_{i - 1} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 3,...,n - 1 $$

(18)

where L_i > 0 are design parameters.

Differentiating (18) and noting (1), we have

$$ \begin{aligned} \dot{V}_{i} & = \frac{{z_{i} \dot{z}_{i} }}{{L_{i}^{2} - z_{i}^{2} }} + \dot{V}_{i - 1} = \frac{{z_{i} \left( {\dot{x}_{i} - \dot{\alpha }_{i - 1} } \right)}}{{L_{i}^{2} - z_{i}^{2} }} + \dot{V}_{i - 1} \\ & = \frac{{z_{i} \left( {x_{i + 1} + \theta^{T} \varphi_{i} \left( {\overline{x}_{i} } \right) + d_{i} \left( {\overline{x}_{i} ,t} \right) - \dot{\alpha }_{i - 1} } \right)}}{{L_{i}^{2} - z_{i}^{2} }} + \dot{V}_{i - 1} \\ & = \frac{{z_{i} \left( {z_{i + 1} + \alpha_{i} + \theta^{T} \varphi_{i} \left( {\overline{x}_{i} } \right) + d_{i} \left( {\overline{x}_{i} ,t} \right) - \dot{\alpha }_{i - 1} } \right)}}{{L_{i}^{2} - z_{i}^{2} }} + \dot{V}_{i - 1} \\ \end{aligned} $$

(19)

Similar to (15), the virtual controllers α_i are developed to be

$$ \begin{aligned} \alpha_{i} & = - \hat{\theta }^{T} \varphi_{i} \left( {\overline{x}_{i} } \right) - \hat{x}_{ei} + \dot{\alpha }_{{\left( {i - 1} \right)c}} - k_{i} z_{i} - \frac{{z_{i - 1} \left( {L_{i}^{2} - z_{i}^{2} } \right)}}{{\left( {L_{i - 1}^{2} - z_{i - 1}^{2} } \right)}} \\ &\quad - \frac{{\omega_{i}^{2} z_{i} }}{{2\left( {L_{i}^{2} - z_{i}^{2} } \right)}} - \frac{{\sum_{k = 1}^{i - 1} {\left( {\omega_{k} \frac{{\partial \alpha_{i - 1} }}{{\partial x_{k} }}} \right)^{2} } z_{i} }}{{2\left( {L_{i}^{2} - z_{i}^{2} } \right)}} \\ \end{aligned} $$

(20)

where k_i > 0 are design parameters,$\dot{\alpha }_{i - 1} = \dot{\alpha }_{{\left( {i - 1} \right)c}} + \dot{\alpha }_{{\left( {i - 1} \right)u}}$, $\dot{\alpha }_{{\left( {i - 1} \right)c}}$ and $\dot{\alpha }_{{\left( {i - 1} \right)u}}$ are the calculable part and incalculable part, respectively.

$$ \begin{aligned} \dot{\alpha }_{{\left( {i - 1} \right)c}} &= \frac{{\partial \alpha_{i - 1} }}{\partial t} + \sum_{k = 1}^{i - 1} {\frac{{\partial \alpha_{i - 1} }}{{\partial x_{k} }}} \hat{\dot{x}}_{k} + \sum_{k = 1}^{i - 1} {\frac{{\partial \alpha_{i - 1} }}{{\partial \hat{x}_{ek} }}} \dot{\hat{x}}_{ek} + \frac{{\partial \alpha_{i - 1} }}{{\partial \hat{\theta }}}\dot{\hat{\theta }} \hfill \\ \dot{\alpha }_{{\left( {i - 1} \right)u}} &= \sum_{k = 1}^{i - 1} {\frac{{\partial \alpha_{i - 1} }}{{\partial x_{k} }}} \tilde{\dot{x}}_{k} \hfill \\ \end{aligned} $$

(21)

Then, we have

$$ \begin{aligned} \dot{V}_{i} & = \dot{V}_{i - 1} - \frac{{k_{i} z_{i}^{2} }}{{L_{i}^{2} - z_{i}^{2} }} + \frac{{z_{i} z_{i + 1} }}{{L_{i}^{2} - z_{i}^{2} }} + \frac{{z_{i} \left( {d_{i} \left( {\overline{x}_{i} ,t} \right) + \tilde{\theta }^{T} \varphi_{i} \left( {\overline{x}_{i} } \right) - \hat{x}_{ei} - \dot{\alpha }_{{\left( {i - 1} \right)u}} } \right)}}{{L_{i}^{2} - z_{i}^{2} }} \\ &\quad -\, \frac{{z_{i} z_{i - 1} }}{{L_{i - 1}^{2} - z_{i - 1}^{2} }} - \frac{{\omega_{i}^{2} z_{i}^{2} }}{{2\left( {L_{i}^{2} - z_{i}^{2} } \right)^{2} }} - \frac{{\sum_{k = 1}^{i - 1} {\left( {\omega_{k} \frac{{\partial \alpha_{i - 1} }}{{\partial x_{k} }}} \right)^{2} } z_{i}^{2} }}{{2\left( {L_{i}^{2} - z_{i}^{2} } \right)^{2} }} \\ \end{aligned} $$

(22)

From (22), we have

$$ \begin{aligned} \dot{V}_{i} &= \frac{{z_{i + 1} z_{i} }}{{L_{i}^{2} - z_{i}^{2} }} - \sum_{k = 2}^{i} {\frac{{k_{k} z_{k}^{2} }}{{L_{k}^{2} - z_{k}^{2} }}} + \sum_{k = 2}^{i} {\frac{{z_{k} \left( {d_{k} \left( {\overline{x}_{k} ,t} \right) + \tilde{\theta }^{T} \varphi_{k} \left( {\overline{x}_{k} } \right) - \hat{x}_{ek} } \right)}}{{L_{k}^{2} - z_{k}^{2} }}} - \sum_{k = 2}^{n} {\frac{{z_{k}^{2} \sum_{j = 1}^{k - 1} {\left( {\omega_{j} \frac{{\partial \alpha_{k - 1} }}{{\partial x_{j} }}} \right)^{2} } }}{{2\left( {L_{k}^{2} - z_{k}^{2} } \right)^{2} }}} \hfill \\ &\quad -\, \sum_{k = 2}^{i} {\frac{{z_{k} \dot{\alpha }_{{\left( {k - 1} \right)u}} }}{{L_{k}^{2} - z_{k}^{2} }}} - \sum_{k = 2}^{i} {\frac{{\omega_{k}^{2} z_{k}^{2} }}{{2\left( {L_{k}^{2} - z_{k}^{2} } \right)^{2} }}} - \frac{{\rho^{ - 1} k_{1} z_{1}^{2} }}{{1 - z_{1}^{2} }} + \frac{{z_{1} }}{{1 - z_{1}^{2} }}\rho^{ - 1} \left( {\tilde{\theta }^{T} \varphi_{1} \left( {x_{1} } \right) - \hat{x}_{e1} + d_{1} \left( {x_{1} ,t} \right)} \right) - \frac{{\omega_{1}^{2} \rho^{ - 2} z_{1}^{2} }}{{2\left( {1 - z_{1}^{2} } \right)^{2} }} \hfill \\ \end{aligned} $$

(23)

Step n: Choose nth positive definite function as follows:

$$ V_{n} = \frac{1}{2}\log \frac{{L_{n}^{2} }}{{L_{n}^{2} - z_{n}^{2} }} + V_{n - 1} $$

(24)

where L_n > 0 is a design parameter.

Differentiating V_n, substituting (1) into it yields

$$ \begin{aligned} \dot{V}_{n} & = \frac{{z_{n} \dot{z}_{n} }}{{L_{n}^{2} - z_{n}^{2} }} + \dot{V}_{n - 1} = \frac{{z_{n} \left( {\dot{x}_{n} - \dot{\alpha }_{n - 1} } \right)}}{{L_{i}^{2} - z_{i}^{2} }} + \dot{V}_{n - 1} \\ &= \frac{{z_{n} \left( {u + \theta^{T} \varphi_{n} \left( x \right) + d_{n} \left( {x,t} \right) - \dot{\alpha }_{n - 1} } \right)}}{{L_{n}^{2} - z_{n}^{2} }} + \dot{V}_{n - 1} \\ \end{aligned} $$

(25)

The input u is designed as

$$ \begin{aligned} u & = - \hat{\theta }^{T} \varphi_{n} \left( x \right) - \hat{x}_{en} + \dot{\alpha }_{{\left( {n - 1} \right)c}} - k_{n} z_{n} - \frac{{z_{n - 1} \left( {L_{n}^{2} - z_{n}^{2} } \right)}}{{\left( {L_{n - 1}^{2} - z_{n - 1}^{2} } \right)}} \\ &\quad -\, \frac{{\omega_{n}^{2} z_{n} }}{{2\left( {L_{n}^{2} - z_{n}^{2} } \right)}} - \frac{{\sum_{k = 1}^{n - 1} {\left( {\omega_{k} \frac{{\partial \alpha_{n - 1} }}{{\partial x_{k} }}} \right)^{2} } z_{n} }}{{2\left( {L_{n}^{2} - z_{n}^{2} } \right)}} \\ \end{aligned} $$

(26)

where k_n > 0 is a design parameter, $\dot{\alpha }_{n - 1} = \dot{\alpha }_{{\left( {n - 1} \right)c}} + \dot{\alpha }_{{\left( {n - 1} \right)u}}$, $\dot{\alpha }_{{\left( {n - 1} \right)c}}$ denotes the calculable part, $\dot{\alpha }_{{\left( {n - 1} \right)u}}$ denotes the incalculable part.

$$ \begin{aligned} \dot{\alpha }_{{\left( {n - 1} \right)c}} &= \frac{{\partial \alpha_{n - 1} }}{\partial t} + \sum_{k = 1}^{n - 1} {\frac{{\partial \alpha_{n - 1} }}{{\partial x_{k} }}} \hat{\dot{x}}_{k} + \sum_{k = 1}^{n - 1} {\frac{{\partial \alpha_{n - 1} }}{{\partial \hat{x}_{ek} }}} \dot{\hat{x}}_{ek} + \frac{{\partial \alpha_{n - 1} }}{{\partial \hat{\theta }}}\dot{\hat{\theta }} \hfill \\ \dot{\alpha }_{{\left( {n - 1} \right)u}} &= \sum_{k = 1}^{n - 1} {\frac{{\partial \alpha_{n - 1} }}{{\partial x_{k} }}} \tilde{\dot{x}}_{k} \hfill \\ \end{aligned} $$

(27)

When the following conditions hold:

• (1) Suitable parameters k_i, ω_i and L_i are selected to satisfy

  $$ c_{i + 1} \ge \left| {\alpha_{i} } \right|_{\max } + L_{i + 1} $$

• (2) The initial conditions z_i(0) satisfy

  $$ \left| {z_{1} \left( 0 \right)} \right| \le \rho_{0} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left| {z_{i} \left( 0 \right)} \right| \le L_{i} ,i = 2,...,n $$

The following two theorems are carried out to ensure the stability of the closed-loop system.

Theorem 1

If the disturbances d_i, i = 1,…, n, are time-invariant in system (1), i.e., h_i (t) = 0, with the proposed controller (26) with the adaptation law as follows:

$$\begin{aligned} \dot{\hat{\theta }} &= \Gamma \left( \sum_{j = 2}^{n} \frac{{z_{j} \varphi_{j} \left( x \right)}}{{L_{j}^{2} - z_{j}^{2} }} - \sum_{k = 2}^{n} \frac{{z_{k} \sum_{j = 1}^{k - 1} {\frac{{\partial \alpha_{k - 1} }}{{\partial x_{j} }}} \varphi_{j} \left( {\overline{x}_{j} } \right)}}{{L_{k}^{2} - z_{k}^{2} }}\right.\\ & \quad +\left. \, \sum_{i = 1}^{n} {\varepsilon_{i}^{T} PB_{1} \varphi_{i} } + \frac{{z_{1} }}{{1 - z_{1}^{2} }}\rho^{ - 1} \varphi_{1} \left( {\overline{x}_{1} } \right) \right)\end{aligned} $$

(28)

where $\Gamma > 0$ is a diagonal adaptation rate matrix. Then, all signals of closed-loop system can be guaranteed to be bounded with prescribed performance tracking, the constraints of full states are not violated, and asymptotic track performance is also achieved, i.e., z₁ → 0 as t → ∞.

Proof

See Appendix 1.

Theorem 2

If the disturbances d_i, i = 1,..., n, are time-variant, i.e., $h_{i} (t) \ne 0$, all signals are bounded with the proposed control law (26), prescribed performance tracking is obtained and the constraints of full states are not violated. The following positive definite Lyapunov function

$$ V_{b} = V_{n} + \sum_{i = 1}^{n} {\frac{1}{2}\varepsilon_{i}^{T} P\varepsilon_{i} } $$

(29)

is bounded by

$$ V_{b} \left( t \right) \le \exp \left( { - \lambda t} \right)V_{b} \left( 0 \right) + \frac{\sigma }{\lambda }\left[ {1 - \exp \left( { - \lambda t} \right)} \right] $$

(30)

where $\lambda = \left\{ {2\rho_{0}^{ - 1} k_{1} ,{\kern 1pt} 2k_{2} ,{\kern 1pt} {\kern 1pt} ...,2k_{n} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{2\omega_{1} - n - 1}}{{2\lambda_{\max } \left( P \right)}},{\kern 1pt} {\kern 1pt} ...,{\kern 1pt} {\kern 1pt} \frac{{2\omega_{n} - n - 1}}{{2\lambda_{\max } \left( P \right)}}} \right\}_{\min }$, λ_max(P) is the maximum eigenvalue of matrix P, $\sigma = \sum_{i = 1}^{n} {\frac{{\left\| {PB_{2} } \right\|^{2} \left| {h_{i} \left( t \right)} \right|_{\max }^{2} }}{{2\omega_{i}^{2} }}}$.

Proof.

See Appendix 2.

4 Simulation

Two simulation examples are carried out to testify the validity of the proposed algorithm as follows.

Example 1.

A spring, mass and damper system given in [3, 39] is considered. The dynamic model is modeled as follows:

$$ \begin{aligned}& \dot{x}_{1} = x_{2} \hfill \\ & \dot{x}_{2} = \frac{u}{m} - \theta^{T} \varphi + d\left( t \right) \hfill \\ \end{aligned} $$

(31)

where x₁ is the position and x₂ is the velocity, θ = [θ₁, θ₂]^T = [k/m, c/m]^T, $\varphi = \left[ {x_{1} ,x_{2} } \right]^{{\text{T}}}$. The system parameters are found in Table 1.

Table 1 Parameters of the spring, mass and damper system

The ESO is constructed for (31):

$$ \left\{ \begin{aligned} \dot{\hat{x}}_{1} &= x_{2} - 3\omega_{1} \left( {x_{1} - \hat{x}_{1} } \right) \hfill \\ \dot{\hat{x}}_{2} = \frac{u}{m} + \hat{\theta }^{T} \varphi + \hat{x}_{e} - 3\omega_{1}^{2} \left( {x_{1} - \hat{x}_{1} } \right) \hfill \\ \dot{\hat{x}}_{e} &= - \omega_{1}^{3} \left( {x_{1} - \hat{x}_{1} } \right) \hfill \\ \end{aligned} \right. $$

(32)

The controller is designed as

$$ u = m\left( {\hat{\theta }^{T} \varphi - \hat{x}_{e} + \dot{\alpha }_{1} - k_{2} z_{2} - \frac{{\rho^{ - 1} z_{1} \left( {L_{2}^{2} - z_{2}^{2} } \right)}}{{1 - z_{1}^{2} }} - \frac{{\omega_{1}^{4} z_{2} }}{{2\left( {L_{2}^{2} - z_{2}^{2} } \right)}}} \right) $$

(33)

The virtue controller is designed as

$$ \alpha_{1} = \dot{x}_{1d} + \dot{\rho }z_{1} - k_{1} z_{1} $$

(34)

The adaptation law is designed as

$$ \dot{\hat{\theta }} = \Gamma_{1} \left( {\frac{{z_{2} \varphi }}{{L_{2}^{2} - z_{2}^{2} }} + \varepsilon_{1}^{T} PB_{1} \varphi } \right) $$

(35)

where $\Gamma_{1} > 0$ is a diagonal adaptation rate matrix, $\varepsilon_{1} = \left[ {\varepsilon_{11} ,\varepsilon_{12} ,\varepsilon_{13} } \right]^{{\text{T}}} = \left[ {\tilde{x}_{1} ,\tilde{x}_{2} /\omega_{1} ,\tilde{x}_{e} /\omega_{1}^{2} } \right]^{{\text{T}}}$, $B_{1} = \left[ {0,1,0} \right]^{T}$.

The parameters of the proposed controller (i.e., APC) are selected as k₁ = 200, k₂ = 500, L₂ = 2, ω₁ = 200, θ₀ = 100, $\hat{\theta }\left( 0 \right)$ = [5, 3]^T, $\Gamma_{1} = \left[ {5.7,{\kern 1pt} {\kern 1pt} 2.2} \right]^{{\text{T}}}$, ρ₀ = 0.3, ρ_∞ = 0.012, k = 0.0009, c₁ = 0.8, c₂ = 2. The desired trajectory y_d(t) = 0.5sin(0.5πt)[1 − exp(−t³)], the initial value of x₁ is set as x₁(0) = 0.2, d(t) = sin(2πt).

Remark 3

As the accurate disturbance estimation can be guaranteed by increasing the observer parameters, in order to test the performance of ESO, large disturbance is added into the system; In addition, the initial value of x₁(0) is assigned to be 0.2 to test the effectiveness of the prescribed performance control and state constraint control.

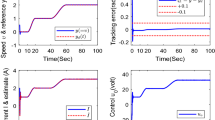
The simulation results are exhibited in Figs. 2, 4, 5, 6, 7 and 8. Figure 2 shows the desired trajectory x_1d and output state x₁. After a short transient response process, the output trajectory can track the desired trajectory quite well. Figure 3 presents the control input u. The tracking error e(t) and prescribed performance bounds are given in Fig. 4. Obviously, the output tracking error of the proposed controller converges to the neighborhood of zero and the prescribed performance bounds are not violated. From Figs. 5 and 6, it can be seen that the proposed controller can meet the requirements of state constraints. The parameters estimation is presented in Fig. 7. The real parameters of the system are estimated accurately. Figure 8 illustrates d and disturbance estimations. Obviously, the actual disturbances are obtained by ESO.

Fig. 2

Desired trajectory x_1d(t) and the trajectory x₁(t)

Fig. 3

Control input u

Fig. 4

Tracking error e(t) and prescribed performance bounds

Fig. 5

Output x₁

Fig. 6

Output x₂

Fig. 7

Parameter estimations

Fig. 8

Disturbance d and disturbance estimation

Example 2.

A single inverted pendulum (SIP) system [40, 41] is given as follows:

$$ \left\{ \begin{array}{l} \dot{x}_{1} = x_{2} \hfill \\ \dot{x}_{2} = \beta_{{1}} \left( x \right)u + \theta^{T} \varphi + d\left( t \right) \hfill \\ \end{array} \right. $$

(36)

where $\theta^{T} = \left[ {\theta_{1} ,\theta_{2} } \right] = \left[ {1,1} \right]$, $\varphi = \left[ {f_{1} \left( x \right), - f_{2} \left( x \right)} \right]^{{\text{T}}}$, $f_{1} \left( x \right) = \frac{{g\sin x_{1} }}{{l\left( {4/3 - {{m\cos^{2} x_{1} } \mathord{\left/ {\vphantom {{m\cos^{2} x_{1} } {\left( {m_{c} + m} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {m_{c} + m} \right)}}} \right)}}$, $f_{2} \left( x \right) = \frac{{{{mx_{2}^{2} \cos x_{1} \sin x_{1} } \mathord{\left/ {\vphantom {{mx_{2}^{2} \cos x_{1} \sin x_{1} } {\left( {m_{c} + m} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {m_{c} + m} \right)}}}}{{4/3 - {{m\cos^{2} x_{1} } \mathord{\left/ {\vphantom {{m\cos^{2} x_{1} } {\left( {m_{c} + m} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {m_{c} + m} \right)}}}}$, $\beta_{{1}} \left( x \right) = \frac{{{{\cos x_{1} } \mathord{\left/ {\vphantom {{\cos x_{1} } {\left( {m_{c} + m} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {m_{c} + m} \right)}}}}{{l\left( {4/3 - {{m\cos^{2} x_{1} } \mathord{\left/ {\vphantom {{m\cos^{2} x_{1} } {\left( {m_{c} + m} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {m_{c} + m} \right)}}} \right)}}$.

The SIP is described by the states found in Table 2.

Table 2 Parameters of SIP

The ESO is constructed for (36):

$$ \left\{ \begin{array}{l} \dot{\hat{x}}_{1} = x_{2} - 3\omega_{1} \left( {x_{1} - \hat{x}_{1} } \right) \hfill \\ \dot{\hat{x}}_{2} = \beta_{{1}} \left( x \right)u + \hat{\theta }^{T} \varphi_{2} + \hat{x}_{e} - 3\omega_{1}^{2} \left( {x_{1} - \hat{x}_{1} } \right) \hfill \\ \dot{\hat{x}}_{e} = - \omega_{1}^{3} \left( {x_{1} - \hat{x}_{1} } \right) \hfill \\ \end{array} \right. $$

(37)

The controller is designed as

$$ u = \left( { - \hat{\theta }^{T} \varphi - \hat{x}_{e} + \dot{\alpha }_{1} - k_{2} z_{2} - \frac{{\rho^{ - 1} z_{1} \left( {L_{2}^{2} - z_{2}^{2} } \right)}}{{1 - z_{1}^{2} }} - \frac{{\omega_{1}^{4} z_{2} }}{{2\left( {L_{2}^{2} - z_{2}^{2} } \right)}}} \right)/\beta_{1} $$

(38)

The virtue controller is designed as

$$ \alpha_{1} = \dot{x}_{1d} + \dot{\rho }z_{1} - k_{1} z_{1} $$

(39)

The adaptation law is designed as

$$ \mu = \Gamma_{1} \left( {\frac{{z_{2} \varphi }}{{L_{2}^{2} - z_{2}^{2} }} + \varepsilon_{1}^{T} PB_{1} \varphi } \right) $$

(40)

where $\Gamma_{1} > 0$ is a diagonal adaptation rate matrix, $\varepsilon_{1} = \left[ {\varepsilon_{11} ,\varepsilon_{12} ,\varepsilon_{13} } \right]^{{\text{T}}} = \left[ {\tilde{x}_{1} ,\tilde{x}_{2} /\omega_{1} ,\tilde{x}_{e} /\omega_{1}^{2} } \right]^{{\text{T}}}$, $B_{1} = \left[ {0,1,0} \right]^{T}$.

In this simulation, the desired trajectory y_d(t) = 2sin(πt)[1 − exp(−0.01t³)], d = 30sin(2πt). In order to prove the validity of disturbance compensation term, adaptive law, prescribed control performance of the proposed controller, the initial values of the states are x₁(0) = 0.2. The parameters of the proposed controller (i.e., APC) are given as k₁ = 5, k₂ = 50, L₂ = 2, ω₁ = 300, θ₀ = 20, $\hat{\theta }\left( 0 \right)$ = [1.6, 1.6]^T, $\Gamma_{1} = \left[ {10,{\kern 1pt} {\kern 1pt} 4.2} \right]^{{\text{T}}}$, ρ₀ = 0.3, ρ_∞ = 0.0005, k = 0.003, c₁ = 0.4, c₂ = 2.

The simulation results are shown in Figs. 9, 10, 11, 12, 13, 14 and 15. Figure 9 shows the desired trajectory x_1d and output state x₁. The output trajectory can track the desired trajectory quite quickly and well. Figure 10 presents the control input u. The tracking error e(t) and prescribed performance bounds are given in Fig. 11. Obviously, the output tracking error of the proposed controller converges to the neighborhood of zero within the bounds of the prescribed performance function limitation. From Fig. 12 and Fig. 13, it can be seen that the requirements of state constraints can be satisfied by the proposed controller. As presented in Fig. 14, the real parameters of the system are estimated accurately. Figure 15 illustrates d and disturbance estimations. Obviously, the actual disturbances are obtained by ESO.

Fig. 9

Desired trajectory x_1d(t) and the trajectory x₁(t)

Fig. 10

Control input u

Fig. 11

Tracking error e(t) and prescribed performance bounds

Fig. 12

Output x₁ of two controllers

Fig. 13

Output x₂ of two controllers

Fig. 14

Parameter estimations

Fig. 15

Disturbance d and disturbance estimation

5 Conclusion

In this study, an ESO-based adaptive prescribed performance controller is developed for a class of nonlinear systems with full-state constraints and uncertainties. Adaptive control for the system parametric uncertainties and multiple ESOs for disturbances are integrated into the prescribed performance and full-state constraints design via backstepping technique to achieve prescribed performance tracking of output error without violation of full states. The global stability of the proposed control approach is proved. Finally, two simulation examples are employed to demonstrate the performance of the proposed method.

Appendices

Appendix 1

Proof of Theorem 1. If the disturbances d_i, i = 1,..., n, are time-invariant, the following positive definite Lyapunov function is defined with x_ei = d_i in this case

$$ V_{a} = V_{n} + \sum_{i = 1}^{n} {\frac{1}{2}\varepsilon_{i}^{T} P\varepsilon_{i} } + \frac{1}{2}\tilde{\theta }^{T} \Gamma^{ - 1} \tilde{\theta } $$

(41)

Differentiating V_n, substituting (5) into it yields

$$ \begin{aligned} \dot{V}_{a} & = \dot{V}_{n} + \sum_{i = 1}^{n} {\left( {\frac{1}{2}\dot{\varepsilon }_{i}^{T} P\varepsilon_{i} + \frac{1}{2}\varepsilon_{i}^{T} P\dot{\varepsilon }_{i} } \right)} - \tilde{\theta }^{T} \Gamma^{ - 1} \dot{\hat{\theta }} \\ &= \dot{V}_{n} - \tilde{\theta }^{T} \Gamma^{ - 1} \dot{\hat{\theta }} + \sum_{i = 1}^{n} {\left( {\frac{1}{2}\left( {\omega_{i} A\varepsilon_{i} + B_{1} \tilde{\theta }^{T} \varphi_{i} } \right)^{T} P\varepsilon_{i} + \frac{1}{2}\varepsilon_{i}^{T} P\left( {\omega_{i} A\varepsilon_{i} + B_{1} \tilde{\theta }^{T} \varphi_{i} } \right)} \right)} \\ &= \dot{V}_{n} - \tilde{\theta }^{T} \Gamma^{ - 1} \dot{\hat{\theta }} + \sum_{i = 1}^{n} {\left( {\frac{1}{2}\omega_{i} \varepsilon_{i}^{T} A^{T} P\varepsilon_{i} + \frac{1}{2}\omega_{i} \varepsilon_{i}^{T} PA\varepsilon_{i} + \varepsilon_{i}^{T} PB_{1} \tilde{\theta }^{T} \varphi_{i} } \right)} \\ \end{aligned} $$

(42)

As the matrix A is Hurwitz,$A^{T} P + PA = - 2I$ is established, noting (23)–(26), we have

$$ \begin{aligned} \dot{V}_{a}& \le - \sum_{j = 2}^{n} {\frac{{k_{j} z_{j}^{2} }}{{L_{j}^{2} - z_{j}^{2} }}} - \frac{{\rho^{ - 1} k_{1} z_{1}^{2} }}{{1 - z_{1}^{2} }} + \sum_{j = 2}^{n} {\frac{{z_{j} \tilde{\theta }^{T} \varphi_{j} \left( {\overline{x}_{j} } \right)}}{{L_{j}^{2} - z_{j}^{2} }}} { + }\sum_{k = 2}^{n} {\frac{{z_{k} \left( {d_{k} \left( {\overline{x}_{k} ,t} \right) - \hat{x}_{ek} } \right)}}{{L_{k}^{2} - z_{k}^{2} }}} \hfill \\ &\quad -\, \sum_{k = 2}^{n} {\frac{{z_{k} \dot{\alpha }_{{\left( {k - 1} \right)u}} }}{{L_{k}^{2} - z_{k}^{2} }}} - \sum_{k = 2}^{n} {\frac{{z_{k}^{2} \sum_{j = 1}^{k - 1} {\left( {\omega_{j} \frac{{\partial \alpha_{k - 1} }}{{\partial x_{j} }}} \right)^{2} } }}{{2\left( {L_{k}^{2} - z_{k}^{2} } \right)^{2} }}} - \sum_{k = 2}^{n} {\frac{{\omega_{k}^{2} z_{k}^{2} }}{{2\left( {L_{k}^{2} - z_{k}^{2} } \right)^{2} }}} + \frac{{\rho^{ - 1} z_{1} }}{{1 - z_{1}^{2} }}\tilde{\theta }^{T} \varphi_{1} \left( {\overline{x}_{1} } \right) \hfill \\ &\quad +\, \frac{{\rho^{ - 1} z_{1} }}{{1 - z_{1}^{2} }}\left( {d_{1} \left( {x_{1} ,t} \right) - \hat{x}_{e1} } \right) - \frac{{\omega_{1}^{2} \rho^{ - 2} z_{1}^{2} }}{{2\left( {1 - z_{1}^{2} } \right)^{2} }} - \tilde{\theta }^{T} \Gamma^{ - 1} \dot{\hat{\theta }} - \sum_{i = 1}^{n} {\omega_{i} \left\| {\varepsilon_{i} } \right\|^{2} } + \sum_{i = 1}^{n} {\varepsilon_{i}^{T} PB_{1} \tilde{\theta }^{T} \varphi_{i} } \hfill \\ & = - \sum_{j = 2}^{n} {\frac{{k_{j} z_{j}^{2} }}{{L_{j}^{2} - z_{j}^{2} }}} - \frac{{\rho^{ - 1} k_{1} z_{1}^{2} }}{{1 - z_{1}^{2} }} + \sum_{j = 2}^{n} {\frac{{z_{j} \tilde{\theta }^{T} \varphi_{j} \left( {\overline{x}_{j} } \right)}}{{L_{j}^{2} - z_{j}^{2} }}} + \frac{{\rho^{ - 1} z_{1} }}{{1 - z_{1}^{2} }}\tilde{\theta }^{T} \varphi_{1} \left( {\overline{x}_{1} } \right){ + }\sum_{k = 2}^{n} {\frac{{z_{k} \tilde{x}_{ek} \left( {\overline{x}_{k} ,t} \right)}}{{L_{k}^{2} - z_{k}^{2} }}} \hfill \\ &\quad -\, \sum_{k = 2}^{n} {\frac{{z_{k} \sum_{j = 1}^{k - 1} {\frac{{\partial \alpha_{k - 1} }}{{\partial x_{j} }}\left( {\tilde{\theta }^{T} \varphi_{j} \left( {\overline{x}_{j} } \right) + \tilde{x}_{ej} \left( {\overline{x}_{j} ,t} \right)} \right)} }}{{L_{k}^{2} - z_{k}^{2} }}} - \sum_{k = 2}^{n} {\frac{{z_{k}^{2} \sum_{j = 1}^{k - 1} {\left( {\omega_{j} \frac{{\partial \alpha_{k - 1} }}{{\partial x_{j} }}} \right)^{2} } }}{{2\left( {L_{k}^{2} - z_{k}^{2} } \right)^{2} }}} - \sum_{k = 2}^{n} {\frac{{\omega_{k}^{2} z_{k}^{2} }}{{2\left( {L_{k}^{2} - z_{k}^{2} } \right)^{2} }}} \hfill \\ &\quad +\, \frac{{\rho^{ - 1} z_{1} }}{{1 - z_{1}^{2} }}\tilde{x}_{e1} - \frac{{\omega_{1}^{2} \rho^{ - 2} z_{1}^{2} }}{{2\left( {1 - z_{1}^{2} } \right)^{2} }} - \tilde{\theta }^{T} \Gamma^{ - 1} \dot{\hat{\theta }} - \sum_{i = 1}^{n} {\omega_{i} \left\| {\varepsilon_{i} } \right\|^{2} } + \sum_{i = 1}^{n} {\varepsilon_{i}^{T} PB_{1} \tilde{\theta }^{T} \varphi_{i} } \hfill \\ \end{aligned} $$

(43)

Utilizing the Young’s inequality, we obtain

$$ \begin{aligned} \sum_{k = 2}^{n} {\frac{{z_{k} \tilde{x}_{ek} }}{{L_{k}^{2} - z_{k}^{2} }}} &\le \sum_{k = 2}^{n} {\frac{{\omega_{k}^{2} z_{k}^{2} }}{{2\left( {L_{k}^{2} - z_{k}^{2} } \right)^{2} }}} + \sum_{k = 2}^{n} {\frac{{\varepsilon_{k2}^{2} }}{2}} \hfill \\ \sum_{k = 2}^{n} {\frac{{z_{k} \sum_{j = 1}^{k - 1} {\frac{{\partial \alpha_{k - 1} }}{{\partial x_{j} }}\tilde{x}_{ej} \left( {\overline{x}_{j} ,t} \right)} }}{{L_{k}^{2} - z_{k}^{2} }}} &\le \sum_{k = 2}^{n} {\frac{{z_{k}^{2} \sum_{j = 1}^{k - 1} {\left( {\omega_{j} \frac{{\partial \alpha_{k - 1} }}{{\partial x_{j} }}} \right)^{2} } }}{{2\left( {L_{k}^{2} - z_{k}^{2} } \right)^{2} }}} + \sum_{k = 2}^{n} {\sum_{j = 1}^{k - 1} {\frac{{\varepsilon_{j2}^{2} }}{2}} } \hfill \\ \frac{{\rho^{ - 1} }}{{1 - z_{1}^{2} }}z_{1} \tilde{x}_{e1}& \le \frac{{\omega_{1}^{2} \rho^{ - 2} z_{1}^{2} }}{{2\left( {1 - z_{1}^{2} } \right)^{2} }} + \frac{{\varepsilon_{12}^{2} }}{2} \hfill \\ \end{aligned} $$

(44)

Substituting (28) and (44) into (43), then we have

$$ \begin{aligned} \dot{V}_{a} &\le - \sum_{j = 2}^{n} {\frac{{k_{j} z_{j}^{2} }}{{L_{j}^{2} - z_{j}^{2} }}} - \frac{{\rho^{ - 1} k_{1} z_{1}^{2} }}{{1 - z_{1}^{2} }} - \sum_{i = 1}^{n} {\omega_{i} \left\| {\varepsilon_{i} } \right\|^{2} } + \sum_{k = 2}^{n} {\sum_{j = 1}^{k - 1} {\frac{{\varepsilon_{j2}^{2} }}{2}} } + \sum_{k = 1}^{n} {\frac{{\varepsilon_{k2}^{2} }}{2}} \hfill \\ &\quad -\, \tilde{\theta }^{T} \left( {\Gamma^{ - 1} \dot{\hat{\theta }} - \sum_{j = 2}^{n} {\frac{{z_{j} \varphi_{j} \left( {\overline{x}_{j} } \right)}}{{L_{j}^{2} - z_{j}^{2} }}{ + }\sum_{k = 2}^{n} {\frac{{z_{k} \sum_{j = 1}^{k - 1} {\frac{{\partial \alpha_{k - 1} }}{{\partial x_{j} }}} \varphi_{j} \left( {\overline{x}_{j} } \right)}}{{L_{k}^{2} - z_{k}^{2} }} - \sum_{i = 1}^{n} {\varepsilon_{i}^{T} PB_{1} \varphi_{i} - \frac{{\rho^{ - 1} z_{1} }}{{1 - z_{1}^{2} }}\varphi_{1} \left( {\overline{x}_{1} } \right)} } } } \right) \hfill \\ &\le - \sum_{j = 2}^{n} {\frac{{k_{j} z_{j}^{2} }}{{L_{j}^{2} - z_{j}^{2} }}} - \frac{{\rho^{ - 1} k_{1} z_{1}^{2} }}{{1 - z_{1}^{2} }} - \sum_{i = 1}^{n} {\frac{{2\omega_{i} - n}}{2}\left\| {\varepsilon_{i} } \right\|^{2} } \hfill \\ &= - W \hfill \\ \end{aligned} $$

(45)

According to Lyapunov’s theorem, V_a is uniformly ultimately bounded; thus, errors z_i, $\tilde{\theta }$, and $\tilde{\varepsilon }$ are bounded. This further guarantees the boundedness of e₁. Moreover, the adaptive parameters $\hat{\theta }$ and $\hat{x}_{ei}$ are all bounded. As x₁ = e(t) + x_1d(t), $z_{1} = e\left( t \right)/\rho \left( t \right)$, $\left| {z_{1} } \right| \le 1$ with Assumption 2 and (8), we have $\left| {x_{1} } \right| \le c_{1}$, and x₁ is bounded. α₁ in (12) is a function of x₁, z₁,$\hat{\theta }$,$\dot{x}_{1d}$ and $\hat{x}_{e1}$. Since the boundedness of x₁, z₁, $\hat{\theta }$, $\dot{x}_{1d}$ and $\hat{x}_{e1}$, α₁ is bounded. As $\left| {x_{2} } \right| \le \left| {\alpha_{1} } \right|_{\max } + \left| {z_{2} } \right|$ and $\left| {z_{2} } \right| \le L_{2}$, we obtain $x_{2} \le c_{2}$ and α₂ is bounded. Similarly,$\left| {x_{i + 1} } \right|$, α_i, i = 3, …, n-1 and the control input u are bounded. Consequently, all signals in the closed-loop system are bounded, prescribed performance tracking is obtained and full states are ensured to remain in the constrained field.

Appendix 2

Proof of Theorem 2. If the disturbances d_i, i = 1,..., n, are time-variant, x_ei = $d_{i} \left( {\overline{x}_{i} ,t} \right) + \tilde{\theta }^{T} \varphi_{i} \left( {\overline{x}_{i} } \right)$. With (6), differentiating V_b defined in (29), we have

$$ \dot{V}_{b} = \dot{V}_{n} + \sum_{i = 1}^{n} {\left( {\frac{1}{2}\omega_{i} \varepsilon_{i}^{T} A^{T} P\varepsilon_{i} + \frac{1}{2}\omega_{i} \varepsilon_{i}^{T} PA\varepsilon_{i} + \varepsilon_{i}^{T} PB_{2} \frac{{h_{i} \left( t \right)}}{{w_{i} }}} \right)} $$

(46)

As $A^{T} P + PA = - 2I$, noting (23), (25) and (28), we have

$$ \begin{aligned} \dot{V}_{b} &\le \dot{V}_{n} - \sum_{i = 1}^{n} {\omega_{i} \left\| {\varepsilon_{i} } \right\|^{2} } + \sum_{i = 1}^{n} {\varepsilon_{i}^{T} PB_{2} \frac{{h_{i} \left( t \right)}}{{\omega_{i} }}} \hfill \\ &\le - \sum_{j = 2}^{n} {\frac{{k_{j} z_{j}^{2} }}{{L_{j}^{2} - z_{j}^{2} }}} - \frac{{\rho^{ - 1} k_{1} z_{1}^{2} }}{{1 - z_{1}^{2} }}{ + }\sum_{k = 2}^{n} {\frac{{z_{k} \left( {d_{k} \left( {\overline{x}_{k} ,t} \right) + \tilde{\theta }^{T} \varphi_{k} \left( {\overline{x}_{k} } \right) - \hat{x}_{ek} } \right)}}{{L_{k}^{2} - z_{k}^{2} }}} \hfill \\ &\quad -\, \sum_{k = 2}^{n} {\frac{{z_{k} \sum_{j = 1}^{k - 1} {\frac{{\partial \alpha_{k - 1} }}{{\partial x_{j} }}\left( {\tilde{x}_{ej} \left( {\overline{x}_{j} ,t} \right)} \right)} }}{{L_{k}^{2} - z_{k}^{2} }}} - \sum_{k = 2}^{n} {\frac{{z_{k}^{2} \sum_{j = 1}^{k - 1} {\left( {\omega_{j} \frac{{\partial \alpha_{k - 1} }}{{\partial x_{j} }}} \right)^{2} } }}{{2\left( {L_{k}^{2} - z_{k}^{2} } \right)^{2} }}} - \sum_{k = 2}^{n} {\frac{{\omega_{k}^{2} z_{k}^{2} }}{{2\left( {L_{k}^{2} - z_{k}^{2} } \right)^{2} }}} \hfill \\ &\quad+\, \frac{{\rho^{ - 1} z_{1} }}{{1 - z_{1}^{2} }}\left( {d_{1} \left( {x_{1} ,t} \right) + \tilde{\theta }^{T} \varphi_{1} \left( {\overline{x}_{1} } \right) - \hat{x}_{e1} } \right) - \frac{{\omega_{1}^{2} \rho^{ - 2} z_{1}^{2} }}{{2\left( {1 - z_{1}^{2} } \right)^{2} }} - \sum_{i = 1}^{n} {\omega_{i} \left\| {\varepsilon_{i} } \right\|^{2} } + \sum_{i = 1}^{n} {\varepsilon_{i}^{T} PB_{2} \frac{{h_{i} \left( t \right)}}{{\omega_{i} }}} \hfill \\ &\le - \sum_{j = 2}^{n} {\frac{{k_{j} z_{j}^{2} }}{{L_{j}^{2} - z_{j}^{2} }}} - \frac{{\rho^{ - 1} k_{1} z_{1}^{2} }}{{1 - z_{1}^{2} }} - \sum_{i = 1}^{n} {\omega_{i} \left\| {\varepsilon_{i} } \right\|^{2} } + \sum_{j = 2}^{n} {\sum_{k = 1}^{j - 1} {\frac{{\varepsilon_{k2}^{2} }}{2}} } + \frac{1}{2}\sum_{i = 1}^{n} {\left\| {\varepsilon_{i} } \right\|^{2} } + \sum_{i = 1}^{n} {\frac{{\left\| {\varepsilon_{i} } \right\|^{2} }}{2}} + \sum_{i = 1}^{n} {\frac{{\left\| {PB_{2} } \right\|^{2} \left| {h_{i} \left( t \right)} \right|^{2} }}{{2\omega_{i}^{2} }}} \hfill \\ &\le - \sum_{j = 2}^{n} {\frac{{k_{j} z_{j}^{2} }}{{L_{j}^{2} - z_{j}^{2} }}} - \frac{{\rho^{ - 1} k_{1} z_{1}^{2} }}{{1 - z_{1}^{2} }} - \sum_{i = 1}^{n} {\frac{{2\omega_{i} - n - 1}}{2}\left\| {\varepsilon_{i} } \right\|^{2} } + \sum_{i = 1}^{n} {\frac{{\left\| {PB_{2} } \right\|^{2} \left| {h_{i} \left( t \right)} \right|^{2} }}{{2\omega_{i}^{2} }}} \hfill \\ \end{aligned} $$

(47)

As $\log \frac{{L_{j}^{2} }}{{L_{j}^{2} - z_{j}^{2} }} \le \frac{{z_{j}^{2} }}{{L_{j}^{2} - z_{j}^{2} }}$ in the interval z_j < L_j [42], then

$$ \begin{gathered} \dot{V}_{b} \le - \sum_{j = 2}^{n} {k_{j} \log \frac{{L_{j}^{2} }}{{L_{j}^{2} - z_{j}^{2} }}} - \rho^{ - 1} k_{1} \log \frac{1}{{1 - z_{1}^{2} }} - \sum_{i = 1}^{n} {\frac{{2\omega_{i} - n - 1}}{{2\lambda_{\max } \left( P \right)}}\varepsilon_{i}^{T} P\varepsilon_{i} } + \sigma \hfill \\ \le - \lambda V_{a} + \sigma \hfill \\ \end{gathered} $$

(48)

which leads to (30). Similar to the proof of Theorem 1, all signals in the closed-loop system are also bounded and prescribed performance tracking is obtained without violation of constraints of the full states.