Finite-time stability of nonlinear systems with state-dependent delayed impulses

Abstract

This paper addresses the issue of finite-time stability (FTS) and finite-time contractive stability (FTCS) of nonlinear systems involving state-dependent delayed impulsive perturbation. Several sufficient conditions are obtained by using theories of impulsive control and Lyapunov stability. The relation between impulsive perturbation and state-dependent delay is established to achieve FTS and FTCS. For time-varying nonlinear system and nonlinear system with fixed parameters, we derive some sufficient conditions based on the main thought of this paper, respectively. Finally, three numerical examples are provided to illustrate the effectiveness and validity of achieved results.

1 Introduction

In plenty cases of practical situations, there should consider the behavior of systems over a period of time, which is finite. For instance, in the process of some chemical experiments, will the pressure or humidity or other parameters be kept within suitable bounds in a fixed time interval? Furthermore, under the circumstance of launching a satellite from neighborhood of a place A to neighborhood of the destination D, will the satellite be placed into the appropriate orbit? Thus, Kamenkov [7] introduced the concept of FTS in 1953. Dorato pointed out that FTS is a much more natural concept of “stability” in contrast with classical Lyapunov stability [3]. Specifically, there are two main aspects of differences. First, FTS processes systems which operating time is limited to a finite-time interval. Second, a prescribed bound of variables is essentially required by FTS. It should be emphasized that there is another concept of FTS, which has been extensively considered in mountains of publications, e.g., [2, 5, 10, 12, 26, 28, 38]. The latter FTS refers to the case that states of a system converge to the equilibrium at setting time, which is finite. A great variety of research regarding FTS has been devoted to because of its wide range of applications over many practical areas. Authors in [16] investigated the problem of FTS for time-varying systems by applying the Lyapunov–Razumikhn technique to deal with the time delay. In particular, this paper deeply investigated FTS for linear time-varying systems with time-varying parameters by constructing an auxiliary function. In [26], the concept of FTS was developed into the interconnected impulsive switched system and the problem of FTS for interconnected switching systems with impulses was researched. In 1967, Weiss and Infante presented the concept of FTCS to describe the state of a system operates within a smaller specified bound, compared with the initial one, at some instant $\sigma <T$ under the premise of FTS [33]. Thereafter, there has been considerable research concerning the FTCS [27].

The phenomenon of impulses is one of the indispensable topics when scientists and researchers investigate the real world, such as pharmacokinetics, transition of satellite orbit, frequency modulate systems, and secure communication [15, 29, 36]. In these cases, the impulsive differential equation (IDE) provides a natural way to describe systems with discontinuous motions. In 1989, Lakshmikantham and Simeonov [8] presented some general results of the IDE, which provided a researching foundation for the follow-up studies. After then, the domain of IDE has been a hot issue over decades and been broadly studied pertaining to the stability and other properties of solutions to IDE, see [1, 17, 18]. Research on the stability of impulsive systems generally can be split into two groups. One group considers the fixed-time impulses [11, 20, 31], and the other one pays particular attention to the variable-time impulses [32, 37]. There has been a lot of interesting research on the FTS or finite-time synchronization of impulsive systems. Author in [21] presented a general approach to analyze the key point for FTS and fixed-time convergence for the impulsive systems. Issues of FTS for nonlinear systems with impulsive effects were investigated in [22] via the method of average dwell time.

Delayed impulses is a notion to depict the scenario that states at impulsive moments are not merely dependent on current states of the system but as well the historical ones. For example, in the process of information transfer via the impulsive control, there exist sampling and transmission delays caused by data rate of the link [24]. Most existing studies concern the time delay in impulses either fixed or in the form of integral. In [19], the synchronization issue of complex dynamical networks via pinning impulsive control was considered. Delays in impulses were assumed as $\tau _k$, meaning that different impulsive instants may have different scale of delays which is more suitable to depict practical situation. Another synchronization issue of chaotic neural networks with delayed impulses was studied in [34]. Distributed time delay was taken into consideration in impulsive input, in other words, states of impulsive instants rely on the historical period of states of the system. Authors in [30] investigated the issue of exponential synchronization of coupled Lur’e networks involving proportional delay. The proportional delay considered in Ref. [30] is a type of unbounded time-varying delay. While in many cases, the time delay may differ based on states of the system. For instance, in a sampling and impulsive control system, the data needed to be frequently sampled if states of the system increase sharply for better control performance; while the states of the system run steadily, the sample period can be longer for lower control cost. Thus, the notion of state-dependent delay came into researcher’s vision. Li in [13] brought up a kind of state-dependent delay $\tau =\tau (t_k,\ x(t_k^-))$, where the scale of time-delay is determined by historical states of the system. In [13], the authors provided some sufficient criteria of locally uniform stability, locally uniformly asymptotical stability and locally exponential stability of nonlinear differential systems under the effects of state-dependent delayed impulses. Besides, from the viewpoint of control, authors presented some interesting results with respect to the issue of stabilities of nonlinear systems via state-dependent delayed impulsive control [14]. Although both issues of state-dependent delayed impulsive perturbation and control of nonlinear systems were investigated and some novel results were obtained, there have been rare research concerning those issues in the framework of FTS so far.

Hinted by the above discussion, we shall address the problem of FTS and FTCS for nonlinear systems with the state-dependent delayed impulsive perturbation. By employing theories and techniques stem from the impulsive differential equation, we derive some sufficient conditions to ensure the FTS and FTCS of nonlinear systems with state-dependent delayed impulses. We drop the restriction of smoothness on the state-dependent delay. Alternatively, we use a ${\mathcal {K}}$ function to constrain the delay term. Furthermore, we estimate the Lyapunov function which is subjected to the state-dependent delayed impulsive perturbation via the comparison principle. The rest of this article is structured as follows. Some notions and basic definitions which will be used afterward are introduced in Sect. 2; in Sect. 3, we analyze the issue of FTS and FTCS for nonlinear systems with state-dependent delayed impulsive perturbation and obtain some sufficient criteria; we offered three numerical examples in Sect. 4 to illustrate the validity of our results; conclusions are concluded in Sect. 5 together with further work.

2 Preliminaries

Notations $\Vert \cdot \Vert$ is a notation of the Euclidean norm of n-dimensional real spaces ${\mathbb {R}}^n$. ${\mathbb {R}}$ denotes the set of real numbers. ${\mathbb {R}}_+$ and ${\mathbb {Z}}_+$ are the sets of positive real and integers, respectively. ${\mathbb {R}}^{n\times m}$ represents the $n\times m$-dimensional real spaces. Matrix $\mathbf {\Gamma }> 0$, means the matrix $\mathbf {\Gamma }$ is symmetric and positive definite. $\mathbf {\Gamma }^T$ is the transpose of the matrix $\mathbf {\Gamma }$. $\mathbf {\Gamma }^{-1}$ denotes the inverse of $\mathbf {\Gamma }$. For symmetric matrices ${\mathscr {M}}$ and ${\mathscr {N}}$, ${\mathscr {M}}>{\mathscr {N}}$ indicates that ${\mathscr {M}}-{\mathscr {N}}$ is positive and definite. I stands for the identity matrix with appropriate dimensions. ${\varLambda }=\{1,\ 2,\ldots ,n\}$. $\star$ denotes the symmetric block in a symmetric matrix. ${\mathcal {K}}=\{f(\cdot )\in C| \, f(0)=0, \, \forall x>0,\ f(x)>0 \, \hbox {and} \, f \, \hbox {is strictly increasing in} \, x\}$. For any set $I\subseteq {\mathbb {R}}$ containing the origin and the set $D\subseteq {\mathbb {R}}$, $C(I,\ D)=\{f:I\rightarrow D$ and f is continuous$\}$. $C_{\xi }\doteq C([t_0-\xi ,\ t_0],\ {\mathbb {R}}^n)$ equipped with the norm $\Vert \psi \Vert _{\xi }=\hbox {sup}_{s\in [t_0-\xi ,\ t_0]} \Vert \psi (s)\Vert$.

Consider the nonlinear system subject to impulses involving state-dependent delay, described by

$$\begin{aligned} \left\{ \begin{array}{lllll} {\dot{x}}(t)=f(t,\ x(t)),\ t\ge t_0\ge 0,\ t\ne t_k,\\ x(t_k)=J_k(t_k^--\tau ,\ x(t_k^--\tau )), \\ \tau =\tau (t_k,\ x(t_k^-)), k\in {\mathbb {Z}}_+ \\ x_{t_0}=\psi , \end{array}\right. \end{aligned}$$

(1)

where $x\in {\mathbb {R}}^n$ is the state vector, $f\in C({\mathbb {R}}_+\times {\mathbb {R}}^n,\ {\mathbb {R}}^n)$, $J_k \in C( {\mathbb {R}}\times {\mathbb {R}}^n,\ {\mathbb {R}}^n)$, $k\in {\mathbb {Z}}_+$, $\tau \in C({\mathbb {R}}_+\times {\mathbb {R}}^n,\ [0,\ \xi ])$, $x_{t_0}=\{x(t+s):\ s\in [t_0-\xi ,\ t_0]\}$, $0\le \tau \le +\infty$. $\psi \in C_{\xi }$ is the initial condition. To exclude the Zeno phenomenon, impulsive instants $t_k$ satisfy $0\le t_0<t_1<\cdots <t_k\rightarrow +\infty$, as $k\rightarrow \infty$, $k\in {\mathbb {Z}}_+$. Without loss of generality, we assume that each solution of (1) is right continuous, that is, $\lim _{t\rightarrow t_k^+}x(t)=x(t_k)$.

Suppose that the function f satisfies conditions (H1)–(H3) in Ref. [18], so that solutions of the system (1) exist. Assume that $x(t)=x(t,\ t_0, \, \psi )$ is a solution of (1) started from the point $(t_0,\ \psi )$. Furthermore, for any $t\ge t _0$, $f(t,\ x)=0$ and $J_k(t,\ x)=0$, iff $x=0$, $k\in {\mathbb {Z}}_+$. In this case, the system (1) always has a trivial solution $(x=0)$. Some basic definitions which will be used in the next section are given in the following.

Definition 1

Function V: $[t_0-\xi ,\ \infty )\times {\mathbb {R}}^n\rightarrow {\mathbb {R}}_+$, is said to be included in the class ${\mathcal {V}}$ if

• 1. V is continuous on $[t_{k-1},\ t_k)\times {\mathbb {R}}^n$ and

  $$\begin{aligned} \displaystyle \lim \limits _{(m,\ n)\rightarrow (m^-,\ n)}V(t,\ x)=V(m^-,\ n); \end{aligned}$$

• 2. $V(t,\ x)$ is locally Lipchitiz in x with $V(t,\ 0)\equiv 0$.

Definition 2

[4] Given three positive constants $\alpha ,\ \beta$, T, with $\alpha <\beta$. System (1) is said to be FTS with respect to $(\alpha ,\ \beta ,\ T )$, provided that for any trajectory x(t), the condition $\Vert \psi \Vert _\xi <\alpha$ indicates that $\Vert x(t)\Vert <\beta$, for all $t\in [t_0,\ t_0+T]$.

Remark 1

It should be strongly stressed that $\alpha$, $\beta$, T are all a prior in a relevant problem. What is worth noting is that FTS differs from the concept of stability in the sense of Lyapunov [23]. A system which is FTS can be not Lyapunov stability, and vice versa. FTS requires a solution to a given problem stay within the prescribed bound over finite-time interval. Next, the finite-time analog of asymptotical stability is introduced as FTCS.

Definition 3

[33] Given five positive constants $\alpha ,\ \beta$, $\gamma ,\ \sigma$ and T, with $\gamma<\alpha <\beta$ and $\sigma \in (0,\ T)$, system (1) is FTCS with respect to $(\alpha ,\ \beta ,\ \gamma ,\ \sigma ,\ T)$, if $\Vert \psi \Vert _{\xi }<\alpha$ implies

• (1) $\Vert x(t)\Vert <\beta ,\ \forall t\in [t_0,\ t_0+T]$;

• (2) $\Vert x(t)\Vert <\gamma ,\ \forall t\in [t_0+\sigma ,\ t_0+T]$.

Remark 2

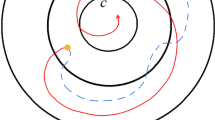
FTS identifies a case that the state of a system begins within a given initial bound and will operate below an assigned bound over finite time, as is shown in Fig. 1. Moreover, the concept of FTCS characterizes the “contractive behavior” of the state based on Definition 3, that is, the state will additionally enter a smaller prescribed bound compared with initial one before the terminal time. Illustration of FTCS mentioned above is given by Fig. 2 in trajectory behavior. Therefore, FTCS requires stronger conditions in comparison with FTS.

Fig. 1

Trajectory of the case of FTS

Fig. 2

Trajectory of the case of FTCS

3 Main results

In this section, we shall present some Lyapunov-based conditions for both FTS and FTCS of nonlinear system (1). For the investigating purpose, we claim that $\alpha ,\ \beta ,\ \gamma ,\ \sigma ,\ T$ are all pre-given positive constants with $\gamma<\alpha <\beta$, $t_0<\sigma <T$. We always assume the initial condition satisfy $0<\Vert \psi \Vert <\alpha$.

Theorem 1

Suppose that there exist constants $\mu _k\ge 1,\ k\in {\mathbb {Z}}_+,\ \delta \in {\mathbb {R}}_+$, functions $\omega _1,\ \omega _2,\ \kappa \in {\mathcal {K}}$, $V\in {\mathcal {V}}$, $L\in C({\mathbb {R}}_+,\ {\mathbb {R}}_+)$ and $H\in C({\mathbb {R}},\ {\mathbb {R}}_+)$, such that

• (I) $\omega _1(\Vert x\Vert )\le V(t,\ x)\le \omega _2(\Vert x\Vert )$, $\forall t\in [t_0-\xi ,\ t_0+T];$

• (II) $D^+V(t,\ x(t))\le -H(t)L(V(t,\ x(t))$, $t\in [t_{k-1}$, $t_k);$

• (III) $V(t_k,\ x(t_k))\le \mu _k V(t_k^--\tau ,\ x(t_k^--\tau ))$, $\tau =\tau (t_k,\ x(t_k^-))$, $k\in {\mathbb {Z}}_+$, furthermore $x(t)=x(t,\ t_0,\ \psi )$ is the solution of the system (1) through $(t_0,\ \psi )$;

• (IV) $\tau (t,\ u)\le \kappa (\Vert u\Vert )$, $t\in {\mathbb {R}}_+,\ u\in {\mathbb {R}}^n$;

• (V) $ln\mu _k+\displaystyle \int ^{t_k}_{t_k-{\mathscr {K}}}\sup _{u\in (0,\ \omega _2(\alpha ))}H(s)\frac{L(u)}{u}\mathrm{d}s \le \delta \displaystyle \int ^{t_k}_{t_k-\eta } \inf _{u\in (0,\ \omega _2(\alpha ))}H(s)\frac{L(u)}{u}\mathrm{d}s$, where ${\mathscr {K}}=\kappa \left( \omega _1^{-1}(\omega _2(\alpha ))\right)$, $\eta \doteq \hbox {inf}_{k\in {\mathbb {Z}}_+}\{t_k-t_{k-1}\};$

• (VI) $(\delta -1)\displaystyle \int ^t_{t_0} \displaystyle H(s)\frac{L(u)}{u}\mathrm{d}s\le \ln \displaystyle \frac{\omega _1(\beta )}{ \omega _2(\alpha )}$, $\forall t\in [t_0, t_0+T]$.

Then, system (1) is FTS w.r.t. $(\alpha ,\ \beta ,\ T)$.

Additionally, if

$$\begin{aligned} (1-\delta )\displaystyle \int ^{t_0+\sigma }_{t_0} \displaystyle H(s)\frac{L(u)}{u}\mathrm{d}s\ge |\ln \displaystyle \frac{\omega _1(\gamma )}{\omega _2(\alpha )}|, \end{aligned}$$

(2)

then, the system (1) is FTCS w.r.t. $(\alpha ,\ \beta , \gamma ,\ \sigma , T)$

Proof

Let x(t) denote the solution of system (1) through $(t_0,\ \psi )$. Define the Lyapunov function as $V(t)=V(t, x(t))$.

To begin, we shall verify

$$\begin{aligned} V(t)>0,\ \forall t\ge t_0-\xi . \end{aligned}$$

(3)

For $t\in [t_0-\xi ,\ t_0]$, because of the assumption on the initial condition that $0<\Vert \psi \Vert <\alpha$, it is obvious that $V(t)>0$.

For $t\in [t_0,\ t_1)$, $\psi (t_0)\ne 0$ implies $V(t)>0$. Suppose $V(t_1^+)=0$, that is,

$$\begin{aligned} x(t_1^+)=J_1(t_1^--\tau ,\ x(t_1^--\tau _1))=0, \end{aligned}$$

where $\tau _1=\tau (t_1,\ x(t_1^-))$, which yields that $x(t_1^--\tau _1)=0$. It contradicts the above induction. so $V(t_1^+)>0$, and

$$\begin{aligned} V(t)>0,\ \forall t\in [t_1,\ t_2). \end{aligned}$$

Utilizing this method iteratively, we can show that the inequality (3) holds for all $t\ge t_0-\xi$.

Next, we make the following claim. For $t\ge t_0$,

$$\begin{aligned} V(t)&\le \displaystyle \prod \limits _{t_0<t_k\le t}\mu _k \omega _2(\Vert \psi \Vert _{\xi }) \nonumber \\&\quad \times \exp \left( -\int _{t_0}^{t}H(s)\frac{L(V(s))}{V(s)}\mathrm{d}s\right) \nonumber \\&\quad \times \exp \left( \sum \limits _{t_0<t_k\le t}\int _{t_k-\tau (t_k,\ x(t_k^-))}^{t_k}H(s)\frac{L(V(s))}{V(s)}\mathrm{d}s\right) . \end{aligned}$$

(4)

For simple representation, we define ${\mathbb {L}}(s,\ u)=H(s)\displaystyle \frac{L(u)}{u}$. The proof of (4) is formulated based on the mathematical induction. For $t\in [t_0,\ t_1)$, it is clear that

$$\begin{aligned} V(t)\le V(t_0)\le \omega _2(\Vert \psi \Vert _{\xi }), \end{aligned}$$

and

$$\begin{aligned} V(t)&\le V(t_0)\exp (-\int _{t_0}^t{\mathbb {L}}(s,\ V)\mathrm{d}s)\nonumber \\&\le \omega _2(\Vert \psi \Vert _{\xi }) \exp \left( -(1-\delta )\int ^{t}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) , \end{aligned}$$

(5)

which indicates that the inequality (4) holds for $t\in [t_0,\ t_1)$.

By condition (I), we can arrive that, for all $t\in [t_0,\ t_1)$,

$$\begin{aligned} V(t)\le \omega _2(\Vert \psi \Vert _{\xi }), \end{aligned}$$

and

$$\begin{aligned} \Vert x(t)\Vert \le \omega _1^{-1}\left( \omega _2(\Vert \psi \Vert _{\xi })\right) <\omega _1^{-1}\left( \omega _2(\alpha )\right) , \end{aligned}$$

which combining with condition (IV) derives that

$$\begin{aligned} \tau _1=\tau _1(t_1,\ x(t_1^-))\le \kappa (\Vert x(t_1^-) \Vert )\le {\mathscr {K}}. \end{aligned}$$

(6)

Using (6) and condition (V), we have

$$\begin{aligned}&\mu _1 \exp \left( \int ^{t_1}_{t_1-\tau _1}{\mathbb {L}}(s,\ V) \mathrm{d}s \right) \nonumber \\&\quad \le \mu _1 \exp \left( \int ^{t_1}_{t_1-{\mathscr {K}}}{\mathbb {L}}(s,\ V) \mathrm{d}s \right) \nonumber \\&\quad \le \exp \left( \delta \int ^{t_1}_{t_1-\eta }{\mathbb {L}}(s,\ V) \mathrm{d}s \right) \nonumber \\&\quad \le \exp \left( \delta \int ^{t_1}_{t_0}{\mathbb {L}}(s,\ V) \mathrm{d}s \right) . \end{aligned}$$

(7)

It then follows from condition (III) that

$$\begin{aligned} V(t_1)&\le \mu _1V(t_1^--\tau _1)\nonumber \\&\le \mu _1 \left\{ \begin{array}{llll} V(t_0)\exp \left( -\displaystyle \int ^{t_1-\tau _1}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) ,\ \\ t_1-\tau _1\ge t_0,\\ \omega _2(\Vert \psi \Vert _\xi ),\ t-\tau _1<t_0, \end{array}\right. \nonumber \\&\quad \le \mu _1 \left\{ \begin{array}{llll} V(t_0)\exp \left( -\displaystyle \int ^{t_1-\tau _1}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) ,\\ t_1-\tau _1\ge t_0,\\ \omega _2(\Vert \psi \Vert _\xi )\exp \left( -\displaystyle \int ^{t_1-\tau _1}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) ,\ \\ t-\tau _1<t_0, \end{array}\right. \nonumber \\&\quad \le \mu _1 \omega _2(\Vert \psi \Vert _\xi )\exp \left( -\displaystyle \int ^{t_1-\tau _1}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) \nonumber \\&\quad \le \mu _1 \omega _2(\Vert \psi \Vert _\xi )\exp \left( -\displaystyle \int ^{t_1}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) \nonumber \\&\qquad \times \exp \left( \displaystyle \int _{t_1-\tau _1}^{t_1}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) . \end{aligned}$$

(8)

For $t\in [ t_1,\ t_2)$,

$$\begin{aligned} V(t)\le&V(t_1) \exp (-\int ^{t}_{t_1}{\mathbb {L}}(s,\ V)\mathrm{d}s),\nonumber \\ \le&\mu _1 \omega _2(\Vert \psi \Vert _\xi )\exp \left( -\displaystyle \int ^{t}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) \nonumber \\&\times \exp \left( \displaystyle \int _{t_1-\tau _1}^{t_1}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) . \end{aligned}$$

(9)

Thus, (4) holds for $t\in [t_1,\ t_2)$. By substituting (7) into (9), we can get

$$\begin{aligned} V(t)\le \omega _2(\Vert \psi \Vert _\xi )\exp \left( -(1-\delta )\int ^{t}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) . \end{aligned}$$

As a consequence,

$$\begin{aligned} \omega _1(\Vert x\Vert )\le V(t)\le \omega _2(\Vert \psi \Vert _\xi ),\ \forall t\in [t_1,\ t_2), \end{aligned}$$

and

$$\begin{aligned} \Vert x(t)\Vert&\le \omega _1^{-1}\left( \omega _2(\Vert \psi \Vert _\xi )\right) \\&< \omega _1^{-1}\left( \omega _2(\alpha )\right) , \forall t\in [t_1,\ t_2). \end{aligned}$$

Suppose that (4) holds for $t\in [t_{l-1},\ t_l)$, $l\ge 2$, which implies

$$\begin{aligned} \left\{ \begin{array}{ll} V(t)&{}\le \displaystyle \prod _{k= 1}^{l-1}\mu _k\omega _2(\Vert \psi \Vert _\xi )\exp \left( -\displaystyle \int ^{t}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) \\ &{}\quad \times \exp \left( \displaystyle \sum _{k = 1}^{l-1}\displaystyle \int ^{t_k}_{t_k-\tau (t_k,\ x(t_k^-))}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) , \\ V(t)&{}\le \omega _2(\Vert \psi \Vert _\xi )\exp \left( -(1-\delta )\displaystyle \int ^{t}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) ,\\ \Vert x(t)\Vert &{}\le \omega _1^{-1}\left( \omega _2(\Vert \psi \Vert _\xi )\right) . \end{array} \right. \end{aligned}$$

(10)

The next thing to do is to verify that for $t\in [t_l,\ t_{l+1})$, the following inequalities hold,

$$\begin{aligned} \left\{ \begin{array}{ll} V(t)&{}\le \displaystyle \prod _{k= 1}^{l}\mu _k\omega _2(\Vert \psi \Vert _\xi )\exp \left( -\displaystyle \int ^{t}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) \\ &{}\quad \times \exp \left( \displaystyle \sum _{k = 1}^{l}\displaystyle \int ^{t_k}_{t_k-\tau (t_k,\ x(t_k^-))}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) , \\ &{}V(t)\le \omega _2(\Vert \psi \Vert _\xi )\exp \left( -(1-\delta )\displaystyle \int ^{t}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) ,\\ \Vert x(t)\Vert \le &{}\omega _1^{-1}\left( \omega _2(\Vert \psi \Vert _\xi )\right) . \end{array} \right. \nonumber \\ \end{aligned}$$

(11)

With the help of condition (III) and (10), we can get

$$\begin{aligned} V(t_l)&\le \mu _lV(t-\tau _l) \\&\le \mu _l \left\{ \begin{array}{llll} \displaystyle \prod _{k= 1}^{l-1}\mu _k\omega _2(\Vert \psi \Vert _\xi )\exp \left( -\displaystyle \int ^{t_l-\tau _l}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) \\ ~~~\times \exp \left( \displaystyle \sum _{k = 1}^{l-1}\displaystyle \int ^{t_k}_{t_k-\tau (t_k,\ x(t_k^-))}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) , \\ ~~~\left( t_l-\tau _l\ge t_{l-1}\right) , \\ \displaystyle \prod _{k= 1}^{l-2}\mu _k\omega _2(\Vert \psi \Vert _\xi )\exp \left( -\displaystyle \int ^{t_l-\tau _l}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) \\ ~~~\times \exp \left( \displaystyle \sum _{k = 1}^{l-2}\displaystyle \int ^{t_k}_{t_k-\tau (t_k,\ x(t_k^-))}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) , \\ ~~~\left( t_{l-2}\le t_l-\tau _l<t_{l-1}\right) , \\ \vdots \\ \omega _2(\Vert \psi \Vert _\xi ),\ t_l-\tau _l<t_0, \end{array}\right. \\&\le \mu _l \omega _2(\Vert \psi \Vert _\xi )\exp \left( -\displaystyle \int ^{t_l-\tau _l}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) \\&~~\times \exp \left( \displaystyle \sum _{k = 1}^{l-1}\displaystyle \int ^{t_k}_{t_k-\tau (t_k,\ x(t_k^-))}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) , \\&\le \mu _l \omega _2(\Vert \psi \Vert _\xi )\exp \left( -\displaystyle \int ^{t_l}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) \\&~~\times \exp \left( \displaystyle \sum _{k = 1}^{l}\displaystyle \int ^{t_k}_{t_k-\tau (t_k,\ x(t_k^-))}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) . \end{aligned}$$

As demonstrated before, for $t\in [t_l,\ t_{l+1})$, we have

$$\begin{aligned} V(t)&\le V(t_l^+)\exp \left( \int _{t_l}^t{\mathbb {L}}(s,\ V)\mathrm{d}s \right) \\&\le \displaystyle \prod _{k= 1}^{l}\mu _k\omega _2(\Vert \psi \Vert _\xi )\exp \left( -\displaystyle \int ^{t}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) \\&\quad \times \exp \left( \displaystyle \sum _{k = 1}^{l}\displaystyle \int ^{t_k}_{t_k-\tau (t_k,\ x(t_k^-))}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) . \end{aligned}$$

According to the fact that

$$\begin{aligned} \Vert x(t_l^-)\Vert \le \omega _1^{-1}\left( \omega _2(\Vert \psi \Vert _\xi )\right) , \end{aligned}$$

one can get

$$\begin{aligned} \tau _l=\tau (t_l,\ x(t_l^-))\le \kappa (\Vert x(t_l^-)\Vert )\le {\mathscr {K}}. \end{aligned}$$

By employing condition (V) successively, the following inequality can be derived

$$\begin{aligned}&\displaystyle \prod _{k= 1}^{l}\mu _k\exp \left( \displaystyle \sum _{k = 1}^{l}\displaystyle \int ^{t_k}_{t_{k}-\tau (t_k,\ x(t_k^-))}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) \\&~~\le \displaystyle \prod _{k= 1}^{l}\mu _k\exp \left( \displaystyle \sum _{k = 1}^{l}\displaystyle \int ^{t_k}_{t_{k}-{\mathscr {K}}}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) \\&~~\le \exp \left( \delta \displaystyle \int ^{t_k}_{t_{k}-{\mathscr {K}}}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) . \end{aligned}$$

Accordingly, for any $t\in [t_l,\ t_{l+1})$, with $t<t_0+T$,

$$\begin{aligned} V(t)\le \omega _2(\Vert \psi \Vert _\xi )\exp \left( -(1-\delta )\displaystyle \int ^{t}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) . \end{aligned}$$

(12)

Inserting the condition (VI) into (12), and using the condition (I), we could arrive that, for $t\in [t_0,\ t_0+T]$,

$$\begin{aligned} \omega _1(\Vert x(t)\Vert )&\le V(t)\\&<\omega _2(\alpha )\exp \left( -(1-\delta )\displaystyle \int ^{t}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) ,\\&<\omega _1(\beta ), \end{aligned}$$

which implies that

$$\begin{aligned} \Vert x(t)\Vert <\beta ,\ \forall t\in [t_0,\ t_0+T]. \end{aligned}$$

Therefore, the system (1) is FTS w.r.t. $(\alpha ,\ \beta ,\ T)$.

If the additional condition (2) holds. Another step is to prove FTCS of system (1). Taking condition (I), (2) and (12) into consideration, one can get, for $t_0+\sigma \le t\le t_0+T$,

$$\begin{aligned} \omega _1(\Vert x(t)\Vert )&\le V(t)\\&\le \omega _2(\Vert \psi \Vert _\xi )\exp \left( -(1-\delta )\displaystyle \int ^{t_0+\sigma }_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) \\&\le \omega _2(\Vert \psi \Vert _\xi )\exp \left( -(1-\delta )\displaystyle \int ^{t}_{t_0}{\mathbb {L}}(s,\ V)\mathrm{d}s\right) \\&<\omega _1(\gamma ), \end{aligned}$$

which indicates

$$\begin{aligned} \Vert x(t)\Vert <\gamma , \forall t\in [t_0+\sigma ,\ t_0+T]. \end{aligned}$$

Then, the system (1) is FTCS with respect to $(\alpha ,\ \beta$, $\gamma ,\ \sigma ,\ T)$. The proof is completed. $\square$

Remark 3

In fact, condition (V) can be relaxed as follows

$$\begin{aligned}&ln\mu _k+\displaystyle \int ^{t_k}_{t_k-{\mathscr {K}}}H(s)\frac{L(u)}{u}\mathrm{d}s \\&\quad \le \delta \displaystyle \int ^{t_k}_{t_k-\eta }H(s)\frac{L(u)}{u}\mathrm{d}s, \end{aligned}$$

for any $u\in (0,\ \omega _2(\alpha ))$ and $k\in {\mathbb {Z}}_+$.

Remark 4

The crucial point of Theorem 1 is to handle the delay term in impulses. The delay is state-dependent, in other words, it varies in accordance with the past state of the system (1). Thereby, we established a relation between the delay term (${\mathscr {K}}$) and the impulsive perturbation (the impulsive strength $\mu _k$, and the lower bound of impulsive interval $\eta$) by introducing a parameter $\delta$ and constructing the condition (V) in Theorem 1. In addition, the choice of $\delta$ is also dependent on the prescribe bound, which could be reflected in condition (VI) and the additional condition (2).

Remark 5

The parameter $\delta$ corresponds the pre-given information of bounds, the impulsive perturbation and the state-dependent delay together and can be adjusted according to specific situations. Specifically, considering condition (VI) for the case that $\omega _1(\beta )<\omega _2(\alpha )$, the range of $\delta$ is restricted to $(0,\ 1)$. While if $\omega _1(\beta )\ge \omega _2(\alpha )$, the range of $\delta$ is ${\mathbb {R}}_+$.

Remark 6

Lots of publications have considered the problem of the stability for different kinds of systems, see [6, 9, 25, 35]. Compared with results in [13], firstly, we drop the restriction of smoothness on the delay function $\tau =\tau (x(t^-), t)$. A ${\mathcal {K}}$-class function $\kappa$ is used to constrain the state-dependent delay $\tau$. Secondly, we develop the local uniformly asymptotically stability of nonlinear systems with state-dependent delayed impulsive perturbation to the FTS and FTCS of which. It should be noted that both FTS and FTCS could be regarded as the local properties of solutions, since we just consider the boundedness of solution over finite-time interval.

Choose special forms of functions H(s) and L(u) in Theorem 1, the following results could be obtained.

Corollary 1

Suppose the condition (IV) in Theorem 1 holds. The system (1) is FTS w.r.t. $(\alpha ,\ \beta , T)$, if there exist positive constants $\omega _1,\ \omega _2,\ h,\ m$, $\mu \ge 1$, $\delta$ and functions $V\in {\mathcal {V}}$, $\kappa \in {\mathcal {K}}$, such that $\tau (u)\le \kappa (\Vert u\Vert ),\ u\in {\mathbb {R}}^n$, and the following conditions hold,

• (1) $\omega _1\Vert x\Vert ^m\le V(t,\ x)\le \omega _2\Vert x\Vert ^m$, $\forall x\in [t_0-\xi ,\ t_0+T];$

• (2) $D^+V(t,\ x(t)\le -h V(t,\ x(t)$, $t\in [t_{k-1},\ t_k);$

• (3) $V(t_k,\ x(t_k))\le \mu V(t_k^--\tau ,\ x(t_k^--\tau ))$, $\tau =\tau (t_k, x(t_k^-))$, $k\in {\mathbb {Z}}_+$;

• (4) $\mu \le \exp (h\delta \eta -h{\mathcal {M}})$, where ${\mathcal {M}}=\kappa (\displaystyle \root m \of {\frac{\omega _2 }{\omega _1}}\alpha )$, $\eta =\inf _{k\in {\mathbb {Z}}_+}\{t_k-t_{k-1}\};$

• (5) $(\delta -1)h(t-t_0)\le \displaystyle \ln \frac{\omega _1\beta ^m}{\omega _2\alpha ^m}$, $\forall t\in [t_0,\ t_0+T]$.

Then system (1) is FTS w.r.t. $(\alpha ,\ \beta ,\ T)$.

Furthermore, if

$$\begin{aligned} (1-\delta )h\delta \sigma \ge \displaystyle |\ln \frac{\omega _1\gamma ^m}{\omega _2\alpha ^m}|, \end{aligned}$$

system (1) is FTCS w.r.t. $(\alpha ,\ \beta ,\ \gamma ,\ \sigma ,\ T)$.

Corollary 2

Assume that conditions (I), (III), (IV) and (VI) in Theorem 1 are satisfied. Suppose $\delta \eta >{\mathscr {K}}$, and there exists function ${\hat{L}} \in C({\mathbb {R}}_+,\ {\mathbb {R}}_+)$, satisfying

$$\begin{aligned} D^+V(t)\le {\hat{L}}(V),\ t\in [t_{k-1},\ t_k). \end{aligned}$$

If the following inequality holds,

$$\begin{aligned} \displaystyle \frac{\sup \limits _{k\in {\mathbb {Z}}_+}\ln \mu _k}{\delta \eta -{\mathscr {K}}}\le \inf \limits _{u\in (0,\ \omega _2(\alpha ))}\frac{{\hat{L}}(u)}{u}, \end{aligned}$$

then the system (1) is FTS w.r.t. $(\alpha ,\ \beta ,\ T)$. In addition, the system (1) is FTCS w.r.t. $(\alpha ,\ \beta ,\ \gamma , \sigma ,\ T)$ with (2).

We now turn to the case of time-varying nonlinear systems and investigate the corresponding issue of FTS and FTCS. A type of time-varying nonlinear system is given as

$$\begin{aligned} \left\{ \begin{array}{lllll} {\dot{x}}(t)=-A(t)x(t)+B(t)g(x(t)), \\ t\ge t_0\ge 0,\ t\ne t_k,\\ x_{t_0}=\psi . \end{array}\right. \end{aligned}$$

(13)

The impulsive perturbation is given,

$$\begin{aligned} x(t_k)=I_kx(t_k^--\tau ),\ \tau =\tau (x(t_k^-)), \end{aligned}$$

(14)

where $A(t)=\left( a_{ij}(t)\right) _{n\times n}$, $B(t)=\left( \ b_{ij}(t)\right) _{n\times n}\in C({\mathbb {R}}_+$, ${\mathbb {R}}^{n\times n})$, and $I_k=\left( {\mathscr {I}}^{(k)}\right) _{n\times n},\ k \in {\varLambda }$. $g(x)=(g_1(x_1), g_2(x_2), \ldots , g_n(x_n))^T$, satisfying

$$\begin{aligned} |g_i(x)-g_i(y)|\le l_i|x-y|, \end{aligned}$$

where $x,\ y \in {\mathbb {R}}$ and $l_i>0,\ i\in {\varLambda }$ are Lipschitizian constants. Furthermore, we assume that $g_i(0)\equiv 0,\ i\in {\varLambda }$. Then system (13) can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{lllll} \dot{x_i}(t)=-\sum \limits _{j=1}^na_{ij}(t)x_j(t)+\sum \limits _{j=1}^nb_{ij}(t)g_j(x(t)), \\ t\ge t_0\ge 0,\ t\ne t_k,\\ x_i(t_k)=\sum \limits _{j=1}^n{\mathscr {I}}_{ij}^{(k)}x_j(t_k^--\tau ),\ \tau =(x(t_k^-)),\\ x_{t_0}=\psi . \end{array}\right. \end{aligned}$$

(15)

Theorem 2

Suppose that $a_{ii}(t)>0, i\in {\varLambda }$, and there exist constants $\delta >0$, $\mu _k\ge 1$ and functions ${\mathcal {H}}(t)\in C({\mathbb {R}}_+,\ {\mathbb {R}}_+)$, $V\in {\mathcal {V}},$ $\kappa \in {\mathcal {K}}$, complying with $\tau (u)\le \kappa (\Vert u\Vert ),\ u\in {\mathbb {R}}^n$, and the following conditions,

• (I)
  $$\begin{aligned} {\mathcal {H}}(t)\le & {} 2 \min \limits _i a_{ii}(t)-{\mathop {\mathop {\hbox {max}}\limits _{i}}\limits _{i\ne j}}\sum \limits _{j=1}^n|a_{ij}(t)|\\&- {\mathop {\mathop {\hbox {max}}\limits _{j}}\limits _{j\ne i}} \sum \limits _{i=1}^n|a_{ij}(t)| \\&-\max \limits _i\sum \limits _{j=1}^n|b_{ij}(t)|l_j- \max \limits _j\sum \limits _{i=1}^n|b_{ij}(t)|l_j; \end{aligned}$$

• (II) $\sum _{i=1}^n\sum _{j=1}^n({\mathscr {I}}_{ij}^{(k)})^2\le \mu _k,\ k\in {\mathbb {Z}}_+;$

• (III) $\ln \mu _k+\displaystyle \int _{t_k-{\mathcal {M}}}^{t_k}{\mathcal {H}}(s)\mathrm{d}s\le \delta \displaystyle \int _{t_k-\eta }^{t_k}{\mathcal {H}}(s)\mathrm{d}s$, where ${\mathcal {M}}=\kappa (\alpha ),\ \eta =\inf _{k\in {\mathbb {Z}}_+}\{t_k-t_{k-1}\}$;

• (IV) $(1-\delta )\displaystyle \int _{t_0}^{t_0+T}{\mathcal {H}}(s)\mathrm{d}s\le 2\ln \displaystyle \frac{\beta }{\alpha }$.

Then, system (15) is FTS w.r.t. $(\alpha ,\ \beta ,\ T)$. If the additional condition holds, that is,

$$\begin{aligned} (\delta -1)\int _{t_0}^{t_0+\sigma }{\mathcal {H}}(s)ds\ge 2|\ln \frac{\gamma }{\alpha }|. \end{aligned}$$

(16)

Then, system (15) is FTCS w.r.t. $(\alpha ,\ \beta ,\ \gamma ,\ \sigma ,\ T)$.

Proof

Choose the Lyapunov function with the form of

$$\begin{aligned} V(t)=\Vert x(t)\Vert ^2=\sum \limits _{i=1}^nx_i^2(t). \end{aligned}$$

Then take the derivative along the solution x(t) of system (15). Combining the condition (I), it yields that for $t\ne t_k$,

$$\begin{aligned}&D^+V(t)\nonumber \\&\quad = 2\sum \limits _{i=1}^nx_i(t){\dot{x}}_i(t)\nonumber \\&\quad =-2\sum \limits _{i=1}^n\sum \limits _{j=1}^na_{ij}(t) x_i(t)x_j(t) \nonumber \\&\qquad +2\sum \limits _{i=1}^n\sum \limits _{j=1}^nb_{ij}(t) x_i(t)g_j(x(t))\nonumber \\&\qquad \quad 2\sum \limits _{i=1}^na_{ii}(t)x_i^2(t)-2\sum \limits _{\begin{array}{c} i=1\\ i\ne j\end{array}}^n\sum \limits _{j=1}^na_{ij}(t)x_i(t)x_j(t)\nonumber \\&\qquad +2\sum \limits _{i=1}^n\sum \limits _{j=1}^nb_{ij}(t) x_i(t)g_j(x(t))\nonumber \\&\quad \le -2\sum \limits _{i=1}^na_{ii}(t)x_i^2(t) \nonumber \\&\qquad +{\mathop {\mathop {\hbox {max}}\limits _{i}}\limits _{i\ne j}}\sum \limits _{j=1}^n|a_{ij}(t)|\sum \limits _{i=1}^n x_i^2(t)\nonumber \\&\qquad +{\mathop {\mathop {\hbox {max}}\limits _{j}}\limits _{j\ne i}}\sum \limits _{i=1}^n|a_{ij}(t)| \sum \limits _{i=1}^n x_i^2(t) \nonumber \\&\qquad +\max \limits _i\sum \limits _{j=1}^n|b_{ij}(t)|l_j\sum \limits _{i=1}^n x_i^2(t)\nonumber \\&\qquad +\max \limits _j\sum \limits _{i=1}^n|b_{ij}(t)|l_j \sum \limits _{i=1}^nx_i^2(t)\nonumber \\&\quad \le -{\mathcal {H}}(t) V(t). \end{aligned}$$

(17)

When $t=t_k$, it follows from the impulsive perturbation function (14) and the condition (II) that

$$\begin{aligned} V(t_k)=&\sum \limits _{i=1}^nx_i(t_k)\nonumber \\ =&\sum \limits _{i=1}^n\sum \limits _{j=1}^n ({\mathscr {I}}_{ij}^{(k)})^2 x_j^2(t_k^--\tau )\nonumber \\ \le&\mu _k \sum \limits _{j=1}^nx_j^2(t_k^--\tau )\nonumber \\ =&\mu _k V(t_k^--\tau ). \end{aligned}$$

(18)

Base on Theorem 1, we can arrive that the system (15) is FTS w.r.t. $(\alpha ,\ \beta ,\ T)$. Moreover, with the help of formula (16), the system (15) could realize FTCS w.r.t. $(\alpha ,\ \beta ,\ \gamma ,\ \sigma ,\ T)$. The proof is completed. $\square$

Remark 7

For systems in practical implications, due to complex mechanisms and unmeasured disturbance, it is unavoidable to investigate dynamical behaviors of systems with time-varying parameters. Theorem 2 provides a possible way to analyze the FTS and the FTCS of time-varying system with state-dependent delayed impulsive perturbation based on the Lyapunov stability theory and the theories of the impulsive differential equation. However, it should be mentioned that we do not find a general way to construct the function ${\mathcal {H}}(t)$, namely, up to now, the function ${\mathcal {H}}(t)$ could only be chosen by trial and error. Besides, the choice of Lyapunov function as $V(t)=\Vert x(t)\Vert ^2$ in Theorem 2 is to simplify the calculation process. The Lyapunov function could also be taken in a more general form as $V(t)=x^T(t)Px(t),\ P>0\in {\mathbb {R}}^{n\times n}$. The detailed corresponding results are omitted here.

In what follows, we are concentrated on analyzing issues of FTS and FTCS of nonlinear systems with fixed parameters under state-dependent delayed impulsive perturbation. The model is described by

$$\begin{aligned} \left\{ \begin{array}{lllll} {\dot{x}}(t)=-Ax(t)+Bg(x(t)),\ t\ge t_0\ge 0,\ t\ne t_k,\\ x(t_k)=I_kx(t_k^--\tau ),\ \tau =\tau (x(t_k^-)),\\ x_{t_0}=\psi , \end{array}\right. \end{aligned}$$

(19)

where $A,\ B\in {\mathbb {R}}^{n\times n}$. The other illustrations of system (19) is same as those of the system (15). Applying the LMI technique, we can acquire the following corollary.

Corollary 3

If there exists a $n\times n$ positive and definite matrix P, a diagonal matrix $Q\in {\mathbb {R}}^{n\times n}$, $Q>0$, positive constants $h,\ \mu ,\ l_i,\ \delta$, functions $V\in {\mathcal {V}}$, $\kappa \in {\mathcal {K}}$, such that $\tau (u)\le \kappa (\Vert u\Vert ),\ u\in {\mathbb {R}}^n$, and the following conditions hold,

• (1)
  $$\begin{aligned} \left[ \begin{array}{ccc} -\mu P&{} I_k^TP\\ *&{}-P \end{array}\right] \le 0; \end{aligned}$$
• (2)
  $$\begin{aligned} \left[ \begin{array}{ccc} -PA-A^TP+L_gQL_g+h P&{} PB\\ *&{}-Q \end{array}\right] \le 0; \end{aligned}$$

  where $L_g=diag(l_1,\ l_2, \ldots , l_n).;$

• (3) $\mu \le \exp (h\delta \eta -h{\mathcal {M}})$, where ${\mathcal {M}}{=}\kappa (\displaystyle \sqrt{\frac{\lambda _{\mathrm{max}}(P) }{\lambda _{\mathrm{min}}(P)}}\alpha )$, $\eta =\inf _{k\in {\mathbb {Z}}_+}\{t_k-t_{k-1}\};$

• (4) $(\delta -1)h\delta (t-t_0)\le \ln \displaystyle \frac{\lambda _{\mathrm{min}}(P)\beta ^2 }{\lambda _{\mathrm{max}}(P)\alpha ^2}$, $\forall t\in [t_0,\ t_0+T]$.

Then, the system (19) is FTS w.r.t. $(\alpha ,\ \beta ,\ T).$

Furthermore, if

$$\begin{aligned} (1-\delta )h\sigma \ge |\ln \displaystyle \frac{\lambda _{\mathrm{min}}(P)\gamma ^2 }{\lambda _{\mathrm{max}}(P)\alpha ^2}|, \end{aligned}$$

the system (19) is FTCS w.r.t. $(\alpha ,\ \beta ,\ \gamma ,\ \sigma ,\ T)$.

Remark 8

Set the Lyapunov function $V(t)= x^T(t)$ Px(t). It is not complicated to obtain the above result, so the detailed proof is omitted here. Corollary 3 is derived in the framework of the LMI technique. The superiority of this method lying that it could be numerically solved by employing the LMI toolbox in the MATLAB software. In addition, it has less conservative compared with other methods since only the negative definiteness of the linear matrix could obtain the expected results instead of negativeness of every component.

4 Examples

In this section, we will provide three examples to demonstrate the validity and reliability of the above results in Segment 3.

Example 1

A one-dimensional nonlinear system with the effects of state-dependent delayed impulses is given as

$$\begin{aligned} \left\{ \begin{array}{lllll} {\dot{x}}(t)=-x(t)\displaystyle \frac{1}{1+|x(t)|},\ t\ge 0,\ t\ne t_k,\\ x(t_k)=(1.15+\displaystyle \frac{1}{10k})x(t_k^--\tau ),\ k\in {\varLambda },\\ x_{t_0}=\psi , \end{array}\right. \end{aligned}$$

(20)

where $\tau =0.1\cdot \sin t \cdot |x|$.

In this case, we consider that $\alpha =3.2,\ \beta =5,\ \gamma =2,\ \sigma =8.5,\ T=10$. Choose the Lyapunov function $V(t)=|x|$, then the functions $\omega _1(\cdot ),\ \omega _2(\cdot )$ can be chosen as $\omega _1(u)=\omega _2(u)=u,\ u\in {\mathbb {R}}_+$. Apparently, $H(t)=1$, $L(u)=u\cdot \displaystyle \frac{1}{1+u}$, $\kappa (u)=0.1|u|,\ u\in {\mathbb {R}}_+$ and ${\mathscr {K}}=0.33$.

Fig. 3

State trajectories of the system (20). a The case of FTS with $\eta =1$; b the case of FTCS with $\eta =1.1$; c the case of divergence with $\eta =0.8$

(I) FTS.

For the FTS of system (20), we choose $\delta =0.6$, $\mu =1.25$. According to Theorem 1, one may derive that $\eta =1$, in other words, the impulsive-time sequence satisfies $t_{k+1}-t_k\ge 1$, $k\in {\mathbb {Z}}_+$. For simulation, we take impulsive instants $t_k=1, 2, \ldots , k$, $k\in {\mathbb {Z}}_+.$ It can be shown from Fig. 3a that the system (20) is FTS w.r.t. $(3,\ 5,\ 10)$.

(II) FTCS.

If we choose $\delta =0.5$, $\eta =1.2$, which leads to the satisfaction of (2) in Theorem 1. We can conclude that the system (20) is FTCS w.r.t. $(3,\ 5, \, 2,\ 8.5,\ 10)$, which can be demonstrated by Fig. 3b with the impulsive instants are set as $t_k= 1.1k$, $k\in {\mathbb {Z}}_+$. However, if we change the impulsive interval slightly as $t_{k+1}-t_k=0.8$, and keep the other parameters as the same, it is easy to check this case does not satisfy Theorem 1. It can be observed from Fig. 3c that the state diverged from the bound $\beta =5$ sharply. In a word, the more frequently the impulsive perturbation occurs, the system is more easy to be divergent.

Remark 9

Figure 3a shows that the system is finite-time stability but not asymptotic stability, which can illustrate the difference between FTS and AS in the sense of Lyapunov.

It can be observed that the additional condition (2) resulting in a lager lower bound of impulsive interval, which means that impulsive perturbation should occur infrequently compared with the case of FTS to realize the FTCS.

Example 2

Consider the nonlinear systems (13) with the parameters

$$\begin{aligned} A(t)&=\left[ \begin{array}{ccc} 4+0.5e^{-t}&{}\quad -1\\ -1&{}\quad 4+e^{-t} \end{array}\right] ,\\ B(t)&=\left[ \begin{array}{ccc} 1+\sin (t)&{}\quad -\cos (t)\\ \sin (t)&{}\quad 1-\cos (t) \end{array}\right] , \end{aligned}$$

with the impulsive perturbation (14)

$$\begin{aligned} I_k=\displaystyle \frac{\sqrt{2}}{2}\left[ \begin{array}{ccc} \sin (k)&{}\quad -\cos (k)\\ \sin (\displaystyle \frac{1}{3k})&{}\quad -\cos (\displaystyle \frac{1}{3k}) \end{array}\right] . \end{aligned}$$

$\tau (x)=\sqrt{\displaystyle \frac{|x_1x_2|}{2}}$, $g_1(s)=g_2(s)=\tanh (s),\ s\in {\mathbb {R}}$. For this case, let $\alpha =4.5,\ \beta =6,\ \gamma =1,\ \sigma =6,\ T=8$. Note that $\kappa (u)=\displaystyle \frac{\Vert u\Vert }{2}$, $u\in {\mathbb {R}}^n$, $l_1=l_2=1$, $\mu _k=1.42$, ${\mathcal {M}}=2.25$. We choose $\delta =5$, ${\mathcal {H}}(t)=e^{-t}$. It follows from Theorem 2 that when $\eta \ge 0.9$, the system (15) is FTCS w.r.t. $(4.5,\ 6,\ 1,\ 6,\ 8)$. Here we take $\eta =0.9$, for numerical simulation; see Fig. 4. While if we change the impulsive interval slightly as $t_{k+1}-t_k=0.7$, and $\mu _k=2$, keep the other parameters unchanged. It is easy to verify that it does not satisfy Theorem 2, in other words under this circumstance, system (15) cannot be FTCS w.r.t. $(4.5,\ 6,\ 1,\ 6,\ 8)$, which is shown in Fig. 5. Note that in the $t-x_1-x_2$ plane, the phase portrait, which is shown in Fig. 5b, gives both the case of FTCS and not FTCS, where the only difference is the impulsive interval.

Fig. 4

a Trajectories of states $x_1(t)$, $x_2(t)$, and |x| of system (15); b phase portrait for the case of FTCS of system (15) with impulsive perturbation involving state-dependent delay

Fig. 5

a Trajectories of states of system (15) with $\eta =0.7$, $\mu =2$; b phase portraits for cases of system (15) with $\eta =1.3$, and $\eta =0.7$

Remark 10

It should be noticed that Theorem 2 provides a feasible method to explore the finite-time stability for time-varying systems, but these conditions are somehow conservative. In the future, we would like to investigate this problem further to obtain some principles with less conservative and to get a general way to construct the function ${\mathcal {H}}(t)$.

Fig. 6

a State trajectories of $x_i(t)$, $i=1,2,3$, and |x| in Example 3 with the initial bound $\alpha =5.5$; b Trajectories of |x| of the system (19) with different initial bounds $\alpha =5.5$ and $\alpha =8.5$

Example 3

Next, we consider a 3-D nonlinear system (19) with $g=0.5\Vert x+1\Vert -0.5\Vert x-1\Vert$, $\tau (x)=\displaystyle \frac{\sqrt{x^Tx}}{2}$. Parameter matrices $A,\ B$ are given by

$$\begin{aligned} A=\left[ \begin{array}{ccc} 2.4&{}\quad -0.2&{}\quad -0.8\\ -0.48&{}\quad 2.3&{}\quad -1.5\\ -0.5&{}\quad -0.8&{}\quad 2.5 \end{array}\right] ,\\ B=\left[ \begin{array}{ccc} -0.15&{}\quad 0.2&{}\quad -0.1\\ -0.5&{}\quad 0.6&{}\quad 0.3\\ -0.2&{}\quad -0.3&{}\quad -0.8 \end{array}\right] . \end{aligned}$$

The impulsive matrix is

$$\begin{aligned} I_k=\left[ \begin{array}{ccc} 0.5+\sin (k)&{}\quad 0&{}\quad 0\\ 0&{}\quad \tanh (k)&{}\quad 0\\ 0&{}\quad 0&{}\quad 1+e^{-k} \end{array}\right] . \end{aligned}$$

Obviously, $l_j=1,\ \kappa (u)=\displaystyle \frac{\Vert u\Vert }{2},\ u\in {\mathbb {R}}^n$. Choose $\alpha =5.5,\ \beta =8,\ \gamma =1,\ \sigma =6,\ T=10$, $\delta =0.9,\ \eta =1.1,\ \mu =4$, ${\mathcal {M}}=3.6$, and $h=4$, a feasible solution solved by the MATLAB software is

$$\begin{aligned} P=\left[ \begin{array}{ccc} 0.606 &{}\quad 0.063&{}\quad 0.158\\ 0.063&{}\quad 0.559&{}\quad 0.204\\ 0.158&{}\quad 0.204&{}\quad 0.686 \end{array}\right] ,\\ Q=\left[ \begin{array}{ccc} 0.565 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0.565 &{}\quad 0\\ 0 &{}\quad 0&{}\quad 0.565 \end{array}\right] . \end{aligned}$$

Then, it follows from Corollary 3 that system (19) with the state-dependent delayed impulsive perturbation is FTCS w.r.t. $(5.5,\ 8,\ 1,\ 6,\ 10)$, see Fig. 6a. If we slightly change the initial bound $\alpha =8.5$ and keep other parameters as the same, conditions in Corollary 3 do not hold at all. Figure 6b reflects visually that in this case the system (19) is not FTCS w.r.t. $(8.5,\ 9,\ 1,\ 6,\ 10)$. Larger initial bounds may lead to invalidity of FTCS because of the dependence of solution on initial value.

5 Conclusions

In this paper, we have studied the issue of FTS and FTCS for nonlinear systems with impulses involving state-dependent delay. Some sufficient conditions are obtained by employing techniques based on the theory of impulsive differential equation. The key point of this paper lies in tackling the past information in delay terms and adopting it into the construction of Lyapunov function as a constraint. The reliability of obtained results is demonstrated by three numerical examples. As is known to all, time-varying systems are noticeably sophisticated to be investigated, due to their varied structure. We present a viable way to analyze the FTS and FTCS of the time-varying nonlinear systems with state-dependent delayed impulses. It should be noted that a more general model, which is consist of the state of $x(t_k^-)$ at impulsive instants, that is, the impulsive jump function has the form $x(t)=I_k(t_k^-,\ t_k^--\tau )$, needs to be further investigated. Since the method in this paper is somehow conservative, more methods and tools need to be developed for future research. It would be an interesting work to consider how to derive some less conservative conditions for FTS and FTCS of nonlinear systems with impulsive perturbation involving the state-dependent delay. Besides, our results are focused on nonlinear systems without time-delay. Next, delayed nonlinear systems could also be further taken into consideration.