Finite-time stabilization of nonlinear systems using an event-triggered controller with exponential gains

Abstract

This paper investigates the finite-time stabilization for a class of nonlinear systems by proposing a new event-triggered controller. The novelty lies in that, by introducing an exponential term, the control gains are exponential alterable in the interval of two adjacent event instants. Moreover, based on the proposed controller, a specific event-triggered scheme with a new type of error function is also derived to stabilize the concerned system in a finite time. In addition, a positive lower bound of the inter-execution is obtained, such that the Zeno behaviors can be avoided. Finally, illustrative examples are provided to verify that the overall amount of triggered events can be reduced by utilizing the proposed method in this paper.

1 Introduction

Stabilization of nonlinear systems is an eternal subject in the field of nonlinear control theory, such as exponential stabilization, asymptotic stabilization and finite-time stabilization [1,2,3,4]. Widely regarded as an interesting topic in recent years, finite-time stabilization of nonlinear systems has been paid much attentions [5,6,7,8]. As suggested in the pioneering work of S. Bhat and D. Bernstein [9, 10], the key feature of finite-time stabilization is to render system states to its equilibrium point/periodic orbits in finite time and to keep them then after, in which the settling time can be estimated [11]. Compared with traditional Lyapunov asymptotic stability, exponential stabilization and others, it has faster convergence speed, better disturbance rejection and better robustness to uncertainties [12,13,14,15,16]. In [7], by proposing a discontinuous state-feedback and adaptive control method, finite-time stabilization problem of delayed memristive neural networks was studied. Authors in [8] investigated the finite-time distributed state estimation issue for discrete-time nonlinear systems over sensor networks. In [15], a finite-time filter was designed for switched systems through a suitable event-driven communication scheme, and then, finite-time boundedness and input–output finite-time stability were simultaneously considered.

Nowadays, since almost all practical systems are implemented over digital platforms and communicated via a sharing network, how to reduce unnecessary samplings is an important issue due to the limited bandwidth and communication resources [16,17,18]. As we all know, the traditional time-driven communication, in which the signal transmissions are always implemented in a periodic manner, has hard implementation and bad predictability when focusing on the communication resources (e.g., bandwidth of the network). Thus, the time-driven communication becomes less preferable since such a communication manner would lead to unnecessary data transmissions. As such, event-triggered mechanism (ETM) has been proposed and paid a steadily growing interest [19,20,21,22,23,24,25,26,27,28,29]. The main feature of ETM is that the event-triggered controllers are designed by using the transmission data, which are sampled at the event instants. Combining with an error function, the event-triggered scheme is constructed and the event sequences are generated to determine whether the fresh data should be transmitted and the controller should be updated or not. For instance, in [16], by using an asynchronous switching scheme, the event-triggered finite-time control problem for networked switched linear systems has been investigated; in [20], the event-based synchronization control for memristive neural networks with time-varying delay was investigated; a decentralized state-dependent triggering scheme for interconnected systems was proposed in [25]. Consequently, for the stabilization of nonlinear systems in a finite time, how to generate necessary time sequences and reduce controller update times via ETM is an interesting question.

What is more, according to the existing results on the finite-time stabilization of various systems [17, 18, 27,28,29], it can be seen that almost all event-triggered controllers are the basic ones, such as $u(t)=K_{r(t)}x(t_kh)$ in [27], $u_i(t)=-\beta \mathrm{sig}(\sum _{j\in N_i}a_{ij}(x_i(t_k^i)-x_j(t_k^i)))^\alpha$ in [28] and $u(t)=K_{\sigma (t)}{\hat{x}}(t_r)$ in [29]. It is not difficult to find one disadvantage that these control gains are prescribed constants in the interval of two consecutive event times (e.g., $K_{r(t)}x(t_kh)$ and $K_{\sigma (t)}{\hat{x}}(t_r)$). If it is continuous for a long time, the corresponding event-triggered conditions can be violated easily and the amount of events will be increased. Naturally, how to design the event-triggered scheme and controller to further decrease the trigger rate of events is a valuable problem. On the other hand, there are also some other approaches that have been explored to design new event-triggered controllers or related schemes [23]. For example, authors in [22, 24, 25] utilized the idea of exponential approximation method to design control laws; in [26]; by designing the threshold parameter as an adaptive one, an adaptive event-triggering scheme was proposed. However, it is noticed that these methods are not suitable for dealing with finite-time stabilization issue of nonlinear systems due to the introduction of some redundant computing problems. For instance, in [24], an error function was chosen as $e_i(t)=\exp (A(t-t_k^i))x_i(t_k^i)-x_i(t)$, in which the event-triggered condition cannot be achieved in solving finite-time stabilization problem; an adaptive-triggered law $\dot{\sigma _i}(t)=-\,\,\kappa _i\sigma _i^2(t)\varphi _i^\mathrm{T}\varPhi _i\varphi _i(t)$ was introduced with several additional parameters in [26]. On the other hand, authors in [30] introduced exponential time-varying gains to solve sampled-data stabilization and estimation issues. And it was concluded that the introduction of time-varying gains is beneficial to the enlargement of sampling intervals while preserving the stability of the system. With these in mind, it cannot help think that whether or not there exists another approach to design the event-triggered controller and the corresponding event-triggered scheme to investigate finite-time stabilization issue, which motivates this present paper.

Motivated by above discussions, in this brief, finite-time stabilization problem for a class of nonlinear systems is studied via ETM; in special, a new event-triggered controller equipped with exponential gains is designed via an exponential gain approach. The core idea of the exponential gain approach is to make the control gains exponential alterable in the interval of two adjacent event instants by introducing an exponential term. Then, combining with the newly designed controller, a specific event-triggered scheme with a new type of error function is proposed. In this way, the considered system achieves stability in a finite time. Moreover, the inter-execution is lower bounded by a positive constant, and it is assured that Zeno behaviors will be avoided.

The remainder of this paper is organized as follows. In Sect. 2, some preliminaries are described. Section 3 develops the main results. In Sect. 4, illustrative examples are provided. Section 5 concludes this paper.

Notations$R, R^n$ and $R^{n\times n}$ denote the space of real numbers, the n-dimensional Euclidean space and the set of $n\times n$ real matrices, respectively. Given column vector $x=(x_1,x_2\ldots , x_n)^\mathrm{T}\in R^n, ||x||$ denotes the 2-norm of x and $x^{\sigma }=(x_{1}^{\sigma }, x_{2}^{\sigma },\ldots , x_{n}^{\sigma } )^\mathrm{T}$. $\mathrm{diag}\{\cdots \}$ denotes a diagonal matrix.

2 Preliminaries

Consider a class of nonlinear systems described as follows:

$$\begin{aligned} {\dot{x}}(t)=Ax(t)+A_d f(x(t))+u(t) \end{aligned}$$

(1)

where $A\in R^{n\times n}, A_d\in R^{n\times n}$ are known constant matrices; $x(t)=[x_{1}(t),x_{2}(t),\ldots , x_{n}(t)]^\mathrm{T}\in R^{n}$ represents the state vector; $u(t)\in R^n$ is the controller to be designed. $f(\cdot )=[f_1(\cdot ),f_2(\cdot ),\cdots ,f_n(\cdot ) ]^\mathrm{T}\in R^n$ is a nonlinear function satisfying the Lipschitz condition with constant L.

The objective of this paper is to design suitable event-triggered controller to stabilize nonlinear system (1) in a finite time. Before proceeding the main results, some useful lemmas are provided as follows.

Lemma 1

[7] Assume that $V(t):R^n \rightarrow R$ is C-regular and that $x(t) :[0, +\infty ) \rightarrow R^n$ is absolutely continuous on any compact subinterval of $[0, +\infty )$. If there exists a continuous function $\varUpsilon : [0, +\infty ) \rightarrow R^n$, with $\varUpsilon (\varrho )>0$ for $\varrho \in (0,+\infty )$, such that

$$\begin{aligned} \frac{\mathrm{d}V(t)}{\mathrm{d}t}\le -\varUpsilon ( V(t)),\ \ \int _0^{V(0)}\frac{1}{\varUpsilon (\varrho )}\mathrm{d}\varrho ={\mathcal {T}}^*< +\infty \end{aligned}$$

then we have $V(t)=0$ for $t\ge {\mathcal {T}}^*$. If $\varUpsilon (\varrho )=K_1\varrho +K_2\varrho ^\vartheta$ for all $\varrho \in (0,+\infty )$ holds, where $\vartheta \in (0,1)$ and $K_1, K_2 >0$, then the settling time is estimated by

$$\begin{aligned} {T}^*=\frac{1}{K_1(1-\vartheta )}\ln \frac{K_1V^{1-\vartheta }(0)+K_2}{K_2}. \end{aligned}$$

Lemma 2

[31] For any nonnegative real numbers $\xi _1, \xi _2, \ldots , \xi _n$, if $0<r\le 1, \sum _{i=1}^n \xi _i^r\ge \Big (\sum _{i=1}^n\xi _i\Big )^r.$

3 Main results

In this section, we will develop the main results step by step. A new type of event-triggered controller equipped with exponential gains is designed in Sect. 3.1 to achieve finite-time stabilization of nonlinear system (1). And then, based on the newly designed controller, the corresponding stability analysis will be given in Sect. 3.2.

3.1 Control scheme

At the first of this subsection, an exponential gain approach for designing a new event-triggered controller is given, which aims at reducing the amount of samplings and transmission signals under ETM. Then, the specific event-triggered controller is designed and a specific event-triggering scheme is proposed to achieve the finite-time stabilization of nonlinear system (1).

As we all know, the common event-triggered controllers are always designed as $u(t)=-\kappa x(t_k), \ \text {for} \ t_k \in [t_k, t_{k+1})$, in which $\kappa$ is the control gain; $t_0, t_1,\ldots , t_k,{\ldots }$ denote the event instances when the controller is updated; $x(t_k),x(t_{k+1})\cdots$ denote the transmission signals. By defining the event-triggered scheme or condition, the triggered time sequences are generated in achieving the stabilization and control synthesis of systems. The main feature of this control law is that the control inputs are updated when the event-triggered condition is violated, and the original control input $-\kappa x(t)$ is replaced by $-\kappa x(t_k)$. However, since the control gains are fixed in the interval of two consecutive event times (i.e., $[t_k, t_{k+1})$), the event-triggered condition is easy to be violated. Over the long haul, the amount of samplings or triggered events will increase, and a higher triggering rate will be induced until the control objective is realized.

Fig. 1

The comparison between $u(t)=-\kappa x(t_k)$ (denoted as the red dot line) and $u(t)=-e^{-\eta (t-t_k)}\kappa x(t_k)$ (denoted as the blue solid line). Each jump in all curves denotes that an event is triggered, and the corresponding time is the event instance. (Color figure online)

With that in mind, in the following, we propose an exponential gain approach to design new controllers under ETM, in which an exponential term $e^{-\eta (t-t_k)}$ ($\eta \ge 0$ is a given scalar) is introduced. The core idea is that that control gain becomes monotonically increasing or decreasing instead of fixed on $[t_k, t_{k+1})$. The illustrate figures are given in Fig. 1. From Fig. 1a( or b), when $x(t)>0$ and x(t) is monotonically decreasing (or increasing) in any an interval of two consecutive event instances, instead of the traditional gains $-\kappa x(t_k)$, $-e^{-\eta (t-t_k)}\kappa x(t_k)$ is monotonically increasing( or decreasing). Similarly, from Fig. 1c( or b), when $x(t)<0$ and x(t) is monotonically decreasing (or increasing) on $[t_k, t_{k+1})$, instead of the traditional gains $-\kappa x(t_k)$, control gains of the new controller with exponential gains are monotonically increasing( or decreasing).

Motivated by the above discussions, the new event-triggered controller equipped with exponential gains is designed for finite-time stabilization of nonlinear system (1):

$$\begin{aligned} u(t)=&-e^{-\eta (t-t_k)}\alpha x(t_k) -e^{-\eta (t-t_k)}\beta x^\sigma (t_k) \end{aligned}$$

(2)

where $\eta \ge 0$ are given scalars; $\sigma$ is positive scalar satisfying $0<\sigma <1$; $\alpha , \beta$ are the gain coefficients to be determined. According to the proof in [22], it is obvious that the negative sign “−” is used to guarantee the decay characteristics of the added term so as to preserve the stability of the concerned system. And it may lead to a substantial enlargement of the maximum sampling intervals, which is beneficial to the decrease in the amount of events in this paper.

Traditionally, the error function is chosen as $e(t)=x(t)-x(t_k)$, and the event instances are generated by the classical event-triggered scheme $t_{k+1}=\inf \{t>t_k|e^\mathrm{T}(t)\varOmega e(t)>\varepsilon x^\mathrm{T}(t)\varOmega x(t)\}$, in which $\varOmega$ is a positive definite matrix and $\varepsilon$ is the threshold value. However, due to new controller (2) equipped with $x^\sigma (t_k)$, the related criteria are difficult to be derived, even impossible if the original one continues to be used. Consequently, in order to realize control law (2) proposed specially for finite-time stabilization issue in this paper, we will give a specific event-triggered scheme in the following.

First, an auxiliary function is introduced as follows, which depends on the current states.

$$\begin{aligned} \chi (t)=-\alpha x(t)-\beta x^\sigma (t) \end{aligned}$$

(3)

Then, the new error function e(t) is defined as

$$\begin{aligned} e(t)=&-\alpha x(t)-\beta x^\sigma (t)+e^{-\eta (t-t_k)}\alpha e(t_k)\nonumber \\&+e^{-\eta (t-t_k)}\beta x^\sigma (t_k) \end{aligned}$$

(4)

Finally, the event-triggered scheme is given as:

$$\begin{aligned} t_{k+1}&=\inf \{t> t_k|\ ||e(t)||>\varepsilon \varpi ||x(t)||\}, \end{aligned}$$

(5)

$$\begin{aligned}&\qquad \text {for}\ t \in [t_k, t_{k+1}) \end{aligned}$$

(6)

where $\varepsilon \in (0,1)$ is the threshold value. Notice that $\varpi$ is a scalar to be designed in the latter, which depends on the related parameters of the system and controller. In the proposed event-triggered mechanism, data releases and transmissions are determined by event generator (5). Noticing that the event-triggered condition can be regarded as an index indicating whether the system performance is getting worse than the requirement. And when the event-triggered condition $||e(t)||>\varepsilon \varpi ||x(t)||$ is achieved, the next event instant $t_{k+1}$ occurs. In this way, many unnecessary transmissions can be avoided. Consequently, it is capable of improving the efficiency in communication resource utilization and prolonging the lifetime of network components [34].

Remark 1

Different from existing results in [24,25,26, 28, 29], a new type of exponential gain approach has been proposed to design new controller and related event-triggered scheme. The main superiority is that the developed control gains are equipped with an exponential term (i.g. $-e^{-\eta (t-t_k)}k$). Combining with Fig. 1, it can be found that the new control gain can be self-adjusting as time goes by. Compared with the prescribed fixed parameters (i.g. k) in existing results, the exponential control inputs are not easy to be updated frequently at event instances, and then, the overall amount of samplings will be decreased.

Remark 2

It is worthy noticing that a new event-triggered scheme (5) is designed for finite-time stabilization of (1) by defining a new error function (4). Different with traditional error functions between x(t) and $x(t_k)$ in [20] or $\varPhi (t)x(t_k)$ in [23], the conspicuous feature of new event-triggered scheme is that the error function is defined between the control inputs u(t) and an auxiliary function $\chi (t)$. Thus, for nonlinear systems under the control law equipped with $x^\sigma (\cdot )$ (e.g., (2)), (4) will simplify analysis and derivation process in developing the related criteria.

3.2 Finite-time stabilization

In this subsection, the stability criterion is developed to guarantee finite-time stabilization of system (1). Furthermore, the positive lower bound of the inter-execution is given, which ensures the nonexistence of Zeno behaviors.

Theorem 1

For given scalars $0<\varepsilon <1, \eta \ge 0, \alpha >0$, $\beta >0$, $0<\sigma <1$, nonlinear system (1) can be stabilized in a finite time via event–triggered controller (2) under event-triggered scheme (5) with

$$\begin{aligned} \varpi =\frac{(2\alpha \lambda _{min}(P)-2\lambda _{max}(PA)-2\lambda _{max}(PA_d)L)}{2\lambda _{min}(P)} \end{aligned}$$

(7)

for $t \in [t_k, t_{k+1})$, if there is a positive definite diagonal matrix $P\in R^{n \times n}$ such that

$$\begin{aligned} 2\alpha \lambda _{min}(P)>2\lambda _{max}(PA)+2\lambda _{max}(PA_d)L \end{aligned}$$

(8)

where $\lambda _{max}(PA)$ and $\lambda _{max}(PA_d)$ are the largest eigenvalue of PA and $PA_d$, respectively; $\lambda _{min}(P)$ is the smallest eigenvalue of P. Furthermore, the settling time for finite-time stabilization can be estimated as

$$\begin{aligned} T=\frac{2}{{\tilde{\alpha }}(1-\sigma )} \ln \frac{{\tilde{\alpha }}V^{\frac{1-\sigma }{2}}(0)+{\tilde{\beta }}}{{\tilde{\beta }}} \end{aligned}$$

(9)

where ${\tilde{\alpha }}=2(1-\varepsilon )\varpi , {\tilde{\beta }}=2\beta \lambda _{min}(P)\lambda _{max}^{-\frac{1+\sigma }{2}}(P)$.

Proof

Consider the following Lyapunov function

$$\begin{aligned} V(t)=x^\mathrm{T}(t)Px(t). \end{aligned}$$

(10)

Differentiating V(t), it yields that

$$\begin{aligned} {\dot{V}}(t)=\,&2x^\mathrm{T}(t)P{\dot{x}}(t)\nonumber \\ =\,&2x^\mathrm{T}(t)P(Ax(t))+A_df(x(t))+u(t))\nonumber \\ =\,&2x^\mathrm{T}(t)P(Ax(t){+}A_df(x(t)){-}e^{-\eta (t-t_k)}\alpha x(t_k)\nonumber \\&-e^{-\eta (t-t_k)}\beta x^\sigma (t_k))\nonumber \\ =\,&2x^\mathrm{T}(t)PAx(t)+2x^\mathrm{T}(t)PA_df(x(t))\nonumber \\&+2x^\mathrm{T}(t)P(-e^{-\eta (t-t_k)}\alpha x(t_k)\nonumber \\&-e^{-\eta (t-t_k)}\beta x^\sigma (t_k)) \end{aligned}$$

(11)

According to error function (4), (11) can be derived as

$$\begin{aligned} {\dot{V}}(t)=\,&2x^\mathrm{T}(t)PAx(t))+2x^\mathrm{T}(t)PA_df(x(t))\nonumber \\ {}&+2x^\mathrm{T}(t)P(-e(t)-\alpha x(t)-\beta x^\sigma (t)) \end{aligned}$$

(12)

Since f(x(t)) is a Lipschitz function with a constant L, the following inequality can be obtained

$$\begin{aligned} {\dot{V}}(t)\le \,&2\lambda _{max}(PA)||x(t)||^2 +2\lambda _{max}(PA_d)L||x(t)||^2\nonumber \\&+2\lambda _{min}(P)||x(t)||||e(t)||\nonumber \\&-2\alpha \lambda _{min}(P)||x(t)||^2-2\beta x(t)^\mathrm{T}P x^\sigma (t)\nonumber \\ =\,&-(2\alpha \lambda _{min}(P) -2\lambda _{max}(PA)\nonumber \\&-2\lambda _{max}(PA_d)L)\times ||x(t)||^2\nonumber \\&+2\lambda _{min}(P)||x(t)||||e(t)||\nonumber \\&-2\beta x(t)^\mathrm{T}P x^\sigma (t) \end{aligned}$$

(13)

$\square$

According to condition (7), it can be obtained that

$$\begin{aligned}&2\alpha \lambda _{min}(P)-2\lambda _{max}(PA)-2\lambda _{max}(PA_d)L \end{aligned}$$

(14)

$$\begin{aligned}&\quad \quad = 2\varpi \lambda _{min}(P) \end{aligned}$$

(15)

Substituting (14) in (13), it yields that

$$\begin{aligned} {\dot{V}}(t)\le&-2\varpi \lambda _{min}(P)||x(t)||^2\nonumber \\&+2\lambda _{min}(P)||x(t)||||e(t)||\nonumber \\&-2\beta x(t)^\mathrm{T}P x^\sigma (t)\nonumber \\ \le&\,2\lambda _{min}(P)||x(t)||(||e(t)||-\varpi ||x(t)||)\nonumber \\&-2\beta x(t)^\mathrm{T}P x^\sigma (t)) \end{aligned}$$

(16)

Through introducing a parameter $\varepsilon \in (0,1)$, we can obtain that

$$\begin{aligned} {\dot{V}}(t)\le&\,2\lambda _{min}(P)||x(t)||(||e(t)||-\varepsilon \varpi ||x(t)||\nonumber \\&+(\varepsilon -1)\varpi ||x(t)||)-2\beta x(t)^\mathrm{T}P x^\sigma (t) \end{aligned}$$

(17)

From event-triggering scheme (5), it implies that $||e(t)||-\varepsilon \varpi ||x(t)||\le 0$, and then

$$\begin{aligned} {\dot{V}}(t)\le&-2\lambda _{min}(P)(\varepsilon -1)\varpi ||x(t)||^2\nonumber \\&-2\beta x(t)^\mathrm{T}P x^\sigma (t)) \end{aligned}$$

(18)

Since $0<\sigma <1$, we have $0<\frac{1+\sigma }{2}<1$. Then, by Lemma 2, it is derived that

$$\begin{aligned} -2\beta x^\mathrm{T}P x^\sigma (t))\le&-2\beta \lambda _{min}(P)\sum _{i=1}^n \sum _{j=1}^n(x_{ij}^2(t))^{\frac{1+\sigma }{2}}\nonumber \\ \le&-2\beta \lambda _{min}(P)(x^\mathrm{T}(t)x(t))^{\frac{1+\sigma }{2}}\nonumber \\ \le&-2\beta \lambda _{min}(P)\lambda _{max}^{-\frac{1+\sigma }{2}} (P)V^{\frac{1+\sigma }{2}}(t)\nonumber \\ =\,&-{\tilde{\beta }}V^{\frac{1+\sigma }{2}}(t). \end{aligned}$$

(19)

And then, we have

$$\begin{aligned} {\dot{V}}(t)\le&-{\tilde{\alpha }} V(t)-{\tilde{\beta }}V^{\frac{1+\sigma }{2}}(t). \end{aligned}$$

(20)

According to Lemma 1, it can be concluded that nonlinear system (1) can be stabilized in a finite time via the newly designed controller (2) and event-triggered scheme (5). Furthermore, the settling time can be estimated by (9). This completes the proof.

Next, Zeno behaviors will be checked, which is always described as infinitely fast switching in an interval of two consecutive event times. Based on the contrapositive of the Zeno’s definition in [32], it can be seen that if the inter-execution time $\{t_{k+1}-t_k\}>0$ on $t_k$ is verified, there will not exist Zeno behaviors.

Theorem 2

Consider nonlinear system (1), if all conditions in Theorem 1 hold, then the inter-execution time $\{t_{k+1}-t_k\}$ is lower bounded by a positive constant $\xi$ as follows:

$$\begin{aligned} \xi =\frac{\varepsilon \varpi }{(\hbar +\psi )^2+\varepsilon \varpi (\hbar +\psi )} \end{aligned}$$

(21)

where $\hbar =\Big (\alpha +\beta \sigma \big (2V(0)\big )^{\frac{\sigma -1}{2}}\Big )$, $\psi =(\alpha -||A||+||A_d||L)$.

Proof

Let $\varphi (t)=\frac{||e(t)||}{||x(t)||}$. Then, the derivative of $\varphi (t)$ is

$$\begin{aligned} {\dot{\varphi }}(t)=&\frac{||{\dot{e}}(t)||||x(t)||}{||x(t)||^2} +\frac{||e(t)||||{\dot{x}}(t)||}{||x(t)||^2} \end{aligned}$$

(22)

$\square$

Based on (4), (22) can be rewritten as

$$\begin{aligned} \dot{\varphi _i}(t)\le&\frac{(\alpha +\beta \sigma ||x_i(t)||^{\sigma -1})||{\dot{x}}(t)||}{||x(t)||}+\frac{||e(t)||||{\dot{x}}(t)||}{||x(t)||||x(t)||} \end{aligned}$$

(23)

Furthermore, due to ${\dot{V}}(t)\le 0$, the following inequality is derived on the basis of lemma 2.

$$\begin{aligned} {\dot{\varphi }}(t)\le&\frac{\Big (\alpha +\beta \sigma \big (2V(0)\big )^{\frac{\sigma -1}{2}}\Big )||{\dot{x}}(t)||}{||x(t)||} {+}\frac{||e(t)||||{\dot{x}}(t)||}{||x(t)||||x(t)||}\nonumber \\ \le&\frac{\hbar ||{\dot{x}}(t)||}{||x(t)||}+\frac{||e(t)||||{\dot{x}} (t)||}{||x(t)||||x(t)||} \nonumber \\ \le&\bigg (\hbar +\frac{||e(t)||}{||x(t)||}\bigg )\frac{||{\dot{x}}(t)||}{||x(t)||} \end{aligned}$$

(24)

Substituting (1) and (2) in (24), it yields the following inequality

$$\begin{aligned} \dot{\varphi _i}(t)\le&\big (\hbar +\varphi _i(t)\big )\bigg ( (\alpha -||A||+||A_d||L)\nonumber \\&+\beta ||x(t)||^{\sigma -1}+\frac{||e(t)||}{||x(t)||}\bigg )\nonumber \\ \le&\big (\hbar +\varphi (t)\big )\bigg ( \psi +\beta (2V(0))^{\frac{\sigma -1}{2}} +\frac{||e(t)||}{||x(t)||}\bigg )\nonumber \\ \le&\big (\hbar +\varphi _i(t)\big )\big (\psi +\varphi _i(t)\big )\nonumber \\ \le&\big (\hbar +\psi +\varphi _i(t)\big )^2 \end{aligned}$$

(25)

Define the inter-execution time $\{t_{k+1}-t_k\}\ge \xi$. On the other hand, $\frac{{\dot{\varGamma }}(t)}{\varGamma (t)^2}=1$ can be obtained from (25) when $\varGamma (t)=\hbar +\psi +\varphi _i(t)$. Then, integrating this equality from 0 to $\xi$, we has

$$\begin{aligned} 1/\varGamma (0,\varphi _0)-1/\varGamma (\xi ,0)=\xi \end{aligned}$$

(26)

where $\varGamma (0,\varphi _0)=\hbar +\psi +\varphi _i(0,\varphi _0)$, $\varGamma (\xi ,0)=\hbar +\psi +\varphi _i(\xi ,0)$. Since the initial condition of (25) is $\varphi (0,\varphi _0)$, we can obtain that

$$\begin{aligned} \varphi (\xi ,0)=&\frac{\hbar +\psi +\varphi _0-(\hbar +\psi ) (1-\xi (\hbar +\psi +\varphi _0))}{1-\xi (\hbar +\psi +\varphi _0)}\nonumber \\ =&\frac{\xi (\hbar +\psi )^2}{1-\xi (\hbar +\psi )} \end{aligned}$$

(27)

According to event-triggered scheme (4) and (7), $\varphi (\xi ,0)=\varepsilon \varpi$ is guaranteed when next event is triggered. Then, (27) leads to

$$\begin{aligned} \xi =\frac{\varepsilon \varpi }{(\hbar +\psi )^2+\varepsilon \varpi (\hbar +\psi )} \end{aligned}$$

(28)

According to condition (8), then inter-execution time $\{t_{k+1}-t_k\}=\xi >0$. Above all, for whole system (1), the Zeno behaviors are avoided. This completes the proof.

Remark 3

In existing results on finite-time stabilization and control synthesis for various systems via ETM [17, 18, 27,28,29], almost all controllers are always chosen as the common ones, such as $u(t)=K_{r(t)}x(t_kh)$ in [27], $u_i(t)=-\beta \mathrm{sig}(\sum _{j\in N_i}a_{ij}(x_i(t_k^i)-x_j(t_k^i)))^\alpha$ in [28] and $u(t)=K_{\sigma (t)}{\hat{x}}(t_r)$ in [29]. It is worth noticing that the control gains in the interval of two adjacent events are fixed, which are preset off-line. Aiming at relaxing this issue, in this brief, we introduce an event-triggered controller with exponential gains (2) and specific event-triggered scheme (5) to investigate the finite-time stabilization for a class of nonlinear systems. Equipping an exponential term into the control gains, the control inputs will become exponential alterable in the interval of two event times. According to the previous proof process, it can be found that this exponential gain approach is beneficial to the enlargement of event interval while preserving the control performance. Additionally, when $\eta =0$, the new event-triggered control law with exponential gains will degrade into the existing ones.

Remark 4

It is worthy noticing that concerned system (1) in this paper can describe many types of practical systems, such as Chua’s circuit [33] and neural dynamical systems [1]. Obviously, the proposed control strategy is also suitable for these variety of systems. In addition, the exponential gain approach proposed in this paper can be still used to design controllers for a broad class of systems, whose input matrix is not the identity matrix or dimension of the output does not coincide with that of state. Limited by the space, the main work of this paper is the introduction of the scheme with exponential gains for a class of nonlinear system (1), and the research on more general systems will be made in the future work.

Remark 5

In Theorem 1, stability criterion has been developed to ensure the finite-time stabilization of nonlinear system. In order to explain the solution steps of the controller, we give a feasible design procedure of $\alpha , \beta$ and P.

4 Numerical examples

In this section, two numerical examples are provided to illustrate the validity of obtained results in this paper.

Example 1

Consider a nonlinear system (1) with $A=\begin{bmatrix}-\frac{19}{7}&9&0\\1&-1&1\\0&-14.25&0\end{bmatrix}$, $A_d=\begin{bmatrix}0.02&0&0\\0&0.03&0\\0&0&0.04\end{bmatrix}$. The nonlinear function f(s) is chosen as $f(s)=0.04\sin (s)$ satisfying the Lipschitz condition with $L=0.05$. Under initial values $x(0)=[-3.5\ 1\ -1]^\mathrm{T}$, Fig. 2 shows the unstable dynamic behaviors of the nonlinear system without controller.

Fig. 2

State responses without controller

Next, under proposed event-triggered scheme (5), the event-triggered controller with exponential gains (2) will be utilized to stabilize the unstable system in a finite time. We choose the related parameters are $\alpha =6, \beta =0.06$, $\sigma =1/3, \eta =1, \varepsilon =0.2, P=\mathrm{diag}\{2, 2, 2\}$. Thus, $\varpi =9.4342$ and the event-triggered scheme is described as $t_{k+1}=\inf \{t> t_k|\ ||e(t)||>1.88684||x(t)||\},\ \text {for}\ t \in [t_k, t_{k+1})$. Thus, by Theorem 1, the closed-loop control system is finite-time stable. And the settling time can be estimated as $T=2.1377$ s by (9). The simulation results with the same initial condition are shown in Fig. 3. Obviously, the concerned system under newly designed controller (2) is stable when $t=2$ s.

Fig. 3

State responses with controller

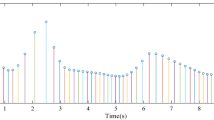
In addition, in order to further describe the event-triggering scheme and input updates, Fig. 4 is provided, in which ||e(t)|| and u(t) are plotted. From the relationships between measurement errors ||e(t)|| and $\varepsilon \varpi ||x(t)||$ shown in Fig. 4a, it is demonstrated that the events are triggered when $||e(t)||>\varepsilon \varpi ||x(t)||$ at $t_k$. Then, combining with Fig. 4b, it is clear that the control inputs are updated at the same instants when the events are triggered. The simulation results tell us that the number of events is $\varGamma =32$, which takes 3.2% of the data that should have been transmitted. Consequently, compared with existing results, control law (2) and stability criteria proposed in this paper are not merely to stabilize the nonlinear system in a finite time, but save the resources by reducing the number of sampled-data transmissions. What is more, the release interval between the adjacent release instants is shown in Fig. 5. It tells us that not all data are necessary to be transmitted to update the controller, and the release interval is alterable according to event-triggered scheme (5).

Fig. 4

a The fluttering of the error ||e(t)|| and $\varepsilon \varpi ||x(t)||$. b The control inputs

It is noticed that the newly proposed event-triggered controller (2) is degraded into the common one when $\eta =0$, which can represent the used event-triggered controllers in [20, 21]. Then, in order to explain the improvements of controller (2) with exponential gain, some simulations are made when $\eta =2$ and $\eta =0$. And other related parameters are still unchanged with the previous work. The comparison results are shown in Fig. 6. From Fig. 6, it can be seen that the release interval between the adjacent release instants with $\eta =2$ is larger than the ones when $\eta =0$. Furthermore, the simulations tell us that $\varGamma _{\eta =2}= 30$ and $\varGamma _{\eta =0}= 43$. Consequently, it can be concluded that the amount of samplings or triggering events can be decreased when the exponential term is introduced.

Example 2

In order to further verify the effectiveness and priority of the main results obtained in this paper, the finite-time master–slave synchronization of dynamic networks with 5 Chua’s circuit is investigated in this example.

The Chua’s circuit, i.e., the master system, is described as

$$\begin{aligned} {\dot{s}}(t)=As(t)+Bg(s(t))) \end{aligned}$$

(29)

where $s(t)=(s_1(t),s_2(t),s_3(t))^\mathrm{T}, B=54/7 \mathrm{diag}\{1,0, 0\}$, $g(s(t))=0.5(|s_1(t)+1|-|s_1(t)-1|, 0, 0)^\mathrm{T}$,

$A=\begin{bmatrix}-\frac{19}{7}&9&0\\1&-1&1\\0&-14.28&0\end{bmatrix}$. Under the initial condition $s(0)=(0.5,0.2,0.3)^\mathrm{T}$, the structure and trajectory of (29) are shown in Figs. 7 and 8.

The considered dynamic networks, i.e., the slave system, is described as

$$\begin{aligned} {\dot{x}}_i(t)=Ax_i(t)+Bg_i(x(t))+\sum _{j=1}^5\mu _{ij}\varPhi x_j(t)+u_i(t)) \end{aligned}$$

(30)

where $i=1,2,3,4,5, x_i(t)=(x_{i1}(t),x_{i2}(t),x_{i3}(t))^\mathrm{T}$, $\varPhi =\mathrm{diag}(1,1,1), {\mathcal {U}}=\mu _{5\times 5}=7\begin{bmatrix}-2&0&1&0&1\\ 1&-3&1&0&1\\ 1&1&-4&1&1\\ 1&1&0&-4&2\\ 1&2&1&1&-5\end{bmatrix}$.

Fig. 5

The release interval between the adjacent release instants

Fig. 6

The comparison of release interval between the adjacent release instants when $\eta =0$ (denoted as the blue stem line with “$\bigtriangleup$” mark) and $\eta =2$ (denoted as the red stem line with “$+$” mark). (Color figure online)

Fig. 7

The structure of the Chua’s circuit

Fig. 8

The trajectory of (29) with initial condition $x(0)=(0.5,0.2,0.3)^\mathrm{T}$

Fig. 9

The trajectories of the error system between (29) and (30). a Subsystem 1 with initial condition $x_1(0)=(-6,-3,5)^\mathrm{T}$. b Subsystem 2 with initial condition $x_2(0)=(-4.8,6.2,-3.7)^\mathrm{T}$. c Subsystem 3 with initial condition $x_3(0)=(5.8,-6.7,3.5)^\mathrm{T}$. d Subsystem 4 with initial condition $x_4(0)=(-4.5,6.0,-3.2)^\mathrm{T}$. e Subsystem 5 with initial condition $x_5(0)=(5.4,-6.2,3.1)^\mathrm{T}$

In the following, the event-triggered controller with exponential gains (2) is designed to realize the finite-time synchronization of (29) and (30). The threshold parameters of event-triggered scheme (5) for 5 subsystems are chosen as the same as $\varepsilon _1=0.6$. According to the conditions in Theorem 1, the related parameters of $u_1$, $u_2, u_3, u_4$ and $u_5$ for 5 Chua’s circuits are chosen as $\alpha _1=21, \alpha _2=20, \alpha _3=22, \alpha _4=20$, $\alpha _5=22, \beta _1=\beta _3=\beta _5=0.02$, $\beta _2=\beta _4=0.01, \eta _1=\eta _2=\eta _3=\eta _4=\eta _5=5$, $\sigma =1/3$. Then, under the initial conditions $x_1(0)=(-6,-3,5)^\mathrm{T}, x_2(0)=(-4.8,6.2,-3.7)^\mathrm{T}$, $x_3(0)=(5.8,-6.7,3.5)^\mathrm{T}, x_4(0)=(-4.5,6.0,-3.2)^\mathrm{T}$, $x_5(0)=(5.4,-6.2,3.1)^\mathrm{T}$, the trajectory of the error system between (29) and (30) is shown in Fig. 9, in which the error system between the master and slave systems is denoted as $r_i(t)=x_i(t)-s(t)$.

Fig. 10

The fluttering of the error ||e(t)|| and $\varepsilon \varpi ||r(t)||$. a Subsystem 1. b Subsystem 2. c Subsystem 3. d Subsystem 4. e Subsystem 5

According to the state responses of the error system in Fig. 9, it indicates that the synchronization between (30) and (29) is achieved at $t=0.6$ s, which is smaller than the estimate of the settling time $T=2.045$ by Theorem 1. Thus, it can be concluded that under the proposed event-triggered controller with exponential gains, the finite-time stabilization of the error system can be realized. In addition, in order to further explain the triggering dynamics of (5), the fluttering of the error ||e(t)|| and $\varepsilon \varpi ||r(t)||$ is shown in Fig. 10. It is obvious that only necessary events will be triggered when ||e(t)|| surpasses $\varepsilon \varpi ||r(t)||$. In this way, unnecessary date releases, and transmissions and control updates can be avoided. Consequently, the proposed controller and the related results can further reduce the amount of samplings or events, and then, the limited bandwidth and recourses can be saved.

5 Conclusion

An exponential gain approach has been proposed to design the event-triggered controller in this paper to decrease the rate of triggering in event-triggered control process. By introducing an exponential term, the new control gains became exponentially decreasing or increasing in the interval of two consecutive event times. Significantly, a novel event-triggered controller with exponential gain and a specific event-triggered scheme has been designed to stabilize the considered system in a finite time. In order to avoid Zeno behaviors, a positive lower bound for the inter-execution has been obtained. Finally, two illustrative examples have been provided to show the effectiveness of the main results. In the future, based on the proposed ETM in this paper, it is interesting to investigate finite-time stabilization and control synthesis issues for other class of nonlinear systems with time delays. And how to improve the proposed exponential gain method and design event-triggered controller are worthy to be studied, so as to further save the limited bandwidth and resources.