Adaptive robust decoupling control of multi-arm space robots using time-delay estimation technique

Abstract

The most distinctive difference between a space robot and a base-fixed robot is its free-flying/floating base, which results in the dynamic coupling effect. The mounted manipulator motion will disturb the position and attitude of the base, thereby deteriorating the operational accuracy of the end effector. This paper focuses on decoupling or counteracting the coupling between the manipulator and the base. The dynamics model of multi-arm space robots is established using the composite rigid dynamics modeling approach to analyze the dynamic coupling force/torque. An adaptive robust controller that is based on time-delay estimation (TDE) and sliding mode control (SMC) is designed to decouple the multi-arm space robot. In contrast to the online computation method, the proposed controller compensates for the dynamic coupling via the TDE technique and the SMC can complement and reinforce the robustness of the TDE. The global asymptotic stability of the proposed decoupling controller is mathematically proven. Several contrastive simulation studies on a dual-arm space robot system are conducted to evaluate the performance of the TDE-based SMC controller. The results of qualitative and quantitative analysis illustrate that the proposed controller is simpler and yet more effective.

1 Introduction

Space robots are typical vehicle–manipulator systems [1] that have both the maneuverability of satellites and the operational ability of manipulators to accomplish various on-orbit servicing (OOS) tasks [2, 3]. As the difficulty of OOS tasks has increased, multi-arm space robots have developed to be the mainstream direction. Typical examples include the Robotic Servicing of Geosynchronous Satellites and the Restore-L programs [4]. Due to the dynamic coupling effect between the robotic arms and the base, the reaction force/torque induced by the arm motion will produce translation/rotation disturbances at the base [5], which severely affects the motion accuracy [6] of space robots in some operational tasks, such as on-orbit assembly [7] and on-orbit refueling [8]. Thus, decoupling or minimizing the dynamic coupling has become a hot spot in this field [9, 10]. Researchers have proposed various creative motion planning and control methods to address this issue.

From the aspect of motion planning, Dubowsky and Torres [11] proposed a pioneering work method concerning disturbance maps and enhanced disturbance maps, which aimed to find a feasible trajectory in the joint space that resulted in a relatively low base disturbance. Nakamura and Mukherjee [12] investigated the nonholonomic redundancy of free-floating space robots and proposed a bidirectional method to plan the manipulator with a guaranteed base attitude. Nenchevl et al. [13] utilized the reaction null-space (RNS) strategy to map the base motion in the null-space of the generalized Jacobian matrix of free-floating space robots; however, the dynamic singularity problem restricts the performance of this method. Based on the RNS planning, Abdul Hafez et al. [14] extended this method with the task function approach to realize the reactionless motion planning of multi-arm space robots. Chu et al. [15] proposed a control strategy using the particle swarm optimization extreme learning machine (PSO-ELM) algorithm to track the dynamic changes in the planned path. Xu et al. [16] proposed a coordinated motion planning strategy for planning dual-arm space robot systems, in which one arm is called the mission arm and the other is called the auxiliary arm, where the essential principle is based on the concept of the dynamic balance [17], i.e., using the auxiliary arm to balance the mission arm. Similarly, Wang et al. [18] used the constrained PSO to plan a dual-arm space robot that can avoid dynamic singularities. Moreover, Zhang and Liu [19] proposed a motion planning strategy that considers the base berth position and the grasping area to improve the efficiency of trajectory planning. Most motion planning methods focus on the joint trajectory planning of amounted manipulators with a free-floating base. For the free-floating mode, the base is not controlled, so the system will save fuel. However, in various situations, such as on-orbit capture or on-orbit assembly, two or three arms must coordinately manipulate together in real time [20, 21] and the base needs to keep stable for communication with the earth.

Free-flying space robots can actively control their bases to solve this problem. For the active compensation control strategies of free-flying space robots, Longman et al. [22] divided the entire control system into two subsystems, namely the manipulator control system and the base control system, and the coupling force and torque can be compensated by the Newton–Euler recursive equations. This model-based compensation strategy is also used in Refs. [9, 10]. In fact, the active compensation method using the Newton–Euler equations can be regarded as a typical torque feedforward method and is also referred to as the computed torque control (CTC) method, which is a conventional and classical decoupling control method for robotic arm systems [23]. Similarly, Oda and Ohkami [24] utilized the angular momentum conservation to estimate the coupling torque and proposed a feedforward control to compensate for the base attitude disturbance. In fact, space robots are multiple-input multiple-output (MIMO) systems, and researchers have designed monolithic controllers to coordinately control the entire system. Papadopoulos and Dubowsky [25] proposed a Jacobian transpose controller for coordinately controlling the manipulator and the satellite base, which can realize point-to-point motion but is not suitable for continuous trajectory tracking in operational space. Kumar et al. [26] used feedforward neural networks to learn the nonlinear dynamics of a space robot and developed an adaptive controller for coordinating the manipulator and the base attitude. Shi et al. [27] utilized the diagonalization technique to transform a MIMO system into multiple single-input single-output systems and developed three types of controllers including the CTC, SMC, and model predictive control approaches to control the entire system, respectively. Jayakody et al. [28] utilized a virtual control input vector to decouple the MIMO system and proposed an adaptive SMC for controlling the space robot system. Wang et al. [29] proposed a coordination controller for capturing a tumbling target and regulating the base attitude concurrently. Zong et al. [30] proposed a concurrent learning algorithm to identify unknown parameters for minimizing the base disturbance.

In summary, the motion planning approaches [11,12,13,14,15,16,17,18,19] mainly focus on free-floating space robots, and the kinematic redundancy of the manipulator is the prerequisite condition for eliminating the coupling. Although the RNS approach [13] can be used in real-time scenarios, it requires that the dimensions of the null-space are sufficiently large for generating reactionless joint trajectories. Motion control approaches [9, 10], [22,23,24,25,26,27,28] are mainly focused on the free-flying space robot with single arm, which is relatively simple. The CTC performance depends on the accuracy of the dynamics model, which will degrade when disturbances or uncertainties exist. The SMC is a robust control approach that outputs high control gains to suppress disturbances or uncertainties; however, its high-frequency switching action leads to the control chattering effect. Some adaptive control methods can reinforce the SMC, but they usually require a high computing capacity to estimate the parameters of uncertainties. Compared with the single-arm space robot system, the dynamics model of the multi-arm space robot systems is more complicated, and the coupling effect of the multi-arm space robot system occurs not only between the robotic arm and the base but also among the robotic arms. Thus, for the multi-arm space robot, the CTC-based decoupling method will be not suitable due to the high computational burden on calculating model parameters. However, the TDE technique provides us an easy solution to address this tough issue. The TDE is an effective control method proposed by Hisa and Gao [31] for controlling industrial manipulators, which uses the previously observed information and control input to estimate the current unknown dynamics of continuous variable dynamic systems [32]. In this paper, we propose a TDE-based SMC to realize the decoupling control of the multi-arm space robot system. The main contributions of this paper are listed as follows:

• (1) To the best of our knowledge, we are the first to use the TDE method to address the decoupling control of the multi-arm space robot system. The transient learning ability of the TDE is suitable to estimate the coupling dynamics, and the TDE-based SMC is intrinsically adaptive and robust.

• (2) Compared with the CTC and the CTC-based SMC, the TDE-based SMC uses online estimation rather than online computation to compensate for the nonlinear term, so the proposed controller is simpler and more efficient.

The remainder of this paper is organized as follows: The dynamic equation of a multi-arm space robot is introduced in Sect. 2. The dynamic coupling analysis and the decoupling controller design are investigated in Sect. 3. Four contrastive simulation studies are conducted to verify the effectiveness of the proposed method in Sect. 4. Finally, the conclusions are concluded in Sect. 5.

2 Dynamics modeling of multi-arm space robots

2.1 Modeling assumptions

Before we introduce the dynamics model of the multi-arm space robot system, the basic modeling assumptions are given as follows: (1) The entire system consists of rigid bodies. (2) The multi-arm space robot system is not affected by gravity, i.e., $g = 0$. (3) If some disturbances or uncertainties are impacting on the system, their boundaries are limited and known.

2.2 Notation definitions

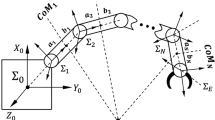
As shown in Fig. 1, the space robot system includes a satellite base (denoted as body 0) and N serial robotic arms with nA bodies, where the kth arm has nk ($k = 1,2, \ldots ,N$) bodies and degrees of freedom (DOFs), and n1 + n2 + … + nN = nA. The related symbols are defined in Table 1. If not otherwise specified, all the vectors are defined in the inertial frame $\sum_{\text{I}}$.

Fig. 1

Schematic diagram of a multi-arm space robot system

Table 1 Notation definitions

2.3 Composite rigid body dynamics modeling

In this subsection, we will deduce the model using an efficient algorithm, i.e., the composite rigid dynamics algorithm [33], which combines the Lagrange method and the Newton–Euler recursive method.

Based on assumptions (1) and (2), we know that the energy of the space robot system is mainly embodied in its kinetic energy. Here, the kinetic energy of the entire system can be calculated as

$$ \begin{aligned} {\text{\rm T}} &= \frac{1}{2}(\varvec{\omega}_{0}^{\text{T}} \varvec{I}_{0}\varvec{\omega}_{0} + m_{0} \varvec{v}_{0}^{\text{T}} \varvec{v}_{0} ) \\ & \quad + \frac{1}{2}\sum\limits_{k = 1}^{N} {\left( {\sum\limits_{i = 1}^{nk} {\left( {\varvec{\omega}_{i}^{{k{\text{T}}}} \varvec{I}_{i}^{k}\varvec{\omega}_{i}^{k} + m_{i}^{k} \varvec{v}_{i}^{{k{\text{T}}}} \varvec{v}_{i}^{k} } \right)} } \right)} \\ \end{aligned} $$

(1)

$$ \varvec{\omega}_{i}^{k} =\varvec{\omega}_{0} + \sum\limits_{j = 1}^{i} {\varvec{z}_{j}^{k} \dot{\theta }_{j}^{k} } $$

(2)

$$ \varvec{v}_{i}^{k} = \varvec{v}_{0} +\varvec{\omega}_{0} \times (\varvec{r}_{i}^{k} - \varvec{r}_{ 0} ) + \sum\limits_{j = 1}^{i} {\left( {\varvec{z}_{j}^{k} \times (\varvec{r}_{i}^{k} - \varvec{P}_{j}^{k} )} \right)} \dot{\theta }_{j}^{k} $$

(3)

where $m_{0}$ and $m_{i}^{k}$ are the masses of the base and body i of arm-k, respectively; $\varvec{I}_{0}$ and $\varvec{I}_{i}^{k}$ are the inertial tensors of the base and body i of arm-k, respectively; $\varvec{\omega}_{0}$ and $\varvec{\omega}_{i}^{k}$ are the angular velocities of the base and body i of arm-k, respectively; and $\varvec{v}_{0}$ and $\varvec{v}_{i}^{k}$ are the linear velocities of the base and the CoM of body i of arm-k, respectively. According to the Lagrange method, the general dynamics model of the multi-arm space robot can be expressed as

$$ \underbrace {{\left[ {\begin{array}{*{20}c} {\varvec{H}_{\text{B}} } & {\varvec{H}_{\text{BM}}^{1} } & \ldots & {\varvec{H}_{\text{BM}}^{N} } \\ {\varvec{H}_{\text{BM}}^{{1{\text{T}}}} } & {\varvec{H}_{\text{M}}^{1} } & {\mathbf{0}} & {\mathbf{0}} \\ \vdots & {\mathbf{0}} & \ddots & {\mathbf{0}} \\ {\varvec{H}_{\text{BM}}^{{N{\text{T}}}} } & {\mathbf{0}} & {\mathbf{0}} & {\varvec{H}_{\text{M}}^{N} } \\ \end{array} } \right]}}_{\varvec{H}}\underbrace {{\left[ {\begin{array}{*{20}c} {{\ddot{\varvec{X}}} _{0} } \\ { {\ddot{\varvec{\theta}}} _{\text{M}}^{1} } \\ \vdots \\ {\ddot{\varvec{\theta }}_{\text{M}}^{N} } \\ \end{array} } \right]}}_{{{\ddot{\varvec{q}}} }} + \underbrace {{\left[ {\begin{array}{*{20}c} {\varvec{C}_{\text{B}} } \\ {\varvec{C}_{\text{M}}^{1} } \\ \vdots \\ {\varvec{C}_{\text{M}}^{N} } \\ \end{array} } \right]}}_{\varvec{C}} = \underbrace {{\left[ {\begin{array}{*{20}c} {\varvec{F}_{\text{B}} } \\ {\varvec{\tau}_{\text{M}}^{1} } \\ \vdots \\ {\varvec{\tau}_{\text{M}}^{N} } \\ \end{array} } \right]}}_{\varvec{F}} $$

(4)

where $\varvec{H}$ is the inertial matrix of the system; $\varvec{H}_{\text{B}}$ and $\varvec{H}_{\text{M}}^{k}$ are the inertia matrices of the base and arm-k, respectively; $\varvec{H}_{\text{BM}}^{k}$ is the coupling matrix between the base and arm-k; $\varvec{C}$ is the generalized Coriolis and centrifugal force term of the system, which is also called the nonlinear bias force term; $\varvec{C}_{\text{B}}$ and $\varvec{C}_{\text{M}}^{k}$ are the Coriolis and centrifugal force terms that correspond to the base and arm-k, respectively; $\varvec{F}$ is the generalized driving force and torque term of the system; $\varvec{F}_{\text{B}}$ is the driving force and torque term corresponding to the base; $\varvec{\tau}_{\text{M}}^{k}$ is the driving torque term corresponding to the arm-k; ${\ddot{\varvec{q}}}$ is the generalized acceleration term; and ${\ddot{\varvec{X}}} _{ 0} {\mathbf{ = }}[\dot{\varvec{v}}_{0}^{\text{T}} , \, \dot{\varvec{\omega }}_{0}^{\text{T}} ]^{\text{T}}$ is the generalized acceleration of the base. In Eq. (4), the inertial matrix H and the nonlinear bias force C are coefficients of the dynamics equation, which are the functions of state variables.

As the composite rigid dynamics algorithm synthesizes the forward dynamics and the inverse dynamics, the inertial matrix H can be deduced according to the kinetic energy equation, and the nonlinear bias force term C can be deduced by the Newton–Euler equations. Equation (1) can be transformed into

$$ {\text{T}} = \frac{1}{2}\dot{\varvec{q}}^{\text{T}} {\varvec{H}}\dot{\varvec{q}} $$

(5)

Thus, we can deduce

$$ \varvec{H}{ = }\left[ {\begin{array}{*{20}c} {M\varvec{E}} & { - M\tilde{\varvec{r}}_{{ 0 {\text{S}}}} } & {\varvec{J}_{{{\text{T}}\omega }}^{1} } & {, \ldots ,} & {\varvec{J}_{{{\text{T}}\omega }}^{N} } \\ {M\tilde{\varvec{r}}_{{ 0 {\text{S}}}} } & {\varvec{H}_{\omega } } & {\varvec{H}_{\omega \varphi }^{1} } & {, \ldots ,} & {\varvec{H}_{\omega \varphi }^{N} } \\ {\varvec{J}_{{{\text{T}}\omega }}^{{1{\text{T}}}} } & {\varvec{H}_{\omega \varphi }^{{1{\text{T}}}} } & {\varvec{H}_{\text{M}}^{1} } & {\mathbf{0}} & {\mathbf{0}} \\ \vdots & \vdots & {\mathbf{0}} & \ddots & {\mathbf{0}} \\ {\varvec{J}_{{{\text{T}}\omega }}^{{N{\text{T}}}} } & {\varvec{H}_{\omega \varphi }^{{N{\text{T}}}} } & {\mathbf{0}} & {\mathbf{0}} & {\varvec{H}_{\text{M}}^{N} } \\ \end{array} } \right] $$

(6)

$$ \varvec{H}_{\text{B}} = \left[ {\begin{array}{*{20}c} {M\varvec{E}} & { - M\tilde{\varvec{r}}_{{0{\text{S}}}} } \\ {M\tilde{\varvec{r}}_{{0{\text{S}}}} } & {\varvec{H}_{\omega } } \\ \end{array} } \right], \varvec{H}^{k}_{\text{BM}} = \left[ {\begin{array}{*{20}c} {\varvec{J}^{k}_{\text{T}\omega}} \\ {{\varvec{H}}^{k}_{{\omega\varphi}} } \\ \end{array} } \right] $$

(7)

where $\varvec{E}$ is the identity matrix; $\tilde{\varvec{r}}$ is the skew-symmetric matrix of $\varvec{r}$; and other parameters are expressed as

$$ M = m_{0} + \sum\limits_{k = 1}^{N} {\left( {\sum\limits_{i = 1}^{nk} {m_{i}^{k} } } \right)} $$

(8a)

$$ \varvec{r}_{{0{\text{S}}}} = \varvec{r}_{\text{S}} - \varvec{r}_{0} $$

(8b)

$$ \varvec{H}_{\omega } = \varvec{I}_{0} + \sum\limits_{k = 1}^{N} {\left( {\sum\limits_{i = 1}^{nk} {(\varvec{I}_{i}^{k} + m_{i}^{k} \tilde{\varvec {r}}_{0i}^{k\text{T}} \tilde{\varvec{r}}_{0i}^{k})} } \right)} $$

(8c)

$$ \varvec{J}_{{{\text{T}\omega }}}^{k} = \sum\limits_{i = 1}^{nk} {m_{i}^{k} \varvec{J}_{{{\text{T}}i}}^{k} } $$

(8d)

$$ \varvec{H}_{\omega \varphi }^{k} = \sum\limits_{i = 1}^{nk} {\left( {\varvec{I}_{i}^{k} \varvec{J}_{Ri}^{k} + m_{i}^{k} \tilde{\varvec{r}}_{0i}^{k} \varvec{J}_{Ti}^{k} } \right)} $$

(8e)

$$ \varvec{H}_{\text{M}}^{k} = \sum\limits_{i = 1}^{nk} {\left( {\varvec{J}_{{{\text{R}}i}}^{{k{\text{T}}}} \varvec{I}_{i}^{k} \varvec{J}_{{{\text{R}}i}}^{k} + m_{i}^{k} \varvec{J}_{{{\text{T}}i}}^{{k{\text{T}}}} \varvec{J}_{{{\text{T}}i}}^{k} } \right)} $$

(8f)

while the intermediate parameters are expressed as

$$ \varvec{r}_{\text{S}} = \frac{{m_{0} \varvec{r}_{0} + \sum\limits_{k = 1}^{N} {\left( {\sum\limits_{i = 1}^{nk} {m_{i}^{k} } \varvec{r}_{i}^{k} } \right)} }}{M} $$

(9a)

$$ \varvec{r}_{0i}^{k} = \varvec{r}_{i}^{k} - \varvec{r}_{0} $$

(9b)

$$ \varvec{J}_{{{\text{T}}i}}^{k} = \left[ {\varvec{z}_{1}^{k} \times (\varvec{r}_{i}^{k} - \varvec{P}_{1}^{k} ) \, , \ldots ,\varvec{z}_{i}^{k} \times (\varvec{r}_{i}^{k} - \varvec{P}_{i}^{k} ), \, {\mathbf{0}} ,\ldots ,{\mathbf{0}}} \right] $$

(9c)

$$ \varvec{J}_{{{\text{R}}i}}^{k} = \left[ {\varvec{z}_{1}^{k} , \ldots ,\varvec{z}_{i}^{k} , \, {\mathbf{0}} ,\ldots ,{\mathbf{0}}} \right] $$

(9d)

The nonlinear bias force term C is independent from the system acceleration term ${\ddot{\varvec{q}}}$, and we can calculate it under the Newton–Euler recursion framework [33] by setting ${\ddot{\varvec{q}}} = {\mathbf{0}}$. Here, the recursive computations include two steps: the outward recursion of the velocity and acceleration terms and the inward recursion of the force and torque terms. We can rewrite Eqs. (2) and  (3) to obtain the outward velocity recursions ($i = 1,2, \ldots ,nk$) as

$$ \varvec{\omega}_{i}^{k} =\varvec{\omega}_{i - 1}^{k} + \varvec{z}_{i}^{k} \dot{\theta }_{i}^{k} $$

(10)

$$ \varvec{v}_{i}^{k} = \varvec{v}_{i - 1}^{k} +\varvec{\omega}_{i - 1}^{k} \times \varvec{b}_{i - 1}^{k} +\varvec{\omega}_{i}^{k} \times \varvec{a}_{i}^{k} $$

(11)

The acceleration recursions are obtained as

$$ \dot{\varvec{\omega }}_{i}^{k} = \dot{\varvec{\omega }}_{i - 1}^{k} +\varvec{\omega}_{i - 1}^{k} \times \varvec{z}_{i}^{k} \dot{\theta }_{i}^{k} + \varvec{z}_{i}^{k} \ddot{\theta }_{i}^{k} $$

(12)

$$ \begin{aligned} \dot{\varvec{v}}_{i}^{k} = \dot{\varvec{v}}_{i - 1}^{k} + \dot{\varvec{\omega }}_{i - 1}^{k} \times \varvec{b}_{i - 1}^{k} +\varvec{\omega}_{i - 1}^{k} \times (\varvec{\omega}_{i - 1}^{k} \times \varvec{b}_{i - 1}^{k} ) \hfill \\ \, &+ \dot{\varvec{\omega }}_{i}^{k} \times \varvec{a}_{i}^{k} +\varvec{\omega}_{i}^{k} \times (\varvec{\omega}_{i}^{k} \times \varvec{a}_{i}^{k} ) \hfill \\ \end{aligned} $$

(13)

According to the Newton–Euler equations,

$$ \varvec{f}_{{{\text{R}}0}} = m_{0} \dot{\varvec{v}}_{0} $$

(14)

$$ \varvec{n}_{{{\text{R}}0}} = \varvec{I}_{0} \dot{\varvec{\omega }}_{0} +\varvec{\omega}_{0} \times \varvec{I}_{0}\varvec{\omega}_{0} $$

(15)

$$ \varvec{f}_{{{\text{R}}i}}^{k} = m_{i}^{k} \dot{\varvec{v}}_{i}^{k} $$

(16)

$$ \varvec{n}_{{{\text{R}}i}}^{k} = \varvec{I}_{i}^{k} \dot{\varvec{\omega }}_{i}^{k} +\varvec{\omega}_{i}^{k} \times \varvec{I}_{i}^{k}\varvec{\omega}_{i}^{k} $$

(17)

where $\varvec{f}_{{{\text{R}}0}}$ and $\varvec{n}_{{{\text{R}}0}}$ are the resulting force and torque of the base, and $\varvec{f}_{{{\text{R}}i}}^{k}$ and $\varvec{n}_{{{\text{R}}i}}^{k}$ are the resulting force and torque of body i of arm-k.

Meanwhile, the inward force and torque recursions ($i = nk - 1, \, nk - 2, \ldots ,1$) are formulated as

$$ \varvec{f}_{i}^{k} = \varvec{f}_{{{\text{R}}i}}^{k} + \varvec{f}_{i + 1}^{k} $$

(18)

$$ \varvec{n}_{i}^{k} = \varvec{n}_{{{\text{R}}i}}^{k} + \varvec{n}_{i + 1}^{k} - \varvec{f}_{i}^{k} \times \varvec{a}_{i}^{k} + \varvec{f}_{i + 1}^{k} \times \varvec{b}_{i}^{k} $$

(19)

$$ \varvec{f}_{0} = \varvec{f}_{{{\text{R}}0}} + \sum\limits_{k = 1}^{N} {\varvec{f}_{1}^{k} } $$

(20)

$$ \varvec{n}_{0} = \varvec{n}_{{{\text{R}}0}} + \sum\limits_{k = 1}^{N} {\varvec{n}_{1}^{k} } $$

(21)

where $\varvec{f}_{i}^{k}$ and $\varvec{n}_{i}^{k}$ are the force and torque of body i-1 acting on body i in arm-k. If $i = nk$ ,there exist the relationships $\varvec{f}_{nk}^{k} = \varvec{f}_{{{\text{R}}nk}}^{k}$ and $\varvec{n}_{nk}^{k} = \varvec{n}_{{{\text{R}}nk}}^{k} + \varvec{f}_{nk}^{k} \times \varvec{a}_{nk}^{k}$. The driving torque of joint i of arm-k can be derived as

$$ \tau_{i}^{k} = \varvec{n}_{i}^{k} \varvec{z}_{i}^{k} $$

(22)

Furthermore, we rewrite the nonlinear bias force C in the matrix form. According to Eqs. (10)–(22), we can express

$$ \varvec{C}\text{ = }\left[ {\begin{array}{*{20}c} {\varvec{C}_{\text{B}} } \\ {\varvec{C}_{\text{M}}^{1} } \\ \vdots \\ {\varvec{C}_{\text{M}}^{N} } \\ \end{array} } \right]\text{ = }\left[ {\begin{array}{*{20}c} {\varvec{c}_{\text{B}} } & {\varvec{c}_{\text{BM}}^{1} } & \ldots & {\varvec{c}_{\text{BM}}^{N} } \\ {\varvec{c}_{\text{MB}}^{1} } & {\varvec{c}_{\text{M}}^{1} } & {\mathbf{0}} & {\mathbf{0}} \\ \vdots & {\mathbf{0}} & \ddots & {\mathbf{0}} \\ {\varvec{c}_{\text{MB}}^{N} } & {\mathbf{0}} & {\mathbf{0}} & {\varvec{c}_{\text{M}}^{N} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{\varvec{X}}_{0} } \\ {\dot{\varvec{\theta }}_{\text{M}}^{1} } \\ \vdots \\ {\dot{\varvec{\theta }}_{\text{M}}^{N} } \\ \end{array} } \right]\text{ = }f_{\text{NE}} ({\ddot{\varvec{q}}} \text{ = }{\mathbf{0}}) $$

(23)

where $\varvec{c}_{\text{B}}$, $\varvec{c}_{\text{M}}^{k}$, and $\varvec{c}_{\text{BM}}^{k}$ are the nonlinear Coriolis and centrifugal force matrices that correspond to the base, arm-k, and base and arm-k coupling term, respectively, and $f_{\text{NE}} ( \cdot )$ represents the Newton–Euler recursive function. Therefore, we have derived the nominal dynamics equation of the multi-arm space robot system, namely $\varvec{H}\ddot{\varvec{q}} + \varvec{C} = \varvec{F}$.

3 Coupling analysis and decoupling control strategy

In this section, we will analyze the dynamic coupling effect on the multi-arm space robot system qualitatively. As the TDE has an intrinsic adaptability, we aim to design a controller with a simple structure to address this tough issue. Here, a simple TDE-based SMC is proposed to realize the decoupling control, and the classical boundary layer method is used to alleviate the SMC chattering. Meanwhile, we want to evaluate and demonstrate the merits of the TDE, so the conventional CTC and the CTC-based SMC are introduced for contrastive studies.

3.1 Qualitative analysis of the dynamic coupling

Early research [22, 24] focused on the satellite with a single arm. The traditional approach is very intuitive, which divides the entire system into two subsystems, namely the base control system and the manipulator control system, as illustrated in Fig. 2. Also, two independent controllers are designed to control the two subsystems, respectively. However, for a multi-arm space robot system, the dynamic coupling occurs not only between arms and the base but also between arms [14]. Thus, the traditional decoupling strategy will be difficult to use in this occasion.

Fig. 2

Traditional subsystem decoupling strategy [22]

According to Eqs. (4) and (23), we obtain the dynamics equation for a dual-arm space robot, which can be divided into three subsystems as follows:

$$ \varvec{H}_{\text{M}}^{ 1} {\ddot{\varvec{\theta}}} _{\text{M}}^{ 1} { + }\varvec{c}_{\text{M}}^{ 1} \dot{\varvec{\theta }}_{\text{M}}^{ 1} + \varvec{H}_{\text{BM}}^{{ 1 {\text{T}}}} {\ddot{\varvec{X}}} _{ 0} + \varvec{c}_{\text{MB}}^{ 1} \dot{\varvec{X}}_{ 0} =\varvec{\tau}_{\text{M}}^{1} $$

(24a)

$$ \varvec{H}_{\text{M}}^{ 2} {\ddot{\varvec{\theta}}} _{\text{M}}^{ 2} { + }\varvec{c}_{\text{M}}^{2} \dot{\varvec{\theta }}_{\text{M}}^{2} + \varvec{H}_{\text{BM}}^{{ 2 {\text{T}}}} {\ddot{\varvec{X}}} _{ 0} { + }\varvec{c}_{\text{MB}}^{2} \dot{\varvec{X}}_{ 0} =\varvec{\tau}_{\text{M}}^{2} $$

(24b)

$$ \varvec{H}_{\text{B}} {\ddot{\varvec{X}}} _{ 0} { + }\varvec{c}_{\text{B}} \dot{\varvec{X}}_{ 0} { + }\varvec{H}_{\text{BM}}^{ 1} {\ddot{\varvec{\theta}}} _{\text{M}}^{ 1} { + }\varvec{c}_{\text{BM}}^{ 1} \dot{\varvec{\theta }}_{\text{M}}^{ 1} { + }\varvec{H}_{\text{BM}}^{2} {\ddot{\varvec{\theta}}} _{\text{M}}^{2} { + }\varvec{c}_{\text{BM}}^{2} \dot{\varvec{\theta }}_{\text{M}}^{2} { = }\varvec{F}_{\text{B}} $$

(24c)

where $\varvec{H}_{\text{BM}}^{{ 1 {\text{T}}}} {\ddot{\varvec{X}}} _{ 0} + \varvec{c}_{\text{MB}}^{ 1} \dot{\varvec{X}}_{ 0}$ is the coupling term that corresponds to the base disturbance impacting on Arm-1. According to Eqs. (24c) and (24b), we know that this dynamic coupling will affect Arm-2; namely, the coupling occurs between two arms. Therefore, the strategy of the subsystem decoupling control is not suitable for multi-arm space robots. In fact, throughout the entire dynamics equation, namely Eq. (4), the term $\varvec{H}\ddot{\varvec{q}}$ is a linear term, but the bias force term C is a nonlinear term. Thus, we will directly design a decoupling strategy based on the entire MIMO system, and the online computation and online estimation methods will be adopted to compensate the nonlinear term.

3.2 Conventional CTC

The conventional CTC is equivalent to using the Newton–Euler equations to calculate the coupling force/torque. As illustrated in Fig. 3, the conventional CTC incorporates the computation of the nonlinear bias force term C and the PD control into the controller, which can realize the decoupling and linearization of the system.

Fig. 3

Conventional CTC decoupling strategy

The control law of the CTC is expressed as

$$ \varvec{F} = \varvec{Hu} + \varvec{C} $$

(25a)

$$ \varvec{u} = {\ddot{\varvec{q}}} _{\text{d}} + \varvec{K}_{\text{D}} \dot{\varvec{e}} + \varvec{K}_{\text{P}} \varvec{e} $$

(25b)

where $\varvec{q}_{\text{d}}$, $\dot{\varvec{q}}_{\text{d}}$, and ${\ddot{\varvec{q}}} _{\text{d}}$ are the desired position, velocity, and acceleration signals, respectively; $\varvec{u}$ is the PD control with a bias term ${\ddot{\varvec{q}}} _{\text{d}}$; $\varvec{e} = \varvec{q}_{\text{d}} - \varvec{q}$ is the position error vector; $\dot{\varvec{e}}$ and $\ddot{\varvec{e}}$ are the velocity and acceleration error vectors, respectively; and $\varvec{K}_{\text{P}}$ and $\varvec{K}_{\text{D}}$ are the proportional and derivative gain matrices, respectively, which are diagonal and positive definite. Substituting Eq. (25) into Eq. (4) yields

$$ {\ddot{\varvec{q}}} = \varvec{u} \Leftrightarrow {\ddot{\varvec{e}}} + \varvec{K}_{\text{D}} \dot{\varvec{e}} + \varvec{K}_{\text{P}} \varvec{e} = {\mathbf{0}} $$

(26)

Its stability can be easily proven by differentiating the following positive-definite quadratic Lyapunov function:

$$ V = \frac{1}{2}\dot{\varvec{e}}^{\text{T}} \dot{\varvec{e}} + \frac{1}{2}\varvec{e}^{\text{T}} \varvec{K}_{\text{P}} \varvec{e} \Rightarrow \dot{V} = - \dot{\varvec{e}}^{\text{T}} \varvec{K}_{\text{D}} \dot{\varvec{e}} \le 0 $$

(27)

3.3 CTC-based SMC

For the conventional CTC, its control performance mainly depends on the accuracy of the system model, and it is difficult to deal with disturbances and uncertainties. If we consider disturbances and uncertainties, the nominal model can be modified to

$$ \varvec{H}\ddot{\varvec{q}} + \varvec{C} + \varvec{f}_{\text{D}} + \varvec{f}_{\text{U}} = \varvec{F} $$

(28)

where $\varvec{f}_{\text{D}} = \left[ {f_{\text{D1}} ,\ldots , { }f_{Di} , \ldots ,f_{\text{Dn}} } \right]^{\text{T}}$ denotes the disturbance force/torque vector with the ith element restricted by its bound, i.e., $\left| {f_{Di} } \right| \le D_{i}$, and $\varvec{f}_{\text{U}} = [f_{\text{U1}} ,\ldots , { }f_{{{\text{U}}i}} ,\ldots , \, f_{{{\text{U}}n}} ]^{\text{T}}$ denotes the uncertain dynamics, i.e., $\varvec{f}_{\text{U}} = \Delta \varvec{H}\ddot{\varvec{q}} + \Delta \varvec{C}$, with the ith element restricted by its bound, i.e., $\left| {f_{{{\text{U}}i}} } \right| \le U_{i}$.

SMC is a well-known robust method that maintains the robustness of the system against disturbances and model uncertainties with a fast response and satisfactory transient performance. Thus, based on the decoupling principle of the CTC, we design a CTC-based SMC controller, as illustrated in Fig. 4.

Fig. 4

CTC-based SMC decoupling strategy

First, we design a sliding surface vector as follows:

$$ \varvec{s} = \dot{\varvec{e}} + \varvec{\varLambda e} $$

(29)

where $\varvec{\varLambda}$ is the sliding surface matrix which is a diagonal and positive-definite matrix. Differentiating Eq. (29) with respect to time yields

$$ \dot{\varvec{s}} = {\ddot{\varvec{e}}} + \varvec{\varLambda} \dot{\varvec {e}} = {\ddot{\varvec{q}}} _{d} - {\ddot{\varvec{q}}} + \varvec{\varLambda} \dot{\varvec{e}} $$

(30)

According to Eq. (4), we can obtain ${\ddot{\varvec{q}}} = \varvec{H}^{ - 1} (\varvec{F} - \varvec{C})$. By setting $\dot{\varvec{s}}$ to be zero, we can obtain an equivalent control law

$$ \varvec{F}_{\text{CTCeq}} = \varvec{H}({\ddot{\varvec{q}}} _{d} + \varvec{\varLambda} \dot{\varvec{e}}) + \varvec{C} $$

(31)

where $\varvec{F}_{\text{CTCeq}}$ is the equivalent control law based on the nominal model, which keeps the system trajectory moving on the sliding surface without considering disturbances or uncertainties. Thus, the control law of the CTC-based SMC is expressed as

$$ \varvec{F} = \varvec{F}_{\text{CTCeq}} + \varvec{G}{\text{sgn}}(\varvec{s} ) $$

(32)

where $\varvec{G} = {{diag}}(G_{1} , \ldots ,G_{i} , \ldots ,G_{n} )$ is the switching gain matrix, which is diagonal and positive definite, and its ith diagonal element is set to meet the condition $G_{i} > D_{i} + U_{i}$; ${\text{sgn}}( \cdot )$ is the sign function, and ${\text{sgn}}(\varvec{s} ) = [{\text{sgn}}(s_{1} ) ,\ldots , {\text{sgn}}(s_{i} ) ,\ldots , {\text{sgn}}(s_{n} ) ]^{\text{T}}$; and $\varvec{G}{\text{sgn}}(\varvec{s} )$ is the robust switching term against disturbances and uncertainties. Its stability can be evaluated by selecting the following Lyapunov function:

$$ V = \frac{1}{2}\varvec{s}^{\text{T}} \varvec{s} $$

(33)

Differentiating Eq. (33) with respect to time and substituting Eq. (28) and Eq. (32) into it yield

$$ \begin{aligned} \dot{V} = \varvec{s}^{\text{T}} \dot{\varvec{s}} \hfill \\ \, = \varvec{s}^{\text{T}} ({\ddot{\varvec{q}}} _{\text{d}} - {\ddot{\varvec{q}}} + \varvec{\varLambda} \dot{\varvec{e}}) \, \hfill \\ \, = \varvec{s}^{\text{T}} ({\ddot{\varvec{q}}} _{\text{d}} - \varvec{H}^{ - 1} (\varvec{F} - \varvec{C} - \varvec{f}_{\text{D}} - \varvec{f}_{\text{U}} ) + \varvec{\varLambda} \dot{\varvec{e}}) \hfill \\ \, = \varvec{s}^{\text{T}} ({\ddot{\varvec{q}}} _{\text{d}} - \varvec{H}^{ - 1} (\varvec{F}_{\text{CTCeq}} + \varvec{G}{\text{sgn}}(\varvec{s} )- \varvec{C} - \varvec{f}_{\text{D}} - \varvec{f}_{\text{U}} ) + \varvec{\varLambda} \dot{\varvec{e}}) \hfill \\ \, = \varvec{s}^{\text{T}} (\varvec{H}^{ - 1} )(\varvec{f}_{\text{D}} { + }\varvec{f}_{\text{U}} - \varvec{G}{\text{sgn}}(\varvec{s} )) \hfill \\ \, = \varvec{s}^{\text{T}} (\varvec{H}^{ - 1} )(\varvec{f}_{\text{D}} + \varvec{f}_{\text{U}} ) - \left| {\varvec{s}^{\text{T}} } \right|(\varvec{H}^{ - 1} )\varvec{G^{\prime}} \hfill \\ \end{aligned} $$

(34)

where $\varvec{G^{\prime}} = [G_{1} , \ldots ,G_{i} , \ldots ,G_{n} ]^{\text{T}}$ is the corresponding switching gain vector and its ith element is equal to the ith diagonal element of the switching gain matrix $\varvec{G}$. As $G_{i} > D_{i} + U_{i}$ and $\varvec{H}^{ - 1}$ is a diagonal and positive-definite matrix, we can deduce that $\dot{V} \le 0$. Thus, its stability is proven.

As the discontinuous sign function ${\text{sgn}} (\cdot )$ is used for generating the high frequently switching action in the control input, which usually causes the control chattering effect, many effective methods are proposed to regulate the switching term for alleviating the chattering effect, such as the supervising control [35], the super-twisting algorithm [36], and the fuzzy logic method [37]. In consideration of the simplicity and effectiveness of the controller design, the classical boundary layer method [38, 39] is adopted in this study. Here, ${\text{sat}}(\varvec{s} ,\varvec{\psi}) = [{\text{sat}}(s_{1} ,\psi_{1} ) ,\ldots , {\text{sat}}(s_{i} ,\psi_{i} ) ,\ldots , {\text{sat}}(s_{n} ,\psi_{n} ) ]^{\text{T}}$ is used to replace ${\text{sgn}}(\varvec{s} )$, and the ith boundary layer function ${\text{sat}}(s_{i} , \psi_{i} )$ is defined as

$${\text{sat(}}s_{i} {\text{, }}\psi _{i} {\text{)}} = \left\{ {\begin{array}{*{20}c} {\frac{{s_{i} }}{{\left| {s_{i} } \right|}},{\text{ if}}\left| {s_{i} } \right| > \psi _{i} } \\ {\frac{{s_{i} }}{{\psi _{i} }},{\text{ if}}\left| {s_{i} } \right| \le \psi _{i} } \\ \end{array} } \right. $$

(35)

where $\varvec{\psi}= [\psi_{1} , \ldots ,\psi_{i} , \ldots ,\psi_{n} ]^{\text{T}}$ is the boundary layer width vector, and $\psi_{i}$ is the ith boundary layer width.

As shown in Fig. 5, it is obvious that if the boundary layer width $\psi_{i}$ approaches to zero, ${\text{sat}}(s_{i} , { }\psi_{i} )$ will become the real sign function ${\text{sgn}}(s_{i} )$. For alleviating the chattering problem, the boundary layer creates a buffer area, which can attenuate the high-frequency switching control around the sliding surface, so $\psi_{i}$ works as a threshold for entering the buffer area. If $\psi_{i}$ increases, the control input will be smooth, but the robustness of the controller will degrade, which may cause a steady-state error. Thus, the selection of the boundary layer width is a crucial problem for the trade-off between the control accuracy and the chattering. Generally, if no chattering occurs, we will set the width of the boundary layer as small as possible, and the dynamics within the strip can be called the “quasi-sliding mode.” Sometimes, the system should be controlled in the presence of disturbances or unknown uncertainties. If the disturbance and uncertainty cause the state variable to be far away from the steady state, i.e., $\left| \varvec{e} \right|$ has a large value, we can increase the switching gain $\varvec{G}$ to reduce the steady-state error. If the disturbances and uncertainties cause a high-frequency oscillation of the state variable around the boundary layer, we can increase the width of the boundary layer to alleviate it.

Fig. 5

Boundary layer function

3.4 TDE-based SMC

Compared with the first two controllers, the TDE [31] does not require the online computation of the model parameters $\varvec{H}$ and $\varvec{C}$. The main strategy of the TDE controller is to incorporate a new constant diagonal gain matrix to reformat the dynamics equation and to use the time-delay information to estimate the new unknown nonlinear term. Thus, the TDE-based controller is an intrinsically adaptive controller, and the SMC can increase the robustness of the controller. The block scheme of the TDE-based SMC is illustrated in Fig. 6.

Fig. 6

TDE-based SMC decoupling strategy

First, by introducing a constant diagonal matrix $\bar{\varvec{H}}$ and combining it with Eq. (28), we can obtain a new form of the dynamics equation as follows:

$${\bar{ \varvec {H}}\ddot{q}} + \varvec{N} = \varvec{F} $$

(36a)

$$ \varvec{N} = (\varvec{H} - \bar{\varvec{H}} ){\ddot{\varvec{q}}} \text{ + }\varvec{C} + \varvec{f}_{\text{D}} + \varvec{f}_{\text{U}} $$

(36b)

where $\varvec{N}$ is a new nonlinear term that includes the Coriolis which is unknown but bounded. According to Eq. (36a), which is unknown but bounded. According to Eq. (36a), $\bar{\varvec{H}}$ is a diagonal matrix, and if we can estimate the term $\varvec{N}$ with a certain degree of accuracy and compensate for it in real time, we will decouple and linearize Eq. (36a). As the space robot is a continuous variable dynamic system, $\varvec{N}$ can be estimated by the TDE, and the dynamics model, namely Eq. (36a), is modified to be

$${\bar{ \varvec {H}}\ddot{q}} + \hat{\varvec{N}} = \varvec{F} $$

(37a)

$$ \hat{\varvec{N}} \approx \varvec{N}\text{(}t - \delta \text{)} $$

(37b)

where $\hat{\varvec{N}}$ is the estimation of $\varvec{N}$; $\varvec{N}\text{(}t - \delta \text{)}$ is the TDE term that represents $\varvec{N}$ at the previous time; and $\delta$ is the sampling period of the control system, which directly affects the online estimation accuracy of the TDE and is usually set to be sufficiently small. According to Eq. (36a), we know that

$$ \varvec{N}\text{(}t - \delta \text{) = }\varvec{F}\text{(}t - \delta \text{)} - {\bar{\varvec {H}}\ddot{q}}\text{(}t - \delta \text{)} $$

(38)

As illustrated in Fig. 6, the TDE-based SMC is similar to the CTC-based SMC, wherein the sliding surface vector is designed to be the same as Eq. (29), namely $\varvec{s} = \dot{\varvec{e}} + \varvec{\varLambda e}$. Differentiating $\varvec{s}$ with respect to time and setting $\dot{\varvec{s}}$ to be zero, we can obtain an equivalent control based on Eq. (37a):

$$ \varvec{F}_{\text{TDEeq}} = \bar{\varvec{H}}({\ddot{\varvec{q}}} _{\text{d}} + \varvec{\varLambda} \dot{\varvec{e}}) + \hat{\varvec{N}} $$

(39)

where $\varvec{F}_{\text{TDEeq}}$ is the equivalent control law based on the modified model. The control law of the TDE-based SMC is

$$ \varvec{F} = \varvec{F}_{\text{TDEeq}} + \varvec{G}{\text{sgn}}(\varvec{s} ) $$

(40)

where $\varvec{G}{\text{sgn}}(\varvec{s} )$ is the same as in Eq. (32), which is the robustness term against disturbances and uncertainties.

For its stability, we select the same Lyapunov function candidate as used in Eq. (33) and differentiate it with respect to time. Furthermore, according to Eq. (36a), we obtain

$$ \begin{aligned} \dot{V}& = \varvec{s}^{\text{T}} ({\ddot{\varvec{q}}} _{\text{d}} - \bar{\varvec{H}}^{ - 1} (\varvec{F} - \varvec{N}) + \varvec{\varLambda} \dot{\varvec{e}}) \hfill \\ \, &= \varvec{s}^{\text{T}} ({\ddot{\varvec{q}}} _{\text{d}} - \bar{\varvec{H}}^{ - 1} (\varvec{F}_{\text{TDEeq}} + \varvec{G}{\text{sgn}}(\varvec{s} )- \varvec{N}) + \varvec{\varLambda} \dot{\varvec{e}}) \hfill \\ \, &= \varvec{s}^{\text{T}} \bar{\varvec{H}}^{ - 1} (\varvec{N} - \hat{\varvec{N}} - \varvec{G}{\text{sgn}}(\varvec{s} )) \hfill \\ \, &= \varvec{s}^{\text{T}} \bar{\varvec{H}}^{ - 1} (\varvec{N} - \hat{\varvec{N}}) - \left| {\varvec{s}^{\text{T}} } \right|(\bar{\varvec{H}}^{ - 1} )\varvec{G^{\prime}} \hfill \\ \end{aligned} $$

(41)

where $\varvec{\varepsilon}{ = }\varvec{N} - \hat{\varvec{N}}$ denotes the TDE error vector. According to Ref. [31], we know that $\varvec{\varepsilon}$ is bounded, i.e., the ith element of $\varvec{\varepsilon}$ satisfies $\left| {\varepsilon_{i} } \right| \le E_{i}$, and we can deduce $\dot{V} < 0$ by setting $G_{i} > E_{i}$; hence, its stability is proven. Likewise, the boundary layer function ${\text{sat}}(\varvec{s},\varvec{\psi} )$ is used to replace ${\text{sgn}}(\varvec{s} )$ in Eq. (41). A detailed proof of the boundedness of ε is provided in Appendix.

In summary, the conventional CTC and the CTC-based SMC are model-based decoupling control methods, because the online parameter computation is needed to compensate the nonlinear bias force term. Although the CTC-based decoupling strategy is intuitive and explicit, it strongly depends on the accuracy of the system model. Disturbances or uncertainties may deteriorate its control performance. Moreover, if the model parameters of the multi-arm space robot system are high dimensional, the online computation burden for the CTC decoupling method will increase accordingly. However, the TDE technique provides us a new perspective, which incorporates a constant diagonal gain matrix to reformulate the dynamics equation and uses the control input and output information from the previous sampling time to estimate the new nonlinear term. Via its transient learning nature and simple decoupling principle, the TDE and SMC can complement and reinforce each other.

4 Numerical simulation

In this section, the simulations in contrast to the conventional CTC and the CTC-based SMC are made to verify the advantages of the TDE-based SMC, where we use a 2D dual-arm space robot (in Fig. 7) through three case studies, namely the nominal model, the model with disturbances, and the model with disturbances and uncertainties. Additionally, to verify the computational efficiency of the TDE-based SMC, another case study on analyzing different delay lengths is conducted after the three case studies above.

Fig. 7

Dual-arm space robot system

As shown in Fig. 7, the dual-arm space robot aims at grasping a floating target, where the base is controlled to perform the station-keeping maneuver and Arm-1 and Arm-2 are controlled to grasp the target. The initial base position is set as $\varvec{r}_{0} = [0.8,{ 1} . 5]^{\text{T}} (m)$, and the initial attitude angle is set as $\theta_{0} = - 15^{ \circ }$. The position of the target’s Tip-1 and Tip-2 is set as $\varvec{P}_{\text{T1}} = [3.2,{ 1} . 4]^{\text{T}} (m)$ and $\varvec{P}_{\text{T2}} = [3.04471,{ 0} . 8 2 0 4 4]^{\text{T}} (m)$, respectively. The attitude angles for grasping Tip-1 and Tip-2 are set as $\theta_{\text{T1}} = - 60^{ \circ }$ and $\theta_{\text{T2}} = 30^{ \circ }$, respectively. The fifth-order polynomial curves [19] are used to plan joint trajectories, and the terminal time is set as: $t_{\text{f}} = 10{\text{ s}}$. As the base is kept still, we can easily obtain the planned joint trajectories as shown in Fig. 8. The D-H parameters of the dual-arm space robot are specified in Table 2 and the initial parameters are given in Table 3, where the presuperscript ${}^{i}( \cdot )^{k}$ denotes that the parameter is defined in body i frame of arm-k, i.e.,$\sum_{i}^{k}$. Meanwhile, the desired grasping process of the dual-arm space robot is illustrated in Fig. 9.

Fig. 8

Planned joint trajectories

Table 2 D-H parameters of the dual-arm space robot

Table 3 Inertial parameters of the dual-arm space robot

Fig. 9

Grasping process of the dual-arm space robot

4.1 Case A: The nominal model

In this case, we will evaluate the control performances of the three controllers using the nominal model, namely Eq. (4).

For the conventional CTC, the proportional and derivative gain matrices $\varvec{K}_{\text{P}}$ and $\varvec{K}_{\text{D}}$ are diagonal and positive definite, and the system can achieve the global asymptotic stability. Since Eq. (26) is a decoupled model, and the suitable $\varvec{K}_{\text{P}}$ and $\varvec{K}_{\text{D}}$ can be easily obtained by the trial-and-error method. Usually, we first set the order of magnitude of $\varvec{K}_{\text{P}}$, each element of which can be roughly estimated according to the inertial parameters of the system in Table 3. Then, we set $\varvec{K}_{\text{D}}$ to improve the dynamic performance of the system. Here, the proportional and derivative gain matrices are set as $\varvec{K}_{\text{P}} = {{diag}}$(1,500,000, 1,600,000, 8,000,000, 80,000, 40,000, 10,000, 80,000, 40,000, 10,000) and $\varvec{K}_{\text{D}} =$${diag}$(500,000, 500,000, 150,000, 2500, 1000, 550, 2500, 1000, 550), respectively. In addition, we can seek the optimal parameters of $\varvec{K}_{\text{P}}$ and $\varvec{K}_{\text{D}}$ by some heuristic algorithms such as particle swarm optimization [40, 41].

For the CTC-based SMC, we need to set the sliding surface matrix $\varvec{\varLambda}$, the switching gain matrix $\varvec{G}$, and the boundary layer width vector $\varvec{\psi}$. In general, $\varvec{\varLambda}$ just affects the sliding surface structure, so any diagonal and positive-definite matrices can meet the requirement. In Section III, the settings of $\varvec{G}$ and $\varvec{\psi}$ have been discussed before. Here, we set $\varvec{\varLambda}= diag$(1, 1, 1, 1, 1, 1, 1, 1, 1), $\varvec{G} = diag$(0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3), and $\varvec{\psi}\text{ = }$[4, 4, 4, 4, 4, 4, 4, 4, 4]^T × 10⁻³.

For the TDE-based SMC, the sampling period should be sufficiently small for guaranteeing the TDE accuracy, and we choose $\delta = 1{\text{ms}}$. The space robot controller runs at a 1 ms rate, which is the same as the research in [42]. The constant diagonal matrix of the TDE-based SMC is set as $\bar{\varvec{H}} = diag$(10, 10, 20, 1, 1, 1, 1, 1, 1). The sliding surface matrix, the switching gain matrix, and the boundary layer width vector are set to be the same with the parameters of the CTC-based SMC. Figure 10 shows the state error and the driving force and torque of three different controllers.

Fig. 10

Control results in Case A

4.2 Case B: The model with disturbances

In this case, disturbances are considered in the model, where the disturbance force/torque signals are assumed as follows:

$$\left\{ {\begin{array}{*{20}l} {f_{{{\text{DBx}}}} = f_{{{\text{DBy}}}} = \tau _{{{\text{DBz}}}} = 0.2(sin(0.5\pi t) + sin(2\pi t))} \hfill \\ {\tau _{{{\text{D1}}}}^{1} = \tau _{{{\text{D2}}}}^{1} = \tau _{{{\text{D3}}}}^{1} = 0.05(sin(2.5\pi t) + \sin (0.4\pi t))} \hfill \\ {\tau _{{{\text{D1}}}}^{2} = \tau _{{{\text{D2}}}}^{2} = \tau _{{{\text{D3}}}}^{2} = 0.05(sin(2.5\pi t) + \sin (0.4\pi t))} \hfill \\ \end{array} } \right. $$

(42)

where $f_{\text{DBx}}$ and $f_{\text{DBy}}$ are the base disturbance forces in the two axis directions of $\sum_{\text{B}}$; $\tau_{\text{DBz}}$ is the base disturbance torque; and $\tau_{{{\text{D}}i}}^{\text{k}}$ is the disturbance torque of joint i in arm-k.

For the conventional CTC, the control parameters are the same as the control parameters used in Case A. For the CTC-based SMC, the switching gain matrix is ${\varvec{G}} = {diag}$ (0.5, 0.5, 0.5, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3), and the other parameters are the same as the control parameters used in Case A. For the TDE-based SMC, the switching gain matrix is ${\varvec{G}} = {diag}$ (0.5, 0.5, 0.5, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3), and the other parameters are the same as the control parameters used in Case A. Their control performances are shown in Fig. 11.

Fig. 11

Control results in Case Bn

4.3 Case C: The model with disturbances and uncertainties

In this case, disturbances and uncertainties are considered in the simulation, where the disturbance force/torque signals are identical to those in Case B, namely as defined in Eq. (42). For the uncertainty, we assume that each robotic arm carries an unknown payload to track the planned trajectories and to keep the base still. Thus, the uncertainty is caused by the unknown payload, which leads to the inertial parameter changes of the end link of each arm. Here, we assume that the inertial parameters of link 3 with EE of each arm (Table 3) are changed to be $m_{3}^{1} = m_{3}^{2} = 13 \, kg$ and ${}^{3}I_{\text{z}}^{1} = {}^{3}I_{\text{z}}^{2}$$= 1.3 \, kg \cdot m^{2}$, and herein, the model uncertainties are unknown to the controller.

For the conventional CTC, the CTC-based SMC, and the TDE-based SMC, the control parameters are the same as the control parameters used in Case B. The corresponding control results are presented in Fig. 12.

Fig. 12

Control results in Case C

4.4 Case D: The TDE-based SMC with different time-delay lengths

In the above three cases, we test the control performances of three different controllers with consideration of disturbances and parameter uncertainties. For the TDE-based SMC, its sampling period is set as $\delta = 1{\text{ms}}$. In fact, the time-delay length (i.e., the sampling period) has a big impact on the control accuracy of the TDE. Usually, the smaller the time-delay length is, the better the control accuracy of the TDE is. In this case, we will compare and analyze the TDE-based SMC with different time-delay lengths ($\delta =$ 0.5 ms, 1 ms, 2 ms, and 4 ms), in which the model with disturbances and uncertainties is identical to the model used in the Case C. The control performance of the TDE-based SMC with $\delta =$ 1 ms is presented in Fig. 12c, and the control results using other delay lengths are shown in Fig. 13.

Fig. 13

Control results of the TDE-based SMC with different time-delay lengths

4.5 Comparison and discussion

For the comparison of three different controllers, we will evaluate the control accuracy and input force/torque quantitatively using the following indicators:

$$ \left\| e \right\|_{\text{RMS}} = \sqrt {\frac{1}{{N_{\text{S}} }}\sum\limits_{i = 1}^{{N_{\text{S}} }} {\left\| {e(i)} \right\|^{2} } } $$

(43a)

$$ \left\| F \right\|_{\text{RMS}} = \sqrt {\frac{1}{{N_{\text{S}} }}\sum\limits_{i = 1}^{{N_{\text{S}} }} {\left\| {F(i)} \right\|^{2} } } $$

(43b)

$$ \left\| \tau \right\|_{\text{RMS}} = \sqrt {\frac{1}{{N_{\text{S}} }}\sum\limits_{i = 1}^{{N_{\text{S}} }} {\left\| {\tau (i)} \right\|^{2} } } $$

(43c)

where $\left\| e \right\|_{\text{RMS}}$ is the root mean square of the control accuracy error; $\left\| F \right\|_{\text{RMS}}$ and $\left\| \tau \right\|_{\text{RMS}}$ are the root mean squares of the control input force and torque, respectively; $e(i)$ is the control accuracy error at the ith sampling; $F(i)$ and $\tau (i)$ are the control input force and torque, respectively, at the ith sampling time; and $N_{\text{S}}$ is the total number of sampling times.

The statistical results of the error indicators and the control inputs of the three different controllers are presented in Tables 4 and 5, respectively. In Case A, the control accuracy of the CTC-based SMC and the TDE-based SMC is 1–2 orders of magnitude higher than the conventional CTC in nearly all the error indicators; their control inputs are within the same order of magnitude. In Case B and Case C, it is obvious that the disturbances and uncertainties degrade the control accuracy of the conventional CTC and the CTC-based SMC, especially in terms of the base attitude accuracy. However, the TDE-based SMC is almost immune to disturbances and uncertainties, and its control performance can be guaranteed at the same order of magnitude.

Table 4 Statistical results of the state errors of the first three case studies

Table 5 Statistical results of the control inputs of the first three case studies

In Case D, the TDE-based SMC with different delay lengths shows different control performances. As shown in Figs. 12c and.13, the controller with $\delta =$ 0.5 ms and the controller with $\delta =$ 1 ms have the same control accuracy in all the error indicators, and the controller with $\delta =$ 2 ms just reduces 1 order of magnitude in the base attitude accuracy. Thus, when the delay length is set as $\delta =$ 1 ms, we can obtain a relatively good performance. For the TDE-based SMC, when the time-delay length is set as $\delta =$ 4 ms, the corresponding error performance degrades slightly, but it is still better than the CTC-based SMC and the conventional CTC. The above analysis illustrated that the TDE-based SMC with a reduced time-delay length can also guarantee the control performance within an acceptable range.

The TDE uses the time-delay information to estimate the unknown nonlinear term, so the TDE-based SMC is an adaptive and robust method. Meanwhile, the case studies above prove its excellent features in the decoupling control.

5 Conclusions and future work

The satellite–manipulator coupling is a significant issue in coordinately controlling multiple-arm space robots in the OOS missions. In this paper, we design three decoupling controllers: the conventional CTC, the CTC-based SMC, and the TDE-based SMC. The results of the first three case studies demonstrate that the TDE-based SMC can outperform the conventional CTC and the CTC-based SMC in terms of control when the model suffers from disturbances and uncertainties. The fourth case study demonstrates that the TDE-based SMC with a reduced time-delay length still achieve a guaranteed control performance. Thanks to the TDE technique, the proposed TDE-based SMC has the following advantages:

• (1) For the decoupling control of multi-arm space robots, the conventional CTC and the CTC-based SMC are model-based methods, which use the online computation to compensate for the nonlinear bias force term $\varvec{C}$ and use the inverse of the inertial matrix $\varvec{H}$ to decouple the system. The TDE-based SMC incorporates a constant diagonal matrix $\bar{\varvec{H}}$ to reformulate the dynamics model and adopts the online estimation of the new nonlinear bias force term $\varvec{N}$, which is a simple and yet efficient decoupling principle with low computational complexity.

• (2) The TDE-based SMC uses the time-delay information to estimate the new nonlinear bias force term $\varvec{N}$; hence, it has intrinsic adaptability, robustness, and model-free traits.

Currently, we verify the TDE-based SMC by the numerical simulation. In the future, we will develop a hardware-in-loop simulation test system for the proposed method.

Appendix

A detailed proof of the boundedness of ε is provided as follows, which is the same as the proof in Refs. [31, 32, 39].

Lemma 1

For the inertial matrix$\varvec{H}$, there exists a constant diagonal matrix$\bar{\varvec{H}}$that satisfies the spectral norm condition, namely$\left\| {\varvec{H}^{ - 1} \bar{\varvec{H}} - \varvec{E}} \right\| < 1$ [34].

Lemma 2

For vectors$\varvec{\alpha}$and$\varvec{\beta}$, if$\varvec{\alpha}= \varvec{A\beta }$, $\varvec{A}$is a symmetric matrix, and$A_{\hbox{max} }$is the maximum eigenvalue of$\varvec{A}$, there exists a conclusion, namely$\left\|\varvec{\alpha}\right\| \le A_{\hbox{max} } \left\|\varvec{\beta}\right\|, \, ({\rm A}_{\hbox{max} }^{k} > 0)$.

According to Eqs. (39) and (40) , we reformulate the control law of the TDE-based SMC as

$$ \varvec{F} = \bar{\varvec{H}}\varvec{u} + \hat{\varvec{N}} $$

(44a)

$$ \varvec{u} = {\ddot{\varvec{q}}} _{\text{d}} + \varvec{\varLambda} \dot{\varvec{e}} + \bar{\varvec{H}}^{ - 1} \varvec{G}{\text{sgn}}(\varvec{s} ) $$

(44b)

Substituting Eqs. (44a) and (37b) into the dynamics equation (Eq. (36a)) yields

$$ \varvec{N}(t) - \varvec{N}\text{(}t - \delta \text{)} = {\bar{\varvec H}\xi }(t) $$

(45a)

$$ \varvec{\xi}(t) = \varvec{u}(t) - {\ddot{\varvec{q}}} (t) $$

(45b)

where$\varvec{\varepsilon}(t) = \varvec{N}(t) - \varvec{N}\text{(}t - \delta \text{)}$. If we want to verify that${\varvec{\varepsilon}}(t)$is bounded, it is equivalent to verify that$\varvec{\xi} (t) = \varvec{u}(t) - \ddot{\varvec{q}}(t)$is bounded. Furthermore, we can obtain

$$ \begin{aligned} & \varvec{H}(t)\varvec{\xi}(t) = \varvec{H}(t)(\varvec{u}(t) - {\ddot{\varvec{q}}} (t)) \\ & = \varvec{H}(t)\varvec{u}(t) - (\varvec{F}(t) - \varvec{C}(t) - \varvec{f}_{\text{D}} (t) - \varvec{f}_{\text{U}} (t)) \\ \end{aligned} $$

(46)

From Eqs. (28), (37b), and (38), we can deduce

$$ \begin{aligned} \hat{\varvec{N}}(t) =&\, (\varvec{H}(t - \delta ) - \bar{\varvec{H}}){\ddot{\varvec{q}}} (t - \delta ) + \varvec{C}(t - \delta ) \\ & + \varvec{f}_{\text{D}} (t - \delta ) + \varvec{f}_{\text{U}} (t - \delta ) \\ \end{aligned} $$

(47)

Substituting Eq. (47) into Eq. (44a) yields

$$ \begin{aligned} \varvec{F}(t) =&\, \bar{\varvec{H}}\varvec{u} + (\varvec{H}(t - \delta ) - \bar{\varvec{H}}){\ddot{\varvec{q}}} (t - \delta ) \\ & + \varvec{C}(t - \delta ) + \varvec{f}_{\text{D}} (t - \delta ) + \varvec{f}_{\text{U}} (t - \delta ) \\ \end{aligned} $$

(48)

Substituting Eq. (48) into Eq. (46) yields

$$ \begin{aligned} \varvec{H}(t)\varvec{\xi}(t) = &\, (\varvec{H}(t) - \bar{\varvec{H}})\varvec{u}(t) + (\bar{\varvec{H}} - \varvec{H}(t - \delta )){\ddot{\varvec{q}}} (t - \delta ) \\ & + \varvec{C}(t) - \varvec{C}(t - \delta ) + \varvec{f}_{\text{D}} (t) - \varvec{f}_{\text{D}} (t - \delta ) \\ & + \varvec{f}_{\text{U}} (t) - \varvec{f}_{\text{U}} (t - \delta ) \\ \end{aligned} $$

(49)

We obtain${\ddot{\varvec{q}}} (t - \delta ) =\varvec{\xi}(t - \delta ) + \varvec{u}(t - \delta )$according to Eq. (45b). Substituting it into Eq. (49) yields

$$ \begin{aligned} \varvec{H}(t)\varvec{\xi}(t) = & (\bar{\varvec{H}} - \varvec{H}(t))(\varvec{\xi}(t - \delta ) + \varvec{u}(t - \delta )) \\ & \quad + (\varvec{H}(t) - \bar{\varvec{H}})\varvec{u}(t) + (\varvec{H}(t) - \varvec{H}(t - \delta )){\ddot{\varvec{q}}} (t - \delta ) \\ & \quad + \varvec{C}(t) - \varvec{C}(t - \delta ) + \varvec{f}_{\text{D}} (t) - \varvec{f}_{\text{D}} (t - \delta ) \\ & \quad + \varvec{f}_{\text{U}} (t) - \varvec{f}_{\text{U}} (t - \delta ) \\ \end{aligned} $$

(50)

Then, we can reformat Eq. (50) as

$$ \varvec{\xi}(t) = \varvec{A}(t)\varvec{\xi}(t - \delta ) +\varvec{\chi}_{1} (t - \delta ) - \varvec{A}(t)\varvec{\chi}_{ 2} (t - \delta ) $$

(51a)

$$ \varvec{A}(t){ = }\varvec{H}^{ - 1} (t)\bar{\varvec{H}} - \varvec{E} $$

(51b)

$$ \begin{aligned}\varvec{\chi}_{1} (t - \delta ) = & \varvec{H}^{ - 1} (t)\{ (\varvec{H}(t) - \varvec{H}(t - \delta )){\ddot{\varvec{q}}} (t - \delta ) \\ & \quad + \varvec{C}(t) - \varvec{C}(t - \delta ) + \varvec{f}_{\text{D}} (t) - \varvec{f}_{\text{D}} (t - \delta ) \\ & \quad + \varvec{f}_{\text{U}} (t) - \varvec{f}_{\text{U}} (t - \delta )\} \\ \end{aligned} $$

(51c)

$$ \varvec{\chi}_{ 2} (t - \delta ) = \varvec{u}(t) - \varvec{u}(t - \delta ) $$

(51d)

Furthermore, we analyze Eq. (51a) in the discrete-time domain. Substituting$t = k\delta$into Eq. (51a) yields

$$ \varvec{\xi}(k) = \varvec{A}(k)\varvec{\xi}(k - 1) +\varvec{\chi}_{1} (k - 1) - \varvec{A}(k)\varvec{\chi}_{ 2} (k - 1) $$

(52)

Via induction and reasoning, we can obtain

$$ \begin{aligned}\varvec{\xi}(k) = \prod\limits_{m = 1}^{k} {\varvec{A}(m)\varvec{\xi}(0)} + \sum\limits_{m = 1}^{k - 1} {\prod\limits_{p = m}^{k - 1} {\varvec{A}(p + 1)} }\varvec{\chi}_{1} (m - 1) \\ { + }\varvec{\chi}_{1} (k - 1) - \sum\limits_{m = 1}^{k} {\prod\limits_{p = m}^{k} {\varvec{A}(p)} }\varvec{\chi}_{2} (m - 1) \\ \end{aligned} $$

(53)

where $\varvec{\xi}(0)$ is the initial value, and we can deduce

$$\begin{aligned} & \left\| {\user2{\varvec{\xi} }(k)} \right\| \le \left\| {\prod\limits_{{m = 1}}^{k} {\user2{A}(m)\user2{\varvec{\xi} }(0)} } \right\| + \left\| {\sum\limits_{{m = 1}}^{{k - 1}} {\prod\limits_{{p = m}}^{{k - 1}} {\user2{A}(p + 1)} } \user2{\varvec{\chi} }_{1} (m - 1)} \right\| \\ & {\text{ + }}\left\| {\user2{\varvec{\chi} }_{1} (k - 1)} \right\| + \left\| {\sum\limits_{{m = 1}}^{k} {\prod\limits_{{p = m}}^{k} {\user2{A}(p)} } \user2{\varvec{\chi }}_{2} (m - 1)} \right\| \\ \end{aligned}$$

(54)

According to Lemma 2, we can deduce

$$ \begin{aligned} \left\| {\varvec{\xi}(k)} \right\| \le = {\rm A}_{\hbox{max} }^{k} \left\| {\varvec{\xi}(0)} \right\| + \sum\limits_{m = 1}^{k - 1} {{\rm A}_{\hbox{max} }^{k - m} } \left\| {\varvec{\chi}_{1} (m - 1)} \right\| \\ { + }\left\| {\varvec{\chi}_{1} (k - 1)} \right\| + \sum\limits_{m = 1}^{k} {{\rm A}_{\hbox{max} }^{k - m + 1} } \left\| {\varvec{\chi}_{2} (m - 1)} \right\| \\ \end{aligned} $$

(55)

According to Lemma 1, we know that$0 < {\rm A}_{\hbox{max} }^{{}} < 1$. Meanwhile,$\left| {\chi_{1i} (k)} \right| < \beta_{1}$and$\left| {\chi_{2i} (k)} \right| < \beta_{2}$, where$\chi_{1i} (k)$and$\chi_{2i} (k)$are, respectively, the ith elements of$\varvec{\chi}_{1} (k)$ and $\varvec{\chi}_{2} (k)$and$\beta_{1}$ and $\beta_{2}$are positive constants. When$k \to \infty$, ${\rm A}_{\hbox{max} }^{k} \to 0$, and we conclude

$$ \left\| {\varvec{\xi}(k)} \right\| \le \frac{{n(\beta_{1} + {\rm A}_{\hbox{max} } \beta_{2} )}}{{1 - {\rm A}_{\hbox{max} } }} $$

(56)

Thus, the boundedness of$\varvec{\xi}(k)$is proven, and the stability of the TDE-based SMC is guaranteed.