1 Introduction

The utilization of space robots [1] is of paramount importance with the increase in space operations including assembly, capturing and construction. Various special tasks (e.g., removal of space debris) can pose a threat to the robotic systems because of the unknown properties of captured objects. In fact, capturing operations by a space robot installed on the spacecraft body need to be limited when the entire system works in a free-floating state [2]. A strong dynamic coupling relationship exists between the spacecraft body and the robotic arm, and the motion of the space robot will lead to instability of the spacecraft body attitude. The ACS (Attitude Control System) of the spacecraft can be employed to ensure the stability of the entire system but with large fuel consumption. The proper path planning of the robotic arm can counteract this effect on the motion of the space robot on spacecraft attitude. No energy problem exists because the sustainable electric energy produced by a solar array can be employed [3]. However, the uncertain properties from the captured unknown object such as space debris can cause the conventional no-disturbance planning methods to be invalid; therefore, precise dynamic knowledge of the entire system is required by the RNS (Reaction Null Space) algorithm or similar [4,5,6,7]. An “identification” process during the post-capture stage was introduced [8,9,10,11] by measuring the property of the captured object and compensating for the path planning and control system. Similar schemes should acquire accurate information of the captured object and bring about high sensor requirements and a delay control issue. To solve this problem, the ARNS (Adaptive Reaction Null Space) method with dynamic changing planning paths for robotic arms [3] during capturing of an unknown object was proposed and introduced to realize the minimum disturbance to the spacecraft body attitude. In this method, the unknown part of the system (the captured object) can be obtained online via the RLS (Recursive Least Square) algorithm and compensation can be made in the form of a time-variable matrix for the path planning equation of the robotic arm. Thus, the delay control issue is solved. The conventional RLS algorithm employed in ARNS exhibits saturation characteristics [12] with the growth of the gain matrix caused by the increased computation, and the online identification for the time-variable term that incorporates the unknown property to construct the planned path will expire, thereby degrading the performance of the path via ARNS. RLS via the forgetting factor [13] could make the ARNS improve its adaptability with limited ability. Furthermore, the SW-RLS algorithm [14] focuses more on the rapidly changed parameters of time-varying systems, and there is no saturation characteristic based on retaining the limited data length by eliminating the older history data.

To realize the reactionless motion for a space robot while capturing an unknown object, an effective reactionless path planning with dynamical changing features is essential. Simultaneously, an efficient control strategy to track the planned path of the space robot is well worth considering because the scheme to realize reactionless motion such as ARNS usually involves ideal path tracking performance, which neglects the effect of the tracking error from the controller and is impossible in reality. To degrade the effects of tracking errors, the control strategy for the controller requires faster tracking speed and less tracking errors to ensure better attitude stability performance for the entire system. Considering the complicated disturbance existing in the control system, such as the abrupt and uncertain changes in system dynamics by capturing an unknown object as well as the original modeling uncertainty of the system, the control strategy to track the adaptive path of a robotic arm needs to be robust and adaptive. Therefore, a single robust controller [15,16,17] or an adaptive controller [18,19,20] can hardly ensure the control performance in capturing the unknown object with abrupt uncertain properties. A compromise is developed with the robust adaptive control strategy [21,22,23,24] to adopt the advantages from both the control strategy, by which the unknown disturbance is learned and compensated via the adaptive strategy, and to reject the model uncertainties via the robust strategy. However, different from the conventional strategy of using the adaptive control to learn the unknown parts of the dynamic system, the space-capturing task attached with the abrupt change in dynamics needs a faster learning and compensating method for the abrupt unknown properties. Traditional adaptive control methods such as a BP (Back Propagation) network [25], RBF (Radial Basis Function) network [25] and fuzzy algorithm [21, 22] exhibit complicated computing processes and are insufficient to deal with the abrupt properties or ensure adaptive speed. Recently, the ELM [26] algorithm was developed for its extremely fast system uncertainty learning and cognizing performance [27, 28]. However, the random input feature settings (input weight, hidden layer bias) of conventional ELM networks could weaken the network performance to some extent because the pre-setting input feature owns the possibility of staying away from its optimal value.

Given the problem, some ameliorated methods by optimizing the input feature of the ELM algorithm have been proposed. Zhu et al. [29] used various types of evolutionary algorithms to determine network input features, which achieved better generalization performance with more compact networks. Particle Swarm Optimization (PSO) was combined with the ELM algorithm in [30] to improve the generalization capacity of the SLFNs (Single-hidden Layer Feed-forward Networks). Xu et al. [31] proposed an evolutionary ELM based on PSO, which can address certain prediction problems more suitably. Han et al. presented an improved ELM algorithm with improved PSO via adaptive inertia in [32] to choose the input feature of the SLFN. In addition, a performance investigation through the PSO-ELM algorithm with various alternative topologies is presented in [33]. The research above with the optimization of the input features of ELM via the PSO algorithm exhibits strong advantages including online parameter adjustment, avoiding optimal input feature value and enhancing the ELM performance. Therefore, in order to satisfy the requirements of faster adaptive performance and higher tracking accuracy for space robots to track the reactionless path, considering the abrupt unknown properties of the manipulating task, a dynamical identification and control strategy without saturation characteristics is developed. This strategy addresses the time-variable matrix for constructing the reactionless path and is necessary to achieve an improved ELM algorithm.

In this paper, an adaptive reactionless path planning and control integrated strategy is proposed for a free-floating space robot while capturing an unknown object, and the work is presented as follows:

  1. (1)

    An adaptive reactionless path planning method is proposed for a space robot, which employs the SW-RLS algorithm to identify and compensate for the unknown properties existing in the system and simultaneously avoids the saturation phenomenon when dealing with time-variable elements during planning.

  2. (2)

    A robust adaptive control strategy is proposed for space robots to track the planned reactionless path, which employs the PSO-ELM algorithm to dynamically learn and compensate for the unknown properties in the form of constructed adaptive control. Herein, the ELM algorithm is used to address the abrupt properties according to its extremely fast learning performance, and the PSO algorithm is used to optimize the input feature of ELM to avoid the optimal value and also to enhance ELM performance. In addition, the designed PD controller is employed to reduce errors associated with computational efficiency, and the robust controller is applied to reject the model uncertainties.

  3. (3)

    To verify the validity of the proposed strategy, simulations of a free-floating space robot with a 4-DOF (Degree of Freedom) robotic arm capturing an unknown object and comparisons with other existing methods are implemented and presented.

This paper is organized as follows. Part II presents the basic dynamic relationship for a free-floating space robot in the post-capture stage, and a dynamic decoupling derivation for the robotic arm is described to construct the basis of the joint controller design. Part III illustrates the form of the ARNS algorithm via SW-RLS algorithm to plan the adaptive reactionless path for the robotic arm, and the details of the proposed robust adaptive control strategy via PSO-ELM are discussed to track the planned path. In Part IV, the simulation is conducted by comparing the performance of the proposed strategy with other conventional strategies. Part V presents the conclusion.

2 Basic dynamics of a free-floating space robot

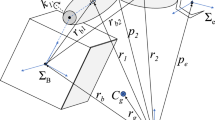
Figure 1 shows a schematic diagram and the vital parameters of a space robot composed of a rigid serial-link robotic arm and the spacecraft. The vectors \({{\varvec{r}}}_{{{\varvec{b}}}}\), \({{\varvec{r}}}_{{{\varvec{i}}} }\) and \({{\varvec{r}}}_{{{\varvec{g}}}}\) denote the centroid position of the spacecraft, link i and the entire robotic system, respectively, expressed in inertial frame. Considering that the system works in a free-floating state without any external forces or torque, i.e., without the employment of momentum exchange devices, the only disturbances of the robotic system are derived from interior factors such as joint friction, measurement noises and model uncertainty. Thus, the robotic system is subject to the law of linear and angular momentum conservation in the post-capture stage. The detailed kinematics and dynamics of a space robot can be found in [2], by which the dynamic equation can be rewritten as follows.

From [2], the basic dynamic equation of the system before capturing can be expressed by Eq. (1).

$$\begin{aligned} {{\varvec{M}}}({{\varvec{q}}})\ddot{{\varvec{q}}}+{{\varvec{C}}}({{\varvec{q}}}, \dot{{\varvec{q}}})\dot{{\varvec{q}}}+{{\varvec{d}}}={\varvec{\tau }} \end{aligned}$$
(1)

Equation (1) illustrates the precise dynamic knowledge of the whole system in the pre-capture stage, without the property of captured object, and the dynamic parameters are regarded as prior data. The matrix \({{\varvec{M(q)}}}\) in Eq. (1) denotes the dynamic inertial matrix of the system, and \({{\varvec{C}}}({{\varvec{q}}},\dot{{\varvec{q}}})\) contains the centrifugal force and Coriolis force of the system; \({{\varvec{d}}}\) denotes the interior disturbance term, and \({\varvec{\tau }}\) is the generalized force composed of the actuating torque of the motors installed on each joint; \({{\varvec{q}}}\) denotes the generalized variable term, which is composed of the angular displacement of each joint.

Fig. 1
figure 1

Space robot in the post-capture stage

Full size image

Given the capturing operation involving an unknown object with appending dynamic parameters, the dynamic parameters of the entire system might be changed, and the dynamic equation of the entire system in the post-capture stage will be rewritten again as Eq. (2). In this equation, \({\hat{{\varvec{M}}}}({{\varvec{q}}})\) and \({\hat{{\varvec{C}}}}({{\varvec{{q}}}},\dot{{\varvec{{q}}}})\) contain the uncertain properties from the captured object, so the uncertain dynamic parameter can be defined by Eq. (3),

$$\begin{aligned}&{\hat{{\varvec{M}}}}({{\varvec{q}}})\ddot{{\varvec{q}}}+{\hat{{\varvec{C}}}}({{\varvec{q}}},\dot{{\varvec{q}}})\dot{{\varvec{q}}}+{{\varvec{d}}}={\varvec{\tau }}\nonumber \\&{\tilde{{\varvec{M}}}}({{\varvec{q}}})={\hat{{\varvec{M}}}}({{\varvec{q}}})-{{\varvec{M}}}({{\varvec{q}}}) \end{aligned}$$
(2)
$$\begin{aligned}&{\tilde{{\varvec{C}}}}({{\varvec{q}}},\dot{{\varvec{q}}})={\hat{{\varvec{C}}}}({{\varvec{q}}},\dot{{\varvec{q}}})-{{\varvec{C}}}({{\varvec{q,}}}\dot{{\varvec{q}}}) \end{aligned}$$
(3)

where \({\tilde{{\varvec{M}}}}({{\varvec{q}}})\) and \({\tilde{{\varvec{C}}}}({{\varvec{q}}},\dot{{\varvec{q}}})\) result from the captured object.

Fig. 2
figure 2

Adaptive reactionless control strategy for space robotic

Full size image

To simplify the form of the existing uncertainties in the system, the composite disturbance \({{\varvec{D}}}\) is defined with Eq. (4) that includes the unknown properties as well as the interior disturbance \({{\varvec{d}}}\).

$$\begin{aligned}&{\varvec{\tau }} ={\hat{{\varvec{M}}}}({{\varvec{q}}})\ddot{{\varvec{q}}}+{\hat{{\varvec{C}}}}({{\varvec{q}}},\dot{{\varvec{q}}})\dot{{\varvec{q}}}+{{\varvec{d}}}\nonumber \\&\quad ={{\varvec{M}}}({{\varvec{q}}})\ddot{{\varvec{q}}}+{{\varvec{C}}}({{\varvec{q}}},\dot{{\varvec{q}}})\dot{{\varvec{q}}}+{{\varvec{d}}}+{\tilde{{\varvec{M}}}}({{\varvec{q}}})\ddot{{\varvec{q}}}+{\tilde{{\varvec{C}}}}({{\varvec{q}}},\dot{{\varvec{q}}})\dot{{\varvec{q}}} \nonumber \\&\quad ={{\varvec{M}}}({{\varvec{q}}})\ddot{{\varvec{q}}}+{{\varvec{C}}}({{\varvec{q}}},\dot{{\varvec{q}}})\dot{{\varvec{q}}}+{{\varvec{D}}} \nonumber \\&{{\varvec{D}}}={{\varvec{d}}}+{\tilde{{\varvec{M}}}}({{\varvec{q}}})\ddot{{\varvec{q}}}+{\tilde{{\varvec{C}}}}({{\varvec{q}}},\dot{{\varvec{q}}})\dot{{\varvec{q}}} \end{aligned}$$
(4)

\({{\varvec{M}}}({{\varvec{q}}})=diag\left\{ {M_{11}\ldots M_{ii}\ldots M_{nn} } \right\} \) in Eq.(4) is a constant diagonal matrix with n\(\times \)n elements, i.e., \(M_{ii} \) is a constant-valued nominal term of the ith subsystem via axis inertia. Therefore, Eq. (4) can be rewritten by Eq. (5).

$$\begin{aligned} \ddot{{{\varvec{q}}}}=-{{\varvec{M}}}({{\varvec{q}}})^{-1}({{\varvec{C}}}({{\varvec{q}}},\dot{{{\varvec{q}}}})\dot{{{\varvec{q}}}}+{{\varvec{D}}})+{{\varvec{M}}}({{\varvec{q}}})^{-1}{\varvec{\tau }} \end{aligned}$$
(5)

Now, combining the term \(-{{\varvec{M}}}({{\varvec{q}}})^{-1}({{\varvec{C}}}({{\varvec{q}}},\dot{{{\varvec{q}}}})\dot{{{\varvec{q}}}}+{{\varvec{D}}})\) into a newly defined uncertain term \({{\varvec{D}}}'\), the dynamic Eq. (5) can be transformed into Eq. (6),

$$\begin{aligned} \ddot{{\varvec{q}}}={{\varvec{{D}'}}}+{{\varvec{M}}}({{\varvec{q}}})^{-1}{\varvec{\tau }} \end{aligned}$$
(6)

where \({{\varvec{{D}'}}}=({D}'(1) \,\,{D}'(2)\ldots {D}'(\hbox {n}))\).

Noting that \({{\varvec{M}}}({{\varvec{q}}})\) is invertible with a diagonal form, it is straightforward to verify that Eq. (6) can be decoupled through the proper transformation. The decoupled form is illustrated by Eq. (7), with an uncertain \({D}'(i)\) for the ith subsystem.

$$\begin{aligned} \ddot{q}_i ={D}'(i)+M_{ii} ^{-1}\tau _i \end{aligned}$$
(7)

Then, the system error of control r for the robotic system is redefined and expressed as Eq. (8),

$$\begin{aligned}&{{\varvec{r}}}=\dot{{\varvec{e}}}+{\varvec{\varLambda }} {{\varvec{e}}} \nonumber \\&\dot{{\varvec{e}}}=\dot{{\varvec{q}}}-\dot{{\varvec{q}}}_{{\varvec{d}}} \nonumber \\&{{\varvec{e}}}={{\varvec{q}}}-{{\varvec{q}}}_{{\varvec{d}}} \end{aligned}$$
(8)

where \({{\varvec{q}}}\) and \({{\varvec{q}}}_{{\varvec{d}}}\) denote the actual and desired generalized variable terms, respectively, and \(\dot{{\varvec{q}}}\) and \(\dot{{\varvec{q}}}_{{\varvec{d}}} \) denote the derivation of them, respectively. \({{\varvec{e}}}\) represents the position tracking error, and \({\varvec{\varLambda }}\) represents the diagonal matrix with positive diagonal elements. Therefore, the reference output \(\dot{{\varvec{q}}}_{{\varvec{r}}} \) can be defined and expressed via Eq. (9a) and fulfill the relationship via Eq. (9b) based on Eqs. (4) and (8).

$$\begin{aligned}&\dot{{\varvec{q}}}_{{\varvec{r}}} =\dot{{\varvec{q}}}_{{\varvec{d}}} +{\varvec{\varLambda }} {{\varvec{e}}} \end{aligned}$$
(9a)
$$\begin{aligned}&{{\varvec{M}}}\ddot{{\varvec{q}}}_{{\varvec{r}}} +{{\varvec{C}}}\dot{{\varvec{q}}}_{{\varvec{r}}} +{{\varvec{D}}}-{\varvec{\tau }} ={{\varvec{M}}}(\ddot{{\varvec{q}}}_{{\varvec{d}}} +{\varvec{\varLambda }} \dot{{\varvec{e}}})\nonumber \\&\qquad +{{\varvec{C}}}(\dot{{\varvec{q}}}_{{\varvec{d}}} +{\varvec{\varLambda }} {{\varvec{e}}})+{{\varvec{D}}}-({{\varvec{M}}}\ddot{{\varvec{q}}}+{{\varvec{C}}}\dot{{\varvec{q}}}+{{\varvec{D}}}) \nonumber \\&\quad ={{\varvec{M}}}(\ddot{{\varvec{q}}}_{{\varvec{d}}} +{\varvec{\varLambda }} {\varvec{\dot{e}}}-\ddot{{\varvec{q}}})+\,{{\varvec{C}}}(\dot{{\varvec{q}}}_{{\varvec{d}}} +{\varvec{\varLambda }} {{\varvec{e}}}-\dot{{\varvec{q}}}) \nonumber \\&\quad ={{\varvec{M}}}(\ddot{{\varvec{e}}}+{\varvec{\varLambda }} \dot{{\varvec{e}}})+{{\varvec{C}}}(\dot{{\varvec{e}}}+{\varvec{\varLambda }} {\varvec{e}})\nonumber \\&\quad ={{\varvec{M}}}\dot{{\varvec{r}}}+{{\varvec{Cr}}} \end{aligned}$$
(9b)

3 Adaptive reactionless control strategy

To realize the reactionless motion of the robotic arm, the integrated adaptive reactionless control strategy involves adaptive path planning and the corresponding control strategy. The adaptive path planning would be adaptively updated by the SW-RLS because of the existing time-variable elements in the coefficient matrix of the ARNS algorithm. In addition, the robust adaptive control strategy via PSO-ELM algorithm is proposed to fast track the planned adaptive path of the robotic arm to ensure enough robustness and the adaptive nature of the system control performance. The schematic of the proposed adaptive reactionless control strategy is illustrated in Fig. 2.

3.1 Adaptive reactionless path planning via SW-RLS

The space robot is subject to the law of linear/angular momentum conservation when the system operates in the post-capture stage, and thereby, the total linear and angular momentum of the system can be reformed by Eq. (10) according to [3], with expressed P (linear momentum) and L (angular momentum), respectively.

$$\begin{aligned} \left[ {\begin{array}{l} {{\varvec{P}}} \\ {{\varvec{L}}} \\ \end{array}} \right] =\left[ {\begin{array}{ll} m{{\varvec{I}}}&{}m{\tilde{{\varvec{r}}}}^{T}_{0g} \\ 0&{}{{\varvec{H}}}_\omega \\ \end{array}} \right] \left[ {\begin{array}{l} {{\varvec{v}}}_0 \\ {\varvec{\omega }} _0 \\ \end{array}} \right] +\left[ {\begin{array}{l} {{\varvec{J}}}_{T\omega } \\ {{\varvec{H}}}_{\omega \phi } \\ \end{array}} \right] \dot{{\varvec{q}}}+\left[ {\begin{array}{c} 0 \\ {{\varvec{r}}}_g \times {{\varvec{P}}} \\ \end{array}} \right] \end{aligned}$$
(10)

In the above, the expressions \({{\varvec{v}}}_{0}\) and \({\varvec{\omega }} _0 \) represent the linear velocity and angular velocity of the spacecraft, respectively, expressed in the inertial frame; \(\dot{{\varvec{q}}}\) represents the derivation of the generalized variable \({{\varvec{q}}}\), i.e., joint rate; m denotes the total mass of the robotic system; and \({{\varvec{I}}}\) is the identity matrix. The coefficient matrix of \([{{\varvec{v}}}_{0 }\,\,\,{\varvec{\omega }}_0 ]^{\mathrm{T}}\) and \(\dot{{\varvec{q}}}\) is based on the inertial matrix and coupling inertial matrix, accordingly.

Given the angular momentum of the robotic system from Eq. (10), with initial momentum \({{\varvec{P}}}_{0}\), \({{\varvec{L}}}_{0}\) is expressed as follows:

$$\begin{aligned} {{\varvec{L}}}={{\varvec{H}}}_{\omega } {\varvec{\omega }}_0 +{{\varvec{H}}}_{\omega \phi } \dot{{\varvec{q}}}+{{\varvec{r}}}_g \times {{\varvec{P}}}_0 ={{\varvec{L}}}_0 \end{aligned}$$
(11)

i.e.,

$$\begin{aligned} {{\varvec{H}}}_\omega {\varvec{\omega }} _0 +{{\varvec{H}}}_{\omega \phi } \dot{{\varvec{q}}}={{\varvec{L}}}_0 -{{\varvec{r}}}_g \times {{\varvec{P}}}_0 \end{aligned}$$
(12)

Based on the RNS algorithm [4,5,6,7], the desired path planning of the robotic arm to realize reactionless motion for the spacecraft can be obtained by Eq. (13),

$$\begin{aligned} \dot{{\varvec{q}}}_{d|\mathrm{RNS}} ={{\varvec{H}}}_{\omega \phi }^+ ({{\varvec{L}}}_0 -{{\varvec{r}}}_g \times {{\varvec{P}}}_0 )+({{\varvec{I}}}-{{\varvec{H}}}_{\omega \phi }^+ {{\varvec{H}}}_{\omega \phi } ){\dot{\varvec{\zeta }}} \end{aligned}$$
(13)

where \({\dot{\varvec{\zeta }}}\) is the arbitrary vector (\({\dot{\varvec{\zeta }}}\in {{\varvec{R}}}^{n})\) mapped into the null space of \({{\varvec{H}}}_{\omega \phi } \), and to ensure the initial velocity of each joint is available, the \({\dot{\varvec{\zeta }}}\) should be defined as a vector with nonzero elements [3,4,5,6,7]; \({{\varvec{H}}}_{\omega \phi }^+ \) represents the pseudo-inverse of \({{\varvec{H}}}_{\omega \phi }\).

Then, considering the captured unknown object with unknown properties, the coefficient matrix (base inertial matrix, coupling inertial matrix) incorporating the uncertain dynamic parameter cannot be obtained precisely, which affects the desired path \(\dot{{\varvec{q}}}_\mathrm{RNS} \) to realize the absolutely reactionless motion. Therefore, the ARNS algorithm is employed to realize the adjustment online for the coefficient matrix to obtain the precise property of the post-capture system.

Equation (12) is rewritten, illustrated by Eq. (14), in which the signal\(\wedge \)represents the current estimate value that incorporates the dynamic parameter of the captured unknown object. Then, Eqs. (13) and (14) are combined and expressed by Eq. (15),

$$\begin{aligned}&\dot{{\varvec{q}}}={\hat{{\varvec{H}}}}_{\omega \phi }^+ ({{\varvec{L}}}_0 -{{\varvec{r}}}_g \times {{\varvec{P}}}_0 )-{\hat{{\varvec{H}}}}_{\omega \phi }^+ {\hat{{\varvec{H}}}}_\omega {\varvec{\omega }} _0 \nonumber \\&\qquad +\,\left( {{\varvec{I}}}-{\hat{{\varvec{H}}}}_{\omega \phi }^+ {\hat{{\varvec{H}}}}_{\omega \phi } \right) {\dot{\varvec{\zeta }}} \end{aligned}$$
(14)
$$\begin{aligned}&\dot{{\varvec{q}}}_{d|\mathrm{RNS}} -\dot{{\varvec{{q}}}}=({{\varvec{H}}}_{\omega \phi }^+ -{\hat{{\varvec{H}}}}_{\omega \phi }^+ )({{\varvec{L}}}_0 -{{\varvec{r}}}_g \times {{\varvec{P}}}_0 )\nonumber \\&\qquad +\,{\hat{{\varvec{H}}}}_{\omega \phi }^+ {\hat{{\varvec{H}}}}_\omega {\varvec{\omega }} _0 +({\hat{{\varvec{H}}}}_{\omega \phi }^+ {\hat{{\varvec{H}}}}_{\omega \phi } -{{\varvec{H}}}_{\omega \phi }^+ {{\varvec{H}}}_{\omega \phi } ){\dot{\varvec{\zeta }}} \nonumber \\&\quad =[{{\varvec{K}}}_1 {{\varvec{{K}}}}_2 {{\varvec{{K}}}}_3 ]\left[ {\begin{array}{l} {{\varvec{1}}} \\ {\varvec{\omega }} _0 \\ {\dot{\varvec{\zeta }}} \\ \end{array}} \right] \end{aligned}$$
(15)

where matrix \({{\varvec{K}}}_{1}\), \({{\varvec{K}}}_{2}\) and \({{\varvec{K}}}_{3}\) owns the time-variable elements, expressed as follows.

$$\begin{aligned}&{{\varvec{{K}}}}_1 =\left( {{\varvec{H}}}_{\omega \phi }^+ -{\hat{{\varvec{H}}}}_{\omega \phi }^+ \right) ({{\varvec{L}}}_0 -{{\varvec{r}}}_g \times {{\varvec{P}}}_0 ) \nonumber \\&{{\varvec{{K}}}}_2 ={\hat{{\varvec{H}}}}_{\omega \phi }^+ {\hat{{\varvec{H}}}}_\omega \nonumber \\&{{\varvec{{K}}}}_3 =\left( {\hat{{\varvec{H}}}}_{\omega \phi }^+ {\hat{{\varvec{H}}}}_{\omega \phi } -{{\varvec{H}}}_{\omega \phi }^+ {{\varvec{H}}}_{\omega \phi } \right) \end{aligned}$$
(16)

Based on Eq. (15), the precise coefficient matrix \({{\varvec{K}}}_{1}, {{\varvec{K}}}_{2}\) and \({{\varvec{K}}}_{3}\) means that \(\dot{{\varvec{{q}}}}\) can ultimately converge to the desired path \(\dot{{\varvec{{q}}}}_{d|\mathrm{RNS}} \) to realize reactionless motion for the robotic arm [3]. Thus, the identification algorithm SW-RLS is used to obtain the coefficient matrix online to deal with the time-variable parameters from \({{\varvec{K}}}_{1}, {{\varvec{K}}}_{2}\) and \({{\varvec{K}}}_{3}\). The simplified linear regression forms of Eq. (15) are defined with Eq. (17) as follows:

$$\begin{aligned} {\varvec{\varPsi }} {\varvec{\Theta }} ={\varvec{\varPhi }} \end{aligned}$$
(17)

where \({\varvec{\Theta }}\) denotes the coefficient matrix \([{{\varvec{{K}}}}_1 {{\varvec{{K}}}}_2 {{\varvec{{K}}}}_3 ]^{T}\); \({\varvec{\varPsi }},{\varvec{\varPhi }}\) denote the terms \(\left[ 1 \, {\varvec{\omega }} _0 \, \dot{\varvec{{\zeta }}} \right] ^{\mathrm{T}}\)and \([\dot{{\varvec{{q}}}}_{d|\mathrm{RNS}} -\dot{{\varvec{{q}}}}]^{\mathrm{T}}\), respectively.

Fig. 3
figure 3

Proposed control strategy for the joint controller

Full size image

The details of the SW-RLS algorithm can be found in [14] and are expressed below with Eq. (18). New data are being added to the algorithm via Eq. (18a), and the older data are removed via Eq. (18b) to avoid the saturation phenomenon. From Eq. (18), k denotes the kth iteration for the corresponding elements and \(\hat{\varvec{{\Theta }}}_{(k)} \) is an estimate of \({\varvec{\Theta }}\) from iteration k; u denotes the length of the slide window; \({\varvec{\varepsilon }} _1 \) and \({\varvec{\varepsilon }}_2 \) denote the priori and posteriori residual error, respectively; \({{\varvec{PN}}}\) is the inverse of the autocorrelation matrix with the initial setting \({{\varvec{PN}}}_{(0)} =\delta {{\varvec{I}}}\) for \(\delta >1\).

$$\begin{aligned}&{\varvec{\varepsilon }} _1 ={\varvec{\varPhi }} _{(k+1)} -{\varvec{\varPsi }}_{(k+1)} \hat{\varvec{{\Theta }}}_{(k)} \nonumber \\&\Delta _{1(k+1)} =\frac{{{\varvec{PN}}}_{(k)} {\varvec{\varPsi }} _{(k+1)} }{{{\varvec{I}}}+{\varvec{\varPsi }} _{(k+1)}^{\mathrm{T}} {{\varvec{PN}}}_{(k)} {\varvec{\varPsi }} _{(k+1)} } \end{aligned}$$
(18a)
$$\begin{aligned}&{{\varvec{PN}}}_{1(k+1)} =[{{\varvec{I}}}-\Delta _{{1}(k+1)} {\varvec{\varPsi }} _{(k+1)}^{\mathrm{T}} ]{{\varvec{PN}}}_{(k)} \nonumber \\&\hat{{\varvec{{\Theta }}}}_{1(k+1)} =\hat{\varvec{{\Theta }}}_{(k)} +\Delta _{1(k+1)} {\varvec{\varepsilon }} _1 \nonumber \\&{\varvec{\varepsilon }} _2 ={\varvec{\varPhi }} _{(k-u+1)} -{\varvec{\varPsi }} _{(k-u+1)}\hat{\varvec{{\Theta }}}_{1(k+1)}\nonumber \\&\Delta _{(k+1)} =\frac{{{\varvec{PN}}}_{1(k+1)} {\varvec{\varPsi }} _{(k-u+1)} }{{-{\varvec{I}}}+{\varvec{\varPsi }} _{(k-u+1)}^{\mathrm{T}} {{\varvec{PN}}}_{1(k+1)} {\varvec{\varPsi }} _{(k-u+1)} } \nonumber \\&{{\varvec{PN}}}_{(k+1)} =[{{\varvec{I}}}-\Delta _{{(k+1)}} {\varvec{\varPsi }} _{(k-u+1)}^{\mathrm{T}} ]{{\varvec{PN}}}_{1(k+1)} \nonumber \\&\hat{\varvec{{\Theta }}}_{(k+1)} =\hat{\varvec{{\Theta }}}_{1(k+1)} +\Delta _{(k+1)} {\varvec{\varepsilon }} _2 \end{aligned}$$
(18b)

According to the description in Eqs. (15–18), the reactionless path with dynamical changing performance can be obtained, as shown in Eq. (19) as follows:

$$\begin{aligned} \dot{{\varvec{{q}}}}_{d|\mathrm{RNS}} =\dot{{\varvec{{q}}}}+\hat{\varvec{{\Theta }}}\left[ {\begin{array}{l} \mathbf{1} \\ {{\varvec{\omega }}} _0 \\ \dot{\varvec{{\zeta }}} \\ \end{array}} \right] \end{aligned}$$
(19)

in which \(\dot{{\varvec{{q}}}}_{d|\mathrm{RNS}} =[\dot{q}_{d1|\mathrm{RNS}} ,\dot{q}_{d2|\mathrm{RNS}} ,\ldots ,\dot{q}_{dn|\mathrm{RNS}} ]^{T}\) denotes the planned angular velocity for each joint installed on the space robot.

3.2 Robust adaptive control strategy via the PSO-ELM algorithm

In this section, the robust adaptive control strategy using the PSO-ELM algorithm is proposed. According to Eq. (7), in order to compensate for the uncertain term \({D}'(i)\) for the ith subsystem and to realize the desired tracking for each joint installed on the robotic arm, the proposed control strategy for each joint is preferentially involved through the decoupling Eq. (7) illustrated as Fig. 3.

To address the uncertain term \({D}'(i)\), the proposed control torque \(\bar{{\tau }}_i \) of joint i takes the form of (20), where \(\tau _{Ai} \) denotes the adaptive controller to learn and compensate for the uncertain or unknown properties existing in the system. This then employs the ELM algorithm attached with PSO optimization to realize quick tracking and performance enhancement. \(\tau _{Ri} \) denotes the robust control strategy to reject the model uncertainties, and \(\tau _{PDi} \) denotes the conventional proportion and differentiation control strategy to reduce the error with computational efficiency.

$$\begin{aligned} \bar{\tau }_i =M_{ii} (\tau _{Ai} +\tau _{Ri} +\tau _{PDi} ) \end{aligned}$$
(20)

Combining Eqs. (20) and (7) into Eq. (21) is illustrated as follows; thus, the proper choice of \(\tau _{Ai} \) and \(\tau _{Ri} \) can compensate for the existing uncertain term \({D}'(i)\), as described in the next section.

$$\begin{aligned} {D}'(i)=\ddot{q}_i -\tau _{Ai} -\tau _{Ri} -\tau _{PDi} \end{aligned}$$
(21)

3.3 Adaptive control term via the PSO-ELM algorithm

The ELM algorithm is employed to construct an adaptive control strategy to quickly compensate for the abrupt properties of the control system. The PSO algorithm is employed to optimize the input feature of the ELM network to address any input feature variation from the optimal value. The schematic of the PSO-ELM algorithm is illustrated in Fig. 4.

Fig. 4
figure 4

ELM network diagram

Full size image

The input vector \({{\varvec{x}}}_{{{\varvec{i}}}}\) is defined in Eq. (22) for the network as follows:

$$\begin{aligned} {{\varvec{x}}}_i =[\ddot{{\varvec{{q}}}}_{{{\varvec{di}}}}~\dot{{\varvec{{q}}}}_{{{\varvec{di}}}}~{{\varvec{q}}}_{{{\varvec{di}}}}~{{\varvec{e}}}_i~ \dot{{\varvec{{e}}}}_i ] \end{aligned}$$
(22)

Therefore, the input and output for the hidden layer can be obtained by Eqs. (23) and (24), respectively, with an input weight matrix \({{\varvec{A}}}_{i}\), hidden bias \(b_{i}\) and activation function \({{\varvec{g}}}_{i}\).

$$\begin{aligned}&{{\varvec{f}}}_i ({{\varvec{x}}}_i )={{\varvec{A}}}_i {{\varvec{x}}}_i +b_i \end{aligned}$$
(23)
$$\begin{aligned}&{{\varvec{h}}}_i ={{\varvec{g}}}_i ({{\varvec{f}}}_i ({{\varvec{x}}}_i ))={{\varvec{g}}}_i ({{\varvec{A}}}_i {{\varvec{x}}}_i +b_i ) \end{aligned}$$
(24)

The output \(\tau _{Ai} \) of the network can be obtained via Eq. (25), with the output weight matrix \({\varvec{\beta }} _i \).

$$\begin{aligned} \tau _{Ai} ={{\varvec{h}}}_i {\varvec{\beta }} _i \end{aligned}$$
(25)

Therefore, the proposed adaptive law for \({\varvec{\beta }} _i \) is proposed and presented by Eq. (26) as follows:

$$\begin{aligned}&\dot{\hat{{\varvec{{\beta }}}}}_i =[\dot{\hat{{\beta }}}_{i1} \dot{\hat{{\beta }}}_{i2} \ldots \dot{\hat{{\beta }}}_{ij} \ldots ] \nonumber \\&\dot{\hat{{\beta }}}_{ij} =\gamma _{ij} {{\varvec{h}}}_i r_i (j=1,2,\ldots ,l) \nonumber \\&\hat{{\tau }}_{Ai} ={{\varvec{h}}}_i \hat{{\varvec{{\beta }}}}_i \end{aligned}$$
(26)

where \(\dot{\hat{{\varvec{{\beta }}}}}_i \) denotes the estimated growth rate of the estimated weight matrix \(\hat{{\varvec{{\beta }}}}_i \); l is the amount of hidden layer nodes; \(\gamma \) denotes the step-length regulatory factor; \(\hat{{\tau }}_{Ai} \) represents the estimated output torque, i.e., the output of the adaptive controller. Residual error still exists between \(\hat{{\tau }}_{Ai} \) and \(\tau _{Ai} \), compensated by the robust controller exhibited in Sect. 4. The stability analysis of the proposed adaptive law (26) can be verified by the constructed Lyapunov function illustrated below.

To avoid the input weight \({{\varvec{A}}}_{i}\) and the hidden bias \({{\varvec{b}}}_{i}\) of the ELM network varying from the optimal value, \({{\varvec{A}}}_{i }\)   and \({{\varvec{b}}}_{i}\)   elements are set as the particles requiring optimization, and these elements are reformed into set \({{\varvec{S}}}\), with amount m as follows:

$$\begin{aligned} {{\varvec{S}}}=(s_1 ,s_2 ,\ldots ,s_i ,\ldots ,s_m )^{T} \end{aligned}$$
(27)

The PSO algorithm is then used to optimize the particles \({{\varvec{S}}}\), according to the principle obtaining the least value of the fitness function \(F({{\varvec{S}}})\), which is chosen by the control tracking error \({\varvec{e}}\) in this paper. Thus, if the tracking error \({{\varvec{e}}}\) exhibits a downtrend, the obtained particles move toward the optimal value. Then, the update via Eq. (28) is adopted; however, if the tracking error is on the rise, the original particle values are maintained.

$$\begin{aligned}&v_i^{k+1} =wv_i^k +c_1 R_1 (p_i^k -s_i^k )+c_2 R_2 (g_i^k -s_i^k ) \nonumber \\&s_i^{k+1} =s_i^k +v_i^{k+1} \end{aligned}$$
(28)

From Eq. (28), elements \(s_{i}\) and \(v_i \) represent the position and velocity of particle i, respectively; \(p_i \) and \(g_i \) denote the best partial position and best global position for particle i, respectively, obtained by the empirical data from the experimental tests; w denotes the inertial weight serving as a tradeoff between the global and local exploration capabilities of the swarm; \(c_{1}\) and \(c_{2}\) are the weights of the stochastic acceleration terms, determined in advance and pulling each particle toward \(p_{i}\) and \(g_{i}\); R1 and R2 are the random variables from the range of [0,1]; k denotes the kth iteration for the corresponding elements. To avoid overrun, the limitations for the position and velocity are set as \(s_i \in [S_{\min } ,S_{\max } ]\) and \(v_i \in [V_{\min } ,V_{\max } ]\), respectively.

Therefore, based on Eqs. (27) and (28), particles S, i.e., the optimized input feature A \(_{i}\), b \(_{i}\) of the ELM network, is associated with improved performance of the adaptive control term via the optimized ELM algorithm.

4 Robust control term

The main purpose for the robust control term in this paper is to reject model uncertainties. The residual errors are produced by the adaptive control process with Eq. (26), i.e., error \(E_{i }\) by Eq. (29), shown as follows:

$$\begin{aligned} E_i =\tau _{Ai} -\tau _{Ai}^*={{\varvec{h}}}_i {\varvec{\beta }} _i -{{\varvec{h}}}_i {\varvec{\beta }} _i^{*} \end{aligned}$$
(29)

where \(\tau _{Ai}^{*} \) denotes the optimal approximation of \(\tau _{Ai} \). Noting that there exists an upper bound of \(E_i \) with \(|E_i |\le {E}_{i\_\max }\), the basic form of the robust control term can be illustrated by Eq. (30), where \(\hat{{\tau }}_{Ri} \) represents the estimated output of the robust control term and \(r_{i}\) represents the ith element of system error \({{\varvec{r}}}\).

$$\begin{aligned} \hat{{\tau }}_{Ri} ={E}_{i\_\max } sign(r_i ) \end{aligned}$$
(30)

Therefore, the estimated output of the proposed control strategy \(\hat{{\varvec{{\tau }}}}\) for the robotic arm can be obtained by Eq. (31) through Eqs. (20) and (30) in which the positive definite matrix \({{\varvec{K}}}\) represents the gain of the PD control strategy.

$$\begin{aligned}&\hat{{\varvec{{\tau }}}}_ =[\hat{{\tau }}_1 \hat{{\tau }}_2 \ldots \hat{{\tau }}_i \ldots \hat{{\tau }}_n ] \nonumber \\&\hat{{\tau }}_i =\hat{{\tau }}_{PDi} +\hat{{\tau }}_{Ai} +\hat{{\tau }}_{Ri} \nonumber \\&\quad \,\, ={{\varvec{K}}}r_i +{{\varvec{h}}}_i \hat{{\varvec{{\beta }}}}_i+ {E}_{i\_\max } \cdot sign(r_i ) \end{aligned}$$
(31)

5 Stability analysis of the proposed control strategy

Considering the following Lyapunov function:

$$\begin{aligned}&{{\varvec{Q}}}=\frac{1}{2}{{\varvec{r}}}^{T}{{\varvec{M}}}r+\frac{1}{2}\sum _{i=1}^n {\sum _{j=1}^l {\frac{1}{\gamma _{ij} }\tilde{\beta }_{ij} \tilde{\beta }_{ij} } } \nonumber \\&\tilde{\beta }_{ij} =\hat{{\beta }}_{ij} -\beta _{ij}^*\end{aligned}$$
(32)

the first derivation of (32) is derived through Eqs. (9) and (31).

$$\begin{aligned}&\dot{{\varvec{{Q}}}}={{\varvec{r}}}^{T}{{\varvec{M}}}\dot{{\varvec{{r}}}}+\frac{1}{2}{{\varvec{r}}}^{T}\dot{{\varvec{{M}}}}{{\varvec{r}}}+\sum _{i=1}^n {\sum _{j=1}^l {\frac{1}{\gamma _{ij} }\tilde{\beta }_{ij} \dot{\hat{{\beta }}}_{ij} } } \nonumber \\&\quad ={{\varvec{r}}}^{T}({{\varvec{M}}}\ddot{{\varvec{{q}}}}_r +{{\varvec{C}}}\dot{{\varvec{{q}}}}_r +{{\varvec{D}}}-{\varvec{\tau }} -{{\varvec{Cr}}})\nonumber \\&\qquad +\,\frac{1}{2}{{\varvec{r}}}^{T}\dot{{\varvec{{M}}}}{{\varvec{r}}}+\sum _{i=1}^n {\sum _{j=1}^l {\frac{1}{\gamma _{ij} }\tilde{\beta }_{ij} \dot{\hat{{\beta }}}_{ij} } } \nonumber \\&\quad ={{\varvec{r}}}^{T}({{\varvec{M}}}\ddot{{\varvec{{q}}}}_r +{{\varvec{C}}}\dot{{\varvec{{q}}}}_r \nonumber \\&\qquad +\,{{\varvec{D}}}-{{\varvec{Kr}}}-\sum _{i=1}^n {{{\varvec{h}}}_i \hat{{\varvec{{\beta }}}}_i } -{\mathbf{E }}_{\max } \cdot sign({{\varvec{r}}})-{{\varvec{Cr}}})\nonumber \\&\qquad +\,\frac{1}{2}{{\varvec{r}}}^{T}\dot{{\varvec{{M}}}}{{\varvec{r}}}+\sum _{i=1}^n {\sum _{j=1}^l {\frac{1}{\gamma _{ij} }\tilde{\beta }_{ij} \dot{\hat{{\beta }}}_{ij} } } \nonumber \\&\quad ={{\varvec{r}}}^{T}\left( \sum _{i=1}^n {{{\varvec{h}}}_i {\varvec{\beta }} _i} \right. \nonumber \\&\left. \qquad -\sum _{i=1}^n {{{\varvec{h}}}_i \hat{{\varvec{{\beta }}}}_i } -{{\varvec{Kr}}}-{\mathbf{E }}_{\max } \cdot sign({{\varvec{r}}})-{{\varvec{Cr}}}\right) \nonumber \\&\qquad +\,\frac{1}{2}{{\varvec{r}}}^{T}\dot{{\varvec{{M}}}}{{\varvec{r}}}+\sum _{i=1}^n {\sum _{j=1}^l {\frac{1}{\gamma _{ij} }\tilde{\beta }_{ij} \dot{\hat{{\beta }}}_{ij} } } \nonumber \\&\quad ={{\varvec{r}}}^{T}\left( \sum _{i=1}^n {{{\varvec{h}}}_i {\varvec{\beta }} _i^*}\right. \nonumber \\&\left. \qquad -\sum _{i=1}^n {{{\varvec{h}}}_i \hat{\varvec{{\beta }}}_i } -{{\varvec{Kr}}}-\mathbf{{E} }_{\max } \cdot sign({{\varvec{r}}})\right) +{{\varvec{r}}}^{T}\sum _{i=1}^n {E_i }\nonumber \\&\qquad -\frac{1}{2}{{\varvec{r}}}^{T}(2{{\varvec{C}}}-\dot{{\varvec{{M}}}}){{\varvec{r}}}+\sum _{i=1}^n {\sum _{j=1}^l {\frac{1}{\gamma _{ij} }\tilde{\beta }_{ij} \dot{\hat{{\beta }}}_{ij} } } \nonumber \\&\quad =-\sum _{i=1}^n {{{\varvec{h}}}_i \tilde{\varvec{{\beta }}}_i } r_i -{{\varvec{r}}}^{T}{{\varvec{Kr}}}-{{{\varvec{E}}}}_{\max } \cdot {{\varvec{r}}}^{T}sign({{\varvec{r}}})\nonumber \\&\qquad +\,{{\varvec{r}}}^{T} \sum _{i=1}^n {E_i } +\sum _{i=1}^n {\sum _{j=1}^l {\frac{1}{\gamma _{ij} }\tilde{\beta }_{ij} \dot{\hat{{\beta }}}_{ij} } } \end{aligned}$$
(33)

Combining Eqs. (26) and (33), the relationship of Eq. (34) can be obtained as follows:

$$\begin{aligned}&\dot{{\varvec{{Q}}}}=-\,{{\varvec{r}}}^{T}{{\varvec{Kr}}}-{\mathbf{E }}_{\max } {{\varvec{r}}}^{T}sign({{\varvec{r}}})+{{\varvec{r}}}^{T}\sum _{i=1}^n {E_i } \nonumber \\&\quad =-\,{{\varvec{r}}}^{T}{{\varvec{Kr}}}-{{\varvec{r}}}^{T}({\mathbf{E }}_{\max } \cdot sign({{\varvec{r}}})\nonumber \\&\qquad -\sum _{i=1}^n {E_i } )\le -{{\varvec{r}}}^{T}{{\varvec{Kr}}}-\sum _{i=1}^n {({E}_{i\_\max } -E_i } )\left| {r_i } \right| \le 0\nonumber \\ \end{aligned}$$
(34)

Therefore, the stability condition is sufficient according to Eq. (34), which proves the stability of the proposed control law.

6 Numerical simulation

In this section, the validity of the proposed control strategy is verified with a planar dynamic model of a space robot with a 4-DOF robotic arm operating in the free-floating mode as established by the Matlab/Simulink software, as shown in Fig. 5. The sampling period is 0.001 s for the established simulation platform. The entire system operating in the post-capture stage has initial linear/angular motion with the initial angular velocity of 0.25 rad/s for a captured object during the pre-captured stage, in addition to precise knowledge about the spacecraft as well as the robotic arm and unknown dynamic parameters about the captured object in the end-effector. The geometric and inertial parameters of the system employed in the model are shown in Table 1, where \(a_{i}\) and \(b_{i}\) denote the position vector from the joint i to the centroid of link i and also from the center of link i to the joint (i + 1), respectively; \(I_{i}\) denotes the inertial tensor along the z axis; link 0 represents the spacecraft, and the attitude angle and joint angle can be expressed by \(\alpha \) and \({\theta }_{i}\), respectively. The parameter setting and initial condition of the model are illustrated by Table 2, and the interior disturbance term d in the robotic system is set by the function \(d_{i }\) = (0.8 * sign(\(\dot{q}_i )\) + 5 * sin(10t) + 2 * rand(0,1)) for each joint, where the signal of rand(0,1) means the value is randomly produced from the range of (0,1).

Fig. 5
figure 5

Space robot with a 4-DOF robotic arm

Full size image
Table 1 Geometric and inertial parameters of the space robot
Full size table
Table 2 Parameter setting of the dynamic simulation
Full size table
Fig. 6
figure 6

Total linear/angular momentum measurement via Eq. (10)

Full size image
Fig. 7
figure 7

Adaptive reactionless path planning via various algorithms

Full size image
Fig. 8
figure 8

Position tracking error of each joint controller via various control strategies

Full size image

The total linear/angular momentum of the system in the post-capture stage is shown in Fig. 6, where the entire system is shown to be subject to the law of linear/angular momentum conservation. In the simulation, the adaptive reactionless path planning is considered via the SW-RLS algorithm and the conventional RLS algorithm, and the planned path via the two various algorithms can be obtained with the parameter settings in Table 2 and illustrated in Fig. 7. It can be concluded that the planned path for the robotic arm via the SW-RLS algorithm exhibits a time-variable feature that keeps pace with Eq. (16), yet the planned path via the conventional RLS exhibits a saturation phenomenon that cannot track the time-variable property of the coefficient matrix.

Then, several various control schemes are employed to track the planned path produced by the SW-RLS algorithm, expressed as follows:

  1. Scheme 1.

    Adaptive control strategy via the RBF algorithm: 60 hidden layer nodes (l= 60); the adaptive law conforming to Eq. (26); the center \({{\varvec{f}}}_{iC} \), the width \(\sigma \) and the bias of hidden nodes affiliated with rand(− 1,1), rand(0,1) and rand(0,1), respectively; the activation function selected by the radial basis function with \({{\varvec{h}}}_i =\exp (-({{{\varvec{f}}}}_{i} (x)-{{\varvec{f}}}_{iC} )^{2}/(2\sigma )^{2})\); the output of controller \(\hat{{\tau }}_i =\hat{{\tau }}_{PDi} +\hat{{\tau }}_{Ai} \) with corresponding K in Table 2.

  2. Scheme 2.

    Adaptive control strategy via the ELM algorithm: all initial conditions are in accordance with scheme 1 except that the activation function is selected by the sigmoid function with \({{\varvec{h}}}_i =1/(1+\exp (-{{\varvec{f}}}_{i} (x))\).

  3. Scheme 3.

    Robust adaptive control strategy via the ELM algorithm: all initial conditions are in accordance with scheme 2 except an appending robust controller with the output of \(\hat{{\tau }}_i =\hat{{\tau }}_{PDi} +\hat{{\tau }}_{Ai} +\hat{{\tau }}_{Ri} \).

  4. Scheme 4.

    Proposed control strategy: all initial conditions are in accordance with scheme 3 except the optimization of the input weight matrix for the ELM algorithm via the PSO.

The comparison of the tracking results for control Schemes 1–4 is shown in Fig. 8 and Tables 3, 4, with tracking performance and tracking error, respectively. Then, the angular velocity of the spacecraft is measured, as shown in Fig. 9, which exhibits the existing disturbance from the motion of the robotic arm to the spacecraft as well as to the attitude stability.

Table 3 Mean values of position tracking errors for each joint controller (5–40 s)
Full size table
Table 4 Position tracking steady-state mean square errors for each joint controller (5–40 s)
Full size table
Fig. 9
figure 9

Angular velocity measurement of the spacecraft via various control strategies

Full size image
Table 5 Mean value of spacecraft angular velocity (5–40 s)
Full size table
Table 6 Position tracking steady-state mean square of spacecraft angular velocity (5–40 s)
Full size table

According to the tracking results from Fig. 8 and Table 3, the adaptive control strategy via ELM exhibits better speed performance compared with adaptive control strategy via RBF, although the accuracy performances of the steady-state error for the two schemes are both inferior to the robust adaptive control strategy via ELM because of the appending of the robust control strategy. The proposed control strategy via the PSO-ELM algorithm exhibits slight tracking accuracy improvement and shorter transient time; however, an extremely negligible delay of speed exists compared with the robust adaptive control strategy via the ELM algorithm, which reflects the optimization process of the PSO algorithm to seek and update the optimal input weight matrix of the network. In addition, Fig. 9 and Tables 5 and 6 exhibit the stability of the spacecraft attitude after capturing an unknown object, where the reactionless control strategy via the proposed scheme shows faster and relatively less angular spacecraft velocity as well as the least disturbance, which validates the proposed method in this paper.

7 Conclusion

An adaptive reactionless path planning and control integrated strategy is proposed for free-floating space robots while capturing unknown objects, achieving the reactionless motion of a robotic arm and ensuring the stability of the base attitude of the spacecraft. A SW-RLS algorithm is introduced to avoid the saturation feature and to construct adaptive reactionless path planning, and a composite control strategy via the PSO-ELM algorithm is proposed to track the dynamic changing planning path with the speed and accuracy enhancement of tracking performance. The notable feature of the proposed design is that it requires neither accurate system modeling nor any information about the unknown properties. Most importantly, the design can dynamically realize the reactionless path tracking performance although there are uncertain and abrupt dynamic parameters from the captured object. The simulation results validate the proposed method in this paper, which makes it significant for on-orbit operations in the future.