1 Introduction

Ceramic motorised spindles have high precision and reliability and have been widely used in high-speed machining. As a key component of ceramic motorised spindles, the ceramic angular contact ball bearing directly affects the operating accuracy of the spindle and thus influences the overall performance. Therefore, much research has been conducted on bearings regarding different aspects, e.g. analyses of the dynamic performance of bearings [1,2,3,4,5], discussions on their sliding behaviour [6,7,8], predictions of their lifetime [9, 10], and studies on the characteristics of bearings with localised defects [11,12,13,14,15]. All parts of a bearing affect its dynamic performance, e.g. lubricants, lubrication mode, and oil film pressure [16,17,18], bearing stiffness [19, 20], bearing friction torque [21, 22], bearing contact angle [23], material, deformation, and pocket shape of the cage [24]. Further, the thermal performance of a bearing cannot be ignored during operation [25,26,27]. When pre-tightening forces applied to the bearing are varied, as well as the bearing clearance, pressure distribution, and bearing configuration, the bearing will exhibit a different dynamic behaviour [28,29,30,31]. The influences of the surface roughness and waviness in the raceway, surface waviness of balls, and ball number on precision bearings are critical [32,33,34,35]. A deformation of the outer ring of the bearing will alter the fit clearance between the outer ring and housing, thereby affecting the load distribution of the bearing [36]. Li et al. measured the vibrations at the bearing nodes with a double-section interpolation iteration method [37]. Tomovic discussed the influences of the radial internal clearance value and number of rolling elements on the rigid-rotor vibrations in unloaded rolling-element bearings [38]. Wu, P\(\mathring{\mathrm{u}}\)st, and Hu analysed the vibration characteristics of bearings in different applications [39,40,41]. These studies contribute to improving the bearing performance. However, research on ceramic bearings is still rare.

Fig. 1
figure 1

Schematic diagram of coordinate systems for ball bearing

Full size image

The bearing noise is an important index to evaluate the bearing performance. Factors such as the bearing structure, dimensional accuracy of all components, and lubrication condition will affect the working state of the bearing, resulting in different noise characteristics of the bearing. According to the literature on bearing research, few reports on the acoustic performance of rolling bearings exist. Rho and Bouaziz investigated the acoustic properties of a hydrodynamic journal bearing using the sound pressure level (SPL) of the oil film including the rotor imbalance and the elastic deformation of the bearing liner [42, 43], respectively. However, the mechanism of bearing noise, distribution characteristics of noise, and noise characteristics of each component have not been thoroughly analysed.

Rolling-element bearings are commonly composed of four components, each of which produces different nonlinear noises according to different working parameters. Therefore, the nonlinear dynamic differential equations for the vibration of each component of a rolling-element bearing are established in the study, and the radiation noise of the bearing is investigated using the multi-sound source method. In this study, a ceramic angular contact ball bearing in a high-speed motorised spindle [26] is used as the research object. First, the nonlinear dynamic model is proposed in a speed range of 10,000–40,000 r \(\hbox {min}^{-1}\). Then, the radiation noise of each bearing component is calculated using different sound source models, and the total radiation noise of the bearing is obtained using the principle of sound field superposition. The numerical simulation results are verified through the corresponding experiments. Finally, the frequency spectrum characteristics of the radiation noise regarding each component are analysed.

2 Vibration equations of components

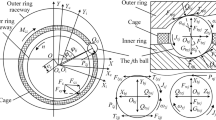
Generally, in actual operations, the outer ring of the bearing is assembled into the bearing pedestal, but it can still vibrate. The inner ring rotates at a constant speed. It is assumed that the centre of mass and geometrical centre of each component are the same. The movement of the cage is guided by the inner ring. To better analyse the vibration and noise characteristics of the high-speed ceramic angular contact ball bearing, the coordinate systems of the bearing are set up as shown in Fig. 1.

As shown in Fig. 1, the inertial coordinate system {O; X, Y, Z} is fixed, and coordinate origin O is fixed to the initial centre of the bearings. The X-axis represents the bearing rotation axis, which is parallel to the ground. The Y- and Z-axes represent the horizontal radial and vertical radial directions, respectively. The following notation is used to describe the components: ball (b), inner ring (i), outer ring (o), cage (c), cage pocket (p), and ordinal number (j) for balls or cage pockets. In the coordinate system of the \(j{\mathrm{th}}\) ball {\(O_{\mathrm{b}j}; X_{\mathrm{b}j}, Y_{\mathrm{b}j}, Z_{\mathrm{b}j}\)}, the origin \(O_{\mathrm{b}j}\) represents the centre of mass of the ball, the \(X_{\mathrm{b}j}\) axis is the axial direction of the bearing, the \(Y_{\mathrm{b}j}\) axis is the circumferential direction of the bearing, and the \(Z_{\mathrm{b}j}\) axis is the radial direction of the bearing. The coordinate system {\(O_{\mathrm{b}j};X_{\mathrm{b}j},Y_{\mathrm{b}j},Z_{\mathrm{b}j}\)} moves with the revolution of the ball but does not spin with origin \(O_{\mathrm{b}j}\). Each ball has an independent coordinate system. In the coordinate system of the cage, {\(O_\mathrm{c}; X_\mathrm{c}, Y_\mathrm{c}, Z_\mathrm{c}\)}, origin \(O_\mathrm{c}\) coincides with the centre of mass of the cage; the \(X_\mathrm{c}\) axis is the axial direction of the cage; and the \(Y_\mathrm{c}\) and \(Z_\mathrm{c}\) axes show the radial direction of the cage and are parallel to the Y- and Z-axes of the initial condition, respectively. The coordinate system {\(O_\mathrm{c}; X_\mathrm{c}, Y_\mathrm{c}, Z_\mathrm{c}\)} moves and spins with the centre of mass of the cage. The same properties apply to the coordinate system of the inner ring, \(\{O_\mathrm{i}; X_\mathrm{i}, Y_\mathrm{i}, Z_\mathrm{i}\}\), and that of the outer ring, \(\{O_{\mathrm{o}}; X_{\mathrm{o}},Y_{\mathrm{o}}, Z_{\mathrm{o}}\}\). The coordinate system \(\{O_{\mathrm{p}j}; X_{\mathrm{p}j},Y_{\mathrm{p}j}, Z_{\mathrm{p}j}\}\) belongs to the \(j{\mathrm{th}}\) cage pocket in which origin \(O_{\mathrm{p}j}\) coincides with the geometric centre of the pocket. The \(X_{\mathrm{p}j}\) axis is parallel to the axial direction of the cage; the \(Y_{\mathrm{p}j}\) axis stands for the circumferential direction of the cage; the \(Z_{\mathrm{p}j}\) axis represents the radial direction of the cage. The coordinate system {\(O_{\mathrm{p}j}; X_{\mathrm{p}j}, Y_{\mathrm{p}j}, Z_{\mathrm{p}j}\)} moves and rotates with the cage. In addition, the \(j{\mathrm{th}}\) cage pocket corresponds to the \(j{\mathrm{th}}\) ball, and each cage pocket has its own coordinate system. The directions of the coordinate axes in all coordinate systems conform to the right-hand rule of the Cartesian coordinate system.

Fig. 2
figure 2

Schematic diagram of forces acting on ceramic ball

Full size image

The bearing noise mainly comes from the vibration, which can be classified as inherit noise caused by inherent vibrations of the structure, noise caused by vibrations of the profile error, as well as the friction and impact noise caused during the operation. The radiation noise of the bearing is caused by the superposition of noises of all components, i.e. balls, inner ring, cage, and outer ring. The vibration characteristics of each component are analysed below.

2.1 Differential equations of vibrations for rolling element

As an important component of angular contact ball bearings, the balls contact all components, i.e. the cage, inner ring, and outer ring. It is supposed that all balls are equal in mass and size, and the sizes of the cage pockets, which are distributed uniformly along the circumference, are the same. Figure 2 illustrates the forces acting on a ball when the ceramic ball bearing operates at a high speed.

In Fig. 2, \(\alpha _{\mathrm{i}j}\) and \(\alpha _{\mathrm{o}j}\) are the contact angles between the \(j{\mathrm{th}}\) ball and inner and outer raceways; \(Q_{\mathrm{i}j}\) and \(Q_{\mathrm{o}j}\) are the normal contact forces between the \(j{\mathrm{th}}\) ball and inner and outer raceways, respectively; \(T_{{\eta } {\mathrm{i}j}}, T_{{\eta } \mathrm{o}j}, T_{{\xi } \mathrm{i}j}\), and \(T_{{\xi } \mathrm{o}j}\) are the traction forces of the contact surface between the \(j{\mathrm{th}}\) ball and raceways; \(Q_{\mathrm{c}xj}\), \(Q_{\mathrm{c}yj}\), and \(Q_{\mathrm{c}zj}\) are the decomposition components of the collision force between the \(j{\mathrm{th}}\) ball and cage; \(G_{\mathrm{b}yj}\) and \(G_{\mathrm{b}zj}\) are the decomposition components of the gravity of the \(j{\mathrm{th}}\) ball; \(P_{\eta } j\) and \(P_{{\xi } j}\) are the friction forces acting on the surface of the \(j{\mathrm{th}}\) ball, including rolling and sliding friction forces; \(F_{\mathrm{b}xj}\), \(F_{\mathrm{b}yj}\), and \(F_{\mathrm{b}zj}\) are the components of the hydrodynamic force acting on the centre of the \(j{\mathrm{th}}\) ball; \(F_{{\eta } \mathrm{i}j}, F_{{\eta } \mathrm{o}j}, F_{{\xi } \mathrm{i}j}\), and \(F_{{\xi } \mathrm{o}j}\) are the hydrodynamic friction forces at the lubricant inlet of the contact zone of ball and raceways, including rolling and sliding friction forces; \(J_{x}\), \(J_{y}\), and \(J_{z}\) are the components of the moment of inertia for a ball rotated around its own centre; \(\omega _{xj}\), \(\omega _{yj}\), and \(\omega _{zj}\) are the components of the spin angular velocity of the \(j{\mathrm{th}}\) ball in its own coordinate system; and \({\dot{\omega }}_{xj} , {\dot{\omega }}_{yj} \), and \({\dot{\omega }}_{zj} \) are the components of the spin angular acceleration of the \(j{\mathrm{th}}\) ball in its own coordinate system.

The normal contact forces can be obtained through Hertz contact theory [6], and the traction forces can be calculated [7] by \(\eta VS _{c}/h_{c}\), where \(\eta \) is the lubricant viscosity; V is the relative velocity of the ball and raceways; \(S_{c}\) is the contact area; and \(h_{c}\) is the film thickness. For the detailed calculation of the other forces, please refer to ref. [44].

The differential equation [24] for the vibration of the \(j{\mathrm{th}}\) ceramic ball can be described as

$$\begin{aligned}&F_{\mathrm {b}xj} +F_{\eta \mathrm {o}j} \cos \alpha _{\mathrm {o}j} -F_{\eta \mathrm {i}j} \cos \alpha _{\mathrm {i}j}\nonumber \\&\quad +\,T_{\mathrm {\eta i}j} \mathrm {cos}\alpha _{\mathrm {i}j} -T_{\mathrm {\eta o}j} \cos \alpha _{\mathrm {o}j} \nonumber \\&\quad +\,Q_{\mathrm {i}j} \sin \alpha _{\mathrm {i}j} -Q_{\mathrm {o}j} \sin \alpha _{\mathrm {o}j}\nonumber \\&\quad +\,Q_{\mathrm {c}xj} -P_{\mathrm {\eta }j} =m_\mathrm {b} \ddot{x}_{\mathrm {b}j} \nonumber \\&F_{\mathrm {b}yj} +F_{\xi \mathrm {i}j} -F_{\xi \mathrm {o}j}\nonumber \\&\quad +\,T_{\xi \mathrm {o}j} -T_{\xi \mathrm {i}j} +G_{\mathrm {b}yj} +Q_{\mathrm {c}yj} =m_\mathrm {b} \ddot{y}_{\mathrm {b}j} \nonumber \\&F_{\mathrm {b}zj} -F_{\eta \mathrm {o}j} \sin \alpha _{\mathrm {o}j} +F_{\mathrm{R}\eta \mathrm {i}j} \sin \alpha _{\mathrm {i}j}\nonumber \\&\quad -\,T_{\mathrm {\eta i}j} \sin \alpha _{\mathrm {i}j} +T_{\mathrm {\eta o}j} \sin \alpha _{\mathrm {o}j} \nonumber \\&\quad +\,Q_{\mathrm {i}j} \cos \alpha _{\mathrm {i}j} -Q_{\mathrm {o}j} \cos \alpha _{\mathrm {o}j} -G_{\mathrm {b}zj} \nonumber \\&\quad +\,Q_{\mathrm {c}zj} -P_{\mathrm {\xi }j} =m_\mathrm {b} \ddot{z}_{\mathrm {b}j} \nonumber \\&{[}(T_{\xi \mathrm {i}j} -F_{\xi \mathrm {i}j} )\cos \alpha _{\mathrm {i}j} +(T_{\xi \mathrm {o}j} -F_{\xi \mathrm {o}j} )\cos \alpha _{\mathrm {o}j} \nonumber \\&\quad +\,Q_{czj} -P_{\xi j} ]\frac{D_\mathrm {W} }{2}-J_x {\dot{\omega }}_{xj} =I_\mathrm {b} {\dot{\omega }}_{\mathrm {b}xj} \nonumber \\&(T_{\eta \mathrm {i}j} -F_{\eta \mathrm {i}j} +T_{\eta \mathrm {o}j} -F_{\eta \mathrm {o}j} )\frac{D_\mathrm {W} }{2} -J_y {\dot{\omega }}_{yj} =I_\mathrm {b} {\dot{\omega }}_{\mathrm {b}yj}\nonumber \\&\quad +\,I_\mathrm {b} \omega _{\mathrm {b}zj} {\dot{\theta }}_{\mathrm {b}j} \nonumber \\&{[}(T_{\xi \mathrm {i}j} -F_{\xi \mathrm {i}j} )\sin \alpha _{\mathrm {i}j} +(T_{\xi \mathrm {o}j} -F_{\xi \mathrm {o}j} )\sin \alpha _{\mathrm {o}j} \nonumber \\&\quad +\,Q_{cxj} -P_{\eta j} ]\frac{D_\mathrm {W} }{2}-J_z {\dot{\omega }}_{zj} =I_\mathrm {b} {\dot{\omega }}_{\mathrm {b}zj} \nonumber \\&\quad +\,I_\mathrm {b} \omega _{\mathrm {b}yj} {\dot{\theta }}_{\mathrm {b}j} \end{aligned}$$
(1)

where \(D_\mathrm{W}\) is the diameter of the ceramic ball; \(m_\mathrm{b}\) is its mass; \(\ddot{x}_{{\mathrm {b}j}} , \ddot{y}_{{\mathrm {b}j}} \), and \(\ddot{z}_{\mathrm {b}j} \) are the displacement accelerations of the barycentre of the \(j{\mathrm{th}}\) ball along the direction of each coordinate axis in the coordinate system \(\{O; X, Y,Z\}; \omega _{\mathrm{b}xj}, \omega _{\mathrm{b}yj}\), and \(\omega _{\mathrm{b}zj}\) are the angular velocities of the \(j{\mathrm{th}}\) ball in the coordinate system \(\{O; X, Y, Z\}; \dot{\omega }_{{\mathrm {b}xj}} , {\dot{\omega }}_{\mathrm {b}yj} \), and \(\dot{\omega }_{\mathrm {b}zj} \) are the angular accelerations of the \(j{\mathrm{th}}\) ball in the coordinate system \(\{O; X, Y, Z\}; \dot{\theta }_{\mathrm {b}j} \) is the orbit speed of the \(j{\mathrm{th}}\) ball in the coordinate system \(\{O; X, Y, Z\}; and I_{b}\) are the moments of inertia of the ball in the coordinate system \(\{O; X, Y, Z\}\).

Fig. 3
figure 3

Schematic diagram of forces acting on cage

Full size image
Fig. 4
figure 4

Schematic diagram of forces acting on inner ring

Full size image

2.2 Differential equations of vibrations on cage

During the operation of the bearing, the cage contacts only the ball, and friction and impact are generated. The forces of the \(j{\mathrm{th}}\) ceramic ball on the cage of the bearing are shown in Fig. 3.

In Fig. 3, \(e_\mathrm{c}\) is the eccentricity between origin \(O_\mathrm{c}\) in the cage coordinate system \(\{O_\mathrm{c}; X_\mathrm{c}, Y_\mathrm{c}, Z_\mathrm{c}\}\) and origin O in the inertial coordinate system \(\{O; X, Y, Z\}; \phi _{\mathrm{c}} \) is the deflection angle of the coordinate system \(\{O_\mathrm{c}; Y_\mathrm{c}, Z_\mathrm{c}\}\) relative to \(\{O; Y, Z\}; \phi _{\mathrm {p}j} \) is the position angle of the \(j{\mathrm{th}}\) pocket; \(\phi _{\mathrm {b}j} \) is the position angle of the \(j{\mathrm{th}}\) ceramic ball relative to the cage; \({\phi }'_{\mathrm {b}j} \) is the cosine angle of \(\phi _{\mathrm {b}j} \); \(F_{\mathrm{c}y}\), and \(F_{\mathrm{c}z}\) are the components of the hydrodynamic force acting on the cage; and \(M_{\mathrm{c}x}\) is the friction moment acting on the cage.

The differential equation [24] for the vibration of the cage can be described as

$$\begin{aligned}&\sum _{j=1}^N {[(P_{\mathrm {\eta }j} -Q_{\mathrm {c}xj} )]} =m_{\mathrm{c}} \ddot{x}_{\mathrm{c}} \nonumber \\&F_{\mathrm {c}y} +\sum _{j=1}^N {[(P_{\mathrm {\xi }j} -Q_{\mathrm {c}zj} )\cos \phi _{\mathrm {b}j} -Q_{\mathrm {c}yj} \sin \phi _{\mathrm {b}j} ]} =m_{\mathrm{c}} \ddot{y}_{\mathrm{c}} \nonumber \\&F_{\mathrm {c}z} +\sum _{j=1}^N [(P_{\mathrm {\xi }j} -Q_{\mathrm {c}zj} )\sin \phi _{\mathrm {b}j} +Q_{\mathrm {c}yj} \cos \phi _{\mathrm {b}j} ] =m_{\mathrm{c}} \ddot{z}_{\mathrm{c}}\nonumber \\&\sum _{j=1}^N {\left[ (P_{\mathrm {\xi }j} -Q_{\mathrm {c}zj} )\frac{D_{\mathrm{W}} }{2}-Q_{\mathrm {c}yj} \frac{d_m }{2}\right] } +M_{\mathrm {c}x}\nonumber \\&\quad =I_{\mathrm {c}x} {\dot{\omega }}_{\mathrm {c}x} -(I_{\mathrm {c}y} -I_{\mathrm {c}z} )\omega _{\mathrm {c}y} \omega _{\mathrm {c}z} \nonumber \\&\sum _{j=1}^N {(P_{\mathrm {\eta }j} -Q_{\mathrm {c}xj} )\frac{d_m }{2}\cos \phi _{\mathrm {p}j} } =I_{\mathrm {cy}} {\dot{\omega }}_{\mathrm {c}y} -(I_{\mathrm {c}z} -I_{\mathrm {c}x} )\omega _{\mathrm {c}z} \omega _{\mathrm {c}x} \nonumber \\&\sum _{j=1}^N {(P_{\mathrm {\eta }j} -Q_{\mathrm {c}xj} )\frac{d_m }{2}\hbox {sin}\phi _{\mathrm {p}j} } =I_{\mathrm {cz}} {\dot{\omega }}_{\mathrm {c}z} -(I_{\mathrm {c}x} -I_{\mathrm {c}y} )\omega _{\mathrm {c}x} \omega _{\mathrm {c}y}\nonumber \\ \end{aligned}$$
(2)

where \(m_\mathrm{c}\) is the mass of the cage; \(d_{m}\) is the pitch diameter of the bearing; N is the number of the ceramic ball; \(\ddot{x}_{\mathrm{c}} \), \(\ddot{y}_{\mathrm{c}} \), and \(\ddot{z}_{\mathrm{c}} \) are the displacement accelerations of the barycentre of the cage along the direction of each coordinate axis in the coordinate system \(\{O; X, Y, Z\}; \omega _{\mathrm{c}x}, \omega _{\mathrm{c}y}\), and \(\omega _{cz}\) are the angular velocities of the cage in the coordinate system \(\{O; X, Y, Z\}; {\dot{\omega }}_{\mathrm {c}x} , {\dot{\omega }}_{\mathrm {c}y} \), and \({\dot{\omega }}_{\mathrm {c}z} \) are the angular accelerations of the cage in the coordinate system \(\{O; X, Y, Z\}; and I_{\mathrm{c}x}, I_{\mathrm{c}y}\), and \(I_{\mathrm{c}z}\) are the moments of inertia of the cage in the coordinate system \(\{O; X, Y, Z\}\).

Fig. 5
figure 5

Schematic diagram of forces acting on outer ring

Full size image

2.3 Differential equations of vibrations on inner ring

Vibrations of the inner ring are mainly caused by the contact friction between ball and inner ring. The forces of the \(j{\mathrm{th}}\) ceramic ball on the inner ring of the bearing are shown in Fig. 4.

In Fig. 4, \(\varphi _{\mathrm{i}j}\) is the position angle of the \(j{\mathrm{th}}\) ceramic ball relative to the inner ring.

The differential equation [24] for the vibration of the inner ring can be described as

$$\begin{aligned}&F_{\mathrm {i}x} +\sum _{j=1}^N {[(F_{\mathrm {\eta i}j} -T_{\mathrm {\eta i}j} )\cos \alpha _{\mathrm {i}j} -Q_{\mathrm {i}j} \sin \alpha _{\mathrm {i}j} ]} =m_{\mathrm{i}} \ddot{x}_{\mathrm{i}} \nonumber \\&F_{\mathrm {i}y} +\sum _{j=1}^N [(T_{\mathrm {\xi i}j} -F_{\mathrm {\xi i}j} )\cos \varphi _{\mathrm {i}j}\nonumber \\&\quad -\,(T_{\mathrm {\eta i}j} -F_{\mathrm {\eta i}j} )\sin \alpha _{\mathrm {i}j} \sin \varphi _{\mathrm {i}j}\nonumber \\&\quad +Q_{\mathrm {i}j} \cos \alpha _{\mathrm {i}j} \sin \varphi _{\mathrm {i}j} ] =m_{\mathrm{i}} \ddot{y}_{\mathrm{i}} \nonumber \\&F_{\mathrm {i}z} +\sum _{j=1}^N [(T_{\mathrm {\xi i}j} -F_{\mathrm {\xi i}j} )\sin \varphi _{\mathrm {i}j}\nonumber \\&\quad +\,(T_{\mathrm {\eta i}j} -F_{\mathrm {\eta i}j} )\sin \alpha _{\mathrm {i}j} \cos \varphi _{\mathrm {i}j}\nonumber \\&\quad -\,Q_{\mathrm {i}j} \cos \alpha _{\mathrm {i}j} \cos \varphi _{\mathrm {i}j} ] =m_{\mathrm{i}} \ddot{z}_{\mathrm{i}} \nonumber \\&M_{\mathrm {i}x} +\sum _{j=1}^N {(F_{\mathrm {\xi i}j} -T_{\mathrm {\xi i}j} )r_{\mathrm {i}j} } =I_{\mathrm {i}x} {\dot{\omega }}_{\mathrm {i}x} -(I_{\mathrm {i}y} -I_{\mathrm {i}z} )\omega _{\mathrm {i}y} \omega _{\mathrm {i}z} \nonumber \\&M_{\mathrm {i}y} +\sum _{j=1}^N {[Q_{\mathrm {i}j} \sin \alpha _{\mathrm {i}j} +(T_{\mathrm {\eta i}j} -F_{\mathrm {\eta i}j} )\cos \alpha _{\mathrm {i}j} ]r_{\mathrm {i}j} \cos \varphi _{\mathrm {i}j} }\nonumber \\&\quad -\sum _{j=1}^N {\left[ (T_{\mathrm {\xi i}j} -F_{\mathrm {\xi i}j} )\frac{D_{\mathrm{W}} }{2}k_{\mathrm{i}} \sin \alpha _{\mathrm {i}j} \sin \varphi _{\mathrm {i}j} \right] } \nonumber \\&\quad =I_{\mathrm {i}y} {\dot{\omega }}_{\mathrm {i}y} -(I_{\mathrm {i}z} -I_{\mathrm {i}x} )\omega _{\mathrm {i}z} \omega _{\mathrm {i}x} \nonumber \\&M_{\mathrm {i}z} +\sum _{j=1}^N {[Q_{\mathrm {i}j} \sin \alpha _{\mathrm {i}j} +(T_{\mathrm {\eta i}j} -F_{\mathrm {\eta i}j} )\cos \alpha _{\mathrm {i}j} ]r_{\mathrm {i}j} \sin \varphi _{\mathrm {i}j} }\nonumber \\&\quad +\sum _{j=1}^N {\left[ (T_{\mathrm {\xi i}j} -F_{\mathrm {\xi i}j} )\frac{D_{\mathrm{W}} }{2}k_{\mathrm{i}} \sin \alpha _{\mathrm {i}j} \cos \varphi _{\mathrm {i}j} \right] } \nonumber \\&\quad =I_{\mathrm {i}z} {\dot{\omega }}_{\mathrm {i}z} -(I_{\mathrm {i}x} -I_{\mathrm {i}y} )\omega _{\mathrm {i}x} \omega _{\mathrm {i}y} \end{aligned}$$
(3)

where \(m_\mathrm{i}\) is the mass of the inner ring; \(F_{\mathrm{i}x}\), \(F_{\mathrm{i}y}\), and \(F_{\mathrm{i}z}\) are the external loads acting on the inner ring; \(M_{\mathrm{i}x}, M_{\mathrm{i}y}\), and \(M_{\mathrm{i}z}\) are the external torques acting on the inner ring; \({\ddot{x}}_{\mathrm{i}} \), \(\ddot{y}_{\mathrm{i}} \), and \(\ddot{z}_{\mathrm{i}}\) are the displacement accelerations of the barycentre of the inner ring along the direction of each coordinate axis in the coordinate system \(\{O; X, Y, Z\}; \omega _{\mathrm{i}x}, \omega _{\mathrm{i}y},\) and \(\omega _{\mathrm{i}z}\) are the angular velocities of the inner ring in the coordinate system \(\{O; X, Y, Z\}; \dot{\omega }_{\mathrm {i}x} , {\dot{\omega }}_{\mathrm {i}y} \), and \(\dot{\omega }_{\mathrm {i}z} \) are the angular accelerations of the inner ring in the coordinate system \(\{O; X, Y, Z\}; I_{\mathrm{i}x}, I_{\mathrm{i}y}\), and \(I_{\mathrm{i}z}\) are the moments of inertia of the inner ring in the coordinate system \(\{O; X, Y, Z\}; k_\mathrm{i}\) is the inner ring raceway curvature radius coefficient; and \(r_{\mathrm{i}j}\) is the raceway radius of the inner ring and can be calculated by

$$\begin{aligned} r_{\mathrm {i}j} =\frac{d_{{m}} }{2}-\frac{D_{\mathrm{W}} }{2}k_{\mathrm{i}} \cos \alpha _{\mathrm {i}j} \end{aligned}$$
(4)

2.4 Differential equations of vibrations on outer ring

Since the outer ring of the bearing is installed inside the bearing pedestal and does not rotate with the rotating inner ring, the outer ring is subject to the force of the bearing pedestal. The forces acting on the outer ring comprise the contact force and dynamic friction forces caused by the interaction between outer ring and balls. The forces of the \(j{\mathrm{th}}\) ceramic ball on the outer ring of the bearing are shown in Fig. 5.

In Fig. 5, \(\phi _{\mathrm{o}j}\) is the position angle of the \(j{\mathrm{th}}\) ceramic ball relative to the outer ring.

The differential equation for the vibration of the outer ring can be described as

$$\begin{aligned}&F_{\mathrm {o}x} +\sum _{j=1}^N {[(T_{\mathrm {\eta o}j} -F_{\mathrm {\eta o}j} )\cos \alpha _{\mathrm {o}j} +Q_{\mathrm {o}j} \sin \alpha _{\mathrm {o}j} ]} =m_{\mathrm{o}} \ddot{x}_{\mathrm{o}} \nonumber \\&F_{\mathrm {o}y} -\sum _{j=1}^N \left[ (T_{\mathrm {\xi o}j} -F_{\mathrm {\xi o}j} )\cos \varphi _{\mathrm {o}j}\right. \nonumber \\&\quad \left. -\,(T_{\mathrm {\eta o}j} -F_{\mathrm {\eta o}j} )\sin \alpha _{\mathrm {o}j} \sin \varphi _{\mathrm {o}j} \right. \nonumber \\&\quad \left. +\,Q_{\mathrm {o}j} \cos \alpha _{\mathrm {o}j} \sin \varphi _{\mathrm {o}j} \right] =m_{\mathrm{o}} \ddot{y}_{\mathrm{o}} \nonumber \\&F_{\mathrm {o}z}-\sum _{j=1}^N \left[ \left( T_{\mathrm {\xi o}j} -F_{\mathrm {\xi o}j} \right) \sin \varphi _{\mathrm {o}j} \right. \nonumber \\&\quad \left. +\,\left( T_{\mathrm {\eta o}j} -F_{\mathrm {\eta o}j} \right) \sin \alpha _{\mathrm {o}j} \cos \varphi _{\mathrm {o}j}\right. \nonumber \\&\quad \left. -\,Q_{\mathrm {o}j} \cos \alpha _{\mathrm {o}j} \cos \varphi _{\mathrm {o}j} \right] =m_{\mathrm{o}} \ddot{z}_{\mathrm{o}} \nonumber \\&M_{\mathrm {o}x}+\sum _{j=1}^N {(T_{\mathrm {\xi o}j} -F_{\mathrm {\xi o}j} )r_{\mathrm {o}j} } =I_{\mathrm {o}x} {\dot{\omega }}_{\mathrm {o}x} -\left( I_{\mathrm {o}y} \right. \nonumber \\&\quad \left. -\,I_{\mathrm {o}z} \right) \omega _{\mathrm {o}y} \omega _{\mathrm {o}z} \nonumber \\&M_{\mathrm {o}y} +\sum _{j=1}^N \left[ Q_{\mathrm {o}j} \sin \alpha _{\mathrm {o}j} +\left( T_{\mathrm {\eta o}j} \right. \right. \nonumber \\&\quad \left. \left. -\,F_{\mathrm {\eta o}j} \right) \cos \alpha _{\mathrm {o}j} \right] r_{\mathrm {o}j} \cos \varphi _{\mathrm {o}j}\nonumber \\&\quad +\sum _{j=1}^N {\left[ (T_{\mathrm {\xi o}j} -F_{\mathrm {\xi o}j} )\frac{D_{\mathrm{W}} }{2}k_{\mathrm{o}} \sin \alpha _{\mathrm {o}j} \sin \varphi _{\mathrm {o}j} \right] } \nonumber \\&\quad =I_{\mathrm {o}y} {\dot{\omega }}_{\mathrm {o}y} -(I_{\mathrm {o}z} -I_{\mathrm {o}x} )\omega _{\mathrm {o}z} \omega _{\mathrm {o}x} \nonumber \\&M_{\mathrm {o}z} +\sum _{j=1}^N \left[ Q_{\mathrm {o}j} \sin \alpha _{\mathrm {o}j} +\left( T_{\mathrm {\eta o}j} \right. \right. \nonumber \\&\quad \left. \left. -\,F_{\mathrm {\eta o}j} \right) \cos \alpha _{\mathrm {o}j} \right] r_{\mathrm {o}j} \sin \varphi _{\mathrm {o}j}\nonumber \\&\quad -\sum _{j=1}^N {\left[ (T_{\mathrm {\xi o}j} -F_{\mathrm {\xi o}j} )\frac{D_{\mathrm{W}} }{2}k_{\mathrm{o}} \sin \alpha _{\mathrm {o}j} \cos \varphi _{\mathrm {o}j} \right] } \nonumber \\&\quad =I_{\mathrm {o}z} {\dot{\omega }}_{\mathrm {o}z} -(I_{\mathrm {o}x} -I_{\mathrm {o}y} )\omega _{\mathrm {o}x} \omega _{\mathrm {o}y} \end{aligned}$$
(5)

where \(m_\mathrm{o}\) is the mass of the outer ring; \(F_{\mathrm{o}x}\), \(F_{\mathrm{o}y}\), and \(F_{\mathrm{o}z}\) are the external loads acting on the outer ring; and \(M_{\mathrm{o}x}, M_{\mathrm{o}y}\), and \(M_{\mathrm{o}z}\) are the external torques acting on the outer ring. Here, these external forces and moments acting on the outer ring come from the pedestal. They are calculated by \(F_{\mathrm{o}x}=K_{\mathrm{o}{x}}x_\mathrm{o}, F_{\mathrm{o}y}=K_{\mathrm{o}y}y_{o}, F_{\mathrm{o}z}=K_{\mathrm{o}z}z_{o}, M_{\mathrm{o}x}=S_{\mathrm{o}x}R_{o}\psi _{\mathrm{o}x}, M_{oy}=S_{\mathrm{o}y}R_{o}\psi _{\mathrm{o}y}\), and \(M_{\mathrm{o}z}=S_{\mathrm{o}z}R_{o}\psi _{\mathrm{o}z}\) based on lumped spring–mass system models [45], where \(K_{\mathrm{o}x}, K_{\mathrm{o}y}, K_{\mathrm{o}z}, S_{\mathrm{o}x}, S_{\mathrm{o}y}\), and \(S_{\mathrm{o}z}\) are the stiffness coefficients of the springs, \(R_{\mathrm{o}}\) is the radius of the outer ring, and \(\psi _{\mathrm{o}x}, \psi _{\mathrm{o}y}\), and \(\psi _{\mathrm{o}z}\) are the angular displacements of the outer ring in the coordinate system \(\{O; X, Y, Z\}. \ddot{x}_{\mathrm{o}} , \ddot{y}_{\mathrm{o}} \), and \(\ddot{z}_0 \) are the displacement accelerations of the barycentre of the outer ring along the direction of each coordinate axis in the coordinate system \(\{O; X, Y, Z\}; \omega _{\mathrm{o}x}, \omega _{\mathrm{o}y}\), and \(\omega _{\mathrm{o}z}\) are the angular velocities of the outer ring in the coordinate system \(\{O; X, Y, Z\}; \dot{\omega }_{\mathrm {o}x} , {\dot{\omega }}_{\mathrm {o}y} \), and \(\dot{\omega }_{\mathrm {o}z} \) are the angular accelerations of the outer ring in the coordinate system \(\{O; X, Y, Z\}; I_{\mathrm{o}x}, I_{\mathrm{o}y}\), and \(I_{\mathrm{o}z}\) are the moments of inertia of the outer ring in the coordinate system \(\{O; X, Y, Z\}; k_{o}\) is the outer ring raceway curvature radius coefficient; and \(r_{\mathrm{o}j}\) is the raceway radius of the outer ring and can be calculated by

$$\begin{aligned} r_{\mathrm {o}j} =\frac{d_{{m}} }{2}+\frac{D_{\mathrm{W}} }{2}k_{\mathrm{o}} \cos \alpha _{\mathrm {o}j} \end{aligned}$$
(6)

3 Equivalent noise model

The rolling-element bearing consists of four components, i.e. inner ring, outer ring, rolling body, and cage. During the operation, friction and shock vibrations will be produced between the bearing components, leading to friction and impact noise. To analyse the noise characteristics of the ceramic angular contact ball bearing, the noise produced by each component of the bearing is investigated. That is, the noise characteristics of the inner ring, outer ring, ball, and cage are determined in order to locate the position of the noise source. The radiation noise of the bearing is the superposition of the noise of the four components.

The sound source models of four components of bearings, including ball sound source, point sound source, piston sound source, and cylindrical sound source, are developed according to the structural characteristics of a ceramic angular contact ball bearing [46, 47]. The acoustic conditions of the mathematical model regarding the noise are assumed as follows:

  1. (1)

    The propagation medium for the sound wave is a perfect fluid, i.e. no energy loss occurs during the movement of the medium.

  2. (2)

    The medium is uniform, continuous, and well distributed. On a macroscopic level, it is a static state, i.e. the initial velocity is zero when no sound disturbance exists.

  3. (3)

    The medium and its neighbourhood are in an adiabatic condition, i.e. no heat exchange occurs during the propagation of the sound wave.

Therefore, the wave equation [46] for the propagation of a small-amplitude wave in a perfect fluid can be described as

$$\begin{aligned} \nabla ^{2}p-\frac{1}{c_0^2 }\cdot \frac{\partial ^{2}p}{\partial t^{2}}=0 \end{aligned}$$
(7)

where \(\nabla ^{2}\) denotes the Laplace operator. Different forms exist in different coordinate systems; p is the sound pressure, \(c_{0}\) the sound velocity, and t the time.

3.1 Ball sound source

It is assumed that a sphere with radius \(r_{0}\) exists. Its surface emits sound waves uniformly with the microscale \(\xi = {dr}\) in the vicinity of \(r_{0}\). The wave equation with spherical coordinates is

$$\begin{aligned} \frac{\partial ^{2}p}{\partial r^{2}}+\frac{2}{r}\cdot \frac{\partial p}{\partial r}=\frac{1}{c_0^2 }\cdot \frac{\partial ^{2}p}{\partial t^{2}} \end{aligned}$$
(8)

where r is the distance between observation point and ball centre.

The general solution [46] of Eq. (8) is

$$\begin{aligned} p(r,t)=\frac{A}{r}\cdot e^{j(\omega t-kr)}+\frac{B}{r}\cdot e^{j(\omega t+kr)} \end{aligned}$$
(9)

where A and B are plurals usually, \(\omega \) is the angular velocity, \(k = 2\pi /\lambda _{0}\) the wave number, \(\lambda _{0}\) the wavelength, and j denotes an imaginary unit.

The first part of Eq. (9) represents an outwardly propagating spherical wave of radiation (divergent), and the second part represents a reflected spherical wave (convergent) going towards the ball sound source. Here, the freely travelling wave of the radiation towards unbounded space is discussed. No reflected wave exists, i.e. \(B = 0\). Hence,

$$\begin{aligned} p(r,t)=\frac{A}{r}\cdot e^{j(\omega t-kr)} \end{aligned}$$
(10)

where the modulus of A / r is the sound pressure amplitude.

According to the kinetic equation, the particle velocity along the radial coordinate r can be obtained as

$$\begin{aligned} v_r =-\frac{1}{j\omega \rho _0 }\frac{\partial p}{\partial r}=\frac{A}{r\rho _0 c_0 }\left( 1+\frac{1}{jkr}\right) e^{j(\omega t-kr)} \end{aligned}$$
(11)

where \(\rho _{0}\) is the static density of the medium.

Since the velocity of a medium particle at the surface of the sound source is equal to the vibration velocity on the surface of the sound source [46, 48, 49], the following boundary condition exists:

$$\begin{aligned} v_r |_{r=r_0 } =u \end{aligned}$$
(12)

where u is the vibration velocity on the surface of the sound source and obtained by solving the differential equations of each bearing component as a sound source.

Therefore, A can be calculated using Eq. (13).

$$\begin{aligned} A=\frac{\rho _0 c_0 kr_0^2 u}{1+(kr_0 )^{2}}(kr_0 +j) \end{aligned}$$
(13)

Then, the radiation sound pressure equation of the pulsating spherical source is obtained as

$$\begin{aligned} p(r,t)=\frac{\rho _0 c_0 kr_0^2 u}{r\sqrt{1+(kr_0 )^{2}}}e^{j\left( \omega t-kr+\arctan \frac{1}{kr_0 }\right) } \end{aligned}$$
(14)

The pulsating spherical-source model describes a zero-order spherical source. The model is therefore not fully applicable to radiation noise caused by a ceramic ball. Here, a first-order spherical source [50] is used to describe the radiation sound pressure of the ceramic ball, which can be written as

$$\begin{aligned}&p_b (r,\theta ,t)\nonumber \\&=\frac{\rho _0 c_0 kr_0^3 u\cos \theta }{2r^{2}}\sqrt{1+(kr)^{2}}e^{j\left( \omega t-kr-\arctan \frac{1}{kr}\right) }\nonumber \\ \end{aligned}$$
(15)

where \(p_{b}\) is the radiation sound pressure of a ball sound source and \(\theta \) is the azimuth angle of the observation point.

To obtain the radiation sound pressure of the \(j{\mathrm{th}}\) ceramic ball, its vibration velocity in the ball sound source is calculated by

$$\begin{aligned} u_{\mathrm {b}bj} =\sqrt{{\dot{x}}_{\mathrm {b}j}^2 +\dot{y}_{\mathrm {b}j}^2 +{\dot{z}}_{\mathrm {b}j}^2 } \end{aligned}$$
(16)

where \(u_{{\mathrm{b}}bj}\) is the vibration velocity of the \(j{\mathrm{th}}\) ball in the ball sound source. \({\dot{x}}_{\mathrm {b}j} \), \(\dot{y}_{\mathrm {b}j} \), and \({\dot{z}}_{\mathrm {b}j} \) are the velocities of the barycentre of the \(j{\mathrm{th}}\) ball along the direction of each coordinate axis in the coordinate system \(\{O; X, Y, Z\}\).

By substituting Eq. (16) into Eq.(15), the radiation sound pressure of a ceramic ball in the ball sound source is obtained as

$$\begin{aligned} p_{\mathrm {b}bj} (r,\theta ,t)= & {} \frac{\rho _0 c_0 kr_0^3 \sqrt{1+(kr)^{2}}\cos \theta }{2r^{2}}\nonumber \\&\sqrt{{\dot{x}}_{\mathrm {b}j}^2 +{\dot{y}}_{\mathrm {b}j}^2 +{\dot{z}}_{\mathrm {b}j}^2 }e^{j(\omega t-kr-\arctan \frac{1}{kr})}\nonumber \\ \end{aligned}$$
(17)

where \(p_{\mathrm{b}bj}\) represents the radiation sound pressure of the \(j{\mathrm{th}}\) ball in the ball sound source.

3.2 Point sound source

When the sound source radius of the pulsating sphere is far smaller than the sound wave length, i.e. \({ kr}_{0}\rightarrow 0\), the sound source is called a point sound source. When the point sound source radiates energy into the half-space, the intensity of the point source is denoted as \(Q_{0} = 2\pi \hbox {r}_{0}^{2}u\). Hence, the sound pressure equation of radiation for the sound source can be described as [46]

$$\begin{aligned} p_d (r,t)= & {} \frac{\rho _0 c_0 k}{2\pi r}Q_0 e^{j\left( \omega t-kr+\frac{\pi }{2}\right) }\nonumber \\= & {} \frac{\rho _0 c_0 kr_0^2 u}{r}e^{j\left( \omega t-kr+\frac{\pi }{2}\right) } \end{aligned}$$
(18)

where \(p_{d}\) represents the radiation sound pressure of a point sound source.

The combination of point sources can handle any complex surface sound source. Here, the point source is used to calculate the turnover vibration radiation sound pressure of each bearing component. The vibration velocity of each bearing component in the point sound source can be determined using

$$\begin{aligned} \begin{array}{lll} u_{\mathrm {b}dj} =\frac{D_{\mathrm{w}} }{4}\sqrt{\omega _{\mathrm {b}xj}^2 +\omega _{\mathrm {b}yj}^2 +\omega _{\mathrm {b}zj}^2 } \\ u_{\mathrm {c}d} =\frac{R_{\mathrm{c}} }{2}\sqrt{4\omega _{\mathrm {c}x}^2 +\omega _{\mathrm {c}y}^2 +\omega _{\mathrm {c}z}^2 } \\ u_{\mathrm {i}d} =\frac{R_{\mathrm{i}} }{2}\sqrt{4\omega _{\mathrm {i}x}^2 +\omega _{\mathrm {i}y}^2 +\omega _{\mathrm {i}z}^2 } \\ u_{\mathrm {o}d} =\frac{R_{\mathrm{o}} }{2}\sqrt{4\omega _{\mathrm {o}x}^2 +\omega _{\mathrm {o}y}^2 +\omega _{\mathrm {o}z}^2 } \\ \end{array} \end{aligned}$$
(19)

where \(u_{\mathrm{b}dj}, u_{\mathrm{c}d}, u_{\mathrm{i}d}\), and \(u_{\mathrm{o}d}\) are the vibration velocities of the \(j{\mathrm{th}}\) ball, cage, inner ring, and outer ring in point sound source, respectively. \(R_\mathrm{c}\) and \(R_\mathrm{i}\) are the radii of the cage and inner ring.

Therefore, the radiation sound pressure of each bearing component in the point sound source can be obtained as

$$\begin{aligned} \begin{array}{lll} p_{\mathrm {b}dj} (r,t)=\frac{\rho _0 c_0 kr_0^2 D_{\mathrm{w}} }{4r}\sqrt{\omega _{\mathrm {b}xj}^2 +\omega _{\mathrm {b}yj}^2 +\omega _{\mathrm {b}zj}^2 }e^{j\left( \omega t-kr+\frac{\pi }{2}\right) } \\ p_{\mathrm {c}d} (r,t)=\frac{\rho _0 c_0 kr_0^2 R_{\mathrm{c}} }{2r}\sqrt{4\omega _{\mathrm {c}x}^2 +\omega _{\mathrm {c}y}^2 +\omega _{\mathrm {c}z}^2 }e^{j\left( \omega t-kr+\frac{\pi }{2}\right) } \\ p_{\mathrm {i}d} (r,t)=\frac{\rho _0 c_0 kr_0^2 R_{\mathrm{i}} }{2r}\sqrt{4\omega _{\mathrm {i}x}^2 +\omega _{\mathrm {i}y}^2 +\omega _{\mathrm {i}z}^2 }e^{j\left( \omega t-kr+\frac{\pi }{2}\right) } \\ p_{\mathrm {o}d} (r,t)=\frac{\rho _0 c_0 kr_0^2 R_{\mathrm{o}} }{2r}\sqrt{4\omega _{\mathrm {o}x}^2 +\omega _{\mathrm {o}y}^2 +\omega _{\mathrm {o}z}^2 }e^{j\left( \omega t-kr+\frac{\pi }{2}\right) } \\ \end{array} \end{aligned}$$
(20)

where \(p_{\mathrm{b}dj}\), \(p_{\mathrm{c}d}\), \(p_{\mathrm{i}d}\), and \(p_{\mathrm{o}d}\) represent the radiation sound pressures of the \(j{\mathrm{th}}\) ball, cage, inner ring, and outer ring in the point sound source, respectively.

3.3 Piston sound source

The piston sound source is obtained by combining many point sound sources. The end-surface vibration noise of a bearing ring is a piston sound source. It is assumed that the end surface of the ring is divided into many infinitely small surfaces, dS, and each is treated as a point sound source. The intensity of the point sound source is denoted as \({\mathrm{d}}Q_{0} = u {\mathrm{d}}S\). Since the vibration of only half a sphere contributes to the half-space sound field, the sound pressure emitted from the end surface of the ring can be expressed as [46]

$$\begin{aligned} p=\int \mathop {\int }\limits _S {j\frac{\rho _0 c_0 k}{2\pi h}ue^{j(\omega t-kh)}\mathrm{d}S} \end{aligned}$$
(21)

where S is the end surface area of the ring and h is the distance from observation point to point sound source.

Fig. 6
figure 6

Schematic diagram of coordinate systems for piston sound source

Full size image

As shown in Fig. 6, the sound field is rotational symmetric relative to the X-axis of the piston sound centre. In the sound field, the point P is placed in the XOZ plane, and analysed by geometry, the relational expressions can be obtained as follows:

$$\begin{aligned} h= & {} \sqrt{r^{2}+l^{2}-2rl\cos (\vec {r},\vec {l})} \end{aligned}$$
(22)
$$\begin{aligned} \cos (\vec {r},\vec {l})= & {} \sin \theta \cos \varphi \end{aligned}$$
(23)

where l is the distance between the surface, dS, and coordinate origin, O, and \(\varphi \) is the azimuth angle of the surface, dS. When the distance from the observation point to the centre of the piston sound source is far greater than the radius of the piston,

$$\begin{aligned} h\approx r-l\sin \theta \cos \varphi \end{aligned}$$
(24)

By replacing Eq. (24) into (21), the sound pressure can be expressed as

$$\begin{aligned} p=j\frac{\rho _0 c_0 k}{2\pi r}e^{j(\omega t-kr)}\int \int {e^{jkl\sin \theta \cos \varphi }l\mathrm{d}l\mathrm{d}\varphi } \end{aligned}$$
(25)

According to the properties of the Bessel function, the sound pressure can be obtained using

$$\begin{aligned} p(r,\theta ,t)= & {} j\frac{\rho _0 c_0 u_0 e^{j(\omega t-kr)}}{r\sin \theta }\nonumber \\&\left[ \frac{D}{2}J_1 \left( k\frac{D}{2}\sin \theta \right) -\frac{d}{2}J_1 \left( k\frac{d}{2}\sin \theta \right) \right] \nonumber \\ \end{aligned}$$
(26)

where D and d are the external and internal diameters of the ring, respectively.

Based on the low frequency near the field characteristic of the piston sound source, the sound pressure equation for the vibration radiation of the ring end surface can be obtained as

$$\begin{aligned} p_p (r,\theta ,t)=\frac{\rho _0 c_0 ku}{8r}(D^{2}-d^{2})e^{j\left( \omega t-kr+\frac{\pi }{2}\right) } \end{aligned}$$
(27)

where \(p_{p}\) is the radiation sound pressure of a piston sound source.

The end-surface vibration radiation pressure of the cage is also calculated with a piston sound source.

In the piston sound source, the vibration velocities of the cage, inner ring, and outer ring are calculated as

$$\begin{aligned} \begin{array}{l} u_{\mathrm {c}p} ={\dot{x}}_{\mathrm{c}} \\ u_{\mathrm {i}p} ={\dot{x}}_{\mathrm{i}} \\ u_{\mathrm {o}p} ={\dot{x}}_{\mathrm{o}} \\ \end{array} \end{aligned}$$
(28)

where \(u_{{\mathrm{c}}p}, u_{\mathrm{{i}}p}\), and \(u_{{\mathrm{o}}p}\) are the vibration velocities of the cage, inner ring, and outer ring in the piston sound source, respectively. \({\dot{x}}_{\mathrm{c}}, {\dot{x}}_{\mathrm{i}} \), and \({\dot{x}}_{\mathrm{o}} \) are, respectively, the velocities of the barycentre of the cage, inner ring, and outer ring along the X-direction in the coordinate system \(\{O; X, Y, Z\}\).

Therefore, the radiation sound pressures of the cage, inner ring, and outer ring in the piston sound source can be obtained as

$$\begin{aligned} \begin{array}{l} p_{\mathrm {c}p} (r,\theta ,t)=\frac{\rho _0 c_0 k{\dot{x}}_{\mathrm{c}} }{8r}(D^{2}-d^{2})e^{j\left( \omega t-kr+\frac{\pi }{2}\right) } \\ p_{\mathrm {i}p} (r,\theta ,t)=\frac{\rho _0 c_0 k{\dot{x}}_{\mathrm{i}} }{8r}(D^{2}-d^{2})e^{j\left( \omega t-kr+\frac{\pi }{2}\right) } \\ p_{\mathrm {o}p} (r,\theta ,t)=\frac{\rho _0 c_0 k{\dot{x}}_{\mathrm{o}} }{8r}(D^{2}-d^{2})e^{j\left( \omega t-kr+\frac{\pi }{2}\right) } \\ \end{array} \end{aligned}$$
(29)

where \(p_{{\mathrm{c}}p}, p_{\mathrm{{i}}p}\), and \(p_{\mathrm{{o}}p}\) represent the radiation sound pressures of the cage, inner ring, and outer ring in the piston sound source, respectively.

3.4 Cylindrical sound source

A cylindrical sound source is used for the radial vibrations of a bearing ring. By assuming an infinite medium and that the length of the cylindrical bearing ring surface is infinite, the axis perpendicular to the ring oscillates at a vibration velocity of u. Further, it is assumed that the x-axis coincides with the cylindrical axis. Thus, the sound pressure p is independent of the X coordinate. The sound wave equation can be simplified as

$$\begin{aligned} \frac{\partial ^{2}p}{\partial r^{2}}+\frac{1}{r}\frac{\partial p}{\partial r}=\frac{1}{c^{2}}\frac{\partial ^{2}p}{\partial t^{2}} \end{aligned}$$
(30)

By only addressing the sound field radiation from the sound source surface to the distant space, the sound pressure [51] can be calculated with

$$\begin{aligned} p(r,\theta ,t)=A_1 \cdot H_1^{(2)} (kr)\cdot \cos \theta \cdot e^{j(\omega t-kr)} \end{aligned}$$
(31)

Here,

$$\begin{aligned} A_1= & {} \frac{-j\rho _0 c_0 u}{{J}'_1 (ka)-j{N}'_1 (ka)} \end{aligned}$$
(32)
$$\begin{aligned} H_1^{(2)} (kr)= & {} J_1 (kr)-jN_1 (kr) \end{aligned}$$
(33)

where \(J_{1}\), \(N_{1}\), and \(H_{1}^{(2)}\) are the first-order Bessel function, first-order Neumann function, and Hankel function of the second kind, respectively; \(J_{1}'\) and \(N_{1}'\) are the derivatives of \(J_{1}\) and \(N_{1}\), respectively, and a is the cylindrical radius.

By substituting Eqs. (32) and (33) into (31), the sound pressure can be denoted as

$$\begin{aligned} p(r,\theta ,t){=}\frac{-j\rho _0 c_0 ue^{j(\omega t{-}kr)}}{{J}'_1 (ka){-}j{N}'_1 (ka)}[J_1 (kr){-}jN_1 (kr)]\cos \theta \nonumber \\ \end{aligned}$$
(34)

For a low-frequency emission, i.e. \(a<< \lambda _{0}\) and \(ka<< 1\), according to the expansion of the Bessel function, \(z_{0}<< 1\),

$$\begin{aligned} \begin{array}{l} J_1 (z_0 )\approx \frac{z_0 }{2} ,\\ N_1 (z_0 )\approx -\frac{2}{\pi z_0 } \\ {J}'_1 (z_0 )\approx \frac{1}{2},\\ {N}'_1 (z_0 )\approx \frac{2}{\pi z_0^2 } \\ \end{array} \end{aligned}$$
(35)

By substituting Eq. (35) into (34), the sound pressure can be determined using

$$\begin{aligned} p(r,\theta ,t)= & {} \frac{\rho _0 c_0 ue^{j(\omega t-kr)}}{\frac{1}{4}+\left( {\frac{2}{\pi k^{2}a^{2}}} \right) ^{2}}\nonumber \\&\left[ \left( {\frac{1}{\pi kr}+\frac{r}{\pi ka^{2}}} \right) \right. \nonumber \\&\left. -j\left( {\frac{kr}{4}-\frac{4}{\pi ^{2}k^{3}ra^{2}}} \right) \right] \cos \theta \end{aligned}$$
(36)

The following terms are defined:

$$\begin{aligned} A_0= & {} \frac{\rho _0 c_0 }{\frac{1}{4}+\left( {\frac{2}{\pi k^{2}a^{2}}} \right) ^{2}}\cos \theta \end{aligned}$$
(37)
$$\begin{aligned} B_r= & {} \frac{1}{\pi kr}+\frac{r}{\pi ka^{2}} \end{aligned}$$
(38)
$$\begin{aligned} B_i= & {} \frac{kr}{4}-\frac{4}{\pi ^{2}k^{3}ra^{2}} \end{aligned}$$
(39)

Consequently, the sound pressure caused by the radial vibration of the ring cylinder can be expressed as

$$\begin{aligned} p_c (r,\theta ,t)=A_0 u\sqrt{B_r^2 +B_i^2 }e^{j\left( \omega t-kr-\arctan \frac{B_i }{B_r }\right) } \end{aligned}$$
(40)

where \(p_{c}\) represents the radiation sound pressure of a cylindrical sound source.

The cylindrical sound source model can also be used to calculate the radial vibration radiation pressure of the cage.

In the cylindrical sound source, the vibration velocities of the cage, inner ring, and outer ring are calculated as

$$\begin{aligned} \begin{array}{lll} u_{\mathrm {c}c} =\sqrt{{\dot{y}}_{\mathrm{c}}^2 +{\dot{z}}_{\mathrm{c}}^2 } \\ u_{\mathrm {i}c} =\sqrt{{\dot{y}}_{\mathrm{i}}^2 +{\dot{z}}_{\mathrm{i}}^2 } \\ u_{\mathrm {o}c} =\sqrt{{\dot{y}}_{\mathrm{o}}^2 +{\dot{z}}_{\mathrm{o}}^2 } \\ \end{array} \end{aligned}$$
(41)

where \(u_{\mathrm{c}c}, u_{{\mathrm{i}}c}\), and \(u_{\mathrm{o}c}\) are the vibration velocities of the cage, inner ring, and outer ring in cylindrical sound source, respectively. \({\dot{y}}_{\mathrm{c}}, {\dot{y}}_{\mathrm{i}} , {\dot{y}}_{\mathrm{o}} , {\dot{z}}_{\mathrm{c}} , {\dot{z}}_{\mathrm{i}} \), and \({\dot{z}}_{\mathrm{o}} \) are, respectively, the velocities of the barycentre of the cage, inner ring, and outer ring along the Y- and Z-direction in the coordinate system \(\{O; X, Y, Z\}\).

Therefore, the radiation sound pressures of the cage, inner ring, and outer ring in cylindrical sound source can be obtained as

$$\begin{aligned} \begin{array}{lll} p_{\mathrm {c}c} (r,\theta ,t)=A_0 \sqrt{B_r^2 +B_i^2 }\sqrt{{\dot{y}}_{\mathrm{c}}^2 +{\dot{z}}_{\mathrm{c}}^2 }e^{j\left( \omega t-kr-\arctan \frac{B_i }{B_r }\right) } \\ p_{\mathrm {i}c} (r,\theta ,t)=A_0 \sqrt{B_r^2 +B_i^2 }\sqrt{{\dot{y}}_{\mathrm{i}}^2 +{\dot{z}}_{\mathrm{i}}^2 }e^{j\left( \omega t-kr-\arctan \frac{B_i }{B_r }\right) } \\ p_{\mathrm {o}c} (r,\theta ,t)=A_0 \sqrt{B_r^2 +B_i^2 }\sqrt{{\dot{y}}_{\mathrm{o}}^2 +{\dot{z}}_{\mathrm{o}}^2 }e^{j\left( \omega t-kr-\arctan \frac{B_i }{B_r }\right) } \\ \end{array}\nonumber \\ \end{aligned}$$
(42)

where \(p_{\mathrm{c}c}, p_{\mathrm{i}c}\), and \(p_{\mathrm{o}c}\) represent the radiation sound pressure of the ball, cage, inner ring, and outer ring in cylindrical sound source, respectively.

3.5 Sound pressure level (SPL)

By solving the differential equations of the vibration for each bearing component, the vibration velocity of each bearing component is obtained, and the velocity is substituted into the above sound source model to obtain the sound pressure of the analysis field point. By superposing multiple sound sources, the total sound pressure of each bearing component can be obtained as

$$\begin{aligned} \begin{array}{l} p_{\mathrm {b}j} =\sqrt{p_{\mathrm {b}bj}^2 +p_{\mathrm {b}dj}^2 } \\ p_{\mathrm{c}} =\sqrt{p_{\mathrm {c}p}^2 +p_{\mathrm {c}c}^2 +p_{\mathrm {c}d}^2 } \\ p_{\mathrm{i}} =\sqrt{p_{\mathrm {i}p}^2 +p_{\mathrm {i}c}^2 +p_{\mathrm {i}d}^2 } \\ p_{\mathrm{o}} =\sqrt{p_{\mathrm {o}p}^2 +p_{\mathrm {o}c}^2 +p_{\mathrm {o}d}^2 } \\ \end{array} \end{aligned}$$
(43)

where \(p_{\mathrm{b}j}, p_{\mathrm{c}}, p_{\mathrm{i}}\), and \(p_{\mathrm{o}}\) represent the total radiation sound pressure of the ball, cage, inner ring, and outer ring, respectively.

The sound pressure of a certain sound source is measured by assuming a continuous time interval at a certain fixed position. The effective sound pressure [42] is obtained as

$$\begin{aligned} p_e =\sqrt{\frac{1}{T}\int _0^T {p^{2}\mathrm{d}t} } \end{aligned}$$
(44)

where \(p_{e}\) denotes the effective sound pressure value; T, the sampling time; and p, the instantaneous sound pressure.

Therefore, the effective SPL at the measurement point can be calculated from

$$\begin{aligned} L_p =20\log _{10} \frac{p_e }{p_{\mathrm{ref}} } \end{aligned}$$
(45)

where \(p_{\mathrm{ref}} = 2 \times 10^{-5}\) Pa is the referenced SPL.

According to the principle of sound field superposition [46], the overall SPL for the noise of the ceramic angular contact ball bearing at a certain measuring point can be calculated as

$$\begin{aligned} SPL=10\log _{10} \left( \sum _{i=1}^Z {10^{\frac{L_{pi} }{10}}} \right) \end{aligned}$$
(46)

where \(L_{pi}\) is the SPL of the \(i{\mathrm{th}}\) sound source at the measuring point and Z the total number of sound sources.

The dynamic behaviour of each component of the ceramic angular contact ball bearing is analysed, and the noise is calculated by combining various types of sound sources to obtain the total noise of the bearing. This method is the so-called multi-sound source method. In the method, according to the vibration characteristics of each component, a combination of multiple sound sources is applied to calculate the radiation noise of each bearing component, e.g. the radiation noise of the rings is obtained by superposing the noises of the point sound source, piston sound source, and cylindrical sound source. Furthermore, based on the principle of sound field superposition, the total noise of the bearing is obtained by superposing the radiation noises of all bearing components. The flowchart for whole solution process is shown in Fig. 7.

Fig. 7
figure 7

Flowchart for whole solution process

Full size image

4 Numerical simulation and experimental verification

4.1 Numerical simulation

In this study, high-speed ceramic angular contact ball bearings are installed in a motorised spindle, and the pre-tightening force of the bearing is set to 500 N. The rings, balls, and cage are made of GCr15 steel, silicon nitride ceramics, and bakelite, respectively. The specifications of the ceramic angular contact ball bearing and spindle are listed in Table 1. It is assumed that the bearing operates with a perfect lubrication and remains in the steady state during operation. Here, the nonlinear dynamic differential equations are solved by gear stiff integration algorithm with variable steps [52]. Then, the vibration velocities on the sound source surfaces are obtained and substituted into the noise model for calculating the radiation noise. The noise variations of the high-speed ceramic angular contact ball bearing during the unloaded operation in a speed range of 10,000–40,000 r \(\hbox {min}^{-1}\) are studied. The speed variation step size is set to 1000 r \(\hbox {min}^{-1}\).

Table 1 Specifications of the ceramic angular contact ball bearing and spindle
Full size table

Four field points are analysed to discuss the change law of the SPL for a ceramic angular contact ball bearing with rotational speed. The analysis points 1, 2, and 3 are located along the radial direction and the analysis point 4 along the axial direction. The analysis points 1, 2, and the bearing centre are positioned on a straight line perpendicular to gravity. Further, points 1 and 2 are 105 mm and 150 mm away from the bearing axis, respectively. The analysis point 3 is above the bearing and 105 mm away from the bearing axis. The analysis point 4 is located on the bearing axis and 75.5 mm away from the end surface of the bearing. The SPL at the analysis points can be obtained through Eq. (46). The calculation results based on the multi-sound source method are shown in Fig. 8.

Regarding the SPL trend at each point in Fig. 8, first, the radiation noise of the ceramic angular contact ball bearing gradually increases with increasing rotation speed of the bearing. Then, it reaches a peak value and begins to decrease. The maximum peak value of the SPL occurs at a rotation speed of 28,000 r \(\hbox {min}^{-1}\), which is called the critical speed. The SPL varies steeply near the critical speed. Although the overall trend of the SPL at each point is similar, there are still differences in SPL and its variations at different locations. The SPL of point 2 is smaller than that of point 1 at any rotation speed, and the SPL of point 4 is between points 1 and 2. It seems that the SPL at point 3 is not significantly related to the SPL at other points. The SPL of point 3 is larger than that of point 1 for a rotation speed range of 16,000–27,000 r \(\hbox {min}^{-1}\), and lower than that of point 1 at other speeds. Above 32,000 r \(\hbox {min}^{-1}\), the SPL at point 3 is smaller than that at the other three points.

Fig. 8
figure 8

SPL of bearing at analysis points

Full size image
Fig. 9
figure 9

Measurement scheme of bearing noise

Full size image
Fig. 10
figure 10

Experimental and calculated results. a point 1, b point 2, c point 3, and d point 4

Full size image

4.2 Experimental verification

To obtain the sound pressure distribution of the radiation noise for the ceramic angular contact ball bearing, the measurement scheme of Fig. 9 is adopted in this study. When observing from the front end of the motorised spindle, the bearing rotates clockwise. To ensure the consistency of the measuring points and the calculation field points, the measuring points 1 and 2 are positioned on the left side of the motorised spindle, point 3 is above the motorised spindle, and point 4 is in front of the motorised spindle. The positions of points 1 and 2 are 55 mm and 100 mm away from the outer surface of the motorised spindle (105 mm and 150 mm away from the bearing axis) regarding the horizontal diameter, respectively. Measuring point 3 is located 55 mm away from the outer surface of the motorised spindle (105 mm away from the bearing axis) regarding the vertical diameter. Point 4 is on the bearing axis and 60 mm away from the front surface of the motorised spindle (75.5 mm away from the end surface of the bearing). The sound pressure sensors (INV9206-I, China Orient Institute of Noise and Vibration) are placed at the measuring points. The sound pressure signal of each measuring point is collected by a data collector (INV3018C, China Orient Institute of Noise and Vibration) and transmitted to the computer to further process the sound pressure data and analyse the radiation sound field characteristics of the ceramic angular contact ball bearing.

The environmental temperature in the laboratory is \(22^{\circ }\hbox {C}\), and the background noise is lower than 45 dB. The cooling system for the motorised spindle is composed of a water cooling system, and the motorised spindle is lubricated through an oil–gas lubrication system. The flow rates of cooling water, air, and oil are set to \(0.3\,\hbox {m}^{3}\,\hbox {h}^{-1}, 4.84 \hbox {m}^{3}\, \hbox {h}^{-1}\), and \(0.8 \hbox {cm}^{3}\,\hbox {h}^{-1}\), respectively. The sound pressure distribution characteristics of the bearing radiation noise are analysed by measuring the noise pressure for spindle rotation speeds of 10,000 r \(\hbox {min}^{-1}\), 15,000 r \(\hbox {min}^{-1}\), 20,000 r \(\hbox {min}^{-1}\), 25,000 r \(\hbox {min}^{-1}\), 26,000 r \(\hbox {min}^{-1}\), 27,000 r \(\hbox {min}^{-1}\), 28,000 r \(\hbox {min}^{-1}\), 29,000 r \(\hbox {min}^{-1}\), 30,000 r \(\hbox {min}^{-1}\), 35,000 r \(\hbox {min}^{-1}\), and 40,000 r \(\hbox {min}^{-1}\), respectively. The measured SPLs and the calculated results of the four measuring points are shown in Fig. 10.

As shown in Fig. 10, at the selected field points, a consistent variation trend exists between calculated values and experimental results: the radiation noise first increases with increasing rotation speed of the spindle, and the SPL has a high peak value at a critical speed of 28,000 r \(\hbox {min}^{-1}\). Then, the noise decreases with increasing rotation speed. The experimental values at each rotation speed are smaller than the calculated values except for 20,000 r \(\hbox {min}^{-1}\). The average relative errors of the field points 1 to 4 at all selected rotation speeds are 1.74%, 1.62%, 1.89%, and 1.75%, respectively. Further, the overall average relative error is 1.75%. The maximum difference between calculated and experimental results is 2.36 dB with a relative error of 2.83% (point 3 with rotation speed of 30,000 r \(\hbox {min}^{-1}\)). The minimum difference between calculated and experimental results is 0.24 dB with a relative error of 0.28% (point 1 with rotation speed of 26,000 r \(\hbox {min}^{-1}\)). The error is relatively large above 30,000 r \(\hbox {min}^{-1}\). The results show that the bearing noise is the main constituent of the motorised-spindle noise. They simultaneously verify the effectiveness and accuracy of the proposed multi-sound source method in predicting the radiation noise of a ceramic angular contact ball bearing.

According to the theoretical directivity of the sound field, even if the analysis point is at identical distances from the sound source, the noise in different directions varies. For example, the maximum values in Fig. 10a, c are different. In the condition of the ideal sound propagation and equivalent analysis, the calculated results obviously show the sound field directivity. However, in the actual measurements, the radiation noise of the bearing will be disturbed by various factors such as the attenuation of sound propagation, and absorption of the bearing noise by the motorised spindle housing. The experimental results at the maximum value of Fig. 10a, c present a similar value. They do not have obvious directionality compared with the calculation results. Therefore, the SPL in Fig. 10c has a better approximation of the maximum value, whereas Fig. 10a presents a larger discrepancy.

To get detailed information of the bearing noise, the radiation noise characteristics and contribution of each component are further analysed.

5 Acoustic characteristics of the bearing

For a more detailed analysis of the acoustic characteristics of the ceramic angular contact ball bearing, the radiation noise of each component is analysed separately in the frequency domain. The eigenfrequency for each component has a prominent contribution to the radiation noise of the ceramic angular contact ball bearing and can be calculated by applying Eq. (47):

$$\begin{aligned} \begin{array}{l} f_{\mathrm{b}} =\frac{d_{{m}} }{2D_{\mathrm{W}} }f_{\mathrm{r}} \left( 1-\frac{D_{\mathrm{W}}^2 }{d_{{m}}^2 }\cos ^{2}\alpha \right) \\ f_{\mathrm{c}} =\frac{1}{2}f_{\mathrm{r}} \left( 1-\frac{D_{\mathrm{W}} }{d_{\mathrm{m}} }\cos \alpha \right) \\ f_{\mathrm{i}} =\frac{N}{2}f_{\mathrm{r}} \left( 1+\frac{D_{\mathrm{W}} }{d_{\mathrm{m}} }\cos \alpha \right) \\ f_{\mathrm{o}} =\frac{N}{2}f_{\mathrm{r}} \left( 1-\frac{D_{\mathrm{W}} }{d_{\mathrm{m}} }\cos \alpha \right) \\ \end{array} \end{aligned}$$
(47)

where \(f_{\mathrm{r}}\) is the rotation frequency of the bearing; \(f_{\mathrm{b}}, f_{\mathrm{c}}, f_{\mathrm{i}}\), and \(f_{\mathrm{o}}\) represent the eigenfrequencies of the ball, cage, inner-ring raceway, and outer-ring raceway, respectively; and \(\alpha \) is the contact angle of the bearing.

The eigenfrequencies can be obtained based on the structural parameters of the ceramic angular contact ball bearing in Table 1. Table 2 lists the rotation frequency and the eigenfrequencies of all components when the bearing operates at rotation speeds of 20,000 r \(\hbox {min}^{-1}\), 25,000 r \(\hbox {min}^{-1}\), 28,000 r \(\hbox {min}^{-1}\), and 30,000 r \(\hbox {min}^{-1}\).

Considering Table 2, the eigenfrequency of the inner-ring raceway is the largest and no more than 4000 Hz. Therefore, the acoustic characteristics of each component are investigated in the frequency range of 0–4000 Hz with steps of 20 Hz. Here, the analysis point 1 is taken as reference. The radiation noise characteristics of each component and their contribution to the total bearing noise can be obtained based on the multi-sound source method.

Table 2 Bearing speed and characteristic frequency
Full size table
Fig. 11
figure 11

Frequency spectrum for the calculated radiation noise of balls under different rotation speeds. a\(n=20,000\, \hbox {r}\,\hbox {min}^{-1}\), b\(n=25,000\, \hbox {r}\, \hbox {min}^{-1}\), c\(\hbox {n}=28,000\, \hbox {r}\, \hbox {min}^{-1}\), and d\(n=30,000\, \hbox {r}\, \hbox {min}^{-1}\)

Full size image
Fig. 12
figure 12

Frequency spectrum for the calculated radiation noise of cage under different rotation speeds. a\(n=20,000\, \hbox {r}\, \hbox {min}^{-1}\), b\(n=25,000\, \hbox {r}\, \hbox {min}^{-1}\), c\(n=28,000\, \hbox {r}\, \hbox {min}^{-1}\), and d\(n=30,000\, \hbox {r}\, \hbox {min}^{-1}\)

Full size image

5.1 Radiation noise of ceramic balls

Under ideal working conditions, the frequency spectrum for the radiation noise of the ceramic balls is shown in Fig. 11.

According to the four subgraphs in Fig. 11, the radiation noise of the ball presents distinct peaks in medium- and low-frequency bands, and the ball noise peaks contain the eigenfrequencies of all components. The changes in SPLs at all eigenfrequencies along with the rotation speed show a similar trend, which changes nonlinearly with increasing rotation speed. The SPL has its maximum at the ball eigenfrequency. The noises for the eigenfrequencies of the inner and outer ring exhibit only little differences, and the SPL at the eigenfrequency of the outer ring is slightly larger than at that of the inner ring. With increasing rotation speed, the SPL at the rotation frequency becomes obviously larger than that at the eigenfrequency of the cage and at twice the rotation frequency. The SPL at twice the rotation frequency gradually increases from a value below the cage eigenfrequency noise to a value above. The SPL of each eigenfrequency noise at a speed of 28,000 r \(\hbox {min}^{-1}\) is higher than that of other rotation speeds, which is consistent with the total noise.

5.2 Radiation noise of cage

The cage is subject to the impact and friction of the balls. Moreover, the force of the lubrication fluid has an impact. The frequency spectrum for the radiation noise of the cage is shown in Fig. 12.

Figure 12 exhibits three remarkably high peaks in the noise spectrum of the cage. They appear at the eigenfrequencies of the cage, ball, and rotation frequency, respectively. The eigenfrequency of the cage contributes the most noise, followed by the rotation frequency. The peak values in Fig. 12c are larger than those in other subgraphs; i.e. the noise at a rotation speed of 28,000 r \(\hbox {min}^{-1}\) is higher than that at other rotation speeds. The SPLs of three peaks at a rotation speed of 25,000 r \(\hbox {min}^{-1}\) are below those at 30,000 r \(\hbox {min}^{-1}\) and above those at 20,000 r \(\hbox {min}^{-1}\). The noise varies nonlinearly with increasing rotation speed, and the tendency is consistent with the behaviour of the overall radiation noise.

5.3 Radiation noise of inner ring

As a power-transmitting element for the bearing, the inner ring is fastened to the shaft and its rotation speed remains that of the shaft. Considering the characteristics of the inner-ring sound source, the frequency spectrum of the radiation noise for the inner ring under different rotation speeds is calculated, as shown in Fig. 13.

Fig. 13
figure 13

Frequency spectrum for the calculated radiation noise of inner ring under different rotation speeds. a\(n=20,000\, \hbox {r}\, \hbox {min}^{-1}\), b\(n=25,000\, \hbox {r}\, \hbox {min}^{-1}\), c\(n=28,000\, \hbox {r}\, \hbox {min}^{-1}\), and d\(n=30,000\, \hbox {r}\, \hbox {min}^{-1}\)

Full size image

According to Fig. 13, the SPL for radiation noise of the inner ring consists of six main peaks, which are at the eigenfrequency of each component, rotation frequency, and double rotation frequency, respectively. Further, the peak values shift to the right with increasing rotation speed. The variation in the eigenfrequency contribution in the radiation noise of the inner ring is more complex. According to the six peaks, the SPL for the inner-ring eigenfrequency noise is maximum and the minimum SPL is at twice the rotation frequency. The contribution of ball eigenfrequency to the radiation noise for the inner ring decreases gradually, and the contributions of rotation frequency and outer-ring eigenfrequency to the radiation noise for the inner ring increase gradually. The eigenfrequency of the cage contributes less to the radiation noise for the inner ring at low rotation speed, and the contribution increases with increasing rotation speed. However, the change is not obvious. The variation in the feature noise at the eigenfrequency of each component with the rotation speed is in accordance with that of the total noise.

Fig. 14
figure 14

Frequency spectrum for the calculated radiation noise of outer ring under different rotation speeds. a\(n=20,000\, \hbox {r}\, \hbox {min}^{-1}\), b\(n=25,000\,\hbox {r}\, \hbox {min}^{-1}\), c\(n=28,000\,\hbox {r}\, \hbox {min}^{-1}\), and d\(n=30,000\, \hbox {r}\, \hbox {min}^{-1}\)

Full size image

5.4 Radiation noise of outer ring

Although the outer ring is assembled into the bearing pedestal, it is still subject to the force of the balls and pedestal, thereby resulting in a vibration and noise. The frequency spectrum for the radiation noise of the outer ring is shown in Fig. 14.

Figure 14 displays the variation in the frequency spectrum, detected from the radiation noise of the outer ring, with the rotation speed. There are six major peaks in each frequency spectrum, which appear at the eigenfrequency of each component, rotation frequency, and double rotation frequency, respectively. The contribution of the rotation frequency increases with increasing rotation speed. At a speed of 28,000 r \(\hbox {min}^{-1}\), its SPL is close to the SPL of the outer ring eigenfrequency and has exceeded the SPL of the ball eigenfrequency. The contribution of the outer ring eigenfrequency seems to be decreasing. However, its SPL still has the largest value. The SPL at the eigenfrequency of the inner ring increases first and then decreases with increasing rotation speed. The SPL at the eigenfrequency of the cage has always been greater than that at the double rotation frequency, and their contributions have little change. The radiation noises at the eigenfrequency of each component vary nonlinearly with increasing rotation speed, and they all have a similar trend with the overall radiation noise.

5.5 Comparison of radiation noise among bearing components

Figure 15 compares the radiation noise of the bearing components under different rotation speeds. The SPL values from point 1 at each component under different speeds will provide more insight into the radiation noise source and effect of the speed. As shown in Fig. 15, the radiation noise of each component increases with increasing rotation speed. The maximum SPL of each component appears at a rotation speed of 28,000 r \(\hbox {min}^{-1}\), where the radiation noise of the outer ring is larger than that of the inner ring. Therefore, the outer ring can be considered the main noise source, followed by the inner ring. The radiation noise of the ball is between those of the cage and inner ring.

5.6 Spectrum characteristics of radiation noise for the bearing

In order to reveal the difference between the calculated and the experimental results more intuitively, Fig. 16 presents the spectrum diagram of the radiation noise for the ceramic angular contact ball bearing at the speed of 28,000 r \(\hbox {min}^{-1}\). According to Fig. 16, the calculated results are close to the experimental results, and the rotation frequency contributes most to the radiation noise. The maximum difference between calculated and experimental results is 3.4 dB with a relative error of 4.12% (at \(f_{\mathrm{b}}\)). The minimum difference between calculated and experimental results is 1.15 dB with a relative error of 1.34% (at f). In the calculated results, the contribution of each eigenfrequency to the radiation noise is consistent with the experimental results. When the frequency is less than \( f_{\mathrm{c}}\), the fluctuation of the experimental results is slightly larger than that of the calculated results. On the whole, the radiation noise of the calculated results is larger than that of the experimental results in the range of the analysis frequency. The deviation between the two results may be caused by the simplification of the parameters in the calculated model or the systematic error during experimental testing. It can be seen from the comparison that the results of the calculation can basically reflect the experimental results, which indicates that the multi-sound source method can be applied to the prediction of the radiation noise for the ceramic angular contact ball bearings.

Fig. 15
figure 15

Comparison of the calculated radiation noise for bearing components under different rotation speeds

Full size image

6 Discussion

The overall radiation noise of the bearing increases first and then decreases with increasing rotation speed. However, owing to the increasingly intense motion of the bearing with increasing rotation speed, the SPL of the radiation noise cannot be reduced to values below the SPL of the low rotation speed. Although field points 1 and 2 are in the same radial direction and maintain a fixed distance, the SPLs of the two points are not strictly in a linear relation. At a rotation speed of 20,000 r \(\hbox {min}^{-1}\), the experimental results are always larger than the calculated values because of the magnetic-field resonances of the motorised spindle in the experiment. In addition, the background noise is lower than 45 dB in the paper, which has a little effect on the experimental results according to the principle of sound field superposition.

Fig. 16
figure 16

Spectrum characteristics of the radiation noise for the bearing

Full size image

The rotation frequency noise is found in the spectrum of the radiation noise for each component. This indicates that the rotation frequency noise is a fundamental constituent of the radiation noise of the bearing. In addition, the double rotation frequency has a certain contribution to the radiation noise of the bearing. In the noise spectrum of each bearing component, the eigenfrequency of each component contributes the most noise to its own acoustic spectrum. The high hard-brittleness ceramic ball contacts with all components and produces friction and impact noise, causing obvious eigenfrequency noise of the ball. The stiffness and natural frequency of the cage are both low and the impact between the cage and the balls is violent, resulting in obvious eigenfrequency noise of the cage. However, the cage has a strong absorptive capacity to noise, so the cage noise is relatively smaller than the ceramic ball.

The radiation noise characteristics of the bearing components alter nonlinearly with increasing spindle speed. This is consistent with the trend of the overall radiation noise of the bearing. The radiation noise of the outer ring is the main source contributing to the total noise of the bearing. This might be because the outer ring is subject to the greater force of the ball, which causes the larger vibration noise of the outer ring. The inner ring is mainly affected by the friction force of the ball. However, the contribution of the inner ring to the total radiation noise of the bearing is slightly below that of the outer ring due to the influence of the centrifugal force caused by high-speed motion. The radiation noise from the ball is greater than that from the cage but smaller than that from the inner ring. Since the cage material has the ability to absorb impact energy, it has a relatively small contribution to the total radiation noise of the bearing. According to the analyses above, the friction noise is the main component of the bearing radiation noise. The stiffness and natural frequency of the components have a great influence on the radiation noise.

Furthermore, other types of bearings such as deep groove ball bearing, which are equipped with similar structures, have similar dynamic behaviours with the angular contact ball bearing during operation, which cause vibration and noise. Therefore, the multi-sound source method can also be applied to calculate the radiation noise of other bearings.

7 Conclusion

To address the differential equation for the vibration of bearing components and the characteristics of different sound sources, a multi-sound source method for the noise calculation of high-speed ceramic angular contact ball bearing is presented in this paper. The radiation noise of the ceramic angular contact ball bearing affecting a high-speed motorised spindle at different field points and varied rotation speeds are calculated using numerical simulations. The accuracy of the proposed method is verified with contrast experiments. The results show that the calculated values are in good agreement with the experimental results. The maximum difference measures 2.36 dB, and the relative error is not more than 2.83%. The radiation noise of the bearing has an obvious sound field directivity. On this basis, the characteristics of the radiation noise of the bearing components are analysed in detail. According to the analysis, the friction noise is the main component of radiation noise of the bearing. The stiffness and natural frequency of the components have a great influence on the radiation noise. The noise of the balls is lower than that of the inner ring but is above that of the cage. Further, the noise of the outer ring is slightly greater than that of the inner ring. The eigenfrequency of each component is the main contributor to the radiation noise in the own frequency spectrum of each component. The rotation frequency noise appears in the noise frequency spectrum of each component. This paper provides a theoretical basis for improving the acoustic performance of bearings and their application in high-speed motorised spindles. In addition, this method can be used to analyse the radiation noise of other equipment with the bearing as the sound source.