Keywords

1 Introduction

In recent years, as high-speed rotary machines with roller bearings found wide applications, their dynamics properties were extensively studied. An analysis of rolling element bearing dynamic behavior is important to predict the system vibration responses. When rolling element bearings are operated at high speed, they generate vibrations and noise. The principal forces, which drive these vibrations, are the time varying nonlinear contact forces, which exist between the various components of the bearings, i.e., the rolling elements, and races with the rotor. In the rotor bearing assembly supported by perfect rolling element bearings, the vibration spectrum is dominated by the vibrations at the natural frequency and the ball passage frequency (BPF). By vibration monitoring, down time and risk of accident in highly productive industrial plants (power generation, steel production), traffic systems (automotive, railway, aircraft), industrial manufacturing (textile, machine tool industry) and domestic appliances (washing machine) can be minimized.

Ball passage vibrations were first documented, by Perret [1] and Meldau [2] as a static running accuracy problem. Tamura and Tsuda [3] performed a theoretical study of radial spring characteristics of a ball bearing based on the work of Perret [1] and Meldau [2]. They suggested that an increase in the number of the balls in a bearing reduces its untoward effects. However, its nature and importance was not properly understood until a research by Gustafsson et al. [4], who called this vibration as variable compliance. BPF is an inherent frequency of the system. They studied the effects of waviness and pointed out that lower order ring waviness affects the amplitude of the vibrations at the ball passage frequency. They showed that clearance is an important parameter for ball passage vibrations (BPV). They observed that vibrations at higher harmonics of the ball passage frequency are also present in the vibration spectrum and their amplitudes depend on the radial load, radial clearance, rotational speed and the order of harmonics. Wardle [5] has studied theoretically the relation between the frequency harmonics of waviness and bearing dynamic performance. Aktürk [6] has studied some characteristic parameters affecting the natural frequency of a rotating shaft supported by defect-free ball bearings. The conclusion of this work shows that large values of axial preload cause stiffer spring characteristics and result in higher natural frequency values. As the number of balls is increased, the system becomes stiffer, since a larger number of balls support the shaft. The change in natural frequency is cyclic for the change in ball set position. The number of changes is equal to the number of rolling elements in the bearing. This is also the reason for ball passage vibrations.

Recently, Tiwari et al. [7] investigated the stability of a rigid rotor supported by deep-grooved ball bearings and described the unstable ranges for different radial clearances but the stability of a rolling bearing rotor system containing local surface defects has not been studied before. Harsha and Kankar [8] developed an analytical model to predict nonlinear dynamic response in a rotor bearing system due to surface waviness. The conclusion of this work shows that for the outer race waviness, the severe vibrations occur when the number of balls and waves are equal. Harsha et al. [9] have studied the stability analysis of a rotor bearing system due to surface waviness and number of balls. They suggested that the system express dynamic behaviors that are extremely sensitive to small variations of the system parameters, such as number of balls and number of waves.

In this paper, a theoretical investigation has been conducted to observe the effect of race waviness with varying the number of waves on the vibration characteristics of a balanced rotor bearing system. A nonlinear damping formula, correlating the contact damping force with the equivalent contact stiffness and contact deformation rate (determined by the surface profiles and radial speed of inner/outer races and rollers), is developed to improve model fidelity.

2 Problem Formulation

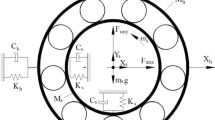
For investigating the structural vibration characteristics of rolling element bearing, a model of bearing assembly can be considered as a spring mass damper system. Elastic deformation between races and rolling elements gives a non-linear force deformation relation, which is obtained by Hertzian theory. In the mathematical modeling, the rolling element bearing is considered as spring mass system and rolling elements act as non-linear contact spring as shown in Fig. 1Since, the Hertzian forces arise only when there is contact deformation, the springs are required to act only in compression. In other words, the respective spring force comes into play when the instantaneous spring length is shorter than its unstressed length, otherwise the separation between balls and the races takes place and the resultant force is set to zero. The excitation is because of the varying compliance vibrations of the bearing which arise because of the geometric and elastic characteristics of the bearing assembly varying according to the cage position.

Fig. 1
figure 1_30

Mass – spring-damper model of rolling element bearings

Full size image

2.1 Mathematical Modeling

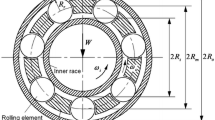
The rolling element bearing model considered here has equi-spaced balls rolling on the surfaces of the inner and outer races. For developing the theoretical model it is assumed that the outer race is fixed rigidly to the support and the inner race is fixed rigidly to the rotor and there is no bending of races.

$${\omega }_{\mathit{cage}}\, =\, {\omega }_{\mathit{rotor}}\,\left ( \frac{r} {r\, +\, R}\right )$$
(1)

The ball passage frequency is given by

$${\omega }_{bp}\, =\, {\omega }_{\mathit{cage}}\,\, \times \, {N}_{b}$$
(2)

where N b is the number of balls.

2.2 Race Waviness

When the rolling element is moving round the inner race, it follows the rolling surface contours continuously. It is assumed that there exists no slip condition i.e., rolling element always in contact with inner race and also it is assumed that the inner race surface has a circumferential sinusoidal wavy feature. The amplitude of wavy surface is often measured with respect to central point at a certain angle from the reference axis. Hence the sinusoidal wave is:

$$\Pi = {\Pi }_{p}\sin \left (2\pi \frac{L} {\lambda }\right )$$
(3)

The inner race has circumferential sinusoidal wavy surface (Fig. 2a), therefore the radial clearance consists of a constant part and a variable part. Hence the amplitude of the wave of inner race is:

$${ \left (\Pi \right )}_{in} = \left ({\Pi }_{O}\right ) + \left ({\Pi }_{p}\right )\sin \left (2\pi \frac{L} {\lambda }\right )$$
(4)

Here Π p is the maximum amplitude of wave and Π o is initial wave amplitude (or constant clearance) as shown in Fig. 2b. The arc length (L) of the wave of inner race at the contact angle is:

$$L = r{\theta }_{j}$$
(5)

For an imperfect surface with Nwaves, the wavelength (λ) inversely proportional to the number of waves N w is:

$$\lambda \propto \frac{1} {{N}_{w}}$$
(6)

For the inner race the wavelength is ratio of length of the inner race circumference to the number of waves on circumference, which is:

$$\lambda = \frac{2r\pi } {{N}_{w}}$$
(7)

The amplitude of the waves of inner race at the contact angle is:

$${ \left (\Pi \right )}_{\mathit{in}} = \left ({\Pi }_{O}\right ) + \left ({\Pi }_{p}\right )\sin \left ({N}_{w}{\theta }_{j}\right )$$
(8)
Fig. 2
figure 2_30

(a)Contact between inner race and rolling element. (b)Wave of the race

Full size image

2.3 Formulation of Equations of Motion

A real rotor-bearing system is generally very complicated and difficult to model. First the expression for energies of the individual components of the bearing is formulated. Using these energies, the equations of motion are derived with the help of Lagrange’s equation.

2.3.1 Energy Expression of the Rolling Element Bearings

The total energy of system is considered to be the sum of kinetic energy, potential energy, strain energy of the springs representing contact and dissipation energy due to contact damping. The detail description of the energy expressions due to different parts of rolling bearings, which have been already derived in the papers published by Harsha [8, 9], are used in this paper. The contacts between rolling elements and races are treated as nonlinear springs, whose stiffness is obtained by Hertzian theory of elasticity. In those previous papers a constant damping value was chosen, but here a nonlinear viscous damping model is adopted.

2.3.1.1 Energy Dissipation

The lubrication is assumed to behave in a Newtonian way. Hence, a viscous damping model is adopted in which the dissipative forces are proportional to the time derivate of the mutual approach. The resulting equation yields:

$${F}_{d}\, =\,\, c\,\left (\delta \right )\,{\dot{\delta }}^{{}^{q} }$$
(9)

where cδ is also a function of the contact geometry, the material properties of the elastic bodies, the properties of lubricant and the contact surface velocities.

2.3.1.2 Contact Damping

For the jth rolling element the equivalent contact stiffness between the rolling element and race is

$${k}_{\mathit{Eq}}\, = \dfrac{3} {2}\,{k}_{\mathit{contact}}\ {\delta }^{1/2}$$
(10)

The deforming forces for the jth rolling element and inner race is

$${F}_{d{\_}\mathit{in}}\,\, =\,\, {c}_{\mathit{in}}\,\,{k}_{\mathit{Eq}}\,{\left (\dot{{\delta }}_{\mathit{in}}\right )}_{+}^{q}\,$$
(11)
$${F}_{d{\_}\mathit{in}}\, = \frac{3} {2}\,{c}_{\mathit{in}}\,\left ({k}_{\mathit{in}{\_}\mathit{contact}}\right )\,{\delta }_{in\,+}^{1/2}\,{\dot{{\delta }}_{ in\,+}}^{{}^{q} }$$
(12)

Similarly, the damping force for the jth rolling element with the outer race is:

$${F}_{d{\_}\mathit{out}} = {c}_{\mathit{out}}{\delta }_{out+}{k}_{eq}$$
(13)
$${F}_{d{\_}\mathit{out}}\, = \frac{3} {2}\,{c}_{\mathit{out}}\,\left ({k}_{\mathit{out}{\_}\mathit{contact}}\right )\,{\delta }_{\mathit{out}\,+}^{1/2}\,{\dot{{\delta }}_{\mathit{ out}\,\,+}}^{{}^{q} }$$
(14)

Hence total energy dissipation at both contact points of rolling element with inner and outer race is

$$\begin{array}{rcl} \hspace{-20.0pt}{E}_{\mathit{dissipation}} = \frac{3} {2\left (q\, +\, 1\right )}\,{\sum }_{j=1}^{{N}_{r.e.} }& & \left [\left \{\,{c}_{\mathit{in}}\,\left ({k}_{\mathit{in}{\_}\mathit{contact}}\right )\,{\delta }_{{\mathit{in}\,}_{+}}^{3/2}\,\,{\dot{{\delta }}_{\mathit{ in}\ +}}^{{}^{q+1} }\right \}\right. \\ & & \quad + \left.\left \{{c}_{\mathit{out}}\,\left ({k}_{\mathit{out}{\_}\mathit{contact}}\right )\,{\delta }_{{\mathit{out}\,}_{+}}^{3/2}\,\,{\dot{{\delta }}_{\mathit{ out}+}}^{{}^{q\,+1} }\right \}\right ]\end{array}$$
(15)

2.4 Equations of Motion

The kinetic energy and potential energy contributed by the inner race, outer race, balls, rotor and springs, can be differentiated with respect to the generalized coordinates ρ j (j= 1, 2, …,N b ),x in , and y in to obtain the equations of motion. For the generalized coordinates ρ j , where j= 1, 2, …,N b , the equations are:

$$\begin{array}{rcl} \ddot{{\rho }}_{j}& +& g\sin {\theta }_{j} + {\rho }_{j}\dot{{\theta }}^{2} - \frac{1} {{m}_{j}}\left ({k}_{\mathit{in}{\_}\mathit{contact}}\right )\,{\left [{\delta }_{\mathit{in}}\right ]}_{+}^{3/2}\frac{\partial {\chi }_{j}} {\partial {\rho }_{j}} +\, \frac{1} {{m}_{j}}\left ({k}_{\mathit{out}{\_}\mathit{contact}}\right )\,{\left [{\delta }_{\mathit{out}}\right ]}_{+}^{3/2} \\ & +& \frac{1} {2\,{m}_{j}} \frac{\partial \,\left [\left ({k}_{\mathit{in}{\_}\mathit{contact}}\right )\,\left ({\left [{\delta }_{in}\right ]}_{+}^{3/2}\right )\right ]} {\partial {\rho }_{j}} \,{\left [{\delta }_{\mathit{in}}\right ]}_{+}^{2} \\ & +& \frac{1} {2\,{m}_{j}} \frac{\partial \,\left [\left ({k}_{\mathit{out}{\_}\mathit{contact}}\right )\,\left ({\left [{\delta }_{out}\right ]}_{+}^{1/2}\right )\right ]} {\partial {\rho }_{j}} \,{\left [{\delta }_{\mathit{out}}\right ]}_{+}^{2} \\ \end{array}$$
$$\begin{array}{rcl} & & + \frac{3} {2{m}_{j}}{ \sum }_{j=1}^{{N}_{r.e.} }\left \{{c}_{\mathit{in}}\left ({k}_{\mathit{in}{\_}\mathit{contact}}\right ){\delta }_{\mathit{in}+}^{3/2}{\left (-{\chi }_{ j}\right )}^{q}\,\frac{\partial {\chi }_{j}} {\dot{\partial {\rho }}_{j}} \right \} \\ & & + \frac{3} {2{m}_{j}}{ \sum }_{j=1}^{{N}_{r.e.} }{c}_{\mathit{out}}\left ({k}_{\mathit{out}{\_}\mathit{contact}}\right ){\delta }_{\mathit{out}+}^{3/2}\,{\left (-\dot{{\rho }}_{ j}\right )}^{q}\, = 0\,\,\,j = 1,2,\ldots,{N}_{ r.e.}\end{array}$$
(16)

For the generalized coordinate x in the equation is:

$$\begin{array}{rcl} \ddot{x}& - \frac{1} {{m}_{\mathit{rotation}}} { \sum }_{j=1}^{{N}_{r.e.}}\left ({k}_{\mathit{in}{\_}\mathit{contact}}\right ){\left [{\delta }_{\mathit{in}}\right ]}_{+}^{3/2} \frac{\partial {\chi }_{j}} {\partial {x}_{in}} & \\ & + \frac{3} {2{m}_{\mathit{rotation}}} { \sum }_{j=1}^{{N}_{r.e.}}\left \{{c}_{\mathit{in}}\left ({k}_{\mathit{in}{\_}\mathit{contact}}\right ){\delta }_{\mathit{in}+}^{3/2}{\left (-\dot{{\chi }}_{j}\right )}^{q}\, \frac{\partial \dot{{\chi }}_{j}} {\partial \dot{{x}}_{\mathit{in}}} \right \} = \frac{{F}_{u}\,\sin \left ({\omega }_{s}\,t\right )} {{m}_{\mathit{rotation}}} &\end{array}$$
(17)

For the generalized coordinate { y} { in}the equation is:

$$\begin{array}{rcl} & +g - \frac{1} {{m}_{\mathit{rotation}}} { \sum }_{j=1}^{{N}_{r.e.}}\left ({k}_{\mathit{in}{\_}\mathit{contact}}\right ){\left [{\delta }_{\mathit{in}}\right ]}_{+}^{3/2} \frac{\partial {\chi }_{j}} {\partial {y}_{\mathit{in}}} & \\ & + \frac{3} {2{m}_{\mathit{rotation}}} { \sum }_{j=1}^{{N}_{r.e.}}\left \{{c}_{\mathit{in}}\left ({k}_{\mathit{in}{\_}\mathit{contact}}\right ){\delta }_{\mathit{in}+}^{3/2}{\left (-\dot{{\chi }}_{j}\right )}^{q}\, \frac{\partial \dot{{\chi }}_{j}} {\partial \dot{{y}}_{\mathit{in}}} \right \} = \frac{\left (W+{F}_{u}\,\sin \left ({\omega }_{s}\,t\right )\right )} {{m}_{\mathit{rotation}}} &\end{array}$$
(18)

where \({m}_{\mathit{rotation}} = \left ({m}_{\mathit{inner}} + {m}_{\mathit{rotor}}\right )\).

This is a system of (N b + 2) coupled non-linear differential equations. There is no external radial force allowed to act on the bearing system and no external mass is attached to the outer race. The “ + ” sign as subscript in these equations signifies that if the expression inside the bracket is greater than zero, then the rolling element at angular location θ j is loaded giving rise to restoring force and if the expression inside bracket is negative or zero, then the rolling element is not in the load zone, and restoring force is set to zero. The deformation of spring at inner race χ j , is derived in [9, 10], and is used in the present paper.

3 Methods of Solution

The two coupled non-linear second order differential equations are solved by numerical integration which is a time domain approach. The non-analytic nature of the stiffness term renders the system equations difficult for analytical solution.

3.1 Numerical Integration

The equations of motion (10–12) are solved using the modified Newmark-β method to obtain the radial displacement, velocity and acceleration of the rolling elements. With inclusion of damping, transient vibrations are eliminated and peak steady state amplitudes of vibration can be estimated. To observe the nonlinear behavior of the system, parameters of the ball bearing are selected and are shown in Table 1. The time step for the numerical integration is taken as \(\Delta t = 1{0}^{-5}\)sec.

Table 1 Geometric and physical properties used for the ball bearings
Full size table

4 Results and Discussion

The equations of motion are solved by modified Newmark-β method to obtain the radial displacement and velocity of the rolling elements. The predicted vibrations are clearly observed in case of two waves, as shown in Fig. 3a. A dominant peak appears at 2ω inner = 166. 67 Hz with the other peaks at super harmonics of the rotor speed \(3{\omega }_{\mathit{inner}} = 250\,\mathrm{Hz},\ 4{\omega }_{\mathit{inner}} = 333.5\)Hz, and at the wave passage frequency (WPF) \({\omega }_{\mathit{wp}} = {N}_{b}\left ({\omega }_{\mathit{inner}} - {\omega }_{\mathit{cage}}\right ) = 400\)Hz. Other peaks also appear which are more complicated at (2/3)\({\omega }_{\mathit{wp}} - 2{\omega }_{\mathit{inner}} = 100\)Hz. However, a more complicated response is observed for three waves. A dominant peak of relatively smaller amplitude is observed at 3ω inner = 250 Hz, implying a change of shape in the vibration spectrum. The other peaks are observed at \({\omega }_{\mathit{wp}} - 3/2{\omega }_{\mathit{inner}} = 275\)Hz, and at \({\omega }_{\mathit{wp}} + 3/2{\omega }_{\mathit{inner}} = 525\)Hz as shown in Fig. 3b. However, when damping is not considered in the model, the peak excitation occurs in vertical displacement, and is at 1 micron [9].

Fig. 3
figure 3_30

FFT for defective bearings, (a) N w = 2, (b) N w = 3, (c) N w = 5, (d) N w = 8, (e) N w = 12

Full size image

For five waves a dominant peak of relatively smaller amplitude (0.14) is observed at 5ω inner = 416. 65 Hz, implying a change of shape in the vibration spectrum. The other peaks are observed at \(3/2{\omega }_{\mathit{wp}} - 5{\omega }_{\mathit{inner}} = 183.35\)Hz for horizontal and vertical displacement response as shown in Fig. 3c. For eight waves, the vibrations are predicted at wave passage frequency (ω wp ) = 400 Hz, where q= 1 and k= 0 in Eq. (13), as shown in Fig. 3d. The amplitude of peak is 0.25 μm. But when damping is not considered in the model, the peak excitation occurs in vertical displacement, and is at 10 μm [9], which is quite high. Hence, the peak excitation is drastically reduced mainly due to damping effect. For waviness of order 12, the predicted peak is either at ω wp − 4ω cage or at 2ω wp − 4ω inner depending on the parameter qand kchosen in Eq. (13). The peak for 12 waves are at \(2{\omega }_{\mathit{wp}} - 4{\omega }_{\mathit{inner}} = 467\)Hz where q= 2 and k= 4 in Eq. (13) as shown in Fig. 3e.

Fig. 3
figure 4_30

(continued)

Full size image

Vibration amplitudes in the spectrum for 12 waves become negligible ( < 1.5 μm). However, there is another peak at \({\omega }_{\mathit{wp}} + 4{\omega }_{\mathit{inner}} = 733.5\)Hz, where q= 1 and k= 4 in Eq. (13). A clear transformation from q= 1 to 2 can be observed in the vibration spectrum obtained for the waviness of order 12. Results of Fig. 3a–e are summarized in Table 2.

Table 2 Summary of inner race waviness
Full size table

5 Conclusions

A lumped parameter model has been introduced in this paper to investigate structural vibrations in rolling element bearings. Using this model, effect of race waviness with varying the number of waves, nonlinear stiffness and nonlinear damping on the vibration response of the bearing have been studied. With the addition of the damping, the peak amplitude of vibration reduced drastically. The foregoing results provide the following conclusion:

  1. a.

    The frequency of the vibrations due to inner race waviness depends on the waviness order given as n= qN b ± kand frequency of vibration caused by waviness is \(\omega ={ \mathit{qN}}_{b}\left ({\omega }_{\mathit{inner}} - {\omega }_{\mathit{cage}}\right ) \pm k{\omega }_{\mathit{inner}}\). However, this equation is applicable to major peaks only.

  2. b.

    For the inner race waviness order (n), the peaks or its super-harmonics are observed at wave passage frequency (WPF) \({\omega }_{\mathit{wp}} = {N}_{b}\left ({\omega }_{\mathit{inner}} - {\omega }_{\mathit{cage}}\right )\).