1 Introduction

Water waves are one of the most common phenomena in nature, the study of which helps the design of the related industries, such as the energy development, marine and offshore engineering, hydraulic engineering and mechanical engineering [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. Media with the negative refractive index are among the carrier media in fiber optics and can be applied in the fabrications of the optical guiding elements in integrated circuit and bidirectional optical waveguide coupling devices [24,25,26,27,28,29]. References [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45] have used the derivative nonlinear Schrödinger (DNLS) equations to model the nonlinear phenomena in some fluids, optical fibers and inhomogeneous plasmas.

In hydrodynamics, long waves have been governed by the Korteweg–de Vries equation in the shallow-water limit, whereas short waves, by the nonlinear Schrödinger equation in the deepwater limit, more precisely when \(KH > 1.363\), where K is the carrier wavenumber and H is the unperturbed water depth [46, 48]. However, through the combination of the asymptotic analysis and numerical simulations, in the framework of the higher-order DNLS equations with variable coefficients, it has been discovered that a wave packet in the deep water can penetrate into the shallow water (\(KH< 1.363\)) and propagate stably, depending on the initial value in deep water with a certain parameter related to the velocity of the wave packet [45]. It has been said that in the neighborhood of the “critical” \(KH \approx 1.363\) [49], cubic nonlinearity weakens considerably, and higher-order nonlinear and dispersive effects need to be restored [48, 50, 51]. Higher-order, higher-dimensional, or even time-fractional DNLS equations have been introduced to describe the nonlinear phenomena in hydrodynamics [48, 52,53,54,55,56,57,58,59].

With the uneven bottom into consideration so that H is allowed to be slowly varying with the space, a higher-order DNLS equation with time-dependent coefficients has been derived [45]. In the study of media with negative refractive index, negative permittivity and permeability have been considered [27, 28]. Due to the inhomogeneities of media and nonuniformities of boundaries, time-dependent coefficients have been incorporated in the DNLS equations for describing the real physical backgrounds [29, 42,43,44,45, 47].

A quintic time-dependent-coefficient DNLS equation [42, 43],

$$\begin{aligned}&i{u_t}+ \lambda \left( t \right) {u_{xx}}+ i\alpha \left( t \right) {\left| u \right| ^2}{u_x} + \mu \left( t \right) {\left| u \right| ^2}u \nonumber \\&\quad + \,\nu \left( t \right) {\left| u \right| ^4}u = 0, \end{aligned}$$
(1)

has arisen in the study of hydrodynamic wave packets and media with the negative refractive index, where u(x, t) is the wave envelope for the free water surface displacement or envelope of the electric field, t and x denote not only the propagation distance and retarded time in the context of optical fiber physics, but also the slow time and spatial coordinate traveling with the group velocity in hydrodynamics, while \(\mu (t)\), \(\nu (t)\), \(\lambda (t)\) and \(\alpha (t)\) represent the cubic nonlinearity, quintic nonlinearity, dispersion and self-steepening coefficients, respectively [42]. Additionally, special cases of Eq. (1) have been seen in the following:

  • When \([\lambda (t), \alpha (t), \mu (t), \nu (t)]=[\hat{\lambda },\hat{\alpha },\hat{\mu },\hat{\nu }]\), Eq. (1) has been reduced to a quintic DNLS equation describing the hydrodynamic wave packets and the medium with negative refractive index, where \(\hat{\lambda }\), \(\hat{\alpha }\), \(\hat{\mu }\) and \(\hat{\nu }\) are the constants [44, 45]. Deformation and destruction of a water wave packet propagating shoreward from the deep to shallow water have been described [45]. Gray solitons on a continuous-wave background have been derived via two integrals of motion [44], and the explicit power series solutions, singular and dark solitons have been constructed [60].

  • When \([\lambda (t), \alpha (t), \mu (t), \nu (t)]=[\frac{\alpha }{2},0,-\frac{q_1}{\alpha },-\frac{q_2}{\alpha }]\), Eq. (1) has been reduced to the equation describing the Madelung fluid, where \(\alpha \), \(q_1\) and \(q_2\) are the constants [61]. Bright and gray/dark solitary waves are derived [61].

  • When \([{\lambda (t),\alpha (t),\mu (t),\nu (t)}] = [{-1,\kappa ,0,0}]\), Eq. (1) has been reduced to the Chen–Lee–Liu equation for the nonlinear optical pulses in a quadratic nonlinear crystal involving the self-steepening without any concomitant self-phase modulation, where \(\kappa \) is a constant [62]. When \(\kappa =1\), soliton, breather, multi-rogue wave and rational solutions have been constructed [41].

Bright and kink solitons for Eq. (1) have been derived via the trial equation method [37], and the N-soliton solutions for Eq. (1) have been constructed via the bilinear forms [43]. By the way, it has been demonstrated that: A dark soliton is a nonlocalized traveling wave formed as a result of nonlinear resonance of a bore with a periodic wave, and appears as an intensity dip in an infinitely extended constant background [63, 64]; Anti-dark soliton exists in the form of a bright pulse on a nonzero continuous-wave background [65]; Gray soliton exists under the background plane, with its amplitude less than the high of the background plane [61]; Dark and anti-dark solitons coexist on the same background in the normal dispersion regime [40]. It has also been proved analytically that a random frequency shift of a dark soliton results in a time jitter \(\sqrt{2}\) times lower than that from the bright solitons [66, 67], i.e., the dark solitons are more resistant to the perturbations than the bright ones [40].

However, to our knowledge, the bilinear forms for Eq. (1) different from those in Ref. [43] and dark/anti-dark/gray solitons with the nonzero background for Eq. (1) have not been investigated. In Sect. 2, we will construct such bilinear forms, and derive the N-soliton solutions for Eq. (1) under certain conditions. In Sect. 3, properties of the two solitons will be derived via the asymptotic analysis. In Sect. 4, conditions for the dark, anti-dark and gray solitons will be derived. In Sect. 5, interactions between/among the anti-dark, gray and dark solitons, as well as the effects of \(\alpha (t)\), \(\lambda (t)\) and \(\mu (t)\) on the interactions will be discussed under two cases. In Sect. 6, we will give the conclusions.

2 Bilinear forms and N-soliton solutions for Eq. (1)

Introducing the transformation \(u = g/f\), we construct the bilinear forms for Eq. (1), which are different from those in Ref. [43], as follows

$$\begin{aligned}&\left[ {i{D_t} + \lambda (t)D_x^2+\frac{{\chi _1(t)}^2}{2\lambda (t)}+{\chi _2(t)}} \right] \left( {g \cdot f} \right) = 0, \end{aligned}$$
(2a)
$$\begin{aligned}&\lambda (t){D_x}\left( {f \cdot {f^*}} \right) + \chi _1(t){\left| f \right| ^2} - \frac{1}{2}i\alpha (t){\left| g \right| ^2} = 0,\end{aligned}$$
(2b)
$$\begin{aligned}&\lambda \left( t \right) D_x^2\left( {f \cdot {f^ * }} \right) + \chi _2(t){\left| f \right| ^2} - \frac{1}{2}i\alpha ( t){D_x}\left( {g \cdot {g^ * }} \right) \nonumber \\&\quad - \left[ \mu (t)-i\frac{{\chi _1(t)}}{4\lambda (t)}\alpha (t)\right] {\left| g \right| ^2} = 0, \end{aligned}$$
(2c)

with the condition [43]

$$\begin{aligned} {\alpha (t)}^2 + 8\lambda (t)\nu (t) = 0, \end{aligned}$$
(3)

where g and f are complex differentiable function with respect to x and t, \(g^*\) and \(f^*\), respectively, denote the complex conjugate of f and g, \(\chi _1(t)\) and \(\chi _2(t)\) are the nonzero complex functions of t, the bilinear operators \(D_{t}\) and \(D_{x}\) are defined by [68]

$$\begin{aligned}&D_x^\iota D_t^\tau \left( {\Theta \cdot \Upsilon } \right) ={{\left( {\frac{\partial }{{\partial x}} - \frac{\partial }{{\partial x'}}} \right) }^\iota }\nonumber \\&\quad {\left. {{{\left( {\frac{\partial }{{\partial t}} - \frac{\partial }{{\partial t'}}} \right) }^\tau } \Theta \left( {x,t} \right) \Upsilon \left( {x',t'} \right) } \right| _{t' = t,x' = x}}, \end{aligned}$$
(4)

\(\Theta (x,t)\) is a differentiable function with respect to x and t, \(\Upsilon (x^{'},t^{'})\) is a differentiable function with respect to the formal variables \(x^{'}\) and \(t^{'}\), while \(\iota \) and \(\tau \) are both the nonnegative integers.

Based on Bilinear Forms (2), the N-soliton solutions for Eq. (1) can be expressed as

$$\begin{aligned} u = \frac{g_{N}}{f_{N}}, \end{aligned}$$
(5)

where N is a positive integer. Then, \(g_N\) and \(f_N\) in Eq. (5) are derived as

$$\begin{aligned} {g_{N}} = \mathcal {G} e^{i\left[ \eta _1 x +m_1(t) \right] },~~{f_{N}}= \mathcal {F} e^{i\left[ \eta _2 x +m_2(t) \right] } \end{aligned}$$
(6)

with

$$\begin{aligned}&\mathcal {G}=1 + \sum \limits _{n = 1}^N{\left[ \sum \limits G_{N_1,\ldots ,N_n}\exp {\sum \limits _{\rho = 1}^n{\left( \theta _{N_\rho } + 2i\phi _{N_\rho }\right) }}\right] },\\&\mathcal {F}=1 + \sum \limits _{n =1}^N{\left[ \sum \limits F_{N_1,\ldots ,N_n}\exp {\sum \limits _{\rho = 1}^n{ \theta _{N_\rho }}}\right] },\\&\theta _j=k_j x+\omega _j(t),~G_{N_1,\ldots ,N_n}=F_{N_1,\ldots ,N_n} \prod \limits _{\rho =1}^{n}{ \frac{G_{N_\rho }}{F_{N_\rho }} },\\&F_{N_1,\ldots ,N_n}=\prod \limits _{\rho =1}^{n}{F_{N_\rho }}\times \prod \limits _{1\le N_l,N_d \le n}^{N_l<N_d}{H_{N_l,N_d}},\\&\chi _1(t)=\frac{1}{2}i\left[ \alpha (t)-4\eta _2\lambda (t)\right] ,\\&\chi _2(t)=-\frac{1}{2}\left( 2\eta _1+\eta _2\right) \alpha (t)+\frac{{\alpha (t)}^2}{8\lambda (t)}\\&\quad +4\eta _2^2\lambda (t)+\mu (t), \end{aligned}$$

where

$$\begin{aligned}&\omega _j(t)=k_j\int \left[ 2\left( \eta _2 - \eta _1\right) \lambda (t)-\alpha (t)\right] {\mathrm{d}}t\\&\quad \pm \frac{1}{2}\int {\Lambda _j}{\mathrm{d}}t,\\&m_1(t)=\frac{1}{2}\left( \eta _2 - 2\eta _1\right) \int \alpha (t){\mathrm{d}}t \\&\quad + \int \mu (t){\mathrm{d}}t + m_2(t)\\&\quad + \left( \eta _2^2 + 2\eta _1\eta _2 - \eta _1^2\right) \int \lambda (t){\mathrm{d}}t,\\&{F_j}=\exp \left( 2i\phi _j\right) \frac{\Lambda _j+2k_j\left[ \alpha (t)+ik_j \lambda (t)\right] }{\Lambda _j+2k_j\left[ \alpha (t)-ik_j \lambda (t)\right] }{G_j},\\&H_{s,h}=\frac{\Lambda _s\Lambda _h + k_s k_h \left( 8k_sk_j\lambda (t)^2-\Gamma _{s,h}\right) }{\Lambda _s\Lambda _h - k_s k_h \Gamma _{s,h}},\\&\Lambda _j=\sqrt{k_j^2\left\{ \Omega -4\lambda (t)\left[ k_j^2\lambda (t)+2\mu (t)\right] \right\} },\\&\Gamma _{s,h}=\Omega +4\lambda (t)\left[ k_sk_h\lambda (t)-2\mu (t)\right] ,\\&\Omega ={\alpha (t)}^2 + 4\left( 2\eta _1 -3\eta _2\right) \alpha (t)\lambda (t), \end{aligned}$$

\(\eta _1\), \(\eta _2\) and \(k_j\)’s are the real constants, \(G_j\)’s are the complex constants, \(\sum \limits \) means a summation over all possible subscripts \(\{N_1,\ldots ,N_n\}\) chosen from the set \(\{1,2,\ldots ,N\}\) under the condition that \(N_1 \le \cdots \le N_\rho \le N_{\rho +1} \le \cdots \le N_n\), while \(\rho \), j, s, h, l, d and \(N_j\)’s are the integers.

Since \(\omega _j(t)\)s are the real functions, it is required that \(\Lambda _j\)’s are real, i.e.,

$$\begin{aligned}&{\alpha (t)}^2+ 4\left( 2\eta _1 - 3 \eta _2\right) \alpha (t)\lambda (t)\nonumber \\&\quad - \,4{\lambda (t)}^2k_j^2-8\lambda (t)\mu (t)\ge 0. \end{aligned}$$
(7)

Due to \(\chi _1(t)\ne 0\) and \(\chi _2(t)\ne 0\), N-Soliton Solutions (5) needs to satisfy that

$$\begin{aligned} \begin{aligned}&\alpha (t)-4\eta _2\lambda (t)\ne 0,\\&\frac{{\alpha (t)}^2}{8\lambda (t)} -\frac{1}{2}\left( 2\eta _1+\eta _2\right) \alpha (t)+4\eta _2^2\lambda (t)+\mu (t)\ne 0. \end{aligned} \end{aligned}$$
(8)

If \(\chi _1(t)= 0\) or \(\chi _2(t)= 0\), N-Soliton Solutions (5), respectively, need to satisfy that

$$\begin{aligned} \alpha (t)=4\eta _2\lambda (t),~~\text {or}~~\mu (t)=4\eta _2(\eta _1-\eta _2)\lambda (t). \end{aligned}$$
(9)

Under Constraints (7)–(9), the N-soliton solutions with the nonzero background for Eq. (1) can be expressed as N-Soliton Solutions (5), which are different from those in Ref. [43].

However, different from the above, when \(\chi _1(t)=0\) and \(\chi _2(t)=0\), i.e., \(\alpha (t)=4\eta _2\lambda (t)\) and \(\mu (t)=4\eta _2(\eta _1-\eta _2)\lambda (t)\), the solutions given by N-Soliton Solutions (5) are still different from those in Ref. [43], although the bilinear forms are the same as those in Ref. [43], which is caused by the expansion forms of \(f_N\) and \(g_N\), namely, Expressions (6).

3 Asymptotic analysis

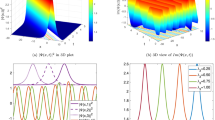
When \(N=2\), we can obtain the two-soliton solutions for Eq. (1) as

$$\begin{aligned} \begin{aligned} u&=\frac{g_2}{f_2}=e^{i[(\eta _1-\eta _2)x+m_1(t)-m_2(t)]}\frac{1+G_1e^{\theta _1+2i\phi _1}+G_2e^{\theta _2+2i\phi _2} +G_{1,2}e^{\theta _1+\theta _2+2i(\phi _1+\phi _2)}}{1+F_1e^{\theta _1}+F_2e^{\theta _2}+F_{1,2} e^{\theta _1+\theta _2}}. \end{aligned} \end{aligned}$$
(10)

Then, we can derive \(|u|^2\) as

$$\begin{aligned} \begin{aligned} |u|^2&=\frac{1+G_1e^{\theta _1+2i\phi _1}+G_2e^{\theta _2+2i\phi _2} +G_{1,2}e^{\theta _1+\theta _2+2i(\phi _1+\phi _2)}}{1+F_1e^{\theta _1}+F_2e^{\theta _2}+F_{1,2}e^{\theta _1+\theta _2}}\frac{1+G_1^{*}e^{\theta _1-2i\phi _1}+G_2^{*}e^{\theta _2-2i\phi _2} +G_{1,2}^{*}e^{\theta _1+\theta _2-2i(\phi _1+\phi _2)}}{1+F_1^{*}e^{\theta _1}+F_2^{*}e^{\theta _2}+F_{1,2}^{*}e^{\theta _1+\theta _2}}. \end{aligned}\nonumber \\ \end{aligned}$$
(11)

Under \(G_{1,2}\ne 0\), we assume that

$$\begin{aligned} k_1>k_2>0~~\text {and}~~\omega _2(t)/k_2>\omega _1(t)/k_1. \end{aligned}$$
(12)
Table 1 Properties of the solitonic interaction for the two-dark-soliton solutions
Full size table

If \(\theta _1\) is fixed, \(\theta _2\) can be expressed as \(\theta _2=\frac{k_2}{k_1}\theta _1+k_2\left[ \frac{\omega _2(t)}{k_2} -\frac{\omega _1(t)}{k_1}\right] \). When \(t\rightarrow -\infty \), we have \(e^{\theta _2}\rightarrow 0\); when \(t\rightarrow +\infty \), we have \(e^{-\theta _2}\rightarrow 0\). So we can derive

$$\begin{aligned} S_1^-=&\lim _{\begin{array}{c} t\rightarrow -\infty \\ (\theta _1\,\text {fixed}) \end{array}}|u|^2 = 1-\Bigg |\text {sech}\left( \frac{\theta _1}{2} +\frac{1}{2}\ln F_1\right) \Bigg |^2\nonumber \\&\times \left[ \left| \sin \left( \phi _1-\frac{1}{2}i\ln G_1\right) \right| ^2 -\frac{|1-F_1|^2}{4|\sqrt{G_1}|^2}\right] ,\end{aligned}$$
(13a)
$$\begin{aligned} S_1^+=&\lim _{\begin{array}{c} t\rightarrow +\infty \\ (\theta _1\,\text {fixed}) \end{array}}|u|^2 \nonumber \\ =&1-\left| \text {sech}\left( \frac{\theta _1}{2}+\frac{1}{2}\ln \left( F_1 H_{1,2}\right) \right) \right| ^2\nonumber \\&\times \left[ \left| \sin \left( \phi _1-\frac{1}{2}i\ln \left( G_1H_{1,2}\right) \right) \right| ^2\nonumber \right. \\&\left. -\frac{|1-F_1H_{1,2}|^2}{4|\sqrt{G_1H_{1,2}}|^2}\right] , \end{aligned}$$
(13b)

where \(S_1^-\) and \(S_1^+\) denote the asymptotic expressions for the soliton \(S_1\) before and after the interaction, respectively.

If \(\theta _2\) is fixed, \(\theta _1\) can be expressed as \(\theta _1=\frac{k_1}{k_2}\theta _2+k_1\left[ \frac{\omega _1(t)}{k_1} -\frac{\omega _2(t)}{k_2}\right] \). When \(t\rightarrow -\infty \), we have \(e^{-\theta _1}\rightarrow 0\); when \(t\rightarrow +\infty \), we have \(e^{\theta _1}\rightarrow 0\). So we can derive

$$\begin{aligned} S_2^-=&\lim _{\begin{array}{c} t\rightarrow -\infty \\ (\theta _2\,\text {fixed}) \end{array}}|u|^2 \nonumber \\ =&1-\left| \text {sech}\left( \frac{\theta _2}{2}+\frac{1}{2}\ln \left( F_2 H_{1,2}\right) \right) \right| ^2\nonumber \\&\times \left[ \left| \sin \left( \phi _2-\frac{1}{2}i\ln \left( G_2 H_{1,2} \right) \right) \right| ^2 \nonumber \right. \\&\left. - \frac{|1-F_2H_{1,2}|^2}{4|\sqrt{G_2H_{1,2}}|^2} \right] ,\end{aligned}$$
(14a)
$$\begin{aligned} S_2^+=&\lim _{\begin{array}{c} t\rightarrow +\infty \\ (\theta _2\,\text {fixed}) \end{array}}|u|^2 = 1-\left| \text {sech}\left( \frac{\theta _2}{2} +\frac{1}{2}\ln F_2\right) \right| ^2\nonumber \\&\times \left[ \left| \sin \left( \phi _2-\frac{1}{2}i\ln G_2 \right) \right| ^2 - \frac{|1-F_2|^2}{4|\sqrt{G_2}|^2}\right] , \end{aligned}$$
(14b)

where \(S_2^-\) and \(S_2^+\) denote the asymptotic expressions for the soliton \(S_2\) before and after the interaction, respectively.

Based on Expressions (13) and (14), the relevant properties of the two solitons during the interaction, including the widths \(W_j\)\((j=1,2)\), amplitudes \(A_j^{\pm }\), velocities \(V_j^{\pm }\) and phase shifts \(\Delta _j\), are listed in Table 1, where \(\Phi _j\), \(\Psi _j\), \(V_j\) and \(\Delta \) can be written as

$$\begin{aligned}&\Phi _j=\left| \sin \left( \phi _j-\frac{1}{2}i\ln G_j \right) \right| ^2 -\left| \cosh \left[ \frac{\ln \left( -F_j\right) }{2}\right] \right| ^2,\\&\Psi _j=\left| \sin \left( \phi _j-\frac{1}{2}i\ln (G_j H_{1,2})\right) \right| ^2\\&\qquad \quad -\left| \cosh \left[ \frac{\ln \left( -F_jH_{1,2}\right) }{2}\right] \right| ^2,\\&V_j=\alpha (t)+2(\eta _1-\eta _2)\lambda (t)-\frac{\Lambda _j}{2k_j}\\&\qquad \quad +i4k_j\lambda (t)^2\frac{[2k_j\alpha (t)\lambda (t)^{-1}+\Lambda _j\lambda (t)^{-1}]_t}{4k_j^4\lambda (t)^2+[2k_j\alpha (t)+\Lambda _j]^2},\\&\Delta =-\left[ \ln (H_{1,2})\right] _t\\&\quad =8\frac{ 4\lambda (t)\left[ \lambda (t)^{\prime }\mu (t)-\lambda (t)\mu (t)^{\prime }\right] }{\left[ 4k_1^2\lambda (t)^2 + k_1^{-2}\Lambda _1^2\right] \Lambda _1\Lambda _2k_1^{-2}k_2^{-2}\lambda (t)^{-1}}\\&\qquad \, +8\frac{\left[ 2(\eta _1-3\eta _2)\lambda (t)+\alpha (t)\right] \left[ \lambda (t)\alpha (t)^{\prime }-\alpha (t)\lambda (t)^{\prime }\right] }{\left[ 4k_1^2\lambda (t)^2 + k_1^{-2}\Lambda _1^2\right] \Lambda _1\Lambda _2k_1^{-2}k_2^{-2}\lambda (t)^{-1}}, \end{aligned}$$

where \((\bullet )^\prime =\frac{\partial }{\partial t}(\bullet )\).

Without loss of generality, we consider the case of \(\eta _1=-\eta _2=1\) and \(\phi _j=\frac{\pi }{2}\) for illustrating the asymptotic expressions of the two-dark-soliton solutions for Eq. (1). When \(\phi _j=\frac{\pi }{2}\), \(\Phi _j\) and \(\Psi _j\) are reduced as

$$\begin{aligned} \Phi _j= & {} \Psi _j=\frac{\text {Re}(G_j+F_j)}{2|G_j|}=\frac{2k_j^2\lambda (t) }{\sqrt{\text {Re}(G_j)^2+\text {Im}(G_j)^2} }\nonumber \\&\times \frac{ 2 \text {Re}(G_j) k_j^2\lambda (t) + \text {Im}(G_j)\left[ \Lambda _j+2k_j\alpha (t) \right] }{4k_j^4\lambda (t)^2+\left[ \Lambda _j+2k_j\alpha (t)\right] ^2}, \nonumber \\ \end{aligned}$$
(15)

where \(\text {Re}(\bullet )\) and \(\text {Im}(\bullet )\) denote the real and imaginary parts of the element \(\bullet \), respectively.

Based on Table 1, we can observe \(A_j^{\pm }\)’s \((j=1,2)\), \(V_j^{\pm }\)’s and \(\Delta _j\)’s are related to t, while \(W_j\)’s are constant. Besides, under \(\Delta =0\) or \(\Delta \ne 0\), the properties of the two solitons \(S_j\)’s have different situations.

Table 2 Conditions of the dark, anti-dark and gray solitons
Full size table

Assuming that

$$\begin{aligned} \frac{\alpha (t)}{\lambda (t)}=\rho _1,~~\frac{\mu (t)}{\lambda (t)}=\rho _2, \end{aligned}$$
(16)

where \(\rho _1\) and \(\rho _2\) are the proportional coefficients, and then we can obtain two cases according to \(\Delta =0\) and \(\Delta \ne 0\) as follows:

Case 1.:

\(\rho _1\) and \(\rho _1\) are the constant.

In this case, \(\Delta =0\), i.e., \(\ln H_{1,2}=\mathrm{const}.\) We can obtain \(V_j^-=V_j^+\) and \(A_j^-=A_j^+\), which implies that the velocity, amplitude and width of the soliton \(S_j\) are unchanged after the interaction except that there is a phase shift, while the interaction is elastic.

Case 2.:

\(\rho _1\)and\(\rho _2\)are related tot.

In this case, \(\Delta \ne 0\), i.e., \(\ln H_{1,2}\ne \mathrm{const}\). We can observe \(V_j^-\ne V_j^+\) and \(A_j^-=A_j^+\), which implies that the velocity of the soliton \(S_j\) is changed after the interaction, while the interaction is inelastic.

Note that: Under Expressions (16) and Constraints (7)–(9), without loss of generality, setting \(\eta _1=-\eta _2=1\), we will investigate these situations under \(\rho _1\ne -4\) or \(\rho _2\ne -8\).

4 Conditions for the dark, anti-dark and gray solitons

According to \(A_j^{\pm }\) in Table 1 and Eq. (15), we can obtain the dark, anti-dark and gray solitons under the different conditions listed in Table 2.

According to Constraint (7), we can obtain

$$\begin{aligned} |k_j|<\frac{1}{2}\sqrt{\rho _1^2+20\rho _1-8\rho _2}\,\text {and}\,\rho _2<\frac{5}{2}\rho _1+\frac{1}{8}\rho _1^2.\nonumber \\ \end{aligned}$$
(17)

Based on Table 2, expressions of the conditions of the dark, anti-dark and gray solitons are derived as follows:

  • According to \(\Phi _j=1\), we can reduce the condition for the dark solitons as

    $$\begin{aligned} \begin{aligned}&2k_j^2\lambda (t)\Big \{ \text {Im}(G_j)\Lambda _j + 2k_j\left[ \text {Im}(G_j)\alpha (t) \right. \\&\quad \left. +\, k_j\text {Re}(G_j)\lambda (t)\right] \Big \} -\sqrt{{\text {Im}(G_j)}^2+{\text {Re}(G_j)}^2}\\&\quad \Big \{\left[ \Lambda _j + 2k_j\alpha (t)\right] ^2 +4k_j^4\lambda (t)^2\Big \}=0. \end{aligned}\nonumber \\ \end{aligned}$$
    (18)

  • According to \(\Phi _j<0\), we can reduce the condition for the anti-dark solitons as

    $$\begin{aligned}&\lambda (t)\Big \{ \text {Im}(G_j)\Lambda _j + 2k_j\left[ \text {Im}(G_j)\alpha (t) \right. \nonumber \\&\quad \left. + k_j\text {Re}(G_j)\lambda (t)\right] \Big \}<0. \end{aligned}$$
    (19)

  • According to \(0<\Phi _j<1\), we can reduce the condition for the gray solitons as

    $$\begin{aligned} \begin{aligned}&\lambda (t)\Big \{ \text {Im}(G_j)\Lambda _j + 2k_j \left[ \text {Im}(G_j)\alpha (t) \right. \\&\quad \left. +\, k_j\text {Re}(G_j)\lambda (t)\right] \Big \}>0,\\&2k_j^2\lambda (t)\Big \{ \text {Im}(G_j)\Lambda _j \\&\quad + 2k_j\left[ \text {Im}(G_j)\alpha (t) + k_j\text {Re}(G_j)\lambda (t)\right] \Big \}\\&\quad -\sqrt{{\text {Im}(G_j)}^2+{\text {Re}(G_j)}^2}\\&\qquad \Big \{\left[ \Lambda _j + 2k_j\alpha (t)\right] ^2+4k_j^4\lambda (t)^2\Big \}<0. \end{aligned} \end{aligned}$$
    (20)

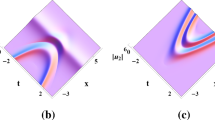
According to the above discussion, the three types of solitons, including the dark, anti-dark and gray solitons, are derived under Conditions (18)–(20), as seen in Fig. 1.

Fig. 1
figure 1

Solitons via N-Soliton Solutions (5) under \(N=2\) with \(-\alpha (t)=\lambda (t)=-\frac{1}{4}\mu (t)=1\) and \(k_{1}=k_{2}=1.5\); a\(G_{1}=G_{2}=1\); b\(G_{1}=G_{2}=1-i\); c\(G_{1}=G_{2}=-1+i\)

Full size image

5 Discussions

Under Constraints (7) and (8), according to N-Soliton Solutions (5), we will analyze the interactions between or among the solitons and illustrate the effects of \(\lambda (t)\), \(\alpha (t)\) and \(\mu (t)\) on the interactions with Case 1 and 2, respectively.

5.1 Interactions between two solitons

  • \(\rho _1\) and \(\rho _2\) are the constants.

Because \(\rho _1\) and \(\rho _2\) are constants, under \(\Delta =0\) and \(\eta _1=-\eta _2=1\), the velocity \(V_j^{\pm }=V_j\)\((j=1,2)\), and \(V_j\) is reduced as

$$\begin{aligned} V_j= & {} \alpha (t)+4\lambda (t)\nonumber \\&-\frac{\text {sign}(k_j)}{2}|\lambda (t)|\sqrt{\rho _1^2+20\rho _1-8\rho _2-4k_j^2},\nonumber \\ \end{aligned}$$
(21)

which indicates that \(V_j\)’s are related to \(\rho _1\), \(\rho _2\) and \(\lambda (t)\). With other parameters fixed, we obtain that \(V_j\) is proportional to \(k_j\) whether under \(k_j>0\) or \(k_j<0\), whereas \(V_j\) under \(k_j<0\) is bigger than that under \(k_j>0\).

Fig. 2
figure 2

Interactions between the two solitons via N-Soliton Solutions (5) under \(N=2\) with \(-\alpha (t)=\lambda (t)=-\frac{1}{4}\mu (t)=1\), \(k_{1}=-0.5\) and \(k_{2}=0.6\); a interaction between the anti-dark and gray solitons with \(G_{1}=-1+i\) and \(G_{2}=1-i\); b interaction between the dark and gray solitons with \(G_{1}=1-i\) and \(G_{2}=1\); c interaction between the anti-dark and dark solitons with \(G_{1}=-1+i\) and \(G_{2}=1\)

Full size image
Fig. 3
figure 3

Interactions between the gray and anti-dark solitons via N-Soliton Solutions (5) under \(N=2\) with \(-\alpha (t)=\lambda (t)=-\frac{1}{4}\mu (t)=1\), \(G_{1}=-1+i\), \(G_{2}=1\) and \(k_2=1.5\); a\(k_{1}=0.95\); b\(k_{1}=1\); c\(k_{1}=1.1\)

Full size image
Fig. 4
figure 4

Effects of \(\lambda (t)\), with the same parameters as those in Fig. 3c except that a\(\lambda (t)=1.1\); b\(\lambda (t)=1.2\); c\(\lambda (t)=1.3\)

Full size image
Fig. 5
figure 5

Effects of \(\alpha (t)\), with the same parameters as those in Fig. 3c except that a\(\alpha (t)=-1.1\); b\(\alpha (t)=-1.2\); c\(\alpha (t)=-1.25\)

Full size image
Fig. 6
figure 6

Effects of \(\mu (t)\), with the same parameters as those in Fig. 3c except that a\(\mu (t)=-3.9\); b\(\mu (t)=-3.8\); c\(\mu (t)=-3.7\)

Full size image

Under Conditions (18), (19) and (20), interactions, between the anti-dark and gray solitons, between the dark and gray solitons, as well as between the anti-dark and dark solitons, are described in Fig. 2a–c, respectively. We observe that \(V_j\) and \(\Phi _j\) are invariable in Fig. 2 and the propagation of the soliton \(S_1\) is faster than that of the soliton \(S_2\) due to \(V_1>V_2\), which implies that the interactions are elastic.

Interactions between the gray and anti-dark solitons are described in Fig. 3. Amplitude in the interaction center increases with \(k_1\) increasing. With \(V_2\) unchanged, time of the interaction between the anti-dark soliton \(S_1\) and gray soliton \(S_2\) decreases as \(V_1\) increases. Especially, under \(k_1=1.1\) the amplitude is more than six times as high as the background.

Effects of \(\lambda (t)\), \(\alpha (t)\) and \(\mu (t)\) on the interactions between the gray and anti-dark solitons are analyzed in Figs. 4, 5 and 6, respectively. According to \(\Phi _j\) and \(V_j\)\((j=1,2)\), under \(k_{1}=1.1\) and \(k_2=1.5\), we observe that: the amplitude in the interaction center decreases not only as any one of \(\mu (t)\) and \(\lambda (t)\) increases, but also as \(\alpha (t)\) decreases, whereas the amplitudes of the anti-dark and gray solitons increase not only as any one of \(\lambda (t)\) and \(\mu (t)\) increases, but also as \(\alpha (t)\) decreases; \(V_j\)’s are proportional to \(\lambda (t)\) and \(\mu (t)\), respectively, whereas \(V_j\)’s decrease first and then increase with \(\alpha (t)\) increasing.

Fig. 7
figure 7

The same as Fig. 2 except that \(-\alpha (t)=\lambda (t)=-\frac{1}{4}\mu (t)=\text {cosh}(t)\)

Full size image
Fig. 8
figure 8

The same as Fig. 2 except that \(k_{1}=0.3\), \(k_{2}=0.1\) and \(\alpha (t)=\lambda (t)=\mu (t)=\text {cos}(t)+1.1\)

Full size image

When \(\alpha (t)\), \(\lambda (t)\) and \(\mu (t)\) are real functions with respect to t, under \(\rho _1=-1\) and \(\rho _2=-4\), the interactions with \(\lambda (t)=\text {cosh}(t)\), between the anti-dark and dark solitons, between the gray and dark soliton, as well as between the anti-dark and gray solitons, are described in Fig. 7a–c, respectively. Under \(\rho _1=\rho _2=1\), interactions with \(\lambda (t)=\text {cos}(t)+1.1\) are described in Fig. 8. Amplitude in the interaction center has a nonlinear superposition effect. According to Eq. (21), the velocities of the solitons in Figs. 7 and 8 are recorded as \(V_{7,j}\) and \(V_{8,j}\), respectively, as well as derived as

$$\begin{aligned} V_{7,j}= & {} \text {cosh}(t)\left[ 3-\frac{1}{2}\text {sign}(k_j) \sqrt{13-4k_j^2}\right] ,\\ V_{8,j}= & {} \left[ \text {cos}(t)+\frac{11}{10}\right] \left[ 5-\frac{1}{2}\text {sign}(k_j)\sqrt{13-4k_j^2}\right] . \end{aligned}$$

Because \(V_{7,j}\) and \(V_{8,j}\) are the functions with respect to t, the interactions in Figs. 7 and 8 are inelastic. Especially, propagations of the two solitons in Fig. 8 have the periodicity due to \(V_{8,j}\), while \(A_j\)’s increase as |t| increases in Fig. 8.

Fig. 9
figure 9

Interactions between the anti-dark and dark solitons, with the same as Fig. 2c except that \(k_{1}=0.3\), \(k_{2}=0.1\) and \(\alpha (t)=\lambda (t)=1\); a\(\mu (t)=-{\text {cos}^2(t)}-1.1\); b\(\mu (t)=-{\text {cos}^2(t)}+1.1\); c\(\mu (t)={\text {cos}^2(t)}+1.1\)

Full size image
Fig. 10
figure 10

The same as Fig. 2 except that \(k_{1}=0.3\), \(k_{2}=0.1\), \(\alpha (t)=\lambda (t)=1\) and \(\mu (t)=-\text {cosh}(t)\)

Full size image

  • \(\rho _1\)and\(\rho _2\)are related tot.

Because \(\rho _1\) and \(\rho _2\) are related to t, then \(\Delta \ne 0\), and then \(V_j^{\pm }\) and \(A_j^{\pm }\)\((j=1,2)\) are more complex than that under the condition that \(\rho _1\) and \(\rho _2\) are constants, where \(V_j\) and \(\Phi _j\) are rewritten as

$$\begin{aligned} V_j=\,&\alpha (t)+4\lambda (t)\nonumber \\&-\frac{k_j|\lambda (t)|}{2|k_j|} \sqrt{\rho _1^2+20\rho _1-8\rho _2-4k_j^2}\nonumber \\&+\frac{ik_j\left[ 2k_j\rho _1+\sqrt{\rho _1^2+20\rho _1-8\rho _2-4k_j^2} \right] _t}{4k_j^4+\left[ 2k_j\rho _1+\sqrt{\rho _1^2+20\rho _1-8\rho _2-4k_j^2}\right] ^2}, \end{aligned}$$
(22a)
$$\begin{aligned} \Phi _j=&\frac{2k_j^2}{\sqrt{\text {Re}(G_j)^2+\text {Im}(G_j)^2}}\nonumber \\&\times \left\{ \frac{\text {Im}(G_j)\sqrt{\rho _1^2+20\rho _1-8\rho _2-4k_j^2}}{4k_j^4+\left[ 2k_j\rho _1+\sqrt{\rho _1^2+20\rho _1-8\rho _2-4k_j^2}\right] ^2}\right. \nonumber \\&+\left. \frac{2k_j^2\text {Re}(G_j)+2k_j\rho _1\text {Im}(G_j)}{4k_j^4+\left[ 2k_j\rho _1+\sqrt{\rho _1^2+20\rho _1-8\rho _2-4k_j^2}\right] ^2}\right\} . \end{aligned}$$
(22b)

According to Eq. (22), under \(\rho _1=1\), when \(\rho _2\) is a periodic function of t, \(V_j\) and \(A_j\) are the periodic functions of t, and the corresponding solitons propagate periodically. When \(\rho _2\) increases from \(-{\text {cos}^2(t)}-1.1\) to \(-{\text {cos}^2(t)}+1.1\) and then to \({\text {cos}^2(t)}+1.1\), for the anti-dark and dark solitons, the corresponding \(V_j\) decreases in turn, whereas the corresponding \(\Phi _j\) increases in turn, as seen in Fig. 9a–c.

Fig. 11
figure 11

Interaction among the dark, gray and anti-dark solitons via N-Soliton Solutions (5) under \(N=3\) with \(-\alpha (t)=\lambda (t)=-\frac{1}{4}\mu (t)=1\), \(G_{1}=1\), \(G_{2}=1-i\), \(G_{3}=-1+i\), \(k_{1}=1.5\), \(k_{2}=-0.5\) and \(k_{3}=-1\); a\(-\alpha (t)=\lambda (t)=-\frac{1}{4}\mu (t)=1\); b\(-\alpha (t)=\lambda (t)=-\frac{1}{4}\mu (t)=\text {cosh}(\frac{t}{4})\); c\(-\alpha (t)=\lambda (t)=\text {cosh}(\frac{t}{4})\) and \(\mu (t)=-4\)

Full size image

Especially, when \(\rho _1=1\) and \(\rho _2=-\text {cosh}(t)\), the interactions between any two of the dark, anti-dark and gray solitons are described in Fig. 10. According to Eq. (22), we can observe that: when t tends to be infinite, \(\Phi _j\) tends to be zero, whereas \(V_j\) tends to be infinite, which is affected by \(\text {cosh}(t)\).

5.2 Interactions among three or four solitons

Anti-dark, gray and dark solitons coexist on the nonzero background, as seen in Fig. 11. According to \(\Phi _j\) and \(V_j\), the waveforms and velocities of the anti-dark, gray and dark solitons all remain unchanged after the interaction, which indicates that the interaction is elastic, as seen in Fig. 11a, whereas the interactions in Fig. 11b, c are inelastic due to the changes with t of the waveforms and velocities of the solitons.

Fig. 12
figure 12

Interactions among the dark, gray and anti-dark solitons via N-Soliton Solutions (5) under \(N=4\) with \(G_{1}=1\), \(G_{2}=1-i\), \(G_{3}=-1+i\), \(G_{4}=1-i\), \(k_{1}=1.5\), \(k_{2}=-0.5\), \(k_{3}=-0.6\) and \(k_{4}=-0.4\); a\(-\alpha (t)=\lambda (t)=-\frac{1}{4}\mu (t)=1\); b\(-\alpha (t)=\lambda (t)=-\frac{1}{4}\mu (t)=\text {cos}(t) +1.1\); c\(\alpha (t)=\lambda (t)=\text {sech}(t)\) and \(\mu (t)=-4\)

Full size image

Under \(N=4\), interactions among the four solitons, including one gray soliton, one dark soliton and two anti-dark solitons, are described in Fig. 12. When \(\rho _1=\frac{1}{4}\rho _2=-1\), then \(\Delta =0\), and then whether \(V_j\)’s are invariable or variable depends on whether \(\alpha (t)\) and \(\lambda (t)\) are constants or functions of t, as seen in Fig. 12a, b, respectively. When \(\rho _1=1\) and \(\rho _2=-4\text {cosh}(t)\), then \(\Delta \ne 0\), and then the interaction among the four solitons occurs on the nonzero background with \(\alpha (t)=\lambda (t)=\text {sech}(t)\), as seen in Fig. 12c.

6 Conclusions

Water waves are one of the most common phenomena in nature, while the media with negative refractive index are among the carrier media in fiber optics. Due to the inhomogeneities of the media and nonuniformities of the boundaries in the real physical backgrounds, a quintic DNLS equation with the time-dependent coefficients, i.e., Eq. (1), which describes certain hydrodynamic wave packets or medium with the negative refractive index, has been investigated. Under Constraints (7)–(9), we have derived Bilinear Forms (2) for Eq. (1), which are different from those in Ref. [43], and obtained N-Soliton Solutions (5) for Eq. (1) with respect to the nonzero background. Under Assumptions (12), properties of the two solitons, including the amplitudes \(A_j^{\pm }\)’s (\(j=1,2\)), velocities \(V_j^{\pm }\)’s, widths \(W_j\)’s and phase shifts \(\Delta _j\)’s, have been derived via the asymptotic analysis and listed in Table 1. Conditions for the dark, anti-dark and gray solitons have been deduced in Table 2. Three types of the solitons have been described in Fig. 1.

Under Condition (3), quintic nonlinearity coefficient \(\nu (t)\) has been demonstrated to be related to the dispersion coefficient \(\lambda (t)\) and self-steepening coefficient \(\alpha (t)\). Interactions between the two solitons and effects of \(\alpha (t)\), \(\lambda (t)\) and the cubic nonlinearity coefficient \(\mu (t)\) on the interactions have been investigated under two cases:

Case 1,:

where \(\frac{\alpha (t)}{\lambda (t)}\) and \(\frac{\mu (t)}{\lambda (t)}\) are the constants.

  • When \(\alpha (t)\), \(\lambda (t)\) and \(\mu (t)\) are the constants, interactions, between any two of the dark, anti-dark and gray solitons, have been seen to be elastic, as seen in Fig. 2. Amplitude at the center of the interaction between the anti-dark and gray solitons has been found to increase not only with the decrease of \(\alpha (t)\) but also with the increase of any of \(\lambda (t)\), \(\mu (t)\) and \(k_j\), while \(A_j^{\pm }\)’s increase not only with the increase of \(\alpha (t)\) but also with the decrease of any of \(\lambda (t)\), \(\mu (t)\) and \(k_j\), as seen in Figs. 3, 4, 5 and 6.

  • When \(\alpha (t)\), \(\lambda (t)\) and \(\mu (t)\) are related to t, under \(\frac{\alpha (t)}{\lambda (t)}=-1\) and \(\frac{\mu (t)}{\lambda (t)}=-4\), we have found that: when \(\lambda (t)=\text {cosh}(t)\) or \(\text {cos}(t)+1.1\), the interactions in Figs. 7 or 8 is inelastic due to the changes of \(V_j^{\pm }\)’s; propagation of the two solitons in Fig. 8 is periodic due to \(\lambda (t)=\text {cos}(t)+1.1\).

Case 2,:

where\(\frac{\alpha (t)}{\lambda (t)}\)and\(\frac{\mu (t)}{\lambda (t)}\)are related tot.

  • When \(\frac{\alpha (t)}{\lambda (t)}=1\), we have found that: When \(\frac{\mu (t)}{\lambda (t)}\) increases from \(-{\text {cos}^2(t)}-1.1\) to \(-{\text {cos}^2(t)}+1.1\) and then to \({\text {cos}^2(t)}+1.1\), propagation of the two solitons remains periodic, while the corresponding \(V_j\)’s decrease and \(A_j\)’s increase, as seen in Fig. 9; when \(\frac{\mu (t)}{\lambda (t)}=-\text {cosh}(t)\), under \(\lambda (t)=1\), \(\Phi _j\) tends to zero and \(V_j\) tends to the infinity as t tends to the infinity, which is affected by \(\text {cosh}(t)\), as seen in Fig. 10.

Anti-dark, dark and gray solitons have been found to coexist on the same nonzero background, as shown in Fig. 11; interactions among the three or four solitons have been investigated: when \(\frac{\alpha (t)}{\lambda (t)}=-1\) and \(\frac{\mu (t)}{\lambda (t)}=-4\), velocities and waveforms for the three solitons remain unchanged after the interaction under \(\lambda (t)=1\), indicating that the interaction in Fig. 11a is elastic, whereas the velocities for the three solitons change after the interaction under \(\lambda (t)=\text {cosh}(\frac{t}{4})\), indicating that the interaction in Fig. 11b is inelastic; under \(\frac{\alpha (t)}{\lambda (t)}=-1\) and \(\frac{\mu (t)}{\lambda (t)}=-4\text {sech}(\frac{t}{4})\), interaction in Fig. 11c is inelastic due to the changes in the velocities for the solitons. Interaction is elastic in Fig. 12a due to the invariance of the waveforms and velocities for the four solitons, whereas interaction is inelastic in Fig. 12b, c due to the changes of the waveforms and velocities for the four solitons.