1 Introduction

The application of nonlinear evolution equations (NLEEs) has covered in the filed of mathematical physics and engineering, and their solutions which are important for describing nonlinear physical phenomena. In almost all the branches of physics, such as plasma physics and optical fibers (Moslem 2011; Bailung et al. 2011), the traces of NLEEs can be found. Solitons have been defined by physical system in early work and these solutions of nonlinear dispersive partial differential equations are also very important in the study of physical phenomena (Zhang and Ma 2015a, b; Liu et al. 2018; Ma 2015; Jiangen et al. 2017; Deng and Gao 2017; Ji-Guang et al. 2015; He et al. 2013). Recently, more and more studies have found that optical solitons in optical fibers with nonlinearity can be described well by the nonlinear Schrödinger (NLS) equation (Zhang and Si 2010; Trombettoni and Smerzi 2001; Biswas and Konar 2006; Biswas 2003; Dai et al. 2010; Belmonte-Beitia et al. 2008; Agrawal 2000; Gangwar et al. 2007; Krishnan et al. 2015; Sardar et al. 2016; Mirzazadeh et al. 2015, 2016). Optical solitons can be structured by a variety of different approaches, including the sine-cosine method (Yan 2001), the tanh–coth method (Heris and Lakestani 2013; Manafian Heris and Lakestani 2014; Wazwaz 2006), inverse scattering transformation (Ablowitz et al. 1974), the symbol calculation method (Tian and Zhang 2010; Tian 2017) and so on. Not only that, but the symmetries, Bäcklund transformation, conservation laws and Darboux transformation (Latha and Vasanthi 2014) of the nonlinear Schrödinger (NLS) equation also deserve our attention and research. Modulation instability (MI) analysis often be used to analyze whether the modulated envelopes are modulationally stable or not (Moslem et al. 2011). This is of great significance to our research.

In this paper, we mainly studied the quintic derivative nonlinear Schrödinger equation (Rogers and Chow 2012). The models can be found in various physical contexts, including the study of hydrodynamic wave packets and media with negative refractive index. In hydrodynamics, packets of free surface waves are governed by the nonlinear Schrödinger equation to leading order. However, cubic nonlinearity weakens in the parameter regime \(kh \approx 1.363\), where k is the wave number and h is the water depth considerably, and higher order effects need to be restored (Grimshaw and Annenkov 2011). Then, produce a quintic DNLS equation is necessary. Many aspects of this equation are described in other papers. For example, some new exact chirped soliton solutions are obtained by applying the new method to the quintic derivative nonlinear Schrödinger equation (Triki and Wazwaz 2017). But the same type articles are not found when compared with this paper. On the basis of previous work, some new solutions of this equation have not yet been obtained and modulation instability have not been studied.

The paper is organized as follows. In Sect. 2, we introduce the ansatz method to derive the singular solitons and dark solutions of the quintic derivative nonlinear Schrödinger equation. In Sect. 3, the explicit power series solutions for the equation has also been obtained by employing power series method. In Sect. 4, linear stability analysis is used to analyze modulation instability and prove the dark solitons are stable. we investigate the modulation instability (MI) analysis of the equation. In Sect. 5, conclusions and discussions will be given.

2 Mathematical analysis

In this section, the quintic derivative nonlinear Schrödinger equation is given by Rogers and Chow (2012)

$$ iq_{t}+\phi q_{xx}+i\alpha |q|^{2}q_{x}+\mu |q|^{2}q+\upsilon |q|^{4}q=0{.} $$
(2.1)

Introduce the following hypothesis

$$ q(x,t)={u(\xi )}e^{i\theta (x,t)}, $$
(2.2)

where

$$ \xi =x-\lambda t+x_{0}, \quad \theta =-\tau x+\omega t+\varepsilon _{0}, $$
(2.3)

in which \(\omega \), \(\tau \), \(\lambda \), \(x_{0}\) and \(\varepsilon _{0}\) are real constants. Substituting Eq. (2.2) into Eq. (2.1) and separating the real and imaginary parts. The imaginary part can be derived as

$$\lambda +2\tau \phi =\alpha u^{2},$$
(2.4)

while the real part is

$$\phi u^{''}-(\omega +\phi \tau ^{2})u+(\tau \alpha +\mu )u^{3}+\upsilon u^{5}.$$
(2.5)

Equation (2.5) can be reduced to the following form by integrating with respect to \(\xi \)

$$(u^{'})^{2}-\frac{(\omega +\phi \tau ^{2})}{\phi }u^{2}+\frac{(\tau \alpha +\mu )}{2\phi }u^{4}+\frac{\upsilon }{3\phi }u^{6}+2C=0,$$
(2.6)

where C is integration constant. Setting

$$d_{1}=\frac{(\omega +\phi \tau ^{2})}{\phi }, \quad d_{2}=\frac{(\tau \alpha +\mu )}{\phi }, \quad d_{3}=\frac{\upsilon }{\phi }, \quad d_{4}=2C.$$
(2.7)

Then, Eq. (2.6) can be written as

$$(u^{'})^{2}-d_{1}u^{2}+d_{2}\frac{u^{4}}{2}+d_{3}\frac{u^{6}}{3}+d_{4}=0.$$
(2.8)

Let \(u^{2}=v\) and \(u^{'}=\frac{1}{2u}v^{'}\) into Eq. (2.8), we have

$$(v^{'})^{2}-4d_{1}v^{2}+2d_{2}v^{3}+\frac{4}{3}d_{3}v^{4}+4d_{4}v=0.$$
(2.9)

2.1 Singular solitons

In the section, we consider the ansatz method to get the singular solitons solutions for the quintic derivative nonlinear Schrödinger equation. Assuming the following ansatz

$$f(\xi )=\sigma {\mathrm{csch}}^{n}(\nu \xi ),$$
(2.10)

where \(\nu \) is the wave number and \(\sigma \), \(\nu \), n are parameters to be determined later. The derivative of Eq. (2.10) can be represented as

$$\begin{aligned}&f^{'}(\xi )=-\sigma n\nu {\mathrm{csch}}^{n}(\nu \xi )\coth (\nu \xi ),\\&f^{''}(\xi )=\sigma n\nu ^{2}\left[ (n+1){\mathrm{csch}}^{n+2}(\nu \xi )+n{\mathrm{csch}}^{n}(\nu \xi )\right] ,\\&f^{'''}(\xi )=-\sigma n\nu ^{3}\left[ (n+1)(n+2){\mathrm{csch}}^{n+2}(\nu \xi )+n^{2}{\mathrm{csch}}^{n}(\nu \xi )\right] \coth (\nu \xi ),\\&\ldots \ . \end{aligned}$$
(2.11)

Substituting Eq. (2.10) into the imaginary part Eq. (2.4), we have

$${\mathrm{csch}}^{2n}(\nu \xi )=\frac{\lambda +2\tau \phi }{\alpha \sigma ^{2}}=0,$$
(2.12)

then

$$\lambda =-2\tau \phi .$$
(2.13)

What is more, we can get the transforms of Eq. (2.9) by substituting Eqs. (2.10) and (2.11) into Eq. (2.9)

$$ \begin{aligned}&\sigma ^{2}n^{2}\nu ^{2}{\mathrm{csch}}^{2n+2}(\nu \xi )+\sigma ^{2}n^{2}\nu ^{2}{\mathrm{csch}}^{2n}(\nu \xi )-4d_{1}\sigma ^{2}{\mathrm{csch}}^{2n}(\nu \xi )\\&\quad +2d_{2}\sigma ^{3}{\mathrm{csch}}^{3n}(\nu \xi )+\frac{4}{3}d_{3}\sigma ^{4}{\mathrm{csch}}^{4n}(\nu \xi )+4d_{4}\sigma {\mathrm{csch}}^{n}(\nu \xi )=0. \end{aligned}$$
(2.14)

By balancing the highest-order exponents of \({\mathrm{csch}}^{2n+2}(\nu \xi )\) and \({\mathrm{csch}}^{4n}(\nu \xi )\) functions, we get

$$ 2n+2=4n\Leftrightarrow n=1{.}$$
(2.15)

Therefore, the Eq. (2.14) can be written as

$$ \begin{aligned}&\sigma ^{2}\nu ^{2}{\mathrm{csch}}^{4}(\nu \xi )+\sigma ^{2}\nu ^{2}{\mathrm{csch}}^{2}(\nu \xi )-4d_{1}\sigma ^{2}{\mathrm{csch}}^{2}(\nu \xi )\\&\quad +2d_{2}\sigma ^{3}{\mathrm{csch}}^{3}(\nu \xi )+\frac{4}{3}d_{3}\sigma ^{4}{\mathrm{csch}}^{4}(\nu \xi )+4d_{4}\sigma {\mathrm{csch}}(\nu \xi )=0. \end{aligned}$$
(2.16)

Collecting the coefficients of the same exponent of \({\mathrm{csch}}^{i}(\nu \xi )\) to zero (\(i=1,2,3,4\)), we have

$${4d_{4}\sigma = 0, \quad \nu ^{2}-4d_{1}=0, \quad -4d_{1}\sigma ^{2}=0, \quad \nu ^{2}+\frac{4}{3}d_{3}\sigma ^{2}=0.}$$
(2.17)

Solving the system above, we get

$$ \nu =2\sqrt{\frac{(\omega +\phi \tau ^{2})}{\phi }}, \quad \sigma =\sqrt{-\frac{3(\omega +\phi \tau ^{2})}{\upsilon }},$$
(2.18)

where must be satisfied

$$\phi (\omega +\phi \tau ^{2})>0, \quad \upsilon (\omega +\phi \tau ^{2})<0.$$
(2.19)

Substituting the Eqs. (2.13) and (2.18) into Eq. (2.10), the ansatz \(f(\xi )\) can be represented as follows

$$f(\xi )=\sqrt{-\frac{3(\omega +\phi \tau ^{2})}{\upsilon }}{\mathrm{csch}}^{\frac{1}{2}}\left( 2\sqrt{\frac{(\omega +\phi \tau ^{2})}{\phi }}(x+2\tau \phi t+x_{0})\right).$$
(2.20)

Finally, the singular solitons solutions for the quintic derivative nonlinear Schrödinger equation can be alternatively written as

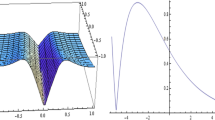
$$q(x,t)=e^{i(-\tau x+\omega t+\varepsilon _{0})}\sqrt{-\frac{3(\omega +\phi \tau ^{2})}{\upsilon }}{\mathrm{csch}}^{\frac{1}{2}}\left( 2\sqrt{\frac{(\omega +\phi \tau ^{2})}{\phi }}(x+2\tau \phi t+x_{0})\right).$$
(2.21)

Figure 1 showed that the profile of the squared of module (\(|q(x,t)|^{2}\)) of Eq. (2.21) of the quintic derivative nonlinear Schrödinger equation.

Fig. 1
figure 1

The squared of module of Eq. (2.21) at \(w=1\), \(\phi =1\), \(\tau =1\), \(\upsilon =1\)

Full size image

2.2 Tanh–coth method

In the section, we introduce the new independent variable reads

$$g(\xi )=\tanh (\xi ),$$
(2.22)

where \(f(\xi )=U(\xi )\). The derivative of Eq. (2.22) can be represented as

$$ \begin{aligned}&\frac{dU}{d\xi }=(1-g^{2})\frac{dU}{dg},\\&\frac{d^{2}U}{d\xi ^{2}}=-2g(1-g^{2})\frac{dU}{dg}+(1-g^{2})^{2}\frac{d^{2}U}{dg^{2}},\\&\frac{d^{3}U}{d\xi ^{3}}=2(1-g^{2})(3g^{2}-1)\frac{dU}{dg}-6g(1-g^{2})^{2}\frac{d^{2}U}{dg^{2}}+(1-g^{2})^{3}\frac{d^{3}U}{dg^{3}},\\&\ldots \ . \end{aligned}$$
(2.23)

Taking the solution of Eq. (2.9) has the following form

$$U(\xi )=\sum _{k=0}^{q}a_{k}g^{k}+\sum _{k=1}^{q}b_{k}g^{-k},$$
(2.24)

where \(a_{k}\) and \(b_{k}\) are arbitrary constant. Eq. (2.9) can be expressed in the form by substituting Eqs. (2.2) and (2.23) into Eq. (2.9)

$$ (1-g^{2})^{2}\left( \frac{dU_{1}}{dg}\right) ^{2}-4d_{1}U_{1}^{2}+2d_{2}U_{1}^{3}+\frac{4}{3}d_{3}U_{1}^{4}+4d_{4}U_{1}=0. $$
(2.25)

The parameter q of Eq. (2.25) can be derived by balancing the highest-order exponents of \(U_{1}^{4}\) and \((\frac{dU_{1}}{dg})^{2}\), we get

$$ 4q=(q+1)^{2}\Leftrightarrow q=1. $$
(2.26)

Then, we obtain

$$\begin{aligned}&U_{1}=a_{0}+a_{1}g+b_{1}g^{-1},\\&U_{1}^{'}=a_{1}-b_{1}g^{-2}. \end{aligned}$$
(2.27)

Substituting Eq. (2.27) into Eq. (2.25) and collecting the coefficients of the same exponent of \(g^{k}\) to zero(\(k=-4,-3,-2,-1,0,1,2,3,4\)), we get a set of algebraic equations

$$\begin{aligned} \left\{ \begin{aligned}&\frac{4}{3}d_{3}b_{1}^{4}-b_{1}^{2}=0,\\&\frac{16}{3}d_{3}a_{0}b_{1}^{3}+2d_{2}b_{1}^{3}=0,\\&6d_{2}a_{0}b_{1}^{2}+8d_{3}a_{0}^{2}b_{1}^{2}+\frac{16}{3}d_{3}a_{1}b_{1}^{3}+2a_{1}b_{1}-4d_{1}b_{2}^{2}+2b_{1}^{2}=0,\\&-8d_{1}a_{0}b_{1}+6d_{2}a_{0}^{2}b_{1}+6d_{2}a_{1}b_{1}^{2}+\frac{16}{3}d_{3}a_{0}^{3}b_{1}+4d_{4}b_{1}+16d_{3}a_{0}a_{1}b_{1}^{2}=0,\\&12d_{2}a_{0}a_{1}b_{1}+16d_{3}a_{0}^{2}a_{1}b_{1}-8d_{1}a_{1}b_{1}+8d_{3}a_{1}^{2}b_{1}^{2}-4a_{1}b_{1}+\frac{4}{3}d_{3}a_{0}^{4}+4d_{4}a_{0}\\&\quad -a_{1}^{2}-b_{1}^{2}-4d_{1}a_{0}^{2}+2d_{2}a_{0}^{3}=0,\\&-8d_{1}a_{0}a_{1}+6d_{2}a_{0}^{2}a_{1}+6d_{2}a_{1}^{2}b_{1}+\frac{16}{3}d_{3}a_{0}^{3}a_{1}+4d_{4}a_{1}+16d_{3}a_{0}a_{1}^{2}b_{1}=0,\\&6d_{2}a_{0}a_{1}^{2}+8d_{3}a_{0}^{2}a_{1}^{2}+\frac{16}{3}d_{3}a_{1}^{3}b_{1}+2a_{1}b_{1}-4d_{1}a_{1}^{2}+2a_{1}^{2}=0,\\&\frac{16}{3}d_{3}a_{0}a_{1}^{3}+2d_{2}a_{1}^{3}=0,\\&\frac{4}{3}d_{3}a_{1}^{4}-a_{1}^{2}=0. \end{aligned} \right. \end{aligned}$$
(2.28)

Solving the system above, we get

$$a_{0}=-\sqrt{\frac{3}{d_{3}}}, \quad a_{1}=b_{1}=-\sqrt{\frac{3}{4d_{3}}}, \quad d_{1}=-4, \quad d_{2}=\frac{8\sqrt{3d_{3}}}{3}, \quad d_{4}=0.$$
(2.29)

Substituting Eqs. (2.13) and (2.29) into Eq. (2.27), we have

$$U_{1}(\xi )=\left\{ -\sqrt{\frac{3}{4d_{3}}}\left[ 2+\tanh (x+2\tau \phi t+x_{0})+\coth (x+2\tau \phi t+x_{0})\right] \right\} ^{\frac{1}{2}}. $$
(2.30)

Therefore, the solution for the quintic derivative nonlinear Schrödinger equation can be written as (Fig. 2)

$$q(x,t)=e^{i(-\tau x+\omega t+\varepsilon _{0})}\left\{ -\sqrt{\frac{3}{4d_{3}}}\left[ 2+\tanh (x+2\tau \phi t+x_{0})+\coth (x+2\tau \phi t+x_{0})\right] \right\} ^{\frac{1}{2}}. $$
(2.31)
Fig. 2
figure 2

The squared of module of Eq. (2.31) at \(\phi =1\), \(\tau =1\), \(\upsilon =1\), \(x_{0}=0\)

Full size image

3 The explicit power series solutions

Using assumption as follows

$$q(x,t)=p(\xi )e^{i(\alpha _{1}x+\beta t+\theta _{0})}, $$
(3.1)

where \(p(\xi )=p(l_{1}x-vt+\theta _{1})\) is a real-valued function. We substitute Eq. (3.1) into Eq. (2.1), one can get

$$G_{1}p^{''}+G_{2}p^{'}+G_{3}p^{2}p^{'}+G_{4}p+G_{5}p^{3}+\upsilon p^{5}=0, $$
(3.2)

in which \(G_{1}=\phi l_{1}^{2}\), \(G_{2}=-iv+2i\phi \alpha _{1}l_{1}\), \(G_{3}=i\alpha l_{1}\), \(G_{4}=-\alpha _{1}^{2}\phi +i\beta \), \(G_{5}=-\alpha \alpha _{1}+\mu \). Now, we consider the form of solutions of Eq. (3.2)

$$ p(\xi )=c_{0}+c_{1}\xi +c_{2}\xi ^{2}+\cdots =\sum _{n=0}^{\infty }c_{n}\xi ^{n}. $$
(3.3)

Putting Eq. (3.3) into Eq. (3.2), we get

$$ \begin{aligned}&2G_{1}c_{2}+G_{1}\sum _{n=1}^{\infty }(n+1)(n+2)c_{n+2}\xi ^{n}+G_{2}c_{1}+G_{2}\sum _{n=1}^{\infty }(n+1)c_{n+1}\xi ^{n}+G_{3}c_{0}^{2}c_{1}\\&\quad +G_{3}\sum _{n=1}^{\infty }\sum _{i=0}^{n}(n-i+1)c_{q}c_{i-q}c_{n-i+1}\xi ^{n}+G_{4}c_{0}+G_{4}\sum _{n=1}^{\infty }c_{n}\xi ^{n}+G_{5}c_{0}^{3}+\upsilon c_{0}^{5}\\&\quad +G_{5}\sum _{n=1}^{\infty }\sum _{i=0}^{n}\sum _{q=0}^{i}c_{q}c_{i-q}c_{n-i}\xi ^{n}+\upsilon \sum _{n=1}^{\infty }\sum _{i=0}^{n}\sum _{q=0}^{i}\sum _{r=0}^{q}\sum _{a=0}^{r}c_{a}c_{r-a}c_{q-r}c_{i-q}c_{n-i}\xi ^{n}=0. \end{aligned} $$
(3.4)

When \(n=0\), we can derived

$$c_{2}=\frac{-(G_{2}c_{1}+G_{3}c_{0}^{2}c_{1}+G_{4}c_{0}+G_{5}c_{0}^{3}+\upsilon c_{0}^{5})}{2G_{1}},$$
(3.5)

where \(2G_{1}\ne 0\). When \(n\ge 1\), we have

$$ \begin{aligned} c_{n+2}&=\frac{1}{G_{1}(n+1)(n+2)}\left[ G_{2}(n+1)c_{n+1}+G_{3}\sum _{i=0}^{n}\sum _{q=0}^{i}(n-i+1)c_{q}c_{i-q}c_{n-i+1}\right. \\&\left. \quad +\,G_{4}c_{n}+G_{5}\sum _{i=0}^{n}\sum _{q=0}^{i}c_{q}c_{i-q}c_{n-i}+\upsilon \sum _{i=0}^{n}\sum _{q=0}^{i}\sum _{r=0}^{q}\sum _{a=0}^{r}c_{a}c_{r-a}c_{q-r}c_{i-q}c_{n-i}\right] .\end{aligned}$$
(3.6)

According to the Eq. (3.6), \(c_{m}\) \((m=3,4,5,\ldots )\) can be derived. For example

$$ \begin{aligned} c_{3}&=\frac{1}{6G_{1}}\left[ 2G_{2}c_{2}+G_{3}(2c_{0}^{2}c_{2}+2c_{0}c_{1}^{2})+G_{4}c_{1}+3G_{5}c_{0}^{2}c_{1}+5\upsilon c_{0}^{4}c_{1}\right] \\&=\frac{1}{6G_{1}}\left[ (2G_{2}+2G_{3}c_{0}^{2})\left( \frac{-(G_{2}c_{1}+G_{3}c_{0}^{2}c_{1}+G_{4}c_{0}+G_{5}c_{0}^{3}+\upsilon c_{0}^{5})}{2G_{1}}\right) \right. \\&\left. \quad +\,2G_{3}c_{0}c_{1}^{2}+G_{4}c_{1}+3G_{5}c_{0}^{2}c_{1}+5\upsilon c_{0}^{4}c_{1}\right] . \end{aligned} $$
(3.7)

It is generally true that the power series solution has no practical significance for the Eq. (2.1). Therefore, it is necessary to prove the convergence of the power series solution. Based on the results provided in Rudin (2004), the Eq. (3.6) can be enlarged as

$$ \begin{aligned} |c_{n+2}|&\le K\left[ |c_{n+1}|+\sum _{i=0}^{n}\sum _{q=0}^{i}|c_{q}||c_{i-q}||c_{n-i+1}|+|c_{n}|+\sum _{i=0}^{n}\sum _{q=0}^{i}|c_{q}||c_{i-q}||c_{n-i}|\right. \\&\left. \quad +\sum _{i=0}^{n}\sum _{q=0}^{i}\sum _{r=0}^{q}\sum _{a=0}^{r}|c_{a}||c_{r-a}||c_{q-r}||c_{i-q}||c_{n-i}|\right] , \end{aligned} $$
(3.8)

in which \(K=max\{|G_{2}|,|G_{3}|,|G_{4}|,|G_{5}|,|v|\}\). Then we introduce a new power series as follows

$$ B(\xi )=\sum _{n=0}^{\infty }b_{n}\xi ^{n}, \quad b_{i}=|c_{i}|, (i=0,1,\ldots ). $$
(3.9)

From what has been discussed above, we have

$$ \begin{aligned} b_{n+2}&=K\left[ |c_{n+1}|+\sum _{i=0}^{n}\sum _{q=0}^{i}|c_{q}||c_{i-q}||c_{n-i+1}|+|c_{n}|+\sum _{i=0}^{n}\sum _{q=0}^{i}|c_{q}||c_{i-q}||c_{n-i}|\right. \\&\left. \quad +\sum _{i=0}^{n}\sum _{q=0}^{i}\sum _{r=0}^{q}\sum _{a=0}^{r}|c_{a}||c_{r-a}||c_{q-r}||c_{i-q}||c_{n-i}|\right] . \end{aligned} $$
(3.10)

It is easy to find that \(|c_{n}|\le b_{n}\), \(n=0,1,2,\ldots \). Then we can say that the series \(B(\xi )\) is a majorant series of Eq. (3.3). Next, if the positive radius of convergence of the series \(B(\xi )\) exists, the proof is complete. Considering expression Eq. (3.9), we obtain

$$ \begin{aligned} B(\xi )&=b_{0}+b_{1}\xi +K\left[ \sum _{n=0}^{\infty }|b_{n+1}|\xi ^{n+2}+\sum _{n=0}^{\infty }\sum _{i=0}^{n}\sum _{q=0}^{i}|b_{q}||b_{i-q}||b_{n-i+1}|\xi ^{n+2}\right. \\&\left. \quad +\sum _{n=0}^{\infty }\sum _{i=0}^{n}\sum _{q=0}^{i}|b_{q}||b_{i-q}||b_{n-i}|\xi ^{n+2}+\sum _{n=0}^{\infty }|b_{n}|\xi ^{n+2}\right. \\&\left. \quad +\sum _{n=0}^{\infty }\sum _{i=0}^{n}\sum _{q=0}^{i}\sum _{r=0}^{q}\sum _{a=0}^{r}|b_{a}||b_{r-a}||b_{q-r}||b_{i-q}||b_{n-i}|\xi ^{n+2}\right] \\&=b_{0}+b_{1}\xi +K[\xi B(\xi )+\xi ^{2}B(\xi )+\xi ^{2}B(\xi )^{3}+\xi B(\xi )^{3}+\xi ^{4}B(\xi )^{5}+N(\xi )]. \end{aligned} $$
(3.11)

Then the implicit functional equation with respect to \(\xi \) can be written as

$$ \mathbb {B}(\xi ,B)=B(\xi )-b_{0}-b_{1}\xi -K[\xi B(\xi )+\xi ^{2}B(\xi )+\xi ^{2}B(\xi )^{3}+\xi B(\xi )^{3}+\xi ^{4}B(\xi )^{5}+N(\xi )]=0. $$
(3.12)

We can know that \(\mathbb {B}\) is analytical in a neighborhood of \((0,b_{0})\). Furthermore, \(\mathbb {B}(0,b_{0})=0\) and \(\frac{\partial }{\partial B}(0,b_{0})\ne 0\). According to Rudin (2004), we reach the convergence (Fig. 3). Finally, \(p(\xi )\) can be changed as follows

$$ \begin{aligned} p(\xi )&=c_{0}+c_{1}\xi +c_{2}\xi ^{2}+\sum _{n=1}^{\infty }c_{n+2}\xi ^{n+2}\\&=\Bigg \{c_{0}+c_{1}(l_{1}x-vt+\theta _{1})+\frac{-(G_{2}c_{1}+G_{3}c_{0}^{2}c_{1}+G_{4}c_{0}+G_{5}c_{0}^{3}+\upsilon c_{0}^{5})}{2G_{1}}(l_{1}x-vt+\theta _{1})^{2} \\&\quad +\sum _{n=1}^{\infty }\frac{1}{G_{1}(n+1)(n+2)}\Bigg [G_{2}(n+1)c_{n+1}+G_{3}\sum _{i=0}^{n}\sum _{q=0}^{i}(n-i+1)c_{q}c_{i-q}c_{n-i+1}\\&\quad +\,G_{4}c_{n}+G_{5}\sum _{i=0}^{n}\sum _{q=0}^{i}c_{q}c_{i-q}c_{n-i}+\upsilon \sum _{i=0}^{n}\sum _{q=0}^{i}\sum _{r=0}^{q}\sum _{a=0}^{r}c_{a}c_{r-a}c_{q-r}c_{i-q}c_{n-i}\Bigg ]\\&\quad \times (l_{1}x-vt+\theta _{1})^{n+2}\Big \}e^{i(\alpha _{1}x+\beta t+\theta _{0})}. \end{aligned}$$
(3.13)
Fig. 3
figure 3

The explicit power series solutions of Eq. (3.13) at \(n=1\), \(c_{0}=1\), \(c_{1}=1\), \(c_{2}=1\), \(c_{3}\), \(l_{1}=1\), \(\alpha _{1}=1\), \(\phi =1\), \(\upsilon =1\), \(\mu =1\), \(v=2\), \(\alpha =0\), \(\beta =0\), \(\theta _{1}=0\)

Full size image

4 Linear stability analysis

It is easy to know that whether some nonlinear Schrödinger equation are modulationally stable or not by using the modulation instability (MI) analysis. Based on the linear stability analysis, the constant solutions of Eq. (2.1) have the following form

$$ q=q_{0}e^{i(kx+\omega t)}.$$
(4.1)

Substituting Eq. (4.1) into Eq. (2.1), we get

$$ \omega =-\phi k^{2}-(\alpha k-\mu )q_{0}^{2}+\upsilon q_{0}^{4},$$
(4.2)

where \(q_{0}\), \(\phi \), \(\mu \), \(\upsilon \) and k are all real constants. In order to find the linear stability analysis of Eq. (2.1), the constant solutions q can be written as

$$ q=(q_{0}+\vartheta \tilde{q})e^{i(kx+\omega t)}, $$
(4.3)

where \(\vartheta \) is a disturbance parameter, and \(\tilde{q}\) is defined as

$$ \tilde{q}=q_{1}e^{i(\hat{k} x-\varpi t)}+q_{2}e^{-i(\hat{k} x-\varpi t)}, $$
(4.4)

where \(q_{1}\) and \(q_{2}\) are both the coefficients of the linear combination, \(\hat{k}\) and \(\hat{\omega }\) are real disturbance wave numbers and real disturbance frequency, respectively. Substituting Eq. (4.3) into Eq. (2.1), we have

$$ M_{1}\tilde{q}+i\tilde{q}_{t}+iM_{2}\tilde{q}_{x}+\phi \tilde{q}_{xx}+M_{3}\tilde{q}^{*}=0, $$
(4.5)

where \(*\) means complex conjugate, and

$$ \begin{aligned}&M_{1}=-\omega -\phi k^{2}-2\alpha kq_{0}^{2}+2\mu q_{0}^{2}+3\upsilon q_{0}^{4},\\&M_{2}=2k\phi +\alpha q_{0}^{2},\\&M_{3}=-\alpha kq_{0}^{2}+\mu q_{0}^{2}+2\upsilon q_{0}^{4}. \end{aligned}$$
(4.6)

Then, we substitute Eq. (4.4) into Eq. (4.5) and linearize equations about \(q_{1}\) and \(q_{2}\) can be derived as

$$ \begin{aligned}&\psi _{11}q_{1}+\psi _{12}q_{2}=0,\\&\psi _{21}q_{1}+\psi _{22}q_{2}=0, \end{aligned} $$
(4.7)

in which

$$ \begin{aligned}&\psi _{11}=M_{1}+\varpi -M_{2}\hat{k}-\phi \hat{k}^{2},\\&\psi _{12}=M_{3},\\&\psi _{21}=M_{3},\\&\psi _{22}=M_{1}-\varpi +M_{2}\hat{k}-\phi \hat{k}^{2}. \end{aligned} $$
(4.8)

Equation (4.7) have nonzero solutions if and only if the determinant

$$\begin{aligned} \begin{vmatrix} \psi _{11}&\psi _{12} \\ \psi _{21}&\psi _{22} \end{vmatrix} =0. \end{aligned}$$
(4.9)

Substituting Eq. (4.8) into Eq. (4.9), we can obtain the following dispersion relation about \(\varpi \)

$$ \varpi =(2k\phi +\alpha q_{0}^{2})\hat{k}\pm \sqrt{\Delta }, $$
(4.10)

with

$$ \begin{aligned} \Delta =&\left[ (-\omega -\phi k^{2}-2\alpha kq_{0}^{2}+2\mu q_{0}^{2}+3\upsilon q_{0}^{4})-\phi \hat{k}^{2}+(-\alpha kq_{0}^{2}+\mu q_{0}^{2}+2\upsilon q_{0}^{4})\right] \\&\times \left[ (-\omega -\phi k^{2}-2\alpha kq_{0}^{2}+2\mu q_{0}^{2}+3\upsilon q_{0}^{4})-\phi \hat{k}^{2}-(-\alpha kq_{0}^{2}+\mu q_{0}^{2}+2\upsilon q_{0}^{4})\right] . \end{aligned}$$
(4.11)

If \(\Delta \ge 0\), \(\varpi \) is real and it is easy to know that the steady state is stable against small perturbation. Otherwise, when \(\Delta <0\), the \(\varpi \) is complex and the steady state are unstable.

5 Conclusions and discussions

In this paper, we mainly studied the quintic derivative nonlinear Schrödinger equation. On the one hand, different types of solutions of Eq. (2.1) which include singular solitons and dark solitons have derived by using the ansatz method. What is more, we also provide the explicit power series solutions for the equation by employing power series method. These solutions are presented via 3-dimensional plots and density plots with choosing some special parameters. On the other hand, we investigate the modulation instability (MI) analysis. In future, symmetries and conservation laws of the quintic derivative nonlinear Schrödinger equation are worth exploring.