Abstract
The paper proposes an adaptive coordinated control scheme on free-floating space manipulators at the dynamic level, with kinematic and dynamic uncertainties. The free-floating space manipulator can be controlled to realize the end-effector trajectory tracking task and the spacecraft attitude regulation task simultaneously, based on the carefully designed prescribed performance error transformations and the reaction null space. In face of nonlinearly parametric feature of the uncertain free-floating space manipulators, a novel attractive manifold control method is proposed by introducing the nonlinear filters on dynamics of the free-floating space manipulators. The parameter estimation error terms can converge to zero, independent of persistent excitation conditions. The proposed adaptive coordinated control scheme can guarantee that both the end-effector tracking error and the spacecraft attitude regulation error possess the prescribed control performances, in the presence of the nonlinearly parametric feature and the nonzero linear and angular momenta of the free-floating space manipulators. The simulation results show the effectiveness of the proposed control scheme.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Space manipulators are essential tools to realize unmanned on-orbit serving missions, such as on-orbit assembly, capture of a tumbling spacecraft and orbital debris removal. The space manipulator consists of base spacecraft and the mounted manipulator. There are three common control modes for the space manipulators: free-floating mode, attitude-controlled mode and free-flying mode [1]. For the free-floating mode, both position and attitude of the base spacecraft are not controlled by the actuators (e.g., thrusters, momentum wheels). The space manipulators are usually in the free-floating mode when they are close to the space targets. The reason is that if the actuators of the base spacecraft are suddenly firing, there may be a undesirable collision between the space manipulator and the space target [2]. Even through the momentum wheels are utilized in the base spacecraft such that the on-off mode of operation is avoided, the influence of the inaccurate and transient behavior of the attitude control system (ACS) to the on-orbit serving missions should not be overlooked, which means that it is preferable to turn off the ACS of the base spacecraft during the on-orbit serving missions [3]. Moreover, compared with the other control modes, the free-floating mode of the space manipulator can save the non-renewable fuel in the base spacecraft and hence can prolong the lifespan of the space manipulator, once the base spacecraft is actuated by thrusters [4].
It should be pointed out that the free-floating space manipulator (FFSM) possesses two salient features, and hence is distinct from the fixed-base robotic manipulators. First, the FFSM will encounter kinematic and dynamic uncertainties [5,6,7,8,9,10], when it is controlled to perform the on-orbit serving missions. However, the FFSM dynamics suffers from nonlinearly parametric issue, leading to infeasibility of the adaptive control schemes that rely on linear parameterization of the robotic dynamics [11]. Moreover, in several on-orbit serving missions, the spacecraft attitude of the FFSM should be maintained to the desired orientation to achieve the information communication between the Earth and the space manipulator, implying that the base spacecraft and the mounted manipulator should be coordinated controlled [12,13,14]. However, since the base spacecraft is not fixed and the space manipulator is in the free-floating mode, there exist coupling effects between the base spacecraft and the mounted manipulator [15,16,17]. Owing to the coupling effects of the FFSM, the manipulator motion will generate reaction torque toward the base spacecraft, resulting in the undesirable rotation of the base spacecraft, and the spacecraft attitude rotation in turn changes the end-effector pose of the FFSM. Therefore, it is highly desirable to investigate the coordinated control of the FFSMs to realize the end-effector pose tracking task and the spacecraft attitude regulation task simultaneously, subject to kinematic and dynamic uncertainties [18].
First, a great deal of theoretical progress has been made on the robust and adaptive control of the uncertain FFSM [19,20,21,22,23,24,25,26]. In face of the parameter uncertainties of the FFSM, an adaptive control scheme on the uncertain free-flying space manipulator is designed in [19] to achieve the end-effector trajectory tracking task. As for the FFSM, a novel control scheme named the normal-form-augmentation-based approach is proposed in [20], where the spacecraft motion is represented by an extended robotic manipulator, and correspondingly, the obtained kinematics and dynamics of the whole system can be linear toward physical parameters of the FFSM, which facilitates the adaptive controller design of the FFSM. However, for the above normal-form-augmentation-based approach, the spacecraft acceleration is required to obtain the extended robotic manipulator, and the kinematic uncertainties are also not considered [21]. In [22], a novel passivity-based adaptive control method is designed to realize trajectory tracking control of the FFSM with kinematic and dynamic uncertainties, without the need of spacecraft acceleration information. The carefully designed inverted chain controllers are also proposed in [23, 24] for the trajectory tracking of the uncertain FFSM. Notice that although the neural network can be also utilized to approximate the uncertain FFSM dynamics and to obtain the corresponding adaptive controller [25, 26], only the uniform ultimate boundedness of the end-effector tracking error is ensured, compared with the results in [19,20,21,22,23,24,25,26] ensuring zero-error trajectory tracking. The size of the neural network and the according computational burden will be also increased if the tracking accuracy is needed to be improved.
Besides, notice that the methods in [20,21,22,23,24,25,26] depend on the assumption on the zero linear and angular momenta of the FFSM. In face of this problem, an optimal control scheme on the free-flying space manipulator is proposed in [27], where the nonzero and time-varying linear and angular momenta of the space manipulator are considered. As for the FFSM, the usage of the spacecraft thruster is reduced to prolong the lifespan of the FFSM, and the FFSM end-effector is free from the contact force and torque when the FFSM is not in contact with the space targets. Besides, the external disturbances imposed on the FFSM (such as the gravity gradient torque) are small since the FFSM is maneuvered in the micro-gravity space environment [28, 29]. This means that the linear and angular momenta of the FFSM can be viewed as constants within a time interval, as long as the FFSM is not in contact with the space targets. In [30], a feedback-linearization-based impedance control scheme is constructed on the free-floating space manipulator with the known and nonzero linear/angular momenta. A torque feedback control scheme on the FFSM is then designed in [31], and the effects of the nonzero linear/angular momenta of the FFSM can be compensated by the according adaptive laws. However, the control schemes in [30, 31] rely on the deterministic model of the FFSM.
Unfortunately, several control schemes (such as the results in [19,20,21,22,23,24,25,26, 30, 31]) only take the end-effector trajectory tracking into account, and the base spacecraft regulation is not considered. Inspired by reaction null-space control method [32,33,34], an adaptive reaction null-space control method is proposed in [35] to realize the coordinated control of the uncertain FFSM. Compared with the previous reaction null-space control method, the adaptive reaction null-space control method does not require additional high sensor measurements to obtain the exact parameter values of the FFSM [35]. However, the proposed control schemes in [35] can only lower the effects of the reaction force caused by robotic motion to the base spacecraft, and the spacecraft attitude regulation is not considered. This implies that the spacecraft attitude would possibly deviate from the desired orientation if the control schemes in [35] are utilized. Xu et al. [36] go further to propose a novel adaptive reaction null-space control scheme on the uncertain FFSM, such that the end-effector trajectory tracking task and the spacecraft attitude regulation task can be realized simultaneously. However the adaptive reaction null-space control schemes in [35, 36] are derived only at the kinematic level. Besides, the end-effector attitude tracking is not considered in [36], which is essential to accomplish several on-orbit serving missions such as the orbital capture of the space targets.
Moreover, to realize the on-orbit serving missions, the FFSM needs to possess good transient and steady control performance, such as fast convergence speed, small overshoot and small steady error [37,38,39]. In recent years, prescribed performance control (PPC) has been presented in [40,41,42,43], which renders the tracking or regulation error converge with arbitrary large convergence speed and arbitrary small overshoot, to a sufficient small residual set. This method has been successfully applied into the marine surface vessels [44], the servo mechanisms [45,46,47] and the vehicle suspensions [48]. A funnel controller with the smooth dead-zone inverse is proposed in [49] to realize the joint-space tracking control of the robotic manipulator with the asymmetric dead zone. A neural-network-based controller is constructed in [50] to render the joints of the robotic manipulator track the desired joint-space trajectory, without the need of the inverse of the estimate of the inertia matrix. Karayiannidis and Doulgeri [51] propose a joint regulation/tracking control scheme on robotic manipulators with prescribed control performance, without exact parameter information of robotic manipulators. A more general control framework is derived in [52] to realize prescribed performance trajectory tracking of the fully actuated Euler–Lagrange system, where the Nussbaum function is utilized to guarantee the convergence of the tracking error. In [53], a dynamic learning scheme with neural network approximator is designed for the uncertain robotic manipulators, where the trajectory tracking error in the joint space can possess prescribed control performance and the convergence of the neural network weight estimates can be ensured based upon specific partial persistent excitation condition. A joint-space prescribed performance PID control scheme is proposed for uncertain robotic manipulators with actuator faults [54]. Yang et al. [55] propose a novel neural-network-based control scheme on the bimanual robots, such that the grasped object can follow the reference trajectory in the task space with the guaranteed control performance. The prescribed performance control method can be also applied into force/position control of the robotic manipulators [56], such that the robotic manipulator can remain contact with the planar surface and track the desired end-effector pose trajectory simultaneously.
However, the literature [49,50,51,52,53,54,55,56] focuses on prescribed performance control of the fixed-base robotic manipulators. Due to the kinematic and dynamic couplings of the FFSM, the spacecraft attitude regulation and the end-effector pose tracking are two interacted tasks. Therefore, it is infeasible to employ the control scheme on the fixed-base robotic manipulator into the FFSM [57]. Recently, Zhou et al. [58] propose a robust prescribed performance control scheme on the uncertain FFSM, where a linear switching surface is utilized to cope with kinematic and dynamic uncertainties. However, the control method in [58] relies on the assumption that angular velocity and angular acceleration of the FFSM are both bounded in priori, and besides only the end-effector trajectory tracking task of the FFSM is considered. Therefore, it deserves further study on prescribed performance coordinated control of the uncertain FFSM, such that the spacecraft attitude regulation error and the end-effector trajectory tracking error can meet the corresponding prescribed control performances, in the presence of the nonlinearly parametric feature and the nonzero linear and angular momenta.
This paper is devoted to the adaptive coordinated control of the uncertain FFSM, subject to the nonlinearly parametric feature and the nonzero linear and angular momenta. The contributions of this paper are summarized as follows:
(i) A coordinated control scheme on the FFSM is designed to accomplish two coupled control tasks simultaneously, that is, the spacecraft attitude regulation and the end-effector pose tracking. This means that the proposed control scheme differs from those in [49,50,51,52,53,54,55,56] that focuses on the fixed-base robotic manipulators. By means of the adaptive reaction null space and the prescribed performance functions, both the spacecraft attitude regulation error and the end-effector pose tracking error can meet the respective prescribed performance requirements and converge to zero, and therefore, the couplings effects of the FFSM are overcome. The effects of the uncertain kinematic parameter, and the nonzero linear and angular momenta are attenuated by a series of carefully designed updated laws. Hence, the proposed control scheme is distinct from the control schemes in [35] and [58] (which cannot stabilize the spacecraft attitude).
(ii) A novel attractive manifold control method is proposed to cope with nonlinear parameterization of the FFSM. Notice that for the FFSM, several adaptive control methods based upon linear parameterized model are inapplicable. Therefore, a nonlinear filter on the FFSM dynamics is constructed, and the estimate of the dynamic parameter is updated by the estimation error of the joint velocity. Since the updated law on the dynamic parameter is not designed directly on the FFSM dynamics, the nonlinearly parametric issue of the FFSM is overcome. Furthermore, the proposed attractive manifold control method renders the parameter estimation error terms converge to zeros, independent of the persistent excitation conditions, implying that the influences of the dynamic uncertainties are attenuated. By means of the proposed attractive manifold method, the control input can be constructed at the dynamic level and ensures zero-error regulation/tracking, compared with the control schemes in [35, 36] (which are only designed at the kinematic level).
The remaining part of this paper is organized as follows: The kinematic and dynamic modeling of the FFSM is provided in Sect. 2. The adaptive coordinated control scheme on the FFSM with prescribed control performance is designed in Sect. 3. The according simulation results are shown in Sect. 4. The conclusions are given in Sect. 5.
2 Preliminaries
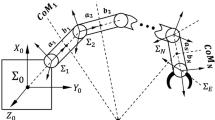
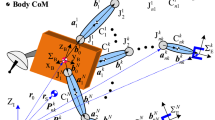
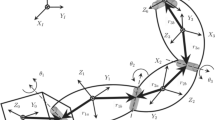
The motion of the FFSM is determined by the motion of the base spacecraft and the motion of the mounted manipulator. First, denote \(q_{m} \in {\mathbb {R}}^{m_{1}}\) as the joint angle of the FFSM, \(p_{e} \in {\mathbb {R}}^{m_{2}}\) as the FFSM end-effector position in the inertia frame, \(q_{e} \in {\mathbb {R}}^{m_{3}}\) as the FFSM end-effector attitude in the inertia frame, \(p_{b} \in {\mathbb {R}}^{m_{2}}\) as the position of the base spacecraft centroid in the inertia frame, \(q_{b} \in {\mathbb {R}}^{m_{3}}\) as the attitude of the base spacecraft in the inertia frame and \(z_{e} = \mathrm{{col}}(p_{e},q_{e}) \in {\mathbb {R}}^{m_{2} + m_{3}}\) as the FFSM end-effector pose in the inertia frame. Note that \(m_{2} = m_{3} = 3\) when the spatial FFSM is employed, and in this condition, the variables \(q_{b}\) and \(q_{e}\) can be viewed as the modified Rodriguez parameters (MRPs) of the base spacecraft attitude and the end-effector attitude, respectively. Besides, \(m_{2} = 2\) and \(m_{3} = 1\) when the planar FFSM is considered, and in this condition, the variables \(q_{b}\) and \(q_{e}\) are the rotation angles of the base spacecraft and the end-effector. Then, denote \(q \triangleq \mathrm{{col}}(q_{b},q_{m}) \in {\mathbb {R}}^{m_{1} + m_{3}}\) and \(w \triangleq \mathrm{{col}}(w_{b},w_{m}) \in {\mathbb {R}}^{m_{1} + m_{3}}\).
2.1 Kinematic modeling of the FFSMs
Denote \(v_{b} \triangleq {\dot{p}}_{b} \in {\mathbb {R}}^{m_{2}}\) and \(w_{b} \in {\mathbb {R}}^{m_{3}}\) as the linear and angular velocities of the base spacecraft satisfying the following equation
where the matrix \(L_{b}(q_{b}) \in {\mathbb {R}}^{m_{3} \times m_{3}}\) with \(L_{b}^{T}L_{b} \ge \lambda _{b}{\mathbf {E}}_{m_{3}}\) and \(\lambda _{b} > 0\).
Additionally, the FFSM end-effector position and attitude \({p}_{e}\) and \({q}_{e}\) obey the following kinematic equations, respectively [57]
where \(w_{m} \in {\mathbb {R}}^{m_{1}}\) is the joint velocity of the FFSM, \(J_{pb}(q) \in {\mathbb {R}}^{m_{2} \times m_{3}}\), \(J_{pm}(q) \in {\mathbb {R}}^{m_{2} \times m_{1}}\), \(J_{qb}(q) \in {\mathbb {R}}^{m_{3} \times m_{3}}\) and \(J_{qm}(q) \in {\mathbb {R}}^{m_{3} \times m_{1}}\) are the corresponding Jacobian matrices, and \(v_{0} \in {\mathbb {R}}^{m_{2}}\) is the nonzero constant velocity stemming from the nonzero linear momentum of the FFSM.
The kinematic equations of the FFSM (2a)–(2b) can be also rewritten in a compact form as
where \(J_{b}(q) = [J_{pb}(q);J_{qb}(q)] \in {\mathbb {R}}^{(m_{2} + m_{3}) \times m_{3}}\), \(J_{m}(q) = [J_{pm}(q);J_{qm}(q)] \in {\mathbb {R}}^{(m_{2} + m_{3}) \times m_{1}}\), and \({\bar{v}}_{0} = \mathrm{{col}}(v_{0},{\mathbf {0}}_{m_{3}})\), and \(z_{e}\) is the FFSM end-effector pose in the inertia frame defined before.
For the kinematics of the FFSM (3), the following property holds.
Property 1
The kinematic equation (3) of the FFSM is linear toward parameter \(\theta _{z} \in {\mathbb {R}}^{n_{1}}\), that is,
where \(Y_{z}(q,w) \in {\mathbb {R}}^{(m_{2} + m_{3}) \times n_{1}}\) is the according regressor matrix.
2.2 Dynamic modeling of the FFSMs
The FFSM dynamics is formulated as [57]:
where \({\dot{w}}_{b} \in {\mathbb {R}}^{m_{3}}\) is angular acceleration of the base spacecraft, \({\dot{w}}_{m} \in {\mathbb {R}}^{m_{1}}\) is joint acceleration of mounted manipulator, \(u_{m} \in {\mathbb {R}}^{m_{1}}\) is input torque of the mounted manipulator, \(M_{bb}(q,p_{b}) \in {\mathbb {R}}^{m_{3} \times m_{3}}\) is inertia matrix of the base spacecraft, \(M_{mm}(q) \in {\mathbb {R}}^{m_{1} \times m_{1}}\) is inertia matrix of the mounted manipulator, \(M_{bm}(q,p_{b}) \in {\mathbb {R}}^{m_{3} \times m_{1}}\) is coupled inertia matrix between the base spacecraft and the mounted manipulator, \(C_{bb}(q,w,p_{b},v_{b})\)\(\in {\mathbb {R}}^{m_{3} \times m_{3}}\) is centrifugal and Coriolis matrix of the base spacecraft, \(C_{mm}(q,w,p_{b})\)\(\in {\mathbb {R}}^{m_{1} \times m_{1}}\) is centrifugal and Coriolis matrix of the mounted manipulator, and \(C_{bm}(q,w,p_{b},v_{b})\)\(\in {\mathbb {R}}^{m_{3} \times m_{1}}\) and \(C_{mb}(q,w,p_{b},v_{b}) \in \)\({\mathbb {R}}^{m_{1} \times m_{3}}\) are coupled centrifugal and Coriolis matrices between the mounted manipulator and the base spacecraft.
Notice that Eq. (5a) depicts the dynamic couplings between the spacecraft attitude motion and the mounted manipulator motion [59]. Due to the fact that the space manipulator is in the free-floating mode, the base spacecraft is driven by the joint motion of the mounted manipulator. Hence, Eq. (5a) can be rewritten as
where
is the reaction torque exerted on the base spacecraft by the manipulator motion [59].
For the sake of simplicity, Eqs. (5a)–(5b) can be rewritten as
where \({u} \triangleq \mathrm{{col}}({\mathbf {0}}_{m_{3}};u_{m}) \in {\mathbb {R}}^{m_{1} + m_{3}}\), and the matrices \(M(q,p_{b})\)\(\in {\mathbb {R}}^{(m_{1} + m_{3}) \times (m_{1} + m_{3})}\) and \(C(q,w,p_{b},v_{b})\)\(\in {\mathbb {R}}^{(m_{1} + m_{3}) \times (m_{1} + m_{3})}\) are
Note that the matrix M is uniformly bounded and positive definite [22]. This means that there exist \(\lambda _{M,\mathrm{{min}}}\)\(> 0\) and \(\lambda _{M,\mathrm{{max}}} > 0\) such that \(\lambda _{M,\mathrm{{min}}}{\mathbf {E}}_{m_{1} + m_{3}}< M < \lambda _{M,\mathrm{{max}}}{\mathbf {E}}_{m_{1} + m_{3}}\). It can be seen in Eqs. (5a)–(5b) and (8) that the matrices in the FFSM dynamics contain the information on the centroid position and the linear velocity of the base spacecraft. For the sake of simplicity, the variables in the matrices, like \(M(q,p_{b})\) and \(C(q,w,p_{b},v_{b})\), will be omitted when there is no confusion in the context.
From (5a)–(5b), it can be seen that there exist dynamic couplings between the base spacecraft and the mounted manipulator. Substitute the spacecraft angular acceleration \({\dot{w}}_{b}\) in (5a) into (5b), and we can obtain the reduced form of the FFSM dynamics as [4]:
where the matrices \(M_{mm}^{*} \in {\mathbb {R}}^{m_{1} \times m_{1}}\), \(C_{mb}^{*} \in {\mathbb {R}}^{m_{1} \times m_{3}}\) and \(C_{mm}^{*}\)\(\in {\mathbb {R}}^{m_{1} \times m_{1}}\) are
For the FFSM dynamics (8), the following property holds.
Property 2
The matrices and vectors in the FFSM dynamics (8) are linear toward dynamic parameter \(\theta _{d} \in {\mathbb {R}}^{n_{2}}\), and correspondingly denote
where \(\varsigma _{1} \in {\mathbb {R}}^{m_{1} + m_{3}}\), \(\varsigma _{2} \in {\mathbb {R}}^{m_{1} + m_{3}}\), \(\varsigma _{3} \in {\mathbb {R}}^{m_{1} + m_{3}}\), matrix \({\dot{M}} \in {\mathbb {R}}^{(m_{1} + m_{3}) \times (m_{1} + m_{3})}\) is defined as \({\dot{M}}\)\(\triangleq \frac{d M}{d t}\), and \(Y_{d}(q,w,p_{b},v_{b},\varsigma _{1},\varsigma _{2},\varsigma _{3}) \in {\mathbb {R}}^{(m_{1} + m_{3}) \times n_{2}}\) is the corresponding regressor matrix.
2.3 Principle of the angular momentum conservation
Note that the space manipulator is in the free-floating mode, and therefore, the FFSM motion obeys the principle of angular momentum conservation, which can be formulated as [36]:
where \(A_{0} \in {\mathbb {R}}^{m_{3}}\) is nonzero constant angular momentum of the FFSM, \(H_{bb}(q,p_{b}) \in {\mathbb {R}}^{m_{3} \times m_{3}}\) and \(H_{bm}(q,p_{b})\)\(\in {\mathbb {R}}^{m_{3} \times m_{1}}\).
Then, the following property holds [22].
Property 3
The angular momentum conservation equation (13) is linear to the parameter \(\theta _{b} \in {\mathbb {R}}^{n_{3}}\), that is,
where \(Y_{b} \in {\mathbb {R}}^{m_{3} \times n_{3}}\) is the corresponding regressor matrix.
It is noted from (4) and (14) that \(v_{0}\) and \(A_{0}\) are components of \(\theta _{z}\) and \(\theta _{b}\), respectively. Besides, based upon (13) and (14), it is obtained that
Remark 1
In several on-orbit serving missions, it is desirable to reduce the usage of the actuators of the base spacecraft. This means that the space manipulator is usually in the free-floating mode during the on-orbit serving missions. This is because when the space manipulator is near the space target, any abrupt action of the actuators of the base spacecraft may result in the unwanted collision between the space manipulator and the space target [2]. Even through the base spacecraft is equipped with the momentum wheels, it is still preferable to close the ACS of the base spacecraft during the on-orbit serving missions, owing to the inaccurate and transient behavior of the ACS [3]. Moreover, when the base spacecraft is actuated by the thrusters, the non-renewable fuels in the base spacecraft can be saved and the lifespan of the space manipulator can be prolonged in the free-floating mode [4].
Furthermore, as long as the FFSM end-effector is not in contact with the space targets, the FFSM will be free from the contact force and torque. Moreover, the FFSM is maneuvered in the micro-gravity environment, and the external disturbances exerted on the FFSM, such as the gravity gradient, are small. In all, the linear and angular momenta of the FFSM can be viewed as constants within a time interval.
Remark 2
As pointed out in [20, 22], when the FFSM is deterministic, the control methods that are designed for fixed-base robotic manipulators are also applicable into the FFSMs based upon the reduced form of the FFSM dynamics (10) (see [32,33,34] and references therein). However, note that the matrices \(M_{mm}^{*}\) (11a), \(C_{mb}^{*}\) (11b) and \(C_{mm}^{*}\) (11c) contain the matrix \(M_{bb}^{-1}\), the inverse of the matrix \(M_{bb}\). This means that the reduced form of the FFSM dynamics (10) is not linear toward the dynamic parameter \(\theta _{d}\), which differs from the fixed-base robotic manipulators. Since the previous adaptive control methods on the fixed-base robotic manipulators rely on the linear parameterization model, they are inapplicable to the uncertain FFSMs [22].
Moreover, the following lemma will be utilized hereinafter [60].
Lemma 1
For a function \(f(t): {\mathbb {R}}^{+} \rightarrow {\mathbb {R}}^{n}\), if it is uniformly continuous on t and satisfies \(f(t) \in {\mathcal {L}}^{p}(1 \le p \le +\,\infty )\), then it is obtained that \(\lim _{t \rightarrow +\infty }f(t) = {\mathbf {0}}_{n}\).
3 Adaptive prescribed performance coordinated control of the FFSMs
In this section, we construct a coordinated control scheme on the uncertain FFSM to achieve the end-effector trajectory tracking task and the spacecraft attitude regulation task simultaneously. Denote \(p_{e,d}(t) \in {\mathbb {R}}^{m_{2}}\) and \(q_{e,d}(t) \in {\mathbb {R}}^{m_{3}}\) as the desired end-effector position and attitude trajectory in the inertia frame, respectively, denote \(z_{e,d}(t) \triangleq \mathrm{{col}}(p_{e,d}(t),q_{e,d}(t)) \in {\mathbb {R}}^{m_{2} + m_{3}}\) as the desired end-effector pose trajectory in the inertia frame, and denote \(q_{b,d} \in {\mathbb {R}}^{m_{3}}\) as the desired attitude of the base spacecraft in the inertia frame. Accordingly, denote the end-effector position tracking error as \(\varDelta p_{e}(t) \triangleq p_{e}(t) - p_{e,d}(t) \in {\mathbb {R}}^{m_{2}}\), the end-effector attitude tracking error as \(\varDelta q_{e}(t) \triangleq q_{e}(t) - q_{e,d}(t) \in {\mathbb {R}}^{m_{3}}\), the end-effector pose tracking error as \(\varDelta z_{e}(t) = [\varDelta p_{e}(t);\varDelta q_{e}(t)]\)\(\in {\mathbb {R}}^{m_{2}+m_{3}}\), and the spacecraft attitude regulation error as \(\varDelta q_{b}(t) \triangleq q_{b}(t) - q_{b,d} \in {\mathbb {R}}^{m_{3}}\). The proposed coordinated control scheme renders the FFSM end-effector track the desired trajectory \(z_{e,d}(t)\) and the spacecraft attitude converge to the desired attitude \(q_{b,d}\) simultaneously. This means that for the end-effector pose tracking error \(\varDelta z_{e}(t) \triangleq z_{e}(t) - z_{e,d}(t) \in {\mathbb {R}}^{m_{2} + m_{3}}\), the time derivative of the end-effector pose tracking error \(\varDelta {\dot{z}}_{e}(t) \triangleq {\dot{z}}_{e}(t) - {\dot{z}}_{e,d}(t) \in {\mathbb {R}}^{m_{2} + m_{3}}\), the spacecraft attitude regulation error \(\varDelta q_{b}(t) \triangleq q_{b}(t) - q_{b,d} \in {\mathbb {R}}^{m_{3}}\), and the spacecraft angular velocity \(w_{b}(t) \in {\mathbb {R}}^{m_{3}}\), the FFSM should be controlled to realize \(\lim _{t \rightarrow +\infty }\)\(\varDelta z_{e}(t) = {\mathbf {0}}_{m_{2} + m_{3}}\), \(\lim _{t \rightarrow +\infty }\varDelta {\dot{z}}_{e}(t) = {\mathbf {0}}_{m_{2} + m_{3}}\), \(\lim _{t \rightarrow +\infty }\)\(\varDelta q_{b}(t)\)\(= {\mathbf {0}}_{m_{3}}\), and \(\lim _{t \rightarrow +\infty }w_{b}(t) = {\mathbf {0}}_{m_{3}}\). Note that the reference end-effector pose trajectory \(z_{e,d}(t)\) and the corresponding time derivatives \({\dot{z}}_{e,d}(t)\) and \(\ddot{z}_{e,d}(t)\) are all uniformly bounded.
3.1 Prescribed performance control and error transformations
It should be pointed out that compared with the control schemes in [35, 36], both the end-effector pose tracking error \(\varDelta z_{e}(t)\) and the spacecraft attitude regulation error \(\varDelta q_{b}(t)\) should satisfy the prescribed control performances in this paper. To be specific, for the spacecraft attitude regulation error \(\varDelta q_{b}(t) = [\varDelta q_{b,1}(t);\ldots ;\)\(\varDelta q_{b,m_{3}}(t)]\) and the end-effector tracking error \(\varDelta z_{e}(t) = \)\([\varDelta z_{e,1}(t);\ldots ;\varDelta z_{e,m_{2}+m_{3}}(t)]\), they should satisfy the following prescribed performance constraints which are defined element-wisely as
for \(i = 1,\ldots ,m_{3}\), and
for \(i = 1,\ldots ,m_{2}+m_{3}\) [40, 41]. In (16)–(17), \(\rho _{b,i}(t)\) and \(\rho _{z,i}(t)\) are decaying functions of time defined as
In Eqs. (16)–(17) and (18a)–(18b), \(\rho _{b,i}^{0}\), \(\rho _{z,i}^{0}\), \(\rho _{b,i}^{\infty }\), \(\rho _{z,i}^{\infty }\), \(\beta _{b,i}\), \(\beta _{z,i}\), \(\sigma _{b,i}\) and \(\sigma _{z,i}\) are all positive constants with \(\rho _{b,i}^{\infty } < \rho _{b,i}^{0}\) and \(\rho _{z,i}^{\infty } < \rho _{z,i}^{0}\), which means that the functions \(\rho _{b,i}(t)\) and \(\rho _{z,i}(t)\) are both positive at all the time with \(\rho _{b,i}(t) \ge \rho _{b,i}^{\infty }\) and \(\rho _{z,i}(t) \ge \rho _{z,i}^{\infty }\), and are both monotonically decreasing. The parameters \(\sigma _{b,i}\) and \(\sigma _{z,i}\) are set such that \(0 < \sigma _{b,i} \le 1\) and \(0 < \sigma _{z,i} \le 1\).
Notice that the parameters \(\rho _{b,i}^{0}\) and \(\rho _{z,i}^{0}\) are the initial values of functions \(\rho _{b,i}(t)\) and \(\rho _{z,i}(t)\), respectively, and their values are chosen based upon the initial pose of the FFSM end-effector and the initial value of the desired trajectory. To be specific, the parameters \(\rho _{b,i}^{0}\) and \(\rho _{z,i}^{0}\) are set such that the relations (16) and (17) are satisfied at the initial instant, that is, \(|\varDelta q_{b,i}(0)| < \rho _{b,i}^{0}\) for \(i=1,\ldots ,m_{3}\) and \(|\varDelta z_{e,i}(0)| < \rho _{z,i}^{0}\) for \(i=1,\ldots ,m_{2} + m_{3}\).
Taking the derivatives of \(\rho _{b,i}(t)\) (18a) and \(\rho _{z,i}(t)\) (18b) yields
and correspondingly, it is obtained that \(\lim _{t \rightarrow +\infty }{\dot{\rho }}_{b,i}(t)\)\(= \lim _{t \rightarrow +\infty }{\dot{\rho }}_{z,i}(t) = 0\).
Based upon (16) and (17), denote that \(s_{b,i}(t) \triangleq \rho _{b,i}^{-1}(t)\varDelta q_{b,i}(t)\) and \(s_{z,i}(t) \triangleq \rho _{z,i}^{-1}(t)\varDelta z_{e,i}(t)\), and the prescribed performance error transformations on \(s_{b,i}(t)\) and \(s_{z,i}(t)\) are designed as
where the transformation functions \(R_{b,i}(\cdot )\) and \(R_{z,i}(\cdot )\) are constructed as
For the function \(R_{b,i}(\cdot )\), it satisfies \(R_{b,i}(\cdot ): (-\sigma _{b,i},1) \rightarrow (-\infty ,+\infty )\) when \(s_{b,i}(0) \ge 0\) and \(R_{b,i}(\cdot ): (-1,\sigma _{b,i}) \rightarrow (-\infty ,+\infty )\) when \(s_{b,i}(0) < 0\). It is also obtained from (21a) that the \(\psi _{b,i}(t) = 0\) if and only if \(s_{b,i}(t) = 0\), and \(\psi _{b,i}(t)\) approaches zero if and only if \(s_{b,i}(t)\) approaches zero. These properties also hold for the function \(R_{z,i}(\cdot )\).
Then, denote \(\psi _{b}(t) \triangleq \mathrm{{col}}(\psi _{b,1}(t),\ldots ,\psi _{b,m_{3}}(t)) = \mathrm{{col}}(R_{b,1}(s_{b,1}(t)),\ldots ,R_{b,m_{3}}(s_{b,m_{3}}(t))) \in {\mathbb {R}}^{m_{3}}\) and \(\psi _{z}(t) \triangleq \mathrm{{col}}(\psi _{z,1}(t),\ldots ,\psi _{z,m_{2}+m_{3}}(t)) = \mathrm{{col}}(R_{z,1}(s_{z,1}(t)),\ldots , R_{z,m_{2}+m_{3}}(s_{z,m_{2}+m_{3}}(t))) \in {\mathbb {R}}^{m_{2}+m_{3}}\). Invoking (20a)–(20b) and (21a)–(21b), the derivatives of \(\psi _{b}(t)\) and \(\psi _{z}(t)\) are
where \(\rho _{b} \triangleq \mathrm{{diag}}(\rho _{b,1},\ldots ,\rho _{b,m_{3}})\), \(\rho _{z} \triangleq \mathrm{{diag}}(\rho _{z,1},\ldots ,\)\(\rho _{z,m_{2}+m_{3}})\), \(\rho _{b}^{-1} = \mathrm{{diag}}(\rho _{b,1}^{-1},\)\(\ldots ,\rho _{b,m_{3}}^{-1})\), \(\rho _{z}^{-1} = \mathrm{{diag}}(\rho _{z,1}^{-1}\)\(,\ldots ,\rho _{z,m_{2}+m_{3}}^{-1})\), \({\dot{\rho }}_{b} = \mathrm{{diag}}({\dot{\rho }}_{b,1},\ldots ,{\dot{\rho }}_{b,m_{3}})\), \({\dot{\rho }}_{z} = \mathrm{{diag}}(\)\({\dot{\rho }}_{z,1},\ldots ,\)\({\dot{\rho }}_{z,m_{2}+m_{3}})\), \(s_{b} \triangleq \rho _{b}^{-1}\varDelta q_{b} = \mathrm{{col}}(s_{b,1},\ldots ,s_{b,m_{3}})\), \(s_{z} \triangleq \rho _{z}^{-1}\varDelta z_{e}\)\(= \mathrm{{col}}(s_{z,1};\ldots ; \)\(s_{z,m_{2}+m_{3}})\), \(\varPhi _{b}\)\((s_{b},\rho _{b}) \triangleq \mathrm{{diag}}(\varPhi _{b,1}(s_{b,1},\rho _{b,1}),\ldots ,\varPhi _{b,m_{3}}(s_{b,m_{3}},\rho _{b,m_{3}}))\) with \(\varPhi _{b,i}\)\((s_{b,i},\rho _{b,i}) \triangleq \frac{d R_{b,i}(s_{b,i})}{d s_{b,i}}\rho _{b,i}^{-1}\), and \(\varPhi _{z}(s_{z},\rho _{z}) \triangleq \mathrm{{diag}}(\varPhi _{z,1}\)\((s_{z,1},\rho _{z,1}),\ldots ,\varPhi _{z,m_{2}+m_{3}}(s_{z,m_{2}+m_{3}},\rho _{z,m_{2}+m_{3}}))\) with \(\varPhi _{z,i}(s_{z,i},\rho _{z,i}) \triangleq \frac{d R_{z,i}(s_{z,i})}{d s_{z,i}}\rho _{z,i}^{-1}\). In addition, from the structure of \(R_{b,i}(\cdot )\) (21a) and \(R_{z,i}(\cdot )\) (21b), it is obtained that
once \(\Vert \psi _{b}(t)\Vert < +\infty \), and
once \(\Vert \psi _{z}(t)\Vert < +\infty \).
Remark 3
Note that the parameters \(\rho _{b,i}^{0}\), \(\rho _{z,j}^{0}\), \(\beta _{b,i}\), \(\beta _{z,j}\), \(\sigma _{b,i}\) and \(\sigma _{z,j}\), for \(i=1,\ldots ,m_{3}\) and \(j=1,\ldots ,m_{2} + m_{3}\), are essential to determine the control performance of the proposed scheme. First, the parameters \(\rho _{b,i}^{0}\), \(i=1,\ldots ,m_{3}\) and \(\rho _{z,j}^{0}\), \(j=1,\ldots ,m_{2} + m_{3}\), are selected such that the prescribed performance constraints (16)–(17) are satisfied at the initial instant. Then, parameters \(\beta _{b,i}\), \(i=1,\ldots ,m_{3}\), and \(\beta _{z,j}\), \(j=1,\ldots ,m_{2} + m_{3}\), are chosen to determine the transient regulation/tracking performance of the spacecraft attitude regulation error \(\varDelta q_{b}\) and the end-effector pose tracking error \(\varDelta z_{e}\), respectively. Once the prescribed performance constraints (16)–(17) are satisfied at all the time, it can be obtained that the signals \(\varDelta q_{b,i}(t)\) and \(\varDelta z_{e,j}(t)\), for \(i=1,\ldots ,m_{3}\) and \(j=1,\ldots ,m_{2} + m_{3}\), can converge with at least \(\exp (-\beta _{b,i}t)\) and \(\exp (-\beta _{z,j}t)\) exponential rates into the sets \(\varTheta _{b,i} \triangleq \{\varDelta q_{b,i} ~|~ |\varDelta q_{b,i}| < 2\rho _{b,i}^{\infty }\}\) and \(\varTheta _{b,j} \triangleq \{\varDelta z_{e,j}\)\(~|~ |\varDelta z_{e,j}| < 2\rho _{z,j}^{\infty }\}\), respectively. Moreover, the parameters \(\sigma _{b,i}\) and \(\sigma _{b,i}\), for \(i=1,\ldots ,m_{3}\) and \(j=1,\ldots ,m_{2}+m_{3}\), are selected to determine the overshoots of the signals \(\varDelta q_{b}\) and \(\varDelta z_{e}\). That is to say, the overshoots of the signals \(\varDelta q_{b,i}(t)\), \(i=1,\ldots ,m_{3}\), and \(\varDelta z_{e,j}(t)\), \(j=1,\ldots ,m_{2} + m_{3}\) will be less than \(\sigma _{b,i}\rho _{b,i}^{0}\) and \(\sigma _{z,i}\rho _{z,i}^{0}\), respectively, once the prescribed performance constraints (16)–(17) hold at all the time.
Remark 4
It should be noted that as long as \(\psi _{b}(t)\) is uniformly bounded, the spacecraft attitude regulation error \(\varDelta q_{b}(t)\) can satisfy prescribed control performance (16) [40, 41]. Similarly, as long as signal \(\psi _{z}(t)\) is uniformly bounded, the end-effector pose tracking error \(\varDelta z_{e}(t)\) can also satisfy prescribed control performance (17) [40, 41]. Therefore, we can turn to designing control schemes on the FFSMs such that the prescribed performance error signals \(\psi _{b}(t)\) and \(\psi _{z}(t)\) are uniformly bounded, which means that the corresponding prescribed control performances (16)–(17) can be satisfied. On the other hand, the end-effector pose tracking error \(\varDelta z_{e}(t)\) and the spacecraft attitude regulation error \(\varDelta q_{b}(t)\) of the FFSM should satisfy prescribed control performances (16)–(17) simultaneously in the presence of the nonlinearly parametric feature and the nonzero linear and angular momenta, which is different from the fixed-base robot manipulators. Therefore, it is worth investigating the adaptive prescribed performance coordinated control of the FFSM.
3.2 Adaptive prescribed performance control for spacecraft attitude regulation at the kinematic level
To regulate the spacecraft attitude, the following adaptive prescribed performance controller is designed at the kinematic level
where \({\hat{H}}_{bb} \triangleq {H}_{bb}(q_{b},{\hat{\theta }}_{b})\), \({\hat{H}}_{bm} \triangleq {H}_{bm}(q_{b},q_{m},{\hat{\theta }}_{b})\) and \({\hat{A}}_{0}\) are the estimates of \({H}_{bb}\), \({H}_{bm}\) and \({A}_{0}\), respectively, \({\hat{\theta }}_{b}\) is the estimate of the parameter \({\theta }_{b}\), matrix \({\hat{H}}_{bm}^{\dagger }\) is the pseudo-inverse of the matrix \({\hat{H}}_{bm}\), \(k_{b}\) is a positive constant, \(L_{b}\) is introduced in (1), and the signals \(\psi _{b}\) and \(\varPhi _{b}\) are introduced in the previous subsection. Note that \({\hat{A}}_{0}\) is the component of \({\hat{\theta }}_{b}\). The vector \(\xi \in {\mathbb {R}}^{m_{1}}\) in (25) is introduced to achieve trajectory tracking of the FFSM end-effector and will be designed in the next subsection.
Pre-multiplying both sides of (25) by the matrix \({\hat{H}}_{bm}\) leads to
where \({\hat{H}}_{bm}{\hat{H}}_{bm}^{\dagger } = {\mathbf {E}}_{m_{3}}\) and \({\hat{H}}_{bm}({\mathbf {E}}_{m_{1}} - {\hat{H}}_{bm}^{\dagger }{\hat{H}}_{bm}) = {\mathbf {0}}_{m_{3} \times m_{1}}\) are utilized. The corresponding sliding vector \(w_{m,r} \in {\mathbb {R}}^{m_{1}}\) is obtained as
Note that \({\hat{\theta }}_{b}\) is the estimate of \({\theta }_{b}\), and its updated law is designed as
where \(Y_{b}(q_{b},q_{m},w_{b},w_{m})\) is the regressor matrix that is defined in (14), and \(\varGamma _{1}\) is a positive constant. Denote the estimation error of \(\theta _{b}\) as \({\tilde{\theta }}_{b} \triangleq \theta _{b} - {\hat{\theta }}_{b}\). Correspondingly based upon (15) and (28), the derivative of \({\tilde{\theta }}_{b}\) is obtained as
It can be seen in (29) that \({\tilde{\theta }}_{b}(t)\) is uniformly bounded, and the parameter \(\varGamma _{1}\) determines the decaying rate of \({\tilde{\theta }}_{b}(t)\).
From (14) and (15), it is obtained that
Substituting (26) and (27) into (30) yields
In view of the Young’s inequality, it is obtained from (31) that
where \(\lambda _{hb} > 0\) is defined such that \(\lambda _{hb}^{2} {\mathbf {E}}_{m_{3}} > {\hat{H}}_{bb}^{-T}{\hat{H}}_{bb}^{-1}\). Substitute (31) into the attitude kinematics of the base spacecraft \({\dot{q}}_{b} = L_{b}w_{b}\) and the derivative of \(\varDelta q_{b} = q_{b} - q_{b,d}\) is obtained as
Substituting (33) into (22a) also yields
Then, denote a Lyapunov function candidate \(V_{b}\) as \(V_{b} \triangleq \frac{c_{1}}{2\varGamma _{1}}\Vert {\tilde{\theta }}_{b}\Vert ^{2} + \frac{1}{2}\Vert \psi _{b}\Vert ^{2}\), where \(c_{1} \triangleq \frac{4\lambda _{b}^{2}}{k_{b}}\). From (29), (32), (34), the Young’s inequality and the relation \(L_{b}L_{b}^{T}\)\(\ge \lambda _{b}{\mathbf {E}}_{m_{3}}\), the derivative of \(V_{b}\) is scaled as
where \(c_{2} \triangleq \mathrm{{min}}\{\frac{1}{12k_{b}},\frac{c_{1}}{12\lambda _{hb}^{2}}\}\) and \(c_{3} > 0\) is set such that \(c_{3}{\mathbf {E}}_{m_{1}} > (3c_{2} + \frac{2}{k_{b}}) \lambda _{hb}^{2} {\hat{H}}_{bm}^{T}{\hat{H}}_{bm}\).
3.3 Adaptive prescribed performance coordinated control of the FFSMs at the kinematic level
When the FFSM performs on-orbit serving missions, not only should the base spacecraft realize attitude regulation, but also the FFSM end-effector should track desired trajectory. In view of the virtual controller at the kinematic level (25), the auxiliary variable \(\xi \) is designed as
where \({\hat{U}} \triangleq {\mathbf {E}}_{m_{1}} - {\hat{H}}_{bm}^{\dagger }{\hat{H}}_{bm}\), \({\hat{J}}_{m} \triangleq {J}_{m}(q_{b},q_{m},{\hat{\theta }}_{z})\), and \(\hat{{\bar{v}}}_{0}\) are the estimates of \({U} \triangleq {\mathbf {E}}_{m_{1}} - {H}_{bm}^{\dagger }{H}_{bm}\), \({J}_{m}\) and \({\bar{v}}_{0}\), respectively, \({\hat{\theta }}_{z}\) is the estimate of the parameter \({\theta }_{z}\), \(k_{z}\) is a positive constant, \(k_{b} > 0\), \({\dot{z}}_{e,d}\) is time derivative of desired end-effector pose trajectory \(z_{e,d}(t)\), and the signals \(\psi _{z}\) and \(\varPhi _{z}\) are defined in Sect. 3.1. Note that the matrices \({\hat{H}}_{bm}^{\dagger }\), \({\hat{H}}_{bb}\), \(L_{b}\) and the vector \({\hat{A}}_{0}\) have been defined in (25), and the matrix \(({\hat{J}}_{m}{\hat{U}})^{\dagger }\) is the pseudo-inverse of the matrix \({\hat{J}}_{m}{\hat{U}}\).
Pre-multiplying both side of (25) by the matrix \({\hat{J}}_{m}\) and substituting (36) lead to
where the relation \({\hat{J}}_{m}{\hat{U}}({\hat{J}}_{m}{\hat{U}})^{\dagger } = {\mathbf {E}}_{m_{2}+m_{3}}\) is utilized. Then, from (3), (4), (27) and (37), the derivative of \(\varDelta z_{e}(t)\) is obtained as
where matrix \({\hat{J}}_{b} \triangleq J_{b}(q,{\hat{\theta }}_{z})\) is the estimate of the matrix \(J_{b}\), \({\tilde{\theta }}_{z} \triangleq \theta _{z} - {\hat{\theta }}_{z}\) is the estimation error of the parameter \(\theta _{z}\), and \(Y_{z}\) is the corresponding regressor matrix defined in (4). Substituting (38) into (22b) yields
Besides, in order to obtain the adaptive law on \({\hat{\theta }}_{z}\), denote vector \(\hat{{\dot{z}}}_{e}\) as
Correspondingly denote \(\tilde{{\dot{z}}}_{e} \triangleq {\dot{z}}_{e} - \hat{{\dot{z}}}_{e}\), and it is obtained from (3), (4) and (40) that
where \({\tilde{J}}_{b} \triangleq J_{b}(q_{b},q_{m},{\tilde{\theta }}_{z}) = J_{b} - {\hat{J}}_{b}\), \({\tilde{J}}_{m} \triangleq J_{m}(q_{b},q_{m},{\tilde{\theta }}_{z})\)\( = J_{m} - {\hat{J}}_{m}\) and \(\tilde{{\bar{v}}}_{0} \triangleq {\bar{v}}_{0} - \hat{{\bar{v}}}_{0}\) are estimation errors of \(J_{b}\), \(J_{m}\) and \({\bar{v}}_{0}\), respectively. Then, the corresponding adaptive law on \({\hat{\theta }}_{z}\) is designed as
where \(\varGamma _{2}\) is a positive constant. From (41) and (42), the derivative of estimation error \({\tilde{\theta }}_{z} = \theta _{z} - {\hat{\theta }}_{z}\) is obtained as
It is obtained from (43) that \({\tilde{\theta }}_{z}(t)\) is uniformly bounded, and the parameter \(\varGamma _{2}\) determines decaying rate of \({\tilde{\theta }}_{z}(t)\).
Then, denote a Lyapunov function candidate \(V_{z}\) as \(V_{z} \triangleq \frac{1}{2}\Vert \psi _{z}\Vert ^{2} + \frac{2}{k_{z}\varGamma _{2}}\Vert {\tilde{\theta }}_{z}\Vert ^{2}\). Taking the derivative of \(V_{z}\) along with (39) and (43) leads to
where the Young’s inequality is utilized and \(\mu _{J} > 0\) is set such that \(\mu _{J}{\mathbf {E}}_{m_{3} \times m_{3}} > {\hat{J}}_{b}^{T}{\hat{J}}_{b}\) and \(\mu _{J}{\mathbf {E}}_{m_{1} \times m_{1}} \ge {\hat{J}}_{m}^{T}{\hat{J}}_{m}\). Then, denote \(V_{k} \triangleq V_{z} + c_{4}V_{b}\), where \(c_{4} \triangleq \frac{4\mu _{J}}{c_{2}k_{z}}\). The derivative of \(V_{k}\) according to (35) and (44) is scaled as
where \(c_{5} \triangleq \frac{2\mu _{J}}{k_{z}} + c_{3}c_{4} > 0\).
3.4 Attractive manifold control of the FFSMs at the dynamic level
As pointed out in Remark 2 and [20,21,22], since the reduced form of the FFSM dynamics is nonlinearly parameterized toward dynamic parameter \(\theta _{d}\), several adaptive control methods on the uncertain fixed-base robotic manipulators, including the attractive manifold control method in [62,63,64,65], are inapplicable to the uncertain FFSMs. In this paper, we propose a novel attractive manifold control method to overcome nonlinearly parametric feature of the uncertain FFSMs. First, the estimate of w, that is, \({\hat{w}} \triangleq \mathrm{{col}}({\hat{w}}_{b},{\hat{w}}_{m})\), is introduced which obeys the following dynamic equation
where matrices \({\hat{M}} \triangleq M(q,{\hat{\theta }}_{d})\), \(\hat{{\dot{M}}} \triangleq {\dot{M}}(q,w,{\hat{\theta }}_{d})\) and \({\hat{C}} \triangleq C(q,w,{\hat{\theta }}_{d})\) are the estimates of the matrices M(q), \({\dot{M}}(q,w)\) and C(q, w), respectively, and \({\hat{\theta }}_{d}\) is the estimate of uncertain parameter \({\theta }_{d}\). Besides in (46), \({\tilde{w}} \triangleq w - {\hat{w}} = \mathrm{{col}}({\tilde{w}}_{b},{\tilde{w}}_{m})\) is the estimation error of w, \(k_{de}\) is a positive constant, and \(\eta _{x} \in {\mathbb {R}}^{m_{1} + m_{3}}\) is an auxiliary variable which will be designed later.
Subtracting (46) from (8) yields
where \({\tilde{M}} \triangleq M - {\hat{M}} = M(q,{\tilde{\theta }}_{d})\), \(\tilde{{\dot{M}}} \triangleq {\dot{M}} - \hat{{\dot{M}}} = {\dot{M}}(q,w,{\tilde{\theta }}_{d})\) and \({\tilde{C}} \triangleq C - {\hat{C}} = C(q,w,{\tilde{\theta }}_{d})\) is estimation errors of M, \({\dot{M}}\) and C, respectively, and \({\tilde{\theta }}_{d} \triangleq \theta _{d} - {\hat{\theta }}_{d}\) is estimation error of dynamic parameter \(\theta _{d}\). Note that from Property 2, the matrices in (12) are linear toward dynamic parameter \(\theta _{d}\). Therefore, based on (12), Eq. (47) can be rewritten as
where \(Y_{d,c} \triangleq Y_{d}(q,w,\dot{{\hat{w}}} - k_{de}{\tilde{w}},{\tilde{w}},{w})\) such that
For the regressor matrix \(Y_{d,c}\), an auxiliary variable \(Y_{d,f}(t) \in {\mathbb {R}}^{(m_{1} + m_{3}) \times n_{2}}\) is introduced and obeys the following dynamic equation
Then, for the estimate of the uncertain dynamic parameter \(\theta _{d}\), that is, \({\hat{\theta }}_{d}\), its adaptive law is designed as
where \(\varGamma _{3}\) is a positive constant. Correspondingly, the auxiliary variable \(\eta _{x}\) in (46) is designed as
where the adaptive law on \({\hat{\theta }}_{d}\) (51) is utilized.
Substituting (50) and (52) into (48) and adding term \(Y_{d,f}\dot{{\tilde{\theta }}}_{d} - k_{de}Y_{d,f}{\tilde{\theta }}_{d}\) on both sides of (48) yield
Denote
and therefore, Eq. (53) can be simplified as
It can be seen from (55) that the variable e(t) decays to zero with \(\exp (-k_{de} t)\) exponential convergence rate. Then, in view of (51) and (54), the derivative of \({\tilde{\theta }}_{d} = {\theta }_{d} - {\hat{\theta }}_{d}\) can be obtained as
Denote \(V_{\theta ,d} \triangleq \frac{1}{2\varGamma _{3}}\Vert {\tilde{\theta }}_{d}\Vert ^{2}\), and according to (56) and \(\lambda _{M,\mathrm{{min}}}{\mathbf {E}}_{m_{1} + m_{3}} < M\), the derivative of \(V_{\theta ,d}\) is bounded as
Since the signal e(t) converges to zero with \(\exp (-k_{de} t)\) exponential rate, it can be obtained that \(e(t) = e(0)\)\(\exp (-k_{de}t)\). Thus, it is further obtained from (57) that
It can be seen in (58) that \({\tilde{\theta }}_{d}(t)\) is uniformly bounded. The parameter \(\varGamma _{3}\) in (56) determines the decaying rate of \({\tilde{\theta }}_{d}(t)\).
Besides, according to (54) and the Young’s inequality, it is obtained that
where \(\lambda _{M,\mathrm{{min}}} > 0\) is defined in the preliminaries with \(\lambda _{M,\mathrm{{min}}}{\mathbf {E}}_{m_{1} + m_{3}} \le M(q)\).
To derive the control input, denote \(Y_{d,f} = [Y_{d,f1};\)\(Y_{d,f2}]\), where matrix \(Y_{d,f1} \in {\mathbb {R}}^{m_{3} \times n_{2}}\) is the first \(m_{3}\) rows of the matrix \(Y_{d,f}\) and matrix \(Y_{d,f2} \in {\mathbb {R}}^{m_{1} \times n_{2}}\) is the last \(m_{1}\) rows of the matrix \(Y_{d,f}\). Then, the dynamic equation of the variable \({\hat{w}}\) (46) can be rewritten as
where matrices \({\hat{M}}_{bb}\), \({\hat{M}}_{bm}\) and \({\hat{M}}_{mm}\) are the estimates of the matrices \({M}_{bb}\), \({M}_{bm}\) and \({M}_{mm}\), respectively, and vectors \(\zeta _{b} \in {\mathbb {R}}^{3}\) and \(\zeta _{m} \in {\mathbb {R}}^{m_{1}}\) are defined as
and matrices \({\hat{C}}_{bb}\), \({\hat{C}}_{bm}\), \({\hat{C}}_{mb}\), \({\hat{C}}_{mm}\), \(\hat{{\dot{M}}}_{bb}\), \(\hat{{\dot{M}}}_{bm}\) and \(\hat{{\dot{M}}}_{mm}\) in (61a)–(61b) are the estimates of the matrices \({C}_{bb}\), \({C}_{bm}\), \({C}_{mb}\), \({C}_{mm}\), \({{\dot{M}}}_{bb}\), \({{\dot{M}}}_{bm}\) and \({{\dot{M}}}_{mm}\), respectively.
Substituting \(\dot{{\hat{w}}}_{b}\) in (60a) into (60b) leads to
where
Then, denote \({\hat{w}}_{m,r} \triangleq {\hat{w}}_{m} - w_{m,c}\), where \({\hat{w}}_{m}\) is the estimate of \(w_{m}\) defined before, and correspondingly, \({\hat{w}}_{m,r}\) is the estimate of \(w_{m,r}\) which satisfies \({\hat{w}}_{m,r} = {w}_{m,r} - {\tilde{w}}_{m}\). The control input \(u_{m}\) is designed as
where \(k_{d}\) is a positive constant. Substituting (64) into (62) leads to
Then, denote \(V_{d} \triangleq \frac{\Vert {\tilde{\theta }}_{d}\Vert ^{2}}{2\varGamma _{3}} + \frac{\Vert e\Vert ^{2}}{k_{de}\lambda _{M,\mathrm{{min}}}} + \frac{\lambda _{M,\mathrm{{min}}}\Vert {\hat{w}}_{m,r}\Vert ^{2}}{4k_{d}}\). In view of (55), (56), (59), (65), the Young’s inequality and the relation \(\Vert w_{m,r}\Vert ^{2} = \Vert {\tilde{w}}_{m} + {\hat{w}}_{m,r}\Vert ^{2} \le \frac{3}{2}\Vert {\tilde{w}}_{m}\Vert ^{2} + 3\Vert {\hat{w}}_{m,r}\Vert ^{2}\), the derivative of \(V_{d}\) can be scaled as
Then, denote \(c_{t} \triangleq \frac{16c_{5}}{\lambda _{M,\mathrm{{min}}}}\) and \(V_{c} \triangleq V_{k} + c_{t}V_{d}\). The derivative of \(V_{c}\) in view of (45) and (66) is bounded as
3.5 Stability analysis
In view of the proposed adaptive prescribed performance coordinated control scheme (25), (28), (36), (42), (46), (50), (51) and (64), the following result is obtained.
Theorem 1
For the uncertain FFSM (3) and (5a)-(5b), the controller with the form (25), (28), (36), (42), (46), (50), (51) and (64) is employed. The parameters \(\rho _{b,i}^{0}\), \(i=1,\ldots ,m_{3}\), and \(\rho _{z,i}^{0}\), \(i=1,\ldots ,m_{2}+m_{3}\), are set such that \(|\varDelta q_{b,i}(0)| < \rho _{b,i}^{0}\) and \(|\varDelta z_{e,i}(0)| < \rho _{z,i}^{0}\). Then, the signals \({\psi }_{b}(t)\), \({\psi }_{z}(t)\), \({\tilde{\theta }}_{b}(t)\), \({\tilde{\theta }}_{z}(t)\), \({\tilde{w}}(t)\), \(Y_{d,f}(t)\), \({\tilde{\theta }}_{d}(t)\), e(t), \({\hat{w}}_{m,r}(t)\), \({w}_{m,r}(t)\), and w(t) are all uniformly bounded, and \(\lim _{t \rightarrow +\infty }\varDelta q_{b}(t) = {\mathbf {0}}_{m_{3}}\), \(\lim _{t \rightarrow +\infty }\)\(w_{b}(t) = {\mathbf {0}}_{m_{3}}\), \(\lim _{t \rightarrow +\infty }\)\(\varDelta z_{e}(t) = {\mathbf {0}}_{m_{2}+m_{3}}\), \(\lim _{t \rightarrow +\infty }\varDelta {\dot{z}}_{e}(t) = {\mathbf {0}}_{m_{2}+m_{3}}\), \(\lim _{t \rightarrow +\infty }Y_{b}(t)\)\({\tilde{\theta }}_{b}(t) = {\mathbf {0}}_{m_{3}}\), \(\lim _{t \rightarrow +\infty }Y_{z}(t){\tilde{\theta }}_{z}(t)\)\(= {\mathbf {0}}_{m_{2} + m_{3}}\), \(\lim _{t \rightarrow +\infty }\)\(Y_{d,f}(t){\tilde{\theta }}_{d}(t) = {\mathbf {0}}_{m_{1} + m_{3}}\), \(\lim _{t \rightarrow +\infty }\)\({\tilde{w}}(t) = {\mathbf {0}}_{m_{1} + m_{3}}\), and \(\lim _{t \rightarrow +\infty }\)\(w_{m,r}(t) = {\mathbf {0}}_{m_{1}}\). Moreover, the prescribed control performances on the spacecraft attitude regulation error \(\varDelta q_{b}(t)\) (16) and the end-effector pose tracking error \(\varDelta z_{e}(t)\) (17) are both satisfied.
Proof
The proof of Theorem 1 can be divided into the following three steps.
Step 1 The uniform boundedness of \(V_{c}(t)\).
The proof procedure of Step 1 is inspired by [44] and [61].
Notice that the relations (35), (45), (66) and (67) are obtained at the time instant t, based upon the boundedness of the signals \(\psi _{b}(t)\) and \(\psi _{z}(t)\) at the time instant t. Therefore, it should be proved first that the signals \(\varDelta q_{b}(t)\) and \(\varDelta z_{e}(t)\) meet the prescribed performance constraints (16) and (17) at all the time, respectively. Denote \(\chi (t) \triangleq (\varDelta q_{b}(t), \varDelta z_{e}(t))\).
Suppose that for the signal \(\chi (t)\), the prescribed performance constraints (16)–(17) are not satisfied at all the time. Hence, denote \(t_{M} \ge 0\) as the minimum time instant when \(\chi (t)\) violates the prescribed performance constraints (16)–(17). Due to the fact that \(|\varDelta q_{b,i}(0)| < \rho _{b,i}^{0}\) for \(i=1,\ldots ,m_{3}\) and \(|\varDelta z_{e,i}(0)| < \rho _{z,i}^{0}\) for \(i=1,\ldots ,m_{2}+m_{3}\), it is obtained that \(0 < t_{M} \le +\infty \). This means that the signal \(\chi (t)\) meets the prescribed performance constraints (16)–(17) when \(t \in [0,t_{M})\).
Besides, it can be seen in (29), (43), (55) and (65) that \(Y_{b}(t){\tilde{\theta }}_{b}(t) \in {\mathcal {L}}_{2}[0,t_{M})\), \(Y_{z}(t){\tilde{\theta }}_{z}(t) \in {\mathcal {L}}_{2}[0,t_{M})\), e(t) \(\in {\mathcal {L}}_{2}[0,t_{M})\), \({\hat{w}}_{m,r}(t) \in {\mathcal {L}}_{\infty }[0,t_{M})\). Correspondingly, from (56), it is further that \(Y_{d,f}(t){\tilde{\theta }}_{d}(t) \in {\mathcal {L}}_{2}[0,t_{M})\). Hence, it can be seen from (54) that \({\tilde{w}}(t) \in {\mathcal {L}}_{2}[0,t_{M})\), and accordingly for \(w_{m,r}(t) = {\hat{w}}_{m,r}(t) + {\tilde{w}}_{m}(t)\), we have \(w_{m,r}(t) \in {\mathcal {L}}_{2}[0,t_{M})\). According to the definition of \({\dot{\rho }}_{b}(t)\) (19a), \({\dot{\rho }}_{z}(t)\) (19b), \(s_{b}(t)\) and \(s_{z}(t)\), it is also obtained that \({\dot{\rho }}_{b}(t) \in {\mathcal {L}}_{\infty }[0,t_{M})\), \({\dot{\rho }}_{z}(t) \in {\mathcal {L}}_{\infty }[0,t_{M})\), \(s_{b}(t) \in {\mathcal {L}}_{\infty }[0,t_{M})\) and \(s_{z}(t) \in {\mathcal {L}}_{\infty }[0,t_{M})\), and correspondingly \({\dot{\rho }}_{b}(t)s_{b}(t) \in {\mathcal {L}}_{\infty }[0,t_{M})\) and \({\dot{\rho }}_{z}(t)s_{z}(t) \in {\mathcal {L}}_{\infty }[0,t_{M})\).
In addition, denote \(V_{\psi ,b} \triangleq \frac{1}{2}\Vert \psi _{b}\Vert ^{2}\) and \(V_{\psi ,z} \triangleq \frac{1}{2}\Vert \psi _{z}\Vert ^{2}\). According to the definition of the time instant \(t_{M}\), it is obtained that \(\psi _{b}(t)\) and \(\psi _{z}(t)\) are both finite for any \(t \in [0,t_{M})\). According to (34) and (39) and the Young’s inequality, the derivative of \(V_{\psi ,b}\) at any time instant \(t \in [0,t_{M})\) is scaled as
where \(L_{b}L_{b}^{T} \ge \lambda _{b}{\mathbf {E}}_{m_{3}}\), \(\lambda _{hb}^{2} {\mathbf {E}}_{m_{3}} > {\hat{H}}_{bb}^{-T}{\hat{H}}_{bb}^{-1}\) and \(c_{3}{\mathbf {E}}_{m_{1}}\)\(> (3c_{2} + \frac{2}{k_{b}}) \lambda _{hb}^{2} {\hat{H}}_{bm}^{T}{\hat{H}}_{bm}\) are utilized. Then, for any \(t \in [0,t_{M})\), it is obtained from (68) that
Due to the fact that \(w_{m,r}(t) \in {\mathcal {L}}_{2}[0,t_{M})\), \(Y_{b}(t){\tilde{\theta }}_{b}(t) \in {\mathcal {L}}_{2}[0,t_{M})\) and \({\dot{\rho }}_{b}(t)s_{b}(t) \in {\mathcal {L}}_{\infty }[0,t_{M})\), it can be seen that all the integral terms of the right side of (69) are uniformly bounded in \([0,t_{M})\). This implies that \(V_{\psi ,b}(t)\) is also uniformly bounded in \([0,t_{M})\), and \(\psi _{b}(t)\) is also uniformly bounded in \([0,t_{M})\). Accordingly, \(\varPhi _{b}(t)\) and \(L_{b}(t)\) are also uniformly bounded in \([0,t_{M})\) owing to the uniform boundedness of \(\psi _{b}(t)\) in \([0,t_{M})\).
Additionally, in view of (32), (39) and the Young’s inequality, the derivative of \(V_{\psi ,z}\) is scaled as
where \(\mu _{J}{\mathbf {E}}_{m_{3}} > {\hat{J}}_{b}^{T}{\hat{J}}_{b}\), \(\mu _{J}{\mathbf {E}}_{m_{1}} \ge {\hat{J}}_{m}^{T}{\hat{J}}_{m}\) and \(c_{3}{\mathbf {E}}_{m_{1}} > (3c_{2} + \frac{2}{k_{b}}) \lambda _{hb}^{2} {\hat{H}}_{bm}^{T}{\hat{H}}_{bm}\) are used. Integrating both sides of (70) leads to
for \(t \in [0,t_{M})\). Note that based upon the previous proof, we have \(L_{b}^{T}(t)\varPhi _{b}(t)\psi _{b}(t) \in {\mathcal {L}}_{\infty }[0,t_{M})\). Besides, it has been proved that \(Y_{z}(t){\tilde{\theta }}_{z}(t) \in {\mathcal {L}}_{2}[0,t_{M})\), \({\dot{\rho }}_{z}(t)s_{z}(t) \in {\mathcal {L}}_{\infty }[0,t_{M})\), \(Y_{b}(t){\tilde{\theta }}_{b}(t) \in {\mathcal {L}}_{2}[0,t_{M})\) and \(w_{m,r}(t) \in {\mathcal {L}}_{2}[0, t_{M})\). Therefore, it can be seen that all the integral terms in the right-hand side of (71) are uniformly bounded in \([0,t_{M})\), and accordingly \(V_{\psi ,z}(t)\) is uniformly bounded in \([0,t_{M})\). This implies that \(\psi _{z}(t)\) and \(\varPhi _{z}(t)\) are also uniformly bounded in \([0,t_{M})\).
In all, according to the above analysis, it is obtained that \(\psi _{b}(t)\) and \(\psi _{z}(t)\) are uniformly bounded in \([0,t_{M})\). This contradicts with the assumption that the regulation/tracking error \(\chi (t) = (\varDelta q_{b}(t), \varDelta z_{e}(t))\) violates the prescribed performance constraints (16)–(17) when \(t = t_{M}\). Hence, this assumption is invalid and, due to the generality of the time instant \(t_{M}~(0 < t_{M} \le +\infty )\), it is obtained that both \(\psi _{b}(t)\) and \(\psi _{z}(t)\) are uniformly bounded, and the prescribed performance constraints (16)–(17) are always satisfied for \(\chi (t)\) in \([0,+\infty )\).
Then, it will be proved that \(V_{c}(t)\) is uniformly bounded. Since it has been proved that the prescribed performance constraints (16)–(17) are satisfied in \([0,+\infty )\), the aforementioned inequality (67) is always established in [0, \(+\infty )\), and the relations \(|s_{b,i}(t)| < 1\) for \(i=1,\ldots ,\)\(m_{3}\) and \(|s_{z,i}(t)| < 1\) for \(i=1,\ldots ,m_{2}+m_{3}\) are also always established in \([0,+\infty )\). Correspondingly, due to the fact that \({\dot{\rho }}_{b}(t)\) and \({\dot{\rho }}_{z}(t)\) are both uniformly bounded in \([0,+\infty )\), \({\dot{\rho }}_{b}(t)s_{b}(t)\) and \({\dot{\rho }}_{z}(t)s_{z}(t)\) are also uniformly bounded in \([0,+\infty )\).
Due to the fact that \(\lim _{t \rightarrow +\infty }{\dot{\rho }}_{b}(t) = {\mathbf {0}}_{m_{3} \times m_{3}}\) and \(\lim _{t \rightarrow +\infty }{\dot{\rho }}_{z}(t) = {\mathbf {0}}_{(m_{2}+m_{3}) \times (m_{2}+m_{3})}\) from (19a)–(19b), denote \(\acute{\lambda }(t)\)\( \triangleq \mathrm{{max}}\{\frac{1}{k_{z}}\Vert {\dot{\rho }}_{z}(t)\Vert ^{2},\frac{1}{\lambda _{b}k_{b}}\Vert {\dot{\rho }}_{b}(t)\Vert ^{2}\}\), and it is obtained that \(\lim _{t \rightarrow +\infty }\acute{\lambda }(t) = 0\). This means that there exists \(t_{N} > 0\) such that \(\acute{\lambda }(t) \le \mathrm{{min}}\{2k_{z},k_{b}\lambda _{b}\}\) for any \(t \ge t_{N}\). Notice that according to the previous proof, it is obtained that \({\dot{\rho }}_{b}(t)s_{b}(t)\) and \({\dot{\rho }}_{z}(t)s_{z}(t)\) are uniformly bounded in \([0,t_{N}]\), meaning that \(V_{c}(t)\) is also uniformly bounded in \([0,t_{N}]\) based upon (67). Moreover, for any time instant \(t \in [t_{N},+\infty )\), the derivative of \(V_{c}(t)\) in (67) can be further scaled as
where
and the relations \(\varPhi _{b}\varPhi _{b}^{T} \ge 4{\mathbf {E}}_{m_{3}}\) and \(\varPhi _{z}\varPhi _{z}^{T} \ge 4{\mathbf {E}}_{m_{2}+m_{3}}\) when \(\Vert \psi _{b}\Vert < +\infty \) and \(\Vert \psi _{z}\Vert < +\infty \), \(L_{b}L_{b}^{T} \ge \lambda _{b}{\mathbf {E}}_{m_{3}}\) and (23)–(24) are utilized. From (72)–(73), it is obtained that \(V_{c}(t)\) is also uniformly bounded in \([t_{N},+\infty )\). In all, it is concluded that \(V_{c}(t)\) is uniformly bounded in \([0,+\infty )\).
Step 2 The asymptotical convergence of signal \(\varPi (t)\).
First, due to uniform boundedness of \(V_{c}(t)\), the signals \(\psi _{b}(t)\), \(\varPhi _{b}(t)\), \({\tilde{\theta }}_{b}(t)\), \({\hat{\theta }}_{b}(t)\), \(\psi _{z}(t)\), \(\varPhi _{z}(t)\), \({\tilde{\theta }}_{z}(t)\), \({\hat{\theta }}_{z}(t)\), e(t), \({\tilde{\theta }}_{d}(t)\), \({\hat{\theta }}_{d}(t)\), \({\hat{w}}_{m,r}(t)\) and \(w_{m,r}(t)\) are all uniformly bounded. Remind that it has been proved that the signals \(s_{b}(t)\) and \(s_{z}(t)\) are both uniformly bounded and, together with the uniform boundedness of \(\rho _{b}(t)\) and \(\rho _{z}(t)\), it is also obtained that \(\varDelta q_{b}(t) = \rho _{b}(t)s_{b}(t)\) and \(\varDelta z_{e}(t) = \rho _{z}(t)s_{z}(t)\) are both uniformly bounded. Due to uniform boundedness of \({\hat{\theta }}_{b}(t)\), the matrices \({\hat{H}}_{bb}(t)\), \({\hat{H}}_{bb}^{-1}(t)\), \({\hat{H}}_{bm}(t)\), \({\hat{H}}_{bm}^{\dagger }(t)\), \({\hat{U}}(t)\) are also uniformly bounded. Similarly, owing to the uniform boundedness of \({\hat{\theta }}_{z}(t)\), the matrices \({\hat{J}}_{b}(t)\) and \({\hat{J}}_{m}(t)\) are also uniformly bounded. According to the uniform boundedness of \({\hat{J}}_{m}(t)\) and \({\hat{U}}(t)\), it is obtained that \({\hat{J}}_{m}(t){\hat{U}}(t)\) and \(({\hat{J}}_{m}(t){\hat{U}}(t))^{\dag }\) are both uniformly bounded. Note that the estimates of \(A_{0}\) and \(v_{0}\), that is, \({\hat{A}}_{0}(t)\) and \({\hat{v}}_{0}(t)\), are the components of \({\hat{\theta }}_{b}(t)\) and \({\hat{\theta }}_{z}(t)\), respectively, which means that both \({\hat{A}}_{0}(t)\) and \({\hat{v}}_{0}(t)\) are also uniformly bounded in view of the uniform boundedness of \({\hat{\theta }}_{b}(t)\) and \({\hat{\theta }}_{z}(t)\). It is also noted that \(q_{b}(t)\) and \(L_{b}(t)\) are both uniformly bounded due to the uniform boundedness of \(\varDelta q_{b}(t) = q_{b}(t) - q_{b,d}\). In all, in view of (25) and (36), the signals \(w_{m,c}(t)\) are uniformly bounded. Accordingly, the signals \(w_{m}(t) = w_{m,c}(t) + w_{m,r}(t)\), \(w_{b}(t)\)\(= H_{bb}^{-1}(t)A_{0} - H_{bb}^{-1}(t)H_{bm}(t)\)\(w_{m}(t)\) and \(w(t) = \mathrm{{col}}(w_{b}(t),\)\(w_{m}(t))\) are all uniformly bounded, due to the uniform boundedness of \(w_{m,c}(t)\) and \(w_{m,r}(t)\).
Then, we will prove that the signals \({\dot{\psi }}_{b}(t)\), \({\dot{\psi }}_{z}(t)\), \({\dot{\varPhi }}_{b}(t)\), \({\dot{\varPhi }}_{z}(t)\) and \({\dot{e}}(t)\) are uniformly bounded. From the structures of the regressor matrices \(Y_{b}(t)\) (14) and \(Y_{z}(t)\) (4), it is obtained that \(Y_{b}(t)\) and \(Y_{z}(t)\) are both uniformly bounded, owing to the uniform boundedness of w(t). In view of the uniform boundedness of \({\tilde{\theta }}_{b}(t)\), \(Y_{b}(t)\), \(\psi _{b}(t)\), \(\varPhi _{b}(t)\), \({\hat{H}}_{bb}^{-1}(t)\), \(L_{b}(t)\), \(w_{m,r}(t)\), \({\hat{H}}_{bm}(t)\), \(s_{b}(t)\) and \({\dot{\rho }}_{b}(t)\), it is obtained that \(\varDelta {\dot{q}}_{b}(t)\) in (33) and \({\dot{\psi }}_{b}(t)\) in (34) are both uniformly bounded. Correspondingly, \({\dot{s}}_{b}(t)\) is also uniformly bounded in view of the uniform boundedness of \(\varDelta {q}_{b}(t)\), \(\varDelta {\dot{q}}_{b}(t)\), \(\rho _{b}^{-1}(t)\) and \({\dot{\rho }}_{b}(t)\), and \({\dot{\varPhi }}_{b}(t)\) is also uniformly bounded owing to the uniform boundedness of \(\psi _{b}(t)\), \(s_{b}(t)\) and \({\dot{s}}_{b}(t)\). Similarly, from (22b) and (38), the signals \(\varDelta {\dot{z}}(t)\) and \({\dot{\psi }}_{z}(t)\) are also uniformly bounded due to the uniform boundedness of w(t), \(v_{0}\), \({\dot{z}}_{e,d}(t)\), \(J_{b}(t)\), \(J_{m}(t)\), \(\varPhi _{z}(t)\), \({\dot{\rho }}_{z}(t)\) and \(s_{z}(t)\). Accordingly, \({\dot{s}}_{z}(t)\) and \({\dot{\varPhi }}_{z}(t)\) are also uniformly bounded due to uniform boundedness of \(\varDelta z_{e}(t)\), \(\varDelta {\dot{z}}_{e}(t)\), \(\rho _{z}^{-1}(t)\), \({\dot{\rho }}_{z}(t)\), \(s_{z}(t)\), \(\psi _{z}(t)\). Besides, \({\dot{e}}(t)\) in (55) is also uniformly bounded in view of the uniform boundedness of e(t).
Next, the uniform boundedness of \({\dot{w}}_{m,c}(t)\) will be verified. From (29) and (43), the signals \(\dot{{\tilde{\theta }}}_{b}(t)\), \(\dot{{\hat{\theta }}}_{b}(t)\), \(\dot{{\tilde{\theta }}}_{z}(t)\) and \(\dot{{\hat{\theta }}}_{z}(t)\) are all uniformly bounded in view of the uniform boundedness of \(Y_{b}(t)\), \(Y_{z}(t)\), \({\tilde{\theta }}_{b}(t)\) and \({\tilde{\theta }}_{z}(t)\). Accordingly, the signals \(\dot{{\hat{A}}}_{0}(t)\) and \(\dot{{\hat{v}}}_{0}(t)\), which are the components of \(\dot{{\hat{\theta }}}_{b}(t)\) and \(\dot{{\hat{\theta }}}_{z}(t)\), respectively, are also uniformly bounded. Correspondingly, in view of the uniform boundedness of \({\hat{\theta }}_{b}(t)\), \(\dot{{\hat{\theta }}}_{b}(t)\), \({\hat{\theta }}_{z}(t)\), \(\dot{{\hat{\theta }}}_{z}(t)\), w(t), \({\hat{H}}_{bm}(t)\), \({\hat{H}}_{bm}^{\dagger }(t)\), \({\hat{U}}(t)\) and \({\hat{J}}_{m}(t)\), it is obtained that \(({\hat{H}}_{bb}(t))^{'}\), \(({\hat{H}}_{bm}(t))^{'}\), \(({\hat{H}}_{bm}^{\dagger }(t))^{'}\), \(({\hat{U}}(t))^{'}\), \(({\hat{J}}_{m}(t))^{'}\), \(({\hat{J}}_{b}(t))^{'}\) and \(({\hat{J}}_{m}(t){\hat{U}}(t))^{'}\) are all uniformly bounded. Based upon the uniform boundedness of \({\hat{J}}_{m}(t){\hat{U}}(t)\), \(({\hat{J}}_{m}(t){\hat{U}}(t))^{\dag }\) and \(({\hat{J}}_{m}(t){\hat{U}}(t))^{'}\), the matrix \((({\hat{J}}_{m}(t){\hat{U}}(t))^{\dag })^{'}\) is also uniformly bounded. Besides, based upon the uniform boundedness of \(q_{b}(t)\) and \(w_{b}(t)\), it is obtained that \({\dot{L}}_{b}(t)\) is also uniformly bounded. In all, according to the uniform boundedness of the signals \(\psi _{b}(t)\), \(\varPhi _{b}(t)\), \(L_{b}(t)\), \({\hat{H}}_{bb}(t)\), \({\hat{A}}_{0}(t)\), \({\hat{H}}_{bm}(t)\), \({\hat{H}}_{bm}^{\dagger }(t)\), \({\hat{U}}(t)\), \({\hat{J}}_{m}(t)\), \(({\hat{J}}_{m}(t){\hat{U}}(t))^{\dagger }\), \(\psi _{z}(t)\), \(\varPhi _{z}(t)\), \({\dot{z}}_{e,d}(t)\), \({\hat{v}}_{0}(t)\) and the corresponding derivatives, it is obtained that \({\dot{w}}_{m,c}(t)\) is uniformly bounded.
In addition, it will be proved that the control input \(u_{m}(t)\) is uniformly bounded. Note that \(\dot{{\hat{w}}}_{m,r}(t)\) in (65) is uniformly bounded due to the uniform boundedness of \({\hat{w}}_{m,r}(t)\). \(\dot{{\hat{w}}}_{m}(t) = {\dot{w}}_{m,c}(t) + \dot{{\hat{w}}}_{m,r}(t)\) is also uniformly bounded due to the uniform boundedness of \({\dot{w}}_{m,c}(t)\) and \(\dot{{\hat{w}}}_{m,r}(t)\). Similarly, \({\hat{w}}_{m}(t) = w_{m,c}(t) + {\hat{w}}_{m,r}(t)\) is uniformly bounded due to uniform boundedness of \(w_{m,c}(t)\) and \({\hat{w}}_{m,r}(t)\). \({\tilde{w}}_{m}(t) = w_{m}(t) - {\hat{w}}_{m}(t)\) is also uniformly bounded, owing to the uniform boundedness of \(w_{m}(t)\) and \({\hat{w}}_{m}(t)\). Therefore, it is obtained that \(Y_{d,c}(t)\) in (49) is also uniformly bounded. The signals \(Y_{d,f}(t) = [Y_{d,f1}(t);Y_{d,f2}(t)]\) and \({\dot{Y}}_{d,f}(t)\) in (50) are also uniformly bounded, according to the uniform boundedness of \(Y_{d,c}(t)\). The estimation error \({\tilde{w}}(t)\) in (54) is also uniformly bounded due to the uniform boundedness of e(t), M(t), \(Y_{d,f}(t)\) and \({\tilde{\theta }}_{d}(t)\). Correspondingly, \({\hat{w}}(t) = w(t) - {\tilde{w}}(t)\) is uniformly bounded. Besides, due to the uniform boundedness of w(t) and \({\hat{\theta }}_{d}(t)\), it is obtained that the matrices \(\hat{{\dot{M}}}_{bb}(t)\), \(\hat{{\dot{M}}}_{bm}(t)\), \(\hat{{\dot{M}}}_{bm}^{T}(t)\), \(\hat{{\dot{M}}}_{mm}(t)\), \({\hat{C}}_{bb}(t)\), \({\hat{C}}_{bm}(t)\), \({\hat{C}}_{mb}(t)\), \({\hat{C}}_{mm}(t)\), \({\hat{M}}_{bb}(t)\), \({\hat{M}}_{bm}(t)\), \({\hat{M}}_{bm}^{T}(t)\), \({\hat{M}}_{mm}(t)\) are all uniformly bounded. Therefore, it is obtained that \({\hat{M}}_{mm}^{*}\) in (63a), \(\zeta _{b}(t)\) in (61a) and \(\zeta _{m}(t)\) in (61b) are all uniformly bounded. The vector \(\zeta _{m}^{*}(t)\) in (63b) is also uniformly bounded, according to the uniform boundedness of \(\zeta _{b}(t)\), \(\zeta _{m}(t)\), \({\hat{M}}_{bb}(t)\) and \({\hat{M}}_{bm}^{T}(t)\). In all, it is obtained that the control input \(u_{m}(t)\) in (64) is uniformly bounded, based upon the uniform boundedness of \(\zeta _{m}^{*}(t)\), \({\hat{M}}_{mm}^{*}(t)\), \(\dot{{w}}_{m,c}(t)\) and \({\hat{w}}_{m,r}(t)\).
Moreover, it will be proved that signals \(({Y}_{b}(t){\tilde{\theta }}_{b}(t))^{'}\), \(({Y}_{z}(t){\tilde{\theta }}_{z}(t))^{'}\), and \(({Y}_{d,f}(t){\tilde{\theta }}_{d}(t))^{'}\) are uniformly bounded. According to the uniform boundedness of \(Y_{d,f}(t)\) and \({\tilde{w}}(t)\), it is obtained from (51) that \(\dot{{\hat{\theta }}}_{d}(t)\) and \(\dot{{\tilde{\theta }}}_{d}(t)\) are uniformly bounded. Therefore, \(({Y}_{d,f}(t){\tilde{\theta }}_{d}(t))^{'}\) is uniformly bounded, according to the uniform boundedness of \(Y_{d,f}(t)\), \({\dot{Y}}_{d,f}(t)\), \({\tilde{\theta }}_{d}(t)\) and \(\dot{{\tilde{\theta }}}_{d}(t)\). Besides, due to the uniform boundedness of w(t), the matrix C(q(t), w(t)) is also uniformly bounded. Correspondingly, according to the uniform boundedness of \(u_{m}(t)\), w(t), C(q(t), w(t)) and M(q(t)), it is obtained that \({\dot{w}}(t) = [{\dot{w}}_{b}(t);{\dot{w}}_{m}(t)]\) in (8) is also uniformly bounded. Due to the uniform boundedness of the signals w(t) and \({\dot{w}}(t)\), it is obtained from the structures of the regressor matrices \(Y_{b}(t)\) (14) and \(Y_{z}(t)\) (4) that \({\dot{Y}}_{b}(t)\) and \({\dot{Y}}_{z}(t)\) are also uniformly bounded. Therefore, based on the uniform boundedness of the signals \(Y_{b}(t)\), \({\tilde{\theta }}_{b}(t)\), \(Y_{z}(t)\), \({\tilde{\theta }}_{z}(t)\) and their derivatives, it is obtained that both \((Y_{b}(t){\tilde{\theta }}_{b}(t))^{'}\) and \((Y_{z}(t){\tilde{\theta }}_{z}(t))^{'}\) are also uniformly bounded. Additionally, due to the uniform boundedness of \(\dot{{\hat{\theta }}}_{d}(t)\) and \(Y_{d,f}(t)\), it is obtained that \(\eta _{x}(t)\) in (52) is uniformly bounded. \({\dot{M}}(t)\) is also uniformly bounded due to the uniform boundedness of w(t). Therefore, due to the uniform boundedness of M(t), \({\dot{M}}(t)\), \({\tilde{w}}(t)\), \(Y_{d,c}(t)\), \({\tilde{\theta }}_{d}(t)\) and \(\eta _{x}(t)\), the signal \(\dot{{\tilde{w}}}(t) = [\dot{{\tilde{w}}}_{b}(t);\dot{{\tilde{w}}}_{m}(t)]\) in (48) is also uniformly bounded. Correspondingly, \({\dot{w}}_{m,r}(t) = \dot{{\hat{w}}}_{m,r}(t) + \dot{{\tilde{w}}}_{m}(t)\) is also uniformly bounded due to the uniform boundedness of \(\dot{{\hat{w}}}_{m,r}(t)\) and \(\dot{{\tilde{w}}}_{m}(t)\).
In all, it is obtained that \({\dot{\psi }}_{b}(t)\), \((Y_{b}(t){\tilde{\theta }}_{b}(t))^{'}\), \({\dot{\psi }}_{z}(t)\), \((Y_{z}(t){\tilde{\theta }}_{z}(t))^{'}\), \({\dot{w}}_{b}(t)\), \((Y_{d,f}(t){\tilde{\theta }}_{d}(t))^{'}\), \(\dot{{\hat{w}}}_{m,r}(t)\), \({\dot{e}}(t)\), \({\dot{w}}_{m,r}(t)\), \(\dot{{\tilde{w}}}(t)\) are all uniformly bounded. Besides, from (72)–(73), it is further obtained that
which means that \(\psi _{b}(t) \in {\mathcal {L}}_{2}\), \(Y_{b}(t){\tilde{\theta }}_{b}(t) \in {\mathcal {L}}_{2}\), \(\psi _{z}(t) \in {\mathcal {L}}_{2}\), \(Y_{z}(t){\tilde{\theta }}_{z}(t) \in {\mathcal {L}}_{2}\), \({w}_{b}(t) \in {\mathcal {L}}_{2}\), \(Y_{d,f}(t){\tilde{\theta }}_{d}(t) \in {\mathcal {L}}_{2}\), \({{\hat{w}}}_{m,r}(t) \in {\mathcal {L}}_{2}\), \(e(t) \in {\mathcal {L}}_{2}\), \({w}_{m,r}(t) \in {\mathcal {L}}_{2}\), \({{\tilde{w}}}(t) \in {\mathcal {L}}_{2}\). Based upon Lemma 1 in Section 2, it is obtained that \(\lim _{t \rightarrow +\infty }\psi _{b}(t) = {\mathbf {0}}_{m_{3}}\), \(\lim _{t \rightarrow +\infty }Y_{b}(t){\tilde{\theta }}_{b}(t) = {\mathbf {0}}_{m_{3}}\), \(\lim _{t \rightarrow +\infty }\psi _{z}(t) = {\mathbf {0}}_{m_{2}+m_{3}}\), \(\lim _{t \rightarrow +\infty }Y_{z}(t){\tilde{\theta }}_{z}(t) = {\mathbf {0}}_{m_{2}+m_{3}}\), \(\lim _{t \rightarrow +\infty }w_{b}(t)\)\(= {\mathbf {0}}_{m_{3}}\), \(\lim _{t \rightarrow +\infty }Y_{d,f}(t){\tilde{\theta }}_{d}(t) = {\mathbf {0}}_{m_{1}+m_{3}}\), \(\lim _{t \rightarrow +\infty }{\hat{w}}_{m,r}(t)\)\(= {\mathbf {0}}_{m_{1}}\), \(\lim _{t \rightarrow +\infty }e(t) = {\mathbf {0}}_{m_{1} + m_{3}}\), \(\lim _{t \rightarrow +\infty }w_{m,r}(t) = {\mathbf {0}}_{m_{1}}\), \(\lim _{t \rightarrow +\infty }{\tilde{w}}(t) = {\mathbf {0}}_{m_{1} + m_{3}}\). Besides based upon (23)–(24), it is further obtained that \(\lim _{t \rightarrow +\infty }s_{b}(t) = {\mathbf {0}}_{m_{3}}\) and \(\lim _{t \rightarrow +\infty }s_{z}(t) = {\mathbf {0}}_{m_{2} + m_{3}}\), and correspondingly \(\lim _{t \rightarrow +\infty }\varDelta q_{b}(t) = \lim _{t \rightarrow +\infty }\)\(\rho _{b}(t) s_{b}(t) = {\mathbf {0}}_{m_{3}}\) and \(\lim _{t \rightarrow +\infty }\varDelta z_{e}(t)\)\(= \lim _{t \rightarrow +\infty }\)\(\rho _{z}(t)s_{z}(t) = {\mathbf {0}}_{m_{2} + m_{3}}\).
Step 3 The prescribed control performances on the spacecraft attitude regulation error \(\varDelta q_{b}(t)\) and the end-effector pose tracking error \(\varDelta z_{e}(t)\).
From the previous proof, it is obtained that the prescribed performance error signals \(\psi _{b}(t)\) and \(\psi _{z}(t)\) are both uniformly bounded. Therefore, based on Remark 4, it is obtained that the spacecraft attitude regulation error \(\varDelta q_{b}(t)\) and the end-effector pose tracking error \(\varDelta z_{e}(t)\) can satisfy the prescribed control performances (16)–(17), respectively. Besides, in the previous proof, it is verified that \(\lim _{t \rightarrow +\infty }w_{b}(t) = {\mathbf {0}}_{m_{3}}\). Furthermore, due to the fact that \(\lim _{t \rightarrow +\infty }w_{b}(t) = {\mathbf {0}}_{m_{3}}\), \(\lim _{t \rightarrow +\infty }w_{m,r}(t) = {\mathbf {0}}_{m_{1}}\), \(\lim _{t \rightarrow +\infty }\psi _{z}(t) = {\mathbf {0}}_{m_{2} + m_{3}}\) and \(\lim _{t \rightarrow +\infty } Y_{z}(t){\tilde{\theta }}_{z}(t) = {\mathbf {0}}_{m_{2} + m_{3}}\), it is obtained from (38) that \(\lim _{t \rightarrow +\infty }\varDelta {\dot{z}}_{e}(t)\)\(= {\mathbf {0}}_{m_{2} + m_{3}}\). The proof of this Theorem is complete. \(\square \)
Remark 5
According to the proposed control scheme, the base spacecraft and the mounted manipulator can be coordinated controlled to realize the spacecraft attitude regulation task and the end-effector pose tracking task simultaneously. Besides, compared with the adaptive null-space control methods in [35, 36], the proposed control scheme can further ensure the prescribed control performances on the spacecraft attitude regulation error \(\varDelta q_{b}(t)\) and the end-effector pose tracking error \(\varDelta z_{e}(t)\) (16)–(17) simultaneously.
Remark 6
The attractive manifold control methods have been put forward to achieve adaptive control of several controlled systems [62,63,64,65]. For instance, in [63], the attractive manifold control method has been utilized to achieve trajectory tracking control of the uncertain fully actuated robotic manipulators with the following dynamic equation
where \(q_{f}\), \({\dot{q}}_{f}\) and \(\ddot{q}_{f}\) are the joint angle, joint velocity and joint acceleration of the robotic manipulator, \(M_{f}(q_{f})\), \(C_{f}(q_{f},{\dot{q}}_{f})\) and \(G_{f}(q_{f})\) is the inertia matrix, the centrifugal/Coriolis matrix, the potential force vector of the robotic manipulator, and \(u_{f}\) is the control input. In [63], the robotic manipulator (75) is controlled to track the desired trajectory \(q_{f,d}(t)\). Denote the tracking error as \(\varDelta q_{f}(t) \triangleq q_{f}(t) - q_{f,d}(t)\), and accordingly \(\varDelta {\dot{q}}_{f}(t) \triangleq {\dot{q}}_{f}(t) - {\dot{q}}_{f,d}(t)\) and \(\varDelta \ddot{q}_{f}(t) \triangleq \ddot{q}_{f}(t) - \ddot{q}_{f,d}(t)\). Then, it is obtained from (75) that
The proposed attractive manifold controller in [63] is designed on the above tracking error dynamic equation (76). For the dynamic parameter \(\theta _{f}\) in (76), the proposed adaptive controller in [63] can ensure that the uncertain parameter estimation error term on \(\theta _{f}\) can converge to zero independent of the persistent excitation condition.
However, it should be noted that the method in [63] is designed for the fully actuated robotic manipulator (75) and besides depends on the linearly parametric feature of the robotic dynamics, that is,
where \(W(q_{f},{\dot{q}}_{f},\ddot{q}_{f,d})\) is the according regressor matrix. Unfortunately, owing to the free-floating mode of the space manipulator, the FFSM is an underactuated system. Besides, the reduced form of the FFSM dynamics (10) is nonlinearly parameterized toward the dynamic parameter. Hence, the attractive manifold method in [63] is inapplicable toward the FFSM.
In this paper, a novel attractive manifold control method is proposed. A nonlinear filter on the FFSM dynamics is constructed in (46), and the designed updated law on the dynamic parameter estimate (51) is driven by estimation error of the joint velocity. Different from the methods in [62, 63] in which the updated laws on the uncertain parameters are designed directly on the tracking error equations (like Eq. (76)), the proposed adaptive law is constructed on the dynamic equation on the estimation error of the joint velocity (47), and correspondingly, the nonlinearly parametric issue of the FFSM is overcome. Hence, compared with [35, 36], the proposed control scheme can be designed at the dynamic level.
Remark 7
Similar to [62,63,64,65], the proposed attractive manifold control method renders parameter estimation error term decay to zero, that is,
independent of the persistent excitation condition which is the prerequisite for the several adaptive control methods to render the parameter estimation error terms converge to zero. Once the parameter estimation error term \(Y_{d,f}{\tilde{\theta }}_{d}\) falls to zero, that is, \(Y_{d,f}{\tilde{\theta }}_{d} = {\mathbf {0}}_{m_{1} + m_{3}}\), it is obtained from (54) and (55) that
This means that the estimation error \({\tilde{w}}(t) = ({\tilde{w}}_{b}^{T}(t),\)\({\tilde{w}}_{m}^{T}(t))^{T}\) can tend to zero with \(\exp (-k_{de}t)\) exponential convergence rate. Besides, since \({\hat{w}}_{m,r}(t)\) in (65) also tends to zero with \(\exp (-k_{d}t)\) exponential convergence rate, it is obtained that the sliding vector \(w_{m,r} = {\hat{w}}_{m,r} + {\tilde{w}}_{m}\) can also tend to zero with exponential convergence rate. In addition, the proposed adaptive control method also ensures that the parameter estimation error terms \(Y_{b}(t){\tilde{\theta }}_{b}(t)\) and \(Y_{z}(t){\tilde{\theta }}_{z}(t)\) tend to zero, independent of the persistent excitation conditions. This means that \(\lim _{t \rightarrow +\infty }\)\(\varPhi _{b}(t)L_{b}(t){\hat{H}}_{bb}^{-1}(t)Y_{b}(t){\tilde{\theta }}_{b}(t) = {\mathbf {0}}_{m_{3}}\) in (34) and \(\lim _{t \rightarrow +\infty }\varPhi _{z}(t)Y_{z}(t){\tilde{\theta }}_{z}(t) = {\mathbf {0}}_{m_{2} + m_{3}}\) in (39). In all, the proposed adaptive control method can eliminate the influences of kinematic and dynamic uncertainties of the FFSM, independent of the persistent excitation conditions.
4 Simulation results
In this section, a 4-DOF planar FFSM (see Fig. 1) is taken as an example to show the control performances of the proposed control scheme [36]. For this planar FFSM, its base spacecraft is equipped with a 4-DOF manipulator, which means that \(m_{1} = 4\). For the end-effector pose tracking task of this planar FFSM, the number of task variables is \(m_{2} + m_{3} = 3\). For the spacecraft attitude regulation task of this planar FFSM, the number of task variable is \(m_{3} = 1\) [36]. Therefore, it is obtained that \(m_{1} = m_{2} + 2m_{3}\), which means that the DOFs of the mounted manipulators are enough to realize the spacecraft attitude regulation task and the end-effector pose tracking task simultaneously [36].
The system parameters are chosen based upon [36] and are given in Table 1, where the base spacecraft is labeled 0, \(m_{0}\) represents the mass of the base spacecraft, \(m_{i}\), \(i=1,2,3,4\), represents the mass of the ith link, \(I_{0}\) stands for the moment of inertia of the base spacecraft, \(I_{i}\), \(i=1,2,3,4\), stands for the moment of inertia of the ith link, and the physical meanings of \(l_{i}\) and \(l_{c,i}\), \(i=0,1,2,3,4\), can be seen in Fig. 1. The structure of matrices in (3), (5a), (5b) and (13) can be seen in [36]. Besides, the nonzero constant velocity \(v_{0}\) and the nonzero constant angular momentum \(A_{0}\) are \(v_{0} = [0.0988;0.0943]~\mathrm{m/s}\) and \(A_{0} = -1.6467~\mathrm{kg}\, \mathrm{m}^{2}/\mathrm{s}\), and correspondingly, the uncertain parameters \(\theta _{z} \in {\mathbb {R}}^{n_{1}}\), \(\theta _{d} \in {\mathbb {R}}^{n_{2}}\) and \(\theta _{b} \in {\mathbb {R}}^{n_{3}}\) are \(\theta _{z} = [0.0988, ~ 0.0943, ~ 0.6277\)\( 1.1550, ~ 1.2600, ~ 1.3542]^{T}\), \(\theta _{d} = [34.5482, ~\) 20.0140, 11.9952, \(~ 3.1686, ~ 11.9952, 12.6126,\) 4.1234, 6.8544, 4.4982, \(~ 2.2409]^{T}\) and \(\theta _{b} = [-1.6467, ~ 34.5482, ~ 20.0140,\)\(~ 11.9952, 3.1686,\) 11.9952, 12.6126, \(4.1234, ~ 6.8544, ~ 4.4982, 2.2409]^{T}\).
Besides, the desired attitude in the inertia frame is \(q_{b,d} = 0\), and the desired trajectory of the end-effector pose in the inertia frame is set as
where the first two rows of \(z_{e,d}(t)\) constitute the desired end-effector position trajectory, and the last row of \(z_{e,d}(t)\) is the desired end-effector attitude trajectory.
In order to verify the control performance of the proposed control scheme, two control schemes are employed as compared control scheme. The first control scheme resembles the proposed control scheme but does not consider the prescribed performance requirements (16)–(17), in order to show the transient and steady control performance of the proposed control scheme. The second control scheme only considers the prescribed performance control of the FFSM end-effector, but overlooks the requirement of spacecraft attitude regulation, to show the coordinated control performance of the proposed control scheme.
4.1 Compared simulation results between the proposed control scheme and the control scheme without prescribed performance requirement
In this case, the corresponding control scheme without the prescribed control performances is employed as compared control scheme, to verify the control performances of the proposed control scheme [66]. To be specific, in the compared control scheme, the variables \(\psi _{b}(t)\) (20a), \(\psi _{z}(t)\) (20b), \(\rho _{b}(t)\) (18a) and \(\rho _{z}(t)\) (18b) are replaced by \(\varDelta q_{b}(t)\), \(\varDelta z_{e}(t)\), 1 and \({\mathbf {E}}_{3}\), respectively. Correspondingly, it means that the variables \(s_{b}(t)\), \(s_{z}(t)\), \(\varPhi _{b}(t)\) and \(\varPhi _{z}(t)\) are also replaced by \(\varDelta q_{b}(t)\), \(\varDelta z_{e}(t)\), 1 and \({\mathbf {E}}_{3}\), respectively, and \({\dot{\rho }}_{b}(t) = {\mathbf {0}}\) and \({\dot{\rho }}_{z}(t) = {\mathbf {0}}_{3 \times 3}\) for the compared control scheme.
The control parameters of proposed control scheme are set as \(k_{b} = 0.04\), \(\varGamma _{1} = 10\), \(k_{z} = 0.04\), \(\varGamma _{2} = 10\), \(k_{de} = 0.3\), \(k_{d} = 0.8\), \(\varGamma _{3} = 10\), \(\rho _{b}^{0} = 0.4\), \(\rho _{z,1}^{0} = \rho _{z,2}^{0} = 1\), \(\rho _{z,3}^{0} = 0.2\), \(\rho _{b}^{\infty } = 0.03\), \(\rho _{z,1}^{\infty } = \rho _{z,2}^{\infty } = 0.08\), \(\rho _{z,3}^{\infty } = 0.05\), \(\beta _{b} = 0.22\), \(\beta _{z,1} = \beta _{z,2} = \beta _{z,3} = 0.22\), \(\sigma _{b} = 0.8\), \(\sigma _{z,1} = \sigma _{z,2} = \sigma _{z,3} = 0.8\). As for the compared control scheme, its control parameters are set the same as the counterparts of the proposed control scheme, expect for the control parameters in the decaying functions of time \(\rho _{b}(t)\) (18a) and \(\rho _{z}(t)\) (18b). The initial values of the system variables and control variables can be seen in Table 2.
The control performances of proposed and compared control schemes are shown in Figs. 2 and 3. In Figs. 2 and 3, the proposed control scheme is denoted as case 1, and the compared control scheme is denoted as case 2. Besides, the black dotted lines in Fig. 2a–d depict the corresponding decaying functions of time (18a)–(18b), and the regions surrounded by these black dotted lines are the prescribed performance constraints. If, in Fig. 2a–d, the spacecraft attitude regulation error \(\varDelta q_{b}(t)\) and the end-effector pose tracking error \(\varDelta z_{e}(t) = [\varDelta z_{e,1}(t);\)\(\varDelta z_{e,2}(t);\)\(\varDelta z_{e,3}(t)]\) are within the corresponding prescribed performance constraints, it means that the corresponding control scheme satisfies the prescribed control performances (16)–(17).
The control performances of the proposed control scheme are analyzed first. Notice that in Fig. 2a–d, both the spacecraft attitude regulation error \(\varDelta q_{b}(t)\) and the end-effector pose tracking error \(\varDelta z_{e}(t) = [\varDelta z_{e,1}(t);\)\(\varDelta z_{e,2}(t);\varDelta z_{e,3}(t)]\) of the proposed control scheme can converge to zeros within 10s, and satisfy prescribed control performances (16)–(17). Besides, in Fig. 2e–g, the spacecraft angular velocity \(w_{b}(t)\), the time derivative of the end-effector position tracking error \(\varDelta {\dot{p}}_{e}(t)\), and the time derivative of the end-effector attitude tracking error \(\varDelta {\dot{q}}_{e}(t)\) of the proposed control scheme can all converge to zero within 10s. In Fig. 2h, the joint velocity \(w_{m}(t)\) of the proposed control scheme is bounded.
In addition, as shown in Fig. 3a–d, the uncertain parameter estimation errors \({\tilde{\theta }}_{b}(t)\), \({\tilde{\theta }}_{z}(t)\) and \({\tilde{\theta }}_{d}(t)\) of the proposed control scheme can converge into the neighborhoods of the desired equilibriums within 15s, and the variable \(Y_{d,f}(t)\) of the proposed control scheme is bounded. This means that the parameter estimation error terms \(Y_{b}(t){\tilde{\theta }}_{b}(t)\), \(Y_{z}(t){\tilde{\theta }}_{z}(t)\) and \(Y_{d,f}(t){\tilde{\theta }}_{d}(t)\) of the proposed control scheme can also converge into the neighborhoods of the desired equilibriums asymptotically. Moreover in Fig. 3e–f, the estimation error \({\tilde{w}}(t)\) of the proposed control scheme can also converge to zero within 8s, the control input \(u_{m}(t)\) of the proposed control scheme is bounded, and the maximum value of \(\Vert u_{m}(t)\Vert \) is nearly \(6.38~\mathrm{N}\,\mathrm{m}\).
On the other hand, in Fig. 3a–c, the compared control scheme can also ensure the convergence properties of the parameter estimation errors \({\tilde{\theta }}_{b}(t)\), \({\tilde{\theta }}_{z}(t)\) and \({\tilde{\theta }}_{d}(t)\). In Fig. 3d, e, the auxiliary variable \(Y_{d,f}(t)\) of the compared control scheme is bounded, and the estimation error \({\tilde{w}}(t)\) of the compared control scheme can also converge to zero. In Fig. 3f, the control input \(u_{m}(t)\) of the compared control scheme is also bounded, and the maximum value of \(\Vert u_{m}(t)\Vert \) is nearly \(3.75~\mathrm{N}\,\mathrm{m}\), which is smaller than that of the proposed control scheme.
However, the compared control scheme does not possess the same control performance as the proposed control scheme. First, in Fig. 2a–d, it can be seen that both the spacecraft attitude regulation error \(\varDelta q_{b}(t)\) and the end-effector pose tracking error \(\varDelta z_{e}(t)\)\(= [\varDelta z_{e,1}(t);\)\(\varDelta z_{e,2}(t);\)\(\varDelta z_{e,3}(t)]\) of the compared control scheme violate the prescribed control performances (16)-(17). This is because the compared control scheme does not take the prescribed control performances (16)–(17) into consideration. Besides, in Fig. 2e–g, the spacecraft angular velocity \(w_{b}(t)\), the time derivative of the end-effector position tracking error \(\varDelta {\dot{p}}_{e}(t)\) and the time derivative of the end-effector attitude tracking error \(\varDelta {\dot{q}}_{e}(t)\) of the compared control scheme do not converge as fast as the counterparts of the proposed control scheme.
4.2 Compared simulation results between the proposed control scheme and the control scheme without spacecraft attitude regulation
In this subsection, the control scheme that only considers the end-effector pose tracking and neglects the spacecraft attitude regulation is introduced as a compared control scheme. Different from the proposed control scheme, the controller of this compared control scheme at the kinematic level is designed as
The updated law on the parameter estimates \({\hat{\theta }}_{z}\) (42), the updated law on the parameter estimate \({\hat{\theta }}_{d}\) (51), the filters (46) and (50) and the control input (64) are still employed in this compared control scheme. It can be seen that the spacecraft attitude regulation error \(\varDelta q_{b}(t)\) and the corresponding prescribed performance error \(\psi _{b}\) do not appear in (81), which means that the spacecraft attitude regulation is not considered in the compared control scheme.
The control parameters of this compared control scheme are still the same as the counterparts of the proposed control scheme. The simulation results on the proposed control scheme and the compared control scheme can be seen in Fig. 4. In Fig. 4a–h, the proposed control scheme is denoted as case 1, the above compared control scheme is denoted as case 3, and the corresponding decaying functions on time are also shown in Fig. 4a–d as the black dotted lines.
On the one hand, in Fig. 4b–d, the end-effector pose tracking error of the compared control scheme obeys the prescribed performance requirement (17). The time derivatives of the end-effector position and attitude tracking errors also converge to zero within 10s in Fig. 4d, e. On the other hand, compared with the proposed control scheme, the spacecraft attitude regulation error of the compared control scheme violates the prescribed performance requirement (16) in Fig. 4a, and the corresponding spacecraft angular velocity does not converge to zero in Fig. 4e. Moreover, in Fig. 4h, the reaction torque \({\mathcal {F}}_{r}(t)\) of the compared control scheme does not fall to zero within 20 s, compared with the proposed control scheme whose reaction torque falls to zero within 7 s.
The reason of these differences in Fig. 4a, e, h is that the spacecraft attitude regulation is not taken in consideration in this compared control scheme. Notice that there exists dynamic couplings (5a) between the base spacecraft and the mounted manipulator, and hence, the manipulator motion of the FFSM will induce reaction torque toward the base spacecraft. However, since the requirement on the spacecraft attitude regulation is overlooked in this compared control scheme, the FFSM will not be controlled to reduce the spacecraft attitude regulation error, even if the spacecraft attitude is far away from the desired attitude. Therefore, the uncontrolled reaction torque of the compared control scheme will alter the base spacecraft attitude, such that the spacecraft attitude deviates from the desired attitude. On the other hand, the proposed control scheme takes the requirement on the spacecraft attitude regulation into account. Hence, for the proposed control scheme, its spacecraft attitude regulation error obeys the prescribed performance requirement (16) and converges to zero in Fig. 4a, its spacecraft angular velocity falls to zero in Fig. 4e, and its reaction torque exerted on the base spacecraft also converges to zero in Fig. 4h.
5 Conclusions
In this paper, the coordinated control of the uncertain FFSM is investigated. Both the prescribed performance error transformations and the reaction null space are carefully designed to realize the spacecraft attitude regulation task and the end-effector trajectory tracking task simultaneously. Besides, in face of the nonlinearly parameterized feature of the FFSM, a novel attractive manifold control method is proposed, and the convergence of the parameter estimation error terms does not rely on the persistent excitation conditions. Based upon the proposed adaptive coordinated control scheme, both the spacecraft attitude regulation error and the end-effector pose tracking error can meet the prescribed control performances, in the presence of the nonlinearly parametric feature and the nonzero linear and angular momenta of the FFSM. Future work will focus on the detumbling control of the uncertain space manipulator with prescribed control performance.
Abbreviations
- \({\mathbf {E}}_{n}\) :
-
\((n \times n)\)-dimensional identity matrix
- \({\mathcal {L}}_{\infty }\) :
-
Space on the essentially bounded functions
- \({\mathcal {L}}_{p}\) :
-
Space on the p-order-integrable functions
- \(\theta _{b}\) :
-
Parameters in the angular momentum conservation equation
- \(\theta _{d}\) :
-
Parameters in the dynamic equation of the free-floating space manipulator
- \(\theta _{z}\) :
-
Parameters in the kinematic equation of the free-floating space manipulator
- \(A_{0}\) :
-
Nonzero angular momentum of the free-floating space manipulator
- \(C_{bb}\) :
-
Centrifugal and Coriolis matrix of the base spacecraft
- \(C_{bm}\) :
-
Centrifugal and Coriolis matrix of the base spacecraft and the manipulator
- \(C_{mb}\) :
-
Centrifugal and Coriolis matrix of the manipulator and the base spacecraft
- \(C_{mm}\) :
-
Centrifugal and Coriolis matrix of the manipulator
- \(I_{i}\) :
-
Inertia of the ith link
- \(J_{pb}\) :
-
Jacobian matrix between the spacecraft angular velocity and the end-effector linear velocity
- \(J_{pm}\) :
-
Jacobian matrix between the manipulator joint angular velocity and the end-effector linear velocity
- \(J_{qb}\) :
-
Jacobian matrix between the spacecraft angular velocity and the end-effector angular velocity
- \(J_{qm}\) :
-
Jacobian matrix between the manipulator joint angular velocity and the end-effector angular velocity
- \(l_{c,i}\) :
-
Distance between the ith link centroid and the \((i+1)\)th joint
- \(l_{i}\) :
-
Length of the ith link
- \(M_{bb}\) :
-
Spacecraft inertia matrix
- \(M_{bm}\) :
-
Coupled inertia matrix between the base spacecraft and the mounted manipulator
- \(m_{i}\) :
-
Mass of the ith link
- \(M_{mm}\) :
-
Inertia matrix of the mounted manipulator
- \(p_{e}\) :
-
End-effector position in the inertia frame
- \(q_{b}\) :
-
Base spacecraft attitude in the inertia frame
- \(q_{e}\) :
-
End-effector attitude in the inertia frame
- \(q_{m}\) :
-
Joint angle
- \(u_{m}\) :
-
Joint torque of the manipulator
- \(v_{0}\) :
-
Nonzero linear velocity of the free-floating space manipulator in the inertia frame
- \(w_{b}\) :
-
Base spacecraft angular velocity in the inertia frame
- \(w_{m}\) :
-
Joint angular velocity
- \(z_{e}\) :
-
Base spacecraft pose in the inertia frame
References
Moosavian, S.A.A., Papadopoulos, E.: Free-flying robots in space: an overview of dynamics modeling, planning and control. Robotica 25(5), 537–547 (2007)
Hirzinger, G., Landzettel, K., Brunner, B., et al.: DLR’s robotics technologies for on-orbit servicing. Adv. Robot. 18(2), 139–174 (2004)
Xu, Y.S., Kanade, T.: Space Robotics: Dynamics and Control. Springer, New York (1992)
Papadopoulos, E., Dubowsky, S.: On the nature of control algorithms for free-floating space manipulators. IEEE Trans. Robot. Autom. 7(6), 750–758 (1991)
Cheah, C.C., Liu, C., Slotine, J.J.E.: Adaptive Jacobian tracking control of robots with uncertainties in kinematic, dynamic and actuator models. IEEE Trans. Autom. Control 51(6), 1024–1029 (2006)
Zhang, B., Jia, Y.M., Matsuno, F., Endo, T.: Task-space synchronization of networked mechanical systems with uncertain parameters and communication delays. IEEE Trans. Cybern. 47(8), 2288–2298 (2017)
Duan, P.H., Duan, Z.S., Wang, J.Y.: Task-space fully distributed tracking control of networked uncertain robotic manipulators without velocity measurements. Int. J. Control 92, 1–14 (2017). https://doi.org/10.1080/00207179.2017.1395911
Zhao, L.Y., Ji, J.C., Liu, J., Wu, Q.J., Zhou, J.: Tracking task-space synchronization of networked Lagrangian systems with switching topology. Nonlinear Dyn. 83(3), 1673–1685 (2016)
Ge, M.F., Guan, Z.H., Yang, C., Chen, C.Y., Zheng, D.F., Chi, M.: Task-space coordinated tracking of multiple heterogeneous manipulators via controller-estimator approaches. J. Frankl. Inst. 353(15), 3722–3738 (2016)
Yao, X.Y., Ding, H.F., Ge, M.F.: Task-space tracking control of multi-robot systems with disturbances and uncertainties rejection capability. Nonlinear Dyn. 92(4), 1649–1664 (2018)
Flores-Abad, A., Ma, O., Pham, K., Ulrich, S.: A review of space robotics technologies for on-orbit servicing. Prog. Aerosp. Sci. 68(4), 1–26 (2014)
Vafa, Z., Dubowsky, S.: On the dynamics of space manipulators using the virtual manipulator, with applications to path planning. J. Astronaut. Sci. 38(4), 441–472 (1990)
Nakamura, Y., Mukherjee, R.: Nonholonomic path planning of space robots via a bidirectional approach. IEEE Trans. Robot. Autom. 7(4), 500–514 (1991)
Torres, M.A., Dubowsky, S.: Minimizing spacecraft attitude disturbances in space manipulator systems. J. Guid. Control Dyn. 15(4), 1010–1017 (1992)
Parlaktuna, O., Ozkan, M.: Adaptive control of free-floating space manipulators using dynamically equivalent manipulator model. Robot. Auton. Syst. 46(3), 185–193 (2004)
Moosavian, S.A.A., Papadopoulos, E.: On the kinematics of multiple manipulator space free-flyers and their computation. J. Robot. Syst. 15(4), 207–216 (1998)
Rybus, T., Seweryn, K., Sasiadek, J.Z.: Control system for free-floating space manipulator based on nonlinear model predictive control (NMPC). J. Intell. Robot. Syst. 85(3–4), 491–509 (2017)
Aghili, F.: Coordination control of a free-flying manipulator and its base attitude to capture and detumble a noncooperative satellite. In: Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 2365–2372 (2009)
Wee, L.B., Walker, M.W., McClamroch, N.H.: An articulated-body model for a free-flying robot and its use for adaptive motion control. IEEE Trans. Robot. Autom. 13(2), 264–277 (1997)
Gu, Y.L., Xu, Y.S.: A normal form augmentation approach to adaptive control of space robot systems. In: Proceedings of the IEEE Conference on Robotics and Automation, pp. 731–737 (1993)
Parlaktuna, O., Ozkan, M.: Adaptive control of free-floating space robots in Cartesian coordinates. Adv. Robot. 18(9), 943–959 (2004)
Wang, H.L., Xie, Y.C.: Passivity based adaptive Jacobian tracking for free-floating space manipulators without using spacecraft acceleration. Automatica 45(6), 1510–1517 (2009)
Abiko, S., Hirzinger, G.: Adaptive control for a torque controlled free-floating space robot with kinematic and dynamic model uncertainty. In: Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 2359–2364 (2009)
Abiko, S., Hirzinger, G.: An adaptive control for a free-floating space robot by using inverted chain approach. In: Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 2236–2241 (2007)
Sanner, R.M., Vance, E.E.: Adaptive control of free-floating space robots using “neural” networks. In: Proceedings of the American Control Conference, pp. 2790–2794 (1995)
Taveira, F.P.A., Siqueira, A.A.G., Terra, M.H.: Adaptive nonlinear H\(\infty \) controllers applied to a free-floating space manipulator. In: Proceedings of the 2006 IEEE International Conference on Control Applications, pp. 1476–1481 (2006)
Seweryn, K., Banaszkiewicz, M.: Optimization of the trajectory of a general free-flying manipulator during the rendezvous maneuver. In: Proceedings of the AIAA Guidance, Navigation and Control Conference, p. 7273 (2008)
Vladimmir, A.C.: Spacecraft Attitude Dynamics and Control. Malabar Krieger Publishing Company, Florida (1991)
Kane, T.R., Likins, P.W., Levinson, D.A.: Spacecraft Dynamics. McGraw-Hill Book Coporation, New York (1983)
Nakanishi, H., Yoshida, K.: Impedance control for free-flying space robots-basic equations and applications. In: Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 3137–3142 (2006)
Giordano, A.M., Garofalo, G., De Stefano, M., Ott, C., Albu-Schaffer, A.: Dynamics and control of a free-floating space robot in presence of nonzero linear and angular momenta. In: Proceedings of IEEE 55th Conference on Decision and Control (CDC), pp. 7527–7534 (2016)
Ran, X., Peng, S., Yushan, Z.: Zero reaction coordinated motion planning for free-floating space manipulators. In: Proceedings of Chinese Control Conference (CCC), pp. 5830–5834 (2015)
Nenchev, D.N., Yoshida, K., Vichitkulsawat, P., Uchiyama, M.: Reaction null-space control of flexible structure mounted manipulator systems. IEEE Trans. Robot. Autom. 15(6), 1011–1023 (1999)
James, F., Shah, S.V., Singh, A.K., Krishna, K.M., Misra, A.K.: Reactionless maneuvering of a space robot in precapture phase. J. Guid. Control Dyn. 39(10), 2419–2425 (2016)
Nguyen-Huynh, T.C., Sharf, I.: Adaptive reactionless motion and parameter identification in postcapture of space debris. J. Guid. Control Dyn. 36(2), 404–414 (2013)
Xu, S.F., Wang, H.L., Zhang, D.Z., Yang, B.H.: Adaptive zero reaction motion control for free-floating space manipulators. IEEE Trans. Aerosp. Electron. Syst. 52(3), 1067–1076 (2016)
Yang, Y.N., Hua, C.C., Guan, X.P.: Synchronization control for bilateral teleoperation system with prescribed performance under asymmetric time delay. Nonlinear Dyn. 81(1–2), 481–493 (2015)
Sun, D., Naghdy, F., Du, H.P.: Time domain passivity control of time-delayed bilateral telerobotics with prescribed performance. Nonlinear Dyn. 87(2), 1253–1270 (2017)
Yang, Y.N., Ge, C., Wang, H., Li, X.Y., Hua, C.C.: Adaptive neural network based prescribed performance control for teleoperation system under input saturation. J. Frankl. Inst. 352(5), 1850–1866 (2015)
Bechlioulis, C.P., Rovithakis, G.A.: Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance. IEEE Trans. Autom. Control 53(9), 2090–2099 (2008)
Bechlioulis, C.P., Rovithakis, G.A.: Adaptive control with guaranteed transient and steady state tracking error bounds for strict feedback systems. Automatica 45(2), 532–538 (2009)
Yang, C.G., Jiang, Y.M., He, W., Na, J., Li, Z.J., Xu, B.: Adaptive parameter estimation and control design for robot manipulators with finite-time convergence. IEEE Trans. Ind. Electron. 65(10), 8112–8123 (2018)
Han, S.I., Lee, J.M.: Improved prescribed performance constraint control for a strict feedback non-linear dynamic system. IET Control Theory Appl. 7(14), 1818–1827 (2013)
Zhang, J.X., Yang, G.H.: Fault-tolerant leader–follower formation control of marine surface vessels with unknown dynamics and actuator faults. Int. J. Robust Nonlinear Control 28(14), 4188–4208 (2018)
Wang, S.B., Yu, H.S., Yu, J.P., Na, J., Ren, X.M.: Neural-network-based adaptive funnel control for servo mechanisms with unknown dead-zone. IEEE Trans. Cybern. (2018). https://doi.org/10.1109/TCYB.2018.2875134
Wang, S.B., Na, J., Ren, X.M., Yu, H.S., Yu, J.P.: Unknown input observer-based robust adaptive funnel motion control for nonlinear servomechanisms. Int. J. Robust Nonlinear Control 28(18), 6163–6179 (2018)
Na, J., Chen, Q., Ren, X.M., Guo, Y.: Adaptive prescribed performance motion control of servo mechanisms with friction compensation. IEEE Trans. Ind. Electron. 61(1), 486–494 (2014)
Na, J., Huang, Y.B., Wu, X., Gao, G.B., Herrmann, G., Jiang, J.Z.: Active adaptive estimation and control for vehicle suspensions with prescribed performance. IEEE Trans. Control Syst. Technol. 26(6), 2063–2077 (2017)
Tang, X.Q., Chen, Q., Nan, Y., Na, J.: Backstepping funnel control for prescribed performance of robotic manipulators with unknown dead zone. In: Proceedings of the 27th Chinese Control and Decision Conference (CCDC), pp. 1508–1513 (2015)
Xie, X.L., Hou, Z.G., Cheng, L., Ji, C., Tan, M., Yu, H.: Adaptive neural network tracking control of robot manipulators with prescribed performance. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 225(6), 790–797 (2011)
Karayiannidis, Y., Doulgeri, Z.: Model-free robot joint position regulation and tracking with prescribed performance guarantees. Robot. Auton. Syst. 60(2), 214–226 (2012)
Zhao, K., Song, Y.D., Ma, T.D., He, L.: Prescribed performance control of uncertain Euler–Lagrange systems subject to full-state constraints. IEEE Trans. Neural Netw. Learn. Syst. 29(8), 3478–3489 (2018)
Wang, M., Yang, A.: Dynamic learning from adaptive neural control of robot manipulators with prescribed performance. IEEE Trans. Syst. Man Cybernet. Syst. 47(8), 2244–2255 (2017)
Cao, Y., Song, Y.D.: Adaptive PID-like fault-tolerant control for robot manipulators with given performance specifications. Int. J. Control (2018). https://doi.org/10.1080/00207179.2018.1468928
Yang, C.G., Jiang, Y.M., Li, Z.J., He, W., Su, C.Y.: Neural control of bimanual robots with guaranteed global stability and motion precision. IEEE Trans. Ind. Inform. 13(3), 1162–1171 (2017)
Bechlioulis, C.P., Doulgeri, Z., Rovithakis, G.A.: Guaranteeing prescribed performance and contact maintenance via an approximation free robot force/position controller. Automatica 48(2), 360–365 (2012)
Xu, Y.S., Shum, H.Y., Kanade, T., Lee, J.J.: Parameterization and adaptive control of space robot systems. IEEE Trans. Aerosp. Electron. Syst. 30(2), 435–451 (1994)
Zhou, Z.G., Zhang, Y.A., Zhou, D.: Robust prescribed performance tracking control for free-floating space manipulators with kinematic and dynamic uncertainty. Aerosp. Sci. Technol. 71(12), 568–579 (2017)
Abiko, S., Yoshida, K.: Adaptive reaction control for space robotic applications with dynamic model uncertainty. Adv. Robot. 24(8–9), 1099–1126 (2010)
Lozano, R., Brogliato, B., Egeland, O., Maschke, B.: Dissipative Systems Analysis and Control: Theory and Applications. Springer, Berlin (2013)
Zhang, J.X., Yang, G.H.: Prescribed performance fault-tolerant control of uncertain nonlinear systems with unknown control directions. IEEE Trans. Autom. Control 62(12), 6529–6535 (2017)
Seo, D.E., Akella, M.R.: High-performance spacecraft adaptive attitude-tracking control through attracting-manifold design. J. Guid. Control Dyn. 31(4), 884–891 (2008)
Seo, D.E., Akella, M.R.: Non-certainty equivalent adaptive control for robot manipulator systems. Syst. Control Lett. 58(4), 304–308 (2009)
Lee, K.W., Singh, S.N.: Noncertainty-equivalent adaptive wing-rock control via Chebyshev neural network. J. Guid. Control Dyn. 37(1), 123–133 (2013)
Sun, L., Zheng, Z.W.: Nonlinear adaptive trajectory tracking control for a stratospheric airship with parametric uncertainty. Nonlinear Dyn. 82(3), 1419–1430 (2015)
Sui, S., Tong, S.C., Li, Y.M.: Observer-based fuzzy adaptive prescribed performance tracking control for nonlinear stochastic systems with input saturation. Neurocomputing 158(3), 100–108 (2015)
Acknowledgements
This work was supported by the NSFC (61327807, 61521091, 61520106010, 61134005) and the National Basic Research Program of China (973 Program: 2012CB821200, 2012CB821201).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that no conflict of interest exists in the submission of the manuscript.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Lu, X., Jia, Y. Adaptive coordinated control of uncertain free-floating space manipulators with prescribed control performance. Nonlinear Dyn 97, 1541–1566 (2019). https://doi.org/10.1007/s11071-019-05071-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-019-05071-w