1 Introduction

Teleoperation system has emerged as a useful tool to accomplish tasks in remote or hazardous environments [1–4]. A typical teleoperator is composed of human operator, master manipulator, communication channel, slave manipulator and remote environment [5]. On being manipulated by a human operator, the controlled coupling between the master and slave manipulators is utilized by the slave manipulator for carrying out tasks remotely. For the practical teleoperation design, the synchronization transient-state performance is very important. Take the telesurgery as an example, in real life, the telesurgery can minimize healthcare cost and make specialist doctors available throughout the world, saving people’s life and improving health care systems. Meanwhile, the telesurgery requires a higher performance than other applications, because the work performance influences the patient’s health status, even his life. However, the existing teleoperation control design methods cannot guarantee the transient-state performance, and even the steady-state performance cannot be guaranteed in the presence of system uncertainties and external disturbances. Therefore, an effective control scheme can guarantee that both the transient-state and the steady-state performances are significant for bilateral teleoperation system.

Synchronization control of the master and the slave has been widely investigated, and a vast number of publications are produced. The breakthrough to the bilateral teleoperation problem with time delay was achieved in [6], in which the concepts from network theory, passivity and scattering theory were used to analyze mechanisms responsible for loss of stability and a time delay compensation scheme was derived to guarantee stability independent of the constant time delay. Niemeyer and Slotine [7] proposed the wave variable idea to deal with the time delay issue. Nevertheless, the classic scattering transformation may give rise to position drift. A new teleoperation scheme was proposed in [8] to improve the position-tracking performance. To improve the haptic feedback fidelity, a new scattering method was developed in [9]. In [10], a simple PD controller was proposed and a delay-dependent stability condition was derived. Unfortunately, the stability proof hinges upon unverifiable assumption on the human operators and the contact environment. Additionally, recently, Hua and Liu [11] proposed the delay- dependent LMI stability criteria for the closed-loop teleoperation system with time-varying delays. Consider the unknown gravity term, Hua and Yang [12] proposed a new adaptive-based control method to estimate the unknown gravity term online. Forouzantabar et al. [13] proposed an adaptive NN control for bilateral teleoperation system with unsymmetrical stochastic delays in communication channel. The synchronization problem for nonlinear bilateral teleoperator with interval time-varying delay was investigated in [14]. However, the above literatures on the master and slave synchronization control problem deal solely with the steady-state problem rather than the system performance in a transient situation.

It has been early recognized that transient-state control performance deserves further research [15]. The tracking control for nonlinear system with prescribed transient behavior was investigated in [16]. In recent years, to achieve the prescribed transient behavior, the prescribed performance control (PPC) has attracted many attentions. The main thought of PPC is that the tracking error should converge to an arbitrarily predefined small residual set with convergence rate not less than a prespecified value, exhibiting a maximum overshoot less than a sufficiently small prespecified constant [17]. By employing the neural networks, a new controller for a robot manipulator was proposed in [18] to guarantee the tracking error of the system bounded by prescribed decreasing boundary. The preset performance control problem for the flexible joint robot with unknown and possibly variable elasticity was addressed in [19]. Recently, the PPC was employed to control complex high-order nonlinear system [20, 21]. However, as far as we know, there are few results on PPC for networked bilateral teleoperation system with time delay.

It is well known that robotic manipulator is complicated, dynamically coupled, highly time-varying and highly nonlinear system. Moreover, with the limitation of modeling method and the complex external task environment, teleoperation system is inevitably subject to structured and unstructured uncertainties. Fuzzy logical system (FLs) was introduced by Zadeh in 1965, as one of the most popular intelligent computation approaches, which was proved to be an essential tool for solving some various classes of engineering problems. Recently, the adaptive fuzzy approximation approach was also used in controlling MIMO nonlinear system and nonlinear time delay system [22–26]. Tong et al. [27] proposed a fuzzy output feedback controller combining the backstepping method and the stochastic small-gain approach. By using sliding mode control theory, a neuro-fuzzy-based control scheme for a spherical rolling robot was designed in [28]. For pure-feedback stochastic nonlinear system with input constraints, a robust adaptive fuzzy tracking control method was proposed in [29]. The adaptive fuzzy method was used in controlling teleoperation system under time-varying delay in [30]. In this paper, the adaptive fuzzy method will be applied to compensate the uncertainties in the master–slave model and the external disturbances.

In this paper, the adaptive fuzzy-based prescribed performance control scheme is designed for the bilateral teleoperation system with asymmetric time delays. The contributions of this paper can be summarized as follows: (1) To satisfy the high-performance requirements, both the prespecified transient-state performance and steady-state performance are provided for bilateral teleoperation system by designing a PPC algorithm. (2) System uncertainties and external disturbances are not necessary to be known. (3) The damping forces from the human operator and the remote environment are considered.

The rest of paper is organized as follows. Section 2 presents some preliminary knowledge for the dynamics of teleoperation system with the related properties and the knowledge for FLs. In Sect. 3, the specific design process for the new controller is given. Moreover, the control performance is proved by employing proper Lyapunov functions. The simulation and experiment results are presented in Sect. 4. Finally, Sect. 5 concludes with a summary of the obtained results.

2 Problem formulation

2.1 Dynamic models of master and slave

The Euler–Lagrange equations of motion for n-link master and slave manipulators are given as

$$\begin{aligned} \left\{ \begin{array}{l} M_{m}\left( q_{m}\right) \ddot{q}_{m}+C_{m}\left( q_{m} ,\dot{q}_{m}\right) \dot{q}_{m}+G_{m}\left( q_{m}\right) \\ \quad +F_{m}\dot{q}_{m}+f_{cm}(\dot{q}_{m})+\tau _{dm}=\tau _{m}+F_{h}\\ M_{s}\left( q_{s}\right) \ddot{q}_{s}+C_{s}\left( q_{s} ,\dot{q}_{s}\right) \dot{q}_{s}+G_{s}\left( q_{s}\right) \\ \quad +F_{s}\dot{q}_{s}+f_{cs}(\dot{q}_{s})+\tau _{ds}=\tau _{s}-F_{e} \end{array} \right. \end{aligned}$$
(1)

where \(i=m\) for the master and \(i=s\) is the slave; \(q_{i}, \dot{q}_{i}, \ddot{q}_{i}\in \mathbb {R}^{n}\) are the joint positions, velocities, accelerations; \(M_{i} (q_{i})\in \mathbb {R}^{n\times n}\) are the positive-definite inertia matrices; \(C_{i}\left( q_{i},\dot{q}_{i}\right) \in \mathbb {R}^{n\times n}\) are the matrices of centripetal and coriolis torques; \(G_{i}\left( q_{i}\right) \in \mathbb {R}^{n}\) are the gravitational torques; \(F_{i}\) denote the viscous friction coefficients; \(f_{ci}(\dot{q}_{i})\) \(\in \mathbb {R}^{n}\) are the coulomb friction; \(\tau _{di}\in \mathbb {R}^{n}\) are the bounded external disturbances, i.e., \(\left\| \tau _{di}\right\| \le \bar{\tau }_{di}, \bar{\tau }_{di}\) are positive constants; \(F_{h}, F_{e}\in \mathbb {R}^{n}\) are the torques exerted by the human operator and the environment interaction, respectively; \(\tau _{i}\,\in \mathbb {R}^{n}\) are the applied torques.

Important properties of the nonlinear dynamic models (1) are presented as follows [9]:

Property 1

The inertia matrix \(M_{i}(q_{i})\) is a symmetric function, and there exist lower and upper bounds, i.e.,

$$\begin{aligned} 0<\lambda _{m}(M_{i}(q_{i}))I\le M_{i}(q_{i})\le \lambda _{M}(M_{i}(q_{i}))I \end{aligned}$$
(2)

where \(I\) is the identity matrix with the corresponding dimension. \(\lambda _{m}(\cdot )\) and \(\lambda _{M}(\cdot )\) represent the minimum and maximum eigenvalues for \(\cdot \), respectively.

Property 2

For all \(q_{i}, x, y\in \mathbb {R}^{n}\), there exists a positive scalar \(v_{i}\) such that

$$\begin{aligned} \left\| C(q_{i},x)y\right\| \le v_{i}\left\| x\right\| \left\| y\right\| \end{aligned}$$

Property 3

The matrix \(\dot{M}_{i}(q_{i})-2C_{i}(q_{i},\dot{q}_{i})\) is skew-symmetric, i.e.,

$$\begin{aligned} \eta ^\mathrm{T}(\dot{M}_{i}(q_{i})-2C_{i}(q_{i},\dot{q}_{i}))\eta =0,\quad \forall \eta \in \mathbb {R}^{n} \end{aligned}$$

Property 4

There exists a positive scalar \(\mu _{G_i}\) such that \(\left\| G_{i}(q_{i})\right\| \le \mu _{G_i}\).

For a given vector, \(\left\| \cdot \right\| \) denotes the vector Euclidean norm and the corresponding induced matrix norm.

2.2 Fuzzy logic system

During the past years, FLs have been extensively used as universal approximators for controller design of dynamic systems with precise model unknown. A fuzzy system is a collection of fuzzy IF–THEN rules of the form:

$$\begin{aligned} R^{\left( j\right) }&:\hbox {IF}\,z_{1}\left( t\right) \hbox {is}\, A_{1}^{j} \hbox {and} \cdots \hbox {and}\, z_{n}\left( t\right) \hbox {is}\,A_{n}^{j}\\&\hbox {THEN}\, y\left( t\right) \hbox {is}\, B^{j}.\nonumber \end{aligned}$$
(3)

By using the strategy of singleton fuzzification, product inference and center-average defuzzification, the output of the fuzzy system is

$$\begin{aligned} y\left( z\left( t\right) \right) =\frac{\sum _{j=1}^{l}y^{j}\left( \prod _{i=1}^{n}\mu _{A_{i}^{j}}\left( z_{i}\left( t\right) \right) \right) }{\sum _{j=1}^{l}\prod _{i=1}^{n}\mu _{A_{i}^{j}}\left( z_{i}\left( t\right) \right) }, \end{aligned}$$
(4)

where \(\mu _{A_{i}^{j}}\left( z_{i}\left( t\right) \right) \) is the membership function of linguistic variable \(z_{i}\left( t\right) \), and \(y^{j}\) is the point in \(\mathbb {R}\) at which \(\mu _{B^{j}}\) achieves its maximum value [assume that \(\mu _{B^{i} }\left( y^{i}\right) =1\)].

Introducing the concept of the fuzzy basic function vector \(\varphi \left( z\left( t\right) \right) \) gives

$$\begin{aligned} y\left( z\left( t\right) \right) =W^\mathrm{T}\left( t\right) \varphi \left( z\left( t\right) \right) , \end{aligned}$$
(5)

where

$$\begin{aligned}&W\left( t\right) =\left( y^{1}\left( t\right) ,y^{2}\left( t\right) ,\ldots ,y^{l}\left( t\right) \right) ^\mathrm{T},\\&\varphi \left( z\left( t\right) \right) =\left( \varphi _{1}\left( z\left( t\right) \right) ,\varphi _{2}\left( z\left( t\right) \right) ,\ldots ,\varphi _{l}\left( z\left( t\right) \right) \right) ^\mathrm{T}, \end{aligned}$$

and \(\varphi _{j}\left( z\left( t\right) \right) \) is defined as

$$\begin{aligned} \varphi _{j}\left( z\left( t\right) \right) =\frac{\prod _{i=1}^{n} \mu _{A_{i}^{j}}\left( z_{i}\left( t\right) \right) }{\sum _{j=1}^{l} \prod _{i=1}^{n}\mu _{A_{i}^{j}}\left( z_{i}\left( t\right) \right) }. \end{aligned}$$

Based on the universal approximation theorem, there exists the optimal approximation parameter \(W^{*}\) such that \(W^{*\mathrm{T}}\varphi \left( z\left( t\right) \right) \) can approximate a nonlinear function \(F_{1}\left( z\left( t\right) \right) \) to any desired degree over a compact set \(\Omega _{z}\). The parameter \(W^{*}\) is defined as follows.

$$\begin{aligned} W^{*}=\arg \min _{W\in \Omega _{W}}\left( \sup _{z\in \Omega _{z}}\left| W^\mathrm{T}\left( t\right) \varphi \left( z\left( t\right) \right) -\bar{F}\left( z\left( t\right) \right) \right| \right) , \end{aligned}$$

where \(\Omega _{W}\) and \(\Omega _{z}\) denote the sets of suitable bounds on \(W\left( t\right) \) and \(z\left( t\right) \), respectively. The minimum approximation error satisfies

$$\begin{aligned} F_{1}\left( z\left( t\right) \right) =W^{*\mathrm{T}}\varphi \left( z\left( t\right) \right) +\varepsilon (z(t)) \end{aligned}$$
(6)

where \(\left\| \varepsilon (z(t))\right\| \le \varepsilon ^{*}\) over \(z\left( t\right) \in \Omega _{z}\), and \(\varepsilon ^{*}\) is a positive scalar.

Actually, because of the existence of friction and backlash, the dynamic functions of manipulators are piecewise continuous functions possibly. Make a supposition that \(F\left( z\left( t\right) \right) \) is a piecewise function, which can be expressed as \(F\left( z\left( t\right) \right) =F_{1}\left( z\left( t\right) \right) +F_{2}\left( z\left( t\right) \right) \), where \(F_{1}\left( z\left( t\right) \right) \) is the continuous part and \(F_{2}\left( z\left( t\right) \right) \) is the bounded piecewise term. Therefore, we have

$$\begin{aligned} F\left( z\left( t\right) \right)&=W^{*\mathrm{T}}\varphi \left( z\left( t\right) \right) +\varepsilon (z(t))+F_{2}\left( z\left( t\right) \right) \\&=W^{*\mathrm{T}}\varphi \left( z\left( t\right) \right) +\bar{\varepsilon }(z(t))\nonumber \end{aligned}$$
(7)

where \(\bar{\varepsilon }(z(t))=\varepsilon (z(t))+F_{2}\left( z\left( t\right) \right) \) with \(\left\| \bar{\varepsilon }(z(t))\right\| \le \bar{\varepsilon }^{*}\) is the piecewise function approximation error and \(\bar{\varepsilon }^{*}\) is the upper bound of the approximation error.

3 Main results

Let \(x_{m1}=q_{m}, x_{s1}=q_{s}, x_{m2}=\dot{q}_{m}\) and \(x_{s2}=\dot{q}_{s}\), then Eq. (1) can be rewritten as the following strictly feedback form

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{m1}=x_{m2}\\ M_{m}(x_{m1})\dot{x}_{m2}=-C_{m}\left( x_{m1},x_{m2}\right) x_{m2} -G_{m}\left( x_{m1}\right) \\ \quad -F_{m}x_{m2}-f_{cm}(x_{m2})-\tau _{dm}+\tau _{m}+F_{h}\\ \dot{x}_{s1}=x_{s2}\\ M_{s}(x_{s1})\dot{x}_{s2}=-C_{s}\left( x_{s1},x_{s2}\right) x_{s2} -G_{s}\left( x_{s1}\right) \\ \quad -F_{s}x_{s2}-f_{cs}(x_{s2})-\tau _{ds}+\tau _{s}-F_{e} \end{array} \right. \end{aligned}$$
(8)

Definition 1

[15–18]: A smooth function \(\rho (t):\mathbb {R}^{+}\rightarrow \mathbb {R}^{+}-\{0\}\) will be called a performance function if \(\rho (t)\) is decreasing and \(\hbox {lim}_{t\rightarrow \infty } \rho (t)=\rho (\infty )>0\).

Apparently, we can give next definition

$$\begin{aligned} \left\{ \begin{array} {l} -\delta \rho (t)<e(t)<\rho (t)\\ -\rho (t)<e(t)<\delta \rho (t) \end{array} \begin{array} {l} \quad \hbox {if}\; e(0)\ge 0\\ \quad \hbox {if}\; e(0)<0 \end{array} \right. \end{aligned}$$
(9)

for all \(t\ge 0\), where \(0<\delta \le 1\) and \(\rho (t)\) a performance function associated with \(e(t)\).

Remark 1

The constant \(\rho (\infty )\) represents the maximum allowable size of the tracking error \(e(t)\) at the steady state. Furthermore, the decreasing rate of \(\rho (t)\) introduces a lower bound on the required speed of convergence of \(e(t)\), while the maximum overshoot is prescribed less than \(\delta \rho (t)\), which may even become zero by setting \(\delta =0\). Thus, the appropriate selections of the performance function \(\rho (t)\), as well as of the design constant \(\delta \), impose behavioral bounds on the system synchronization error.

3.1 Error transformation

The master–slave trajectory synchronization errors are defined as follows

$$\begin{aligned}&e_{m}(t)=x_{m1}(t)-x_{s1}(t-T_{s}),\nonumber \\&e_{s}(t) = x_{s1}(t)-x_{m1}(t-T_{m}) \end{aligned}$$
(10)

where \(T_{m}\) is the communication time delay from the master side to the slave side and \(T_{s}\) is the time delay in inverse direction. In this subsection, we propose the error transformation capable of transforming the original tracking error into a new variable. As it was originally stated, the prescribed performance is achieved if each element \(e_{j}(t)\), \(j=1,2,\ldots ,n\) of the tracking error \(e(t)\) evolves within a predefined region that is bounded by a decaying function of time. More specifically, we define

$$\begin{aligned} \epsilon _{mj}(t)=R\left( \frac{e_{mj}(t)}{\rho _{m}(t)}\right) ,\quad \epsilon _{sj}(t)=R\left( \frac{e_{sj}(t)}{\rho _{s}(t)}\right) \end{aligned}$$
(11)

where \(\epsilon _{ij}(t)\in \mathbb {R}^{n}\) is the transformed error vector; \(\rho _{i}(t)=\left( \rho _{i}(0)-\rho _{i}(\infty )\right) e^{-\alpha _{i}t}+\rho _{i}(\infty )\) is a scalar performance function; \(R\left( \frac{e_{i}(t)}{\rho _{i}(t)}\right) =\left[ R\left( \frac{e_{i1}(t)}{\rho _{i} (t)}\right) ,\ldots ,R\left( \frac{e_{in}(t)}{\rho _{i}(t)}\right) \right] ^\mathrm{T}\) \((i=m,s)\). The definition for \(R(\cdot )\) is shown as follows.

$$\begin{aligned} R(e_{ij}(t)/\rho _{i}(t))=\left\{ \begin{array}{c} \ln \frac{e_{ij}(t)/\rho _{i}(t)+\delta }{\delta -\delta e_{ij}(t)/\rho _{i}(t)}\\ \ln \frac{\delta e_{ij}(t)/\rho _{i}(t)+\delta }{\delta -e_{ij}(t)/\rho _{i}(t)} \end{array} \begin{array}{c} \quad \text {if }e_{ij}(0)\ge 0\\ \quad \text {if }e_{ij}(0)<0 \end{array} \right. \end{aligned}$$
(12)

Remark 2

With the definition for the \(R(\cdot )\), we know that \(R(\cdot )\) is smooth, strictly increasing function operating on each element of the vector argument, i.e., \(R(\cdot )\): \((-\delta ,1)\rightarrow (-\infty ,+\infty )\) when \(e_{ij}(0)\ge 0\) and \(R(\cdot )\): \((-1,\delta )\rightarrow (-\infty ,+\infty )\) when \(e_{ij}(0)<0\). It is obvious that by keeping \(\epsilon _{ij}(t)\) bounded, the prescribed performance (9) will be satisfied. Moreover, when \(\epsilon _{ij}(t)\rightarrow 0\), the \(e_{ij}(t)\) will converge to zero. Therefore, the controllers should be designed to guarantee the boundedness of \(\epsilon _{ij}(t)\) in order the achieve the prescribed performance.

To avoid cluttering the notation, the argument of all time signals will be omitted except for the case when it appears delayed.

3.2 Controller design and performance analysis

In this subsection, the controller design with the case that the human operator and environment providing damping torques will be presented. The external torques for the teleoperation system are given as \(F_{h}=-D_{m} \dot{q}_{m}\) and \(F_{e}=D_{s}\dot{q}_{s}\), where \(D_{m}\) and \(D_{s}\) represent the positive-definite diagonal damping matrices for the human operator and the remote environment.

Theorem 1

Consider the closed-loop teleoperation system described by (8) and the master and slave controllers are chosen as (25), with the fuzzy tuning laws

$$\begin{aligned} \overset{\cdot }{\hat{W}}_{i}=-\Gamma _{i}\varphi (Z_{i})\Delta x_{i2}^\mathrm{T} \end{aligned}$$
(13)

and the parameter adaptive tuning laws

$$\begin{aligned} \overset{\cdot }{\hat{\theta }}_{i}=\frac{\left\| \Delta x_{i2}\right\| ^{2}}{\left\| \Delta x_{i2}\right\| +e^{-\kappa _{i}t}} \end{aligned}$$
(14)

where \(\Gamma _{i}\) is a positive-definite diagonal matrix; \(\kappa _{i}\) is a positive constant; the definition of \(\Delta x_{i2}\) will be given below \((i=m,s)\). Then with the external torques \(F_{h}=-D_{m}\dot{q}_{m}\) and \(F_{e}=D_{s}\dot{q}_{s}\), the system is stable and the synchronization errors converge to zero as \(t\rightarrow \infty \) independent of the asymmetric time delay. Moreover, the synchronization errors will not violate the boundaries.

Proof

In this paper, the new controller design process will be given in two steps.

Step1: Differentiating \(\epsilon _{m}\) and \(\epsilon _{s}\) with respect to time, yields

$$\begin{aligned} \dot{\epsilon }_{m}&=\frac{1}{\rho _{m}}\frac{\partial R}{\partial (e_{m}/\rho _{m})}\left( x_{m2}-x_{s2}(t-T_{s})-\frac{\dot{\rho }_{m}e_{m}}{\rho _{m} }\right) \nonumber \\ \dot{\epsilon }_{s}&=\frac{1}{\rho _{s}}\frac{\partial R}{\partial (e_{s}/\rho _{s})}\left( x_{s2}-x_{m2}(t-T_{m})-\frac{\dot{\rho }_{s}e_{s}}{\rho _{s} }\right) \end{aligned}$$
(15)

where

$$\begin{aligned} \frac{\partial R}{\partial (e_{ij}/\rho _{i})}=\left\{ \begin{array}{cc} \hbox {diag}\{\frac{1+\delta }{(\delta +e_{ij}/\rho _{i})(1-e_{ij}/\rho _{i})}\}&{} \quad \text {if }e_{ij}(0)\ge 0\\ \hbox {diag}\{\frac{1+\delta }{(\delta -e_{ij}/\rho _{i})(1+e_{ij}/\rho _{i})}\}&{} \quad \text {if }e_{ij}(0)<0 \end{array}\right. \end{aligned}$$

with the definition of \(0<\delta \le 1\), by keeping \(\epsilon _{ij}\) bounded, we will have \(\frac{\partial R}{\partial (e_{ij}/\rho _{i})}\ne 0\); thus, the \(\left( \frac{\partial R}{\partial (e_{ij}/\rho _{i})}\right) ^{-1}\) will always exist.

The auxiliary desired trajectory \(x_{m2d}, x_{s2d}\) of \(x_{m2}, x_{s2}\) are designed as follows.

$$\begin{aligned} x_{m2d} =&-k_{m1}\left( \frac{\partial R}{\partial (e_{m}/\rho _{m})}\right) ^{-1}\rho _{m}\epsilon _{m}+x_{s2}(t-T_{s})\nonumber \\&\quad +\frac{\dot{\rho }_{m}}{\rho _{m}} e_{m}\nonumber \\ x_{s2d} =&-k_{s1}\left( \frac{\partial R}{\partial (e_{s}/\rho _{s})}\right) ^{-1}\rho _{s}\epsilon _{s}+x_{m2}(t-T_{m})\nonumber \\&\quad +\frac{\dot{\rho }_{s}}{\rho _{s}}e_{s} \end{aligned}$$
(16)

where \(k_{m1}, k_{s1}\) are positive-definite diagonal matrices.

Substituting the designed auxiliary variables into Eq. (15) with \(\Delta x_{m2}=x_{m2}-x_{m2d}\) , \(\Delta x_{s2}=x_{s2}-x_{s2d}\), we can obtain that

$$\begin{aligned} \dot{\epsilon }_{m}&=\frac{1}{\rho _{m}}\frac{\partial R}{\partial (e_{m}/\rho _{m})}\Delta x_{m2}-k_{m1}\epsilon _{m}\\ \dot{\epsilon }_{s}&=\frac{1}{\rho _{s}}\frac{\partial R}{\partial (e_{s}/\rho _{s})}\Delta x_{s2}-k_{s1}\epsilon _{s}\nonumber \end{aligned}$$
(17)

Consider the Lyapunov function candidate

$$\begin{aligned} V_{1}=\frac{1}{2}\epsilon _{m}^\mathrm{T}\epsilon _{m}+\frac{1}{2}\epsilon _{s} ^\mathrm{T}\epsilon _{s} \end{aligned}$$
(18)

According to Eq. (17), the time derivative of \(V_{1}\) is

$$\begin{aligned} \dot{V}_{1} =\,&\epsilon _{m}^\mathrm{T}\dot{\epsilon }_{m}+\epsilon _{s}^\mathrm{T} \dot{\epsilon }_{s}\nonumber \\ =\,&\epsilon _{m}^\mathrm{T}\frac{1}{\rho _{m}}\frac{\partial R}{\partial (e_{m} /\rho _{m})}\Delta x_{m2}-\epsilon _{m}^\mathrm{T}k_{m1}\epsilon _{m}\nonumber \\&+\epsilon _{s}^\mathrm{T}\frac{1}{\rho _{s}}\frac{\partial R}{\partial (e_{s} /\rho _{s})}\Delta x_{s2}-\epsilon _{s}^\mathrm{T}k_{s1}\epsilon _{s} \end{aligned}$$
(19)

Step 2: Design the input torques \(\tau _{m}\) and \(\tau _{s}\) to make \(\Delta x_{m2}\) and \(\Delta x_{s2}\) converge to zero as \(t\rightarrow \infty \).

According to definitions of the \(\Delta x_{m2}\) and \(\Delta x_{s2}\), we have

$$\begin{aligned} M_{m}(x_{m1})\Delta \dot{x}_{m2} =\,&M_{m}(x_{m1})\dot{x}_{m2}-M_{m} (x_{m1})\dot{x}_{m2d}\nonumber \\ =&-C_{m}\left( x_{m1},x_{m2}\right) x_{m2}-G_{m}\left( x_{m1}\right) \nonumber \\&-\,F_{m}x_{m2}-f_{cm}(x_{m2})-\tau _{dm} \nonumber \\&+\,\tau _{m}+F_{h}-M_{m}(x_{m1})\dot{x}_{m2d} \end{aligned}$$
(20)

and

$$\begin{aligned} M_{s}(x_{s1})\Delta \dot{x}_{s2} =\,&M_{s}(x_{s1})\dot{x}_{s2}-M_{s} (x_{s1})\dot{x}_{s2d}\nonumber \\ =&-C_{s}\left( x_{s1},x_{s2}\right) x_{s2}-G_{s}\left( x_{s1}\right) \nonumber \\&-F_{s}x_{s2}-f_{cs}(x_{s2})-\tau _{ds}+\tau _{s}\nonumber \\&-F_{e}-M_{s}(x_{s1})\dot{x} _{s2d} \end{aligned}$$
(21)

Consider the Lyapunov function candidate

$$\begin{aligned} V_{2}=\frac{1}{2}\Delta x_{m2}^\mathrm{T}M_{m}(x_{m1})\Delta x_{m2}+\frac{1}{2}\Delta x_{s2}^\mathrm{T}M_{s}(x_{s1})\Delta x_{s2} \end{aligned}$$
(22)

Differentiating \(V_{2}\) with respect time and using Property 3 of the dynamics equation, it can be obtained that

$$\begin{aligned} \dot{V}_{2}=\,&\Delta x_{m2}^\mathrm{T}M_{m}(x_{m1})\Delta \dot{x}_{m2}+\frac{1}{2}\Delta x_{m2}^\mathrm{T}\dot{M}_{m}(x_{m1})\Delta x_{m2}\nonumber \\&+\,\Delta x_{s2}^\mathrm{T}M_{s}(x_{s1})\Delta \dot{x}_{s2}+\frac{1}{2}\Delta x_{s2}^\mathrm{T}\dot{M}_{s}(x_{s1})\Delta x_{s2}\nonumber \\ =\,&\Delta x_{m2}^\mathrm{T}(\tau _{m}-G_{m}\left( x_{m1}\right) -M_{m}(x_{m1} )\dot{x}_{m2d}\nonumber \\&-C_{m}(x_{m1},x_{m2}) x_{m2d}-D_{m}x_{m2}-F_{m}x_{m2}\nonumber \\&-f_{cm}(x_{m2})-\tau _{dm}) +\, \Delta x_{s2}^\mathrm{T}(\tau _{s}-G_{s}\left( x_{s1}\right) \nonumber \\&-M_{s}(x_{s1})\dot{x}_{s2d}-C_{s}(x_{s1},x_{s2})x_{s2d}\nonumber \\&-\,D_{s}x_{s2}-F_{s}x_{s2}-f_{cs}(x_{s2})-\tau _{ds}) \end{aligned}$$
(23)

Let \(F_{m}(Z_{m})=M_{m}(x_{m1})\dot{x}_{m2d}+C_{m}(x_{m1},x_{m2})x_{m2d} +G_{m}\left( x_{m1}\right) +D_{m}x_{m2d}+F_{m}x_{m2}+f_{cm}(x_{m2})\) and \(F_{s}(Z_{s})=M_{s}(x_{s1})\dot{x}_{s2d}+C_{s}(x_{s1},x_{s2})x_{s2d} +G_{s}\left( x_{s1}\right) +D_{s}x_{s2d}+F_{s}x_{s2}+f_{cs}(x_{s2})\); \(Z_{m}=\left[ \dot{x}_{s2}^\mathrm{T}(t-T_{s}),x_{s2}^\mathrm{T}(t-T_{s}),x_{s1}^\mathrm{T} (t-T_{s}),x_{m2}^\mathrm{T},x_{m1}^\mathrm{T}\right] ^\mathrm{T}\) and \(Z_{s}=\big [\dot{x}_{m2}^\mathrm{T} (t-T_{m}),x_{m2}^\mathrm{T}(t-T_{m}),x_{m1}^\mathrm{T}(t-T_{m}),x_{s2}^\mathrm{T},x_{s1}^\mathrm{T}\big ]^\mathrm{T}\). Then (23) can be rewritten as

$$\begin{aligned} \dot{V}_{2} =\,&\Delta x_{m2}^\mathrm{T}(\tau _{m}-F_{m}(Z_{m})-D_{m}\Delta x_{m2})-\Delta x_{m2}^\mathrm{T}\tau _{dm}\nonumber \\&\quad +\,\Delta x_{s2}^\mathrm{T}(\tau _{s}-F_{s}(Z_{s})-D_{s}\Delta x_{s2})-\Delta x_{s2}^\mathrm{T}\tau _{ds} \end{aligned}$$
(24)

where the controller \(\tau _{i}\) can be designed as follows.

$$\begin{aligned} \tau _{i}=&-k_{i2}\Delta x_{i2}+\hat{F}_{i}(Z_{i})-\frac{1}{\rho _{i}} \frac{\partial R}{\partial (e_{i}/\rho _{i})}\epsilon _{i}\nonumber \\&-\,\frac{\Delta x_{i2} }{\left\| \Delta x_{i2}\right\| +e^{-\kappa _{i}t}}\hat{\theta }_{i} \end{aligned}$$
(25)

where \(\hat{F}_{i}(Z_{i})=\hat{W}_{i}^\mathrm{T}\varphi (Z_{i})\) is the approximation of \(F_{i}(Z_{i})\) using FLs; \(\hat{\theta }_{i}\) is used to estimate the upper bound of the fuzzy approximation error and the bounded external disturbances, i.e., \(\theta _{i}=\left\| \bar{\varepsilon }_{i} (Z_{i})+\tau _{di}\right\| \); \(k_{i2}\) is a positive-definite diagonal matrix; \(i=m,s\).

Additionally, to streamline the presentation, we give the following definitions:

$$\begin{aligned} \tilde{F}_{i}(Z_{i})&=F_{i}(Z_{i})-\hat{F}_{i}(Z_{i})\nonumber \\&=(W_{i}^{*\mathrm{T}}-\hat{W}_{i}^\mathrm{T})\varphi (Z_{i})+\bar{\varepsilon }_{i} (Z_{i}) \end{aligned}$$
(26)

Thus, we rewrite (24) as follows.

$$\begin{aligned} \dot{V}_{2} =&-\Delta x_{m2}^\mathrm{T}k_{m2}\Delta x_{m2}+\Delta x_{m2}^\mathrm{T} (\hat{F}_{m}(Z_{m})-F_{m}(Z_{m}))\nonumber \\&-\,\Delta x_{m2}^\mathrm{T}D_{m}\Delta x_{m2}-\Delta x_{m2}^\mathrm{T}\frac{\Delta x_{m2}\hat{\theta }_{m}}{\left\| \Delta x_{m2}\right\| +e^{-\kappa _{m}t}}\nonumber \\&-\,\Delta x_{m2}^\mathrm{T}\left( \frac{1}{\rho _{m}} \frac{\partial R}{\partial (e_{m}/\rho _{m})}\epsilon _{m}+\tau _{dm}\right) \nonumber \\&-\,\Delta x_{s2}^\mathrm{T}k_{s2}\Delta x_{s2}+\Delta x_{s2}^\mathrm{T}(\hat{F} _{s}(Z_{s})-F_{s}(Z_{s}))\nonumber \\&-\,\Delta x_{s2}^\mathrm{T}D_{s}\Delta x_{s2}-\Delta x_{s2}^\mathrm{T}\frac{\Delta x_{s2}\hat{\theta }_{s}}{\left\| \Delta x_{s2}\right\| +e^{-\kappa _{s}t}}\nonumber \\&-\,\Delta x_{s2}^\mathrm{T}\left( \frac{1}{\rho _{s}} \frac{\partial R}{\partial (e_{s}/\rho _{s})}\epsilon _{s}+\tau _{ds}\right) \end{aligned}$$
(27)

Furthermore, with Eq. (26)

$$\begin{aligned} \dot{V}_{2} =&-\Delta x_{m2}^\mathrm{T}k_{m2}\Delta x_{m2}-\Delta x_{m2}^\mathrm{T} D_{m}\Delta x_{m2}\nonumber \\&-\,\Delta x_{m2}^\mathrm{T}\tilde{W}_{m}^\mathrm{T}\varphi (Z_{m}) -\Delta x_{m2}^\mathrm{T}(\tau _{dm}+\bar{\varepsilon }_{m}(Z_{m}))\nonumber \\&-\,\Delta x_{s2}^\mathrm{T}k_{s2}\Delta x_{s2}-\Delta x_{s2}^\mathrm{T}D_{s}\Delta x_{s2}\nonumber \\&-\,\Delta x_{s2}^\mathrm{T}\tilde{W}_{s}^\mathrm{T}\varphi (Z_{s})-\Delta x_{s2}^\mathrm{T} (\tau _{ds}+\bar{\varepsilon }_{s}(Z_{s}))\nonumber \\&-\,\Delta x_{m2}^\mathrm{T}\frac{1}{\rho _{m}}\frac{\partial R}{\partial (e_{m}/\rho _{m})}\epsilon _{m}-\Delta x_{s2}^\mathrm{T}\frac{1}{\rho _{s}} \frac{\partial R}{\partial (e_{s}/\rho _{s})}\epsilon _{s}\nonumber \\&-\,\frac{\left\| \Delta x_{m2}\right\| ^{2}\hat{\theta }_{m} }{\left\| \Delta x_{m2}\right\| +e^{-\kappa _{m}t}}-\frac{\left\| \Delta x_{s2}\right\| ^{2}\hat{\theta }_{s}}{\left\| \Delta x_{s2}\right\| +e^{-\kappa _{s}t}} \end{aligned}$$
(28)

where \(\tilde{W}_{m}=W_{m}^{*}-\hat{W}_{m}\) and \(\tilde{W}_{s}=W_{s}^{*}-\hat{W}_{s}\).

Consider the Lyapunov function candidate

$$\begin{aligned} V =\,&V_{1}+V_{2}+\frac{1}{2}\hbox {tr}(\tilde{W}_{m}^\mathrm{T}\Gamma _{m}^{-1}\tilde{W} _{m})+\frac{1}{2}\hbox {tr}(\tilde{W}_{s}^\mathrm{T}\Gamma _{s}^{-1}\tilde{W}_{s} )\nonumber \\&\quad +\,\frac{1}{2}(\theta _{m}-\hat{\theta }_{m})^{2}+\frac{1}{2}(\theta _{s}-\hat{\theta }_{s})^{2} \end{aligned}$$
(29)

With the fuzzy adaptive law (13), the time derivative of \(V\) satisfies

$$\begin{aligned} \dot{V}=&-\epsilon _{m}^\mathrm{T}k_{m1}\epsilon _{m}-\Delta x_{m2}^\mathrm{T}k_{m2}\Delta x_{m2}\nonumber \\&-\,\Delta x_{m2}^\mathrm{T}D_{m}\Delta x_{m2}-\Delta x_{m2}^\mathrm{T}(\tau _{dm} +\bar{\varepsilon }_{m}(Z_{m}))\nonumber \\&-\frac{\left\| \Delta x_{m2}\right\| ^{2}\hat{\theta }_{m} }{\left\| \Delta x_{m2}\right\| +e^{-\kappa _{m}t}}-\Delta x_{m2} ^\mathrm{T}\tilde{W}_{m}^\mathrm{T}\varphi (Z_{m})\nonumber \\&+\,{tr}\big (\tilde{W}_{m}^{T}\varphi _{m}(Z_{m}\big )\Delta x_{m2}^{T})-(\theta _{m}-\hat{\theta }_{m})\overset{\cdot }{\hat{\theta }} _{m}\nonumber \\&-\epsilon _{s}^\mathrm{T}k_{s1}\epsilon _{s}-\Delta x_{s2}^\mathrm{T}k_{s2}\Delta x_{s2}-\Delta x_{s2}^\mathrm{T}D_{s}\Delta x_{s2}\nonumber \\&-\, \Delta x_{s2}^\mathrm{T}(\tau _{ds} +\bar{\varepsilon }_{s}(Z_{s}))\nonumber \\&-\frac{\left\| \Delta x_{s2}\right\| ^{2}\hat{\theta }_{s} }{\left\| \Delta x_{s2}\right\| +e^{-\kappa _{s}t}}-\Delta x_{s2} ^\mathrm{T}\tilde{W}_{s}^\mathrm{T}\varphi (Z_{s})\nonumber \\&+\, {tr}\big (\tilde{W}_{s}^{T}\varphi _s(Z_{s})\Delta x_{s2}^{T}\big )-(\theta _{s}-\hat{\theta }_{s})\overset{\cdot }{\hat{\theta }}_{s} \end{aligned}$$
(30)

Further, with the parameter adaptive laws (14), we have

$$\begin{aligned} \dot{V} \le&-\epsilon _{m}^\mathrm{T}k_{m1}\epsilon _{m}-\Delta x_{m2}^\mathrm{T} k_{m2}\Delta x_{m2}-\Delta x_{m2}^\mathrm{T}D_{m}\Delta x_{m2}\nonumber \\&+\, \left\| \Delta x_{m2}\right\| \left\| \tau _{dm}+\bar{\varepsilon }_{m}(Z_{m})\right\| \nonumber \\&-\epsilon _{s}^\mathrm{T}k_{s1}\epsilon _{s}-\Delta x_{s2}^\mathrm{T}k_{s2}\Delta x_{s2}-\Delta x_{s2}^\mathrm{T}D_{s}\Delta x_{s2}\nonumber \\&+\, \left\| \Delta x_{s2}\right\| \left\| \tau _{ds}+\bar{\varepsilon }_{s}(Z_{s})\right\| \nonumber \\&-\frac{\left\| \Delta x_{m2}\right\| ^{2}}{\left\| \Delta x_{m2}\right\| +e^{-\kappa _{m}t}}\hat{\theta }_{m}-\frac{\left\| \Delta x_{s2}\right\| ^{2}}{\left\| \Delta x_{s2}\right\| +e^{-\kappa _{s}t} }\hat{\theta }_{s}\nonumber \\&-(\theta _{m}-\hat{\theta }_{m})\frac{\left\| \Delta x_{m2}\right\| ^{2}}{\left\| \Delta x_{m2}\right\| +e^{-\kappa _{m}t}}\nonumber \\&-\, (\theta _{s} -\hat{\theta }_{s})\frac{\left\| \Delta x_{s2}\right\| ^{2}}{\left\| \Delta x_{s2}\right\| +e^{-\kappa _{s}t}} \end{aligned}$$
(31)

with \(\theta _{m}=\left\| \tau _{dm}+\bar{\varepsilon }_{m}(Z_{m})\right\| \) and \(\theta _{s}=\left\| \tau _{ds}+\bar{\varepsilon }_{s}(Z_{s})\right\| \), we have

$$\begin{aligned} \dot{V} \le&-\epsilon _{m}^\mathrm{T}k_{m1}\epsilon _{m}-\Delta x_{m2}^\mathrm{T} k_{m2}\Delta x_{m2}\nonumber \\&-\, \Delta x_{m2}^\mathrm{T}D_{m}\Delta x_{m2}+e^{-\kappa _{m}t} \theta _{m}\nonumber \\&-\epsilon _{s}^\mathrm{T}k_{s1}\epsilon _{s}-\Delta x_{s2}^\mathrm{T}k_{s2}\Delta x_{s2}\nonumber \\&-\, \Delta x_{s2}^\mathrm{T}D_{s}\Delta x_{s2}+e^{-\kappa _{s}t}\theta _{s} \end{aligned}$$
(32)

Integrating both sides of the above equation from \(t=0\) to \(T\), yields

$$\begin{aligned} V(T)-V(0)\le&-\int _{0}^{T}(\epsilon _{m}^\mathrm{T}k_{m1}\epsilon _{m}+\epsilon _{s}^\mathrm{T}k_{s1}\epsilon _{s}\nonumber \\&+\, \Delta x_{m2}^\mathrm{T}k_{m2}\Delta x_{m2}+\Delta x_{s2}^\mathrm{T}k_{s2}\Delta x_{s2}\nonumber \\&+\Delta x_{m2}^\mathrm{T}D_{m}\Delta x_{m2}+\Delta x_{s2}^\mathrm{T}D_{s}\Delta x_{s2})\hbox {d}t\nonumber \\&+\, \theta _{m}\int _{0}^{T}e^{-\kappa _{m}t}dt+\theta _{s}\int _{0} ^{T}e^{-\kappa _{s}t}\hbox {d}t \end{aligned}$$
(33)

Since \(V(T)\ge 0\), \(\int _{0}^{T}e^{-\kappa _{m}t}\hbox {d}t<\infty \) and \(\int _{0} ^{T}e^{-\kappa _{s}t}\hbox {d}t<\infty \) hold

$$\begin{aligned}&\underset{T\rightarrow \infty }{\lim }\sup \frac{1}{T}\int _{0}^{T}\left( \epsilon _{m}^\mathrm{T}k_{m1}\epsilon _{m}+\epsilon _{s}^\mathrm{T}k_{s1}\epsilon _{s}+\Delta x_{m2}^\mathrm{T}k_{m2}\Delta x_{m2}\right. \nonumber \\&\left. \quad \quad +\,\Delta x_{s2}^\mathrm{T}k_{s2}\Delta x_{s2}+\Delta x_{m2}^\mathrm{T}D_{m}\Delta x_{m2}+\Delta x_{s2}^\mathrm{T}D_{s}\Delta x_{s2}\right) \hbox {d}t\nonumber \\&\quad \le (V(0)+\theta _{m}\int _{0}^{T}e^{-\kappa _{m}t}\hbox {d}t + \theta _{s}\int _{0} ^{T}e^{-\kappa _{s}t}\hbox {d}t)\underset{T\rightarrow \infty }{\lim }\frac{1}{T}\!=\!0 \end{aligned}$$
(34)

From (18), (22), (29) and (32), with \(V\ge 0\) and \(\dot{V}\le 0\), we have that \(\epsilon _{m}\), \(\epsilon _{s}\) are bounded and \(\epsilon _{m}\), \(\epsilon _{s}\), \(\Delta x_{m2}\), \(\Delta x_{s2}\) converge to zero as \(t\rightarrow \infty \). Therefore, from Eq. (11) and the definitions of \(\Delta x_{m2}\), \(\Delta x_{s2}\), the prescribed synchronization performance is obtained. Moreover, the position synchronization errors asymptotically converge to zero as \(t\rightarrow \infty \).

Remark 3

The steady-state performance has been investigated in many literatures for the bilateral teleoperation system [6–14]. However, to our best knowledge, there are almost no transient-state performance control results for teleoperation system. In this paper, an appropriate function that characterizes the convergence rate, maximum overshoot, and steady-state error is adopted and incorporated into an output error transformation, and thus, the stabilization of the transformed system is sufficient to achieve original synchronization control with prescribed performance. Moreover, with the prescribed control performance, the controller gains are easily selected.\(\square \)

Remark 4

For the practical teleoperation design, the synchronization accuracy and synchronization time are very important. The existing teleoperation control design methods can guarantee that the synchronization error converges to zero asymptotically. It is well known that the state variables reach zero when \(t\rightarrow \infty \) for the asymptotical stability. It is obvious that, only the stability performance can be guaranteed with the asymptotical stability. For some precise teleoperation job, for example tele-surgery, we expect the synchronization error converges to a satisfied region in finite time, i.e., not only the steady-state performance, but also the transient-state performance also should be obtained. With the proposed control scheme (25), the synchronization errors between the master manipulator and the slave manipulator will converge to zero with the prescribed convergence speed.

Remark 5

The PPC-based synchronization controllers are designed for the master and the slave robots in the presence of system uncertainties and external disturbances. Compared with the literature about teleoperation system [6–11], the influence from the unknown system parameter and the external disturbance is compensated successfully. The FLs is used to estimate the system uncertainties. Moreover, adaptive method is also applied to compensate the fuzzy estimation error and the bounded external disturbance. Good synchronization performance is achieved by combining of the FLs and the adaptive method.

Remark 6

In this paper, the damping forces from the human operator and the external disturbances are considered. Similarly, with the new controller (25), the prescribed synchronization control performance also can be guaranteed when the closed-loop teleoperation system presented as (8) in free motion, i.e., \(F_{h}=F_{e}=0\).

4 Simulation and experiment

4.1 Simulation on a teleoperation of 2-DOF planar manipulators

In order to show the effectiveness of the proposed scheme, some simulations are presented in this section, in which the local and remote manipulators are modeled as a pair of 2-DOF serial links. For simplicity, the identical master and slave manipulators are chosen. The specific definitions for the model are same as [10], and the friction functions are set as follows.

$$\begin{aligned} F_{i}(\dot{q}_{i})+f_{ci}(\dot{q}_{i})=F(\dot{q})+f_{c}(\dot{q}),\quad \text {for }i=m,s \end{aligned}$$

with

$$\begin{aligned} F\dot{q}+f_{c}(\dot{q})=\left[ \begin{array}{c} f_{d1}\dot{q}_{1}+k_{1}\hbox {sgn}(\dot{q}_{1})\\ f_{d2}\dot{q}_{2}+k_{2}\hbox {sgn}(\dot{q}_{2}) \end{array}\right] \end{aligned}$$

For simulation, we choose the parameters as \(m_{1}=1\)kg, \(m_{2}=1\)kg, \(l_{1}=0.5\)m, \(l_{2}=0.5\)m, \(g=9.81\hbox {m}/\hbox {s}^{2}\), \(f_{d1}=3\), \(f_{d2}=4\), \(k_{1} =5\), \(k_{2}=4\), \(\tau _{di}=\left[ \begin{array}{c} 0.3q_{_{1}}\dot{q}_{_{1}}\sin t\\ 0.3q_{_{2}}\dot{q}_{_{2}}\sin t \end{array}\right] \). \(\rho _{m}(0)=\rho _{s}(0)=1.5\), \(\rho _{m}(\infty )=\rho _{s}(\infty )=0.02\), \(\delta =1\), \(\alpha _{m}=\alpha _{s}=1.4\). The controller parameters are set as \(k_{m1}=\hbox {diag}(15,15)\), \(k_{m2}=\hbox {diag}(30,15)\), \(k_{s1}=\hbox {diag}(20,20)\), \(k_{s2}=\hbox {diag}(30,15)\). The initial joint configurations of the master and slave are set as \(q_{m}(0)=[0.2pi\) \(0.1pi]^\mathrm{T}\) and \(q_{s}(0)=[0.1pi\) \(0.12pi]^\mathrm{T}\) . The velocities of master and the slave manipulators are set as \(\dot{q} _{m}=\left[ \begin{array}{ll} 0&0 \end{array} \right] ^\mathrm{T}\), \(\dot{q}_{s}=\left[ \begin{array}{ll} 0&0 \end{array} \right] ^\mathrm{T}\). We set \(D_{m}=D_{s}=\hbox {diag}(10,10)\). The asymmetric constant time delays are chosen as \(T_{m}=0.5\)s and \(T_{s}=0.7\)s.

Consider the case that the human operator and the remote environment insert damping torques. The human operator inserting torques are shown in Fig. 1, and the environment inserting torques are shown in Fig. 2. To illustrate the effectiveness of the proposed control method (25), the comparisons with the traditional controller are presented. When set \(\varepsilon _{i}=e_{i}\), \(\rho _{i}=1\), \(\dot{\rho }_{i}=0\) and \(\partial R=I_{n}\), the adaptive fuzzy-based prescribed performance controllers proposed in this paper are changed into traditional adaptive fuzzy controllers as follows.

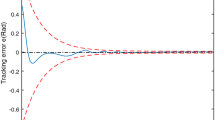
$$\begin{aligned} \tau _{m} =&-k_{m2}(x_{m2}-x_{s2}(t-T_{s}))+\hat{F}_{m}(Z_{m})\nonumber \\&-\, e_{m}-\frac{x_{m2}-x_{s2}(t-T_{s})}{\left\| x_{m2}-x_{s2} (t-T_{s})\right\| +e^{-\kappa _{m}t}}\hat{\theta }_{m}\\ \tau _{s} =&-k_{s2}(x_{s2}-x_{m2}(t-T_{m}))+\hat{F}_{s}(Z_{s})\nonumber \\&-\, e_{s}-\frac{x_{s2}-x_{m2}(t-T_{m})}{\left\| x_{s2}-x_{m2} (t-T_{m})\right\| +e^{-\kappa _{s}t}}\hat{\theta }_{s}\nonumber \end{aligned}$$
(35)

With the proposed controller (25) and the general adaptive fuzzy controller (35), the joint position errors for master are shown in Figs. 3 and 4. The joint position errors for the slave are shown in Figs. 5 and 6. As we can see in these four figures, with the proposed PPC-based controller (25), the synchronization errors are prevented from transgressing the constrained region during the transient stages. Thus, both the transient-state performance and the steady-state performance can be guaranteed. However, with the general adaptive fuzzy controller (35), the synchronization errors will transgress the boundaries during the transient stages. Therefore, it is clear that with the same controller gain, the system with the prescribed performance controller can achieve a better synchronization performance. The control torques for the master manipulator and the slave manipulator are shown in Figs. 7 and 8, respectively.

Fig. 1
figure 1

The human insert torques

Full size image
Fig. 2
figure 2

The environment insert torques

Full size image
Fig. 3
figure 3

The position errors of the first joint at master side

Full size image
Fig. 4
figure 4

The position errors of the second joint at master side

Full size image
Fig. 5
figure 5

The position errors of the first joint at slave side

Full size image
Fig. 6
figure 6

The position errors of the second joint at slave side

Full size image
Fig. 7
figure 7

The control torques at master side

Full size image
Fig. 8
figure 8

The control torques at slave side

Full size image

Next, we will consider the case that the human operator inserts a nonpassive force, while there is no contact force between the slave manipulator and the remote environment. We apply a human force \(F\) to the master site in the Y-direction, which is shown in Fig. 9. The human-input force is \(0\) at \(0\) s and then increases to \(10\) N and it decreases to zero from \(1\) to \(2\) s. The simulation results are used to verify the following: (1) When we move the master robot, does the slave track the trajectory of the master. (2) When the human-input force changes to zero, does the synchronization error between the master and slave positions converge to zero and the synchronization error stay in the constrained region. The synchronization errors of the master and the slave are shown in Figs. 10 and 11. From these figures, we can see that the prescribed performance also can be guaranteed when the teleoperation system in free motion.

Fig. 9
figure 9

The human operator insert forces

Full size image
Fig. 10
figure 10

The position errors at master side

Full size image
Fig. 11
figure 11

The position errors at slave side

Full size image

4.2 Experiment on a teleoperated pair of 3-DOF PHANToM manipulator

The teleoperation system for the experiments consists of two Phantom Premium \(1.5A\) robots (SensAble Technologies, Inc.), which have three DOFs (see Fig. 12). The two robotic manipulators are connected by two computers that are connected via the Internet network. The network environment can be set in the network-simulator block. The controller is established with the MATLAB software. First, we set the time delay as \(T_{m}=100\) ms and \(T_{s}=100\) ms. The joint positions for the master and the slave are shown in Fig. 13. It should be noticed that the three sub-figures in Fig. 13 stand for the first joint, the second joint and the third joint, respectively. The position errors at the slave side are shown in Fig. 14. Then the time delays are set as \(T_{m}=500\) ms and \(T_{s}=500\) ms. The experimental results of joint positions and the position errors are shown in Figs. 15 and 16, respectively. Finally, we set the time delays are \(T_{m}=800\) ms and \(T_{s}=800\) ms. The experimental results of joint position and the position errors are shown in Figs. 17 and 18, respectively. From these figures, it is clear that when we move the master, the slave can track the trajectory of the master. Moreover, the synchronization errors are always within the prescribed performance boundaries.

Fig. 12
figure 12

Teleoperation system

Full size image
Fig. 13
figure 13

The joint position of the master and the slave

Full size image
Fig. 14
figure 14

The position errors at slave side

Full size image
Fig. 15
figure 15

The joint position of the master and the slave

Full size image
Fig. 16
figure 16

The position errors at slave side

Full size image
Fig. 17
figure 17

The joint position of the master and the slave

Full size image
Fig. 18
figure 18

The position errors at slave side

Full size image

5 Conclusion

This paper has studied the prescribed performance synchronization control problem for the networked bilateral teleoperation system with asymmetric time delay. In the presence of the system uncertainties and the external disturbances, we propose a new adaptive fuzzy-based PPC design method. With the new controller, the synchronization errors between the master and the slave converge to zero asymptotically. Moreover, the prescribed transient performance is guaranteed. Finally, the simulation and experiment are both performed, and the results verify the effectiveness of the presented control approach. In the future, the PPC will be extended to more complex systems like stochastic systems and other application domains [31–33].