1 Introduction

The design of nonlinear missile interception guidance and control algorithm is among the most important and difficult components of modern missile missions. This type of problem has been widely studied during the past decades [1,2,3,4,5]. However, it is still difficult to design an optimal or near-optimal control strategy [6,7,8]. The main theoretical and practical challenges raising in these problems are the inherent nonlinearities of the missile–target dynamics, uncertainties in the aerodynamic model, target maneuver capability, measurement noises and variable/mission constraints.

To enhance the performance of interception, various robust control algorithms have been investigated [10, 11]. For example, Zhu et al. [10] applied a modified sliding-mode control to generate the guidance law, wherein the target acceleration was handled by the extended state observer. Similarly, in [11], considering the model uncertainties and target movement, a stochastic optimal guidance law was designed based on the Markov chain approximation technique. However, the reported works do not address the inside constraints such as the state and control limits or the velocity increment. In practical missile systems, these requirements should be considered in the controller designs.

The problem addressed in this research is a receding horizon pseudospectral control (RHPC) design for the integrated missile interception guidance and control problems. Traditionally, missile guidance and control systems are designed separately as two loops [2, 4]. That is, an inner loop autopilot is constructed in order to track the acceleration command generated by the outer loop guidance algorithm. However, such a design usually leads to large design iterations and does not fully exploit the relationships between different subsystems, thereby resulting in suboptimal performance [12]. In recent years, there has been a growing interest in the design of integrated guidance law and flight control system. For instance, in [9] the authors proposed an integrated sliding-mode controller for the guidance and control of interceptors. Besides, Panchal et al. [12] proposed a continuous-time predictive control-based integrated guidance and control algorithm to fulfill the 2-D missile–target interception mission. It was shown in these investigations that the end-game performance of the interceptor can be effectively enhanced by taking into account the coupling between the guidance and control dynamics. This is mainly because in a dual-control structure, additional degrees of freedom and more missile state information can be used. Due to these advantages, the integrated design of the missile guidance and control system, referred as integrated guidance and control (IGC) [13], is considered in this investigation.

The missile–target IGC algorithm designed in this work is mainly based on the implementation of model predictive control (MPC). The motivation of the use of receding horizon control (RHC) or MPC relies on its ability to deal with control and state constraints that naturally arise in practical applications [14, 15]. Contributions made to apply MPC can be found in the literature [16,17,18,19]. For example, Li et al. [16] proposed a neural network-based robust MPC algorithm to generate the optimal missile guidance law. Zhao et al. [17] designed an MPC-based algorithm in order to generate the multi-missile guidance law. Weiss et al. [18] implemented an MPC algorithm to solve the spacecraft rendezvous and docking problems. Wen et al. [19] developed a specific MPC scheme with output feedback for a deorbiting electrodynamic tether system. Recently, control algorithms based on pseudospectral methods have become popular to offer a promising alternative to MPC [15, 20, 21]. Pseudospectral methods can be used to solve optimal control problems under constraints using a specific discretization of the solution [23,24,25]. The main advantage with pseudospectral methods is that a high approximation accuracy can be achieved with much less temporal nodes, which means the size of the resulting static NLP problem can be decreased significantly. Therefore, the application of pseudospectral methods in MPC schemes can have positive influences in terms of improving the real-time computational performance.

One of the key components of the RHC schemes is the optimization process [16, 25,26,27]. Since the RHPC algorithm solves an open-loop optimal control problem at each sampling instant, the effectiveness and efficiency are largely affected by the optimization procedure employed. In order to meet the high real-time requirements of the RHPC scheme constructed in Sect. 3, a recently proposed NLP sensitivity-based optimization technique [28] is applied and embedded in the RHPC framework. This algorithm applies the implicit function theory, where the optimal solution is found around a continuously updated reference solution. A detailed description of this near-optimal gradient-based method can be found in [28, 29]. By applying this technique, the complicated solution finding can be avoided by approximating the optimal solution inexactly. This indicates that the online computational performance of the proposed RHPC method can be improved.

The main contributions of the work reported in this paper are twofold. Firstly, prior to performing the MPC-based IGC algorithm, the presence of noise in the measurement of the model state is decreased by implementing an MHE technique. Secondly, different from the work carried out in [16], the online MHE+MPC optimization model is solved using a pseudospectral method so as to improve the solution finding accuracy. Moreover, the computational performance of the optimization process is enhanced by analyzing the NLP sensitivity of the solutions at two consecutive update time instants. It is worth noting that currently there are many effective state estimation methods available in the literature. For example, the use of extended Kalman filter (EKF) and particle filter (PF) is two well-known state estimation strategies. The EKF is one of the most widely applied state estimate approaches for nonlinear process control due to its strong generality. To apply the EKF, the nonlinear system equation will be linearized such that the classical KF becomes applicable. One main challenge of using EKF is that in some applications, the calculation of the Jacobian might become nontrivial. Besides, it requires the system nonlinearity to be mild such that the linearization of the system equation will not result in large divergence or approximation error. On the other hand, the PF applies a set of samples/particles in order to approximate the posterior density function. Compared with the EKF, it does not require to compute the Jacobian and needs less computational power. Moreover, if the size of the particle set goes to infinity, the PF can achieve asymptotically optimal estimation performance. However, a major disadvantage of the PF is that it usually suffers from the phenomena of degeneracy, and it tends to be sensitive with respect to the initial guess value. The MHE approach deals with the state estimation by formulating an optimization model defined over a finite moving horizon. This technique has the capability in handling nonlinear system dynamics as well as variable constraints. Furthermore, by applying the MHE state estimator, the assumption of specific error distribution is no longer necessary. Although solving an optimization model online may result in a high computational burden, the implementation of the sensitivity-based optimization method can effectively deal with this issue, thus making the MHE a potentially useful alternative for the considered missile–target intercept problem.

The rest of this paper is organized as follows. The overall interception strategy and the nonlinear dynamics of the three-dimensional missile–target system are provided in Sect. 2. The main results are provided in Sect. 3, where a moving horizon state estimation is combined with a RHPC scheme to achieve the interception in the presence of measurement noises. Numerical simulations are provided in Sect. 4 to illustrate the effectiveness of the proposed IGC strategies. The concluding remarks are given in Sect. 5.

2 Missile–target nonlinear model

2.1 2-D missile–target engagement

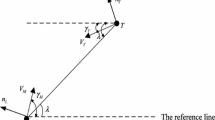
Let us consider a standard 2-D geometry of planar interception scenario illustrated in Fig. 1. The corresponding nonlinear kinematics are given by [2, 4, 10]:

$$\begin{aligned}&{\dot{r}}=V_{T}\cos {(\theta -\varphi _{T})}-V_{M}\cos {(\theta -\varphi _{M})}\nonumber \\&{\dot{\theta }} = (-V_{T}\sin {(\theta -\varphi _{T})}+V_{M}\sin {(\theta -\varphi _{M})})/r\nonumber \\&{\dot{\varphi }}_{M} = \frac{A_{M}}{V_{M}}\nonumber \\&{\dot{\varphi }}_{T} = \frac{A_{T}}{V_{T}} \end{aligned}$$
(1)

where r is the range along the line of sight (LOS). \(V_{T}\) and \(A_{T}\) are target velocity and acceleration, respectively. Correspondingly, \(V_{M}\) and \(A_{M}\) represent the missile velocity and acceleration. \(\theta \) stands for the LOS angle. \(\varphi _{M}\) and \(\varphi _{T}\) are the flight path angle of the missile and target.

Fig. 1
figure 1

Missile–target engagement geometry

Full size image

Then, by considering the normal acceleration as the control input, the following state-space model of missile–target engagement formulation can be constructed [4, 10]:

$$\begin{aligned}&{\dot{r}}= V_{r}\nonumber \\&\dot{V_{r}} = \frac{V_{\theta }^{2}}{r}+A_{Tr}-A_{M}\sin {(\theta -\varphi _{M})}\nonumber \\&{\dot{\theta }} = \frac{V_{\theta }}{r}\nonumber \\&\dot{V_{\theta }} =-\frac{V_{r}V_{\theta }}{r}+A_{T\theta }-A_{M}\cos {(\theta -\varphi _{M})} \end{aligned}$$
(2)

where \(V_{r} = V_{T}\cos {(\theta -\varphi _{T})}-V_{M}\cos {(\theta -\varphi _{M})}\), \(V_{\theta }=-V_{T}\sin {(\theta -\varphi _{T})}+V_{M}\sin \)\((\theta -\varphi _{M})\). \(V_{\theta }\) can be treated as a transversal component of relative velocity rotating with the LOS. \(A_{Tr}=A_{T}\sin {(\theta -\varphi _{T})}\) and \(A_{T\theta }=A_{T}\cos {(\theta -\varphi _{T})}\). \(A_{Tr}\) and \(A_{T\theta }\) can be described as the projection components of the target acceleration.

During the engagement, the target maneuver is considered to be given by the first-order lag dynamics given by:

$$\begin{aligned} {\dot{A}}_{T} = (A_{T}^{c}-A_{T})/\tau _{T} \end{aligned}$$
(3)

where \(A_{T}^{c}\) is the commanded target acceleration, while \(\tau _{T}\) is the time constant associated with the target dynamics. Subsequently, the pitch plane dynamics for the missile should be constructed so as to describe the missile attitude related to the inertial frame. That is,

$$\begin{aligned} \begin{array}{l} {\dot{\alpha }} = q-(L_{\alpha }^{\beta }f_{1}(\alpha )+L_{\delta }f_{2}(\alpha +\delta ))/V_{M} \\ {\dot{q}} = M_{\alpha }^{\beta }f_{3}(\alpha )+ M_{\delta }f_{4}(\alpha +\delta )+M_{q}q\\ {\dot{\delta }} = (\delta _{c}-\delta )/\tau _{s} \end{array} \end{aligned}$$
(4)

where \(\alpha \) denotes the angle of attack; q stands for the pitch rate; \(\delta \) and \(\delta _{c}\) are, respectively, the actual and demanded deflection angles. Similar to Eq. (3), \(\delta \) is established by the first-order dynamics with the time constant \(\tau _{s}\). \(L_{\alpha }^{\beta }\), \(L_{\delta }\), \(M_{\alpha }^{\beta }\), \(M_{\delta }\) and \(M_{q}\) are the aerodynamic forces and pitch moments acting on the missile, respectively. \(f_{i}, i=1,2,3,4\), are saturation functions denoting the nonlinear aerodynamic characteristics of the missile. Based on the engagement equations and pitch plane dynamics, the integrated model is then established. Let us rewrite the dynamic equations by defining the state variable in a more compact form (e.g., \(x=[r, V_{r}, \theta , V_{\theta }, A_{T}, \alpha , q, \delta ]^{T}=[x_{1},x_{2},x_{3}\), \(x_{4},x_{5},x_{6},x_{7},x_{8}]^{T}\)). Then Eqs. (2)–(4) in the state space can be given by:

$$\begin{aligned} {\dot{x}} = f(x(t),u(t),t) \end{aligned}$$
(5)

where \(f\in \mathfrak {R}^{8}\) is the right-hand side of the dynamic Eqs. (2)–(4). \(u=\delta _{c}\) is the control input.

In this study, we aim at the integrated guidance and control law design in the presence of model uncertainties and noise measurements of the state model. The objective is to design an optimization-based predictive controller such that the state variables (given by Eq. (2)) can be stabilized to the origin.

2.2 3-D missile–target engagement

The mission scenario can be easily extended to a 3-D case. To better illustrate the 3-D engagement system, equations of motion for the missile and target are constructed separately as follows:

$$\begin{aligned} \begin{array}{l} \hbox {Missile}{:} \left\{ \begin{array}{l} {\dot{X}}_{M} = V_{M}\sin {\varphi _{Ma}}\cos {\varphi _{Me}}\\ {\dot{Y}}_{M} = V_{M}\cos {\varphi _{Ma}}\sin {\varphi _{Me}}\\ {\dot{Z}}_{M} = V_{M}\sin {\varphi _{Me}} \end{array}\right. \\ \hbox {Target}{:}\left\{ \begin{array}{l} {\dot{X}}_{T} = V_{T}\sin {\varphi _{Ta}}\cos {\varphi _{Te}}\\ {\dot{Y}}_{T} = V_{T}\cos {\varphi _{Ta}}\sin {\varphi _{Te}}\\ {\dot{Z}}_{T} = V_{T}\sin {\varphi _{Te}} \end{array} \right. \end{array} \end{aligned}$$
(6)

where \(\varphi _{Ma}\), \(\varphi _{Ta}\), \(\varphi _{Me}\) and \(\varphi _{Te}\) are azimuth and elevation angles of the missile and target, respectively. Based on Eq. (6), the 3-D dynamic model of the missile–target engagement system is constructed as follows:

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{l} {\dot{r}} = V_{T}\cos (\theta _{y}-\varphi _{Te})\cos (\theta _{z}-\varphi _{Ta})\\ \qquad -V_{M}\cos (\theta _{y}-\varphi _{Me})\cos (\theta _{z}-\varphi _{Ma})\\ {\dot{\theta }}_{z} = (V_{T}\sin (\theta _{z}-\varphi _{Ta})-V_{M}\sin (\theta _{z} \\ \qquad -\varphi _{Ma}))/r\\ {\dot{\theta }}_{y} = (V_{T}\cos (\theta _{z}-\varphi _{Ta})\sin (\theta _{y}-\varphi _{Te})\\ \qquad -V_{M}\cos (\theta _{z}-\varphi _{Ma})\sin (\theta _{y}\\ \qquad -\varphi _{Me}))/r\cos \theta _{z}\\ {\dot{\varphi }}_{Ta} = A_{Ty}/V_{T}\\ {\dot{\varphi }}_{Te} = A_{Tz}/V_{T}\\ {\dot{\varphi }}_{Ma} = A_{My}/V_{M}\\ {\dot{\varphi }}_{Me} = A_{Mz}/V_{M} \end{array} \right. \end{array} \end{aligned}$$
(7)

where \(\theta _{y}\) and \(\theta _{z}\) are the LOS angles. Eq. (7) can be analogized using the 2-D engagement system given by Eq. (1). The target acceleration is again modeled as: \({\dot{A}}_{Ty}=(A_{Ty}^{c}-A_{Ty})/\tau _{T}\) and \({\dot{A}}_{Tz}=(A_{Tz}^{c}-A_{Tz})/\tau _{T}\), where \(A_{Ty}\) and \(A_{Tz}\) stand for the yaw and pitch lateral accelerations. A detailed description of the 3-D case missile–target interception geometry is depicted in Fig. 2.

Remark 1

It is worth remarking that in some relative references and the missile–target dynamic model used in this paper, the effect of gravity was omitted to simplify the engagement formulation. For the design of guidance and control command, the gravitational effects can be taken into account by simply subtracting the gravity from the acceleration command. This strategy considers the gravity implicitly, and it might result in some deviations from the real system. Future works should be carried out in order to explicitly incorporate gravity compensation into the missile–target engagement system such that the effect of gravity can be optimally compensated.

Fig. 2
figure 2

3-D missile–target engagement geometry

Full size image

3 Receding horizon pseudospectral control

3.1 Discrete approximation model

For the numerical solutions of the RHPC problems, the multi-interval Legendre–Gauss–Radau (LGR) pseudospectral method is applied to parameterize the continuous-time equations of state dynamics given by Eq. (5) [20, 23,24,25]. The motivation of the use of pseudospectral algorithm relies on its high accuracy in function approximation. A detailed introduction with respect to the different classes of pseudospectral methods can be found in [23]. The time horizon is divided into \({\tilde{N}}\) mesh intervals \([t_{i},t_{i+1}]\) for \(i=1,\ldots ,{\tilde{N}}\). The mesh grid points are equally spaced and the \(\Theta \) is assumed to be the length of the mesh interval. By using the Lagrange interpolation, the state and control variables are discretized over the ith time interval as:

$$\begin{aligned} x^{(i)}(t)\approx X^{(i)}(t)= & {} \mathop \sum \limits _{j=1}^{N_{k}+1}x_{j}^{(i)}L_{j}^{(i)}(t) =\Phi ^{(i)}x^{(i)} \end{aligned}$$
(8)
$$\begin{aligned} u^{(i)}(t)\approx U^{(i)}(t)= & {} \mathop \sum \limits _{j=1}^{N_{k}}u_{j}^{(i)}L_{j}^{(i)}(t) = \Phi ^{(i)}u^{(i)} \end{aligned}$$
(9)

where \(j=1,2,\ldots ,N_{k}\), \(N_{k}\) is the number of LGR collocation points. \(t_{j}\in [t_{i},t_{i+1}]\) can be obtained by solving \(P_{K-1}(t)+P_{K}(t)=0\), where \(P_{K}\) is the Kth-order Legendre polynomial. \(a(\cdot )\) is a positive weight function. \(\Phi ^{(i)} = [L_{1}^{(i)},L_{2}^{(i)},\ldots ,L_{N_{k}}^{(i)}]\) where \(L_{j}^{(i)}\) is the Lagrange interpolation basis function.

One advantage of using pseudospectral approximation is that the derivative of the state equations (e.g., \({\dot{x}}(t)=f(x(t),u(t),t)\)) can be obtained by differentiating the approximation function:

$$\begin{aligned} \begin{array} {ll} {\dot{x}}^{(i)}(t) = \frac{dx^{(i)}(t)}{dt} &{} \approx \frac{dx^{(i)}(t)}{dt}\\ &{}= \sum \limits _{j=1}^{N_{k}+1}\frac{d}{dt}(\frac{a(t)}{a(t_{j})}L_{j}^{(i)}(t))x_{j}^{(i)} \end{array} \end{aligned}$$
(10)

Note that the term \(\frac{d}{dt}(\frac{a(t)}{a(t_{j})}L_{j}(t))\) can be obtained at collocation points and it can be compacted into a differentiation matrix. That is,

$$\begin{aligned} D_{jk} = \frac{d}{dt}(\frac{a(t)}{a(t_{j})}L_{j}^{(i)}(t))\mid _{t=t_{j}} \end{aligned}$$
(11)

where \(D_{jk}\) denotes the elements of the \(N_{k}\times (N_{k}+1)\) differentiation matrix and can be calculated by the following equation:

$$\begin{aligned} D_{jk} = \left\{ \begin{array}{ll} \frac{-N_{k}(N_{k}+2)}{4}, &{} k=j=0\hbox {;} \\ \frac{L_{N_{k}}(t_{j})}{L_{N_{k}}(t_{k})}\frac{1}{t_{j}-t_{k}}, &{} k\ne j, \quad 1\le k, \quad j\le N_{k}\hbox {;} \\ \frac{-1}{2(1-t_{j})}, &{} 1\le k=j\le N_{k}\hbox {} \end{array} \right. \nonumber \\ \end{aligned}$$
(12)

In order to clearly show the approximation accuracy of the Legendre–Gauss–Radau pseudospectral method (LGRPM), Fig. 3 shows a comparison between the approximations of an open-loop optimal control solutions using LGRPM and zero-order hold (ZOH) functions (commonly used in the MPC framework [16, 18]).

Fig. 3
figure 3

Approximation comparison of an open-loop optimal control problem

Full size image

This example can also be understood as a convergence analysis of open-loop solution to the exact solution and the problem formulation associated with it is defined as follows:

$$\begin{aligned} \begin{array}{cl} \hbox {minimize} &{} J = \frac{1}{2}\displaystyle {\int _{0}^{1}[ u(t)^{2}+x(t)u(t)+1.25x(t)^{2}]}dt\\ \hbox {subject to} &{} {\dot{x}}(t) = 0.5x(t)+u(t), \quad x(0) = 1 \end{array} \end{aligned}$$

The exact state and control trajectories to this problem are:

$$\begin{aligned} \begin{array}{l} x^{*}(t)=\frac{\cosh {(1-t)}}{\cosh {(1)}} \\ u^{*}(t)=-\frac{\sinh {(1-t)}+0.5\cosh {(1-t)}}{\cosh {(1)}} \end{array} \end{aligned}$$

The approximation errors are measured using the maximum base ten logarithm of the state and control variables. That is,

$$\begin{aligned} \begin{array}{l} E_{x}=\max \limits _{j}\log _{10}|x_{j}-x^{*}(t_{j})| \\ E_{u}=\max \limits _{j}\log _{10}|u_{j}-u^{*}(t_{j})| \end{array} \end{aligned}$$

As shown in Fig. 3, LGRPM can produce almost identical results with the exact solution. However, ZOH functions cannot achieve such a high accuracy. In addition, the algorithm will steer the approximation error to zero as the number of basis functions increases.

Remark 2

It is worth noting that one well-known issue with pseudospectral optimal control is the choice of collocation points. For optimal control of underactuated nonlinear dynamical systems (e.g., the missile dynamical system), the approximation to the dynamics may be poor if the current mesh grid is chosen improperly. This brings the development of mesh refinement strategies. That is, the current mesh grid will be updated several times in order to achieve higher accuracy. In recent years, many effective mesh refinement strategies that can be embedded in the pseudospectral methods have been developed. In this paper, we are interested in applying the pseudospectral method to solve the MHE and MPC formulation. A detailed analysis of the approximation error order of the pseudospectral method is beyond the scope of this paper. We refer to [33] for such an analysis.

Remark 3

One important issue of mesh refinement-based pseudospectral methods is that it may result in several calls to the NLP solver and a significant computational cost. Due to the lack of physical knowledge of the system dynamics and the uncertainties/noises in the model, it is usually hard to select a proper accuracy threshold of the mesh refinement process. Therefore, to make a trade-off between the approximation accuracy and real-time applicability, the multi-interval LGR pseudospectral method with fixed number of collocation points is applied to produce a relatively dense mesh grid. This mesh grid setting is given in the simulation section and perturbations of this number will only result in negligible differences of the results.

3.2 Moving horizon estimation

As a technique based on numerical optimization, the nonlinear MPC constructs a series of optimal control problems to optimize a specified objective function while accounting for the system dynamics and constraints [26]. The design of optimization-based controllers is usually based on the assumption of full state feedback. However, in some practical applications (e.g., the missile interception guidance and control), there might be some measurement noises in the system, and thus, the state variables are not directly available [11, 12]. To address this problem, an MHE technique is developed by constructing an online suboptimization problem.

In the absence of measurement noise, the relationships between the measurable outputs and the integrated missile–target state variables are defined as \(y=h(x)\). \(h(\cdot )\) is a mapping from the missile–target state space to the measurable output space. Note that in many practical scenarios, only a part of states are available for measurement. In these cases, it is necessary to reconstruct the state information using a limited number of measurement. For the MHE optimization process, the solution finding is carried out using the latest \({\bar{N}}\) measurements \(y_{j}^{i}\) obtained at the sampling time instants \(t_{j}^{i}\), where \(i=1,\ldots ,{\bar{N}}\). Using the LGRPM method to approximate the dynamics, the MHE subproblem can then be formulated as follows:

$$\begin{aligned} \begin{array}{cll} \hbox {minimize} &{} J_{MHE} = \sum \limits _{i=1}^{{\bar{N}}} \Vert h(z_{j}^{(i)})-y_{j} \Vert _{2}^{2} &{}\\ &{} &{} \\ \hbox {subject to} &{} \forall t_{j}^{(i)}\in [t_{i},t_{i+1}] &{} \\ &{} \displaystyle {\sum _{k=1}^{N_{k}+1}}D_{jk}^{(i)}z_{j}^{(i)} = \frac{t_{i+1}-t_{i}}{2}f(z_{j}^{(i)}, u_{j}^{(i)}, t_{j}^{(i)})&{} \\ &{} z_{j} - z_{max} \le 0 &{}\\ &{} u_{j} - u_{max} \le 0 &{} \end{array}\nonumber \\ \end{aligned}$$
(13)

where \(z_{j}\) stands for the state estimation at time instant \(t_{j}\), whereas \(h(z_{j})\) is the actual measured value. Usually, an initial state estimation term should also be introduced in the objective function. However, for the missile–target intercept problem, it is assumed to have a known initial state vector of the engagement system.

The motivation for the use of MHE over standard tools such as the extended Kalman filter (EKF) relies on its ability in dealing with highly nonlinear system dynamics (e.g., the nonlinear missile–target engagement system considered in this study). The EKF is computationally efficient, but it requires both the variances of the noises to be small and the system nonlinearities to be mild such that the linearization of dynamics can still be valid. On the other hand, utilizing the MHE algorithm requires more computational efforts since it needs to solve the nonconvex nonlinear optimization problems related to the MHE formulation. However, one advantage of using the MHE formulation (13) is that only the latest \({\bar{N}}\) measurements are taken into account instead of all the \(N_{k}\) measurements. Therefore, the computational complexity can be reduced significantly and the online performance can also be improved.

The objective function of Eq. (13) is a measure of the missile–target state estimation errors. It is worth noting that the state estimate at the time instant \(t_{k+1}\) (e.g., \(z_{N_{k}+1}^{({\bar{N}})}\)) is used as the initial condition of the subsequent model predictive pseudospectral control step.

3.3 Receding horizon pseudospectral control

MPC can be regarded as an iterative optimization process that produces control moments by performing a moving horizon trajectory optimization [26, 27]. The control is periodically recalculated with the current state as an initial condition, thus providing a feedback action that can improve robustness to uncertainties and disturbances.

By using the updated initial condition \(x_{1}^{(1)}=z_{N_{k}+1}^{({\bar{N}})}\), the moving prediction horizon of the kth RHPC optimization problem becomes \([t_{k+1}, t_{k+1}+T]\), where \(T={\widetilde{N}}\Theta \). That is, the moving horizon of the RHPC formulation consists of \({\widetilde{N}}\) sampling intervals. Considering that the control objective of the RHPC is to drive the missile–target system given by Eq. (5) to the origin, the following stage cost function can be formulated:

$$\begin{aligned} J_{\textit{RHPC}}= & {} \displaystyle {\sum _{i=1}^{{\widetilde{N}}}}\displaystyle {\int _{t_{k+1}}^{t_{k+1}+{\widetilde{N}}\Theta }}(x^{(i)})^{T}Qx^{(i)}+(u^{(i)})^{T}Ru^{(i)}dt \nonumber \\ \end{aligned}$$
(14)

where \(i=1,\ldots ,{\widetilde{N}}\). \(Q\in \mathfrak {R}^{4\times 4}\) is a semi-definite matrix. \(R\in \mathfrak {R}^{1\times 1}\) is a symmetric positive definite matrix. By introducing \(\psi (x^{(i)}, u^{(i)}, t^{(i)})=(x^{(i)})^{T}Qx^{(i)}+(u^{(i)})^{T}Ru^{(i)}\) and using a Gauss quadrature to approximate the integral term, the RHPC cost can be rewritten as:

$$\begin{aligned} \begin{array}{c} {\bar{J}}_{\mathrm{RHPC}} = \displaystyle {\sum _{i=1}^{{\widetilde{N}}}}\displaystyle {\sum _{j=1}^{N_{k}}}\omega _{j}\psi (x_{j}^{(i)}, u^{(i)}, t_{j}^{(i)})\\ \end{array} \end{aligned}$$
(15)

where \(\omega _{j}\) is the LGR weight and defined as:

$$\begin{aligned} \omega _{j} = \int _{-1}^{+1}L_{j}(t)\mathrm{d}t \end{aligned}$$
(16)

According to [23], Eq. (16) can be rewritten as:

$$\begin{aligned} \omega _{j} = \left\{ \begin{array}{l@{\quad }l} \frac{2}{(N_{k}+1)^{2}}, &{} j=0; \\ \frac{1}{(N_{k}+1)^{2}}\frac{1-t_{j}}{[L_{N_{k}}(t_{j})]^{2}}, &{} j\ne 0 \end{array} \right. \end{aligned}$$
(17)

Therefore, the RHPC formulation is considered as an online optimal control problem which has the minimum value of cost function defined by Eq. (15) subject to the state, control and nonlinear algebraic constraints. Specifically, the RHPC optimization model can be given by:

$$\begin{aligned}&\begin{array}{lll} \hbox {minimize} &{} {\bar{J}}_{\textit{RHPC}} = \displaystyle {\sum _{i=1}^{{\widetilde{N}}}}\displaystyle {\sum _{j=1}^{N_{k}}}\omega _{j}\psi (x_{j}^{(i)}, u_{j}^{(i)}, t_{j}^{(i)}) &{}\\ \hbox {subject to} &{} \displaystyle {\sum _{k=1}^{N_{k}+1}}D_{jk}^{(i)}x_{j}^{(i)} = \frac{t_{i+1}-t_{i}}{2}f(x_{j}^{(i)}, u_{j}^{(i)}, t_{j}^{(i)})&{} \\ &{} x_{j}^{(i)} - x_{\mathrm{max}} \le 0 &{}\\ &{} u_{j}^{(i)} - u_{\mathrm{max}} \le 0 &{} \end{array}\nonumber \\ \end{aligned}$$
(18)

3.4 NLP optimality and approximated KKT conditions

One significant challenge of the optimization-based control strategies is that the computational cost associated with it can be high and usually cannot be afforded online [16, 28, 35]. To deal with this problem, a NLP sensitivity-based optimization method is applied and embedded in the RHPC framework. This technique improves the computational performance, by solving an easier, approximate problem.

Based on the constructed online optimization formulation shown in Eq. (18), the corresponding augmented Lagrange function is then given by:

$$\begin{aligned} {\mathscr {L}}= & {} \displaystyle {\sum _{i=1}^{{\widetilde{N}}}}\displaystyle {\sum _{j=1}^{N_{k}}}\omega _{j}\psi (x_{j}^{(i)}, u_{j}^{(i)}, t_{j}^{(i)}) + \lambda _{1}(x_{1}^{(i)}-z_{N_{k}+1}^{({\bar{N}})})\nonumber \\&+ \displaystyle {\sum _{j=1}^{N_{k}}}\lambda _{j}^{T}\left( \displaystyle {\sum _{k=1}^{N_{k}+1}}D_{jk}^{(i)}x_{j}^{(i)}-\frac{{\widetilde{N}}\Theta }{2}f(x_{j}^{(i)},u_{j}^{(i)},t_{j}^{(i)})\right) \nonumber \\&+ \displaystyle {\sum _{j=1}^{N_{k}}}\nu _{j}^{T}(x_{j}^{(i)} - x_{\mathrm{max}}) + \displaystyle {\sum _{j=1}^{N_{k}}}\mu _{j}^{T}(u_{j}^{(i)} - u_{\mathrm{max}})\nonumber \\ \end{aligned}$$
(19)

where \(\lambda _{j}, \nu _{j},\)\(\mu _{j}, j=1,\ldots ,N_{k}\) are vectors of the Lagrange multipliers. For simplicity in the presentation, the superscript representing the index of time interval is ignored in the following equations. The optimal solution of the optimization problem (18) should satisfy the first-order optimality or Karush–Kuhn–Tucker (KKT) conditions given by:

$$\begin{aligned} \begin{array}{l} \nabla _{\lambda _{1}}{\mathscr {L}} = x_{1}-z_{N_{k}+1}^{({\bar{N}})} = 0 \\ \nabla _{\lambda _{j}}{\mathscr {L}} = \displaystyle {\sum _{k=1}^{N_{k}+1}}D_{jk}x_{j}-\frac{{\widetilde{N}}\Theta }{2}f_{j} = 0\\ \nabla _{x_{j}}{\mathscr {L}} = \omega _{j}\nabla _{x_{j}}\psi _{j} + \displaystyle {\sum _{k=1}^{N_{k}+1}}\frac{\lambda _{k}}{\omega _{j}}D_{kj} - \frac{{\widetilde{N}}\Theta }{2}A_{j}^{T}\frac{\lambda _{j}}{\omega _{j}}\\ \qquad \qquad \quad +\,\nu _{j} = 0\\ \nabla _{u_{j}}{\mathscr {L}} = \omega _{j}\nabla _{u_{j}}\psi _{j} -\frac{{\widetilde{N}}\Theta }{2}B_{j}^{T}\frac{\lambda _{j}}{\omega _{j}}+\mu _{j} = 0 \end{array}\nonumber \\ \end{aligned}$$
(20)

where \(f_{j}:=f(x_{j},u_{j},t_{j})\), \(\psi _{j}:=\psi (x_{j},u_{j},t_{j})\), \(A_{j}^{T}:=\nabla _{x_{j}}f_{j}\) and \(B_{j}^{T}:=\nabla _{u_{j}}f_{j}\), respectively. By defining \(p:=z_{N_{k}+1}^{({\bar{N}})}\), the first-order nonlinear equations can be rewritten in a more condensed form:

$$\begin{aligned} \zeta (s(p,N_{k}+1),p) = 0 \end{aligned}$$
(21)

where \(s(p,N_{k}+1)\) is the solution vector and is given by \(s(p,N_{k}+1)^{T}=[x_{1}^{T},u_{1}^{T},\lambda _{1}^{T}, \nu _{1}^{T}, \mu _{1}^{T}\)\( x_{2}^{T},u_{2}^{T},\lambda _{2}^{T}, \nu _{2}^{T}, \mu _{2}^{T} \ldots , x_{N_{k}}^{T}, u_{N_{k}}^{T}, \lambda _{N_{k}}^{T}, \nu _{N_{k}}^{T}, \mu _{N_{k}}^{T}]\). The optimal solution is then defined as: \(s^{*}(p,N_{k}+1)\). NLP solvers based on Newton iteration search for a given solution \(s^{*}(p_{0},N_{k}+1)\) by successive linearization of Eq. (21) (e.g., first-order Taylor expansion) around the current searching point \(s^{j}\)\((p_{0},N_{k}+1)\), where j is the iteration index. This can be described as:

$$\begin{aligned} K(p_{0},N_{k}+1)\Delta {s}= & {} -\zeta (s(p_{0},N_{k}+1),p_{0})\nonumber \\ K(p_{0},N_{k}+1)= & {} \frac{\partial \zeta }{\partial s}|_{(s(p_{0},N_{k}+1),p_{0})} \end{aligned}$$
(22)

where K is the KKT matrix. Equation (22), combined with suitable adjustments to monitor the step length \(\Delta s\) (e.g., line search or trust region techniques), yields the optimal solution \(s^{*}(p_{0},N_{k}+1)\).

In order to improve the online performance of the optimization algorithm, the effect of perturbations on p around the nominal solution is analyzed. Then, these sensitivity results are used to approximate solutions to the neighboring problems. The general idea of the sensitivity-based optimization can be understood as exploiting the similarity between the solutions of the optimization problem at two consecutive update time instants. To achieve the approximation, the following theory regarding NLP sensitivity is introduced [28, 29].

Theorem 1

[28, 30] Consider the RHPC optimization problem given by Eq. (18) with \(f(\cdot )\) and \(\psi (\cdot )\) that are twice continuously differential in a neighborhood of the nominal solution \(s^{*}(p_{0},N_{k}+1)\), if the nominal solution \(s^{*}(p_{0},N_{k}+1)\) can satisfy the linear independence constraint qualifications (LICQ) [28, 30] and second-order sufficient conditions (SOSC) [28, 30], then

  1. 1.

    \(s^{*}(p_{0},N_{k}+1)\) is an isolated local optimal solution of the problem, and the associated Lagrange multipliers are unique.

  2. 2.

    For p in a neighborhood of \(p_{0}\), there exist a unique, continuous and differentiable vector function \(s^{*}(p,\)\(N_{k}+1)\), which is a local optimal solution satisfying the LICQ and SSOC conditions.

  3. 3.

    There exists positive constants \(c_{1}\) and \(c_{2}\) such that \(|s^{*}(p,N_{k}+1)-s^{*}(p_{0},N_{k}+1)|\le c_{1}|p-p_{0}|\), and the optimal values satisfy \(|J_{N_{k}+1}(p)-J_{N_{k}+1}(p_{0})|\le c_{2}|p-p_{0}|\).

The results in Theorem 1 allow the application of the implicit function theory to Eq. (21) at the nominal solution point \(s^{*}(p_{0},N_{k}+1)\):

$$\begin{aligned}&K^{*}(p_{0},N_{k}+1)\frac{\partial s^{*}}{\partial p} \nonumber \\&\quad = - \frac{\partial \zeta (s(p,N_{k}+1), p)}{\partial p}|_{s^{*}(p_{0},N_{k}+1)} \end{aligned}$$
(23)

where \(K^{*}(p_{0},N_{k}+1)\) is the KKT matrix calculated at \(s^{*}(p_{0},N_{k}+1)\). The right-hand side term of Eq. (23) is \(\frac{\partial \zeta (s(p,N_{k}+1), p)}{\partial p}|_{s^{*}(p_{0},N_{k}+1)}=[-I_{n_{x}},0,\ldots ,0]\), where \(n_{x}\) is the degrees of freedom of the state equations. Assuming that the nominal solution \(s^{*}(p_{0}, N_{k}+1)\) can satisfy SSOC and LICQ, the KKT matrix can then be used to calculate the sensitivity matrix shown in Eq. (23). Based on these results, the estimation of the neighboring problem can be approximated by:

$$\begin{aligned} {\tilde{s}}(p, N_{k}+1) = s^{*}(p_{0}, N_{k}+1) + \frac{\partial s^{*}}{\partial p}(p-p_{0}) \end{aligned}$$
(24)

where \({\tilde{s}}\) stands for the approximation of \(s^{*}(p,N_{k}+1)\). Based on the continuity and differentiability assumptions, there exists a positive constant \(c_{3}\) such that \(|{\tilde{s}}(p, N_{k}+1)-s^{*}(p,N_{k}+1)|\le c_{3}|p-p_{0}|^{2}\).

The calculation of the sensitivity matrix in Eq. (23) (e.g., \(\frac{\partial \zeta (s(p,N_{k}+1), p)}{\partial p}\)) requires \(n_{x}\) backsolves. This process is usually expensive especially when the size of the system becomes larger. To deal with this problem, the step length \(\Delta s(p,N_{k}+1)={\tilde{s}}(p, N_{k}+1)-s^{*}(p_{0},N_{k}+1)\) is obtained by linearization of KKT conditions at the nominal solution point \(s^{*}(p_{0},N_{k}+1)\). That is,

$$\begin{aligned}&K^{*}(p_{0},N_{k}+1)\Delta s(p,N_{k}+1) \nonumber \\&\quad = -\zeta (s^{*}(p_{0},N_{k}+1), p) \end{aligned}$$
(25)

where \(\zeta (s^{*}(p_{0},N_{k}+1), p)\) corresponds to the KKT matrix calculated at the nominal solution. \(\Delta s\) can be described as a Newton step starting from the nominal solution to the solution of the neighboring problem such that \({\tilde{s}}(p, N_{k}+1)\) can satisfy Eq. (24). The main advantage of this approximation process is that only a single backsolve is required to compute the sensitivity matrix. Compared with addressing the NLP problem to obtain new solutions, this update costs negligible time. Moreover, it is worth noting that if \(f(\cdot )\) and \(\psi (\cdot )\) are convex quadratic functions, \({\tilde{s}}(p, N_{k}+1)=s^{*}(p,N_{k}+1)\), which means the approximate solution is exactly equivalent to the optimal solution.

It should be noted that the change of the active sets concerning the inequality constraints may affect the results of the sensitivity analysis. If \(\Delta s(p,N_{k}+1)={\tilde{s}}(p, N_{k}+1)-s^{*}(p_{0},N_{k}+1)\) is large enough to result in a change with respect to the current active set, approximation of the KKT conditions becomes nonsmooth. This indicates that Eq. (24) does not hold true and the updated solution \({\tilde{s}}(p, N_{k}+1)\) might violate the box constraints. Besides, Theorem 1 does not hold at the points where the change of active set occurs. As a result, the continuity and differentiability of \(s^{*}(p,N_{k}+1)\) with respect to p cannot be preserved. One way to tackle this problem is to use the generalized SOSC condition as well as the relaxed set of constraint qualifications [29, 35].

3.5 Implementation consideration

In order to better present the proposed algorithm, the overall procedures of the MHE algorithm and the MPC method are summarized, respectively, in Algorithms 1 and 2.

figure a
figure b

According to Algorithm 2, for the MPC loop, the control variable is recalculated at each time step, thereby providing feedback to reduce the effects caused by uncertainties or model errors. Apart from the structure of the MPC algorithm, it is also important to know how the MPC scales as the problem grows. Therefore, a computational complexity analysis with the number of operations required to solve an iteration of MPC versus the dimensionality, number of collocation points as well as the time horizon of the problem is provided. Suppose that an optimal control problem which contains \(n_{x}\) state variables, \(n_{u}\) control variables and \(N_{k}\) LGR points is applied to discretize the system. If the mesh grid consists of \({\tilde{N}}\) sampling intervals and the length of the mesh interval is \(\Theta \), then \({\mathcal {O}}({\tilde{N}}\Theta (n_{x}(N_{k}+1)+n_{u}N_{k})^{3})\) operations are required to solve the formulation [16, 22].

4 Simulation studies

4.1 Parameter specification

In order to verify the effectiveness of the proposed RHPC-based IGC approach, numerical simulations were carried out. All the simulation results were carried out using MATLAB under Windows 7 and Intel (R) i7-3520M CPU, 2.90 GHZ, with 12.00 GB RAM. The parameters of the RHPC algorithm are chosen as: \({\bar{N}}=2\), \({\widetilde{N}}=3\), \(N_{k}=4\). Q and R are obtained according to the Bryson’s rule [34]. The lower and upper bounds of the state and control variables are chosen as: \(r\in [0, 20000]\), \(V_{r}, V_{\theta }\in \)\([-5000, 5000]\), \(\theta \in [-40, 40]\), \(\alpha \in [-20, 20]\), \(A_{M}\in [-350, 350]\) and \(\delta \in [-20, 20]\), respectively. Besides, the pitch rate and raw rate should vary in the region \([-250, 250]\).

The initial positions of the missile are assigned as: \(X_{M}(0)= 0\)m, \(Y_{M}(0)=0\) and \(Z_{M}=0\). The missile initial flight path angle and velocity are chosen as \(\varphi _{M}=35\)deg and \(V_{M}=1800~\hbox {m}/\hbox {s}\), respectively. Correspondingly, the initial flight path angle and velocity of the target are set as \(\varphi _{T}=50^{\circ }\) and \(V_{T}=2000~\hbox {m}/\hbox {s}\). The initial range along the LOS is \(r=12{,}000~\hbox {m}\). In addition, the initial LOS angle is \(\theta =40^{\circ }\), and the measurement of the LOS is taken as a first-order lag system. It is supposed that the target acceleration is given by \(A_{T}=(150+d_{A_{T}})\sin {\pi t}\) (\(\hbox {m}^{2}/\hbox {s}\)).

Moreover, to evaluate the performance of the MHE approach against measurement noises, it is assumed that the measurements of the missile–target range r, target acceleration \(A_{T}\) and the LOS angle (\(\theta _{y}\) and \(\theta _{z}\)) are disturbed by \(d=[d_{r}, d_{A_{T}}\), \(d_{\theta _{y}}, d_{\theta _{z}}]\), where d is the zero mean Gaussian noise with standard deviation of 10 m, 2 m/s and 1 mrad. The missile model-dependent parameters are set as: \({\bar{L}}_{\alpha }^{\beta }= {\bar{L}}_{\alpha }- {\bar{L}}_{\delta }\), \({\bar{L}}_{\alpha }=1070.1~\hbox {m}/\hbox {s}^{2}\), \({\bar{L}}_{\delta }=191.8~\hbox {m}/\hbox {s}^{2}\), \({\bar{M}}_{\alpha }^{\beta }= {\bar{M}}_{\alpha }- {\bar{M}}_{\delta }\), \({\bar{M}}_{\alpha } =-353.4~\hbox {s}^{-2}\), \({\bar{M}}_{\delta }=-283.3~\hbox {s}^{-2}\), \({\bar{M}}_{q}=-14.8~\hbox {s}^{-1}\). Since the RHPC optimization problem is formulated as a large-dimensional NLP problem, the scaling process becomes important to obtain a robust and rapid convergence to the optimal solution. Therefore, all the optimization variables are scaled using the strategy suggested in [34]. For the numerical simulation, the trajectory sampling step is set to 0.2 s. The NLP problems arising from the MPC and MHE formulations are addressed using the primal–dual interior point algorithm (e.g., the IPOPT optimizer [36]). The update of the NLP sensitivity is carried out manually via MATLAB.

4.2 Interception results

The performance of the proposed IGC design is firstly evaluated for a sample run. In this case, no model uncertainty and measurement noise are considered. The missile–target engagement trajectories, together with the state measurement results, are displayed in Figs. 4 and 5. The corresponding estimation error evolutions are presented in Fig. 6.

Fig. 4
figure 4

3-D missile–target engagement trajectory (no uncertainty and noise)

Full size image
Fig. 5
figure 5

State estimation performance (no uncertainty and noise)

Full size image
Fig. 6
figure 6

Estimation error profiles (no uncertainty and noise)

Full size image

The result displayed in Fig. 4 shows that the missile can engage the target successfully with a 0.032 m miss distance. According to the state estimation results shown in Figs. 5 and 6, the plant states can be estimated satisfactorily and the estimation error can be steered to a small neighborhood of the origin. Therefore, these results demonstrate that the MHE algorithm can have a good performance in terms of estimating state variables for the missile–target engagement system. In terms of the computational performance, the average processing time for generating the solution of each RHPC optimization problem is around 0.1721 s in this case, which is smaller than the trajectory update time.

Next, this sample run was performed by considering the measurement noise as well as the parameter uncertainty (e.g., the missile aerodynamic parameters \({\bar{L}}\), \({\bar{M}}\) were assumed to be varied randomly by ± 10% from the model values). Figure 7 depicts the time history of the 3-D intercept geometry obtained by applying the RHPC-based IGC method.

The corresponding state estimation trajectory results are then plotted in Fig. 8. It should be noted that in the last two figures (e.g., Fig. 8h and i), \(A_{Ty}\) and \(A_{Tz}\) stand for the normal target acceleration profiles along the elevation plane and azimuth plane. From these figures, it can be observed that by performing the MHE process and minimizing its least-squares objective function given by Eq. (13), the plant states can still be estimated satisfactorily in the presence of measurement noises.

The performance of applying other state estimation approaches such as the EKF and the PF for the missile–target interception problem is also analyzed. Numerical simulations were performed and the state estimation error profiles obtained using different estimation methods are depicted in Fig. 9. The result presented in Fig. 9 shows that the MHE and PF methods perform better than the EKF in the initial state estimation. Moreover, in the later stage of simulation, the estimation error achieved via the MHE method remains nearly zero, while the estimation errors achieved via the EKF and PF both increase. In other words, the MHE method tends to converge faster to the real value than its counterparts. Moreover, the MHE approach is likely to be more stable than the EKF and PF during the entire estimation process. Therefore, it is suggested to apply the MHE in dealing with the state estimation problem of the missile–target interception task.

Fig. 7
figure 7

3-D missile–target engagement trajectory (with uncertainty and noise)

Full size image

The results obtained via the proposed control scheme are compared against other typical missile guidance and control strategies, for example a primal–dual neural network (PDNN)-based predictive control scheme design reported in [16] and an integrated sliding-mode guidance and control (SMGC) design studied in [3]. For the PDNN method, the state and control input constraints are taken care by means of performance index weightings. On the other hand, the SMGC control scheme utilizes the control saturation function to handle constraints.

Fig. 8
figure 8

State estimation performance (with uncertainty and noise)

Full size image

The comparative time histories with respect to the missile acceleration, control input and attitude angles are plotted in Fig. 10, from where it can be seen that the proposed RHPC-based IGC law can produce state and control trajectories without violating the pre-specified state and control constraints in the absence of model uncertainties and measurement noises. (The control moments acting on the missile are provided in Fig. 10e–f.) As for SMGC results, although the control constraints are guaranteed via the use of saturation functions, constraint violations can be found in the missile acceleration and angular rate trajectories. Similar phenomena are found in the PDNN results. Hence, using performance index weightings may fail to satisfy the state constraints and result in constraint violations. Actually, imposing state constraints might further restrict the allowable control regions implicitly. As indicated in Fig. 10, the algorithm has to sacrifice using its maximum allowable control moments in order to satisfy the missile acceleration and attitude angle constraints.

Fig. 9
figure 9

Performance of different estimation methods (with uncertainty and noise)

Full size image

Based on the results shown in Figs. 7, 8, 9 and 10, it is obtained that the RHPC method achieves an engagement time 3.303 s, which indicates the interception can be fulfilled within short time for the interception mission investigated in this study. Besides, the miss distance for this sample run as well as the average computation time for the RHPC optimization process are 0.324 m and 0.1729 s, respectively. These two factors are slightly greater than the case that no model uncertainty and measurement noises are considered. This can be explained that the performance of the proposed control scheme might be degraded due to the consideration of these noises and uncertainties. However, according to the design of the RHPC scheme stated in Sect. 3 of this paper, the optimization procedure is repeated online at each sampling instant and the final state values of the previous process will be applied as the initial conditions of the continuing control loop. This receding manner can provide feedbacks such that the effects of uncertainty and model errors are reduced significantly, thereby improving the robustness of the control algorithm.

Fig. 10
figure 10

Performance of the proposed IGC law (with uncertainty and noise)

Full size image

To further verify the performance of the proposed optimization-based predictive IGC scheme, it is necessary to run a large number of simulations using the Monte Carlo method. It is well known that the Monte Carlo simulation is a powerful tool to analyze the effectiveness and robustness of a design by allowing consideration of the influences of different system noises and uncertainties. In total, 500 Monte Carlo simulations were performed for the missile–target engagement mission. Simulation results show that the proposed optimization-based predictive control algorithm can lead the state estimation error to a small value and achieve the hit for most of the cases with an average miss distance of 0.0362 m and an average interception time of 3.305 s when the stochastic disturbances and measurement noises are included in the missile–target system. A graph of the average runtime per iteration of MPC is plotted in Fig. 11. It is further calculated that the mean value of this runtime array is about 0.1723 s, which is again smaller than the trajectory update time. Hence, based on the results presented in Fig. 11, the real-time applicability can be preserved by applying the proposed control scheme.

Fig. 11
figure 11

Average runtime per iteration of MPC

Full size image

4.3 Comparative study

Comparative studies were also performed to compare the missile intercept accuracy achieved by applying the proposed IGC solver with other alternative MPC-based controllers, for instance a differential dynamic programming (DDP)-based MPC controller and a direct sequential quadratic programming (DSQP)-based MPC controller. Moreover, to make a fair comparison, all the algorithm-dependent parameters are tuned optimally as suggested in relative investigations [19, 30,31,32]. For the purpose of comparison, it is worth mentioning that the missile’s target accuracy is a critical factor for its effectiveness. Therefore, this is used as the main criteria to evaluate the performance of different controller designs.

Figure 12 illustrates the miss distance distribution obtained using the different guidance and control strategies. The last subplot in Fig. 12 shows the corresponding cumulative miss distance statistics for all the engagement cases. Cumulative miss distance chart, also known as Single Shot Kill Probability (SSKP), is an effective way to visualize guided missile system performance in a Monte Carlo sense. Figure 12 shows that the DSQP-based method performs better than the proposed method and the DDP-based controller in terms of the SSKP value. (A higher SSKP value can be obtained with a small value of miss distance.)

Fig. 12
figure 12

Miss distance distribution and SSKP results for different methods

Full size image

Regarding the real-time performance, it should be noted that based on our experiments, a penalty might be found in computational time for the increased accuracy and fidelity. Consequently, a relatively small index of accuracy (e.g., \(1\times 10^{-4}\)) is applied in the optimization process and the comparative study in order to enhance the real-time applicability of different control schemes as well as to make a fair comparison. The average computational time required by the proposed method, DSQP and DDP for the solution of each MPC optimization problem are 0.1723 s, 0.5743 s and 0.6611 s, respectively. The proposed approach achieves real-time applicability as the optimization time is smaller than the trajectory update time. Therefore, it can be concluded that compared with other algorithms studied in this investigation, the proposed RHPC-based algorithm can preserve the real-time applicability without scarifying the interception accuracy significantly. (This is reflected by Fig. 12, where a relatively high SSKP value can be obtained by applying the proposed strategy.)

4.4 Effect of parameter uncertainty

In this subsection, the effect of parameter uncertainty on the computational time and the interception accuracy is studied. By assuming the missile aerodynamic parameters are varied randomly by \(\pm ~10\%\), \(\pm ~15\%\) and \(\pm ~20\%\) from the model values, the sensitivity results of the MPC-based controllers with respect to modeling errors are displayed in Figs. 13, 14 and 15.

Fig. 13
figure 13

Effect of parameter uncertainty: DSQP results

Full size image
Fig. 14
figure 14

Effect of parameter uncertainty: RHPC results

Full size image
Fig. 15
figure 15

Effect of parameter uncertainty: DDP results

Full size image
Table 1 Comparative results for different methods
Full size table

The maximum, average and minimum miss distance (MD) values, alone with the average computational time consumed for each MPC optimization process, are summarized in Table 1. According to the results presented in Figs. 13, 14 and 15 and Table 1, it is apparent that an increasing uncertainty effect will result in a decrease in the interception accuracy and an increase in terms of the computational time. It is worth noting that in Table 1, another comparative study denoted as warm-start DSQP (wsDSQP) was carried out. In this strategy, the NLP problem is solved directly using the solution of the previous time step as an initial guess. Compared with the normal DSQP solution, the computational as well as the interception performance obtained by using the wsDSQP can be improved to some extent. However, the real-time applicability of wsDSQP is still not achieved.

For all the uncertain cases, the proposed RHPC control scheme with the sensitivity-based optimization method is able to preserve the real-time applicability and achieve a competitive interception accuracy. However, it is found that the real-time applicability will lose when the uncertainty interval is increase to ± 25%, as the average running time for solving the optimization problem will be increased to around 0.2738 s.

5 Conclusion

In this paper, an optimization-based predictive control strategy was constructed and implemented to solve the missile integrated guidance and control problem in the presence of model parameter uncertainties and measurement noises. A multiple interval pseudospectral method was applied to discretize the moving horizon state estimation and predictive control problems. Then the resulting NLP formulation was solved via a sensitivity-based nonlinear programming approach. In order to reduce the computational complexity and match real-time requirements, the NLP sensitivity information was applied to approximate the optimal solution. Numerical simulations were conducted to illustrate the effectiveness and robustness of the proposed method. The results show that the integrated guidance and control scheme investigated in this paper can achieve the preceding requirements for the missile interception mission.

However, there are some issues left in terms of applying the proposed control scheme for addressing the missile–target interception problem. For example, the performance of the sensitivity-based optimization technique might be affected significantly if large noises and model errors are considered. As a result, the processing speed will be decreased, thereby restricting the implementation of longer predictive horizons. In addition, the current missile dynamic model is relatively simple and more complex aerodynamic models should be applied. This will inevitably increase the computational burden of the optimizer since a more dense mesh grid is required to have an accurate approximation of the dynamics. These issues will be the main subjects of our future research.