1 Introduction

The convergence rate is determined for the orthogonal collocation method developed in [1, 2] where the collocation points are the Gauss quadrature abscissas, or equivalently, the roots of a Legendre polynomial. Other sets of collocation points that have been studied in the literature include the Lobatto quadrature points [3, 4], the Chebyshev quadrature points [5, 6], the Radau quadrature points [7–10], and extrema of Jacobi polynomials [11]. We show that if the continuous problem has a smooth solution and the Hamiltonian satisfies a strong convexity assumption, then the discrete problem has a local minimizer that converges exponentially fast at the collocation points to a solution of the continuous control problem. In other work [12, 13], Kang considers control systems in feedback linearizable normal form and shows that when the Lobatto discretized control problem is augmented with bounds on the states and control and on certain Legendre polynomial expansion coefficients, then the objectives in the discrete problem converge to the optimal objective of the continuous problem at an exponential rate. Kang’s analysis does not involve coercivity assumptions, but instead employs bounds in the discrete problem. Also, in [14] a consistency result is established for a scheme based on Lobatto collocation.

These collocation schemes based on the roots of orthogonal polynomials or their derivatives all employ approximations to the state based on global polynomials. Previously, convergence rates have been obtained when the approximating space consists of piecewise polynomials as in [15–21]. In this earlier work, convergence is achieved by letting the mesh spacing tend to zero, while keeping fixed the degree of the approximating polynomials on each mesh interval. In contrast, for schemes based on global polynomials, convergence is achieved by letting the degree of the approximating polynomials and the number of collocation points tend to infinity. This leads to an exponential convergence rate for problems with a smooth solution.

2 Preliminaries

A convergence rate is established for an orthogonal collocation method applied to an unconstrained control problem of the form

$$\begin{aligned} \left. \begin{array}{cll} \text{ minimize } &{}C(\mathbf{{x}}(1))&{}\\ \text{ subject } \text{ to } &{}\dot{\mathbf{{x}}}(t)= \mathbf{{f(x}}(t), \mathbf{{u}}(t)),&{} \; t\in [-1,1],\\ &{}\mathbf{{x}}(-1)=\mathbf{{x}}_0,&{} (\mathbf{{x}}, \mathbf{{u}}) \in \mathcal{{C}}^1(\mathbb {R}^n) \times \mathcal{{C}}^0 (\mathbb {R}^m), \end{array} \right\} \end{aligned}$$
(1)

where the state \({\mathbf{{x}}}(t)\in \mathbb {R}^n\), \(\dot{\mathbf{{x}}} := \displaystyle \frac{\hbox {d}}{\hbox {d}t}{\mathbf{{x}}}\), the control \({\mathbf{{u}}}(t)\in {\mathbb R}^m\), \({\mathbf{{f}}}: {\mathbb R}^n \times {\mathbb R}^m\rightarrow {\mathbb R}^n\), \(C: {\mathbb R}^n \rightarrow {\mathbb R}\), and \({\mathbf{{x}}}_0\) is the initial condition, which we assume is given; \(\mathcal{{C}}^k\) denotes the space of k times continuously differentiable functions. Although there is no integral (Lagrange) cost term appearing in (1), it could be included in the objective by augmenting the state with an \((n+1)\)st component \(x_{n+1}\) with initial condition \(x_{n+1} (-1) = 0\) and with dynamics equal to the integrand of the Lagrange term. It is assumed that \(\mathbf{{f}}\) and C are at least continuous. Let \(\mathcal{{P}}_N\) denote the space of polynomials of degree at most N defined on the interval \([-1, +1]\), and let \(\mathcal{{P}}_N^n\) denote the n-fold Cartesian product \(\mathcal{{P}}_N \times \cdots \times \mathcal{{P}}_N\). We analyze a discrete approximation to (1) of the form

$$\begin{aligned} \begin{array}{cl} \text{ minimize } &{}C(\mathbf{{x}}(1))\\ \text{ subject } \text{ to } &{}\dot{\mathbf{{x}}}(\tau _i)= \mathbf{{f(x}}(\tau _i), \mathbf{{u}}_i),\quad 1 \le i \le N,\\ &{}\mathbf{{x}}(-1)=\mathbf{{x}}_0, \quad \mathbf{{x}} \in \mathcal{{P}}_N^n. \end{array} \end{aligned}$$
(2)

The collocation points \(\tau _i, 1 \le i \le N\), are where the equation should be satisfied, and \(\mathbf{{u}}_i\) is the control approximation at time \(\tau _i\). The dimension of \(\mathcal{{P}}_N\) is \(N+1\), while there are \(N+1\) equations in (2) corresponding to the collocated dynamics at N points and the initial condition. In this paper, we collocate at the Gauss quadrature points, which are symmetric about \(t = 0\) and satisfy

$$\begin{aligned} -1 < \tau _1 < \tau _2 < \cdots < \tau _N < +1 . \end{aligned}$$

In addition, the analysis utilizes two noncollocated points \(\tau _0 = -1\) and \(\tau _{N+1} = +1\).

To state our convergence results in a precise way, we need to introduce a function space setting. Let \(\mathcal{{C}}^k (\mathbb {R}^n)\) denote the space of k times continuously differentiable functions \(\mathbf{{x}}: [-1, +1] \rightarrow \mathbb {R}^n\). For the space of continuous functions, we use the sup-norm \(\Vert \cdot \Vert _\infty \) given by

$$\begin{aligned} \Vert \mathbf{{x}}\Vert _\infty = \sup \{ |\mathbf{{x}} (t)| : t \in [-1, +1] \} , \end{aligned}$$
(3)

where \(| \cdot |\) is the Euclidean norm. For \(\mathbf{{y}} \in \mathbb {R}^n\), let \(\mathcal{{B}}_\rho (\mathbf{{y}})\) denote the ball with center \(\mathbf{{y}}\) and radius \(\rho \):

$$\begin{aligned} \mathcal{{B}}_\rho (\mathbf{{y}}) = \{ \mathbf{{x}} \in \mathbb {R}^n : |\mathbf{{x}} - \mathbf{{y}}| \le \rho \} . \end{aligned}$$

The following regularity assumption is assumed to hold throughout the paper.

Smoothness. The problem (1) has a local minimizer \((\mathbf{{x}}^*, \mathbf{{u}}^*)\) in \(\mathcal{{C}}^1 (\mathbb {R}^n) \times \mathcal{{C}}^0 (\mathbb {R}^m)\), and the first two derivatives of f and C are continuous on the closure of an open set \(\Omega \) and on \(\mathcal{{B}}_\rho (\mathbf{{x}}^*(1))\) respectively, where \(\Omega \subset \mathbb {R}^{m+n}\) has the property that for some \(\rho > 0\),

$$\begin{aligned} \mathcal{{B}}_\rho (\mathbf{{x}}^*(t),\mathbf{{u}}^*(t)) \subset \Omega \text{ for } \text{ all } t \in [-1, +1]. \end{aligned}$$

Let \({\varvec{\lambda }}^*\) denote the solution of the linear costate equation

$$\begin{aligned} \dot{{\varvec{\lambda }}}^*(t)=-\nabla _xH({\mathbf{{x}}}^*(t), {\mathbf{{u}}}^*(t), {{\varvec{\lambda }}}^*(t)), \quad {{\varvec{\lambda }}}^*(1)=\nabla C({\mathbf{{x}}}^*(1)), \end{aligned}$$
(4)

where H is the Hamiltonian defined by \(H({\mathbf{{x}}}, {\mathbf{{u}}}, {{\varvec{\lambda }}}) ={{\varvec{\lambda }}}^\mathsf{T}{\mathbf{{f}}}({\mathbf{{x}}}, {\mathbf{{u}}})\). Here \(\nabla C\) denotes the gradient of C. By the first-order optimality conditions (Pontryagin’s minimum principle), we have

$$\begin{aligned} \nabla _u H({\mathbf{{x}}}^*(t), {\mathbf{{u}}}^*(t), {{\varvec{\lambda }}}^*(t)) = \mathbf{{0}} \end{aligned}$$
(5)

for all \(t \in [-1, +1]\).

Since the discrete collocation problem (2) is finite dimensional, the first-order optimality conditions (Karush–Kuhn–Tucker conditions) imply that when a constraint qualification holds [22], the gradient of the Lagrangian vanishes. By the analysis in [2], the gradient of the Lagrangian vanishes if and only if there exists \({\varvec{\lambda }} \in \mathcal{{P}}_N^n\) such that

$$\begin{aligned} \dot{{\varvec{\lambda }}}(\tau _i)= & {} -\nabla _x H\left( {\mathbf{{x}}} (\tau _i),{\mathbf{{u}}}_i, {{\varvec{\lambda }}} (\tau _i) \right) , \quad 1 \le i \le N, \end{aligned}$$
(6)
$$\begin{aligned} {{\varvec{\lambda }}}(1)= & {} \nabla C(\mathbf{{x}}(1)), \end{aligned}$$
(7)
$$\begin{aligned} \mathbf{{0}}= & {} \nabla _u H\left( {\mathbf{{x}}}(\tau _i),{\mathbf{{u}}}_i, {{\varvec{\lambda }}} (\tau _i) \right) , \quad 1\le i\le N. \end{aligned}$$
(8)

The assumptions that play a key role in the convergence analysis are the following:

  1. (A1)

    The matrix \(\nabla ^2 C(\mathbf{{x}}^*(1))\) is positive semidefinite and for some \(\alpha > 0\), the smallest eigenvalue of the Hessian matrix

    $$\begin{aligned} \nabla ^2_{(x,u)} H(\mathbf{{x}}^* (t), \mathbf{{u}}^* (t), {\varvec{\lambda }}^* (t) ) \end{aligned}$$

    is greater than \(\alpha \), uniformly for \(t \in [-1, +1]\).

  2. (A2)

    The Jacobian of the dynamics satisfies

    $$\begin{aligned} \Vert \nabla _x \mathbf{{f}} (\mathbf{{x}}^*(t), \mathbf{{u}}^*(t))\Vert _\infty \le \beta < 1/2 \quad \text{ and } \quad \Vert \nabla _x \mathbf{{f}} (\mathbf{{x}}^*(t), \mathbf{{u}}^*(t))^\mathsf{T}\Vert _\infty \le \beta \end{aligned}$$

    for all \(t \in [-1, +1]\) where \(\Vert \cdot \Vert _\infty \) is the matrix sup-norm (largest absolute row sum), and the Jacobian \(\nabla _x \mathbf{{f}}\) is an n by n matrix whose ith row is \((\nabla _x f_i)^\mathsf{T}\).

The coercivity assumption (A1) ensures that the solution of the discrete problem is a stationary point. The condition (A2) arises in the theoretical convergence analysis since the solution of the problem (1) is approximated by polynomials defined on the entire time interval \([-1, +1]\). In contrast, when the solution is approximated by piecewise polynomials as in [15–21], this condition is not needed. To motivate why this condition arises, suppose that the system dynamics \(\mathbf{{f}}\) has the form \(\mathbf{{f}}(\mathbf{{x}}, \mathbf{{u}}) = \mathbf{{Ax}} + \mathbf{{g}}(\mathbf{{u}})\) where \(\mathbf{{A}}\) is an n by n matrix. Since the dynamics are linear in the state, it follows that for any given \(\mathbf{{u}}\) with \(\mathbf{{g}}(\mathbf{{u}})\) absolutely integrable, we can invert the continuous dynamics to obtain the state \(\mathbf{{x}}\) as a function of the control \(\mathbf{{u}}\). The dynamics in the discrete approximation (2) are also a linear function of the discrete state evaluated at the collocation points; however, the invertibility of the matrix in the discrete dynamics is not obvious. If the system matrix satisfies \(\Vert \mathbf{{A}}\Vert _\infty < 1/2\), then we will show that the matrix for the discrete dynamics is invertible with its norm uniformly bounded as a function of N, the degree of the polynomials. Consequently, it is possible to solve for the state as a function of the control in the discrete problem (2). When \(\Vert \mathbf{{A}}\Vert _\infty > 1/2\), the matrix for the discrete dynamics could be singular for some choice of N. In general, (A2) could be replaced by any condition that ensures the solvability of the linearized dynamics for the state in terms of the control, and the stability of this solution under perturbations in the dynamics.

When the dynamics of the control problem are nonlinear, the convergence analysis leads us to study the linearized dynamics around \((\mathbf{{x}}^*, \mathbf{{u}}^*)\), and (A2) implies that the linearized dynamics in the discrete problem (2) are invertible with respect to the state. In contrast, if the global polynomials are replaced by piecewise polynomials on a uniform mesh of width h, then (A2) is replaced by

$$\begin{aligned} \Vert \nabla _x \mathbf{{f}} (\mathbf{{x}}^*(t), \mathbf{{u}}^*(t))\Vert _\infty < 1/h \quad \text{ and } \quad \Vert \nabla _x \mathbf{{f}} (\mathbf{{x}}^*(t), \mathbf{{u}}^*(t))^\mathsf{T}\Vert _\infty < 1/h, \end{aligned}$$

which is satisfied when h is sufficiently small. In other words, when h is sufficiently small, it is possible to solve for the discrete states in terms of the discrete controls, independent of the degree of the polynomials on each mesh interval. These schemes where both the mesh width h and the degree of the polynomials p on each mesh interval are free parameters have been referred to as hp-collocation methods [9, 10].

In addition to the two assumptions, the analysis employs two properties of the Gauss collocation scheme. Let \(\omega _j\), \(1 \le j \le N\), denote the Gauss quadrature weights, and for \(1 \le i \le N\) and \(0 \le j \le N\), define

$$\begin{aligned} D_{ij} = \dot{L}_j (\tau _i), \quad \text{ where } L_j (\tau ) := \prod ^N_{\begin{array}{c} k=0\\ k\ne j \end{array}} \frac{\tau -\tau _k}{\tau _j-\tau _k}. \end{aligned}$$
(9)

\(\mathbf{{D}}\) is a differentiation matrix in the sense that \((\mathbf{{Dp}})_i = \dot{p} (\tau _i)\), \(1 \le i \le N\), where \(p \in \mathcal{{P}}_N\) is the polynomial that satisfies \(p(\tau _j) = p_j\) for \(0 \le j \le N\). The submatrix \(\mathbf{{D}}_{1:N}\) consisting of the tailing N columns of \(\mathbf{{D}}\) has the following properties:

  1. (P1)

    \(\mathbf{{D}}_{1:N}\) is invertible and \(\Vert \mathbf{{D}}_{1:N}^{-1}\Vert _\infty \le 2\).

  2. (P2)

    If \(\mathbf{{W}}\) is the diagonal matrix containing the Gauss quadrature weights \({\varvec{\omega }}\) on the diagonal, then the rows of the matrix \([\mathbf{{W}}^{1/2} \mathbf{{D}}_{1:N}]^{-1}\) have Euclidean norm bounded by \(\sqrt{2}\).

The fact that \(\mathbf{{D}}_{1:N}\) is invertible is established in [2, Prop.1]. The bounds on the norms in (P1) and (P2), however, are more subtle. We refer to (P1) and (P2) as properties rather than assumptions since the matrices are readily evaluated, and we can check numerically that (P1) and (P2) are always satisfied. In fact, numerically we find that \(\Vert \mathbf{{D}}_{1:N}^{-1}\Vert _\infty = 1 + \tau _N\) where the last Gauss quadrature abscissa \(\tau _N\) approaches \(+1\) as N tends to \(\infty \). On the other hand, we do not yet have a general proof for the properties (P1) and (P2). A prize for obtaining a proof is explained on William Hager’s Web site (Google William Hager 10,000 yen). In contrast to these properties, conditions (A1) and (A2) are assumptions that are only satisfied by certain control problems.

If \(\mathbf{{x}}^N \in \mathcal{{P}}_N^n\) is a solution of (2) associated with the discrete controls \(\mathbf{{u}}_i\), \(1 \le i \le N\), and if \({\varvec{\lambda }}^N \in \mathcal{{P}}_N^n\) satisfies (6)–(8), then we define

$$\begin{aligned} \begin{array}{llllllll} \mathbf{{X}}^N &{}= [ &{}\mathbf{{x}}^N(-1), &{} \mathbf{{x}}^N(\tau _1), &{} \ldots , &{} \mathbf{{x}}^N(\tau _N), &{} \mathbf{{x}}^N(+1) &{}], \\ \mathbf{{X}}^* &{}= [ &{}\mathbf{{x}}^*(-1), &{} \mathbf{{x}}^*(\tau _1), &{} \ldots , &{} \mathbf{{x}}^*(\tau _N), &{} \mathbf{{x}}^*(+1) &{}], \\ \mathbf{{U}}^N &{}= [ &{}&{} \mathbf{{u}}_1, &{} \ldots , &{} \mathbf{{u}}_N\; &{} &{}], \\ \mathbf{{U}}^* &{}= [ &{}&{} \mathbf{{u}}^*(\tau _1), &{} \ldots , &{} \mathbf{{u}}^*(\tau _N)&{} &{} ], \\ {\varvec{\Lambda }}^N &{}= [ &{}{\varvec{\lambda }}^N(-1), &{} {\varvec{\lambda }}^N(\tau _1), &{} \ldots , &{} {\varvec{\lambda }}^N(\tau _N), &{} {\varvec{\lambda }}^N(+1) &{}], \\ {\varvec{\Lambda }}^* &{}= [ &{}{\varvec{\lambda }}^*(-1), &{} {\varvec{\lambda }}^*(\tau _1), &{} \ldots , &{} {\varvec{\lambda }}^*(\tau _N), &{} {\varvec{\lambda }}^*(+1) &{}]. \end{array} \end{aligned}$$

The following convergence result relative to the vector \(\infty \)-norm (largest absolute element) is established:

Theorem 2.1

If \((\mathbf{{x}}^*, \mathbf{{u}}^*)\) is a local minimizer for the continuous problem (1) with \((\mathbf{{x}}^*, {\varvec{\lambda }}^*) \in \mathcal{{C}}^\eta \) for some \(\eta \ge 4\) and both (A1)–(A2) and (P1)–(P2) hold, then for N sufficiently large, the discrete problem (2) has a stationary point \((\mathbf{{X}}^N, \mathbf{{U}}^N)\) and an associated discrete costate \({\varvec{\Lambda }}^N\), and there exists a constant c independent of N and \(\eta \) such that

$$\begin{aligned}&\max \left\{ \Vert \mathbf{X}^N-\mathbf{X}^*\Vert _\infty , \Vert \mathbf{U}^N-\mathbf{U}^*\Vert _\infty , \Vert {{\varvec{\Lambda }}}^N-{{\varvec{\Lambda }}}^*\Vert _\infty \right\} \nonumber \\&\quad \le \left( \displaystyle {\frac{c}{N}} \right) ^{p-3} \left( \Vert {\mathbf{{x}}^*}^{(p)}\Vert _\infty + \Vert {{\varvec{\lambda }}^*}^{(p)}\Vert _\infty \right) , \quad p = \min \{\eta , N+1\}. \end{aligned}$$
(10)

Moreover, if \(\nabla ^2 C(\mathbf{{x}}^*(1))\) is positive definite, then \((\mathbf{{X}}^N, \mathbf{{U}}^N)\) is a local minimizer of (2). Here the superscript (p) denotes the (p)th derivative.

Although the discrete problem only possesses discrete controls at the collocation points \(-1 < \tau _i < +1\), \(1 \le i \le N\), an estimate for the discrete control at \(t = -1\) and \(t = +1\) could be obtained from the minimum principle (5) since we have estimates for the discrete state and costate at the end points. Alternatively, polynomial interpolation could be used to obtain estimates for the control at the end points of the interval.

The paper is organized as follows. In Sect. 3, the discrete optimization problem (2) is reformulated as a nonlinear system of equations obtained from the first-order optimality conditions, and a general approach to convergence analysis is presented. Section 4 obtains an estimate for how closely the solution to the continuous problem satisfies the first-order optimality conditions for the discrete problem. Section 5 proves that the linearization of the discrete control problem around a solution of the continuous problem is invertible. Section 6 establishes an \(L^2\) stability property for the linearization, while Sect. 7 strengthens the norm to \(L^\infty \). This stability property is the basis for the proof of Theorem 2.1. Numerical examples illustrating the exponential convergence result are given in Sect. 8.

Notation. The meaning of the norm \(\Vert \cdot \Vert _\infty \) is based on context. If \(\mathbf{{x}} \in \mathcal{{C}}^0 (\mathbb {R}^n)\), then \(\Vert \mathbf{{x}}\Vert _\infty \) denotes the maximum of \(|\mathbf{{x}}(t)|\) over \(t \in [-1, +1]\), where \(| \cdot |\) is the Euclidean norm. If \(\mathbf{{A}} \in \mathbb {R}^{m \times n}\), then \(\Vert \mathbf{{A}}\Vert _\infty \) is the largest absolute row sum (the matrix norm induced by the vector sup-norm). For a vector \(\mathbf{{v}} \in \mathbb {R}^m\), \(\Vert \mathbf{{v}}\Vert _\infty \) is the maximum of \(|v_i|\) over \(1 \le i \le m\). We let \(|\mathbf{{A}}|\) denote the matrix norm induced by the Euclidean vector norm. The dimension of the identity matrix \(\mathbf{{I}}\) is often clear from context; when necessary, the dimension of \(\mathbf{{I}}\) is specified by a subscript. For example, \(\mathbf{{I}}_n\) is the n by n identity matrix. \(\nabla C\) denotes the gradient, a column vector, while \(\nabla ^2 C\) denotes the Hessian matrix. Throughout the paper, c denotes a generic constant which has different values in different equations. The value of this constant is always independent of N. \(\mathbf{{1}}\) denotes a vector whose entries are all equal to one, while \(\mathbf{{0}}\) is a vector whose entries are all equal to zero, and their dimension should be clear from context. Finally, \(\bar{\mathbf{{X}}} \in \mathbb {R}^{nN}\) is the vector obtained by vertically stacking \(\mathbf{{X}}_i \in \mathbb {R}^n\), \(1 \le i \le N\).

3 Abstract Setting

As shown in [2], the discrete problem (2) can be reformulated as the nonlinear programming problem

$$\begin{aligned} \begin{array}{ll} \text{ minimize } &{}C(\mathbf{{X}}_{N+1})\\ \text{ subject } \text{ to } &{}\sum _{j=0}^N{D}_{ij}{\mathbf{{X}}}_j ={\mathbf{{f}}}({\mathbf{{X}}}_i,{\mathbf{{U}}}_i), \quad 1\le i\le N, \quad \mathbf{{X}}_0=\mathbf{{x}}_0,\\ &{}{\mathbf{{X}}}_{N+1}={\mathbf{{X}}}_0+\sum _{j=1}^N\omega _j{\mathbf{{f}}}({\mathbf{{X}}}_j,{\mathbf{{U}}}_j). \end{array} \end{aligned}$$
(11)

As indicated before Theorem 2.1, \(\mathbf{{X}}_i\) corresponds to \(\mathbf{{x}}^N(\tau _i)\). Also, Garg et al. [2] show that the equations obtained by setting the gradient of the Lagrangian to zero are equivalent to the system of equations

$$\begin{aligned} \sum _{j=1}^{N+1}{D}_{ij}^\dag {{\varvec{\Lambda }}}_j= & {} -\nabla _x H\left( {\mathbf{{X}}}_i,{\mathbf{{U}}}_i, {{\varvec{\Lambda }}}_i\right) , \quad 1 \le i \le N, \end{aligned}$$
(12)
$$\begin{aligned} {{\varvec{\Lambda }}}_{N+1}= & {} \nabla C(\mathbf{{X}}_{N+1}), \end{aligned}$$
(13)
$$\begin{aligned} \mathbf{{0}}= & {} \nabla _u H\left( {\mathbf{{X}}}_i,{\mathbf{{U}}}_i, {{\varvec{\Lambda }}}_i\right) , \quad 1\le i\le N, \end{aligned}$$
(14)

where

$$\begin{aligned} {D}_{ij}^\dag= & {} -\displaystyle \left( \frac{\omega _j}{\omega _i}\right) {D}_{ji}, \quad 1\le i \le N,\quad 1\le j \le N, \end{aligned}$$
(15)
$$\begin{aligned} {D}_{i,N+1}^\dag= & {} -\sum _{j=1}^N{D}_{ij}^\dag , \quad 1\le i\le N. \end{aligned}$$
(16)

Here \({\varvec{\Lambda }}_i\) corresponds to \({\varvec{\lambda }}^N(\tau _i)\). The relationship between the discrete costate \({\varvec{\Lambda }}_i\), the KKT multipliers \({\varvec{\lambda }}_i\), \(1 \le i \le N\), associated with the discrete dynamics, and the multiplier \({\varvec{\lambda }}_{N+1}\) associated with the equation for \(\mathbf{{X}}_{N+1}\) is

$$\begin{aligned} \omega _i {{\varvec{\Lambda }}}_i={\varvec{\lambda }}_i+ \omega _i {\varvec{\lambda }}_{N+1} \quad \text{ when }\quad 1\le i \le N, \quad \text{ and } \quad {{\varvec{\Lambda }}}_{N+1}={\varvec{\lambda }}_{N+1}. \end{aligned}$$
(17)

The first-order optimality conditions for the nonlinear program (11) consist of the Eqs. (12)–(14) and the constraints in (11). This system can be written as \(\mathcal{{T}}(\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}) = \mathbf{{0}}\) where

$$\begin{aligned} (\mathcal{{T}}_1, \mathcal{{T}}_2, \ldots , \mathcal{{T}}_5) (\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}) \in \mathbb {R}^{nN} \times \mathbb {R}^n \times \mathbb {R}^{nN} \times \mathbb {R}^n \times \mathbb {R}^{mN} . \end{aligned}$$

The five components of \(\mathcal{{T}}\) are defined as follows:

$$\begin{aligned} \mathcal{{T}}_{1i}(\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }})= & {} \left( \sum _{j=0}^N{D}_{ij}{} \mathbf{X}_j \right) -\mathbf{f}(\mathbf{X}_i,\mathbf{U}_i), \quad 1\le i\le N ,\\ \mathcal{{T}}_2(\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }})= & {} \mathbf{X}_{N+1}-\mathbf{X}_0-\sum _{j=1}^N\omega _j\mathbf{f}(\mathbf{X}_j,\mathbf{U}_j), \\ \mathcal{{T}}_{3i}(\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }})= & {} \left( \sum _{j=1}^{N+1}{D}_{ij}^\dag {{\varvec{\Lambda }}}_j \right) + \nabla _x H(\mathbf{X}_i,\mathbf{U}_i, {{\varvec{\Lambda }}}_i), \quad 1 \le i \le N , \\ \mathcal{{T}}_4(\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }})= & {} {{\varvec{\Lambda }}}_{N+1}-\nabla _x C(\mathbf {X}_{N+1}), \\[.05in] \mathcal{{T}}_{5i}(\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }})= & {} \nabla _u H(\mathbf{X}_i, \mathbf{U}_i, {{\varvec{\Lambda }}}_i), \quad 1\le i\le N . \end{aligned}$$

Note that in formulating \(\mathcal{{T}}\), we treat \(\mathbf{{X}}_0\) as a constant whose value is the given starting condition \(\mathbf{{x}}_0\). Alternatively, we could treat \(\mathbf{{X}}_0\) as an unknown and then expand \(\mathcal{{T}}\) to have a sixth component \(\mathbf{{X}}_0 - \mathbf{{x}}_0\). With this expansion of \(\mathcal{{T}}\), we need to introduce an additional multiplier \({\varvec{\Lambda }}_0\) for the constraint \(\mathbf{{X}}_0 - \mathbf{{x}}_0\); it turns out that \({\varvec{\Lambda }}_0\) approximates \({\varvec{\lambda }}^*(-1)\). To achieve a slight simplification in the analysis, we employ a five-component \(\mathcal{{T}}\) and treat \(\mathbf{{X}}_0\) as a constant, not an unknown.

The proof of Theorem 2.1 reduces to a study of solutions to \(\mathcal{{T}}(\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}) = \mathbf{{0}}\) in a neighborhood of \((\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*)\). Our analysis is based on Dontchev et al. [17, Proposition3.1], which we simplify below to take into account the structure of our \(\mathcal{{T}}\). Other results like this are contained in Theorem 3.1 of [16], in Proposition 5.1 of Hager [19], and in Theorem 2.1 of Hager [23].

Proposition 3.1

Let \(\mathcal {X}\) be a Banach space and \(\mathcal {Y}\) be a linear normed space with the norms in both spaces denoted \(\Vert \cdot \Vert \). Let \(\mathcal {T}\): \(\mathcal {X} \longmapsto \mathcal {Y}\) with \(\mathcal {T}\) continuously Fréchet differentiable in \(\mathcal{{B}}_r({\varvec{\theta }}^*)\) for some \({\varvec{\theta }}^* \in \mathcal {X}\) and \(r> 0\). Suppose that

$$\begin{aligned} \Vert \nabla \mathcal {T}({\varvec{\theta }})-\nabla \mathcal {T}({\varvec{\theta }}^*)\Vert \le \varepsilon \text{ for } \text{ all } {\varvec{\theta }} \in {\mathcal B}_r({\varvec{\theta }}^*) \end{aligned}$$

where \(\nabla \mathcal {T}({\varvec{\theta }}^*)\) is invertible, and define \(\mu := \Vert \nabla \mathcal {T}({\varvec{\theta }}^*)^{-1}\Vert \). If \(\varepsilon \mu < 1\) and \(\left\| \mathcal {T}\left( {\varvec{\theta }}^*\right) \right\| \le \) \((1-\mu \varepsilon )r/\mu \), then there exists a unique \({\varvec{\theta }} \in {\mathcal B}_r({\varvec{\theta }}^*)\) such that \(\mathcal {T}({\varvec{\theta }})=\mathbf{{0}}\). Moreover, we have the estimate

$$\begin{aligned} \Vert {\varvec{\theta }}-{\varvec{\theta }}^*\Vert \le \frac{\mu }{1-\mu \varepsilon } \left\| \mathcal {T}\left( {\varvec{\theta }}^*\right) \right\| \le r. \end{aligned}$$
(18)

We apply Proposition 3.1 with \({\varvec{\theta }}^* = (\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*)\) and \({\varvec{\theta }} = (\mathbf{{X}}^N, \mathbf{{U}}^N, {\varvec{\Lambda }}^N)\). The key steps in the analysis are the estimation of the residual \(\left\| \mathcal {T}\left( {\varvec{\theta }}^*\right) \right\| \), the proof that \(\nabla \mathcal {T}({\varvec{\theta }}^*)\) is invertible, and the derivation of a bound for \(\Vert \nabla \mathcal {T}({\varvec{\theta }}^*)^{-1}\Vert \) that is independent of N. In our context, we use the \(\infty \)-norm for both \(\mathcal{{X}}\) and \(\mathcal{{Y}}\). In particular,

$$\begin{aligned} \Vert {\varvec{\theta }}\Vert =\Vert (\mathbf{X},\mathbf{U}, {{\varvec{\Lambda }}})\Vert _\infty =\max \{\Vert \mathbf X\Vert _\infty , \Vert \mathbf U\Vert _\infty ,\Vert {\varvec{\Lambda }}\Vert _\infty \}. \end{aligned}$$
(19)

For this norm, the left side of (10) and the left side of (18) are the same. The norm on \(\mathcal{{Y}}\) enters into the estimation of both the residual \(\Vert \mathcal {T}({\varvec{\theta }}^*)\Vert \) in (18) and the parameter \(\mu := \Vert \nabla \mathcal {T}({\varvec{\theta }}^*)^{-1}\Vert \). In our context, we think of an element of \(\mathcal{{Y}}\) as a vector with components \(\mathbf{{y}}_i\), \(1 \le i \le 3N + 2\), where \(\mathbf{{y}}_i \in \mathbb {R}^n\) for \(1 \le i \le 2N + 2\) and \(\mathbf{{y}}_i \in \mathbb {R}^m\) for \(i > 2N + 2\). For example, \(\mathcal{{T}}_1(\mathbf{{X}},\mathbf{{U}}, {\varvec{\Lambda }}) \in \mathbb {R}^{nN}\) corresponds to the components \(\mathbf{{y}}_i \in \mathbb {R}^n\), \(1 \le i \le N\).

4 Analysis of the Residual

We now establish a bound for the residual.

Lemma 4.1

If \((\mathbf{{x}}^*, {\varvec{\lambda }}^*) \in \mathcal{{C}}^{\eta }\) and \(p = \min \{\eta , N+1\} \ge 4\), then there exits a constant c independent of N and \(\eta \) such that

$$\begin{aligned} \Vert \mathcal {T}(\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*)\Vert _\infty \le \left( \displaystyle {\frac{c}{N}} \right) ^{p-3} \left( \Vert {\mathbf{{x}}^*}^{(p)}\Vert _\infty + \Vert {{\varvec{\lambda }}^*}^{(p)}\Vert _\infty \right) . \end{aligned}$$
(20)

Proof

By the definition of \(\mathcal{{T}}\), \(\mathcal{{T}}_4 (\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*) = \mathbf{{0}}\) since \(\mathbf{{x}}^*\) and \({\varvec{\lambda }}^*\) satisfy the boundary condition in (4). Likewise, \(\mathcal{{T}}_5(\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*) = \mathbf{{0}}\) since (5) holds for all \(t \in [-1, +1]\); in particular, (5) holds at the collocation points.

Now let us consider \(\mathcal{{T}}_1\). By Garg et al. [2, Eq. (7)],

$$\begin{aligned} \sum _{j=0}^N D_{ij} \mathbf{{X}}_j^* = \dot{\mathbf{{x}}}^I(\tau _i), \quad 1 \le i \le N, \end{aligned}$$

where \(\mathbf{{x}}^I \in \mathcal{{P}}_N^n\) is the (interpolating) polynomial that passes through \(\mathbf{{x}}^*(\tau _i)\) for \(0 \le i \le N\). Since \(\mathbf{{x}}^*\) satisfies the dynamics of (1), it follows that \(\mathbf{{f}}(\mathbf{{X}}_i^*, \mathbf{{U}}_i^*) = \dot{\mathbf{{x}}}^* (\tau _i)\). Hence, we have

$$\begin{aligned} \mathcal{{T}}_{1i}(\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*) = \dot{\mathbf{{x}}}^I(\tau _i) - \dot{\mathbf{{x}}}^*(\tau _i) . \end{aligned}$$
(21)

By Hager et al. [24, Prop. 2.1], we have

$$\begin{aligned} \Vert \dot{\mathbf{{x}}}^I - \dot{\mathbf{{x}}}^*\Vert _\infty \le \left( 1+2N^2\right) \inf _{\mathbf{{q}} \in \mathcal {P}_{N}^n}\left\| \dot{\mathbf{{x}}}-\dot{\mathbf{{q}}}\right\| _\infty + N^2(1+L_N) \inf _{\mathbf{{q}} \in \mathcal {P}_{N}^n}\left\| \mathbf{{x}}-\mathbf{{q}}\right\| _\infty , \end{aligned}$$
(22)

where \(L_N\) is the Lebesgue constant of the point set \(\tau _i\), \(0 \le i \le N\). In [24, Thm. 4.1], we show that \(L_N = O(\sqrt{N})\). It follows from Elschner [25, Prop. 3.1] that for some constant c, independent of N, we have

$$\begin{aligned} \inf _{\mathbf{{q}} \in \mathcal {P}_{N}^n}\left\| \mathbf{{x}}-\mathbf{{q}}\right\| _\infty \le \left( \frac{c}{N+1} \right) ^\eta \Vert {\mathbf{{x}}^*}^{(\eta )}\Vert _\infty \end{aligned}$$
(23)

and

$$\begin{aligned} \inf _{\mathbf{{q}} \in \mathcal {P}_{N}^n}\left\| \dot{\mathbf{{x}}}-\dot{\mathbf{{q}}}\right\| _\infty \le \left( \frac{c}{N} \right) ^{\eta -1} \Vert {\mathbf{{x}}^*}^{(\eta )}\Vert _\infty \end{aligned}$$
(24)

whenever \(N+1 \ge \eta \). In the case that \(N+1 < \eta \), the smoothness requirement \(\eta \) can be relaxed to \(N+1\) to obtain similar bounds. Since the first bound (23) is dominated by (24), it follows that the first term in (22) dominates the second term, and we have

$$\begin{aligned} \Vert \dot{\mathbf{{x}}}^I - \dot{\mathbf{{x}}}^*\Vert _\infty \le \left( \frac{c}{N} \right) ^{p-3} \Vert {\mathbf{{x}}^*}^{(p)}\Vert _\infty \end{aligned}$$
(25)

where \(p = \min \{\eta , N+1 \}\). The bound (25) is valid in both cases \(N+1 \ge \eta \) and \(N+1 < \eta \). By (21) and (25), \(\mathcal{{T}}_{1}(\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*)\) complies with the bound (20).

Next, let us consider

$$\begin{aligned} \mathcal{{T}}_2 (\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*) = \mathbf{{x}}^* (1) - \mathbf{{x}}^*(-1) - \sum _{j=1}^N \omega _j \mathbf{{f}}(\mathbf{{x}}^*(\tau _j), \mathbf{{u}}^*(\tau _j)) . \end{aligned}$$
(26)

By the fundamental theorem of calculus and the fact that N-point Gauss quadrature is exact for polynomials of degree up to \(2N - 1\), we have

$$\begin{aligned} \mathbf{{0}} = \mathbf{x}^I(1)-\mathbf{x}^I(-1)-\int _{-1}^1\dot{\mathbf{x}}^I(t)dt = \mathbf{x}^I(1)-\mathbf{x}^*(-1)-\sum _{j=1}^N\omega _j\dot{\mathbf{x}}^I(\tau _j) \end{aligned}$$
(27)

since \(\mathbf{{x}}^I(-1) = \mathbf{{x}}^*(-1)\). Subtract (27) from (26) to obtain

$$\begin{aligned} \mathcal{{T}}_2 (\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*) = \mathbf{x}^*(1)-\mathbf{x}^I(1)+\sum _{j=1}^N\omega _j\left( \dot{\mathbf{x}}^I(\tau _j) -\dot{\mathbf{x}}^*(\tau _j)\right) . \end{aligned}$$
(28)

Since \(\omega _j > 0\) and their sum is 2,

$$\begin{aligned} \left| \sum _{j=1}^I\omega _j\left( \dot{\mathbf{x}}^I(\tau _j) -\dot{\mathbf{x}}^*(\tau _j)\right) \right| \le 2\Vert \dot{\mathbf{{x}}}^I - \dot{\mathbf{{x}}}^*\Vert _\infty . \end{aligned}$$
(29)

Likewise,

$$\begin{aligned} | \mathbf{x}^*(1)-\mathbf{x}^I(1)| = \left| \int _{-1}^{+1} \left( \dot{\mathbf{{x}}}^*(t) - \dot{\mathbf{{x}}}^I(t) \right) dt \right| \le 2\Vert \dot{\mathbf{{x}}}^* - \dot{\mathbf{{x}}}^I\Vert _\infty . \end{aligned}$$
(30)

We combine (28)–(30) and (25) to see that \(\mathcal{{T}}_2 (\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*)\) complies with the bound (20).

Finally, let us consider \(\mathcal{{T}}_3\). By Garg et al. [2, Thm. 1],

$$\begin{aligned} \sum _{j=1}^{N+1} D_{ij}^\dagger {\varvec{\Lambda }}_j^* = \dot{{\varvec{\lambda }}}^I(\tau _i), \quad 1 \le i \le N, \end{aligned}$$

where \({\varvec{\lambda }}^I \in \mathcal{{P}}_N^n\) is the (interpolating) polynomial that passes through \({\varvec{\Lambda }}^*_j = {\varvec{\lambda }}(\tau _j)\) for \(1 \le j \le N+1\). Since \({\varvec{\lambda }}^*\) satisfies (4), it follows that \(\dot{{\varvec{\lambda }}}^*(\tau _i) =\) \(-\nabla _x H(\mathbf{X}_i^*,\mathbf{U}_i^*, {{\varvec{\Lambda }}}_i^*)\). Hence, we have

$$\begin{aligned} \mathcal{{T}}_{3i}(\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*) = \dot{{\varvec{\lambda }}}^I(\tau _i) - \dot{{\varvec{\lambda }}}^*(\tau _i) . \end{aligned}$$

In exactly the same way that \(\mathcal{{T}}_1\) in (21) was handled, we conclude that \(\mathcal{{T}}_{3}(\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*)\) complies with the bound (20). This completes the proof. \(\square \)

5 Invertibility

In this section, we show that the derivative \(\nabla \mathcal{{T}} ({\varvec{\theta }}^*)\) is invertible. This is equivalent to showing that for each \(\mathbf{{y}} \in \mathcal{{Y}}\), there is a unique \({\varvec{\theta }} \in \mathcal{{X}}\) such that \(\nabla \mathcal{{T}} ({\varvec{\theta }}^*)[{\varvec{\theta }}] = \mathbf{{y}}\). In our application, \({\varvec{\theta }}^* = (\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*)\) and \({\varvec{\theta }} = (\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }})\). To simplify the notation, we let \(\nabla \mathcal{{T}}^*[\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}]\) denote the derivative of \(\mathcal{{T}}\) evaluated at \((\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*)\) operating on \((\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }})\). This derivative involves the following six matrices:

$$\begin{aligned} \begin{array}{ll} \mathbf{A}_i=\nabla _x\mathbf{f}(\mathbf{x}^*(\tau _i),\mathbf{u}^*(\tau _i)), &{}\mathbf{B}_i=\nabla _u\mathbf{f}(\mathbf{x}^*(\tau _i),\mathbf{u}^*(\tau _i)),\\ \mathbf{Q}_i=\nabla _{xx}H\left( \mathbf{x}^*(\tau _i),\mathbf{u}^*(\tau _i), {{\varvec{\lambda }}}^*(\tau _i)\right) , &{}\mathbf{S}_i=\nabla _{ux}H\left( \mathbf{x}^*(\tau _i),\mathbf{u}^*(\tau _i), {{\varvec{\lambda }}}^*(\tau _i)\right) ,\\ \mathbf{R}_i=\nabla _{uu}H\left( \mathbf{x}^*(\tau _i),\mathbf{u}^*(\tau _i), {{\varvec{\lambda }}}^*(\tau _i)\right) , &{}\mathbf{T}=\nabla ^2C(\mathbf{x}^*(1)). \end{array} \end{aligned}$$

With this notation, the five components of \(\nabla \mathcal{{T}}^*[\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}]\) are as follows:

$$\begin{aligned} \nabla \mathcal{{T}}_{1i}^*[\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}]= & {} \left( \sum _{j=1}^N{D}_{ij}{} \mathbf{X}_j \right) - \mathbf{{A}}_i \mathbf{{X}}_i - \mathbf{{B}}_i \mathbf{{U}}_i, \quad 1\le i\le N ,\\ \nabla \mathcal{{T}}_2^*[\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}]= & {} \mathbf{X}_{N+1}-\sum _{j=1}^N\omega _j (\mathbf{{A}}_j \mathbf{{X}}_j + \mathbf{{B}}_j \mathbf{{U}}_j), \\ \nabla \mathcal{{T}}_{3i}^*[\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}]= & {} \left( \sum _{j=1}^{N+1}{D}_{ij}^\dag {{\varvec{\Lambda }}}_j \right) + \mathbf{{A}}_i^\mathsf{T}{\varvec{\Lambda }}_i + \mathbf{{Q}}_i \mathbf{{X}}_i + \mathbf{{S}}_i \mathbf{{U}}_i, \quad 1 \le i \le N , \\ \nabla \mathcal{{T}}_4^*[\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}]= & {} {{\varvec{\Lambda }}}_{N+1} -\mathbf{{T}} \mathbf{{X}}_{N+1}, \\ \nabla \mathcal{{T}}_{5i}^*[\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}]= & {} \mathbf{{S}}_i^\mathsf{T}\mathbf{{X}}_i + \mathbf{{R}}_i \mathbf{{U}}_i + \mathbf{{B}}_i^\mathsf{T}{\varvec{\Lambda }}_i, \quad 1\le i\le N . \end{aligned}$$

Notice that \(\mathbf{{X}}_0\) does not appear in \(\nabla \mathcal{{T}}^*\) since \(\mathbf{{X}}_0\) is treated as a constant whose gradient vanishes.

The analysis of invertibility starts with the first component of \(\nabla \mathcal{{T}}^*\).

Lemma 5.1

If (P1) and (A2) hold, then for each \(\mathbf{{q}} \in \mathbb {R}^n\) and \(\mathbf{{p}} \in \mathbb {R}^{nN}\) with \(\mathbf{{p}}_i \in \mathbb {R}^n\), \(1 \le i \le N\), the linear system

$$\begin{aligned} \left( \sum _{j=1}^{N}{D}_{ij}{} \mathbf{X}_j \right) - \mathbf{{A}}_i \mathbf{{X}}_i= & {} \mathbf{{p}}_{i} \quad 1\le i\le N , \end{aligned}$$
(31)
$$\begin{aligned} \mathbf{X}_{N+1} -\sum _{j=1}^N\omega _j \mathbf{{A}}_j \mathbf{{X}}_j= & {} {\mathbf{{q}}}, \end{aligned}$$
(32)

has a unique solution \(\mathbf{{X}}_j \in \mathbb {R}^{n}\), \(1 \le j \le N+1\). This solution has the bound

$$\begin{aligned} \Vert \mathbf{{X}}_j\Vert _\infty\le & {} 2\Vert \mathbf{{p}}\Vert _\infty /(1-2\beta ) , \quad 1 \le j \le N, \end{aligned}$$
(33)
$$\begin{aligned} \Vert \mathbf{{X}}_{N+1}\Vert _\infty\le & {} \Vert \mathbf{{q}}\Vert _\infty + 4\beta \Vert \mathbf{{p}}\Vert _\infty / (1-2\beta ). \end{aligned}$$
(34)

Proof

Let \(\bar{\mathbf{{X}}}\) be the vector obtained by vertically stacking \(\mathbf{{X}}_1\) through \(\mathbf{{X}}_N\), let \({\mathbf{{A}}}\) be the block diagonal matrix with i-th diagonal block \(\mathbf{{A}}_i\), \(1 \le i \le N\), and define \(\bar{\mathbf{{D}}} = \mathbf{D}_{1:N}\otimes \mathbf{I}_n\) where \(\otimes \) is the Kronecker product. With this notation, the linear system (31) can be expressed \((\bar{\mathbf{{D}}} - {\mathbf{{A}}}) \bar{\mathbf{{X}}} = \mathbf{{p}}\). By (P1) \(\mathbf{D}_{1:N}\) is invertible which implies that \(\bar{\mathbf{{D}}}\) is invertible with \(\bar{\mathbf{{D}}}^{-1} = \mathbf{D}_{1:N}^{-1}\otimes \mathbf{I}_n\). Moreover, \(\Vert \bar{\mathbf{D}}^{-1}\Vert _\infty =\) \(\Vert \mathbf{D}_{1:N}^{-1}\Vert _\infty \le 2\) by (P1). By (A2) \(\Vert {\mathbf{{A}}}\Vert _\infty \le \beta \) and \(\Vert \bar{\mathbf{{D}}}^{-1}{\mathbf{{A}}}\Vert _\infty \le \) \(\Vert \bar{\mathbf{{D}}}^{-1}\Vert _\infty \Vert {\mathbf{{A}}}\Vert _\infty \le 2\beta \). By Horn and Johnson [26, p. 351], \(\mathbf{I}-\bar{\mathbf{D}}^{-1}{} \mathbf{A}\) is invertible since \(\beta < 1/2\) and \(\left\| (\mathbf{I}-\bar{\mathbf{D}}^{-1}\mathbf{A})^{-1}\right\| _\infty \le \) \(1/(1-2\beta )\). Consequently, \(\bar{\mathbf{{D}}} - {\mathbf{{A}}} =\) \(\bar{\mathbf{{D}}}(\mathbf{{I}} - \bar{\mathbf{{D}}}^{-1}{\mathbf{{A}}})\) is invertible, and

$$\begin{aligned} \Vert (\bar{\mathbf{{D}}} - {\mathbf{{A}}})^{-1}\Vert _\infty \le \Vert (\mathbf{{I}} - \bar{\mathbf{{D}}}^{-1}{\mathbf{{A}}})^{-1}\Vert _\infty \Vert \bar{\mathbf{{D}}}^{-1}\Vert _\infty \le 2/(1-2\beta ). \end{aligned}$$

Thus there exists a unique \(\bar{\mathbf{{X}}}\) such that \((\bar{\mathbf{{D}}} - {\mathbf{{A}}}) \bar{\mathbf{{X}}} = \mathbf{{p}}\), and (33) holds. By (32), we have

$$\begin{aligned} \Vert \mathbf{{X}}_{N+1}\Vert _\infty \le \Vert \mathbf{{q}}\Vert _\infty + \sum _{j=1}^N \omega _j \Vert \mathbf{{A}}_j\Vert _\infty \Vert \mathbf{{X}}_j\Vert _\infty . \end{aligned}$$

Hence, (34) follows from (33) and the fact that the \(\omega _j\) are positive and sum to 2 and \(\Vert \mathbf{{A}}_j \Vert _\infty \le \beta \) by (A2). \(\square \)

Next, we establish the invertibility of \(\nabla \mathcal{{T}}^*\).

Proposition 5.1

If (A1), (A2), and (P1) hold, then \(\nabla \mathcal{{T}}^*\) is invertible.

Proof

We formulate a strongly convex quadratic programming problem whose first-order optimality conditions reduce to \(\nabla \mathcal{{T}}^*[\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}] = \mathbf{{y}}\). Due to the strong convexity of the objective function, the quadratic programming has a solution and there exists \({\varvec{\Lambda }}\) such that \(\nabla \mathcal{{T}}^*[\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}] = \mathbf{{y}}\). Since \(\mathcal{{T}}^*\) is square and \(\nabla \mathcal{{T}}^*[\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}] = \mathbf{{y}}\) has a solution for each choice of \(\mathbf{{y}}\), it follows that \(\nabla \mathcal{{T}}^*\) is invertible.

The quadratic program is

$$\begin{aligned} \left. \begin{array}{cl} \text{ minimize } &{}\frac{1}{2} \mathcal {Q}(\mathbf{X},\mathbf{U}) + \mathcal{{L}}(\mathbf{{X}}, \mathbf{{U}}) \\ \text{ subject } \text{ to } &{}\sum _{j=1}^N{D}_{ij}{} \mathbf{X}_j =\mathbf{A}_i\mathbf{X}_i+ \mathbf{B}_i\mathbf{U}_i+\mathbf{y}_{1i}, \quad 1\le i \le N, \\ &{}\mathbf{X}_{N+1}= \mathbf{{y}}_2 + \sum _{j=1}^N\omega _j \left( \mathbf{A}_j\mathbf{X}_j+\mathbf{B}_j\mathbf{U}_j \right) , \end{array} \right\} \end{aligned}$$
(35)

where the quadratic and linear terms in the objective are

$$\begin{aligned} \mathcal {Q}(\mathbf{X},\mathbf{U})= & {} \mathbf{X}_{N+1}^\mathsf{T}\mathbf{T}{} \mathbf{X}_{N+1} + \mathcal{{Q}}_0(\bar{\mathbf{{X}}}, \mathbf{{U}}) \end{aligned}$$
(36)
$$\begin{aligned} \mathcal{{Q}}_0(\bar{\mathbf{{X}}}, \mathbf{{U}})= & {} \sum _{i=1}^N\omega _i \left( \mathbf{X}_i^\mathsf{T}\mathbf{Q}_i\mathbf{X}_i +2\mathbf{X}_i^\mathsf{T}\mathbf{S}_i\mathbf{U}_i +\mathbf{U}_i^\mathsf{T}\mathbf{R}_i\mathbf{U}_i\right) , \nonumber \\ \mathcal{{L}}(\mathbf{{X}}, \mathbf{{U}})= & {} \mathbf{{y}}_4^\mathsf{T}\mathbf{{X}}_{N+1} + \mathcal{{L}}_0(\bar{\mathbf{{X}}}, \mathbf{{U}}), \nonumber \\ \mathcal{{L}}_0(\bar{\mathbf{{X}}}, \mathbf{{U}})= & {} - \sum _{i=1}^N\omega _i \left( \mathbf{{y}}_{3i}^\mathsf{T}\mathbf{{X}}_i + \mathbf{{y}}_{5i}^\mathsf{T}\mathbf{{U}}_i \right) . \end{aligned}$$
(37)

The first-order optimality conditions for (35) reduce to \(\nabla \mathcal{{T}}^*[\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}] = \mathbf{{y}}\). See Garg et al. [2] for the manipulations needed to obtain the first-order optimality conditions in this form.

Notice that the state variable \(\mathbf{{X}}_{N+1}\) in the quadratic program (35) can be expressed as a function of \(\bar{\mathbf{{X}}}\), \(\mathbf{{U}}\), and the parameter \(\mathbf{{y}}_2\). After making this substitution, we obtain a new quadratic \(\bar{\mathcal{{Q}}}\) and a new linear term \(\bar{\mathcal{{L}}}\) in the objective:

$$\begin{aligned} \bar{\mathcal {Q}}(\bar{\mathbf{X}},\mathbf{U})= & {} \mathcal{{Q}}_0(\bar{\mathbf{{X}}}, \mathbf{{U}}) + \mathcal{{Q}}_1(\bar{\mathbf{{X}}}, \mathbf{{U}}), \nonumber \\ \mathcal{{Q}}_1(\bar{\mathbf{{X}}}, \mathbf{{U}})= & {} \left( \sum _{i=1}^N\omega _i (\mathbf{A}_i\mathbf{X}_i+\mathbf{B}_i\mathbf{U}_i) \right) ^\mathsf{T}\mathbf{{T}} \left( \sum _{i=1}^N\omega _i (\mathbf{A}_i\mathbf{X}_i+\mathbf{B}_i\mathbf{U}_i) \right) , \nonumber \\ \bar{\mathcal{{L}}}(\bar{\mathbf{{X}}}, \mathbf{{U}})= & {} \mathcal{{L}}_0(\bar{\mathbf{{X}}}, \mathbf{{U}}) + \sum _{i=1}^N \omega _i (\mathbf{{y}}_4+ 2\mathbf{{Ty}}_2)^\mathsf{T}(\mathbf{{A}}_i \mathbf{{X}}_i + \mathbf{{B}}_i \mathbf{{U}}_i). \nonumber \end{aligned}$$

Hence, the elimination of \(\mathbf{{X}}_{N+1}\) from the quadratic program (35) leads to the reduced problem

$$\begin{aligned} \left. \begin{array}{cl} \text{ minimize } &{}\frac{1}{2} \bar{\mathcal {Q}}(\bar{\mathbf{X}},\mathbf{U}) + \bar{\mathcal{{L}}}(\bar{\mathbf{{X}}}, \mathbf{{U}}) \\ \text{ subject } \text{ to } &{}\sum _{j=1}^N{D}_{ij}{} \mathbf{X}_j =\mathbf{A}_i\mathbf{X}_i+ \mathbf{B}_i\mathbf{U}_i+\mathbf{y}_{1i}, \quad 1\le i \le N. \end{array} \right\} \end{aligned}$$
(38)

By (A1), we have

$$\begin{aligned} \bar{\mathcal{{\mathcal {Q}}}}(\bar{\mathbf{X}},\mathbf{U})\ge \alpha \left( \sum _{i=1}^N \omega _i\left( |\mathbf{X}_i|^2 +|\mathbf{U}_i|^2\right) \right) . \end{aligned}$$
(39)

Since \(\alpha \) and \({\varvec{\omega }}\) are strictly positive, the objective of (38) is strongly convex with respect to \(\bar{\mathbf{{X}}}\) and \(\mathbf{{U}}\), and by Lemma 5.1, the quadratic programming problem is feasible. Hence, there exists a unique solution to both (35) and (38) for any choice of \(\mathbf{{y}}\), and since the constraints are linear, the first-order necessary optimality conditions hold. Consequently, \(\nabla \mathcal{{T}}^*[\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}] = \mathbf{{y}}\) has a solution for any choice of \(\mathbf{{y}}\) and the proof is complete. \(\square \)

6 \(\omega \)-Norm Bounds

In this section, we obtain a bound for the \((\mathbf{{X}}, \mathbf{{U}})\) component of the solution to \(\nabla \mathcal{{T}}^*[\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}] = \mathbf{{y}}\) in terms of \(\mathbf{{y}}\). We bound the Euclidean norm of \(\mathbf{{X}}_{N+1}\), while the other components of the state and the control are bounded in the \(\omega \)-norm defined by

$$\begin{aligned} \Vert \bar{\mathbf{X}}\Vert _\omega ^2= \sum _{i=1}^N\omega _i|\mathbf{X}_i|^2 \quad \text{ and } \quad \Vert \mathbf{U}\Vert _\omega ^2= \sum _{i=1}^N\omega _i|\mathbf{U}_i|^2. \end{aligned}$$
(40)

This defines a norm since the Gauss quadrature weight \(\omega _i > 0\) for each i. Since the \((\mathbf{{X}}, \mathbf{{U}})\) component of the solution to \(\nabla \mathcal{{T}}^*[\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}] = \mathbf{{y}}\) is a solution of the quadratic program (35), we will bound the solution to the quadratic program.

First, let us think more abstractly. Let \(\pi \) be a symmetric, continuous bilinear functional defined on a Hilbert space \(\mathcal{{H}}\), let \(\ell \) be a continuous linear functional, let \(\phi \in \mathcal{{H}}\), and consider the quadratic program

$$\begin{aligned} \min \left\{ \frac{1}{2}\pi (v+\phi ,v+\phi ) + \ell (v+\phi ): v\in \mathcal{{V}} \right\} , \end{aligned}$$

where \(\mathcal{{V}}\) is a subspace of \(\mathcal{{H}}\). If w is a minimizer, then by the first-order optimality conditions, we have

$$\begin{aligned} \pi (w, v) + \pi (\phi , v) + \ell (v) = 0 \quad \text{ for } \text{ all } v \in \mathcal{{V}}. \end{aligned}$$

Inserting \(v = w\) yields

$$\begin{aligned} \pi (w,w) = -(\pi (w, \phi ) + \ell (w)). \end{aligned}$$
(41)

We apply this observation to the quadratic program (38). We identify \(\ell \) with the linear functional \(\bar{\mathcal{{L}}}\), and \(\pi \) with the bilinear form associated with the quadratic \(\bar{\mathcal{{Q}}}\). The subspace \(\mathcal{{V}}\) is the null space of the linear operator in (38), and \(\phi \) is a particular solution of the linear system. For the particular solution of the linear system in (38), we take \(\bar{\mathbf{{X}}} = {\varvec{\chi }}\) and \(\mathbf{{U}} = \mathbf{{0}}\), where \({\varvec{\chi }}\) denotes the solution to (31) given by Lemma 5.1 for \(\mathbf{{p}} = \mathbf{{y}}_1\). The complete solution of (38) is the particular solution \(({\varvec{\chi }}, \mathbf{{0}})\) plus the minimizer over the null space, which we denote \((\mathbf{{X}}^{\mathcal{{N}}}, \mathbf{{U}}^{\mathcal{{N}}})\).

In the relation (41) describing the null space component \((\mathbf{{X}}^{\mathcal{{N}}}, \mathbf{{U}}^{\mathcal{{N}}})\) of the solution, \(\pi (w,w)\) corresponds to \(\bar{\mathcal{{Q}}}(\bar{\mathbf{{X}}}^{\mathcal{{N}}}, \mathbf{{U}}^{\mathcal{{N}}})\). The terms on the right side of (41) correspond to

$$\begin{aligned} \pi (w, \phi )= & {} \sum _{i=1}^N \omega _i \left[ ({\varvec{\chi }}_i^\mathsf{T}\mathbf{{Q}}_i + \mathbf{{z}}^\mathsf{T}\mathbf{{A}}_i )\mathbf{{X}}_i^{\mathcal{{N}}} + ({\varvec{\chi }}_i^\mathsf{T}\mathbf{{S}}_i + \mathbf{{z}}^\mathsf{T}\mathbf{{B}}_i)\mathbf{{U}}_i^{\mathcal{{N}}} \right] , \quad \text{ and }\\ \ell (w)= & {} \sum _{i=1}^N \omega _i \left[ \left( (\mathbf{{y}}_4+2\mathbf{{Ty}}_2)^\mathsf{T}\mathbf{{A}}_i - \mathbf{{y}}_{3i}^\mathsf{T}\right) \mathbf{{X}}_i^{\mathcal{{N}}} + \left( (\mathbf{{y}}_4+2\mathbf{{Ty}}_2)^\mathsf{T}\mathbf{{B}}_i - \mathbf{{y}}_{5i}^\mathsf{T}\right) \mathbf{{U}}_i^{\mathcal{{N}}} \right] , \end{aligned}$$

where

$$\begin{aligned} \mathbf{{z}} = \mathbf{{T}}\left( \sum _{i=1}^N \omega _i \mathbf{{A}}_i {\varvec{\chi }}_i \right) . \end{aligned}$$

(A1) implies that the quadratic term has the lower bound

$$\begin{aligned} \pi (w, w) = \bar{\mathcal{{Q}}}(\bar{\mathbf{{X}}}^{\mathcal{{N}}}, \mathbf{{U}}^{\mathcal{{N}}}) \ge \alpha (\Vert \bar{\mathbf{{X}}}^{\mathcal{{N}}}\Vert _\omega ^2 + \Vert \mathbf{{U}}^{\mathcal{{N}}}\Vert _\omega ^2) . \end{aligned}$$
(42)

The terms corresponding to \(\pi (w, \phi )\) and \(\ell (w)\) can all be bounded in terms of the \(\omega \)-norms of \(\bar{\mathbf{{X}}}\) and \(\mathbf{{U}}\) and \(\Vert \mathbf{{y}}\Vert \). For example, by the Schwarz inequality, we have

$$\begin{aligned} \sum _{i=1}^N \omega _i \mathbf{{y}}_{3i}^\mathsf{T}\mathbf{{X}}_i^{\mathcal{{N}}}\le & {} \left( \sum _{i=1}^N \omega _i |\mathbf{{y}}_{3i}|^2 \right) ^{1/2} \left( \sum _{i=1}^N \omega _i |\mathbf{{X}}_{i}^{\mathcal{{N}}}|^2 \right) ^{1/2} \nonumber \\\le & {} \sqrt{2} \Vert \mathbf{{y}}_3\Vert _\infty \left( \Vert \bar{\mathbf{{X}}}^{\mathcal{{N}}}\Vert _\omega ^2 + \Vert \mathbf{{U}}^{\mathcal{{N}}}\Vert _\omega ^2 \right) ^{1/2} . \end{aligned}$$
(43)

The last inequality exploits the fact that the \(\omega _i\) sum to 2 and \(|\mathbf{{y}}_{3i}| \le \Vert \mathbf{{y}}_3\Vert _\infty \). To handle the terms involving \({\varvec{\chi }}\) in \(\pi (w,\phi )\) and \(\ell (w)\), we utilize the upper bound \(|{\varvec{\chi }}_j| \le 2 \Vert \mathbf{{y}}\Vert _\infty /(1-2\beta )\) given in (33). Hence, we have

$$\begin{aligned} |\mathbf{{z}}|\le & {} |\mathbf{{T}}|\sum _{i=1}^N \omega _i |\mathbf{{A}}_i| \left[ 2\Vert \mathbf{{y}}\Vert _\infty /(1-2\beta ) \right] \le \left[ 2\beta /(1-2\beta ) \right] |\mathbf{{T}}| \Vert \mathbf{{y}}\Vert _\infty \sum _{i=1}^N \omega _i \\= & {} \left[ 4\beta /(1-2\beta ) \right] |\mathbf{{T}}| \Vert \mathbf{{y}}\Vert _\infty , \end{aligned}$$

where we used (A2) to obtain the bound

$$\begin{aligned} |\mathbf{{A}}_i| = \sqrt{|\mathbf{{A}}_i^\mathsf{T}\mathbf{{A}}_i|} \le \sqrt{\Vert \mathbf{{A}}_i^\mathsf{T}\mathbf{{A}}_i\Vert _\infty } \le \sqrt{\Vert \mathbf{{A}}_i^\mathsf{T}\Vert _\infty \Vert \mathbf{{A}}_i\Vert _\infty } \le \beta . \end{aligned}$$
(44)

Combine upper bounds of the form (43) with the lower bound like (42) to conclude that \(\Vert \bar{\mathbf{{X}}}^{\mathcal{{N}}}\Vert _\omega \) and \(\Vert \mathbf{{U}}^{\mathcal{{N}}}\Vert _\omega \) are bounded by a constant times \(\Vert \mathbf{{y}}\Vert _\infty \). The complete solution of (38) is the null space component that we just bounded plus the particular solution \(({\varvec{\chi }}, \mathbf{{0}})\). Again, since \(\Vert {\varvec{\chi }}_j\Vert _\infty \le 2 \Vert \mathbf{{y}}\Vert _\infty /(1-2\beta )\), we deduce that the complete solution \((\bar{\mathbf{{X}}}, \mathbf{{U}})\), null space component plus particular solution, has \(\Vert \bar{\mathbf{{X}}}\Vert _\omega \) and \(\Vert \mathbf{{U}}\Vert _\omega \) bounded by a constant times \(\Vert \mathbf{{y}}\Vert _\infty \). Finally, the equation for \(\mathbf{{X}}_{N+1}\) in (35) yields

$$\begin{aligned} |\mathbf{{X}}_{N+1}| \le |\mathbf{{y}}_2| + \sum _{i=1}^N \omega _i \left[ |\mathbf{{A}}_i| | \mathbf{{X}}_i| + |\mathbf{{B}}_i| |\mathbf{{U}}_i| \right] . \end{aligned}$$

Again, the Schwarz inequality gives bounds such as

$$\begin{aligned} \sum _{i=1}^N \omega _i |\mathbf{{A}}_i| | \mathbf{{X}}_i| \le \left( \sum _{i=1}^N \omega _i |\mathbf{{A}}_i|^2\right) ^{1/2} \Vert \bar{\mathbf{{X}}}\Vert _\omega \le \sqrt{2}\beta \Vert \bar{\mathbf{{X}}}\Vert _\omega , \end{aligned}$$

where the last inequality is due to (44) and the fact that the \(\omega _i\) sum to 2. Since \(\Vert \bar{\mathbf{{X}}}\Vert _\omega \) and \(\Vert \mathbf{{U}}\Vert _\omega \) are bounded by a constant times \(\Vert \mathbf{{y}}\Vert _\infty \), so is \(|\mathbf{{X}}_{N+1}|\). This yields the following:

Lemma 6.1

If (A1), (A2), and (P1) hold, then there exists a constant c, independent of N, such that the solution \((\mathbf{{X}}, \mathbf{{U}})\) of (35) satisfies \(|\mathbf{{X}}_{N+1}| \le c\Vert \mathbf{{y}}\Vert _\infty \), \(\Vert \bar{\mathbf{{X}}}\Vert _\omega \le c \Vert \mathbf{{y}}\Vert _\infty \), and \(\Vert \mathbf{{U}}\Vert _\omega \le c \Vert \mathbf{{y}}\Vert _\infty \).

7 Infinity Norm Bounds

We now need to convert these \(\omega \)-norm bounds for \(\mathbf{{X}}\) and \(\mathbf{{U}}\) into \(\infty \)-norm bounds and, at the same time, obtain an \(\infty \)-norm estimate for \({\varvec{\Lambda }}\). By Lemma 5.1, the solution to the dynamics in (35) can be expressed

$$\begin{aligned} \bar{\mathbf{{X}}} = (\mathbf{{I}} - \bar{\mathbf{{D}}}^{-1}{\mathbf{{A}}})^{-1} \bar{\mathbf{{D}}}^{-1} \mathbf{{BU}} + (\bar{\mathbf{{D}}} - \mathbf{{A}})^{-1}\mathbf{{y}}_1, \end{aligned}$$
(45)

where \(\mathbf{{B}}\) is the block diagonal matrix with ith diagonal block \(\mathbf{{B}}_i\). Taking norms and utilizing the bounds \(\Vert (\bar{\mathbf{{D}}} - \mathbf{{A}})^{-1}\mathbf{{y}}_1 \Vert _\infty \le \) \(2 \Vert \mathbf{{y}}_1\Vert _\infty /(1-2\beta )\) and \(\left\| (\mathbf{I}-\bar{\mathbf{D}}^{-1}{} \mathbf{A})^{-1}\right\| _\infty \le 1/(1-2\beta )\) from Lemma 5.1, we obtain

$$\begin{aligned} \Vert \bar{\mathbf{{X}}}\Vert _\infty \le \left( \Vert \bar{\mathbf{{D}}}^{-1} \mathbf{{BU}}\Vert _\infty + 2 \Vert \mathbf{{y}}_1\Vert _\infty \right) /(1-2\beta ) . \end{aligned}$$
(46)

We now write

$$\begin{aligned} \bar{\mathbf{{D}}}^{-1} \mathbf{{BU}} = [\mathbf{{D}}_{1:N}^{-1}\otimes \mathbf{{I}}_n] \mathbf{{BU}} = [(\mathbf{{W}}^{1/2} \mathbf{{D}}_{1:N})^{-1} \otimes \mathbf{{I}}_n] \mathbf{{BU}}_\omega , \end{aligned}$$
(47)

where \(\mathbf{{W}}\) is the diagonal matrix with the quadrature weights on the diagonal and \(\mathbf{{U}}_\omega \) is the vector whose ith element is \(\sqrt{\omega _i} \mathbf{{U}}_i\). Note that the \(\sqrt{\omega _i}\) factors in (47) cancel each other. An element of the vector \(\bar{\mathbf{{D}}}^{-1} \mathbf{{BU}}\) is the dot product between a row of \((\mathbf{{W}}^{1/2} \mathbf{{D}}_{1:N})^{-1} \otimes \mathbf{{I}}_n\) and the column vector \(\mathbf{{BU}}_\omega \). By (P2) the rows of \((\mathbf{{W}}^{1/2} \mathbf{{D}}_{1:N})^{-1} \otimes \mathbf{{I}}_n\) have Euclidean length bounded by \(\sqrt{2}\). By the properties of matrix norms induced by vector norms, we have

$$\begin{aligned} |\mathbf{{BU}}_\omega | \le |\mathbf{{B}}| |\mathbf{{U}}_\omega | = |\mathbf{{B}}| \Vert \mathbf{{U}}\Vert _\omega . \end{aligned}$$
(48)

Thus thinking of \(\bar{\mathbf{{D}}}^{-1} \mathbf{{BU}}\) in (47) as being the dot product of \(\mathbf{{BU}}_\omega \) with a vector of length at most \(\sqrt{2}\), where the Euclidean length of \(\mathbf{{BU}}_\omega \) is estimated in (48), we have

$$\begin{aligned} \Vert \bar{\mathbf{{D}}}^{-1} \mathbf{{BU}}\Vert _\infty \le \sqrt{2} |\mathbf{{B}}| \Vert \mathbf{{U}}\Vert _\omega . \end{aligned}$$
(49)

Combine Lemma 6.1 with (46) and (49) to deduce that \(\Vert \bar{\mathbf{{X}}}\Vert _{\infty } \le c \Vert \mathbf{{y}}\Vert _\infty \), where c is independent of N. Since \(|\mathbf{X}_{N+1}| \le c\Vert \mathbf{{y}}\Vert _\infty \) by Lemma 6.1, it follows that

$$\begin{aligned} \Vert {\mathbf{{X}}}\Vert _{\infty } \le c \Vert \mathbf{{y}}\Vert _\infty . \end{aligned}$$
(50)

Next, we use the third and fourth components of the linear system

$$\begin{aligned} \nabla \mathcal{{T}}^*[\mathbf{{X}}, \mathbf{{U}},{\varvec{\Lambda }}] = \mathbf{{y}} \end{aligned}$$
(51)

to obtain bounds for \({\varvec{\Lambda }}\). These equations can be written

$$\begin{aligned} \bar{\mathbf{{D}}}^\dagger \bar{{\varvec{\Lambda }}} + \bar{\mathbf{{D}}}_{N+1}^\dagger {\varvec{\Lambda }}_{N+1} + {\mathbf{{A}}}^\mathsf{T}\bar{{\varvec{\Lambda }}} + {\mathbf{{Q}}} \bar{\mathbf{{X}}} + {\mathbf{{S}}} {\mathbf{{U}}} = \mathbf{{y}}_3 \end{aligned}$$
(52)

and

$$\begin{aligned} {\varvec{\Lambda }}_{N+1} - \mathbf{{TX}}_{N+1} = \mathbf{{y}}_4 , \end{aligned}$$
(53)

where \(\bar{\mathbf{{D}}}^\dagger = \mathbf{D}_{1:N}^\dagger \otimes \mathbf{I}_n\), \(\bar{\mathbf{{D}}}_{N+1}^\dagger = \mathbf{{D}}_{N+1}^\dagger \otimes \mathbf{{I}}_n\) and \(\mathbf{{D}}_{N+1}^\dagger \) is the \((N+1)\)th column of \(\mathbf{{D}}^\dagger \), \(\bar{{\varvec{\Lambda }}}\) is obtained by vertically stacking \({\varvec{\Lambda }}_1\) through \({\varvec{\Lambda }}_N\), and \({\mathbf{{Q}}}\) and \({\mathbf{{S}}}\) are block diagonal matrices with ith diagonal blocks \(\mathbf{{Q}}_i\) and \(\mathbf{{S}}_i\), respectively.

We show in Proposition 10.1 of the “Appendix” that \(\mathbf{{D}}_{1:N} = -\mathbf{{J}} \mathbf{{D}}_{1:N}^\dagger \mathbf{{J}}\), where \(\mathbf{{J}}\) is the exchange matrix with ones on its counterdiagonal and zeros elsewhere. It follows that \(\mathbf{{D}}_{1:N}^{-1} = -\mathbf{{J}} (\mathbf{{D}}_{1:N}^\dagger )^{-1}\mathbf{{J}}\). Consequently, the elements in \(\mathbf{{D}}_{1:N}^{-1}\) are the negative of the elements in \((\mathbf{{D}}_{1:N}^\dagger )^{-1}\), but rearranged as in (60). As a result, \((\mathbf{{D}}_{1:N}^\dagger )^{-1}\) also possesses properties (P1) and (P2), and the analysis of the discrete costate closely parallels the analysis of the state. The main difference is that the costate equation contains the additional \({\varvec{\Lambda }}_{N+1}\) term along with the additional equation (53). By (53) and the previously established bound \(\Vert {\mathbf{{X}}}\Vert _{\infty } \le c \Vert \mathbf{{y}}\Vert _\infty \), it follows that

$$\begin{aligned} \Vert {\varvec{\Lambda }}_{N+1}\Vert _{\infty } \le c \Vert \mathbf{{y}}\Vert _\infty , \end{aligned}$$
(54)

where c is independent of N. Since \(\mathbf{{D}}^\dagger \mathbf{{1}} = \mathbf{{0}}\), we deduce that \((\mathbf{{D}}_{1:N}^\dagger )^{-1} \mathbf{{D}}_{N+1}^\dagger = -\mathbf{{1}}\). It follows that

$$\begin{aligned} (\bar{\mathbf{{D}}}^\dagger )^{-1} \bar{\mathbf{{D}}}_{N+1}^\dagger = [(\mathbf{D}_{1:N}^\dagger )^{-1}\otimes \mathbf{I}_n] [\mathbf{{D}}_{N+1}^\dagger \otimes \mathbf{{I}}_n] = -\mathbf{{1}}\otimes \mathbf{{I}}_n . \end{aligned}$$

Exploiting this identity, the analog of (45) is

$$\begin{aligned} \bar{{\varvec{\Lambda }}} = (\mathbf{{I}} + (\bar{\mathbf{{D}}}^\dagger )^{-1}{\mathbf{{A}}}^\mathsf{T})^{-1} [(\mathbf{{1}}\otimes \mathbf{{I}}_n){\varvec{\Lambda }}_{N+1} + (\bar{\mathbf{{D}}}^\dagger )^{-1} (\mathbf{{y}}_3 - {\mathbf{{Q}}} \bar{\mathbf{{X}}} - {\mathbf{{S}}} {\mathbf{{U}}})] . \end{aligned}$$

Hence, we have

$$\begin{aligned} \Vert \bar{{\varvec{\Lambda }}}\Vert _\infty \le \Vert (\mathbf{{1}}\otimes \mathbf{{I}}_n){\varvec{\Lambda }}_{N+1} + (\bar{\mathbf{{D}}}^\dagger )^{-1} (\mathbf{{y}}_3 - {\mathbf{{Q}}} \bar{\mathbf{{X}}} - {\mathbf{{S}}} {\mathbf{{U}}})\Vert _\infty /(1-2\beta ) . \end{aligned}$$
(55)

Moreover, \(\Vert (\mathbf{{1}}\otimes \mathbf{{I}}_n){\varvec{\Lambda }}_{N+1} \Vert _\infty \le c\Vert \mathbf{{y}}\Vert _\infty \) by (54), \(\Vert (\bar{\mathbf{{D}}}^\dagger )^{-1} \mathbf{{y}}_3\Vert _\infty \le 2 \Vert \mathbf{{y}}_3\Vert _\infty \), and \(\Vert (\bar{\mathbf{{D}}}^\dagger )^{-1} {\mathbf{{Q}}} \bar{\mathbf{{X}}}\Vert _\infty \le \) \(2 \Vert {\mathbf{{Q}}}\Vert _\infty \Vert \bar{\mathbf{{X}}}\Vert _\infty \) where \(\Vert \bar{\mathbf{{X}}}\Vert _\infty \) is bounded by (50). The term \(\Vert (\bar{\mathbf{{D}}}^\dagger )^{-1} {\mathbf{{S}}} {\mathbf{{U}}})\Vert _\infty \) is handled exactly as \(\Vert \bar{\mathbf{{D}}}^{-1} \mathbf{{BU}}\Vert _\infty \) was handled in the state equation (45). Combine (54) with (55) to conclude that \(\Vert {{\varvec{\Lambda }}}\Vert _\infty \le c \Vert \mathbf{{y}}\Vert _\infty \) where c is independent of N.

Finally, let us examine the fifth component of the linear system (51). These equations can be written

$$\begin{aligned} \mathbf{{S}}_i^\mathsf{T}\mathbf{{X}}_i + \mathbf{{R}}_i \mathbf{{U}}_i + \mathbf{{B}}_i^\mathsf{T}{\varvec{\Lambda }}_i = \mathbf{{y}}_{5i}, \quad 1\le i\le N . \end{aligned}$$

By (A1) the smallest eigenvalue of \(\mathbf{{R}}_i\) is greater than \(\alpha > 0\). Consequently, the bounds \(\Vert \mathbf{{X}}\Vert _\infty \le c \Vert \mathbf{{y}}\Vert _\infty \) and \(\Vert {\varvec{\Lambda }}\Vert _\infty \le c \Vert \mathbf{{y}}\Vert _\infty \) imply the existence of a constant c, independent of N, such that \(\Vert \mathbf{{U}}\Vert _\infty \le c \Vert \mathbf{{y}}\Vert _\infty \). In summary, we have the following result:

Lemma 7.1

If (A1)–(A2) and (P1)–(P2) hold, then there exists a constant c, independent of N, such that the solution of \(\nabla \mathcal{{T}}^*[\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}] = \mathbf{{y}}\) satisfies

$$\begin{aligned} \max \left\{ \Vert \mathbf{{X}}\Vert _\infty , \Vert \mathbf{{U}}\Vert _\infty , \Vert {\varvec{\Lambda }}\Vert _\infty \right\} \le c \Vert \mathbf{{y}}\Vert _\infty . \end{aligned}$$

Let us now prove Theorem 2.1 using Proposition 3.1. By Lemma 7.1, \(\mu = \Vert \nabla \mathcal{{T}}(\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*)^{-1}\Vert _\infty \) is bounded uniformly in N. Choose \(\varepsilon \) small enough that \(\varepsilon \mu < 1\). When we compute the difference \(\nabla \mathcal{{T}}(\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}) - \nabla \mathcal{{T}}(\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*)\) for \((\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }})\) near \((\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*)\) in the \(\infty \)-norm, the \(\mathbf{{D}}\) and \(\mathbf{{D}}^\dagger \) constant terms cancel, and we are left with terms involving the difference of derivatives of \(\mathbf{{f}}\) or C up to second order at nearby points. By the smoothness assumption, these second derivatives are uniformly continuous on the closure of \(\Omega \) and on a ball around \(\mathbf{{x}}^*(1)\). Hence, for r sufficiently small, we have

$$\begin{aligned} \ \Vert \nabla \mathcal {T}(\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }})- \nabla \mathcal {T}(\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*)\Vert _\infty \le \varepsilon \end{aligned}$$

whenever

$$\begin{aligned} \max \{\Vert \mathbf{{X}} -\mathbf{{X}}^*\Vert _\infty , \Vert \mathbf{{U}} -\mathbf{{U}}^*\Vert _\infty , \Vert {\varvec{\Lambda }} - {\varvec{\Lambda }}^*\Vert _\infty \} \le r. \end{aligned}$$
(56)

Since the smoothness \(\eta \ge 4\) in Theorem 2.1, let us choose \(\eta = 4\) in Lemma 4.1 and then take \(\bar{N}\) large enough that \(\left\| \mathcal {T}\left( \mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*\right) \right\| \le (1-\mu \varepsilon )r/\mu \) for all \(N \ge \bar{N}\). Hence, by Proposition 3.1, there exists a solution to \(\mathcal{{T}}(\mathbf{{X}},\mathbf{{U}}, {\varvec{\Lambda }}) = \mathbf{{0}}\) satisfying (56). Moreover, by (18) and (20), the estimate (10) holds.

Notice that the smoothness parameter \(\eta \) does not enter into the discretization. We chose \(\eta = 4\) to establish the existence of a unique solution to \(\mathcal{{T}}(\mathbf{{X}},\mathbf{{U}}, {\varvec{\Lambda }}) = \mathbf{{0}}\) satisfying (56). Once we know that the solution exists, larger values for \(\eta \) can be inserted in the error bound (10) if the problem solution has more than 4 continuous derivatives. In particular, if the problem solution has an infinite number of continuous derivatives that are nicely bounded, then we might take \(\eta = N+1\) in (10).

The analysis shows the existence of a solution to \(\mathcal{{T}}(\mathbf{{X}},\mathbf{{U}}, {\varvec{\Lambda }}) = \mathbf{{0}}\), which corresponds to the first-order necessary optimality conditions for either (11) or (2). To complete the proof, we need to show that this stationary point is a local minimizer when the assumption that \(\nabla ^2 C(\mathbf{{x}}^*(1))\) is positive semidefinite is strengthened to positive definite. After replacing the KKT multipliers by the transformed quantities given by (17), the Hessian of the Lagrangian is a block diagonal matrix whose ith diagonal block, \(1 \le i \le N\), is \(\omega _i \nabla _{(x,u)}^2 H(\mathbf{{X}}_i, \mathbf{{U}}_i, {\varvec{\Lambda }}_i)\), where H is the Hamiltonian, and whose \((N+1)\)st diagonal block is \(\nabla ^2 C(\mathbf{{X}}_{N+1})\). In computing the Hessian, we assume that the \(\mathbf{{X}}\) and \(\mathbf{{U}}\) variables are arranged in the following order: \(\mathbf{{X}}_1\), \(\mathbf{{U}}_1\), \(\mathbf{{X}}_2\), \(\mathbf{{U}}_2\), \(\ldots \), \(\mathbf{{X}}_N\), \(\mathbf{{U}}_N\), \(\mathbf{{X}}_{N+1}\). By the strengthened version of (A1), the Hessian is positive definite when evaluated at \((\mathbf{{X}}^*, \mathbf{{U}}^*, {\varvec{\Lambda }}^*)\). By continuity of the second derivative of C and \(\mathbf{{f}}\) and by the convergence result (10), we conclude that the Hessian of the Lagrangian, evaluated at the solution of \(\mathcal{{T}}(\mathbf{{X}}, \mathbf{{U}}, {\varvec{\Lambda }}) = \mathbf{{0}}\) satisfying (56), is positive definite for N sufficiently large. Hence, by the second-order sufficient optimality condition [22, Thm.12.6], \((\mathbf{{X}},\mathbf{{U}})\) is a strict local minimizer of (11). This completes the proof of Theorem 2.1.

8 Numerical Illustrations

The first example we study is

$$\begin{aligned}&\text{ minimize } \;\; \textstyle {\frac{1}{2}} \displaystyle {\int _0^1 } \left[ u(t)^2 + x(t)u(t) + \textstyle {\frac{5}{4}}x(t)^2 \right] \; dt \\&\begin{array}{ll} \text{ subject } \text{ to }&{x}'(t) = .5x(t) + u(t), \quad x(0) = 1, \end{array} \nonumber \end{aligned}$$
(57)

with the optimal solution

$$\begin{aligned} x^*(t) = \frac{\cosh (1-t)}{\cosh (1)}, \quad u^*(t) = - \frac{\sinh (1 - t) + .5 \cosh (1-t)}{\cosh (1)} . \end{aligned}$$

To put this problem in the form of (1), we could introduce a new state variable y with dynamics

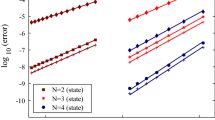
$$\begin{aligned} y'(t) = \frac{1}{2}\left( u(t)^2 + x(t)u(t) + 1.25 x(t)^2 \right) , \quad y(0) = 0, \end{aligned}$$

in which case the objective is y(1). Finally, we make the change of variable \(t = (1+\tau )/2\) to obtain the form (1). For this problem, (A1)–(A2) are satisfied so we expect the error to decay at least as fast as the bound given in Theorem 2.1. Since the derivatives of the hyperbolic functions are nicely bounded, exponential convergence is expected. Figure 1 plots the logarithm of the error in the sup-norm at the collocation points. Fitting the data of Fig. 1 by straight lines, we find that the error is \(O(10^{-1.5N})\) roughly.

Fig. 1
figure 1

The base 10 logarithm of the error in the sup-norm at the collocation points as a function of the polynomial degree for example (57)

Full size image

Although the assumptions (A1)–(A2) are sufficient for exponential convergence, the following example indicates that these assumptions are conservative. Let us consider the unconstrained control problem

$$\begin{aligned} \min \left\{ -x(2) : \dot{x}(t) = \textstyle {\frac{5}{2}}(-x(t) + x(t)u(t) - u(t)^2), \; x(0) = 1 \right\} . \end{aligned}$$
(58)

The optimal solution and associated costate are

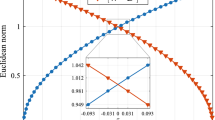
$$\begin{aligned} x^*(t)= & {} 4/a(t), \quad a(t) = 1 + 3 \exp (2.5t), \\ u^*(t)= & {} x^*(t)/2, \\ \lambda ^* (t)= & {} -a^2(t) \exp (-2.5t)/[\exp (-5) + 9 \exp (5) + 6]. \end{aligned}$$

This violates (A2) since \(\Vert \nabla _x f(\mathbf{{x}}^* (t), \mathbf{{u}}^* (t))\Vert _\infty \) is around 5/2 for t near 2. Nonetheless, as shown in Fig. 2, the logarithm of the error decays nearly linearly; the error behaves like \(c 10^{-0.6 N}\) for either the state or the control and \(c 10^{-0.8N}\) for the costate.

Fig. 2
figure 2

The base 10 logarithm of the error in the sup-norm as a function of the number of collocation points for example (58)

Full size image

A more complex problem with a known solution is

$$\begin{aligned} \min \int _0^1 \left[ 2x_1^2 x_2^2 + 1.25/x_2^2 + u_2/x_2 + u_1^2 + u_2^2 \right] dt , \end{aligned}$$
(59)

subject to the dynamics

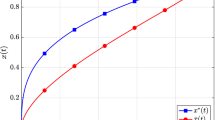
$$\begin{aligned} \begin{array}{ll} \dot{x}_1 = x_1 + u_1/x_2 + u_2 x_1x_2 , &{} \quad x_1(0) = 1, \\ \dot{x}_2 = -x_2(0.5 + u_2x_2), &{} \quad x_2(0) = 1. \end{array} \end{aligned}$$

The argument “(t)” on the states and controls was suppressed. The solution of the problem is

$$\begin{aligned} x_1^*(t)= & {} \frac{\cosh (1-t) (2 \exp (3t) + \exp (3))}{(2+\exp (3))\exp (3t/2)\cosh (1)}, \\ x_2^*(t)= & {} \frac{\cosh (1)}{\cosh (1-t)}, \\ u_1^*(t)= & {} \frac{2(\exp (3t) - \exp (3))}{(2+\exp (3))\exp (3t/2)}, \\ u_2^*(t)= & {} \frac{-\cosh (1-t)(\tanh (1-t)+0.5)}{\cosh (1)} . \end{aligned}$$

Figure 3 plots the logarithm of the sup-norm error in the state and control as a function of the number of collocation points. The convergence is again exponentially fast,

Fig. 3
figure 3

The base 10 logarithm of the error in the sup-norm as a function of the number of collocation points for example (59)

Full size image

9 Conclusions

A Gauss collocation scheme is analyzed for an unconstrained control problem. When the problem has a smooth solution with \(\eta \) continuous derivatives and with a Hamiltonian that satisfies a strong convexity assumption, we show that the discrete problem has a local minimizer in a neighborhood of the continuous solution, and as the degree N of the approximating polynomials increases, the error in the sup-norm at the collocation point is \(O(N^{3-p})\), where \(p = \min \{\eta , N+1\}\). Numerical examples confirm the exponential convergence.