1 Introduction

The submarine-launched missile, one of the most critical parts of the triad nuclear powers for every country, plays a crucial role in military strategies. The launching point of the submarine-launched missile is random in the presence of high-speed maneuver of the submarine underwater [1]. Meanwhile, the seawater is a strong barrier for the propagation of electromagnetic waves, such that the radar cannot detect the submarine effectively. Therefore, the submarine-launched missile has the characteristics of good concealment, strong ability to attack suddenly, high survivability, and formidable deterrence [2].

In most circumstances, the whole flight stage of the submarine-launched missile consists of three parts: the underwater stage, the water-exit stage and the aerial stage. The missile rises through the thrust of the underwater engine until its body is completely out of water in the water-exit stage [3]. However, the attitude and trajectory of the missile are seriously affected by the ocean currents, sea waves and sea winds during the water-exit process. This can make the missile deviate from the designed motion state and result in unstable flight or even an unsuccessful launch. Furthermore, the submarine-launched missile causes a series of complex changes in the flow field, such as the development and collapse of vacuoles, which produces complicated dynamic characteristics. Additionally, the flow filed evolution process adversely acts on the missile due to the pressure or even the impact load generated by cavity collapses, which constantly changes the strained condition of the missile, thus forming a complex fluid solid coupling process [4]. Therefore, the water-exit dynamic model of the submarine-launched missile is complicated and difficult to describe accurately. Moreover, the attitude tracking control design for the submarine-launched missile is also one of the most challenging problems for engineers in the presence of highly complex nonlinear dynamics, external disturbances, couplings, and uncertainties.

The initial conditions for the aerial stage of the submarine-launched missile are essential. Thus, the attitude information needs to be accurately obtained at the end of the water-exit process. Although the classical proportional–integral–derivative (PID) controller has already been developed based on the dynamical models linearized around the fixed flight points, most of the existing approaches cannot satisfy the precision demands of attitude tracking [5,6,7,8]. To further improve the performance and reliability of the control system, an adaptive longitudinal trajectory tracking control method based on backstepping technique is presented in [9]. However, the steady-state error is comparatively large. A sliding mode attitude control law based on the feedback linearization is also presented for a submarine-launched missile in the presence of strong nonlinearity of submerged buoy space motion and interference uncertainty [10]. Nevertheless, system chattering is inevitable in this case. With the development of modern control theories, multiple new control laws are proposed to ensure the robust, accurate, and rapid response to the attitude tracking controller in the presence of large disturbances and uncertainties. Unfortunately, the research of attitude tracking control system design for submarine-launched missiles is rare in the existing literature. In other fields, finite-time attitude tracking control [11], smooth backstepping sliding mode control [12], adaptive output feedback integral sliding mode attitude tracking control [13], and disturbance observer-based attitude tracking control [14,15,16,17,18] are widely utilized, especially for spacecrafts that have better performance than traditional ones. Many scholars, such as Utkin [19], Filippov [20], Roxin [21], Drakunov [22], Perruquetti [23], Defoort [24], and Baccioti [25], have also studied the finite-time stability theories to prove the stability of the corresponding controllers. In recent years, the fixed-time convergence sliding mode control has become a research focus [26,27,28]. In fact, the fixed-time strategy has been applied to many areas, such as mobile robots [29], multiagent systems [30, 31], fractional order chaotic systems [32] and power systems [33]. Different from finite-time stability, fixed-time stability can guarantee convergence within finite time, whose upper bound is a constant independent of initial conditions, which facilitates convergence time estimation and controller design to satisfy the severe settling time constraint [32]. This phenomenon was initially discovered in the context of systems that are homogeneous in the bi-limit [34]. Fixed-time stability was widely studied by Cruz-Zavala [35], Polyakov [36] and Fridman [37]. Moreover, fixed-time stability is an extension of finite-time stability and demands boundedness of the settling time function for a globally finite-time stable system [38]. The main tool for analysis of fixed-time stability is the Lyapunov function method [39, 40]. Compared with other sliding mode controls, the fixed-time sliding mode control obtains faster convergence in both the reaching phase and the sliding phase [41]. Furthermore, it can guarantee that the steady-state error is within a smaller convergence region for attitude tracking especially in the field of submarine-launched missiles.

In this study, we present a novel adaptive non-singular fixed-time fast terminal sliding mode control (ANFFTSMC) for a submarine-launched missile. The proposed ANFFTSMC consists of a non-singular fixed-time fast terminal sliding mode surface (NFFTSMS), a fixed-time disturbance observer and a fixed-time differentiator. To the best of our knowledge, this paper might be the first attempt to design a fixed-time attitude tracking control for submarine-launched missiles. The main contribution of this paper includes:

  1. 1.

    The complicated nonlinear water-exit dynamic model of submarine-launched missiles is completely established in the presence of engine thrust and multiple disturbances for the first time. Then, the attitude tracking control system design for the complicated dynamic model is transformed into a simple second-order state equation, which simplifies the control system.

  2. 2.

    The derivative of the attitude command, which can be constructed to be a novel NFFTSMS, is obtained by a fixed-time differentiator. Moreover, the proposed NFFTSMS can avoid singularity without adding additional parameters, and achieve faster convergence and a more compact structure than the existing approaches.

  3. 3.

    Unlike the existing attempts to design the sliding mode controller, the proposed ANFFTSMC is developed based on the total disturbances that are estimated by the fixed-time disturbance observer. The proposed controller does not require the bounded disturbances in advance. Also, the control parameters are not required to be equal to or greater than the disturbances.

This paper is organized as follows. In Sect. 2, the water-exit dynamic model of submarine-launched missiles is developed. After that, Sect. 3 presents a novel adaptive non-singular fixed-time fast terminal sliding mode control. Then, Sect. 4 provides the simulations and results. Lastly, Sect. 5 briefly concludes this work.

Notation In this paper, the bold italic variable \({\varvec{X}}\) is denoted as a vector and \({\varvec{X}}=\left[ {{\begin{array}{ccc} {X_{x} } &{} {X_{y} } &{} {X_{z} } \\ \end{array} }} \right] ^{\mathrm{T}}\). The italic variable X is the norm of the vector \({\varvec{X}}\).

Fig. 1
figure 1

Two typical trajectories of the submarine-launched missile

Full size image

2 Water-exit dynamic model

In most cases, a submarine-launched missile is launched at a depth of 30 m or even 100 m beneath the ocean. Meanwhile, the submarine-launched missile has two typical trajectories in the water-exit process, which correspond to the vertical launching mode and the oblique launching mode. The two typical trajectories are shown by the yellow and blue lines, respectively, in Fig. 1.

This section establishes the nonlinear attitude kinematics and dynamics model of the submarine-launched missile in the water-exit process. Figure 2 defines the body coordinate system \(Ox_{1} y_{1} z_{1} \) and the ground coordinate system \(O_{e} x_{0} y_{0} z_{0} \). It also presents the force analysis of the water-exit process.

Fig. 2
figure 2

Definition of two coordinate systems and force analysis of the water-exit process

Full size image

where O is the barycenter, \(O_{e}\) is the launch point, c is the center of buoyancy, and G is gravity. N denotes the buoyancy, and P represents the thrust of the main engine for the submarine-launched missile. \(\varvec{R}_{\alpha } =\left[ {{\begin{array}{ccc} {R_{\alpha x} } &{} {R_{\alpha y} } &{} {R_{\alpha z} } \\ \end{array} }} \right] ^{\mathrm{T}}\) represents the fluid viscosity force. \(\varvec{R}_{\omega } =\left[ {{\begin{array}{ccc} {R_{\omega x} } &{} {R_{\omega y} } &{} {R_{\omega z} } \\ \end{array} }} \right] ^{\mathrm{T}}\) denotes the fluid viscosity damping force and \(\varvec{R}=\left[ {{\begin{array}{ccc} {R_{x} } &{} {R_{y} } &{} {R_{z} } \\ \end{array} }} \right] ^{\mathrm{T}}\) stands for the fluid inertia force. The coordinate transform matrix from \(O_{e} x_{0} y_{0} z_{0} \) to \(Ox_{1} y_{1} z_{1} \) is given by

$$\begin{aligned} {\varvec{B}}_{G} =\left[ {{\begin{array}{ccc} {\cos \varphi \cos \psi } &{} {\sin \varphi \cos \psi } &{} {-\sin \psi } \\ {\cos \varphi \sin \psi \sin \gamma -\sin \varphi \cos \gamma } &{} {\sin \varphi \sin \psi \sin \gamma +\cos \varphi \cos \gamma } &{} {\cos \psi \sin \gamma } \\ {\cos \varphi \sin \psi \cos \gamma +\sin \varphi \sin \gamma } &{} {\sin \varphi \sin \psi \cos \gamma -\cos \varphi \sin \gamma } &{} {\cos \psi \cos \gamma } \\ \end{array} }} \right] \end{aligned}$$
(1)

where \(\varphi \), \(\psi \) and \(\gamma \) represent the pitch angle, yaw angle and roll angle, respectively, for the submarine-launched missile [42]. Subsequently, these forces or torques will be analyzed in detail in the following parts.

2.1 Fluid inertia force and torque

The submarine-launched missile is considered to be axisymmetric, and the seawater is assumed as the ideal fluid. Therefore, the fluid momentum \(\varvec{Q}_{f} \) and fluid moment of momentum \(\varvec{K}_{f} \) are described as follows in [43].

$$\begin{aligned} \left[ {{\begin{array}{c} {Q_{fx} } \\ {Q_{fy} } \\ {Q_{fz} } \\ {K_{fx} } \\ {K_{fy} } \\ {K_{fz} } \\ \end{array} }} \right] =\left[ {{\begin{array}{cccccc} {\lambda _{11} } &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} {\lambda _{22} } &{} 0 &{} 0 &{} 0 &{} {\lambda _{26} } \\ 0 &{} 0 &{} {\lambda _{33} } &{} 0 &{} {\lambda _{35} } &{} 0 \\ 0 &{} 0 &{} 0 &{} {\lambda _{44} } &{} 0 &{} 0 \\ 0 &{} 0 &{} {\lambda _{53} } &{} 0 &{} {\lambda _{55} } &{} 0 \\ 0 &{} {\lambda _{62} } &{} 0 &{} 0 &{} 0 &{} {\lambda _{66} } \\ \end{array} }} \right] \left[ {{\begin{array}{c} {V_{x} } \\ {V_{y} } \\ {V_{z} } \\ {\omega _{x} } \\ {\omega _{y} } \\ {\omega _{z} } \\ \end{array} }} \right] \end{aligned}$$
(2)

where \(V_{i} \left( {i=x,y,z} \right) \) is the velocity of the submarine-launched missile in the body coordinate system \(Ox_{1} y_{1} z_{1} \), \(\omega _{i} \left( {i=x,y,z} \right) \) is the angular velocity and \(\lambda _{ij} \left( {i=1,2, \ldots 6,j=1,2, \ldots ,6} \right) \) is the added mass. By employing the momentum theorem and the moment of momentum theorem, the inertia force and torque of the ideal fluid for the submarine-launched missile are described as

$$\begin{aligned} -{\varvec{R}}= & {} \frac{\hbox {d}\varvec{Q}_{f} }{\hbox {d}t}+\varvec{\omega }\times \varvec{Q}_{f}\nonumber \\ -{\varvec{M}}= & {} \frac{\hbox {d}\varvec{K}_{f} }{\hbox {d}t}+\varvec{\omega }\times \varvec{K}_{f} +\varvec{V}\times \varvec{Q}_{f} \end{aligned}$$
(3)

2.2 Fluid viscosity force and torque

The definition of fluid viscosity force \(\varvec{R}_{\alpha } \) and torque \(\varvec{M}_{\alpha } \) is similar to that of aerodynamic force and torque for the aircraft, which yields

$$\begin{aligned} {\varvec{R}}_{\alpha }= & {} \left[ {{\begin{array}{ccc} {-C_{x} \frac{1}{2}\rho V^{2}S} &{} {\frac{1}{2}\rho V^{2}SC_{y}^{\alpha } \alpha } &{} {\frac{1}{2}\rho V^{2}SC_{z}^{\beta } \beta } \\ \end{array} }} \right] ^{\mathrm{T}} \nonumber \\ \varvec{M}_{\alpha }= & {} \left[ {{\begin{array}{ccc} {\frac{1}{2}\rho V^{2}SLm_{x}^{\beta } \beta } &{} {\frac{1}{2}\rho V^{2}SLm_{y}^{\beta } \beta } &{} {\frac{1}{2}\rho V^{2}SLm_{z}^{\alpha } \alpha } \\ \end{array} }} \right] ^{\mathrm{T}} \end{aligned}$$
(4)

where \(\rho \), S, V and L represent the density of seawater, the cross-sectional area of the missile, the velocity of the missile and the length of the missile, respectively. \(\alpha \) and \(\beta \) are the angle of attack and angle of sideslip, respectively. \(C_{x} \), \(C_{y}^{\alpha }\) and \(C_{z}^{\beta }\) denote fluid viscosity force coefficients. \(m_{x}^{\beta } \), \(m_{y}^{\beta } \) and \(m_{z}^{\alpha } \) represent fluid viscosity torque coefficients.

2.3 Fluid viscosity damping force and torque

The fluid viscosity damping force \(\varvec{R}_{\omega }\) and torque \(\varvec{M}_{\omega }\) are defined as

$$\begin{aligned} \varvec{R}_{\omega }= & {} \left[ 0 \quad {C_{y}^{\bar{{\omega }}_{z} } \frac{1}{2}\rho V^{2}S\omega _{z} } \quad {C_{z}^{\bar{{\omega }}_{y} } \frac{1}{2}\rho V^{2}S\omega _{y} } \right] ^{\mathrm{T}} \nonumber \\ \varvec{M}_{\omega }= & {} \left[ {\frac{1}{2}\rho V^{2}SL\left( {m_{x}^{\bar{{\omega }}_{x} } \omega _{x} +m_{x}^{\bar{{\omega }}_{y} } \omega _{y} } \right) }\right. \nonumber \\&\left. \quad {\frac{1}{2}\rho V^{2}SL\left( {m_{y}^{\bar{{\omega }}_{x} } \omega _{x} +m_{y}^{\bar{{\omega }}_{y} } \omega _{y} } \right) }\quad {m_{z}^{\bar{{\omega }}_{z} } \frac{1}{2}\rho V^{2}SL\omega _{z} } \right] ^{\mathrm{T}}\nonumber \\ \end{aligned}$$
(5)

where \(C_{y}^{\bar{{\omega }}_{z} } \) and \(C_{z}^{\bar{{\omega }}_{y} } \) are damping force coefficients. \(m_{x}^{\bar{{\omega }}_{x} } \), \(m_{x}^{\bar{{\omega }}_{y} } \), \(m_{y}^{\bar{{\omega }}_{x} } \), \(m_{y}^{\bar{{\omega }}_{y} } \) and \(m_{z}^{\bar{{\omega }}_{z} } \) are damping torque coefficients.

2.4 Buoyancy and its torque

The buoyancy of the submarine-launched missile is given by

$$\begin{aligned} N=\rho V_{L} g \end{aligned}$$
(6)

where \(V_{L}\) is the volume of displacement for the submarine-launched missile and g is the acceleration of gravity. It is worth noting that N is pointing along the \(O_{e} y_{0} \) direction; thus we have

$$\begin{aligned} {\varvec{N}}={\varvec{B}}_{G} \left[ {{\begin{array}{c} 0 \\ N \\ 0 \\ \end{array} }} \right] =\left[ {{\begin{array}{c} {N\sin \varphi \cos \psi } \\ {N\left( {\sin \varphi \sin \psi \sin \gamma +\cos \varphi \cos \gamma } \right) } \\ {N\left( {\sin \varphi \sin \psi \cos \gamma -\cos \varphi \sin \gamma } \right) } \\ \end{array} }} \right] \end{aligned}$$
(7)

Similarly, the torque of buoyancy is defined as

$$\begin{aligned} \varvec{M}_{N} =\left[ {{\begin{array}{c} {N\left( {\sin \varphi \sin \psi \sin \gamma +\cos \varphi \cos \gamma } \right) z_{c} -N\left( {\sin \varphi \sin \psi \cos \gamma -\cos \varphi \sin \gamma } \right) y_{c} } \\ {-N\sin \varphi \cos \psi z_{c} +N\left( {\sin \varphi \sin \psi \cos \gamma -\cos \varphi \sin \gamma } \right) x_{c} } \\ {N\sin \varphi \cos \psi y_{c} -N\left( {\sin \varphi \sin \psi \sin \gamma +\cos \varphi \cos \gamma } \right) x_{c} } \\ \end{array} }} \right] \end{aligned}$$
(8)

where \(x_{c} ,y_{c} \) and \(z_{c} \) represent the position of buoyancy in the body coordinate system \(Ox_{1} y_{1} z_{1} \). \(\varvec{M}_{N} \) is the torque vector of buoyancy.

2.5 Gravity

Gravity G is pointing along the negative direction of \(O_{e} y_{0} \); thus we have

$$\begin{aligned} {\varvec{G}}= & {} {\varvec{B}}_{G} \left[ {{\begin{array}{c} 0 \\ {-G} \\ 0 \\ \end{array} }} \right] \nonumber \\= & {} \left[ {{\begin{array}{c} {-G\sin \varphi \cos \psi } \\ {-G\left( {\sin \varphi \sin \psi \sin \gamma +\cos \varphi \cos \gamma } \right) } \\ {-G\left( {\sin \varphi \sin \psi \cos \gamma -\cos \varphi \sin \gamma } \right) } \\ \end{array} }} \right] \end{aligned}$$
(9)

2.6 Thrust of the main engine and its control torque

Figure 3 displays the main engine distribution of the submarine-launched missile. The control commands are four swing angles \(\delta _{1} \), \(\delta _{2} \), \(\delta _{3} \) and \(\delta _{4} \), which are also given in Fig. 3.

Fig. 3
figure 3

Main engine distribution of the submarine-launched missile

Full size image

Thus, the four swing angles can be converted into the equivalent three-channel swing angles independent of one another, such as \(\delta _{\varphi } ,\delta _{\psi } \) and \(\delta _{\gamma } \). According to Fig. 3, it can be drawn that

$$\begin{aligned} \delta _{\varphi }= & {} \frac{\delta _{3} +\delta _{4} -\delta _{1} -\delta _{2} }{4} \nonumber \\ \delta _{\psi }= & {} \frac{\delta _{2} +\delta _{3} -\delta _{1} -\delta _{4} }{4} \nonumber \\ \delta _{\gamma }= & {} \frac{\delta _{1} +\delta _{2} +\delta _{3} +\delta _{4} }{4} \end{aligned}$$
(10)

The thrust value of the four main engines is consistent. Therefore, the corresponding control forces and control torques are developed as follows.

$$\begin{aligned} \varvec{P}=\left[ {{\begin{array}{c} P \\ {\frac{\sqrt{2} }{2}P\delta _{\varphi } } \\ {-\frac{\sqrt{2} }{2}P\delta _{\psi } } \\ \end{array} }} \right] ,\varvec{M}_{P} =\left[ {{\begin{array}{c} {-P\delta _{\gamma } r} \\ {-\frac{\sqrt{2} }{2}P(x_{R} -x_{T} )\delta _{\psi } } \\ {-\frac{\sqrt{2} }{2}P(x_{R} -x_{T} )\delta _{\varphi } } \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$
(11)

where \(x_{R}\) is the distance between the position of main engines and vertex of the missile, \(x_{T} \) is the distance between the barycenter and vertex of the missile, and P denotes the total thrust. The four main engines are uniformly installed along a circle and the radius of the circle is r.

2.7 Multiple disturbances

  1. (1)

    Sea wave

To facilitate the description of the motion for the submarine-launched missile, a new variable l is defined to describe the distance between the vertex of the missile and sea level in the \(Ox_{1}\) direction.

$$\begin{aligned} l=\frac{Y+x_{T} \sin \theta -h}{\sin \theta } \end{aligned}$$
(12)

where Y is the position of the submarine-launched missile in the ground coordinate system \(O_{e} x_{0} y_{0} z_{0} \), h is the depth of the launching point, and \(\theta \) is the trajectory inclination angle. The disturbance forces caused by the six levels of sea waves can be obtained as follows in [9].

$$\begin{aligned} R_{dy} =\left\{ {\begin{array}{l} \hbox {0.00391}l^{3}+\hbox {0.1436}l^{2}-\hbox {0.1892}l-\hbox {89.68}{\begin{array}{*{20}c} &{} {-15\le l\le 0} &{} \\ \end{array} } \\ \hbox {0.0003077}l^{3}-\hbox {0.4629}l^{2}+\hbox {12.72}l-\hbox {89.12}{\begin{array}{*{20}c} &{} {0<l\le 15} \\ \end{array} } \\ \end{array}} \right. \nonumber \\\end{aligned}$$
(13)
$$\begin{aligned} R_{dz} =\left\{ {\begin{array}{l} 0.0\hbox {1512}l^{3}+0.\hbox {4}0\hbox {3}l^{2}+0.\hbox {2167}l-\hbox {42.48}{\begin{array}{*{20}c} &{} {-15\le l<0} &{} \\ \end{array} } \\ -0.0\hbox {4748}l^{3}+0.\hbox {39}0\hbox {8}l^{2}+\hbox {7.681}l-\hbox {43.12}{\begin{array}{*{20}c} &{} {0\le l\le 15} \\ \end{array} } \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(14)

where \(R_{dx} =0\), \(\varvec{R}_{d} =\left[ {{\begin{array}{ccc} {R_{dx} } &{} {R_{dy} } &{} {R_{dz} } \\ \end{array} }} \right] ^{\mathrm{T}}\) denotes the disturbance vector in the presence of sea waves and the unit is \(\hbox {kN}\).

  1. (2)

    Sea wind

The sea wind will result in disturbance force \(P_{w} \). It can be described as

$$\begin{aligned} P_{w} =QC_{wx} K_{z} \end{aligned}$$
(15)

where \(Q=0.5\rho _{1} V_{wz}^{2} \), Q denotes the wind pressure, \(\rho _{1} \) represents the air density, \(K_{z} \) is usually set to \(K_{z} =1\), \(V_{wz} \) represents the wind velocity and \(C_{wx} \) denotes the aerodynamic drag coefficient. The wind direction is denoted by \(\phi \). Hence, the disturbance forces produced by the sea wind can be indicated as

$$\begin{aligned} \left[ {{\begin{array}{c} {P_{wdx} } \\ {P_{wdy} } \\ {P_{wdz} } \\ \end{array} }} \right] =\left[ {{\begin{array}{c} {P_{w} \cos \phi } \\ 0 \\ {-P_{w} \sin \phi } \\ \end{array} }} \right] \end{aligned}$$
(16)

Thus, the disturbance force in the ground coordinate system \(O_{e} x_{0} y_{0} z_{0} \) can be transformed into that in the body coordinate system \(Ox_{1} y_{1} z_{1} \). The corresponding force \(\varvec{P}_{wt} \) and torque \(\varvec{M}_{w} \) will be obtained by the following equation.

$$\begin{aligned} \varvec{P}_{wt}= & {} \left[ {{\begin{array}{c} {P_{wtx} } \\ {P_{wty} } \\ {P_{wtz} } \\ \end{array} }} \right] ={\varvec{B}}_{G} \left[ {{\begin{array}{c} {P_{w} \cos \phi } \\ 0 \\ {-P_{w} \sin \phi } \\ \end{array} }} \right] \end{aligned}$$
(17)
$$\begin{aligned} \varvec{M}_{w}= & {} \left[ {{\begin{array}{c} 0 \\ {P_{wtz} Dl\left( {x_{T} -\frac{l}{2}} \right) } \\ {P_{wty} Dl\left( {x_{T} -\frac{l}{2}} \right) } \\ \end{array} }} \right] \end{aligned}$$
(18)

where D is the diameter of the submarine-launched missile.

  1. (3)

    Ocean current

The ocean current is similar to the wind in the atmosphere for the missile. It will result in the added angle of attack \(\alpha _{wp} \) and added angle of sideslip \(\beta _{w_{p} } \). As shown in [42], we have

$$\begin{aligned} \alpha _{wp}= & {} -\arctan \frac{w_{p} \cos A\sin \theta }{V-w_{p} \cos A\cos \theta } \nonumber \\ \beta _{w_{p} }= & {} \arctan \frac{w_{p} \sin A}{V} \end{aligned}$$
(19)

where \(w_{p} \) is the flow velocity of the seawater, A represents the wind direction, and V is the velocity of the missile. The total angle of attack \(\alpha \) and the total angle of sideslip \(\beta \) are replaced by \(\alpha +\alpha _{w_{p} } \) and \(\beta +\beta _{w_{p} } \), respectively. With the added angle of attack and added angle of sideslip, there exist large disturbances in the fluid viscosity force \(\varvec{R}_{\alpha } \) and torque \(\varvec{M}_{\alpha } \).

2.8 Kinematics and dynamics model of the submarine-launched missile

The momentum \(\varvec{Q}\) and moment of momentum \(\varvec{K}\) of the submarine-launched missile are described as follows [43].

$$\begin{aligned} \varvec{Q}= & {} m(\varvec{V}+\varvec{\omega }\times \varvec{r}_{c} ) \nonumber \\ {\varvec{K}}= & {} {\varvec{J}}_{0} \varvec{\omega }+\varvec{r}_{c} \times m\varvec{V} \end{aligned}$$
(20)

where m is the mass of the submarine-launched missile, and \(\varvec{r}_{c} =\left[ {{\begin{array}{ccc} {x_{c} } &{} {y_{c} } &{} {z_{c} } \\ \end{array} }} \right] ^{\mathrm{T}}\) is the position vector of buoyancy in the body coordinate system. \(\varvec{J}_{0} =\hbox {diag}\left( {\left[ {{\begin{array}{ccc} {J_{x} } &{} {J_{y} } &{} {J_{z} } \\ \end{array} }} \right] } \right) \) represents the rotational inertia matrix. By employing the momentum theorem and the moment of momentum theorem, the dynamics model of the submarine-launched missile is described as

$$\begin{aligned}&\frac{\hbox {d}\varvec{Q}}{\hbox {d}t}+\varvec{\omega }\times \varvec{Q}=\varvec{R}+\varvec{R}_{\alpha } +\varvec{R}_{\omega }\nonumber \\&\qquad +\,\varvec{N}+\varvec{G}+\varvec{P}+\varvec{R}_{d} +\varvec{P}_{wt} \nonumber \\&\quad \frac{\hbox {d}\varvec{K}}{\hbox {d}t}+\varvec{\omega }\times \varvec{K}+\varvec{V}\times \varvec{Q}=\varvec{M}+\varvec{M}_{\alpha }\nonumber \\&\qquad +\,\varvec{M}_{\omega } +\varvec{M}_{N} +\varvec{M}_{P} +\varvec{M}_{w} \end{aligned}$$
(21)

Therefore, multiple disturbances are included in the dynamic model, such as \(\varvec{R}_{\alpha } \), \(\varvec{R}_{d} \), \(\varvec{P}_{wt} \), \(\varvec{M}_{\alpha } \) and \(\varvec{M}_{w} \).

Expanding Eq. (21) yields

$$\begin{aligned}&\left( {m+\lambda _{11} } \right) \dot{{V}}_{x} +m\dot{{\omega }}_{y} z_{c} -m\dot{{\omega }}_{z} y_{c}\nonumber \\&\qquad +\,m \left[ V_{z} \omega _{y} -V_{y} \omega _{z} +y_{c} \omega _{y} \omega _{x} +z_{c} \omega _{x} \omega _{z}\right. \nonumber \\&\left. \qquad -x_{c} \left( {\omega _{y}^{2} +\omega _{z}^{2} } \right) \right] \nonumber \\&\quad =-\,C_{x} \frac{1}{2}\rho V^{2}S+(N-G)\sin \varphi \cos \psi \nonumber \\&\qquad +P+P_{wtx} \end{aligned}$$
(22)
$$\begin{aligned}&\left( {m+\lambda _{22} } \right) \dot{{V}}_{x} +\left( {mx_{c} +\lambda _{26} } \right) \dot{{\omega }}_{z} -mz_{c} \dot{{\omega }}_{x}\nonumber \\&\qquad +\,m \left[ V_{x} \omega _{z} -V_{z} \omega _{x} +x_{c} \omega _{y} \omega _{x} +z_{c} \omega _{y} \omega _{z}\right. \nonumber \\&\left. \qquad -y_{c} \left( {\omega _{z}^{2} +\omega _{x}^{2} } \right) \right] \nonumber \\&\quad =\frac{1}{2}\rho V^{2}S\left( {C_{y}^{\alpha } \alpha +C_{y}^{\bar{{\omega }}_{z} } \bar{{\omega }}_{z} } \right) +(N-G)\nonumber \\&\qquad \left( {\sin \varphi \sin \psi \sin \gamma +\cos \varphi \cos \gamma } \right) \nonumber \\&\qquad +\,\frac{\sqrt{2} }{2}P\delta _{\varphi } +R_{dy} +P_{wty} \end{aligned}$$
(23)
$$\begin{aligned}&\left( {m+\lambda _{33} } \right) \dot{{V}}_{z} +my_{c} \dot{{\omega }}_{x} -\left( {mx_{c} -\lambda _{35} } \right) \dot{{\omega }}_{y}\nonumber \\&\qquad +\,m\left[ V_{y} \omega _{x} -V_{x} \omega _{y} +x_{c} \omega _{z} \omega _{x} +y_{c} \omega _{y} \omega _{z}\right. \nonumber \\&\left. \qquad -z_{c} \left( {\omega _{x}^{2} +\omega _{y}^{2} } \right) \right] \nonumber \\&\quad =\frac{1}{2}\rho V^{2}S\left( {C_{z}^{\beta } \beta +C_{z}^{\bar{{\omega }}_{y} } \omega _{y} } \right) +(N-G)\nonumber \\&\qquad \left( {\sin \varphi \sin \psi \cos \gamma -\cos \varphi \sin \gamma } \right) \nonumber \\&\qquad -\,\frac{\sqrt{2} }{2}P\delta _{\psi } +R_{dz} +P_{wtz} \end{aligned}$$
(24)
$$\begin{aligned}&\left( {J_{x} +\lambda _{44} } \right) \dot{{\omega }}_{x} +my_{c} \dot{{V}}_{z} -mz_{c} \dot{{V}}_{y} \nonumber \\&\qquad +\,my_{c} \left( {V_{y} \omega _{x} -V_{x} \omega _{y} } \right) \nonumber \\&\qquad +\,mz_{c} \left( {V_{z} \omega _{x} -V_{x} \omega _{z} } \right) +(J_{z} -J_{y} )\omega _{y} \omega _{z} \nonumber \\&\quad =\frac{1}{2}\rho V^{2}SL\left( {m_{x}^{\beta } \beta +m_{x}^{\bar{{\omega }}_{x} } \omega _{x} +m_{x}^{\bar{{\omega }}_{y} } \omega _{y} } \right) \nonumber \\&\qquad +\,N\left( {\sin \varphi \sin \psi \sin \gamma +\cos \varphi \cos \gamma } \right) z_{c} \nonumber \\&\qquad -N\left( {\sin \varphi \sin \psi \cos \gamma -\,\cos \varphi \sin \gamma } \right) y_{c} -P\delta _{\gamma } r\nonumber \\ \end{aligned}$$
(25)
$$\begin{aligned}&\left( {J_{y} +\lambda _{55} } \right) \dot{{\omega }}_{y} +mz_{c} \dot{{V}}_{x} -\left( {mx_{c} -\lambda _{35} } \right) \dot{{V}}_{z}\nonumber \\&\qquad +\,mz_{c} (V_{z} \omega _{y} -V_{y} \omega _{z} )\nonumber \\&\qquad +\,mx_{c} (V_{x} \omega _{y} -V_{y} \omega _{x} )+(J_{x} -J_{z} )\omega _{x} \omega _{z} \nonumber \\&\quad =\frac{1}{2}\rho V^{2}SL\left( {m_{y}^{\beta } \beta +m_{y}^{\bar{{\omega }}_{x} } \omega _{x} +m_{y}^{\bar{{\omega }}_{y} } \omega _{y} } \right) \nonumber \\&\qquad -N\sin \varphi \cos \psi z_{c} \nonumber \\&\qquad +\,N\left( {\sin \varphi \sin \psi \cos \gamma -\cos \varphi \sin \gamma } \right) x_{c}\nonumber \\&\qquad -\frac{\sqrt{2} }{2}P(x_{R} -x_{T} )\delta _{\psi } +M_{wy} \end{aligned}$$
(26)
$$\begin{aligned}&\left( {J_{z} +\lambda _{66} } \right) \dot{{\omega }}_{z} +\left( {mx_{c} +\lambda _{26} } \right) \dot{{V}}_{y}\nonumber \\&\qquad -\,my_{c} \dot{{V}}_{x} +mx_{c} (V_{x} \omega _{z} -V_{z} \omega _{x} )\nonumber \\&\qquad +\,my_{c} (V_{y} \omega _{z} -V_{z} \omega _{y} )+(J_{y} -J_{x} )\omega _{x} \omega _{y} \nonumber \\&\quad =\frac{1}{2}\rho V^{2}SL\left( {m_{z}^{\alpha } \alpha +m_{z}^{\bar{{\omega }}_{z} } \omega _{z} } \right) +N\sin \varphi \cos \psi y_{c}\nonumber \\&\qquad -\,N\left( {\sin \varphi \sin \psi \sin \gamma +\cos \varphi \cos \gamma } \right) x_{c} \nonumber \\&\qquad -\,\frac{\sqrt{2} }{2}P(x_{R} -x_{T} )\delta _{\varphi } +M_{wz} \end{aligned}$$
(27)

The attitude kinematic equations are presented as

$$\begin{aligned} \dot{{\varphi }}= & {} \frac{1}{\cos \psi }\left( {\omega _{y} \sin \gamma +\omega _{z} \cos \gamma } \right) \nonumber \\ \dot{{\psi }}= & {} \omega _{y} \cos \gamma -\omega _{z} \sin \gamma \nonumber \\ \dot{{\gamma }}= & {} \omega _{x} -\omega _{y} \tan \psi \sin \gamma -\omega _{z} \tan \psi \cos \gamma \end{aligned}$$
(28)

For the convenience of description of the added mass, some new variables are defined as

(29)

Moreover, the kinematic equations of the submarine-launched missile are developed as

$$\begin{aligned} \left[ {{\begin{array}{c} {\dot{{X}}} \\ {\dot{{Y}}} \\ {\dot{{Z}}} \\ \end{array} }} \right] =\left( {{\varvec{B}}_{G} } \right) ^{\mathrm{T}}\left[ {{\begin{array}{c} {V_{x} } \\ {V_{y} } \\ {V_{z} } \\ \end{array} }} \right] \end{aligned}$$
(30)

where X, Y and Z denote the position of the submarine-launched missile. Thus, the trajectory inclination angle \(\theta \) and trajectory deflection angle \(\psi _{v} \) are, respectively, calculated by

(31)

where \(V=\sqrt{V_{x}^{2} +V_{y}^{2} +V_{z}^{2} } \). Furthermore, the mass satisfies

$$\begin{aligned} m=m_{0} -\hbox {d}m\cdot t \end{aligned}$$
(32)

where \(m_{0}\) is the initial mass of the missile, \(\hbox {d}m\) represents the consumption rate of the fuel and t denotes the running time of the submarine-launched missile.

The relationships among the angle of attack \(\alpha \), the angle of sideslip \(\beta \) and the bank angle \(\gamma _{v} \) are depicted by [42].

$$\begin{aligned} \sin \beta= & {} \cos \left( {\theta {-}\varphi } \right) \cos \psi _{v} \sin \psi \cos \gamma \nonumber \\&+\sin \left( {\varphi {-}\theta } \right) \cos \psi _{v} \sin \gamma {-}\sin \psi _{v} \cos \psi \cos \gamma \nonumber \\&-\sin \alpha \cos \beta {=}\cos \left( {\theta {-}\varphi } \right) \cos \psi _{v} \sin \psi \sin \gamma \nonumber \\&+\sin \left( {\theta {-}\varphi } \right) \cos \psi _{v} \cos \gamma {-}\sin \psi _{v} \cos \psi \sin \gamma \nonumber \\&\cos \psi _{v} \sin \gamma _{v} {=}\cos \alpha \cos \psi \sin \gamma {-}\sin \psi \sin \alpha \nonumber \\ \end{aligned}$$
(33)

Next, we will simplify the dynamic model to design the attitude control system. Define \({\varvec{X}}_{1} =\left[ {{\begin{array}{ccc} \varphi &{} \psi &{} \gamma \\ \end{array} }} \right] ^{\mathrm{T}}\), \({\varvec{X}}_{2} =\left[ {{\begin{array}{ccc} {\omega _{x} } &{} {\omega _{y} } &{} {\omega _{z} } \\ \end{array} }} \right] ^{\mathrm{T}}\) and \(\varvec{U}=\left[ {{\begin{array}{ccc} {\delta _{\varphi } } &{} {\delta _{\psi } } &{} {\delta _{\gamma } } \\ \end{array} }} \right] ^{\mathrm{T}}\). Combining Eqs. (25), (26) and (27) yields

$$\begin{aligned} \varvec{\dot{{X}}}_{1}= & {} \varvec{HX}_{2} \nonumber \\ \varvec{\dot{{X}}}_{2}= & {} \varvec{J}^{-1}\varvec{BU}+\varvec{J}^{-1}\varvec{D}_{1} \end{aligned}$$
(34)

where \(\varvec{J}\), \(\varvec{H}\), \(\varvec{\dot{{H}}}\), \(\varvec{J}\) and \(\varvec{D}_{1} \) are given in “Appendix”.

Differentiating Eq. (34) with respect to time obtains

$$\begin{aligned} \varvec{\ddot{{X}}}_{1}= & {} \varvec{\dot{{H}}X}_{2} +\varvec{H\dot{{X}}}_{2} \nonumber \\= & {} \varvec{\dot{{H}}X}_{2} +\varvec{H}\left( {\varvec{J}^{-1}\varvec{BU}+\varvec{J}^{-1}\varvec{D}_{1} } \right) \end{aligned}$$
(35)

According to Eq. (34) and (35), the following second-order attitude tracking error dynamic system is presented as

$$\begin{aligned} \varvec{\dot{{e}}}_{1}= & {} \varvec{e}_{2} \nonumber \\ \varvec{\dot{{e}}}_{2}= & {} \varvec{\dot{{H}}X}_{2} +\varvec{H}\left( {\varvec{J}^{-1}\varvec{BU}+\varvec{J}^{-1}\varvec{D}_{1} } \right) -\varvec{\ddot{{X}}}_{1}^{c} \end{aligned}$$
(36)

where \({\varvec{X}}_{1}^{c} =\left[ {{\begin{array}{ccc} {\varphi ^{c}} &{} {\psi ^{c}} &{} {\gamma ^{c}} \\ \end{array} }} \right] ^{\mathrm{T}}\) is the attitude command vector, and \(\varvec{\dot{{X}}}_{1}^{c} =\left[ {{\begin{array}{ccc} {\dot{{\varphi }}^{c}} &{} {\dot{{\psi }}^{c}} &{} {\dot{{\gamma }}^{c}} \\ \end{array} }} \right] ^{\mathrm{T}}\) represents the derivative of the attitude command. \(\varvec{e}_{1} \varvec{=X}_{1} -{\varvec{X}}_{1}^{c} \) and \(\varvec{e}_{2} \varvec{=\dot{{X}}}_{1} -\varvec{\dot{{X}}}_{1}^{c} =\varvec{HX}_{2} -\varvec{\dot{{X}}}_{1}^{c} \) denote the attitude tracking errors.

Simplifying Eq. (36) yields

$$\begin{aligned} \varvec{\dot{{e}}}_{1}= & {} \varvec{e}_{2} \nonumber \\ \varvec{\dot{{e}}}_{2}= & {} \varvec{d}+{\varvec{B}}_{1} \varvec{U} \end{aligned}$$
(37)

where \(\varvec{d=\dot{{H}}X}_{2} +\varvec{HJ}^{-1}\varvec{D}_{1} -\varvec{\ddot{{X}}}_{1}^{c} \) and \({\varvec{B}}_{1} =\varvec{HJ}^{-1}{\varvec{B}}\).

Remark 1

According to Eq. (37), the attitude tracking control problem for a complicated dynamic model of the submarine-launched missile has been transformed into a simple second-order control system. After that, it is convenient to apply the corresponding modern control methods.

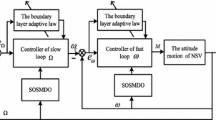
3 Adaptive non-singular fixed-time fast terminal sliding mode control

3.1 Definitions and Lemmas

Consider the following system

$$\begin{aligned} \dot{{x}}=f(x(t)),x(0)=0,f(x(0))=0 \end{aligned}$$
(38)

where \(x\in R^{n}\) and \(f(x):R^{n}\rightarrow R^{n}\) is a nonlinear function.

Definition 1

[44] If the origin of system (38) is Lyapunov stable, then system (38) is said to be finite-time stable and there exists a settling time function \(T:R^{n}\rightarrow R^{n}\), such that for every \(x_{0} \in R^{n}\), the solution \(x\left( {t,x_{0} } \right) \) of the system satisfies \(\lim \nolimits _{t\rightarrow T\left( {x_{0} } \right) } x\left( {t,x_{0} } \right) =0\).

Definition 2

[44] System (38) is said to be fixed-time stable if it is globally finite-time stable. Thus, it will converge to the origin within the bounded convergence time \(T\left( {x_{0} } \right) \). In this case, there exists a positive constant \(T_\mathrm{max} \) such that \(T\left( {x_{0} } \right) <T_\mathrm{max} \).

Lemma 1

[28] For system (38), suppose there exists a Lyapunov functionV(x), parameters \(\alpha _{1} ,\beta _{1} ,p,q,k\in R^{+}\), \(pk<1\) and \(qk>1\), such that \(\dot{{V}}(x)\le -\left( {\alpha _{1} V(x)^{p}+\beta _{1} V(x)^{q}} \right) ^{k}\). Then, the system is fixed-time stable. Furthermore, the upper bound of the convergence time is given as follows.

$$\begin{aligned} T\le \frac{1}{\alpha _{1}^{k} \left( {1-pk} \right) }+\frac{1}{\beta _{1}^{k} \left( {qk-1} \right) } \end{aligned}$$
(39)

Lemma 2

[45] For any \(x_{i} \in R,i=1,2\ldots ,n\), \(\left( {\sum \nolimits _{i=1}^n {\left| {x_{i} } \right| } } \right) ^{v}\le \sum \nolimits _{i=1}^n {\left| {x_{i} } \right| }^{v}\), where \(v\in R^{+}\) and \(v\in (0,1]\).

Lemma 3

[41] For any \(x_{i} \in R,i=1,2\ldots ,n\) ,If \(v\in R^{+}\) and \(v_{1} >1\) ,we have \(\left( {\sum \nolimits _{i=1}^n {\left| {x_{i} } \right| } } \right) ^{v_{1} }\le n^{v_{1} -1}\sum \nolimits _{i=1}^n {\left| {x_{i} } \right| }^{v_{1} }\).

Notation 1

[46] In this paper, we use \(\left\| {\cdot } \right\| \) for the Euclidean norm of vectors and induced norm of matrices. For a given vector \(\varvec{x}=\left[ {x_{1} ,x_{2} ,\ldots ,x_{n} } \right] ^{\mathrm{T}}\), \(\hbox {sig}^{p}(\varvec{x})=\left[ \left| {x_{1} } \right| ^{p}\hbox {sign}(x_{1} ),\left| {x_{2} } \right| ^{p}\hbox {sign}(x_{2} ),\ldots ,\left| {x_{n} } \right| ^{p}\right. \left. \hbox {sign}(x_{n} ) \right] ^{\mathrm{T}}\), \(\hbox {sig}^{p}(x)=\left| x \right| ^{p}\hbox {sign}(x) \quad \hbox {sign}(\varvec{x})=\left[ {\hbox {sign}(x_{1} ),\hbox {sign}(x_{2} ),\ldots ,\hbox {sign}(x_{n} )} \right] ^{\mathrm{T}}\), where sign(.) denotes the sign function.

Assumption 1

[41] The disturbances \(\varvec{d}\) in Eq. (37) are assumed to be bounded and satisfy \(\left\| {\varvec{d}} \right\| \le d_{m} \), where \(d_{m} \) is a positive constant and \(\varvec{d}_{m} \) is the vector of the max value of the disturbances.

3.2 Control design

This section presents a novel adaptive non-singular fixed-time fast terminal sliding mode control. To guarantee that both \(\varvec{e}_{1} \) and \(\varvec{e}_{2} \) in Eq. (37) converge to zero within a fixed time regardless of the initial states, a novel non-singular fixed-time fast terminal sliding mode surface (NFFTSMS) is developed as follows [41].

$$\begin{aligned} \varvec{S}=\varvec{\Gamma }\left( {\varvec{e}_{1} } \right) \varvec{e}_{1} +\hbox {sig}^{\gamma _{2} }\left( {\varvec{e}_{2} } \right) \end{aligned}$$
(40)

where \(\varvec{e}_{1} \in R^{3},\varvec{e}_{2} \in R^{3}\) and \(\varvec{\Gamma }\left( {\varvec{e}_{1} } \right) \) is a diagonal matrix. Moreover, the diagonal elements of \(\varvec{\Gamma }\left( {\varvec{e}_{1} } \right) \) are given by

$$\begin{aligned} \Gamma \left( {e_{1i} } \right)= & {} \left( {\alpha _{1} \left| {e_{1i} } \right| ^{p-1/k\gamma _{2} }+\beta _{1} \left| {e_{1i} } \right| ^{q-1/k\gamma _{2} }} \right) ^{k\gamma _{2} } \nonumber \\ {\varvec{\Gamma }} \left( {\varvec{e}_{1} } \right)= & {} \hbox {diag}\left( {\left[ {{\begin{array}{ccc} {{{\Gamma }} \left( {e_{1x} } \right) } &{} {\Gamma \left( {e_{1y} } \right) } &{} {\Gamma \left( {e_{1z} } \right) } \\ \end{array} }} \right] } \right) \end{aligned}$$
(41)

where \(i=x,y,z\), \(\alpha _{1}>0,\beta _{1}>0,k>1,\gamma _{2} >1\) and p, q are positive parameters satisfying \(qk>1\) and \(1/\gamma _{2}<pk<1\).

Similarly, \(\hbox {sig}^{\gamma _{2} }\left( {\varvec{e}_{2} } \right) \) can be denoted as

$$\begin{aligned} \hbox {sig}^{\gamma _{2} }\left( {\varvec{e}_{2} } \right) =\left[ {{\begin{array}{ccc} {\hbox {sig}^{\gamma _{2} }\left( {{e}_{2x} } \right) } &{} {\hbox {sig}^{\gamma _{2} }\left( {{e}_{2y} } \right) } &{} {\hbox {sig}^{\gamma _{2} }\left( {{e}_{2z} } \right) } \\ \end{array} }} \right] ^{\mathrm{T}} \end{aligned}$$
(42)

Theorem 1

If the sliding mode surface satisfies \(\varvec{S}=\varvec{0}\), \(\varvec{e}_{1} =0\) and \(\varvec{e}_{2} =0\) can be reached within a fixed convergence time \(T_{0} \) regardless of the initial states. Thus, we obtain the upper bound of the convergence time

$$\begin{aligned} T_{0} \le \frac{1}{\alpha _{1}^{k} \left( {1-pk} \right) }+\frac{1}{\beta _{1}^{k} \left( {qk-1} \right) } \end{aligned}$$
(43)

Proof

When the sliding mode surface satisfies \(\varvec{S}=\varvec{0}\), we have

$$\begin{aligned} \varvec{\dot{{e}}}_{1} =-\,\hbox {sig}^{k}\left( {\alpha _{1} \hbox {sig}^{p}\left( {\varvec{e}_{1} } \right) +\beta _{1} \hbox {sig}^{q}\left( {\varvec{e}_{1} } \right) } \right) \end{aligned}$$
(44)

Next, consider a new variable \(\Phi _{i} =\left| {e_{1i} } \right| ^{1-pk},\left( {i=x,y,z} \right) \), Eq. (44) can be rewritten as

$$\begin{aligned} \dot{{\Phi }}_{i} =-\left( {1-pk} \right) \left( {\alpha _{1} +\beta _{1} \Phi _{i}^{\mu } } \right) ^{k} \end{aligned}$$
(45)

where \(\mu =\left( {q-p} \right) /\left( {1-pk} \right) \). By integrating Eq. (45), we obtain

$$\begin{aligned} T_{0}= & {} \lim \limits _{\Phi _{i} \rightarrow \infty } \frac{1}{1-pk}\int _0^{\Phi _{i} } {\frac{1}{\left( {\alpha _{1} +\beta _{1} \Phi _{i}^{\mu } } \right) ^{k}}} \hbox {d}\Phi _{i} \nonumber \\= & {} \lim \limits _{\Phi _{i} \rightarrow \infty } \frac{1}{1-pk}\left( \int _1^{\Phi _{i} } {\frac{1}{\left( {\alpha _{1} +\beta _{1} \Phi _{i}^{\mu } } \right) ^{k}}} \hbox {d}\Phi _{i}\right. \nonumber \\&\left. +\,\int _0^1 {\frac{1}{\left( {\alpha _{1} +\beta _{1} \Phi _{i}^{\mu } } \right) ^{k}}} \hbox {d}\Phi _{i} \right) \nonumber \\\le & {} \lim \limits _{\Phi _{i} \rightarrow \infty } \frac{1}{1-pk}\left( {\int _1^{\Phi _{i} } {\frac{1}{\beta _{1} \Phi _{i}^{\mu k} }} \hbox {d}\Phi _{i} +\int _0^1 {\frac{1}{\alpha _{1}^{k} }} \hbox {d}\Phi _{i} } \right) \nonumber \\= & {} \frac{1}{1-pk}\left( {\frac{1}{\beta _{1}^{k} \left( {\mu k-1} \right) }+\frac{1}{\alpha _{1}^{k} }} \right) \nonumber \\= & {} \frac{1}{\alpha _{1}^{k} \left( {1-pk} \right) }+\,\frac{1}{\beta _{1}^{k} \left( {qk-1} \right) } \end{aligned}$$
(46)

This completes the proof of Theorem 1. \(\square \)

Remark 2

It is worth noting that this sliding mode surface is partly motivated by the reference [41]. Compared with other sliding mode surfaces, the proposed NFFTSMS can avoid singularity without adding additional parameters and achieve faster convergence and a more compact structure.

To design the non-singular fixed-time fast terminal sliding mode control, a nonlinear function is defined as

$$\begin{aligned} \eta \left( x \right) =\left\{ {{\begin{array}{ll} \sin \left( {\frac{\pi }{2}\frac{x^{2}}{\tau ^{2}}} \right) ,&{} \left| x \right| \le \tau \\ 1&{} , \left| x \right| >\tau \\ \end{array} }} \right. \end{aligned}$$
(47)

where \(\tau >0\) is an unknown parameter that needs to be designed. \(\eta \left( x \right) \) is a non-negative function, when \(x\rightarrow 0\), there is \(\eta \left( x \right) /x\rightarrow 0\).

In fact, the derivative of the attitude command \(\varvec{\dot{{X}}}_{1}^{c} \) is usually unavailable in the process of real flight. Therefore, \(\varvec{e}_{2} \) is unknown in Eq. (40). To solve this problem, a fixed-time differentiator can be developed based on the reference [47]. Accordingly, we have

$$\begin{aligned} \dot{{v}}_{1}= & {} v_{2} -k_{1} \hbox {sig}^{a_{1} }\left( {v_{1} -\chi ^{c}} \right) -\kappa _{1} \hbox {sig}^{b_{1} }\left( {v_{1} -\chi ^{c}} \right) \nonumber \\ \dot{{v}}_{2}= & {} -k_{2} \hbox {sig}^{a_{3} }\left( {v_{1} -\chi ^{c}} \right) -\kappa _{2} \hbox {sig}^{b_{3} }\left( {v_{1} -\chi ^{c}} \right) \end{aligned}$$
(48)

where \(\chi ^{c}\) can be set as \(\varphi ^{c}\), \(\psi ^{c}\) or \(\gamma ^{c}\), \(v_{1} \) is the estimated value of \(\chi ^{c}\), \(v_{2} \) is the derivative of \(\chi ^{c}\) which corresponds to \(\dot{{\varphi }}^{c}\), \(\dot{{\psi }}^{c}\) or \(\dot{{\gamma }}^{c}\). Therefore, \(\varvec{\dot{{X}}}_{1}^{c} \) is obtained and \(\varvec{e}_{2} \) will be calculated. Moreover, the convergence time of the differentiator is set as \(T_{d} \) and the exact value can be found in Theorem 2 in the reference [47].

Subsequently, a fixed-time disturbance observer for Eq. (37) is established by [47].

$$\begin{aligned} \varvec{\dot{{Z}}}_{1}= & {} \varvec{Z}_{2} -k_{1} \hbox {sig}^{a_{1} }\left( {\varvec{Z}_{1} -\varvec{e}} \right) -\kappa _{1} \hbox {sig}^{b_{1} }\left( {\varvec{Z}_{1} -\varvec{e}} \right) \nonumber \\ \varvec{\dot{{Z}}}_{2}= & {} \varvec{Z}_{3} {-}k_{2} \hbox {sig}^{a_{2} }\left( {\varvec{Z}_{1} {-}\varvec{e}} \right) {-}\kappa _{2} \hbox {sig}^{b_{2} }\left( {\varvec{Z}_{1} {-}\varvec{e}} \right) +{\varvec{B}}_{1} \varvec{U} \nonumber \\ \varvec{\dot{{Z}}}_{3}= & {} -k_{3} \hbox {sig}^{a_{3} }\left( {\varvec{Z}_{1} -\varvec{e}} \right) -\kappa _{3} \hbox {sig}^{b_{3} }\left( {\varvec{Z}_{1} -\varvec{e}} \right) \end{aligned}$$
(49)

where \(\varvec{Z}_{1} \in R^{3},\varvec{Z}_{2} \in R^{3}\varvec{,Z}_{3} \in R^{3}\). \(k_{1} ,k_{2} ,k_{3} ,\kappa _{1} ,\kappa _{2} \) and \(\kappa _{3} \) are observer gains. \(a_{1} \in \left( {1-\varepsilon ,1} \right) \), \(\varepsilon \) is a sufficiently small number, \(a_{2} =2a_{1} -1\) and \(a_{3} =3a_{1} -2\). Similarly, \(b_{1} \in \left( {1,1+\varepsilon _{1} } \right) \), \(b_{2} =2b_{1} -1\), \(b_{3} =3b_{1} -2\) and \(\varepsilon _{1} \) is also sufficiently small. The resulting observer estimation error system for errors \(\varvec{\xi }_{1} =\varvec{Z}_{1} -\varvec{e}_{1} \), \(\varvec{\xi }_{2} =\varvec{Z}_{2} -\varvec{\dot{{e}}}_{1} \) and \(\varvec{\xi }_{3} =\varvec{Z}_{3} -\varvec{d}\) takes the following form

$$\begin{aligned} \varvec{\dot{{\xi }}}_{1}= & {} \varvec{\xi }_{2} -k_{1} \hbox {sig}^{a_{1} }\left( {\varvec{Z}_{1} -\varvec{e}} \right) -\kappa _{1} \hbox {sig}^{b_{1} }\left( {\varvec{Z}_{1} -\varvec{e}} \right) \nonumber \\ \varvec{\dot{{\xi }}}_{2}= & {} \varvec{\xi }_{3} -k_{2} \hbox {sig}^{a_{2} }\left( {\varvec{Z}_{1} -\varvec{e}} \right) -\kappa _{2} \hbox {sig}^{b_{2} }\left( {\varvec{Z}_{1} -\varvec{e}} \right) \nonumber \\ \varvec{\dot{{\xi }}}_{3}= & {} -\,k_{3} \hbox {sig}^{a_{3} }\left( {\varvec{Z}_{1} -\varvec{e}} \right) -\kappa _{3} \hbox {sig}^{b_{3} }\left( {\varvec{Z}_{1} -\varvec{e}} \right) \end{aligned}$$
(50)

Theorem 2

Consider the observer (49) and the corresponding estimation error system (50). The errors \(\varvec{\xi }_{1} ,\varvec{\xi }_{2} \) and \(\varvec{\xi }_{3} \) converge to the origin and the observer states \(\varvec{Z}_{1} ,\varvec{Z}_{2} \varvec{,Z}_{3} \) converge to the state variables \( \varvec{e}\) , \(\varvec{\dot{{e}}}_{1} \) and \(\varvec{d}\), respectively, within a fixed time \(T_{1} \).

$$\begin{aligned} T_{1} \le \frac{\lambda _{\max }^{\rho _{1} } \left( {P_{1} } \right) }{r_{1} \rho _{1} }+\frac{1}{r_{2} \sigma \gamma ^{\sigma }} \end{aligned}$$
(51)

where \(\rho _{1} =1-a_{1} \), \(\sigma =b_{1} -1\), \(\lambda _{\min } \left( {Q_{1} } \right) >0\) is the minimum eigenvalue of the matrix \(Q_{1} \), \(\lambda _{\max } \left( {P_{1} } \right) >0\) is the maximum eigenvalue of the matrix \(P_{1} \), \(r_{1} =\lambda _{\min } \left( {Q_{1} } \right) /\lambda _{\max } \left( {P_{1} } \right) ,r_{2} =\lambda _{\min } \left( {Q_{2} } \right) /\lambda _{\max } \left( {P_{2} } \right) \), and \(\gamma \le \lambda _{\min } \left( {P_{2} } \right) \) is a positive number. \(Q_{1} \) and \(Q_{2} \) are positive definite matrices and the matrices \(P_{1} ,P_{2}\) satisfy

$$\begin{aligned} P_{1} A_{1} +A_{1}^{\mathrm{T}} P_{1} =-\,Q_{1} \nonumber \\ P_{2} A_{2} +A_{2}^{\mathrm{T}} P_{2} =-\,Q_{2} \end{aligned}$$
(52)

where \(A_{1} \) and \(A_{2} \) are defined as

$$\begin{aligned} A_{1} =\left[ {{\begin{array}{ccc} {-\,k_{1} } &{} 1 &{} 0 \\ {-\,k_{2} } &{} 0 &{} 1 \\ {-\,k_{3} } &{} 0 &{} 0 \\ \end{array} }} \right] ,A_{2} =\left[ {{\begin{array}{ccc} {-\,\kappa _{1} } &{} 1 &{} 0 \\ {-\,\kappa _{2} } &{} 0 &{} 1 \\ {-\,\kappa _{3} } &{} 0 &{} 0 \\ \end{array} }} \right] \end{aligned}$$
(53)

Theorem 2 can be proved by the reference [47].

Next, by employing the proposed NFFTSMS in Eq. (40), an adaptive non-singular fixed-time fast terminal sliding mode control (ANFFTSMC) is designed. Thus we have

$$\begin{aligned} \varvec{u}= & {} -{\varvec{B}}_{1}^{-1}\left[ \frac{1}{\gamma _{2} }\left( {\varvec{\bar{{\Gamma }}}\left( {\varvec{e}_{1} } \right) +\varvec{\Gamma }\left( {\varvec{e}_{1} } \right) } \right) \hbox {sig}^{2-\gamma _{2} }\left( {\varvec{e}_{2} } \right) \right. \nonumber \\&+\,\frac{1}{\gamma _{2} }\hbox {diag}\left\{ {\eta \left( {\left| {\varvec{e}_{2} } \right| ^{\gamma _{2} -1}} \right) } \right\} \nonumber \\&\hbox {diag}\left\{ {\left( {\left| {\varvec{e}_{2} } \right| ^{1-\gamma _{2} }} \right) } \right\} \hbox {sig}^{\gamma _{5} }\left( {\sigma _{1}\hbox {sig}^{\gamma _{3} }\left( {\varvec{S}} \right) {+}\sigma _{2} \hbox {sig}^{\gamma _{4} }\left( {\varvec{S}} \right) } \right) \nonumber \\&\left. +\,\hbox {diag}\left( {\Upsilon \left| {\varvec{Z}_{3} } \right| _{\max } } \right) {\hbox {sign}}\left( {\varvec{S}} \right) \right] \end{aligned}$$
(54)

where \(\gamma _{5} >1,\gamma _{3} \gamma _{5} <1\), \(\Upsilon >1\) and \(\gamma _{4} \gamma _{5} >1\). \(\sigma _{1} \) and \(\sigma _{2} \) are two positive constants. \(\varvec{Z}_{3}\) represents the estimate value of the multiple disturbances in Eq. (37), which has the form of \(\varvec{Z}_{3} =\varvec{d}\) within a fixed time \(T_{1} \). \(\left| {\varvec{Z}_{3} } \right| _{\max } =\left[ {{\begin{array}{ccc} {\left| {\varvec{Z}_{3x} } \right| _{\max } } &{} {\left| {\varvec{Z}_{3y} } \right| _{\max } } &{} {\left| {\varvec{Z}_{3z} } \right| _{\max } } \\ \end{array} }} \right] ^{\mathrm{T}}\) denotes the max value of the disturbances, which can be updated online. \(\varvec{\bar{{\Gamma }}}\left( {\varvec{e}_{1} } \right) \) is a diagonal matrix which has the diagonal elements as

$$\begin{aligned} \varvec{\bar{{\Gamma }}}\left( {e_{1i} } \right) =k\gamma _{2} \left( {\alpha _{1} \left| {e_{1i} } \right| ^{p-1/k\gamma _{2} }+\beta _{1} \left| {e_{1i} } \right| ^{q-1/k\gamma _{2} }} \right) ^{k\gamma _{2} -1}\Lambda \end{aligned}$$
(55)

where \(\Lambda =\alpha _{1} \left( {p-\frac{1}{k\gamma _{2} }} \right) \left| {e_{1i} } \right| ^{p-1/k\gamma _{2} }+\beta _{1} \left( {q-\frac{1}{k\gamma _{2} }} \right) \left| {e_{1i} } \right| ^{q-1/k\gamma _{2} }\) and \(i=x,y,z\).

The following theorem presents the fixed-time stability of the proposed ANFFTSMC in Eq. (54) for the second-order system (37).

Theorem 3

Consider system (37) and the controller (54), the state variables \(\varvec{e}_{1} \) and \(\varvec{e}_{2}\) will converge to the origin within a fixed time and the upper bound of the convergence time is given as follows.

$$\begin{aligned} T<T_{\max } =T_{0} +T_{1} +T_{2} +T_{d} +T_{L} \end{aligned}$$
(56)

where

$$\begin{aligned} T_{2}= & {} \frac{2}{2^{\left( {1+\gamma _{3} \gamma _{5} } \right) /2}\sigma _{1}^{\gamma _{5} } 3^{\gamma _{5} -1}\left( {1-\gamma _{3} \gamma _{5} } \right) }\\&+\frac{2}{2^{\left( {1+\gamma _{4} \gamma _{5} } \right) /2}3^{\gamma _{5} -1}\left( {\gamma _{4} \gamma _{5} -1} \right) } \\ T_{L}= & {} \left( {\tau ^{1/\left( {\gamma _{2} -1} \right) }} \right) /\left( {\left\| {\Upsilon \left| {\varvec{Z}_{3} } \right| _{\max } -\varvec{d}_{m} } \right\| } \right) \end{aligned}$$

Proof

Consider the following Lyapunov function candidate

$$\begin{aligned} \varvec{V}_{S} \varvec{=}\frac{1}{2}\varvec{S}^{\mathrm{T}}\varvec{S} \end{aligned}$$
(57)

The derivative of \(\varvec{V}_{S} \) is

$$\begin{aligned} \varvec{\dot{{V}}}_{S}= & {} \varvec{S}^{\mathrm{T}}\varvec{\dot{{S}}} \nonumber \\= & {} \varvec{S}^{\mathrm{T}}\left( {\frac{\hbox {d}{\varvec{\Gamma }} \left( {\varvec{e}_{1} } \right) }{\hbox {d}t}\varvec{e}_{1} +{\varvec{\Gamma }} \left( {\varvec{e}_{1} } \right) \varvec{e}_{2} +\gamma _{2} \hbox {diag}\left\{ {\left| {\varvec{e}_{2} } \right| ^{\gamma _{2} -1}} \right\} \varvec{\dot{{e}}}_{2} } \right) \nonumber \\= & {} \varvec{S}^{\mathrm{T}}\left( \bar{{{\varvec{\Gamma }} }}\left( {\varvec{e}_{1} } \right) \varvec{e}_{1} +{\varvec{\Gamma }} \left( {\varvec{e}_{1} } \right) \varvec{e}_{2} +\gamma _{2} \hbox {diag}\left\{ {\left| {\varvec{e}_{2} } \right| ^{\gamma _{2} -1}} \right\} \right. \nonumber \\&\left. \left( {\varvec{d}+{\varvec{B}}_{1} \varvec{U}} \right) \right) \end{aligned}$$
(58)

Substituting the ANFFTSMC into Eq. (58) yields

$$\begin{aligned} \dot{{\varvec{V}}}_S= & {} -{\varvec{S}}^{T}\hbox {diag}\left\{ {\eta \left( {\left| {{\varvec{e}}_2 } \right| ^{\gamma _2 -1}} \right) } \right\} \nonumber \\&\hbox {sig}^{\gamma _5 }\left( {\sigma _1 \hbox {sig}^{\gamma _3 }\left( {\varvec{S}} \right) +\sigma _2 \hbox {sig}^{\gamma _4 }\left( {\varvec{S}} \right) } \right) \nonumber \\&-\,\gamma _2 {\varvec{S}}^{T}\hbox {diag}\left\{ {\left( {\left| {{\varvec{e}}_2 } \right| ^{\gamma _2 -1}} \right) } \right\} \nonumber \\&\left( {\hbox {diag}\left( {\left| {{\varvec{Z}}_3 } \right| } \right) \hbox {sign}\left( \varvec{S} \right) -{\varvec{d}}} \right) \nonumber \\\le & {} -\,\sum _{i=1}^3 \left( \sigma _1 \eta ^{1/\gamma _5 }\left( {\left| {{\varvec{e}}_{2i} } \right| ^{\gamma _2 -1}} \right) \left| {\varvec{S}_i } \right| ^{1/\gamma _5 +\gamma _3 }\right. \nonumber \\&\left. +\,\sigma _2 \eta ^{1/\gamma _5 }\left( {\left| {{\varvec{e}}_2 } \right| ^{\gamma _2 -1}} \right) \left| {\varvec{S}_i } \right| ^{1/\gamma _5 +\gamma _4 } \right) ^{\gamma _5 } \nonumber \\&-\,\gamma _2 \sum _{i=1}^3 {\left| {{\varvec{e}}_{2i} } \right| ^{\gamma _2 -1}} \left| {\varvec{S}_i } \right| \left( {\Upsilon \left| {\varvec{Z}_3 } \right| _{\max } -\,\left| {\varvec{d}_i } \right| } \right) \end{aligned}$$
(59)

With the proposed fixed-time disturbance observer and Theorem 2, we have \(\varvec{Z}_{3} =\varvec{d}\) within a fixed time \(T_{1} \) and \(\Upsilon \left| {\varvec{Z}_{3} } \right| _{\max } -\left| {\varvec{d}_{i} } \right| >0\). Meanwhile, according to Lemma 2 and Lemma 3, Eq. (59) can be written as

$$\begin{aligned} \varvec{\dot{{V}}}_{S}\le & {} -\sum \limits _{i=1}^3 \left( \sigma _{1} \eta ^{1/\gamma _{5} }\left( {\left| {\varvec{e}_{2i} } \right| ^{\gamma _{2} -1}} \right) \left| {\varvec{S}_{i} } \right| ^{1/\gamma _{5} +\gamma _{3} }\right. \nonumber \\&\left. +\,\sigma _{2} \eta ^{1/\gamma _{5} }\left( {\left| {\varvec{e}_{2} } \right| ^{\gamma _{2} -1}} \right) \left| {\varvec{S}_{i} } \right| ^{1/\gamma _{5} +\gamma _{4} } \right) ^{\gamma _{5} } \nonumber \\\le & {} -3^{1-\gamma _{5} }\left( \sigma _{1} \min \left( {\eta ^{1/\gamma _{5} }\left( {\left| {\varvec{e}_{2i} } \right| ^{\gamma _{2} -1}} \right) } \right) \right. \nonumber \\&\sum \limits _{i=1}^3 {\left( {\left| {\varvec{S}_{i} } \right| ^{2}} \right) ^{\left( {1+\gamma _{3} \gamma _{5} } \right) /\left( {2\gamma _{5} } \right) }} \nonumber \\&\left. +\,\sigma _{2} \min \left( {\eta ^{1/\gamma _{5} }\left( {\left| {\varvec{e}_{2i} } \right| ^{\gamma _{2} -1}} \right) } \right) \right. \nonumber \\&\left. \sum \limits _{i=1}^3 {\left( {\left| {\varvec{S}_{i} } \right| ^{2}} \right) ^{\left( {1+\gamma _{4} \gamma _{5} } \right) /\left( {2\gamma _{5} } \right) }} \right) ^{\gamma _{5} } \nonumber \\\le & {} {-}3^{1{-}\gamma _{5} } \nonumber \\&\left( {\tau _{m} \varvec{V}_{S}^{\left( {1{+}\gamma _{3} \gamma _{5} } \right) /\left( {2\gamma _{5} } \right) } {+}\upsilon _{m} \varvec{V}_{S}^{\left( {1+\gamma _{4} \gamma _{5} } \right) /\left( {2\gamma _{5} } \right) } } \right) ^{\gamma _{5} }\end{aligned}$$
(60)

where \(\tau _{m} =2^{\left( {1+\gamma _{3} \gamma _{5} } \right) /\left( {2\gamma _{5} } \right) }\sigma _{1} \min \left( {\eta ^{1/\gamma _{5} }\left( {\left| {\varvec{e}_{2i} } \right| ^{\gamma _{2} -1}} \right) } \right) \), \(\upsilon _{m} =2^{\left( {1+\gamma _{4} \gamma _{5} } \right) /\left( {2\gamma _{5} } \right) }\sigma _{2} \min \left( {\eta ^{1/\gamma _{5} }\left( {\left| {\varvec{e}_{2i} } \right| ^{\gamma _{2} -1}} \right) } \right) \). If \(\varvec{e}_{2i} \ne 0\), then \(\eta \left( {\left| {\varvec{e}_{2i} } \right| ^{\gamma _{2} -1}} \right) >0\), \(\left( {i=1,2,3} \right) \). Two new variables are defined as follows for the convenience of the proof of the proposed ANFFTSMC.

$$\begin{aligned} \Omega _{1}= & {} \left\{ {\left. {\left( {\varvec{e}_{1i} ,\varvec{e}_{2i} } \right) } \right| \left| {\varvec{e}_{2i} } \right| ^{\gamma _{2} -1}\ge \tau ,\forall i=x,y,z} \right\} \nonumber \\ \Omega _{2}= & {} \left\{ {\left. {\left( {\varvec{e}_{1i} ,\varvec{e}_{2i} } \right) } \right| \left| {\varvec{e}_{2i} } \right| ^{\gamma _{2} -1}<\tau ,\forall i=x,y,z} \right\} \end{aligned}$$
(61)

If the error system states \(\varvec{e}_{1i} \) and \(\varvec{e}_{2i} \) reach the region \(\Omega _{1} \), we have \(\eta \left( {\left| {\varvec{e}_{2i} } \right| ^{\gamma _{2} -1}} \right) =1\) based on Eq. (47). Therefore, \(\tau _{m} \) and \(\upsilon _{m} \) are positive constants regardless of the system states. They can be simplified as

$$\begin{aligned} \tau _{m}= & {} 2^{\left( {1+\gamma _{3} \gamma _{5} } \right) /\left( {2\gamma _{5} } \right) }\sigma _{1} \nonumber \\ \upsilon _{m}= & {} 2^{\left( {1+\gamma _{4} \gamma _{5} } \right) /\left( {2\gamma _{5} } \right) }\sigma _{2} \end{aligned}$$
(62)

Equation (60) can be converted into

$$\begin{aligned} \varvec{\dot{{V}}}_{S}\le & {} -3^{1-\gamma _{5} }\left( 2^{\left( {1+\gamma _{3} \gamma _{5} } \right) /\left( {2\gamma _{5} } \right) }\sigma _{1} \varvec{V}_{S}^{\left( {1+\gamma _{3} \gamma _{5} } \right) /\left( {2\gamma _{5} } \right) }\right. \nonumber \\&\left. +\,2^{\left( {1+\gamma _{4} \gamma _{5} } \right) /\left( {2\gamma _{5} } \right) }\sigma _{2} \varvec{V}_{S}^{\left( {1+\gamma _{4} \gamma _{5} } \right) /\left( {2\gamma _{5} } \right) } \right) ^{\gamma _{5}} \end{aligned}$$
(63)

Based on Lemma 1 and Eq. (63), the system states \(\varvec{e}_{1i} \) and \(\varvec{e}_{2i} \) will be driven on the sliding mode surface \(\varvec{S}=\varvec{0}\) within a bounded time \(T_{2} \).

$$\begin{aligned} T_{2}= & {} \frac{2}{2^{\left( {1+\gamma _{3} \gamma _{5} } \right) /2}\sigma _{1}^{\gamma _{5} } 3^{\gamma _{5} -1}\left( {1-\gamma _{3} \gamma _{5} } \right) }\nonumber \\&+\frac{2}{2^{\left( {1+\gamma _{4} \gamma _{5} } \right) /2}3^{\gamma _{5} -1}\left( {\gamma _{4} \gamma _{5} -1} \right) } \end{aligned}$$
(64)

Furthermore, if \(\varvec{e}_{2i} \ne 0\), we have \(0<\left| {\varvec{e}_{2i} } \right| ^{\gamma _{2} -1}<\tau \) in the region \(\Omega _{2} \). It can be similarly verified according to the definition of \(\tau _{m} \) and \(\upsilon _{m} \) that \(\tau _{m} >0\) and \(\upsilon _{m} >0\). Thus, based on Lemma 1 and Eq. (60), the sliding mode surface \(\varvec{S}_{i} =0\) is still an attractor in the region \(\Omega _{2} \). Next, we will verify that the region \(\Omega _{2} \) is not an attractor area except for the origin. Substituting the ANFFTSMC into Eq. (37) yields

$$\begin{aligned} \varvec{\dot{{e}}}_{2}= & {} -\frac{1}{\gamma _{2} }\left( {\varvec{\bar{{\Gamma }}}\left( {\varvec{e}_{1} } \right) +\varvec{\Gamma }\left( {\varvec{e}_{1} } \right) } \right) \hbox {sig}^{2-\gamma _{2} }\left( {\varvec{e}_{2} } \right) \nonumber \\&-\,\frac{1}{\gamma _{2} }\hbox {diag}\left\{ {\eta \left( {\left| {\varvec{e}_{2} } \right| ^{\gamma _{2} -1}} \right) } \right\} \nonumber \\&\hbox {diag}\left\{ {\left( {\left| {\varvec{e}_{2} } \right| ^{1-\gamma _{2} }} \right) } \right\} \nonumber \\&\hbox {sig}^{\gamma _{5} }\left( {\sigma _{1} \hbox {sig}^{\gamma _{3} }\left( {\varvec{S}} \right) +\sigma _{2} \hbox {sig}^{\gamma _{4} }\left( {\varvec{S}} \right) } \right) \nonumber \\&-\,\hbox {diag}\left( {\Upsilon \left| {\varvec{Z}_{3} } \right| _{\max } } \right) {\hbox {sign}}\left( {\varvec{S}} \right) +\varvec{d} \end{aligned}$$
(65)

If \(\varvec{e}_{2i} \rightarrow 0\), Eq. (65) can be simplified as

$$\begin{aligned} \varvec{\dot{{e}}}_{2} =-\hbox {diag}\left( {\Upsilon \left| {\varvec{Z}_{3} } \right| _{\max } } \right) \hbox {sign}\left( {\varvec{S}} \right) +\varvec{d} \end{aligned}$$
(66)

If \(\varvec{S}_{i} >0\), then \(\varvec{\dot{{e}}}_{2} \le \varvec{d}_{m} -\Upsilon \left| {\varvec{Z}_{3} } \right| _{\max } <0\), and if \(\varvec{S}_{i} <0\), then \(\varvec{\dot{{e}}}_{2}>\Upsilon \left| {\varvec{Z}_{3} } \right| _{\max } -\varvec{d}_{m} >0\), where \(\varvec{d}_{m} \) is the vector of the max value of the disturbances. Therefore, the system states will transgress the region \(\Omega _{2}\) into \(\Omega _{1} \) monotonically within the time \(T_{L} =\left( {\tau ^{1/\left( {\gamma _{2} -1} \right) }} \right) /\left( {\left\| {\Upsilon \left| {\varvec{Z}_{3} } \right| _{\max } -\varvec{d}_{m} } \right\| } \right) \). It is obvious that the system states from anywhere will be driven on the proposed sliding mode surface \(\varvec{S}=\varvec{0}\). Moreover, according to Theorem 1, the system states \(\varvec{e}_{1i} \) and \(\varvec{e}_{2i} \) will converge to the origin within a fixed time \(T<T_{0} +T_{1} +T_{2} +T_{d} +T_{L} \). This completes the proof of Theorem 3. \(\square \)

Remark 3

The proposed controller is developed based on the NFFTSMS and the total disturbances that are estimated by the fixed-time disturbance observer. Compared with other non-singular fixed-time fast terminal sliding mode controllers, the proposed ANFFTSMC does not require the bounded disturbances in advance, and the control parameters are not required to be equal to or greater than the disturbances.

4 Simulations and results

In this section, to prove the effectiveness of the proposed adaptive non-singular fixed-time fast terminal sliding mode control (ANFFTSMC) in Eq. (54), various results of the numerical simulation are presented. The fluid coefficients and parameters of the submarine-launched missile are listed in Tables 1 and 2 [43].

Table 1 Fluid coefficients of the submarine-launched missile
Full size table
Table 2 Parameters of the submarine-launched missile
Full size table
Fig. 4
figure 4

Attitude tracking results under the PID controller and ANFFTSMC

Full size image

4.1 Simulation results for the vertical launching mode

The proposed control algorithm will be first tested for the vertical launching mode, and the initial parameters are set to be \(x=0,y=0,z=0\), \(\varphi =89^{\circ },\psi =1^{\circ },\gamma =1^{\circ }\), \(V_{x} =0.5,V_{y} =0,V_{z} =0\) and \(\omega _{x} =\hbox {0.001},\omega _{y} =\hbox {0.001},\omega _{z} =\hbox {0.001}\). The expected attitude commands are chosen as \(\varphi ^{c}=90^{\circ },\psi ^{c}=0^{\circ }\) and \(\gamma ^{c}=0^{\circ }\). Meanwhile, the depth of the launching point for the submarine-launched missile is \(h=30\,\hbox {m}\), and the simulation sampling step is 5ms. The control command is limited within [\(-15^{\circ }\), \(15^{\circ }\)]. Moreover, the PID controller parameters for both the pitch channel and the yaw channel are set as \(\left( {\hbox {10},\hbox {2},\hbox {6}} \right) \), and the roll channel is \(\left( {\hbox {5.0},1.\hbox {7}} \right) \). Furthermore, the control parameters of ANFFTSMC are selected to be \(\alpha _{1} =1.5\), \(\beta _{1} =1.5\), \(p=0.4\), \(q=0.7\), \(k=2\), \(\gamma _{2} =5/3\), \(\gamma _{3} =1/3\), \(\gamma _{4} =3/4\), \(\gamma _{5} =1.85\), \(\tau =0.005\), \(\sigma _{1} =1.0\), \(\Upsilon =2\) and \(\sigma _{2} =1.0\). The parameters of the fixed-time disturbance observer are selected to be \(a_{1} =0.9\), \(a_{2} =2a_{1} -1\), \(a_{3} =3a_{1} -2\), \(b_{1} =1.8\), \(b_{1} =2b_{1} -1\), \(b_{1} =3b_{1} -2\) and the observer gains are set as \(k_{1} =\kappa _{1} =24\), \(k_{2} =\kappa _{2} =216\) and \(k_{3} =\kappa _{3} =864\) [47]. As for the parameter uncertainty, its bias is set to be 20% for the density of the seawater, and 10% for the fluid coefficients of the submarine-launched missile. The sea current velocity is \(w_{p} =1.5\hbox { m/s}\); the air density is \(\rho _{1} =1.225\); the sea wind velocity is \(V_{wz} =30\hbox { m/s}\); the aerodynamic drag coefficient is \(C_{wx} =0.5\) and the wind direction is \(\phi =60^{\circ }\).

To reduce the chattering of the control system, the switching function \(\hbox {sign}(x)\) will be replaced by a hyperbolic tangent function \(\tanh (x)=\left( {e^{x}-e^{-x}} \right) /\left( {e^{x}+e^{-x}} \right) \). The simulation results of the submarine-launched missile with six degrees of freedom (6DOF) in the water-exit process are shown in Figs. 4, 5, 6, 7, 8, 9.

Fig. 5
figure 5

Attitude tracking error results

Full size image
Fig. 6
figure 6

Angular velocity results under the PID controller and ANFFTSMC

Full size image
Fig. 7
figure 7

Simulation results of the total angle of attack and the total angle of sideslip

Full size image
Fig. 8
figure 8

Control commands under the PID controller and ANFFTSMC

Full size image
Fig. 9
figure 9

Fixed-time disturbance observer results

Full size image

From Figs. 4, 5, 6, it can be seen that the proposed ANFFTSMC has a more satisfactory performance than the PID controller in spite of multiple disturbances including sea winds, sea waves and ocean currents, etc. The attitude tracking error of the three channels for the ANFFTSMC is \(<\,0.003^{\circ }\), while the attitude tracking error of the PID controller is \(0.56^{\circ }\). Hence, the simulation results indicate that the ANFFTSMC has less overshoot and smaller steady-state error than the PID control law. Meanwhile, the total angle of attack and the total angle of sideslip are shown in Fig. 7, which indicate large fluid viscosity forces and torques. The responses of control commands are shown in Fig. 8, where the ANFFTSMC’s control commands are larger than the PID controller’s. Also, the ANFFTSMC has stronger robustness in the presence of multiple disturbances especially near the sea level. Moreover, the control command is more exquisite during the water-exit process especially from 2.0 to 2.5 s, which indicates large disturbances for the submarine-launched missile. From Fig. 9, it can be seen that, for multiple disturbances and un-modeled dynamics, the proposed fixed-time disturbance observer has excellent estimated performance.

4.2 Simulation results for the oblique launching mode

Next, the simulation is carried out on the missile launched in oblique launching mode. The initial parameters are set to \(\varphi =46^{\circ },\psi =0.5^{\circ },\gamma =0.5^{\circ }\) and other parameters are the same as those in Sect. 4.1. Moreover, the expected attitude commands are designed as follows

$$\begin{aligned} \left\{ {\begin{array}{l} \varphi ^{c}=45+5t \\ \psi ^{c}=2\sin \left( {\pi t/6} \right) \\ \gamma ^{c}=\sin \left( {\pi t/6} \right) \\ \end{array}} \right. \end{aligned}$$
(67)

The simulation results of the oblique launching mode are shown in Figs. 10, 11, 12, 13 and 14.

Fig. 10
figure 10

Attitude tracking results for the oblique launching mode

Full size image
Fig. 11
figure 11

Attitude tracking error results for the oblique launching mode

Full size image
Fig. 12
figure 12

Control commands for the oblique launching mode

Full size image
Fig. 13
figure 13

Simulation results of the differentiator

Full size image
Fig. 14
figure 14

Simulation results of the fixed-time disturbance observer for the oblique launching mode

Full size image

From Figs. 10, 11, it can be seen that the simulation results indicate the effectiveness of the proposed ANFFTSMC with respect to the oblique launching mode for the submarine-launched missile. Moreover, the tracking error for the three channels is \(<\,0.03^{\circ }\). Meanwhile, the curves of the control commands are smooth in Fig. 12. As can be seen in Figs. 13, 14, both the differentiator and the proposed fixed-time disturbance observer show satisfactory performances for the oblique launching mode, which exhibits strong robustness of the proposed control scheme.

5 Conclusion

In this work, a novel fixed-time attitude tracking control named as ANFFTSMC is presented for a submarine-launched missile with multiple disturbances. The proposed ANFFTSMC is designed by employing a NFFTSMS, a fixed-time disturbance observer and a fixed-time differentiator. Compared with other sliding mode surfaces, the proposed NFFTSMS can avoid singularity without adding additional parameters and achieve faster convergence and a more compact structure. Moreover, the proposed ANFFTSMC does not require the bounded disturbances in advance, and the control parameters do not need to be equal to or greater than the disturbances. Simulations are carried out to demonstrate the strong robustness and effectiveness of the proposed control scheme in comparison with the PID control law. The proposed fixed-time disturbance observer and the differentiator exhibit satisfactory performances in the 6DOF simulations. Moreover, the proposed control scheme achieves an attitude tracking error of \(0.03^{\circ }\), which satisfies the requirement of the control system design.