Sinusoidal control and limit cycle analysis of the dissipative Chaplygin sleigh

Abstract

In this paper, we investigate the behavior of an underactuated mixed-dynamic nonholonomic system, a Chaplygin sleigh, subjected to viscous dissipation and sinusoidal forcing. The viscous dissipation is in the allowable directions of motion and preserves the nonholonomic constraint. The inclusion of such dissipative effects produces limit cycle oscillations in a reduced velocity space. We find analytical approximations to such limit cycles and use these to determine sinusoidal inputs to control the speed of the sleigh. We further show small changes to the sinusoidal input can steer the sleigh to any desired direction. Invariant structures like limit cycles can be expected to be seen in the dynamics of other nonholonomic systems when the effects of viscous dissipation are included. The findings we report here are therefore applicable to a broad class of both terrestrial and aquatic locomotion systems with nonholonomic constraints.

1 Introduction

The Chaplygin sleigh is a canonical system in the study of nonholonomic mechanics [1,2,3,4,5]. The sleigh has a wheel or a knife edge at one end, which does not allow any velocity in a transverse direction, see Fig. 1. The Chaplygin sleigh is a mixed-dynamic system [6] with one nonholonomic constraints and three degrees of freedom with the equations of motion of the sleigh having a drift term. One of the first papers to investigate the control of the motion of the sleigh was by Osborne and Zenkov [7], where the means of control was a particle that could move anywhere on the sleigh. With these two degrees of actuation, it was shown that the sleigh could be steered to pass through any point in the configuration space or workspace. A modified version of the sleigh, called the Chaplygin beanie, was introduced in [8]. The Chaplygin beanie contained an actuated balanced rotor pinned to the sleigh. The sleigh with the balanced rotor is an underactuated control system, since it has only one control input, the torque on the rotor. In [8], it was shown that any desirable change in the heading angle of the sleigh can be achieved through proportional control, but the speed of the sleigh could not be controlled. This is because for the classical sleigh the energy can only increase. This has also been discussed in [9, 10]. A consequence is that limit cycles in the reduced velocity space are only possible when some energy dissipation is introduced. An open loop control of the sleigh’s heading was proposed in [11] for the Chaplygin sleigh with the balanced rotor. Other variants of the Chaplygin sleigh are also addressed in recent works [12,13,14,15].

A piecewise smooth constraint was considered in [16, 17] which allowed the sleigh to slip in the transverse direction at the knife edge if the constraining force of friction exceeded a threshold. The Coulomb friction model produced stick-slip motion of the sleigh such that the speed and heading of the sleigh could be controlled for a small range of velocities. Separately, in the context of nonholonomic systems, the effects of viscous dissipation in the form of Reyleigh dissipation function were considered in [18] where the effects of the dissipation on several gaits of the snakeboard were shown. In [19], the motion planning problem for the snakeboard in the presence of viscous dissipation was investigated. The viscous dissipation in these cases preserves the nonholonomic constraint, but dissipates energy at a rate proportional to square of the velocity in the direction orthogonal to the nonholonomic constraint. A viscous sleigh was also recently considered in [20], where regular and chaotic dynamics were shown for the case of impulsive torques.

The introduction of viscous friction is motivated by the fact that dissipation of kinetic energy exists in robotic systems with nonholonomic constraints even in the absence of slip-induced dissipation. A second motivation is due to recent work related to a fish-like swimming robot. The interaction between a Joukowski foil-shaped body and the fluid through vortex shedding has been shown to be an affine nonholonomic constraint [21, 22]. Moreover, this constraint has a formal similarity to that of the constraint on the Chaplygin sleigh. Experimental data related to the motion of a swimming robot propelled by an internal rotor show that its motion is very similar to that of the Chaplygin sleigh [23]. The Chaplygin sleigh thus serves as a terrestrial analogue of swimming robots, and this analogy can be exploited to understand the more complicated dynamics of fluid–robot interaction.

In this paper, an extension of previous work [24], we investigate the motion of a Chaplygin sleigh under the influence of viscous dissipation. The sleigh’s motion is controlled through the torque applied on a balanced rotor pinned to the sleigh. The locomotion characteristics of many animals, including those of fish, show that rhythmic or periodic actuation for instance through central pattern generators plays an important role [25]. There has also been a rich history within the area of nonholonomic mechanics, where motion planning was achieved through sinusoidal inputs [26]. Motivated by this, we consider the dynamics of the sleigh when the balanced rotor executes sinusoidal motion. Such motion of the rotor is shown to lead to limit cycles in the reduced velocity space of the sleigh. We then use the harmonic balance method [27, 28] to control both the speed and the heading of the sleigh. While motion planning of mixed-dynamic nonholonomic systems has been studied extensively in the past, see for instance, [29, 30], the work presented here is the first to exploit the limit cycles in the reduced velocity space to control the motion of the sleigh.

Fig. 1

Chaplygin sleigh with a balanced rotor. The rotor is placed at distance of b from the rear contact

2 Equations of motion

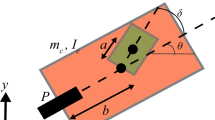
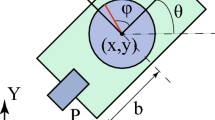
A schematic diagram of the Chaplygin sleigh is shown in Fig. 1. The sleigh has mass m and moment of inertia I. The point P represents the point of contact of sharp knife edge or wheel with the ground. At this point, the sleigh is not allowed to slip in the transverse direction. The axes $X_b$ and $Y_b$ are body fixed where $X_b$ is aligned with the line between P and the center of mass. The position of the center of mass of the sleigh is denoted by (x, y), and the orientation of the sleigh is $\theta$. The distance between P and the center of mass is b. The sleigh carries a balanced rotor ($I_\mathrm{r}$), whose center coincides with the center of mass of the sleigh. The relative angle that the rotor makes with the body axes is denoted by $\phi$. The configuration manifold for the system is $Q=SE2\times S^1$, where $S^1$ is the shape or base manifold that is parametrized by the relative angle the rotor makes with the $X_b$-axis. The so-called fiber manifold is SE2 that is parameterized by the x, y coordinates of the center of mass of the sleigh and the orientation of the body axis with respect to the fixed inertial axis. The equations of motion are derived using the Lagrange multiplier method. The generalized coordinates are $q = (x,y,\theta , \phi )$, and the generalized velocities are ${\dot{q}} = ({\dot{x}},{\dot{y}},{\dot{\theta }}, {\dot{\phi }})$. Since there are no potential forces, the Lagrangian is the kinetic energy of the sleigh (1),

$$\begin{aligned} {\mathscr {L}} = \frac{1}{2}m({\dot{x}}^2+{\dot{y}}^2) +\frac{1}{2}I{\dot{\theta }}^2+\frac{1}{2}I_{r}({\dot{\theta }}+{\dot{\phi }})^2. \end{aligned}$$

(1)

The system is subject to the following nonholonomic constraint (2), which ensures that the transverse velocity ( along the $Y_b$ direction) of the point of contact P be equal to zero,

$$\begin{aligned} -{\dot{x}}\sin {\theta } + {\dot{y}}\cos {\theta } - b{\dot{\theta }} = 0 \end{aligned}$$

(2)

with Pfaffian one form being

$$\begin{aligned} -\sin {\theta }\hbox {d}x + \cos {\theta }\hbox {d}y - b \hbox {d}\theta = 0. \end{aligned}$$

The viscous dissipation is due to the longitudinal velocity of the sleigh, $u = {\dot{x}}\cos (\theta )+{\dot{y}}\sin (\theta )$ along the body $X_b$-axis. The Rayleigh dissipation function is

$$\begin{aligned} R_w =\frac{1}{2}cu^2 = \frac{1}{2}c({\dot{x}}\cos {\theta }+{\dot{y}}\sin {\theta })^2. \end{aligned}$$

The Euler–Lagrange equations are of the following form

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\left( \frac{\partial {\mathscr {L}}}{\partial \dot{q^k}}\right) -\frac{\partial {\mathscr {L}}}{\partial q^k}= C_k\lambda + Q_{q^k} \end{aligned}$$

(3)

where $\lambda$ is the Lagrange multiplier, $C_{k}$ is the coefficient corresponding to one forms $dq_k$, and $Q_{q_k} =-\frac{\partial R_w}{\partial q_k}$ is the dissipation force due to dissipation at the wheel. The dissipation forces are calculated as

$$\begin{aligned} Q_{x}&= -\,c({\dot{x}}\cos ^2{\theta }+{\dot{y}}\sin {\theta }\cos {\theta })\\ Q_{y}&= -\,c({\dot{y}}\sin ^2{\theta }+{\dot{x}}\sin {\theta }\cos {\theta })\\ Q_{\omega }&= 0. \end{aligned}$$

With this formulation, the Euler–Lagrange equations are readily obtained to be

$$\begin{aligned} m{\ddot{x}}&=-\,\lambda \sin (\theta )+Q_x\\ m{\ddot{y}}&=\lambda \cos (\theta )+Q_y\\ m{\ddot{\theta }}&=-\,b\lambda -I_\mathrm{r}{\ddot{\phi }}+Q_{\theta }. \end{aligned}$$

The velocities of the center of the cart can be written in terms of the velocity of the point P and the angular velocity of the sleigh, $\omega ={\dot{\theta }}$, to obtain the reconstruction equations which define the path of the body on the fiber manifold.

$$\begin{aligned} {\dot{x}}&= u \cos {\theta } - \omega b\sin {\theta } \end{aligned}$$

(4)

$$\begin{aligned} {\dot{y}}&= u \sin {\theta } + \omega b\cos {\theta }. \end{aligned}$$

(5)

$$\begin{aligned} {\ddot{x}} = {\dot{u}}\cos {\theta } - u\omega \sin {\theta } -\omega ^2 b \cos {\theta } - {\dot{\omega }}b \sin {\theta }\\ {\ddot{y}} = {\dot{u}}\sin {\theta } + u\omega \cos {\theta }- \omega ^2 b \sin {\theta } + {\dot{\omega }}b\cos {\theta }. \end{aligned}$$

Using the above expressions, the equations of motion can be reduced to

$$\begin{aligned} {\dot{u}}&=b\omega ^2-\frac{c}{m}u \end{aligned}$$

(6)

$$\begin{aligned} {\dot{\omega }}&=\frac{-\,mbu\omega }{I+I_\mathrm{r}+mb^2} -\frac{I_\mathrm{r}{\ddot{\phi }}}{I+I_\mathrm{r}+mb^2} \end{aligned}$$

(7)

$$\begin{aligned} {\dot{\theta }}&= \omega . \end{aligned}$$

(8)

In the absence of any actuation from the rotor, i.e., ${\ddot{\phi }}$, the system has one globally asymptotically stable fixed point at $(u,\omega )=(0,0)$.

3 Sinusoidal motion of the rotor

We analyze the behavior of the sleigh when the balanced rotor executes sinusoidal motion. In the dynamical system described by (6) and (7), we set $-\,I_\mathrm{r}{\ddot{\phi }} = A\sin {\varOmega t}$. We first show that the velocity of the sleigh is bounded for any sinusoidal input. We further show that the average kinetic energy of the sleigh, averaged over a time period $T=\frac{2\pi }{\varOmega }$, converges to a constant value.

3.1 Bounded velocities

We first establish that the dynamical system (6) and (7) has no fixed points when $-\,I_\mathrm{r}{\ddot{\phi }} = A\sin {\varOmega t}$. For if such a fixed point exists, it must satisfy

$$\begin{aligned} b\omega ^2-\frac{c}{m}u = 0\\ \frac{-\,mbu\omega +A\sin {\varOmega t}}{I+I_\mathrm{r}+mb^2} =0. \end{aligned}$$

This requires that $m^2b^2\omega ^3 = Ac\sin (\varOmega t)$ which is not satisfied by any fixed value of $\omega$ if $A\ne 0$.

Next, we consider four possible scenarios in which u(t) or $\omega (t)$ could be unbounded and show that these contradict (6) and (7).

• 1. Suppose $u\rightarrow -\infty$. By examining (6) ${\dot{u}} >0$ if $u<0$. Therefore u(t) cannot be a decreasing function if $u<0$ and the case $u\rightarrow -\,\infty$ can be ruled out.

• 2. Suppose $u\rightarrow \infty$, and $\omega \in {\mathscr {C}} \subset \mathbb {R}$, a bounded subset. Let $\omega _\mathrm{max}$ be the highest value of $\omega \in {\mathscr {C}}$. Then, for $u > \frac{mb\omega ^2_\mathrm{max}}{c}$, ${\dot{u}}<0$. Therefore, u will have to be a decreasing function for large enough values of u contradicting the assumption that $u \rightarrow \infty$.

• 3. Suppose $\omega \rightarrow \infty$ or $\omega \rightarrow -\infty$ and $u\in {\mathscr {C}} \subset \mathbb {R}$, a bounded subset. Once again, (6) prohibits such unbounded behavior. We can infer that this is not possible because if $u_\mathrm{min}\le u\le u_\mathrm{max}$, then for $\omega ^2>\frac{c}{bm}u_\mathrm{max}$, ${\dot{u}}>0$ and u must increase past $u_\mathrm{max}$.

• 4. Suppose $u\rightarrow \infty$, $\omega \rightarrow \infty$ or $\omega \rightarrow -\,\infty$. From (7) we can see that if $u>0$ and $\omega >0$, then $\omega$ must be a decreasing function when $u\omega > \frac{I_\mathrm{r}A}{mb}$. Therefore, $\omega$ cannot become positively unbounded. Similarly, if $u>0$ and $\omega <0$ then for $-u\omega > \frac{I_\mathrm{r}A}{mb}$, ${\dot{\omega }}>0$ and $\omega$ must increase. So, $\omega$ cannot become negatively unbounded.

We can therefore conclude that the solution of (6) and (7) has to be bounded.

3.2 Bounded average kinetic energy

The kinetic energy of the sleigh is bounded, since the velocities u and $\omega$ are bounded. Furthermore, numerics indicate that starting from rest the kinetic energy of sleigh varies periodically after an initial transient. Figure 2a shows the evolution of the kinetic energy of sleigh due to the sinusoidal motion of the rotor. The kinetic energy initially increases from zero and then decays somewhat before beginning to oscillate periodically. Figure 2b shows a plot of the kinetic energy at points $t=t_0+kT$ for $t\ge 50$, $k=1,2,3\ldots$, where $T= \frac{2\pi }{\varOmega }$. The value of the kinetic energy at these time intervals $L(t_0+kT)$ reaches a constant. This indicates that the kinetic energy of the sleigh varies periodically when the rotor is forced to execute sinusoidal motion.

Fig. 2

a Kinetic energy ${\mathscr {L}}$ over time and b The kinetic energy of the sleigh at intervals of time T for $t>50$

The change in kinetic energy in a time period T is

$$\begin{aligned} \int _{t_0}^{t_0+T}\frac{\hbox {d}}{\hbox {d}t}{\mathscr {L}}\hbox {d}t = \int _{t_0}^{t_0+T}\left( I_\mathrm{r}{\dot{\phi }}{\ddot{\phi }}+I_\mathrm{r}{\dot{\phi }}{\dot{\omega }}-cu^2\right) \hbox {d}t\nonumber \\ \end{aligned}$$

(9)

where (6) and (7) are used to substitute for ${\dot{u}}$. Since $-\,I_\mathrm{r}{\ddot{\phi }} = A\sin {\varOmega t}$, the first integral $\int _{t_0}^{t_0+T}I_\mathrm{r}{\dot{\phi }}{\ddot{\phi }} \hbox {d}t$ on R.H.S of (9) vanishes. The second integral can be reduced through integration by parts to obtain

$$\begin{aligned} \int _{t_0}^{t_0+T}I_\mathrm{r}{\dot{\phi }}{\dot{\omega }}\hbox {d}t={\dot{\phi }}\omega \Big |_{t_0}^{t_0+T}-\int _{t_0}^{t_0+T}I_\mathrm{r}{\ddot{\phi }}\omega \hbox {d}t. \end{aligned}$$

The change in kinetic energy of the sleigh in one time period of actuation is

$$\begin{aligned} \int _{t_0}^{t_0+T}\frac{\hbox {d}}{\hbox {d}t}{\mathscr {L}}\hbox {d}t ={\dot{\phi }}\omega \Big |_{t_0}^{t_0+T}-\int _{t_0}^{t_0+T}(I_\mathrm{r}{\ddot{\phi }}\omega -cu^2)\hbox {d}t.\nonumber \\ \end{aligned}$$

(10)

Setting $t_0 = nT$ for $n \ge 1$, one can obtain a sequence, $\{\varDelta E_n\}$ of changes in the kinetic energy of the sleigh in each time period,

$$\begin{aligned} \varDelta E_n = \int _{nT}^{(n+1)T}\frac{\hbox {d}}{\hbox {d}t}{\mathscr {L}}\hbox {d}t. \end{aligned}$$

The sequence $\{\varDelta E_n\}$ is bounded since the total energy of the sleigh is bounded. By virtue of the Bolzano–Weierstrass theorem, the bounded sequence contains a convergent subsequence. The sequence $\{\varDelta E_n\}$ converges to zero if solutions to (6) and (7) converge to a limit cycle with frequency that is an integer multiple of the forcing frequency $\varOmega$. A sufficient condition for this is that the velocities are u and $\omega$ converge to periodic functions with frequencies that are integer multiples of the forcing frequency $\varOmega$, with appropriate time T-averages. The first term on the L.H.S of (10) vanishes since ${\dot{\phi }}(t_0)\omega (t_0) = {\dot{\phi }}(t_0+T)\omega (t_0+T)$. The next two terms on the L.H.S of (10) sum to zero if the time T-average of $I_\mathrm{r}{\ddot{\phi }}\omega -cu^2$ is zero. This follows from a basic result in analysis that a function f(t) is T-periodic if and only if

$$\begin{aligned} \int _{t_0}^{t_0+T}f(t)\hbox {d}t = {\overline{f}}T \end{aligned}$$

for any $t_0$, where ${\overline{f}}$ is time T-average of the function f. Therefore, a period-T limit cycle exists in the reduced velocity space if and only if the change in energy of the sleigh in a time interval T on the limit cycle is zero,

$$\begin{aligned} \varDelta E= -\int _{t_0}^{t_0+T}(I_\mathrm{r}{\ddot{\phi }}\omega -cu^2)\hbox {d}t = 0. \end{aligned}$$

(11)

3.3 Limit cycles in the reduced velocity space

Figure 3a–c shows the results of a simulation of (6)–(8) under input of the form $-\,I_\mathrm{r}{\ddot{\phi }}=A\sin (\varOmega t)$ and Fig. 3d shows the path of the sleigh in the $x-y$ plane obtained through the reconstruction equation (4)–(5).

Fig. 3

Simulation of chaplygin sleigh with $(u(0),\omega (0))=(0,0)$ with the input being $I_\mathrm{r}{\ddot{\phi }} = -2\sin {t}$, i.e., $A=2$ and $\varOmega =1$

We see from Fig. 3a–c that the velocities u and $\omega$ are T-periodic. The solutions to (6) and (7) converge to a limit cycle in the velocity space as shown in Fig. 4. The figure 8 shape of the limit cycle is due to the fact that the frequency of oscillations in u is double the frequency of oscillations in $\omega$ as shown in Fig. 3a, b. A similar phenomenon has been observed in the twistcar [31] under periodic input.

Fig. 4

Trajectory of the sleigh with $(u(0),\omega (0))=(0,0)$ (dashed line) and predicted limit cycle from harmonic balance method (solid line). The input is $I_\mathrm{r}{\ddot{\phi }} = -2\sin {t}$, i.e., $A=2$ and $\varOmega =1$

Figure 3d shows that sinusoidal motion of the rotor can cause the sleigh to exhibit serpentine motion. Furthermore, after the initial transient motion decays, the average heading of the sleigh remains constant, say $\theta _c$ with some fixed time T-average velocity $v_\mathrm{net}$. Let $(x(t_1),y(t_1))$ be a point on the path of the sleigh in the $x-y$ plane that is generated by the limit cycle in the reduced velocity space, then $v_\mathrm{net}$ is defined as

$$\begin{aligned} v_\mathrm{net}{=}\frac{1}{T}\sqrt{(x(t_1{+}T){-}x(t_1))^2{+}(y(t_1+T)-y(t_1))^2}.\nonumber \\ \end{aligned}$$

(12)

The average velocity $v_\mathrm{net}$ is the velocity which would actually be useful in developing motion planning for the sleigh under sinusoidal inputs.

In this paper, we address the problem of controlling $v_\mathrm{net}$ by choosing A. First, we employ the harmonic balance technique to show that given A the limit cycle can be accurately predicted. Then we take A to be an unknown and apply averaging to reduce the problem of controlling $v_\mathrm{net}$ to solving a nonlinear system of equations. We then employ the Newton–Raphson algorithm to solve the system and obtain A. Finally, we check the accuracy of our prediction with simulations.

4 Approximate solution of the limit cycle

An approximate solution to the limit cycle can be found using the harmonic balance method. Following this approach and motivated by the numerical simulation, 3 we will make the ansatz that u and $\omega$ are T-periodic functions The harmonic balance technique assumes the outputs of a system to be sinusoidal and attempts to use the equations of motion to predict the limiting trajectory. From the simulations, we see that only harmonics up to the second order appear in the velocities. We use this as motivation to neglect periodic terms with frequency greater than $2\varOmega$. Suppose that u and $\omega$ are of the form

$$\begin{aligned} u&=u_c+a_1 \sin {\varOmega t}+a_2 \cos {\varOmega t}\\&\quad +A_u \sin {2\varOmega t}+B_u \cos {2\varOmega t}\\ \omega&= A_w \sin {\varOmega t}+B_w \cos {\varOmega t} \\&\quad + b_1\sin {2\varOmega t}+b_2 \cos {2\varOmega t}. \end{aligned}$$

The angular velocity will assumed to periodic with zero mean since numerical simulations such as those shown in Fig. 4 indicate that limit cycles in the velocity space are symmetric about $\omega$ axis. The assumed form of u and $\omega$ will be substituted into (6) and (7). In applying the harmonic balance approach, we will substitute our assumed solutions into the equations of motion and equate coefficients on both sides. Consider ${\dot{u}}$, substituting the assumed periodic form into (6) and (7),

$$\begin{aligned} \begin{aligned} {\dot{u}}&=A_w^2bm+B_w^2bm-2cu_c-\frac{c}{m}(a_1 \sin {\varOmega t}\\&\quad +a_2 \cos {\varOmega t})\\&\quad +(2A_w B_wb-2A_u c)\sin {2\varOmega t}\\&\quad +(-A_w^2bm+b_w^2bm-2B_u c)\cos {2\varOmega t}\ldots \end{aligned}\\ \end{aligned}$$

A direct differentiation of the assumed periodic form of u yields

$$\begin{aligned} {\dot{u}}&=-\varOmega a_2 \sin {\varOmega t}+\varOmega a_1 \cos {\varOmega t}\\&\quad -2\varOmega A_u \sin {2\varOmega t}+2\varOmega A_w \cos {2\varOmega t}. \end{aligned}$$

Equating coefficients of $\sin {\varOmega t}$ and $\cos {\varOmega t}$, we get

$$\begin{aligned} -\varOmega a_2 = -\frac{c}{m} a_1,\quad \varOmega a_1 = -\frac{c}{m} a_2 \end{aligned}$$

which is only satisfied if $a_1=a_2=0$. Substituting the assumed periodic form of $\omega$ and u into the right-hand side of (7),

$$\begin{aligned} {\dot{\omega }}&=\frac{(-A_uB_wbm+A_wB_ubm-2A_ubmu_c+2A)}{mb^2+I+I_\mathrm{r}}\nonumber \\&\quad \sin (\varOmega t)\nonumber \\&\quad +\frac{(-A_uA_wbm-B_ub_2bm-2B_wbmu_c)}{mb^2+I+I_\mathrm{r}}\nonumber \\&\quad \cos (\varOmega t)\ldots \end{aligned}$$

(13)

The interesting thing to note is that no second-order harmonics appear in the (13). By equating coefficients of $\sin (2\varOmega t)$ and $\cos (2\varOmega t)$ with the derivative of our assumed $\omega$, we get simply

$$\begin{aligned} -\,2\varOmega b_3 = 0,\quad 2\varOmega b_4 = 0 \end{aligned}$$

or $b_3=b_4=0$. Therefore, the velocity u has only secondharmonics while the angular velocity, $\omega$ has only first harmonic,

$$\begin{aligned} u&=u_c+A_u \sin (2\varOmega t)+B_u \cos (2\varOmega t) \end{aligned}$$

(14)

$$\begin{aligned} \omega&= A_w \sin (\varOmega t)+B_w \cos (\varOmega t). \end{aligned}$$

(15)

In order for this solution to exist, it must satisfy (6)–(7). Substituting (14) and (15) into (6)–(7) and simplifying,

$$\begin{aligned} {\dot{u}}&=A_w^2bm+B_w^2bm-2cu_c\\&\quad +(2A_wB_wb-2A_u c)\sin (2\varOmega t)\\&\quad +(-A_w^2bm+B_w^2bm-2B_uc)\cos (2\varOmega t)\ldots \\ {\dot{\omega }}&=\frac{(-A_uB_wbm+A_wB_ubm-2A_wbmu_c+2A)}{mb^2+I+I_\mathrm{r}}\\&\quad \sin (\varOmega t)\\&\quad +\frac{(-A_uA_wbm-B_uB_wbm-2B_wbmu_c)}{mb^2+I+I_\mathrm{r}}\\&\quad \cos (\varOmega t)\ldots \end{aligned}$$

The higher harmonics are neglected as part of the harmonic balance method. We will later justify this assumption with numerical results. A direct differentiation of (14) and (15) gives

$$\begin{aligned} {\dot{u}}&=-\,2\varOmega B_u \sin (2\varOmega t)+2\varOmega A_u \cos (2\varOmega t) \\ {\dot{\omega }}&= -\,\varOmega B_w \sin (\varOmega t)+\varOmega A_w \cos (\varOmega t). \end{aligned}$$

To determine $u_c$ and the coefficients $A_u$, $B_u$, $A_w$ and $B_w$, we simply equate the coefficients of the above two systems. This yields the following system of nonlinear equations

$$\begin{aligned} 0&=A_w^2bm+B_w^2bm-2cu_c \end{aligned}$$

(16a)

$$\begin{aligned} -\,4m\varOmega B_u&=2A_wB_wbm-2A_u c \end{aligned}$$

(16b)

$$\begin{aligned} 4m\varOmega A_u&=-A_w^2bm+B_w^2bm-2B_uc \end{aligned}$$

(16c)

$$\begin{aligned} -\,2\alpha \varOmega B_w&=-A_uB_wbm+A_wB_ubm\nonumber \\&\quad -2A_wbmu_c+2A \end{aligned}$$

(16d)

$$\begin{aligned} 2\alpha \varOmega A_w&=-A_uA_wbm-B_uB_wbm-2B_wbmu_c. \end{aligned}$$

(16e)

where we denote $\alpha =mb^2+I+I_\mathrm{r}$ to keep the notation compact. We employ the Newton–Raphson method to solve the equations (16) numerically.

To illustrate the calculation of the coefficients, we choose the sleigh parameters and the input, ${\ddot{\phi }}$ to be the same as the parameters for the simulation in Fig. 4. Performing the calculations yields $u_c = 0.6341$, $A_u=0.1103$, $B_u =0.1071$, $A_w =0.2069$ and $B_w = -0.7689$ after just 4 iterations of the Newton–Raphson method. To compare this solution with the numerical simulation, we may define $C_u=\sqrt{A_u^2+B_u^2}$ and $C_w=\sqrt{A_w^2+B_w^2}$, which are the amplitudes of u and $\omega$, respectively. In a similar manner, we will define $C_u^*$ and $C_w^*$ to be the amplitude of u and $\omega$ on the limit cycle in the numerical simulation. This allows us to define the error between the limit cycle solution obtained through the harmonic balance method and the limit cycle solution obtained through a numerical simulation,

$$\begin{aligned} e = \sqrt{(u_c-u_c^*)^2+(C_u-C_u^*)^2+(C_w-C_w^*)^2}.\nonumber \\ \end{aligned}$$

(17)

The error was found to be $e=8.6e-3$ which is two orders of magnitude smaller than the values of the coefficient $(u_c, A_u, B_u, A_w, B_w)$. In Fig. 4, we can see further agreement between the analytical solution of the limit cycle and one obtained through direct numerics. The dotted graph shows a trajectory with generic initial values of $(u,\omega )$ converging to the analytically predicted limit cycle (solid line).

Recall the expression for the change in the kinetic energy of the sleigh over time period (10). By substituting (14) and (15) into (11), we get

$$\begin{aligned} \varDelta E = AA_w-c(A_u^2+B_u^2+2u_c^2) = 0. \end{aligned}$$

(18)

Recall that the harmonic balance approximation satisfies (16a-e). We can take the following combinations: Suppose we denote by $X_1$ and $X_2$ the following expressions,

$$\begin{aligned} X_1&=(\hbox {R.H.S}(16b)A_u+(\hbox {R.H.S}(16c)B_u=0\\ X_2&=(\hbox {R.H.S}16dA_u+(\hbox {R.H.S}16eB_u=0, \end{aligned}$$

then

$$\begin{aligned} \frac{1}{2}(X_1 {+} X_2) = 0{=}AA_w-c(A_u^2+B_u^2+2u_c^2)= \varDelta E.\nonumber \\ \end{aligned}$$

(19)

which matches with (18). This confirms that the solution of the limit cycle obtained through the harmonic balance approach is such that the time T-average of the energy of the sleigh on the limit cycle is constant.

5 Feedforward velocity control of the sleigh

The harmonic balance method can be used to determine the input, $I_\mathrm{r}{\ddot{\phi }} = -\,A \sin {\varOmega t}$ required for the sleigh to move at a prescribed $v_\mathrm{net}$ or average velocity. This is equivalent to controlling the velocity of the sleigh to lie on a chosen limit cycle in the reduced velocity space. The asymptotic angle $\theta _c$ is due to the transient phase of the motion, and it is not predicted by the Harmonic balance approach. However, special cases can treated and in this section we develop a technique for controlling $v_\mathrm{net}$.

5.1 Average velocity of the sleigh

We first derive an expression for the average velocity of the sleigh, when its longitudinal velocity and angular velocity lie on a limit cycle. We will choose the input control parameter to be the amplitude of the torque on the rotor, A, and leave the input frequency $\varOmega$ constant. Equations (6) and (7) are independent of $\theta$, so the eventual value of the heading does not influence the average speed of the sleigh. Therefore, in calculating $v_\mathrm{net}$ we may set $\theta _c=0$. This simplifies $v_\mathrm{net}$ (23) to

$$\begin{aligned} v_\mathrm{net} = \frac{1}{T}(x(t_1+T)-x(t_1)) = \frac{1}{T}\int _{t_1}^{t_1+T} {\dot{x}}\hbox {d}t. \end{aligned}$$

(20)

This average velocity can then be put in terms of u and $\omega$ using (4)

$$\begin{aligned} v_\mathrm{net} = \frac{1}{T}\int _{t_1}^{t_1+T} ( u \cos {\theta } - \omega b\sin {\theta })\hbox {d}t. \end{aligned}$$

(21)

Without any loss of generality, we may choose $t_1=0$. We can simplify the second of the integrals on the right-hand side of (21),

$$\begin{aligned} \frac{1}{T}\int _{0}^{T}\omega b\sin {\theta }\hbox {d}t&= -\frac{b}{T}\int _{\theta (0)}^{\theta (T)}\sin {\theta }\hbox {d}\theta \nonumber \\&=\frac{b}{T}(\cos (\theta (T))-\cos (\theta (0)). \end{aligned}$$

(22)

where used $\omega \hbox {d}t = \hbox {d}\theta$ to change the variable of integration.

We will now use (14) and (15) to compute the integrals in (21) and (22). Furthermore, we can also obtain $\theta (T)$ through such a substitution

$$\begin{aligned} \theta (T) = \theta (0) + \int _0^T\omega \hbox {d}t = \theta (0). \end{aligned}$$

This follows from the fact that $\omega$ is periodic with zero mean. The average velocity $v_\mathrm{net}$ is then

$$\begin{aligned} v_\mathrm{net} = \frac{1}{T}\int _{0}^{T}u(t) \cos (\theta (t))\hbox {d}t. \end{aligned}$$

(23)

5.2 Feedforward velocity control

The integral leftover in (23) cannot be evaluated analytically, since a substitution of the expression for $\theta$ leads to terms such as $\cos (\sin {\varOmega t})$ in the integrand. This integral will therefore be computed numerically in an iterative manner. Considering the amplitude of the input torque on the rotor, A to be an unknown (23) together with (16) form a system of 6 equations and 6 unknowns in A and the variables $(u_c,A_u,B_u,A_w,B_w)$. Solving this system for some desired $v_\mathrm{net}$ and finding the A required will allow us to control the velocity of the sleigh. In order to solve the system of six equations, we once again employ the Newton–Raphson algorithm.

To illustrate this process, suppose we want the sleigh to be on a limit cycle such that $v_\mathrm{net}=0.2$. Solving system (23), (16) yields the solution $(u_c,A_u,B_u,A_w,B_w,A) = (0.2106,0.0466,0.0208,-\,0.0400,0.4571,-\,1.1403)$ after 9 iterations of the Newton Raphson algorithm. This means that we must choose $A=-1.1403$ to get a translational speed of $v_\mathrm{net}=0.2$.

The error in $v_\mathrm{net}$ between the calculation (23) that relies on the harmonic balance approach with respect to the value obtained from a direct numerical simulation, can be quantified as

$$\begin{aligned} e_v = ||v_\mathrm{net}-v_{net}^*|| \end{aligned}$$

(24)

where $v_\mathrm{net}^*$ is the average velocity of the sleigh found from the simulation using (20). The results of the simulation of the motion of the sleigh due to the chosen input, $A=-1.1403$ and $\varOmega =1$ are shown in Fig. 5. The velocity u of the rear wheel/knife edge is a periodic function with a nonzero mean, while the angular velocity of the sleigh is a periodic function with zero mean. The heading angle of the sleigh, $\theta$, is also periodic with a nonzero mean, which is the average heading of the sleigh.

Fig. 5

Simulation of Chaplygin sleigh with $(u(0),\omega (0))=(0,0)$. The input is torque has amplitude $A=-\,1.1403$ and frequency $\varOmega =1$

The actual net translational velocity was found to converge to $v_\mathrm{net}^*=0.20049$, while our control algorithm gave a $v_\mathrm{net} = 0.2$ with an error of $4.9\times 10^{-4}$. A plot of the error against $t_2$ can be seen in Fig. 6. The error is large initially, when $u(t), \omega (t)$ are far from the limit cycle. As these velocities converge to the limit cycle, $\limsup e_v(t) \rightarrow 0$.

Fig. 6

Error in $v_\mathrm{net}$ for the Chaplygin sleigh with $(u(0),\omega (0))=(0,0)$. The input is torque has amplitude $A=-1.1403$ and frequency $\varOmega =1$

6 Simultaneous control of $v_\mathrm{net}$ and $\theta _c$

The average orientation of the sleigh $\theta _c$ is due to the transient phase of motion, when the angular velocity of the sleigh is far from being a periodic function. This means that we cannot use the harmonic balance approach to determine the average heading. It is also possible that in practice the average orientation of the sleigh would not remain constant due to unaccounted-for dynamic effects and disturbances. This motivates the use of feedback to control the heading of the sleigh.

6.1 Integral control of the average heading angle

Since the velocities $(u,\omega )$ of the sleigh converge to a limit cycle, we wish to use a controller that does not depend on the immediate state. The steady feedforward sinusoidal input takes care of the fast dynamics. For this reason, we define our error in terms of an integral over one time period (25). By defining the feedback error in this way, we ensure that the integral control remains close to zero once the sleigh is on the limit cycle and has achieved its desired orientation $\theta _\mathrm{r}$.

$$\begin{aligned} e_{\theta }(t) = \int _{t-T}^{t}(\theta (t)-\theta _\mathrm{r}) \hbox {d}t. \end{aligned}$$

(25)

This allows us to add a feedback term $T_I = -K_I e_{\theta }$ to the torque which accounts for deviations from the reference angle $\theta _\mathrm{r}$. The input torque becomes

$$\begin{aligned} -I_\mathrm{r}{\ddot{\phi }}=A\sin (\varOmega t)+T_I \end{aligned}$$

(26)

where the first term, designed through harmonic balance method, generates forward motion. The second term adjusts the heading angle of the sleigh. As the trajectory approaches the limit cycle in the reduced velocity space with the desired orientation, the second term in (26) converges to zero.

6.2 Simulation

We demonstrate the ability of the proposed control law to steer the sleigh with results of a simulation. The sleigh will be required to track $v_\mathrm{net} = 0.2$, while first having an average heading of $\theta = 0$ and later making a turn to $\theta = \frac{\pi }{2}$ still tracking $v_\mathrm{net} = 0.2$. The reference angle is

$$\begin{aligned} \theta _\mathrm{r} = {\left\{ \begin{array}{ll} 0 &{} t< 150 \\ \frac{\pi }{2} &{} t\ge 150 . \end{array}\right. } \end{aligned}$$

Fig. 7

Simulation of the chaplygin sleigh tracking a turn with $(u(0),\omega (0))=(0,0)$. The sleigh first tracks a reference of $\theta _\mathrm{r}=0$, and then at $t=150 s$ the control objective is changed to $\theta _\mathrm{r}=\frac{\pi }{2}$. The integral control parameter is $K_I=0.003$

The results of the simulation of the sleigh completing this maneuver are in Fig. 7. From Fig. 7a, c we see that the sleigh acquires a large heading angle from the initial swing of the rotor; however, the integral control quickly begins to correct for it and the sleigh’s average heading converges to zero. After $t=150$, the sleigh begins to turn, ultimately changing its average heading by 90$^{\circ }$. The overshoot and settling time depend on the integral control parameter $K_I$. In this case, it takes approximately 90 s for error in the average heading angle to become negligible. Simultaneously, a constant amplitude sinusoidal torque is applied determined from harmonic balance method that ensures that the average speed of the sleigh converges to $v_\mathrm{net}=0.2$, as seen in Fig. 7b. The graph of $T_I$ is shown in Fig. 8a, and the graph of the total input torque is shown in Fig. 8b. The input torque, $T_I$, to steer the sleigh is small compared to the torque required to propel the sleigh forward. The sleigh with average straight line motion can therefore be easily steered by small changes to the total input torque.

Fig. 8

Required input for turning simulation. Input due to integral control is shown in (a) and total input in (b)

We see that the input required to drive $\theta _c$ is small compared to the input we are already applying to propel the sleigh. We also see in Fig. 8a that the input due to the integral control goes to zero during both stages of motion as we hoped.

7 Effect of forcing amplitude and frequency on motion

The motion of the sleigh due to changes in the amplitude and frequency of oscillation of the rotor shows a rich variety of dynamics. The effect of variations in the forcing amplitude A and the frequency $\varOmega$ on the average longitudinal velocity $u_0$ of the knife edge and hence the average velocity $v_\mathrm{net}$ of the sleigh is shown in 9.

Fig. 9

Velocity of the sleigh for different inputs. a shows $u_0$ and b shows $v_\mathrm{net}$ for amplitudes of up to 40 and values of $\varOmega$ up to 20

The average longitudinal velocity of the wheel $u_0$ only increases with amplitude and shows little variation with respect to the forcing frequency $\varOmega$ at low amplitudes. This means that the instantaneous speed of the sleigh along its path is higher for higher-amplitude input. The average velocity of the sleigh in the plane $v_\mathrm{net}$ appears to reach a local maximum and then decreases to zero before increasing again for higher amplitudes.

Fig. 10

Velocity of the sleigh for different amplitudes. a shows $u_0$ and b shows $v_\mathrm{net}$ for amplitudes of up to 1000 with $\varOmega$ set to 15.5

Figure 10 shows a plot of $u_0$ and $v_\mathrm{net}$ for a fixed $\varOmega$ and a large range of amplitudes. We note that although $u_0$ monotonically increases with A, $v_\mathrm{net}$ can decrease or increase.

Fig. 11

Trajectories of the sleigh for four different values of A with $\varOmega =1$. Each starts with $(u,\omega )=(0,0)$. Each trajectory is shown for $t>4T$ allowing for the velocities u and $\omega$ to converge to the limit cycle. The trajectories for the transient phase are not shown

Figure 11 shows the transitions in steady paths of the sleigh in $x-y$ plane as A increases. These are the paths of the sleigh when the velocities u and $\omega$ are on or very close to the limit cycle in the reduced velocity space. The net displacement of the sleigh in a time period T shrinks, with the path curving back onto itself, as illustrated in the paths for $A=5$ and $A=10$. As A increases further, path of the sleigh forms a closed loop at $A \approx 16.82$. This is when $v_\mathrm{net}$ converges to zero for the first time. As A increases further, $v_\mathrm{net}$ becomes nonzero again and the figure eight path breaks open to produce a net displacement, as shown for $A=20$. Larger values of A lead to the path increasingly close onto itself, eventually leading to another closed path for $A\approx 175.4$ as shown in Fig. 12b.

Fig. 12

Simulations of the chaplygin sleigh executing a closed trajectory in the (x, y) plane. Input parameters are $\varOmega = 1$ and a $A=16.82$, b $A=175.4$

8 Conclusion and discussion

The motion of the Chaplygin sleigh under the effect of viscous dissipation and periodic forcing exhibits a stable limit cycle in the reduced velocity space. We find an analytical approximation for the limit cycle solution with the use of the harmonic balance method. Furthermore, we use the harmonic balance method to control the average velocity of the sleigh by using the amplitude of the rotor’s motion as a control input. We also show that the heading of the sleigh could be controlled simultaneously using integral control. The utility of the proposed approach was demonstrated through simulations.

The analysis of the limit cycles of the Chaplygin sleigh in this paper opens the possibility that other mixed-dynamic nonholonomic systems that are subject to viscous friction in the allowable directions of motion also have stable limit cycles in their reduced velocity or nonholonomic momentum space when subjected to periodic forcing. The algorithm to control to the average velocity and heading can then be useful in the motion planning for other nonholonomic systems and robots based on them.