Analysis of Underactuated Dynamic Locomotion Systems Using Perturbation Expansion: The Twistcar Toy Example

Abstract

Underactuated robotic locomotion systems are commonly represented by nonholonomic constraints where in mixed systems, these constraints are also combined with momentum evolution equations. Such systems have been analyzed in the literature by exploiting symmetries and utilizing advanced geometric methods. These works typically assume that the shape variables are directly controlled, and obtain the system’s solutions only via numerical integration. In this work, we demonstrate utilization of the perturbation expansion method for analyzing a model example of mixed locomotion system—the twistcar toy vehicle, which is a variant of the well-studied roller-racer model. The system is investigated by assuming small-amplitude oscillatory inputs of either steering angle (kinematic) or steering torque (mechanical), and explicit expansions for the system’s solutions under both types of actuation are obtained. These expressions enable analyzing the dependence of the system’s dynamic behavior on the vehicle’s structural parameters and actuation type. In particular, we study the reversal in direction of motion under steering angle oscillations about the unfolded configuration, as well as influence of the choice of actuation type on convergence properties of the motion. Some of the findings are demonstrated qualitatively by reporting preliminary motion experiments with a modular robotic prototype of the vehicle.

1 Introduction

Underactuated systems whose dynamics is governed by nonholonomic constraints have been a subject of extensive research for several decades (Bloch 2003; Bloch et al. 2005; Neimark and Fufaev 2004). While the earliest example of a nonholonomic system is the classical Chaplygin’s sleigh (Stanchenko 1989), other typical examples of such systems are wheeled toy vehicles such as snakeboard (Ostrowski et al 1994), roller racer (Krishnaprasad and Tsakiris 2001; Ostrowski et al. 1995; Zenkov et al. 1998; Bullo and Žefran 2002) and more (Chitta et al. 2005; Chitta and Kumar 2003; Kelly et al. 2012; Dear et al, 2013). In addition, the dynamics of simple models of swimming robots also share a similar structure, particularly microswimmers governed solely by viscous drag effects (Shapere and Wilczek 1989; Hatton and Choset 2013; Gutman and Or 2016), as well as the opposite physical extreme of large robots performing inertia-dominated swimming in “perfect” (inviscid) fluid (Kanso et al. 2005; Melli et al. 2006).

In the literature on robotic locomotion (Kelly and Murray 1995; Ostrowski and Burdick 1998), many works have analyzed various locomotion systems subject to nonholonomic constraints, studying aspects such as nonlinear controllability and gait generation. One simple subclass of locomotion systems is principal kinematic systems (Shammas et al. 2007), whose motion is time-invariant and depends only on geometric trajectories of shape variables (e.g. joint angles). On the other hand, the snakeboard and roller-racer examples belong to the more general class of mixed systems, where the motion is dynamic and governed also by momentum evolution in time. In a majority of previous works, it has been assumed that the controlled inputs are shape variables, which can be prescribed directly or via closed-loop feedback control in order to follow periodic trajectories (gaits). On the other hand, there are many practical cases where the controlled actuation is mechanical, i.e. forces or torques. For example, robotic microswimmers are often actuated by applying a time-varying external magnetic field which generates torques on magnetized parts of the swimmer (Dreyfus et al. 2005; Gutman and Or 2014). Moreover, many systems do not employ closed-loop control due to practical limitations and apply open-loop oscillatory inputs instead (Vela et al. 2002).

In order to analyze locomotion systems under oscillatory inputs, Vela and Burdick (2003a), Vela and Burdick (2003b) developed an averaging theory for studying asymptotic solutions while assuming small-amplitude inputs. This theory utilizes separation of scales in the system’s solution into fast oscillatory dynamics and slow ’averaged’ dynamics. While this technique seems fairly general, it has been applied in Vela and Burdick (2003a), Vela and Burdick (2003b) mainly for studying controllability and feedback stabilization of locomotion systems, where the controlled inputs were again limited to shape variables, i.e. kinematic actuation. Another asymptotic method which has recently been employed for locomotion dynamics, and to microswimmers in particular Gutman and Or (2014), Wiezel and Or (2016), is perturbation expansion (Nayfeh 2008). The main advantage of this method is that it results in explicit expressions for the system’s approximate solution under small-amplitude inputs, in contrast to other works in which solutions of the nonlinear equations of motion could only be obtained via numerical integration. The explicit expressions obtained from perturbation expansion enable analyzing dependence of the system’s dynamic behavior on structural parameters and can also be utilized for optimizing the system’s performance. To best of our knowledge, the perturbation expansion method has not yet been applied to mixed locomotion systems governed by nonholonomic constraints combined with momentum evolution.

Fig. 1

a The twistcar toy vehicle, and b its planar two-link model

The goal of this work is to demonstrate the utility of perturbation expansion method for analysis of mixed locomotion systems, by providing a detailed investigation of a particular example problem—the twistcar, which is a popular children’s toy vehicle shown in Fig. 1a. The twistcar has two axles of passive wheels and its only actuation is through cyclic oscillations of the steering handlebar, which makes it a highly underactuated system. Nonholonomic constraints are induced by the assumption that the wheels cannot slip sideways along the directions of their axles. We consider oscillatory inputs of either steering handlebar angle (kinematic) or the applied steering torque (mechanical). Perturbation expansion method is used in order to obtain explicit solutions under small amplitude approximation. It is shown that the cases of steering angle input and torque inputs differ fundamentally in terms of convergence or divergence of the vehicle’s orientation angle. The latter case is further analyzed by obtaining the averaged solution which evolves on a slower time scale. Moreover, we show that changing the vehicle’s structural parameters can have a drastic effect on the dynamics, and may even result in reversal of the direction of the vehicle’s net motion.

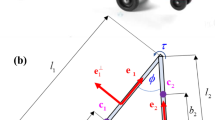
The simple planar model of the twistcar, shown in Fig. 1b, is in fact very similar to the roller-racer model, which has been studied extensively in the literature on nonholonomic mechanics (Krishnaprasad and Tsakiris 2001; Ostrowski et al. 1995; Zenkov et al. 1998; Bullo and Žefran 2002). The main difference between the two models is the fact that in the twistcar (TC), the relative angle of the steering link oscillates about $\phi =0$ whereas in the roller-racer (RR) the link is “unfolded” and oscillates about $\phi =\pi$. The works (Krishnaprasad and Tsakiris 2001; Ostrowski et al. 1995; Zenkov et al. 1998; Bullo and Žefran 2002) have made two additional simplifying assumptions on the roller-racer model, which are questionable: first, they assumed that the steering link has zero mass and nonzero moment of inertia, which is unphysical. Second, they assumed that the center-of-mass of the body link is located on the back axle (i.e. $l_{1}=0$ in Fig. 1b), while in reality this may result in tendency of the vehicle to tip over. Like many other works on robotic locomotion systems, Krishnaprasad and Tsakiris (2001), Ostrowski et al. (1995), Zenkov et al. (1998), Bullo and Žefran (2002) also assumed that the actuation input is the steering angle $\phi ({t})$ rather than the applied steering torque $\tau {(t)}$. All these assumptions are relaxed in our present study. Furthermore, in order to make our analysis accessible to a broader audience of the robotics research community, we chose not to use advanced notions of geometric mechanics such as Lie groups and Riemannian geometry as in previous works. Instead, the results are presented using elementary terminology of linear algebra, vector calculus, and ordinary differential equations.

The organization of the paper is as follows. The next section introduces the problem statement and notation, formulates the equation of motion, and presents numerical simulation results that demonstrate interesting phenomena in the system’s dynamic behavior. Section 3 introduces asymptotic analysis of the system via perturbation expansion method under small-amplitude inputs of either steering angle or torque, and also analyzes the system’s averaged dynamics in the latter case. Closed-form expressions for the solution are obtained, and their analysis explains the phenomena observed via numerical simulations. Section 4 reports preliminary motion experiments on a robotic prototype, that qualitatively demonstrate some of the theoretical results. The closing section contains a concluding discussion of the results, their limitations, and outlook for future extensions of the research.

2 Problem Formulation, Numerical Simulations and Reduced Equations

We now introduce the twistcar model, formulate its dynamic equations, and show some simulation examples. The planar two-link model of the twistcar is shown in Fig. 1b. For simplicity, it is assumed that the mass of the steering link is negligible and both links have zero moment of inertia. The body link is thus represented by a mass m concentrated at a point p which is located at a distance of $l_{1}$ from the rear axle.

2.1 Constrained Equations of Motion

The generalized coordinates that describe the vehicle’s motion are chosen as the vector $\mathbf{q}=(x, y, \theta , \phi )^{\mathrm{T}}$, where x, y denote the position of p, $\theta$ is the orientation angle of the body link, and $\phi$ is the steering joint’s relative angle. Components of the velocity of p expressed in the body-fixed frame $(x^{\prime },y^{\prime })$ in Fig. 1b are defined as

$$\begin{aligned} \left( {{\begin{array}{c} {v_x } \\ {v_y } \\ \end{array} }} \right) =\left( {{\begin{array}{c@{\quad }c} {\cos \theta }&{} {-\sin \theta } \\ {\sin \theta }&{} {\cos \theta } \\ \end{array} }} \right) \left( {{\begin{array}{c} {{\dot{x}}} \\ {{\dot{y}}} \\ \end{array} }} \right) \end{aligned}$$

(1)

A key factor in the vehicle’s motion is the inability of the two pairs of passive wheels on the axles to slip sideways. This imposes limitations on the feasible velocities $\dot{\mathbf{q}}$ which are manifested by the two nonholonomic constraints:

$$\begin{aligned} \mathbf{W}(\mathbf{q}){\dot{\mathbf{q}}}= & {} 0,\,\,\,\hbox {where} \nonumber \\ \mathbf{W}(\mathbf{q})= & {} \left( {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {\sin \theta } &{} {-\cos \theta } &{} {l_1 } &{} 0 \\ {\sin (\theta +\phi )} &{} {-\cos (\theta +\phi )} &{} {l_3 -l_2 \cos \phi } &{} {l_3 } \\ \end{array} }} \right) \end{aligned}$$

(2)

The dynamic equations of motion can then be obtained using constrained Lagrange’s equations (cf Murray et al. 1994) as:

$$\begin{aligned} \mathbf{M}{\ddot{\mathbf{q}}}= & {} \mathbf{E}\tau +\mathbf{W}(\mathbf{q})^{\mathrm{T}}{\varvec{\Lambda }}, \hbox { where } \nonumber \\ \mathbf{M}= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} m &{} 0 &{} 0 &{} 0 \\ 0 &{} m &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} }} \right] , \quad \mathbf{E}=\left[ {{\begin{array}{l} 0 \\ 0 \\ 0 \\ 1 \\ \end{array} }} \right] , \end{aligned}$$

(3)

and ${\varvec{\Lambda }}=(\lambda _{1}, \lambda _{2})^{\mathrm{T} }$ is the vector of Lagrange’s multipliers representing the generalized constraint forces. Note that the matrix of inertia M in (3) is singular due to our assumptions of massless steering link, hence the accelerations $\ddot{\mathbf{q}}$ cannot be obtained directly from (3). Differentiation of the nonholonomic constraints (2) with respect to time yields:

$$\begin{aligned} \mathbf{W}(\mathbf{q}){\ddot{\mathbf{q}}}+{\dot{\mathbf{W}}}(\mathbf{q},{ \dot{\mathbf{q}}}){\dot{\mathbf{q}}}=0. \end{aligned}$$

(4)

Combining Eqs. (3) and (4), one obtains the final equations of motion as a linear system:

$$\begin{aligned} \left( {{\begin{array}{c@{\quad }c} \mathbf{M}&{} {-\mathbf{W}^{T}} \\ \mathbf{W}&{} 0 \\ \end{array} }} \right) \left( {{\begin{array}{c} {\ddot{\mathbf{q}}} \\ {\varvec{\Lambda }} \\ \end{array} }} \right) =\left( {{\begin{array}{c} {\mathbf{E}{{{\tau }}}} \\ {-\dot{\mathbf{W}}\dot{\mathbf{q}}} \\ \end{array} }} \right) \end{aligned}$$

Importantly, this 6$\,\times \,$6 linear system has full rank in spite of the singularity of M. Defining the state vector $\mathbf{x}=(\mathbf{q},{\dot{\mathbf{q}}})$, the procedure described above yields a state equation of the form $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x},t)$, where the steering torque $\tau ({t})$ is considered as a given controlled input. In case where the steering angle $\phi ({t})$ is the controlled input, one has to rearrange the linear system formed by (3) and (4) so that $\tau ({t})$ is an unknown to be solved while the acceleration ${\ddot{\phi }}{(t)}$ is known.

2.2 Numerical Simulation Results

In order to motivate the explicit asymptotic analysis of the system, we now present some simulations results where the system’s nonlinear equations of motion are numerically integrated using ode45 command of MATLAB. Nominal values for the parameters are chosen as $m=30\,\hbox {kg}$, $l_{1}=l_{2}=0.5\,\hbox {m}$, $l_{3}=0.2\,\hbox {m}$. A movie with animations of all numerical simulations appears in the multimedia extension.

First, the case of steering angle actuation is considered, with the given harmonic input $\phi {(t)}=0.6\hbox {sin(t)}$ in radians, under initial conditions of $\mathbf{q}(0)=0~\hbox {and}~{\dot{x}}(0)=0$ while the initial values of ${\dot{y}}(0),{{\dot{\theta }}}(0)$ are enforced by the constraints (2). Figure 2a, b plot the body angle $\theta {(t)}$ and the forward speed $v_{x}{(t)}$, defined in (1). Figure 2c plots the trajectory of the point mass p in (x, y)-plane and snapshots of the vehicle at times $t=\{0,2\pi ,4\pi ,6\pi \}$. It can be seen that the vehicle accelerates forward but its body angle undergoes diverging oscillations that result in a diverging curve of motion trajectory of p. Interestingly, while $\theta {(t)}$ oscillates at the actuation frequency $\omega$, $v_{x}{(t)}$ appears to oscillate at twice the frequency, $2\omega$.

Fig. 2

Numerical simulation results of TC under harmonic input of steering angle: a forward speed $v_{x}{(t)}$, b body angle $\theta {(t)}$. c Motion trajectory of the point p and snapshots of the vehicle

Next, motion under the roller-racer configuration is simulated, where the steering angle input is given by $\phi {(t)}=\pi +0.6\hbox {sin}{(t)}$. Figure 3 shows the forward speed $v_{x}{(t)}$ under two different lengths of the steering link: nominal value of $l_{3}=0.2\,\hbox {m}$, and larger value of $l_{3}=0.6\,\hbox {m}$. Remarkably, the simulation results indicate a reversal in the direction of motion—a short steering link causes backward motion while a long steering link causes forward motion. The body angle $\theta {(t)}$, which is not shown, displays behavior of diverging oscillations, similar to the previous simulation results shown in Fig. 2b.

Fig. 3

Simulation results of speed $v_{x}{(t)}$ under RR configuration where $\phi {(t)}$ oscillates about $\pi$, for $l_{3}=0.2$ (solid) and $l_{3}=0.6$ (dashed)

The last simulated case is of torque actuation which is given by the harmonic input $\tau =\hbox {sin}{(t)}$ in Nm. Two initial values of the steering angle $\phi (0)$ were considered, 0 and $\pi$, which correspond to TC and RR configurations, respectively. All other coordinates are initially zero, as well as initial velocities $\dot{\mathbf{q}}(0)=0$. Figure 4a shows plots of the body angle $\theta {(t)}$ in solid line and steering angle $\phi {(t)}$ in dashed line, for $\phi (0)=0$. A noticeable difference from the previous case is the fact that both angles now undergo slowly decaying oscillations. This implies that the vehicle slowly converges toward motion along a straight line, as shown in the snapshots and trajectory of p in (x, y)-plane in Fig. 4b. The forward speed $v_{x}{(t)}$ is shown in Fig. 4c. It indicates that after an initial transient, the speed undergoes slowly decaying oscillations about mean acceleration. Under roller-racer initial condition of $\phi (0)=\pi$, the dotted line in Fig. 4a denotes the simulated solution of the steering angle $\phi {(t)}$. It can be seen that $\phi {(t)}$ rapidly diverges away from $\pi$ and converges toward oscillations about $2\pi$, i.e. the steering link flips back to TC configuration.

The main goal of this work is to analyze solutions of the system using perturbation expansion in order to explain the interesting phenomena observed in numerical simulations. As a preparatory step toward this analysis, the equations of motion are normalized and reduced, as discussed next.

2.3 Normalization and Reduction of the Dynamic Equations

First, the equations of motion are normalized by the total body length $l=l_{1}+l_{2}$, the mass m, and actuation frequency $\omega$, so that velocities, forces and torques are scaled by $l\omega$, ${ml}\omega ^{2}$ and ${ml}^{2}\omega ^{2}$, respectively. Additionally, two nondimensional parameters are defined as $\alpha = l_{3}/l$ and $\beta =l_{1}/l$. For convenience, we keep the same notation unchanged for all nondimensional quantities, while velocities and accelerations are expressed with respect to the nondimensional time $\omega {t}$.

Fig. 4

Simulation results under harmonic torque input $\tau {(t)}$: a Angles $\theta {(t)}$ (solid) and $\phi {(t)}$ (dashed) for $\phi (0)=0$, and $\phi {(t)}$ for $\phi (0)=\pi$ (dotted). b Motion trajectory of point p and snapshots of the vehicle for $\phi (0)=0$. c Forward speed $v_{x}{(t)}$ for $\phi (0)=0$

Next, we exploit the invariance of the equations of motion with respect to rigid body motion of the vehicle (gauge symmetry, cf. Shapere and Wilczek 1989; Kelly and Murray 1995), and rewrite the dynamics in terms of a vector $\mathbf{v}_b =(v_x ,v_y ,{\dot{\theta }},{\dot{\phi }})^{\mathrm{T}}$. The nonholonomic constraints (2) in terms of $\mathbf{v}_{b}$ in their nondimensional form are given by

$$\begin{aligned} \mathbf{W}_b {(}\phi )\mathbf{v}_b =0,\,\,\hbox { where }{} \mathbf{W}_b (\phi {)}=\left( {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0&{} {-1}&{} \beta &{} 0 \\ {\sin \phi }&{} {-\cos \phi }&{} {\alpha -(1-\beta )\cos \phi }&{} \alpha \\ \end{array} }} \right) . \end{aligned}$$

(5)

The nondimensional equation of motion in terms of $\mathbf{v}_{b}$ is obtained from (3) by differentiating (1) with respect to time as

$$\begin{aligned}&\mathbf{M}_b \dot{\mathbf{v}}_b +\mathbf{B}_b (\mathbf{v}_b )=\mathbf{E}\tau +\mathbf{W}_b (\phi )^{\mathrm{T}}{\varvec{\Lambda }} , \quad \hbox {where} \nonumber \\&\mathbf{M}_b =\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} }} \right] \;,\; \mathbf{B}_b =\left[ {{\begin{array}{c} {-{\dot{\theta }}v_y } \\ {{\dot{\theta }}v_x } \\ 0 \\ 0 \\ \end{array} }} \right] . \end{aligned}$$

(6)

Combining (6) with the time-derivative of (5), i.e. $\mathbf{W}_b \dot{\mathbf{v}}_b +{\dot{\mathbf{W}}}_b \mathbf{v}_b =0$, yields a linear 6$\,\times \,$6 system in $\dot{\mathbf{v}}_b$ and ${\varvec{\Lambda }}$ as:

$$\begin{aligned} \left( {{\begin{array}{c@{\quad }c} {\mathbf{M}_b }&{} {\mathbf{W}_b^\mathrm{T} } \\ {\mathbf{W}_b }&{} 0 \\ \end{array} }} \right) \left( {{\begin{array}{c} {\dot{\mathbf{v}}_b } \\ {\varvec{\Lambda }} \\ \end{array} }} \right) =\left( {{\begin{array}{c} \mathbf{E} \\ 0 \\ \end{array} }} \right) \tau -\left( {{\begin{array}{c} {\mathbf{B}_b (\mathbf{v}_b )} \\ {{\dot{\mathbf{W}}}_b \mathbf{v}_b } \\ \end{array} }} \right) \end{aligned}$$

(7)

It can be shown that the determinant of the 6$\,\times \,$6 matrix in (7) is $\alpha ^{2}\beta ^{2}$, which gives another reason why the case of $\beta =0$, assumed in previous studies of this model, is unphysical. In case where the steering angle $\phi {(t)}$ is the controlled input, one has to swap the unknown $\tau {(t)}$ with ${\ddot{\phi }}{(t)}$, which amounts to simply interchanging the fourth column of the 6$\,\times \,$6 matrix with the column vector (E,0) in the right hand side of (7).

The last step of the reduction is the use of two permissible velocities v, u that automatically satisfy the nonholonomic constraint (5), which are defined by the relation:

$$\begin{aligned} \mathbf{v}_b= & {} \mathbf{w}_v (\phi )v+\mathbf{w}_u (\phi )u,\hbox { where} \nonumber \\ \mathbf{w}_v \left( \phi \right)= & {} \left( {{\begin{array}{c} {\cos \phi -\alpha } \\ {\beta \sin \phi } \\ {\sin \phi } \\ 0 \\ \end{array} }} \right) , \mathbf{w}_u \left( \phi \right) =\left( {{\begin{array}{c} {\alpha (\beta ^{2}+1)\sin \phi } \\ {\alpha \beta (\alpha -\cos \phi )} \\ {\alpha (\alpha -\cos \phi )} \\ {-(\alpha -\cos \phi )^{2}-(1+\beta ^{2})\sin ^{2}\phi } \\ \end{array} }} \right) . \end{aligned}$$

(8)

The two orthogonal vector fields $\mathbf{w}_{v}$ and $\mathbf{w}_{u}$ span the null-space of the constraint matrix $\mathbf{W}_{b}$ in (5). Moreover, $\mathbf{w}_{v}$ represents velocity field under constant steering angle $({\dot{\phi }}=0)$, i.e. motion of the vehicle along a circular arc. Substituting (8) into (6), one obtains the reduced equations of motion in their final form, as:

$$\begin{aligned} {\dot{v}}= & {} f\left( {v,u,\phi ,\tau } \right) \hbox {=}f_v (\phi )v^{2}+f_u (\phi )u^{2}+f_{uv} (\phi )uv+f_\tau (\phi )\tau \end{aligned}$$

(9)

$$\begin{aligned} {\dot{u}}= & {} g\left( {v,u,\phi ,\tau } \right) \hbox {=}g_v (\phi )v^{2}+g_u (\phi )u^{2}+g_{uv} (\phi )uv+g_\tau (\phi )\tau \end{aligned}$$

(10)

$$\begin{aligned} {\dot{\phi }}= & {} h(u,\phi )=h_u (\phi )u. \end{aligned}$$

(11)

The explicit expressions of the functions $f_{v}(\phi ), g_{u}(\phi )$ etc. in Eqs. (9–11), appear in Table 1. The three scalar ODEs (8)–(10) encapsulate all the dynamics of the twistcar, while the body velocities $\mathbf{v}_{b}$ can be obtained from (8), and the body motion can be obtained by integrating for $\theta {(t)}$ and then integrating (1) for x(t), y(t).

Table 1 Expressions in equations (9)–(12)

In case where the angle $\phi {(t)}$ is given as the controlled input, one can find u(t) and ${\dot{u}}({t})$ from (11) and then eliminate $\tau {(t)}$ from (10) into (9) in order to obtain a single linear time-varying ODE in the variable v(t) as:

$$\begin{aligned} {\dot{v}}=F\left( {\phi (t),{\dot{\phi }}(t)} \right) v+G\left( {\phi (t),{\dot{\phi }}(t),{\ddot{\phi }}(t)} \right) , \end{aligned}$$

(12)

where the functions F, G in (12) are also given in Table 1.

3 Perturbation Expansion Analysis

We now derive the leading-order solution of the dynamics in (9)–(11) or (12) by utilizing the method of perturbation expansion (Nayfeh 2008), assuming small-amplitude deviations from a nominal steering link angle of $\phi =0$ or $\phi =\pi$.

3.1 The Case of Steering Angle Oscillatory Input

It is first assumed that the steering angle is prescribed as

$$\begin{aligned} \phi {(t)}= \mathop {\phi }\nolimits _{0} +\, \varepsilon \hbox {sin}{(t)} \end{aligned}$$

(13)

where $\varepsilon \ll 1$ and $\phi _{0}=0$ or $\pi$ for TC or RR configuration, respectively. The variables u(t) and v(t) in (9–10) and body angle $\theta {(t)}$ are expanded into power series in $\varepsilon$ as:

$$\begin{aligned} \begin{array}{l} v(t)=v_0 (t)+\varepsilon v_1 (t)+{\varepsilon }^{2}v_2 (t)+{\varepsilon }^{3}v_3 (t)+\cdots \\ u(t)=u_0 (t)+\varepsilon u_1 (t)+{\varepsilon }^{2}u_2 (t)+{\varepsilon }^{3}u_3 (t)+\cdots \\ \theta (t)=\uptheta _0 (t)+\varepsilon \theta _1 (t)+\varepsilon ^{2}\theta _2 (t)+{\varepsilon }^{3}\theta _3 (t)+\cdots \\ \end{array} \end{aligned}$$

(14)

Then, the functions F and G in (12) are expanded into Taylor series in their arguments as

$$\begin{aligned} F\left( {\phi ,{\dot{\phi }}} \right)= & {} F\left( {0,0} \right) +\frac{1}{1!}\left( \phi \frac{\partial }{\partial \phi }+{\dot{\phi }}\frac{\partial }{\partial {\dot{\phi }}} \right) F\left( {\phi ,{\dot{\phi }}} \right) \nonumber \\&+\frac{1}{2!}\left( \phi \frac{\partial }{\partial \phi }+\dot{\phi }\frac{\partial }{\partial {\dot{\phi }}} \right) ^{2}F\left( {\phi ,{\dot{\phi }}} \right) +\cdots \\ G\left( {\phi ,{\dot{\phi }},{\ddot{\phi }}} \right)= & {} G\left( {0,0,0} \right) +\frac{1}{1!}\left( {\phi \frac{\partial }{\partial \phi }+{\dot{\phi }}\frac{\partial }{\partial {\dot{\phi }}}+\ddot{\phi }\frac{\partial }{\partial {\ddot{\phi }}}} \right) G\left( {\phi ,{\dot{\phi }},{\ddot{\phi }}} \right) \nonumber \\&+\,\frac{1}{2!}\left( {\phi \frac{\partial }{\partial \phi }+\dot{\phi }\frac{\partial }{\partial {\dot{\phi }}}+\ddot{\phi }\frac{\partial }{\partial {\ddot{\phi }}}} \right) ^{2}G\left( {\phi ,{\dot{\phi }},{\ddot{\phi }}} \right) +\cdots \nonumber \end{aligned}$$

(15)

where all the derivatives in (14) are evaluated at $\phi =\phi _{\mathrm{o}} , {\dot{\phi }}{=}{\ddot{\phi }}\hbox {=}0.$ The leading-order expressions for the forward speed $v_{\mathrm{x}}$ and orientation angle $\theta$ are summarized in the following proposition.

Proposition 1

Consider the twistcar model under oscillatory input of steering angle $\phi {(t)}$ as given in (13). Under initial condition of $v(0)=v_{0}$ for (12), the leading-order solution of (6) is given by:

$$\begin{aligned} v_x (t)= & {} (\sigma -\alpha )v_0 {+}\varepsilon ^{2}\left( {\frac{\beta (\sigma \alpha {-}\beta )}{4(\sigma {-}\alpha )}v_0 {+}\frac{\alpha \beta (\alpha {+}\sigma \beta )}{2(\sigma -\alpha )^{2}}t} \right. \nonumber \\&\left. {+\,\frac{\alpha \beta (\alpha -\sigma \beta )}{4(\sigma {-}\alpha )^{2}}\sin (2t){+}\frac{\beta (\beta {-}\sigma \alpha )}{4(\sigma {-}\alpha )}v_0 \cos (2t)} \right) {+}O(\varepsilon ^{3}) \end{aligned}$$

(16)

$$\begin{aligned} \theta {(t)}= & {} \varepsilon \left( {v_0 \sigma (1{-}\cos t){+}\frac{\alpha }{\sigma {-}\alpha }\sin (t)} \right) \nonumber \\&+\,\varepsilon ^{3}\left( {\frac{\sigma \left( {\alpha ^{2}{-}3\sigma \alpha \beta {+}\sigma \alpha {+}3\beta ^{2}{-}2} \right) }{8(\sigma {-}\alpha )^{2}}v_0 (\cos t-1)} \right. \nonumber \\&-\,\frac{\alpha (\sigma \alpha {-}5\sigma \alpha \beta {-}5\beta ^{2}+2\beta ^{2}{-}1)}{8(\sigma {-}\alpha )^{3}}\sin t-\,\frac{\alpha \left( {\sigma \alpha \beta -\sigma \alpha +\beta ^{2}-2\beta ^{2}+1} \right) }{24(\sigma -\alpha )^{3}}\sin (3t) \nonumber \\&\left. {-\,\frac{\sigma (\alpha ^{2}{-}3\sigma \alpha \beta +\sigma \alpha +3\beta ^{2}{-}2)}{72(\sigma {-}\alpha )^{2}}v_0 (1{-}\cos (3t))-\frac{\alpha \beta \left( {\sigma \alpha +\beta } \right) }{2(\sigma {-}\alpha )^{3}}t\cos t} \right) \nonumber \\&+\,O(\varepsilon ^{4}) , \end{aligned}$$

(17)

where $\sigma =1$ for $\phi _{0}$ = 0 and $\sigma =-1$ for $\phi _{0}=\pi$.

Proof

We first obtain the leading-order solution of v(t) by expanding (12). Substituting (13)– (15) into (12) and rearranging in $\varepsilon$-orders yields a series of differential equations for $v_{i}{(t)}$, which are solved iteratively. The zero-order equation is null, ${\dot{v}}_0 =0$, which implies that $v_{0}$ = constant, and so is $v_{1}$. The second-order part of (12) is given by:

$$\begin{aligned} {\dot{v}}_2 =\frac{(1{-}\sigma \alpha +\beta )(1{-}\beta )}{(\sigma -\alpha )^{2}}v_0 \sin t\cos t+\frac{\alpha (\alpha \beta +\sigma \beta ^{2}+\sigma )}{(\sigma -\alpha )^{3}}\cos ^{2}t-\frac{\sigma \alpha }{(\sigma -\alpha )^{3}}\sin ^{2}t. \end{aligned}$$

Integration then yields the leading-order expression for v:

$$\begin{aligned} v\left( t \right)= & {} v_0 +\varepsilon ^{2}\left( {\frac{\alpha \beta (\alpha +\sigma \beta )}{2(\sigma -\alpha )^{3}}t+\frac{\alpha (\alpha \beta +\sigma \beta ^{2}+2\sigma )}{4(\sigma -\alpha )^{3}}\sin (2t)} \right. \nonumber \\&\left. {+\,\frac{(\sigma \alpha -\beta -1)(1-\beta )}{4(\sigma -\alpha )^{2}}v_0 \left( {\cos (2t)-1} \right) } \right) +O\left( {\varepsilon ^{3}} \right) \end{aligned}$$

(18)

Next, expanding $1/h_{u}(\phi )$ in (11) as a Taylor series in $\phi$ and substituting (13), one obtains the expression for u(t) as

$$\begin{aligned} u(t)\hbox {=}-\varepsilon \frac{\cos t}{(\sigma -\alpha )^{2}}+{\varepsilon }^{3}\frac{(\beta ^{2}+\sigma \alpha )}{4(\sigma -\alpha )^{4}}\left( {\cos t-\cos (3t)} \right) +O({\varepsilon }^{4}) . \end{aligned}$$

(19)

For the forward speed $v_{{x}}$, the relation (8) implies that $v_{{x}}=(\cos \phi -\alpha )v+\upalpha (\beta ^{2}+1)u\sin \phi$. Expanding about $\phi =\phi _{0}$ and using (14) and (15), one obtains:

$$\begin{aligned} v_x (t){=}\left( \sigma -\frac{\varepsilon ^{2}\sigma \sin ^{2}t}{2}-\alpha \right) (v_0 +\varepsilon ^{2}v_2 (t))+\sigma \alpha (\beta ^{2}+1)\varepsilon ^{2}u_1 (t)\sin t+O(\varepsilon ^{3}). \end{aligned}$$

Substituting the expressions for $v_{2}$ and $u_{1}$ from (18) and (19) and rearranging, one obtains the expansion of $v_{{x}}{(t)}$ in (16).

For the angular velocity, the relation (8) implies that ${\dot{\theta }}=v\hbox {sin}\phi +u\alpha (\alpha -\cos \phi ).$ Expanding about $\phi =\phi _{0}$ and using (13) and (14), one obtains:

$$\begin{aligned} {\dot{\theta }}(t)= & {} \sigma \left( \varepsilon \sin t-\frac{\varepsilon ^{3}}{6}\sin ^{3}t\right) (v_0 +\varepsilon ^{2}v_2 (t))\\&+\,\alpha \left( \alpha -\sigma +\frac{\sigma \varepsilon ^{2}}{2}\sin ^{2}t\right) (\varepsilon u_1 (t)+\varepsilon ^{3}u_3 (t))+O(\varepsilon ^{3}). \end{aligned}$$

Substituting the expressions for $v_{2}$, $u_{1}$ and $u_{3}$ from (18) and (19) and integrating under zero initial conditions, the body angle $\theta (t)$ is then obtained as in (17). $\square$

The results in (16–17) explain the interesting observations from numerical simulations, as follows. First, (16) implies that the forward speed $v_{x}(t)$ undergoes oscillations in twice the actuation frequency while its mean value grows with constant rate a which is proportional to ${\varepsilon }^{2}$, given by:

$$\begin{aligned} a=\varepsilon ^{2}\frac{\alpha \beta (\alpha +\sigma \beta )}{2\left( {\sigma -\alpha } \right) ^{3}} . \end{aligned}$$

(20)

Second, in (17) we not only obtained the leading-order terms for the body angle $\theta {(t)}$, but also terms of $O({\varepsilon }^{3})$. The last term in (17) indicates that $\theta {(t)}$ undergoes oscillations whose amplitude slowly diverges as ${\varepsilon }^{3}t\cos (t)$.

Fig. 5

Comparison of simulation results (solid) and leading-order approximation (dashed) under harmonic input of steering angle $\phi {(t)}$: a Forward speed $v_{x}{(t)}$ and b body angle $\theta {(t)}$. c Log–log plot of mean forward acceleration as a function of amplitude $\varepsilon$

In order to demonstrate the validity of the small-amplitude approximate solution, Fig. 5a, b plot the solutions of $\theta {(t)}$ and $v_{x}{(t)}$, respectively, for $\phi _{0}=0$, $\alpha =0.2$, $\beta =0.5$ and $\varepsilon =0.5$, where the dashed curves denote leading-order expressions from (16) and (17) while the solid curves are obtained from numerical integration of (6). In order to test the scaling of the mean forward acceleration a in (20) as ${\varepsilon }^{2}$, simulations under a range of values of amplitudes $\varepsilon$ were performed, and the slope of the time-varying average of $v_{x}{(t)}$ was obtained using least-squares linear regression and plotted in solid curve on a log-log scale in Fig. 5c, while the dashed line represents the leading-order term in (20) which is proportional to ${\varepsilon }^{2}$. The results show good agreement for values up to $\varepsilon \approx 0.5$ rad (5% error). Note that the discrepancy between the approximate and numerical solutions is increasing with time t. This is because in theory, the perturbation expansion in (14) is valid as long as the terms $u_{\mathrm{i}}$, $v_{\mathrm{i}}, \theta _{\mathrm{i}}$ remain as small as O(1). Since both $v_{2}(t)$ and $\theta _{3}(t)$ contain (secular) terms that diverge linearly in time, the expansion is formally valid only for short times.

Next, we analyze the dependence of the mean forward acceleration a on the vehicle’s parameters. From (20), it can be seen that a vanishes for $\alpha =0$ or $\beta =0$. That is, using the assumption $\beta =0$ as in previous works (Krishnaprasad and Tsakiris 2001; Ostrowski et al. 1995; Zenkov et al. 1998; Bullo and Žefran 2002) implies that the leading-order acceleration is only of order ${\varepsilon }^{3}$. For oscillations about TC configuration $\phi _{0}=0$, substituting $\sigma =1$ into (20) reveals that $a>0$ for all $\beta >0$ and $0<\alpha <1$. On the other hand, in case of oscillations about RR configuration $\phi _{0}=\pi$, substituting $\sigma =-1$ into (20) reveals that the sign of a depends on the sign of $\alpha -\beta$, or physically the length difference $l_{3}-l_{1}$. In case where $l_{3}>l_{1}$ the vehicle accelerates forward $(a>0)$, whereas in the case where $l_{3}<l_{1}$ it accelerates backwards $(a<0)$. This is precisely the explanation to the direction reversal obtained in the simulation results in Fig. 3.

While for TC configuration $(\sigma =1)$ the mean acceleration a grows monotonically with $\alpha$ and $\beta$, for RR configuration $(\sigma =-1)$ it is natural to seek for optimal values of $\alpha$ and $\beta$ that maximize ${\vert }a{\vert }$. Substituting $\sigma =-1$ into (20) and using elementary calculus, it can be shown that a has no global extremum in both $\alpha$ and $\beta$ lying within the interval (0,1). Nevertheless, for a given value of $\alpha$, the optimal value for $\beta$ is $\beta ^{*}=\alpha /2$, which gives maximal forward acceleration. On the other hand, if the value of $\beta$ is given then the optimal value of $\alpha$ is $\alpha ^{*}=\beta /(\beta +2)$, which gives a minimum value for $a<0$, i.e. maximal backward acceleration. These optimal values can be incorporated into design considerations of the vehicle.

3.2 The Case of Steering Torque Oscillatory Input

It is now assumed that controlled input is the steering torque $\tau {(t)}$, whose (normalized) value is prescribed as

$$\begin{aligned} \tau {(t)}=\varepsilon \hbox {sin}{(t)}, \end{aligned}$$

(21)

where $\varepsilon \ll 1$. The following proposition gives the leading-order solution of the dynamic equations of motion.

Proposition 2

Consider the twistcar model under oscillatory input of steering torque $\tau \hbox {(t)}$ as given in (21). Under initial steering angle of $\phi (0)=\pi$, the RR configuration is unstable, and the angle $\phi {(t)}$ diverges away from $\pi$. Under initial condition of $\phi (0)=u(0)=0$ and $v(0)=v_{0}>0$, the steady-state solution of (9)–(11), after a decaying transient, is given to leading order as:

$$\begin{aligned} \phi \left( {t} \right)= & {} \varepsilon (b_\phi \sin t+c_\phi \cos t)+O({\varepsilon }^{2}) \end{aligned}$$

(22)

$$\begin{aligned} u\left( {t} \right)= & {} \varepsilon \left( {b_u \sin t+c_u \cos t} \right) +O({\varepsilon }^{2}) \end{aligned}$$

(23)

$$\begin{aligned} v\left( {t} \right)= & {} v_0 +{\varepsilon }^{2}(a_v t+b_v \sin \left( {2t} \right) +c_v \left( {1-\cos \left( {2t} \right) } \right) +O({\varepsilon }^{3}) \end{aligned}$$

(24)

where all the coefficients in (22–24) are given in Table 2. The steady-state expressions for the body angle $\theta (t)$ and forward speed $v_{{x}}(t)$ are given to leading order as:

$$\begin{aligned} \theta (t)= & {} \varepsilon \frac{1-\alpha }{\alpha \beta \left( {(1-\alpha )^{2}v_0^2 +\beta ^{2}} \right) }\left( {(1-\alpha )(1-\cos t)v_0 -\beta \sin t} \right) +O({\varepsilon }^{3}) \end{aligned}$$

(25)

$$\begin{aligned} v_x (t)= & {} (1-\alpha )v_0 +{\varepsilon }^{2}\left( {a_x {t +}b_x \sin \mathrm{(2t)}+c_x {(\cos \mathrm{(2t)}-1)}} \right) +O({\varepsilon }^{3}) \end{aligned}$$

(26)

where the constants $a_{x}, b_{x}, c_{x}$ are also given in Table 2.

Table 2 Expressions in equations (22)–(26)

Proof

All functions of $\phi$ in the reduced dynamic equations (9–11) are expanded about $\phi =0$ or $\phi =\pi$. Expanding $\phi {(t)}=\varepsilon \phi _{1}{(t)}+{\varepsilon }^{2}\phi _{2}{(t)}+{\cdots }$ and substituting (14) into (9)–(11) while assuming $u_{0}=0$, the zero-order dynamics again implies that $v_{0}=$constant. The first-order dynamics is then obtained in matrix form as:

$$\begin{aligned} \left[ {{\begin{array}{c} {\dot{v}_1 } \\ {\dot{u}_1 } \\ {\dot{\phi }_1 } \\ \end{array} }} \right] =\left[ {{\begin{array}{c@{\quad }c@{\quad }c} 0&{} 0&{} 0 \\ 0&{} {\frac{(\alpha \hbox {-}\sigma )(\alpha \hbox {+}\sigma \beta )}{\alpha \beta }v_0 }&{} {\frac{\sigma }{\alpha \beta }v_0^2 } \\ 0&{} {-(\alpha -\sigma )^{2}}&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{c} {v_1 } \\ {u_1 } \\ {\phi _1 } \\ \end{array} }} \right] +\left[ {{\begin{array}{c} 0 \\ {-\frac{1}{\alpha ^{2}\beta ^{2}}} \\ 0 \\ \end{array} }} \right] \sin (t) \end{aligned}$$

(27)

where ${\sigma } =1$ for expansion about $\phi =0$ and ${\sigma } =-1$ for $\phi =\pi$. This is the linearized dynamics of $(v, u, \phi )$ about $v=v_{0}$, u=0, and either $\phi =0$ or $\phi =\pi$. One can see that the first-order dynamics of v in (20) is zero, hence its leading-order dynamics is of $O({\varepsilon }^{2})$. The solution of (27) for u(t) and $\phi {(t)}$ consists of steady-state response of the form $\hbox {sin}({t}+\psi )$ and transient response of the form $\hbox {e}^{{{\lambda }_{{i}}}{t}}$, where $\lambda _{1,2}$ are eigenvalues of the 2$\,\times \,$2 lower sub-matrix in (27), which are given as

$$\begin{aligned} \lambda _1 =\frac{(\alpha -\sigma )}{\beta }v_o ,\hbox { }\lambda _2 =\frac{(\alpha -\sigma )}{\alpha }\sigma v_o \hbox { .} \end{aligned}$$

(28)

In case of expansion about $\phi =\pi$ where $\sigma =-1$, it can be verified that either $\lambda _{1}$ or $\lambda _{2}$ is a positive real number for any $v_{0}\ne 0$. Therefore, one concludes that the RR configuration is an unstable (relative) equilibrium of the linearized system (27). This explains the divergence of solutions from $\phi =\pi$ under torque input, which was observed in numerical simulations (dashed line in Fig. 4a). For the TC configuration where $\sigma =1$, i.e. expansion about $\phi =0$, both eigenvalues have negative real part for $v_{0}>0$, implying that the transient response is decaying in time. The steady-state solutions of $u_{1}{(t)}$ and $\phi _{1}{(t)}$ in the linear system (27) are then obtained directly as in (22), (23).

The second-order dynamics of v(t) is obtained by expanding (9) in $\phi$ and then substituting (14), as:

$$\begin{aligned} \begin{aligned} {\dot{v}}_2 (t)= & {} -\alpha (\alpha ^{2}\beta +\alpha \beta ^{2}-\alpha \beta -\beta ^{2}+\alpha -1)u_1^2 \left( t \right) +\frac{1}{\beta (1-\alpha )}v_0^2 \phi _1^2 (t) \\&-\,\frac{\alpha \beta ^{2}-\beta ^{3}-\alpha \beta -\alpha }{\beta }v_0 u_1 (t)\phi _1 (t)+\frac{1}{\alpha \beta ^{2}(1-\alpha )}\phi _1 (t)\sin \left( t \right) \end{aligned} \end{aligned}$$

(29)

Substituting the expressions for $u_{1}{(t)}$ and $\phi _{1}{(t)}$ from (22), (23) and integrating, one obtains the solution of $v_{2}{(t)}$, and its steady-state part is given in (24)

For the angular velocity, the relation (8) implies that ${\dot{\theta }}=v\hbox {sin}\phi +u\alpha (\alpha -\cos \phi ).$ Expanding about $\phi =0$ and using the expansions of $\phi (t), u(t), v(t)$ in (23)–(25), one obtains:

$$\begin{aligned} {\dot{\theta }}=\varepsilon \frac{1-\alpha }{\alpha \left( {(1-\alpha )^{2}v_0^2 +\beta ^{2}} \right) }\left( {\frac{(1-\alpha )v_0 }{\beta }\sin t-\cos t} \right) +O\left( {\varepsilon ^{3}} \right) \end{aligned}$$

Integrating under zero initial conditions, the leading-order solution of the body angle $\theta {(t)}$ is obtained as in (25). Finally, the relation (8) implies that $v_{\mathrm{x}}=(\hbox {cos}\phi -\alpha )v+\upalpha (\beta ^{2}+1){u}\hbox {sin}\phi$. Expanding about $\phi =0$ and using the expansions of $\phi (t)$, u(t), v(t) in (22)–(24) then gives (26). $\square$

In order to verify the expressions in Proposition 2, Fig. 6a–c plot numerical simulation values of the forward speed $v_{x}{(t)}$, steering angle $\phi {(t)}$ and body angle $\theta {(t)}$, respectively, in solid lines for parameter values of $\alpha =0.2$, $\beta =0.5$, $v_{0}=3$ and $\varepsilon =0.25$. The leading-order approximations in (26), (22) and (25) are overlaid in dashed lines on the plots. Approximation errors in $\phi {(t)}$, $\theta {(t)}$ also appear in solid lines in Figs. 7a, b. The fast decay of transient response is hardly visible in the plots (according to (28), its slowest component is $\hbox {e}^{-4.8{t}})$. It can be seen that the steady-state approximation works well for short times, yet for longer times its deviation from the exact solution is diverging. More importantly, the leading-order approximation does not capture the slow decay in oscillation amplitudes of $\phi {(t)}$, $\theta {(t)}$ and v(t), observed in numerical simulations. One reason for this discrepancy is the fact that for long times, the diverging term ${\varepsilon }^{2}a_{v}{t}$ in (24) is no longer of $O({\varepsilon }^{2})$, which violates the inherent assumption of $\varepsilon$-scales in the expansion (14). More importantly, the leading-order solution is based on expansion about a nominal constant value of $v=v_{0}$ while the actual mean value of v(t) increases with time due to the acceleration term ${\varepsilon }^{2}{a}_{v}{t}$ in (24). In particular, the oscillation amplitudes of $\phi {(t)}$, $\theta {(t)}$ and v(t) in the leading-order solution (22–24), which are given by the b, c coefficients in Table 2, depend on $v_{0}$ in a monotonically decreasing way, so that the growth in v(t) causes the slow convergence of the oscillations. It has been demonstrated in Chakon (2015) that updating the value of $v_{0}$ according to that of v(t) every several periods improves the accuracy of the approximation drastically. This motivates the use of a “continuous update” of $v_{0}$, which is implemented by the averaging scheme of v(t) discussed next.

Fig. 6

Comparison of simulation results (solid) and leading-order approximation (dashed) under harmonic input of steering torque $\tau {(t)}$: a forward speed $v_{x}{(t)}$, b steering angle $\phi {(t)}$, and c body angle $\theta {(t)}$

Fig. 7

Comparison of simulation results and improved time-varying approximation under harmonic input of steering torque $\tau {(t)}$: a solid velocity v(t), stars extrema of v(t), circles moving average $\bar{{v}}_{{k}}$ , dashed $\bar{{v}}{(t)}$. b error in $\phi (t)$, and c error in $\theta {(t)}$: solid constant $v_{0}$, dashed updated $\bar{{v}}{(t)}$

3.3 Improved Solution with Time-Averaged Speed

We now introduce an improved solution under oscillatory input of steering torque, which is based on time-averaging of the speed v(t). From the leading-order solution (24), it is observed that v(t) oscillates about a time-varying average value, which is denoted by $\bar{{v}}{(t)}$, whose slow rate of change is given by $\hbox {d}\bar{{v}}{/\hbox {d}t=}{\varepsilon }^{2}a_v$, where $a_{v}$ is given in Table 2 and depends on the initial value $v_{0}$. A continuous update of the approximate solution in (22)–(24) can thus be obtained by replacing every instance of $v_{0}$ in the coefficients in Table 2 with the slowly-varying average $\bar{{v}}{(t)}$. The time evolution of $\bar{{v}}{(t)}$ is then governed by a nonlinear ODE, given by:

$$\begin{aligned} \frac{\hbox {d}\bar{{v}}}{\hbox {d}t}={\varepsilon }^{2}a_v ={\varepsilon }^{2}\frac{(\alpha +\beta )(1-\alpha )}{2\alpha \beta \left( {(1-\alpha )^{2}\bar{{v}}^{2}+\alpha ^{2}} \right) \left( {(1-\alpha )^{2}\bar{{v}}^{2}+\beta ^{2}} \right) } \end{aligned}$$

(30)

Using separation of variables, an implicit solution for $\bar{{v}}{(t)}$ in (30) under initial condition $\bar{{v}}{(0)=}\bar{{v}}_0$ is obtained as

$$\begin{aligned}&\frac{2\alpha \beta }{\varepsilon ^{2}(\alpha +\beta )(1-\alpha )}\left( {(1-\alpha )^{4}(\bar{{v}}^{5}-\bar{{v}}_0^5 )} \right. \nonumber \\&\quad +\,(1-\alpha )^{2}(\alpha ^{2}+\beta ^{2})(\bar{{v}}^{3}-\bar{{v}}_0^3 )\left. {+\alpha ^{2}\beta ^{2}(\bar{{v}}-\bar{{v}}_0 )} \right) =t \end{aligned}$$

(31)

The solution $\bar{{v}}{(t)}$ in (31) for $\varepsilon {=}0.25, \bar{{v}}_0 {=}3$ is plotted as a dashed line in Fig. 7a, overlaid with the solid line of numerical solution v(t) of (9). In order to compare $\bar{{v}}{(t)}$ with the time-varying average of v(t) obtained numerically, the circles denote discrete-time approximation of $\bar{{v}}{(t)}$ by taking a moving average of local extremum points $v_{{k}}$ (marked by *) as $\bar{{v}}_{{k}} =(v_{{{k}-1}} +2v_{{k}} +v_{{{k}+1}} ){/4.}$ It can be seen that after an initial transient, $\bar{{v}}{(t)}$ displays good agreement with the moving average $\bar{{v}}_{{k}}$. Next, we calculate the improved approximation for the angles $\phi {(t)}$, $\theta {(t)}$ in (22), (23), which is obtained by replacing every instance of $v_{0}$ in Table 2 with the time-varying mean value $\bar{{v}}{(t)}$, whose solution is given in (31). The results are shown in Fig. 7b, c, where the solid lines are approximation errors of $\phi {(t)}$, $\theta {(t)}$ under constant $v_{0}$ whereas the dashed lines are errors under the improved approximation using $\bar{{v}}{(t)}$. The plots reveal significant improvement in the approximations for long times.

Finally, this improved solution can also be used in order to find explicit expressions for the decay rate of the oscillation amplitudes of the angles $\phi {(t)}$ and $\theta {(t)}$ for long times. At long times, the mean forward speed $\bar{{v}}$ is large so that the term $\bar{{v}}^{5}$ in (31) is dominating. Thus, it is concluded that for long times, the solution of (31) is $\bar{{v}}{(t)}\approx d_{{\phi }}{t}^{0.2}$, where $d_{{\phi } }$ is given in Table 2. Substituting this into the amplitude coefficients $b_{{\theta }}, c_{{\theta }}, b_{{\phi }}, c_{{\phi }}$ in Table 2 and assuming that $\bar{{v}}{(t)}\gg \alpha {,}\beta$ , it is then concluded that for long times, the oscillation amplitude of $\phi {(t)}$ decays as $d_{{\phi }}{t}^{-0.4}$ while the oscillation amplitude of $\theta {(t)}$ decays as $d_{{\theta }}{t}^{-0.2}$, where $d_{{\phi }}$ and $d_{{\theta }}$ appear in Table 2.

Fig. 8

Comparison of amplitudes at extremum values of $\phi$ and $\theta$ (‘*’) with the expressions for their long-time decay rate (dashed) on log-log scale.

In order to verify these expressions for long-time decay rates, Fig. 8 plots on a log-log scale the discrete series of absolute-valued peak values of $\phi {(t)}$ and $\theta {(t)}$, marked by * (minus steady-state value for $\theta$), for $\varepsilon {=}0.5, \bar{{v}}_0 {=1}$. The dashed lines denote the long-time approximate expressions $d_{{\phi }}{t}^{-0.4}$ and $d_{{\theta }}{t}^{-0.2}$, represented as straight lines with slopes of $-0.4$ and $-0.2$, respectively, on the log–log scale. The plot indicates that this approximation captures the true decay rate of the angles $\phi {(t)}$ and $\theta {(t)}$ for long times, which completes the analytic corroboration of all significant phenomena that were observed in numerical simulations.

Fig. 9

The vehicle’s robotic prototype: a Twistcar configuration, b roller-racer configuration

4 Preliminary Experiments

Preliminary motion experiments on a modular robotic prototype of the twistcar vehicle were conducted, which only demonstrate some qualitative aspects of the theoretical results presented in this work. Movies of these representative experiments appear in the multimedia extension. The robotic prototype, which was constructed from VEX robotics kit, is shown in Fig. 9. A DC servo motor (7.2 V 2000 mAh) with built-in incremental encoder and batteries is mounted at the steering joint, and controlled by an on-board microcontroller via RobotC environment of VEX. This basic controller only enables dictating instantaneous power, which is proportional to angular velocity, and is not suitable for more advanced feedback control. Additionally, the motor shaft suffered from static friction torque which stops the motor when the power signal is below some threshold, precluding the use of sinusoidal reference signals. Therefore, we chose to use a square-wave input of power, which results in triangular wave for the steering angle $\phi {(t)}$ with amplitude of $\pm 53^{\circ }$. The first motion experiment was at TC configuration (oscillations about $\phi =0$), and the second experiment was at RR configuration (oscillations about $\phi =\pi$). Snapshot images from the two experiments are shown in Fig. 10a, b. The experiments demonstrate forward motion at twistcar configuration and backwards motion at roller–racer configuration, as predicted by the theoretical results. The experiments clearly show deviation of the motion trajectory from a straight line to an arc. Nevertheless, due to lack of accurate position measurements, it is not clear whether the source of this deviation is diverging oscillations of the body angle $\theta$, asymmetric oscillations of the steering angle $\phi$ due to inaccurate manual homing and encoder’s drift, or asymmetry in rolling friction at the wheel’s bearings.

Finally, the purpose of the third experiment was demonstration of reversing the direction of motion of the roller-race due to change in the ratio $l_{1}/l_{3}$. In this experiment, a rectangular heavy box was attached to the vehicle’s back axle, shifting the body’s center-of-mass backwards $l_{1}<l_{3}$, which, according to the theory, results in forward motion. Then the box is removed, so that the center-of-mass position now satisfies $l_{1}>l_{3}$ and consequently, the direction is reversed and the vehicle begins to move backwards, as expected. Illustration of this experiment is shown in Fig. 10c, d. This experiment suffered from high sensitivity and low repeatability, probably due to wear and misalignment of the motor shaft, which caused increased static friction and backlashes. Additionally, intermittent events of sideways slippage of the wheels were clearly observed for all motion experiments, which were not accounted by the theoretical model. Some future improvements of the experiments as well as the theoretical model are discussed in the next section.

Fig. 10

Movie snapshots from experiments under steering angle input of triangular wave: a Twistcar configuration, b roller–racer configuration. c, d Reversal of motion direction of the roller–racer by removing a massive box that changes the distance $l_{1}$

5 Conclusion

In this work we have utilized the method of perturbation expansion in order to explicitly analyze the leading-order dynamics of the twistcar vehicle which is governed by momentum evolution and nonholonomic constraints of no-slip at the wheels. We have relaxed some unphysical assumptions made by previous works on the roller-racer model and considered both cases of steering torque and steering angle actuation of harmonic input. Interesting dynamic phenomena have been observed numerically and justified analytically, such as direction reversal of the roller-racer depending on the vehicle’s parameters, and influence of the choice of controlled input on convergence of the angles’ oscillations. Preliminary motion experiments with a robotic prototype demonstrated the influence of vehicle’s parameters on the direction of motion under open-loop controlled steering angle of triangular wave.

Some limitations of the work and proposed extensions of the research are listed as follows. First, the few preliminary experiments shown here were conducted on a prototype with limited control capabilities. We currently design an advanced robotic prototype, equipped with a more sophisticated microcontroller for closed-loop control of either steering torque or steering angle, which will enable overcoming mechanical backlashes and static friction at the shaft. The new setup will also include position measurement system, either by odometry using encoders on both wheels of the back axle, or by using a camera tracking system, in order to enable quantitative measurements of the vehicle’s motion. Motivated by observed events of wheels’ sideways slippage, we currently investigate extension of the theoretical model in order to include stick-slip transition under Coulomb’s friction model (cf. Fedonyuk and Tallapragada 2015) as well as the effects of backlashes and frictional torques at the joints, which all give rise to a hybrid dynamical system. Finally, the work can be extended to design of more applicative control laws for steering and path following of the vehicle.