1 Introduction

Locomotion, the act of self-propulsion, is an inherent ability in animals. Legged animals walk, fish swim, birds fly and bacteria use their flagella as propellers. Of the different gaits utilized, the undulatory and oscillatory gaits that are observed in snakes and fish, respectively, have distinctly made their way into robotic locomotion. Using tools from geometric mechanics, Ostrowski [1] decomposed undulatory locomotion into two principal components: changes in the internal shape of a system and changes in position and orientation of the system. This led to the observation that the relationship between shape changes and locomotion stems from a connection on a trivial principal fiber bundle.

Several mechanical systems mimicking undulatory and oscillatory locomotion have been presented in literature. In [2], Hirose and Morishima designed and implemented an articulated robot that ‘crawls’ in a manner similar to snakes. Lewis et al. [3] used cyclic variations in the base space to produce net displacement in the fiber space of their famous undulatory locomotor, the Snakeboard. More recently, Kelly et al. [4] demonstrated oscillatory locomotion in the Chaplygin Beanie, whereby oscillations in the heading generated longitudinal translation. In 1995, Krishnaprasad and Tsakiris [5] studied the motion and control of the Roller Racer. The Roller Racer is a two-link planar mechanical system with passive wheels attached at the center of mass of each link; it is a single module SE(2)-snake. This system undergoes oscillatory locomotion through cyclic variations of the inter-link angle, which generates forward propulsion. Even though it is the simplest mobile articulated system, the Roller Racer produces rich dynamics. Jouffroy [6] and Jouffroy and Jouffroy [7] were attracted by this fact and used the racer as a framework for studying Central Pattern Generators, which arise in many biological activities such as digestion and locomotion. Moreover, being a mechanical system with nonholonomic constraints and symmetry, Bullo and Zefran [8] and Lewis [9] explored its controllability through methods of affine connections and Lie brackets. In [10], a commercial scooter referred to as the Trikke was modeled as a modified Roller Racer due to the large resemblance between the two.

Throughout the literature, every dynamic analysis of the racer assumes that the mass and linear momentum of one of the links is much smaller than the other and thus can be ignored. This is evident in the Trikke and in the prototype built in [5]. In this paper, we present a generalization of the racer commonly treated in the literature, by admitting two links with masses of the same order of magnitude. We refer to this system as the Land-shark. The Land-shark closely resembles the Landfish developed in [17], with the difference that the nonholonomic constraints are imposed at both ends of the system rather than one, meaning that the Land-shark is more general. This introduces a new complexity to the system. This simple modification reveals that the mass and geometric parameters of the system can give significant insight about the locomotive capabilities of the system and that for specific combinations of mass and geometry, changing the pattern of movement (i.e., gait) being used does not affect these capabilities. The more important result is that, for certain mass and geometric parameters, the derivative of the nonholonomic momentum can sometimes change sign throughout its course. It follows that, as opposed to the Trikke and Roller Racer, and subject to certain geometric conditions, starting from rest, the Land-shark can be accelerated, decelerated and brought to a complete halt by solely using its single control input.

Furthermore, this paper extends the motion analysis to include the effects of frictional slip on the Land-shark’s locomotive capabilities. To do this, a friction model proposed by the authors in [11] is used. The aforementioned friction model was initially proposed for modeling skidding effects on the nonholonomic rolling motion of a unicycle. By applying it to the Land-shark, we explore its scope of applicability to nonholonomic systems that exhibit oscillatory motion.

Accordingly, the main contributions of the paper are as follows. We show that the momentum of the Land-shark can be increased and decreased by merely controlling its only input (the inter-link/steering angle), which allows for bringing the system to a complete stop. Furthermore, we develop a tool for analyzing the motion of two-link nonholonomic swimmers is presented. This tool is based on the partitioning of the parameter space of possible masses and geometries depending on the momentum behavior, which is possible after reducing the equations of motion. This reveals that the mass and geometric parameters of the system can give significant insight about the locomotive capabilities of the system. It can also be used as a preliminary tool for designing Land-sharks, given the desired momentum behavior. In principle, parameter space partitioning should be extendable to analyze the motion of other mobile articulated systems, after reducing their respective equations of motion. Finally, we explore the generality and applicability of a previously proposed model of locomotion in the presence of frictional slip to the oscillatory locomotion of the Land-Shark. The advantage of this friction model is that it preserves the inherent symmetry of the equations of motion, hinting at the ‘possibility’ for their reduction even in the presence of skidding effects.

The remainder of this paper is organized as follows. In Sect. 2, we analyze the dynamics and then reduce the equations of motion. In Sect. 3, we present the partitioning of the parameter space and highlight its usefulness in designing gaits. In Sect. 4, we investigate the locomotion of the system in the presence of frictional slip and we verify a friction model proposed in earlier work. Finally, Sect. 5 discusses the importance of the proposed friction model and Sect. 6 concludes the paper and explores the directions of future work.

2 Dynamics of the Land-shark

In this section, we develop the dynamic model of the Land-shark by identifying its configuration space, parameters and the nonholonomic constraints acting on it. After computing the Euler–Lagrange equations of motion, we use tools from geometric mechanics to achieve a reduced set of equations of motion. Finally, by defining the scaled nonholonomic momentum [13], we further simplify the system and the result is a reduction in the number and order of the equations of motion from six equations (four second order and two first order) to four first-order equations.

Fig. 1
figure 1

Configuration variables of the Land-shark

Full size image

2.1 Configuration space

The Land-shark comprises two planar links connected by an actuated revolute joint. A passive wheel set is attached at the center of mass of each link, with the wheel axis perpendicular to the line joining the link’s center of mass to the revolute joint. This gives rise to nonholonomic constraints that prevent skidding of the wheel sets.

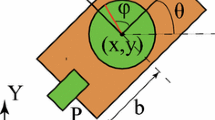
Figure 1 illustrates the configuration variables of the Land-shark (the discrepancy between the sizes of the links is for illustrative purposes only). Let \(2L_1\) and \(2L_2\) denote the lengths of the links, \(M_1\) and \(M_2\) their masses, and \(J_1\) and \(J_2\) their moments of inertia about their centers of mass. The configuration of the Land-shark is described by the four-dimensional vector of generalized coordinates \(q = (x, y, \theta , \phi )\) where (x, y) denotes the position of the center of mass of the robot, \(\theta \) denotes its orientation, all expressed relative to the fixed inertial frame \(\{X,Y\}\), and \(\phi \) denotes half the inter-link angle. We consider the orientation of the robot to be aligned parallel to the bisector of the inter-link angle. As such, denoting by \(\alpha \) and \(\beta \) the angles that the first and second links make with the horizontal, respectively, then the inter-link angle is \(\beta -\alpha =2\phi \) and the orientation of the robot is \(\theta =\alpha +\phi \). For further clarification of the choice of generalized coordinates, we have attached the body frame at the robot’s center of mass in Fig. 1.

2.2 Euler–Lagrange equations

The next step is to use the Lagrangian formulation to develop the equations of motion. Let \(p_1\) and \(p_2\) denote the locations of the centers of mass, with respect to the fixed inertial frame, and therefore the locations of the wheel sets, as shown in Fig. 1. Let

$$\begin{aligned} p_1=(u,v), \end{aligned}$$
(1)

then

$$\begin{aligned} p_2 = {(u+L_1\cos \alpha +L_2\cos \beta ,v+L_1\sin \alpha +L_2\sin \beta ).}\nonumber \\ \end{aligned}$$
(2)

To compute the positions of the centers of mass in terms of the configuration variables, \(q_i\), we must perform a change in variables from \((u,v,\alpha ,\beta )\) to \((x,y,\theta ,\phi )\). Since, (x, y) denotes the center of mass, we have

$$\begin{aligned} (x,y)=\frac{M_1 p_1+M_2 p_2}{M_1+M_2}, \end{aligned}$$
(3)

One can compute the required change in variables to be:

$$\begin{aligned} u= & {} x - \frac{M_2}{M1+M2}\left( L_1 \cos \alpha + L_2\cos \beta \right) \end{aligned}$$
(4)
$$\begin{aligned} v= & {} y - \frac{M_2}{M1+M2}\left( L_1 \sin \alpha + L_2\sin \beta \right) \end{aligned}$$
(5)
$$\begin{aligned} \alpha= & {} \theta -\phi \end{aligned}$$
(6)
$$\begin{aligned} \beta= & {} \theta +\phi . \end{aligned}$$
(7)

Since the potential energy is zero, the Lagrangian is equal to the kinetic energy:

$$\begin{aligned} L = \frac{M_1}{2} v_1^Tv_1 + \frac{M_2}{2} v_2^Tv_2 + \frac{M_1 L_1^2}{2} \dot{\alpha }^2 + \frac{M_2 L_2^2}{2} \dot{\beta }^2, \end{aligned}$$
(8)

where \(v_i = \frac{\mathrm{{d}}{\mathrm{{d}}t}}{p}_i\). As mentioned earlier, the passive wheels attached to each link constrain the motion of the respective contact point. The wheels are not allowed to slide sideways, and this kinematic restriction can be modeled as two nonholonomic constraints, each acting on one wheel set. Assuming ideal, no-slipping conditions, the constraints are given by

$$\begin{aligned} C_1 : \begin{pmatrix}-\sin \alpha \cos \alpha \end{pmatrix} v_1&= 0, \end{aligned}$$
(9)
$$\begin{aligned} C_2 : \begin{pmatrix}-\sin \beta \cos \beta \end{pmatrix} v_2&= 0. \end{aligned}$$
(10)

Rewriting the above constraints in terms of the configuration variables and expressing them in matrix form, we arrive at

$$\begin{aligned} \omega (q) \dot{q}&= 0, \end{aligned}$$
(11)

where

$$\begin{aligned} \omega (q) = \begin{pmatrix} -\sin (\theta -\phi ) &{} -\sin (\theta +\phi ) \\ \cos (\theta -\phi ) &{} \cos (\theta +\phi ) \\ \frac{-L_1-\cos (2 \phi ) L_2}{\frac{M_1}{M_2}+1} &{} \frac{\cos (2 \phi ) L_1+L_2}{1+\frac{M_2}{M_1}} \\ \frac{L_1-\cos (2 \phi ) L_2}{\frac{M_1}{M_2}+1} &{} \frac{L_2-\cos (2 \phi ) L_1}{1+\frac{M_2}{M_1}} \\ \end{pmatrix}^\mathrm{{T}}. \end{aligned}$$
(12)

These nonholonomic constraints are the essence of the self-propulsion of the system. When the Land-shark undergoes oscillatory motion through the actuation of the inter-link angle, the reaction/constraint forces that arise to enforce the nonholonomic constraints propel the system and allow locomotion.

Finally, one can compute the governing equations of motion by using the Euler–Lagrange equations:

$$\begin{aligned} \frac{d}{dt}\frac{\partial L(q,\dot{q})}{\partial \dot{q}_i} - \frac{\partial L(q, \dot{q})}{\partial q_i} + \lambda _j \omega ^j_i(q)&= \tau _i, \end{aligned}$$
(13)

where \(\lambda _j\) are the Lagrange multipliers that represent the reaction forces enforcing the nonholonomic constraints and \(\tau _i\) is the vector of generalized forces given by

$$\begin{aligned} \tau = \begin{pmatrix}0&0&0&\tau _\phi \end{pmatrix}^\mathrm{{T}}, \end{aligned}$$
(14)

where \(\tau _\phi \) is the torque control input of the inter-link angle, the only actuated degree of freedom.

2.3 Reduced equations of motion

The configuration space of the Land-shark Q has a principal fiber bundle structure \(Q = G \times R = \mathrm{{SE(2)}} \times \mathbb {S}\) with fiber coordinates \(g = (x,y,\theta )\) and base coordinate \(r=\phi \). From the literature [19], it is well known that the Lagrangian and the nonholonomic constraints are invariant under group action, and this symmetry can be exploited to reduce the equations of motion. This is done by expressing the Lagrangian and the constraints in terms of the body-frame coordinates. The reduced Lagrangian and constraints are defined as follows:

$$\begin{aligned} l(r,\dot{r},\xi )&= L(g^{-1}g, r, T_g L_{g^{-1}} \dot{g}, \dot{r}) \end{aligned}$$
(15)
$$\begin{aligned} c_i(r,\dot{r},\xi )&= C_i(g^{-1}g, r, T_g L_{g^{-1}} \dot{g}, \dot{r}), \end{aligned}$$
(16)

where \(\xi \) is the body velocity, defined as the group velocity pulled back to the Lie Algebra

$$\begin{aligned} \xi = T_g L_{g^{-1}} \dot{g}. \end{aligned}$$
(17)

Similarly, one can compute the reduced constraint matrix, \(\tilde{\omega }(r)\), to arrive at

$$\begin{aligned} \tilde{\omega }(r)&= \begin{pmatrix} \sin (\phi ) &{} -\sin (\phi ) \\ \cos (\phi ) &{} \cos (\phi ) \\ \frac{-L_1-\cos (2 \phi ) L_2}{\frac{M_1}{M_2}+1} &{} \frac{\cos (2 \phi ) L_1+L_2}{1+\frac{M_2}{M_1}} \\ \frac{L_1-\cos (2 \phi ) L_2}{\frac{M_1}{M_2}+1} &{} \frac{L_2-\cos (2 \phi ) L_1}{1+\frac{M_2}{M_1}} \\ \end{pmatrix}^\mathrm{{T}}. \end{aligned}$$
(18)

It is worth noting that, due to the invariance with respect to the fiber group action, \(\tilde{\omega }(r)\) is independent of any fiber variable.

Since the fiber space, SE(2), is three-dimensional and since there are two nonholonomic constraints acting on the system, there must be a direction along which the constraints do not act. It is along this direction that one can define the nonholonomic momentum variable [19], p, as

$$\begin{aligned} p = \mathcal {N}(\tilde{\omega }(r))\frac{\partial l(r, \dot{r}, \xi )}{\partial \xi }, \end{aligned}$$
(19)

where \(\mathcal {N}(\tilde{\omega }(r))\) is a basis for the null space of \(\tilde{\omega }(r)\). For the Land-shark, the nonholonomic momentum is given by

$$\begin{aligned}&p = \frac{\frac{M_1 M_2}{2} }{ \sin (\phi )} \left( \left( \frac{L_2}{M_1}+\frac{L_1}{M_2}\right) \cos (2 \phi )+\,\frac{L_1}{M_1}+\frac{L_2}{M_2}\right) \xi _x \nonumber \\&\qquad _ + \frac{\frac{M_1 M_2}{2} }{\cos (\phi )} \left( \left( \frac{L_2}{M_1}-\frac{L_1}{M_2}\right) \cos (2 \phi )+\,\frac{L_1}{M_1}-\frac{L_2}{M_2} \right) \xi _y\nonumber \\&\qquad _+\frac{m_1+m_2+l_0}{m_0}\xi _\theta + \frac{ m_2 - m_1}{m_0}\dot{\phi }, \end{aligned}$$
(20)

where \(l_0 = 2 L_1 L_2 M_1 M_2 \cos (2 \phi )\), \(m_0 = M_1+M_2\), \(m_1 = L_1^2 M_1 \left( M_1+2 M_2\right) \) and \(m_2 = L_2^2 M_2 \left( 2 M_1+M_2\right) \). Using this nonholonomic momentum alongside the reduced nonholonomic constraints, we can develop the reconstruction equation [1], which allows us to reconstruct the group trajectory and unfold the global motion of the system. Following that, using the first three equations of (13), i.e., the equations of motion of the Lie group variables, the inverse of the pull back action in (17) and its derivative, and the reconstruction equation, one can develop the momentum evolution equation, governing the behavior of \(\dot{p}\). We omit the reconstruction and momentum evolution equations for now since we will present a reduced and much simpler form in the next subsection.

2.4 Scaled momentum

In [13] and [14], Shammas et al. introduced the notion of the scaled momentum, \(\rho \). By noting that the momentum evolution equation \(\dot{p}\) is first order and it has an integrating factor, f(r), Shammas defined the scaled momentum as follows:

$$\begin{aligned} \rho&= f(r) p \end{aligned}$$
(21)
$$\begin{aligned}&= \frac{\sin (\phi ) \cos (\phi )}{\sqrt{2 L_2 L_1 \cos (2 \phi )+L_1^2+L_2^2}} p. \end{aligned}$$
(22)

This scaled momentum allows for further simplification of the reconstruction equation and the momentum evolution equation. Thus, we have reduced the original set of six equations of motion [two first order in (11) and four second order in (13)] to four first-order equations, namely the reconstruction equation and the scaled momentum evolution equation. These are shown in (23) and (24).

$$\begin{aligned} \xi= & {} \left( \begin{array}{c} \frac{2 L_1 L_2 \left( L_1 M_1-L_2 M_2\right) \sin (2 \phi ) \cos (\phi )}{m_0 \left( 2 L_2 L_1 \cos (2 \phi )+L_1^2+L_2^2\right) }\\ -\frac{2 L_1 L_2 \left( L_1 M_1+L_2 M_2\right) \sin (\phi ) \sin (2 \phi )}{m_0 \left( 2 L_2 L_1 \cos (2 \phi )+L_1^2+L_2^2\right) } \\ \frac{\left( L_1-L_2\right) \left( L_1+L_2\right) }{2 L_2 L_1 \cos (2 \phi )+L_1^2+L_2^2}\\ \end{array} \right) \dot{\phi }\nonumber \\{}&+ \begin{pmatrix} \frac{2 \cos (\phi ) \left( L_1 \left( \cos (2 \phi ) M_1+M_2\right) +L_2 \left( M_1+\cos (2 \phi ) M_2\right) \right) }{\sqrt{L_1^2+2 \cos (2 \phi ) L_2 L_1+L_2^2} m_0^2} \\ -\frac{2 \sin (\phi ) \left( L_1 \left( \cos (2 \phi ) M_1-M_2\right) +L_2 \left( M_1-\cos (2 \phi ) M_2\right) \right) }{\sqrt{L_1^2+2 \cos (2 \phi ) L_2 L_1+L_2^2} m_0^2} \\ \frac{2 \sin (2 \phi )}{\sqrt{L_1^2+2 \cos (2 \phi ) L_2 L_1+L_2^2} m_0} \end{pmatrix}\rho \nonumber \\ \end{aligned}$$
(23)
$$\begin{aligned} \dot{\rho }= & {} -\begin{pmatrix}\frac{2 L_1 L_2 \left( L_2 L_1 \left( M_1-M_2\right) \cos (2 \phi )+L_1^2 M_1-L_2^2 M_2\right) }{\left( 2 L_2 L_1 \cos (2 \phi )+L_1^2+L_2^2\right) {}^{3/2}}\end{pmatrix}\dot{\phi }^2.\nonumber \\ \end{aligned}$$
(24)

3 Parameter space partitioning

Inspecting the scaled momentum evolution equation (24) one can solve for robot parameters, \(M_1\), \(M_2\), \(L_1\), and \(L_2\), for which the scaled momentum, \(\rho \), has a particular desired behavior. The sign of the first derivative of the scaled momentum is indicative of this behavior. A positive sign indicates that the scaled momentum is increasing and thus the system is accelerating, whereas a negative sign indicates that the Land-shark is decelerating. On this basis, one may partition the parameter space into different regions, each representing a characteristic response of the scaled momentum.

3.1 Monotonically increasing momentum

In order for the scaled momentum to be increasing monotonically, we require that \(\dot{\rho }>0\) at all times. Examining Eq. (24), this condition reduces to

$$\begin{aligned} \left( L_2 L_1 \left( M_2-M_1\right) \cos (2 \phi )-L_1^2 M_1+L_2^2 M_2\right) > 0, \end{aligned}$$

since the denominator is always positive. Rearranging the inequality, we arrive at

$$\begin{aligned} \cos (2\phi )>\frac{L_1^2 M_1-L_2^2 M_2}{L_1 L_2 \left( M_2-M_1\right) } \quad \text {for} \quad \frac{M_2}{M_1}>1, \end{aligned}$$

or

$$\begin{aligned} \cos (2\phi )<\frac{L_1^2 M_1-L_2^2 M_2}{L_1 L_2 \left( M_2-M_1\right) } \quad \text {for} \quad \frac{M_2}{M_1}<1. \end{aligned}$$

Denoting \(\frac{L_1^2 M_1-L_2^2 M_2}{L_1 L_2 \left( M_2-M_1\right) }\) as \(\varLambda \), the inequalities derived above will hold at all times when

$$\begin{aligned} \varLambda <-1 \quad \text {for} \quad \frac{M_2}{M_1}>1, \end{aligned}$$

or

$$\begin{aligned} \varLambda >1 \quad \text {for} \quad \frac{M_2}{M_1}<1\;, \end{aligned}$$

since \(-1<\cos (2\phi )<1\).

Lemma 1

The scaled momentum will increase monotonically at all times for the following geometric parameters of the Land-shark: Either \((\frac{M_2}{M_1}>1\) & \(\frac{L_2}{L_1}>1)\) or \((\frac{M_2}{M_1}<1\) & \(\frac{M_2}{M_1}>\frac{L_1}{L_2})\).

The proof of Lemma 1 is given in “Appendix.”

3.2 Monotonically decreasing momentum

To achieve a monotonically decreasing momentum, the first derivative of the scaled momentum should remain negative at all times. Following the same analysis used in the previous section, this requirement reduces to

$$\begin{aligned} \cos (2\phi )<\varLambda \quad \text {for} \quad \frac{M_2}{M_1}>1, \end{aligned}$$

or

$$\begin{aligned} \cos (2\phi )>\varLambda \quad \text {for} \quad \frac{M_2}{M_1}<1. \end{aligned}$$

The inequalities expressed above will be respected at all times provided that

$$\begin{aligned} \varLambda>1 \quad \text {for} \quad \frac{M_2}{M_1}>1, \end{aligned}$$

or

$$\begin{aligned} \varLambda<-1 \quad \text {for} \quad \frac{M_2}{M_1}<1. \end{aligned}$$

Lemma 2

The scaled momentum will decrease monotonically at all times for the following geometric parameters of the Land-shark: Either \( \left( \frac{M_2}{M_1}<1 \& \frac{L_2}{L_1}<1\right) \) or \( \left( \frac{M_2}{M_1}>1 \& \frac{M_2}{M_1}<\frac{L_1}{L_2}\right) \).

The proof of Lemma 2 is given in “Appendix.”

3.3 Gait-dependent momentum

Throughout the analysis in the previous sections, the behavior of the scaled momentum was independent of the gaits, i.e., for any Land-shark with parameters satisfying Lemmas 1 or 2, the momentum would increase or decrease monotonically, regardless of the locomotive gait employed. We would like to explore the possibility of finding a region in the parameter space whereby the behavior of the momentum is not monotonic and that in fact, it may increase or decrease depending on the gait being utilized. More formally, in this section we seek to answer the following question: Is it possible to find regions in the parameter space of the Land-shark where the momentum behavior is not monotonic but rather gait-dependent? (i.e., \(\dot{\rho }\) may switch sign).

Studying the inequalities presented in the previous sections, one can deduce that this gait-dependent behavior is attainable when

$$\begin{aligned} -1<\varLambda <1. \end{aligned}$$

Lemma 3

A nonmonotonic behavior of the scaled nonholonomic momentum, whereby it may increase or decrease depending on the gait, will be observed for the following geometric parameters of the Land-shark: Either \( \left( \frac{M_2}{M_1}>1 \; \& \frac{M_2}{M_1}>\frac{L_1}{L_2} \; \& \; \frac{L_2}{L_1}<1\right) \) or \( \left( \frac{M_2}{M_1}<1 \; \& \; \frac{M_2}{M_1}<\frac{L_1}{L_2} \; \& \; \frac{L_2}{L_1}>1 \right) \).

Table 1 Simulation parameters and gaits
Full size table

The proof of Lemma 3 is given in “Appendix.”

Lemma 3 is a very important result, and it serves as the fundamental difference between the Land-shark and the two-link systems presented in literature. In [10] and [5], the authors proved for the Trikke and the Roller Racer, respectively, that these systems cannot be stopped after motion starting from rest using only the actuated inter-link angle. However, this is not the case for the Land-shark. As opposed to the Roller Racer and Trikke, certain regions exist within the parameter space of the Land-shark whereby the first derivative of the scaled nonholonomic momentum changes sign. This indicates that it is possible to stop the system after motion starting from rest by solely oscillating the only actuated degree of freedom, i.e., the inter-link angle. For these transition regions, the first derivative of the scaled nonholonomic momentum changes sign whenever the state of the following inequality changes from True to False or from False to True:

$$\begin{aligned} \cos (2\phi )<\varLambda \;. \end{aligned}$$
(25)

We refer to this inequality as the momentum transition inequality (MTI).

Fig. 2
figure 2

Parameter space partitioning based on the sign of \(\dot{\rho }\)

Full size image

Figure 2 illustrates the results expressed in Lemmas 1, 2 and 3 by partitioning the parameter space depending on the sign of the first derivative of the scaled nonholonomic momentum. Four different regions exist, each with a distinct behavior of the scaled momentum. The regions labeled by and depict the parameter ratios for which the first derivative of the scaled momentum is, respectively, either positive or negative for any arbitrary input. The other two regions labeled as and denote regions for which the first derivative of the scaled momentum will change sign from positive to negative or from negative to positive, for certain base variable values. The difference between these two regions is that violating the MTI produces an acceleration in the region and a deceleration in the region.

Figure 2 serves as an intuitive tool for designing Land-sharks, depending on the desired momentum behavior. If one requires that the Land-shark moves in a manner such that the scaled momentum increases monotonically and keeps building up, then the only requirement is that the parameters must belong to the region and any arbitrary gait can be used. The same analysis applies to the region. If one desires that the Land-shark builds up momentum for some time and then starts decelerating, then the parameters must belong to the region and the gait designed must violate the MTI for the first portion of the gait and comply with it for the second portion of the gait. Or it must belong to the region and the gait must violate the MTI at first and then satisfy it.

3.4 Simulations

For the sake of experimental validation of the partitioning presented above, we present four different simulations of the Land-shark, ranging over different regions of the parameter space. Table 1 displays the parameters and gaits used for simulating motion in each region. Figure 3 presents the results of the simulations by showing the evolution of the system’s velocity in the x-direction versus time (since all the gaits chosen moved the Land-shark in the x-direction only).

Fig. 3
figure 3

Simulation results for Land-sharks in different regions of the parameter space

Full size image

It is evident from Fig. 3 that the partitioning of the parameter space presented above is genuine. Indeed, the Land-shark possessing parameters within the region accelerated endlessly, irrespective of whether the gait switched or not, whereas the one lying in the region decelerated monotonically. As for the and regions, it is evident that the system’s velocity can increase or decrease by switching the gait as one desires. It is noteworthy to mention that a change in the sign of \({\dot{x}}\) indicates that the Land-shark has started to move and build up momentum in the opposite direction.

In order for the system to reach a complete stop (note that this is only possible in the and regions), one has to simply stop actuating the inter-link angle at the instant when the system’s velocity becomes zero, and before the Land-shark starts moving and building momentum in the opposite direction. Figure 4 illustrates the motion in the \(x-y\) plane of the linkage point of the Land-shark simulated in Fig. 3. It is clear that after moving about 1.8 meters, the Land-shark is merely moving in place and seizing actuation at this point would keep it in place. If the gait is applied for a longer time, the Land-shark would proceed to move in the opposite direction (to the left).

Fig. 4
figure 4

Reaching a complete stop with a Land-shark from the region

Full size image

As such, we have successfully demonstrated that Land-sharks within this region can be stopped using only the inter-link angle. In [5], this was only achievable by locking the inter-link angle, i.e., \({\dot{\phi }}(t)=0\), and including friction in the model.

4 Locomotion in the presence of frictional slip

In this section, we consider an additional complexity to the locomotion: frictional slip. In reality, the ideal nonholonomic constraints imposed by the wheels are sometimes violated due to wheel skidding and slipping, and this gives rise to nonideal constraints [15, 16]. To exaggerate these frictional effects, we investigate the locomotion of the Land-shark under conditions of high wheel slippage, such as roads covered with loose dirt, ice or oil and/or driving conditions that cause tire deformation. This need arises in many applications such as search and rescue operations or unmanned missions to the moon.

In earlier work [11], we devised a novel friction model and applied it to the nonholonomic rolling motion of a vertical disk (unicycle). We successfully demonstrated its validity by comparing it to a dissipative friction model from the literature [12]. For the scope of this paper, we build upon the results of the previous work and take things one step further by applying the methods of this friction model to the oscillatory locomotion of the Land-shark, in order to explore its scope of applicability and validity. Assessing the friction model’s validity for two different methods of nonholonomic locomotion is an important step toward establishing its generality for nonholonomic mechanical systems in future analysis.

4.1 Friction models

It is well known that there are two types of slipping; lateral and longitudinal. Lateral slipping is referred to as skidding. When a wheel skids, it slides in a direction perpendicular to that toward which it is pointing. Longitudinal slipping occurs when the wheel slips along its direction of motion. Since the wheel sets of the Land-shark are passive and are not actuated, we will only consider skidding effects. A skidding wheel moves along a direction different than that toward which it is pointing (i.e., the wheel heading). In other words, the velocity vector of the wheel forms an angle \(\delta \) with its heading \(\alpha \), which we refer to as the skid angle. Figure 5 clarifies this by comparing the motion of a normal wheel to that undergoing skidding.

Fig. 5
figure 5

a A wheel undergoing normal motion. b A wheel undergoing lateral slipping

Full size image

The main characteristic of our friction model is that the nonholonomic constraints are rotated by an angle \(\delta \), the skid angle. This is done because, as the wheel skids, the effective direction of zero velocity, i.e., the effective direction of no skidding, is no longer perpendicular to \(\alpha \) but it is rather perpendicular to \(\alpha +\delta \), as shown in Fig. 5. The new nonholonomic constraints become

$$\begin{aligned}&C_1 : \begin{pmatrix}-\sin (\alpha +\delta ) \cos (\alpha +\delta )\end{pmatrix} v_1 = 0, \end{aligned}$$
(26)
$$\begin{aligned}&C_2 : \begin{pmatrix}-\sin (\beta +\gamma ) \cos (\beta +\gamma )\end{pmatrix} v_2 = 0, \end{aligned}$$
(27)

where \(\delta \) and \(\gamma \) are the skid angles of the first and second wheel sets, respectively. Expressing the constraints in this manner, we preserve their frictionless property and thus we can now approximate frictional slip effects without adding dissipative forces to the equations of motion. This is a significant feature of the model, which will prove useful later on. In [11], we hypothesized that the skid angles are related to the constraint forces acting on the respective wheel, and three different friction models were developed, each with a distinct relation. Regarding the Land-shark, we will use the Linear Lagrange Multipliers friction model. This model assumes that the relation between the skid angles and the constraint forces is as follows:

$$\begin{aligned} \delta (t)= & {} a_1\lambda _1(t), \end{aligned}$$
(28)
$$\begin{aligned} \gamma (t)= & {} a_2\lambda _2(t), \end{aligned}$$
(29)

where, as mentioned earlier, \(\lambda _j\) are the respective Lagrange multipliers that enforce the nonholonomic constraints and the constants \(a_1\) and \(a_2\) are parameters that depend on several factors, mainly the road conditions [11].

4.2 Simulations

To explore the validity of this friction model, we simulated it on several Land-sharks from different parameter space regions and compared to those simulated under the Sidek model, a dynamic dissipative friction model for wheeled mobile robots with lateral slip [12]. Figure 6 displays the results of four of these simulations, by showing the evolution of the x coordinate versus time, since the gaits used caused a net displacement in the x direction only. The results of the ideal, no-slip case are also shown for comparison purposes.

It is evident from the simulation results that the proposed Linear model closely follows the Sidek model and this proves the validity of the model to a great extent. In fact, we do not expect an exact match between our proposed model and the Sidek model for several reasons. The Sidek model is devised for Wheeled Mobile Robots undergoing typical nonholonomic motion through active wheels. It is not guaranteed that such a model can be extended to oscillatory and undulatory types of locomotion such as those at hand. Moreover, the Sidek model employs the Pacejka Magic formula [18] for the skid angle. This formula is tailored to suit race cars where the wheels are deformed elastically and the speeds and masses of the cars are many orders of magnitude larger than those witnessed in the Land-shark.

Fig. 6
figure 6

Simulation results for Land-sharks in the presence of frictional slip. a Region, b Region, c Region, d Region

Full size image

Another important observation is the effect of frictional slip on the motion of the Land-shark. As one can deduce from Fig. 6 by comparing to the ideal no-slip case, wheel slippage merely affects the magnitude of the displacement and hence the magnitude of the momentum, over the period of the simulation. However, the overall behavior of the system in terms of increasing or decreasing momentum exactly follows that of the ideal case. In other words, if the ideal case shows an increase in velocity, then so does the slipping case, and the same applies for a decrease in velocity. This can be inferred from the fact that the shape of the curve of displacement remains quadratic after including slippage effects. In fact, the results are intuitive; the system behaves in the same manner in the presence of frictional slip but achieves smaller magnitudes of acceleration/deceleration due to the dissipation of energy. The implications of this result will be discussed shortly. It is noteworthy to mention that Krishnaprasad and Tsakiris [5] investigated the effects of viscous friction and concluded that it results in restricting the Roller Racer to a constant velocity and prevents it from building up momentum monotonically. This was manifested in the linear graph of displacement produced by including the viscous friction effects.

4.3 Parameter space partitioning with frictional slip

Now that the correctness of the friction model has been verified we are ready to tackle problem of partitioning the parameter space in the presence of frictional slip. In particular, we would like to determine whether the nonholonomic momentum of the system will exhibit an identical behavior in the presence of frictional slip and thus whether the utilization of this partitioning as a motion analysis tool remains appropriate in the case of wheel slippage. The results of the simulations in Fig. 6 can be employed to arrive at a solution to the parameter space partitioning problem in the presence of slippage effects. As was deduced earlier, wheel slippage only affects the magnitudes of the attainable momentum, yet the overall behavior, whether be it increasing or decreasing, remains unchanged. This paves the way for utilizing the parameter space partitioning developed in Fig. 2 to analyze the motion of the Land-shark even in the presence of frictional slip. To conclude, the parameter space partitioning can be employed as a motion analysis tool for Land-sharks in both the ideal, no-slip case and for the case of slipping.

5 Discussion

It is noteworthy at this point to mention the importance of the proposed friction model and its desirable features. The locomotion of nonholonomic mechanical systems and the reduction in their equations of motion in the presence of dissipative forces was treated in [20,21,22,23]. However, the dissipative forces considered therein were simple viscous forces, which were assumed to be linear in the generalized velocities and derivable from a Rayleigh dissipation function. The reduction techniques employed in these works are therefore not applicable to the problem at hand, where complex, nonlinear dissipative forces arise due to wheel skidding, such as the tire forces modeled by Pacejka’s Magic formula [18]. For the proposed friction model, the aim was to develop a model that approximates frictional slip but without the need to add dissipative forces, in order to preserve any underlying symmetries in the equations of motion, for the sake of reduction.

The results in Fig. 6 show that the proposed friction model can accurately capture the effect of wheel slippage on the motion of the Land-shark, without the need to add nonlinear dissipative forces to the equations of motion. We hypothesize that such a model for frictional slip (eqs. 30–33) will not impede the reduction in the equations of motion of the system. This is because the skid angles are a modeled as functions of the Lagrange multipliers, which are in turn a function of the base space variables and velocities. This means that the constraints should in principle remain invariant under the group action and hence retain their original symmetry. However, we do not have a formal proof of this yet, and this will be the focus of future work.

6 Conclusions and future work

In this paper, a generalization of two-link mobile articulated systems, referred to as the Land-shark, is introduced. It resembles the common Roller Racer with the slight variation that the mass of one of the links is not ignored. Through reduction tools commonly used in geometric mechanics, the equations of motion are reduced to only four first-order equations: the three-dimensional reconstruction equation and an equation describing the evolution of the scaled nonholonomic momentum. This reduction revealed that the simple variations in the system parameters have drastic effects on its dynamics. By partitioning the parameter space into regions based on the sign of the derivative of the momentum, two regions are discovered within which the momentum changes sign depending on whether a certain inequality involving the base variable is satisfied or not. This led to the conclusion that, as opposed to the Roller Racer, the Land-shark can use its only actuated degree of freedom to come to a halt.

In addition to that, a friction model developed in earlier work was applied in an effort to gain some insight about its scope of applicability. The model proved to be of good accuracy and it displays an advantageous feature toward solving the motion planning problem in the presence of frictional slip.

For future work, we aim to exploit this advantageous feature of the friction model, namely the symmetry-preserving property, to reduce the equations of motion for Land-sharks navigating in the presence of frictional slip. The authors are also interested in investigating time-optimal gaits and trajectories for this system.