1 Introduction

There is a significant number of equipment and machines which can be modeled as one degree-of-freedom oscillators with time variable mass (see [1, 2]). The model corresponds for the leaky tap [3], to the micro-cantilever-based resonators in MEMS, where the mass disturbance is induced by adsorption and desorption of surrounded molecules [4], for damped mass variable oscillatory systems [5, 6] etc. The model is suitable to explain some phenomena in physics [7], chemistry [8], biology [9, 10] and mechanical engineering considering centrifuges, sieves, pumps, compressors, transportation devices, etc. In the system mass is varying slowly during time. The device is usually driven with a motor. The excitation force is supposed to be a periodic time function usually a harmonic one. For the most device motor system the excitation force of the motor has an influence on the working device, but the influence of the device on the motion of the motor is neglected [11, 12]. For that case it is said that the energy source and the system are ideal. However, in the real systems there is an interaction between the driving source and the working machine. The driving source has an influence on the device, but the device affects the motion of the motor. This source and the system are called non-ideal ones [13] This type of interaction is widely investigated (see for example [14,15,16] and the references in them). Unfortunately, mass variable—motor non-ideal systems are not considered, yet, in spite of the fact that the problem of insufficient driving energy in the mass variable system also exists. Our interest is to analyze the influence of the mass variation on the properties of the non-ideal system.

The aim of the paper is to determine the effect of mass variation in the non-ideal mass variable machine-motor system. Due to the non-ideal source the mathematical model of the system contains beside equations whose number corresponds to degrees-of-freedom, an additional differential equation which defines the motor motion due to interaction of the driving torque and oscillator. In this paper the one degree-of-freedom oscillator and the motor with linear torque are considered. The model has two coupled second order differential equations. In the paper the equations are qualitatively and quantitatively analyzed, and the influence of the mass variation parameters is investigated. Based on the obtained results the prediction of motion of the system is possible.

The paper is divided in five sections. In the Sect. 2, the model of the oscillator - motor system is formed. Two coupled second order equations. with time variable parameters describe the motion of the system. The reactive force, which is the product of the mass time derivative and of the velocity of mass variation, is also taken into account. Vibrations close to the resonant regime are considered. The problem is not easy to be solved analytically. An approximate analytical solving method is developed based on the well-known averaging procedure. The obtained averaged equations are applied for analyzing of the continuous slow variable mass non-ideal systems. In Sect. 3 the qualitative analysis of the non-ideal system with oscillator with variable mass is introduced. The continual mass variation is substituted with the discontinual mass variation in small time intervals. Then the motion of the system is investigated as a succession series of steady-state dynamics of the non-ideal system with the oscillator with constant mass. In Sect. 4 the analytically obtained results in Sect. 2 are compared with numerical ones for the cases discussed in Sect. 3. The peaks in amplitude-frequency and torque diagrams are obtained. Based on the obtained results the quantitative description of the phenomena is given. The influence of the system parameters on the oscillation properties of the system is discussed. The paper ends with conclusion.

2 Oscillator with time variable mass driven by a non-ideal source

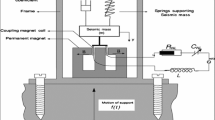
In Fig. 1 the model of an oscillator with time variable mass \(m_{1}\) connected with a motor which is a non-ideal energy source is plotted. The motor is settled on a cart whose mass \(m_{1}\) is varying in time due to leaking of the contain with velocity u. It is supposed that the mass variation is slow in time. The connection of the oscillating cart to the fixed element has the rigidity k and damping c.

Fig. 1
figure 1

Model of the non-ideal mass variable system

Full size image

The motor has the moment of inertia J, unbalance \(m_{2}\) and eccentricity d. The excitation torque of the motor, \(\mathcal {M}\left( \dot{\varphi } \right) \), is the function of the angular velocity \(\dot{\varphi }\)

$$\begin{aligned} \mathcal {M}\left( \dot{\varphi }\right) =M_{0}\left( 1-\frac{\dot{\varphi }}{ \Omega _{0}}\right) , \end{aligned}$$
(1a)

where \(\Omega _{0}\) is the steady-state angular velocity. This mathematical model corresponds to asynchronous AC motor [17].

To describe the motion of the system, let us assume the two generalized coordinates: the displacement of the oscillator x and the rotation angle of the motor \(\varphi \). Variation of the mass of the oscillator is assumed to be slow and to be the function of the slow time \(\tau =\varepsilon t\), where \(\varepsilon<<1\) is a small constant parameter. Equations of motion of the system with time variable mass are in general [2]

$$\begin{aligned} \frac{\text {d}}{\text {d}t}\frac{\partial T}{\partial \dot{x}}-\frac{\partial T}{\partial x} +\frac{\partial U}{\partial x}= & {} Q_{x}+Q_{R},\nonumber \\ \frac{\text {d}}{\text {d}t}\frac{\partial T}{\partial \dot{\varphi }}-\frac{\partial T}{ \partial \varphi }+\frac{\partial U}{\partial \varphi }= & {} Q_{\varphi }, \end{aligned}$$
(2)

where T is the kinetic energy, U is the potential energy, \(Q_{x}\) and \( Q_{\varphi }\) are generalized forces and \(Q_{R}\) is the generalized reactive force caused by mass variation. If the mass is added or separated with the absolute velocity u in x direction, the generalized reactive force is the product of the velocity u and mass variation \(\text {d}m_{1}/\text {d}t\), i.e.,

$$\begin{aligned} Q_{R}=\frac{\text {d}m_{1}}{\text {d}t}u. \end{aligned}$$
(3)

The non-conservative force in x direction is the damping force \(Q_{x}=-\,c \dot{x}\) with the damping coefficient c,  while the generalized force \( Q_{\varphi }\) corresponds to the torque \(\mathcal {M}(\dot{\varphi })\) applied to motor. The kinetic energy of the system is

$$\begin{aligned} T= & {} \frac{1}{2}[m_{1}(\tau )+m_{2}]\dot{x}^{2}+\frac{1}{2}(J+m_{2}d^{2})\dot{\varphi }^{2}\nonumber \\&-\,m_{2}d\dot{x}\dot{\varphi }\sin \varphi . \end{aligned}$$
(4)

and the potential energy of the system is

$$\begin{aligned} U=\frac{kx^{2}}{2}. \end{aligned}$$
(5)

Using (4) and (5) and also (3) equations of motion are due to (2)

$$\begin{aligned}&{[}m_{1}(\tau )+m_{2}]\ddot{x}+c\dot{x}+kx \nonumber \\&\quad = \frac{\text {d}m_{1}(\tau )}{\text {d}t}(u- \dot{x})\nonumber \\&\qquad +\,m_{2}d\left( \ddot{\varphi }\sin \varphi +\dot{\varphi }^{2}\cos \varphi \right) , \end{aligned}$$
(6)
$$\begin{aligned}&\left( J+m_{2}d^{2}\right) \ddot{\varphi }=m_{2}d\ddot{x}\sin \varphi + \mathcal {M}\left( \dot{\varphi }\right) . \end{aligned}$$
(7)

Assuming that the velocity u is sufficiently small, Eqs. (6) and (7) transform into

$$\begin{aligned}&{[}m_{1}(\tau )+m_{2}]\ddot{x}+c\dot{x}+kx\nonumber \\&\quad =-\frac{\text {d}m_{1}(\tau )}{\text {d}t} \dot{x} +\,m_{2}d\left( \ddot{\varphi }\sin \varphi +\dot{\varphi }^{2}\cos \varphi \right) , \end{aligned}$$
(8)
$$\begin{aligned}&\left( J+m_{2}d^{2}\right) \ddot{\varphi }=m_{2}d\ddot{x}\sin \varphi + \mathcal {M}\left( \dot{\varphi }\right) . \end{aligned}$$
(9)

Let us rewrite (8) and (9) into

$$\begin{aligned}&\ddot{x}+\omega ^{2}(\tau )x =-\,\varepsilon \zeta (\tau )\dot{x}-\frac{ \varepsilon }{m_{1}(\tau )+m_{2}}\frac{\text {d}m_{1}(\tau )}{\text {d}\tau }\dot{x} \nonumber \\\end{aligned}$$
(10)
$$\begin{aligned}&\qquad \qquad \qquad \qquad +\,\varepsilon \mu (\tau )\left( \ddot{\varphi }\sin \varphi +\dot{\varphi }^{2}\cos \varphi \right) , \nonumber \\&\ddot{\varphi } =\varepsilon \eta \ddot{x}\sin \varphi +\varepsilon \gamma \mathcal {M}\left( \dot{\varphi }\right) , \end{aligned}$$
(11)

where

$$\begin{aligned} \omega ^{2}(\tau )= & {} \frac{k}{m_{1}(\tau )+m_{2}},\quad \varepsilon \zeta (\tau )=\frac{c}{m_{1}(\tau )+m_{2}},\quad \varepsilon \gamma \nonumber \\= & {} \frac{1}{J+m_{2}d^{2}} \nonumber \\ \varepsilon \mu (\tau )= & {} \frac{m_{2}d}{m_{1}(\tau )+m_{2}},\quad \varepsilon \eta =\frac{m_{2}d}{J+m_{2}d^{2}}. \end{aligned}$$
(12)

In Eqs. (10) and (11) the right-hand side terms are of the order of small parameter \(\varepsilon \). Analyzing the dimensionless parameters (12) it is obvious that the dimensionless frequency \(\omega \), damping \(\zeta \) and excitation \(\gamma \) are functions of slow time. Namely, the mass variation affects these values. To give the correct analyzes of the problem it is necessary to solve Eqs. (10) and ( 11).

2.1 First order differential equations

Let us transform the second order differential Eqs. (10) and (11) into a system of first order ones by introducing the new variables a(t), \(\varphi (t),\) \(\psi (t)\) and \(\Omega (t)\) which satisfy the relations

$$\begin{aligned} x= & {} a(t)\cos (\varphi (t)+\psi (t)), \end{aligned}$$
(13)
$$\begin{aligned} \dot{x}= & {} -\,a(t)\omega (\tau )\sin (\varphi (t)+\psi (t)), \end{aligned}$$
(14)

and

$$\begin{aligned} \dot{\varphi }(t)=\Omega (t). \end{aligned}$$
(15)

Using the time derivative of (13)

$$\begin{aligned} \dot{x}= & {} \dot{a}(t)\cos (\varphi (t)+\psi (t))-a(t)(\dot{\varphi }(t)\nonumber \\&+\,\dot{\psi }(t))\sin (\varphi (t)+\psi (t)). \end{aligned}$$
(16)

and comparing (16) with (14) the following constraint is obtained

$$\begin{aligned} 0=\dot{a}\cos (\varphi +\psi )-a(\Omega +\dot{\psi })\sin (\varphi +\psi ), \end{aligned}$$
(17)

where we have the simplified notation \(a=a(t)\), \(\psi =\psi (t)\), \(\varphi =\varphi (t)\), \(\Omega =\Omega (t)\). Substituting (13), (14) and the time derivative of (14)

$$\begin{aligned} \ddot{x}=-\,(\dot{a}\omega +a\dot{\omega })\sin (\varphi +\psi )-a\omega (\dot{ \varphi }+\dot{\psi })\cos (\varphi +\psi ), \end{aligned}$$

into (10) and (11), we have

$$\begin{aligned}&-\,(\dot{a}\omega +a\dot{\omega })\sin (\varphi +\psi )-a\omega (\Omega +\dot{\psi })\cos (\varphi +\psi ) \nonumber \\&\quad =\varepsilon \zeta a\omega \sin (\varphi +\psi )\nonumber \\&\qquad +\,\frac{\varepsilon }{ m_{1}(\tau )+m_{2}}\frac{\text {d}m_{1}(\tau )}{\text {d}\tau }a\omega \sin (\varphi +\psi )\nonumber \\&\qquad +\,\varepsilon \mu \omega ^{2}\cos \varphi +\varepsilon ^{2}\ldots \end{aligned}$$
(18)
$$\begin{aligned}&\dot{\Omega } =-\,\varepsilon \eta [\dot{a}\sin (\varphi +\psi )\nonumber \\&\qquad +\,a(\omega +\dot{\psi })\cos (\varphi +\psi )]\omega \sin \varphi \nonumber \\&\qquad +\,\varepsilon \gamma \mathcal {M}\left( \dot{\varphi }\right) +\varepsilon ^{2}\ldots \end{aligned}$$
(19)

Equations (15), (17), (18) and (19) represent the first order differential equations of motion which are the transformed version of (10) and (11) in new variables. After some modification we have (15) and

$$\begin{aligned} \dot{a}= & {} -\left( \varepsilon \zeta a+\frac{\varepsilon }{m_{1}(\tau )+m_{2} }\frac{\text {d}m_{1}(\tau )}{\text {d}\tau }a\right. \nonumber \\&\left. +\,\frac{\varepsilon a}{\omega }\frac{\text {d}\omega }{ \text {d}\tau }\right) \sin ^{2}(\varphi +\psi ) \nonumber \\&-\,\varepsilon \mu \frac{\Omega ^{2}}{\omega }\sin (\varphi +\beta )\cos \varphi , \end{aligned}$$
(20)
$$\begin{aligned} \dot{\psi }= & {} (\omega -\Omega )-\varepsilon \mu \frac{\Omega ^{2}}{a\omega } \cos \varphi \cos (\varphi +\psi ) \nonumber \\&-\,\frac{\sin 2(\varphi +\psi )}{2a\omega }\left( \varepsilon a\frac{\text {d}\omega }{\text {d}\tau }+\varepsilon \zeta a\omega \right. \nonumber \\&\left. +\,\frac{\varepsilon a\omega }{m_{1}(\tau )+m_{2}}\frac{\text {d}m_{1}(\tau )}{\text {d}\tau }\right) , \end{aligned}$$
(21)
$$\begin{aligned} \dot{\Omega }= & {} -\varepsilon \frac{\text {d}\omega }{\text {d}\tau }+\varepsilon \gamma \mathcal {M}\left( \dot{\varphi }\right) \nonumber \\&-\,\varepsilon \eta a\omega ^{2}\cos (\varphi +\psi )\sin \varphi . \end{aligned}$$
(22)

Equations (15) and (20)–(22) are coupled strong nonlinear equations.

2.2 Averaging procedure

For simplicity let us introduce the averaging over the period of the trigonometric function \(\varphi \). The averaged Eqs. (20)–(22) are

$$\begin{aligned} \dot{a}= & {} -\frac{1}{2}\left( \varepsilon \zeta a+\frac{\varepsilon a}{ m_{1}(\tau )+m_{2}}\frac{\text {d}m_{1}(\tau )}{\text {d}\tau }+\frac{\varepsilon a}{\omega } \frac{\text {d}\omega }{\text {d}\tau }\right) \nonumber \\&-\,\frac{1}{2}\varepsilon \mu \frac{\Omega ^{2}}{\omega }\sin \psi , \end{aligned}$$
(23)
$$\begin{aligned} \dot{\psi }= & {} (\omega -\Omega )-\frac{\varepsilon \mu \Omega ^{2}}{2a\omega } \cos \psi , \end{aligned}$$
(24)
$$\begin{aligned} \dot{\Omega }= & {} -\,\varepsilon \frac{\text {d}\omega }{\text {d}\tau }+\varepsilon \gamma \mathcal {M}\left( \dot{\varphi }\right) +\frac{1}{2}\varepsilon \eta a\omega ^{2}\sin \psi . \end{aligned}$$
(25)

Using the relation

$$\begin{aligned} \frac{2}{\omega (\tau )}\frac{\text {d}\omega (\tau )}{\text {d}\tau }=-\frac{1}{m_{1}(\tau )+m_{2}}\frac{\text {d}m_{1}(\tau )}{\text {d}\tau }, \end{aligned}$$
(26)

the Eq. (23) reads

$$\begin{aligned} \dot{a}=-\frac{1}{2}\left( \varepsilon \zeta a-\frac{\varepsilon a}{\omega } \frac{\text {d}\omega }{\text {d}\tau }+\varepsilon \mu \frac{\Omega ^{2}}{\omega }\sin \psi \right) . \end{aligned}$$
(27)

In (24), (25) and (27) the frequency \(\omega \) is the function of the ‘slow time’ \(\tau \).

3 Influence of mass variation on the dynamics of the system

Let us consider the system with constant mass when \(m_{1}=\text {const}\). Then the dimensionless values \(\omega \), \(\zeta \) and \(\gamma \) in (12) are also constant. Assuming that the mass of the system is constant and omitting the terms with the second and higher order of the small parameter \( \varepsilon \), relations (10) and (11) simplify into

$$\begin{aligned}&\ddot{x}+\omega ^{2}x =-\varepsilon \zeta \dot{x}+\varepsilon \mu \dot{\varphi }^{2}\cos \varphi , \end{aligned}$$
(28)
$$\begin{aligned}&\ddot{\varphi } =\varepsilon \eta \ddot{x}\sin \varphi +\varepsilon \gamma \mathcal {M}\left( \dot{\varphi }\right) . \end{aligned}$$
(29)

According to (20)–(22) and to transformations (13)–(15), Eqs. (28) and (29) are rewritten in new variables a, \(\psi \) and \(\Omega \)

$$\begin{aligned} \dot{a}= & {} -\varepsilon \zeta a\sin ^{2}(\varphi +\psi )\nonumber \\&-\,\varepsilon \mu \frac{ \Omega ^{2}}{\omega }\sin (\varphi +\psi )\cos \varphi ,\end{aligned}$$
(30)
$$\begin{aligned} \dot{\psi }= & {} (\omega -\Omega )-\varepsilon \mu \frac{\Omega ^{2}}{a\omega }\cos (\varphi +\psi )\cos \varphi \nonumber \\&-\,\varepsilon \zeta \frac{\sin 2(\varphi +\psi )}{2}, \end{aligned}$$
(31)
$$\begin{aligned} \dot{\Omega }= & {} \varepsilon \gamma \mathcal {M}\left( \Omega \right) -\varepsilon \eta a\omega ^{2}\cos (\varphi +\psi )\sin \varphi . \end{aligned}$$
(32)

Equations (30)–(32) are coupled and strong nonlinear.

Fig. 2
figure 2

a Intersection of the amplitude-frequency diagram and various values of motor torque; b intersection of the motor torque and amplitude-frequency diagrams for various values of mass

Full size image

3.1 Averaging procedure. Steady-state motion

After averaging over the period of the trigonometric function \(\varphi \) the averaged equations follow as

$$\begin{aligned} \dot{a}= & {} -\frac{1}{2}\varepsilon \zeta a-\frac{1}{2}\varepsilon \mu \frac{ \Omega ^{2}}{\omega }\sin \psi , \end{aligned}$$
(33)
$$\begin{aligned} \dot{\psi }= & {} (\omega -\Omega )-\frac{\varepsilon \mu \Omega ^{2}}{2a\omega } \cos \psi , \end{aligned}$$
(34)
$$\begin{aligned} \dot{\Omega }= & {} \varepsilon \gamma \mathcal {M}\left( \dot{\varphi }\right) + \frac{1}{2}\varepsilon \eta a\omega ^{2}\sin \psi , \end{aligned}$$
(35)

which correspond to (24), (25) and (27) where \(\frac{\text {d}m_{1}(\tau )}{\text {d}\tau }=0\), i.e., \(\frac{\text {d}\omega }{\text {d}\tau }=0\).

Let us consider the case when discontinual mass variation occurs. The transient motion is eliminated, and the steady-state motion, when \(\dot{a}=0,\) \(\dot{\psi }=0\) and \(\dot{\Omega }=0\), is analyzed. Equations (33)–( 35) transform into

$$\begin{aligned} \frac{\varepsilon \mu \Omega ^{2}}{2\omega }\sin \psi= & {} -\frac{1}{2} \varepsilon \zeta a, \end{aligned}$$
(36)
$$\begin{aligned} \frac{\varepsilon \mu \Omega ^{2}}{2\omega }\cos \psi= & {} (\omega -\Omega )a, \end{aligned}$$
(37)
$$\begin{aligned} \frac{1}{2}\varepsilon \eta a\omega ^{2}\sin \psi= & {} -\varepsilon \gamma \mathcal {M}\left( \dot{\varphi }\right) . \end{aligned}$$
(38)

Using relations (36) and (37) the amplitude -frequency relation is obtained

$$\begin{aligned} a=\frac{\varepsilon \mu \Omega ^{2}}{\omega \sqrt{(\varepsilon \zeta )^{2}+4(\omega -\Omega )^{2}}}. \end{aligned}$$
(39)

Eliminating \(\psi \) in the Eqs. (36) and (38), we have

$$\begin{aligned} \frac{(\varepsilon \eta )(\varepsilon \zeta )\omega ^{3}}{2\varepsilon \mu \Omega ^{2}}a^{2}=\varepsilon \gamma \mathcal {M}\left( \dot{\varphi }\right) \equiv \varepsilon \gamma M_{0}\left( 1-\frac{\Omega }{\Omega _{0}}\right) . \end{aligned}$$
(40)

Based on (39) and (40) the influence of the mass variation for the small amount is analyzed.

3.2 Qualitative analysis

Let us compare the properties of the systems with various values of mass. The characteristic points, which represent the intersection of curves (39) and (40), will be analyzed. In Fig. 2 the points of intersection of amplitude-frequency and characteristic curve are presented: in Fig. 2a the intersection of an amplitude-frequency curve and various characteristic curves and in Fig. 2 b for one characteristic curve and amplitude-frequency curves for various values of mass are plotted.

In Fig. 2a the intersection of the amplitude-frequency diagram for \(m_{1}=m_{10}\) and various values of motor torque are plotted. It can be seen that there may be one, two (for boundary cas) or three points of intersection (two of them are stable and one is unstable). In Fig. 2b only one motor characteristic for \(m_{1}=m_{10}\) is plotted. It is worth to say that the influence of the small mass variation on the motor characteristic is negligible.

Fig. 3
figure 3

The motion of the lower Intersection point for increasing mass: a \(m_{1}=m_{10}\), b \( m_{1}=1.03m_{10}\) and c \(m_{1}=1.06m_{10}\)

Full size image

The intersection of this motor characteristic and of amplitude-frequency diagrams obtained for various values of mass \(m_{1}\) is plotted in Fig. 2b. It is seen that for \(m_{1}=m_{10}\) there are three intersection points. If the mass is higher than \(m_{10}\), i.e., \( m_{1}=1.1m_{10}\), the amplitude-frequency diagram is moving to left and the number of intersections decreases from three to only one. If the mass is smaller than \(m_{10}\), i.e., \(m_{1}=0.9m_{10}\), the amplitude-frequency diagram is moving to right and the number of intersection points decreases from three to one.

Fig. 4
figure 4

The motion of the upper Intersection point for increasing mass: a \(m_{1}=m_{10}\), b \( m_{1}=1.03m_{10}\) and c \(m_{1}=1.06m_{10}\)

Full size image

It can be concluded that the value of mass has an influence on the number and position of characteristic points.

Besides, it is concluded that the mass variation has an influence on the amplitude of vibration, i.e., on the position of the intersection points. The intersection points correspond to the so-called almost steady-state positions. In Fig. 3a–c the influence of mass increase on the position of the characteristic point with small amplitude and high frequency (lower steady-state position) is plotted. The amplitude of the steady-state position decreases from 1 to 3, while the frequency increases. The second characteristic point, the so-called upper steady-state position, also moves due to mass increase (see Fig. 4a–c). First the intersection point moves toward higher amplitude and smaller frequency (point 2) and then jumps to the position 3 with small amplitude and high frequency.

4 Comparison of the analytical and numerical solution

Let us compare the previously obtained results with the numerical solution of the equations of motion (10) and (11). We assume the mass-time variation diagram (see Fig. 5). For \(t\in [0,200]\) the mass is constant, while for \(t>200\) mass is increasing for \(\varepsilon >0\) and decreasing for \(\varepsilon <0\).

Fig. 5
figure 5

Mass–time diagrams

Full size image

The parameters of the system are: \(J=1,\) \(m_{10}=1,\) \(m_{2}=0.1,\) \( k=1.1,\) \(c=0.1,\) \(M_{0}=0.1\) and \(d=0.5.\) The solution of (10) and (11) is obtained using the Runge-Kutta procedure. Three problems are considered: one, the mass is constant for the time interval \(t\in [0,200),\) second when the mass of the oscillator is slowly increasing (\( \varepsilon >0\)) for \(t\geqslant 200\), and third, when the mass is slowly decreasing (\(\varepsilon <0\)) in time for\( t\geqslant 200\)

Fig. 6
figure 6

a Frequency-time diagram for upper steady-state position, b displacement-time diagram for upper steady-state position, c frequency-time diagram for lower steady-state position and d displacement-time diagram for lower steady-state position. Mass is constant (gray line) and mass is increasing (black mass)

Full size image

In Fig. 6 the displacement and frequency time history diagrams are plotted for the case when mass increases in time and \(\varepsilon =0.001>0\). For the diagrams in Fig. 6a, b the initial conditions are \(x(0)=0, \dot{x}(0)=0,\varphi (0)=0.001\) and \(\dot{\varphi }(0)=0,\)while for Fig. 6c, d the initial conditions are \(x(0)=0,\dot{x}(0)=0,\varphi (0)=0.001\) and \(\dot{\varphi }(0)=1.09.\) The first group of initial values correspond to the so-called upper steady-state position, while the second to the ‘lower’ steady-state position.

Fig. 7
figure 7

a Frequency-time diagram for upper steady-state position, b displacement-time diagram for upper steady-state position, c frequency-time diagram for lower steady-state position and d displacement-time diagram for lower steady-state position. Mass is constant (black line) and mass is decreasing (gray mass)

Full size image

It is worth to say that dependently on the initial conditions there are two steady-state frequency - time diagrams. This conclusion was already obtained in the previous section by applying the qualitative analysis. In this section both steady-state positions are investigated. In Fig. 6a the frequency-time diagram for upper steady-state position is plotted. For the constant mass, after the transient motion, the frequency is constant while for the mass increase the frequency increases, too. In Fig. 6b the corresponding displacement-time diagram for the upper steady-state position is shown. For the constant mass (gray line) the displacement has the constant value. For the case when the mass is increasing the amplitude decreases (black line). The same tendency of motion is evident for the lower steady-state position (Fig. 6c, d).

In Fig. 7 the case when the mass is decreasing with parameter \( \varepsilon =-\,0.001<0\) is plotted. Two groups of initial values are considered: in Fig. 7a, b it is \(x(0)=0,\dot{x}(0)=0,\varphi (0)=0.001\) and \(\dot{\varphi }(0)=0\) and in Fig. 7c, d it is \( x(0)=0,\dot{x}(0)=0,\varphi (0)=0.001\) and \(\dot{\varphi }(0)=1.09\).

Fig. 8
figure 8

\(x-t\) diagrams obtained analytically (black line) and numerically (gray line) for increasing mass and initial conditions \(x(0)=0,\dot{x}(0)=0,\) \(\varphi (0)=0.001\): a \(\dot{\varphi }(0)=0\) and b \(\dot{\varphi }(0)=1.09\)

Full size image

Analyzing Fig. 7a, c it can be seen that if the mass is constant, the frequency-time diagram is constant, too, while if the mass decreases the frequency tends to decrease in time. Motion around two steady-state positions exists. The upper steady-state position (gray line; Fig. 7b) is constant for constant mass, but the mass decrease causing the value of displacement to decrease in time (gray line). For the lower steady-state position which corresponds to the constant mass the displacement-time (gray line) is constant. However, due to mass decrease the displacement increases from that steady-state position up to the upper steady-state one and then decreases in time (black line) (Fig. 7d).

Fig. 9
figure 9

\(x-t\) diagrams obtained analytically (black line) and numerically (gray line) for decreasing mass and initial conditions \(x(0)=0, \dot{x}(0)=0,\) \(\varphi (0)=0.001\): a \(\dot{\varphi }(0)=0\) and b \(\dot{\varphi }(0)=1.09\)

Full size image

It is of interest to compare the analytical solutions of the averaged Eqs. (15), (24), (25) and (27) with numerical solution of (10) and (11). In Fig. 8 the displacement-time diagrams for the increasing mass around the both steady-state positions are plotted. The analytically obtained result (full black line) is on the top of the numerical solution (gray line). The agreement is excellent.

In Fig. 9 the displacement-time diagrams obtained analytically (black line) and numerically (gray line) for the case when the mass is decreasing are plotted. The both almost steady-state positions are considered. For the upper steady-state solution the agreement between analytical averaged solution and of the numerical solution is better than for the lower steady-state position. However, for higher time values the analytical solution is the envelope of the oscillatory numerical result. The tendency of amplitude is to increase with decrease in mass in time.

In Fig. 6b, d the transition phenomena from one steady-state motion to another due to mass increase is evident. The transient from the steady-state of the system with constant mass to the upper steady-state is jump-like (see Fig. 6b), while to the lower steady-state is monotone (see Fig. 6d). The same conclusion is obtained analytically by analyzing the amplitude variation shown in Fig. a, b. It is worth to say that the transient from one to another steady states in the systems where mass is decreasing is different. The transition from the steady-state which corresponds to constant mass to the steady states of decreasing mass is much more gradual (see Fig. 7b, d). The same result is obtained analytically and presented in Fig. 9.

5 Conclusion

It can be concluded:

  1. 1.

    There is an interaction between the amplitude-frequency property of the non-ideal mass variable system and the driving torque. Mass variation causes variation of extreme values of the amplitude of vibration in time. Besides, in contrary to the ideal systems, mass variation causes the change in number of the ‘almost’ steady-state motions of the system. The change is connected with jump in the amplitude-frequency property of the system. The phenomenon is usually called Sommerfeld effect. It is concluded that it is detected in the investigated non-ideal system with time variable mass, too.

  2. 2.

    The intersection between the amplitude-frequency diagram and the motor torque characteristics represents the ‘almost’ steady-state position. Number of these intersections varies with mass variation in time and may be one or three: two of them are stable and one is unstable. This number is varying in time with mass variation. Namely, if the mass is increasing the amplitude-frequency diagram is moving to left and the number of intersections with the torque characteristics may decrease from three to only one. In opposite, if the mass is decreasing, the amplitude-frequency diagram is moving to right.

  3. 3.

    The ‘almost’ steady-state vibration is with time variable amplitude. If the mass is increasing, the amplitude of vibration is decreasing. Otherwise, if the mass is decreasing the amplitude is increasing.

  4. 4.

    The influence of the slow variable mass in time on the motor characteristics is negligible.

  5. 5.

    The qualitative analysis of the non-ideal system with mass variable oscillator is suitable to be done by analyzing the series of equations of motion with constant mass but successively assumed increasing or decreasing mass values.

  6. 6.

    The solution of the averaged equations of motion for the non-ideal system with time variable mass is on the top of the exact numerical solution. The difference between analytical and numerical solution is negligible.

  7. 7.

    Finally, we concluded that the mass variation is suitable to be applied as a method for control of motion in non-ideal systems.