1 Introduction

Energy harvesting is the term associated with any localized power generation without the need of a main power grid to energize important and sensitive electronic devices continuously. These devices include micro-electromechanical systems [1], health monitoring sensors [2], wireless sensors [3, 4], medical implants [5], and cameras [6]. During recent years, flow-induced vibrations with respect to energy harvesting potential and design have been studied for different kinds of aeroelastic instabilities, such as vortex-induced vibrations (VIV) in circular cylinders [7,8,9,10], flutter in airfoil sections [11,12,13,14], galloping exhibited by prismatic structures [15, 16] and wake galloping induced by bluff body placed in the wake of another one [17, 18].

For energy harvesting by VIV that is the topic of interest in current work, the performed study by Akaydin et al. [19] is of considerable importance. They placed piezoelectric cantilever beams in wakes of circular cylinders at high Reynolds number. They synchronized natural frequency of their generators with the unsteady turbulent flow’s predominant frequency to maximize the generated piezoelectric voltage. They observed a reasonable agreement between their simulation results and experimental data. Molino-Minero-Re et al. [20] considered cylinders of different sizes attached to a cantilever beam having piezoelectric generators. They analyzed performance of the energy harvesters and observed power of up to 0.31 mW. Akaydin et al. [8] performed an experimental study in a wind tunnel on their designed VIV energy harvester. They analyzed the performance of their system and reported a 0.1 mW power generation at a wind speed of 1.192 m/s. A nonlinear distributed-parameter model for piezoelectric energy harvester having a circular cylinder as tip mass and subjected to VIV by wind flow was proposed by Dai et al. [21]. They validated their model with experimental results of Akaydin et al. [8], and discussed effects of the wind speed, cylinder’s tip mass, length of the piezoelectric layer and electrical load resistance on the response of the energy harvester. Zhang and Wang [22] investigated VIV and wake-induced vibrations of a rigid circular cylinder attached with two cantilever beams. A bigger cylinder was placed upstream in order to induce wake galloping in a smaller cylinder. For VIV, they indicated an optimum value of electrical load resistance for maximum generated power. For the wake-induced galloping, they found out that vibration of the small cylinder is controlled by the vortex frequency of the large one. Their work also pointed to an optimum gap between the two cylinders to maximize harvested power.

The immense importance of aeroelastic oscillations and especially VIV for power harvesting applications has been established. When it comes to the transduction mechanisms for scavenging energy out of these ambient vibrations, it is evident from above that most of the researchers have given attention to piezoelectric transducers. The ease of placement in small volumes and ability to harness energy over a large range of frequencies have made them a good choice. Recently, few researches have reported the use of another important transduction mechanism that is electromagnetic induction, which turns out to be a good choice for harnessing energy from relative motions. The work of Zhu et al. [23] consisted of an airfoil placed on a cantilever spring. The airflow over the airfoil causes the cantilever to oscillate that has a magnet attached to it that cuts the coil placed near it. They got a power output as high as 1.6 mW for a wind speed of 5 m/s. The use of electromagnetic induction for wake galloping was also proposed by Jung and Lee [17]. They carried out experiments in a wind tunnel using the prototype device they developed, for harnessing energy by wake galloping. They indicated power generation of 370 mW under a wind speed of 4.5 m/s.

De Marqui and Erturk [24] considered two separate cases of two degree of freedom airfoils: one with a piezoelectric transducer and other having electromagnetic induction in the plunge direction. They studied influences of several dimensionless parameters on linear flutter speed as well as electrical power output for both the transducers. Dias et al. [25, 26] simultaneously used a hybrid piezoelectric-electromagnetic formation in an airfoil for power generation. Based on their electroaeroelastic modeling and simulations, their work gave a direction for designing and optimizing airfoil-based hybrid energy harvesters. Recently, Javed et al. [27] were the first to propose and investigate a hybrid transduction mechanism for galloping energy harvesters. The transduction mechanism consisted of a piezoelectric layer and a magnet in the vicinity of a coil. They considered a coupled electroaeroelastic lumped-parameter model for the harvester. The effect of each external load resistance on the onset speed of galloping was discussed. Moreover, for a range of wind speeds, they investigated effects of the external load resistances on the harvested power. A complete comparative analysis was also carried out that revealed decreased powers in individual circuits in hybrid, as compared to each separate transducer. They mentioned that use of hybrid transduction mechanisms is very beneficial to operate multiple electronic devices.

Fig. 1
figure 1

A schematic of the hybrid piezoelectric-electromagnetic energy harvester subjected to vortex-induced vibrations

Full size image

The effectiveness of using hybrid transducers studied before is further investigated in this study, when considering VIV phenomenon of a circular cylinder. Researchers till this date have focused on piezoelectric transduction for energy harvesting by VIV. In this work, our objective mainly is to study the performance of vortex-induced oscillations exhibited for energy harvesting when considering two transduction mechanisms, namely electromagnetic and piezoelectric working simultaneously. To do so, a nonlinear distributed-parameter model for the hybrid energy harvesting system is first derived. The harvester, in present case, consists of a circular cylinder attached to the free end of a multilayered cantilever beam, which is partially covered by a unimorph piezoelectric patch along with a magnet attached to the beam that cuts a coil when the beam vibrates. The influences of the external load resistances of the respective piezoelectric and electromagnetic circuitries on the coupled damping and energy generated are studied. Moreover, the impacts of the magnet placement/location and mass on the coupled frequency and damping as well as performance of the hybrid energy harvester are deeply investigated. A comparison is drawn at the end between the VIV hybrid energy harvester and its classical counterparts performing individually, for same wind flow conditions.

2 Electroaeroelastic modeling of hybrid VIV energy harvesters

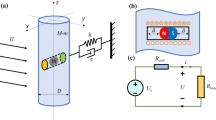
The current section deals with mathematical modeling of the proposed hybrid VIV harvester. The idea is to harvest energy from wind flowing past a circular cylinder that is attached as a tip mass at the end of a cantilever beam by two separate transducers simultaneously, as shown in Fig. 1. The cantilever beam is multilayered with a portion of it covered by a piezoelectric layer on one side that is unimorph. The other side consists of a magnet with a coil placed in its close vicinity. It should be mentioned that magnet shown in schematic in Fig. 1 is actually at other side of the beam. Because of the incoming wind flow, the tip mass cylinder exhibits vortex-induced oscillations for a well-defined range of wind speeds. The flexure of the beam is translated into electrical power by strains produced in the piezoelectric layer attached on the beam. Moreover, a magnet attached on the other side of the beam converts transverse deflection of the beam into useful electrical energy by cutting the coil placed near it. This new proposed concept of using two separate transduction mechanisms for harnessing energy from VIV in this particular piezoelectric-electromagnetic configuration needs to be thoroughly investigated. To this end, a nonlinear electroaeroelastic coupled dynamical model for the parameters given in Table 1 is first developed.

Table 1 Parameters of the electromagnetic-piezoelectric energy harvester
Full size table

To develop a reduced-order model of the hybrid VIV energy harvester, the Euler–Lagrange equations are utilized. To this end, total kinetic energy, potential energy, and non-conservative work are first determined. As for the kinetic energy of the dynamical system under consideration, it is written as:

$$\begin{aligned} T= & {} \frac{1}{2}\int \limits _0^{Lp} {m_1 \left[ {\frac{\partial w \left( {x,t} \right) }{\partial t}} \right] ^{2}} \text {d}X\nonumber \\&+\, \frac{1}{2}\int \limits _{L\mathrm{p}}^L {m_2 \left[ {\frac{\partial w\left( {x,t} \right) }{\partial t}} \right] ^{2}} \text {d}X\nonumber \\&+\,\frac{1}{2}m_0 \left[ {\left. {\frac{\partial w\left( {x,t} \right) }{\partial t}} \right| _{x=L0} } \right] ^{2}\nonumber \\&+\, \frac{1}{2}M_t \left[ {\left. {\frac{\partial w\left( {x,t} \right) }{\partial t}} \right| _{x=L} +\left. {\frac{D_t }{2}\frac{\partial ^{2}w \left( {x,t} \right) }{\partial x\partial t}} \right| _{x=L} } \right] ^{2} \nonumber \\&+\,\frac{1}{2}J_t \left[ {\left. {\frac{\partial ^{2}w\left( {x,t} \right) }{\partial x\partial t}} \right| _{x=L} } \right] ^{2} \end{aligned}$$
(1)

where w represents the deflection of the beam, \(M_{t}\) denotes mass of the cylinder attached at tip of the beam, \(J_{t}\) is mass moment of inertia in the tip mass cylinder, and \(m_{1}\) and \(m_{2}\) denote the masses per unit length which depend on placement of the piezoelectric layer. The first portion of the beam \(0 \le x \le L_\mathrm{p}\) with the substrate and the piezoelectric layers has a mass given by:

$$\begin{aligned} m_1 =b_\mathrm{s} \rho _\mathrm{s} t_\mathrm{s} +b_\mathrm{p} \rho _\mathrm{p} t_\mathrm{p} \end{aligned}$$
(2)

For the second portion of the beam \(L_{\mathrm{p}}<x \le L\) with only aluminum substrate, the mass is given by:

$$\begin{aligned} m_2 =b_\mathrm{s} \rho _\mathrm{s} t_\mathrm{s} \end{aligned}$$
(3)

where \(b_\mathrm{s}\) and \(b_\mathrm{p}\) are width of the aluminum and piezoelectric layers, respectively. In Eqs. (2) and (3), \(t_\mathrm{s}\) and \(t_\mathrm{p}\) are thicknesses of the aluminum substrate and piezoelectric layers, respectively. Moreover, the substrate and piezoelectric densities are given by \(\rho _\mathrm{s}\) and \(\rho _\mathrm{p}\), respectively.

Concerning the potential energy of the energy harvester, it consists of elastic energy of the beam, potential energy due to the piezoelectric material, potential energy stored in the magnetic field, and electromagnetic potential energy of the coil that can be expressed as:

$$\begin{aligned} U= & {} \frac{1}{2}\int \limits _0^{L_\mathrm{p} } {[EI_1 } {w}''^{2}]\text {d}x+\frac{1}{2}\int _{L_\mathrm{p} }^L {\left[ {EI_2 {w}''^{2}} \right] \text {d}x} \nonumber \\&-\,\int \limits _0^{L_\mathrm{p} } {e_{31} b_\mathrm{p} \frac{\left( {y_1 +y_2 } \right) }{2}{w}''V^{p}(\hbox {t})\text {d}x} \nonumber \\&-\,\frac{1}{2}\frac{\in _{33} b_\mathrm{p} L_\mathrm{p} }{h_\mathrm{p} }V^{{p}{2}}\hbox {(t)}\nonumber \\&-\frac{1}{2}L_\mathrm{c} \dot{Q}^{{e}{2}}+C_{Bl} \dot{Q}^{e}w\left( {L_0 ,t} \right) \end{aligned}$$
(4)

where \(V^{p}\) represents generated voltage across the external load resistance \(R_\mathrm{p}\) of the piezoelectric transducer, \(e_{31}\) is the piezoelectric coupling coefficient and the permittivity at constant strain is given by \(\in _{33}\). Moreover, \(Q^{e}\) represents the extracted charge from the electromagnetic circuit, \(C_{Bl}\) denotes the electromagnetic coupling and \(L_\mathrm{c}\) is inductance of the coil placed near the magnet. It is important to note that in Eq. (4),

$$\begin{aligned} EI_1= & {} \frac{1}{3}E_\mathrm{s} b_\mathrm{s} \left( {y_1^3 -y_0^3 } \right) +\frac{1}{3}E_\mathrm{p} b_\mathrm{p} \left( {y_2^3 -y_1^3 } \right) \end{aligned}$$
(5)
$$\begin{aligned} EI_2= & {} \frac{1}{12}b_1 E_\mathrm{s} t_\mathrm{s}^3 \end{aligned}$$
(6)

where \(E_\mathrm{s }\) and \(E_\mathrm{p}\) are elastic moduli of the substrate and piezoelectric layers, respectively.

As presented in Fig. 2, positions of the aluminum substrate and piezoelectric layers with respect to the neutral axis are given by:

$$\begin{aligned} y_0= & {} -\overline{y} \nonumber \\ y_1= & {} t_\mathrm{s} -\overline{y} \nonumber \\ y_2= & {} \left( {t_\mathrm{s} +t_\mathrm{p} } \right) -\overline{y} \nonumber \\ \overline{y}= & {} (2E_\mathrm{p} t_\mathrm{p} b_\mathrm{p} t_\mathrm{s} +E_\mathrm{s} b_\mathrm{s} t_\mathrm{s} ^{2}\nonumber \\&+\,E_\mathrm{p} b_\mathrm{p} t_\mathrm{p} ^{2})/(2E_\mathrm{p} t_\mathrm{p} b_\mathrm{p} +2E_\mathrm{s} t_\mathrm{s} b_\mathrm{s} ) \end{aligned}$$
(7)
Fig. 2
figure 2

Schematic depicting the position of the neutral axis and the layers in the beam

Full size image

When it comes to non-conservative work of the dynamical system under investigation, it is composed of work due to the power dissipated through the electromagnetic and piezoelectric transducers across their respective external load resistances and work due to the aerodynamic and viscous damping forces [21]. Therefore, the non-conservative work is expressed as:

$$\begin{aligned} \delta W= & {} -(R_\mathrm{i} +R_\mathrm{c} )\dot{Q}^{e}\delta Q^{e}-R_\mathrm{p} \dot{Q}^{p}\delta Q^{p}\nonumber \\&-\,\int \limits _0^L \left[ {c_m \frac{\partial w\left( {x,t} \right) }{\partial t}} \right] \delta w \left( {x,t} \right) \text {d}x \nonumber \\&+\,F_\mathrm{L} \delta \left[ {w\left( {L,t} \right) + \left. {L_\mathrm{c} \frac{\partial w\left( {x,t} \right) }{\partial x}} \right| _{x=L} } \right] \end{aligned}$$
(8)

where \(R_\mathrm{i}\) and \(R_\mathrm{p}\) represent, respectively, the electrical load resistances for the electromagnetic-inductive circuit and piezoelectric circuit, \(R_\mathrm{c}\) is indicative of internal resistance of the coil, \(Q^{p}\) denotes charge produced across the piezoelectric transducer and \(c_{m}\) is viscous damping coefficient of the energy harvesting system. In Eq. 8, \(F_\mathrm{L}\) represents aerodynamic force generated by the flowing wind in the transverse direction over the cylinder. The \(F_\mathrm{L}\) is responsible for the non-conservative work by the aerodynamic force and is given by Facchinetti [28]. According to Facchinetti et al. [28], this aerodynamic force caused by flowing wind over a circular cylinder can be expressed as:

$$\begin{aligned} F_\mathrm{L} \left( t \right)= & {} \frac{C_\mathrm{L} \rho _0 D_t U^{2}L_\mathrm{D} }{2}-\frac{C_\mathrm{D} \rho _0 D_t UL_\mathrm{D} }{2}\nonumber \\&\left[ {\left. {\frac{\partial w\left( {x,t} \right) }{\partial t}} \right| _{x=L} +\left. {\frac{D_t }{2}\frac{\partial ^{2}w\left( {x,t} \right) }{\partial x\partial t}} \right| _{x=L} } \right] \end{aligned}$$
(9)

where \(C_\mathrm{L}=\frac{C_\mathrm{L0} s(t)}{2}\) is the fluctuating lift coefficient, \(C_\mathrm{L0}\) and \(C_\mathrm{D }\) are the steady lift and mean sectional drag coefficients that can be taken as 0.3 and 1.2, respectively, in the region of well-developed wake [28]. Moreover, \(\rho _0 \) denotes density of the fluid, \(L_\mathrm{D}\) is length of the circular cylinder and U is the incoming wind speed.

The determination of the fluctuating lift coefficient on a circular cylinder is very challenging. This topic has been extensively explored in the past few decades. The reason researchers resort to use phenomenological models for modeling aerodynamic force is their ease of application in terms of computation time and computational cost together with decent accuracy offered compared to direct numerical simulations (DNS). Facchinetti et al. [28] modeled the forcing on the wake of a circular cylinder by using a modified van der Pol oscillator. They evaluated their wake oscillator model’s parameters (\(C_\mathrm{L0}\), \(C_\mathrm{D}\), \(\lambda \), and A) by using experimental and computational results. Dai et al. [29] worked on suppression of VIV oscillations of a circular cylinder by using a nonlinear energy sink and used Facchinetti’s model. They compared resulting experimental measurements with the wake oscillator modeled response of circular cylinder for two different mass ratios. The output of the system using the model was found to be in excellent agreement with the experimental results. This excellent agreement is due to the modified wake oscillator model that Facchinetti et al. [28] have proposed. In this study, we use the modified van der Pol wake oscillator proposed by Facchinetti et al. [28] in order to relate the lift fluctuating force to acceleration of the circular cylinder as follows:

$$\begin{aligned}&\ddot{s}+\lambda \omega _\mathrm{s} \left( {s^{2}-1} \right) \dot{s}+\omega _\mathrm{s}^2 s\nonumber \\&\quad =\frac{A}{D_t }\sum _{i=1}^n {\left( {\left[ {\frac{\partial ^{2}w\left( {x,t} \right) }{\partial t^{2}}+\frac{D_t }{2}\frac{\partial ^{3}w\left( {x,t} \right) }{\partial x\partial t^{2}}} \right] } \right) } \end{aligned}$$
(10)

where s or s(t) describes the behavior of the near wake and stands for the lift acting on the cylinder. \(\omega _s\) is the vortex-shedding frequency that is defined as \(\omega _\mathrm{s} =\frac{2\pi s_t }{D_t }U\), where \(s_t \) represents the Strouhal number. The values of \(\lambda \) and A are constants and are identified from the experimental measurements whereas U represents the freestream velocity. The same flow conditions without turbulence and same range of Reynolds number as Facchinetti et al. [28] are considered, and therefore same values for the constants are utilized.

To derive a nonlinear reduced-order model of the considered electromagnetic-piezoelectric VIV energy harvester, the Galerkin procedure is employed in order to obtain an ordinary-differential equation having infinite degrees of freedom instead of a partial-differential equation. To this end, displacement of the piezoelectric-electromagnetic energy harvester is expressed in the following form:

$$\begin{aligned} w\left( {x,t} \right) =\sum _{k=1}^\infty {\varphi _{jk} } \left( x \right) f_k (t) \end{aligned}$$
(11)

where \(\varphi _{jk} \left( x \right) \) indicates mode shape and \(f_k \left( \hbox {t} \right) \) are modal coordinates of the cantilever beam with tip mass. The mode shapes of partially covered beam are used in this study, as performed by Abdelkefi and Barsallo [30]. For more details about determination of the exact mode shapes of partially covered cantilever beam, the reader is referred to the work presented in [30]. The mode shapes are then normalized using the following orthogonality conditions:

$$\begin{aligned}&\int \limits _0^{L_\mathrm{p} } {\varphi _{1s} \left( x \right) } m_1 \varphi _{1r} \left( x \right) \text {d}x+\int \limits _{L_\mathrm{p} }^L {\varphi _{2s} \left( x \right) } m_2 \varphi _{2r} \left( x \right) \text {d}x\nonumber \\&\quad +\,\left[ \varphi _{2s} \left( L \right) +\frac{D_t }{2}{\varphi }'_{2s} \left( L \right) \right] M_t \left[ \varphi _{2r} \left( L \right) \right. \nonumber \\&\left. \quad +\frac{D_t }{2}{\varphi }'_{2r} \left( L \right) \right] +\left[ {{\varphi }'_{2s} \left( L \right) J_t {\varphi }'_{2r} \left( L \right) } \right] \nonumber \\&\quad +\,\varphi _{2s} \left( {L_0 } \right) m_0 \varphi _{2r} \left( {L_0 } \right) =\delta _{rs} \end{aligned}$$
(12)
$$\begin{aligned}&\int \limits _0^{L_\mathrm{p} } {\frac{d^{2}\varphi _{1s} \left( x \right) }{\text {d}x^{2}}} EI_1 \frac{d^{2}\varphi _{1r} \left( x \right) }{\text {d}x^{2}}\text {d}x\nonumber \\&\quad +\int \limits _{L_\mathrm{p} }^L {\frac{d^{2}\varphi _{2s} \left( x \right) }{\text {d}x^{2}}} EI_2 \frac{d^{2}\varphi _{2r} \left( x \right) }{\text {d}x^{2}}\text {d}x=\delta _{rs} \omega _r^2 \end{aligned}$$
(13)

Using Euler–Lagrange equations which are given by the following relations:

$$\begin{aligned}&\frac{\partial }{\partial t}\frac{\partial L_g }{\partial \dot{f}_k }-\frac{\partial L_g }{\partial f_k }=\frac{\delta W}{\delta f_k }\quad (k=1,2,\ldots ,n) \end{aligned}$$
(14)
$$\begin{aligned}&\frac{\partial }{\partial t}\frac{\partial L_g }{\partial \dot{Q}^{e}}-\frac{\partial L_g }{\partial Q^{e}}=\frac{\delta W}{\delta Q^{e}}=-\,(R_\mathrm{p} +R_\mathrm{c} )\dot{Q}^{e} \end{aligned}$$
(15)
$$\begin{aligned}&\frac{\partial }{\partial t}\frac{\partial L_g }{\partial \dot{\eta }^{p}}-\frac{\partial L_g }{\partial \eta ^{p}}=\frac{\delta W}{\delta \eta ^{p}}=-\,\frac{V^{p}}{R_\mathrm{p} } \end{aligned}$$
(16)

where \(L_g =T-U\) represents the Lagrangian and \(\dot{\eta }^{p}=V^{p}\). The nonlinear reduced-order model of such piezoelectric-electromagnetic energy harvesting system subjected to vortex-induced vibrations can be expressed as:

$$\begin{aligned}&\ddot{f}_k \left( t \right) +2\varsigma _k \omega _k \dot{f}_k \left( t \right) + \left( {\frac{C_\mathrm{D} \rho _0 D_t UL_\mathrm{D} }{2}} \right) \nonumber \\&\left[ {\varphi _k \left( L \right) +\frac{D_t }{2} \varphi _k ^{\prime }\left( L \right) } \right] \nonumber \\&\quad \times \left[ {\sum _{j=1}^n {\left( {\varphi _j \left( L \right) +\frac{D_t }{2}\varphi _j ^{\prime }\left( L \right) } \right) } \dot{f}_j } \right] +\omega _k^2 f_k \left( t \right) \nonumber \\&\quad +\,C_{Bl} \varphi _k \left( {L_0 } \right) i^{e}- \frac{e_{31} \left( {y_1 +y_2 } \right) b_\mathrm{p} }{2}{\varphi }'_k \left( {L_\mathrm{p} } \right) V^{p}\left( t \right) \nonumber \\&={C_{\mathrm{L}0}} \rho _0 D_t U^{2}L_\mathrm{D} \left[ {\varphi _k \left( L \right) +\frac{D_t }{2}{\varphi }'_k \left( L \right) } \right] \Big /4\times s\left( t \right) \nonumber \\&\quad (k=1,2,\ldots ,n) \end{aligned}$$
(17)
$$\begin{aligned}&L_{c} \frac{di^{e}}{dt}+\left( {R_\mathrm{i} +R_\mathrm{c} } \right) i^{e}\nonumber \\&\,\quad -\,C_{Bl} \sum _{k=1}^n {\varphi _k \left( {L_0 } \right) \dot{f}_k \left( t \right) } =0 \end{aligned}$$
(18)
$$\begin{aligned}&\frac{\in _{33}^s b_\mathrm{p} L_\mathrm{p}}{t_\mathrm{p} }\dot{V}^{p}\left( t \right) +\frac{V^{p}\left( t \right) }{R_\mathrm{p} }\nonumber \\&\quad +\,\sum _{k=1}^n {\frac{e_{31} \left( {y_1 +y_2 } \right) b_\mathrm{p} }{2}{\varphi }'_k \left( {L_\mathrm{p} } \right) \dot{f}_{_k } \left( t \right) } =0 \end{aligned}$$
(19)
$$\begin{aligned}&\ddot{s}+\lambda \omega _\mathrm{s} \left( {s^{2}-1} \right) \dot{s}+\omega _\mathrm{s}^2 s\nonumber \\&\quad =\frac{A}{D_t }\sum _{k=1}^n {\left( {\left[ {\varphi _k \left( L \right) +\frac{D_t }{2}{\varphi }'_k \left( L \right) } \right] \ddot{f}_k } \right) } \end{aligned}$$
(20)

In the above expressions, n denotes the number of used modes in the Galerkin discretization.

3 System’s parameters impacts on the coupled frequency and damping of the hybrid VIV energy harvester

For understanding complete dynamics of the piezoelectric-electromagnetic VIV energy harvesting system, a linear analysis should be first carried out. In fact, this type of analysis reveals valuable information about the harvester’s predicted behavior. The current section deals with examining the effects or impacts of different parameters of the hybrid energy harvester including the external load resistances, wind speed, and location and mass of magnet on its coupled damping and frequency. To this end, the nonlinear terms in the reduced-order model presented in Eqs. (17)–(20) are neglected. Furthermore, only first mode in the Galerkin discretization is considered in current linear analysis because the harvester presented is designed for low wind speeds, and hence for low shedding frequencies. The resulting equations are presented in the form of \(\dot{X}=BX\) where B is indicative of the linear state space matrix and \(X=\left[ {X_1 X_2 X_3 X_4 X_5 X_6 } \right] ^{t}\), where \(X_1 =f_1 \), \(X_2 =\dot{f_1 }\), \(X_3 =V^{p}\), \(X_4 =s\),\(X_5 =\dot{s}\) and \(X_6 =i^{e}\) are the state variables. The obtained linear matrix B of the governing equations of hybrid energy harvester is given by:

$$\begin{aligned} B=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0&{} 1&{} 0&{} 0&{} 0&{} 0 \\ {-\omega ^{2}}&{} {-2\varsigma \omega -\frac{C_\mathrm{D} \rho _0 D_t L_\mathrm{D} U}{2}\times \psi ^{2}}&{} \theta &{} \alpha &{} 0&{} {-C_{BL} \varphi (L_0 )} \\ 0&{} {\frac{\theta }{C_\mathrm{p} }}&{} {\frac{-1}{R_\mathrm{p} C_\mathrm{p} }}&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 1&{} 0 \\ {\frac{-\omega ^{2}}{D_t }\times A\times \psi }&{} {A/D_t \times \psi \times \left( {-\frac{C_\mathrm{D} \rho _0 D_t L_t U}{2}\times \psi ^{2}-2\varsigma \omega } \right) }&{} {-A/D_t \times \psi \times \theta }&{} {-\omega _\mathrm{s}^2 +\frac{A}{D_t }\times \psi \times \alpha }&{} {\lambda \omega _\mathrm{s} }&{} {-\frac{A}{D_t }\times C_{BL} \times \psi \times \varphi (L_0 )} \\ 0&{} {C_{BL} \times \varphi (L_0 )/L_\mathrm{c} }&{} 0&{} 0&{} 0&{} {-\left( {R_\mathrm{i} +R_\mathrm{c} } \right) /L_\mathrm{c} } \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$
(21)

where

$$\begin{aligned} \psi =\varphi \left( L \right) +\frac{D_t }{2}{\varphi }'\left( L \right) . \end{aligned}$$

This matrix with its six eigenvalues \(\lambda _{1}\) to \(\lambda _{6}\) holds important information about governing behavior of the hybrid energy harvesting system. The first two eigenvalues \(\lambda _{1}\) and \(\lambda _{2}\) regulate the physics of the mechanical system. They are complex conjugates for all the incoming wind speeds with real part pointing to the coupled damping of the hybrid VIV energy harvester, whereas imaginary part is indicative of the system’s coupled frequency. The fourth and fifth eigenvalues \(\lambda _{4}\) and \(\lambda _{5}\) correspond to the modified van der Pol wake oscillator model that has been used. The two transducers used for harnessing energy are responsible for \(\lambda _{3}\) and \(\lambda _{6}\) in linear state space matrix B. These two eigenvalues always remain real and negative because of dissipative effect of their external and internal load resistances. Due to our interest in understanding overall behavior of the system, we present the effects or impacts of different important governing parameters on hybrid energy harvester’s coupled damping and frequency. Both of these quantities are of valuable interest in predicting the overall behavior of the VIV energy harvesting system.

3.1 External load resistances’ impact on the coupled frequency and damping

The presence of electrical circuitries in the form of transducers underlines the importance of analyzing effects of the external load resistances on behavior of the hybrid energy harvester. For a zero wind speed \(U=0\,\hbox {m/s}\), the variations of the coupled damping and frequency are shown in Fig. 3a and b, where the external load resistance \(R_\mathrm{p}\) in the piezoelectric circuitry varies from a short-circuit configuration to an open-circuit one. It is observed that the coupled damping of the hybrid energy harvester exhibits a maximum value for a particular value of \(R_\mathrm{p}\) that comes out to be almost equal to \(1.6\times 10^{5}\,\Omega \) for the considered parameters of the system. It follows from plotted curves in Fig. 3a that an increase in the electromagnetic-inductive load resistance \(R_\mathrm{i}\) is accompanied with a decrease in the magnitude of coupled damping of the hybrid energy harvesting system. The difference in overall associated change due to \(R_\mathrm{i}\) on the coupled damping and frequency of the hybrid energy harvesting system as compared to \(R_\mathrm{p}\) is attributed to the added resistive-shunt damping effect because of the internal resistance of coil \(R_\mathrm{c}\) and the external load resistance in electromagnetic-inductive circuit. Inspecting the plotted curves in Fig. 3a, it is noted that higher values of \(R_\mathrm{i}\) can drive the system to a decreased coupled damping. This result is also evident from the plotted curves in Fig. 4a. The change in coupled damping and frequency of system due to \(R_\mathrm{p}\) is far greater than \(R_\mathrm{i}\) as evident from Fig. 4. The reason as already stated is due to internal resistance of the coil \(R_\mathrm{c}\). An important point to mention is that the coupled frequency of system is not significantly affected by \(R_\mathrm{p}\). A slight increase is observed between \(R_\mathrm{p}= 10^{4}\) and \(10^{6}\,\Omega \), when the coupled frequency increases from 27.28 to 27.84 rad/s as depicted in Fig. 3b. Moreover, \(R_\mathrm{i}\) has negligible effect on the coupled frequency, as shown in Figs. 3b and 4b. Interestingly, the effect of \(R_\mathrm{p}\) on the coupled damping or frequency of the harvester is far greater than \(R_\mathrm{i}\).

Fig. 3
figure 3

The variation of a coupled damping, b frequency as a function of piezoelectric load resistances \(R_\mathrm{p}\) for different electromagnetic-inductive load resistances \(R_\mathrm{i}\) for a zero wind speed and when \(L_{0}=110\times 10^{-3}\) m and \(m_{0}=1\times 10^{-3}\,\hbox {kg}\)

Full size image
Fig. 4
figure 4

The variations of a coupled damping, b frequency as a function of electromagnetic-inductive load resistances \(R_\mathrm{i}\) for different piezoelectric load resistances \(R_\mathrm{p}\), for a zero wind speed and when \(L_{0}=110\times 10^{-3}\,\hbox {m}\) and \(m_{0} =1\times 10^{-3}\,\hbox {kg}\)

Full size image
Fig. 5
figure 5

The variations of a coupled damping, b frequency as a function of piezoelectric load resistance \(R_\mathrm{p}\) for different masses of magnet \(m_{0}\) when \(L_{0} = 110\times 10^{-3}\,\hbox {m}\) and \(R_\mathrm{i}= 10\,\Omega \)

Full size image
Fig. 6
figure 6

The variations of a coupled damping, b frequency as a function of electromagnetic load resistance \(R_\mathrm{i}\) for different masses of magnet \(m_{0}\) when \(L_{0}=110\times 10^{-3}\,\hbox {m}\) and \(R_\mathrm{p} =1.6\times 10^{5}\,\Omega \)

Full size image
Fig. 7
figure 7

The variations of a coupled damping, b frequency as a function of piezoelectric load resistance \(R_\mathrm{p}\) for different locations of magnet \(L_{0}\) when \(R_\mathrm{i}=10\,\Omega \) and \(m_{0}=1\times 10^{-3}\,\hbox {kg}\)

Full size image
Fig. 8
figure 8

The variations of a coupled damping, b frequency as a function of electromagnetic-inductive load resistance \(R_\mathrm{i}\) for different locations of magnet \(L_{0}\) when \(R_\mathrm{p}=1.6\times 10^{5}\,\Omega \) and \(m_{0}=1\times 10^{-3}\,\hbox {kg}\)

Full size image

In VIV, coupled frequency of the system is of utmost importance considering the fact that the synchronization or lock-in only happens when shedding frequency \(\omega _\mathrm{s}\) comes close to the hybrid energy harvesting system’s coupled frequency. A change of coupled frequency would have a significant impact on the oscillating amplitudes of harvester as well as the levels of harvested power from both transducers. The negligible change of coupled frequencies as a result of varying \(R_\mathrm{p }\) and \(R_\mathrm{i }\) is beneficial in terms of keeping the same lock-in region. It is pertinent to mention that the piezoelectric properties are exceptionally important in terms of showing significant effect of the load resistance \(R_\mathrm{p}\) on coupled frequency of hybrid energy harvester. The chosen piezoelectric layer properties limit the extensive change in the coupled frequency as a result of change of \(R_\mathrm{p}\), that is actually beneficial for efficient energy harvesting as synchronization region does not change for the same shedding frequency and wind flow conditions. Therefore, it can be deduced from the current analyses that external load resistance values in the respective circuits would actually govern only the amplitudes of induced current in the electromagnetic circuit, generated voltage in the piezoelectric circuit and harvested power from both transducers.

3.2 Location and mass of the magnet impact on the coupled frequency and damping

The effect of mass of magnet \(m_{0}\) is depicted in Figs. 5a and 6a and it is concluded that it has no significant effect on the system’s coupled damping for different values of \(R_\mathrm{p}\) and \(R_\mathrm{i}\). Figures 5b and 6b show a very little change (which is negligible) in the coupled frequency of the system with use of magnet of different masses \(m_{0}\) for different values of \(R_\mathrm{p}\) and \(R_\mathrm{i}\). When it comes to the different locations of the magnet on beam, the plotted curves in Figs. 7 and 8 show that the placement of the magnet has a negligible effect on the coupled frequency of the hybrid energy harvester. On the other hand, the plots in Figs. 7 and 8 show a considerable increase in the coupled damping of the system as the magnet is moved away from the supported side, towards the free end, i.e., tip mass. This behavior is attributed towards large deflections of the beam that are predicted for locations of the magnet closer to its free end and therefore high resistive-shunt damping in the electromagnetic circuit is obtained, as compared to magnet’s placements closer to beam’s clamped side.

Fig. 9
figure 9

The variation of a coupled damping, b frequency as a function of incoming wind speed U for different piezoelectric load resistances \(R_\mathrm{p}\) when \(L_{0}=110\times 10^{-3}\,\hbox {m}, R_\mathrm{i}=10\,\Omega \), and \(m_{0}=1\times 10^{-3}\,\hbox {kg}\)

Full size image
Fig. 10
figure 10

The variations of a coupled damping, b frequency as a function of incoming wind speed U for different electromagnetic-inductive load resistances \(R_\mathrm{i}\) when \(L_{0}=110\times 10^{-3}\,\hbox {m}\), \(R_\mathrm{p}=1.6\times 10^{5}\,\Omega \), and \(m_{0}=1\times 10^{-3}\,\hbox {kg}\)

Full size image

It is concluded from the presented linear analysis that placement of the magnet although does not change harvester’s coupled frequency, strongly changes its coupled damping owing to small or large resistive-shunt damping in the electromagnetic circuit that depends on placement of the magnet on the beam and the coil in its close vicinity.

3.3 Wind speed impact on the coupled frequency and damping

The effects of the wind speed on the coupled damping and frequency are extremely important, considering the fact that large amplitude VIV happens only for a definite range of wind speeds. Figures 9 and 10 show the variations of the coupled damping and frequency with respect to the incoming wind speed U. It can be observed that when the wind speed is between 1 and 2.5 m/s, the coupled damping shows maximum values. When it comes to the coupled frequency, it can be observed that it decreases up to \(U = {1.2}{-}1.3\hbox {\,m/s}\) and then shows an increase till around 1.9–2 m/s, before settling down to a more or less constant value as demonstrated in Figs. 9b and 10b. These trends are plotted for different values of \(R_\mathrm{p}\) and \(R_\mathrm{i}\), and the impacts of the external load resistances on the coupled damping and frequencies for wind speed between 0 and 2.5 m/s are found to be similar to previous results; the only difference being that previous analyses of Figs. 3–8 were performed with \(U=0 \,\,\hbox {m/s}\).

4 Hybrid piezoelectric-electromagnetic energy harvester’s performance

4.1 Galerkin approach: convergence analysis

In order to utilize the developed nonlinear reduced-order model and determine the hybrid energy harvester’s performance, a convergence analysis is first performed by considering different number of modes in the Galerkin discretization in the developed model in Eqs. (17)–(20). The displacement of cylinder is calculated from Eq. (11) by w(L, t) where L is the length of the cantilever beam and is the location of the attached tip mass from the fixed supporting end. The summation for Eq. (11) is carried out for \(k= 1\) to n where n is 7 and observing which mode onwards the response does not vary. The same \(k = 1\) to 7 is also performed for Eqs. (17)–(20) as well, as Eqs. (11) and (17)–(20) are coupled anyways. The harvested average power levels in the piezoelectric circuit \(P_\mathrm{p\,avg}\), and in the electromagnetic circuit \(P_\mathrm{i\,avg}\), maximum piezoelectric generated voltage \(V_\mathrm{p}\) or \(V_\mathrm{pmax}\), maximum electromagnetic current \(i^{e}\), and the resulting maximum tip displacement y of the cylinder are evaluated at different wind speeds U for different number of modes n. It can be concluded from Fig . 11a–e that considering only one mode that is \(n = 1\) in the Galerkin discretization, does not accurately predict the response of the hybrid energy harvester. In fact, it underestimates or overestimates the behavior of the system. It is established from the results that any number of modes greater than one can precisely estimate the performance of the hybrid energy harvester. In the rest of this analysis, three modes in the Galerkin discretization are considered. The convergence at n modes means, that the results of modes \(n{-}1\), n, \(n+1 {\ldots }\) are the same. It is evident from Fig. 11 that convergence reaches for three modes. It should also be mentioned that for all the cases simulated and in the sections that follow, Runge–Kutta is used for solving Eqs. (11) and (17)–(20) for different wind speeds U. In each simulation for solving Eqs. (11) and (17)–(20) for a particular U, it is ensured that steady-state response is reached by considering enough time. Only constant increasing/forward steps in the wind speed are considered in the bifurcation/response diagrams to keep the focus on the hybrid energy harvester performance.

Fig. 11
figure 11

The variation of response of the hybrid energy harvester for different number of considered modes in Galerkin discretization a harvested piezoelectric power, b harvested electromagnetic-inductive power, c harvested piezoelectric voltage, d harvested electromagnetic current, e displacement of cylinder when \(L_{0}=110\times 10^{-3}\,\hbox {m}\), \(R_\mathrm{p}=1.6\times 10^{5}\,\Omega , R_\mathrm{i} = 10\,\Omega \), and \(m_{0} =1\times 10^{-3}\,\hbox {kg}\)

Full size image

4.2 External load resistance’s impact on the hybrid energy harvester’s performance

The proposed hybrid VIV energy harvester with two separate transduction mechanisms comes with two separate electrical circuitries, each associated with its own transduction mechanism. The prediction of the effectiveness of the energy harvester’s operation would be incomplete without investigating the effects of the external load resistances on the response of the energy harnessing system as demonstrated in the linear analysis as well. The linear analysis revealed a strong effect of \(R_\mathrm{p}\) and \(R_\mathrm{i}\) on the coupled damping, that pointed to an impact on the overall behavior of the system.

It should be mentioned here, that the change in incoming wind speed changes the qualitative dynamics of the system, as the cylinder and beam only oscillate with high amplitudes of oscillation for a certain range of wind speed. The change in qualitative dynamics of a system due to some governing parameter, which in this case is incoming wind speed, is called bifurcation and therefore a bifurcation diagram in the current work refers to response of system versus incoming wind speed. For analyzing performance of the hybrid energy harvester as a result of a change of \(R_\mathrm{p}\) in the piezoelectric layer, five different \(R_\mathrm{p}\) load resistances are considered that vary from short- to open-circuit configurations with inductive load resistance \(R_\mathrm{i}\) set equal to \(10\,\Omega \). The bifurcation/response diagrams for the definite range of wind speeds in which the synchronization or lock-in region takes place, and maximum response that comes out would be the focus of interest. From the linear analysis, it is already established that very less (near to negligible) change in the coupled frequency of the energy harvester is observed for a change of the piezoelectric load resistance and virtually no change is observed for a change in the electromagnetic-inductive load resistance. Therefore, a shift of the synchronization region for different values of external load resistances is not expected. The concern is the strong effect of the external load resistances on the coupled damping of the system that is demonstrated in Figs. 9 and 10. The definite range of wind speeds in which there is a sharp change in the coupled damping comes out to be between U = 1.2 and 1.9 m/s based on the performed linear analysis, and this is the focus of interest in all the bifurcation/response diagrams that will be plotted.

It should be mentioned here that all analyses are performed by using the developed nonlinear reduced-order model of Eqs. (17–20). The predicted average harvested piezoelectric power \(P_{\mathrm{p}\,\mathrm{avg}}\), inductive power \(P_{\mathrm{i}\,\mathrm{avg}}\), maximum generated piezoelectric voltage \(V_\mathrm{p}\), maximum electromagnetic current \(i^{e}\), and maximum tip displacement y of the circular cylinder are plotted in Fig. 12a–e with respect to the incoming wind flow speed. All of these quantities besides \(P_{\mathrm{p}\,\mathrm{avg}}\) and \(P_{\mathrm{i\,avg}}\), that are plotted here and in the rest of the paper, are maximum and not root mean square (RMS). It can be observed from Fig. 12e that the tip displacement y shows a decrease from maximum when \(R_\mathrm{p}=10^{3}\,\Omega \) up to minimum at \(R_\mathrm{p}=1.6\times 10^{5}\,\Omega \) going through the considered \(R_\mathrm{p}=4\times 10^{4}\,\Omega \), for the range of U in synchronization region. This is followed by an increase in the tip displacement up to the open-circuit configuration \(R_\mathrm{p}=10^{8}\,\Omega \) going through the considered \(R_\mathrm{p}=5\times 10^{5}\,\Omega \). The tip displacement of the circular cylinder is again maximum at \(R_\mathrm{p}=10^{8}\,\Omega \). These responses corroborate with the obtained results in Figs. 3, 5, and 7 where it was pointed that a critical load resistance (\(R_\mathrm{p}=1.6\times 10^{5}\,\Omega \)) takes place for maximum coupled damping, and two different external load resistances in the piezoelectric circuit can give same magnitude of coupled damping of the hybrid energy harvester. Furthermore, the electromagnetic current \(i^{e}\) and average harvested inductive power \(P_\mathrm{i\, avg}\) show the same trend as observed in the tip displacement of the harvester. The reason behind this is that \(R_\mathrm{i}\) is set equal to \(10\,\Omega \). This tendency can be seen in Fig. 12b and d. The maximum generated piezoelectric voltage \(V_\mathrm{p}\), on the other hand, exhibits a trend where the voltage increases from short- to open-circuit configuration of the external resistance \(R_\mathrm{p}\). Interestingly, the average harvested power \(P_\mathrm{p\, avg}\) shows unique behavior as compared to other already observed responses, where very low and high \(R_\mathrm{p}\) are giving low harvested power levels whereas intermediate piezoelectric load resistances are found to be suitable for harnessing maximum wind energy for the wind speeds in the synchronization region.

Fig. 12
figure 12

Bifurcation diagrams of the hybrid energy harvester for different piezoelectric load resistances a harvested piezoelectric power, b harvested electromagnetic power, c generated piezoelectric voltage, d generated electromagnetic current, and e displacement of the cylinder when \(R_\mathrm{i}=10\,\Omega \), \(L_{0}=100\times 10^{-3}\) m, and \(m_{0} = 1\times 10^{-3}\) kg

Full size image

The impact of the electromagnetic-inductive load resistances on the performance of the hybrid energy harvesting system is examined in Fig. 13a–e when \(R_\mathrm{i}=10^{-2}\,\Omega \), \(10\,\Omega \), \(50\,\Omega \), \(10^{2}\,\Omega \) and \(10^{3}\,\Omega \) and setting \(R_\mathrm{p}=1.6\times 10^{5}\,\Omega \). The bifurcation/response diagram of the tip displacement shows an increment for an increase in \(R_\mathrm{i}\) as was evident from the linear analysis that showed a decrease in the coupled damping. The average harvested power \(P_\mathrm{p\,avg}\) and maximum generated voltage \(V_\mathrm{p}\) across the piezoelectric circuitry shows exactly the same trend as the tip displacement y, because \(R_\mathrm{p}\) is kept constant for the performed analyses. When it comes to \(i^{e}\), it is demonstrated that it is maximum for a short-circuit configuration of \(R_\mathrm{i}=10^{-2}\,\Omega \) whereas it keeps on decreasing as the external resistance is increased up to the open-circuit values. Interestingly, the average harvested electromagnetic power \(P_\mathrm{i\,avg}\) is maximum for \(R_\mathrm{i}=10\,\Omega \) or also exhibits a high value for another intermediate resistance value of \(R_\mathrm{i}=50\,\Omega \). The behavior of \(i^{e}\) and \(P_{{i} _\mathrm{avg}}\) is demonstrated in Fig. 13b and d, respectively.

Fig. 13
figure 13

Bifurcation diagrams of the hybrid energy harvester for different electromagnetic load resistances a harvested piezoelectric power, b harvested electromagnetic power, c generated piezoelectric voltage, d generated electromagnetic current, and e displacement of the cylinder when \(R_\mathrm{p}=1.6\times 10^{5}\,\Omega \), \(L_{0}=100\times 10^{-3}\) m, and \(m_{0} =1\times 10^{-3}\) kg

Full size image

The performance analysis of the hybrid harvester with respect to different piezoelectric and electromagnetic-inductive external load resistances was carried out. It is observed that no shift or change in the synchronization or lock-in region, that is average or maximum amplitudes of responses with respect to wind speeds, is observed as a result of change of \(R_\mathrm{p}\) or \(R_\mathrm{i}\). It is established that there are optimum values of the external load resistances for respective electrical circuitries that can maximize the harvested power in the proposed hybrid arrangement, by vortex-induced oscillations.

4.3 Mass and location of magnet impact on the hybrid energy harvester’s performance

The influence of the location and mass of the magnet on the proposed hybrid energy harvester is investigated. The linear results previously pointed to no effect of the mass of magnet on both the coupled damping and frequency. No effect of the coupled damping implies no change in magnitude of the response of the harvester, whereas no frequency change further indicates no shift in synchronization region. In order to substantiate the initial prediction of the effect of the magnet’s mass, a nonlinear analysis is carried out using the developed nonlinear reduced-order model.

The synchronization region for the wind speeds which should be our focus of interest in the bifurcation/response diagrams is estimated from the linear analysis presented in Figs. 9 and 10. The incoming wind speed changes the qualitative dynamics of the system as the cylinder only oscillates with high amplitudes of oscillation for a certain range of wind speed. The change in qualitative dynamics of a system due to some governing parameter, which in this case is incoming wind speed, is called bifurcation and therefore the response versus the incoming flow speed diagrams in Fig. 14a–e are called bifurcation diagrams. It should be mentioned that the linear analysis was performed with \(m_{0}=1\times 10^{-3}\) kg, but Figs. 5 and 6 that see the variation of \(m_{0}\) are not forecasting a change of coupled frequency and therefore no shift in synchronous region anyways. Consequently, the bifurcation/response diagrams of the hybrid energy harvester are recorded for three different considered masses, namely \(m_{0}=1\times 10^{-3}\) kg, \(m_{0}=3\times 10^{-3}\) kg, \(m_{0}=5\times 10^{-3}\) kg for a definite range of wind speeds established before. It is demonstrated in Fig. 14a–e that there is no effect of the mass of magnet even when it is increased from 1 to 5 g. This result is exceptionally important and useful considering the fact that for effective energy harvesting, masses of magnet can be chosen freely (between 1 and 5 g), without any concerns about its negative impact on the magnitude of the harvested power in both piezoelectric and electromagnetic circuitries.

Fig. 14
figure 14

Bifurcation diagrams of the hybrid energy harvester for different masses of the magnet a harvested piezoelectric power, b harvested electromagnetic power, c generated piezoelectric voltage, d generated electromagnetic current, and e displacement of the cylinder when \(R_\mathrm{p}=1.6\times 10^{5}\,\Omega \), \(R_\mathrm{i} = 10\,\Omega \), and \( L_{0}=110\times 10^{-3}\) m

Full size image
Fig. 15
figure 15

Bifurcation diagrams of the hybrid energy harvester for different locations of the magnet a harvested piezoelectric power, b harvested electromagnetic power, c generated piezoelectric voltage, d generated electromagnetic current, and e displacement of the cylinder when \(R_\mathrm{p}=1.6\times 10^{5}\,\Omega \), \(R_\mathrm{i}=10\,\Omega \), and \( m_{0}=1\times 10^{-3}\) kg

Full size image

The cantilever beam with piezoelectric layer on one side is considered in this study as already discussed. This gives room to place the magnet on any location of the beam and the electromagnetic coil in its vicinity. The placement of the magnet on the harvester beam is examined in order to understand the response and the dynamics of the system. The linear analysis presented in Figs. 7 and 8 shows that the coupled damping increases as the magnet is placed closer to the tip end of the cantilever beam. It was indicated that the coupled frequency of the system remains virtually unaffected and hence it is predicted that no considerable shift in the synchronous region happens. As stated, it is shown from the obtained linear analysis results that the coupled damping is strongly affected by the location of the magnet. Hence, a huge impact/effect on the magnitude of responses of the hybrid system is expected.

The output responses of the system are plotted with respect to the wind speeds in Fig. 15a–e when \(L_{0}=0.2\,\mathrm{L}\), \(L_{0}=0.4\,\mathrm{L}\), \(L_{0}=0.6\,\mathrm{L}\), and \(L_{0}=0.8\,\mathrm{L}\). A careful examination reveals that sharp increase in the coupled damping, as a result of shifting the magnet position away from the supporting end of the beam, is translated into a decrease in the tip displacement of the oscillating tip mass cylinder, as shown in Fig. 15e. More importantly, it should be noted that this increase in the coupled damping and decrease in the displacement as \(L_{0}\) is increased is also accompanied by a decrease in the harvested piezoelectric power \(P_\mathrm{p\,avg}\) and generated voltage \(V_\mathrm{p}\) as depicted in Fig. 15a and c. The voltage \(V_\mathrm{p}\) decreases from peak voltage of 15.2–5.8 V in the synchronization regions which translate into 720\(\upmu \)W and 105\(\upmu \)W of average power \(P_\mathrm{p\,avg}\), respectively, when the location of magnet is moved from 0.2 to 0.8 L away from supporting end of the beam. Interestingly, the generated electromagnetic current \(i^{e}\) and power \(P_{i\mathrm{avg}}\) have an opposite effect where both of them show a considerable increase as the magnet is shifted closer to the tip mass away from the beam support, as depicted in Fig. 15b and d. It is noted that maximum generated \(i^{e}\) shows an increase from nearly 0.5 mA to around 4 mA, whereas harvested inductive power \(P_\mathrm{i\,avg}\) shows an increase from an average power of 1.31 to 82\(\upmu \)W in the synchronization region. These opposite trends in piezoelectric and electromagnetic circuitries are evident. Indeed, as large transverse deflections of the beam appear near and at the tip mass of the beam, and as the magnet is attached closer to the tip of the beam, higher amount of current and correspondingly harvested inductive power are obtained. This large drawn current across the electromagnetic transducer increases the coupled damping of the system due to the presence of the coupling term \(C_{Bl} \varphi _k \left( {L_0 } \right) i^{e}\) in Eq. 17, that consequently decreases the generated voltage \(V_\mathrm{p}\) and harvested power \(P_\mathrm{p\,avg}\) of the piezoelectric transducer.

It is established that the magnet location is of utmost importance for an efficient design of a hybrid energy harvesting system. The increase in the harvested electromagnetic power by a closer placement of magnet to the tip mass comes at the expense of decreasing the harvested piezoelectric power. Therefore, a careful choice of the magnet placement is needed in order to ensure a continuous supply of power from two different devices according to their separate required needs.

4.4 Relationship between the hybrid energy harvester’s performance and the input parameters

Aeroelastic energy harvesters are designed to be operated in well-defined locations and for specific environmental conditions. A careful selection of the designed parameters ensures efficient energy harvesting for a particular place with a particular range of wind speeds. In order to make that choice of right parameters, a careful analysis which determines the effects of the critical parameters should be carried out while considering operational wind speeds. The proposed VIV hybrid energy harvester has been shown to be strongly dependent on the external load resistances and the placement of the magnet. In order to determine the effects of the external load resistances on the behavior of the energy harvester, individual responses are plotted as a function of these two external resistances for different wind speeds within the synchronization region, that is the region of interest for energy generation purposes. The hybrid energy harvester’s response for different wind speeds gives an insight in the system’s behavior, which would help in choosing the optimum range or values of the external load resistances for a specific wind speed for effective energy harvesting.

The different responses of the hybrid energy harvesting system with respect to the external piezoelectric load resistance \(R_\mathrm{p}\) are plotted in Fig. 16a–e. It follows from these plotted curves that maximum average piezoelectric power \(P_{\mathrm{p}\,\mathrm{avg}}\) is obtained for two different values of \(R_\mathrm{p}\). This behavior is consistent for different considered wind speeds in the synchronization region. The behavior of the generated voltage \(V_\mathrm{p}\) is rather different where it increases, from short- to open-circuit values of \(R_\mathrm{p}\). It is observed that an increase in \(R_\mathrm{p}\) 10\(^{4}\,\Omega \) to \(10^{7}\,\Omega \) is accompanied by a sharp increase in \(V_\mathrm{p}\) whereas it stabilizes after that. When it comes to the harvested electromagnetic power \(P_\mathrm{i\,avg}\), electromagnetic current \(i^{e}\), and the tip displacement y of the harvester, a sharp decrease and increase is observed between \(10^{4}\,\Omega \) to 10\(^{7}\,\Omega \) that is explained due to the increase in the coupled damping of the system between these external piezoelectric load resistances as explained by the linear analysis in Figs. 3, 5 and 7. An increase in the wind speed only increases the magnitude of the responses with the overall qualitative trend remaining the same. The same behavior of \(P_\mathrm{i}\) and \( i^{e}\) is also explained because the external electromagnetic load resistance during the whole analysis is kept constant as \(R_\mathrm{i}=10\,\Omega \).

Fig. 16
figure 16

Variations of the response of the hybrid energy harvester as a function of the external piezoelectric load resistance for different considered wind speed values a harvested piezoelectric power, b harvested electromagnetic power, c generated piezoelectric voltage, d induced electromagnetic current, and e tip displacement of the system for \(R_\mathrm{i}=10\,\Omega \), \(m_{0}=1\times 10^{-3}\) kg, and \(L_{0}=110\times 10^{-3}\) m

Full size image

The trends of harvested power, generated voltage, induced current and tip displacement of the energy harvester, y, with respect to the electromagnetic load resistance \(R_\mathrm{i}\), for three different wind speeds are plotted in Figs. 17a–e. It is interesting to observe that \(P_\mathrm{p\,avg}\), \(V_\mathrm{p}\), and y are showing an increase with increase in \(R_\mathrm{i}\), that is agreeing with the decrease in the coupled damping as \(R_\mathrm{i}\) is increased from its short- to open-circuit values. This reason is also explained because \(R_\mathrm{p}\) is kept constant at \(R_\mathrm{p}=10^{3}\,\Omega \). The harvested electromagnetic power \(P_\mathrm{i\,avg}\), on the other hand, shows a peak at a particular \(R_\mathrm{i}\). This maximum \(P_\mathrm{i\,avg}\) of 95 \(\upmu \)W is obtained for external resistances between \(R_\mathrm{i}=16\,\Omega \) and \(18\,\Omega \) when \(U=1.8\hbox {m/s}\). The reason of these particular external load resistances \(R_\mathrm{i}\) responsible for maximizing \(P_\mathrm{i\,avg}\) is explained due to their closeness in value with internal resistance of the coil that is kept at \(R_\mathrm{c}=16\,\Omega \). This behavior remains persistent with other considered speed values in synchronization region as well. Importantly, very low and high values of \(R_\mathrm{i}\) generate very low powers in the electromagnetic circuitry. When it comes to flow of current \(i^{e}\) in the electromagnetic circuitry, Fig. 17d depicts its variation with respect to \(R_\mathrm{i}\). The external load resistances of \(R_\mathrm{i}\) where on the one hand produce maximum flow of current \(i^{e}\) for its short-circuit configuration, produce minimum values once \(R_\mathrm{i}\) is increased to an open-circuit configuration. Values of \(R_\mathrm{i}\) between 1 and 100 \(\Omega \) sharply reduce the \(i^{e}\) from 6 to 1 mA when \(U=1.8\,\hbox {m/s}\), whereas the decrease from \(100\,\Omega \) to open-circuit value is rather gradual. It should be mentioned that the behavior of all the responses with respect to the external electromagnetic load resistances is qualitatively same for wind speeds in the synchronization region that is the zone of interest for energy harvesting purposes.

Fig. 17
figure 17

Variations of the response of the hybrid energy harvester as a function of the external electromagnetic load resistance for different considered wind speed values a harvested piezoelectric power, b harvested electromagnetic power, c generated piezoelectric voltage, d induced electromagnetic current, and e tip displacement of the system for \(R_\mathrm{p}=10^{3}\,\Omega \), \(m_{0}=1\times 10^{-3}\) kg, and \( L_{0}=110\times 10^{-3}\) m

Full size image

The dependence of performance of proposed hybrid harvester was investigated with the variation of external load resistances on individual outputs. It was demonstrated that a careful choice of the external load resistances in respective circuitries of transducers maximizes power outputs and would result in efficient energy harvesting.

Fig. 18
figure 18

Comparison between the bifurcation diagrams of the hybrid energy harvester and its classical counterparts when \(R_\mathrm{p}=1.6\times 10^{5}\,\Omega \), \(R_\mathrm{i}=10\,\Omega \), \( m_{0}=1\times 10^{-3}\) kg and \( L_{0}=110\times 10^{-3}\) m

Full size image
Fig. 19
figure 19

Comparison between the bifurcation diagrams of the hybrid energy harvester and its classical counterparts when \(R_\mathrm{p}=10^{3}\,\Omega \), \(R_\mathrm{i}=10\,\Omega \), \( m_{0}=1\times 10^{-3}\) kg and \( L_{0}=110\times 10^{-3}\) m

Full size image
Table 2 Comparison between the coupled frequency of a fully functional hybrid energy harvester and classical energy harvesters PE or EM as well as hybrid with nonfunctional piezoelectric EHNP or electromagnetic circuit PHNE
Full size table

5 Comparative analyses between hybrid electromagnetic-piezoelectric VIV energy harvesters and their classical counterparts

The idea of simultaneous use of two different transduction mechanisms utilizing VIV oscillations needs further scrutiny to conclude its effectiveness. In order to understand the limitations and benefits, a hybrid transduction utilizing VIV has to offer, a comparative study is performed between hybrid VIV energy harvester under investigation and their pure classical counterparts. Two different transduction mechanisms working simultaneously under wind flow increase the overall coupled damping of the system as compared to a pure classical piezoelectric VIV (PE) or a pure classical electromagnetic VIV (EM). This is due to the presence of the resistive-shunt damping effect from both transducers. It should be mentioned that a classical harvester here refers to a single functioning transducer being present and used on the harvester. Therefore, a qualitative as well as quantitative comparison between piezoelectric circuitry of hybrid VIV (PH) and PE, as well as electromagnetic circuitry of hybrid VIV (EH) and EM needs to be drawn and discussed. Furthermore, a hybrid VIV energy harvester can be operated for pure piezoelectric energy harvesting by short circuiting the electromagnetic circuitry (PHNE). This actually implies that there is a nonfunctional magnet and electromagnetic circuitry on the energy harvester. This case is not separately considered in this study as the mass of the magnet does not affect the system’s response as demonstrated above. Therefore, this case is the same as PE. Similarly, hybrid energy harvesting system can be used for pure electromagnetic energy harvesting by short circuiting the piezoelectric transducer (EHNP). This case is really important as this means that the piezoelectric layer is physically attached to the cantilever beam but due to short-circuit in its circuitry, only electromagnet transduction is working. The working of EHNP would be totally different than pure classical EM because the natural frequency of the dynamical system changes due to the physical presence of a nonfunctional piezoelectric layer, and therefore a shift in the synchronization region is expected for similar flow conditions. This EHNP in Figs. 18 and 19 is referred to as “Power by EM (with piezoelectric layer)” and represented by a black dotted line. In order to simulate all the different cases of PE, EM, PH, EH, PHNE and EHNP, the parameter values of Table 1 are used as required. For instance, PE as mentioned refers to a pure classical piezoelectric VIV. In this configuration, there is no need to use electromagnet transducer’s properties from Table 1 as compared to a case of PH and EH which requires us to use all the parameter values of Table 1. The same goes for the rest of the cases.

The power output of a classical piezoelectric VIV harvester (PE) is compared to that of a piezoelectric transducer of the proposed hybrid VIV mechanism (PH) for \(R_\mathrm{p}=1.6\times 10^{5}\,\Omega \) in Fig. 18a. Clearly, the power generated by PH is a little less than its classical counterpart PE. The \(R_\mathrm{i}\) is kept at a value of \(10\,\Omega \) for hybrid VIV and could have been fixed at any other random value to draw a comparison with a sole working classical piezoelectric harvester. The same hybrid energy harvester electromagnetic circuitry (EH) power \(P_\mathrm{i\,avg}\) is compared to that of a classical EM harvester solely working with an electromagnet. The EM VIV system with no piezoelectric layer exhibits a totally different coupled frequency as compared to its hybrid counterpart with a piezoelectric layer. Table 2 highlights this fact and it can be seen that EM shows a reduced frequency of 18.08 rad/s as compared to the proposed two transducers hybrid VIV configuration which exhibits a natural frequency equals to 27.56 rad/s. This behavior means that a smaller shedding frequency, \(\omega _\mathrm{s}=\frac{2\pi \times s_t \times U}{D}\), is required for the EM to generate energy in the synchronization or lock-in region, as evidently shown in Fig. 18a. The electromagnetic power generated by electromagnetic-inductive circuitry EH is far less than EM. This is predicted because the coupled damping of the system is increased due to the presence of a piezoelectric layer that is also generating power in piezoelectric circuit. More importantly, as described above, if the hybrid energy harvester is used as a pure EM by short circuiting piezoelectric layer that is EHNP, then the coupled frequency of the system remains the same as of a hybrid one. Figure 18b demonstrates the harvested electromagnetic power \(P_\mathrm{i\,avg}\) from this EHNP with a nonfunctioning piezoelectric layer is larger than both its counterparts EH and EM ones.

The plotted curves in Fig. 19a and b show comparison between the bifurcation diagrams of the hybrid energy harvester and its classical counterparts when \(R_\mathrm{p}=10^{3}\,\Omega \) and \(R_\mathrm{i}=10\,\Omega \). The harvested piezoelectric power from PH again comes out to be lower than its sole working classical piezoelectric VIV counterpart that is PE. For harvested electromagnetic power \(P_\mathrm{i\,avg}\), pure classical EM again shows a shift in the synchronous region and lower wind speed is required to harvest energy whereas power generated by EH is again smaller than that of EHNP with both of them sharing the same synchronization region that is same wind speed range. The only difference is that EH is only a fraction smaller in magnitude than EHNP and greater than classical EM. The different coupled frequencies exhibited by these systems are presented in Table 2.

A comparison is carried out between hybrid VIV and single transducer working harvesters. It is concluded that if the external load resistances are carefully chosen, then, the energy generated from the proposed VIV working in hybrid arrangement produces nearly same power as a classical piezoelectric harvester whereas it can produce greater power from the electromagnetic circuitry as compared to its classical sole electromagnetic counterpart. Moreover, if the hybrid energy harvester is made to function with a single transducer by short circuiting the other one, then, the power generated would be more than the prior hybrid one. Nevertheless, the importance of VIV hybrid energy harvesters for powering multiple electronic gadgets as compared to individual classical harvesters is clear. The average power required by civil engineering application sensors and health monitoring gadgets are in the order of 1 \(\upmu \)W to 1000 \(\upmu \)W [1,2,3,4]. If more than one electronic gadget need to be fed with electrical power, individual piezoelectric and electromagnetic energy harvesters would cover more space whereas a hybrid energy harvester is effective in saving space as well as producing comparable levels of harvested power as compared to classical counterparts.

6 Conclusions

Energy harvesting by converting vortex-induced oscillations of a circular cylinder was investigated by simultaneously using piezoelectric and electromagnetic transduction mechanisms. The hybrid energy harvester is composed of a piezoelectric cantilever beam with a tip mass circular cylinder and a magnet placed on the beam. The magnet has a coil placed in its close vicinity. The nonlinear reduced-order model was developed, and numerical study was performed by varying different parameters and drawing parallel between the proposed hybrid configuration and its classical pure piezoelectric and electromagnetic-inductive counterparts. This hybrid energy harvester’s response came out to be significantly dependent on the external load resistances present in the respective circuitries as well as the location of the magnet on the beam. The mass of the magnet was found to have negligible impact on the response of the hybrid energy harvester. It was also indicated that a careful choice of the piezoelectric layer properties can minimize the effect of the external load resistances on the coupled frequency of the harvester and enable the hybrid energy harvester to work effectively in a range of wind speeds. It was also demonstrated that a smart selection of the external load resistances helps achieve similar piezoelectric and electromagnetic levels of harvested power from the proposed hybrid configuration for powering multiple electronic devices instead of using many individual single operating harvesters.