1 Introduction

Converting ambient and aeroelastic vibrations, using piezoelectric transducers, to electric power has been proposed for powering micro-electromechanical systems [1, 2] and heath monitoring and wireless sensors [3] and for replacing small batteries that have a finite life span and require hard and expensive maintenance [4, 5]. To date, most of energy harvesting from mechanical vibrations concentrated on exploiting ambient vibrations [6–12]. More recently, few investigations [13–20] focused on the conversion of aeroelastic vibrations of wings to electrical power. These investigations have been mostly concerned with aeroelastic responses of streamlined surfaces, such as wings. In comparison to wing flutter, the galloping aeroelastic instability results in large oscillations. This is very beneficial when using piezoelectric transducers because the harvested voltage is directly related to the oscillation amplitude.

As the wind speed exceeds a critical value, an elastic bluff body undergoes transverse oscillations, called galloping. Den Hartog [21] was the first to study and explain the galloping phenomenon. He used the quasi steady hypothesis to describe the aerodynamic loads. He also developed a criterion for the occurrence of galloping. Several studies [22–33] investigated the effects of various parameters on the behavior of the galloping of different structures. Barrero-Gil et al. [34] investigated theoretically the possibility of using transverse galloping to extract energy. Specific methods on how to harvest this energy were not discussed. Based on previous numerical and experimental data, Barrero-Gil et al. [33, 34] modeled the transverse aerodynamic force using a cubic polynomial for high Reynolds numbers and a seven-order polynomial for Reynolds numbers below 200. Barrero-Gil et al. [33] investigated the possibility of transverse galloping of a square cylinder at low Reynolds numbers (Re<200). They showed that a square cylinder cannot gallop below a Reynolds number of 159.

The objective of this work is to investigate the possibility of designing enhanced piezoelectric energy harvesters that exploit the galloping of square cylinders. Particularly, we aim to determine the power levels that can be generated from these oscillations for low and high Reynolds numbers by modeling the aerodynamic loads using the quasi steady approximation. To this end, we attach a piezoelectric transducer to the transverse degree of freedom of the cylinder. We develop a phenomenological model for the global coupled (transverse displacement and electrical circuit) system in Sect. 2. In Sect. 3, we perform a linear analysis to determine the effects of the electrical load resistance and the Reynolds number on the onset of galloping, which is due to a Hopf bifurcation. In Sect. 4, we perform a nonlinear analysis, based on the normal form of this bifurcation, to determine the effects of the load resistance and the Reynolds number on the harvested power, voltage output, and transverse displacement. Conclusions are presented in Sect. 5.

2 Mathematical modeling of transverse galloping

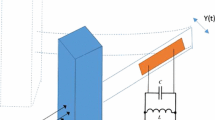
We consider a galloping-based piezo-aeroelastic energy harvester consisting of an elastically-mounted square cylinder and a piezoelectric transducer attached to its transverse degree of freedom, as shown in Figs. 1(a) and 1(b). When this system is subjected to an incoming flow, the cylinder undergoes galloping in the transverse direction as the wind speed exceeds a critical value. The governing equations of the coupled electromechanical system are written as

(1)
(2)

where m is the total mass per unit length, D is the characteristic dimension of the body normal to the incoming flow, U is the velocity of the incoming flow, ρ is the fluid density, ω n is the cylinder natural frequency, ξ is the mechanical damping ratio, θ and χ are the electromechanical coupling coefficients, V is the harvested voltage across the load resistance R, C p is the capacitance of the piezoelectric layer, and F y and C y are respectively the aerodynamic force per unit length and force coefficient in the normal direction to the incoming flow.

Fig. 1
figure 1

(a) Simplified and (b) three-dimensional schematics of piezo-aeroelastic energy harvester based on transverse galloping of a square cylinder

Full size image

Generally, in transverse galloping, the characteristic time scale of the structure oscillation, which is approximately equal to \(\frac{2 \pi}{\omega_{n}}\), is much larger than the characteristic time scale of the flow which is O(\(\frac{D}{U}\)). Furthermore, if the vortex shedding frequency is much larger than the natural frequency of the oscillating square cylinder, the quasi steady hypothesis can be used to evaluate the aerodynamic force [26]. In this work, we consider two configurations that cover low and high Reynolds number (Re) regimes of galloping square cylinders. For Reynolds numbers below 200, Barrero-Gil et al. [33] showed that the transverse aerodynamic force can be estimated by the odd terms in a seventh-order polynomial function of \(\frac{\dot{y}}{U}\), that is,

(3)

Here, \(\frac{\dot{y}}{U}=\tan\alpha\), where α is the angle of attack. Based on the numerical results of Sohankar et al. [35], the coefficients in Eq. (3) are estimated by Barrero-Gil et al. [33] as

The aerodynamic coefficient C y is directly related to the lift and drag coefficients C l and C d , respectively, by C y =−[C l cos(α)+C d sin(α)].

At high Reynolds numbers, Barrero-Gil et al. [34] showed that the aerodynamic force coefficient can be approximated by a cubic polynomial expansion of \(\frac{\dot{y}}{U}\) with the coefficients being independent of the Reynolds number. Then the transverse aerodynamic force can be written in the form

(4)

where a 1 and a 3 are empirical coefficients obtained by fitting C y with a cubic polynomial of \(\dot{y}/U\).

The Den Hartog stability criterion [21] states that a section of a structure on a flexible support is susceptible to galloping when the linear coefficient a 1 is positive. For the energy harvester considered here, the onset of galloping is determined when the electromechanical damping of the system changes from a positive to a negative value. The nonlinear coefficient a 3 is always negative, because as the angle of attack increases, C y increases, achieves a maximum value, and then decreases. For this work, our focus is on a square cylinder. The linear and nonlinear coefficients used to determine the transverse aerodynamic force are empirically determined from the experiments of Parkinson and Smith [22]; that is, a 1=2.3 and a 3=−18.

Two different configurations are considered in this work: low and high Reynolds number configurations. In the low Reynolds number configuration, D is set equal to 1 mm, m=0.044 kg, ω n =10 rad/s, ξ=7.102×10−6, and the speed is limited to a maximum value of 2 m/s so that the Reynolds number remains below 200. The galloping parameters in this configuration are the same as those used by Barrero-Gil et al. [33]. The transverse aerodynamic force is estimated by Eq. (3). In the high Reynolds number configuration, D is set equal to 1.5 cm, m=0.44 kg, ω n =62.83 rad/s, and ξ=0.0013.

3 Effects of the electrical load resistance and Reynolds number on the onset of galloping

Introducing the piezoelectric transducer and load resistance causes the global frequency and damping of the electromechanical system to be different from those of the mechanical system (without the piezoelectric transducer). These effects can be determined from the analysis of the linear system in which only the first term of the aerodynamic force is considered. Introducing the following state variables:

(5)

we rewrite the linear part of the coupled equations of motion as

(6)
(7)
(8)

Clearly, these equations have the form

(9)

where

$$B =\left [ { \begin{array}{c@{\quad}c@{\quad}c} 0 & 1 & 0 \\ -\omega_n^2 & - (2 \xi\omega_n - \frac{1}{2} \frac{\rho U D a_1}{m}) &\frac{\theta}{m} \\ \noalign{\vspace*{6pt}} 0 & -\frac{\theta}{C_p} & -\frac{1}{ R C_p} \\ \end{array} } \right ] $$

and a 1=−2.7+0.017Re in the low Reynolds number configuration and a 1=2.3 in the high Reynolds number configuration.

The matrix B(U) has a set of three eigenvalues λ i , i=1,2,3. The first two eigenvalues are similar to those of a pure galloping problem in the absence of the piezoelectricity effect. The third eigenvalue is a result of the electromechanical coupling. This eigenvalue (λ 3) is always real negative as in the case of piezoelectric systems subjected to base or aeroelastic excitations [10–12, 17]. The first two eigenvalues are complex conjugates (\(\lambda_{2}=\overline{\lambda_{1}}\)). The real part of these eigenvalues represents the damping coefficient and the positive imaginary part corresponds to the global frequency of the coupled system. Because λ 3 is always real negative, the stability of the trivial solution depends only on the first two eigenvalues. The trivial solution is asymptotically stable if the real part of λ 1 is negative. On the other hand, if the real part of λ 1 is positive, the trivial solution is unstable. The speed U g for which λ 1=0 corresponds to the onset of instability or galloping. The matrix B also includes all parameters that affect the linear part of the system. This matrix is used to investigate the effects of the load resistance and the Reynolds number on the onset of galloping.

Figure 2 shows the effect of the electrical load resistance on the onset speed of galloping for both configurations. We note that, in the low Reynolds configuration, the galloping speed increases with the load resistance to about 2 m/s, corresponding to Re=200, at about 300 Ω. In the absence of the piezoelectric transducer, Barrero-Gil et al. [33] showed that the considered square cylinder does not gallop below a Reynolds number of 159. For the short-circuit configuration in which the load resistance is very small (approximately 10 Ω), our predicted Reynolds number for the onset of galloping matches that obtained by Barrero-Gil et al. [33].

Fig. 2
figure 2

Variations of the galloping speed with the load resistance for both low and high Reynolds number configurations

Full size image

For the high Reynolds numbers, the onset speed of galloping increases as the load resistance increases from low values. It reaches a maximum value near R=105 Ω and decreases to lower speeds for load resistances near 107 Ω, as shown in Fig. 2. In the absence of the piezoelectric transducer, using the Krylov–Bogoliuvov method, Barrero-Gil et al. [34] showed that the onset speed of galloping depends on the damping ratio ξ, the dimensionless mass ration m ∗, and the linear coefficient a 1 by the following relation: U ∗=4m ∗ ξ/a 1 where U ∗=U/(ω n D) and m ∗=m/(ρD 2). For the short-circuit configuration, our onset speeds of galloping match those obtained by Barrero-Gil et al. [34].

4 Nonlinear analysis

4.1 Effect of higher-order terms in the aerodynamic load

In Fig. 3, we compare the level of the harvested power when modeling the transverse aerodynamic force using all terms in Eq. (3) with those obtained when the higher-order terms a 5 and a 7 are neglected. The results show that, for low wind speeds, the first and third terms are sufficient for predicting the bifurcation and characterizing the system behavior and instability. However, for higher wind speeds, between 1.85 m/s and 2 m/s, the level of harvested power is underpredicted when the fifth- and seventh-order terms are neglected. Furthermore, we note that there is no hysteresis when including these higher-order nonlinear terms unlike other systems in which such nonlinear terms resulted in the appearance of hysteresis and unstable branches [36].

Fig. 3
figure 3

Effect of the higher-order nonlinear terms in the model of the aerodynamic force, Eq. (3), on the harvested power when R=100 Ω

Full size image

4.2 Normal form of Hopf bifurcation

Next, we perform a nonlinear analysis of the coupled system to determine the type of instability or bifurcation associated with the proposed galloping-based harvesters. To this end, we add a perturbation term σ U U f to the onset speed and express the air speed as U=U f +σ U U f . Using this expansion, we rewrite the matrix B(U) as

$$B(U)=B(U_f)+\sigma_U B_1(U_f) $$

where

$$B_1(U_f) =\left [ { \begin{array}{c@{\quad }c@{\quad }c} 0 & 0 & 0 \\ 0 & \frac{\rho D (b_1 U_f+2 b_2 U_f^2)}{2 m} & 0 \\ 0 & 0 & 0 \\ \end{array} } \right ] $$

and b 1 and b 2 are related to the linear coefficient a 1 by a 1=b 1+b 2 U. For the low Reynolds number configuration, b 1 and b 2 are set equal to −2.7 and 1.7, respectively; and for the high Reynolds number configuration, b 1 and b 2 are set equal to 2.3 and 0, respectively. Neglecting the higher-order terms (i.e., a 5 and a 7) in the low Reynolds number configuration, we write the equations of motion for both configurations in the following form:

(10)

where

$$\mathbf{C}^T=\left [{ \begin{array}{c} {0, \frac{\rho D (b_3+b_4 U_f+b_5 U_f^2)}{2 m U_f} X_2^3, 0} \\ \end{array} } \right ] $$

where b 3, b 4, and b 5 are related to the nonlinear coefficient a 3 by a 3=b 3+b 4 U+b 5 U 2. For the low Reynolds number configuration, b 3, b 4, and b 5 are set equal to 10, −9.6, and −10, respectively. For the high Reynolds number configuration, b 3, b 4, and b 5 are set equal to −18, 0, and 0, respectively.

Letting G be the matrix whose columns are the eigenvectors of the matrix B(U f ) corresponding to the eigenvalues ±jω 1 and −μ 3 and defining a new vector Y such that X=G Y, we rewrite Eq. (10) as

(11)

Multiplying Eq. (11) from the left by the inverse G −1 of G yields

(12)

where K=G −1 B 1(U f )G and J=G −1 B(U f )G is a diagonal matrix whose elements are the eigenvalues ±jω 1 and −μ 3. We note that \(Y_{2} =\overline{Y_{1}}\), and hence Eq. (12) can be written in component form as

(13)
(14)

where the N i (Y) are trilinear functions of the components of Y.

According to the center-manifold theorem [37], there exists a center manifold

$$Y_3=H_3(Y_1,\bar{Y}_1) $$

such that the dynamics on this manifold is similar to the dynamics of the system represented by Eqs. (13) and (14). Equation (14) is then rewritten as

(15)

Because σ U is small and N 1 and N 3 are cubic functions of the components of Y, H 3 is zero to the third approximation. Keeping only the resonance terms [37] in Eq. (15), we obtain the complex-valued normal form

(16)

where α e depends on the cubic nonlinear coefficients b 3, b 4, and b 5, as shown in Table 1 for both Reynolds number configurations when the load resistance is set equal to 104 Ω.

Table 1 Values of the onset speed of galloping and the real parts of β and α e when R=100 Ω and R=104 Ω for the low and high Reynolds number configurations, respectively
Full size table

Next, we express Y 1 in the polar form

$$ Y_{1}=\frac{1}{2} a e^{j (\omega_1 t+\gamma)} $$
(17)

where a is the amplitude of oscillation and γ is its phase. Substituting Eq. (17) into Eq. (16) and separating the real and imaginary parts, we obtain the following real-valued normal form of the Hopf bifurcation:

(18)
(19)

where β=σ U K 11 and the subscripts r and i denote the real and imaginary parts, respectively.

Equation (18) has three equilibrium solutions:

$$a=0\quad\mbox{and}\quad a=\pm\sqrt{\frac{-4 \beta_r}{\alpha_{er}}} $$

where a=0 is the trivial solution. The two other solutions are nontrivial. The origin is asymptotically stable for β r <0 or β r =0 and α er <0, unstable for β r >0 or β r =0 and α er >0. The nontrivial solutions exist when β r α er <0. They are stable (supercritical Hopf bifurcation) for β r >0 and α er <0 and unstable (subcritical Hopf bifurcation) for β r <0 and α er >0.

The effective nonlinearity α e is a function of the system parameters, including the load resistance and the linear and nonlinear coefficients a 1, b 3, b 4, and b 5. Table 1 shows β r and α er when the electrical load resistance is set equal to 100 Ω for the low Reynolds number configuration and 104 Ω for the high Reynolds number configuration.

For the low Reynolds number configuration, we note that the effective nonlinearity depends on b 3, b 4, and b 5. On the other hand, for the high Reynolds number configuration, it depends only on b 3 because the nonlinear coefficient in this configuration is independent of the Reynolds number. For the proposed values of the b i , we note that the instability is a supercritical Hopf bifurcation for both configurations, as presented in Table 1.

The transverse displacement y, the voltage output V, and harvested power P are related to the amplitude a of the limit cycle by

(20)
(21)
(22)

where (⋅) r and (⋅) i denote the real part and imaginary part, respectively. To validate this analytical solution (normal form of Hopf bifurcation), we compare in Fig. 4 its predictions with those obtained by numerically integrating the high Reynolds number configuration when the electrical load resistance is set equal to R=104 Ω. The results show that the normal form predicts accurately all amplitudes near the onset of galloping. Thus, we conclude that the developed linear and nonlinear analyses provide a methodology to characterize the behavior of transverse galloping near bifurcation for both Reynolds number configurations. In the rest of this investigation, only numerical results are presented.

Fig. 4
figure 4

Comparison between the analytical predictions and the numerical integration of the full system: (a) transverse displacement and (b) harvested power for the high Reynolds number configuration when R=104 Ω

Full size image

5 Effects of the load resistance and Reynolds number on the level of harvested power and transverse displacement

The effects of the load resistance on the transverse displacement and harvested power in the low Reynolds number configuration are shown in Figs. 5(a) and 5(b), respectively. The plots show that increasing the load resistance results in an increase in the onset speed of galloping. Furthermore, the transverse displacement decreases at higher load resistances. This is due to the increase in the electromechanical damping with increasing load resistance. On the other hand, we note that the harvested power increases with the load resistance. Particularly, the level of harvested power is around 0.015 mW for a freestream velocity near 2 m/s.

Fig. 5
figure 5

Variations of the (a) transverse displacement and (b) harvested power with the freestream velocity for different values of the load resistance in the low Reynolds number configuration

Full size image

In the high Reynolds number configuration (freestream velocity between 2 m/s and 15 m/s), we show in Figs. 6(a) and 6(b) variations of the oscillation amplitudes and harvested power with the freestream velocity over a wide range of electrical load resistance. The results show that varying the load resistance changes the onset speed of galloping. Particularly, this speed is the largest when the load resistance has a value near R=105 Ω. The results also show that the load resistance impacts the amplitude of the transverse displacement. Particularly, for R=105 Ω, the transverse displacement is the smallest because the electromechanical damping is the highest. Inspecting the curves in Fig. 6(b), we note that an increase in the load resistance is not accompanied with an increase in the harvested power. Rather, there is an optimum value of the load resistance for maximizing the harvested power. This maximum level is associated with the minimum transverse displacement obtained by using a load resistance of about 105 Ω. For this load resistance, the power that can be generated is around 1.7 W for a wind speed of about 15 m/s. However, the onset of galloping for this configuration is the highest with the wind speed being near 10 m/s. Furthermore, for a wind speed of 4 m/s, this harvester can generate 0.9 mW and 1.2 mW when R=103 Ω and R=107 Ω, respectively, and the displacement is 0.75D.

Fig. 6
figure 6

Variations of the (a) transverse displacement and (b) harvested power with the freestream velocity for different values of the load resistance in the high Reynolds number configuration

Full size image

6 Conclusions

We have investigated the concept of exploiting the galloping phenomenon of a square cylinder to harvest energy over different ranges of wind speeds (Reynolds numbers). The analysis shows that the electrical load resistance and the Reynolds number play an important role in determining the onset of galloping and the harvested power. The harvested energy at high Reynolds numbers is much larger than that at Reynolds numbers below 200. In the low Reynolds number applications, the harvested power can be enhanced by increasing the load resistance. In the high Reynolds number applications, the harvested power can be optimized, with minimum displacement, by properly choosing the load resistance. However, this choice may result in a configuration in which the onset speed of galloping is relatively high.