1 Introduction

Converting vibrations to electric power by using piezoelectric transduction has been the topic of many investigations over the past two decades. Different sources of vibrations, including ambient and aeroelastic vibrations, have been considered. The interest has been in converting these vibrations to electrical power for either operating low-power consumption devices, such as microelectromechanical systems, actuators [1–3], and heath monitoring and wireless sensors [4, 5], or replacing small batteries that have a finite life span or would require hard and expensive maintenance [6, 7]. To date, most of energy harvesting from mechanical vibrations have concentrated on exploiting base excitations. More recently, Bryant and Garcia [8], Erturk et al. [9], De Marqui et al. [10, 11] and Abdelkefi et al. [12–15] investigated conversion of aeroelastic vibrations of wings to electrical power.

A well-known phenomenon in bluff body aerodynamics is the alternate shedding of vortices and the associated unsteady aerodynamic forces acting on the body. When these vortices are shed at a frequency near the natural frequency of the bluff body, lock-in or synchronization takes place and resonant transverse vibrations occur [16–25]. These vibrations are referred to as vortex-induced vibrations (VIV). Williamson and coworkers [26–32] determined that there are different response modes, depending on the mass-damping parameter. Nayfeh and coworkers [33–37] used modern methods of nonlinear dynamics to identify the parameters of phenomenological models that can be used to represent the lift coefficient on a stationary cylinder.

The objective of this work is investigate the possibility of using VIV oscillations of structures to harvest electrical power. Particularly, we aim to determine the power levels that can be generated from VIV oscillations of a circular cylinder and variations of these levels with the freestream velocity. To this end, we attach a piezoelectric transducer to the transverse displacement degree of freedom of the cylinder and develop a representative model for the coupled VIV-energy harvesting problem. Because of the nonlinear mechanisms associated with these vibrations and energy harvesting, we also aim to assess the effects of the load resistance and initial conditions on the harvested power levels.

Generally, high-fidelity simulations of the VIV phenomenon are very expensive in terms of computing power and time. Such simulations can be significantly complicated if three-dimensional effects, turbulence structures, and elasticity are considered. Consequently, assumptions are often made to produce simple and accurate predictions of the VIV phenomenon and the structural response. Different models that are based on the van der Pol oscillator or its combination with other nonlinear oscillators have been proposed for VIV predictions. In this work, a mathematical model that accounts for the coupled lift force, cylinder motion, and harvested voltage is used to investigate and analyze the problem of energy harvesting from VIV oscillations. This model is presented in Sect. 2. In Sect. 3, we perform a linear analysis to determine the effect of the electrical load resistance on the natural frequency of the rigid cylinder and the onset of the synchronization region. In Sect. 4, we perform a nonlinear analysis to determine the level of the power that can be harvested and the effect of the load resistance on the harvested power, voltage output, lift coefficient, and displacement amplitude. A summary and conclusions are presented in Sect. 5.

2 Mathematical model

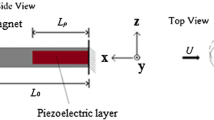
Bishop and Hassan [38] were the first to suggest modeling the lift over a circular cylinder due to vortex shedding by a self-excited oscillator. Hartlen and Currie [39] used a Rayleigh oscillator to model the lift and coupled this oscillator with the motion of the cylinder by a velocity term. A modified van der Pol oscillator was used by Skop and Griffin [20] to represent the lift. Skop and Griffin [21] made a correction to the predicted response frequencies by adding cubic terms to the lift equation. In this work, we use the empirical model of the vortex-induced vibrations of spring-mounted rigid cylinders as developed by Skop and Griffin [21]. In this model, a modified van der Pol equation is used to represent the lift and is coupled to the equation of motion of the cylinder by a velocity term. As shown in Fig. 1, a piezoelectric transducer is attached to the transverse displacement of the cylinder to harvest energy.

Fig. 1
figure 1

Schematic of a piezoelectric energy harvester of a freely oscillating cylinder

Full size image

Coupling between the cylinder motion and the harvested voltage is modeled using the Gauss law. The fluctuating lift coefficient C L induced on a rigid circular cylinder by the vortex-shedding process is modeled by Skop and Griffin [21]

(1)

where Y is the transverse displacement of the cylinder, D is the diameter of the cylinder, and ω s is the shedding frequency, which is related to the freestream velocity U by the Strouhal number S. This relation is given by ω s =2πSU/D. The four coefficients C L0, G, H, and F represent parameters, which can be identified from experimental results. These parameters depend on S G =ξ/μ, where ξ is the nondimensional damping coefficient and μ is the nondimensional mass coefficient. Skop and Griffin [21] provided empirical functions for each of these parameters that are valid in the Reynolds number range between 400 and 105, over which S and C L0 remain constant. These parameters are functions of S G =ξ/μ and are given by

(2)
(3)
(4)
(5)

The equation of motion of a spring-mounted rigid cylinder that includes the effect of the piezoelectric coupling can be expressed as

(6)

where M and L are used to represent the total mass and length of the cylinder and ρ is the fluid density. The natural frequency ω n and the damping ratio ξ of the spring-mass system are measured in a stationary fluid having the same physical properties as the used fluid. In Eq. (6), θ is the electromechanical coupling coefficient and V is the harvested voltage across the load resistance. The electromechanical coupling term appears also in the governing equation of the voltage, which is given by the Gauss law and written as [9, 12]

(7)

where R is the load resistance and C p is the capacitance of the piezoelectric layer.

3 Linear analysis of the electromechanical model

Because the load resistance may affect the structural natural frequency and damping of the harvester, we analyze the coupled electromechanical problem by performing a linear analysis of the governing equation of the cylinder and the Gauss law equation. Using the following state variables:

(8)

we rewrite the equations of motion as

(9)
(10)
(11)

These equations can be expressed in the following matrix form:

(12)

where B includes all parameters that affect the linear part of the system. This matrix is used to investigate the effects of the load resistance, damping ratio, and electromechanical coupling coefficients on the structural natural frequency and then on the onset of synchronization. Below, we consider two different configurations, namely, System 1 and System 2 of Skop and Griffin [20]. The parameters of these two configurations are presented in Table 1.

Table 1 Parameters of the two considered configurations
Full size table

The matrix B in Eq. (12) has a set of three eigenvalues k i , i=1,2,3. These eigenvalues are arranged so that the first two are complex conjugates; that is, \(k_{2}=\bar{k}_{1}\). The third eigenvalue, which is due to the electromechanical coupling, is always negative. These eigenvalues are solutions of the characteristic equation

(13)

where \(\lambda=\frac{k}{\omega_{n}}\). Clearly, the roots of Eq. (13) depend on all linear system parameters: total mass, damping coefficient, electromechanical coupling coefficients, and load resistance.

Considering the parameters presented in Table 1, we obtain from Eq. (13) the following. For System 1:

(14)

For System 2:

(15)

Clearly, the roots, and hence the eigenvalues, of Eqs. (14) and (15) depend on the load resistance R. Figure 2a shows variations of the imaginary and real parts of the complex eigenvalues with the load resistance. In both systems, a steep increase is noted over the load resistance values between 104 Ω and 105 Ω. The imaginary part of this eigenvalue constitutes the dimensional global frequency. For the parameters of System 1, the dimensional frequency is approximately equal to 326.72 rad/s when the load resistance is between 102 Ω and 103 Ω; we refer to this frequency as the short global frequency. Increasing the load resistance causes an increase in the global frequency with a steep increase to values near 530 rad/s when the load resistance is near R=106 Ω; we refer to this frequency as the open global frequency. For the parameters of System 2, the short global frequency is approximately equal to 188.496 rad/s and the open global frequency is approximately equal to 292.33 rad/s. We note that the difference between the open and short global frequencies depends on all of the linear parameters.

Fig. 2
figure 2

Variations of (a) the imaginary parts and (b) the real parts of the electromechanical model with the load resistance for the two considered system parameters

Full size image

As the electromechanical damping, it follows from Fig. 2b that it is maximum for specific values of the load resistance for both considered configurations. We note also that the region of load resistances over which the electromechanical damping is relatively high coincides with the region over which the steep increase in the global frequency occurs. This is true for both configurations. Away from this region, the damping coefficient is small and the global frequency is almost constant for both configurations.

This linear analysis gives a clear idea about the effect of the load resistance on the onset of the synchronization region and the electromechanical damping variations. Particularly, increasing the load resistance can significantly change both of the onset of synchronization and the electromechanical damping. These effects have an impact on the level of harvested power.

4 Nonlinear analysis: effects of load resistance on synchronization regime and harvested power

We investigate the effect of the load resistance on the cylinder displacement, lift coefficient, and harvested power. Furthermore, we study the effect of the load resistance on the short- and open-circuit configurations.

The dependence of the system response on the freestream velocity is shown in Figs. 3 and 4 for both configurations, respectively. We note that, as the freestream velocity is increased, the synchronization region, defined by the region of higher amplitudes, is varied. Furthermore, we note a clear hardening behavior that is associated with resonances near the global frequencies, 326.72 rad/s for R=102 Ω and 532.83 rad/s for R=106 Ω for the first configuration, and near 188.495 rad/s for R=102 Ω and 292.33 rad/s for R=106 Ω for the second configuration. This behavior is a result of the cubic nonlinearity in the lift coefficient. Furthermore, as the load resistance increases from 103 Ω to 105 Ω, the region of synchronization shifts to higher freestream velocities for both configurations. However, the hardening response for these values of the load resistance is not as clear as it is for R=102 Ω and R=106 Ω in both configurations.

Fig. 3
figure 3

Frequency-response curves of the (a) transverse displacement, (b) lift coefficient, and (c) harvested power for different values of the load resistance and for the first configuration

Full size image
Fig. 4
figure 4

Frequency-response curves of the (a) transverse displacement, (b) lift coefficient, and (c) harvested power for different values of the load resistance and for the second configuration

Full size image

The fact that changing the load resistance results in a change in the lock-in or synchronization region is expected from the linear analysis, which shows a delay in the onset of synchronization, in terms of higher freestream velocities, as the load resistance is increased. Furthermore, the high peaks in the transverse displacement when R=102 Ω and R=106 Ω for the first configurations and R=5×102 Ω and R=106 Ω for the second configuration are due to the relatively small electromechanical damping, as aforementioned (Fig. 2b). For the first configuration, we note that both maxima of the transverse displacement are small for the case when R=103 Ω and R=105 Ω. This result is expected because of the high electromechanical damping associated with these values of the load resistance (Fig. 2b). Concerning the second configuration, we note that the maximum transverse displacement is very small when R=105 Ω because, in this case, the electromechanical damping is very large (Fig. 2b).

Variation of the maximum of the lift coefficient with the freestream velocity for different values of the load resistance are shown in Figs. 3b and 4b for the first and second configurations, respectively. The observed variations when R=102 Ω and R=106 Ω for the first configuration and R=5×102 Ω and R=106 Ω for the second configuration are similar to the variations of the displacement in terms of exhibiting a clear hardening behavior. For resistance values near 103 Ω and 105 Ω, the lift coefficients are much smaller in comparison to those for R=102 Ω and R=106 Ω. Furthermore, we note the possibility of anti-resonance for R=103 Ω and R=105 Ω occurring right after the resonance peak in terms of freestream velocities. Figures 3c and 4c show the harvested power for different resistance values, they show maximum power levels near 0.1 and 1 mW that can be attained for R=102 Ω and R=106 Ω for the first configuration and maximum power levels near 0.01 and 0.2 mW that can be attained for R=5×102 Ω and R=106 Ω for the second configuration.

The observed hardening behavior is a result of the nonlinear phenomena associated with vortex-induced vibrations. Although these nonlinearities can be helpful in enhancing the levels of generated power, they can also cause a drop in the harvested power with a slight increase in the freestream velocity. This is due to the presence of an unstable branch, which renders the response to be dependent on the initial conditions. Figures 5a and 5d show variation of the harvested power for different values of the load resistance. The results clearly show a hysteresis associated with the hardening behavior for R=102 Ω and R=106 Ω for the first configuration. This behavior is not observed at the other considered resistances. Concerning the second configuration, the results also show a hysteresis associated with the hardening behavior for R=5×102 Ω, R=103 Ω, and R=106 Ω, as shown in Figs. 6a, 6b, and 6c.

Fig. 5
figure 5

Frequency-response curves of the harvested power for the first configuration and for different values of the load resistance when using different initial conditions

Full size image
Fig. 6
figure 6

Frequency-response curves of the harvested power for the second configuration and for different values of the load resistance when using different initial conditions

Full size image

Figures 7 and 8 show the short- and open-circuit configurations for the harvested power, voltage output, transverse displacement, and lift coefficient for the first and second configurations, respectively. These configurations are defined by setting the shedding frequency equal to the short and open global frequencies for both configurations, which are 326.72 rad/s and 532.83 rad/s for the first configuration and 188.495 rad/s and 292.33 rad/s for the second configuration. These shedding frequencies are obtained at the freestream velocities of 1.486 m/s and 2.423 m/s for R=102 Ω and R=106 Ω, respectively, in the first configuration. Concerning the second configuration, the freestream velocities, which correspond to the shedding frequencies of 188.495 rad/s and 292.33 rad/s, are, respectively, 0.857 m/s and 1.329 m/s. The results show optimum values of the load resistance for both of the short- and open-circuit configurations for which the harvested power is maximized. The harvested power is maximum in the short- and open-circuit configurations when the load resistance is set equal to R=600 Ω and R=3×105 Ω, respectively, for the first configuration. For the second configuration, the harvested power is maximum in the short- and open-circuit configurations when the electrical load resistance is approximately equal to R=700 Ω and R=4×105 Ω, respectively. For both short- and open-circuit configurations, the harvested voltage increases as the load resistance is increased and reaches a constant value. We note that, for the short-circuit configuration, an increase in the load resistance is followed by a decrease in the transverse displacement and lift coefficient before stabilizing at larger values. In the open-circuit configuration, an increase in the load resistance is accompanied with an increase in the transverse displacement and lift coefficient.

Fig. 7
figure 7

Variations of (a) the harvested power, (b) voltage output, (c) maximum transverse displacement, and (d) maximum lift coefficient, for the first configuration, with the load resistance for the short- and open-circuit configurations

Full size image
Fig. 8
figure 8

Variations of (a) the harvested power, (b) voltage output, (c) maximum transverse displacement, and (d) maximum lift coefficient, for the second configuration, with the load resistance for the short- and open-circuit configurations

Full size image

5 Conclusions

We investigate harvesting energy from vortex-induced vibrations (VIV) of a rigid circular cylinder by attaching a piezoelectric transducer to the transverse degree of freedom. We develop the coupled equations governing the lift, cylinder motion, and harvested voltage. The lift on the oscillating cylinder is modeled by a modified van der Pol equation and the Gauss law is used to model the coupling between the harvested voltage and the cylinder motion for two different configurations. The results show that the load resistance influences the onset of the synchronization (the shedding frequency is equal to the cylinder frequency) region and its characteristics. Increasing the load resistance shifts the onset of synchronization to higher freestream velocities. A comparison of the results obtained for the two configurations shows that synchronization depend the linear system parameters. The results also show that the nonlinearity associated with the vortex-induced oscillations results in a hardening behavior and hysteresis. The fast drop in the level of the generated power for some freestream velocities and its dependence on the initial conditions require a careful analysis of the problem of generating power from VIV. Variations in the synchronization region and an the drop in the lift coefficient and cylinder motion associated with energy harvesting from piezoelectric transducers suggest also the potential of using them for VIV control in different regions of freestream velocities.