1 Introduction

Dynamics of optical solitons has exhibited novel and vital properties and exists extensive application in many different real backgrounds of nonlinear optics [1,2,3,4,5]. Spatial and spatiotemporal solitons form with the coaction of diffraction, dispersion nonlinearity and/or external potential [6,7,8,9]. As the subject of intensive theoretical and experimental studies, spatial and spatiotemporal solitons exhibit different types of localized structures including fundamental solitons [10, 11], similaritons [12, 13], vortex solitons [14, 15], Hollow multipole soliton [16, 17], rogue waves [18, 19] and Hermite–Gaussian solitons [15, 20], and so on.

When the optical field frequency approaches a resonant frequency of the optical fiber material, the Kerr nonlinearity is not enough to describe self-focusing effect and cubic–quintic (CQ) nonlinearities are considered. According to the work of Pusharov et al. [21], CQ nonlinearities are introduced into the governing equation of the propagation of optical wave, that is, nonlinear Schrödinger equation (NLSE) by considering the refractive index nonlinearity as \(n=n_0+n_2|u|^2 +n_4|u|^4\), where u is the electric field amplitude, \(n_2=3\chi ^{(3)}/(8n_0), n_4=5\chi ^{(5)}/(16n_0)\) with the linear refractive index coefficient \(n_0\), and two components of the corresponding nonlinear dielectric tensors \(\chi ^{(3)}\) and \(\chi ^{(5)}\). Temporal and spatial solitons in the CQ nonlinear media have extensively studied [22, 23]. Historically, the topological quasi-soliton solutions for the variable-coefficient CQNLSE were reported in the pioneering work of Serkin et al. [24]. Avelar et al. [25] obtained periodic wave and soliton solutions with CQ nonlinearities modulated in space and time. Competing CQ nonlinearity in the bulk medium generates stable vortex solitons [26].

Vector spatial solitons with two or more components can mutually self-trap in the nonlinear medium and have much more application in the control of optical beam diffraction, design of the logic gates, all-optical switching devices and information transformation [27, 28]. When two optical waves of different frequencies co-propagate in a medium and interact nonlinearly through the medium, or when two polarization components of a wave interact nonlinearly at some central frequency, the Manakov equation can describe the propagation of solitons [29]. Multicomponent structures for N fields governed by a coupled NLSE make vector solitons possess richer dynamical propagation behaviors than the scalar solitons [29, 30]. Self-trapping of scalar and vector dipole spatial solitons in 2D Kerr media were studied [31]. However, spatial vector solitons in CQ nonlinear medium are relatively few studied. In this paper, we study spatial vector multipole and vortex solitons in a CQ nonlinear medium and discuss the form and structure pattern of these solitons.

2 Exact vector soliton solutions of CQNLSE

The evolution of vector beams consisting of N mutually incoherent components co-propagating in a CQ nonlinear medium with the spatially modulated refractive index \(n=n_0+n_1R(r)+n_2g_3(r)|u|^{2}+n_4g_5(r)|u|^{4}\) can be described by the following N-coupled (2+1)-dimensional variable-coefficient CQNLSE

$$\begin{aligned} \text {i}\frac{\partial u_k}{\partial z}= & {} -\frac{1}{2}\nabla _\bot ^{2}u_k +g_3(r)\sum _{k=1}^N|u_k|^{2}u_k\nonumber \\&+\, g_5(r)\sum _{k=1}^N|u_k|^{4}u_k+R(r)u_k, \end{aligned}$$
(1)

where \(u_k(z,r,\varphi )(k=1,2, \ldots N)\) are the slowly varying envelopes with the propagation distance z and the polar coordinates r and \(\varphi \) in the transverse plane, as well as the 2D Laplacian \(\nabla _\bot ^{2}=\frac{\partial ^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{\partial ^2}{\partial \varphi ^2}\). The cubic nonlinearity coefficient \(g_3(r)\), quintic nonlinearity coefficient \(g_5(r)\) and the transverse modulation R(r) are all functions of radial coordinate \(r\equiv (x,y)\). The transverse x, y and longitudinal z coordinates, respectively, are normalized to the beam width \(w_0=(2k_0^2n_1)^{-1/4}\) and diffraction length \(L_\mathrm{d}=k_0w_0^2\) with the wave number \(k_0=2\pi n_0/\lambda \) at the input wavelength \(\lambda \). If \(u_k\) represents the macroscopic wave function of the condensate, R(r) is the external potential, Eq. (1) is the coupled CQ Gross–Pitaevskii equation in Bose–Einstein condensates.

We look for the spatially localized stationary exact solution of Eq. (1) in the form

$$\begin{aligned} u_k(r,\varphi ,z)=A (r)\varPhi _k(\varphi )\exp (-i\kappa z), \end{aligned}$$
(2)

where \(\kappa \) is the propagation constant, and A(r) is a real function for the localization demand \(\lim _{r\rightarrow \pm \infty }A(r)=0\).

Substituting Eq. (2) into Eq. (1) leads to

$$\begin{aligned}&\frac{r^2}{A}\left\{ \frac{\partial ^2A}{\partial r^2}+\frac{1}{r}\frac{\partial A}{\partial r}+ 2[\kappa -R(r)]A\right. \nonumber \\&\left. -2g_3(r)A ^{3}-2g_5(r)A ^{5}\right\} =l^2, \end{aligned}$$
(3)
$$\begin{aligned}&-\frac{1}{\varPhi _k}\frac{\partial ^2\varPhi _k}{\partial \varphi ^2}=l^2, \end{aligned}$$
(4)

with the self-consistency condition \(\sum _{k=1}^N|\varPhi _k|^{2}=1\), and the topological charge l.

From Eq. (4), we obtain solution

$$\begin{aligned} \varPhi _k=C_k\cos (l\varphi )+D_k\sin (l\varphi ). \end{aligned}$$
(5)

In the following, we consider two-component case with \(N=2\), thus \(C_1=1,D_1=\text {i} q,C_2=0,C_2=\sqrt{1+q^2}\) with \(q(0\le q\le 1)\). The limit value \(q=1\) corresponds to vortex soliton, and \(q=0\) corresponds to the multipole soliton, where the topological charge \(l=1{-}5\) denotes dipole, quadrupole, hexapole, octopole and dodecagon solitons.

Assuming \(A (r)\equiv \rho (r)U[\chi (r)]\), \(g_3(r)\equiv G_{3}r^{-2}\rho ^{-6}(r)/2,g_5(r)\equiv G_{5}r^{-2}\rho ^{-8}(r)/2\), with \(\chi (r)\equiv \int _{0}^{r}\rho ^{-2} (s)s^{-1}\mathrm{d}s\), Eq. (3) is split into two equations

$$\begin{aligned} \rho ^{\prime \prime }+ & {} \frac{1}{r}\rho ^{\prime }+\left[ 2\kappa -2R(r)-\frac{l^2}{r^{2}}\right] \rho =\frac{E}{r^{2}\rho ^{3}},\nonumber \\- & {} \frac{\mathrm{d}^{2}U}{\mathrm{d}\chi ^{2}}+G_{3}U^{3}+G_{5}U^{5} =E U, \end{aligned}$$
(6)

where \(E,G_3\) and \(G_{5}\) are constants. Note that via the procedure above, the coupled CQNLSE (1) is reduced to solvable stationary CQNLSE (6), which has rich solutions such as Jacobian elliptic function solution and soliton solution [32].

Therefore, it is crucial to construct exact solutions of Eq. (2) to obtain solutions of the underlying coupled CQNLSE (1). Equation (2) is not easily solved. Physical solutions impose several restrictions on \(\rho \): expressions for \(R(r), g_3(r)\) and \(g_5(r)\) hint that \(\rho \) cannot change its sign and diverges (\(\rho \rightarrow \infty \) ) at \(r\rightarrow \infty \); thus, the inhomogeneous nonlinearity strength is bounded and the integration in R(r) converges. If E is a nonzero constant, then Eq. (2) is the Ermakov–Pinney equation [33]; thus, solution of \(\rho (r)\) becomes

$$\begin{aligned} \rho =\sqrt{\frac{1}{r}(\alpha \phi _1^2+2\beta \phi _1\phi _2+\gamma \phi _2^2)}, \end{aligned}$$
(7)

where \(E=(\alpha \gamma -\beta ^2)W^2\) with three constants \(\alpha , \beta , \gamma \) and constant Wronskian \(W=\phi _1\phi _{2r}-\phi _2\phi _{1r}\) with \(\phi _1(r)\) and \(\phi _2(r)\) being two linearly independent solutions of \(\phi _{rr}+[2\kappa -2R(r)-l^2/r^2]\phi =0\).

Especially, when \(E=0\) in Eq. (2), if R(r) is the transverse parabolic modulation with \(R(r)=\frac{1}{2}\omega ^2r^{2}\), then \(\rho \) can be found in terms of the Whittaker’s \(\mathrm{M}\) and \(\mathrm{W}\) functions [34], namely, \(\rho (r)=r^{-1}[c_1M(\kappa /2\sqrt{2\omega },l/2,\sqrt{2\omega }r^2) +c_2W(\kappa /2\sqrt{2\omega },l/2,\sqrt{2\omega }r^2)]\), where the restrictions on \(\rho \) require \(c_{1}c_{2}>0\). Without the transverse modulation with \(\omega =0\), \(\rho \) becomes \(\rho (r)=c_3 B_J(l,\sqrt{2\kappa }r)+c_4B_Y(l,\sqrt{2\kappa }r)\), \(B_{J}\) and \(B_{Y}\) being, respectively, the Bessel functions of the first and second kinds [35], and constants satisfying \(c_{3}c_{4}>0\).

Considering the localization condition \(A(0)=A(\infty )=0\), when \(G_5=-3G_3^2/(16\delta ^2)\) with \(\delta =2\sqrt{E/(m^2+4)}\), Eq. (6) has the following exact solution

$$\begin{aligned} U=\frac{2nm\lambda }{\sqrt{G_3/2}}\frac{\text {sn}\left[ 2n\lambda \chi (r),m\right] }{\sqrt{1+\text {dn}\left[ 2n\lambda \chi (r),m\right] }}, \end{aligned}$$
(8)

where the soliton order number \(n=1,2,3, \ldots \), \(\text {sn}(\cdot )\) and \(\text {dn}(\cdot )\) are the Jacobian elliptic sine function and the Jacobian elliptic function of the third kind, respectively, and \(\lambda \equiv K(m)/\chi (\infty )\) with the complete elliptic integral of the first kind K(m) and modulus m. From solution (8), \(G_3>0\) and \(G_5<0\), thus solution (8) exists only in the focusing cubic and defocusing quintic medium.

Therefore, from Eqs. (2), (5), (7) and (8), we can obtain the spatially localized stationary exact solution of Eq. (1).

Fig. 1
figure 1

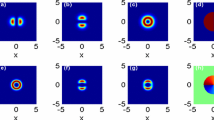
(Color online) Multipole solitons with the intensity of a, e, i, m component \(|u_1|^2\), b, f, j, n component \(|u_2|^2\), c, g, k, o total quantity \(|u|^2=|u_1|^2+|u_2|^2\) and d, h, l, p phase in the presence of the parabolic transverse modulation \(R=\omega ^2 r^{2}/2\). The parameters are chosen as \(c_{1}=0.8,c_2=0.7,\kappa =0.3,\) \(\omega =0.005,G_3=50,q=0,n=1\) with (a)-(d) \(m=1\), (e)-(h) \(m=2\), (i)-(l) \(m=3\), (m)-(p) \(m=4\)

Full size image

3 Vector multipole and vortex solitons

Vector multipole and vortex solitons in the presence of the parabolic transverse modulation \(R=\omega ^2 r^{2}/2\) present abundant structures. Vector multipole and vortex solitons with the intensity of (a), (e), (i) and (m) component \(|u_1|^2\), (b), (f), (j) and (n) component \(|u_2|^2\), (c), (g), (k) and (o) total quantity \(|u|^2=|u_1|^2+|u_2|^2\) and (d), (h), (l) and (p) phase are shown in Figs. 1, 2, 3 and 4.

Fig. 2
figure 2

(Color online) Multipole solitons with the intensity of a, e, i, m component \(|u_1|^2\), b, f, j, n component \(|u_2|^2\), c, g, k, o total quantity \(|u|^2=|u_1|^2+|u_2|^2\) and d, h, l, p phase in presence of the parabolic transverse modulation \(R=\omega ^2 r^{2}/2\). The parameters are chosen as the same as those in Fig. 1 except for \(n=2\)

Full size image

If \(n=1\), the mutually complementary two-petal structures for components \(|u_1|^2\) and \(|u_2|^2\) in Fig. 1a, b constitute a ring structure in Fig. 1c, and the phase of this ring structure is a half-circle in Fig. 1d. The mutually complementary four-“petal” structures for components \(|u_1|^2\) and \(|u_2|^2\) in Fig. 1e, f also constitute a ring structure in Fig. 1g, and the phase of this ring structure is two opposite slices of sectors in Fig. 1h. The mutually complementary six-“petal” structures for components \(|u_1|^2\) and \(|u_2|^2\) in Fig. 1i, j also constitute a ring structure in Fig. 1k, and the phase of this ring structure is three slices of sectors and the angle between two adjacent sectors is 60\(^{\circ }\) in Fig. 1l. The mutually complementary eight-“petal” structures for components \(|u_1|^2\) and \(|u_2|^2\) in Fig. 1m, n also constitute a ring structure in Fig. 1o, and the phase of this ring structure is four slices of sectors, and the angle between two adjacent sectors is 45\(^{\circ }\) in Fig. 1p. Therefore, there exist the mutually complementary 2m-“petal” structures for components \(|u_1|^2\) and \(|u_2|^2\), and the phase is made up of m-slices of sectors. With the add of m, the hole in the center of the ring enlarges.

Fig. 3
figure 3

(Color online) Multipole solitons with the intensity of a, e, i, m component \(|u_1|^2\), b, f, j, n component \(|u_2|^2\), c, g, k, o total quantity \(|u|^2=|u_1|^2+|u_2|^2\) and d, h, l, p phase in the presence of the parabolic transverse modulation \(R=\omega ^2 r^{2}/2\). The parameters are chosen as the same as those in Fig. 1 except for a–d \(m=1,n=3\), e–h \(m=3,n=3\), i–l \(m=1,n=4\), m–p \(m=3,n=4\)

Full size image

With the increase of the soliton order number n, the layer of multipole solitons adds in Figs. 2 and 3. If \(n=2\), the structure and phase of multipole solitons possess two layers in Fig. 2, and if \(n=3,4\), the structures and phases of multipole solitons possess three and four layers, respectively, in Fig. 3. From phase patterns for (d), (h), (l) and (p) in Figs. 1, 2 and 3, we know these ring-like solitons for (c), (g), (k) and (o) in Figs. 1, 2 and 3 are not vortex solitons because the phases are all not a \(2\pi \) jump around their cores.

Fig. 4
figure 4

(Color online) Vortex solitons with the intensity of a, e, i, m component \(|u_1|^2\), b, f, j, n component \(|u_2|^2\), c, g, k, o total quantity \(|u|^2=|u_1|^2+|u_2|^2\) and d, h, l, p phase in presence of the parabolic transverse modulation \(R=\omega ^2 r^{2}/2\). The parameters are chosen as the same as those in Fig. 1 except for \(q=1\) with a–d \(m=1,n=1\), e–h \(m=2,n=2\), i–l \(m=3,n=3\), m–p \(m=4,n=4\)

Full size image

When \(q=1\), vortex solitons with the intensity of (a), (e), (i) and (m) component \(|u_1|^2\), (b), (f), (j) and (n) component \(|u_2|^2\), (c), (g), (k) and (o) total quantity \(|u|^2=|u_1|^2+|u_2|^2\) and (d), (h), (l) and (p) phase are shown in Fig. 4 in presence of the parabolic transverse modulation \(R=\omega ^2 r^{2}/2\). Similar to multipole solitons, the soliton order number n decides the layer of vortex solitons. If \(n=1{-}4\), vortex solitons possess one to four layers, respectively. Moreover, the value of m is related to the number of “petal” for vortex solitons, that is, vortex solitons possess the structures with 2m-“petal.” From these plots in Fig. 4d, h, l, p, all phases exhibit a \(2\pi \) jump around their cores, and thus, these structures in Fig. 4 are all vortex solitons.

We find that localized structures without the transverse modulation are similar to those in the presence of the parabolic transverse modulation in Figs. 1, 2, 3 and 4. For the limit of length, we neglect these related discussions.

4 Summary

In summary, we study a (2+1)-dimensional N-coupled NLSE with spatially modulated cubic–quintic nonlinearity and transverse modulation, and analytically derive vector multipole and vortex soliton solutions. If the modulation depth q is chosen as 0 and 1, vector multipole and vortex solitons are constructed, respectively. The number of “petals” for the multipole solitons and vortex solitons is decided by the value of 2m with the topological charge m, and the number of layers in the multipole solitons and vortex solitons is related to the value of the soliton order number n.