Dynamic modeling and performance analysis of the 3-PRRU 1T2R parallel manipulator without parasitic motion

Abstract

This paper investigates the dynamic modeling and performance analysis of the 3-PRRU parallel manipulator; here, P, R and U denote the prismatic, revolute and universal joints, respectively. The studied 3-PRRU parallel manipulator possesses two rotational and one translational degrees of freedom without parasitic motion. For the dynamic modeling, the Newton–Euler formulation with generalized coordinates is employed to establish the system equations of motion for the 3-PRRU parallel manipulator. Then, the dynamic manipulability ellipsoid which provides a quantitative measure of the ability in manipulating the end-effector is adopted to evaluate the dynamic performance of the studied parallel manipulator. In order to demonstrate the feasibility of the proposed modeling and analysis method, numerical simulations are conducted on dynamic response and performance of the studied manipulator. A prototype is built up based on the proposed parallel manipulator. And the presented modeling method can serve the fundamentals for the optimization and control of the prototype in future work.

1 Introduction

Due to the high positioning accuracy, structure stiffness and load capability, parallel manipulators have been successfully applied in a wide range of aspects, such as motion simulators [1, 2], pick-and-place devices [3, 4] and high-precision machine tools [5, 6]. In these applications, analysis of dynamic performance [7,8,9,10] plays an important role at the stages of optimization and control of parallel manipulators because of the highly nonlinear characteristics of dynamic response.

Fig. 1

CAD model of the 3-PRRU 1T2R parallel manipulator

Dynamic modeling/analysis serves as the fundamental for evaluating the dynamics performance of robot manipulators. The system’s equations of motion (EOM) which provide a direct relation between the corresponding actuation torques and dynamic response are usually required for the definitions of various performance indices. However, due to complexity in kinematics structures, dynamics modeling of the parallel manipulators, especially for the forward problem, is much more difficult than their serial counterparts.

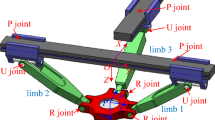
This paper presents a systematic study on the dynamics modeling and performance analysis of a 1T2R spatial parallel manipulator. The studied 3-PRRU parallel manipulator has three identical limbs. Here, P, R and U denote prismatic, revolute and universal joints, respectively. The italic P indicates that the prismatic joints in the limbs are actuated. As shown in Fig. 1, among these PRRU limbs, the first two are arranged within the same plane, while the other is assembled in a perpendicular manner. It has been proved [11] that owing to the particular geometric constraints, this parallel manipulator possesses one translational and two rotational DOFs without parasitic motion. In other words, the end-effector of this parallel manipulator can rotate about a fixed point on its moving platform. Such a feature means that the rotations and translation of the manipulator’s moving platform are decoupled, which significantly reduces the complexity of kinematic model and is preferable for control.

However, most studies on this parallel manipulator were focusing on its kinematic analysis and optimization [11, 12]. There is a lack of thorough investigation on its dynamics and performance. In this paper, the Newton–Euler formulation with generalized coordinates [13], also known as Schiehlen’s method [14], is used to establish the dynamics equations of the studied parallel manipulator in a straightforward manner. Then, both the EOM and the equations of reaction (EOR) can be derived conveniently according to the principle of virtual work [15]. Numerical simulations are provided to verify the correctness of the presented dynamic models through validation with the commercial software Adams/View.

In order to evaluate the dynamic performance of the studied parallel manipulator, the concept of dynamic manipulability ellipsoid (DME) [8] is employed to depict the manipulability, namely the easiness of changing the position and orientation of the manipulator’s end-effector. Distribution of this index within the workspace of the parallel manipulator is obtained in an intuitive manner. And the results will serve as the criteria for structural optimization and motion control of a prototype of the 3-PRRU parallel manipulator.

This paper is organized as follows: Related work on the dynamics modeling of parallel manipulators is reviewed in Sect. 2. Then, Sect. 3 presents the kinematics modeling of the 3-PRRU parallel manipulator, where the positions, velocities and the accelerations of all bodies in the manipulator are derived in closed form in terms of the system’s generalized coordinates. Then, in Sect. 4, dynamics modeling is carried out and the system EOM of the studied parallel manipulator are derived in an analytical form. In order to validate the correctness of the dynamic models, numerical simulations are then conducted in Sect. 5. Thereafter, according to the derived EOM, the index of DME is calculated within the workspace of the parallel manipulator. In this section, the dynamics performance of the studied 3-PRRU parallel manipulator is also discussed for the further optimization in the next stage. At last, some conclusions are drawn in Sect. 6.

2 Related works

From the multi-body system (MBS) dynamics point of view, there are two main methodologies [16], namely the Newton–Euler formulation and Lagrange approach, which can be used to establish the dynamic equations of parallel manipulators.

Geng et al. [17], Bhattacharya et al. [18] and Lebret et al. [19] used Lagrange method to derive the dynamic equations of Stewart–Gough parallel platforms, respectively. Then, Lee et al. [20] derived the EOM for the 3-RPS spatial parallel manipulator using Lagrangian approach. Later, Pendar et al. [21] and Rodriguez et al. [22], respectively, provided further dynamics analysis of this parallel manipulator. In addition, the Lagrangian formulation has also been introduced to the dynamics modeling and analysis for other types of parallel manipulators [23,24,25]. Using the Lagrangian method, Li et al. [24] performed dynamics modeling/analysis of the 3PRC translational parallel kinematic machine by recursive matrix representation. Recently, Kalani et al. [26] presented an improved general formulation for the inverse and direct dynamics of 6-UPS Gough–Stewart parallel robot based on the virtual work method. As well, Deng et al. [27] developed a closed-form dynamics modeling method of a 3-DOF spatial parallel manipulator by combining the Lagrangian formulation with the virtual work principle.

The main advantage of Lagrange formulation is the direct result of a minimal set of ordinary differential equations (ODEs) for the dynamics response of robot manipulators. However, explicit expressions for the kinetic and potential energies are required for all bodies in the manipulator, so that the computational cost of the Lagrange equation will increase vastly when the number of bodies in a MBS increases. Therefore, the derivation of Lagrange equations for a parallel manipulator is extremely complicated, especially when it possesses a relatively complex kinematic structure.

On the other hand, Newton–Euler approach provides a straightforward strategy to establish the dynamic equations of parallel manipulators. Dasgupta et al. [28, 29] developed a general approach for closed-form dynamic formulation of parallel manipulators through the Newton–Euler equations. In their method, the closed-form dynamic equations can be obtained by means of appropriate selection and ordering the equilibrium equations of the legs and platform. Thereafter, Khalil and his colleagues [30, 31] proposed a simple general solution for both inverse and forward dynamics by means of projecting the dynamics of the platform and the legs on the actuated joint axes using particular constructed Jacobian matrices. Using the modular method, Wang et al. [32, 33] established the concept of composite modeling method for the forward dynamics analysis of parallel manipulators based on the Newton–Euler formulation. Besides, other variations of Newton–Euler methods [34,35,36,37] have been proposed for the dynamic modeling of parallel manipulators.

Although, the derivation process for the dynamics modeling by Newton–Euler method is rather straightforward, it results in a set of differential algebra equations (DAE) with a maximum number of coordinates. Since the Newton–Euler equations of all bodies and the constraint equations of all connecting joints are integrated together, the dimension of the DAE for the forward dynamics of parallel manipulators will be huge, and it will be a tedious work to solve them.

Except for the two main methods, other principles such as the theory of screws [38], the Kane’s equations [39, 40], the differential manifold [41], Lie algebra/group theory [42], Hamilton’s equation [43] and the generalized momentum approach [44] have also been employed for the dynamic modeling and simulation of parallel manipulators. In addition, efficient methods [45,46,47] have also been proposed for the nonlinear dynamics analysis of complex systems.

As mentioned above, forward dynamics of parallel manipulators consists of a set of ODE in Lagrangian formulation, or a large number of DAE in Newton–Euler equations. Because of the necessity of the calculation of kinetic and potential energies for all bodies, or the integration of a maximum set of coordinates, enormous computing effort should be paid in both aforementioned formulations. Since the dynamic performance analysis for the parallel manipulators requires a closed-form solution to the system EOM, effective deduction strategy is demanded to calculate the dynamic performance indices in a convenient and efficient manner.

3 Kinematics modeling of the 3-PRRU parallel manipulator

As mentioned above, the studied 3-PRRU parallel manipulator possesses one translational and two rotational DOFs without parasitic motion. To simplify the kinematic analysis, two particular coordinate frames are established on the fixed base and moving platform, respectively, namely the inertia and tool frames $\{\text {S}\}$ and $\{\text {T}\}$ as illustrated in Fig. 1. Hence, the end-effector of the parallel manipulator can only translate along the ${{\varvec{z}}}$-axis of $\{\text {S}\}$ and rotate about ${{\varvec{u}}}$- and ${{\varvec{v}}}$-axis of $\{\text {T}\}$, without introducing any parasitic translations along ${{\varvec{x}}}$ and ${{\varvec{y}}}$-axes, and the rotation about ${{\varvec{w}}}$-axis.

Fig. 2

The sketch of the body-fixed frames and body-joint vectors

3.1 Position analysis

Let the above three pose variables of the manipulator’s end-effector be the generalized coordinates of the whole system. Then, the configuration of the whole parallel manipulator, including all bodies, can be represented in terms of these variables. Firstly, the orientation and position of the moving platform can be expressed directly as

$$\begin{aligned} \mathbf R _P=\exp \left( \hat{\mathbf{e }}_1q_1\right) \exp \left( \hat{\mathbf{e }}_2q_2\right) , \;{{\varvec{p}}}_P=q_3\,{{\varvec{e}}}_3 \end{aligned}$$

(1)

where $q_1$ and $q_2$ denote the rotation angles about the ${{\varvec{u}}}$- and ${{\varvec{v}}}$-axes, respectively. $q_3$ represents the position of $\{\text {T}\}$ with respect to $\{\text {S}\}$ in ${{\varvec{z}}}$ direction. $e_1=[1,0,0]^T$, $e_2=[0,1,0]^T$ and $e_3=[0,0,1]^T$ are unit vectors. And $\hat{\mathbf{e }}_i, i=1,2,3$ are their $3\times 3$ skew-symmetric matrices.

Here, the matrix exponential mapping is introduced to represent the orientations of the links’ body-fixed frames. It can be expressed in an expanded form as

$$\begin{aligned} \exp (\hat{\varvec{\omega }}\theta )=\mathbf I _3+\frac{\sin \theta }{\theta }\hat{\varvec{\omega }}+ \frac{1-\cos \theta }{\theta ^2}\hat{\varvec{\omega }}^2 \end{aligned}$$

(2)

where $\hat{\varvec{\omega }}$ is the $3\times 3$ skew-symmetric matrix associated with the direction of rotation axis $\varvec{\omega }\in {\mathbb {R}}^{3}$.

As shown in Fig. 2, attach a body-fixed frame, denoted by $\left\{ \mathrm {B_{link}}\right\}$, to each link at the center of mass. Then, for the lower links in limbs 1 and 2, the orientations and positions of their body-fixed frames can be obtained as

$$\begin{aligned} \mathbf R _{L_i}=\exp \left( \hat{\mathbf{e }}_1q_1\right) ,\;\;{{\varvec{p}}}_{L_i}={{\varvec{p}}}_{P}+\mathbf R _{P}\varvec{\rho }_{P,i}-\mathbf R _{L_i}\varvec{\rho }_{L_i,2} \end{aligned}$$

(3)

where $\varvec{\rho }_{P,i}, i=1,2,3$ are the position vectors of the universal joints represented in $\{\text {T}\}$, while $\varvec{\rho }_{L_i,2}$ is the vector of the lower link’s universal joint in its local frame $\left\{ \mathrm {B_{L_i}}\right\}$.

Fig. 3

The sketch of the PRRU limbs: a the first and second limbs, b the third limb

For the sliders and upper links in the first two limbs, the poses of their body-fixed frames can be derived as

$$\begin{aligned}&\left\{ \begin{array}{l} \mathbf R _{S_i}=\mathbf E _3\\ {{\varvec{p}}}_{S_i}=b_i{{\varvec{e}}}_2+d_i{{\varvec{e}}}_3-\varvec{\rho }_{S_i,1} \\ \end{array}\right. , \nonumber \\&\left\{ \begin{array}{l} \mathbf R _{U_i}=\exp \left( \hat{\mathbf{e }}_1\alpha _i\right) \\ {{\varvec{p}}}_{U_i}={{\varvec{p}}}_{S_i}+\varvec{\rho }_{S_i,2}-\mathbf R _{U_i}\varvec{\rho }_{U_i,1} \end{array}\right. \end{aligned}$$

(4)

where $\mathbf R _{S_i}$ and ${{\varvec{p}}}_{S_i}, i=1,2$ are the rotation matrix and position vector of the local frame $\left\{ \mathrm {B_{S_i}}\right\}$ which is located at the center of mass and parallel to $\{\text {S}\}$. $\mathbf R _{U_i}$ and ${{\varvec{p}}}_{U_i}$ are those of the upper links’. $\varvec{\rho }_{S_i,1}$ and $\varvec{\rho }_{S_i,2}$ are the body-joint vectors of the slider associated with the prismatic and revolute joints, respectively. $\varvec{\rho }_{U_i,1}$ and $\varvec{\rho }_{U_i,2}$ are those of the upper link associated with revolute joints connected to slider and lower link, respectively. $b_i$ is the position of the prismatic joint in $\{\text {S}\}$. $\mathbf E _3$ is the third-order identity matrix.

As shown in Fig. 3, the joint variable $d_i$ and $\alpha _i$ in Eq. (4) can be obtained as

$$\begin{aligned} \left\{ \begin{array}{l} \alpha _1=-\arccos \frac{y_{B_1}-y_{A_1}}{l_{1,1}},\; d_1=z_{B_1}-l_{1,1}\sin \alpha _1\\ \alpha _2=\arccos \frac{y_{A_2}-y_{B_2}}{l_{2,1}},\; d_2=z_{B_2}+l_{2,1}\sin \alpha _2 \end{array}\right. \end{aligned}$$

where $y_{B_i}$ and $z_{B_i}$ are the y- and z-position of the limb’s second revolute joint with respect to $\{\text {S}\}$. $y_{A_i}=b_i$ denotes the y-position of the limb’s first revolute joint. $l_{i,1}=\Vert \varvec{\rho }_{U_i,2}-\varvec{\rho }_{U_i,1}\Vert$ represents the length of the upper link. The positions of the second revolute joints in the limbs, namely the point $\mathrm {B}_i$, can be derived as ${{\varvec{r}}}_{B_i}={{\varvec{p}}}_{L_i}+\mathbf R _{L_i}\varvec{\rho }_{L_i,1}$.

Since the third limb is constrained within xz-plane of $\{\text {S}\}$, the rotation angles of its universal joint can be derived according to the constraint

$$\begin{aligned} \mathbf R _{P}\exp \left( \hat{\mathbf{e }}_3\theta \right) \exp \left( \hat{\mathbf{e }}_1\varphi \right) {{\varvec{e}}}_2={{\varvec{e}}}_2 \end{aligned}$$

(5)

which relates to the direction of revolute joints in this limb.

Solving Eq. (5), we have

$$\begin{aligned} \left\{ \begin{array}{l} \theta =\arctan \left( -\tan q_1\sin q_2\right) \\ \varphi =\arcsin \left( -\sin q_1\cos q_2\right) \\ \end{array}\right. \end{aligned}$$

Thus, the orientation and position of the lower link in limb 3 can be obtained as

$$\begin{aligned} \mathbf R _{L_3}=\exp \left( \hat{\mathbf{e }}_2\gamma \right) ,\; {{\varvec{p}}}_{L_3}={{\varvec{p}}}_{P}+\mathbf R _{P}\varvec{\rho }_{P,3}-\mathbf R _{L_3}\varvec{\rho }_{L_3,2} \end{aligned}$$

(6)

where $\varvec{\rho }_{L_3,2}$ is the position vector of the universal joint in the lower link’s frame with respect to $\left\{ \mathrm {B_{L_3}}\right\}$. And the rotation angle $\gamma$ can be given by

$$\begin{aligned} \gamma =\arctan \frac{\tan q_2}{\cos q_1} \end{aligned}$$

Similar to (4), the poses of the slider and the upper link in this limb can be represented as

$$\begin{aligned}&\left\{ \begin{array}{l} \mathbf R _{S_3}=\mathbf E _3\\ {{\varvec{p}}}_{S_3}=b_3{{\varvec{e}}}_1+d_3{{\varvec{e}}}_3-\varvec{\rho }_{S_3,1} \\ \end{array}\right. , \nonumber \\&\left\{ \begin{array}{l} \mathbf R _{U_3}=\exp \left( \hat{\mathbf{e }}_2\alpha _3\right) \\ {{\varvec{p}}}_{U_3}={{\varvec{p}}}_{S_3}+\varvec{\rho }_{S_3,2}-\mathbf R _{U_3}\varvec{\rho }_{U_3,1} \end{array}\right. \end{aligned}$$

(7)

where $b_3$ is the x-position of the third prismatic joint in $\left\{ \mathrm {S}\right\}$. $\varvec{\rho }_{U_3,1}$ and $\varvec{\rho }_{S_3,1}$ are body-joint vectors as same as those in the first two limbs. And the variables $d_3$ and $\alpha _3$ of the prismatic and revolute joints are given by

$$\begin{aligned} \alpha _3=\arccos \frac{x_{B_3}-x_{A_3}}{l_{3,1}}, \; d_3=z_{B,3}+l_{3,1}\sin \alpha _3 \end{aligned}$$

where $l_{3,1}=\Vert \varvec{\rho }_{U_3,2}-\varvec{\rho }_{U_3,1}\Vert$ is the length of the upper link. And the position of the second revolute joint can be obtained as ${{\varvec{r}}}_{B_3}={{\varvec{p}}}_{L_3}+\mathbf R _{L_3}\varvec{\rho }_{L_3,1}$.

3.2 Velocity and acceleration analysis

According to (1)–(7), the poses of all links can be obtained once the generalized coordinates ${{\varvec{q}}}=[q_1, q_2, q_3]^T$ are given. Then, the velocities and accelerations of the corresponding links can be derived by means of the time differentiation and represented as functions of ${{{\varvec{q}}}}$, $\dot{{{\varvec{q}}}}$ and $\ddot{{{\varvec{q}}}}$.

The angular and linear velocity of the moving platform can be derived readily as

$$\begin{aligned} \left\{ \begin{array}{l} \varvec{\omega }_{P}=\left( \dot{\mathbf{R }}_{P}\mathbf{R }_{P}^T\right) ^{\vee }={{\varvec{e}}}_{1}\dot{q}_{1}+\exp (\hat{\mathbf{e }}_{1}q_{1}){{\varvec{e}}}_2\dot{q}_2=\mathbf J _{P,R}\,\dot{{{\varvec{q}}}}\\ \,{{\varvec{v}}}_{P}\,=\;\dot{{{\varvec{p}}}}_{P}={{\varvec{e}}}_3\dot{q}_3=\mathbf J _{P,T}\,\dot{{{\varvec{q}}}} \end{array}\right. \end{aligned}$$

(8)

where $\dot{{{\varvec{q}}}}=[\dot{q}_1, \dot{q}_2, \dot{q}_3]^T$ denotes the time differentiation of the generalized coordinates. The corresponding translational and rotational Jacobian matrices are given by $\mathbf J _{P,T}=\left[ {{\varvec{0}}}_3, {{\varvec{0}}}_3, {{\varvec{e}}}_3\right]$ and $\mathbf J _{P,R}=\left[ {{\varvec{e}}}_1, \exp (\hat{\mathbf{e }}_{1}q_{1}){{\varvec{e}}}_2, {{\varvec{0}}}_3\right]$.

In a similar way, the accelerations of the moving platform can be obtained as

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{\varvec{\omega }}}_{P}=\mathbf J _{P,R}\,\ddot{{{\varvec{q}}}}+\varvec{\delta }_{P}\\ \,{\dot{{{\varvec{v}}}}}_{P}\,=\mathbf J _{P,T}\,\ddot{{{\varvec{q}}}}+\varvec{\mu }_{P} \end{array}\right. \end{aligned}$$

(9)

where $\varvec{\delta }_{P}=\hat{\mathbf{e }}_1\exp (\hat{\mathbf{e }}_1q_1){{\varvec{e}}}_2\,\dot{q}_1\dot{q}_2$ and $\varvec{\mu }_P={{\varvec{0}}}_3$.

Using the same strategy, the relative velocities of the local frames of the lower/upper links and slider in the first two limbs can be obtained as

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{l} \varvec{\omega }_{L_i}={{\varvec{e}}}_{1}\dot{q}_{1}=\mathbf J _{L_i,R}\,\dot{{{\varvec{q}}}}\\ \,{{\varvec{v}}}_{L_i}\,=\dot{{{\varvec{p}}}}_P+\hat{\varvec{\omega }}_{P}\mathbf R _{P}\varvec{\rho }_{P,i}-\hat{\varvec{\omega }}_{L_i}\mathbf R _{L_i}\varvec{\rho }_{L_i,2} =\mathbf J _{L_i,T}\,\dot{{{\varvec{q}}}} \end{array}\right. \\ \left\{ \begin{array}{l} \varvec{\omega }_{S_i}={{\varvec{0}}}_3=\mathbf J _{S_i,R}\,\dot{{{\varvec{q}}}}\\ \,{{\varvec{v}}}_{S_i}\,=\dot{d}_i{{\varvec{e}}}_3=\mathbf J _{S_i,T}\,\dot{{{\varvec{q}}}} \end{array}\right. \\ \left\{ \begin{array}{l} \varvec{\omega }_{U_i}={{\varvec{e}}}_{1}\dot{\alpha }_{i}=\mathbf J _{U_i,R}\,\dot{{{\varvec{q}}}}\\ \,{{\varvec{v}}}_{U_i}\,=\dot{{{\varvec{p}}}}_{S_i}-\hat{\varvec{\omega }}_{U_i}\mathbf R _{U_i}\varvec{\rho }_{U_i,1} =\mathbf J _{U_i,T}\,\dot{{{\varvec{q}}}} \end{array}\right. \end{array} \end{aligned}$$

(10)

where the corresponding Jacobian matrices are given by

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{l} \mathbf J _{L_i,R}=[{{\varvec{e}}}_1, {{\varvec{0}}}_3, {{\varvec{0}}}_3]\\ \mathbf J _{L_i,T}=\mathbf J _{P,T}-\hat{\mathbf{r }}_{P,i}\mathbf J _{P,R}+\hat{\mathbf{r }}_{L_i,2}\mathbf J _{L_i,R} \end{array}\right. \\ \left\{ \begin{array}{l} \mathbf J _{S_i,R}=\mathbf 0 _{3\times 3}\\ \mathbf J _{S_i,T}=[{{\varvec{0}}}_3,\cot \alpha _i{{\varvec{e}}}_3,{{\varvec{e}}}_3] (\mathbf J _{L_i,T}-\hat{\mathbf{r }}_{L_i,1}\mathbf J _{L_i,R}) \end{array}\right. \\ \left\{ \begin{array}{l} \mathbf J _{U_i,R}=\frac{1}{l_{i,1}\sin \alpha _i}{{\varvec{e}}}_1{{\varvec{e}}}_2^T(\mathbf J _{L_i,T}-\hat{\mathbf{r }}_{L_i,1}\mathbf J _{L_i,R})\\ \mathbf J _{U_i,T}=\mathbf J _{S_i,T}+\hat{\mathbf{r }}_{U_i,1}\mathbf J _{U_i,R} \end{array}\right. \end{array}\end{aligned}$$

where ${{\varvec{r}}}_{P,i}=\mathbf R _{P}\varvec{{\rho }}_{P,i}$, ${{\varvec{r}}}_{L_i,1}=\mathbf R _{L_i}\varvec{\rho }_{L_i,1}$, ${{\varvec{r}}}_{L_i,2}=\mathbf R _{L_i}\varvec{\rho }_{L_i,2}$ and ${{\varvec{r}}}_{U_i,1}=\mathbf R _{U_i}\varvec{\rho }_{U_i,1}$ are the links’ body-joint vectors expressed in the inertia frame $\left\{ \mathrm {S}\right\}$. And their skew-symmetric matrices (the cross-product operators) satisfy $\hat{\mathbf{r }}_{P,i}=\mathbf R _{P}\hat{\varvec{{\rho }}}_{P,i}\mathbf R _{P}^T$, $\hat{\mathbf{r }}_{L_i,1}=\mathbf R _{L_i}\hat{\varvec{\rho }}_{L_i,1}\mathbf R _{L_i}^T$, $\hat{\mathbf{r }}_{L_i,2}=\mathbf R _{L_i}\hat{\varvec{\rho }}_{L_i,2}\mathbf R _{L_i}^T$ and $\hat{\mathbf{r }}_{U_i,1}=\mathbf R _{U_i}\hat{\varvec{\rho }}_{U_i,1}\mathbf R _{U_i}^T$.

Then, the corresponding accelerations can be represented in the form of

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{l} \dot{\varvec{\omega }}_{L_i}=\mathbf J _{L_i,R}\,\ddot{{{\varvec{q}}}}+\varvec{\delta }_{L_i}\\ \,\dot{{{\varvec{v}}}}_{L_i}\,=\mathbf J _{L_i,T}\,\ddot{{{\varvec{q}}}}+\varvec{\mu }_{L_i} \end{array}\right. \\ \left\{ \begin{array}{l} \dot{\varvec{\omega }}_{S_i}=\mathbf J _{S_i,R}\,\ddot{{{\varvec{q}}}}+\varvec{\delta }_{S_i}\\ \,\dot{{{\varvec{v}}}}_{S_i}\,=\mathbf J _{S_i,T}\,\ddot{{{\varvec{q}}}}+\varvec{\mu }_{S_i} \end{array}\right. \\ \left\{ \begin{array}{l} \dot{\varvec{\omega }}_{U_i}=\mathbf J _{U_i,R}\,\ddot{{{\varvec{q}}}}+\varvec{\delta }_{U_i}\\ \,\dot{{{\varvec{v}}}}_{U_i}\,=\mathbf J _{U_i,T}\,\ddot{{{\varvec{q}}}}+\varvec{\mu }_{U_i} \end{array}\right. \end{array} \end{aligned}$$

(11)

where the coefficients are given by

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{l} \varvec{\delta }_{L_i}={{\varvec{0}}}_3\\ \varvec{\mu }_{L_i}=\hat{\varvec{\omega }}_{P}^2{{{{\varvec{r}}}}}_{P,i}-{\hat{\mathbf{r }}}_{P,i}\varvec{\delta }_{P}-\hat{\varvec{\omega }}_{L_i}^2{{{{\varvec{r}}}}}_{L_i,2} +{\hat{\mathbf{r }}}_{L_i,2}\varvec{\delta }_{L_i} \end{array}\right. \\ \left\{ \begin{array}{l} \varvec{\delta }_{S_i}={{\varvec{0}}}_{3}\\ \varvec{\mu }_{S_i}=[{{\varvec{0}}}_3,\cot \alpha _i{{\varvec{e}}}_3,{{\varvec{e}}}_3] (\varvec{\mu }_{L_i}-\hat{\mathbf{r }}_{L_i,1}\varvec{\delta }_{L_i})\\ \quad \quad \quad +\,l_{i,1}\csc \alpha _i\,\dot{\alpha }_i^2{{\varvec{e}}}_3 \end{array}\right. \\ \left\{ \begin{array}{l} \varvec{\delta }_{U_i}=\frac{1}{l_{i,1}\sin \alpha _i}{{\varvec{e}}}_1{{\varvec{e}}}_2^T(\varvec{\mu }_{L_i}-\hat{\mathbf{r }}_{L_i,1}\varvec{\delta }_{L_i})-\cot \alpha _i\,\dot{\alpha }_i^2{{\varvec{e}}}_1\\ \varvec{\mu }_{U_i}=\varvec{\mu }_{S_i}+{\hat{\mathbf{r }}}_{U_i,1}+{\delta }_{U_i}-\hat{\varvec{\omega }}_{U_i}^2{{\varvec{r}}}_{U_i,1} \end{array}\right. \end{array} \end{aligned}$$

For the third limb, the angular/linear velocities and accelerations of the bodies can also be derived in a similar way. By differentiating the pose functions, we have

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{l} \varvec{\omega }_{L_3}=(\dot{\mathbf{R }}_{L_3}\mathbf R _{L_3}^T)^{\vee }={{\varvec{e}}}_{2}\dot{\gamma }=\mathbf J _{L_3,R}\,\dot{{{\varvec{q}}}}\\ \,{{\varvec{v}}}_{L_3}\,=\dot{{{\varvec{p}}}}_P-\hat{\mathbf{r }}_{P,3}\varvec{\omega }_{P}+\hat{\mathbf{r }}_{L_3,2}\varvec{\omega }_{L_3} =\mathbf J _{L_3,T}\,\dot{{{\varvec{q}}}} \end{array}\right. \\ \left\{ \begin{array}{l} \varvec{\omega }_{S_3}={{\varvec{0}}}_3=\mathbf J _{S_3,R}\,\dot{{{\varvec{q}}}}\\ \,{{\varvec{v}}}_{S_3}\,=\dot{d}_3{{\varvec{e}}}_3=\mathbf J _{S_3,T}\,\dot{{{\varvec{q}}}} \end{array}\right. \\ \left\{ \begin{array}{l} \varvec{\omega }_{U_3}={{\varvec{e}}}_{2}\dot{\alpha }_{3}=\mathbf J _{U_3,R}\,\dot{{{\varvec{q}}}}\\ \,{{\varvec{v}}}_{U_3}\,=\dot{{{\varvec{p}}}}_{S_3}+\hat{\mathbf{r }}_{U_3,1}\varvec{\omega }_{U_3} =\mathbf J _{U_3,T}\,\dot{{{\varvec{q}}}} \end{array}\right. \end{array} \end{aligned}$$

(12)

where the coefficients are given by

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{l} \mathbf J _{L_3,R}=\frac{{{\varvec{e}}}_2{{{\varvec{x}}}}_3^T\hat{\mathbf{w }}}{{{\varvec{w}}}^T\hat{\mathbf{e }}_2{{\varvec{x}}}_3}\mathbf J _{P,R}\\ \mathbf J _{L_3,T}=\mathbf J _{P,T}-\hat{\mathbf{r }}_{P,3}\mathbf J _{P,R}+\hat{\mathbf{r }}_{L_3,2}\mathbf J _{L_3,R} \end{array}\right. \\ \left\{ \begin{array}{l} \mathbf J _{S_3,R}=\mathbf 0 _{3\times 3}\\ \mathbf J _{S_3,T}=[-\cot \alpha _3{{\varvec{e}}}_3,{{\varvec{0}}}_3,{{\varvec{e}}}_3] (\mathbf J _{L_3,T}-\hat{\mathbf{r }}_{L_3,1}\mathbf J _{L_3,R}) \end{array}\right. \\ \left\{ \begin{array}{l} \mathbf J _{U_3,R}=-\frac{{{\varvec{e}}}_2{{\varvec{e}}}_1^T}{l_{3,1}\sin \alpha _3}(\mathbf J _{L_3,T}-\hat{\mathbf{r }}_{L_3,1}\mathbf J _{L_3,R})\\ \mathbf J _{U_3,T}=\mathbf J _{S_3,T}+\hat{\mathbf{r }}_{U_3,1}\mathbf J _{U_3,R} \end{array}\right. \end{array} \end{aligned}$$

where ${{\varvec{w}}}=\mathbf R _{P}\,{{\varvec{e}}}_3$ is the unit vector of the ${{\varvec{w}}}$-axis with respect to $\{\text {S}\}$. ${{\varvec{x}}}_3=\exp (\hat{\mathbf{e }}_2\gamma ){{\varvec{e}}}_1$ is the unit direction vector associated with $O'B_3$.

Then, the corresponding accelerations of the bodies in the third limb can be represented in the form of

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{l} \dot{\varvec{\omega }}_{L_3}=\mathbf J _{L_3,R}\,\ddot{{{\varvec{q}}}}+\varvec{\delta }_{L_3}\\ \,\dot{{{\varvec{v}}}}_{L_3}\,=\mathbf J _{L_3,T}\,\ddot{{{\varvec{q}}}}+\varvec{\mu }_{L_3} \end{array}\right. \\ \left\{ \begin{array}{l} \dot{\varvec{\omega }}_{S_3}=\mathbf J _{S_3,R}\,\ddot{{{\varvec{q}}}}+\varvec{\delta }_{S_3}\\ \,\dot{{{\varvec{v}}}}_{S_3}\,=\mathbf J _{S_3,T}\,\ddot{{{\varvec{q}}}}+\varvec{\mu }_{S_3} \end{array}\right. \\ \left\{ \begin{array}{l} \dot{\varvec{\omega }}_{U_3}=\mathbf J _{U_3,R}\,\ddot{{{\varvec{q}}}}+\varvec{\delta }_{U_3}\\ \,\dot{{{\varvec{v}}}}_{U_3}\,=\mathbf J _{U_3,T}\,\ddot{{{\varvec{q}}}}+\varvec{\mu }_{U_3} \end{array}\right. \end{array} \end{aligned}$$

(13)

where the coefficients are given by

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{l} \varvec{\delta }_{L_3}=\frac{-{{\varvec{e}}}_2}{{{\varvec{w}}}^T\hat{\mathbf{e }}_2{{\varvec{x}}}_3}\left( 2\varvec{\omega }_{P}^T\hat{\mathbf{w }}\hat{\mathbf{e }}_2{{\varvec{x}}}_3\dot{\gamma }+\varvec{\omega }_{P}^T\hat{\mathbf{w }}\hat{\mathbf{x }}_3\varvec{\omega }_{P}+{{\varvec{w}}}_0^T\hat{\mathbf{e }}_2^2{{\varvec{x}}}_3\dot{\gamma }^2\right) \\ \varvec{\mu }_{L_3}=\hat{\varvec{\omega }}_{P}^2{{{{\varvec{r}}}}}_{P,3}-{\hat{\mathbf{r }}}_{P,3}\varvec{\delta }_{P}-\hat{\varvec{\omega }}_{L_3}^2{{{{\varvec{r}}}}}_{L_3,2} +{\hat{\mathbf{r }}}_{L_3,2}\varvec{\delta }_{L_3} \end{array}\right. \\ \left\{ \begin{array}{l} \varvec{\delta }_{S_3}={{\varvec{0}}}_{3}\\ \varvec{\mu }_{S_3}=[-\cot \alpha _3{{\varvec{e}}}_3,{{\varvec{0}}}_3, {{\varvec{e}}}_3] (\varvec{\mu }_{L_3}-\hat{\mathbf{r }}_{L_3,1}\varvec{\delta }_{L_3}+\hat{\varvec{\omega }}_{L_3}^2{{\varvec{r}}}_{L_3,1})\\ \quad \quad -l_{3,1}{{\varvec{e}}}_3{\csc \alpha _3}\dot{\alpha }_3^2 \end{array}\right. \\ \left\{ \begin{array}{l} \varvec{\delta }_{U_3}=-\frac{{{\varvec{e}}}_2{{\varvec{e}}}_1^T}{l_{3,1}\sin \alpha _3}(\varvec{\mu }_{L_3}-\hat{\mathbf{r }}_{L_3,1}\varvec{\delta }_{L_3}+\hat{\varvec{\omega }}_{L_3}^2{{\varvec{r}}}_{L_3,1})\\ \quad \quad -\cot \alpha _3\,\dot{\alpha }_3^2{{\varvec{e}}}_2\\ \varvec{\mu }_{U_3}=\varvec{\mu }_{S_3}+{\hat{\mathbf{r }}}_{U_3,1}\varvec{\delta }_{U_3}-\hat{\varvec{\omega }}_{U_3}^2{{\varvec{r}}}_{U_3,1} \end{array}\right. \end{array} \end{aligned}$$

4 Dynamics modeling of the 3-PRRU parallel manipulator

Using Newton–Euler method with generalized coordinates [13], this section presents the dynamics modeling of the 3-PRRU parallel manipulator. The principle of virtual work is employed to construct the orthogonal space of the system’s constraint forces reacted in the connecting joints. Finally, both EOM and EOR can be derived for the dynamic analysis of the studied parallel manipulator.

4.1 Newton–Euler equations of the bodies

Considered as a spatial rigid body, the Newton–Euler equations of the moving platform can be represented as

$$\begin{aligned} \left\{ \begin{array}{l} \mathbf I _P\,\dot{\varvec{\omega }}_P+\varvec{\varepsilon }_P\,={{\varvec{M}}}_P^a\,+{{\varvec{M}}}_P^n\\ \,m_P\,\dot{{{\varvec{v}}}}_P\,={{\varvec{F}}}_P^a\,+{{\varvec{F}}}_P^n\\ \end{array}\right. \end{aligned}$$

(14)

where $m_P$ and $\mathbf I _P$ denote the mass and inertia tensor of the platform with respect to $\left\{ \mathrm {S}\right\}$. $\varvec{\varepsilon }_P\,=\varvec{\omega }_P\times \left( \mathbf I _P\,\varvec{\omega }_P\right)$ denotes the item including the Coriolis and centrifugal forces. ${{\varvec{M}}}_P^a$ and ${{\varvec{M}}}_P^n$ represent the external and constraint toques exerted on the platform related to its center of mass. ${{\varvec{F}}}_P^a$ and ${{\varvec{F}}}_P^n$ are the corresponding forces applied on the platform.

The moving platform is connected with the limbs through three universal joints. Thus, the forces and torques exerted on it can be represented as linear functions of the constraint forces and torques reacted in the universal joints, as

$$\begin{aligned} \left\{ \begin{array}{l} {{\varvec{M}}}_P^n=\mathbf P _{A_1,R}\varvec{\lambda }_{A_1}+\mathbf P _{A_2,R}\varvec{\lambda }_{A_2}+\mathbf P _{A_3,R}\varvec{\lambda }_{A_3}\\ \qquad \ =\mathbf P _{A,R}\,\varvec{\lambda }_{A}\\ \,{{\varvec{F}}}_P^n\,=\mathbf P _{A_1,T}\varvec{\lambda }_{A_2}+\mathbf P _{A_2,T}\varvec{\lambda }_{A_2}+\mathbf P _{A_3,T}\varvec{\lambda }_{A_3}\\ \qquad \ \, =\mathbf P _{A,T}\varvec{\lambda }_{A}\\ \end{array}\right. \end{aligned}$$

(15)

where

$$\begin{aligned} \left\{ \begin{array}{l} \varvec{\lambda }_{A}=[\varvec{\lambda }_{A_1}^T, \varvec{\lambda }_{A_2}^T, \varvec{\lambda }_{A_3}^T]^T\in {\mathbb {R}}^{12\times 1}\\ \mathbf P _{A,R}=[\mathbf P _{A_1,R}, \mathbf P _{A_2,R}, \mathbf P _{A_3,R}]\in {\mathbb {R}}^{3\times 12}\\ \mathbf P _{A,T}=[\mathbf P _{A_1,T}, \mathbf P _{A_2,T}, \mathbf P _{A_3,T}]\in {\mathbb {R}}^{3\times 12}. \end{array} \right. \end{aligned}$$

where $\varvec{\lambda }_{A_i}\in {\mathbb {R}}^{4\times 1}, i=1, 2, 3$ denote the ideal reaction forces and torques in the universal joint connected to the ith limb. $\mathbf P _{A_i,R}\in {\mathbb {R}}^{3\times 4}$ and $\mathbf P _{A_i,T}\in {\mathbb {R}}^{3\times 4}$ are the transformation matrices related these reaction forces/torques to the body-fixed frame, which are given by

$$\begin{aligned} \left\{ \begin{array}{l} \mathbf P _{A_1,R}=\left[ \hat{\mathbf{r }}_{P,1},\, {{\varvec{u}}}\right] , \, \mathbf P _{A_2,R}=\left[ \hat{\mathbf{r }}_{P,2},\, {{\varvec{u}}}\right] ,\\ \mathbf P _{A_3,R}=\left[ \hat{\mathbf{r }}_{P,3},\, {{\varvec{v}}}\right] \\ \mathbf P _{A_1,T}=\mathbf P _{A_2,T}=\mathbf P _{A_3,T}=\left[ \mathbf E _3, {{\varvec{0}}}_{3\times 1} \right] \end{array} \right. \end{aligned}$$

where $\hat{\mathbf{r }}_{P,i}$ is the skew-symmetric matrices associated with the body-joint vectors of the universal joints on the moving platform with respect to the inertial frame $\left\{ \mathrm {S}\right\}$.

It should be noted that the ideal reactions in the universal joints consist of three forces and one torque since they have two rotational DOFs. The constraint forces are assumed parallel to the coordinate axes of $\left\{ \mathrm {S}\right\}$ and through the center of the universal joint. Meanwhile, the constraint torques in the first and second limbs are parallel to the ${{\varvec{w}}}$-axis of $\left\{ \mathrm {T}\right\}$, while the one in the third limb is parallel to the ${{\varvec{v}}}$-axis.

By substituting (9) and (15) into (14), the Newton–Euler equations of the moving platform can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{l} \;\mathbf I _P\,\mathbf J _{P,R}\,\ddot{{{\varvec{q}}}}={{\varvec{K}}}_{P,R}+{{\varvec{M}}}_P^a\,+\mathbf P _{A,R}\varvec{\lambda }_{A} \\ m_{P}\mathbf J _{P,T}\ddot{{{\varvec{q}}}}={{\varvec{K}}}_{P,T}+\,{{\varvec{F}}}_P^a\,+\,\mathbf P _{A,T}\varvec{\lambda }_{A}\\ \end{array}\right. \end{aligned}$$

(16)

where ${{\varvec{K}}}_{P,R}=-\mathbf I _P\,\varvec{\delta }_{P}-\varvec{\varepsilon }_P$ and ${{\varvec{K}}}_{P,T}=-m_{P}\varvec{\mu }_{P}$.

For other links, the Newton–Euler equations with generalized coordinates can also be derived in the same method.

• Sliders

The Newton–Euler equations can be represented as

$$\begin{aligned} \left\{ \begin{array}{l} \mathbf I _{S_i}\,\dot{\varvec{\omega }}_{S_i}+\varvec{\varepsilon }_{S_i}\,={{\varvec{M}}}_{S_i}^a\,+{{\varvec{M}}}_{S_i}^n\\ \,m_{S_i}\,\dot{{{\varvec{v}}}}_{S_i}\,={{\varvec{F}}}_{S_i}^a\,+{{\varvec{F}}}_{S_i}^n\\ \end{array}\right. \end{aligned}$$

(17)

where the constraint forces ${{\varvec{M}}}_{S_i}^n$ and torques ${{\varvec{F}}}_{S_i}^n$ are given by

$$\begin{aligned} \left\{ \begin{array}{l} {{\varvec{M}}}_{S_i}^n\,=\mathbf S _{P_i,R}\,\varvec{\lambda }_{P_i}+\mathbf S _{A_i,R}\,\varvec{\lambda }_{A_i}\\ {{\varvec{F}}}_{S_i}^n\,\,\, =\mathbf S _{P_i,T}\,\varvec{\lambda }_{P_i}+\mathbf S _{A_i,T}\,\varvec{\lambda }_{A_i}\\ \end{array}\right. \end{aligned}$$

(18)

where $\varvec{\lambda }_{P_i}\in {\mathbb {R}}^{5\times 1}$ and $\varvec{\lambda }_{A_i}\in {\mathbb {R}}^{5\times 1}$ are the ideal constraint forces/torques reacted in the prismatic and first revolute joints of the limbs. The prismatic joints have one translational DOF, such that $\varvec{\lambda }_{P_i}$ consists of two forces and three torques. While $\varvec{\lambda }_{A_i}$ comprises three forces and two torques since the revolute joints have one rotational DOF. The transformation matrices $\mathbf S _{P_i,R}\in {\mathbb {R}}^{3\times 5}$, $\mathbf S _{A_i,R}\in {\mathbb {R}}^{3\times 5}$, $\mathbf S _{P_i,T}\in {\mathbb {R}}^{3\times 5}$ and $\mathbf S _{A_i,T}\in {\mathbb {R}}^{3\times 5}$ can be derived as

$$\begin{aligned}&\left\{ \begin{array}{l} \mathbf S _{P_i,R}=\left[ \mathbf 0 _{3\times 2},\, \mathbf E _3\right] ,\quad \; \mathbf S _{A_1,R}=\left[ \hat{\mathbf{r }}_{S_1,2},\,{{\varvec{e}}}_2,{{\varvec{e}}}_3\right] ,\\ \mathbf S _{A_2,R}=\left[ \hat{\mathbf{r }}_{S_2,2},\,{{\varvec{e}}}_2,{{\varvec{e}}}_3\right] , \mathbf S _{A_3,R}=\left[ \hat{\mathbf{r }}_{S_3,2},\,{{\varvec{e}}}_1,{{\varvec{e}}}_3\right] \\ \end{array}\right. \\&\left\{ \begin{array}{l} \mathbf S _{P_i,T}=\left[ {{\varvec{e}}}_1,\,{{\varvec{e}}}_2, \mathbf 0 _{3\times 3}\right] \\ \mathbf S _{A_i,T}=\left[ \mathbf E _3, \mathbf 0 _{3\times 2}\right] \end{array}\right. \end{aligned}$$

Thus, the Newton–Euler equations of the sliders can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{l} \mathbf I _{S_i}\,\mathbf J _{S_i,R}\,\ddot{{{\varvec{q}}}}={{\varvec{K}}}_{S_i,R}+{{\varvec{M}}}_{S_i}^{a}+\mathbf S _{P_i,R}\varvec{\lambda }_{P_i}\,+\mathbf S _{A_i,R}\varvec{\lambda }_{A_i} \, \\ m_{S_i}\mathbf J _{S_i,T}\ddot{{{\varvec{q}}}}={{\varvec{K}}}_{S_i,T}+\,{{\varvec{F}}}_{S_i}^a\,+\mathbf S _{P_i,T}\varvec{\lambda }_{P_i}\,+\mathbf S _{A_i,T}\varvec{\lambda }_{A_i} \end{array} \right. \end{aligned}$$

(19)

where ${{\varvec{K}}}_{S_i,R}=-\mathbf I _{S_i}\,\varvec{\delta }_{S_i}-\varvec{\varepsilon }_{S_i}$ and ${{\varvec{K}}}_{S_i,T}=-m_{S_i}\varvec{\mu }_{S_i}$.

• Upper links

The Newton–Euler equations of the upper links can be represented as

$$\begin{aligned} \left\{ \begin{array}{l} \mathbf I _{U_i}\,\dot{\varvec{\omega }}_{U_i}+\varvec{\varepsilon }_{U_i}\,={{\varvec{M}}}_{U_i}^{a}\,+{{\varvec{M}}}_{U_i}^{n}\\ \,m_{U_i}\,\dot{{{\varvec{v}}}}_{U_i}\,={{\varvec{F}}}_{U_i}^{a}\,+{{\varvec{F}}}_{U_i}^{n}\\ \end{array}\right. \end{aligned}$$

(20)

where the constraint forces ${{\varvec{M}}}_{U_i}^n$ and torques ${{\varvec{F}}}_{U_i}^n$ are

$$\begin{aligned} \left\{ \begin{array}{l} {{\varvec{M}}}_{U_i}^n\,=\mathbf U _{A_i,R}\,\varvec{\lambda }_{A_i}+\mathbf U _{B_i,R}\,\varvec{\lambda }_{B_i}\\ {{\varvec{F}}}_{U_i}^n\,\,\, =\mathbf U _{A_i,T}\,\varvec{\lambda }_{A_i}+\mathbf U _{B_i,T}\,\varvec{\lambda }_{B_i}\\ \end{array}\right. \end{aligned}$$

(21)

where $\varvec{\lambda }_{B_i}\in {\mathbb {R}}^{5\times 1}$ is the ideal constraint forces/torques reacted in the second revolute joint of the limb. It consists of two forces and three torques same as $\varvec{\lambda }_{A_i}$. The transformation matrices $\mathbf U _{A_i,R}\in {\mathbb {R}}^{3\times 5}$, $\mathbf U _{B_i,R}\in {\mathbb {R}}^{3\times 5}$, $\mathbf U _{A_i,T}\in {\mathbb {R}}^{3\times 5}$ and $\mathbf U _{B_i,T}\in {\mathbb {R}}^{3\times 5}$ can be derived as

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{l} \mathbf U _{A_1,R}=-\left[ \hat{\mathbf{r }}_{U_1,1},\,{{\varvec{e}}}_{2}, {{\varvec{e}}}_{3}\right] \\ \mathbf U _{A_2,R}=-\left[ \hat{\mathbf{r }}_{U_2,1},\,{{\varvec{e}}}_{2}, {{\varvec{e}}}_{3}\right] \\ \mathbf U _{A_3,R}=-\left[ \hat{\mathbf{r }}_{U_3,1},\,{{\varvec{e}}}_{1}, {{\varvec{e}}}_{3}\right] \end{array}\right. ,\\ \left\{ \begin{array}{l} \mathbf U _{B_1,R}=\;\;\;\;\left[ \hat{\mathbf{r }}_{U_1,2},\,{{\varvec{e}}}_{2}, {{\varvec{e}}}_{3}\right] \\ \mathbf U _{B_2,R}=\;\;\;\;\left[ \hat{\mathbf{r }}_{U_2,2},\,{{\varvec{e}}}_{2}, {{\varvec{e}}}_{3}\right] \\ \mathbf U _{B_3,R}=\;\;\;\;\left[ \hat{\mathbf{r }}_{U_3,2},\,{{\varvec{e}}}_{1}, {{\varvec{e}}}_{3}\right] \end{array}\right. ,\\ \left\{ \begin{array}{l} \mathbf U _{A_i,T}=-\left[ \mathbf E _3, \mathbf 0 _{3\times 2}\right] \\ \mathbf U _{B_i,T}=\;\;\;\;\left[ \mathbf E _3, \mathbf 0 _{3\times 2}\right] \end{array}\right. \end{array}\end{aligned}$$

where ${{\varvec{r}}}_{{U_i},1}=\mathbf R _{U_i}\varvec{\rho }_{U_i,1}$ and ${{\varvec{r}}}_{{U_i},2}=\mathbf R _{U_i}\varvec{\rho }_{U_i,2}$ are the body-joint vectors of the revolute joints with respect to $\left\{ \mathrm {S}\right\}$.

Thus, the Newton–Euler equations of the sliders can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{l} \mathbf I _{U_i}\,\mathbf J _{U_i,R}\,\ddot{{{\varvec{q}}}}={{\varvec{K}}}_{U_i,R}+{{\varvec{M}}}_{U_i}^{a}+\mathbf U _{A_i,R}\varvec{\lambda }_{A_i}\,+\mathbf U _{B_i,R}\varvec{\lambda }_{B_i} \, \\ m_{U_i}\mathbf J _{U_i,T}\ddot{{{\varvec{q}}}}={{\varvec{K}}}_{U_i,T}+\,{{\varvec{F}}}_{U_i}^a\,+\mathbf U _{A_i,T}\varvec{\lambda }_{A_i}\,+\mathbf U _{B_i,T}\varvec{\lambda }_{B_i} \end{array} \right. \end{aligned}$$

(22)

where ${{\varvec{K}}}_{U_i,R}=-\mathbf I _{U_i}\,\varvec{\delta }_{U_i}-\varvec{\varepsilon }_{U_i}$ and ${{\varvec{K}}}_{U_i,T}=-m_{U_i}\varvec{\mu }_{U_i}$.

• Lower links

The Newton–Euler equations of the lower links can be represented as

$$\begin{aligned} \left\{ \begin{array}{l} \mathbf I _{L_i}\,\dot{\varvec{\omega }}_{L_i}+\varvec{\varepsilon }_{L_i}\,={{\varvec{M}}}_{L_i}^{a}\,+{{\varvec{M}}}_{L_i}^{n}\\ \,m_{L_i}\,\dot{{{\varvec{v}}}}_{L_i}\,={{\varvec{F}}}_{L_i}^{a}\,+{{\varvec{F}}}_{L_i}^{n}\\ \end{array}\right. \end{aligned}$$

(23)

where the constraint forces ${{\varvec{F}}}_{L_i}^n$ and torques ${{\varvec{M}}}_{L_i}^n$ are be represented as

$$\begin{aligned} \left\{ \begin{array}{l} {{\varvec{M}}}_{L_i}^n\,=\mathbf L _{B_i,R}\,\varvec{\lambda }_{B_i}+\mathbf L _{C_{i},R}\,\varvec{\lambda }_{C_{i}}\\ {{\varvec{F}}}_{L_i}^n\,\,\, =\mathbf L _{B_i,T}\,\varvec{\lambda }_{B_i}+\mathbf L _{C_{i},T}\,\varvec{\lambda }_{C_{i}}\\ \end{array}\right. \end{aligned}$$

(24)

where the transformation matrices $\mathbf L _{B_i,R}\in {\mathbb {R}}^{3\times 5}$, $\mathbf L _{C_{i},R}\in {\mathbb {R}}^{3\times 4}$, $\mathbf L _{B_i,T}\in {\mathbb {R}}^{3\times 5}$ and $\mathbf L _{C_{i},T}\in {\mathbb {R}}^{3\times 4}$ can be derived as

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{l} \mathbf L _{B_1,R}=-\left[ \hat{\mathbf{r }}_{L_1,1},\,{{\varvec{e}}}_{2}, {{\varvec{e}}}_{3}\right] \\ \mathbf L _{B_2,R}=-\left[ \hat{\mathbf{r }}_{L_2,1},\,{{\varvec{e}}}_{2}, {{\varvec{e}}}_{3}\right] \\ \mathbf L _{B_3,R}=-\left[ \hat{\mathbf{r }}_{L_3,1},\,{{\varvec{e}}}_{1}, {{\varvec{e}}}_{3}\right] \end{array}\right. ,\; \left\{ \begin{array}{l} \mathbf L _{C_{1},R}=-\left[ \hat{\mathbf{r }}_{L_1,2},\, {{\varvec{u}}}\right] \\ \mathbf L _{C_{2},R}=-\left[ \hat{\mathbf{r }}_{L_2,2},\,{{\varvec{u}}}\right] \\ \mathbf L _{C_{3},R}=-\left[ \hat{\mathbf{r }}_{L_3,2},\,{{\varvec{v}}}\right] \end{array}\right. \\ \left\{ \begin{array}{l} \mathbf L _{B_i,T}=-\left[ \mathbf E _3, \mathbf 0 _{3\times 2}\right] \\ \mathbf L _{C_{i},T}=-\left[ \mathbf E _3, \mathbf 0 _{3\times 1}\right] \end{array}\right. \end{array} \end{aligned}$$

where ${{\varvec{r}}}_{{U_i},1}=\mathbf R _{U_i}\varvec{\rho }_{U_i,1}$ and ${{\varvec{r}}}_{{U_i},2}=\mathbf R _{U_i}\varvec{\rho }_{U_i,2}$ are the lower links’ body-joint vectors of the revolute and universal joints with respect to $\left\{ \mathrm {S}\right\}$.

Thus, the Newton–Euler equations of the lower links can be rewritten in terms of the system’s generalized coordinates and the constraint forces reacted in their corresponding connecting joints as

$$\begin{aligned} \left\{ \begin{array}{l} \mathbf I _{L_i}\,\mathbf J _{L_i,R}\,\ddot{{{\varvec{q}}}}={{\varvec{K}}}_{L_i,R}+{{\varvec{M}}}_{L_i}^{a}+\mathbf L _{B_i,R}\,\varvec{\lambda }_{B_i}+\mathbf L _{C_{i},R}\,\varvec{\lambda }_{C_{i}} \, \\ m_{L_i}\mathbf J _{L_i,T}\ddot{{{\varvec{q}}}}={{\varvec{K}}}_{L_i,T}+\,{{\varvec{F}}}_{L_i}^a\,+\mathbf L _{B_i,T}\,\varvec{\lambda }_{B_i}+\mathbf L _{C_{i},T}\,\varvec{\lambda }_{C_{i}} \end{array} \right. \end{aligned}$$

(25)

where ${{\varvec{K}}}_{L_i,R}=-\mathbf I _{L_i}\,\varvec{\delta }_{L_i}-\varvec{\varepsilon }_{L_i}$ and ${{\varvec{K}}}_{L_i,T}=-m_{L_i}\varvec{\mu }_{L_i}$.

4.2 System Newton–Euler equations of the parallel manipulator

According to the above analysis, the system Newton–Euler equations of the whole 3-PRRU parallel manipulator can be obtained by concatenating those of all bodies as

$$\begin{aligned} \left\{ \begin{array}{l} \mathbf I \,\dot{\varvec{\omega }}+\varvec{\varepsilon }\,={{\varvec{M}}}^a\,+{{\varvec{M}}}^n\\ \mathbf m \,\dot{{{\varvec{v}}}}\,=\,{{\varvec{F}}}^a\,+{{\varvec{F}}}^n\\ \end{array}\right. \end{aligned}$$

(26)

where the system inertia and force/torque coefficients are given by

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{l} \;\,\mathbf I \;=\,\mathrm {Blkdiag}\left( \mathbf I _P,\, \mathbf I _{L_1},\, \cdots ,\, \mathbf I _{S_3}\right) \\ \,\mathbf m =\,\mathrm {Blkdiag}\left( m_P\mathbf E _3,\, m_{L_1}\mathbf E _3,\, \cdots ,\, m_{S_3}\mathbf E _3\right) \\ \,\varvec{\varepsilon }\,=\,\left[ \varvec{\varepsilon }_P^T,\; \varvec{\varepsilon }_{L_1}^T,\; \cdots ,\; \varvec{\varepsilon }_{S_3}^T\right] ^T \end{array}\right. \\ \left\{ \begin{array}{l} {{\varvec{M}}}^a\,=\,\left[ ({{\varvec{M}}}^a_P)^T, \; ({{\varvec{M}}}^a_{L_1})^T,\;\cdots ,\; ({{\varvec{M}}}^a_{S_3})^T\right] ^T\\ \;{{\varvec{F}}}^a\,=\,\left[ ({{\varvec{F}}}^a_P)^T, \; ({{\varvec{F}}}^a_{L_1})^T,\;\cdots ,\; ({{\varvec{F}}}^a_{S_3})^T\right] ^T\\ \end{array}\right. \\ \left\{ \begin{array}{l} {{\varvec{M}}}^n\,=\,\left[ ({{\varvec{M}}}^n_P)^T, \; ({{\varvec{M}}}^n_{L_1})^T,\;\cdots ,\; ({{\varvec{M}}}^n_{S_3})^T\right] ^T\\ \;{{\varvec{F}}}^n\,=\,\left[ ({{\varvec{F}}}^n_P)^T, \; ({{\varvec{F}}}^n_{L_1})^T,\;\cdots ,\; ({{\varvec{F}}}^n_{S_3})^T\right] ^T\\ \end{array}\right. \end{array}\end{aligned}$$

According to the kinematics analysis presented in the above section, the accelerations of all bodies of the parallel manipulator can be represented in a matrix form as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\varvec{\omega }}=\,\mathbf J _R\,\ddot{{{\varvec{q}}}}+\varvec{\delta }\\ \,\dot{{{\varvec{v}}}}\,=\,\mathbf J _T\,\ddot{{{\varvec{q}}}}+\varvec{\mu } \end{array}\right. \end{aligned}$$

(27)

where

$$\begin{aligned} \,\,\,\,\dot{\varvec{\omega }}= & {} \,\left[ \begin{array}{c} \dot{\varvec{\omega }}_P\\ \dot{\varvec{\omega }}_{L_1}\\ \vdots \\ \dot{\varvec{\omega }}_{S_3}\\ \end{array} \right] ,\, \dot{{{\varvec{v}}}}\,=\,\left[ \begin{array}{c} \dot{{{\varvec{v}}}}_P\\ \dot{{{\varvec{v}}}}_{L_1}\\ \vdots \\ \dot{{{\varvec{v}}}}_{S_3}\\ \end{array} \right] ,\, \mathbf J _R\,=\left[ \begin{array}{c} \mathbf J _{P,\,R}\\ \mathbf J _{L_1,R}\\ \vdots \\ \mathbf J _{S_3,R}\\ \end{array} \right] ,\\ \mathbf J _T\,= & {} \,\left[ \begin{array}{c} \mathbf J _{P,\,T}\\ \mathbf J _{L_1,T}\\ \vdots \\ \mathbf J _{S_3,T}\\ \end{array} \right] ,\, \varvec{\delta }\,=\,\left[ \begin{array}{c} \varvec{\delta }_P\\ \varvec{\delta }_{L_1}\\ \vdots \\ \varvec{\delta }_{S_3}\\ \end{array} \right] ,\, \varvec{\mu }\,=\,\left[ \begin{array}{c} \varvec{\mu }_P\\ \varvec{\mu }_{L_1}\\ \vdots \\ \varvec{\mu }_{S_3}\\ \end{array} \right] \end{aligned}$$

Substituting (27) into Eq. (26), the system Newton–Euler equations of the whole parallel manipulator can be represented as a set of DAEs of the generalized coordinates and the reaction forces as,

$$\begin{aligned} \varvec{\Phi }\,\mathbf H \,\ddot{{{\varvec{q}}}}+{{\varvec{K}}}\left( {{\varvec{q}}},\,\dot{{{\varvec{q}}}}\right) \, =\,\overline{{{\varvec{F}}}}^a\,+\mathbf Q \varvec{\lambda } \end{aligned}$$

(28)

where the items can be determined as

$$\begin{aligned} \left\{ \begin{array}{l} \,\varvec{\Phi }\,=\,\left[ \begin{array}{cc} \mathbf I &{}\mathbf 0 \\ \mathbf 0 &{}\mathbf m \\ \end{array} \right] ,\,\; \mathbf H \,=\,\left[ \begin{array}{c} \mathbf J _R\\ \mathbf J _T\\ \end{array} \right] ,\,\; {{\varvec{K}}}\,=\,\left[ \begin{array}{c} \mathbf J \varvec{\delta }+\varvec{\varepsilon }\\ \mathbf m \varvec{\mu }\\ \end{array} \right] \,\;\\ \overline{{{\varvec{F}}}}^a=\,\left[ \begin{array}{c} {{\varvec{M}}}^a\\ {{\varvec{F}}}^a\\ \end{array} \right] ,\,\; \varvec{\lambda }\,=\left[ \varvec{\lambda }_{C}^T, \; \varvec{\lambda }_{B}^T, \; \varvec{\lambda }_{A}^T, \; \varvec{\lambda }_{P}^T \right] ^T \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{array}{l} \mathbf Q \,=\,\left[ \begin{array}{cccccccc} \mathbf P _{C,\,R}^T &{} \mathbf L _{C,\,R}^T &{} \mathbf 0 &{} \mathbf 0 &{} \mathbf P _{C,\,T}^T &{} \mathbf L _{C,\,T}^T &{} \mathbf 0 &{} \mathbf 0 \\ \mathbf 0 &{} \mathbf L _{B,\,R}^T &{} \mathbf U _{B,\,R}^T &{} \mathbf 0 &{} \mathbf 0 &{} \mathbf L _{B,\,T}^T &{} \mathbf U _{B,\,T}^T &{} \mathbf 0 \\ \mathbf 0 &{} \mathbf 0 &{} \mathbf U _{A,\,R}^T &{} \mathbf S _{A,\,R}^T &{} \mathbf 0 &{} \mathbf 0 &{} \mathbf U _{A,\,T}^T &{} \mathbf S _{A,\,T}^T\\ \mathbf 0 &{} \mathbf 0 &{} \mathbf 0 &{}\mathbf S _{P,\,R}^T &{} \mathbf 0 &{} \mathbf 0 &{} \mathbf 0 &{} \mathbf S _{P,\,T}^T \end{array} \right] ^T \\ \mathbf L _{C,\,X}\,=\,\mathrm {Blkdiag}\left( \mathbf L _{C_1,\,X}, \; \mathbf L _{C_2,\,X}, \;\mathbf L _{C_3,\,X} \right) \quad \;\\ \mathbf L _{B,\,X}\,=\,\mathrm {Blkdiag}\left( \mathbf L _{B_1,\,X},\; \mathbf L _{B_2,\,X}, \;\mathbf L _{B_3,\,X} \right) \\ \mathbf U _{B,\,X}\,=\,\mathrm {Blkdiag}\left( \mathbf U _{B_1,\,X},\;\mathbf U _{B_2,\,X},\;\mathbf U _{B_3,\,X} \right) \quad \\ \mathbf U _{A,\,X}\,=\,\mathrm {Blkdiag}\left( \mathbf U _{A_1,\,X}, \; \mathbf U _{A_2,\,X},\; \mathbf U _{A_3,\,X} \right) \\ \,\mathbf S _{A,\,X}\,=\,\mathrm {Blkdiag}\left( \mathbf S _{A_1,\,X}, \; \mathbf S _{A_2,\,X},\; \mathbf S _{A_3,\,X} \right) \quad \;\;\;\\ \,\mathbf S _{P,\,X}\,=\,\mathrm {Blkdiag}\left( \, \mathbf S _{P_1,\,X}, \; \mathbf S _{P_2,\,X}, \; \mathbf S _{P_3,\,X} \right) \end{array}\right. \end{aligned}$$

where $X \,=\,R \,or \,T$ for rotation and translation, respectively.

According to the principle of virtual work, the ideal constraint forces/torques reacted in the connecting joints do not produce any work to the multi-body system. Then, we have

$$\begin{aligned} \mathbf H ^T\,\mathbf Q \equiv \mathbf 0 \end{aligned}$$

(29)

Then, the constraint forces in Eq. (28) can be eliminated by means of left-multiplying the transpose of $\mathbf H ^T$. And the system equations of motion of the parallel manipulator can be obtained directly as

$$\begin{aligned} \mathbf H ^T\varvec{\Phi }\,\mathbf H \;\ddot{{{\varvec{q}}}}+\mathbf H ^T{{\varvec{K}}}\left( {{\varvec{q}}},\,\dot{{{\varvec{q}}}}\right) \, =\,\mathbf H ^T\,\overline{{{\varvec{F}}}}^a \end{aligned}$$

(30)

where $\overline{{{\varvec{F}}}}^a$ integrates all external forces/torques exerted on the parallel manipulator, including the gravities of all bodies, the driving forces in the actuated joints, and the work load applied to the end-effector.

Meanwhile, the system equations of reaction of the parallel manipulator can be obtained in a similar way as

$$\begin{aligned} \varvec{\lambda }=\,\left( \mathbf Q ^T\varvec{\Phi }^{-1}\mathbf Q \right) ^{-1}\mathbf Q ^T\varvec{\Phi }^{-1}\left( {{\varvec{K}}}-\overline{{{\varvec{F}}}}^a\right) \end{aligned}$$

(31)

where $\mathbf Q ^T\varvec{\Phi }^{-1}\mathbf Q$ is always invertible because the system inertia matrix $\varvec{\Phi }$ is non-singular and $\mathbf Q$ is full rank.

Fig. 4

Constraint forces reacted in the universal joints connected to the moving platform

Comparing with the Lagrange method and convectional Newton–Euler formulation, the advantages of the proposed dynamic modeling method include the following aspects.

Firstly, the derivation process of the parallel manipulator’s forward dynamics is relatively straightforward. As indicated in Sect. 3, the pose of the 3-PRRU parallel manipulator’s end-effector is selected as the system generalized coordinates. Thus, the closed-form solutions to the position, velocity and acceleration analysis can be derived conveniently by taking advantage of the manipulator’s inverse kinematics. Meanwhile, the principle of virtual work can be employed to directly separate the ideal constraint forces reacted in the connecting joints.

Secondly, using the proposed method, both equations of motion and reaction can be analytically derived in the form of ODE and purely linear algebraic equations, respectively. Hence, both the dynamic response and reaction force can be obtained by solving the system’s EOM and EOR separately. And this information is necessary during the performance optimization of the studied parallel manipulator by taking the bodies’ dynamic effects into account.

Furthermore, the proposed method can be extended to a modular dynamic modeling approach by means of taking further consideration into account. For instance, the clearance and friction effects of the connecting joints can also be added as a subsystem into the manipulator’s dynamic models. Then, nonlinear dynamics analysis can be conducted for the manipulators of interest. This aspect will be further studied in our future work.

Table 1 Mass and inertia tensors of the bodies in the 3-PRRU parallel manipulator

Fig. 5

Dynamic response of parallel manipulator under the given load condition: a generalized coordinates; b actuated joints

4.3 Numerical simulation of the manipulator’s dynamic response

Based on the system EOM (30) and EOR (31), the dynamic responses, including the generated movement and the reacted constraint forces/torques, of the studied 3-PRRU parallel manipulator can be obtained directly according to the external load exerted on the manipulator. This section presents a numerical simulation to verify the correctness of the obtained dynamic models.

Fig. 6

Constraint forces reacted in the prismatic joints attached to the fixed base

In the numerical simulation, the preset values of the parallel manipulator’s kinematic parameters illustrated in Fig. 3 are given by $b_1=b_2=0.360\,m$, $b_3=0.315\,m$ for the positions of the prismatic joints, $l_{1,1}=l_{2,1}=l_{3,1}=0.230\,m$, $l_{1,2}=l_{2,2}=l_{3,2}=0.225\,m$ for the lengths of the upper and lower links, and $l_{1,3}=l_{2,3}=0.045\,m$ for the size of the moving platform, respectively. The mass and inertia tensors of the manipulator’s bodies are listed in Table 1. Since all the bodies are symmetric in structure, the inertia tensors are principal ones in their body-fixed frames. The initial pose of the manipulator’s end-effector is set ${{\varvec{q}}}=[0,\,\frac{\pi }{6},\, -0.8]^T rad/m$ and the parallel manipulator is assumed stationary, namely $\dot{{{\varvec{q}}}}=\,{{\varvec{0}}}$, at the beginning of the simulation. And the driving forces in the actuated prismatic joints are assigned to ${{\varvec{F}}}_a=[50,\, 40,\, 25]^T N$ constantly. Meanwhile, a harmonic external load is exerted on the end-effector of the parallel manipulator as ${{\varvec{F}}}_{P}^{a}=[50\sin (4\pi t), -50\cos (4\pi t), 0]^T\,N$ (Fig. 4).

The corresponding simulation results are illustrated in Figs. 5 and 6. It should be noted that all those results have been validated by the commercial code Adams/View. Figure 5 shows the dynamic response of the studied parallel manipulator under a specific load condition. The historic trajectory of the generalized coordinates is obtained by means of the direct integration of the system’s EOM (30) using ODE45 algorithm in MATLAB. Accordingly, the displacements of the active prismatic joints can be specified via the inverse kinematics analysis presented in Sect. 3.

Meanwhile, all constraint forces/torques reacted in the connecting joints can be obtained according to the system’s EOR (31). Figure 4 illustrates the constraint forces reacted in the universal joints. From the results, it is obvious that the external forces along the ${{\varvec{x}}}$-direction of $\left\{ \mathrm {S}\right\}$ are mainly supported by limbs 1 and 2, while the exerted load parallel to the ${{\varvec{y}}}$-axis of $\left\{ \mathrm {S}\right\}$ is mainly distributed into limb 3. Therefore, once there are some large external forces exerted on the end-effector of the parallel manipulator, all its three limbs will bear relatively large loads perpendicular to their assembling planes. And this phenomenon is crucial for the structural design of the bodies in the studied parallel manipulator.

Fig. 7

Dynamic manipulability ellipsoids and the corresponding measure

As illustrated in Fig. 6, horizontal external loads will be transferred to the actuated joints through the limbs. Meanwhile, extra torques about the axes of the prismatic joints will be generated to the limbs. As a result, torsional effects will be caused to the sliders connected to the prismatic joints. Therefore, not only perpendicular forces, but also torsional loads will be exerted on the supporting pillars of the parallel manipulator’s limbs. Since screw-guide mechanisms are used to actuate the prismatic joints of the 3-PRRU parallel manipulator, particular attentions must be paid on the selection of concrete structures and specifications of the actuation systems according to their complex load conditions.

5 Dynamic performance analysis of the 3-PRRU parallel manipulator

Based on the dynamic model obtained in the above section, performance analysis of the 3-PRRU parallel manipulator is conducted in this section. The concept of dynamic manipulability ellipsoid (DME) [8] is used to evaluate the parallel manipulator’s ability in changing the end-effector’s position/orientation under the constraint of the driving forces in the prismatic joints. Then, the distribution of DME index in the whole workspace is also provided in this section.

In the concept of DME, the effect of the links’ dynamics is taken into account in the quantitative evaluation of the ability in manipulating the end-effector of the robot manipulators. Thus, accelerations of the manipulator’s end-effector are calculated to quantify the easiness of changing the pose in various directions under some constraint on the driving forces in the active joints.

Then, for the studied 3-PRRU manipulator, the system dynamic Eq. (30) can be rewritten in the form of

$$\begin{aligned} \mathbf J _d^{-T}\,\mathbf H ^T\,\varvec{\Phi }\,\mathbf H \,\mathbf J _{e}^{+}\,(\dot{\tilde{{{\varvec{v}}}}}_{e}-\dot{\mathbf{J }}_{e}\,\dot{{{\varvec{q}}}})=\,{{\varvec{F}}}_{d}+\mathbf J _d^{-T}\,\mathbf H ^T(\overline{{{\varvec{F}}}}_a-{{\varvec{K}}}) \end{aligned}$$

(32)

where ${{\varvec{F}}}_d=\,\left[ F_{d,1},\, F_{d,2},\, F_{d,3}\right] ^T$ denotes the driving forces applied on the sliders. And the matrix $\mathbf J _{d}$ relates the system’s generalized coordinates to the actuated joints, namely $\dot{{{\varvec{d}}}}=\,\mathbf J _{d}\,\dot{{{\varvec{q}}}}$. The vector $\dot{\tilde{{{\varvec{v}}}}}_{e}=\,\left[ \dot{\varvec{\omega }}_{P}^T,\, \dot{{{\varvec{v}}}}_{P}^T\right] ^T$ integrates the rotational and translational accelerations of the parallel manipulator’s end-effector. Since the end-effector of the manipulator is attached to the moving platform, its Jacobian yields

$$\begin{aligned} \mathbf J _{e}=\,\mathbf J _{P}=\,\left[ \mathbf J _{P,R}^T,\,\mathbf J _{P,T}^T\right] ^T. \end{aligned}$$

According to (32), an ellipsoid can then be obtained to describe the boundary of the end-effector’s accelerations in various directions under the constraint of driving forces as

$$\begin{aligned} \Vert \tilde{{{\varvec{F}}}}\Vert \le 1\Rightarrow \tilde{{{\varvec{a}}}}^T\,\tilde{\mathbf{J }}^{+T}\,\tilde{\mathbf{M }}^T\,\tilde{\mathbf{M }}\,\tilde{\mathbf{J }}^{+}\,\tilde{{{\varvec{a}}}}\le 1 \end{aligned}$$

(33)

where $\tilde{{{\varvec{F}}}}=\,{{\varvec{F}}}_{d}+\mathbf J _d^{-T}\,\mathbf H ^T(\overline{{{\varvec{F}}}}_a-{{\varvec{K}}})$ and $\tilde{{{\varvec{a}}}}=\,\dot{\tilde{{{\varvec{v}}}}}_{e}-\dot{\mathbf{J }}_{e}\,\dot{{{\varvec{q}}}}$ are the generalized driving forces and end-effector acceleration of the parallel manipulator. $\tilde{\mathbf{J }}=\,\mathbf J _{e}\,\mathbf J _{d}^{-1}$ is the Jacobian relating the manipulator’s actuated joints to its end-effector. $\tilde{\mathbf{M }}=\,\mathbf J _d^{-T}\,\mathbf H ^T\,\varvec{\Phi }\,\mathbf H \mathbf J _d^{-1}$ is the system’s reduced inertia matrix.

Moreover, the separated DMEs associated with the rotational and translational aspects of the manipulator can be derived from (33) by replacing the corresponding Jacobians with separate ones. As a consequence, two ellipsoids can be obtained to evaluate the rotational and translation dynamic manipulability, respectively, as

$$\begin{aligned} \Vert \tilde{{{\varvec{F}}}}\Vert \le 1\Rightarrow \left\{ \begin{array}{l} \tilde{{{\varvec{a}}}}_{R}^T\,\tilde{\mathbf{J }}_{R}^{+T}\,\tilde{\mathbf{M }}^T\,\tilde{\mathbf{M }}\,\tilde{\mathbf{J }}_{R}^{+}\,\tilde{{{\varvec{a}}}}_{R}\,\le 1\\ \tilde{{{\varvec{a}}}}_{T}^T\,\tilde{\mathbf{J }}_{T}^{+T}\,\tilde{\mathbf{M }}^T\,\tilde{\mathbf{M }}\,\tilde{\mathbf{J }}_{T}^{+}\,\tilde{{{\varvec{a}}}}_{T}\,\le 1\\ \end{array}\right. \end{aligned}$$

(34)

where $\tilde{{{\varvec{a}}}}_{R}$ and $\tilde{{{\varvec{a}}}}_{T}$ correspond to the rotational and translational aspects of $\tilde{{{\varvec{a}}}}$, respectively. Accordingly, the separate Jacobians are given by $\tilde{\mathbf{J }}_{R}=\,\mathbf J _{P,R}\,\mathbf J _{d}^{-1}$ and $\tilde{\mathbf{J }}_{T}=\,\mathbf J _{P,T}\,\mathbf J _{d}^{-1}$.

Since the studied 3-PRRU parallel manipulator has two rotational and one translation DOF without parasitic motion, the separated DMEs degenerate to a planar ellipse and a line, respectively, as shown in Fig. 7a. It is obvious that the degenerate rotational DME lies on the plane spanned by ${{\varvec{x}}}$ and ${{\varvec{v}}}$, while the translational accelerations only occurs along the ${{\varvec{z}}}$-axis. Furthermore, the axes with the maximum and minimum rotational accelerations on the locating plane can be directly obtained from the degenerate ellipse.

To evaluate the isotropic property of dynamic manipulability, the condition number of $\tilde{\mathbf{M }}\,\tilde{\mathbf{J }}_{R}^{+}$ is adopted as a measure of the manipulator’s dynamic performance as

$$\begin{aligned} w_{_R}=\,\frac{\sigma _{_{R,1}}}{\sigma _{_{R,2}}} \end{aligned}$$

(35)

where $\sigma _{_{R,1}}$ are $\sigma _{_{R,2}}$ are the nonzero singular values of $\tilde{\mathbf{M }}\,\tilde{\mathbf{J }}_{R}^{+}$, and $\sigma _{_{R,1}}\ge \sigma _{_{R,2}}$.

From kinematics analysis, it is known that pure translation of the end-effector only generate a motion of the whole manipulator along the ${{\varvec{z}}}$-axis, so it does not influence the dynamic manipulability performance. Hence, in the performance analysis, the z-coordinate of the end-effector is fixed at the home position, namely $q_3=0$, while for the 2-DOF rotational workspace, a rectangular area is selected in the range of $[-\pi /6, \pi /6]\times [-\pi /4, \pi /6]$ for $q_1$ and $q_2$ by taking the manipulator’s motion limit into account. The workspace is discretized by the two rotation angles $q_1$ and $q_2$, respectively. For each configuration within the above workspace, the isotropic measure $w_{_R}$ is calculated according to (35).

As a result, a surface, as shown Fig. 7b, can be obtained to illustrate the distribution of the studied 3-PRRU parallel manipulator’s dynamic performance within the 2-DOF rotational workspace.

As indicated in the above, the proposed 1T2R parallel manipulator has a partial symmetric structure. Since limbs 1 and 2 are symmetric about the ${{\varvec{xz}}}$-plane of $\left\{ \mathrm {S}\right\}$, the rotation about $q_1$ can be considered as a result of their differential motions. Therefore, the performance index $w_{_R}$ should also be symmetric about $q_1$, which can be verified by the surface obtained in Fig. 7b. As shown in the figure, for a specific $q_2$, the isotropic property of the manipulator’s dynamic performance is symmetric whenever the rotation about $q_1$ is to left or right side. On the other hand, the end-effector’s rotation about $q_2$ is produced only by the third limb, which can be regarded as a planar slider-crank mechanism as shown in Fig. 3b. Thus, the transmission property is different when the angle $\gamma$ is positive or minus.

Further, from Fig. 7a, it is known that the rotational acceleration of $q_1$ is much larger than that of $q_2$. As indicated in the above, the rotation of $q_1$ is generated by the differential motion of two limbs, while $q_2$ is generated by only one. Therefore, the isotropic index $w_{R}$ is not close to 1 even at the home configuration of manipulator, namely $q_1=0, \,q_2=0$. At the mean time, it can be seen that the isotropic property becomes better when the magnitude of $q_1$ increases. This is because the effect of differential motion between limbs 1 and 2 decreases at a more oblique configuration of the manipulator’s end-effector. Then, the ability of rotational accelerations about $q_1$ and $q_2$ becomes closer, so does $w_{R}$ to 1. In addition, a corresponding contour plot is provided in Fig. 7c to demonstrate the distribution property of the dynamic performance index in an intuitive way.

As a general purpose robot manipulator, the condition number (35) is usually minimized as close as 1 to make the dynamic performance of the manipulator as isotropic as possible. In other words, the index surface illustrated in Fig. 7b should be maximally decreased to the horizontal plane $w_{_R}=1$. Then, the studied parallel manipulator has an equal ability in changing the end-effector’s orientation in various directions on the locating plane as illustrated in Fig. 7a. Therefore, the overall distance between the index surface and the plane $w_{_R}=1$ can be defined as an assessment to evaluate the isotropic property of manipulator’s acceleration ability within the workspace.

In future work, two different ways will be carried out to achieve the above subject. One is to employ kinematics and structural optimizations to minimize the index, such that the isotropic property of the dynamic performance can be improved. The other is introducing actuation redundancy to the current design. An extra limb will be added, such that the rotation of $q_2$ is also generated by two limbs. As a result, the ability of rotational accelerations about $q_1$ and $q_2$ can be set more equally.

In addition, the influences of the manipulator’s kinematic parameters and the bodies’ inertia properties on the index of dynamic performance will be further studied based on the modeling and analysis method proposed in this paper, such that optimization can be employed to improve the performance. Moreover, physical experiments will also be conducted on a prototype, which is developed based on the studied 3-PRRU parallel manipulator as shown in Fig. 8, to verify the method presented in this paper.

Fig. 8

A prototype of the 3-PRRU 1T2R parallel manipulator

6 Conclusions

This paper presents the dynamic modeling and performance analysis of the 3-PRRU 1T2R parallel manipulator without parasitic motion. Based on the Newton–Euler formulation with generalized coordinates, both system EOM and EOR are established to predict the dynamic response of the studied parallel manipulator under specific external loads. The proposed modeling method has been validated by means of numerical simulations with the comparison of commercial softwares. From the numerical results, the load transferring property of the studied parallel manipulator has also been investigated. The concept of DME is then adopted to evaluate the dynamic manipulability performance of the 3-PRRU parallel manipulator. And the global distribution of a related measure within the workspace of the parallel manipulator is derived, which will serve as the criteria for further kinematic and structure optimizations of the studied parallel manipulator in future work.