Closed-form dynamic modeling and performance analysis of an over-constrained 2PUR-PSR parallel manipulator with parasitic motions

Abstract

This paper presents an systematic dynamic modeling and performance analysis method of an over-constrained 2PUR-PSR parallel manipulator with parasitic motions, where P, U, S, and R represent the prismatic joint, universal joint, spherical joint, and revolute joint, respectively. The process of the deduction of the over-constrained forces/moment is given. The Newton–Euler approach and natural orthogonal complement method are adopted to establish two types of dynamic models with and without constrained forces/moments with the consideration of the over-constrained forces/moments. The dynamic manipulability ellipsoid, which measures the uniformity of changing the position and orientation of the manipulator’s moving platform, is adopted to evaluate the dynamic performance of the parallel manipulator. To show the feasibility of the proposed method, numerical simulations are conducted to investigate the dynamic models and performance of the 2PUR-PSR manipulator. The actuation forces, constrained forces/moments, and the compatible deformation are calculated. Distribution of the DME index is also obtained. The proposed modeling approach provides a fundamental basis for the structural optimization and control scheme design of the over-constrained parallel manipulator.

1 Introduction

Parallel manipulators (PMs) have been intensively studied for over a decade and have been used in a wide spectrum of applications, from simple pick-and-place operations of an industrial robot to advanced electronic manufacturing, maintenance of nuclear plants robotics [1, 2]. Because of their closed kinematic structures, PMs exhibit better performance in terms of accuracy, rigidity, and payload capacity and show greater potential to deal with numerous tasks [3]. The lower motility PMs, which own less than six degrees of freedom (DOF), can perform most of the aforementioned tasks and have received more and more popularities for their lower cost, lower complexity in structure and easier control [4].

Dynamic modeling serves as the fundamental basis for the dynamic performance analysis and is essential for the structural design and control scheme design of parallel manipulators. However, different applications have different requirements for the dynamic model. For the structural design, the driving forces/torque and the constrained forces/moments should be calculated simultaneously, while for the control scheme design, the dynamic model should be efficient enough for the real-time calculation. Unlike serial manipulators which possess well-established dynamic modeling methods, however, due to the closed kinematic chain, an explicit dynamic formulation of the PMs is much more complicated. Besides, the parasitic motions and over-constraints usually accompany the lower motility PMs, which makes the dynamics even more complicated [5]. Over-constraints would result in deformation for the flexibility of links, which cannot be ignored for high-accurate applications. Most previous studies on low-mobility PMs have focused on kinematics and the corresponding optimal design. The systematic investigation of dynamics and performance analysis of the over-constrained PM with parasitic motions is still an open problem.

Therefore, we aim to propose a systematic precise and efficient method to derive the explicit dynamic formulation and dynamic performance analysis for the over-constrained lower-mobility PM with parasitic motions. We focus on an over-constrained 2PUR-PSR PM, which possesses one translational and two rotational DOFs with parasitic motions, is a three-legged parallel manipulator utilizing the sliders to allow actuators to be mounted on the base.

The literature on the dynamic modeling of PMs mainly falls into four categories: the Newton–Euler method, Lagrange formulation, Kane equation, and principle of virtual power [6]. Using Newton–Euler method, Dasgupta obtained the inverse dynamic models of the Stewart platform [7, 8]. First, the dynamic equation of every isolated rigid body was obtained with the consideration of the internal forces and moments, resulting in a system that can be applied in model-based feed-forward control. By eliminating the internal forces and moments, a closed-form dynamic formulation of the Stewart platform was then derived. Using the same method, Chen established the closed-form dynamic model of the 3PRRU parallel manipulator without parasitic motion or redundant constraints, and the dynamic performance was then analyzed based on the dynamic model [9]. By incorporating the deformation compatible equations, Bi derived the inverse dynamic model of an over-constrained parallel manipulator with the Newton–Euler formulation. This model has the potential to be integrated with control systems to improve dynamic performance under real-time control [10]. However, the Newton–Euler method usually results in a set of differential algebraic equations with a maximum number of coordinates. As the Newton–Euler equations of all bodies and the constraint equations are integrated together, the computation cost is very high.

Many researchers have applied the usual Lagrange formulation to PMs, but the closed kinematic chain requires the introduction of Lagrange multipliers [11], making the Lagrange formulation too complex. To eliminate the multipliers, Stefan proposed a recursive matrix representation for the kinematics of the parallel manipulator and employed a dynamic model for the PM using the minimal parameters derived from the kinematics [12,13,14]. Chen proposed the Udwadia–Kalaba approach to calculate the multipliers and obtained an explicit dynamic model of the Stewart platform [15]. By combining the Lagrange formulation with the virtual work principle, Guiyang established the dynamics of a parallel manipulator with three DOFs [16]. Houssem considered open-loop sub-chains of the PM and derived their dynamics by the Lagrange formulation with respect to an own set of generalized coordinates and velocities. By considering the principle of energy equivalence, the equations can be computed separately for the sub-chains of the robot [17]. Dong established the dynamic model of a planar parallel manipulator with the redundant actuations with the Lagrange equation, and the Lagrange multipliers were eliminated by the expression of the null space of velocity constraint matrix [18]. Briot employed the Lagrange formulation to derive the dynamic model of the 5R parallel manipulator with flexible joints and flexible links, and the Lagrange multipliers were derived based on the dynamic model of the moving platform (MP), and an explicit dynamic model was thus obtained [19, 20]. However, as explicit expressions require the kinetic and potential energies of all components in the manipulator, the computational cost of the Lagrange equation would increase significantly when the number of bodies increases. Hence, for parallel manipulators with closed kinematic chains, dynamic modeling with the Lagrange formulation is too complex.

By integrating Lagrange equation with d’Alembert’s principle, Kane’s equations demonstrate that the sum of total generalized active forces and the total generalized inertia forces for each generalized coordinate of the system equals zero [21]. It can be shown that the constrained forces/moments are eliminated automatically with Kane’s equations, as all selected partial velocities are independent. Using Kane’s equation, Chen derived the rigid-flexible coupled dynamic model of a 3RRR planar parallel manipulator [22]. Cheng derived the dynamic model of a hip joint simulator with a 3SPS + 1PS spatial parallel manipulator. This provided the theoretical basis for the design of a driving system with active branched-chains and the structural parameters of the intermediate branched-chain, as well as for the control system design [23]. However, the deductions of partial velocities and accelerations require tedious calculations due to the closed kinematic chains of PMs, and also the established dynamic model is inappropriate for structural design as constrained forces/moments in connecting joints are automatically eliminated.

The principle of virtual power is another effective dynamic modeling method for multibody system. The process is as following: the generalized forces, including the inertial forces, gravity forces, external forces, and the actuation forces, for individual body are calculated first, and then, the dynamically systematic equilibrium equations depicting the virtual power of the system, which were produced by all forces under instantaneous virtual displacement, are established and held zero. As the constrained forces or moments did not produce work for the system, they are eliminated from the dynamic model; Jaime established the inverse dynamic model of the 4-PRUR PM by means of the screw theory and the principle of virtual work [24]. Hu derived the velocity mapping of the (3-UPU)+(3-UPS+S) serial-parallel manipulator and established the dynamic models with the principle of virtual power, and the actuation forces were derived [25]. Huang first established the 3-DOF Modules of Two Reconfigurable PKM—the Tricept and the TriVariant with the principle of virtual power, and conducted comparison studies of the dynamic performance [26], and then, the dynamic model of the 4-DOF SCARA Type PM was derived with the same method, based on which the dynamic performance indices were optimized [27]. The principle of virtual power is a very efficient control-oriented modeling method for the dynamics of the PM, for which the constrained forces/moments were eliminated. However, the constrained forces/moments are essential for structural design, so the dynamic modeling with the principle cannot satisfy the requirements for structural design and control scheme design simultaneously.

To derive a computationally efficient dynamic model, the concept of the natural orthogonal complement (NOC), which defined the relationship that maps the independent velocities onto the twist of an individual body, is proposed to eliminate the constrained forces/moments or the Lagrange multipliers [28]. In NOC, dynamic modeling of individual body is established first, and then, the NOC matrix is employed to transform the twist of an individual body into independent velocities. The resulting dynamic model is in closed form without including constrained forces, torques, or the Lagrange multipliers. Hence, this method is quite efficient and straightforward and is very suitable for PMs. Using this method, Ganesh established the inverse dynamic model of a translational parallel manipulator and optimized the trajectories [29].

In the aforementioned literature, the research on dynamic modeling of PMs has made considerable achievements; however, relevant studies on the over-constrained PMs with parasitic motions are quite limited. Also, to the author’s knowledge, there is still no generally accepted dynamic index for the over-constrained lower-mobility PM with parasitic motions. In this paper, to satisfy different requirements for the dynamic models of structural and control scheme design, a systematic closed-form dynamic modeling and analysis method of the over-constrained PMs with parasitic motions is presented. The dynamic models with and without constrained forces/moments can be established simultaneously with the Newton–Euler equation and NOC method, and the deformation induced by the over-constrained forces/moments are derived. The dynamic manipulability ellipsoid (DME) [30] for PMs without parasitic motions is employed to evaluate the dynamic performance of the PMs parasitic motions. The 2PUR-PSR PM will be considered to demonstrate the dynamic modeling and the dynamic performance analysis of this type PMs. In the following sections, the NOC method and Newton–Euler equation are used to establish closed-form dynamic model of an over-constrained 2PUR-PSR PM with parasitic motions. The derived model is validated by the comparison with generalized commercial software. Additionally, the dynamic performance is investigated. The dynamic modeling and analysis method presented in this paper is expected to be applicable to other similar PMs with parasitic motions.

2 Kinematics of the 2PUR-PSR parallel manipulator

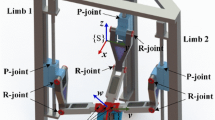
As shown in Fig. 1, the 2PUR-PSR PM considered in this paper consists of a base platform and a MP connected by two identical PUR limbs and one PSR limb. ${A}_1$ and ${A}_2$ represent the intersections of the universal joint, ${A}_3$ is the center point of spherical joint, ${P}_{i} ({i}=1,2,3)$ generally denotes the location of the prismatic joint and the actuated motor in each limb, and the motion of the first two collinear prismatic joints is perpendicularly to the third; ${B}_{i} ({i}=1,2,3)$ represents the revolute joint in the MP connected with each limb, and ${C}_{i}~({i}=1,2,3)$ represents the mass center of the ith link. The reference frame ${O-}{{\varvec{XYZ}}}$ and the moving frame ${P-}{{\varvec{uvw}}}$ are attached to the base and the MP, respectively, with O and P being the origins located at the midpoint of ${A}_1 {A}_2$ and ${B}_1 {B}_2$; the X and u axes are parallel to ${A}_1 {A}_2$ and ${B}_1 {B}_2$, whereas the Z and w axes are perpendicular to the base and the MP; the Y and v axes are then determined through the right-hand rule. In addition, the geometrical parameters of limb 1 and limb 2 are identical, with ${l}_1$ and ${l}_3$ being the length of ${PB}_1$ and ${A}_1 {B}_1$, and the corresponding parameters of limb 3 are ${l}_2$ and ${l}_4$, respectively.

Fig. 1

CAD model of the manipulator

2.1 Inverse position analysis

Inverse position analysis of the 2PUR-PSR PM involves the determination of the position and orientation of each limb for the given position and orientation of the MP. The orientation matrix of the moving frame ${P-}{{\varvec{uvw}}}$ with respect to the reference frame ${O-}{{\varvec{XYZ}}}$ can be derived in terms of three rotational angles $\varphi$, $\theta$ and $\phi$ satisfying the Z-Y-X convention:

$$\begin{aligned} {{\varvec{R}}}_{P}= & {} {{\varvec{R}}}_{{Z,\varphi }} {{\varvec{R}}}_{{Y},\theta } {{\varvec{R}}}_{{X,}\phi } =\left( {{\begin{array}{c@{\quad }c@{\quad }c} {\cos \varphi }&{}\quad {-\sin \varphi }&{}\quad 0 \\ {\sin \varphi }&{}\quad {\cos \varphi }&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1 \\ \end{array} }} \right) \nonumber \\&\times \left( {{\begin{array}{c@{\quad }c@{\quad }c} {\cos \theta }&{}\quad 0&{}\quad {\sin \theta } \\ 0&{}\quad 1&{}\quad 0 \\ {-\sin \theta }&{}\quad 0&{}\quad {\cos \theta } \\ \end{array} }} \right) \left( {{\begin{array}{c@{\quad }c@{\quad }c} 1&{}\quad 0&{}\quad 0 \\ 0&{}\quad {\cos \phi }&{}\quad {-\sin \phi } \\ 0&{}\quad {\sin \phi }&{}\quad {\cos \phi } \\ \end{array} }} \right) \nonumber \\= & {} \left( {{\begin{array}{c@{\quad }c@{\quad }c} {\hbox {c}_\varphi \hbox {c}_\theta }&{}\quad {\hbox {c}_\varphi \hbox {s}_\phi \hbox {s}_\theta -\hbox {c}_\phi \hbox {s}_\varphi }&{}\quad {\hbox {c}_\varphi \hbox {s}_\phi \hbox {s}_\theta -\hbox {c}_\phi \hbox {s}_\varphi } \\ {\hbox {s}_\varphi \hbox {c}_\theta }&{}\quad {\hbox {c}_\varphi \hbox {c}_\phi +\hbox {s}_\phi \hbox {s}_\varphi \hbox {s}_\theta }&{}\quad {\hbox {s}_\varphi \hbox {c}_\phi \hbox {s}_\theta -\hbox {s}_\phi \hbox {c}_\varphi } \\ {-\hbox {s}_\theta }&{}\quad {\hbox {s}_\phi \hbox {c}_\theta }&{}\quad {\hbox {c}_\phi \hbox {c}_\theta } \\ \end{array} }} \right) \end{aligned}$$

(1)

where c and s denote $\cos$ and $\sin$, respectively.

Fig. 2

Coordinate frame of the manipulator

The position of the MP with respect to the reference frame is denoted as ${{\varvec{P}}}_{m} =\left( {{x}~{y}~{z}} \right) ^{\mathrm{T}}$, (see Fig. 2), we can derive the closed loop motion equation as:

$$\begin{aligned}&{{\varvec{p}}}_{m} +{{\varvec{b}}}_{i} -{{\varvec{q}}}_{i} -{{\varvec{L}}}_{i} -{{\varvec{R}}}_{{S,i}} {{\varvec{r}}}_{{S,i,}1}\nonumber \\&\quad -{{\varvec{R}}}_{{S,i}} {{\varvec{r}}}_{{S},{i,}2} =\mathbf{0}_{3\times 1} ,\quad ({i}=1,2,3) \end{aligned}$$

(2)

where ${{\varvec{L}}}_{i}$ is the vector of the ith link, ${{\varvec{R}}}_{{S,i}} ={{\varvec{E}}}_3$, the 3 multiplied by 3 unit matrix, denotes the rotational transformation matrix from the body fixed frame of the ith slider to the base frame, ${{\varvec{r}}}_{{S},{i,}1}$ and ${{\varvec{r}}}_{{S},{i,}2}$ represents the position vector of ${A}_1$ and ${B}_1$ in the body fixed frame ${P}_{i} {-}{{\varvec{x}}}_{{S,i}} {{\varvec{y}}}_{{S,i}} {{\varvec{z}}}_{{S,i}}$, ${{\varvec{q}}}_{i}$ and ${{\varvec{b}}}_{i}$ are positions of the ith actuator and the revolute joint ${B}_{i}$ with respect to the base coordinate frame, with ${{\varvec{q}}}_{i} ={q}_{i} {{\varvec{e}}}_i ({i}=1,2,3)$, ${{\varvec{b}}}_{i} =\left( {-1} \right) ^{{i}+1}{l}_1 {{\varvec{R}}}_{p} {{\varvec{e}}}_{i} ({i}=1,2)$, and ${{\varvec{b}}}_3 ={l}_2 {{\varvec{R}}}_{p} {{\varvec{e}}}_3$, and ${{\varvec{e}}}_{i}$ can be given by:

$$\begin{aligned}&{{\varvec{e}}}_1 ={{\varvec{e}}}_2 =\left( {{\begin{array}{l@{\quad }l@{\quad }l} 0&{} 1&{} 0 \\ \end{array} }} \right) ^{\mathrm{T}},{{\varvec{e}}}_3 =\left( {{\begin{array}{l@{\quad }l@{\quad }l} 1&{} 0&{} 0 \\ \end{array} }} \right) ^{\mathrm{T}},\nonumber \\&{{\varvec{e}}}_4 =\left( {{\begin{array}{l@{\quad }l@{\quad }l} 0&{} 0&{} 1 \\ \end{array} }} \right) ^{\mathrm{T}} \end{aligned}$$

(3)

From the characteristics of the PM, the axis vector ${{\varvec{c}}}_i$ of the revolute joint in each limb is perpendicular to the plane with the normal vector ${{\varvec{q}}}_{i} -{{\varvec{P}}}_{m}$, so the following relationship can be obtained:

$$\begin{aligned} {{\varvec{c}}}_i ^{\mathrm{T}}\left( {{{\varvec{q}}}_i -{{\varvec{P}}}_{m} } \right) =0 \end{aligned}$$

(4)

where ${{\varvec{c}}}_{i} ={{\varvec{R}}}_{p} {{\varvec{c}}}_{{i}0}$, and ${{\varvec{c}}}_{{i}0}$ represents the axis vector of the revolute joint in limb i:

$$\begin{aligned} {{\varvec{c}}}_{1o} ={{\varvec{c}}}_{2o} ={{\varvec{e}}}_3 ,{{\varvec{c}}}_{3o} ={{\varvec{e}}}_1 \end{aligned}$$

(5)

From Eqs. (1)–(4), the constraint relationship can be derived as:

$$\begin{aligned}&x\hbox {c}_\theta \hbox {c}_\varphi -\left( {q_1 -y} \right) \hbox {c}_\theta \hbox {s}_\varphi -z\hbox {s}_\theta =0 \end{aligned}$$

(6)

$$\begin{aligned}&x\hbox {c}_\theta \hbox {c}_\varphi +\left( {q_2 +y} \right) \hbox {c}_\theta \hbox {s}_\varphi -z\hbox {s}_\theta =0 \end{aligned}$$

(7)

$$\begin{aligned}&y\left( {\hbox {c}_\phi \hbox {c}_\varphi +\hbox {s}_\phi \hbox {s}_\theta \hbox {s}_\varphi } \right) +\left( {q_3 -x} \right) \left( {\hbox {c}_\phi \hbox {s}_\varphi -\hbox {s}_\phi \hbox {s}_\theta \hbox {c}_\varphi } \right) \nonumber \\&\quad + z\hbox {s}_\phi \hbox {c}_\theta =0 \end{aligned}$$

(8)

Subtracting Eqs. (7) from (6), we obtain a further relationship:

$$\begin{aligned} \left( {q_1 +q_2 } \right) \hbox {c}_\theta \hbox {s}_\varphi =0 \end{aligned}$$

(9)

In the above equation, $q_1 +q_2$ cannot always be equal to zero; therefore, $\hbox {c}_\theta \hbox {s}_\varphi =0$ must hold. Substituting $\hbox {c}_\theta \hbox {s}_\varphi =0$ into Eq.  (6), if $\hbox {c}_\theta =0$, then $z=0$ would hold permanently, which obviously does not reflect the actual motion of the mechanism. Therefore, $\hbox {s}_\varphi$ must be identically zero, which means $\varphi$ must be 0 or $\pi$. Based on the characteristics of the PM, we assign $\varphi =0$. Hence, the constraint relationship can be expressed as:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\begin{array}{l} \varphi =0 \\ x=z\tan _\theta \\ \end{array}} \\ {y=\left( {q_3 -z\tan _\theta } \right) \hbox {tan}_\phi \hbox {s}_\theta -z\tan _\phi \hbox {c}_\theta } \\ \end{array} }} \right. \end{aligned}$$

(10)

From Eq. (10), the number of independent generalized coordinates is three, and there are two additional parasitic motions. PMs with two rotational DOFs and one rotational DOF have a wide range of applications, so ${\varvec{\eta }} =\left( {{\begin{array}{l@{\quad }l@{\quad }l} {z}&{} \phi &{} {\theta } \\ \end{array} }} \right) ^{\mathrm{T}}$ is chosen as the independent generalized coordinates.

From Eqs. (1) and (9), the positions of the sliders can be obtained as:

$$\begin{aligned} \left\{ {\begin{array}{l} {q}_1 =(-{z}\hbox {c}_\uptheta +\hbox {s}_\uptheta \sqrt{{l}_4^2 -{l}_2^2 \sec _\upphi ^2 \hbox {s}_\uptheta ^2 +{l}_4^2 \tan _\upphi ^2 \hbox {s}_\uptheta ^2 -{z}^{2}\sec _\upphi ^2 +2{l}_2 {z}\sec _\upphi ^2 \hbox {s}_\uptheta }\\ \qquad \quad +\,{l}_2 \hbox {c}_\uptheta \hbox {s}_\uptheta )\tan _\upphi /(\tan _\upphi ^2 \hbox {s}_\uptheta ^2 +1) \\ \qquad \quad +\,\sqrt{{l}_3^2 -{z}^{2}\sec _\uptheta ^2 -{l}_1^2 \hbox {s}_\upphi ^2 -2{l}_1 {z}\sec _\uptheta \hbox {s}_\upphi }+{l}_1 \hbox {c}_\upphi \\ {q}_2 =-({z}\hbox {c}_{\theta } -\hbox {s}_{\theta } \sqrt{{l}_4^2 -{l}_2^2 \sec _\upphi ^2 \hbox {s}_{\theta }^2 +{l}_4^2 \tan _\upphi ^2 \hbox {s}_{\theta }^2 -{z}^{2}\sec _\upphi ^2 +2{l}_2 {z}\sec _\upphi ^2 \hbox {s}_{\theta } }\\ \qquad \quad -{l}_2 \hbox {c}_{\theta } \hbox {s}_{\theta } )\tan _\upphi /(\tan _\upphi ^2 \hbox {s}_{\theta }^2 +1) \\ \qquad \quad -\sqrt{{l}_3^2 -{z}^{2}\sec _{\theta }^2 -{l}_1^2 \hbox {s}_\upphi ^2 -2{l}_1 {z}\sec _{\theta } \hbox {s}_\upphi }-{l}_1 \hbox {c}_\upphi \\ {q}_3 =({l}_2 \hbox {c}_\uptheta + {z}\sec _\upphi ^2 \tan _\uptheta +\sqrt{{l}_4^2 +{l}_4^2 \tan _\upphi ^2 \hbox {s}_\uptheta ^2 -{z}^{2}\sec _\upphi ^2 -{l}_2^2 \sec _\upphi ^2 \hbox {s}_\uptheta ^2 +2{l}_2 {z}\sec _\upphi ^2 \hbox {s}_\uptheta })/(\tan _\upphi ^2 \hbox {s}_\uptheta ^2 +1) \\ \end{array}} \right. \end{aligned}$$

(11)

To describe the inertial characteristics, the local coordinate frames of each limb are established as in Fig. 2, and the body fixed frames ${P}_{i}$ -${{\varvec{x}}}_{{S,i}} {{\varvec{y}}}_{{S,i}} {{\varvec{z}}}_{{S,i}}$ and ${C}_{i}$ -${{\varvec{x}}}_{{C,i}} {{\varvec{y}}}_{{C,i}} {{\varvec{z}}}_{{C,i}}$ are attached to the mass center of the ith slider and link, respectively, while the coordinate axis of ${P}_{i}$ -${{\varvec{x}}}_{{S,i}} {{\varvec{y}}}_{{S,i}} {{\varvec{z}}}_{{S,i}}$ is parallel to the corresponding ones of the base frame. Further, the ${{\varvec{z}}}_{{C,i}}$ axis is parallel to line ${A}_{i} {B}_{i}$, and the ${{\varvec{x}}}_{{C,i}} ({i}=1,2)$ and ${{\varvec{y}}}_{{C,}3}$ are parallel to corresponding revolute axis. In addition, $B_{i} {-}{{\varvec{x}}}_{{B,i}} {{\varvec{y}}}_{{B,i}} {{\varvec{z}}}_{{B,i}}$ is attached to the MP with the ${{\varvec{z}}}_{{B,i}}$ axis normal to the MP, and the ${{\varvec{x}}}_{{B,i}} ({i}=1,2)$ and ${{\varvec{y}}}_{{B,}3}$ axis are parallel with the corresponding axis of $B_{i}$ -${{\varvec{x}}}_{{B,i}} {{\varvec{y}}}_{{B,i}} {{\varvec{z}}}_{{B,i}}$. Hence, the transformation matrix ${{\varvec{R}}}_{i}$ from P-${{\varvec{uvw}}}$ to O-${{\varvec{XYZ}}}$ for the ith limb can be expressed as:

$$\begin{aligned}&{{\varvec{R}}}_{i} ={{\varvec{R}}}_{y_{{C,i}} {,\theta }_{i} } {{\varvec{R}}}_{x_{{C,i}} {,}\upphi _{i} } {{\varvec{R}}}_{x_{{B,i}} {,}\uppsi _{\mathrm{i}} } {{\varvec{R}}}_{{i,p}} ={{\varvec{R}}}_{{L,i}} {{\varvec{R}}}_{x_{{B,i}} {,}\uppsi _{\mathrm{i}} } {{\varvec{R}}}_{{ip}} \nonumber \\&\quad =\left( {{\begin{array}{c@{\quad }c@{\quad }c} {\hbox {c}_{{\theta }_\mathrm{i} } }&{} 0&{} {\hbox {s}_{{\theta }_\mathrm{i} } } \\ 0&{} 1&{} 0 \\ {-\hbox {s}_{{\theta }_\mathrm{i} } }&{} 0&{} {\hbox {c}_{{\theta }_\mathrm{i} } } \\ \end{array} }} \right) \left( {{\begin{array}{c@{\quad }c@{\quad }c} 1&{} 0&{} 0 \\ 0&{} {\hbox {c}_{\upphi _\mathrm{i} } }&{} {-\hbox {s}_{\upphi _\mathrm{i} } } \\ 0&{} {\hbox {s}_{\upphi _\mathrm{i} } }&{} {\hbox {c}_{\upphi _\mathrm{i} } } \\ \end{array} }} \right) \left( {{\begin{array}{c@{\quad }c@{\quad }c} 1&{} 0&{} 0 \\ 0&{} {\hbox {c}_{\uppsi _\mathrm{i} } }&{} {-\hbox {s}_{\uppsi _\mathrm{i} } } \\ 0&{} {\hbox {s}_{\uppsi _\mathrm{i} } }&{} {\hbox {c}_{\uppsi _\mathrm{i} } } \\ \end{array} }} \right) \nonumber \\&\qquad \times \left( {{\begin{array}{c@{\quad }c@{\quad }c} 1&{} 0&{} 0 \\ 0&{} 0&{} {(-1)^{{i}+1}} \\ 0&{} {(-1)^{{i}}}&{} 0 \\ \end{array} }} \right) \nonumber \\&\quad =\left( {{\begin{array}{c@{\quad }c@{\quad }c} {\hbox {c}_{{\theta }_{{\varvec{i}}} } }&{} {(-1)^{{i}}\hbox {s}_{\upphi _\mathrm{i} +\uppsi _\mathrm{i} } \hbox {s}_{{\theta }_{{\varvec{i}}} } }&{} {(-1)^{{i}+1}\hbox {s}_{\upphi _\mathrm{i} +\uppsi _\mathrm{i} } \hbox {s}_{{\theta }_{{\varvec{i}}} } } \\ 0&{} {(-1)^{{i}+1}\hbox {s}_{\upphi _\mathrm{i} +\uppsi _\mathrm{i} } }&{} {(-1)^{{i}+1}\hbox {c}_{\upphi _\mathrm{i} +\uppsi _\mathrm{i} } } \\ {-\hbox {s}_{{\theta }_i } }&{} {(-1)^{{i}}\hbox {c}_{\upphi _\mathrm{i} +\uppsi _\mathrm{i} } \hbox {c}_{{\theta }_{{\varvec{i}}} } }&{} {(-1)^{{i}+1}\hbox {s}_{{\theta }_{i} } \hbox {c}_{\upphi _\mathrm{i} +\uppsi _\mathrm{i} } } \\ \end{array} }} \right) \nonumber \\&\qquad \quad ({i}=1,2) \end{aligned}$$

(12)

$$\begin{aligned} {{\varvec{R}}}_3= & {} {{\varvec{R}}}_{z_{{C,}3} {,\varphi }_3 } {{\varvec{R}}}_{y_{{C,}3} {,\theta }_3 } {{\varvec{R}}}_{x_{{C,}3} {,}\upphi _3 } {{\varvec{R}}}_{y_{{B}3} {,}\uppsi _3 } {{\varvec{R}}}_{3,{p}} ={{\varvec{R}}}_{{L},3} {{\varvec{R}}}_{y_{{B}3} {,}\uppsi _3 } {{\varvec{R}}}_{3,{p}} \nonumber \\= & {} \left( {{\begin{array}{c@{\quad }c@{\quad }c} {\hbox {c}_{{\varphi }_3 } }&{} {-\hbox {s}_{{\varphi }_3 } }&{} 0 \\ {\hbox {s}_{{\varphi }_3 } }&{} {\hbox {c}_{{\varphi }_3 } }&{} 0 \\ 0&{} 0&{} 1 \\ \end{array} }} \right) \left( {{\begin{array}{c@{\quad }c@{\quad }c} {\hbox {c}_{{\theta }_3 } }&{} 0&{} {\hbox {s}_{{\theta }_3 } } \\ 0&{} 1&{} 0 \\ {-\hbox {s}_{{\theta }_3 } }&{} 0&{} {\hbox {c}_{{\theta }_3 } } \\ \end{array} }} \right) \left( {{\begin{array}{c@{\quad }c@{\quad }c} 1&{} 0&{} 0 \\ 0&{} {\hbox {c}_{\upphi _3 } }&{} {-\hbox {s}_{\upphi _3 } } \\ 0&{} {\hbox {s}_{\upphi _3 } }&{} {\hbox {c}_{\upphi _3 } } \\ \end{array} }} \right) \quad \left( {{\begin{array}{c@{\quad }c@{\quad }c} {\hbox {c}_{\uppsi _3 } }&{} 0&{} {\hbox {s}_{\uppsi _3 } } \\ 0&{} 1&{} 0 \\ {-\hbox {s}_{\uppsi _3 } }&{} 0&{} {\hbox {c}_{\uppsi _3 } } \\ \end{array} }} \right) \left( {{\begin{array}{l@{\quad }l@{\quad }l} 0&{} 0&{} 1 \\ 0&{} 1&{} 0 \\ {-1}&{} 0&{} 0 \\ \end{array} }} \right) \nonumber \\= & {} \left( {{\begin{array}{c@{\quad }c@{\quad }c} {-\hbox {c}_{{\varphi }_3 } (\hbox {s}_{\uppsi _3 } \hbox {c}_{{\theta }_3 } +\hbox {c}_{\upphi _3 } \hbox {c}_{\uppsi _3 } \hbox {s}_{{\theta }_3 } )-\hbox {c}_{\uppsi _3 } \hbox {s}_{\upphi _3 } \hbox {s}_{{\varphi }_3 } }&{} {\hbox {c}_{{\varphi }_3 } \hbox {s}_{\upphi _3 } \hbox {s}_{\uppsi _3 } -\hbox {s}_{{\varphi }_3 } \hbox {c}_{\upphi _3 } }&{} {\hbox {c}_{{\varphi }_3 } (\hbox {c}_{\uppsi _3 } \hbox {c}_{{\theta }_3 } -\hbox {c}_{\upphi _3 } \hbox {s}_{\uppsi _3 } \hbox {s}_{{\theta }_3 } )-\hbox {s}_{\uppsi _3 } \hbox {s}_{\upphi _3 } \hbox {s}_{{\varphi }_3 } } \\ {-\hbox {s}_{{\varphi }_3 } (\hbox {s}_{\uppsi _3 } \hbox {c}_{{\theta }_3 } +\hbox {c}_{\upphi _3 } \hbox {c}_{\uppsi _3 } \hbox {s}_{{\theta }_3 } )+\hbox {c}_{\uppsi _3 } \hbox {s}_{\upphi _3 } \hbox {c}_{{\varphi }_3 } }&{} {\hbox {s}_{{\varphi }_3 } \hbox {s}_{\upphi _3 } \hbox {s}_{\uppsi _3 } +\hbox {c}_{{\varphi }_3 } \hbox {c}_{\upphi _3 } }&{} {\hbox {s}_{{\varphi }_3 } (\hbox {c}_{\uppsi _3 } \hbox {c}_{{\theta }_3 } -\hbox {c}_{\upphi _3 } \hbox {s}_{\uppsi _3 } \hbox {s}_{{\theta }_3 } )+\hbox {c}_{\uppsi _3 } \hbox {s}_{\upphi _3 } \hbox {s}_{{\varphi }_3 } } \\ {-\hbox {c}_{\upvarphi _3 } \hbox {s}_{{\theta }_3 } }&{} {\hbox {c}_{{\theta }_3 } \hbox {s}_{\upphi _3 } }&{} {-\hbox {s}_{{\theta }_3 } \hbox {c}_{\uppsi _3 } -\hbox {c}_{{\theta }_3 } \hbox {c}_{\upphi _3 } \hbox {s}_{\uppsi _3 } } \\ \end{array} }} \right) \end{aligned}$$

(13)

where ${{\varvec{R}}}_{{L,i}} ={{\varvec{R}}}_{y_{{C,i}} {,\theta }_{i} } {{\varvec{R}}}_{x_{{C,i}} {,}\upphi _{i} } ({i}=1,2)$ and $\mathbf{R}_{{L},3} =\mathbf{R}_{{z}_{{A3}} {,\varphi }_3 } \mathbf{R}_{{y}_{{A3}} {,\theta }_{3} } \mathbf{R}_{{x}_{{A3}} {,}\upphi _{3} }$ represent the transformation matrix from local coordinate frame of each link to the base frame. $\mathbf{R}_{{i,p}}~({i}=1,2,3)$ represents the transformation matrix from P-${{\varvec{uvw}}}$ to ${{{\varvec{B}}}}_{i} {-}{{\varvec{x}}}_{{{\varvec{B}}},{i}} {{\varvec{y}}}_{{{\varvec{B}}},{i}} {{\varvec{z}}}_{{{\varvec{B}}},{i}}$.

From Eqs. (1), (2), (12) and (13), the relevant trigonometric functions of each limb can be obtained as:

$$\begin{aligned}&{\hbox {c}}_{{\theta }_1 } =\hbox {c}_{\theta } ,\hbox {s}_{{\theta }_1 } =\hbox {s}_{\theta } ,\hbox {c}_{\upphi _1 } =({z}/{\hbox {c}}_{\theta } +{l}_1 \hbox {s}_{\upphi _1 } )/{l}_3 ,\hbox {s}_{\upphi _1 } =\sqrt{1-\hbox {c}_{\upphi _1 }^2 } \end{aligned}$$

(14)

$$\begin{aligned}&\hbox {c}_{{\theta }_2 } =\hbox {c}_{\theta } ,\hbox {s}_{{\theta }_2 } =\hbox {s}_{\theta } ,\hbox {c}_{\upphi _2 } ={\left( {{z}/{\hbox {c}_{\theta } }+{l}_1 \hbox {s}_{\upphi _1 } } \right) }/{{l}_3 },\hbox {s}_{\upphi _2 } =\sqrt{1-\hbox {c}_{\upphi _2 }^2 } \end{aligned}$$

(15)

$$\begin{aligned}&\left\{ {\begin{array}{l} \hbox {c}_{{\varphi }_3 } ={-\left( {{z}\hbox {c}_\upphi -{l}_2 \hbox {c}_\upphi \hbox {s}_{\theta } -\hbox {s}_\upphi ^2 \hbox {c}_{\theta } \hbox {s}_{\theta } \sqrt{{l}_4^2 \hbox {c}_\upphi ^2 -{l}_2^2 \hbox {s}_{\theta }^2 -{z}^{2}+2{l}_2 {z}\hbox {s}_{\theta } +{l}_4^2 \hbox {s}_\upphi ^2 \hbox {s}_{\theta }^2 }} \right) }/\; \\ \qquad \quad \left( {\left( {\hbox {s}_\upphi ^2 \hbox {s}_{\theta }^2 -\hbox {c}_\upphi ^2 } \right) \sqrt{{l}_4^2 \hbox {s}_\upphi ^2 \hbox {c}_{\theta }^2 +{l}_2^2 \hbox {s}_{\theta }^2 -2{l}_2 {z}\hbox {s}_{\theta } +{z}^{2}}} \right) \\ \hbox {s}_{{\varphi }_3 } ={\hbox {s}_\upphi \left( {{l}_2 \hbox {c}_\uptheta ^3 + {z}\hbox {s}_{2{\theta }} /2-{l}_2 \hbox {c}_{\theta } +\hbox {c}_\upphi \hbox {c}_\uptheta ^2 \sqrt{{l}_4^2 \hbox {c}_\upphi ^2 -{l}_2^2 \hbox {s}_\uptheta ^2 - {z}^{2}+2{l}_2 {z}\hbox {s}{\theta }+{l}_4^2 \hbox {s}_\upphi ^2 \hbox {s}_\uptheta ^2 }} \right) }/\; \\ \quad \left( {\hbox {c}_{\theta } \left( {\hbox {c}_\upphi ^2 \hbox {c}_\uptheta ^2 +\hbox {s}_\uptheta ^2 } \right) \sqrt{{l}_4^2 \hbox {s}_\upphi ^2 \hbox {c}_\uptheta ^2 +{l}_2^2 \hbox {s}_\uptheta ^2 -2{l}_2 {z}\hbox {s}_{\theta } + {z}^{2}}} \right) \\ \hbox {c}_{{\theta }_3 } ={-\sqrt{{l}_4^2 \hbox {s}_\upphi ^2 +{l}_2^2 \hbox {s}_\uptheta ^2 + {z}^{2}-2{l}_2 {z}\hbox {s}_{\theta } -{l}_4^2 \hbox {s}_\upphi ^2 \hbox {s}_\uptheta ^2 }}/{{l}_4 },\hbox {s}_{{\theta }_3 } ={-\sqrt{{l}_2^2 \hbox {s}_\uptheta ^2 {-l}_4^2 \hbox {c}_\upphi ^2 +{z}^{2}-2{l}_2 {z}\hbox {s}_{\theta } -{l}_4^2 \hbox {s}_{\psi }^2 \hbox {s}_\uptheta ^2 }}/{{l}_4 } \\ \qquad \hbox {c}_{\upphi _3 } ={-\left( {{z}-{l}_2 \hbox {s}_{\theta } } \right) }/{\sqrt{{l}_4^2 \hbox {s}_\upphi ^2 \hbox {c}_{\theta }^2 +{l}_2^2 \hbox {s}_{\theta }^2 -2{l}_2 {z}\hbox {s}_{\theta } +{z}^{2}}},\hbox {s}_{\upphi _3 } ={-{l}_4 \hbox {c}_{\theta } \hbox {s}_\upphi }/{\sqrt{{l}_4^2 \hbox {s}_\upphi ^2 \hbox {c}_{\theta }^2 +{l}_2^2 \hbox {s}_{\theta }^2 -2{l}_2 {z}\hbox {s}_{\theta } +{z}^{2}}} \\ \end{array}} \right. \end{aligned}$$

(16)

2.2 Velocity and acceleration analysis

The inverse kinematics of the PM is given by Eqs. (11), (14), (15) and (16); the velocities and accelerations can be derived by differentiating with respect to time and represented by the generalized coordinates. Differentiating Eq. (10) with respect to time, the parasitic linear and angular velocity of the MP can be derived as:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\begin{array}{l} {\dot{\varphi }}=0 \\ {\dot{x}}=\tan _\theta {{\dot{z}}}+z\sec _\theta ^2 {{\dot{\theta }}} \\ \end{array}} \\ {\begin{array}{l} {{\dot{y}}}={{\dot{q}}}_3 \hbox {tan}_\phi \hbox {s}_\theta -\hbox {tan}_\phi \hbox {sec}_\theta {{\dot{z}}}\\ \qquad +\,(q_3 \hbox {tan}_\phi \hbox {c}_\theta -z\hbox {tan}_\phi \hbox {s}_\theta \sec _\theta ^2 ){{\dot{\theta }}}\\ \qquad +\,(q_3 \hbox {s}_\theta \sec _\phi ^2 -z\hbox {sec}_\theta \sec _\phi ^2 ){{\dot{\phi }}} \\ =y_z {{\dot{z}}}+y_\theta {{\dot{\theta }}}+y_\phi {{\dot{\phi }}} \\ \end{array}} \end{array} }} \right. \end{aligned}$$

(17)

where the upper dot on a parameter means differentiation with respect to time, and

$$\begin{aligned} y_z= & {} {\left( {\tan _\theta +\frac{-\left( {z-l_2 \hbox {s}_\theta } \right) }{\sqrt{{l}_4^2 +{l}_4^2 \tan _\phi ^2 \hbox {s}_\theta ^2 -\sec _\phi ^2 \left( {z-l_2 {s}_\theta } \right) ^{2}}}} \right) \sec _\phi ^2 \tan _\phi \hbox {s}_\theta }\big /\\&\qquad {\left( {\tan _\phi ^2 \hbox {s}_\theta ^2 +1} \right) -\tan _\varphi \sec _\theta } \\ y_\theta= & {} \left( -\,{l}_2 s_\theta +z\sec _\phi ^2 \sec _\theta ^2 +\frac{{l}_4^2 \tan _\phi ^2 \hbox {s}_\theta {c}_\theta +\sec _\phi ^2 \left( {z-l_2 s_\theta } \right) l_2 {c}_\theta }{\sqrt{{l}_4^2 +{l}_4^2 \tan _\phi ^2 \hbox {s}_\theta ^2 -\sec _\phi ^2 \left( {z-l_2 {s}_\theta }\right) ^{2}}}\right. \\&\qquad \left. -\,2{q}_3 \tan _\phi ^2 {{s}}_\theta {c}_\theta \right) \tan _\phi {{s}}_\theta \big / \\&(\tan _\phi ^2 \hbox {s}_\theta ^2 +1)+\tan _\phi (q_3 {c}_\theta -z \hbox {s}_\theta \sec _\theta ^2 ) \\ y_\phi= & {} \left( 2z\tan _\theta +\frac{{l}_4^2 \hbox {s}_\theta ^2 -\left( {z-l_2 {s}_\theta } \right) ^{2}}{\sqrt{{l}_4^2 +{l}_4^2 \tan _\phi ^2 \hbox {s}_\theta ^2 -\sec _\phi ^2 \left( {z-l_2 {s}_\theta } \right) ^{2}}}\right. \\&\qquad \left. -\,2{q}_3 \hbox {s}_\theta ^2 \right) \tan _\phi ^2 \sec _\phi ^2 {{s}}_\theta \big / \\&\left( {\tan _\phi ^2 \hbox {s}_\theta ^2 +1} \right) +\sec _\phi ^2 \left( {q_3 \hbox {s}_\theta -z\sec _\theta } \right) \end{aligned}$$

From Eqs. (1) and (17), the matrix form of the linear and angular velocities of the MP can be formulated as:

$$\begin{aligned} {{\varvec{t}}}_{p} ={{\varvec{K}}}_{p} \dot{{\varvec{\eta }}} \end{aligned}$$

(18)

where ${{\varvec{t}}}_{p}$ represents the twist of the MP, and

$$\begin{aligned} {{\varvec{t}}}_{p}= & {} \left( {{\begin{array}{l@{\quad }l} {\dot{{{\varvec{P}}}}_{{\varvec{m}}}^{\mathrm{T}} }&{} {{\varvec{\omega }} ^{\mathrm{T}}} \\ \end{array} }} \right) ^{\mathrm{T}}, {{\varvec{K}}}_{p} \\= & {} \left( {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\tan _\theta }&{} {{y}_{z} }&{} 1&{} 0&{} 0&{} 0 \\ 0&{} {{y}_\phi }&{} 0&{} {\cos _\theta }&{} 0&{} {-\sin _\theta } \\ {{z}\sec _\theta ^2 }&{} {\hbox {y}_\theta }&{} 0&{} 0&{} 1&{} 0 \\ \end{array} }} \right) ^{\mathrm{T}} \end{aligned}$$

Differentiating Eq. (2) with respect to time yields:

$$\begin{aligned} {\dot{{{\varvec{P}}}}}_{{{m}}} +{\varvec{\omega }} \times {{\varvec{b}}}_{i} ={\dot{{{\varvec{q}}}}}_{i} +{\varvec{\omega }}_{{L,i}} \times {{\varvec{L}}}_{i} ={{{\dot{q}}}}_{i} {{\varvec{e}}}_{i} +{\varvec{{\omega }}} _{{L,i}} \times {{\varvec{L}}}_{i} \end{aligned}$$

(19)

where ${\varvec{\omega }}$ and ${\varvec{\omega }}_{i}$ represent the angular velocity of the MP and the link in limb i. Taking the dot product with ${{\varvec{L}}}_{i}$ on both sides of Eq. (19) leads to:

$$\begin{aligned} {{\varvec{L}}}_{i}^{\mathrm{T}} \dot{{{\varvec{P}}}}_{m} -{{\varvec{L}}}_{i}^{\mathrm{T}} {\tilde{{{\varvec{b}}}}}_{i} {\varvec{\omega }} ={{\dot{q}}}_{i} {{\varvec{L}}}_{i}^{\mathrm{T}} {{\varvec{e}}}_{i} \end{aligned}$$

(20)

where the upper slash on a vector denotes its skew matrix. Hence, the velocity of the ith actuator can be expressed as:

$$\begin{aligned} {{{\dot{q}}}}_{i} =\left( {{{\varvec{L}}}_{i}^{\mathrm{T}} {{\varvec{e}}}_{{\varvec{i}}} } \right) ^{-1}\left( {{\begin{array}{l@{\quad }l} {{{\varvec{L}}}_{i}^{\mathrm{T}} }&{-{{\varvec{L}}}_{i}^{\mathrm{T}} {\tilde{{{\varvec{b}}}}}_{i} } \end{array} }} \right) {{\varvec{t}}}_{p} \end{aligned}$$

(21)

Rewriting Eq. (21) in matrix form results in the velocity mapping between the linear actuators and the MP:

$$\begin{aligned} {\dot{{{\varvec{q}}}}}={{\varvec{K}}}_{{\varvec{q}}}^{-1} {{\varvec{K}}}_{{\varvec{t}}} {{\varvec{t}}}_{{\varvec{p}}} ={{\varvec{J}}}_{q} {{\varvec{t}}}_{{\varvec{p}}} \end{aligned}$$

(22)

where

$$\begin{aligned}&{{\varvec{q}}}=\left( {{\begin{array}{l@{\quad }l@{\quad }l} {{{{\dot{q}}}}_1 }&{} {{{{\dot{q}}}}_2 }&{} {{{{\dot{q}}}}_3 } \\ \end{array} }} \right) ^{\mathrm{T}}, \quad {{\varvec{K}}}_{{\varvec{q}}} =\left( {{\begin{array}{l@{\quad }l@{\quad }l} {{{\varvec{L}}}_1^{{\varvec{T}}} {{\varvec{e}}}_1 }&{} &{} \\ &{} {{{\varvec{L}}}_2^{{\varvec{T}}} {{\varvec{e}}}_2 }&{} \\ &{} &{} {{{\varvec{L}}}_3^{{\varvec{T}}} {{\varvec{e}}}_3 } \\ \end{array} }} \right) ,\\&{{\varvec{K}}}_{{\varvec{t}}} =\left( {{\begin{array}{l@{\quad }l} {{{\varvec{L}}}_1^{{\varvec{T}}} }&{} {-{{\varvec{L}}}_1^{{\varvec{T}}} {\tilde{{{\varvec{b}}}}}_1 } \\ {{{\varvec{L}}}_2^{{\varvec{T}}} }&{} {-{{\varvec{L}}}_2^{{\varvec{T}}} {\tilde{{{\varvec{b}}}}}_2 } \\ {{{\varvec{L}}}_3^{{\varvec{T}}} }&{} {-{{\varvec{L}}}_3^{{\varvec{T}}} {\tilde{{{\varvec{b}}}}}_3 } \\ \end{array} }} \right) \end{aligned}$$

Taking the cross product with ${{\varvec{L}}}_{i}$ on both sides of Eq. (19) yields the angular velocity of the link in limb i:

$$\begin{aligned} {\varvec{\omega }}_{{L,i}} ={{\varvec{J}}}_{{wi}} {{\varvec{t}}}_{p} \end{aligned}$$

(23)

where

$$\begin{aligned} \left\{ {\begin{array}{l} {{\varvec{J}}}_{{wi}} {=}\frac{\left( {{\begin{array}{l@{\quad }l} {{\tilde{{{\varvec{L}}}}}_{i} -{{\varvec{e}}}_{{\varvec{i}}} \left( {{{\varvec{L}}}_{i}^{\mathrm{T}} {{\varvec{e}}}_{{\varvec{i}}} } \right) ^{-1}{{\varvec{L}}}_{i}^{\mathrm{T}} }&{} {{{\varvec{L}}}_{i}^{\mathrm{T}} {{\varvec{b}}}_{i} {{\varvec{E}}}_3 -{{\varvec{b}}}_{i} {{\varvec{L}}}_{i}^{\mathrm{T}} {+}{{\varvec{e}}}_{{\varvec{i}}} \left( {{{\varvec{L}}}_{i}^{\mathrm{T}} {{\varvec{e}}}_{{\varvec{i}}} } \right) ^{-1}{{\varvec{L}}}_{i}^{\mathrm{T}} {\tilde{{{\varvec{b}}}}}_{i} } \\ \end{array} }}\right) }{{{\varvec{L}}}_{i}^{\mathrm{T}} {{\varvec{L}}}_{i} },\\ \qquad ({i}=1,2) \\ {{\varvec{J}}}_{{w3}} {=}\frac{\left( {{\begin{array}{l@{\quad }l} {{\tilde{{{\varvec{L}}}}}_3 {-}{{\varvec{e}}}_3 \left( {{{\varvec{L}}}_{3}^{\mathrm{T}} {{\varvec{e}}}_3 } \right) ^{-1}{{\varvec{L}}}_3^{\mathrm{T}} }&{} {{{\varvec{L}}}_3^{\mathrm{T}} {{\varvec{b}}}_3 {{\varvec{E}}}_3 -{{\varvec{b}}}_3 {{\varvec{L}}}_3^{\mathrm{T}} {+}{{\varvec{e}}}_3 \left( {{{\varvec{L}}}_3^{\mathrm{T}} {{\varvec{e}}}_3 } \right) ^{-1}{{\varvec{L}}}_3^{\mathrm{T}} {\tilde{{{\varvec{b}}}}}_3 {+}{{\varvec{L}}}_3 {{\varvec{L}}}_3^{\mathrm{T}} } \\ \end{array} }} \right) }{{{\varvec{L}}}_3^{\mathrm{T}} {{\varvec{L}}}_3 } \\ \end{array}} \right. \end{aligned}$$

The linear and angular acceleration of the MP can be obtained by differentiating Eq. (18) with respect to time:

$$\begin{aligned} {\dot{{{\varvec{t}}}}}_{p} ={{\varvec{K}}}_{p} {\ddot{\varvec{\eta }}}+{\dot{{{\varvec{K}}}}}_{p} \dot{{\varvec{\eta }}} \end{aligned}$$

(24)

where ${\ddot{\varvec{\eta }}}$ is the acceleration of the independent generalized coordinates, and

$$\begin{aligned} {\dot{{{\varvec{K}}}}}_{p} =\left( {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\sec _\theta ^2 {{\dot{\theta }}}}&{} {{{{\dot{y}}}}_{z} }&{} 0&{} 0&{} 0&{} 0 \\ {{{{\dot{z}}}}\sec _\theta ^2 +2{z}\tan _\theta \sec _\theta ^2 {{\dot{\theta }}}}&{} {{{{\dot{y}}}}_\theta }&{} 0&{} {-\sin _\theta {{\dot{\theta }}}}&{} 0&{} {-\cos _\theta {{\dot{\theta }}}} \\ 0&{} {{{{\dot{y}}}}_\phi }&{} 0&{} 0&{} 0&{} 0 \\ \end{array} }} \right) ^{\mathrm{T}} \end{aligned}$$

Taking the cross product with ${{\varvec{L}}}_{i}$ on both sides of Eq. (19) and differentiating with respect to time, the angular acceleration of the link in limb i can be obtained as:

$$\begin{aligned} \dot{{\varvec{\omega }}}_{{L,i}} ={{\varvec{J}}}_{{wi}} {{\dot{{{\varvec{t}}}}}}_{p} +{\dot{{\varvec{J}}}}_{{wi}} {{\varvec{t}}}_{p} \end{aligned}$$

(25)

where

$$\begin{aligned} {\dot{{\varvec{J}}}}_{{wi}}= & {} \left( {{\varvec{L}}}_{{{i}}} {\varvec{\omega }} _{{{{{\varvec{L}}}}}_{{\varvec{i}}} }^{\mathrm{T}} -{\varvec{\omega }} _{{{\varvec{L}}}_{{\varvec{i}}} } {{\varvec{L}}}_{{\varvec{i}}}^{\mathrm{T}} +{{\varvec{e}}}_{{\varvec{i}}} \left( \left( {{{\varvec{L}}}_{{{i}}}^{\mathrm{T}} {{\varvec{e}}}_{{\varvec{i}}} } \right) ^{-1}{{\varvec{L}}}_{{{i}}}^{\mathrm{T}} {\tilde{{\varvec{\omega }}}}_{i} \right. \right. \\&\left. +\left( {{{\varvec{L}}}_{{\varvec{i}}}^{\mathrm{T}} {\tilde{{\varvec{\omega }}}}_{{L}_{i} } {{\varvec{e}}}_{{\varvec{i}}} } \right) ^{-1}{{\varvec{L}}}_{i}^{\mathrm{T}} \right) \\&{{\varvec{L}}}_{i}^{\mathrm{T}} \left( {{\tilde{{\varvec{\omega }}}}-{\tilde{{\varvec{\omega }}} }_{i} } \right) {{\varvec{b}}}_{i} {{\varvec{E}}}_3 -{\tilde{{\varvec{\omega }}} }{{\varvec{b}}}_{i} {{\varvec{L}}}_{i}^{\mathrm{T}} +{{\varvec{b}}}_{i} {{\varvec{L}}}_{i}^{\mathrm{T}} {\tilde{{\varvec{\omega }}}}_{i} \\&+\, {{\varvec{e}}}_{{\varvec{i}}} \left( \left( {-\left( {{{\varvec{L}}}_{{\varvec{i}}}^{{\varvec{T}}} {\tilde{{\varvec{\omega }}} }_{{L}_{i} } {{\varvec{e}}}_{{\varvec{i}}} } \right) ^{-1}{{\varvec{L}}}_{i}^{\mathrm{T}} -\left( {{{\varvec{L}}}_{i}^{\mathrm{T}} {{\varvec{e}}}_{{\varvec{i}}} } \right) ^{-1}{{\varvec{L}}}_{{\varvec{i}}}^{{{\varvec{T}}}} {\tilde{{\varvec{\omega }}} }_{{L}_{i} } } \right) {\tilde{{{\varvec{b}}}}}_{i} \right. \\&\left. \left. +\left( {{{\varvec{L}}}_{i}^{\mathrm{T}} {{\varvec{e}}}_{{\varvec{i}}} } \right) ^{-1}{{\varvec{L}}}_{i}^{\mathrm{T}} \left( {{{\varvec{b}}}_{i} {\varvec{\omega }}^{\mathrm{T}}-{\varvec{\omega }} {{\varvec{b}}}_{{\varvec{i}}}^{\mathrm{T}} } \right) \right) \right) \big /{{{\varvec{L}}}_{i}^{\mathrm{T}} {{\varvec{L}}}_{i}}, \left( {{i}=1,2} \right) ,\\ {\dot{{{\varvec{J}}}}}_{{w}3}= & {} \left( {{\varvec{L}}}_3 {\varvec{\omega }} _{{{\varvec{L}}}_3 }^{{\mathrm{T}}} -{\varvec{\omega }} _{{{\varvec{L}}}_3 } {{\varvec{L}}}_{{\varvec{i}}}^{\mathrm{T}} +{{\varvec{e}}}_3 \left( \left( {{{\varvec{L}}}_{3}^{{{\mathrm{T}}}} {{\varvec{e}}}_3 } \right) ^{-1}{{\varvec{L}}}_{3}^{\mathrm{T}} {\tilde{\varvec{\omega }}}_{3} \right. \right. \\&\left. +\left( {{{\varvec{L}}}_3^{{{{\varvec{T}}}}} {\tilde{\varvec{\omega }}} _{{{{L}}}_{3} } {{\varvec{e}}}_3 } \right) ^{-1}{{\varvec{L}}}_{3}^{\mathrm{T}} \right) \\&\quad {{\varvec{L}}}_{3}^{\mathrm{T}} \left( {{\tilde{\varvec{\omega }}}-{\tilde{\varvec{\omega }}}_{3} } \right) {{\varvec{b}}}_{3} {{\varvec{E}}}_3 -{\tilde{\varvec{\omega }}}{{\varvec{b}}}_3 {{\varvec{L}}}_3^{\mathrm{T}} +{{\varvec{b}}}_3 {{\varvec{L}}}_3^{\mathrm{T}} {\tilde{\varvec{\omega }}}_3 \\&+ \left. {{\varvec{e}}}_3 \left( \left( {-\left( {{{\varvec{L}}}_3^{{{{\varvec{T}}}}} {\tilde{\varvec{\omega }}}_{{{{L}}}_{3} } {{\varvec{e}}}_3 } \right) ^{-1}{{\varvec{L}}}_{3}^{\mathrm{T}} -\left( {{{\varvec{L}}}_{3}^{\mathrm{T}} {{\varvec{e}}}_3 } \right) ^{-1}{{\varvec{L}}}_3^{{{{\varvec{T}}}}} {\tilde{\varvec{\omega }}}_{{{{L}}}_{3} } } \right) {{\tilde{{{\varvec{b}}}}}}_{3}\right. \right. \\&\left. +\left( {{{\varvec{L}}}_{3}^{\mathrm{T}} {{\varvec{e}}}_3 } \right) ^{-1}{{\varvec{L}}}_3^{\mathrm{T}} \left( {{{\varvec{b}}}_3 {\varvec{\omega }} ^{\mathrm{T}}-{\varvec{\omega }} {{\varvec{b}}}_3^{\mathrm{T}} } \right) \right) \\&\left. +\,{\tilde{\varvec{\omega }}}_3 {{\varvec{L}}}_3 {{\varvec{L}}}_3^{\mathrm{T}} -{{\varvec{L}}}_3 {\tilde{\varvec{\omega }}}_3 {{\varvec{L}}}_3^{\mathrm{T}} \right) /{{{\varvec{L}}}_3^{\mathrm{T}} {{\varvec{L}}}_3 } \end{aligned}$$

Similarly, the acceleration of the actuators can be obtained as time derivative of Eq. (22):

$$\begin{aligned} {\ddot{{{\varvec{q}}}}}={{\varvec{J}}}_{q} {\dot{{{\varvec{t}}}}}_{p} +{\dot{{\varvec{J}}}}_{q} {{\varvec{t}}}_{p} \end{aligned}$$

(26)

where ${\dot{{\varvec{J}}}}_{q}$ is the time derivative of ${{\varvec{J}}}_{q}$ and can be expressed as:

$$\begin{aligned} {\dot{{\varvec{J}}}}_{q}= & {} -\,{{\varvec{K}}}_{q}^{-1} {\dot{{{\varvec{K}}}}}_{q} {{\varvec{K}}}_{q}^{-1} {{\varvec{K}}}_{t} +{{\varvec{K}}}_{q}^{-1} {\dot{{{\varvec{K}}}}}_{t}\nonumber \\= & {} {{\varvec{K}}}_{q}^{-1} (-{\dot{{{\varvec{K}}}}}_{q} {{\varvec{K}}}_{q}^{-1} {{\varvec{K}}}_{t} +{\dot{{{\varvec{K}}}}}_{t} ) \end{aligned}$$

(27)

where

$$\begin{aligned} {\dot{{{\varvec{K}}}}}_{{\varvec{q}}}= & {} \left( {{\begin{array}{l@{\quad }l@{\quad }l} {({\varvec{\omega }} _{{{\varvec{L}}}_1 } \times {{\varvec{L}}}_1 )^{\mathrm{T}}{{\varvec{e}}}_1 }&{} &{} \\ &{} {({\varvec{\omega }}_{{{\varvec{L}}}_2 } \times {{\varvec{L}}}_2 )^{\mathrm{T}}{{\varvec{e}}}_2 }&{} \\ &{} &{} {({\varvec{\omega }} _{{{\varvec{L}}}_3 } \times {{\varvec{L}}}_3 )^{\mathrm{T}}{{\varvec{e}}}_3 } \\ \end{array} }} \right) ,\\ {\dot{{{\varvec{K}}}}}_{{{{\varvec{t}}}}}= & {} \left( {{\begin{array}{l@{\quad }l} {({\varvec{\omega }} _{{{\varvec{L}}}_1 } \times {{\varvec{L}}}_1 )^{\mathrm{T}}}&{} {-({\varvec{\omega }} _{{{\varvec{L}}}_1 } \times {{\varvec{L}}}_1 )^{\mathrm{T}}{\tilde{{{\varvec{b}}}}}_1 -{{\varvec{L}}}_1^{{\varvec{T}}} {\dot{\tilde{{{\varvec{b}}}}}}_1 } \\ {({\varvec{\omega }} _{{{\varvec{L}}}_2 } \times {{\varvec{L}}}_2 )^{\mathrm{T}}}&{} {-({\varvec{\omega }} _{{{\varvec{L}}}_2 } \times {{\varvec{L}}}_2 )^{\mathrm{T}}{\tilde{{{\varvec{b}}}}}_2 -{{\varvec{L}}}_2^{{\varvec{T}}} {\dot{\tilde{{{\varvec{b}}}}}}_2 } \\ {({\varvec{\omega }} _{{{\varvec{L}}}_3 } \times {{\varvec{L}}}_3 )^{\mathrm{T}}}&{} {-({\varvec{\omega }} _{{{\varvec{L}}}_3 } \times {{\varvec{L}}}_3 )^{\mathrm{T}}{\tilde{{{\varvec{b}}}}}_3 -{{\varvec{L}}}_3^{{\varvec{T}}} {\dot{\tilde{{{\varvec{b}}}}}}_3 } \\ \end{array} }} \right) \\ {\dot{\tilde{{{\varvec{b}}}}}}_{{\varvec{i}}}= & {} \left( {-1} \right) ^{{i}+1}{l}_1 \left( {{\dot{{\varvec{R}}}}_{p} {\tilde{{{\varvec{e}}}}}_{i} {{\varvec{R}}}_{p}^{\mathrm{T}} +{{\varvec{R}}}_{p} {\tilde{{{\varvec{e}}}}}_{i} {\dot{{\varvec{R}}}}_{p}^{\mathrm{T}} } \right) \\= & {} \left( {-1} \right) ^{{i}+1}{l}_1 \left( {{\tilde{{\varvec{\omega }}} }{{\varvec{R}}}_{p} {\tilde{{{\varvec{e}}}}}_{i} {{\varvec{R}}}_{p}^{\mathrm{T}} +{{\varvec{R}}}_{p} {\tilde{{{\varvec{e}}}}}_{i} {{\varvec{R}}}_{p}^{\mathrm{T}} {\tilde{{\varvec{\omega }}}}^{\mathrm{T}}} \right) , ({i}=1,2)\\ {\dot{\tilde{{{\varvec{b}}}}}}_3= & {} {l}_2 \left( {{\tilde{{\varvec{\omega }}}}{{\varvec{R}}}_{p} {\tilde{{{\varvec{e}}}}}_3 {{\varvec{R}}}_{p}^{\mathrm{T}} +{{\varvec{R}}}_{p} {\tilde{{{\varvec{e}}}}}_3 {{\varvec{R}}}_{p}^{\mathrm{T}} {\tilde{{\varvec{\omega }}}}^{\mathrm{T}}} \right) \end{aligned}$$

3 Dynamics of the 2PUR-PSR parallel manipulator

The dynamic modeling of the 2PUR-PSR PM is described in this section. First, the twists of individual bodies, limbs, the system are derived, and thus, the NOC matrix is obtained; then, the Newton–Euler method is used to establish the dynamics model with constrained forces/moments, based on which the NOC matrix and compatible deformation are employed to establish the dynamic models with and without constrained forces/moments.

From Fig. 2, the mass center of the slider and link in ith limb can be expressed as:

$$\begin{aligned} \left\{ {\begin{array}{l} {{\varvec{p}}}_{{S,i}} ={{\varvec{q}}}_{i} +{{\varvec{R}}}_{{S}_{{\varvec{i}}} } {{\varvec{r}}}_{{S,i},1} \\ {{\varvec{p}}}_{{L,i}} ={{\varvec{p}}}_{{S,i}} +{{\varvec{R}}}_{{S,i}} {{\varvec{r}}}_{{S,i,}2} +{{\varvec{R}}}_{{L,i}} {{\varvec{r}}}_{{L},i{,}1} \\ \end{array}} \right. \end{aligned}$$

(28)

where ${{\varvec{r}}}_{L,1,i}$ represents position vector of ${{\varvec{A}}}_{i}$ in the body fixed frame ${C}_{i}$-${{\varvec{x}}}_{{C,i}} {{\varvec{y}}}_{{C,i}} {{\varvec{z}}}_{{C,i}}$.

The velocity of the mass center of the ith slider and link can be obtained by differentiating Eq. (28) with respect to time:

$$\begin{aligned} \left\{ {\begin{array}{l} {\dot{{\varvec{p}}}}_{{S,i}} ={\dot{{{\varvec{q}}}}}_{i} +{\varvec{\omega }} _{{S,i}} \times {{\varvec{R}}}_{{{{{\varvec{S}}}}}_{{{{\varvec{i}}}}} } {{\varvec{r}}}_{{{{{\varvec{S}}}}},{{{{\varvec{i}}}}},1} \\ \qquad =\left( {{\begin{array}{l@{\quad }l} {{{\varvec{E}}}_3 }&{} {-{{\varvec{R}}}_{{{{S}},i}} {\tilde{{{\varvec{r}}}}}_{{{{{\varvec{S,i}}},}}1} {{\varvec{R}}}_{{S,i}}^{\mathrm{T}} } \\ \end{array} }} \right) \left( {{\begin{array}{l@{\quad }l} {{\dot{{{\varvec{q}}}}}_{i}^{\mathrm{T}} }&{} {{\varvec{\omega }} _{{S,i}}^{\mathrm{T}} } \\ \end{array} }} \right) ^{\mathrm{T}} \\ {\dot{{\varvec{p}}}}_{{L,i}} = {\dot{{{\varvec{q}}}}}_{i} +{\varvec{\omega }} _{{L,i}} \times {{\varvec{R}}}_{{L,i}} {{\varvec{r}}}_{{{{{\varvec{L,i}}}}},1} = {\dot{{{\varvec{q}}}}}_{i} -{{\varvec{R}}}_{{L,i}} {\tilde{{{\varvec{r}}}}}_{{{{{\varvec{L,i}}}}},1} {{\varvec{R}}}_{{L,i}}^{\mathrm{T}} {\varvec{\omega }} _{{L,i}}\\ \qquad =\left( {{\begin{array}{l@{\quad }l} {{{\varvec{E}}}_3 }&{} {-{{\varvec{R}}}_{{{{L,i}}}} {\tilde{{{\varvec{r}}}}}_{{{{L}}},{{{i}},}1} {{\varvec{R}}}_{{L,i}}^{\mathrm{T}} } \\ \end{array} }} \right) \left( {{\begin{array}{l@{\quad }l} {{\dot{{{\varvec{q}}}}}_{i}^{\mathrm{T}} }&{} {{\varvec{\omega }} _{{L,i}}^{\mathrm{T}} } \\ \end{array} }} \right) ^{\mathrm{T}} \\ \end{array}} \right. \end{aligned}$$

(29)

where ${\varvec{\omega }}_{{S,i}}$ is the angular velocity of the ith actuator, and ${\varvec{\omega }}_{{S,i}} =\mathbf{0}_{3\times 1}$.

The NOC method employs the concept of twist to describe the velocity field of the individual body, and the twist of the actuator and the link in the ith limb are indicated as ${{\varvec{t}}}_{{S,i}}$ and ${{\varvec{t}}}_{{{\varvec{L,i}}}}$, respectively:

$$\begin{aligned} {{\varvec{t}}}_{{S,i}} =\left( {{\dot{{\varvec{p}}}}_{{S,i}}^{\mathrm{T}}} \quad {{\varvec{\omega }}} _{{S,i}}^{\mathrm{T}} \right) ^{\mathrm{T}},{{\varvec{t}}}_{{L,i}} =\left( {{\dot{{\varvec{p}}}}_{{L,i}}^{\mathrm{T}} }\quad {{\varvec{\omega }} _{{L,i}}^{\mathrm{T}} } \right) ^{\mathrm{T}} \end{aligned}$$

(30)

From Eqs. (29) and (30), the twist of the ith limb is denoted as:

$$\begin{aligned} {\tilde{{{\varvec{t}}}}}_{i} =\left( {{{\varvec{t}}}_{{{\varvec{S,i}}}}^{\mathrm{T}} }\quad {{{\varvec{t}}}_{{{\varvec{L,i}}}}^{\mathrm{T}} } \right) ^{\mathrm{T}}={{\varvec{K}}}_{i} {\varvec{\chi }}_{i} \end{aligned}$$

(31)

where ${\varvec{\chi }}_{i} =\left( {{\dot{{{\varvec{q}}}}}_{i}^\mathrm{T} }\quad {{\varvec{\omega }} _{{L,i}}^{\mathrm{T}} } \right) ^{\mathrm{T}}$ denotes limb independent variables, ${{\varvec{K}}}_{i} =\left( {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {{{\varvec{E}}}_3 }&{} {\mathbf{0}_3 }&{} {{{\varvec{E}}}_3 }&{} {\mathbf{0}_3 } \\ {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {{{\varvec{R}}}_{{{\varvec{L,i}}}}^{\mathrm{T}} {\tilde{{{\varvec{r}}}}}_{{{\varvec{L,i}}},1} {{\varvec{R}}}_{{{\varvec{L,i}}}}}&{} {{{\varvec{E}}}_3 } \\ \end{array} }} \right) ^{\mathrm{T}}$.

Hence, the generalized twists including the limbs and the MP of PM can be expressed as:

$$\begin{aligned} {{\varvec{t}}} = \left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {{\tilde{{{\varvec{t}}}}}_1^{\mathrm{T}} }&{{\tilde{{{\varvec{t}}}}}_2^{\mathrm{T}} }&{{\tilde{{{\varvec{t}}}}}_3^{\mathrm{T}} }&{{{\varvec{t}}}_{p}^{\mathrm{T}} } \end{array} }} \right) ^{\mathrm{T}}={{\varvec{K}}}{\dot{{\varvec{\chi }}}}={{\varvec{T}}}{\dot{\varvec{\eta }}} \end{aligned}$$

(32)

where ${{\varvec{T}}}$ denotes the NOC matrix, ${\varvec{\chi }} =\left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {{\varvec{\chi }} _1^{\mathrm{T}} }&{} {{\varvec{\chi }} _2^{\mathrm{T}} }&{} {{\varvec{\chi }} _3^{\mathrm{T}} }&{} {{{\varvec{t}}}_{p}^{\mathrm{T}} } \\ \end{array} }} \right) ^{\mathrm{T}}$, ${{\varvec{T}}}={{\varvec{KLK}}}_{{\varvec{p}}}$, and

$$\begin{aligned} {{\varvec{K}}}= & {} \left( {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {{{\varvec{K}}}_1 }&{} {\mathbf{0}_{12\times 6} }&{} {\mathbf{0}_{12\times 6} }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_{12\times 6} }&{} {{{\varvec{K}}}_2 }&{} {\mathbf{0}_{12\times 6} }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_{12\times 6} }&{} {\mathbf{0}_{12\times 6} }&{} {{{\varvec{K}}}_3 }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_6 }&{} {\mathbf{0}_6 }&{} {\mathbf{0}_6 }&{} {{{\varvec{E}}}_6 } \\ \end{array} }} \right) ,\nonumber \\ {{\varvec{L}}}= & {} \left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {{{\varvec{E}}}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {{{\varvec{E}}}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_3 }&{} {{{\varvec{E}}}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {{{\varvec{E}}}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {{{\varvec{E}}}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {{{\varvec{E}}}_3 }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {{{\varvec{E}}}_6 } \\ \end{array} }} \right) \\&\times \left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {{{\varvec{e}}}_3 }&{} {\mathbf{0}_{3\times 1} }&{} {\mathbf{0}_{3\times 1} }&{} {\mathbf{0}_{3\times 15} } \\ {\mathbf{0}_{3\times 1} }&{} {{{\varvec{e}}}_1 }&{} {\mathbf{0}_{3\times 1} }&{} {\mathbf{0}_{3\times 15} } \\ {\mathbf{0}_{3\times 1} }&{} {\mathbf{0}_{3\times 1} }&{} {{{\varvec{e}}}_4 }&{} {\mathbf{0}_{3\times 15} } \\ {\mathbf{0}_{15\times 1} }&{} {\mathbf{0}_{15\times 1} }&{} {\mathbf{0}_{15\times 1} }&{} {{{\varvec{E}}}_{15} } \\ \end{array} }} \right) \left( {\begin{array}{l} {{\varvec{J}}}_{{\varvec{q}}} \\ {{\varvec{J}}}_{{w,}1} \\ {{\varvec{J}}}_{{w,}2} \\ {{\varvec{J}}}_{{w,}3} \\ {{\varvec{E}}}_6 \\ \end{array}} \right) \end{aligned}$$

By differentiating Eq. (32) with respect to time, the acceleration mapping between of the individual body and the system independent variables can be expressed as:

$$\begin{aligned} {\dot{{{\varvec{t}}}}}={\dot{{\varvec{T}}}}{\dot{\varvec{\eta }}}+{{\varvec{T}}}{\ddot{\varvec{\eta }}} \end{aligned}$$

(33)

where ${\dot{{\varvec{T}}}}={\dot{{{\varvec{K}}}}}{{\varvec{LK}}}_{{\varvec{p}}} +{{\varvec{K}}}{\dot{{\varvec{L}}}}{{\varvec{K}}}_{{\varvec{p}}} +{{\varvec{KL}}}{\dot{{{\varvec{K}}}}}_{{\varvec{p}}} , {\dot{{{\varvec{K}}}}}_{i} =\left( {{\begin{array}{c@{\quad }c} {\mathbf{0}_3 }&{} {\mathbf{0}_3 } \\ {\mathbf{0}_3 }&{} {\mathbf{0}_3 } \\ {\mathbf{0}_3 }&{} {{{\tilde{{\varvec{\upomega }}}}}_{{L,i}} {\tilde{{{\varvec{r}}}}}_{{L}_{1,i} } -{\tilde{{{\varvec{r}}}}}_{{L}_{1,i} } {{\tilde{{\varvec{\upomega }}}}}_{{L,i}} } \\ {\mathbf{0}_3 }&{} {\mathbf{0}_3 } \\ \end{array} }} \right) , {\dot{{{\varvec{K}}}}}=\left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {{\dot{{{\varvec{K}}}}}_1 }&{} {\mathbf{0}_{12\times 6} }&{} {\mathbf{0}_{12\times 6} }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_{12\times 6} }&{} {{\dot{{{\varvec{K}}}}}_2 }&{} {\mathbf{0}_{12\times 6} }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_{12\times 6} }&{} {\mathbf{0}_{12\times 6} }&{} {{\dot{{{\varvec{K}}}}}_3 }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_6 }&{} {\mathbf{0}_6 }&{} {\mathbf{0}_6 }&{} {\mathbf{0}_6 } \\ \end{array} }} \right) ,$ and

$$\begin{aligned} {\dot{{\varvec{L}}}}= & {} \left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {{{\varvec{E}}}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {{{\varvec{E}}}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_3 }&{} {{{\varvec{E}}}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {{{\varvec{E}}}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {{{\varvec{E}}}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {{{\varvec{E}}}_3 }&{} {\mathbf{0}_6 } \\ {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {\mathbf{0}_3 }&{} {{{\varvec{E}}}_6 } \\ \end{array} }} \right) \\&\times \left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {{{\varvec{e}}}_3 }&{} {\mathbf{0}_{3\times 1} }&{} {\mathbf{0}_{3\times 1} }&{} {\mathbf{0}_{3\times 15} } \\ {\mathbf{0}_{3\times 1} }&{} {{{\varvec{e}}}_1 }&{} {\mathbf{0}_{3\times 1} }&{} {\mathbf{0}_{3\times 15} } \\ {\mathbf{0}_{3\times 1} }&{} {\mathbf{0}_{3\times 1} }&{} {{{\varvec{e}}}_4 }&{} {\mathbf{0}_{3\times 15} } \\ {\mathbf{0}_{15\times 1} }&{} {\mathbf{0}_{15\times 1} }&{} {\mathbf{0}_{15\times 1} }&{} {{{\varvec{E}}}_{15} } \\ \end{array} }} \right) \left( {\begin{array}{l} {\dot{{\varvec{J}}}}_{{\varvec{p}}} \\ {\dot{{\varvec{J}}}}_{{w,}1} \\ {\dot{{\varvec{J}}}}_{{w,}2} \\ {\dot{{\varvec{J}}}}_{{w,}3} \\ \mathbf{0}_6 \\ \end{array}} \right) \end{aligned}$$

For the ith link in the fixed frame ${O-}{{\varvec{XYZ}}}$, the Newton–Euler equation can be derived as:

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\hbox {d}{m}_{{L,i}} {\dot{{\varvec{p}}}}_{{L,i}} }{\hbox {d}{t}}={m}_{{L,i}} {\ddot{{\varvec{p}}}}_{{L,i}} ={{\varvec{f}}}_{{L,i}} +{m}_{{L,i}} {{\varvec{g}}} \\ \frac{\hbox {d}({{\varvec{R}}}_{{L,i}} {{\varvec{I}}}_{{L,i}}^{l} {{\varvec{R}}}_{{L,i}}^{\mathrm{T}} {\varvec{\omega }}_{{L,i}} )}{\hbox {d}{t}}={\dot{{\varvec{R}}}}_{{L,i}} {{\varvec{I}}}_{{L,i}}^{l} {{\varvec{R}}}_{{L,i}}^{\mathrm{T}} {\varvec{\omega }}_{{L,i}} +{{\varvec{R}}}_{{L,i}} {{\varvec{I}}}_{{L,i}}^{l} {\dot{{\varvec{R}}}}_{{L,i}}^{\mathrm{T}} {\varvec{\omega }} _{{L,i}} +{{\varvec{R}}}_{{L,i}} {{\varvec{I}}}_{{L,i}}^{l} {{\varvec{R}}}_{{L,i}}^{\mathrm{T}} {\dot{\varvec{\omega }}}_{{L,i}} \\ \quad \quad ={\tilde{\varvec{\omega }}}_{{L,i}} {{\varvec{R}}}_{{L,i}} {{\varvec{I}}}_{{L,i}}^{l} {{\varvec{R}}}_{{L,i}}^{\mathrm{T}} {\varvec{\omega }} _{{L,i}} +{{\varvec{R}}}_{{L,i}} {{\varvec{I}}}_{{L,i}}^{l} {{\varvec{R}}}_{{L,i}}^{\mathrm{T}} {\tilde{\varvec{\omega }}}_{{L,i}}^{\mathrm{T}} {\varvec{\omega }} _{{L,i}} +{{\varvec{R}}}_{{L,i}} {{\varvec{I}}}_{{L,i}}^{l} {{\varvec{R}}}_{{L,i}}^{T} {\dot{\varvec{\omega }}}_{{L,i}} \\ \quad \quad ={{\varvec{R}}}_{{L,i}} {{\varvec{I}}}_{{L,i}}^{l} {{\varvec{R}}}_{{L,i}}^{\mathrm{T}} {\dot{\varvec{\omega }}}_{{L,i}} +{\tilde{\varvec{\omega }}}_{{L,i}} {{\varvec{R}}}_{{L,i}} {{\varvec{I}}}_{{L,i}}^{l} {{\varvec{R}}}_{{L,i}}^{\mathrm{T}} {\varvec{\omega }} _{{L,i}} ={{\varvec{n}}}_{{L,i}} \\ \end{array}} \right. \end{aligned}$$

(34)

where ${m}_{{L,i}}$ and ${{\varvec{I}}}_{{L,i}}^{l}$ are the mass and the inertial tensor of the ith link in the body fixed frame, and ${{\varvec{g}}}$ denotes the gravity acceleration. ${{\varvec{w}}}_{{L,i}} =\left( {{\begin{array}{l@{\quad }l} {{{\varvec{f}}}_{{L,i}}^{\mathrm{T}} }&{} {{{\varvec{n}}}_{{L,i}}^{\mathrm{T}} } \\ \end{array} }} \right) ^{\mathrm{T}}$ is the wrench in the fixed frame, and can be decomposed into working wrench ${{\varvec{w}}}_{{L,i}}^{a} =\left( {{\begin{array}{l@{\quad }l} {{{\varvec{f}}}_{{L,i}}^{{a}\mathrm{T}} }&{} {{{\varvec{n}}}_{{L,i}}^{{a}\mathrm{T}} } \\ \end{array} }} \right) ^{\mathrm{T}}$ and non-working wrench ${{\varvec{w}}}_{{{\varvec{L,i}}}}^{c} =\left( {{\begin{array}{l@{\quad }l} {{{\varvec{f}}}_{{L,i}}^{{c}\mathrm{T}} }&{} {{{\varvec{n}}}_{{L,i}}^{{c}\mathrm{T}} } \\ \end{array} }} \right) ^{\mathrm{T}}$. The working wrench ${{\varvec{w}}}_{{L,i}}^{{\varvec{a}}}$ denotes wrench due to actuators, external forces/moments gravity or dissipation, while the non-working wrench is caused by the constraint forces and moment and can be expressed as:

$$\begin{aligned} \left\{ {\begin{array}{l} {{\varvec{f}}}_{{L,i}}^{{\varvec{c}}} ={{\varvec{L}}}_{{A,i,T}}^{{\varvec{c}}} {\varvec{\lambda }}_{{A,i}} +{{\varvec{L}}}_{{B,i,T}}^{{\varvec{c}}} {\varvec{\lambda }}_{{B,i}} \\ {{\varvec{n}}}_{{L,i}}^{{\varvec{c}}} ={{\varvec{L}}}_{{A,i,R}}^{{\varvec{c}}} {\varvec{\lambda }}_{{A,i}} +{{\varvec{L}}}_{{B,i,R}}^{{\varvec{c}}} {\varvec{\lambda }}_{{B,i}} \\ \end{array}} \right. \end{aligned}$$

(35)

where ${\varvec{\lambda }}_{{A,i}} \in {{\mathbb {R}}}^{4\times 1}({i}=1,2)$, ${\varvec{\lambda }}_{{A},3} \in {{\mathbb {R}}}^{3\times 1}$ and ${\varvec{\lambda }}_{{B,i}} \in {{\mathbb {R}}}^{5\times 1}$ are the ideal constraint forces/moments generated in the universal joint, spherical joint and the revolute joint of the links. ${{\varvec{L}}}_{{A,i,T}}^{{\varvec{c}}} \in {{\mathbb {R}}}^{3\times 4}({i}=1,2)$, ${{\varvec{L}}}_{{A,i,R}}^{{\varvec{c}}} \in {{\mathbb {R}}}^{3\times 4}({i=}1,2)$, ${{\varvec{L}}}_{{A,}3{,T}}^{{\varvec{c}}} \in {{\mathbb {R}}}^{3\times 3}$, ${{\varvec{L}}}_{{A,}3{,R}}^{{\varvec{c}}} \in {{\mathbb {R}}}^{3\times 3}$, ${{\varvec{L}}}_{{B,i,T}}^{{\varvec{c}}} \in {{\mathbb {R}}}^{3\times 5}$ and ${{\varvec{L}}}_{{B,i,R}}^{{\varvec{c}}} \in {{\mathbb {R}}}^{3\times 5}$ are transformation matrices related with the constraint forces/moments and can be expressed as:

$$\begin{aligned} \left\{ {\begin{array}{l} {{\varvec{L}}}_{{A,}1{,T}}^{{{c}}} ={{\varvec{L}}}_{{A}_{2,{T}} }^{{\varvec{c}}} =\left[ {{{\varvec{E}}}_3 ,\mathbf{0}_{3\times 1} } \right] ,{{\varvec{L}}}_{{A,}3,{T}}^{c} ={{\varvec{E}}}_3 \\ {{\varvec{L}}}_{{A,}1{,{{R}}}}^{c} =\left[ {{{\varvec{R}}}_{{{{L}}},1} {{\tilde{{{\varvec{r}}}}}}_{{{{L}},}1,1} {{\varvec{R}}}_{{{{L}}},1}^{{\varvec{T}}} ,{{\varvec{z}}}_{{c},1} } \right] ,\\ {{\varvec{L}}}_{{A,}3,{{{R}}}}^{c} =-{{\varvec{R}}}_{{{{L}}},3} {{\tilde{{{\varvec{r}}}}}}_{{{{L}}},3,1} {{\varvec{R}}}_{{{{L}}},3}^{{\varvec{T}}},\\ {{\varvec{L}}}_{{A,}2{,{{R}}}}^{c} =\left[ {{{\varvec{R}}}_{{{{L}}},2} {\tilde{{{\varvec{r}}}}}_{{{{L}},}2,1} {{{\varvec{R}}}}_{{{{L}}},2}^{\mathrm{T}} ,{{\varvec{z}}}_{{c},2} } \right] \\ {{\varvec{L}}}_{{B,}1{,T}}^{{{c}}} ={{\varvec{L}}}_{{B,}2{,T}}^{{\varvec{c}}} ={{\varvec{L}}}_{{B,}3{,T}}^{{\varvec{c}}} =-\left[ {{{\varvec{E}}}_3 ,\mathbf{0}_{3\times 2} } \right] \\ {{\varvec{L}}}_{{B,}1{,{{R}}}}^{c} =-\left[ {{{\varvec{R}}}_{{{{L}}},1} {\tilde{{{\varvec{r}}}}}_{{{{L}}},1,2} {{\varvec{R}}}_{{{{L}}},1}^{{\varvec{T}}} ,{{\varvec{v}}},{{\varvec{w}}}} \right] ,\\ {{\varvec{L}}}_{{B,}2{,{{R}}}}^{c} =-\left[ {{{\varvec{R}}}_{{{{L}}},2} {\tilde{{{\varvec{r}}}}}_{{{{L}}},2,2} {{\varvec{R}}}_{{{{L}}},2}^{{\varvec{T}}} ,{{\varvec{v,w}}}} \right] ,\\ {{\varvec{L}}}_{{B,}3{,{{R}}}}^{c} =-\left[ {{{\varvec{R}}}_{{{{L}}},3} {\tilde{{{\varvec{r}}}}}_{{{{L}},}3,2} {{\varvec{R}}}_{{{{L}},}3}^{{\varvec{T}}} ,{{\varvec{u,w}}}} \right] \\ \end{array}} \right. \end{aligned}$$

The matrix form of Eq. (34) can be reformulated as:

$$\begin{aligned} {{\varvec{w}}}_{{L,i}}^{a}= & {} \left( {{\begin{array}{c@{\quad }c} {{m}_{{L,i}} {{\varvec{E}}}_3 }&{} {\mathbf{0}_3 } \\ {\mathbf{0}_3 }&{} {{{\varvec{R}}}_{{L,i}} {{\varvec{I}}}_{{L,i}}^{l} {{\varvec{R}}}_{{L,i}}^{T} } \\ \end{array} }} \right) \left( {\begin{array}{l} {\ddot{{\varvec{p}}}}_{{{{L}},i}} \\ {\dot{\varvec{\omega }}}_{{{{L}},i}} \\ \end{array}} \right) \nonumber \\&+\left( {{\begin{array}{c@{\quad }c} {\mathbf{0}_3 }&{} {\mathbf{0}_3 } \\ {\mathbf{0}_3 }&{} {{{\tilde{{\varvec{\omega }}}}}_{{{{L}},i}} {{\varvec{R}}}_{{{{L}},i}} {{\varvec{I}}}_{{{{L}},i}}^{l} {{\varvec{R}}}_{{{{L}},i}}^{T} } \\ \end{array} }} \right) \left( {\begin{array}{l} {\dot{{\varvec{p}}}}_{{{{L}},i}} \\ {\varvec{\omega }} _{{{{L}},i}} \\ \end{array}} \right) \nonumber \\&-\left( {{\begin{array}{c@{\quad }c} {{{\varvec{L}}}_{{A,i,T}}^{{\varvec{c}}} }&{} {{{\varvec{L}}}_{{B,i,T}}^{{\varvec{c}}} } \\ {{{\varvec{L}}}_{{A,i,{{R}}}}^{{\varvec{c}}} }&{} {{{\varvec{L}}}_{{B,i,{{R}}}}^{{\varvec{c}}} } \\ \end{array} }} \right) \left( {\begin{array}{l} {\varvec{\lambda }}_{{A,i}} \\ {\varvec{\lambda }}_{{B,i}} \\ \end{array}} \right) -\left( {\begin{array}{c} {m}_{{{{L}},i}} {{\varvec{E}}}_3 \\ \mathbf{0}_3 \\ \end{array}} \right) {{\varvec{g}}} \nonumber \\= & {} {{\varvec{M}}}_{{{{L}},i}} {\dot{{{\varvec{t}}}}}_{{{{L}},i}} +{{\varvec{W}}}_{{{{L}},i}} {{\varvec{t}}}_{{{{L}},i}} -{{\varvec{C}}}_{{{{L}},i}} {\varvec{\lambda }}_{{{{L}},i}} -{{\varvec{G}}}_{{{{L}},i}} {{\varvec{g}}} \end{aligned}$$

(36)

From Eq. (36), Newton–Euler equation of the sliders can be given by:

$$\begin{aligned} {{\varvec{w}}}_{{{{S}},i}}^{{\varvec{a}}}= & {} \left( {{\begin{array}{c@{\quad }c} {{m}_{{{{S}},i}} {{\varvec{E}}}_{3} }&{} {\mathbf{0}_3 } \\ {\mathbf{0}_3 }&{} {{{\varvec{R}}}_{{{{S}},i}} {{\varvec{I}}}_{{{{S}},i}}^{{{S}}} {{\varvec{R}}}_{{{{S}},i}}^{T} } \\ \end{array} }} \right) \left( {\begin{array}{l} {\ddot{{\varvec{p}}}}_{{{{S}},i}} \\ \dot{{\varvec{\omega }}}_{{{{S}},i}} \\ \end{array}} \right) \nonumber \\&+\left( {{\begin{array}{c@{\quad }c} {\mathbf{0}_3 }&{} {\mathbf{0}_3 } \\ {\mathbf{0}_3 }&{} {{\tilde{{\varvec{\omega }}} }_{{{{S}},i}} {{\varvec{R}}}_{{{{S}},i}} {{\varvec{I}}}_{{{{S}},i}}^{p} {{\varvec{R}}}_{{{{S}},i}}^{T} } \\ \end{array} }} \right) \left( {\begin{array}{l} {{\dot{{{\varvec{p}}}}}}_{{{{S}},i}} \\ {\varvec{\omega }} _{{{{S}},i}} \\ \end{array}} \right) \nonumber \\&-\left( {{\begin{array}{l@{\quad }l} {{{\varvec{S}}}_{{p,i,T}}^{{\varvec{c}}} }&{} {{{\varvec{S}}}_{{A,i,T}}^{{\varvec{c}}} } \\ {{{\varvec{S}}}_{{p,i,{{R}}}}^{{\varvec{c}}} }&{} {{{\varvec{S}}}_{{A,i,{{R}}}}^{{\varvec{c}}} } \\ \end{array} }} \right) \left( {\begin{array}{l} {\varvec{\lambda }}_{{p,i}} \\ {\varvec{\lambda }}_{{A,i}} \\ \end{array}} \right) -\left( {\begin{array}{c} {m}_{{{{S}},i}} {{\varvec{E}}}_{3} \\ \mathbf{0}_3 \\ \end{array}} \right) {{\varvec{g}}} \nonumber \\= & {} {{\varvec{M}}}_{{{{S}},i}} {\dot{{{\varvec{t}}}}}_{{{{S}},i}} +{{\varvec{W}}}_{{{{S}},i}} {{\varvec{t}}}_{{{{S}},i}} -{{\varvec{w}}}_{{{{S}},i}}^{{\varvec{c}}} -{{\varvec{G}}}_{{{{S}},i}} {{\varvec{g}}} \end{aligned}$$

(37)

where ${m}_{{S,i}}$ and ${{\varvec{I}}}_{{S,i}}^{S}$ represent the mass and inertial tensor of the sliders with the corresponding body fixed coordinate frame. ${{\varvec{w}}}_{{S,i}}^{a} =\left( {{\begin{array}{l@{\quad }l} {{{\varvec{E}}}_3 }&{} {{\tilde{{{\varvec{r}}}}}_{{{\varvec{S,i}}},1}^{{\varvec{T}}} } \\ \end{array} }} \right) ^{\mathrm{T}}{{\varvec{f}}}_{{S,i}}^{a} =\left( {{\begin{array}{l@{\quad }l} {{{\varvec{e}}}_{i}^{\mathrm{T}} }&{} {{{\varvec{e}}}_{i}^{\mathrm{T}} {\tilde{{{\varvec{r}}}}}_{S,{i},1}^{\mathrm{T}} } \\ \end{array} }} \right) ^{\mathrm{T}}{f}_{{S,i}}^{a} ={{\varvec{f}}}_{{CS,i}}^{a}~{f}_{{S,i}}^{a}$ denotes forces and torques generated by the actuators, and ${{\varvec{f}}}_{{S,i}}^{a} ={f}_{{S,i}}^{a} {{\varvec{e}}}_{i}$ is the actuation forces. ${{\varvec{w}}}_{{S,i}}^{{\varvec{c}}} =\left( {{\begin{array}{l@{\quad }l} {{{\varvec{f}}}_{{S,i}}^{{c}\mathrm{T}} }&{} {{{\varvec{n}}}_{{S,i}}^{{c}\mathrm{T}} } \\ \end{array} }} \right) ^{\mathrm{T}}$ denote the ideal constraint forces and moments exerted on the sliders and can be given by:

$$\begin{aligned} \left\{ {\begin{array}{l} {{\varvec{f}}}_{{S,i}}^{c} ={{\varvec{S}}}_{{A,i,T}}^{c} {\varvec{\lambda }}_{{A,i}} +{{\varvec{S}}}_{{p,i,T}}^{c} {\varvec{\lambda }}_{{p,i}} \\ {{\varvec{n}}}_{{S,i}}^{c} ={{\varvec{S}}}_{{A,i,R}}^{c} {\varvec{\lambda }}_{{A,i}} +{{\varvec{S}}}_{{p,i,R}}^{c} {\varvec{\lambda }}_{{p,i}} \\ \end{array}} \right. \end{aligned}$$

where ${\varvec{\lambda }}_{{p,i}} \in {{\mathbb {R}}}^{3\times 5}$ denotes ideal constraint forces and moments caused by the prismatic joints, while the transformation matrices ${{\varvec{S}}}_{{P,}1{,T}}^{{\varvec{c}}}$, ${{\varvec{S}}}_{{P,}1{,R}}^{{\varvec{c}}}$, ${{\varvec{S}}}_{{A,}1{,T}}^{{\varvec{c}}}$ and ${{\varvec{S}}}_{{A,}1{,R}}^{c}$ are given by:

$$\begin{aligned} \left\{ {\begin{array}{l} {{\varvec{S}}}_{{P,}1{,T}}^{{\varvec{c}}} ={{\varvec{S}}}_{{P,}2{,T}}^{{\varvec{c}}} =\left[ {{{\varvec{e}}}_3 ,{{\varvec{e}}}_4 ,\mathbf{0}_3 } \right] ,{{\varvec{S}}}_{{P,}3{,T}}^{{\varvec{c}}} =\left[ {{{\varvec{e}}}_1 ,{{\varvec{e}}}_4 ,\mathbf{0}_3 } \right] \\ {{\varvec{S}}}_{{P,}1{,R}}^{{\varvec{c}}} =\left[ {{\tilde{{{\varvec{r}}}}}_{{{{S}}},1,1} \cdot \left( {{{\varvec{e}}}_3 ,{{\varvec{e}}}_4 } \right) ,{{\varvec{E}}}_3 } \right] ,\\ {{\varvec{S}}}_{{P,}2{,R}}^{{\varvec{c}}} =\left[ {{\tilde{{{\varvec{r}}}}}_{{{{S}}},2,1} \cdot \left( {{{\varvec{e}}}_3 ,{{\varvec{e}}}_4 } \right) ,{{\varvec{E}}}_3 } \right] ,\\ {{\varvec{S}}}_{{P,}3{,R}}^{{\varvec{c}}} =\left[ {{\tilde{{{\varvec{r}}}}}_{{{{S}}},3,1} \cdot \left( {{{\varvec{e}}}_1 ,{{\varvec{e}}}_4 } \right) ,{{\varvec{E}}}_3 } \right] \\ {{\varvec{S}}}_{{A,}1{,T}}^{{\varvec{c}}} ={{\varvec{S}}}_{{A,}2{,T}}^{{\varvec{c}}} =-\left[ {{{\varvec{E}}}_3 ,\mathbf{0}_{3\times 1} } \right] ,{{\varvec{S}}}_{{A,}3{,T}}^{{\varvec{c}}} =-{{\varvec{E}}}_3 \\ {{\varvec{S}}}_{{A,}1{,R}}^{c} =-\left[ {{\tilde{{{\varvec{r}}}}}_{{{S}},1,2}, {{\varvec{z}}}_{{c},1} } \right] ,{{\varvec{S}}}_{{A,}2{,R}}^{{\varvec{c}}} =-\left[ {{\tilde{{{\varvec{r}}}}}_{{{{S}}},2,2} ,{{\varvec{z}}}_{{c},1} } \right] ,\\ {{\varvec{S}}}_{{A,}3{,R}}^{{\varvec{c}}} =-{\tilde{{{\varvec{r}}}}}_{{{{S}}},3,2} \\ \end{array}} \right. \end{aligned}$$

Similarly, matrix form of Newton–Euler equation for the MP can be given by:

$$\begin{aligned} {{\varvec{w}}}_{p}^{a}= & {} \left( {{\begin{array}{c@{\quad }c} {{m}_{p} {{\varvec{E}}}_3 }&{} {\mathbf{0}_3 } \\ {\mathbf{0}_3 }&{} {{{\varvec{R}}}_{p} {{\varvec{I}}}_{p}^{p} {{\varvec{R}}}_{p}^{T} } \\ \end{array} }} \right) \left( {\begin{array}{l} {\ddot{{{\varvec{p}}}}}_{m} \\ {{\dot{{\varvec{\omega }}}}} \nonumber \\ \end{array}} \right) \\&+\left( {{\begin{array}{c@{\quad }c} {\mathbf{0}_3 }&{} {\mathbf{0}_3 } \\ {\mathbf{0}_3 }&{} {{{\tilde{{\varvec{\omega }}}}}{{\varvec{R}}}_{p} {{\varvec{I}}}_{p}^{p} {{\varvec{R}}}_{p}^{T} } \\ \end{array} }} \right) \left( {\begin{array}{l} {\dot{{\varvec{p}}}}_{m} \\ {\varvec{\omega }} \\ \end{array}} \right) \nonumber \\&-\left( {{\begin{array}{l@{\quad }l@{\quad }l} {{{\varvec{P}}}_{{{{P}}}1{,T}}^{{\varvec{c}}} }&{} {{{\varvec{P}}}_{{{{P}},}2{,T}}^{{\varvec{c}}} }&{} {{{\varvec{P}}}_{{{{P}},}3{,T}}^{{\varvec{c}}} } \\ {{{\varvec{P}}}_{{{{P}},}1{,R}}^{{\varvec{c}}} }&{} {{{\varvec{P}}}_{{{{P}},}2{,R}}^{{\varvec{c}}} }&{} {{{\varvec{P}}}_{{{{P}},}3{,R}}^{{\varvec{c}}} } \\ \end{array} }} \right) {\varvec{\lambda }}_{p} -\left( {\begin{array}{l} {m}_{p} {{\varvec{E}}}_3 \\ \mathbf{0}_3 \\ \end{array}} \right) {{\varvec{g}}} \nonumber \\= & {} {{\varvec{M}}}_{p} {\dot{{{\varvec{t}}}}}_{p} +{{\varvec{W}}}_{p} {{\varvec{t}}}_{p} -{{\varvec{w}}}_{{p,i}}^{{\varvec{c}}} -{{\varvec{G}}}_{p} {{\varvec{g}}} \end{aligned}$$

(38)

where ${m}_{p}$ and ${{\varvec{I}}}_{p}^{p}$ represents the mass and inertial tensor of the MP with respect to the corresponding body fixed coordinate frame. ${{\varvec{w}}}_{{p,i}}^{{\varvec{c}}} =\left( {{\begin{array}{l@{\quad }l} {{{\varvec{f}}}_{{p,i}}^{{{{c}}}\mathrm{T}} }&{{{\varvec{n}}}_{{p,i}}^{{c}\mathrm{T}} } \end{array} }} \right) ^{\mathrm{T}}$ denotes the constraint forces and moments of the MP, respectively, and can be represented as:

$$\begin{aligned} \left\{ {\begin{array}{l} {{\varvec{f}}}_{{{{P}},i}}^{{\varvec{c}}} ={{\varvec{P}}}_{{B,}1{,T}}^{{\varvec{c}}} {\varvec{\lambda }}_{{B,}1} +{{\varvec{P}}}_{{B,}2{,T}}^{{\varvec{c}}} {\varvec{\lambda }}_{{B,}2} +{{\varvec{P}}}_{{B,}3{,T}}^{{\varvec{c}}} {\varvec{\lambda }}_{{B,}3} \\ {{\varvec{n}}}_{{{{P}},i}}^{{\varvec{c}}} ={{\varvec{P}}}_{{B,}1{,R}}^{{\varvec{c}}} {\varvec{\lambda }}_{{B,}1} +{{\varvec{P}}}_{{B,}2{,R}}^{{\varvec{c}}} {\varvec{\lambda }}_{{B,}2} +{{\varvec{P}}}_{{B,}3{,R}}^{{\varvec{c}}} {\varvec{\lambda }}_{{B,}3} \\ \end{array}} \right. \end{aligned}$$

Where the transformation matrix ${{\varvec{P}}}_{{B,i,T}}^{{\varvec{c}}} \in {{\mathbb {R}}}^{3\times 5}$ can be derived as:

$$\begin{aligned} \left\{ {\begin{array}{l} {{\varvec{P}}}_{{B,}1{,T}}^{{\varvec{c}}} ={{\varvec{P}}}_{{B}2{,T}}^{{\varvec{c}}} ={{\varvec{P}}}_{{B,}3{,T}}^{{\varvec{c}}} =\left[ {{{\varvec{E}}}_3 ,\mathbf{0}_{3\times 2} } \right] \\ {{\varvec{P}}}_{{B,}1{,R}}^{{\varvec{c}}} =\left[ {{\tilde{{{\varvec{b}}}}}_1 ,{{\varvec{v,w}}}} \right] ,{{\varvec{P}}}_{{B,}2{,R}}^{{\varvec{c}}} =\left[ {{\tilde{{{\varvec{b}}}}}_2 ,{{\varvec{v,w}}}} \right] ,\\ {{\varvec{P}}}_{{B,}3{,R}}^{{\varvec{c}}} =\left[ {{\tilde{{{\varvec{b}}}}}_3 ,{{\varvec{u,w}}}} \right] \\ \end{array}} \right. \end{aligned}$$

Based on Eqs. (36)–(38), the system dynamic equation of the over-constrained PM can be derived as:

$$\begin{aligned} {{\varvec{M}}}{\dot{{{\varvec{t}}}}}+{{\varvec{Wt}}}-{{\varvec{C}}}_\lambda {\varvec{\lambda }} -{{\varvec{Gg}}}={{\varvec{w}}}^{{\mathrm{a}}} \end{aligned}$$

(39)

where ${{\varvec{M}}}$, ${{\varvec{W}}}$ and ${{\varvec{C}}}_\lambda$ denotes extended inertial matrix, extended angular velocity matrix and the extended constraint transformation matrix of the PM, respectively, while ${{\varvec{G}}}$ and ${{\varvec{w}}}^{\mathrm{a}}$ are the gravity matrix and the actuation matrix, which can be represented as:

$$\begin{aligned} \left\{ {\begin{array}{l} {{{\varvec{M}}}} = {{\varvec{blkdiag}}}\left( {{{\varvec{M}}}_{{S,}1} ,{{\varvec{M}}}_{{L,}1} ,{{\varvec{M}}}_{{S,}2} ,{{\varvec{M}}}_{{L,}2} ,{{\varvec{M}}}_{{S,}3} ,{{\varvec{M}}}_{{L,}3} ,{{\varvec{M}}}_{p} } \right) \\ {{\varvec{W}}} = {{\varvec{blkdiag}}}\left( {{{\varvec{W}}}_{{S},1} ,{{\varvec{W}}}_{{L},1} ,{{\varvec{W}}}_{{S},2} ,{{\varvec{W}}}_{{L},2} ,{{\varvec{W}}}_{{S},3} ,{{\varvec{W}}}_{{L},3} ,{{\varvec{W}}}_{p} } \right) \\ {{\varvec{G}}} = \left( {{{\varvec{G}}}_{{S},1}^{\mathrm{T}} ,{{\varvec{G}}}_{{L},1}^{\mathrm{T}} ,{{\varvec{G}}}_{{S},2}^{\mathrm{T}} ,{{\varvec{G}}}_{{L},1}^{\mathrm{T}} ,{{\varvec{G}}}_{{S},3}^{\mathrm{T}} ,{{\varvec{G}}}_{{L},1}^{\mathrm{T}} ,{{\varvec{G}}}_{p}^\mathrm{T} } \right) ^{\mathrm{T}} \\ {\varvec{\lambda }} = \left[ {{\varvec{\lambda }}_{{P},1}^{\mathrm{T}} ,{\varvec{\lambda }}_{{A},1}^{\mathrm{T}} ,{\varvec{\lambda }}_{{B},1}^{\mathrm{T}} ,{\varvec{\lambda }}_{{P},2}^{\mathrm{T}} ,{\varvec{\lambda }}_{{A,}2}^{\mathrm{T}} ,{\varvec{\lambda }}_{{B},2}^{\mathrm{T}} ,{\varvec{\lambda }}_{{P},3}^{\mathrm{T}} ,{\varvec{\lambda }}_{{A},3}^{\mathrm{T}} ,{\varvec{\lambda }}_{{B},3}^{\mathrm{T}} } \right] ^{\mathrm{T}} \\ {{\varvec{w}}}^{\mathrm{a}}=\left( {{{\varvec{w}}}_{{S},1}^{{a}\mathrm{T}} ,{{\varvec{w}}}_{{L},1}^{{a}\mathrm{T}} ,{{\varvec{w}}}_{{S},2}^{{a}\mathrm{T}} ,{{\varvec{w}}}_{{L},2}^{{a}\mathrm{T}} ,{{\varvec{w}}}_{{S},3}^{{a}\mathrm{T}} ,{{\varvec{w}}}_{{L},3}^{{a}\mathrm{T}} ,{{\varvec{w}}}_{p}^{{a}\mathrm{T}} } \right) ^{\mathrm{T}} = {{\varvec{w}}}_{{CS}}^{a}~{{\varvec{f}}}^{{a}},{{\varvec{f}}}^{{a}}\\ =\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {{f}_1^{a} }&{} {{f}_2^{a} }&{} {{f}_3^{a} } \\ \end{array} }} \right] ^{\mathrm{T}} \\ \end{array}} \right. \end{aligned}$$

and

$$\begin{aligned} {{\varvec{C}}}_\lambda= & {} \left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {{{\varvec{C}}}_{{{\varvec{S}}},1} }&{} {\mathbf{0}_{6\times 5} }&{} {\mathbf{0}_{6\times 9} }&{} {\mathbf{0}_{6\times 5} }&{} {\mathbf{0}_{6\times 8} }&{} {\mathbf{0}_{6\times 5} } \\ {\mathbf{0}_{6\times 5} }&{} {{{\varvec{C}}}_{{{\varvec{L}}},1} }&{} {\mathbf{0}_{6\times 9} }&{} {\mathbf{0}_{6\times 5} }&{} {\mathbf{0}_{6\times 8} }&{} {\mathbf{0}_{6\times 5} } \\ {\mathbf{0}_{6\times 5} }&{} {\mathbf{0}_{6\times 9} }&{} {{{\varvec{C}}}_{{{\varvec{S}}},2} }&{} {\mathbf{0}_{6\times 5} }&{} {\mathbf{0}_{6\times 8} }&{} {\mathbf{0}_{6\times 5} } \\ {\mathbf{0}_{6\times 5} }&{} {\mathbf{0}_{6\times 9} }&{} {\mathbf{0}_{6\times 5} }&{} {{{\varvec{C}}}_{{{\varvec{L}}},2} }&{} {\mathbf{0}_{6\times 8} }&{} {\mathbf{0}_{6\times 5} } \\ {\mathbf{0}_{6\times 5} }&{} {\mathbf{0}_{6\times 9} }&{} {\mathbf{0}_{6\times 5} }&{} {\mathbf{0}_{6\times 9} }&{} {{{\varvec{C}}}_{{{\varvec{S}}},3} }&{} {\mathbf{0}_{6\times 5} } \\ {\mathbf{0}_{6\times 5} }&{} {\mathbf{0}_{6\times 9} }&{} {\mathbf{0}_{6\times 5} }&{} {\mathbf{0}_{6\times 9} }&{} {\mathbf{0}_{6\times 5} }&{} {{{\varvec{C}}}_{{{\varvec{L}}},3} } \\ {\mathbf{0}_{6\times 9} }&{} {{{\varvec{P}}}_{{P}1}^{{\varvec{c}}} }&{} {\mathbf{0}_{6\times 8} }&{} {{{\varvec{P}}}_{{P}2}^{{\varvec{c}}} }&{} {\mathbf{0}_{6\times 9} }&{} {{{\varvec{P}}}_{{P}3}^{{\varvec{c}}} } \\ \end{array} }} \right) ,\\ {{\varvec{w}}}_{{CS}}^{{{a}}}= & {} \left( {{\begin{array}{l@{\quad }l@{\quad }l} {{{\varvec{f}}}_{{CS,i}}^{{\varvec{a}}} }&{} {\mathbf{0}_{6\times 1} }&{} {\mathbf{0}_{6\times 1} } \\ {\mathbf{0}_{6\times 1} }&{} {\mathbf{0}_{6\times 1} }&{} {\mathbf{0}_{6\times 1} } \\ {\mathbf{0}_{6\times 1} }&{} {{{\varvec{f}}}_{{CS,i}}^{{\varvec{a}}} }&{} {\mathbf{0}_{6\times 1} } \\ {\mathbf{0}_{6\times 1} }&{} {\mathbf{0}_{6\times 1} }&{} {\mathbf{0}_{6\times 1} } \\ {\mathbf{0}_{6\times 1} }&{} {\mathbf{0}_{6\times 1} }&{} {{{\varvec{f}}}_{{CS,i}}^{{\varvec{a}}} } \\ {\mathbf{0}_{6\times 1} }&{} {\mathbf{0}_{6\times 1} }&{} {\mathbf{0}_{6\times 1} } \\ {\mathbf{0}_{6\times 1} }&{} {\mathbf{0}_{6\times 1} }&{} {\mathbf{0}_{6\times 1} } \\ \end{array} }} \right) , {{\varvec{f}}}^{{a}}=\left( {\begin{array}{l} {f}_1^{a} \\ {f}_2^{a} \\ {f}_3^{a} \\ \end{array}} \right) \end{aligned}$$

According to the principle of virtual power, the ideal constraint forces and moments in the connecting joints don’t produce work in the system dynamics; hence, we can obtain:

$$\begin{aligned} {{\varvec{T}}}^{\mathrm{T}}{{\varvec{C}}}_\lambda =0 \end{aligned}$$

(40)

Based on Eqs. (32), (33) and (40), the system dynamic model without constraint forces/ moments can be reformulated as:

$$\begin{aligned} {{\varvec{T}}}^{\mathrm{T}}{{\varvec{M}}}{{\varvec{T}}}{\ddot{\varvec{\eta }}}+{{\varvec{T}}}^{\mathrm{T}}{{\varvec{M}}}{\dot{{\varvec{T}}}}{\dot{\varvec{\eta }}}+{{\varvec{T}}}^{\mathrm{T}}{{\varvec{W}}}{{\varvec{T}}}{\dot{\varvec{\eta }}}-{{\varvec{T}}}^{\mathrm{T}}{{\varvec{Gg}}} = {{\varvec{T}}}^{\mathrm{T}}{{\varvec{w}}}_{{CS}}^{a}~{{\varvec{f}}}^{{a}} \end{aligned}$$

(41)

Based on the screw theory, the limb 1 and limb 2 simultaneously possess the constraints of translation in u axes and rotation about ${{\varvec{z}}}_{c,i}$ axes, which means that there are two over-constrained motions in the 2R1T PM. Hence, translational deformations along u and rotational deformation about w axes of limb 1 and limb 2 should be equal, which can be derived as:

$$\begin{aligned} \left\{ {\begin{array}{l} \delta _{{i,T,}{{\varvec{u}}}} ={{\varvec{e}}}_3^{\mathrm{T}} {{\varvec{R}}}_{{L,i}}^{-1} \left( {-{m}_{{L,i}} {\ddot{{\varvec{p}}}}_{{L,i}} {+m}_{{L,i}} {{\varvec{g}}}} \right) \left[ {\frac{\left( {{l}_3 -{r}_{{L,}2,{i}} } \right) ^{3}}{3{EI}_{y} }+\frac{{r}_{{L,2,i}} \left( {{l}_3 -{r}_{{L,}2,{i}} } \right) ^{2}}{2{EI}_{y} }} \right] +\frac{{l}_3^3 {{\varvec{e}}}_3^{\mathrm{T}} {{\varvec{R}}}_{{L,i}}^{-1} {{\varvec{L}}}_{{B,i,T}}^{c} {\varvec{\lambda }}_{{B,i}} }{3{EI}_{y} }+\frac{{l}_3^2 {{\varvec{e}}}_1^{\mathrm{T}} {{\varvec{R}}}_{{L,i}}^{-1} {{\varvec{L}}}_{{B,i,R}}^{{\varvec{c}}} {\varvec{\lambda }}_{{B,i}} }{2{EI}_{y} } \\ \delta _{{i,R,}z_{{C,i}} } ={{\varvec{e}}}_4^\mathrm{T} {{\varvec{R}}}_{{L,i}}^{-1} \left( {\frac{-{{\varvec{R}}}_{{L,i}} {{\varvec{I}}}_{{L,i}}^{l} {{\varvec{R}}}_{{L,i}}^\mathrm{T} {\dot{{\varvec{\omega }}}}_{{L,i}} -{\tilde{{\varvec{\omega }}}}_{{L,i}} {{\varvec{R}}}_{{L,i}} {{\varvec{I}}}_{{L,i}}^{l} {{\varvec{R}}}_{{L,i}}^{\mathrm{T}} {\varvec{\omega }} _{{L,i}} }{{GI}_{z} }\left( {{l}_3 -{r}_{{L,}2,{i}} } \right) +\frac{{l}_3 {{\varvec{L}}}_{{B,i,R}}^{c} {\varvec{\lambda }}_{{B,i}} }{{GI}_{z} }} \right) \\ \end{array}} \right. ({i}=1,2) \end{aligned}$$

(42)

where ${I}_{y}$ and ${I}_{z}$ are the area of inertial moments about the body fixed frame ${C}_{i}$ -${{\varvec{x}}}_{{C,i}} {{\varvec{y}}}_{{C,i}} {{\varvec{z}}}_{{C,i}}$, while E and G are Young modulus and shear modulus. Therefore, the compatible deformation conditions can be given by:

$$\begin{aligned} \left\{ {\begin{array}{l} \delta _{1,{T,}{{\varvec{u}}}} =\delta _{2{,T,}{{\varvec{u}}}} \\ \delta _{1{,R,}z_{{C,i}} } =\delta _{2{,R,}z_{{C,i}} } \\ \end{array}} \right. \end{aligned}$$

(43)

Substituting Eq. (43) into (39), constraint force along u and moment about w of revolute joint ${B}_1$ can be represented by other constraint wrenches of revolute joint ${B}_1$ and ${B}_2$; hence, the system dynamic model with the constraints can be derived as:

$$\begin{aligned} {{{\varvec{M}}}}'{{\varvec{T}}}{\ddot{\varvec{\eta }}}+{{{\varvec{M}}}}'{\dot{{\varvec{T}}}}{\dot{{\varvec{\eta }}} }+{{{\varvec{W}}}}'{{\varvec{T}}}\dot{{\varvec{\eta }}}-{{{\varvec{G}}}}'{{\varvec{g}}}={{{\varvec{C}}}}'_\lambda {{\varvec{\lambda }}}' \end{aligned}$$

(44)

where ${{{\varvec{M}}}}'$, ${{{\varvec{W}}}}'$ and ${{{\varvec{G}}}}'$ represent the reformulated inertial matrix, angular velocity matrix, the gravity matrix, respectively, while ${{{\varvec{C}}}}'_\lambda$ and ${\varvec{{\lambda }}}'$ are the reformulated constraint transformation matrix and the wrench and can be given by:

$$\begin{aligned} \left\{ {\begin{array}{l} {{\varvec{M}}}'={{\varvec{M}}}+\Delta {{\varvec{M}}},{{\varvec{W}}}'={{\varvec{W}}}+\Delta {{\varvec{W}}},{{{\varvec{G}}}}'={{\varvec{G}}}\\ \quad +\Delta {{\varvec{G}}},{{{\varvec{C}}}}'_\lambda ={{\varvec{C}}}_\lambda +\Delta {{\varvec{C}}}_\lambda \\ {{\varvec{\lambda }}}{'}=\left[ {\varvec{\lambda }}_{{{\varvec{P}}},1}^{\mathrm{T}} ,{\varvec{\lambda }}_{{{\varvec{A}}},1}^{\mathrm{T}} ,{\varvec{{\lambda }}}{'}_{{{\varvec{B}}},1}^{\mathrm{T}} ,{\varvec{\lambda }}_{{{\varvec{P}}},2}^{\mathrm{T}} ,{\varvec{\lambda }}_{{{\varvec{A}}},2}^{\mathrm{T}} ,{\varvec{\lambda }}_{{{\varvec{B}}},2}^{\mathrm{T}} ,{\varvec{\lambda }}_{{{\varvec{P}}},3}^{\mathrm{T}} ,{\varvec{\lambda }}_{{{\varvec{A}}},3}^{\mathrm{T}} ,\right. \\ \qquad \left. {\varvec{\lambda }}_{{{\varvec{B}}},3}^{\mathrm{T}} ,{{\varvec{f}}}^{{a}\mathrm{T}} \right] ^{\mathrm{T}},{\varvec{{\lambda }}}'_{{B},1} ={\varvec{\lambda }}_{{B},1} (2:4) \\ \end{array}} \right. \end{aligned}$$

where $\Delta {{\varvec{M}}}$, $\Delta {{\varvec{W}}}$, $\Delta {{\varvec{G}}}$, and $\Delta {{\varvec{C}}}_\lambda$ are the increase due to the substitution of constraint force along u and moment about w of revolute joint ${B}_1$, details of which are in the appendix.

Hence, the closed form dynamic models with and without constrained forces/moments of the over-constrained PMs with parasitic motion are established. For Eq. (41), the constrained forces/moments are eliminated, and it is quite straightforward and computational efficient for the dynamic performance analysis, as well as the control scheme design. For Eq. (44), the actuation forces and constrained forces/moments can be computed simultaneously, and it’s essential for structure design. Also, the proposed method utilized the concept of modular dynamic modeling; hence, the clearance and friction can be easily integrated into the system equation; in future studies, the rigid-flexible coupling dynamic model will also be established to obtain rigid-flexible coupling dynamic characteristics and an accurate constraint forces/moments.

4 Dynamic performance analysis of the 2PUR-PSR parallel manipulator

Based on the dynamic model established in Eq. (41), the dynamic performance is investigated in this section. The concept of dynamic manipulability ellipsoid (DME) [30] proposed by Yoshikawa is employed to evaluate the uniformity of the PM’s ability in changing the MP’s position/orientation under the stated driving forces. Then, the distribution and the characteristics of the DME index in the preset workspace are also studied in this section.

The dynamic Eq. (41) can be reformulated as:

$$\begin{aligned} \left( {{{\varvec{T}}}^{\mathrm{T}}{{\varvec{w}}}_{{CS}}^{a} } \right) ^{-1}{{\varvec{T}}}^{\mathrm{T}}{{\varvec{MTK}}}_{p}^{+} {\dot{\tilde{{\varvec{t}}}}}_{p} ={\tilde{{{\varvec{f}}}}}^{{a}} \end{aligned}$$

(45)

where ${{\varvec{K}}}_{p}^{+}$ denotes the pseudoinverse of ${{\varvec{K}}}_{p}$, ${\tilde{{\varvec{f}}}}^{{a}}={{\varvec{f}}}^{{a}}-\left( {{{\varvec{T}}}^{\mathrm{T}}{{\varvec{w}}}_{{CS}}^{a} } \right) ^{-1}\left( {{{\varvec{T}}}^{\mathrm{T}}\left( {{{\varvec{WT}}}+{{\varvec{M}}}{\dot{{\varvec{T}}}}} \right) {\dot{\varvec{\eta }}}-{{\varvec{T}}}^{\mathrm{T}}{{\varvec{Gg}}}} \right)$ and ${\dot{\tilde{{\varvec{t}}}}}_{p} ={\dot{{{\varvec{t}}}}}_{p} -{\dot{{{\varvec{K}}}}}_{p} {\dot{\varvec{\eta }}}$ are the generalized driving force and the MP’s acceleration of the PM, respectively.

The set of all ${\dot{\tilde{{\varvec{t}}}}}_{p}$ which is realizable by a joint driving force such $\left\| {{\tilde{{\varvec{f}}}}^{{a}}} \right\| \le 1$ is an ellipsoid described as:

$$\begin{aligned} {\dot{\tilde{{\varvec{t}}}}}_{p}^{\mathrm{T}} {\tilde{{{\varvec{J}}}}}^{+\mathrm{T}}{\tilde{{{\varvec{M}}}}}^{{T}}{\tilde{{{\varvec{M}}}}}{\tilde{{{\varvec{J}}}}}^{+}{\dot{\tilde{{\varvec{t}}}}}_{p} \le 1 \end{aligned}$$

(46)

where ${\tilde{{{\varvec{M}}}}} = \left( {{{\varvec{T}}}^{\mathrm{T}}{{\varvec{w}}}_{{CS}}^{a} } \right) ^{-\mathrm{T}}{{\varvec{T}}}^{\mathrm{T}}{{\varvec{MT}}}\left( { {{\varvec{T}}}^{\mathrm{T}}{{\varvec{w}}}_{{CS}}^{a} } \right) ^{-1}$ denotes the reduced inertial matrix of the system, and ${\tilde{{{\varvec{J}}}}} = {{\varvec{K}}}_{p} \left( {{{\varvec{T}}}^{\mathrm{T}}{{\varvec{w}}}_{{CS}}^{a} } \right) ^{-1}$ is the Jacobian matrix associating the PM’s actuated joints with the MP.

However, manipulators usually involve translational and rotational motions; hence, the DME should be decomposed into corresponding aspects, and two ellipsoids will be calculated to evaluate the translational and rotational DME:

$$\begin{aligned} \left\{ {\begin{array}{l} {\dot{\tilde{{\varvec{t}}}}}_{{pT}}^{\mathrm{T}} {\tilde{{{\varvec{J}}}}}_{T}^{+\mathrm{T}} {\tilde{{{\varvec{M}}}}}^{{T}}{\tilde{{{\varvec{M}}}}}{{{\tilde{J}}}}_{T}^+ {\dot{\tilde{{\varvec{t}}}}}_{{pT}} \le 1 \\ {\dot{\tilde{{\varvec{t}}}}}_{{pR}}^{\mathrm{T}} {\tilde{{{\varvec{J}}}}}_{R}^{+\mathrm{T}} {\tilde{{{\varvec{M}}}}}^{{T}}{\tilde{{{\varvec{M}}}}}{\tilde{{{\varvec{J}}}}}_{R}^+ {\dot{\tilde{{\varvec{t}}}}}_{{pR}} \le 1 \\ \end{array}} \right. \end{aligned}$$

(47)

where ${\dot{\tilde{{\varvec{t}}}}}_{{p,T}}$ and ${\dot{\tilde{{\varvec{t}}}}}_{{p,R}}$ are the translational and rotational aspect of ${\dot{\tilde{{\varvec{t}}}}}_{p}$.

From kinematic analysis, the manipulator has one translational and two rotational motions with two translational parasitic motions; hence, the dynamic performance might be different when the manipulator moves in different configurations. To evaluate the isotropic property of dynamic manipulability, the condition number and the mean condition number of ${\tilde{{{\varvec{M}}}}}{\tilde{{{\varvec{J}}}}}_{T}^+$ and ${\tilde{{{\varvec{M}}}}}{\tilde{{{\varvec{J}}}}}_{R}^+ \leftarrow$ are adopted as the measure of the manipulator’s dynamic performance as:

$$\begin{aligned} \left\{ {\begin{array}{l} {w}_{T} =\frac{\sigma _{{T,}2} }{\sigma _{{T,}1} }{,}{w}_{R} =\frac{\sigma _{{R,}2} }{\sigma _{{R,}1} } \\ {w}_{{GT}} =\frac{\int {{w}_{T} {dS}_{z} } }{{S}_{z} }{,}{w}_{{GR}} =\frac{\int {{w}_{R} {dS}_{z} } }{{S}_{z} } \\ \end{array}} \right. \end{aligned}$$

(48)

where ${w}_{T}$ and ${w}_{R}$ denote the condition number of ${\tilde{{{\varvec{M}}}}}{\tilde{{{\varvec{J}}}}}_{T}^+$ and ${\tilde{{{\varvec{M}}}}}{\tilde{{{\varvec{J}}}}}_{R}^+$, respectively, $\sigma _{{T,}2}$ and $\sigma _{{T,}1}$ are the nonzero singular value of ${\tilde{{{\varvec{M}}}}}{\tilde{{{\varvec{J}}}}}_{T}^+$, $\sigma _{{R,}2}$ and $\sigma _{{R,}1}$ are the nonzero singular value of ${\tilde{{{\varvec{M}}}}}{\tilde{{{\varvec{J}}}}}_{R}^+$, and $\sigma _{{T,}2} \le \sigma _{{T,}1}$, $\sigma _{{R,}2} \le \sigma _{{R,}1}$, while ${w}_{{GR}}$ and ${w}_{{GT}}$ are the mean value of ${w}_{T}$ and ${w}_{R}$ for the given height z.

Fig. 3

Computed torques of ADAMS model and the proposed model

Table 1 The mass and inertial tensors of the parallel manipulator

5 Numerical study of dynamic response and performance

Based on Eqs. (41) and (44), the actuation forces and the constraint forces/moments can be calculated for the given trajectory. Also, the dynamic performance can be investigated based on the deduced DME (48). This section will verify the correctness of the dynamic model and investigate the dynamic performance of the PM.

In the numerical simulation, the preset values of the parallel manipulator’s kinematic parameters are given by ${l}_1 =30\hbox { mm},{l}_2 =35\hbox { mm}$ for the size of the MP, and ${l}_3 =90\hbox { mm},{l}_4 =95\hbox { mm}$ for the length of the links, and other geometrical and inertial parameters are listed in Table 1. In addition, the inertial tensors are measured in the body fixed frame located in the corresponding mass center. The following trajectory was tested for the dynamic model:

$$\begin{aligned} \left\{ {\begin{array}{l} {z}=60\left( {{6{t}^{5}}/{{t}_{{\varvec{d}}}^5 }-{15{t}^{4}}/{{t}_{{\varvec{d}}}^4 }+{10{t}^{3}}/{{t}_{{\varvec{d}}}^3 }} \right) +20 \\ \uptheta ={20\uppi \left( {{6{t}^{5}}/{{t}_{{\varvec{d}}}^5 }-{15{t}^{4}}/{{t}_{{\varvec{d}}}^4 }+{10{t}^{3}}/{{t}_{{\varvec{d}}}^3 }} \right) }/{180}-{10\uppi }/{180} \\ \upphi ={20\uppi \left( {{6{t}^{5}}/{{t}_{{\varvec{d}}}^5 }-{15{t}^{4}}/{{t}_{{\varvec{d}}}^4 }+{10{t}^{3}}/{{t}_{{\varvec{d}}}^3 }} \right) }/{180}-{10\uppi }/{180} \\ \end{array}} \right. \end{aligned}$$

(49)

where ${t}_{d}$ denotes the desired duration time, and ${t}_{d} =0.5\hbox { s}$.

Based on the given trajectory of the MP, the required joint space trajectory can be calculated using the inverse kinematic model, with which the required actuation forces, the constrained forces/moments and the compatible deformation can be calculated through Eq.  (41) and (44), respectively. The computed actuation forces using the proposed model and the commercial software ADAMS are shown in Fig. 3, and it is evident that the force profiles of the proposed model are the same as the ADAMS model, indicating correctness of the proposed model, which could be employed in the dynamic performance evaluation and accurate dynamic based control design.

Fig. 4

Active and constraint forces and moments in the proposed model

Fig. 5

Compatible deformation of over-constraints

Fig. 6

DME of the parallel manipulator

The constrained forces/moments and the actuation forces computed with the Eq. (48) were illustrated in Fig. 4; the results show that the for the prismatic joints, the peak actuation forces of the first and second limbs are nearly 250N and 190N, respectively, while the value for the third is about 60N. In addition, peak reaction moments of the first and second limbs are much larger than the third limb, which might be explained by the fact that the spherical joint for the third limb cannot bear moments while the universal joints for the first and second limbs could bear moment around the links. Also, reaction forces and moments of different directions show significant differences; therefore, the selection of the linear actuators and joints should be paid attention to the issues.

The compatible deformations are calculated from Eq. (43) and shown in Fig. 5, peak translational deformation along u direction is around 0.0148 mm, and the value for rotational deformation about w is 0.01rad. Hence, for high precision operations such as precision positioning and machining, the compatible deformations cannot be neglected.

As indicated above, the manipulator has one translational and two rotational motions with two translational parasitic motions; the range of z is selected [20 mm, 80 mm], and for the 2DOF rotational motion, a rectangular area is selected in the range of $[-0.175~\hbox {rad},~0.175 \hbox {rad}]\times [{-0.175 ~\hbox {rad},~0.175 \hbox { rad}}]$ for $\theta$ and $\phi$. Thus, the parasitic motions can be calculated from the given independent variables.

As indicated in Fig. 6, the dynamic index ${w}_{R}$ experienced rising and decline stages, which can be explained by the fact that when the manipulator stays in the home position ($\theta =0,\phi =0$), the rotation of the MP about $\theta$ is driven by the two limbs, while for $\phi$, the motion is only produced by the third limb. In the meantime, it can be seen that the isotropic property becomes better when the magnitude of $q_{1}$ increases. That’s because the coupling of the motions is strengthened. Also, unlike the 2R1T parallel manipulators with similar symmetric structure without the parasitic motion [9], symmetric line of the ${w}_{R}$ and ${w}_{T}$ is not parallel with $\phi$ or $\theta$, but has certain slop degree of them; the reason is the existence of the parasitic motion that makes the translation and rotational motion highly coupled, which can also be explained by the similar trend between ${w}_{R}$ and ${w}_{T}$. In addition, with the increase in the magnitude of z to about 70 mm, the dynamic indexes ${w}_{{GT}}$ and ${w}_{{GR}}$ reach their maxima; then, they both decrease, which indicates that the dynamic index has some relevance with the kinematic and structural parameters.

Hence, in future work, the influences of the manipulator’s kinematic parameters and the bodies’ inertia properties on the index of dynamic performance will be further studied based on the modeling and analysis method proposed in this paper, and an integrated optimal design and model-based control will be carried out to improve the performance.

6 Conclusions

This paper presents a systematic dynamic modeling and performance analysis of the over-constrained PM with parasitic motions with the example of the 2PUR-PSR PM. The type and number of over-constrained forces/moments are first analyzed with the algebraic method. Based on the Newton–Euler formulation and the NOC method, the closed-form dynamic models with and without constrained forces/moments are established and have been validated by means of numerical simulations with the comparison of generally accepted commercial software. The concept of DME is then adopted to evaluate the dynamic manipulability performance of the 2PUR-PSR PM. And the distribution characteristics of both translational and rotational condition number and their mean values within the workspace of the parallel manipulator are studied, which indicated that the dynamic performance can be enhanced by kinematic and structure optimizations. The proposed dynamic modeling and performance analysis method can also be applied to other PMs with parasitic motion or over-constraints.

Appendix

$$\begin{aligned}&{{\varvec{C}}}_\lambda ^O =\left( {{\begin{array}{c@{\quad }c} {\frac{{l}_3^3 {{\varvec{e}}}_3^{{\varvec{T}}} {{\varvec{R}}}_{{L,}1}^{-1} {{\varvec{L}}}_{{B}_{{1,T}} }^{{\varvec{c}}} }{3}+\frac{{l}_3^2 {{\varvec{e}}}_1^{{\varvec{T}}} {{\varvec{R}}}_{{L,}1}^{-1} {{\varvec{L}}}_{{B}_{1{,{{R}}}} }^{{\varvec{c}}} }{2}}&{} {-\frac{{l}_3^3 {{\varvec{e}}}_3^{{\varvec{T}}} {{\varvec{R}}}_{{L,}2}^{-1} {{\varvec{L}}}_{{B}_{2{,T}} }^{{\varvec{c}}} }{3}-\frac{{l}_3^2 {{\varvec{e}}}_1^{{\varvec{T}}} {{\varvec{R}}}_{{L,}2}^{-1} {{\varvec{L}}}_{{B}_{{2,{{R}}}} }^{{\varvec{c}}} }{2}} \\ {{l}_3 {{\varvec{e}}}_4^T {{\varvec{R}}}_{{L,1}}^{-1} {{\varvec{L}}}_{{B}_{{1,{{R}}}} }^{{\varvec{c}}} }&{} {{-l}_3 {{\varvec{e}}}_4^T {{\varvec{R}}}_{{L,2}}^{-1} {{\varvec{L}}}_{{B}_{{2,{{R}}}} }^{{\varvec{c}}} } \\ \end{array} }} \right) \\&{{\varvec{C}}}_{M}^{O} =\left( {{\begin{array}{c@{\quad }c} {\left[ {\frac{\left( {{l}_3 -{r}_{{L,}2,1} } \right) ^{3}}{3}+\frac{{r}_{{L,}2,1} \left( {{l}_3 -{r}_{{L,}2,1} } \right) ^{2}}{2}} \right] {{\varvec{e}}}_3^{{\varvec{T}}} {{\varvec{R}}}_{{L,}1}^{-1} {m}_{{L,}1} }&{} {\mathbf{0}_{1\times 3} } \\ {\mathbf{0}_{1\times 3} }&{} {{{\varvec{e}}}_4^{{\varvec{T}}} {{\varvec{R}}}_{{L,}1}^{-1} {{\varvec{R}}}_{{L,}1} {{\varvec{I}}}_{{L,}1}^{l} {{\varvec{R}}}_{{L,}1}^{T} } \\ \end{array} }} \right. \\&\quad \left. {{\begin{array}{c@{\quad }c} {-\left[ {\frac{\left( {{l}_3 -{r}_{{L,}2,2} } \right) ^{3}}{3}+\frac{{r}_{{L,}2,2} \left( {{l}_3 -{r}_{{L,}2,2} } \right) ^{2}}{2}} \right] {{\varvec{e}}}_3^{{\varvec{T}}} {{\varvec{R}}}_{{L,2}}^{-1} {m}_{{L,2}} }&{} {\mathbf{0}_{1\times 3} } \\ {\mathbf{0}_{1\times 3} }&{} {-{{\varvec{e}}}_4^{{\varvec{T}}} {{\varvec{R}}}_{{L,}2}^{-1} {{\varvec{R}}}_{{L,}2} {{\varvec{I}}}_{{L,}2}^{l} {{\varvec{R}}}_{{L,}2}^{T} } \\ \end{array} }} \right) \\&{{\varvec{C}}}_G^{{\varvec{O}}} =\left( {\begin{array}{c} \left[ {\frac{\left( {{l}_3 -{r}_{{L}_{2,1} } } \right) ^{3}}{3}+\frac{{r}_{{L}_{2,1} } \left( {{l}_3 -{r}_{{L}_{2,1} } } \right) ^{2}}{2}} \right] e_3^{{\varvec{T}}} {{\varvec{R}}}_{{L,}1}^{-1} {m}_{{L,}1} -\left[ {\frac{\left( {{l}_3 -{r}_{{L}_{2,2} } } \right) ^{3}}{3}+\frac{{r}_{{L}_{2,2} } \left( {{l}_3 -{r}_{{L}_{2,2} } } \right) ^{2}}{2}} \right] {{\varvec{e}}}_3^{{\varvec{T}}} {{\varvec{R}}}_{{L,}2}^{-1} {m}_{{L,}2} \\ \mathbf{0}_{1\times 3} \\ \end{array}} \right) \\&{{\varvec{C}}}_W^{{\varvec{O}}} =\left( {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0&{} 0&{} 0&{} 0 \\ 0&{} {{{\varvec{e}}}_4^{{\varvec{T}}} {{\varvec{R}}}_{{L,}1}^{-1} {\tilde{{\varvec{\omega }}}}_{{L,}1} {{\varvec{R}}}_{{L,}1} {{\varvec{I}}}_{{L,}1}^{l} {{\varvec{R}}}_{{L,}1}^{T} }&{} 0&{} {-{{\varvec{e}}}_4^{{\varvec{T}}} {{\varvec{R}}}_{{L,}2}^{-1} {\tilde{{\varvec{\omega }}}}_{{L,}2} {{\varvec{R}}}_{{L,}2} {{\varvec{I}}}_{{L,}2}^{l} {{\varvec{R}}}_{{L,}2}^{T} } \\ \end{array} }} \right) \end{aligned}$$

$$\begin{aligned}&{{\varvec{C}}}_{\lambda ,1}^{{\varvec{O}}} =\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {{{\varvec{C}}}_{\lambda ,1}^{{\varvec{O}}} \left( {:,1} \right) }&{} {{{\varvec{C}}}_{\lambda ,1}^{{\varvec{O}}} \left( {:,5} \right) } \\ \end{array} }} \right] \\&{{\varvec{C}}}_{\lambda ,2}^{{\varvec{O}}} =\left[ {{\begin{array}{l@{\quad }l} {{{\varvec{C}}}_{\lambda ,1}^{{\varvec{O}}} \left( {:,2:4} \right) }&{} {{{\varvec{C}}}_{\lambda ,1}^{{\varvec{O}}} \left( {:,6:10} \right) } \\ \end{array} }} \right] \\&{{\varvec{C}}}_{\lambda ,1,2}^{{\varvec{O}}} =-\left( {{{\varvec{C}}}_{\lambda ,1}^{{\varvec{O}}} } \right) ^{-1}{{\varvec{C}}}_{\lambda ,2}^{{\varvec{O}}} , \quad {{\varvec{C}}}_{{M},1,2}^{O} =\left( {{{\varvec{C}}}_{\lambda ,1}^{O} } \right) ^{-1}{{\varvec{C}}}_{M}^{O} , {{\varvec{C}}}_{{W},1,2}^{O}\\&\quad =\left( {{{\varvec{C}}}_{\lambda ,1}^{O} } \right) ^{-1}{{\varvec{C}}}_{W}^{O} , {{\varvec{C}}}_{{G},1,2}^{O} =\left( {{{\varvec{C}}}_{\lambda ,1}^{O} } \right) ^{-1}{{\varvec{C}}}_{G}^{O}\\&\Delta {{\varvec{G}}}=\left( {{\begin{array}{l@{\quad }l} {{{\varvec{C}}}_\lambda }&{} {{{\varvec{w}}}_{{CS}}^{a} } \\ \end{array} }} \right) \left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {\mathbf{0}_{9\times 3} }&{} {{{\varvec{C}}}_{{G},1,2}^{{{\varvec{o}}}\mathrm{T}} \left( {:,1} \right) }&{} {\mathbf{0}_3 }&{} {{{\varvec{C}}}_{{G},1,2}^{{{\varvec{o}}}\mathrm{T}} \left( {:,2} \right) }&{} {\mathbf{0}_{3\times 30} } \\ \end{array} }} \right) ^{\mathrm{T}}\\&\Delta {{\varvec{M}}}=\left( {{\begin{array}{l@{\quad }l} {{{\varvec{C}}}_\lambda }&{} {{{\varvec{w}}}_{{CS}}^{a} } \\ \end{array} }} \right) \\&\left( {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\mathbf{0}_{9\times 6} }&{} {\mathbf{0}_{9\times 6} }&{} {\mathbf{0}_{9\times 6} }&{} {\mathbf{0}_{9\times 6} }&{} {\mathbf{0}_{9\times 18} } \\ {\mathbf{0}_{1\times 6} }&{} {{{\varvec{C}}}_{{M},1,2}^{{\varvec{O}}} \left( {1,1:6} \right) }&{} {\mathbf{0}_{1\times 6} }&{} {{{\varvec{C}}}_{{M},1,2}^{{\varvec{O}}} \left( {1,7:12} \right) }&{} {\mathbf{0}_{1\times 18} } \\ {\mathbf{0}_{3\times 6} }&{} {\mathbf{0}_{3\times 6} }&{} {\mathbf{0}_{3\times 6} }&{} {\mathbf{0}_{3\times 6} }&{} {\mathbf{0}_{3\times 18} } \\ {\mathbf{0}_{1\times 6} }&{} {{{\varvec{C}}}_{{M},1,2}^{{\varvec{O}}} \left( {2,1:6} \right) }&{} {\mathbf{0}_{1\times 6} }&{} {{{\varvec{C}}}_{{M},1,2}^{{\varvec{O}}} \left( {2,7:12} \right) }&{} {\mathbf{0}_{1\times 18} } \\ {\mathbf{0}_{30\times 6} }&{} {\mathbf{0}_{30\times 6} }&{} {\mathbf{0}_{30\times 6} }&{} {\mathbf{0}_{30\times 6} }&{} {\mathbf{0}_{30\times 18} } \\ \end{array} }} \right) ,\\&\Delta {{\varvec{C}}}_\lambda = \left( {{\begin{array}{l@{\quad }l} {{{\varvec{C}}}_\lambda }&{} {{{\varvec{w}}}_{{CS}}^{a} } \\ \end{array} }} \right) \\&\quad \left( {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {E_9 }&{} {\mathbf{0}_{9\times 3} }&{} {\mathbf{0}_{9\times 9} }&{} {\mathbf{0}_{9\times 5} }&{} {\mathbf{0}_{9\times 16} } \\ {\mathbf{0}_{1\times 9} }&{} {{{\varvec{C}}}_{\lambda ,1,2}^{{\varvec{O}}} \left( {1,1:3} \right) }&{} {\mathbf{0}_{1\times 9} }&{} {{{\varvec{C}}}_{\lambda ,1,2}^{{\varvec{O}}} \left( {1,4:8} \right) }&{} {\mathbf{0}_{1\times 16} } \\ {\mathbf{0}_{3\times 9} }&{} {E_3 }&{} {\mathbf{0}_{3\times 9} }&{} {\mathbf{0}_{3\times 5} }&{} {\mathbf{0}_{3\times 16} } \\ {\mathbf{0}_{1\times 9} }&{} {{{\varvec{C}}}_{\lambda ,1,2}^{{\varvec{O}}} \left( {2,1:3} \right) }&{} {\mathbf{0}_{1\times 9} }&{} {{{\varvec{C}}}_{\lambda ,1,2}^{{\varvec{O}}} \left( {2,4:8} \right) }&{} {\mathbf{0}_{1\times 16} } \\ {\mathbf{0}_{30\times 2} }&{} {\mathbf{0}_{30\times 3} }&{} {\mathbf{0}_{30\times 2} }&{} {\mathbf{0}_{30\times 5} }&{} {{{\varvec{E}}}_{30} } \\ \end{array} }} \right) \,,\\&\Delta {{\varvec{W}}} =\left( {{\begin{array}{l@{\quad }l} {{{\varvec{C}}}_\lambda }&{} {{{\varvec{w}}}_{{CS}}^{a} } \\ \end{array} }} \right) \\&\quad \left( {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\mathbf{0}_{9\times 6} }&{} {\mathbf{0}_{9\times 6} }&{} {\mathbf{0}_{9\times 6} }&{} {\mathbf{0}_{9\times 6} }&{} {\mathbf{0}_{9\times 18} } \\ {\mathbf{0}_{1\times 6} }&{} {{{\varvec{C}}}_{{W},1,2}^{{\varvec{O}}} \left( {1,1:6} \right) }&{} {\mathbf{0}_{1\times 6} }&{} {{{\varvec{C}}}_{{W},1,2}^{{\varvec{O}}} \left( {1,7:12} \right) }&{} {\mathbf{0}_{1\times 18} } \\ {\mathbf{0}_{3\times 6} }&{} {\mathbf{0}_{3\times 6} }&{} {\mathbf{0}_{3\times 6} }&{} {\mathbf{0}_{3\times 6} }&{} {\mathbf{0}_{3\times 18} } \\ {\mathbf{0}_{1\times 6} }&{} {{{\varvec{C}}}_{{W},1,2}^{{\varvec{O}}} \left( {2,1:6} \right) }&{} {\mathbf{0}_{1\times 6} }&{} {{{\varvec{C}}}_{{W},1,2}^{{\varvec{O}}} \left( {2,7:12} \right) }&{} {\mathbf{0}_{1\times 18} } \\ {\mathbf{0}_{30\times 6} }&{} {\mathbf{0}_{30\times 6} }&{} {\mathbf{0}_{30\times 6} }&{} {\mathbf{0}_{30\times 6} }&{} {\mathbf{0}_{30\times 18} } \\ \end{array} }} \right) \,, \end{aligned}$$