1 Introduction

Lower-mobility parallel mechanisms (PM) whose degrees of freedom (DOF) are less than six can be implemented in many applications like positioning, orientation and axis-symmetrical machining. If the appropriate architecture of a lower-mobility PM is selected and well optimized, the reduced cost for fabrication, actuation, control and maintenance can be obtained. The DELTA robot [1], Z3 head [2] and Tricept hybrid robot [3] are typical examples of success.

One important category of the lower-mobility PM is the 1T2R PM, where T denotes a translation degrees of freedom (DOF) and R a rotational DOF. The most famous 1T2R PM may be the 3-RPS PM proposed by Hunt [4]. The 3-RPS or its variant 3-PRS PM is rather useful in many applications like Z3 head in machine tool [3], telescope application [5], motion simulator [6], micro-mechanism [7] and coordinate measuring machine [8]. Thus, the 3-RPS or 3-PRS PM has attracted a lot of attention and fruitful research progress regarding kinematics analysis [9,10,11], dimensional synthesis [12,13,14,15], singularity [16, 17] and dynamics [18, 19] has been obtained.

However, as pointed out in our previous work [20], the notion 1T2R or 2R1T is not rigorous because it ignores the information on axes of rotation and the motion of the end-effector cannot simply be regarded as a commutative addition of rotations and translations. Thus, we proposed the concepts of general \(a\hbox {T}b\hbox {R}\) motion and special \(a\hbox {T}b\hbox {R}\) motion to clarify this fact.

The 3-RPS PM proposed by Hunt and its variants belongs to the general 1T2R category. The motion of its moving platform cannot always be decomposed into a product of \((1+2)\) factors, which leads to so-called parasitic motion that is the motion happening in the constrained DOF [21].

A special 1T2R motion can always be decomposed into a product of one translation and two rotations. Using Kong’s virtual chain approach [22], one can understand the three subcategories of the special 1T2R parallel mechanism in a straightforward manner. The first subcategory is called the PU-equivalent parallel mechanism, whose motion is equivalent to a PU serial chain. The family of PU-equivalent PM was first proposed by Li and Herve [20]. The second subcategory is called the UP-equivalent parallel mechanism, whose motion is equivalent to a UP serial chain. The family of UP-equivalent PM was first proposed by Kong and Gosselin [22]. The third subcategory is called the RPR-equivalent parallel mechanism, whose motion is equivalent to a RPR serial chain in which the two axes of rotation do not intersect and remain perpendicular to each other. The family of RPR-equivalent PM was first proposed by Li and Herve [23].

In addition to the general merits of parallel structure: higher rigidity, precision and lower inertia, the advantages of RPR-equivalent parallel mechanisms also include reduced couplings of translation and rotation and specified axes of rotation [20,21,22,23,24]. One RPR-equivalent PM with promising engineering potentials for fields where the manipulator needs to bear large external loads like welding, milling and processing is the 2-URR-RRU PM [23]. However, there is still a lack of investigation on the basic kinematic/dynamic characteristics and optimization of the 2-URR-RRU PM.

The organization of this paper is as follows. Section 2 makes a description of the 2-URR-RRU robot. Section 3 presents the mobility analysis of the 2-URR-RRU PM using screw theory. Sections 4 and 5 present the position and velocity analysis, respectively. In Sect. 6, the dynamic model is established and some simulation results are provided for validation. Section 7 performs the singularity analysis of the PM. Section 8 presents the workspace of the PM considering link interference, singularity and joint limits. Section 9 discusses the force/motion transmission performance of the mechanism. Section 10 conducts optimization of the architecture dimensions.

2 Description of the 2-URR-RRU robot

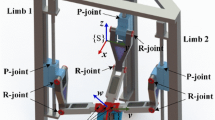
A 2-URR-RRU PM is shown in Fig. 1. The moving platform is connected to the base by three limbs, where limb 1 and limb 2 are URR limbs and limb 3 is an RRU limb. The URR limb is connected to the base by a universal joint (U joint) and to the moving platform by a revolute joint (R joint). The RRU limb is connected to the base by an R joint and to the moving platform by a U joint. Counting from the base, the second R joint of each limb is actuated. The joints are actuated by servo motors and reducers. The first revolute axis of the U joint in limb 1 is coincident with the first revolute axis of the U joint in limb 2. The other revolute axes in limb 1 are parallel to those in limb 2. The first revolute axis of the U joint in limb 3 is parallel to the revolute axis adjacent to the moving platform in limb 1 and limb 2.

Fig. 1
figure 1

CAD model of the 2-URR-RRU PM (at initial configuration)

Full size image

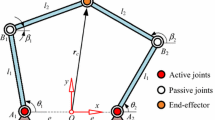
A fixed frame O-XYZ (denoted as {O}) is attached to the base, and the origin O lies at the midpoint of \(\overline{B_1 B_2 }\). The Y-axis and X-axis are set along \(\overline{B_3 O} \) and \(\overline{OB_2}\), respectively, and the Z-axis is determined by the right-hand rule. A moving frame o-uvw (denoted as {o}) is attached to the moving platform, and the origin o lies at the midpoint of \(\overline{A_1 A_2 }\). The u-axis and v-axis are set along \(\overline{A_3 O} \) and \(\overline{OA_2} \), respectively, and the w-axis is determined by the right-hand rule. A limb frame \(B_{i}-x_{i}y_{i}z_{i }\)(denoted as \(\{B_i \}, i=1,2,3\)) is attached to the ith limb. For \(i=1,2\), the \(x_{i}\)-axis and \(y_{i}\)-axis point along the two axes of U joint located at \(B_{i}\), respectively. The angle between Y-axis and \(\overline{B_i C_i}\) is denoted as \(\theta _{i1}\) and that between Y-axis and \(\overline{C_i A_i } \) as \(\theta _{i2} \). For i=3, the axes are the same as those of the frame {O}. The angle between \(x_{3}\)-axis and \(\overline{B_3 C_3 } \) is denoted as \(\theta _{31} \) and that between \(x_{3}\)-axis and \(\overline{C_3 A_3 } \) as \(\theta _{32} \). Besides, \(\triangle A_{1} A_{2} A_{3}\) and \(\triangle B_{1} B_{2} B_{3}\) are all isosceles right triangles, i.e., \(oA_{1} =oA_{2}=oA_{3}=e_{1}\) and \(OB_{1}=OB_{2} =OB_{3}=e_{2}\). The length of each link of limbs is denoted as l. The distance between the origin of the moving frame and the tool tip is defined as H.

3 Mobility analysis

Mobility analysis determines the motion pattern of a manipulator, which is indispensable in mechanical design. Screw theory [25] is used to perform the mobility analysis of the 2-URR-RRU parallel manipulator. In screw theory, a unit screw is defined by a pair of vectors

(1)

where s is a unit vector specifying the direction of the screw axis, r is the position vector of any point on the screw axis in terms of a reference coordinate system, and h denotes pitch.

A screw, , and a set of screws, , are said to be reciprocal if they satisfy the condition

(2)

where “\(\circ \)” denotes reciprocal product and represents the ith screw in the screw set. We call the screw a twist if it represents an instantaneous motion of a rigid body, or a wrench if it represents a force or a couple, or a combination of both, acting on a rigid body.

Let be a twist associated with the jth joint in the ith limb. Let be the jth constraint wrench acting on the moving platform by the ith limb. With respect to frame {O}, the position vectors of points \(A_{i}\) and \(B_{i}\) are as follows. The coordinates of \(A_{1}, A_{2}\) and \(A_{3}\) are \((x_{A_1 } ,y_{A_1 } ,z_{A_1 } ), (x_{A_2 } ,y_{A_2 } ,z_{A_2 } )\) and \((x_{A_3 } ,y_{A_3 } ,z_{A_3 } )\), respectively. The coordinates of \(B_{1}, B_{2}\) and \(B_{3}\) are \((0,-e_2 ,0), (0,e_2 ,0)\) and \((-e_2 ,0,0)\), respectively. The coordinates of \(C_{1}, C_{2}\) and \(C_{3}\) are \((x_{C_1 } ,y_{C_1 } ,z_{C_1 } ), (x_{C_2 } ,y_{C_2 } ,z_{C_2 } )\) and \((x_{C_3 } ,y_{C_3 } ,z_{C_3 } )\), respectively.

In the initial configuration, the twist system of limb 1 is given by

(3)

Using reciprocity between twists and wrenches, the wrench system of limb 1 is obtained as

(4a)

where represents a constraint couple whose axis is perpendicular to the base plane, while represents a constraint force passing through point \(B_{1}\) and parallel to X-axis. Similarly, the constraint wenches of limb 2 and limb 3 are given by:

(4b)

and

(4c)

where or represents a constraint couple whose axis is perpendicular to the base plane, while represents a constraint force passing through point \(B_{2}\) and parallel to X-axis; represents a constraint force passing through point \(A_{3}\) and parallel to Y-axis. Calculating twists that are reciprocal to Eqs. (4a), (4b) and (4c) yields

(5)

The three twists in Eq. (5) represent the three DOFs in the initial configuration, that is, one translation along the Z-axis and two rotations about the u- and Y-axes.

Because a twist or wrench is inherently instantaneous, it is necessary to analyze the mobility of the moving platform in a general configuration. We verify the configuration where the moving platform undergoes a finite translation along the Z-axis and two finite rotations about the u- and Y-axes. In a general configuration as shown in Fig. 2, the twist system of limb 1 is given by

Fig. 2
figure 2

Mobility of the PM at a general configuration

Full size image
(6)

where \(l_{11}, n_{11}\) are direction cosines of the universal joint in \(B_{1}\). The constraint wrench system of limb 1 is obtained as

(7a)

Similarly, the constraint wenches of limb 2 and limb 3 are given by:

(7b)

and

(7c)

where \(l_{22}, n_{22}, l_{33}, n_{33}\) are direction cosines of the universal joints in \(B_{2}\) and \(A_{3}\). Note that the first revolute axes in universal joint \(B_{1}\) and \(B_{2}\) are always parallel to the second revolute axis in universal joint \(A_{3}\), i.e., \((l{ }_{11},0,n_{11} )=(l{ }_{22},0,n_{22} )=(l{ }_{33},0,n_{33} )\). Thus, we have

(7d)

Calculating twists that are reciprocal to Eqs. (7a), (7b) and (7c) yields

(8)

where represents a translation along the w-axis, represents a rotation about the Y-axis, and represents a rotation about the u-axis.

4 Position analysis

4.1 Inverse kinematics

In the inverse kinematics, the position and orientation parameters of the moving platform \((\beta ,\gamma , z_{0})\) are known and the actuated joint parameters \((\theta _{12}, \theta _{22}, \theta _{32})\) are to be found. The rotation matrix of the moving frame relative to base frame is given by

$$\begin{aligned} {\varvec{R}}_A^B ={\varvec{R}}_Y (\beta ){\varvec{R}}_u (\gamma )=\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {\hbox {c}_\beta }&{} {\hbox {s}_\beta \hbox {s}_\gamma }&{} {\hbox {s}_\beta \hbox {c}_\gamma } \\ 0&{} {\hbox {c}_\gamma }&{} {-\hbox {s}_\gamma } \\ {-\hbox {s}_\beta }&{} {\hbox {c}_\beta \hbox {s}_\gamma }&{} {\hbox {c}_\beta \hbox {c}_\gamma } \\ \end{array} }} \right] , \end{aligned}$$
(9)

where “c” stands for cosine and “s” stands for sine. The position vectors of points \(A_{i}\) relative to the frame {o} and {O} are denoted as \({{\varvec{b}}}_i^A\) and \({{\varvec{b}}}_{i}\), respectively. Thus we have

$$\begin{aligned}&\left\{ {\begin{array}{l} {\varvec{b}}_1^A =[{\begin{array}{ccc} 0&{} {-e_1 }&{} 0 \\ \end{array} }]^{\mathrm{T}} \\ {\varvec{b}}_2^A =[{\begin{array}{ccc} 0&{} {e_1 }&{} 0 \\ \end{array} }]^{\mathrm{T}} \\ {\varvec{b}}_3^A =[{\begin{array}{ccc} {-e_1 }&{} 0&{} 0 \\ \end{array} }]^{\mathrm{T}} \\ \end{array}} \right. ,\end{aligned}$$
(10a)
$$\begin{aligned}&{\varvec{b}}_i ={\varvec{R}}_A^B {\varvec{b}}_i^A +{\varvec{P}}, \end{aligned}$$
(10b)

where vector \({\varvec{P}}=\left[ {{\begin{array}{ccc} {x_0 }&{} {y_0 }&{} {z_0 } \\ \end{array} }} \right] ^{\mathrm{T}}\) denotes the position vector of point o in frame {O}. The rotation matrix of frame \(\{B_i\}\) relative to frame {O} is given by

$$\begin{aligned} {\varvec{R}}_1 ={\varvec{R}}_2 =\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {\hbox {c}_\beta }&{} 0&{} {-\hbox {s}_\beta } \\ 0&{} 1&{} 0 \\ {\hbox {s}_\beta }&{} 0&{} {\hbox {c}_\beta } \\ \end{array} }} \right] , {\varvec{R}}_3 =\left[ {{\begin{array}{c@{\quad }c@{\quad }c} 1&{} 0&{} 0 \\ 0&{} 1&{} 0 \\ 0&{} 0&{} 1 \\ \end{array} }} \right] . \end{aligned}$$
(11)

The origins of limb frames represented in frame {O} are

$$\begin{aligned} \left\{ {\begin{array}{l} {\varvec{p}}_1 =\left[ {{\begin{array}{ccc} 0&{} {-e_2 }&{} 0 \\ \end{array} }} \right] ^{\mathrm{T}} \\ {\varvec{p}}_2 =\left[ {{\begin{array}{ccc} 0&{} {e_2 }&{} 0 \\ \end{array} }} \right] ^{\mathrm{T}} \\ {\varvec{p}}_3 =\left[ {{\begin{array}{ccc} {-e_2 }&{} 0&{} 0 \\ \end{array} }} \right] ^{\mathrm{T}} \\ \end{array}} \right. . \end{aligned}$$
(12)

The position vector \({{\varvec{b}}}_{i}\) expressed in frame \(\{B_i \}\) can be written as

$$\begin{aligned} \left\{ {\begin{array}{l} {\varvec{b}}_1^1 =\left[ {{\begin{array}{ccc} 0&{} {lc_{\theta _{11} } +lc_{\theta _{12} } }&{} {ls_{\theta _{11}} +ls_{\theta _{12} } } \\ \end{array} }} \right] ^{\mathrm{T}} \\ {\varvec{b}}_2^2 =\left[ {{\begin{array}{ccc} 0&{} {lc_{\theta _{21} } +lc_{\theta _{22} } }&{} {ls_{\theta _{21} } +ls_{\theta _{22} } } \\ \end{array} }} \right] ^{\mathrm{T}} \\ {\varvec{b}}_3^3 =\left[ {{\begin{array}{ccc} {lc_{\theta _{31} } +lc_{\theta _{32} } }&{} 0&{} {ls_{\theta _{31} } +ls_{\theta _{32} } } \\ \end{array} }} \right] ^{\mathrm{T}} \\ \end{array}} \right. . \end{aligned}$$
(13a)

Moreover, \({{\varvec{b}}}_{i}\) is deduced by

$$\begin{aligned} {\varvec{b}}_i ={\varvec{R}}_i {\varvec{b}}_i^i +{\varvec{p}}_i. \end{aligned}$$
(13b)

Since Eqs. (10b) and (13b) give the position vector of the same point, we have

$$\begin{aligned} \left\{ {\begin{array}{l} \hbox {s}_\beta \left( {l\hbox {s}_{\theta _{11} } +l\hbox {s}_{\theta _{12} } } \right) =e_1 \hbox {s}_\beta \hbox {s}_\gamma -x_0 \\ l\hbox {c}_{\theta _{11} } +l\hbox {c}_{\theta _{12} } =e_2 -e_1 \hbox {c}_\gamma \\ \hbox {c}_\beta \left( {l\hbox {s}_{\theta _{11} } +l\hbox {s}_{\theta _{12} } } \right) =-e_1 \hbox {c}_\beta \hbox {s}_\gamma +z_0 \\ \hbox {s}_\beta \left( {l\hbox {s}_{\theta _{21} } +l\hbox {s}_{\theta _{22} } } \right) =-e_1 \hbox {s}_\beta \hbox {s}_\gamma -x_0 \\ l\hbox {c}_{\theta _{21} } +l\hbox {c}_{\theta _{22} } =-e_2 +e_1 \hbox {c}_\gamma \\ \hbox {c}_\beta \left( {l\hbox {s}_{\theta _{21} } +l\hbox {s}_{\theta _{22} } } \right) =e_1 \hbox {c}_\beta \hbox {s}_\gamma +z_0 \\ l\hbox {c}_{\theta _{31} } +l\hbox {c}_{\theta _{32} } =e_2 -e_1 \hbox {c}_\beta +x_0 \\ l\hbox {s}_{\theta _{31} } +l\hbox {s}_{\theta _{32} } =e_1 \hbox {s}_\beta +z_0 \\ \end{array}} \right. . \end{aligned}$$
(13c)

Based on the mobility analysis and geometrical conditions, we have \({\varvec{P}}=\left[ {{\begin{array}{ccc} {z_0 \hbox {t}_\beta }&{} 0&{} {z_0 } \\ \end{array} }} \right] ^{\mathrm{T}}\), where “t” stands for tangent. Thus Eq. (13c) is simplified:

$$\begin{aligned} \left\{ {\begin{array}{l} l\hbox {s}_{\theta _{11}} +l\hbox {s}_{\theta _{12} } =a_1 ,\,l\hbox {c}_{\theta _{11} } +l\hbox {c}_{\theta _{12} } =c_1 \\ l\hbox {s}_{\theta _{21} } +l\hbox {s}_{\theta _{22} } =a_2 ,\,l\hbox {c}_{\theta _{21} } +l\hbox {c}_{\theta _{22} } =c_2 \\ l\hbox {c}_{\theta _{31} } +l\hbox {c}_{\theta _{32} } =a_3 ,\,l\hbox {s}_{\theta _{31} } +l\hbox {s}_{\theta _{32} } =c_3 \\ \end{array}} \right. , \end{aligned}$$
(13d)

where

$$\begin{aligned} a_1= & {} z_0 \hbox {sec}_\beta -e_1 \hbox {s}_\gamma ,\quad c_1 =e_2 -e_1 \hbox {c}_\gamma , \\ a_2= & {} z_0 \hbox {sec}_\beta +e_1 \hbox {s}_\gamma ,\\ c_2= & {} -e_2 +e_1 \hbox {c}_\gamma , \quad a_3 =e_2 -e_1 \hbox {c}_\beta +z_0 \hbox {t}_\beta ,\\ c_3= & {} e_1 \hbox {s}_\beta +z_0. \end{aligned}$$

Solutions to inverse kinematics can be obtained by solving Eq. (13d):

$$\begin{aligned} \left\{ {\begin{array}{l} \hbox {for}\;i=1,2: \\ \theta _{i2} =2\hbox {atan}\frac{2la_i -\sqrt{(a_i^{2}+c_i^{2})(4l^{2}-a_i^{2}-c_i^{2})}}{a_i^{2}+c_i^{2}+2lc_i} \\ \hbox {for}\;i=3: \\ \theta _{32} =2\hbox {atan}\frac{2lc_3 -\sqrt{(a_3^{2}+c_3^{2})(4l^{2}-a_3^{2}-c_3^{2})}}{a_3^{2}+c_3^{2}+2la_3 } \\ \end{array}} \right. \end{aligned}$$
(14)

Besides, the position vector of the end-effector is denoted as \({\varvec{d}}=\left[ {{\begin{array}{ccc} 0&{} 0&{} H \\ \end{array} }} \right] ^{\mathrm{T}}\). Hence its position vector expressed in {O} is given by

$$\begin{aligned} {\varvec{D}}={\varvec{P}}+{\varvec{R}}_A^B {\varvec{d}}=\left[ {{\begin{array}{c} {H\hbox {s}_\beta \hbox {c}_\gamma +z_0 \hbox {t}_\beta } \\ {-H\hbox {s}_\gamma } \\ {H\hbox {c}_\beta \hbox {s}_\gamma +z_0 } \\ \end{array} }} \right] =\left[ {{\begin{array}{c} {H_x } \\ {H_y } \\ {H_z } \\ \end{array} }} \right] . \end{aligned}$$
(15)

4.2 Forward kinematics

The forward kinematics is solving the position and orientation parameters of the moving platform \((\beta , \gamma , z_{0})\) with the preset joint parameters \((\theta _{12}, \theta _{22}, \theta _{32})\). From Eq. (13d), we have

$$\begin{aligned} a_1^{2}+c_1^{2}-2a_1 l\hbox {s}_{\theta _{12}} -2c_1 l\hbox {c}_{\theta _{12}}= & {} 0,\end{aligned}$$
(16a)
$$\begin{aligned} a_2^{2}+c_2^{2}-2a_2 l\hbox {s}_{\theta _{22} } -2c_2 l\hbox {c}_{\theta _{22} }= & {} 0,\end{aligned}$$
(16b)
$$\begin{aligned} a_3^{2}+c_3^{2}-2a_3 l\hbox {c}_{\theta _{32} } -2c_3 l\hbox {s}_{\theta _{32}}= & {} 0. \end{aligned}$$
(16c)

Square difference of Eqs. (16a) and (16c) results in

$$\begin{aligned} f(\gamma )=z_0 \hbox {sec}_\beta =\frac{u_4 +u_5 -4e_1 e_2 \hbox {c}_\gamma }{4e_1 \hbox {s}_\gamma +2l(\hbox {s}_{\theta _{12} } -\hbox {s}_{\theta _{22}})}, \end{aligned}$$
(17)

where

$$\begin{aligned}&u_4 =2le_1 \hbox {s}_\gamma (\hbox {s}_{\theta _{12} } +\hbox {s}_{\theta _{22} } ), \\&\quad u_5 =2l(\hbox {c}_{\theta _{12} } +\hbox {c}_{\theta _{22} } )(e_1 \hbox {c}_\gamma -e_2 ). \end{aligned}$$

Substituting \(f(\gamma )\) into Eq. (16a), we have

$$\begin{aligned} f_1 (\gamma )+f_2 (\gamma )=0, \end{aligned}$$
(18)

where

$$\begin{aligned} \begin{array}{l} f_1 (\gamma )=\left( {f(\gamma )-e_1 \hbox {s}_\gamma } \right) ^{2}-2l\hbox {s}_{\theta _{12} } \left( {f(\gamma )-e_1 \hbox {s}_\gamma } \right) \\ f_2 (\gamma )=\left( {e_2 -e_1 \hbox {c}_\gamma } \right) ^{2}-2l\hbox {c}_{\theta _{12} } \left( {e_2 -e_1 \hbox {c}_\gamma } \right) \\ \end{array}. \end{aligned}$$

Mathematically, Eq. (18) is a univariate equations of eight degrees, which only numerical solutions are found. Thus the forward kinematics of the 2-URR-RRU PM only has numeric solutions and no analytic solutions.

4.3 Numerical examples

Numerical examples are presented to verify the forward kinematics. The link parameters, four groups of inputs and their corresponding outputs of the PM are listed in Table 1.

The configurations of the moving platform are shown in Fig. 3.

Table 1 The parameters of the input and output links
Full size table
Fig. 3
figure 3

Four solutions of forward kinematics

Full size image

5 Velocity analysis

The Jacobian matrix transforms the rates of actuated joints to the velocity of the end-effector. Differentiating Eq. (14) with respect to time t leads to

$$\begin{aligned}&{\varvec{T}}\left[ {{\begin{array}{ccc} {{\dot{\theta }}_{12} }&{} {{\dot{\theta }}_{22} }&{} {{\dot{\theta }}_{32} } \\ \end{array} }} \right] ^{\mathrm{T}}={\varvec{G}}\left[ {{\begin{array}{lll} {{\dot{\beta }}}&{} {{\dot{\gamma }}}&{} {{\dot{z}}_0 } \\ \end{array} }} \right] ^{\mathrm{T}}, \end{aligned}$$
(19a)
$$\begin{aligned}&{\varvec{T}}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {T_{11} }&{} 0&{} 0 \\ 0&{} {T_{22} }&{} 0 \\ 0&{} 0&{} {T_{33} } \\ \end{array} }} \right] , \end{aligned}$$
(19b)

and

$$\begin{aligned} {\varvec{G}}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {G_{11} }&{} {G_{12} }&{} {G_{13} } \\ {G_{21} }&{} {G_{22} }&{} {G_{23} } \\ {G_{31} }&{} {G_{32} }&{} {G_{33} } \\ \end{array} }} \right] , \end{aligned}$$
(19c)

where

$$\begin{aligned} T_{11}= & {} a_1 l\hbox {c}_{\theta _{12} } -c_1 l\hbox {s}_{\theta _{12} } , \quad T_{22} =a_2 l\hbox {c}_{\theta _{22} } -c_2 l\hbox {s}_{\theta _{22} } ,\\ T_{33}= & {} c_3 lc_{\theta _{32} } -a_3 ls_{\theta _{32} }, \quad G_{11} =z_0 \hbox {sec}_\beta t_\beta (a_1-l\hbox {s}_{\theta _{12} } ) \\ G_{12}= & {} e_1 \hbox {s}_\gamma (c_1-l\hbox {c}_{\theta _{12} } )-e_1 \hbox {c}_\gamma (a_1-l\hbox {s}_{\theta _{12} } ),\\ G_{13}= & {} \hbox {sec}_\beta (a_1 -l\hbox {s}_{\theta _{12} } ), \quad G_{21} =z_0 \hbox {sec}_\beta \hbox {t}_\beta (a_2 -l\hbox {s}_{\theta _{22} } ),\\ G_{22}= & {} e_1 \hbox {c}_\gamma (a_2 -l\hbox {s}_{\theta _{22} } )-e_1 \hbox {s}_\gamma (c_2 -l\hbox {c}_{\theta _{22} } ),\\ G_{23}= & {} \hbox {sec}_\beta (a_2 -l\hbox {s}_{\theta _{22} } ), \\ G_{31}= & {} (e_1 \hbox {s}_\beta +z_0 \hbox {sec}_\beta ^{2})(a_3 -l\hbox {c}_{\theta _{32} } )+e_1 \hbox {c}_\beta (c_3 -l\hbox {s}_{\theta _{32} } ),\\ G_{32}= & {} 0, G_{33} =\hbox {t}_\beta (a_3 -l\hbox {c}_{\theta _{32} } )+(c_3 -l\hbox {s}_{\theta _{32} } ). \end{aligned}$$

Then, the velocity equation of the 2-URR-RRU PM in a non-singular configuration can be written as

$$\begin{aligned} \left[ {{\begin{array}{ccc} {{\dot{\beta }}}&{} {{\dot{\gamma }}}&{} {{\dot{z}}_0 } \\ \end{array} }} \right] ^{\mathrm{T}}={\varvec{G}}^{-1}{\varvec{T}}\left[ {{\begin{array}{ccc} {{\dot{\theta }}_{12} }&{} {{\dot{\theta }}_{22} }&{} {{\dot{\theta }}_{32} } \\ \end{array} }} \right] ^{\mathrm{T}}. \end{aligned}$$
(19d)

6 Dynamics analysis

Newton–Euler method with generalized coordinates [26, 27] is employed for the dynamics modeling of the parallel manipulator.

Let \({\varvec{q}}=[\beta ,\gamma ,l_0 ]^{\mathrm{T}}\) be the generalized coordinate of the system, where \(l_0 \) represents the distance between the origins of \(\{\hbox {o}\}\) and \(\{\hbox {O}\}\). We have

$$\begin{aligned} {\varvec{P}}=l_0 \left[ {{\begin{array}{l} {\hbox {s}_\beta } \\ 0 \\ {\hbox {c}_\beta } \\ \end{array} }} \right] . \end{aligned}$$
(20)

The poses of the upper and lower links in limbs 1 and 2 can be obtained as

$$\begin{aligned}&\left\{ {{\begin{array}{l} {{{\varvec{R}}}_{{U}_i }^B =\exp ({\hat{{{\varvec{e}}}}}_2 {{\beta }} )\exp (-{\hat{{{\varvec{e}}}}}_1 {{\theta }}_{i1} ) } \\ {{\varvec{r}}_{{U}_i }^B ={\varvec{p}}_i -{{\varvec{R}}}_{{U}_i}^B {{\varvec{\rho }}}_{U_i ,1} } \\ \end{array} }} \right. , \end{aligned}$$
(21)
$$\begin{aligned}&\left\{ {{\begin{array}{l} {{{\varvec{R}}}_{{L}_i }^B =\exp ({\hat{{{\varvec{e}}}}}_2 {{\beta }} )\exp (-{\hat{{{\varvec{e}}}}}_1 {{\theta }}_{i2} ) } \\ {{\varvec{r}}_{{L}_i }^B ={{\varvec{P}}}+{\varvec{R}}_A^B {\varvec{b}}_{{i}}^A -{{\varvec{R}}}_{{L}_i}^B {{\varvec{\rho }}}_{L_i ,2} } \\ \end{array} }} \right. , \end{aligned}$$
(22)

where \({{\varvec{e}}}_1 =[1,0,0]^{\mathrm{T}}, {{\varvec{e}}}_2 =[0,1,0]^{\mathrm{T}}\); \({\hat{{{\varvec{e}}}}}_{\mathrm{i}} \;({i}=1,2,3)\) is its 3 \(\times \) 3 skew-symmetrical matrix; \({{\varvec{\rho }}}_{U_i ,1}\) and \({{\varvec{\rho }}}_{U_i ,2} \) are the body-joint vectors of the universal joint and the actuated rotational joint in the upper links’ local frames, \({{\varvec{\rho }}}_{L_i ,1}\) and \({{\varvec{\rho }}}_{L_i ,2}\) are the body-joint vectors of the actuated rotational joint and the rotational joint connected to the platform in the lower links’ local frames.

The local frames of the all the links in limbs 1 and 2 are located at the centers of mass and have their x-axes parallel to the second rotational joint. The poses of the upper and lower links in limb 3 can be obtained as

$$\begin{aligned}&\left\{ {{\begin{array}{l} {{{\varvec{R}}}_{{U}_3 }^B =\exp (-{\hat{{{\varvec{e}}}}}_2 {{\theta }}_{31} ) } \\ {{\varvec{r}}_{{U}_3 }^B ={\varvec{p}}_3 -{{\varvec{R}}}_{{U}_3 }^B {{\varvec{\rho }}}_{U_3 ,1} } \\ \end{array} }} \right. , \end{aligned}$$
(23)
$$\begin{aligned}&\left\{ {{\begin{array}{l} {{{\varvec{R}}}_{{L}_3 }^B =\exp (-{\hat{{{\varvec{e}}}}}_2 {{\theta }}_{32} ) } \\ {{\varvec{r}}_{{L}_3 }^B ={{\varvec{P}}}+{\varvec{R}}_A^B {\varvec{b}}_3^A -{{\varvec{R}}}_{{L}_3 }^B {{\varvec{\rho }}}_{L_3 ,2} } \\ \end{array} }} \right. . \end{aligned}$$
(24)

Then the velocities of the moving platform and all the links can be derived by differentiating Eqs. (20)–(24).

The angular and linear velocity of the moving platform and all the links in limbs 1 and 2 can be obtained as

$$\begin{aligned}&\left\{ {{\begin{array}{l} {{{\varvec{\omega }}}_{\mathrm{A}} =({{\dot{{\varvec{R}}}}}_A^B ({{\varvec{R}}}_A^B )^{\mathrm{T}})^{\vee }={{\varvec{e}}}_2 {\dot{\beta }}+\exp ({\hat{{{\varvec{e}}}}}_2 \beta ){{\varvec{e}}}_1 {\dot{\gamma }}={{\varvec{J}}}_{A,R} {{\dot{{\varvec{q}}}}} } \\ {{{\varvec{v}}}_A ={\dot{{\varvec{P}}}}={{\varvec{J}}}_{A,T} {{\dot{{\varvec{q}}}}}} \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$
(25)
$$\begin{aligned}&\left\{ {{\begin{array}{l} {{{\varvec{\omega }}}_{\mathrm{U}_i } =({{\dot{{\varvec{R}}}}}_{\mathrm{U}_i }^B ({{\varvec{R}}}_{\mathrm{U}_i }^B ) ^{\mathrm{T}})^{\vee }={{\varvec{e}}}_2 {\dot{\beta }}-\exp ({\hat{{{\varvec{e}}}}}_2 \beta ){{\varvec{e}}}_1 {\dot{{{\theta }}}}_{\mathrm{i}1} ={{\varvec{J}}}_{\mathrm{U}_i ,R} {{\dot{{\varvec{q}}}}} } \\ {{{\varvec{v}}}_{\mathrm{U}_i } ={\dot{{\varvec{p}}}}_i -{\hat{{{\varvec{\omega }}}}}_{\mathrm{U}_i} {{\varvec{R}}}_{\mathrm{U}_i }^B {{\varvec{\rho }}}_{U_i ,1} ={{\varvec{J}}}_{\mathrm{U}_i ,T} {{\dot{{\varvec{q}}}}}} \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$
(26)
$$\begin{aligned}&\left\{ {{\begin{array}{l} {{{\varvec{\omega }}}_{\mathrm{L}_i } =({{\dot{{\varvec{R}}}}}_{\mathrm{L}_i }^B ({{\varvec{R}}}_{\mathrm{L}_i }^B )^{\mathrm{T}})^{\vee }={{\varvec{e}}}_2 {\dot{\beta }}-\exp ({\hat{{{\varvec{e}}}}}_2 \beta ) {{\varvec{e}}}_1 {\dot{\theta }}_{\mathrm{i2}} ={{\varvec{J}}}_{\mathrm{L}_i ,R} {{\dot{{\varvec{q}}}}} } \\ {{{\varvec{v}}}_{\mathrm{L}_i } ={\dot{{\varvec{P}}}}+{\hat{{{\varvec{\omega }}}}}_{\mathrm{A}} {{\varvec{R}}}_A^B {\varvec{b}}_{\mathrm{i}}^A -{\hat{{{\varvec{\omega }}}}}_{\mathrm{L}_i } {{\varvec{R}}}_{\mathrm{L}_i }^B {{\varvec{\rho }}}_{L_i ,2} ={{\varvec{J}}}_{\mathrm{L}_i ,T} {{\dot{{\varvec{q}}}}}} \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$
(27)

where \({\dot{{{\theta }}}}_{{ij}} ={{\varvec{M}}}_{ij} {{\dot{{\varvec{q}}}}}\,(i=1,2,3;j=1,2)\) could be obtained from Eqs. (13d) and (14),

$$\begin{aligned} {{\varvec{J}}}_{A,R}= & {} [{{\varvec{e}}}_2 ,\exp ({\hat{{{\varvec{e}}}}}_2 \beta ){{\varvec{e}}}_1 ,{\varvec{0}}_3 ],\\ {{\varvec{J}}}_{A,T}= & {} \left[ {{\begin{array}{c@{\quad }c@{\quad }c} {l_0 \hbox {c}_\beta }&{} 0&{} {\hbox {s}_\beta } \\ 0&{} 0&{} 0 \\ {-l_0 \hbox {s}_\beta }&{} 0&{} {\hbox {c}_\beta } \\ \end{array} }} \right] ,\\ {{\varvec{J}}}_{{U}_i ,R}= & {} [{{\varvec{e}}}_2 ,{\varvec{0}}_3 ,{\varvec{0}}_3 ]-\exp ({ \hat{{{\varvec{e}}}}}_2 \beta ){{\varvec{e}}}_1 {{\varvec{M}}}_{i1} ,\\ {{\varvec{J}}}_{{U}_i ,T}= & {} {\hat{{{\varvec{r}}}}}_{U_i ,1} {{\varvec{J}}}_{{U}_i ,R} ,\\ {{\varvec{J}}}_{{L}_i ,R}= & {} [{{\varvec{e}}}_2 ,{\varvec{0}}_3 ,{\varvec{0}}_3 ]-\exp ({\hat{{{\varvec{e}}}}}_2 \beta ){{\varvec{e}}}_1 {{\varvec{M}}}_{i2} ,\\ {{\varvec{J}}}_{{L}_i ,T}= & {} {{\varvec{J}}}_{A,T} -{\hat{{{\varvec{r}}}}}_{b_i } {{\varvec{J}}}_{A,R} +{\hat{{{\varvec{r}}}}}_{L_i ,2} {{\varvec{J}}}_{L_i ,R} ,\\ {{\varvec{r}}}_{U_i ,1}= & {} {{\varvec{R}}}_{{U}_i }^B {{\varvec{\rho }}}_{U_i ,1} , \quad {{\varvec{r}}}_{b_i } ={{\varvec{R}}}_A^B {\varvec{b}}_{{i}}^A , \quad {{\varvec{r}}}_{L_i ,2} ={{\varvec{R}}}_{{L}_i }^B {{\varvec{\rho }}}_{L_i ,2} . \end{aligned}$$

The angular and linear velocity of the links in limb 3 can be obtained as

$$\begin{aligned}&\left\{ {{\begin{array}{l} {{{\varvec{\omega }}}_{{U}_3 } =-{{\varvec{e}}}_2 {\dot{{{\theta }}}}_{31} =-{{\varvec{e}}}_2 {{\varvec{M}}}_{31} {{\dot{{\varvec{q}}}}}={{\varvec{J}}}_{{U}_3 ,R} {{\dot{{\varvec{q}}}}} } \\ {{{\varvec{v}}}_{{U}_3 } ={\dot{{\varvec{p}}}}_3 -{\hat{{{\varvec{\omega }}}}}_{{U}_3} {{\varvec{R}}}_{{U}_3 }^B {{\varvec{\rho }}}_{U_3 ,1} ={{\varvec{J}}}_{{U}_3 ,T} {{\dot{{\varvec{q}}}}}} \\ \end{array} }} \right. , \end{aligned}$$
(28)
$$\begin{aligned}&\left\{ {{\begin{array}{l} {{{\varvec{\omega }}}_{{L}_3 } =-{{\varvec{e}}}_2 {\dot{{{\theta }}}}_{32} =-{{\varvec{e}}}_2 {{\varvec{M}}}_{32} {{\dot{{\varvec{q}}}}}={{\varvec{J}}}_{{L}_3 ,R} {{\dot{{\varvec{q}}}}} } \\ {{{\varvec{v}}}_{{L}_3 } ={\dot{{\varvec{P}}}}+{\hat{{{\varvec{\omega }}}}}_{{A}} {{\varvec{R}}}_A^B {\varvec{b}}_3^A -{\hat{{{\varvec{\omega }}}}}_{{L}_3 } {{\varvec{R}}}_{{L}_3 }^B {{\varvec{\rho }}}_{L_3 ,2} ={{\varvec{J}}}_{{L}_3 ,T} {{\dot{{\varvec{q}}}}}} \\ \end{array} }} \right. ,\nonumber \\ \end{aligned}$$
(29)

where \({{\varvec{J}}}_{{U}_3 ,R} =-{{\varvec{e}}}_2 {{\varvec{M}}}_{31} , {{\varvec{J}}}_{{U}_3 ,T} ={ \hat{{{\varvec{r}}}}}_{U_3 ,1} {{\varvec{J}}}_{{U}_3 ,R}\),

$$\begin{aligned} {{\varvec{J}}}_{{L}_3 ,R}= & {} -{{\varvec{e}}}_2 {{\varvec{M}}}_{32} , \\ {{\varvec{J}}}_{{L}_3 ,T}= & {} {{\varvec{J}}}_{A,T} -{\hat{{{\varvec{r}}}}}_{b_3} { {\varvec{J}}}_{A,R} +{\hat{{{\varvec{r}}}}}_{L_3 ,2} {{\varvec{J}}}_{L_3 ,R} . \end{aligned}$$

Then the accelerations of the moving platform and all the links can be derived by differentiating Eqs. (25)–(29) as

$$\begin{aligned}&\left\{ {{\begin{array}{l} {{ {\dot{{\varvec{\omega }}}}}_{{A}} ={{\varvec{J}}}_{A,R} {{\ddot{{\varvec{q}}}}}+{{\varvec{\delta }}}_A } \\ {{{\dot{{\varvec{v}}}}}_A ={{\varvec{J}}}_{A,T} {{\ddot{{\varvec{q}}}}}+{{\varvec{\mu }}}_A } \\ \end{array} }} \right. ,\end{aligned}$$
(30)
$$\begin{aligned}&\left\{ {{\begin{array}{l} {{{\dot{{\varvec{\omega }}}}}_{{U}_i } ={{\varvec{J}}}_{{{{U}}}_i ,R} {{\ddot{{\varvec{q}}}}} +{{\varvec{\delta }}}_{{U}_i } } \\ {{{\dot{{\varvec{v}}}}}_{{U}_i } ={{\varvec{J}}}_{{U}_i ,T} {{\ddot{{\varvec{q}}}}} +{{\varvec{\mu }}}_{{U}_i } } \\ \end{array} }} \right. ,\end{aligned}$$
(31)
$$\begin{aligned}&\left\{ {{\begin{array}{l} {{{\dot{{\varvec{\omega }}}}}_{{L}_i } ={{\varvec{J}}}_{{L}_i ,R} {{\ddot{{\varvec{q}}}}} +{{\varvec{\delta }}}_{{L}_i } } \\ {{{\dot{{\varvec{v}}}}}_{{L}_i } ={{\varvec{J}}}_{{L}_i ,T} { {\ddot{{\varvec{q}}}}}+{{\varvec{\mu }}}_{{L}_i } } \\ \end{array} }} \right. , \end{aligned}$$
(32)

where \({{\varvec{\delta }}}_A ={{\dot{{\varvec{J}}}}}_{A,R} {{\dot{{\varvec{q}}}}}={ \hat{{{\varvec{e}}}}}_2 \exp ({\hat{{{\varvec{e}}}}}_2 \beta ){{\varvec{e}}}_1 {\dot{\beta }}{\dot{\gamma }}\),

$$\begin{aligned} {{\varvec{\mu }}}_A= & {} {{\dot{{\varvec{J}}}}}_{A,T} {{\dot{{\varvec{q}}}}}\\= & {} \left[ 2{c}_\beta {\dot{l}}_0 {\dot{\beta }}-{s}_\beta l_0 \dot{\beta }^{2},0,-2{s}_\beta {\dot{l}}_0 {\dot{\beta }}-{c}_\beta l_0 {\dot{\beta }}^{2}\right] ,\\ {{\varvec{\mu }}}_{{U}_i }= & {} {{\dot{{\varvec{J}}}}}_{{U}_i ,T} {\dot{{\varvec{q}}}} ={\hat{{{\varvec{r}}}}}_{U_i ,1} {{\varvec{\delta }}}_{{U}_i } -{ \hat{{{\varvec{\omega }}}}}_{{U}_i }^2 {{\varvec{r}}}_{U_i ,1} ,\\ {{\varvec{\mu }}}_{{L}_i }= & {} {{\dot{{\varvec{J}}}}}_{{L}_i ,T} {\dot{{\varvec{q}}}}\\= & {} {{\varvec{\mu }}}_A -{\hat{{{\varvec{r}}}}}_{b_i } {{\varvec{\delta }}}_A +{ \hat{{{\varvec{\omega }}}}}_A^2 {{\varvec{r}}}_{b_i } +{\hat{{{\varvec{r}}}}}_{L_i ,2} { {\varvec{\delta }}}_{{L}_i } -{\hat{{{\varvec{\omega }}}}}_{{L}_i }^2 {{\varvec{r}}}_{L_i ,2} , \end{aligned}$$

for limbs 1 and 2,

$$\begin{aligned} {{\varvec{\delta }}}_{{U}_i }= & {} {{\dot{{\varvec{J}}}}}_{{U}_i ,R} { {\dot{{\varvec{q}}}}}=-{\dot{\beta }}{\hat{{{\varvec{e}}}}}_2 \exp ({\hat{{{\varvec{e}}}}}_2 \beta ){{\varvec{e}}}_1 {{\varvec{M}}}_{i1} {{\dot{{\varvec{q}}}}}\\&-\exp ({\hat{{{\varvec{e}}}}}_2 \beta ){{\varvec{e}}}_1 {{\dot{{\varvec{M}}}}}_{i1} {{\dot{{\varvec{q}}}}},\\ {{\varvec{\delta }}}_{{L}_i }= & {} {{\dot{{\varvec{J}}}}}_{{L}_i ,R} { {\dot{{\varvec{q}}}}}=-\dot{\beta }{\hat{{{\varvec{e}}}}}_2 \exp ({\hat{{{\varvec{e}}}}}_2 \beta ){{\varvec{e}}}_1 {{\varvec{M}}}_{i2} {{\dot{{\varvec{q}}}}}\\&-\exp ({\hat{{{\varvec{e}}}}}_2 \beta ){{\varvec{e}}}_1 {{\dot{{\varvec{M}}}}}_{i2} {{\dot{{\varvec{q}}}}}, \end{aligned}$$

for limb 3,

$$\begin{aligned} {{\varvec{\delta }}}_{{U}_3 }= & {} {{\dot{{{\varvec{J}}}}}}_{{U}_3 ,R} { {\dot{{\varvec{q}}}}}=-{{\varvec{e}}}_2 {{\dot{{\varvec{M}}}}}_{31} {{\dot{{\varvec{q}}}}},\\ {{\varvec{\delta }}}_{{L}_3 }= & {} {{\dot{{\varvec{J}}}}}_{{L}_3 ,R} { {\dot{{\varvec{q}}}}}=-{{\varvec{e}}}_2 {{\dot{{\varvec{M}}}}}_{32} {{\dot{{\varvec{q}}}}}. \end{aligned}$$

The accelerations of all the parts in the PM can be assembled in a matrix form as

$$\begin{aligned} \left\{ {{\begin{array}{l} {{{\dot{{{\varvec{\omega }}}}}}={{\varvec{J}}}_R {{\ddot{{\varvec{q}}}}}+{{\varvec{\delta }}} } \\ {{{\dot{{\varvec{v}}}}}={{\varvec{J}}}_T {{\ddot{{\varvec{q}}}}}+{{\varvec{\mu }} }} \\ \end{array} }} \right. , \end{aligned}$$
(33)

where

$$\begin{aligned} {{\dot{{\varvec{\omega }}}}}= & {} \left[ {{\begin{array}{c} {{\begin{array}{c} {{{\dot{{\varvec{\omega }}}}}_{{A}} } \\ {{{\dot{{\varvec{\omega }}}}}_{{L}_1 } } \\ \end{array} }} \\ {{{\dot{{\varvec{\omega }}}}}_{{L}_2 } } \\ \vdots \\ {{{\dot{{\varvec{\omega }}}}}_{U_3 } } \\ \end{array} }} \right] _{21\times 1} ,\;{{\dot{{\varvec{v}}}}}=\left[ {{\begin{array}{c} {{\begin{array}{l} {{{\dot{{\varvec{v}}}}}_{{A}} } \\ {{{\dot{{\varvec{v}}}}}_{{L}_1 } } \\ \end{array} }} \\ {{{\dot{{\varvec{v}}}}}_{{L}_2 } } \\ \vdots \\ {{{\dot{{\varvec{v}}}}}_{U_3 } } \\ \end{array} }} \right] _{21\times 1} ,\\ {{\varvec{J}}}_R= & {} \left[ {{\begin{array}{c} {{\begin{array}{c} {{{\varvec{J}}}_{A,R} } \\ {{{\varvec{J}}}_{{{{L}}}_1 ,R} } \\ \end{array} }} \\ {{{\varvec{J}}}_{{L}_2 ,R} } \\ \vdots \\ {{{\varvec{J}}}_{U_3 ,R} } \\ \end{array} }} \right] _{21\times 3} ,\\ {{\varvec{J}}}_T= & {} \left[ {{\begin{array}{c} {{\begin{array}{c} {{{\varvec{J}}}_{A,T} } \\ {{{\varvec{J}}}_{{L}_1 ,T} } \\ \end{array} }} \\ {{{\varvec{J}}}_{{L}_2 ,T} } \\ \vdots \\ {{{\varvec{J}}}_{U_3 ,T} } \\ \end{array} }} \right] _{21\times 3} ,\;{{\varvec{\delta }}}=\left[ {{\begin{array}{c} {{\begin{array}{c} {{{\varvec{\delta }} }_{{A}} } \\ {{{\varvec{\delta }} }_{{L}_1 } } \\ \end{array} }} \\ {{{\varvec{\delta }}}_{{L}_2 } } \\ \vdots \\ {{{\varvec{\delta }}}_{U_3 } } \\ \end{array} }} \right] _{21\times 1} ,\\ {{\varvec{\mu }}}= & {} \left[ {{\begin{array}{c} {{\begin{array}{c} {{{\varvec{\mu }} }_{{A}} } \\ {{{\varvec{\mu }}}_{{L}_1 } } \\ \end{array} }} \\ {{{\varvec{\mu }}}_{{L}_2 } } \\ \vdots \\ {{{\varvec{\mu }}}_{U_3 } } \\ \end{array} }} \right] _{21\times 1} . \end{aligned}$$

The Newton–Euler formulation of the platform can be derived as

$$\begin{aligned} \left\{ {{\begin{array}{l} {{{\varvec{I}}}_A {{\dot{{\varvec{\omega }}}}}_A +{{\varvec{\varepsilon }}}_A ={{\varvec{M}}}_A^a + {{\varvec{M}}}_A^n } \\ {m_A {{\dot{{\varvec{v}}}}}_A ={{\varvec{F}}}_A^a + {{\varvec{F}}}_A^n } \\ \end{array} }} \right. , \end{aligned}$$
(34)

where \({{\varvec{I}}}_A \) represents the \(3\times 3\) inertia tensor with respect to frame \(\{o\}, m_A \) denotes the mass of the platform, \({{\varvec{M}}}_A^a \) and \({{\varvec{F}}}_A^a \) are the equivalent applied moments and forces summarized to the origin of \(\{o\}\). \({{\varvec{M}}}_A^n \) and \({{\varvec{F}}}_A^n \) are the vectors of constraint moments and forces in the joints connected to the platform, which are derived as

$$\begin{aligned} \left\{ {{\begin{array}{l} {{{\varvec{M}}}_A^n ={{\varvec{P}}}_{A_1 ,R} {{\varvec{\lambda }}}_{A_1 } +{{\varvec{P}}}_{A_2 ,R} {{\varvec{\lambda }}}_{A_2 } +{{\varvec{P}}}_{A_3 ,R} {{\varvec{\lambda }}}_{A_3 } ={{\varvec{P}}}_{A,R} {{\varvec{\lambda }}}_A } \\ {{{\varvec{F}}}_A^n ={{\varvec{P}}}_{A_1 ,T} {{\varvec{\lambda }}}_{A_1 } +{{\varvec{P}}}_{A_2 ,T} {{\varvec{\lambda }}}_{A_2 } +{{\varvec{P}}}_{A_3 ,T} {{\varvec{\lambda }}}_{A_3 } ={{\varvec{P}}}_{A,T} {{\varvec{\lambda }}}_A } \\ \end{array} }} \right. ,\nonumber \\ \end{aligned}$$
(35)

where \({{\varvec{\lambda }}}_A =[{{\varvec{\lambda }}}_{A_1 }^T ,{{\varvec{\lambda }} }_{A_2 }^T ,{{\varvec{\lambda }} }_{A_3 }^T ]^{T}\in {\mathbb {R}}^{13\times 1}\) is the ideal constraint force of all the joints connected to the platform,

$$\begin{aligned} {{\varvec{P}}}_{A,R}= & {} \left[ {{{\varvec{P}}}_{A_1 ,R} ,\;{{\varvec{P}}}_{A_2 ,R} ,\;{ {\varvec{P}}}_{A_3 ,R} } \right] \in {\mathbb {R}}^{3\times 13},\\ {{\varvec{P}}}_{A,T}= & {} [{{\varvec{P}}}_{A_1 ,T} ,\;{{\varvec{P}}}_{A_2 ,T} ,\;{{\varvec{P}}}_{A_3 ,T} ]\in {\mathbb {R}}^{3\times 13},\\ {{\varvec{P}}}_{A_1 ,R}= & {} [{\hat{{{\varvec{r}}}}}_{b_1 } ,\;{{\varvec{v}}},\;{{\varvec{w}}}]\in {\mathbb {R}}^{3\times 5}, \\ {{\varvec{P}}}_{A_2 ,R}= & {} [{\hat{{{\varvec{r}}}}}_{b_2 } ,\;{{\varvec{v}}},\;{{\varvec{w}}}]\in {\mathbb {R}}^{3\times 5}, \\ {{\varvec{P}}}_{A_3 ,R}= & {} {\hat{{{\varvec{r}}}}}_{b_3 } \in {\mathbb {R}}^{3\times 3}, \\ {{\varvec{P}}}_{A_1 ,T}= & {} {{\varvec{P}}}_{A_2 ,T} =[{{\varvec{E}}}_3 ,\;{{\varvec{0}}}_{3\times 2} ]\in {\mathbb {R}}^{3\times 5}, \\ {{\varvec{P}}}_{A_3 ,T}= & {} {{\varvec{E}}}_3 =\left[ {{\begin{array}{ccc} 1&{} &{} \\ &{} 1&{} \\ &{} &{} 1 \\ \end{array} }} \right] \in {\mathbb {R}}^{3\times 3}. \end{aligned}$$

The Newton–Euler formulation of the lower links in the limbs can be derived as

$$\begin{aligned} \left\{ {{\begin{array}{l} {{{\varvec{I}}}_{L_i } {{\dot{{\varvec{\omega }}}}}_{L_i } +{{\varvec{\varepsilon }} }_{L_i } ={{\varvec{M}}}_{L_i }^a + {{\varvec{M}}}_{L_i }^n } \\ {m_{L_i } {{\dot{{\varvec{v}}}}}_{L_i } ={{\varvec{F}}}_{L_i }^a + {{\varvec{F}}}_{L_i }^n } \\ \end{array} }} \right. , \end{aligned}$$
(36)

where \({{\varvec{M}}}_{L_i }^n \) and \({{\varvec{F}}}_{L_i }^n \) can be derived as

$$\begin{aligned} \left\{ {{\begin{array}{l} {{{\varvec{M}}}_{L_i }^n ={{\varvec{L}}}_{A_i ,R} {{\varvec{\lambda }}}_{A_i } +{{\varvec{L}}}_{C_i ,R} {{\varvec{\lambda }} }_{C_i } } \\ {{{\varvec{F}}}_{L_i }^n ={{\varvec{L}}}_{A_i ,T} {{\varvec{\lambda }}}_{A_i } +{{\varvec{L}}}_{C_i ,T} {{\varvec{\lambda }}}_{C_i } } \\ \end{array} }} \right. , \end{aligned}$$
(37)

where \({{\varvec{\lambda }}}_{C_i } \in {\mathbb {R}}^{5\times 1}\),

$$\begin{aligned} {\varvec{L}}_{A_1 ,R}= & {} -[{\hat{\varvec{r}}}_{L_1 ,2} ,\;{\varvec{v}},\;{{\varvec{w}}}]\in {\mathbb {R}}^{3\times 5},\; \\ {\varvec{L}}_{A_2 ,R}= & {} -[{\hat{\varvec{r}}}_{L_2 ,2} ,\;{\varvec{v}},\;{{\varvec{w}}}]\in {\mathbb {R}}^{3\times 5},\; \\ {\varvec{L}}_{A_3 ,R}= & {} -{\hat{\varvec{r}}}_{L_3 ,2} \in {\mathbb {R}}^{3\times 3},\; \\ {\varvec{L}}_{C_1 ,R}= & {} [{\hat{\varvec{r}}}_{L_1 ,1} ,\;{\varvec{v}}_{L_1 } ,\;{{\varvec{w}}}_{L_1 } ]\in {\mathbb {R}}^{3\times 5},\; \\ {\varvec{L}}_{C_2 ,R}= & {} [{\hat{\varvec{r}}}_{L_2 ,1} ,\;{\varvec{v}}_{L_2 } ,\;{{\varvec{w}}}_{L_2 } ]\in {\mathbb {R}}^{3\times 5},\; \\ {\varvec{L}}_{C_3 ,R}= & {} [{\hat{\varvec{r}}}_{L_3 ,1} ,\;{{\varvec{u}}}_{L_3 } ,\;{{\varvec{w}}}_{L_3 } ]\in {\mathbb {R}}^{3\times 5},\; \\ {\varvec{L}}_{A_1 ,T}= & {} -{{\varvec{P}}}_{A_1 ,T} ,\\ {\varvec{L}}_{C_i ,T}= & {} [{{\varvec{E}}}_3 ,\;{{\varvec{0}}}_{3\times 2} ]\in {\mathbb {R}}^{3\times 5}. \end{aligned}$$

The Newton–Euler formulation of the upper links in the limbs can be derived as

$$\begin{aligned} \left\{ {{\begin{array}{l} {{{\varvec{I}}}_{U_i } {{\dot{{\varvec{\omega }}}}}_{U_i } +{{\varvec{\varepsilon }} }_{U_i } ={{\varvec{M}}}_{U_i }^a + {{\varvec{M}}}_{U_i }^n } \\ {m_{U_i } {{\dot{{\varvec{v}}}}}_{U_i } ={{\varvec{F}}}_{U_i }^a + {{\varvec{F}}}_{U_i }^n } \\ \end{array} }} \right. , \end{aligned}$$
(38)

where \({{\varvec{M}}}_{U_i }^n \) and \({{\varvec{F}}}_{U_i }^n \) can be derived as

$$\begin{aligned} \left\{ {{\begin{array}{l} {{{\varvec{M}}}_{U_i }^n ={{\varvec{U}}}_{C_i ,R} {{\varvec{\lambda }}}_{C_i } +{{\varvec{U}}}_{B_i ,R} {{\varvec{\lambda }} }_{B_i } } \\ {{{\varvec{F}}}_{U_i }^n ={{\varvec{U}}}_{C_i ,T} {{\varvec{\lambda }}}_{C_i } +{{\varvec{U}}}_{B_i ,T} {{\varvec{\lambda }}}_{B_i } } \\ \end{array} }} \right. , \end{aligned}$$
(39)

where

$$\begin{aligned} {\varvec{U}}_{C_1 ,R}= & {} -[{\hat{\varvec{r}}}_{U_1 ,2} ,\;{{\varvec{v}}}_{L_1 } ,\;{{\varvec{w}}}_{L_1 } ]\in {\mathbb {R}}^{3\times 5}, \\ {\varvec{U}}_{C_2 ,R}= & {} -[{\hat{\varvec{r}}}_{U_2 ,2} ,\;{{\varvec{v}}}_{L_2 } ,\;{{\varvec{w}}}_{L_2 } ]\in {\mathbb {R}}^{3\times 5}, \\ {\varvec{U}}_{C_3 ,R}= & {} -[{\hat{\varvec{r}}}_{U_3 ,2} ,\;{{\varvec{u}}}_{L_3 } ,\;{{\varvec{w}}}_{L_3 } ]\in {\mathbb {R}}^{3\times 5}, \\ {\varvec{U}}_{B_1 ,R}= & {} {\hat{\varvec{r}}}_{U_1 ,1} \in {\mathbb {R}}^{3\times 3},\\ {\varvec{U}}_{B_2 ,R}= & {} {\hat{\varvec{r}}}_{U_2 ,1} \in {\mathbb {R}}^{3\times 3},\\ {\varvec{U}}_{B_3 ,R}= & {} [{\hat{\varvec{r}}}_{U_3 ,1} ,\;{{\varvec{e}}}_1 ,\;{{\varvec{e}}}_3 ]\in {\mathbb {R}}^{3\times 5},\\ {\varvec{U}}_{C_i ,T}= & {} -{{\varvec{L}}}_{C_i ,T}\\ {\varvec{U}}_{B_1 ,T}= & {} {{\varvec{E}}}_3 \in {\mathbb {R}}^{3\times 3},\\ {\varvec{U}}_{B_2 ,T}= & {} {{\varvec{E}}}_3 \in {\mathbb {R}}^{3\times 3},\\ {\varvec{U}}_{B_3 ,T}= & {} [{{\varvec{E}}}_3 ,\;{{\varvec{0}}}_{3\times 2} ]\in {\mathbb {R}}^{3\times 5}. \end{aligned}$$

Then the system dynamics equations can be obtained by assembling the equation of each body as

$$\begin{aligned} \left\{ {{\begin{array}{l} {{{\varvec{I}}{\dot{{\varvec{\omega }}}}}+{{\varvec{\varepsilon }}} ={{\varvec{M}}}^a + {{\varvec{M}}}^n } \\ {{{\varvec{m}}{\dot{{\varvec{v}}}}}={{\varvec{F}}}^a + {{\varvec{F}}}^n } \\ \end{array} }} \right. , \end{aligned}$$
(40)

where

$$\begin{aligned}&{{\varvec{I}}}=\left[ {{\begin{array}{cccc} {{{\varvec{I}}}_A }&{} &{} &{} \\ &{} {{{\varvec{I}}}_{L_1 } }&{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} {{{\varvec{I}}}_{U_3 } } \\ \end{array} }} \right] _{21\times 21} ,\\&{{\varvec{m}}}=\left[ {{\begin{array}{cccc} {m_A {{\varvec{I}}}_3 }&{} &{} &{} \\ &{} {m_{L_1 } {{\varvec{I}}}_3 }&{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} {m_{U_3 } {{\varvec{I}}}_3 } \\ \end{array} }} \right] _{21\times 21} ,\\&{{\varvec{\varepsilon }}}=\left[ {{\begin{array}{l} {{{\varvec{\varepsilon }}}_A } \\ {{{\varvec{\varepsilon }}}_{L_1 } } \\ \vdots \\ {{{\varvec{\varepsilon }}}_{U_3 } } \\ \end{array} }} \right] _{21\times 1} , \quad {{\varvec{M}}}^a =\left[ {{\begin{array}{l} {{{\varvec{M}}}_A^a } \\ {{{\varvec{M}}}_{L_1 }^a } \\ \vdots \\ {{{\varvec{M}}}_{U_3 }^a } \\ \end{array} }} \right] _{21\times 1} ,\\&{{\varvec{M}}}^n =\left[ {{\begin{array}{l} {{{\varvec{M}}}_A^n } \\ {{{\varvec{M}}}_{L_1 }^n } \\ \vdots \\ {{{\varvec{M}}}_{U_3 }^n } \\ \end{array} }} \right] _{21\times 1} ,\\&{{\varvec{F}}}^a =\left[ {{\begin{array}{l} {{{\varvec{F}}}_A^a } \\ {{{\varvec{F}}}_{L_1 }^a } \\ \vdots \\ {{{\varvec{F}}}_{U_3 }^a } \\ \end{array} }} \right] _{21\times 1} , \quad {{\varvec{F}}}^n =\left[ {{\begin{array}{l} {{{\varvec{F}}}_A^n } \\ {{{\varvec{F}}}_{L_1 }^n } \\ \vdots \\ {{{\varvec{F}}}_{U_3 }^n } \\ \end{array} }} \right] _{21\times 1} . \end{aligned}$$

According to the analysis above, the system dynamics equations could be obtained in the generalized coordinates form as

$$\begin{aligned} {{\varvec{\varPhi }} {\varvec{H}}{\ddot{{\varvec{q}}}}}+{{\varvec{K}}}({{\varvec{q}}}, {\dot{{\varvec{q}}}})={\bar{{{\varvec{F}}}}}^{a}+{{\varvec{Q}}{\varvec{\lambda }}}, \end{aligned}$$
(41)

where

$$\begin{aligned}&{{\varvec{\varPhi }}}=\left[ {{\begin{array}{ccc} {{\varvec{I}}}&{} \\ &{} {{\varvec{m}}} \\ \end{array} }} \right] _{42\times 42} , {{\varvec{H}}}=\left[ {{\begin{array}{l} {{{\varvec{J}}}_R } \\ {{{\varvec{J}}}_T } \\ \end{array} }} \right] _{42\times 3} ,\\&{{\varvec{K}}}=\left[ {{\begin{array}{l} {{{\varvec{I}}{\varvec{\delta }} +{\varvec{\varepsilon }} }} \\ {{{\varvec{m}}{\varvec{\mu }}}} \\ \end{array} }} \right] _{42\times 1} , {\bar{{{\varvec{F}}}}}^{a}=\left[ {{\begin{array}{l} {{{\varvec{M}}}^{a}} \\ {{{\varvec{F}}}^{a}} \\ \end{array} }} \right] _{42\times 1} ,\\&{{\varvec{\lambda }} }=\left[ {{\begin{array}{l} {{{\varvec{\lambda }} }_A } \\ {{{\varvec{\lambda }} }_C } \\ {{{\varvec{\lambda }} }_B } \\ \end{array} }} \right] _{42\times 1} ,\\&{{\varvec{Q}}}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {{{\varvec{P}}}_{A,R} }&{} 0&{} 0 \\ {{{\varvec{L}}}_{A,R} }&{} {{{\varvec{L}}}_{C,R} }&{} 0 \\ 0&{} {{{\varvec{U}}}_{C,R} }&{} {{{\varvec{U}}}_{B,R} } \\ {{{\varvec{P}}}_{A,T} }&{} 0&{} 0 \\ {{{\varvec{L}}}_{A,T} }&{} {{{\varvec{L}}}_{C,T} }&{} 0 \\ 0&{} {{{\varvec{U}}}_{C,T} }&{} {{{\varvec{U}}}_{B,T} } \\ \end{array} }} \right] _{42\times 39} ,\\&{{\varvec{L}}}_{A,{X}} =\left[ {{\begin{array}{cccc} {{{\varvec{L}}}_{A_1 ,{X}} }&{} &{} \\ &{} {{{\varvec{L}}}_{A_2 ,{X}} }&{} \\ &{} &{} {{{\varvec{L}}}_{A_3 ,{X}} } \\ \end{array} }} \right] ,\\&{{\varvec{L}}}_{{C},{X}} =\left[ {{\begin{array}{cccc} {{{\varvec{L}}}_{C_1 ,X} }&{} &{} \\ &{} {{{\varvec{L}}}_{C_2 ,{X}} }&{} \\ &{} &{} {{{\varvec{L}}}_{C_3 ,{X}} } \\ \end{array} }} \right] ,\\&{{{\varvec{U}}}}_{{C},{X}} =\left[ {{\begin{array}{cccc} {{{\varvec{U}}}_{C_1 ,X} }&{} &{} \\ &{} {{{\varvec{U}}}_{C_2 ,{X}} }&{} \\ &{} &{} {{{\varvec{U}}}_{C_3 ,{X}} } \\ \end{array} }} \right] ,\\&{{\varvec{U}}}_{{B},{X}} =\left[ {{\begin{array}{cccc} {{{\varvec{U}}}_{B_1 ,{X}} }&{} &{} \\ &{} {{{\varvec{U}}}_{B_2 ,{X}} }&{} \\ &{} &{} {{{\varvec{U}}}_{B_3 ,{X}} } \\ \end{array} }} \right] ,\\&{X}=R\;or\;T. \end{aligned}$$

Left-multiplying Eq. (41) with the transportation of the matrix \({{\varvec{H}}}\), we get

$$\begin{aligned} {{\varvec{H}}}^{{T}}{{\varvec{\varPhi }} {\varvec{H}}{\ddot{{\varvec{q}}}}}+ {{\varvec{H}}}^{{T}}{{\varvec{K}}}({{\varvec{q}}},{{\dot{{\varvec{q}}}}}) ={{\varvec{H}}}^{{T}}{\bar{{{\varvec{F}}}}}^{a}+{{\varvec{H}}}^{{T}} {{\varvec{Q}}{\varvec{\lambda }}}. \end{aligned}$$
(42)

According to the principle of virtual work, the term containing the constraint forces can be eliminated,

$$\begin{aligned} {{\varvec{H}}}^{{T}}{{\varvec{Q}}{\varvec{\lambda }}}=0. \end{aligned}$$
(43)

So the equation of motion of this PM could be derived by rewriting the above equation as

$$\begin{aligned} {{\varvec{H}}}^{{T}}{{\varvec{\varPhi }} {\varvec{H}}{\ddot{{\varvec{q}}}}}= {{\varvec{H}}}^{{T}}{\bar{{{\varvec{F}}}}}^{a}-{{\varvec{H}}}^{{T}}{{\varvec{K}}}({{\varvec{q}}}, {{\dot{{\varvec{q}}}}}). \end{aligned}$$
(44)

Both the forward and inverse dynamic analysis equation could be derived from Eq. (44) which is a set of 3 ordinary differential equations. Left-multiplying Eq. (41) with \({{\varvec{Q}}}^{T}{{\varvec{\varPhi }}}^{-1}\), we get

$$\begin{aligned} {{\varvec{Q}}}^{T}{{\varvec{\varPhi }}}^{-1}{{\varvec{Q}}{\varvec{\lambda }}}= {{\varvec{Q}}}^{T}{{\varvec{\varPhi }}}^{-1}{{\varvec{K}}}({{\varvec{q}}},{{\dot{{\varvec{q}}}}}) -{{\varvec{Q}}}^{T}{{\varvec{\varPhi }}}^{-1}{\bar{{{\varvec{F}}}}}^{a}. \end{aligned}$$
(45)

From Eq. (45), we can get the generalized constraint forces of all the ideal joints.

In order to validate the analysis above, a numerical example is presented here. The initial conditions and mass properties of the manipulator are listed in Table 2 and Table 3.

Table 2 The initial conditions of the manipulator
Full size table
Table 3 The mass properties of the manipulator
Full size table
Fig. 4
figure 4

Rotational accelerations of the platform

Full size image
Fig. 5
figure 5

Constraint forces of the U joint in limb 3

Full size image
Fig. 6
figure 6

Angles of the active joints

Full size image

Then the dynamic responses of the manipulator can be obtained using the approach above. And simulation results are illustrated throughout Figs. 4, 5 and 6. In these figures, the curves subscripted with M are obtained according to the proposed approach in the MATLAB/Simulink environment, while the curves subscripted with A are got from the commercial software Adams/view for the validation of the numerical results. These results validate the correctness of the proposed approach.

7 Singularity analysis

Singularity is an inherent property of a PM. When the PM is at a singularity configuration or in its neighborhood, it becomes uncontrollable. Usually, singularities occurring in PMs are divided into three groups: forward kinematic singularity, inverse kinematic singularity and combined singularity [25].

When \(\left| {\varvec{G}} \right| =0,\left| {\varvec{T}} \right| \ne 0\), the PM is at its forward kinematic singularity configuration. Since G is too complicated to be analytically solved, a numerical method is used for calculating \(\left| {\varvec{G}} \right| \). When the parameters are set as 50\({^{\circ }} \le \beta \le 50{^{\circ }}, -50{^{\circ }} \le \gamma \le 50 {^{\circ }}\), and \(250\,\hbox {mm}\le z_{0} \le 650\,\hbox {mm}\), \(\left| {\varvec{G}} \right| \) is not equal to zero. Hence the PM is not at a forward kinematic singularity configuration under the conditions above. This fact suggests that the forward kinematic singularity of the 2-URR-RRU PM can be avoided by selecting link parameters appropriately.

When \(\left| {\varvec{T}} \right| =0,\left| {\varvec{G}} \right| \ne 0\), the PM is at its inverse kinematic singularity configuration that is also called boundary singularity. Explicitly, when any one of \(T_{11}, T_{22} , T_{33 }\)is equal to zero, \(\left| {\varvec{T}} \right| =0\).

If \(T_{11}=0\), and \(l(a_1 c_{\theta _{12} } -c_1 s_{\theta _{12} } )=0\), we have:

$$\begin{aligned} z_0 =\hbox {c}_\beta \hbox {t}_{\theta _{12} } (e_2 -e_1 \hbox {c}_\gamma ) \end{aligned}$$
(46a)

If \(T_{22}=0\), and \(l(a_2 c_{\theta _{22} }-c_2 s_{\theta _{22} } )=0\), we have:

$$\begin{aligned} z_0 =\hbox {c}_\beta \hbox {t}_{\theta _{22} } (e_1 \hbox {c}_\gamma -e_2 ) \end{aligned}$$
(46b)

If \(T_{33}=0\), and \(l(c_3 \hbox {c}_{\theta _{32}}-a_3 \hbox {s}_{\theta _{32} } )=0\), we have:

$$\begin{aligned} z_0 =\frac{\hbox {t}_{\theta _{32} } (e_2 -e_1 \hbox {c}_\gamma )-e_1 \hbox {s}_\beta }{(1-\hbox {t}_\beta \hbox {t}_{\theta _{32} } )} \end{aligned}$$
(46c)

Thus the 2-URR-RRU PM has three inverse kinematic singular configurations, as shown in Fig. 7.

When \(\left| {\varvec{G}} \right| =0\) and \(\left| {\varvec{T}} \right| =0\), the PM is at its combined singularity configuration. Since \(\left| {\varvec{G}} \right| \ne 0\), the PM has no combined singularities.

Fig. 7
figure 7

Singular configurations. a \(T_{11}=0\), limb 1. b \(T_{22}=0\), limb 2. c \(T_{33}=0\), limb 3

Full size image

8 Workspace

The workspace of a PM is the reachable scope of the end-effector, which should satisfy the limitations of the link length, singularity, joint angles and interference of the manipulator.

Based on the architecture of the 2-URR-RRU PM, three inverse kinematic singularities should be considered. As shown in Fig. 8, the transmission angle \(\theta _i \) should satisfy \(\theta _i =\hbox {acos(}d_{\mathrm{i}} n_{\mathrm{i}} /\left| {d_{\mathrm{i}} } \right| )\le \theta _{i{\mathrm{max}}} \), where \(\theta _{imax} \) is the maximum rotation angle and is defined as \(50^{\circ }\) in this paper. Within the limit of the rotation angles, there is no interference.

The range of \(\beta \), \(\gamma \) and \(z_{0}\) is constrained as

$$\begin{aligned} \left\{ {\begin{array}{l} -\theta _{i{\mathrm{max}}} \le \beta \le \theta _{i{\mathrm{max}}} \\ -\theta _{i{\mathrm{max}}} \le \gamma \le \theta _{i{\mathrm{max}}} \\ 2l\hbox {c}_{\theta _{i{\mathrm{max}}} } \le z_0 \le \sqrt{4l^{2}-(e_2 -e_1 )^{2}} \\ \end{array}} \right. . \end{aligned}$$
(47)

Figure 9 shows the procedure for obtaining the workspace. Figure 10a shows the workspace when \(z_0 =350\hbox {mm}\). Figure 10b shows the workspace when \(z_{0}\) changes.

Fig. 8
figure 8

Angle constraints

Full size image
Fig. 9
figure 9

The procedure of workspace calculation

Full size image
Fig. 10
figure 10

Workspace of the PM

Full size image

9 Force/motion transmission performance

Force/motion transmission performance is one of the main indexes for dimension synthesis of a lower-mobility parallel manipulator. Here we use the indices proposed by Liu et al. [29, 30] to optimize the parameters of the 2-URR-RRU PM. Readers are suggested to refer to [27,28,29] for detailed information of the methodology. The force/motion transmission performance of a manipulator can be divided into two parts: input transmission performance and output transmission performance. Input transmission performance represents the efficiency of power transmitted from the actuated joints to the limbs, while output transmission performance represents the efficiency of power transmitted from limbs to the moving platform. The transmission performance indices are defined as

(48a)

and

(48b)

where \(\lambda _{i}\) and \(\eta _{i}\) denote the input transmission index and output transmission index of the ith limb, respectively, represents the input twist of the ith limb represents the transmission wrench (TWS), and represents the output twist. Obviously, the index range is from zero to one, and the bigger the index is, the better the transmission performance will be. Moreover, LTI is defined as \(\varGamma =\hbox {min}\left\{ {\lambda _i ,\eta _i } \right\} \). According to the definition of transmission angle, it is assumed that when \(\varGamma \ge 0.7\) [30] the manipulator reaches a good-transmission workspace (GTW) in which the manipulator has a good force/motion transmissibility.

Without loss of generality, we take limb 1 for example. The twist system and constraint wrench are given in Eqs. (6) and (7a), respectively. Since the actuated joint of limb 1 is an R joint, we have . The TWS, which is reciprocal to , is given by

(49)

Similarly, the constraint wrenches and TWS of the other two limbs are derived:

(50)

where

$$\begin{aligned} a= & {} l(-\hbox {s}_\beta +\hbox {s}_{\theta _{11} } ), \quad b=l(\hbox {c}_\beta +\hbox {c}_{\theta _{11} } ), \quad f=l(\hbox {s}_{\theta _{21} } +\hbox {s}_\beta ),\\ g= & {} l(\hbox {c}_{\theta _{21} } +\hbox {c}_\beta ), \quad ss=t_\beta (l\hbox {c}_{\theta _{31} } +l\hbox {c}_{\theta _{32} } -e_2 )-l(\hbox {s}_{\theta _{31} } +\hbox {s}_{\theta _{32} } ),\\ z= & {} l(\hbox {c}_{\theta _{31} } +\hbox {c}_{\theta _{32} } ), v=l(\hbox {s}_{\theta _{31} } +\hbox {s}_{\theta _{32} } ). \end{aligned}$$

From Eq. (7b), we can find that and , and thus the constraint wrenches of the PM are and . When limb 1 is actuated and the other two limbs are locked, the screw system is five-dimensional and the PM degenerates to a 1-DOF manipulator. The output motion twist is reciprocal to the screw system above. The other two output motion twists of limb 2 and limb 3 can be derived by the same way:

(51)

where \(m=gl(\hbox {s}_{\theta _{31} } +\hbox {s}_{\theta _{32} } +\hbox {t}_\beta \hbox {c}_{\theta _{31} } +\hbox {t}_\beta \hbox {c}_{\theta _{32} } )\),

$$\begin{aligned} n=e_2 f\hbox {sec}_\beta -e_2 g\hbox {t}_\beta . \end{aligned}$$
Fig. 11
figure 11

LTI for PMs with different architecture parameters: a \(l=500\,\hbox {mm},\;e_1 =250\,\hbox {mm},\;e_2 =400\,\hbox {mm}\); b \(l=500\,\hbox {mm},\;e_1 =300\,\hbox {mm},\;e_2 =400\,\hbox {mm}\); c \(l=500\,\hbox {mm},\;e_1 =300\,\hbox {mm},\; e_2 =445\,\hbox {mm}\); d \(l=445\,\hbox {mm},\;e_1 =300\,\hbox {mm},\;e_2 =445\,\hbox {mm}\)

Full size image

The other two output motion twists of limb 2 and limb 3 can be derived by the same way. Substituting solved TWS and input/output twists into Eqs. (48a) and (48b), we can obtain the force/motion transmission performance of the PM. Figure 11 shows the force/motion transmission performance of the PMs with different architecture parameters. The area covered with slash is GTW, where \(\varGamma \ge 0.7\). The LTI atlases are closely related to parameters \((l,\,e_1 ,\,e_2 )\), so are the GTWs. Figure 11a shows a rectangle-like GTW . Since \(e_1 \) is larger in the second group than that of the first group, the GTW is more narrow along the direction of \(\beta \), as shown in Fig. 11b. For the third group, the parameter \(e_2 \) is larger than that of the second group; thus, the GTW has a wider range of \(\beta \), as shown in Fig. 11c. In the fourth group, \(\gamma \) is smaller than that of the third group, which leads to a GTW with a wider range of \(\beta \) and a more narrow range of \(\gamma \), as shown in Fig. 11d. Besides, due to the architecture of the 2-URR-RRU PM, the GTWs are all symmetrical to \(\gamma \) and asymmetrical to\(\beta \), which depicts the PM has a wider GTW in the range of \([-50^{\circ },0^{\circ }]\) of \(\beta \).

10 Optimization of geometrical parameters

The performance (GTW) of the 2-URR-RRU PM is highly dependent on the geometrical parameters. In actual conditions, the parameters cannot be assigned arbitrarily and should be restricted in an area where the PM possesses good performance [31]. For the 2-URR-RRU PM, we define

$$\begin{aligned} \left\{ {\begin{array}{l} D=(e_1 +e_2 +l)/3 \\ r_1 =e_1 /D\,,r_2 =e_2 /D\,,r_3 =l/D \\ \end{array}} \right. , \end{aligned}$$
(52)

where D is a normalized factor and \(r_i \,(i=1{-}3)\) is a non-dimensional and normalized parameter. To ensure the PM being properly assembled, the three normalized parameters should satisfy

$$\begin{aligned} \left\{ {\begin{array}{l} r_2 >r_1 \\ 0<r_1 \,,r_2 ,r_3 <3 \\ \end{array}} \right. . \end{aligned}$$
(53)

Thus the parameter design space can be planned based on the restrict conditions of Eq. (53), as Fig. 12a shows. The shadow area (\(\Delta \hbox {ABC})\) contains all the possible parameter values. In the plan view, as Fig. 12b shows, the mapping relationships between parameters in spatial space \((r_1 \,,r_2 \,,r_3 )\) and plan space \((s,\,t)\) are derived as

$$\begin{aligned} \left\{ {\begin{array}{l} r_1 =s \\ r_2 =\frac{\sqrt{3}}{2}t-\frac{s}{2} \\ r_3 =3-\frac{\sqrt{3}}{2}t-\frac{s}{2} \\ \end{array}} \right. . \end{aligned}$$
(54)
Fig. 12
figure 12

Parameter design space of a PM. a Spatial view. b Plan view

Full size image

The global transmission index (GTI) can also indicate force/motion transmissibility [30,31,32]. Both the force/motion transmission performance atlas of GTW and GTI are derived by non-dimensional parameters \((s,\,t)\), as shown in Fig. 13. The blank area represents the region where the GTW/GTI is extremely small or there is no GTW/GTI. The optimal solution set should be solved considering actual requirements.

Fig. 13
figure 13

Force/motion transmission indices. a GTW. b GTI

Full size image
Fig. 14
figure 14

Optimum region

Full size image
Table 4 Geometrical parameters and performance indices in the optimum region
Full size table
Fig. 15
figure 15

LTI comparison

Full size image

The steps for the atlas of performance optimization are as follows.

  • Step 1 Given the goals of optimization are \(\hbox {GTW}\ge 1.0\) and \(\hbox {GTI}\ge 0.78\). The optimum region is the intersection of corresponding atlases of GTW and GTI, i.e., the blue area in Fig. 14.

  • Step 2 Choose a group of solution candidate from the optimum region. Given the dimension error of the real body, parameters chosen from boundary region should be avoided. We can select 12 groups of data points in the optimum region, and the non-dimensional parameters can be obtained by Eq. (54), as Table 4 lists.

  • Step 3 The purpose of our optimization is to find the region of highly good performance and not the largest region of relatively good performance. Thus GTI is the preferred factor and GTW the secondary factor. Thus we firstly pick the groups with the largest GTI and secondly select the largest GTW in the picked groups. The data of the 7th group can be regarded as optimal solution, i.e., \(r_1 =0.89\,, r_2 =1.131\,\) and \(r_3 =0.979\).

  • Step 4 The final geometrical parameters are determined by optimal non-dimensional parameters and normalized factor D. Considering occupied area, we set \(D=400\,\hbox {mm}\), and the geometrical parameters are shown in Table 4.

This method provides various solutions of geometrical parameters. To determine the optimum solution, we should consider the performance requirements of the PM. Since the preferred factor is GTI in this paper and the corresponding LTI can depict the performance, we can appeal to LTI atlases to examine the effect of optimization. From Fig. 15, we can find contour line of 0.9 in the LTI atlases after optimization, which verifies the validity of this method.

After optimization, the PM has good motion/force transmissibility in a relatively large collision-free space and its working configurations are far from singularity, which meets the demands of engineering requirements in welding, milling and processing.

11 Conclusions

Overall kinematic/dynamic analysis and optimal design of a 2-URR-RRU PM are presented. Mobility analysis shows that the PM has two rotational DOFs and one translation DOF, which has promising engineering potential. Analytical inverse and numerical forward kinematic models are established. Next, forward and inverse dynamic analysis equation is derived by the Newton–Euler approach, and simulation results are obtained for validation. Based on the Jacobian matrix, it is shown that the PM only has inverse singularities and no forward or combined singularities. The workspace is obtained while considering the practical limits of links and joints. The results demonstrate that the PM has a large workspace without singularities, which is an advantage. Based on motion/force performance indices, the optimal design of the 2-URR-RRU PM is performed, where optimal dimensional parameters are found. It is shown that the PM has a good motion/force transmisibility. This study is helpful to the design and application of the 2-URR-RRU PM.