A novel secure communication scheme based on the Karhunen–Loéve decomposition and the synchronization of hyperchaotic Lü systems

Abstract

This paper proposes a novel secure communication scheme based on the Karhunen–Loéve decomposition and the synchronization of a master and a slave hyperchaotic Lü systems. First, the Karhunen–Loéve decomposition is used as a data reduction tool to generate data coefficients and eigenfunctions that capture the essence of grayscale and color images in an optimal manner. It is noted that the original images can be reproduced using only the most energetic eigenfunctions; this results in computational savings. The data coefficients are encrypted and transmitted using a master hyperchaotic Lü system. These coefficients are then recovered at the receiver end using a sliding mode controller to synchronize two hyperchaotic Lü systems. Simulation results are presented to illustrate the ability of the proposed control law to synchronize the master and slave hyperchaotic Lü systems. Moreover, the original images are recovered by using the decrypted data coefficients in conjunction with the eigenfunctions of the image. Computer simulation results are provided to show the excellent performance of the proposed scheme.

1 Introduction

During the last two decades, many ideas and methods were proposed in the field of secure communication because of the successful application of chaos synchronization [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]. These methods rely on hiding the transmitted signal (the message) in the state variables of the transmitter’s chaotic system. To retrieve the transmitted message, the chaotic system at the receiver end is controlled or synchronized with the chaotic system from the transmitter.

The idea of controlling chaotic systems to follow a desired behavior was introduced by Ott et al. [1]. Later on, using a drive-response approach, Pecora and Carol [2] were able to show that chaotic systems can be synchronized. Since then, chaotic synchronization became a very active research method that can be applied in various fields of engineering, chemistry, biology, ecological systems and secure communication.

In 1993, Wu and Chua [3] introduced a chaotic modulation method using the information signal to manipulate the state variables of the transmitter’s system. Also, Yang and Chua [4] presented a chaotic parameter modulation method to modulate the parameters of the chaotic system of the transmitter.

Many researchers have worked on the synchronization and control of hyperchaotic systems. In 2005, Lu and Cao [5] studied the adaptive synchronization of chaotic and hyperchaotic systems by designing controllers to synchronize the three-dimensional Lorenz system with the first three states of the four-dimensional hyperchaotic Chen system. Also, Park [6] used Lyapunov stability theory to design adaptive control laws to synchronize two hyperchaotic Chen systems. Wang and Song [7] used activation feedback control to synchronize two fractional-order hyperchaotic Lorenz systems. Wang and Song [8] tackled the problem of projective synchronization for the fractional-order unified chaotic system. The synchronization of the fractional-order Liu chaotic system was analyzed by Wang and Wang [9]. Recently, many researchers investigated the usage of different control techniques to synchronize chaotic and hyperchaotic systems; for example, see [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. Chaotic secure communication schemes based on observers were proposed by some researchers; for example, see [35]. Other types of synchronization schemes such as hybrid modulus-phase synchronization [36] were proposed for secure communication purposes. Some researchers have experimentally realized chaotic secure communication systems; for example, see [37]. Other researchers developed chaotic secure video communication schemes [38, 39].

We use the sliding mode control technique in this work for the synchronization of hyperchaotic Lü system. Sliding mode control is known to be a very efficient tool for designing controllers for complex nonlinear systems in order to maintain the system stability and achieve a good performance. This technique reduces the complexity of the overall system by decoupling its motion into lower dimension components [40]. Hence, the design approach is straightforward and can be easily implemented. This gives the sliding mode control technique an advantage over some other techniques that require heavy computing power in order to be implemented. Moreover, the SMC technique is well known for its robustness against parameter uncertainties, unmodeled dynamics and disturbances.

This paper introduces a novel secure communication scheme, which is based on the Karhunen Loéve (K–L) decomposition and the synchronization of hyperchaotic Lü systems. The scheme can be used to transmit text messages or images securely by encrypting the transmitted data. First, the K–L decomposition is used as a data reduction tool to produce data coefficients and eigenfunctions from the text messages or the images to be transmitted. Then, the obtained eigenfunctions are transmitted through a public channel since it is impossible to reconstruct the original data using only the eigenfunctions; the data coefficients are encrypted by adding them to one of the states of the master hyperchaotic Lü system and transmitted. At the receiver end, the master Lü system is synchronized with a slave Lü system to recover the transmitted data coefficients. These coefficients are used to reconstruct the transmitted message/image.

The rest of the paper is organized as follows: In Sect. 2, we give a description of the Karhunen–Loéve decomposition. Sections 3 and 4 present the hyperchaotic Lü system and the controller’s design, respectively. Section 5 describes the proposed secure communication scheme. The simulation results that validate the developed scheme are presented and discussed in Sect. 6 (noise-free) and Sect. 7 (in the presence of noise). Finally, some concluding remarks are given in Sect. 8.

2 The Karhunen–Loéve decomposition

The Karhunen–Loéve (K–L) decomposition is a powerful mathematical tool that can be used to deal with large data sets. The K–L decomposition was used in many applications to solve scientific problems. For example, the K–L decomposition was used as a data reduction tool and as a feature identifier. In 1963, Lorenz [41] proposed the K–L method to analyze meteorological data; in 1967, Lumley [42] used it to identify coherent structures in a turbulent flow. The K–L decomposition method was rediscovered a number of times, and it goes under different names, such as the principal component analysis [43], the Hotelling transform [44], the empirical orthogonal functions [41], the factor analysis [45], the quasiharmonic modes [46], or the proper orthogonal decomposition [42].

Regardless of its different names, the K–L decomposition method is essentially the same. The main idea behind it is to identify coherent structures or eigenfunctions that capture the data in an optimal way [47]. In this paper, the K–L decomposition is used to decompose the data composed of set of images in order to encrypt the data and then transmit it securely. A brief description of K–L decomposition is given below.

Consider a sequence of M real-valued vectors $\{\varphi _i\}^M_{i=1}$ where $\varphi _i$ is a vector of dimension N such that $\varphi _i=[\varphi _1^i,\ \varphi _2^i,\ \ldots ,\ \varphi _N^i]^T$. These vectors can represent text messages or a set of images. The covariance matrix of these vectors can be computed using the direct method as follows:

$$\begin{aligned} {B} = \frac{1}{M}\sum _{i=1}^{M} \varphi _i \ \varphi _i^T. \end{aligned}$$

(1)

The use of the direct method results in an $N \times N$ covariance matrix. This matrix might be too large for practical computation if N is large. Therefore, one of the proposed solutions that makes the computation more tractable is the method of snapshots described by Sirovich [48] and outlined next.

According to the method of snapshots, the covariance matrix B is computed as follows:

$$\begin{aligned} B = [B_{ij}] = \Big [ \frac{1}{M} \langle \varphi _i,\ \varphi _j \rangle \Big ],\ \ i,j=1,\ldots ,M, \end{aligned}$$

(2)

where $\langle \cdot ,\ \cdot \rangle$ represents the usual Euclidian inner product. The eigenvalues $\lambda _i$ and the eigenvectors $V_i$ of the covariance matrix B are then computed. Since the covariance matrix B is symmetric, the eigenvalues $\lambda _i$ and their eigenvectors $V_i$ form a complete orthogonal set.

The eigenfunctions of the data are defined such that,

$$\begin{aligned} \varPsi _k = \sum _{i=1}^{M} V_i^{[k]} \varphi _i, \end{aligned}$$

(3)

where $V_i^{[k]}$ is the ith component of the kth eigenvector. These eigenfunctions form an optimal basis for the representation of the data in the sense that the representation of data in this basis has a smaller mean square error than any representation by other basis. Let $\varphi$ be such that,

$$\begin{aligned} \varphi = \sum _{i=1}^{M} C_i \varPsi _i. \end{aligned}$$

(4)

In Eq. (4), $\varPsi _i$ is the ith eigenfunction and $C_i, \,\, (i=1,\ldots ,M)$ are the data coefficients. The data coefficients $C_i$ show how the images interact; it can be computed by projecting the data vector onto an eigenfunction such that,

$$\begin{aligned} C_i = \Big ( \frac{\varphi \cdot \varPsi _i}{\varPsi _i \cdot \varPsi _i} \Big ), \,\, i=1,\ldots ,M. \end{aligned}$$

(5)

The energy of the data is defined as the sum of the eigenvalues of the covariance matrix such that,

$$\begin{aligned} E = \sum _{i=1}^{M} \lambda _i. \end{aligned}$$

(6)

The energy percentage of each eigenfunction is defined such that:

$$\begin{aligned} E_k = \frac{\lambda _k}{E}, \end{aligned}$$

(7)

where $\lambda _k$ is the eigenvalue associated with the kth eigenfunction.

The original data can be fully reconstructed by using all the eigenfunctions. Moreover, the original data can be approximated by using the most energetic eigenfunctions as follows:

$$\begin{aligned} \tilde{\varphi } = \sum _{i=1}^{K} C_i \varPsi _i, \,\,\, \text{ where }\,\, K < M. \end{aligned}$$

(8)

Remark 1

In some applications of the K–L decomposition, the mean is subtracted from the data vectors to form what is called the caricature vectors which have zero mean; the covariance matrix is then computed using the caricature vectors (see [49]).

3 The Lü hyperchaotic system

This section presents the hyperchaotic systems, which will be used as master and slave systems. These systems are needed for the development of the secure communication scheme.

The master system is taken to be a hyperchaotic Lü system, which is defined by the fourth-order ODE system given below,

$$\begin{aligned} \begin{aligned}&\dot{x}_1 = a(y_1-x_1) + w_1 \\&\dot{y}_1 = -x_1 z_1 + c y_1 \\&\dot{z}_1 = x_1 y_1 - b z_1 + d(t) \\&\dot{w}_1= x_1 z_1 + r w_1, \\ \end{aligned} \end{aligned}$$

(9)

where $x_1,\ y_1,\ z_1$ and $w_1$ are the states of the master system, and $a,\ b,\ c$ and r are the system parameters such that $a,\ b,\ c>0$; d(t) is a bounded noise disturbance such that $|d(t)|\le \zeta$ where $\zeta$ is a known positive bound.

It is easy to check that system (9) is hyperchaotic when $(a,\ b,\ c)=(36,\ 3,\ 20)$, $-0.35<r\le 1.3$, and $d(t)=0$.

The slave system is chosen to be as follows:

$$\begin{aligned} \begin{aligned}&\dot{x}_2 = a(y_2-x_2) + w_2 \\&\dot{y}_2 = -x_2 z_2 + c y_2 + u_1 \\&\dot{z}_2 = x_2 y_2 - b z_2 \\&\dot{w}_2 = x_2 z_2 + r w_2 + u_2, \\ \end{aligned} \end{aligned}$$

(10)

where $x_2,\ y_2,\ z_2$ and $w_2$ are the states of the slave system, and $u_1$ and $u_2$ are the controllers which will be used to synchronize the master and slave systems.

Define the errors, $e_x,\,e_y,\,e_z$ and $e_w$ such that: $e_x = x_2 - x_1$, $e_y = y_2 - y_1$, $e_z = z_2 - z_1$ and $e_w = w_2 - w_1$. In order to synchronize the master and slave systems, the error system is obtained by subtracting the master system in (9) from the slave system in (10). Therefore, we obtain the following error system:

$$\begin{aligned} \begin{aligned}&\dot{e}_x = a(e_y-e_x) + e_w \\&\dot{e}_y = -x_1 e_z - z_1 e_x -e_x e_z + c e_y + u_1 \\&\dot{e}_z = x_1 e_y + y_1 e_x + e_x e_y - b e_z - d(t) \\&\dot{e}_w= x_1 e_z + z_1 e_x + e_x e_z + r e_w + u_2. \\ \end{aligned} \end{aligned}$$

(11)

The synchronization of systems (9) and (10) can be achieved by forcing the errors in system (11) to converge to zero as t tends to infinity.

4 Design of the synchronization controller

This section deals with the design of a sliding mode controller to synchronize the master and the slave Lü systems.

Let $\lambda _1$ and $\lambda _2$ be positive constants. Also, let $K_1$, $K_2$, L and $L_2$ be large enough positive scalars. Define the sliding surfaces $S_1$ and $S_2$ such that:

$$\begin{aligned} S_1&= e_y + \lambda _1 \int e_y \end{aligned}$$

(12)

$$\begin{aligned} S_2&= e_w + \lambda _2 \int e_w . \end{aligned}$$

(13)

Theorem 1

The following controllers:

$$\begin{aligned} u_1 =\,&\, x_1 e_z + z_1 e_x + e_x e_z - c e_y - \lambda _1 e_y \nonumber \\&- K_1 \mathrm{sgn}(S_1) - L_1 S_1 \end{aligned}$$

(14)

$$\begin{aligned} u_2 =&-x_1 e_z - z_1 e_x - e_x e_z - r e_w - \lambda _2 e_w \nonumber \\&- K_2 \mathrm{sgn}(S_2) - L_2 S_2. \end{aligned}$$

(15)

when applied to the error system (11), guarantee the asymptotic convergence of the errors $(e_x,\ e_y,\ e_w)$ to $(0,\ 0,\ 0)$ and the boundedness of the error $e_z$.

Proof

Differentiating the sliding surfaces in (12) and (13) with respect to time along the dynamics in (11) yields the following:

$$\begin{aligned} \dot{S}_1&= \dot{e}_y + \lambda _1 e_y \nonumber \\&= -x_1 e_z - z_1 e_x -e_x e_z + c e_y + u_1 + \lambda _1 e_y \end{aligned}$$

(16)

$$\begin{aligned} \dot{S}_2&= \dot{e}_w + \lambda _2 e_w \nonumber \\&= x_1 e_z + z_1 e_x + e_x e_z + r e_w + u_2 + \lambda _2 e_w. \end{aligned}$$

(17)

By substituting $u_1$ and $u_2$ in the above equations using the proposed controllers given by (14) and (15), one obtains,

$$\begin{aligned} \dot{S}_1&= - L_1 S_1 - K_1 \mathrm{sgn}(S_1) \end{aligned}$$

(18)

$$\begin{aligned} \dot{S}_2&= - L_2 S_2 - K_2 \mathrm{sgn}(S_2). \end{aligned}$$

(19)

Consider the following Lyapunov function candidate:

$$\begin{aligned} V = \frac{1}{2} S_1^2 + \frac{1}{2} S_2^2. \end{aligned}$$

(20)

The time derivative of V along the dynamics in (18) and (19) is such that,

$$\begin{aligned} \dot{V}&= - K_1 S_1 \mathrm{sgn}(S_1) - L_1 S_1^2 - K_2 S_2 \mathrm{sgn}(S_2) - L_2 S_2^2 \nonumber \\&= - K_1 |S_1| - L_1 S_1^2 - K_2 |S_2| - L_2 S_2^2. \end{aligned}$$

(21)

It is clear from (21) that $\dot{V}<0$ for $(S_1,S_2)\ne (0,0)$ since $L_1,\ L_2,$ $K_1, K_2$ are positive scalars. Therefore, V is a positive definite, radially unbounded function whose time derivative along the trajectories in (18)-(19) is negative definite. Hence, it can be concluded that $S_1$ and $S_2$ converge to zero.

Once the sliding surfaces reach zero (i.e., $S_1=0$ and $S_2=0$), we can write,

$$\begin{aligned} e_y + \lambda _1 \int e_y&= 0 \end{aligned}$$

(22)

$$\begin{aligned} e_w + \lambda _2 \int e_w&= 0. \end{aligned}$$

(23)

Since $\lambda _1$ and $\lambda _2$ are positive constants, it can be concluded from (22) and (23) that $\lim \limits _{t\rightarrow \infty }e_y=0$ and $\lim \limits _{t\rightarrow \infty }e_w=0$.

Moreover, the system dynamics on the sliding surfaces ($S_1=0$ and $S_2=0$)  will be such that,

$$\begin{aligned} \dot{e}_x&= -a e_x \end{aligned}$$

(24)

$$\begin{aligned} \dot{e}_z&= - b e_z + y_1 e_x- d(t). \end{aligned}$$

(25)

Equation (24) implies that $\lim \limits _{t\rightarrow \infty }e_x=0$ since $a>0$.

Furthermore, once $e_x$ reaches zero, the dynamics in (25) can be written such that,

$$\begin{aligned} \dot{e}_z = - b e_z - d(t). \end{aligned}$$

(26)

The solution of (26) is given by,

$$\begin{aligned} e_z(t) = e^{-bt} e_z(0) - \int _{0}^{t} e^{-b(t-\tau )} d(\tau ) \mathrm{d}\tau , \end{aligned}$$

(27)

where $e_z(0)$ is the initial value of $e_z(t)$. Since $|d(t)|\le \zeta$, it can be inferred from (27) that,

$$\begin{aligned} e_z(t)\le & {} e^{-bt} |e_z(0)| + \int _{0}^{t} e^{-b(t-\tau )} \zeta \mathrm{d}\tau \nonumber \\= & {} e^{-bt} |e_z(0)| + \frac{\zeta }{b} (1 - e^{-bt})\,\,\,\, \text{ for } \,\,\,\, t \ge 0. \end{aligned}$$

(28)

Since b is a positive scalar, we can conclude that $e_z$ is bounded. Also, using (28) we can write $\lim \limits _{t \rightarrow \infty } e_z(t) \le \frac{\zeta }{b}$ since b is a positive constant which ensures that $e_z(t)$ is bounded.

Therefore, the proposed controllers in (14) and (15), when applied to the error system given in (11), guarantee the asymptotic convergence of $(e_x,\ e_y,\ e_w)$ to $(0,\ 0,\ 0)$, while $e_z$ remains bounded. Hence, the proposed controllers achieve the task of synchronizing the master and slave hyperchaotic Lü systems. $\square$

Remark 2

It should be noted that the proposed control law guarantees the asymptotic convergence of the error e to zero where $e = [e_x\ e_y\ e_z\ e_w]^T$ when $d(t)=0$ (i.e., $\lim \limits _{t\rightarrow \infty }e=0$, when $d(t)=0$).

5 A secure communication scheme

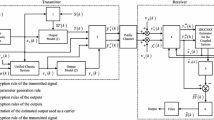
In this section, we propose a novel secure communication scheme based on the K–L decomposition and the synchronization of hyperchaotic Lü systems. This scheme is used to transmit text messages or images securely by encrypting the transmitted data. A block diagram of the proposed secure communication scheme is depicted in Fig. 1. The description of the scheme is presented in the following paragraphs.

Consider a text message or an image (we will call it data) that needs to be transmitted securely. A splitting rule is applied to the data as follows:

• If the data are a text, then it is split into M words,

• If the data are an image, then it is split into M sub-images.

For text messages, the M words are used to form M vectors $\varphi _i$ using the ASCII representation of each word. For images, we consider two cases: grayscale images and color images. An $m \times n$ grayscale image is represented by an $m \times n$ data matrix of the gray level of the pixels, while a true color image (RGB image) of the same size is represented by an $m \times n \times 3$ data matrix that defines the level of red, green and blue color components of each individual pixel. The image given in matrix form can be vectorized by concatenating the rows of the matrix to form M vectors $\varphi _i$ of size $N\times 1$ where $N=m\times n$ for grayscale images and $N=3m\times n$ for RGB images.

Fig. 1

A block diagram representation of the secure communication scheme

Using the K–L decomposition, the eigenfunctions and the data coefficients of the data are generated. The eigenfunctions can be transmitted through a public channel without encryption since it is impossible to reconstruct the original data using only the eigenfunctions. The data coefficients are encrypted by adding them to one of the states of the master hyperchaotic Lü system. This is achieved in the following manner. The data coefficients are transformed into binary format to form a sequence of pulses $\gamma m(t)$ where $\gamma$ is the amplitude of the pulses. This sequence is added to the state $z_1$ of the master Lü system to be encrypted. The states of that system are then sent through a public channel to the receiver. Note that it is assumed that the public channel is a noise-free channel (i.e., $\tilde{x}_1=x_{1},\ \tilde{y}_1=y_1,\ \tilde{z}_1=z_1,\ \tilde{w}_1=w_1$, where $\tilde{x}_1,\ \tilde{y}_1,\ \tilde{z}_1,\$ and $\tilde{w}_1$ are the values of $x_{1},\ y_1,\ z_1$ and $w_1$ at the receiver end of the channel).

It is well known that hyperchaotic systems are very sensitive to initial conditions. Thus, if the transmitted states are intercepted, it will be impossible to retrieve the original data using these states. This is the case because even if the data coefficients are retrieved, the original data cannot be reconstructed because the eigenfunctions of the original data are unknown to the person who intercepted the master Lü system. This makes the transmission of the data secure.

At the receiver end, the slave Lü system is synchronized with the master Lü system using the designed sliding mode controller. A noisy version of the sent message $m_\mathrm{c}(t)$ can then be obtained from the error $e_z = z_2 - z_1$. The original message can be recovered from $m_\mathrm{c}(t)$ using a filter and a threshold detector.

Once the recovered message $\tilde{m}(t)$ is obtained, the transmitted binary data coefficients are recovered and transformed back to real values. These data coefficients can then be used along with the received eigenfunctions to reconstruct the transmitted text or image according to (8).

Remark 3

In the presented approach, the message is added to the dynamics of the master system (known as the inclusion method [50]) rather than adding the message to the output states of the system (known as the masking method [51]). It is required that the amplitude of the message must be small enough to preserve the chaotic behavior of the system. For that purpose, the amplitude of the pulses sequence $\gamma m(t)$ that represents the message can be adjusted by selecting a proper value for $\gamma$. It is noted that some researchers employ user-defined protocols for chaos-based secure communication schemes [52].

Remark 4

One of the powerful features of using the proposed secure communication scheme is the ability to reduce the amount of data which need to be transmitted. This is true since the proposed scheme depends on the K–L decomposition, which is well known as a compression tool. That is, we can reduce the amount of the transmitted data by transmitting only the most energetic eigenfunctions and their corresponding data coefficients.

6 Simulation results

The proposed secure communication scheme is validated through computer simulations, and the obtained results are presented in this section. Two cases are considered: case 1 deals with the transmission of grayscale images, while case 2 corresponds to the transmission of color images. In each case, the original image is split into a number of sub-images. A discussion of these cases is presented in the following subsections.

6.1 Transmitting of a grayscale image

The case of transmitting a grayscale image using the proposed secure communication scheme is presented in this subsection. A $504\times 504$ grayscale image is selected; this image is shown in Fig. 2. It is represented by $504 \times 504$ matrix of the gray-level pixels. This image is split into 64 sub-images where each sub-image is a $63\times 63$ image as shown in Fig. 3.

Fig. 2

Original grayscale image

Fig. 3

Original grayscale image split into 8 $\times$ 8 sub-images

First, the matrices of sub-images matrices are vectorized. Then, the K–L decomposition is applied on the resultant 64 data vectors obtaining 64 eigenfunctions and their corresponding data coefficients. The generated 20 most energetic eigenfunctions, as depicted in Fig. 4, are transmitted through a public channel. Figure 5 shows the energy associated with each eigenfunction. In this figure, the upper plot shows the energy of all eigenfunctions, while the lower plot depicts the energy associated with the rest of the eigenfunctions except the first one. It is clear from this figure that most of the energy (about 97.2 %) is captured by the first eigenfunction.

Fig. 4

The 20 most energetic eigenfunctions

Fig. 5

Energy of the 20 most energetic eigenfunctions

The data coefficients are transformed into binary format; a message $\gamma m(t)$ is then formed where $\gamma$ is taken to be 2 and m(t) is a sequence of pulses with a period of $T=1$ second representing the binary message. Thus, m(t) is defined such that,

$$\begin{aligned} m(t) = \left\{ \begin{array}{ccc} 0, &{} \text {if the bit is 0} &{} \forall t \in [t_0,\ t_0+T] \\ 1, &{} \text {if the bit is 1} &{} \forall t \in [t_0,\ t_0+T]. \end{array} \right. \end{aligned}$$

(29)

For the first 2 seconds, the signal m(t) is set to zero to make sure that the controller has enough time to synchronize the two Lü systems. The message $\gamma m(t)$ is then added as noise to the third state of the master Lü system defined in (9).

The states of the master system are transmitted through a public channel. At the receiver end, the states of the master system are synchronized with the states of the slave system using the proposed sliding mode controller given by the equations (14)–(15). The initial conditions for both the master and slave hyperchaotic Lü systems used in the simulations are such that $x_1(0)=2,\ y_1(0)=1,\ z_1(0)=1,\ w_1(0)=5,\ x_2(0)=4,\ y_2(0)=3,\ z_2(0)=3,\ w_2(0)=1$. The controller design parameters are taken to be: $\lambda _1 = \lambda _2 = 1$, $K_1 = 12$,   $K_2 = 13$,   $L_1=0$,   and $L_2=0$. Moreover, the signum function in the proposed controller is approximated using the tangent hyperbolic function in order to avoid the well-known chattering problem (i.e., the sign function is approximated such that $\hbox {sign}(S)\approx \hbox {tanh}(3S)$).

The synchronization errors between the two systems are plotted for the first 50 seconds in Fig. 6; the asymptotic convergence of $(e_x,\ e_y,\ e_w)$ to $(0,\ 0,\ 0)$ is evident from this figure. Also, it is clear that $e_z$ remains bounded under the application of the proposed controller laws.

Since the slave system at the receiver end is synchronized with the master system, a noisy version of the sent message can be obtained using $m_\mathrm{c}(t) = z_2 - z_1$. Figure 7 shows the recovered signal $m_\mathrm{c}$. To clearly show the details of $m_\mathrm{c}(t)$, the initial part of the recovered signal is depicted in Fig. 8.

Fig. 6

Synchronization errors of the master and slave Lu systems versus time for the first 50 s

Fig. 7

Recovered signal $m_\mathrm{c}(t)$ versus time

Fig. 8

Part of the recovered signal $m_\mathrm{c}(t)$ versus time

The sent message can be then retrieved by filtering $m_\mathrm{c}(t)$ using a threshold detector set at the mean value. This threshold detector (filter) is defined such that:

$$\begin{aligned} \tilde{m}(t) = \left\{ \begin{array}{c c} 0, &{} \text {If}\ \frac{1}{T}\int _{t_0}^{t_0+T}m_\mathrm{c}(t)\mathrm{d}t \le \alpha \\ 1, &{} \text {If}\ \frac{1}{T}\int _{t_0}^{t_0+T}m_\mathrm{c}(t)\mathrm{d}t > \alpha , \end{array} \right. \end{aligned}$$

(30)

where $\alpha$ is the threshold value. In the simulation, $\alpha$ is taken to be 0.4.

Using the recovered signal $\tilde{m}(t)$, the transmitted data coefficients are reconstructed at the receiver end. The reconstructed data coefficients are then used in conjunction with the received eigenfunctions to recover the original image using equation (8). Figure 9 shows the original as well as the recovered image. Figure 9a) depicts the original image, and Fig. 9d shows the recovered image. It is clear from this figure that the proposed secure communication scheme works well.

To show that the proposed scheme posses another feature besides being secure, we plotted the recovered image using some of the eigenfunctions only (see Fig. 9c). The figure shows the ability of the proposed scheme to reduce the amount of data which need to be transmitted since there is very little need to transmit the remaining 29 eigenfunctions and their corresponding data coefficients. It should be noted that a distorted version of the transmitted image is recovered using only the 10 most energetic eigenfunctions as shown in Fig. 9b. Hence, it can be concluded that a sufficient number of eigenfunctions are needed in order to reconstruct the original image.

Fig. 9

a The original image, b the recovered image using 10 eigenfunctions, c the recovered image using 35 eigenfunctions, d the recovered image using all eigenfunctions

6.2 Transmission of color images

This subsection considers the case of transmitting a color image using the proposed secure communication scheme. The original image is shown in Fig. 10; this image has the size of $1000 \times 1000$ pixels. Since it is a true color image (RGB image), it is represented by a $1000 \times 1000 \times 3$ matrix of the levels of red, green and blue components. In order to apply the proposed scheme, this image is split into 64 sub-images with a size of $125\times 125$ pixels each as shown in Fig. 11.

Fig. 10

Original color image. (Color figure online)

Fig. 11

Original color image split into 8 $\times$ 8 sub-images. (Color figure online)

Fig. 12

The 20 most energetic eigenfunctions

Fig. 13

Energies of the 20 most energetic eigenfunctions

The K–L decomposition is then applied to the vectorized version of the sub-images, and the eigenfunctions and the data coefficients are generated. Figure 12 shows the resultant 20 most energetic eigenfunctions expressed as images and transmitted through a public channel. The energy associated with these eigenfunctions is depicted in Fig. 13 where the upper plot shows that most of the energy is captured by the first eigenfunction; it captures $95.73\%$ of the energy. The lower plot shows the energy associated with the rest of the eigenfunctions.

The data coefficients are transformed into binary, and a signal of pulses $\gamma m(t)$ is formed with a pulse width of $T=1$ second, an amplitude of $\gamma = 2$ and m(t) as defined in (29). It should be mentioned that for the first 2 seconds, the signal m(t) was set to zero in order to enable the controller to synchronize the two hyperchaotic Lü systems. This signal to be transmitted is then added to the master Lü system in the transmitter by considering it as noise such that $d(t) = \gamma m(t)$.

The states of the master system are transmitted through a public channel. The states of the slave system at the receiver end are then synchronized with the states of the master system using the proposed sliding mode controller. The initial conditions for both the master and slave systems are taken to be: $x_1(0)=2,\ y_1(0)=1,\ z_1(0)=1,\ w_1(0)=5,\ x_2(0)=4,\ y_2(0)=3,\ z_2(0)=3,\ w_2(0)=1$. The design parameters of the sliding mode controller are selected to be: $\lambda _1 = \lambda _2 = 1$, $K_1 = 12$,   $K_2 = 13$,   $L_1=0$ and $L_2=0$. Also, the signum function is approximated such that $\hbox {sign}(S)\approx \hbox {tanh}(3S)$ to avoid the chattering problem.

Fig. 14

Synchronization errors of the master and slave hyperchaotic Lü systems versus time for the first 50 s

Fig. 15

Recovered signal $m_\mathrm{c}(t)$ versus time for the transmission of the color image. (Color figure online)

Fig. 16

Part of the recovered signal $m_\mathrm{c}(t)$ versus time for the transmission of the color image. (Color figure online)

Fig. 17

a The original color image, b the recovered image using only 15 eigenfunctions, c the recovered image using 35 eigenfunctions, d the recovered color image using all eigenfunctions. (Color figure online)

The synchronization errors versus time are shown in Fig. 14 for the first 50 seconds. It is clear from this figure that the proposed controller forces the asymptotic convergence of $(e_x,\ e_y,\ e_w)$ to $(0,\ 0,\ 0)$ and maintains the boundedness of $e_z$.

The recovered message $m_\mathrm{c}(t) = z_2 - z_1$ is shown in Figs. 15 and 16. A threshold detector as in (30) is used to reconstruct the original image. This reconstructed image is transformed from binary to real (ascii) format in order to obtain the transmitted data coefficients. The received data coefficients are used in conjunction with the received eigenfunctions to recover the original color image (see Fig. 17). Figure 17 shows the original image and the reconstructed image. Figure 17a) depicts the original color image; Fig. 17d) shows the recovered color image with all eigenfunctions used. These two figures clearly indicate that the two images are almost identical. Hence, it can be concluded that the proposed secure communication scheme is able to transmit color images with very high resolution.

Fig. 18

Recovered images considering noise in the transmission channel. a SNR $\,=\,$40 dB and 81 sub-images. b SNR $\,=\,$ 40 dB and 36 sub-images. c SNR $\,=\,$ 35 dB and 81 sub-images. d SNR $\,=\,$35 dB and 36 sub-images. e SNR $\,=\,$ 30 dB and 81 sub-images. f SNR$\,=\,$ 30 dB and 36 sub-images

Moreover, in order to demonstrate the ability of the proposed scheme to reduce the amount of the transmitted data, the original image is reconstructed using only the 35 most energetic eigenfunctions. Note that these eigenfunctions capture $99.75\%$ of the data energy. Figure 17c) shows the recovered color images while using only 35 of the 64 eigenfunctions. It is clear that Fig. 17c is almost identical to the original transmitted image. In addition, Fig. 17b shows the recovered color image while using only 15 of the 64 eigenfunctions. It is clear from the figure that more than 15 eigenfunctions need to be used to be able to reconstruct the original image well.

7 Analysis considering a noisy public channel

In Sect. 6, the proposed scheme was simulated under the assumption that the public channel is a noise-free channel. However, a real transmission channel is exposed to significant noise, which affects the transmitted data [53]. Therefore, we present in this section some results in order to address this concern.

Many simulations were performed considering the case of transmitting a grayscale image, which is shown in Fig. 2. In these simulations, white Gaussian noise was added to the states of the master $L\ddot{u}$ system and eigenfunctions transmitted through the public channel. We considered a different case in every simulation in terms of the signal-to-noise ratio (SNR) of the added noise. Also, two different numbers of sub-images M were considered in each simulation.

The obtained results are shown in Fig. 18. The considered cases of SNR are 40, 35 and 30dB, and the number of sub-images is taken to be either 36 or 81. It can be seen that the proposed scheme shows good results for channels with SNR of 30dB or higher.

8 Concluding remarks

The idea presented in this article constitutes a novel secure communication approach based on the use of Karhunen–Loéve decomposition and the synchronization of master and slave $L\ddot{u}$ hyperchaotic systems. The K–L decomposition is used for data reduction, and the synchronization of the master and slave hyperchaotic Lü systems is used to securely encrypt and decrypt part of the data. A controller is designed to achieve the synchronization of the master and slave hyperchaotic systems, and computer simulations are provided to validate the control design. The proposed communication scheme is then simulated considering the cases of secure transmission and re-construction of grayscale images as well as color images. The simulation results show the excellent performance of the proposed schemes.

The combination of the K–L decomposition with the synchronization of hyperchaotic Lü systems is shown to be a powerful approach in secure communications capable of reducing computational burden. This work establishes a foundation for using K–L decomposition in conjunction with synchronization of hyperchaotic systems in secure communications. Future work will address the use of this technique to securely transmit videos.