1 Introduction

Since the soliton concept was introduced by Zabusky and Kruskal in 1965 [1], a great number of integrable systems have been discovered in the natural and applied sciences [2–11]. Integrable systems exhibit richness and variety of exact solutions such as soliton solutions, periodic solutions, rational solutions and complexiton solutions (see, e.g., [12, 13]).

In recent years, abundant localized structures, like dromions, lumps, ring soliton and oscillated dromion, breathers solution, fractal-dromion and fractal-lump soliton structures [14], were revealed. Besides the usual localized structures, some new localized excitations like peakons, compactons, folded solitary waves and foldon structures were found by choosing some types of lower-dimensional appropriate functions [15–28]. The interaction properties of peakon–peakon, dromion–dromion and foldon–foldon interactions have also investigated [16, 17]. However, within our knowledge, studying the spatiotemporal deformation of multi-soliton such as breather two-soliton and three-soliton under the small perturbation of parameter is still open. Motivated by this reason, we investigate the (2 + 1)D KdV equation

$$\begin{aligned} \displaystyle&u_t-u_{xxx}+3(\mathrm{uv})_x=0,\end{aligned}$$
(1)
$$\begin{aligned}&u_x=v_y, \end{aligned}$$
(2)

Equation (1) was derived by Boiti et al. using the idea of the weak Lax pair. The Painlevé property of it has been proved by Dorizzi et al. And Lie algebraic structure and the infinite-dimensional symmetries have been studied. Some special forms of solitary wave solutions are also reported [26–44].

2 Three-wave method with a perturbation parameter

Multi-wave solutions are important because they reveal the interactions between the inner waves and the various frequency and velocity components. The whole multi-wave solution, for instance, may sometimes be converted into a single soliton of very high energy that propagates over large regions of space without dispersing, and an extremely destructive wave is therefore produced of which the tsunami is a good example. Since all double-wave solutions can be found by using the exp-function method proposed by Fu and Dai [18], we propose an modification of the three-soliton method [6] in this paper (called the three-wave method) for finding coupled wave solutions. Consider a high-dimensional nonlinear evolution equation in the general form

$$\begin{aligned} F(u,u_t,u_x,u_y,u_z,u_{xx}...)=0 \end{aligned}$$
(3)

where \(u=u(x,y,z,t)\) and F is a polynomial of u and its derivatives, t represents time variable, and x, y, z represent spatial variables. The three-wave method operates as follows:

Step 1: By Painleve analysis , a transformation

$$\begin{aligned} \begin{array}{cc} u=T(u_0,f) \end{array} \end{aligned}$$
(4)

is made for some new and unknown function f.

Step 2: Convert Eq. (3) into Hirota bilinear form:

$$\begin{aligned} \begin{array}{cc} G(u_0,D_t,D_x,D_y,D_z...)f\cdot f=0 \end{array} \end{aligned}$$
(5)

where the operator D is the Hirota bilinear operator defined in [2]. The perturbation parameter \(u_0\) plays an important role to the resulting solution, where the spatiotemporal feature in multi-wave propagation including nature of soliton, direction even the shape will change as \(u_0\) makes a small perturbation.

Step 3: Traditionally, we take the following Ansátz to obtain the three-soliton solution

$$\begin{aligned} f= & {} 1+e^{\xi _1}+e^{\xi _2}+e^{\xi _3}+a_{12}e^{\xi _1+\xi _2}+a_{13}e^{\xi _1+\xi _3}\nonumber \\&+\,a_{23}e^{\xi _2+\xi _3}+a_{123}e^{\xi _1+\xi _2+\xi _3} \end{aligned}$$
(6)

cc where

$$\begin{aligned} \begin{array}{ll} \xi _i=a_ix+b_iy+c_iz+d_it,&\quad i=1,2,3 \end{array} \end{aligned}$$
(7)

Here, \(a_{12},a_{13},a_{23}\) and \(a_{123}\) are real constants to be determined. Equation (6) can be rewritten as

$$\begin{aligned} f= & {} e^{\frac{\eta _1}{2}}(e^{-\eta _1}+e^{-\eta _2}+e^{-\eta _3}+e^{-\eta _4}+a_{12}e^{\eta _4}+a_{13}e^{\eta _3}\nonumber \\&+\,a_{23}e^{\eta _2}+a_{123}e^{\eta _1}) \end{aligned}$$
(8)

where

$$\begin{aligned} \displaystyle \eta _1= & {} \frac{\xi _1+\xi _2+\xi _3}{2},\qquad \eta _2=\frac{\xi _1-\xi _2-\xi _3}{2}\end{aligned}$$
(9)
$$\begin{aligned} \displaystyle \eta _3= & {} \frac{-\xi _1+\xi _2-\xi _3}{2}, \qquad \eta _4=\frac{-\xi _1-\xi _2+\xi _3}{2} \end{aligned}$$
(10)

Thus, this three-soliton Ansátz contains four wave variables \(\eta _1,\eta _2,\eta _3\) and \(\eta _4\). Here, we treat it in a different way. We factor out the \(e^{\frac{\eta _1}{2}}\) and decrease the numbers of wave variables to three terms. On the other hand, we set some parameters in a complex way. At last, the above analysis allows us to construct the following assumptions:

$$\begin{aligned} \begin{array}{cc} f=\delta _1\cosh {\xi _1}+\delta _1\cos (\xi _2)+\delta _2\cosh (\xi _3), \end{array} \end{aligned}$$
(11)

or

$$\begin{aligned} \begin{array}{cc} f=\delta _1\cosh {\xi _1}+\delta _1\cos (\xi _2)+\delta _2\sinh (\xi _3), \end{array} \end{aligned}$$
(12)

where \( \delta _j,j=1,2,3\) are constants. In fact, from Eqs. (9) or (10), it is easily seen that it only contains three wave variables. As a result, we call this method “three-wave method.” it is obvious that three-wave method is the reduction and modification of the traditional three-soliton method.

Step 4: Substitute Eq. (9) [or Eq. (10)] in Eq. (5) and collect the coefficients of \(e^{j\xi _1},\sin (\xi _2),\cos (\xi _2),\cosh (\xi _3)\) and \(\sinh (\xi _3)\). Then, equate the coefficients of these terms to zero and obtain a set of over-determined algebraic equations in \(a_i,b_i,c_i\) and \(d_i\)

Step 5: Solve the set of algebraic equations in Step 4 using Maple and solve for \(a_i,b_i,c_i\) and \(\delta _i, i=1,2,3\).

Step 6: Substituting the identified values in Eqs. (4) and (5). Thus, we can deduce the exact multi-wave solutions depended on the parameter for Eq. (3).

Step 7: Make a small perturbation of parameter at the special value to investigate the different spatiotemporal features of multi-wave.

2.1 Application to (2 + 1)-dimensional KdV eqution

Using Painlevé analysis, we assume

$$\begin{aligned} ccu=u_0+2(\mathrm{ln} f)_{xy},\qquad v=v_0+2(\mathrm{ln} f)_{xx}, \end{aligned}$$
(13)

where both \(u_0\) and \(v_0\) are parameters. Then, Eqs. (1) and (2) can be equivalently transformed into the following bilinear form

$$\begin{aligned} (D_yD_t+D_yD_x^3+3u_0D_x^2+3v_0D_xD_y)f\cdot f=0\nonumber \\ \end{aligned}$$
(14)

According to the three-wave method with a perturbation parameter in the previous section, we can assume

$$\begin{aligned} \displaystyle f \left( x,y,t \right)= & {} a_{{1}}\cosh \left( \xi _1 \right) + a_2\cos \left( \xi _2 \right) + a_{{3}}\cosh \left( \xi _3 \right) , \nonumber \\ \displaystyle \xi _i= & {} k_{{i}}x+l_{{i}}y+c_{{i}}t, \end{aligned}$$
(15)

for some constants \(a_i,k_i,l_i,c_i(i=1,2,3)\) to be determined later. Then, by substituting Eq. (13) in Eq. (12) and equating all the coefficients of \(\sin (\xi _i),\cos (\xi _i),\sinh (\xi _i)\) and \(\cosh (\xi _i)\) to be zero, we obtain the set of algebraic equations as follows:

$$\begin{aligned}&2\,l_{{2}}a_{{1}}c_{{1}}+2\,l_{{2}}a_{{1}}{k_{{1}}}^{3}+6\,v_{{0}}a_{{1}}k_{{1}}l_{{2}}=0,\\&2\,l_{{2}}a_{{3}}{k_{{3}}}^{3}+6\,v_{{0}}a_{{3}}k_{{3}}l_{{2}}+2\,l_{{2}}a_{{3}}c_{{3}}+2\,a_{{3}}l_{{3}}c_{{2}}=0,\\&-2\,c_{{2}}l_{{2}}a_{{1}}+6\,u_{{0}}a_{{1}}{k_{{1}}}^{2}=0,\\&2\,a_{{3}}{k_{{3}}}^{3}l_{{3}}-2\,c_{{2}}l_{{2}}a_{{3}}+2\,a_{{3}}c_{{3}}l_{{3}}\\&\quad +\,6\,v_{{0}}a_{{3}}k_{{3}}l_{{3}}+6\,u_{{0}}a_{{3}}{k_{{3}}}^{2}=0,\\&-2\,a_{{3}}l_{{3}}a_{{1}}c_{{1}}-12\,u_{{0}}a_{{1}}k_{{1}}a_{{3}}k_{{3}}-2\,a_{{3}}l_{{3}}a_{{1}}{k_{{1}}}^{3}\\&\quad -\,6\,a_{{3}}{k_{{3}}}^{2}l_{{3}}a_{{1}}k_{{1}} -6\,v_{{0}}a_{{1}}k_{{1}}a_{{3}}l_{{3}}=0,\\&2\,{a_{{3}}}^{2}l_{{3}}c_{{3}}+8\,{a_{{3}}}^{2}{k_{{3}}}^{3}l_{{3}}+6\,u_{{0}}{a_{{1}}}^{2}{k_{{1}}}^{2}\\&\quad +\,6\,u_{{0}}{a_{{3}}}^{2}{k_{{3}}}^{2}-2\,l_{{2}}c_{{2}}+6\,v_{{0}}{a_{{3}}}^{2}k_{{3}}l_{{3}}=0,\\&2\,a_{{3}}c_{{3}}l_{{3}}a_{{1}}+ 2\,a_{{3}}{k_{{3}}}^{3}l_{{3}}a_{{1}}+6\,u_{{0}}a_{{1}}{k_{{1}}}^{2}a_{{3}} +6\,u_{{0}}a_{{3}}{k_{{3}}}^{2}a_{{1}}\\&\quad +\,6\,v_{{0}}a_{{3}}k_{{3}}l_{{3}}a_{{1}}+6\,a_{{3}}k_{{3}}l_{{3}}a_{{1}}{k_{{1}}}^{2}=0. \end{aligned}$$

By solving the above system with the aid of Maple, we obtain

$$\begin{aligned} c_2= & {} \frac{-3k_1k_3\sqrt{k_3^2-k_1^2}}{2},\nonumber \\ c_1= & {} -3v_0k_1-k_1^3,l_3=-\frac{2u_0}{k_3},\nonumber \\ a_{{1}}= & {} {\frac{\sqrt{2\,{a_{{3}}}^{2}{k_{{3}}}^{2}-{k_{{1}}}^{2}{a_{ {3}}}^{2}+{k_{{1}}}^{2}}}{k_{{1}}}},\nonumber \\ l_{{2}}= & {} -2\,\sqrt{- \left( {k_{{1}}}^{2}-{k_{{3}}}^{2} \right) ^{-1}} k_{{1}}u_{{0}}{k_{{3}}}^{-1},\nonumber \\ c_{{3}}= & {} -\frac{1}{2}\left( 3\,{k_{{1}}}^{2}-{k_{{3}}}^{2}+6\,v_{{0}} \right) k_{{3}}. \end{aligned}$$
(16)

where \(k_1,k_3,u_0\) and \(v_0\) are free parameters. Substituting Eq. (14) in Eq. (11), we can derive the explicit soluion of (2 + 1)-dimensional KdV equation:

$$\begin{aligned} u=u_0+\frac{\varXi }{[a_{{1}}\cosh (\xi _1) +\cos (\xi _2) +a_{{3}}\cosh (\xi _3) ] ^{2}},\nonumber \\ \end{aligned}$$
(17)

where

$$\begin{aligned} \varXi= & {} [ b_{{1}}\cosh (\xi _{{1}}) +b_{{2}}\cosh (\xi _{{3}})]\cos (\xi _{{2}})\\&+\,b_{{3}}\cosh (\xi _{{3}})\cosh (\xi _{{1}}) \\&+\, [b_{{ 4}}\sinh (\xi _{{1}}) -b_{{5}}\sin (\xi _{{2}})] \sinh ( \xi _{{3}})\\&+\,b_{{6}}\sin (\xi _{{2}}) \sinh (\xi _{{1}})+b_7. \end{aligned}$$

and the coefficients are determined by

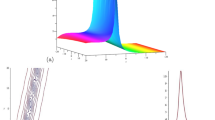
$$\begin{aligned} b_1= & {} 2\,a_{{1}}l_{{1}}k_{ {1}}-2\,l_{{2}}k_{{2}}a_{{1}},\\ b_2= & {} 2\,l_{{3}}k_{{3}}a_{{3}}-2\,l_{{2}}k_{{2}}a_{{3}},\\ b_3= & {} 2\,a_{{3}}l_{{3}}k_{{3}}a_{{1}}+2\,a_{{1}}l_ {{1}}k_{{1}}a_{{3}},\\ b_4= & {} -2\,a_{{1}}k_{{1}}a_{{3}}l_{{3}}-2\,a_{{3} }k_{{3}}a_{{1}}l_{{1}},\\ b_5= & {} 2\,a_{{3}}k_{{3}}l_{{2}}+2\,k_{{2}}a_{{ 3}}l_{{3}},\\ b_6= & {} 2\,a_{{1}}k_{{1}}l_{{2}}+2\,k_{{2}}a_{{1}}l_{{1}},\\ b_7= & {} -2\,k_{{2}}l_{{2}}+2\,{a_{{1}}}^{2}k_{{1}}l_{{1}}+2\,{a_{{3}}}^ {2}l_{{3}}k_{{3}}. \end{aligned}$$

We note that Eq. (12) is just the bilinear equation of Eqs. (1) and (2) under transformation of Eq. (11) when \((u_0,v_0)\) equals to (0, 0), and the transformation (11) is linear respect to \((u_0,v_0)\), so, Eq. (12) is equivalent to the bilinear equation of original equation. Therefore, by studying the variety of spatiotemporal structure of multi-wave of Eq. (12) we can find out some novel nonlinear phenomenon of (2 + 1)D KdV equation when \(u_0\) and \(v_0\) take different values in the neighborhood of (0, 0). Figure (1) shows spatial structure of u(x, y, t) for parameters \(l_{{1}}=0,k_{{2}}=0,k_{{1}}= 0.25,k_{{3}}= 0.5,v_{{0}}=- 0.015,u_{{0}}= 0.1,a_{{3}}=1,t=2\) and \( l_{{1}}=0,k_{{2}}=0,k_{{1}}= 0.25,k_{{3}}= 0.5,v_{{0}}=- 0.015,a_{{3}}=1,t=2,u_{{0}}=- 0.1\).

From Fig. 1, we easily find out the spatiotemporal structures of breather two-soliton happen outstanding change when \((u_0,v_0)\) makes small perturbation at (0, 0), two bright solitons not only change into two dark solitons, but also the shape changes and direction of propagation obviously deflects when \(v_0\) is fixed at a small negative value \(-0.015\) and \(u_0\) are taken \(-0.1\) and 0.1, respectively.

Fig. 1
figure 1

A spatial structure of u in (15) for parameters \( l_{{1}}=0,k_{{2}}=0,k_{{1}}= 0.25, k_{{3}}= 0.5, a_{{3}}=1, t=2,\) a \(u_0=0.1\) and \(v_0=-0.015\), b \(u_0=-0.1\) and \(v_0=-0.015\)

Full size image

In Eq. (14), when \(k_1>k_3\), we obtain three-soliton solution

$$\begin{aligned} u=u_0+\frac{\aleph }{[a_{{1}}\cosh (\xi _1) +\cosh (\xi _2) +a_{{3}}\cosh (\xi _3) ] ^{2} },\nonumber \\ \end{aligned}$$
(18)

where

$$\begin{aligned} \varXi= & {} [b_{{1}}\cosh (\xi _{{1}}) +b_{{2}}\cosh (\xi _{{3}})]\cos (\xi _{{2}})\\&+\,b_{{3}}\cosh (\xi _{{3}}) \cosh (\xi _{{1}}) \\&+\, [b_{{ 4}}\sinh (\xi _{{1}}) -b_{{5}}\sin (\xi _{{2}})] \sinh (\xi _{{3}}) \\&-\,b_{{6}}\sin (\xi _{{2}}) \sinh (\xi _{{1}})+b_7. \end{aligned}$$

and

$$\begin{aligned} \xi _2= & {} -2\,\sqrt{\left( {k_{{1}}}^{2}-{k_{{3}}}^{2} \right) ^{-1}} k_{{1}}u_{{0}}{k_{{3}}}^{-1}y \nonumber \\&+\frac{-3k_1k_3\sqrt{k_1^2-k_3^2}}{2}t, \end{aligned}$$
(19)

Figure 2 exhibits the change in spatiotemporal structure of three solitons when \(v_0\) is fixed at the positive value and \(u_0\) is taken \(-0.1\) and 0.1, respectively. From Fig. 2, we obviously see that the three solitons, i.e., two bright and one dark solitons, not only change into two dark and one bright solitons respectively, but also the propagation direction happens outstanding deflexion of different angles.

Fig. 2
figure 2

A spatial structure of u in (18) for parameters \( l_{{1}}=0, k_{{2}}=0. a_{{3}}=1, t=2, k_{{3}}=1, k_{{1}}=\sqrt{2}\). a \(u_{{0}}=- 0.1\) and \(v_{{0}}=2\), b \(v_0=2, u_0=0.1\)

Full size image

3 Conclusions

In conclusion, using three-wave method with a perturbation parameter, we obtain novel solutions of (2 + 1) KdV equation. We found that the perturbation parameter \(u_0\) plays an important role to the resulting solution, where the spatiotemporal deformation in multi-wave propagation including change between bright and dark multi-soliton each other, deflection with different directions and angles of multi-soliton even the shape will vary as \(u_0\) makes small perturbation in the neighborhood of \( u_0=0 \). These solutions possess many interesting dynamical features as can be seen in the previous sections. Whether there exist other methods to study spatiotemporal variance of multi-wave for other types of high-dimensional system is our future work.