Recursive parameter identification of the dynamical models for bilinear state space systems

Abstract

This paper investigates the recursive parameter and state estimation algorithms for a special class of nonlinear systems (i.e., bilinear state space systems). A state observer-based stochastic gradient (O-SG) algorithm is presented for the bilinear state space systems by using the gradient search. In order to improve the parameter estimation accuracy and the convergence rate of the O-SG algorithm, a state observer-based multi-innovation stochastic gradient algorithm and a state observer-based recursive least squares identification algorithm are derived by means of the multi-innovation theory. Finally, a numerical example is provided to demonstrate the effectiveness of the proposed algorithms.

1 Introduction

System identification is the methodology of establishing mathematical models [1,2,3] and has wide applications in many areas such as linear system modeling [4, 5] and nonlinear system modeling [6,7,8,9]. The identification of linear systems has reached a high level of maturity [10], and nonlinear systems generally exist in industry areas, so their identification has received extensive attention. Bilinear systems are considered as a special class of nonlinear systems and are linear to the state and the control input, respectively, but not to them jointly. The bilinear system is a simple nonlinear extension of a linear system. So it is necessary to introduce some work about the identification of nonlinear systems such as Hammerstein systems. Many nonlinear parameter estimation methods [11,12,13] have been developed, such as the subspace methods [14, 15], the hierarchical methods [16, 17] and the key term separation methods [18]. For example, under the assumption of a white unobserved Gaussian input signal, errorless output observations and an invertible nonlinearity, Vanbeylen et al. [19] proposed a maximum likelihood estimator for Hammerstein systems with output measurements. Ase and Katayama [20] presented a subspace-based method to identify the Wiener–Hammerstein benchmark model by using the orthogonal projection subspace method and the separable least squares method.

The parameter identification [21,22,23] and the design of state observers [24,25,26] for bilinear systems have been carried out throughout the years both for continuous-time bilinear systems [27, 28] and for discrete-time bilinear systems [29, 30]. In the literature, Jan et al. [31] utilized the block pulse functions for the bilinear system identification in order to reduce the computation time. Dai et al. [32] proposed a robust recursive least squares method for bilinear systems identification. dos Santos et al. [33] presented a subspace state space identification algorithm for multi-input multi-output bilinear systems driven by white noise inputs by utilizing the Kalman filter idea.

State space systems can describe not only the system input and output characteristics but also the system internal structure characteristics, and play an important role in dynamical system state estimation [34, 35] and parameter estimation [36]. Many identification methods have been proposed for linear state space systems, but the identification of nonlinear state space systems is still difficult and has not been fully investigated. Schön et al. [37] derived an expectation maximization algorithm for the parameter estimation of nonlinear state space systems using a particle smoother. Marconato et al. [38] presented an identification method for nonlinear state space models on a benchmark problem based on the classical identification techniques and regression methods.

The least squares methods contain the recursive least squares algorithms [39,40,41] and the least squares-based iterative algorithms [42, 43]. In the literature, Arablouei et al. [44] studied an unbiased recursive least squares algorithm for errors-in-variables systems utilizing the dichotomous coordinate-descent iterations. Xu et al. [45] proposed the recursive least squares and multi-innovation stochastic gradient parameter estimation methods for signal modeling. Wan et al. [46] presented a novel method for the T-wave alternans assessment based on the least squares curve fitting technique. This paper addresses the identification issue for the bilinear state space systems with unmeasurable state variables. The basic idea is to transform a bilinear state space system into its observer canonical form and then to derive the recursive parameter estimation algorithms based on the multi-innovation theory and design the state observer to estimate the unknown states. The main contributions of this paper lie in the following.

• By using the gradient search and the state observer, we overcome the difficulty that there exists both unmeasurable states and unknown parameters in the identification models, and propose the state observer-based gradient identification algorithms for bilinear state space systems.

• By utilizing the current innovations and past innovations, this paper presents a state observer-based multi-innovation stochastic gradient (O-MISG) algorithm for bilinear state space systems to improve the parameter estimation accuracy and convergence rates.

To close this section, we give an outline of this paper. Section 2 derives the observer canonical state space model for bilinear systems. Section 3 introduces the identification model for the bilinear state space models. A state estimation-based recursive parameter identification algorithm is presented in Sect. 4. Section 5 provides an illustrative example for the results in this paper. Finally, some concluding remarks are given in Sect. 6.

2 The observer canonical state space model for bilinear systems

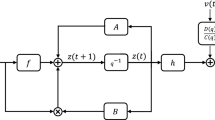
First of all, let us introduce some notation. “$A=:X$” or “$X:=A$” stands for “A is defined as X”; the symbol $\varvec{I}$ ($\varvec{I}_n$) represents an identity matrix of appropriate size ($n\times n$); z denotes a unit forward shift operator like $z\varvec{x}(t)=\varvec{x}(t+1)$ and $z^{-1}\varvec{x}(t)=\varvec{x}(t-1)$; the superscript T symbolizes the vector/matrix transpose; $\hat{\varvec{{\theta }}}(t)$ denotes the estimate of $\varvec{{\theta }}$ at time t.

Consider the bilinear state space system described by

$$\begin{aligned}&\bar{\varvec{x}}(t+1)=\bar{\varvec{A}}\bar{\varvec{x}}(t)+\bar{\varvec{B}}\bar{\varvec{x}}(t)u(t)+\bar{\varvec{f}}u(t), \end{aligned}$$

(1)

$$\begin{aligned}&y(t)=\bar{\varvec{h}}\bar{\varvec{x}}(t)+v(t), \end{aligned}$$

(2)

where $\bar{\varvec{x}}(t):=[\bar{x}_1(t),\bar{x}_2(t),\ldots ,\bar{x}_n(t)]^{\tiny \text{ T }}\in {\mathbb {R}}^n$ is the state vector, $u(t)\in {\mathbb {R}}$ and $y(t)\in {\mathbb {R}}$ are the system input and output variables, $v(t)\in {\mathbb {R}}$ is a random noise with zero mean and variance $\sigma ^2$, and $\bar{\varvec{A}}\in {\mathbb {R}}^{n\times n}$, $\bar{\varvec{B}}\in {\mathbb {R}}^{n\times n}$, $\bar{\varvec{f}}\in {\mathbb {R}}^n$ and $\bar{\varvec{h}}\in {\mathbb {R}}^{1\times n}$ are the parameter matrices/vectors of the system.

Suppose that the system in (1) and (2) is controllable and observable. The bilinear system can be transformed into an observer canonical form under the non-singular linear transformation such as $\bar{\varvec{x}}(t)=\varvec{T}_\mathrm{o}\varvec{x}(t)$, where $\varvec{T}_\mathrm{o}\in {\mathbb {R}}^{n\times n}$ stands for the non-singular matrix. The transformation is as follows.

$$\begin{aligned} \varvec{x}(t+1)= & {} \varvec{T}_\mathrm{o}^{-1}\bar{\varvec{x}}(t+1)=\varvec{T}_\mathrm{o}^{-1}[\bar{\varvec{A}}\bar{\varvec{x}}(t)\nonumber \\&+\bar{\varvec{B}}\bar{\varvec{x}}(t)u(t) +\bar{\varvec{f}}u(t)]\nonumber \\= & {} \varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}\bar{\varvec{x}}(t)+\varvec{T}_\mathrm{o}^{-1}\bar{\varvec{B}}\bar{\varvec{x}}(t)u(t)+\varvec{T}_\mathrm{o}^{-1}\bar{\varvec{f}}u(t)\nonumber \\= & {} \varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}\varvec{T}_\mathrm{o}\varvec{x}(t)+\varvec{T}_\mathrm{o}^{-1}\bar{\varvec{B}}\varvec{T}_\mathrm{o}\varvec{x}(t)+\varvec{T}_\mathrm{o}^{-1}\bar{\varvec{f}}u(t)\nonumber \\= & {} \varvec{A}\varvec{x}(t)+\varvec{B}\varvec{x}(t)u(t)+\varvec{f}u(t), \end{aligned}$$

(3)

$$\begin{aligned} y(t)= & {} \bar{\varvec{h}}\bar{\varvec{x}}(t)+v(t)\nonumber \\= & {} \varvec{h}\varvec{x}(t)+v(t), \end{aligned}$$

(4)

where

$$\begin{aligned} \varvec{A}:= & {} \varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}\varvec{T}_\mathrm{o}= \left[ \begin{array}{ccccc} -a_1 &{} 1 &{} 0 &{} \cdots &{} 0\\ -a_2 &{} 0 &{} 1 &{} \ddots &{} 0\\ \vdots &{}\vdots &{} \ddots &{} \ddots &{} 0\\ -a_{n-1} &{} 0 &{} \cdots &{} 0 &{} 1\\ -a_n &{} 0 &{} \cdots &{} 0 &{} 0 \end{array}\right] \in {\mathbb {R}}^{n \times n},\nonumber \\ \varvec{B}:= & {} \varvec{T}_\mathrm{o}^{-1}\bar{\varvec{B}}\varvec{T}_\mathrm{o}=\left[ \begin{array}{c} \varvec{b}_1 \\ \varvec{b}_2 \\ \vdots \\ \varvec{b}_n \end{array}\right] \in {\mathbb {R}}^{n\times n},\quad \varvec{b}_i\in {\mathbb {R}}^{1\times n},\nonumber \\ \varvec{f}:= & {} \varvec{T}_\mathrm{o}^{-1}\bar{\varvec{f}}=[f_1,f_2,\ldots ,f_n]^{\tiny \text{ T }}\in {\mathbb {R}}^n,\quad \varvec{h}:=\bar{\varvec{h}}\varvec{T}_\mathrm{o}\nonumber \\&=[1,0,\ldots ,0]\in {\mathbb {R}}^{1 \times n}. \end{aligned}$$

(5)

The transformation matrix is given by

$$\begin{aligned} \varvec{T}_\mathrm{o}:=[\bar{\varvec{A}}^{n-1}\varvec{l}_n,\bar{\varvec{A}}^{n-2}\varvec{l}_n,\ldots ,\varvec{l}_n]\in {\mathbb {R}}^{n \times n}, \end{aligned}$$

where $\varvec{l}_n$ is the nth column of $\varvec{T}_\mathrm{ob}$.

$$\begin{aligned} \varvec{T}_\mathrm{ob}:=\left[ \begin{array}{c} \bar{\varvec{h}} \\ \bar{\varvec{h}}\bar{\varvec{A}} \\ \vdots \\ \bar{\varvec{h}}\bar{\varvec{A}}^{n-1} \end{array}\right] ^{-1}\in {\mathbb {R}}^{n \times n}, \end{aligned}$$

where $\varvec{T}_\mathrm{ob}$ is another non-singular matrix which transform the general system into its observability canonical form.

Proof

As $\varvec{T}=[*,\ \varvec{l}_n]$, we have

$$\begin{aligned} \varvec{T}_\mathrm{ob}^{-1}\varvec{T}_\mathrm{ob}:=\left[ \begin{array}{c} \bar{\varvec{h}} \\ \bar{\varvec{h}}\bar{\varvec{A}} \\ \vdots \\ \bar{\varvec{h}}\bar{\varvec{A}}^{n-1} \end{array}\right] [*,\ \varvec{l}_n]=\varvec{I}_n, \end{aligned}$$

and the nth column can be written as

$$\begin{aligned} \left\{ \begin{array}{ccl} \bar{\varvec{h}}\varvec{l}_n&{}=&{}0, \\ \bar{\varvec{h}}\bar{\varvec{A}}\varvec{l}_n&{}=&{}0, \\ \vdots \\ \bar{\varvec{h}}\bar{\varvec{A}}^{n-2}\varvec{l}_n&{}=&{}0, \\ \bar{\varvec{h}}\bar{\varvec{A}}^{n-1}\varvec{l}_n&{}=&{}1. \end{array}\right. \end{aligned}$$

Hence, we have

$$\begin{aligned} \varvec{h}= & {} \bar{\varvec{h}}\varvec{T}_\mathrm{o}=\bar{\varvec{h}}[\bar{\varvec{A}}^{n-1}\varvec{l}_n,\bar{\varvec{A}}^{n-2}\varvec{l}_n,\ldots ,\varvec{l}_n] \\= & {} [\bar{\varvec{h}}\bar{\varvec{A}}^{n-1}\varvec{l}_n,\bar{\varvec{h}}\bar{\varvec{A}}^{n-2}\varvec{l}_n,\ldots ,\bar{\varvec{h}}\varvec{l}_n] \\= & {} [1,0,0,\ldots ,0], \\ \varvec{T}_\mathrm{o}^{-1}\varvec{T}_\mathrm{o}= & {} \varvec{T}_\mathrm{o}^{-1}[\bar{\varvec{A}}^{n-1}\varvec{l}_n,\bar{\varvec{A}}^{n-2}\varvec{l}_n,\ldots ,\varvec{l}_n]\\= & {} [\varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}^{n-1}\varvec{l}_n,\varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}^{n-2}\varvec{l}_n,\ldots ,\varvec{T}_\mathrm{o}^{-1}\varvec{l}_n]{=}\varvec{I}_n, \end{aligned}$$

or

$$\begin{aligned} \varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}^{n-1}\varvec{l}_n= & {} [1,0,0,0,\ldots ,0]^{\tiny \text{ T }}=\varvec{e}_1, \nonumber \\ \varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}^{n-2}\varvec{l}_n= & {} [0,1,0,0,\ldots ,0]^{\tiny \text{ T }}=\varvec{e}_2, \nonumber \\ \varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}^{n-3}\varvec{l}_n= & {} [0,0,1,0,\ldots ,0]^{\tiny \text{ T }}=\varvec{e}_3, \nonumber \\ \vdots \nonumber \\ \varvec{T}_\mathrm{o}^{-1}\varvec{l}_n= & {} [0,0,0,0,\ldots ,1]^{\tiny \text{ T }}=\varvec{e}_n. \end{aligned}$$

(6)

Therefore, we obtain

$$\begin{aligned} \varvec{A}= & {} \varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}\varvec{T}_\mathrm{o} \nonumber \\= & {} \varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}[\bar{\varvec{A}}^{n-1}\varvec{l}_n,\bar{\varvec{A}}^{n-2}\varvec{l}_n,\ldots ,\varvec{l}_n] \nonumber \\= & {} [\varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}^n\varvec{l}_n,\varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}^{n-1}\varvec{l}_n,\varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}^{n-2}\varvec{l}_n,\ldots ,\varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}\varvec{l}_n] \nonumber \\= & {} [\varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}^n\varvec{l}_n,\varvec{e}_1,\varvec{e}_2,\ldots ,\varvec{e}_{n-1}]. \end{aligned}$$

(7)

Suppose that the characteristic equation of $\bar{\varvec{A}}$ can be represented as

$$\begin{aligned} \det [s\varvec{I}_n-\bar{\varvec{A}}]= s^n{+}a_1s^{n-1}{+}a_2s^{n-2}+\cdots +a_n{=}0. \end{aligned}$$

According to the Cayley–Hamilton theorem, we have

$$\begin{aligned} \bar{\varvec{A}}^n+a_1\bar{\varvec{A}}^{n-1}+a_2\bar{\varvec{A}}^{n-2}+\cdots +a_n\varvec{I}_n=\mathbf 0, \end{aligned}$$

or

$$\begin{aligned} \bar{\varvec{A}}^n=-a_1\bar{\varvec{A}}^{n-1}-a_2\bar{\varvec{A}}^{n-2}-\cdots -a_n\varvec{I}_n. \end{aligned}$$

(8)

Pre- and post-multiplying (8) by $\varvec{T}^{-1}$ and $\varvec{l}_n$ gives

$$\begin{aligned} \varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}^n\varvec{l}_n= & {} -a_1\varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}^{n-1}\varvec{l}_n-a_2\varvec{T}_\mathrm{o}^{-1}\bar{\varvec{A}}^{n-2}\varvec{l}_n\nonumber \\&-\cdots -a_n\varvec{T}_\mathrm{o}^{-1}\varvec{l}_n \nonumber \\= & {} -a_1\varvec{e}_1-a_2\varvec{e}_2-\cdots -a_n\varvec{e}_n \nonumber \\= & {} [-a_1,-a_2,\ldots ,-a_n]^{\tiny \text{ T }}. \end{aligned}$$

(9)

By substituting the above equation into (7), the proof is finished. $\square$

The model in (1) and (2) contains $2n^2+2n$ parameters, but the observer canonical form in (3) and (4) contains only $n^2+2n$ parameters. The decrease in the parameters to be identified leads to the reduction in the identification computation because both the initial parameters and the transformed parameters describe the relationship between input and output of the same bilinear state space system.

It is pointed out that this paper does not consider the process noise in the state equation, because if adding the process noise, the problem is more complex and more difficult, more challenging and more interesting, the related work can be found in [15, 47] without considering the process noise. In the future work, we will investigate the case with process noise.

3 The identification model for the bilinear state space system

From (3) to (5), we have the following n equations:

$$\begin{aligned} \left\{ \begin{array}{ccl} x_1(t+1)&{}=&{}-a_1x_1(t)+x_2(t)+\varvec{b}_1\varvec{x}(t)u(t)+f_1u(t),\\ x_2(t+1)&{}=&{}-a_2x_1(t)+x_3(t)+\varvec{b}_2\varvec{x}(t)u(t)+f_2u(t),\\ \vdots \\ x_{n-1}(t+1)&{}=&{}-a_{n-1}x_1(t)+x_n(t)\\ &{}&{} +\varvec{b}_{n-1}\varvec{x}(t)u(t)+f_{n-1}u(t),\\ x_n(t+1)&{}=&{}-a_nx_1(t)+\varvec{b}_n\varvec{x}(t)u(t)+f_nu(t),\end{array}\right. \end{aligned}$$

which can be simplified as

$$\begin{aligned} x_i(t+1)= & {} -a_ix_1(t)+x_{i+1}(t)+\varvec{b}_i\varvec{x}(t)u(t)\nonumber \\&+f_iu(t),\quad i=1,2,\ldots , n-1, \end{aligned}$$

(10)

$$\begin{aligned} x_n(t+1)= & {} -a_nx_1(t)+\varvec{b}_n\varvec{x}(t)u(t)+f_nu(t). \end{aligned}$$

(11)

Multiplying both sides of (10) by $z^{-i}$ gives

$$\begin{aligned} x_i(t-i+1)= & {} -a_ix_1(t-i)+x_{i+1}(t-i)\nonumber \\&+\,\varvec{b}_i\varvec{x}(t-i)u(t-i)+f_iu(t-i).\nonumber \\ \end{aligned}$$

(12)

Summing (12) for i from $i=1$ to $i=(n-1)$, we have

$$\begin{aligned} x_1(t)= & {} -\sum _{i=1}^{n-1}a_ix_1(t-i)+x_n(t-n+1)\nonumber \\&+\sum _{i=1}^{n-1}\varvec{b}_i\varvec{x}(t-i)u(t-i)+\sum _{i=1}^{n-1}f_iu(t-i). \end{aligned}$$

(13)

Then, multiplying both sides of (11) by $z^{-n}$ gives

$$\begin{aligned} x_n(t-n+1)= & {} -a_nx_1(t-n)+\varvec{b}_n\varvec{x}(t-n)u(t-n)\nonumber \\&+f_nu(t-n). \end{aligned}$$

(14)

Substituting (14) into (13), we obtain

$$\begin{aligned} x_1(t)= & {} -\sum _{i=1}^na_ix_1(t-i)+\sum _{i=1}^n\varvec{b}_i\varvec{x}(t-i)u(t-i)\nonumber \\&+\sum _{i=1}^nf_iu(t-i) \nonumber \\= & {} [x_1(t-1),x_1(t-2),\ldots ,x_1(t-n)]\left[ \begin{array}{c} -a_1 \\ -a_2 \\ \vdots \\ -a_n \end{array}\right] \nonumber \\&+[u(t-1),u(t-2),\ldots ,u(t-n)]\left[ \begin{array}{c} f_1 \\ f_2 \\ \vdots \\ f_n \end{array}\right] \nonumber \\&+[\varvec{x}^{\tiny \text{ T }}(t-1)u(t-1),\varvec{x}^{\tiny \text{ T }}(t-2)u(t-2),\ldots ,\nonumber \\&\varvec{x}^{\tiny \text{ T }}(t-n)u(t-n)]\left[ \begin{array}{c} \varvec{b}_1^{\tiny \text{ T }} \\ \varvec{b}_2^{\tiny \text{ T }} \\ \vdots \\ \varvec{b}_n^{\tiny \text{ T }} \end{array}\right] . \end{aligned}$$

(15)

From (4), we have

$$\begin{aligned} y(t)=x_1(t)+v(t). \end{aligned}$$

(16)

Define the information vector $\varvec{{\varphi }}(t)$ and the parameter vector $\varvec{{\theta }}$ as

$$\begin{aligned} \varvec{{\varphi }}(t):= & {} [\varvec{{\varphi }}_x^{\tiny \text{ T }}(t), \varvec{{\varphi }}_{xu}^{\tiny \text{ T }}(t),\varvec{{\varphi }}_u^{\tiny \text{ T }}(t)]^{\tiny \text{ T }}\in {\mathbb {R}}^{n^2+2n},\\ \varvec{{\varphi }}_x(t):= & {} [-x_1(t{-}1),-x_1(t{-}2),\ldots ,-x_1(t{-}n)]^{\tiny \text{ T }}{\in }{\mathbb {R}}^n,\\ \varvec{{\varphi }}_{xu}(t):= & {} [\varvec{x}^{\tiny \text{ T }}(t-1)u(t-1),\varvec{x}^{\tiny \text{ T }}(t-2)u(t\nonumber \\&-2),\ldots ,\varvec{x}^{\tiny \text{ T }}(t-n)u(t-n)]^{\tiny \text{ T }}\in {\mathbb {R}}^{n^2},\\ \varvec{{\varphi }}_u(t):= & {} [u(t-1),u(t-2),\ldots ,u(t-n)]^{\tiny \text{ T }}\in {\mathbb {R}}^n,\\ \varvec{{\theta }}:= & {} [\varvec{a}^{\tiny \text{ T }},\varvec{b}^{\tiny \text{ T }},\varvec{f}^{\tiny \text{ T }}]^{\tiny \text{ T }}\in {\mathbb {R}}^{n^2+2n},\\ \varvec{a}:= & {} [a_1,a_2,\ldots ,a_n]^{\tiny \text{ T }}\in {\mathbb {R}}^n,\\ \varvec{b}:= & {} [\varvec{b}_1, \varvec{b}_2,\ldots , \varvec{b}_n]^{\tiny \text{ T }}\in {\mathbb {R}}^{n^2},\\ \varvec{f}:= & {} [f_1,f_2,\ldots ,f_n]^{\tiny \text{ T }}\in {\mathbb {R}}^n. \end{aligned}$$

Substituting (15) into (16), we obtain the identification model of the bilinear state space system in (3) and (4):

$$\begin{aligned} y(t)= \varvec{{\varphi }}^{\tiny \text{ T }}(t)\varvec{{\theta }}+v(t). \end{aligned}$$

(17)

4 The recursive state and parameter estimation algorithm

The recursive state and parameter estimation algorithm is composed of the state estimation and parameter identification.

4.1 The state estimation algorithm

Although the open-loop observer [26], closed-loop observer [48] and the Kalman filter [35] all can estimate the system states, in the state estimate-based parameter identification methods in this paper, we use the open-loop observer, which can also achieve good performance. From the simulation results, we can see that the estimated states are very close to the actual states of the system (see Figs. 3, 4, 7, 8), which show that the open-loop state observer we propose is valid. Compared with the closed-loop state observer, the open-loop state observer is simpler in structure and has less computation cost. So when the open-loop state observer can satisfy the estimation accuracy, we will give priority to the design of the open-loop state observer instead of the closed-loop state observer to reduce the computation cost. Of course, we may use the closed-loop observer like in Refs. [25] and [48]. Then we carry on the design of the open-loop observer.

If the parameter matrices/vector $\varvec{A}\in {\mathbb {R}}^{n\times n}$, $\varvec{B}\in {\mathbb {R}}^{n\times n}$ and $\varvec{f}\in {\mathbb {R}}^n$ are known, we can apply the following state observer to generate the estimate $\hat{\varvec{x}}(t)$ of the unknown state vector $\varvec{x}(t)$:

$$\begin{aligned} \hat{\varvec{x}}(t+1)= & {} \varvec{A}\hat{\varvec{x}}(t)+\varvec{B}\hat{\varvec{x}}(t)u(t)+\varvec{f}u(t).\nonumber \\ \end{aligned}$$

(18)

When the parameter matrices/vector $\varvec{A}\in {\mathbb {R}}^{n\times n}$, $\varvec{B}\in {\mathbb {R}}^{n\times n}$ and $\varvec{f}\in {\mathbb {R}}^n$ are unknown, we replace them with their estimated parameter matrices/vector $\hat{\varvec{A}}(t)$, $\hat{\varvec{B}}(t)$ and $\hat{\varvec{f}}(t)$ in the following parameter estimation algorithms to compute the estimate $\hat{\varvec{x}}(t)$ of the state vector $\varvec{x}(t)$ and obtain

$$\begin{aligned} \hat{\varvec{x}}(t+1)= & {} \hat{\varvec{A}}(t)\hat{\varvec{x}}(t)+\hat{\varvec{B}}(t)\hat{\varvec{x}}(t)u(t)+\hat{\varvec{f}}(t)u(t).\nonumber \\ \end{aligned}$$

(19)

In (18) and (19), the initial state $\hat{\varvec{x}}(1)$ is usually defined as a real vector with small entries, e.g., $\hat{\varvec{x}}(1)=\mathbf{1}_n/p_0$, where $\mathbf{1}_n:=[1,1,\ldots ,1]^{\tiny \text{ T }}\in {\mathbb {R}}^n$, and $p_0$ is a large number, e.g., $p_0=10^6\gg 1$.

4.2 The state observer-based multi-innovation stochastic gradient algorithm

Based on the identification model in (17), we propose the stochastic gradient (SG) algorithm as

$$\begin{aligned} \hat{\varvec{{\theta }}}(t)= & {} \hat{\varvec{{\theta }}}(t-1)+\frac{\varvec{{\varphi }}(t)}{r(t)}e(t), \end{aligned}$$

(20)

$$\begin{aligned} e(t)= & {} y(t)-\varvec{{\varphi }}^{\tiny \text{ T }}(t)\hat{\varvec{{\theta }}}(t-1), \end{aligned}$$

(21)

$$\begin{aligned} r(t)= & {} r(t-1)+\Vert \varvec{{\varphi }}(t)\Vert ^2,\quad r(0)=1, \end{aligned}$$

(22)

where the norm of a matrix $\varvec{X}$ is defined as $\Vert \varvec{X}\Vert ^2:=\mathrm{tr}[\varvec{X}\varvec{X}^{\tiny \text{ T }}]$, 1 / r(t) represents the convergence factor or the step size, and $e(t):=y(t)-\varvec{{\varphi }}^{\tiny \text{ T }}(t)\hat{\varvec{{\theta }}}(t-1)$ is defined as the scalar innovation. As is known to us, the SG algorithm has slow convergence rates. In order to overcome this weakness, we take advantage of the multi-innovation identification theory and expand the scalar innovation e(t) to an innovation vector (p represents the innovation length):

$$\begin{aligned} \varvec{E}(p,t){:=}\left[ \begin{array}{c} y(t)-\varvec{{\varphi }}^{\tiny \text{ T }}(t)\hat{\varvec{{\theta }}}(t-1) \\ y(t-1)-\varvec{{\varphi }}^{\tiny \text{ T }}(t-1)\hat{\varvec{{\theta }}}(t-1) \\ \vdots \\ y(t-p+1)-\varvec{{\varphi }}^{\tiny \text{ T }}(t-p+1)\hat{\varvec{{\theta }}}(t-1) \end{array}\right] {\in }{\mathbb {R}}^p. \end{aligned}$$

Define the stacked output vector $\varvec{Y}(p,t)$ and the stacked information matrix $\varvec{\varPhi }(p,t)$ as

$$\begin{aligned} \varvec{Y}(p,t):= & {} [y(t),y(t-1),\ldots ,y(t-p+1)]^{\tiny \text{ T }}\in {\mathbb {R}}^p,\\ \varvec{\varPhi }(p,t):= & {} [\varvec{{\varphi }}(t),\varvec{{\varphi }}(t{-}1),\ldots ,\varvec{{\varphi }}(t{-}p{+}1)]\,{\in }\,{\mathbb {R}}^{(n^2+2n)\times p}. \end{aligned}$$

Then the innovation vector $\varvec{E}(p,t)$ can be expressed as

$$\begin{aligned} \varvec{E}(p,t)=\varvec{Y}(p,t)-\varvec{\varPhi }^{\tiny \text{ T }}(p,t)\hat{\varvec{{\theta }}}(t-1). \end{aligned}$$

In the case of $p=1$, we obtain $\varvec{E}(1,t)=e(t)$, $\varvec{\varPhi }(1,t)=\varvec{{\varphi }}(t)$, $\varvec{Y}(1,t)=y(t)$. Equation (20) is equivalent to

$$\begin{aligned} \hat{\varvec{{\theta }}}(t){=}\hat{\varvec{{\theta }}}(t{-}1){+}\frac{\varvec{\varPhi }(t)}{r(t)}[\varvec{Y}(1,t)-\varvec{\varPhi }^{\tiny \text{ T }}(1,t)\hat{\varvec{{\theta }}}(t-1)].\nonumber \\ \end{aligned}$$

(23)

Replacing the “1” in $\varvec{\varPhi }(1,t)$ and $\varvec{Y}(1,t)$ with p obtains

$$\begin{aligned} \hat{\varvec{{\theta }}}(t)= & {} \hat{\varvec{{\theta }}}(t{-}1){+}\frac{\varvec{\varPhi }(t)}{r(t)}[\varvec{Y}(p,t){-}\varvec{\varPhi }^{\tiny \text{ T }}(p,t)\hat{\varvec{{\theta }}}(t-1)],\nonumber \\= & {} \hat{\varvec{{\theta }}}(t-1)+\frac{\varvec{\varPhi }(t)}{r(t)}\varvec{E}(p,t). \end{aligned}$$

(24)

Because the information vector $\varvec{{\varphi }}(t)$ contains the unmeasurable state vector $\varvec{x}(t)$, the algorithm in (20) to (22) cannot be realized. The scheme here is to replace $\varvec{x}(t)$ in $\varvec{{\varphi }}(t)$ with its estimate $\hat{\varvec{x}}(t)$ and to define

$$\begin{aligned} \hat{\varvec{{\varphi }}}(t):= & {} [\hat{\varvec{{\varphi }}}_x^{\tiny \text{ T }}(t), \hat{\varvec{{\varphi }}}_{xu}^{\tiny \text{ T }}(t), \varvec{{\varphi }}_u^{\tiny \text{ T }}(t)]^{\tiny \text{ T }},\nonumber \\ \hat{\varvec{{\varphi }}}_x(t):= & {} [-\hat{x}_1(t{-}1),-\hat{x}_1(t{-}2),\ldots ,-\hat{x}_1(t{-}n)]^{\tiny \text{ T }},\nonumber \\ \hat{\varvec{{\varphi }}}_{xu}(t):= & {} [\hat{\varvec{x}}^{\tiny \text{ T }}(t-1)u(t-1),\hat{\varvec{x}}^{\tiny \text{ T }}(t-2)u(t\nonumber \\&-2),\ldots , \hat{\varvec{x}}^{\tiny \text{ T }}(t-n)u(t-n)]^{\tiny \text{ T }}. \end{aligned}$$

(25)

By using the estimate $\hat{\varvec{{\varphi }}}(t)$ to replace $\varvec{{\varphi }}(t)$ and using the estimate $\hat{\varvec{\varPhi }}(t)$ to replace ${\varvec{\varPhi }}(t)$, the O-MISG algorithm can be derived as

$$\begin{aligned} \hat{\varvec{{\theta }}}(t)= & {} \hat{\varvec{{\theta }}}(t-1)+\frac{\hat{\varvec{\varPhi }}(t)}{r(t)}\varvec{E}(p,t), \end{aligned}$$

(26)

$$\begin{aligned} \varvec{E}(p,t)= & {} \varvec{Y}(p,t)-\hat{\varvec{\varPhi }}^{\tiny \text{ T }}(p,t)\hat{\varvec{{\theta }}}(t-1), \end{aligned}$$

(27)

$$\begin{aligned} r(t)= & {} r(t-1)+\Vert \hat{\varvec{{\varphi }}}(t)\Vert ^2,\quad r(0)=1, \end{aligned}$$

(28)

$$\begin{aligned} \varvec{Y}(p,t)= & {} [y(t),y(t-1),\ldots ,y(t-p+1)]^{\tiny \text{ T }}, \end{aligned}$$

(29)

$$\begin{aligned} \hat{\varvec{\varPhi }}(p,t)= & {} [\hat{\varvec{{\varphi }}}(t),\hat{\varvec{{\varphi }}}(t-1),\ldots ,\hat{\varvec{{\varphi }}}(t-p+1)], \end{aligned}$$

(30)

$$\begin{aligned} \hat{\varvec{{\varphi }}}(t)= & {} [\hat{\varvec{{\varphi }}}_x^{\tiny \text{ T }}(t), \hat{\varvec{{\varphi }}}_{xu}^{\tiny \text{ T }}(t), \varvec{{\varphi }}_u^{\tiny \text{ T }}(t)]^{\tiny \text{ T }}, \end{aligned}$$

(31)

$$\begin{aligned} \hat{\varvec{{\varphi }}}_x(t)= & {} [-\hat{x}_1(t-1),-\hat{x}_1(t-2),\ldots ,\nonumber \\&-\hat{x}_1(t-n)]^{\tiny \text{ T }}, \end{aligned}$$

(32)

$$\begin{aligned} \hat{\varvec{{\varphi }}}_{xu}(t)= & {} [\hat{\varvec{x}}^{\tiny \text{ T }}(t-1)u(t-1),\hat{\varvec{x}}^{\tiny \text{ T }}(t-2)u(t\nonumber \\&-2),\ldots ,\hat{\varvec{x}}^{\tiny \text{ T }}(t-n)u(t-n)]^{\tiny \text{ T }}, \end{aligned}$$

(33)

$$\begin{aligned} \varvec{{\varphi }}_u(t)= & {} [u(t-1),u(t-2),\ldots ,u(t-n)]^{\tiny \text{ T }}, \end{aligned}$$

(34)

$$\begin{aligned} \hat{\varvec{x}}(t+1)= & {} \hat{\varvec{A}}(t)\hat{\varvec{x}}(t)+\hat{\varvec{B}}(t)\hat{\varvec{x}}(t)u(t)\nonumber \\&+\hat{\varvec{f}}(t)u(t),\quad \hat{\varvec{x}}(1)=\mathbf{1}_n/p_0, \end{aligned}$$

(35)

$$\begin{aligned} \hat{\varvec{A}}(t)= & {} \left[ \begin{array}{ccccc} -\hat{a}_1(t) &{} 1 &{} 0 &{} \cdots &{} 0\\ -\hat{a}_2(t) &{} 0 &{} 1 &{} \ddots &{} 0\\ \vdots &{}\vdots &{} \ddots &{} \ddots &{} \vdots \\ -\hat{a}_{n-1}(t) &{} 0 &{} \cdots &{} 0 &{} 1\\ -\hat{a}_n(t) &{} 0 &{} 0 &{} \cdots &{} 0 \end{array}\right] , \end{aligned}$$

(36)

$$\begin{aligned} \hat{\varvec{B}}(t)= & {} \left[ \begin{array}{c} \hat{\varvec{b}}_1(t) \\ \hat{\varvec{b}}_2(t) \\ \vdots \\ \hat{\varvec{b}}_n(t) \end{array}\right] ,\quad \hat{\varvec{b}}_i(t)\nonumber \\&=[\hat{b}_{i1}(t),\hat{b}_{i2}(t),\ldots ,\hat{b}_{in}(t)], \end{aligned}$$

(37)

$$\begin{aligned} \hat{\varvec{f}}(t)= & {} [\hat{f}_1(t), \hat{f}_2(t), \ldots , \hat{f}_{n-1}(t),\hat{f}_n(t)]^{\tiny \text{ T }}. \end{aligned}$$

(38)

When $p=1$, the O-MISG algorithm reduces to the state observer-based stochastic gradient (O-SG) algorithm. Then we study the convergence of the O-SG algorithm by establishing a recursive relation about the parameter estimation error and by using the martingale convergence theorem.

In identification, the output is linear about the parameter space, the algorithms are not sensitive to the initial values and can achieve global minima, and the final parameter estimates do not depend on the initial values. We have the following theorem about the convergence of the proposed algorithms.

Theorem 1

For the system in (17) and the O-SG algorithm in (26) to (38) $(p=1)$, assume that $\{v(t)\}$ is a white noise sequence with zero mean and variance $\sigma ^2$, i.e.,

$$\begin{aligned} \mathrm{E}[v(t)]=0, \quad \mathrm{E}[v^2(t)]{=}\sigma ^2, \quad \mathrm{E}[v(t)v(i)]{=}0, \quad i{\ne } t, \end{aligned}$$

and $r(t)\rightarrow \infty$, and there exist an integer N and a positive constant c independent of t such that the following strong excitation condition holds:

$$\begin{aligned} \sum _{j=0}^{N-1} \frac{\hat{\varvec{{\varphi }}}(j)\hat{\varvec{{\varphi }}}^{\tiny \text{ T }}(j)}{r(j)} \geqslant c\varvec{I}, \quad \mathrm{a.s.}\end{aligned}$$

Then the parameter estimation error given by the O-SG algorithm converges to zero.

The proofs of Theorems1 and 2 in the sequel can be done in a similar way to those in [47, 48].

4.3 The state observer-based recursive least squares algorithm

In order to improve the convergence rate and parameter estimation accuracy of the SG algorithm, we define the output vector $\varvec{Y}(t)$ and the information matrix $\varvec{H}(t)$ as

$$\begin{aligned}&\varvec{Y}(t):=\left[ \begin{array}{c} y(1) \\ y(2) \\ \vdots \\ y(t) \end{array}\right] \in {\mathbb {R}}^t,\nonumber \\&\quad \varvec{H}(t):=\left[ \begin{array}{c} \varvec{{\varphi }}^{\tiny \text{ T }}(1) \\ \varvec{{\varphi }}^{\tiny \text{ T }}(2) \\ \vdots \\ \varvec{{\varphi }}^{\tiny \text{ T }}(t) \end{array}\right] \in {\mathbb {R}}^{t\times ({n^2+2n})}. \end{aligned}$$

(39)

Based on the identification model in (17), we define the criterion function as

$$\begin{aligned} J(\varvec{{\theta }}):= & {} \sum _{j=1}^t[y(j)-\varvec{{\varphi }}^{\tiny \text{ T }}(j)\varvec{{\theta }}]^2 \nonumber \\= & {} [\varvec{Y}(t)-\varvec{H}(t)\varvec{{\theta }}]^{\tiny \text{ T }}[\varvec{Y}(t)-\varvec{H}(t)\varvec{{\theta }}] \nonumber \\= & {} \Vert \varvec{Y}(t)-\varvec{H}(t)\varvec{{\theta }}\Vert ^2. \end{aligned}$$

(40)

According to the least squares principle, and minimizing $J(\varvec{{\theta }})$, we can obtain the following recursive least squares algorithm:

$$\begin{aligned} \hat{\varvec{{\theta }}}(t)= & {} \hat{\varvec{{\theta }}}(t-1)+\varvec{P}(t)\varvec{{\varphi }}(t)[y(t)-\varvec{{\varphi }}^{\tiny \text{ T }}(t)\hat{\varvec{{\theta }}}(t-1)], \nonumber \\\end{aligned}$$

(41)

$$\begin{aligned} \varvec{P}^{-1}(t)= & {} \varvec{P}^{-1}(t-1)+\varvec{{\varphi }}(t) \varvec{{\varphi }}^{\tiny \text{ T }}(t),\quad \varvec{P}(0)\nonumber \\= & {} p_0\varvec{I}_{n^2+2n}>0. \end{aligned}$$

(42)

In order to avoid computing the inversion of the covariance matrix $\varvec{P}(t)$, applying the matrix inversion lemma

$$\begin{aligned} (\varvec{A}+\varvec{B}\varvec{C})^{-1}=\varvec{A}^{-1}-\varvec{A}^{-1}\varvec{B}(\varvec{I}+\varvec{C}\varvec{A}^{-1}\varvec{B})^{-1}\varvec{C}\varvec{A}^{-1} \end{aligned}$$

to (42) gives

$$\begin{aligned} \varvec{P}(t)=\varvec{P}(t-1)-\frac{\varvec{P}(t-1)\varvec{{\varphi }}(t)\varvec{{\varphi }}^{\tiny \text{ T }}(t)\varvec{P}(t-1)}{1+\varvec{{\varphi }}^{\tiny \text{ T }}(t)\varvec{P}(t-1)\varvec{{\varphi }}(t)}.\nonumber \\ \end{aligned}$$

(43)

Defining the gain vector $\varvec{L}(t):=\varvec{P}(t)\varvec{{\varphi }}(t)\in {\mathbb {R}}^{n^2+2n}$, we obtain

$$\begin{aligned} \varvec{L}(t)= & {} \varvec{P}(t{-}1)\varvec{{\varphi }}(t)-\frac{\varvec{P}(t{-}1)\varvec{{\varphi }}(t)\varvec{{\varphi }}^{\tiny \text{ T }}(t)\varvec{P}(t{-}1)\varvec{{\varphi }}(t)}{1{+}\varvec{{\varphi }}^{\tiny \text{ T }}(t)\varvec{P}(t{-}1)\varvec{{\varphi }}(t)}\nonumber \\= & {} \frac{\varvec{P}(t-1)\varvec{{\varphi }}(t)}{1+\varvec{{\varphi }}^{\tiny \text{ T }}(t)\varvec{P}(t-1)\varvec{{\varphi }}(t)}. \end{aligned}$$

(44)

Combining (43) and (44) gives

$$\begin{aligned} \varvec{P}(t)=[\varvec{I}-\varvec{L}(t)\varvec{{\varphi }}^{\tiny \text{ T }}(t)]\varvec{P}(t-1). \end{aligned}$$

(45)

Therefore, the recursive least squares algorithms in (41) and (42) can be equivalent to

$$\begin{aligned} \hat{\varvec{{\theta }}}(t)= & {} \hat{\varvec{{\theta }}}(t-1)+\varvec{L}(t)[y(t)-\varvec{{\varphi }}^{\tiny \text{ T }}(t)\hat{\varvec{{\theta }}}(t-1)], \quad \hat{\varvec{{\theta }}}(0)\nonumber \\= & {} \mathbf{1}_{n^2+2n}/p_0, \end{aligned}$$

(46)

$$\begin{aligned} \varvec{L}(t)= & {} \varvec{P}(t-1)\varvec{{\varphi }}(t)[1+\varvec{{\varphi }}^{\tiny \text{ T }}(t)\varvec{P}(t-1)\varvec{{\varphi }}(t)]^{-1}, \nonumber \\\end{aligned}$$

(47)

$$\begin{aligned} \varvec{P}(t)= & {} [\varvec{I}-\varvec{L}(t)\varvec{{\varphi }}^{\tiny \text{ T }}(t)]\varvec{P}(t-1). \end{aligned}$$

(48)

Aimed at the unmeasurable state variables included in the information vector $\varvec{{\varphi }}(t)$, we replace $\varvec{{\varphi }}(t)$ with its estimates $\hat{\varvec{{\varphi }}}(t)$ in the identification algorithm. Then, combined with the state observer, we can obtain the state observer-based recursive least squares (O-RLS) algorithm:

$$\begin{aligned} \hat{\varvec{{\theta }}}(t)= & {} \hat{\varvec{{\theta }}}(t-1)+\varvec{L}(t)[y(t)-\hat{\varvec{{\varphi }}}^{\tiny \text{ T }}(t)\hat{\varvec{{\theta }}}(t-1)], \quad \hat{\varvec{{\theta }}}(0)\nonumber \\= & {} \mathbf{1}_{n^2+2n}/p_0, \end{aligned}$$

(49)

$$\begin{aligned} \varvec{L}(t)= & {} \varvec{P}(t-1)\hat{\varvec{{\varphi }}}(t)[1+\hat{\varvec{{\varphi }}}^{\tiny \text{ T }}(t)\varvec{P}(t-1)\hat{\varvec{{\varphi }}}(t)]^{-1}, \end{aligned}$$

(50)

$$\begin{aligned} \varvec{P}(t)= & {} [\varvec{I}-\varvec{L}(t)\hat{\varvec{{\varphi }}}^{\tiny \text{ T }}(t)]\varvec{P}(t{-}1),\quad \varvec{P}(0){=}p_0\varvec{I}_{n^2+2n}, \nonumber \\\end{aligned}$$

(51)

$$\begin{aligned} \hat{\varvec{{\varphi }}}(t)= & {} [\hat{\varvec{{\varphi }}}_x^{\tiny \text{ T }}(t), \hat{\varvec{{\varphi }}}_{xu}^{\tiny \text{ T }}(t), \varvec{{\varphi }}_u^{\tiny \text{ T }}(t)]^{\tiny \text{ T }}, \end{aligned}$$

(52)

$$\begin{aligned} \hat{\varvec{{\varphi }}}_x(t)= & {} [-\hat{x}_1(t-1),-\hat{x}_1(t-2),\ldots ,-\hat{x}_1(t-n)]^{\tiny \text{ T }}, \nonumber \\\end{aligned}$$

(53)

$$\begin{aligned} \hat{\varvec{{\varphi }}}_{xu}(t)= & {} [\hat{\varvec{x}}^{\tiny \text{ T }}(t-1)u(t-1),\hat{\varvec{x}}^{\tiny \text{ T }}(t-2)u(t\nonumber \\&-2),\ldots ,\hat{\varvec{x}}^{\tiny \text{ T }}(t-n)u(t-n)]^{\tiny \text{ T }}, \end{aligned}$$

(54)

$$\begin{aligned} \varvec{{\varphi }}_u(t)= & {} [u(t-1),u(t-2),\ldots ,u(t-n)]^{\tiny \text{ T }}, \end{aligned}$$

(55)

$$\begin{aligned} \hat{\varvec{x}}(t+1)= & {} \hat{\varvec{A}}(t)\hat{\varvec{x}}(t)+\hat{\varvec{B}}(t)\hat{\varvec{x}}(t)u(t)+\hat{\varvec{f}}(t)u(t), \end{aligned}$$

(56)

$$\begin{aligned} \hat{\varvec{A}}(t)= & {} \left[ \begin{array}{ccccc} -\hat{a}_1(t) &{} 1 &{} 0 &{} \cdots &{} 0\\ -\hat{a}_2(t) &{} 0 &{} 1 &{} \ddots &{} 0\\ \vdots &{}\vdots &{} \ddots &{} \ddots &{} \vdots \\ -\hat{a}_{n-1}(t) &{} 0 &{} \cdots &{} 0 &{} 1\\ -\hat{a}_n(t) &{} 0 &{} 0 &{} \cdots &{} 0 \end{array}\right] , \end{aligned}$$

(57)

$$\begin{aligned} \hat{\varvec{B}}(t)= & {} \left[ \begin{array}{c} \hat{\varvec{b}}_1(t) \\ \hat{\varvec{b}}_2(t) \\ \vdots \\ \hat{\varvec{b}}_n(t) \end{array}\right] ,\quad \hat{\varvec{b}}_i(t)\nonumber \\= & {} [\hat{b}_{i1}(t),\hat{b}_{i2}(t),\ldots ,\hat{b}_{in}(t)], \end{aligned}$$

(58)

$$\begin{aligned} \hat{\varvec{f}}(t)= & {} [\hat{f}_1(t), \hat{f}_2(t), \ldots , \hat{f}_{n-1}(t),\hat{f}_n(t)]^{\tiny \text{ T }}. \end{aligned}$$

(59)

About the convergence of the parameter estimate $\varvec{{\theta }}(t)$, we have the following theorem.

Theorem 2

Provided that the controllable and observable system in (1) and (2) is stable (i.e., $\varvec{A}$ is stable), for the identification model in (17) and the state observer-based RLS parameter identification algorithm in (49) to (59), suppose that v(t) is a white noise sequence with zero mean and variance $\sigma ^2$, i.e., $\mathrm{E}[v(t)]=0$, $\mathrm{E}[v^2(t)]=\sigma ^2$, $\mathrm{E}[v(t)v(i)]=0(i\ne t)$, and that there exist positive constants $\alpha$ and $\beta$ such that the following persistent excitation conditions holds:

$$\begin{aligned} \alpha \varvec{I}\leqslant \frac{1}{t}\sum _{j=1}^{t}\hat{\varvec{{\varphi }}}(j)\hat{\varvec{{\varphi }}}^{\tiny \text{ T }}(j)\leqslant \beta \varvec{I},\quad \mathrm{a.s.}\end{aligned}$$

(60)

Then the parameter estimation error $\Vert \hat{\varvec{{\theta }}}(t)-\varvec{{\theta }}\Vert$ converges to zero.

Table 1 O-MISG parameter estimates and errors ($\sigma ^2= 0.50^2$)

Fig. 1

O-MISG parameter estimation errors $\delta$ versus t ($\sigma ^2=0.50^2$)

Table 2 O-RLS parameter estimates and errors ($\sigma ^2= 0.50^2$)

Fig. 2

O-RLS parameter estimation errors $\delta$ versus t ($\sigma ^2=0.50^2$)

Fig. 3

State $x_1(t)$ and the estimated state $\hat{x}_1(t)$ against t ($p=8$, $\sigma ^2=0.50^2$)

Fig. 4

State $x_2(t)$ and the estimated state $\hat{x}_2(t)$ against t ($p=8$, $\sigma ^2=0.50^2$)

The identification method proposed in this paper can be extended to multi-input multi-output systems through expanding the single input to multiple inputs and the single output to multiple outputs.

5 Numerical example

Consider the following observer canonical bilinear state space system:

The parameter vector to be identified is

$$\begin{aligned} \varvec{{\theta }}= & {} [a_1,a_2,b_{11},b_{12},b_{21},b_{22},f_1,f_2]^{\tiny \text{ T }}\\&=[-0.19,-0.23,0.01,0.06,\\&\quad 0.15,0.14,1.17,1.14]^{\tiny \text{ T }}. \end{aligned}$$

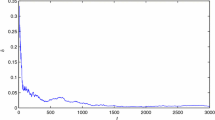
In simulation, the input $\{u(t)\}$ is taken as an uncorrelated persistent excitation signal sequence with zero mean and unit variance, and $\{v(t)\}$ as a white noise sequence with zero mean and variance $\sigma ^2$. Take the data length $L=5000$, and apply the O-MISG algorithm in (26) to (38) and the O-RLS algorithm in (49) to (59) to estimate the states and parameters of this bilinear system. The O-MISG parameter estimates and errors $\delta =\Vert \hat{\varvec{{\theta }}}(t)-\varvec{{\theta }}\Vert /\Vert \varvec{{\theta }}\Vert$ with different innovation length p are shown in Table 1 and Fig. 1 with $\sigma ^2=0.50^2$. The O-RLS parameter estimates and errors $\sigma ^2=0.50^2$ are shown in Table 2 and Fig. 2. The states $x_{i}(t)$ and their estimates $\hat{x}_{i}(t)$ against t are shown in Figs. 3 and 4.

For comparison with the noise variance $\sigma ^2=0.50^2$, Tables 3, 4 and Figs. 5, 6 give the O-MISG and O-RLS parameter estimates and the parameter estimation error curves with $\sigma ^2=0.10^2$. The states $x_{i}(t)$ and their estimates $\hat{x}_{i}(t)$ against t are shown in Figs. 7 and 8.

Table 3 O-MISG parameter estimates and errors ($\sigma ^2= 0.10^2$)

Table 4 O-RLS parameter estimates and errors ($\sigma ^2= 0.10^2$)

Fig. 5

O-MISG parameter estimation errors $\delta$ versus t ($\sigma ^2=0.10^2$)

Fig. 6

O-RLS parameter estimation errors $\delta$ versus t ($\sigma ^2=0.10^2$)

Fig. 7

State $x_1(t)$ and the estimated state $\hat{x}_1(t)$ against t ($p=8$, $\sigma ^2=0.10^2$)

Fig. 8

State $x_2(t)$ and the estimated state $\hat{x}_2(t)$ against t ($p=8$, $\sigma ^2=0.10^2$)

From Tables 1, 2, 3, 4 and Figs. 1, 2, 3, 4, 5, 6, 7, 8, we can draw the following conclusions.

• (1) The O-RLS algorithm is superior to the O-SG algorithm in the parameter estimation accuracy and convergence rates.

• (2) The parameter estimation errors $\delta$ of the O-MISG algorithm become smaller with the innovation length p increasing and converge to zero fast if the innovation length p is large enough, and the data length tends to infinity.

• (3) Under the same innovation length, a smaller noise variance leads to higher parameter estimation accuracy and a faster convergence rate.

• (4) The estimated states are very close to the actual states of the system.

6 Conclusions

This paper considers the parameter identification problems of bilinear state space systems using the multi-innovation theory and the least squares principle. The utilization of the non-singular linear transformation for general bilinear systems reduces the number of the parameters of the identification model, a state observer-based multi-innovation stochastic gradient algorithm and a state observer-based recursive least squares algorithm are derived for observer canonical bilinear state space systems. The convergence analysis indicates that the algorithms proposed are effective and the parameter estimates given by the proposed algorithms can converge to their true values. The numerical simulation results indicate that the designed state observer makes the estimated states close to the actual states of the systems. The O-MISG and O-RLS algorithm can give effective parameter estimates compared with the O-SG algorithm. The multi-innovation identification method can improve the parameter estimate accuracy and the convergence rates compared with the single-innovation identification methods. The proposed algorithms can realize the interactive estimation for unknown states and parameters for bilinear systems.

Although the algorithms in the paper are developed for single-input single-output systems with white noise disturbance, the methods can be extended to identify multiple-input multiple-output systems by expanding the single input to multiple inputs and the single output to multiple outputs. They can also be extended to study identification problems of other linear and nonlinear multivariable systems with colored noises and applied to other fields [49,50,51].