1 Introduction

The parameter identification of linear systems has been mature [31, 32], and many identification methods have been developed, e.g., the recursive identification methods [25] and the iterative identification methods [34, 44]. By comparison, there is a lot of research space for the parameter identification for bilinear stochastic systems. The identification of bilinear systems has been studied for a long history, at least more than four decades. Earlier work on identification for bilinear systems exists: Karanam et al. [26] utilized the Walsh functions for bilinear system identification; Fnaiech and Ljung [19] discussed recursive identification methods for bilinear systems. In respect of nonlinear system identification, the heuristic optimization techniques seem to be very helpful and have been used in system identification [3, 5], control engineering [6, 12, 30], parameter estimation [2, 4] and the Lorenz chaotic systems [1]. By means of the heuristic algorithms, Modares et al. [29] proposed an adaptive particle swarm optimization (PSO) algorithm to estimate the parameters of bilinear systems, increasing the convergence speed and accuracy compared with the basic PSO algorithm. Gibson et al. [20] developed a maximum-likelihood parameter estimation algorithm of bilinear systems. Inspired by the fixed point theory, Li et al. [27] presented an iterative algorithm to recursively identify bilinear models. Lopes dos Santos et al. [28] identified the Wiener–Hammerstein bilinear system using an iterative bilinear subspace identification algorithm.

In the field of nonlinear system identification, much work has been performed for decades [41]. A class of nonlinear systems can be described by a static nonlinearity followed by a linear subsystem. For such nonlinear systems, a decomposition-based Newton iterative identification method [14] and a hierarchical parameter estimation algorithm [33] were developed. Also, Chen et al. [9] presented a hierarchical gradient parameter estimation algorithm for Hammerstein nonlinear systems using the key term separation principle. Wang and Zhang [43] derived an improved least squares identification algorithm for multivariable Hammerstein systems.

The least squares (LS) methods are basic in system identification [18, 39]. For example, for a class of linear-in-parameter output error moving average systems, Wang and Tang proposed an auxiliary model-based recursive least squares (RLS) algorithm [42]; Hu [21] developed iterative and recursive LS algorithms to estimate the parameters of moving average systems; Cao et al. [7] have presented a novel two-dimensional RLS identification approach with soft constraint for batch processes, which can improve the identification performance by exploiting information not only from time direction within a batch but also along batches. Recently, Ding et al. [15] presented an auxiliary model-based least squares algorithm for a dual-rate state space system with time delay using the data filtering and a Kalman state filtering-based least squares iterative parameter estimation algorithm for observer canonical state space systems using decomposition [17].

Multi-innovation identification is an important branch of system identification [13]. The innovation is the valuable information which can improve parameter or state estimation accuracy. In this respect, Ding [13] proposed the innovation-based identification theory and methods, by expanding a scalar innovation to an innovation vector and then to an innovation matrix. Based on this theory, Hu et al. [22] suggested a multi-innovation generalized extended stochastic gradient algorithm for output nonlinear autoregressive moving average systems.

This paper focuses on the parameter identification problems of bilinear stochastic systems. It is organized as follows. Section 2 derives the identification model for bilinear systems. Sections 3 and 4 propose a RLS identification algorithm and a multi-innovation stochastic gradient (MISG) identification algorithm. Section 5 provides two simulation examples to prove the validity of the proposed algorithms. Finally, some concluding remarks are made in Sect. 6.

2 The Identification Model for Bilinear Systems

In this section, we describe a bilinear system and derive its identification model for parameter estimation. Let us define some notation. “\(A=:X\)” or “\(X:=A\)” represents “A is defined as X,” and \(z^{-1}\) stands for a unit forward shift operator with the following properties:

$$\begin{aligned} z^nf(t)= & {} f(t+n),\\ z^nf(t)g(t)= & {} [z^nf(t)]g(t)=f(t+n)g(t),\\ z^n[f(t)g(t)]= & {} f(t+n)z^ng(t)=f(t+n)g(t+n). \end{aligned}$$

Assume that the bilinear systems under consideration have the following observability canonical form [11]:

$$\begin{aligned} \varvec{x}(t+1)= & {} \varvec{A}\varvec{x}(t)+\varvec{B}\varvec{x}(t)u(t)+\varvec{f}u(t), \end{aligned}$$
(1)
$$\begin{aligned} y(t)= & {} \varvec{h}\varvec{x}(t), \end{aligned}$$
(2)

where \(\varvec{x}(t):=[x_1(t), x_2(t), \cdots , x_n(t)]^{\tiny \text{ T }}\) is the n-dimensional state vector, \(u(t)\in {\mathbb R}\) and \(y(t)\in {\mathbb R}\) are the input and output of the system, respectively, and \(\varvec{A}\in {\mathbb R}^{n\times n}\), \(\varvec{B}\in {\mathbb R}^{n\times n}\), \(\varvec{f}\in {\mathbb R}^n\) and \(\varvec{h}\in {\mathbb R}^{1\times n}\) are constant matrices and vectors:

Define the following polynomials:

$$\begin{aligned} A(z):= & {} 1+a_1z^{-1}+a_2z^{-2}+\cdots +a_nz^{-n}, \\ B(z):= & {} b_1z^{-1}+b_2z^{-2}+\cdots +b_nz^{-n}, \\ C(z):= & {} c_1z^{-1}+c_2z^{-2}+\cdots +c_nz^{-n}, \\ D(z):= & {} d_2z^{-2}+d_3z^{-3}+\cdots +d_nz^{-n}. \end{aligned}$$

The coefficients \(c_i\) and \(d_i\) can be determined using \(a_i\), \(b_i\) and \(f_i\). Referring to the method in [11], eliminating the state vector \(\varvec{x}(t)\) in (1)–(2), we have the following input–output relation,

$$\begin{aligned}{}[A(z)+u(t-n)B(z)]y(t)=[C(z)+u(t-n)D(z)]u(t). \end{aligned}$$

Since the practical systems are always interfered with various factors, e.g., stochastic noise, introducing a noise term \(v(t)\in {\mathbb R}\), we have

$$\begin{aligned} {[}A(z)+u(t-n)B(z){]}y(t)=[C(z)+u(t-n)D(z)]u(t)+v(t). \end{aligned}$$
(3)

Define the parameter vector \({\varvec{\theta }}\) and the information vector \({\varvec{\varphi }}(t)\) as

$$\begin{aligned} {\varvec{\theta }}:= & {} [\varvec{a}^{\tiny \text{ T }}, \varvec{b}^{\tiny \text{ T }}, \varvec{c}^{\tiny \text{ T }}, \varvec{d}^{\tiny \text{ T }}]^{\tiny \text{ T }}\in {\mathbb R}^{4n-1},\\ {\varvec{\varphi }}(t):= & {} \left[ {\varvec{\varphi }}_y^{\tiny \text{ T }}(t), u(t-n){\varvec{\varphi }}_y^{\tiny \text{ T }}(t), {\varvec{\varphi }}_u^{\tiny \text{ T }}(t), u(t-n){\varvec{\varphi }}_u^{\tiny \text{ T }}(t)\right] ^{\tiny \text{ T }}\in {\mathbb R}^{4n-1}, \end{aligned}$$

where

$$\begin{aligned} \varvec{a}:= & {} [a_1, a_2, \ldots , a_n]^{\tiny \text{ T }}\in {\mathbb R}^n, \quad \varvec{b}:=[b_1, b_2, \ldots , b_n]^{\tiny \text{ T }}\in {\mathbb R}^n, \\ \varvec{c}:= & {} [c_1, c_2, \ldots , c_n]^{\tiny \text{ T }}\in {\mathbb R}^n, \quad \varvec{d}:=[d_2, d_3, \ldots , d_n]^{\tiny \text{ T }}\in {\mathbb R}^{n-1},\\ {\varvec{\varphi }}_y(t):= & {} [-y(t-1), -y(t-2), \ldots , -y(t-n)]^{\tiny \text{ T }}\in {\mathbb R}^n,\\ {\varvec{\varphi }}_u(t):= & {} [u(t-1), u(t-2), \ldots , u(t-n)]^{\tiny \text{ T }}\in {\mathbb R}^n,\\ {\varvec{\varphi }}_{\bar{u}}(t):= & {} [u(t-2), u(t-3), \ldots , u(t-n)]^{\tiny \text{ T }}\in {\mathbb R}^{n-1}. \end{aligned}$$

Inserting A(z), B(z), C(z) and D(z) into (3) leads to

$$\begin{aligned} y(t)={\varvec{\varphi }}^{\tiny \text{ T }}(t){\varvec{\theta }}+v(t). \end{aligned}$$
(4)

Equation (4) is the identification model of the bilinear system with white noise.

The objective of the paper is to develop new identification methods for estimating the parameters \(a_i\), \(b_i\), \(c_i\) and \(d_i\) or the parameter vectors \(\varvec{a}\), \(\varvec{b}\), \(\varvec{c}\) and \(\varvec{d}\), from the observation data \(\{u(t), y(t): t=1, 2, 3, \ldots \}\).

3 The Recursive Least Squares Identification Algorithm

In this part, aiming at the model in (4), we propose the RLS estimation algorithm so that online identification can be carried out. Using the data with \(t=1,2, \ldots , t\), we define

$$\begin{aligned} \varvec{Y}_t:=\left[ \begin{array}{c} y(1) \\ y(2) \\ \vdots \\ y(t) \end{array}\right] \in {\mathbb R}^t, \quad {\varvec{\varGamma }}_t:=\left[ \begin{array}{c} {\varvec{\varphi }}^{\tiny \text{ T }}(1) \\ {\varvec{\varphi }}^{\tiny \text{ T }}(2) \\ \vdots \\ {\varvec{\varphi }}^{\tiny \text{ T }}(t) \end{array}\right] \in {\mathbb R}^{t\times (4n-1)}, \quad \varvec{V}_t:=\left[ \begin{array}{c} v(1) \\ v(2) \\ \vdots \\ v(t) \end{array}\right] \in {\mathbb R}^t. \end{aligned}$$

According to (4), define a quadratic criterion function

$$\begin{aligned} J({\varvec{\theta }}):= & {} (\varvec{Y}_t-{\varvec{\varGamma }}_t{\varvec{\theta }})^{\tiny \text{ T }} (\varvec{Y}_t-{\varvec{\varGamma }}_t{\varvec{\theta }})\\= & {} \sum _{j=1}^t\left[ \varvec{y}(j)-{\varvec{\varphi }}^{\tiny \text{ T }}(j){\varvec{\theta }}\right] ^2 \end{aligned}$$

Minimizing the criterion function \(J({\varvec{\theta }})\) and letting the partial derivative of \(J({\varvec{\theta }})\) with regard to \({\varvec{\theta }}\) be zero, we obtain the least squares estimate of \({\varvec{\theta }}\):

$$\begin{aligned} \hat{{\varvec{\theta }}}(t)=\left( {\varvec{\varGamma }}_t^{\tiny \text{ T }}{\varvec{\varGamma }}_t\right) ^{-1} {\varvec{\varGamma }}_t^{\tiny \text{ T }}\varvec{Y}_t, \end{aligned}$$
(5)

where \(\hat{{\varvec{\theta }}}(t)\) is the estimate of \({\varvec{\theta }}\) at time t, \(\hat{{\varvec{\theta }}}(0)\) is a very small real vector. To derive the recursive least squares algorithm conveniently, define the covariance matrix \(\varvec{P}(t)\) as

$$\begin{aligned} \varvec{P}^{-1}(t):={\varvec{\varGamma }}_t^{\tiny \text{ T }}{\varvec{\varGamma }}_t\in {\mathbb R}^{4n-1}. \end{aligned}$$
(6)

Using the definition of \({\varvec{\varGamma }}_t\), it follows that

$$\begin{aligned} \varvec{P}^{-1}(t)= & {} \sum _{j=1}^t{\varvec{\varphi }}(j){\varvec{\varphi }}^{\tiny \text{ T }}(j) =\varvec{P}^{-1}(t-1)+{\varvec{\varphi }}(t){\varvec{\varphi }}^{\tiny \text{ T }}(t),\quad \varvec{P}(0)=p_0 \varvec{I}_{4n-1}>0.\qquad \quad \end{aligned}$$
(7)

To avoid computing the matrix inversion of \(\varvec{P}(t)\), applying the matrix inverse lemma [18]

$$\begin{aligned} (\varvec{A}+\varvec{B}\varvec{C})^{-1}=\varvec{A}^{-1}-\varvec{A}^{-1} \varvec{B}(\varvec{I}+\varvec{C}\varvec{A}^{-1}\varvec{B})^{-1}\varvec{C}\varvec{A}^{-1} \end{aligned}$$

to (7) gives

$$\begin{aligned} \varvec{P}(t)=\varvec{P}(t-1)-\varvec{P}(t-1){\varvec{\varphi }}(t) [1+{\varvec{\varphi }}^{\tiny \text{ T }}(t)\varvec{P}(t-1){\varvec{\varphi }}(t)]^{-1} {\varvec{\varphi }}^{\tiny \text{ T }}(t)\varvec{P}(t-1). \end{aligned}$$
(8)

Using (6) and from (5), we have

$$\begin{aligned} \hat{{\varvec{\theta }}}(t)= & {} \varvec{P}(t){\varvec{\varGamma }}_t^{\tiny \text{ T }}\varvec{Y}_t\nonumber \\= & {} \varvec{P}(t)\left[ {\varvec{\varGamma }}_{t-1}^{\tiny \text{ T }}, {\varvec{\varphi }}(t)\right] \left[ \begin{array}{c} \varvec{Y}_{t-1} \\ y(t) \end{array} \right] \nonumber \\= & {} \varvec{P}(t)\left[ {\varvec{\varGamma }}_{t-1}^{\tiny \text{ T }}\varvec{Y}_{t-1}+{\varvec{\varphi }}(t)y(t)\right] \nonumber \\= & {} \varvec{P}(t)\left[ \varvec{P}^{-1}(t-1)\varvec{P}(t-1){\varvec{\varGamma }}_{t-1}^{\tiny \text{ T }}\varvec{Y}_{t-1}+{\varvec{\varphi }}(t)y(t)\right] \nonumber \\= & {} \varvec{P}(t)\left[ \varvec{P}^{-1}(t-1)\hat{{\varvec{\theta }}}(t-1)+{\varvec{\varphi }}(t)y(t)\right] \nonumber \\= & {} \varvec{P}(t)\left[ \varvec{P}^{-1}(t)-{\varvec{\varphi }}(t){\varvec{\varphi }}^{\tiny \text{ T }}(t)\right] \hat{{\varvec{\theta }}}(t-1)+\varvec{P}(t){\varvec{\varphi }}(t)y(t)\nonumber \\= & {} \hat{{\varvec{\theta }}}(t-1)+\varvec{P}(t){\varvec{\varphi }}(t)\left[ y(t)-{\varvec{\varphi }}^{\tiny \text{ T }}(t)\hat{{\varvec{\theta }}}(t-1)\right] . \end{aligned}$$
(9)

Combining (8) and (9), we can obtain the RLS algorithm for estimating the parameter vector \({\varvec{\theta }}\) in (4):

$$\begin{aligned} \hat{{\varvec{\theta }}}(t)= & {} \hat{{\varvec{\theta }}}(t-1)+ \varvec{P}(t){\varvec{\varphi }}(t)\left[ y(t)-{\varvec{\varphi }}^{\tiny \text{ T }}(t)\hat{{\varvec{\theta }}}(t-1)\right] , \end{aligned}$$
(10)
$$\begin{aligned} \varvec{P}(t)= & {} \varvec{P}(t-1)-\varvec{P}(t-1){\varvec{\varphi }}(t)\left[ 1+{\varvec{\varphi }}^{\tiny \text{ T }}(t)\varvec{P}(t-1){\varvec{\varphi }}(t)\right] ^{-1}{\varvec{\varphi }}^{\tiny \text{ T }}(t)\varvec{P}(t-1), \nonumber \\ \end{aligned}$$
(11)
$$\begin{aligned} {\varvec{\varphi }}^{\tiny \text{ T }}(t)= & {} \left[ {\varvec{\varphi }}_y^{\tiny \text{ T }}(t), u(t-n){\varvec{\varphi }}_y^{\tiny \text{ T }}(t), {\varvec{\varphi }}_u^{\tiny \text{ T }}(t), u(t-n){\varvec{\varphi }}_{\bar{u}}^{\tiny \text{ T }}(t)\right] , \end{aligned}$$
(12)
$$\begin{aligned} {\varvec{\varphi }}_u^{\tiny \text{ T }}(t)= & {} \left[ u(t-1), u(t-2), \ldots , u(t-n)\right] , \end{aligned}$$
(13)
$$\begin{aligned} {\varvec{\varphi }}_{\bar{u}}(t)= & {} \left[ u(t-2), u(t-3), \ldots , u(t-n)\right] ^{\tiny \text{ T }}, \nonumber \\ {\varvec{\varphi }}_y^{\tiny \text{ T }}(t)= & {} \left[ -y(t-1), -y(t-2), \ldots , -y(t-n)\right] , \end{aligned}$$
(14)
$$\begin{aligned} \hat{{\varvec{\theta }}}= & {} \left[ \hat{\varvec{a}}^{\tiny \text{ T }}(t), \hat{\varvec{b}}^{\tiny \text{ T }}(t), \hat{\varvec{c}}^{\tiny \text{ T }}(t), \hat{\varvec{d}}^{\tiny \text{ T }}(t)\right] ^{\tiny \text{ T }},\nonumber \\ \hat{\varvec{a}}(t)= & {} \left[ \hat{a}_1(t), \hat{a}_2(t), \ldots , \hat{a}_n(t)\right] ^{\tiny \text{ T }}, \quad \hat{\varvec{b}}(t)=\left[ \hat{b}_1(t), \hat{b}_2(t), \ldots , \hat{b}_n(t)\right] ^{\tiny \text{ T }}, \nonumber \\ \hat{\varvec{c}}(t)= & {} \left[ \hat{c}_1(t), \hat{c}_2(t), \ldots , \hat{c}_n(t)\right] ^{\tiny \text{ T }}, \quad \hat{\varvec{d}}(t)=\left[ \hat{d}_2(t), \hat{d}_3(t), \ldots , \hat{d}_n(t)\right] ^{\tiny \text{ T }}. \end{aligned}$$
(15)

The computational amount of the RLS algorithm for bilinear systems is given in Table 1 and its has \((64n^2-8n-2)\) flops. The RLS algorithm is simple and can be implemented online.

Table 1 Computation load of the RLS algorithm
Full size table

4 The Multi-Innovation Stochastic Gradient Identification Algorithm

Based on the identification model in (4), we can acquire the stochastic gradient (SG) identification algorithm;

$$\begin{aligned} \hat{{\varvec{\theta }}}(t)= & {} \hat{{\varvec{\theta }}}(t-1)+\frac{{\varvec{\varphi }}(t)}{r(t)}e(t), \end{aligned}$$
(16)
$$\begin{aligned} e(t)= & {} y(t)-{\varvec{\varphi }}^{\tiny \text{ T }}(t)\hat{{\varvec{\theta }}}(t-1), \end{aligned}$$
(17)
$$\begin{aligned} r(t)= & {} r(t-1)+\Vert {\varvec{\varphi }}(t)\Vert ^2,\ r(0)=1, \end{aligned}$$
(18)

where the norm of a matrix \(\varvec{X}\) is defined by \(\Vert \varvec{X}\Vert ^2:=\hbox {tr}[\varvec{X}\varvec{X}^{\tiny \text{ T }}]\). It is well known that the SG algorithm has slow convergence rates, in order to improve the situation, expanding the scalar innovation e(t) to an innovation vector [40]:

$$\begin{aligned} \varvec{E}(p,t):=\left[ \begin{array}{c} y(t)-{\varvec{\varphi }}^{\tiny \text{ T }}(t) \hat{{\varvec{\theta }}}(t-1) \\ y(t-1)-{\varvec{\varphi }}^{\tiny \text{ T }}(t-1) \hat{{\varvec{\theta }}}(t-1) \\ \vdots \\ y(t-p+1)-{\varvec{\varphi }}^{\tiny \text{ T }} (t-p+1)\hat{{\varvec{\theta }}}(t-1) \end{array}\right] \in {\mathbb R}^p. \end{aligned}$$
(19)

Define the information matrix \({\varvec{\varPhi }}(p, t)\) and the stacked output vector \(\varvec{Y}(p, t)\) as

$$\begin{aligned} {\varvec{\varPhi }}(p,t):= & {} [{\varvec{\varphi }}(t), {\varvec{\varphi }}(t-1), \ldots , {\varvec{\varphi }}(t-p+1)]\in {\mathbb R}^{(4n-1) \times p}, \\ \varvec{Y}(p,t):= & {} [y(t), y(t-1), \ldots , y(t-p+1)]^{\tiny \text{ T }}\in {\mathbb R}^p. \end{aligned}$$

Then the innovation vector \(\varvec{E}(p, t)\) in (19) can be expressed as

$$\begin{aligned} \varvec{E}(p, t)=\varvec{Y}(p, t)-{\varvec{\varPhi }}^{\tiny \text{ T }}(p, t)\hat{{\varvec{\theta }}}(t-1). \end{aligned}$$

We can obtain the MISG algorithm for bilinear systems:

$$\begin{aligned} \hat{{\varvec{\theta }}}(t)= & {} \hat{{\varvec{\theta }}}(t-1)+\frac{{\varvec{\varPhi }}(p,t)}{r(t)}\varvec{E}(p,t),\ \hat{{\varvec{\theta }}}(0)=\mathbf{1}_{4n-1}/p_0, \end{aligned}$$
(20)
$$\begin{aligned} \varvec{E}(p,t)= & {} \varvec{Y}(p,t)-{\varvec{\varPhi }}^{\tiny \text{ T }}(p,t)\hat{{\varvec{\theta }}}(t-1), \end{aligned}$$
(21)
$$\begin{aligned} r(t)= & {} r(t-1)+\Vert {\varvec{\varPhi }}(p,t)\Vert ^2,\ r(0)=1, \end{aligned}$$
(22)
$$\begin{aligned} \varvec{Y}(p,t)= & {} [y(t), y(t-1), \ldots , y(t-p+1)]^{\tiny \text{ T }}, \end{aligned}$$
(23)
$$\begin{aligned} {\varvec{\varPhi }}(p,t)= & {} [{\varvec{\varphi }}(t), {\varvec{\varphi }}(t-1), \ldots , {\varvec{\varphi }}(t-p+1)], \end{aligned}$$
(24)
$$\begin{aligned} {\varvec{\varphi }}^{\tiny \text{ T }}(t)= & {} \left[ {\varvec{\varphi }}_y^{\tiny \text{ T }}(t), u(t-n){\varvec{\varphi }}_y^{\tiny \text{ T }}(t), {\varvec{\varphi }}_u^{\tiny \text{ T }}(t), u(t-n){\varvec{\varphi }}_{\bar{u}}^{\tiny \text{ T }}(t)\right] , \end{aligned}$$
(25)
$$\begin{aligned} {\varvec{\varphi }}_u^{\tiny \text{ T }}(t)= & {} [u(t-1), u(t-2), \ldots , u(t-n)], \nonumber \\ {\varvec{\varphi }}_{\bar{u}}(t)= & {} [u(t-2), u(t-3), \ldots , u(t-n)]^{\tiny \text{ T }}, \end{aligned}$$
(26)
$$\begin{aligned} {\varvec{\varphi }}_y^{\tiny \text{ T }}(t)= & {} [-y(t-1), -y(t-2), \ldots , -y(t-n)], \end{aligned}$$
(27)
$$\begin{aligned} \hat{{\varvec{\theta }}}(t)= & {} \left[ \hat{\varvec{a}}^{\tiny \text{ T }}(t), \hat{\varvec{b}}^{\tiny \text{ T }}(t), \hat{\varvec{c}}^{\tiny \text{ T }}(t), \hat{\varvec{d}}^{\tiny \text{ T }}(t)\right] ^{\tiny \text{ T }}. \end{aligned}$$
(28)

In this algorithm, \(\varvec{E}(p,t)\in {\mathbb R}^p\) is an innovation vector (i.e., multi-innovation). When \(p=1\), the MISG algorithm reduces to the SG algorithm.

The advantage of the multi-innovation identification method is that it makes full use of the identification innovations and can raise the convergence speed to a certain degree, and the stationarity of data can improve identification accuracy. The computation amount of the MISG algorithm for bilinear systems is \((24pn-5p)\) flops as given in Table 2.

Table 2 Computation load of the MISG algorithm
Full size table
Table 3 RLS parameter estimates and errors
Full size table
Fig. 1
figure 1

RLS parameter estimation errors \(\delta \) versus t

Full size image
Table 4 SG parameter estimates and errors
Full size table
Table 5 MISG gradient parameter estimates and errors
Full size table

Equation (22) can be modified as

$$\begin{aligned} r(t)=r(t-1)+\Vert {\varvec{\varphi }}(t)\Vert ^2,\ r(0)=1. \end{aligned}$$
(29)

In order to track the time-varying parameters, we must introducing a forgetting factor \(\lambda \) in (22) and get

$$\begin{aligned} r(t)=\lambda r(t-1)+\Vert {\varvec{\varPhi }}(p,t)\Vert ^2,\ r(0)=1, \end{aligned}$$
(30)

or

$$\begin{aligned} r(t)=\lambda r(t-1)+\Vert {\varvec{\varphi }}(t)\Vert ^2,\ r(0)=1. \end{aligned}$$
(31)

5 Examples

Example 1

Consider the following bilinear system:

$$\begin{aligned}&[A(z)+u(t-n)B(z)]y(t)=[C(z)+u(t-n)D(z)]u(t)+v(t), \\&A(z)=1+a_1z^{-1}+a_2z^{-2}=1+0.90z^{-1}+0.52z^{-2}, \\&B(z)=b_1z^{-1}+b_2z^{-2}=-0.793z^{-1}-0.312z^{-2}, \\&C(z)=c_1z^{-1}+c_2z^{-2}=0.315z^{-1}-0.6365z^{-2}, \\&D(z)=d_2z^{-2}=-0.2498z^{-2}. \end{aligned}$$

The parameter vector to be estimated is given by

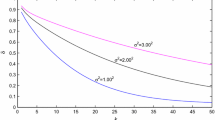
$$\begin{aligned} {\varvec{\theta }}= & {} [a_1, a_2, b_1, b_2, c_1, c_2, d_2]^{\tiny \text{ T }}\\= & {} [0.90, 0.52, -0.793, -0.312, 0.315, -0.6365, -0.2498]^{\tiny \text{ T }}. \end{aligned}$$

In simulation, we adopt an independent persistent excitation signal sequence with zero mean and unit variance as the input \(\{u(t)\}\), and a white noise sequence with zero mean and variance \(\sigma ^2=0.50^2\) as \(\{v(t)\}\). Applying the recursive least squares algorithm in (10)–(15) to compute the parameters estimates \(\hat{{\varvec{\theta }}}(t)\) of the system, the parameter estimates and the estimation errors are given in Table 3, the estimation errors \(\delta \) versus the data length t is shown in Fig. 1. The parameter estimation errors are computed by \(\delta :=\Vert \hat{{\varvec{\theta }}}(t)-{\varvec{\theta }}\Vert /\Vert {\varvec{\theta }}\Vert \).

From Table 3 and Fig. 1, we can see that the RLS parameter estimation errors become smaller with the increase of t.

Fig. 2
figure 2

Parameter estimation errors \(\delta \) versus t

Full size image

Example 2

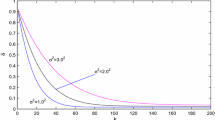
Consider the system in Example 1 and the same simulation conditions. Applying the MISG algorithm to estimate the parameters of this system, the parameter estimates and their errors are shown in Tables 4, 5 and Fig. 2, where Table 4 lists the parameter estimates and errors given by the MISG algorithm when \(p=1\), i.e., the stochastic gradient algorithm.

From Table 5 and Fig. 2, it is observed that the MISG algorithm can identify the parameters of the bilinear system. Meanwhile, the estimation errors become smaller as the innovation length increases. These results show that the proposed algorithms work well for bilinear systems with white noise.

6 Conclusions

This paper derives the identification model of bilinear systems. On the basis of the obtained model, we present a RLS algorithm and an MISG algorithm for bilinear stochastic systems and give the state estimation algorithm. The simulation results indicate that for the multi-innovation identification algorithm, increasing the innovation length can enhance the parameter estimation accuracy, reducing the sensitivity of the algorithm to noise. The algorithms in this paper can be extended to study the identification problems of other bilinear systems, linear and nonlinear systems with colored noise [16, 33, 35], stochastic multivariable systems [36–38], uncertain chaotic delayed nonlinear systems [23] and hybrid switching–impulsive dynamical networks [24], and applied to other fields [8, 10].

When the uncertainty in parameters is small, the obtained parameter estimates are close to their true values. The estimates can be taken as the real parameters for controller design when the errors are tolerable.