1 Introduction

A recent trend of chaos theory is devoted to the development of new chaotic systems which have unique features and unusual behaviours. The behaviours of a dynamical (chaotic/hyperchaotic) system are characterised by its equilibrium points [1]. Many recent papers are reported based on the properties of equilibrium points [1,2,3,4,5,6,7]. Hence, developing a new chaotic system which has unique features and unusual behaviours is the motivation of this paper.

Table 1 Categorisation of the 4-D hyperchaotic/chaotic systems with many number of equilibria
Full size table

The available chaotic or hyperchaotic systems are mainly categorised into two parts. These are self-excited attractors and hidden attractors [8]. The widely known chaotic systems like Lorenz [9], Lu [10], Chen [11] systems and system in [12, 13], etc. belong to self-excited attractors. These attractors have basin of attractions associated with the unstable equilibrium points. However, in case of hidden attractors, basin of attraction does not intersect with any small neighbourhood of any equilibrium points [14]. The analytical investigation, numerical localisation and computation of the hidden chaotic attractors are more difficult compared with the self-excited attractors [15,16,17]. The localisations of the hidden chaotic Chua attractors are discussed in [16, 17]. The control of multistability in the hidden chaotic attractors is reported in [18]. Hidden chaotic attractors are appeared in many applications like in induction motor with bound rotor [19], in convective fluid motion in rotating cavity [20]. The system which has no equilibrium point or only stable equilibrium points or a line of equilibria attractors is the type of hidden attractor [5, 8, 21,22,23,24,25]. Some recent category of hidden attractor is reported with only unstable node equilibrium point in a chaotic system [24].

Usually chaotic or hyperchaotic system has countable number of equilibria; one equilibrium point [26], two equilibrium points [27], three equilibrium points [9] or four equilibrium points [28]. Recently some chaotic or hyperchaotic systems are reported with many equilibrium points like [29, 30]. Some papers are available on these types of systems. Few papers are available on system which has line of equilibria [2, 31, 32]. A 3-D system with curve of equilibria is reported in [33]; a 3-D system with surface of equilibria is reported in [7]; [3, 34] reported a 3-D system with circle of equilibria. Very recently, a 4-D chaotic system with plane of equilibria is reported in [5]. However, most of the reported systems with many number of equilibria are derived from a general algebraic expression [2, 3, 5, 8, 25, 29, 33, 34] using extensive numerical search. The reported 4-D systems with many number of equilibria are summarised in Table 1. Thus, developing the simplest new 4-D chaotic system from a conventional chaotic system which has many number of equilibria (line of equilibria) with unique properties is still a challenging task.

In this paper, the simplest 4-D chaotic system with line of equilibria is reported. The system is different from the category of the rare attractor, or new category of rare attractor [5, 37, 38]. In the proposed system, the basin of attraction of the chaotic attractor intersect the line of equilibria, but some point of basin of attraction may not intersect the line of equilibria. Here, the attractors are generated by choosing arbitrary initial conditions. The proposed system may consider as a new category of hidden attractor. The new system is derived from Rossler type-IV 3-D chaotic system [39]. Following points explain the interesting and unique properties of the proposed 4-D chaotic system:

  1. 1.

    The system has a line of equilibria and is derived from type-IV Rossler 3-D chaotic system [39].

  2. 2.

    The system has only one nonlinear term and a total of eight terms. Thus, the system is the simplest compared with similar available 4-D chaotic or hyperchaotic systems which have many equilibria. This claim is validated from Table 1. Although the system in [5] has seven terms, it consists of five nonlinear terms.

  3. 3.

    The rank of the Jacobian matrix is less than four. However, the system has four distinct Lyapunov exponents for some values of the parameters. Thus, the system behaves as a 4-D system with those values of parameters.

  4. 4.

    The system has chaotic 2-torus nature of Lyapunov exponents. Such nature of a dissipative chaotic system is rare in the literature.

  5. 5.

    The system shows 3-torus and 2-torus (quasi-periodic) and periodic responses other than the chaotic behaviour. The system also exhibits multistability (i.e., coexistence of attractors).

  6. 6.

    The system has asymmetry to its coordinates, planes and spaces. It has only one bifurcation parameter. Asymmetry indicates more disorderness and randomness of the system than to symmetry [40].

The above points also reflect the novelty and contributions of the proposed chaotic system. In 2011 [41] proposed three standard criteria for publication of a new system. These three criteria are as follows [5, 41]:

  1. 1.

    The system should report an important unsolved problem in the literature.

  2. 2.

    The system should exhibit novel behaviour which is not available in the literature.

  3. 3.

    The system should be simple than the similar types of available system.

It is to be noted that a new system should satisfy at least one of the above criteria. Here, the proposed system in this paper satisfies both the second and third conditions. Many tools are used for analysis of a chaotic system. The following tools are used to analyse the proposed chaotic system: bifurcation diagram, Lyapunov spectrum, phase portrait, instantaneous phase plot, Poi-ncaré map, frequency spectrum, recurrence analysis, 0–1 test, sensitivity to initial conditions and hardware circuit realisation.

The rest part of the paper is organised as follows. Section 2 describes the dynamics of the proposed system. The theoretical analyses of the system are presented in Sect. 3. Section 4 describes the numerical findings of the system. The sensitivity to initial conditions of the proposed system is discussed in Sect. 5. Section 6 describes the experimental circuit design and hardware circuit realisation of the proposed system. Finally, conclusions are presented in Sect. 7.

2 Dynamics of the new 4-D chaotic system

In 1979, Rossler proposed some sets (proto types) of chaotic systems [39]. The dynamics of the Rossler type-IV chaotic system is described as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}_{1}=-x_2-x_3\\ {\dot{x}}_2=x_1 \\ {\dot{x}}_3=a\left( x_2-x^2_2\right) -bx_3\\ \end{array}\right. } \end{aligned}$$
(1)

where \(x_{1},\ x_{2},\ x_{3}\) are the state variables. The system exhibits chaotic behaviour with \(a=0.386,\ b=0.2\). System (1) produces attractors for the initial conditions \(x(0)=\) \({(0.7, -0.6, -0.7)}^\mathrm{T}\) and has two equilibrium points \(E_1(0,0,0)\) and \(E_2(0,1.518,-1.581)\). The variable x(0) is the vector of the initial condition of states of system (1) used for numerical simulation. A new 4-D chaotic system is developed by introducing a state feedback control to the second state equation. The dynamics of the new chaotic system is described as:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{x}}_1=-x_2-x_3\\ {\dot{x}}_2=x_1-x_4 \\ {\dot{x}}_3=a\left( x_2-x^2_2\right) -bx_3\\ {\dot{x}}_4=cx_2\\ \end{array}\right. } \end{aligned}$$
(2)

where a, b, c are the parameters and \(x_{1}, x_{2}, x_{3}, x_{4}\) are the state variables. Here in system (2), the parameters \(a=b=0.5\) are kept fixed. But c is considered as the bifurcation parameter. This is because of the fact that the parameters a and b are the parameters of the original system and parameter c is the parameter of the new system. Hence, to see the effect of the new parameters on the new system, it is considered as the bifurcation parameter. However, the parameters a and b are also varied to see their effect, i.e., different dynamical responses of the new system. The results of variation of parameters a, b and c in bifurcation diagram and Lyapunov spectrum are discussed in the numerical finding section. In this paper, all the simulations are carried out using \(ode-45\) solver in MATLAB simulation environment with initial conditions \(x\left( 0\right) ={(0.01, 0.001, 0.001, 0.1)}^\mathrm{T}\). Detailed theoretical and numerical analyses of system (2) are presented in subsequent sections.

3 Theoretical findings

In this section, some theoretical analyses of the proposed system are presented using dissipativity property, symmetrical property and equilibrium points analyses.

3.1 Dissipative and symmetrical property

The divergence of system (2) is described as

$$\begin{aligned} \nabla V=\frac{\partial \dot{x_{1}}}{x_{1}}+\frac{\partial \dot{x_{2}}}{x_{2}}+\frac{\partial \dot{x_{3}}}{x_{3}}+\frac{\partial \dot{x_{4}}}{x_{4}}=-b \end{aligned}$$
(3)

Thus, system (2) is dissipative for \(b>0\). The proposed system has rate of state space contraction equal to \(-1/2\) for \(b=0.5\). The system has no trajectories going to infinity as \(t\rightarrow \infty \). The dissipativity property of a system gives existence of bounded global attractor and analytical localisation of the global attractor in the phase space [42].

The boundedness of the chaotic trajectories of system (2) is proved using the following theorem. The boundness of a chaotic system using the similar approach can be seen in [6, 43].

Theorem 1

Suppose that parameters a, b and c of system (2) are positive. Then, the orbits of system (2) including chaotic orbits are confined in a bounded region.

Proof

Consider a Lyapunov function candidate as in (4)

$$\begin{aligned} v\left( x_1,x_2,x_3,x_4\right) =\frac{1}{2}\left[ cx^2_1+cx^2_2+x^2_3+x^2_4\right] \end{aligned}$$
(4)

The time derivative of (4) is given as

$$\begin{aligned} \dot{v}\left( x_1,x_2,x_3,x_4\right) =cx_1{\dot{x}}_1+cx_2{\dot{x}}_2+x_3{\dot{x}}_3+x_4{\dot{x}}_4 \end{aligned}$$
(5)

Using system dynamics (2), (5) can be written as

$$\begin{aligned} \dot{v}(x_{1},x_{2},x_{3},x_{4})= & {} -cx_{1}x_{3}+ax_{2}x_{3}-ax^{2}_{2}x_{3}-bx^{2}_{3}\\= & {} -{\left( \frac{c}{2\sqrt{b}}x_1+\sqrt{b}x_3\right) }^2\\&+\,\frac{c^2}{4b}x^2_1-{\left( \sqrt{ax_3}x_2-\frac{\sqrt{ax_3}}{2}\right) }^2\\&+\,\frac{a}{4}x^2_3 \end{aligned}$$

Let \(R_0\) be the sufficiently large region so that for all trajectories \((x_{1},x_{2},x_{3},x_{4})\) satisfy

$$\begin{aligned} v(x_{1},x_{2},x_{3},x_{4})=R\quad \hbox {for}~~R>R_{0} \end{aligned}$$

with the following condition

$$\begin{aligned}&\left[ \left( \frac{c}{2\sqrt{b}}x_{1}+\sqrt{b}x_{3}\right) ^{2}+\left( \sqrt{ax_{3}}x_{2}-\,\frac{\sqrt{ax_{3}}}{2}\right) ^{2}\right. \\&\quad \left. >\,\frac{c^{2}}{4b}x^{2}_{1}+\frac{a}{4}x^{2}_{3}\right] \end{aligned}$$

Consequently on the surface

$$\begin{aligned} \left\{ (x_{1},x_{2},x_{3},x_{4})|V(x_{1},x_{2},x_{3},x_{4})\right\} =R. \end{aligned}$$

Since, \(R>R_0\) we can write,

$$\begin{aligned} v(x_{1},x_{2},x_{3},x_{4})<0, \end{aligned}$$

or we can say that, the set

$$\begin{aligned} \left\{ (x_{1},x_{2},x_{3},x_{4})|v(x_{1},x_{2},x_{3},x_{4})\right\} \le R \end{aligned}$$

is a confined region for all the trajectories of system (2). \(\square \)

The system is not invariant under any coordinate, plane and space transformation. Thus, the system is asymmetrical to its coordinates, planes and spaces.

Table 2 The eigenvalues and their corresponding eigenvectors of the new system with \(c=0.014\) at equilibria E
Full size table

3.2 Equilibria and eigenvalues

The equilibria of system (2) can be found by equating each state equation to zero. The equilibria of system (2) are \(E=(x^*_1, 0, 0,x^*_1)\). Thus, it is clear that system (2) has a line of equilibria. The eigenvalues and stability corresponding to the equilibria E can be found by using the Jacobian matrix. The Jacobian matrix of proposed system (2) at equilibria E is given in (6).

$$\begin{aligned} J=\left[ \begin{array}{c@{\quad }c@{\quad }c} 0&-1&\begin{array}{c@{\quad }c} -1 &{} 0 \end{array} \\ 1 &{} 0 &{} \begin{array}{c@{\quad }c} 0 &{} -1 \end{array} \\ \begin{array}{c} 0 \\ 0 \end{array} &{} \begin{array}{c} a \\ c \end{array} &{} \begin{array}{c@{\quad }c} \begin{array}{c} -b \\ 0 \end{array} &{} \begin{array}{c} 0 \\ 0 \end{array} \end{array} \end{array} \right] \end{aligned}$$
(6)

The characteristic equation of (6) is

$$\begin{aligned} \lambda \left( {\lambda }^3+k_1{\lambda }^2+k_2\lambda +k_3\right) =0 \end{aligned}$$
(7)
Table 3 Comparison between Rossler type-IV and the new system
Full size table
Fig. 1
figure 1

Bifurcation diagram of system (2) with \(\ c\in [0.0,\ 0.0629]\ \) and \(a=b=0.5\)

Full size image

where \(k_1=b,\ k_2=c,\ k_3=bc\). It is clear that there is a zero eigenvalue for all equilibrium points of system (2). The eigenvalues and their corresponding eigenvectors of the system for \(a=b=0.5,\ c=0.014\) are given in Table 2. A comparison between the proposed system and the Rossler type-IV chaotic systems is given in Table 3. The proposed system belongs to the category of the hidden attractors since it has line of equilibria [44, 45].

Fig. 2
figure 2

Bifurcation diagram of system (2) with \(\ c\in [0.063,\ 0.25]\ \) and \(a=b=0.5\)

Full size image
Fig. 3
figure 3

Lyapunov spectrum of system (2) with \(\ c\in [0.0,\ 0.0629]\ \) and \(x\left( 0\right) =\left( 0.01,\ 0.001, 0.001,\ 0.1\right) ^\mathrm{T}\)

Full size image

4 Numerical findings

The dynamic behaviours of a self-excited chaotic or hyperchaotic system (having countable equilibrium points) can be obtained with the knowledge of location of equilibria or by considering initial conditions near a equilibrium point. However, for a system with a line of equilibria, it is difficult to obtain the dynamic behaviours with the knowledge of the location of equilibria. The dynamic behaviours of the proposed system are analysed using numerical findings. In this section, different numerical tools are used to analyse the complex dynamic behaviours of the proposed system.

Fig. 4
figure 4

Lyapunov spectrum of system (2) with \(\ c\in [0.063,\ 0.25]\ \) and \(x\left( 0\right) =\left( 0.01,\ 0.001, 0.001,\ 0.1\right) ^\mathrm{T}\)

Full size image
Fig. 5
figure 5

Lyapunov spectrum of system (2) with \(\ a \in [0.4,\ 0.5273]\ \), \(b=0.5, c=0.014\) and \(x\left( 0\right) =\left( 0.01,\ 0.001, 0.001,\ 0.1\right) ^\mathrm{T}\)

Full size image
Fig. 6
figure 6

Lyapunov spectrum of system (2) with \(\ b \in [0.44,\ 0.75]\ \), \(a=0.5, c=0.014\) and \(x\left( 0\right) =\left( 0.01,\ 0.001, 0.001,\ 0.1\right) ^\mathrm{T}\)

Full size image

4.1 Bifurcation and Lyapunov spectrum analyses

The dynamic behaviour of the proposed system for other values of the bifurcation parameter is analysed using bifurcation diagram and Lyapunov spectrum. Both the plots are obtained by variation of one parameter while keeping other fixed. Lyapunov spectrum is obtained using Lyapunov exponents for different values of parameter. Lyapunov exponents are obtained by using Wolf algorithm [46] with observation time \(T=10{,}000\) and sampling size \(\triangle t=0.002\).

The bifurcation diagram of the proposed system with a variation of parameter \(\ c\in [0.0,\ 0.0629]\ \) and \(\ c\in [0.063,\ 0.26]\ \) keeping other parameters fixed are shown in Figs. 1 and 2, respectively. Lyapunov spectrum of the proposed system with the variation of parameter \(\ c\in [0.0,\ 0.0629]\ \) and \(\ c\in [0.063,\ 0.26]\) and keeping other parameters fixed are shown in Figs. 3 and 4, respectively. Both the bifurcation diagrams of the system are generated with 10,000 observation time but discarding initial \(T=9600\) transient time signal, step size \(\triangle t=0.01\) and fixed initial conditions \(x\left( 0\right) ={\left( 0.01,\ 0.001,\ 0.001,\ 0.1\right) }^\mathrm{T}\). It is noted from these figures that the system produces chaotic, chaotic 2-torus and quasi-periodic behaviours (including 2-torus and 3-torus). The 2-torus quasi-periodic behaviour is considered when the nature of the Lyapunov exponents is \(\left( 0,0,\ -,\ -\right) \ \)and 3-torus is considered when the nature of Lyapunov exponents is \((0,0,\ 0,\ -)\). The chaotic 2-torus is named when Lyapunov exponents are \((+,0,0,-)\) as given in [47].

Table 4 Four distinct nature of Lyapunov exponents \((+, 0, - ,-)\) (chaotic) for some values of parameter c of system (2)
Full size table
Table 5 Three distinct nature of Lyapunov exponents \((+, 0, 0 ,-)\) (chaotic 2-torus) for some values of parameter c of system (2)
Full size table
Fig. 7
figure 7

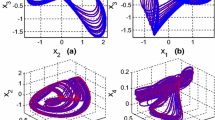
Chaotic attractors of system (2) with \(c=0.014\) and \(x\left( 0\right) ={\left( 0.01,\ 0.001,\ 0.001,\ 0.1\right) }^\mathrm{T}\)

Full size image
Fig. 8
figure 8

Local Lyapunov dimensions for chaotic behaviour on the grid points of the third attractor of system (2) with \(c = 0.014\)

Full size image

Lyapunov spectrum of system (2) with variation of parameters a and b but keeping \(b=0.5, c=0.014\) and \(a=0.5, c=0.014\) fixed are shown in Figs. 5 and 6, respectively. It is seen from Lyapunov spectrum plots that with the variation of parameters a and b, the new system has different dynamical behaviours like chaotic, chaotic 2-torus, quasi-periodic. It is also observed from the Figs. 3,  4,  5 and  6 that the system has almost same ranges of parameters for chaotic behaviour. Lyapunov spectrum for variation of parameter c is shown up to \(a=0.5237\) (Fig. 5). This is because the system response is unbounded after \(a>0.5237\). The same phenomenon is observed in case of the parameter b (Fig. 6) for \(b<0.44\).

The nature of Lyapunov exponents for chaotic and chaotic 2-torus behaviour of system (2) for some values of parameter c are given in Tables 4 and 5, respectively. It is seen from Table  4 that the system has four distinct Lyapunov exponents. This clearly establish that although the Jacobian matrix of the system has rank less than four, but the system behaves as four dimensional for some selected values of parameters. This fact is validated from reference [48].

The chaotic attractors of system (2) are shown in Fig. 7. The attractors of the system are shown considering signal from for 9500 to 10,000 observation time. Thus, the attractors are bounded. The local Lyapunov dimensions (LDs) of the points on the grid of the third attractor (Fig. 7c) of system (2) are shown in Fig. 8. The LDs are shown here only for the grid points where the system has chaotic behaviour. The system has maximum \(K_{DY}\) dimension equal to 3.1271 among the grid points of the third attractor of the system. The other behaviours of system (2) like 3-torus and 2-torus are shown in Figs. 9 and 10, respectively.

Fig. 9
figure 9

Quasi-periodic (3-torus) behaviour of system (2) with \(c=0.0094\) and \(x\left( 0\right) ={\left( 0.01,\ 0.001,\ 0.001,\ 0.1\right) }^\mathrm{T}\) where LEs are \(L_i=(0, 0, 0, -0.50)\)

Full size image
Fig. 10
figure 10

Quasi-periodic (2-torus) behaviour of system (2) with \(c=0.0384\) and \(x\left( 0\right) ={\left( 0.01,\ 0.001,\ 0.001,\ 0.1\right) }^\mathrm{T}\) where LEs are \(L_i=(0, 0, -0.0060, -0.4950)\)

Full size image

4.2 Instantaneous phase and Poincaré map

To validate the chaotic dynamics of system (2), the instantaneous phase (\(\emptyset \)) and Poincaré maps are plotted. The instantaneous phase (\(\emptyset \)) is plotted using Hilbert transformation. Suppose, a chaotic signal x(t) is given in the form of a complex signal s(t), its amplitude (A) and phase \((\emptyset )\) can be written as

$$\begin{aligned} s\left( t\right) =x\left( t\right) +i{\tilde{x}}\left( t\right) =A(t)\hbox {e}^{j\emptyset (t)} \end{aligned}$$
(8)

where

$$\begin{aligned} {\tilde{x}}\left( t\right) =\frac{1}{\pi }P\cdot V\left( \int ^{\infty }_{-\infty }{\frac{x(\tau )}{t-\tau }}d\tau \right) \end{aligned}$$
(9)

where \(P\cdot V\) is the Cauchy principle value in the Hilbert transform (HT). Here, HT is calculated in MATLAB using the technique given in [49]. The instantaneous phase of \(x_2(t)\) and \(x_3(t)\) signals after truncating initial transient part are shown in Fig. 11. The instantaneous phase \((\emptyset )\) of a chaotic signal increases monotonically (inset) as the time increases [49, 50]. It is seen that the instantaneous phase \((\emptyset )\) of the system increases monotonically with time. The monotonous increase in the phase indicates the chaotic behaviour of the system.

The Poincaré maps on the different sections of the plane of system (2) are shown in Figs. 12 and 13. The maps in Figs. 12 and 13 are drawn for \(x_2=0\) and \(x_3=0\), respectively. Different random dots in the Poincaré maps indicate the chaotic behaviour of the system [48]. Poincaré maps in Figs. 12 and 13 are generated for observation time in the ranges \(9500<t<10{,}000\).

Fig. 11
figure 11

The instantaneous phase \((\emptyset )\) of the \(x_2\) and \(x_3\) signals of system (2) with \(c=0.014\) and \(x\left( 0\right) ={\left( 0.01,\ 0.001,\ 0.001,\ 0.1\right) }^\mathrm{T}\) and \(\triangle t=0.001\ \) using HT

Full size image
Fig. 12
figure 12

Poincaré maps on the plane of the system for \(x_2=0\) with \(c=0.014\), \(x\left( 0\right) ={\left( 0.01,\ 0.001,\ 0.001,\ 0.1\right) }^\mathrm{T}\) and \(\triangle t=0.001{:}\) a on \(x_1-x_3\) plane, b on \(x_3-x_4\) plane

Full size image
Fig. 13
figure 13

Poincaré maps on the plane of the system for \(x_3=0\) with \(c=0.014\), \(x\left( 0\right) ={\left( 0.01,\ 0.001,\ 0.001,\ 0.1\right) }^\mathrm{T}\) and \(\triangle t=0.001{:}\) a on \(x_1-x_2\) plane, b on \(x_2-x_4\) plane

Full size image

4.3 Frequency spectrum

The frequency spectra of system (2) are plotted to know the complex dynamic behaviour. The single sided frequency spectra of \(x_2(t)\) and \(x_3(t)\) signals of system (2) are shown in Fig. 14. Random peaks in the spectrum indicate the chaotic behaviour of the proposed system [48].

Fig. 14
figure 14

The frequency spectrum of system (2) with \(c=0.014\) and \(x\left( 0\right) ={\left( 0.01,\ 0.001,\ 0.001,\ 0.1\right) }^\mathrm{T}\) and \(\triangle t=0.001:\) a spectrum of \(x_2(t)\) and b spectrum of \(x_3(t)\)

Full size image

4.4 Recurrence analysis

A recurrence plot (RP) is a graphical visualisation of the repetitions or recurrences of a particular state of a system as its dynamics evolve [49]. It is used to study the reduced phase space plot of a higher dimensional system. In this the recurrence of a state at time i at a different time j is marked within a 2-D square matrix whose column and row correspond to a pair of time scales. The matrix is marked with the black and white dots (usually a black dots for recurrence). A signal \(x_1(t)\) is used from the multi-variable\(\ x\left( t\right) ={[x}_1(t)\),\(\ x_2(t)\) ,..., \(x_m(t)]\) to construct a lower n-D phase space using a time delay \((\tau )\). The reconstructed trajectory in n-D phase space can be written as [49].

$$\begin{aligned} w={[y_1,\ y_2,\ y_3,\ y_4]}^\mathrm{T} \end{aligned}$$
(10)

where \(y_i=[x_i,\ x_{i+\tau },\ \dots ,\ x_{i+(D_\mathrm{E}-1)\tau }]\) and \(m=n-(D_\mathrm{E}-1)\tau \) and \(D_\mathrm{E}\) is the embedding dimension. Any recurrence of state i with state j can be expressed as [49];

$$\begin{aligned} R^{\varepsilon }_{i,\ j}=\varTheta (\varepsilon -\left\| y_i-y_j\right\| ) \end{aligned}$$
(11)

where \(\varTheta \) is the Heaviside function and \(\varepsilon \) is an arbitrary threshold. Here, \(x_2(t)\) signal of system (2) is used for the recurrence plot. A total of 10,000 data points are used. The recurrence plot is obtained by assuming \(\varepsilon =2\), \(D_\mathrm{E}=7\) and the time delay \(\tau =75\). The recurrence plot is shown in Fig. 15. The random distribution of the black dots indicates the chaotic behaviour [49]. The label of x and y in Fig. 15 is considered based on the theory given in [51, 52].

Fig. 15
figure 15

The recurrence plot of \(x_2(t)\) of system (2) with \(c=0.014\) and \(x\left( 0\right) ={\left( 0.01,\ 0.001,\ 0.001,\ 0.1\right) }^\mathrm{T}\), \(\triangle t=0.001,\ D_\mathrm{E}=6\mathrm{,\ }\tau =75.\mathrm{\ }\ \)

Full size image
Fig. 16
figure 16

The 0–1 test of \(x_2(t)\) of system (2) with \(c=0.014\) and \(x\left( 0\right) ={\left( 0.01,\ 0.001,\ 0.001,\ 0.1\right) }^\mathrm{T}\) and \(\triangle t=1\): a dynamics of the translation components \((p_c(n),\ q_c(n))\), b asymptotic growth rate (\(k_c\)) and c mean square displacement \(M_c\left( n\right) \)

Full size image
Fig. 17
figure 17

Bifurcation diagram of system (2) with \(a=b=0.5\)

Full size image

4.5 0–1 test analysis

It is a binary test used to classify the chaotic or periodic behaviour of a system [53]. Here, the dynamics of the system is plotted in a space of translation variable and asymptotic growth rate (\(k_c\)) of the mean square displacement of the trajectories. The chaotic and periodic behaviours are defined based on the values of \(k_c\). The translation variables are defined as [49, 53, 54]:

$$\begin{aligned} {\left\{ \begin{array}{ll} p_c\left( n\right) =\sum ^n_{j=1}{x(j)\mathrm{cos}(jc)}\\ q_c\left( n\right) =\sum ^n_{j=1}{x(j)\mathrm{sin}(jc)} \\ \end{array}\right. } \end{aligned}$$
(12)

where c is a randomly chosen variable constant in the range of \((0-2\pi )\) and x(j) is the time series of any state variable of a dynamical system. If the dynamics is chaotic, then the space of translation variables is a random Brownian-like motion, whereas if the dynamics is regular then the space of the translation variables is a bounded motion. The mean square displacement \(M_c(n)\) obtained using translation variables \((p_c(n),\ q_c(n))\) is defined as [49, 53, 54].

$$\begin{aligned} M_c\left( n\right)&=\mathop {\lim }_{n\rightarrow \infty }\frac{1}{n}\sum ^n_{j=1} \left\{ {\left[ p_c\left( j+n\right) -p_c(j)\right] }^2\right. \nonumber \\&\quad \left. +\, {\left[ q_c\left( j+n\right) -q_c(j)\right] }^2\right\} \end{aligned}$$
(13)
Fig. 18
figure 18

a Coexistences of 2-torus with chaotic attractor and b coexistences of 2-torus with 2-torus of system (2) with \(a=b=0.5, c=0.12\)

Full size image
Fig. 19
figure 19

a Coexistence of 2-torus with chaotic attractor for \(c=0.123\) and b coexistence of 2-torus with 3-torus with \( c=0.119\) of system (2) with \(a=b=0.5\)

Full size image

\(M_c(n)\) grows exponentially for chaotic behaviour whereas it varies periodically for regular/periodic behaviour. The asymptotic growth rate \((k_c)\) is defined as [49, 53, 54]

$$\begin{aligned} k_c={\mathop {\lim }_{n\rightarrow \infty } \frac{{\log M_c(n)\ }}{{\log n\ }}\ } \end{aligned}$$
(14)

The value of \(k_c\approx 1\) determines the chaotic behaviour, and \(k_c\approx 0\) indicates the periodic/regular behaviour. Here, \(x_2(t)\) signal of system (2) is used for 0–1 test. The translation variables, asymptotic growth rate and mean square displacement are shown in Fig. 16. We got \(k_c=0.99691\approx 1\) for \(a=b=0.5, c=0.014\) which confirms the chaotic nature of the new system.

Fig. 20
figure 20

Sensitivity to initial conditions of system (2) with \(x_{3}=0.001\), \(x_{4}=0.1\) and \( x_{1}\in [-2,\ 3]\ , x_{2}\in [-2,\ 5]\ \) where red colour represents the chaotic nature and blue colour represents the unbounded nature of the proposed system. (Color figure online)

Full size image
Fig. 21
figure 21

Sensitivity to initial conditions of system (2) with \(x_{1}=0.01\), \(x_{2}=0.001\) and \(x_{3}\in [-3,\ 2]\ , x_{4}\in [-3,\ 3]\ \) where red colour represents the chaotic nature and blue colour represents the unbounded nature of the proposed system. (Color figure online)

Full size image
Fig. 22
figure 22

Circuit design of chaotic system (2)

Full size image

4.6 Multistability (coexistence of attractors)

Multistability can be determined by observing changes in the responses of bifurcation diagram of the system [55, 56]. The bifurcation diagram of system (2) with variation of the parameter c is replotted to observe the phenomenon of multistability. The bifurcation diagram is plotted considering the final state for each value of c as the initial states for the next value of the bifurcation parameter. The results are shown in Fig. 17. It is observed by comparing Figs. 2 and 17 that the system has changed in behaviour for the bifurcation parameter range \(c \in [0.12,\ 0.14]\ \). In Fig. 17, for \(c=0.12\), it appears that the system has chaotic behaviour, but in Fig. 2 it has periodic behaviour. It is also observed from Fig. 2 that for \(c \in [0.11,\ 0.125]\ \) the system has cascaded reverse period-doubling route to chaos along with one reverse period-doubling route to chaos, but in Fig. 17, there is no cascaded reverse periodic period-doubling route to chaos. Further in Fig. 17, there are four more jump routes to chaos. Thus, it seems that the system has coexistence of different attractors due to changes in initial conditions. The coexistences of (i) quasi-periodic (2-torus) with chaotic attractor and (ii) 2-torus with 2-torus of system (2) are shown in Fig. 18. The coexistences of (i) quasi-periodic (2-torus) with chaotic attractor and (ii) 2-torus with 3-torus of system (2) with \(c=0.123\) and \(c=0.119\), respectively, are shown in Fig. 19.

5 Sensitivity to initial conditions

This section describes the effect of initial conditions on system (2).

System (2) is simulated with different initial conditions in the considered regions of four state variables. The results of two different cases are shown. In the first case, the initial conditions for state variables \(x_{3}(0)=0.001\) and \(x_{4}(0)=0.1\) are kept fixed and \(x_{1}(0)\) and \(x_{2}(0)\) are varied. In the second case, the state variables \(x_{1}(0)=0.01\) and \(x_{2}(0)=0.001\) are kept fixed, and \(x_{3}(0)\) and \(x_{4}(0)\) are varied. The simulated results for the first and second cases are shown in Figs. 20 and 21, respectively. It is seen from both the figures that system (2) is very sensitive to initial conditions.

Fig. 23
figure 23

Chaotic attractors of system (2) using NI Multisim circuit simulation: a in \(y_1-y_3\) plane with scale position 500, 500 mv/div and b in \(y_2-y_3\) plane with scale position 1 V/div, 500 mv/div

Full size image
Fig. 24
figure 24

Hardware circuit design of system (2) on breadboard along with oscilloscope output

Full size image

6 Circuit validation

The circuit designed for the implementation of system (2) is shown in Fig. 22. The circuit validation of the new system is achieved using NI Multisim 12 software. Many chaotic circuits are simulated and verified using NI Multisim [57,58,59,60,61] and PSpice [62,63,64,65]. NI Multisim software is based on actual circuit components. Its simulation results are basically consistent with those of actual circuit results [58]. Here in circuit (Fig. 22), four integration lines are considered correspond to four states of the new system. The supply voltages are considered as ±15 Vdc. The circuit is designed using four capacitors (C1, C2, C3, C4), eleven resistances \((R1,\dots , R12)\), six op-amp (741) and one multiplier (AD633JN). Here, multiplier is used for the nonlinear term\(\ x^2\). It is seem from the chaotic attractors plot (Fig. 7) of the new system that states \(x_1\) and \(x_4\) are in the range of 50 and 60. Thus, the states are scaled with \(y_1=x_1/40, y_2=x_2/10, y_3=x_3/10, y_4=x_4/10\) to make compatible for the circuit simulation and implementable in the hardware circuit. The circuit equation corresponding to each state of scaled system (2) using Kirchhoff’s laws can be obtained as:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{y}}_1=\frac{1}{R c1}\left[ -\frac{R}{R1}y_2-\frac{R}{R2}y_3\right] \\ {\dot{y}}_2=\frac{1}{R c2}\left[ \frac{R}{R5}y_1-\frac{R}{R6}y_4\right] \\ {\dot{y}}_3=\frac{1}{R c3}\left[ \frac{R}{R11}y_2-\frac{0.1R}{R10}y_2y_2-\frac{R}{R9}y_3\right] \\ {\dot{y}}_4=\frac{1}{R c4}\left[ \frac{R}{R12}y_2\right] \\ \end{array}\right. } \end{aligned}$$
(15)
Fig. 25
figure 25

Chaotic attractors using hardware circuit realisation of system (2) in oscilloscope for: a \(x_2-x_3\) plane and b \(x_1-x_3\) plane

Full size image

where the variables \(y_1,\ y_2,y_3,y_4\ \)are the outcomes of the integrators \(U1A,\ U3A,\ U5A,\ U6A\). System (2) is equivalent to (15) with\(\ \tau =t/RC\),\(\ R3=R=R4=R7=R8=100~\hbox {k}\Omega ,\ \ R11=\frac{R}{a}=200~\hbox {k}\Omega \), \(R10=\frac{R}{a}=20~\hbox {k}\Omega \), \(R1=R2=400~\hbox {k}\Omega \), \(R5=25~\hbox {k}\Omega \), \(R9=\frac{R}{b}=200~\hbox {k}\Omega \), \(R12=\frac{R}{c}=7142.85~\hbox {k}\Omega \), \(c1=c2=c3=c4=1nF\) and \(a=b=0.5,\ \ c=0.014.\) Hardware circuit design along with oscilloscope output results of system (2) is shown in Fig. 24. The chaotic attractors of system (2) with \(c=0.014\) obtained using NI Multisim circuit simulation and hardware circuit realisation oscilloscope results are shown in Figs. 23 and 25, respectively. Agilent 1024A 200 MHz digital oscilloscope is used for capturing the experimental results. It is seen from Figs. 23 and 25 that the attractors plot using circuit simulation and hardware circuit realisation validate with the MATLAB simulation results.

7 Conclusions

In this paper, the simplest new 4-D chaotic system with the line of equilibria is reported. The system has only two types of behaviour. These are chaotic (chaotic, chaotic 2-torus) and quasi-periodic (2-torus, 3-torus). The system is unusual with many unique properties. The system exhibits multistability. The system has a total of eight terms including only one nonlinear term and one bifurcation parameter. Hence, the system is the simplest compared with similar 4-D systems (systems with many number of equilibria). The system has chaotic 2-torus with \((+,\ {\approx } 0, \ {\approx } 0,\ -)\) nature of Lyapunov exponents for chaotic behaviour which is rare in the literature. The rank of the Jacobian matrix of the proposed system is three which is less than the dimension of the system. However, the system exhibits four distinct Lyapunov exponents and thereby behaving as a 4-D system for some values of parameter. The system has asymmetry to its coordinates, plane and space. Bifurcation diagram, Lyapunov spectrum, phase portrait, instantaneous phase plot, Poincaré map, frequency spectrum, recurrence analysis, 0–1 test and theoretical analyses are used to analyse the complex dynamic behaviours of the proposed system. The simulation results using MATLAB are validated by using hardware circuit design and realisation. The design and analyses presented in this paper can be further extended by developing some new simplest 4-D/5-D hyperchaotic systems with new complex dynamical behaviours along with their applications.