Dynamical responses of airfoil models with harmonic excitation under uncertain disturbance

Abstract

In this paper, we investigate nonlinear dynamical responses of two-degree-of-freedom airfoil (TDOFA) models driven by harmonic excitation under uncertain disturbance. Firstly, based on the deterministic airfoil models under the harmonic excitation, we introduce stochastic TDOFA models with the uncertain disturbance as Gaussian white noise. Subsequently, we consider the amplitude–frequency characteristic of deterministic airfoil models by the averaging method, and also the stochastic averaging method is applied to obtain the mean-square response of given stochastic TDOFA systems analytically. Then, we carry out numerical simulations to verify the effectiveness of the obtained analytic solution and the influence of harmonic force on the system response is studied. Finally, stochastic jump and bifurcation can be found through the random responses of system, and probability density function and time history diagrams can be obtained via Monte Carlo simulations directly to observe the stochastic jump and bifurcation. The results show that noise can induce the occurrence of stochastic jump and bifurcation, which will have a significant impact on the safety of aircraft.

1 Introduction

A two-degree-of-freedom airfoil (TDOFA) models is a typical self-excited system with rich nonlinear dynamical behaviors, such as limit cycle oscillation, bifurcation, and chaos [1]. The limit cycle oscillation of airfoil is an important problem and normally associated with flutter. In practical aircraft design, the flutter phenomenon is not rare; sometimes they are even very prominent and generally lead to the possible great disaster. Accordingly, predicting the amplitude and frequency of flutter oscillation via the analytical or numerical techniques is very important, and it has been an active area of research for many years.

Many methods have been proposed to investigate the responses of TDOFA systems, such as the harmonic balance method (the describing function method or linearization method) [1,2,3,4,5], the center manifold theory [6], the high-dimensional harmonic balance method [7], the incremental harmonic balance method [8], and the homotopy analysis method [9]. The harmonic balance method is applied to obtain an equivalent linear system, and then, the traditional methods for linear system can be employed [1]. Shen [2] used the first-order harmonic balance method to investigate the approximate analytical solution. Lee et al. [3, 4] investigated the dynamical response of a coupled TDOFA systems with cubic stiffness nonlinearity in both degrees of freedom by the harmonic balance method. Liu and Zhao [5] applied the equivalent linearization method to investigate the bifurcation behavior of an airfoil with a cubic nonlinearity in the pitch degree of freedom, and the comparisons of an approximately analytical solution with the numerical results are presented. Liu et al. [6] analyzed the frequency of the limit cycle oscillation by the center manifold method. Liu et al. [7] investigated the nonlinear TDOFA system by the high-dimensional harmonic balance method. Raghothama et al. [8] applied the incremental harmonic balance method to study the limit cycle flutter of the nonlinear airfoil. In addition, Chen et al. [9] proposed the homotopy analysis method to study the nonlinear aeroelastic system of an airfoil for both weakly and strongly nonlinear terms. Therefore, for the deterministic case, many approximate methods have been well developed to predict the response of system in most flutter cases, such as high flow speeds, weakly and strongly nonlinear systems. The accuracy of the approximate solution can satisfy the realistic requirement.

However, it is noted that random perturbation is usually neglected in most of those airfoil aeroelastic studies. Random factors exist everywhere in real world without exaggeration. Thus, it is necessary to investigate the airfoil system subject to stochastic excitation. In the past few years, with the development and broad application of random dynamical systems, there have been some attempts to consider different techniques in random excited system to get the system responses [10,11,12,13,14,15,16,17,18,19,20]. For instance, Poirel et al. [10, 11] investigated the random flutter of airfoil and they also obtained the numerical results by a probabilistic and statistical method. Du et al. [17] investigated the stochastic resonance in an underdamped quartic double-well potential with noise and time delayed feedback. Hu et al. [18] proposed a moment Lyapunov exponent method to interpret and analyze the stochastic stability for a binary airfoil driven by a non-Gaussian colored noise. Singh et al. [19] investigated the stochastic stability and dynamics of a random two-dimensional airfoil with structurally nonlinear. Xu et al. [20] proposed a new technique to deal with strongly nonlinear stochastic systems with fractional derivative damping and random harmonic excitation.

As we all know, the TDOFA models can be regarded as two coupled Duffing equations. And the dynamical behaviors of Duffing systems with random excitation have been explored successfully in different techniques [21,22,23,24,25]. In this paper, the TDOFA models with harmonic excitation and additive noise will be considered. The steady-state responses will be presented analytically by applying the stochastic averaging method. We also find the stochastic jump for an airfoil flutter system subject to a harmonic excitation and additive noise excitation.

The paper is organized as follows: In Sect. 2, we described the deterministic TDOFA model and based on the deterministic airfoil models, we established the stochastic TDOFA models by introducing the random fluctuations. In Sect. 3, the amplitude–frequency response in deterministic case and the mean-square response in stochastic case can be obtained by applying the averaging method or stochastic averaging method, respectively, and the comparisons of an approximately analytical solution with the numerical results are presented. In Sect. 4, the stochastic jump and bifurcation are investigated based on the steady-state probability density and the response. Conclusion will close this paper in Sect. 5.

2 The description of stochastic TDOFA models

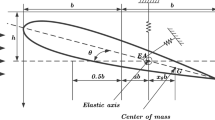
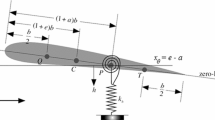
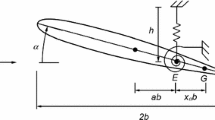
In this section, we introduce a stochastic TDOFA model with cubic stiffness nonlinearity in two degrees of freedom, which oscillates in the pitch and plunge directions. Figure 1 gives the symbols used in the analysis of TDOFA motion. The symbol $\alpha$ represents the airfoil pitch angle, positive if nose up, and h denotes the plunging deflection, positive if downward. The elastic axis is located at a distance ${a_h}b$ from the mid-chord, while the center of mass is located at a distance ${x_\alpha }b$ from the elastic axis, where b is the semi-chord length of the airfoil. Both distances are positive when measured toward the trailing edge of the airfoil.

Fig. 1

Schematic diagram of TDOFA motion

Considering an airfoil placed in a stationary medium, the equations of motion are shown below after neglecting the aerodynamics terms in the equations given by Fung [26]. For nonlinear restoring forces, the coupled bending-torsion equations for the airfoil with cubic stiffness nonlinearity can be written as follows

$$\begin{aligned}&m\ddot{h} + S\ddot{\alpha }+ {C_h}\dot{h} + \bar{G}\left( h \right) = P\left( t \right) , \end{aligned}$$

(1a)

$$\begin{aligned}&S\ddot{h} + {I_\alpha }\ddot{\alpha }+ {C_\alpha }\dot{\alpha }+ \bar{M}\left( \alpha \right) = Q\left( t \right) . \end{aligned}$$

(1b)

where $\bar{G}\left( h \right) = {K_h}\left( {h + {\beta _h}{h^3}} \right)$, $\bar{M}\left( \alpha \right) = {K_\alpha }\left( {\alpha + {\beta _\alpha }{\alpha ^3}} \right)$ denotes the nonlinear plunge and pitch stiffness terms, respectively. The dot over the variables denotes differentiation with respect to the time t. S represents the airfoil static moment about the elastic axis. The symbols m, ${C_h }$, ${C_\alpha }$, and ${I_\alpha }$ denote the airfoil mass per unit length, damping coefficient in plunge, damping coefficient in torsion, and wing mass moment of inertia about elastic axis, respectively. $P\left( t \right)$ and $Q\left( t \right)$ are, respectively, the externally applied force and moment acting on the airfoil.

By introducing the following non-dimensional transformations:

$$\begin{aligned}&\xi = \frac{h}{b},\tau = \frac{{Ut}}{b},{K_\xi } = {K_h},{x_\alpha } = \frac{S}{{bm}},\\&{\omega _\xi } = {\left( {\frac{{{K_\xi }}}{m}} \right) ^{1/2}}, \\&{\omega _\alpha } = {\left( {\frac{{{K_\alpha }}}{{{I_\alpha }}}} \right) ^{1/2}},\varpi = \frac{{{\omega _\xi }}}{{{\omega _\alpha }}},{U^ * } = \frac{U}{{b{\omega _\alpha }}},\\&{r_\alpha } ={\left( {\frac{{{I_\alpha }}}{{m{b^2}}}} \right) ^{1/2}}, \\&{\zeta _\xi } = \frac{{{C_h}}}{{2{{\left( {m{K_h}} \right) }^{1/2}}}},{\zeta _\alpha } = \frac{{{C_\alpha }}}{{2{{\left( {{I_\alpha }{K_\alpha }} \right) }^{1/2}}}},\\&G\left( \xi \right) = \frac{{\overline{G} \left( \xi \right) }}{{{K_\xi }}},\\&M\left( \alpha \right) = \frac{{\overline{M} \left( \alpha \right) }}{{{K_\alpha }}},p\left( \tau \right) = \frac{{P\left( \tau \right) b}}{{m{U^2}}},r\left( \tau \right) = \frac{{Q\left( \tau \right) }}{{m{U^2}r_\alpha ^2}}. \end{aligned}$$

in which ${\omega _\xi }$ and ${\omega _\alpha }$ are the uncoupled natural frequencies in the plunge and pitch degree of freedom, respectively; ${\zeta _\xi }$ and ${\zeta _\alpha }$ are the damping ratios in the plunge and pitch degree of freedom, respectively; ${r _\alpha }$ is the radius of gyration about the elastic axis; and $p\left( \tau \right)$ is the non-dimensional applied force and $r\left( \tau \right)$ is the non-dimensional moment. Therefore, Eqs. (1a), (1b) can be written in a non-dimensional form as

$$\begin{aligned}&\xi '' + {x_\alpha }\alpha '' + 2{\zeta _\xi }\frac{\varpi }{{{U^ * }}}\xi ' + {\left( {\frac{\varpi }{{{U^ * }}}} \right) ^2}G\left( \xi \right) = p\left( \tau \right) ,\nonumber \\ \end{aligned}$$

(2a)

$$\begin{aligned}&\frac{{{x_\alpha }}}{{r_\alpha ^2}}\xi '' + \alpha '' + 2{\zeta _\alpha }\frac{1}{{{U^ * }}}\alpha ' + \frac{1}{{{U^ * }^2}}M\left( \alpha \right) = r\left( \tau \right) . \end{aligned}$$

(2b)

where the prime denotes differentiation with respect to the non-dimensional time $\tau$.

In this paper, we only consider the situation of the externally applied force and moment is harmonic function. Without loss of generality, we assume that the externally applied moment is sinusoidal and the excitation is only applied in the pitch degree of freedom. In this case, $p\left( \tau \right) = 0$ and we write

$$\begin{aligned} Q\left( \tau \right) = {Q_0}\sin \left( {\omega \tau } \right) , \end{aligned}$$

and let

$$\begin{aligned} F = \frac{{{Q_0}}}{{m{U^2}r_\alpha ^2}}, \end{aligned}$$

then the right-hand side of Eq. (2b) becomes $F\sin \left( {\omega \tau } \right)$.

Based on the deterministic systems (2a), (2b), we assume that the harmonic excitation combined with random excitation is only applied in the pitch degree of freedom. In this investigation, we consider the airfoil system is provided with slight coupling and weak nonlinear; then, the stochastic TDOFA models can be obtained as

$$\begin{aligned}&\xi '' + {\varepsilon ^2}{x_\alpha }\alpha '' + 2{\varepsilon ^2}{\zeta _\xi }{\varOmega _\xi }\xi ' + \varOmega _\xi ^2\left( {\xi + {\varepsilon ^2}{\beta _\xi }{\xi ^3}} \right) \nonumber \\&\quad = 0, \end{aligned}$$

(3a)

$$\begin{aligned}&{\varepsilon ^2}\frac{{{x_\alpha }}}{{r_\alpha ^2}}\xi '' + \alpha '' + 2{\varepsilon ^2}{\zeta _\alpha }{\varOmega _\alpha }\alpha ' + \varOmega _\alpha ^2\left( {\alpha + {\varepsilon ^2}{\beta _\alpha }{\alpha ^3}} \right) \nonumber \\&= {\varepsilon ^2}F\sin \left( {\omega \tau } \right) + \varepsilon \eta \left( \tau \right) . \end{aligned}$$

(3b)

in which ${\varOmega _\xi } = \frac{\varpi }{{{U^ * }}}$, ${\varOmega _\alpha } = \frac{1}{{{U^ * }}}$, $0 < \varepsilon \ll 1$ is a small parameter, $\eta \left( \tau \right)$ is a Gaussian white noise and has the following statistical property

$$\begin{aligned} E\left[ {\eta \left( \tau \right) } \right]= & {} 0, ~ E\left[ {\eta \left( \tau \right) \eta \left( {\tau + {\tau _1}} \right) } \right] \nonumber \\= & {} D\delta \left( {{\tau _1}} \right) , ~ {\tau _1} > 0. \end{aligned}$$

(4)

here $E\left[ ~\cdot ~\right]$ denotes the mathematical expectation operator and D is the noise intensity.

Fig. 2

The comparison of two methods: a pitch motion; b plunge motion. “Dot” harmonic balance method, “star” averaging method

3 The theoretical analysis of TDOFA models

3.1 The deterministic TDOFA system

In this subsection, we first consider the deterministic case ($D=0$). Then, Eqs. (3a), (3b) reduce to a deterministic differential equation driven by harmonic excitation, which can be rewritten as

$$\begin{aligned} \xi '' + \omega _\xi ^{ * 2}\xi= & {} {\varepsilon ^2}f\left( {\xi ,\alpha } \right) , \end{aligned}$$

(5a)

$$\begin{aligned} \alpha '' + \omega _\alpha ^{ * 2}\alpha= & {} {\varepsilon ^2}g\left( {\xi ,\alpha } \right) . \end{aligned}$$

(5b)

where

$$\begin{aligned}&\omega _\xi ^{ * 2} = \varOmega _\xi ^2\left( {1 + {\varepsilon ^2}{\sigma _1}} \right) , ~ \omega _\alpha ^{ * 2} = \varOmega _\alpha ^2\left( {1 + {\varepsilon ^2}{\sigma _2}} \right) ,\\&f\left( {\xi ,\alpha } \right) = {\sigma _1}\varOmega _\xi ^2\xi - \left( {{x_\alpha }\alpha '' + 2{\zeta _\xi }{\varOmega _\xi }\xi ' + \varOmega _\xi ^2{\beta _\xi }{\xi ^3}} \right) , \\&g\left( {\xi ,\alpha } \right) = ~ {\sigma _2}\varOmega _\alpha ^2\alpha + F\sin \left( {\omega \tau } \right) \\&\quad \qquad -\left( {\frac{{{x_\alpha }}}{{r_\alpha ^2}}\xi '' + 2{\zeta _\alpha }{\varOmega _\alpha }\alpha ' + \varOmega _\alpha ^2{\beta _\alpha }{\alpha ^3}} \right) . \nonumber \end{aligned}$$

in which ${\sigma _1},{\sigma _2}$ are the detuning parameters of plunge and pitch motion.

In this investigation, we only consider $\omega _\xi ^ * = \omega _\alpha ^ * = \omega$. In this case, the detuning parameters of plunge and pitch motion can be rewritten as

$$\begin{aligned} {\sigma _1} = \left( \frac{\omega ^{2}}{\varOmega _\xi ^2} - 1 \right) \Bigg /{\varepsilon ^{2}}, ~ {\sigma _2} = \left( \frac{\omega ^{2}}{\varOmega _\alpha ^2} - 1 \right) \Bigg / {{\varepsilon ^2}}. \end{aligned}$$

(6)

Now let ${\xi _0},{\alpha _0}$ denote the solutions of systems (5a), (5b), which can be obtained by averaging method. Introducing the Van der Pol transformations as follows

$$\begin{aligned}&{\alpha _0} = {A_0}\left( \tau \right) \cos \left( {{\varPhi _{{\alpha _0}}}} \right) , \nonumber \\&{\alpha '_0} = - \omega {A_0}\left( \tau \right) \sin \left( {{\varPhi _{{\alpha _0}}}} \right) , \end{aligned}$$

(7a)

$$\begin{aligned}&{\xi _0} = {B_0}\left( \tau \right) \cos \left( {{\varPhi _{{\xi _0}}}} \right) , \nonumber \\&{\xi '_0} = - \omega {B_0}\left( \tau \right) \sin \left( {{\varPhi _{{\xi _0}}}} \right) , \end{aligned}$$

(7b)

$$\begin{aligned}&{\varPhi _{{\alpha _0}}} = \omega \tau + {\theta _{{\alpha _0}}}\left( \tau \right) , ~ {\varPhi _{{\xi _0}}} = \omega \tau + {\theta _{{\xi _0}}}\left( \tau \right) . \end{aligned}$$

(7c)

Substituting Eqs. (7a), (7b) into Eqs.  (5a), (5b) then one can obtain

$$\begin{aligned}&{A'_0} = - \frac{{{\varepsilon ^2}}}{\omega }g\left( {{\xi _0},{\alpha _0}} \right) \sin \left( {{\varPhi _{{\alpha _0}}}} \right) , \end{aligned}$$

(8a)

$$\begin{aligned}&{\theta '_{{\alpha _0}}} = - \frac{{{\varepsilon ^2}}}{{\omega {A_0}}}g\left( {{\xi _0},{\alpha _0}} \right) \cos \left( {{\varPhi _{{\alpha _0}}}} \right) , \end{aligned}$$

(8b)

$$\begin{aligned}&{B'_0} = - \frac{{{\varepsilon ^2}}}{\omega }f\left( {{\xi _0},{\alpha _0}} \right) \sin \left( {{\varPhi _{{\xi _0}}}} \right) , \end{aligned}$$

(8c)

$$\begin{aligned}&{\theta '_{{\xi _0}}} = - \frac{{{\varepsilon ^2}}}{{\omega {B_0}}}f\left( {{\xi _0},{\alpha _0}} \right) \cos \left( {{\varPhi _{{\xi _0}}}} \right) . \end{aligned}$$

(8d)

Applying the averaging principle, we arrive at

$$\begin{aligned}&{A'_0} = - \frac{{{\varepsilon ^2}}}{\omega }\frac{1}{{2\pi }}\int _0^{2\pi } {g\left( {{\xi _0},{\alpha _0}} \right) \sin \left( {{\varPhi _{{\alpha _0}}}} \right) } d{\varPhi _{{\alpha _0}}}, \end{aligned}$$

(9a)

$$\begin{aligned}&{\theta '_{{\alpha _0}}} = - \frac{{{\varepsilon ^2}}}{{\omega {A_0}}}\frac{1}{{2\pi }}\int _0^{2\pi } {g\left( {{\xi _0},{\alpha _0}} \right) \cos \left( {{\varPhi _{{\alpha _0}}}} \right) } d{\varPhi _{{\alpha _0}}},\nonumber \\ \end{aligned}$$

(9b)

$$\begin{aligned}&{B'_0} = - \frac{{{\varepsilon ^2}}}{\omega }\frac{1}{{2\pi }}\int _0^{2\pi } {f\left( {{\xi _0},{\alpha _0}} \right) \sin \left( {{\varPhi _{{\xi _0}}}} \right) } d{\varPhi _{{\xi _0}}}, \end{aligned}$$

(9c)

$$\begin{aligned}&{\theta '_{{\xi _0}}} = - \frac{{{\varepsilon ^2}}}{{\omega {B_0}}}\frac{1}{{2\pi }}\int _0^{2\pi } {f\left( {{\xi _0},{\alpha _0}} \right) \cos \left( {{\varPhi _{{\xi _0}}}} \right) } d{\varPhi _{{\xi _0}}}. \end{aligned}$$

(9d)

Substituting the $f\left( {{\xi _0},{\alpha _0}} \right) ,g\left( {{\xi _0},{\alpha _0}} \right)$ into Eqs. (9a)–(9d) and letting $\theta = {\theta _{{\xi _0}}} - {\theta _{{\alpha _0}}}$ yields

$$\begin{aligned}&{A'_0} = - \frac{{{\varepsilon ^2}}}{{2\omega }}\left[ { - {N_2}\sin \left( \theta \right) + {N_3} + F\cos \left( {{\theta _{{\alpha _0}}}} \right) } \right] , \nonumber \\ \end{aligned}$$

(10a)

$$\begin{aligned}&{\theta '_{{\alpha _0}}} = - \frac{{{\varepsilon ^2}}}{{2{A_0}\omega }}\left[ {{N_1} + {N_2}\cos \left( \theta \right) - F\sin \left( {{\theta _{{\alpha _0}}}} \right) } \right] ,\nonumber \\ \end{aligned}$$

(10b)

$$\begin{aligned}&{B'_0} = - \frac{{{\varepsilon ^2}}}{{2\omega }}\left[ {{M_2}\sin \left( \theta \right) + {M_3}} \right] , \end{aligned}$$

(10c)

$$\begin{aligned}&{\theta '_{{\xi _0}}} = - \frac{{{\varepsilon ^2}}}{{2{B_0}\omega }}\left[ {{M_1} + {M_2}\cos \left( \theta \right) } \right] . \end{aligned}$$

(10d)

where

$$\begin{aligned}&{M_1} = {\sigma _1}\varOmega _\xi ^2B_0 - \frac{3}{4}\varOmega _\xi ^2{\beta _\xi }{B^3_0},\\&{N_1} = {\sigma _2}\varOmega _\alpha ^2A_0 - \frac{3}{4}\varOmega _\alpha ^2{\beta _\alpha }{A^3_0},\\&{M_2} = {x_\alpha }{\omega ^2}A_0,{} {N_2} = \frac{{{x_\alpha }}}{{r_\alpha ^2}}{\omega ^2}B_0, \\&{M_3} = 2{\zeta _\xi }{\varOmega _\xi }\omega B_0,{} {N_3} = 2{\zeta _\alpha }{\varOmega _\alpha }\omega A_0. \end{aligned}$$

Base on the steady-state solution of the deterministic system, Eqs. (10a)–(10d) satisfy the following conditions

$$\begin{aligned} {A'_0} = 0, ~ {\theta '_{{\alpha _0}}} = 0, ~ {B'_0} = 0, ~ {\theta '_{{\xi _0}}} = 0. \end{aligned}$$

(11)

Then, one can obtain the following amplitude–frequency relation

$$\begin{aligned}&M_2^2 = M_3^2 + M_1^2, \end{aligned}$$

(12a)

$$\begin{aligned}&{\left( {\frac{{{N_2}{M_3}}}{{{M_2}}} + {N_3}} \right) ^2} + {\left( {{N_1} - \frac{{{N_2}{M_1}}}{{{M_2}}}} \right) ^2} = {F^2}. \end{aligned}$$

(12b)

In order to illustrate the effectiveness of averaging method, the harmonic balance method in Ref. [4] will be used to verify the approach. The system parameters $\varepsilon = 1.0,F = 1.5$ and the values of other system parameters are consistent with the Ref. [4]. In Fig. 2, it is clear that the results obtained by our method show a good agreement with the results obtained by harmonic balance method. Moreover, comparing the method we proposed with the harmonic balance method, the process of calculation of the averaging method seems simpler and also can obtain the same results.

3.2 The stochastic TDOFA system

In this subsection, the perturbation technique will be used to research the effects of the noise and we assume that the noise intensity is small. Let

$$\begin{aligned} \alpha= & {} {\alpha _0} + {\alpha _1} = {A_0}\cos \left( {{\varPhi _{{\alpha _0}}}} \right) + {} {\alpha _1}, \end{aligned}$$

(13a)

$$\begin{aligned} \xi= & {} {\xi _0} + {\xi _1} = {B_0}\cos \left( {{\varPhi _{{\xi _0}}}} \right) + {\xi _1}. \end{aligned}$$

(13b)

where ${\alpha _0} = {A_0}\cos \left( {{\varPhi _{{\alpha _0}}}} \right) , {\xi _0} = {B_0}\cos \left( {{\varPhi _{{\xi _0}}}} \right)$ are the solutions of the deterministic system (5a), (5b) and ${\alpha _1}, {\xi _1}$ are small disturbances.

Substituting Eqs. (13a), (13b) into Eqs. (3a), (3b) and eliminating the high-order small items, we can get ${\alpha _1}, {\xi _1}$ to satisfy the stochastic differential equations as follows

$$\begin{aligned} {\xi ''_1} + \varOmega _\xi ^2{\xi _1}= & {} - {\varepsilon ^2}{f_1}\left( {{\xi _1},{\alpha _1}} \right) , \end{aligned}$$

(14a)

$$\begin{aligned} {\alpha ''_1} + \varOmega _\alpha ^2{\alpha _1}= & {} - {\varepsilon ^2}{g_1}\left( {{\xi _1},{\alpha _1}} \right) + \varepsilon \eta \left( \tau \right) . \end{aligned}$$

(14b)

where

$$\begin{aligned} {f_1}\left( {{\xi _1},{\alpha _1}} \right)= & {} {x_\alpha }{\alpha ''_1} + 2{\zeta _\xi }{\varOmega _\xi }{\xi '_1} + 3\varOmega _\xi ^2{\beta _\xi }\xi _0^2{\xi _1},\\ {g_1}\left( {{\xi _1},{\alpha _1}} \right)= & {} \frac{{{x_\alpha }}}{{r_\alpha ^2}}{\xi ''_1} + 2{\zeta _\alpha }{\varOmega _\alpha }{\alpha '_1} + 3\varOmega _\alpha ^2{\beta _\alpha }\alpha _0^2{\alpha _1}.\end{aligned}$$

On assumption that $\varepsilon$ is small, we introduce the change in variables [27, 28]

$$\begin{aligned}&{\alpha _1} = {A_1}\left( \tau \right) \cos \left( {{\varPhi _{{\alpha _1}}}} \right) , \nonumber \\&{\alpha '_1} = - {\varOmega _\alpha }{A_1}\left( \tau \right) \sin \left( {{\varPhi _{{\alpha _1}}}} \right) , \end{aligned}$$

(15a)

$$\begin{aligned}&{\xi _1} = {B_1}\left( \tau \right) \cos \left( {{\varPhi _{{\xi _1}}}} \right) ,\nonumber \\&{\xi '_1} = - {\varOmega _\xi }{B_1}\left( \tau \right) \sin \left( {{\varPhi _{{\xi _1}}}} \right) , \end{aligned}$$

(15b)

$$\begin{aligned}&{\varPhi _{{\alpha _1}}} = {\varOmega _\alpha }\tau + {\theta _{{\alpha _1}}}\left( \tau \right) , ~ {\varPhi _{{\xi _1}}} = {\varOmega _\xi }\tau + {\theta _{{\xi _1}}}\left( \tau \right) . \end{aligned}$$

(15c)

Substituting Eqs. (15a), (15b) into Eqs. (14a), (14b) and then the stochastic differential equations for ${A_1}\left( \tau \right)$, ${\theta _{{\alpha _1}}}\left( \tau \right)$, ${B_1}\left( \tau \right)$, ${\theta _{{\xi _1}}}\left( \tau \right)$ can be derived as

$$\begin{aligned} {A'_1}\left( \tau \right)= & {} ~ \frac{{{\varepsilon ^2}}}{{{\varOmega _\alpha }}}{g_1}\left( {{\xi _1},{\alpha _1}} \right) \sin \left( {{\varPhi _{{\alpha _1}}}} \right) \nonumber \\&-\frac{\varepsilon }{{{\varOmega _\alpha }}}\eta \left( \tau \right) \sin \left( {{\varPhi _{{\alpha _1}}}} \right) , \end{aligned}$$

(16a)

$$\begin{aligned} {\theta '_{{\alpha _1}}}\left( \tau \right)= & {} ~ \frac{{{\varepsilon ^2}}}{{{\varOmega _\alpha }{A_1}}}{g_1}\left( {{\xi _1},{\alpha _1}} \right) \cos \left( {{\varPhi _{{\alpha _1}}}} \right) \nonumber \\&-\frac{\varepsilon }{{{\varOmega _\alpha }{A_1}}}\eta \left( \tau \right) \cos \left( {{\varPhi _{{\alpha _1}}}} \right) , \end{aligned}$$

(16b)

$$\begin{aligned} {B'_1}\left( \tau \right)= & {} \frac{{{\varepsilon ^2}}}{{{\varOmega _\xi }}}{f_1}\left( {{\xi _1},{\alpha _1}} \right) \sin \left( {{\varPhi _{{\xi _1}}}} \right) , \end{aligned}$$

(16c)

$$\begin{aligned} {\theta '_{{\xi _1}}}\left( \tau \right)= & {} \frac{{{\varepsilon ^2}}}{{{\varOmega _\xi }{B_1}}}{f_1}\left( {{\xi _1},{\alpha _1}} \right) \cos \left( {{\varPhi _{{\xi _1}}}} \right) . \end{aligned}$$

(16d)

Substituting ${f_1}\left( {{\xi _1},{\alpha _1}} \right) , {g_1}\left( {{\xi _1},{\alpha _1}} \right)$ into Eqs. (16a)-(16d) and using the stochastic averaging method, we get the Itô stochastic differential equations as follows

$$\begin{aligned} d{A_1}= & {} \left( { - {\varepsilon ^2}{\zeta _\alpha }{\varOmega _\alpha }{A_1} + \frac{{{\varepsilon ^2}\pi S\left( {{\varOmega _\alpha }} \right) }}{{2{A_1}\varOmega _\alpha ^2}}} \right) d\tau \nonumber \\&+\frac{\varepsilon }{{{\varOmega _\alpha }}}\sqrt{\pi S\left( {{\varOmega _\alpha }} \right) } d{W_1}\left( \tau \right) , \end{aligned}$$

(17a)

$$\begin{aligned} d{\theta _{{\alpha _1}}}= & {} ~ \frac{3}{4}{\varepsilon ^2}{\varOmega _\alpha }{\beta _\alpha }A_0^2d\tau \nonumber \\&+\quad \frac{\varepsilon }{{{\varOmega _\alpha }{A_1}}}\sqrt{\pi S\left( {{\varOmega _\alpha }} \right) } d{W_2}\left( \tau \right) , \end{aligned}$$

(17b)

$$\begin{aligned} d{B_1}= & {} - {\varepsilon ^2}{\zeta _\xi }{\varOmega _\xi }{B_1}d\tau , \end{aligned}$$

(17c)

$$\begin{aligned} d{\theta _{{\xi _1}}}= & {} \frac{3}{4}{\varepsilon ^2}{\varOmega _\xi }{\beta _\xi }B_0^2d\tau . \end{aligned}$$

(17d)

where ${W_1}\left( \tau \right) , {W_2}\left( \tau \right)$ are independent standard Wiener processes and $S\left( {{\varOmega _\alpha }} \right)$ denotes the value of the spectral density of $\eta \left( \tau \right)$ at ${\varOmega _\alpha }$.

Fig. 3

Steady-state probability density of amplitude $A_1$. “Times” numerical result, “solid line” analytical result ($D=0.75$)

Fig. 4

Amplitude–frequency responses: a pitch motion; b plunge motion. “Asterisks” numerical result, “solid line” analytical result ($D=0$)

Clearly, Eq. (17a) implies that ${A_1}\left( \tau \right)$ is a time-homogeneous diffusion process because it does not depend on ${\theta _{{\alpha _1}}}\left( \tau \right)$, ${B_1}\left( \tau \right)$ and ${\theta _{{\xi _1}}}\left( \tau \right)$. So, the probability density function $P\left( {{A_1},\tau } \right)$ of ${A_1}\left( \tau \right)$ satisfies the following Fokker–Plank equation

$$\begin{aligned} \frac{{\partial P}}{{\partial \tau }}= & {} - \frac{\partial }{{\partial {A_1}}}\left[ {\left( { - {\varepsilon ^2}{\zeta _\alpha }{\varOmega _\alpha }{A_1} + {\varepsilon ^2}\frac{{\pi S\left( {{\varOmega _\alpha }} \right) }}{{2\varOmega _\alpha ^2{A_1}}}} \right) P} \right] \nonumber \\&\quad + \frac{{{\varepsilon ^2}\pi S\left( {{\varOmega _\alpha }} \right) }}{{2\varOmega _\alpha ^2}}\frac{{{\partial ^2}P}}{{\partial A_1^2}} \end{aligned}$$

(18)

In the subsection, we just concentrate on the steady-state solution. By letting $\frac{{\partial P\left( {{A_1},\tau } \right) }}{{\partial \tau }} = 0$, the steady-state probability density of ${A_1}\left( \tau \right)$ can be written as

$$\begin{aligned} P\left( {{A_1}} \right) = \frac{{{A_1}}}{{{\sigma ^2}}}\exp \left( { - \frac{{A_1^2}}{{2{\sigma ^2}}}} \right) , ~ {\sigma ^2} = \frac{{\pi S\left( {{\varOmega _\alpha }} \right) }}{{2{\zeta _\alpha }\varOmega _\alpha ^3}}. \end{aligned}$$

(19)

Now we carry out numerical simulation to verify the correctness of the analytical solution (see Fig. 3). We can see that the numerical result of steady-state probability density is coincident with the analytical result.

Appling Eq. (19), we can obtain the first- and second-order moments of ${A_1}\left( \tau \right)$ as follows

$$\begin{aligned} E\left( {{A_1}} \right)= & {} \int _0^{ + \infty } {{A_1} \cdot P\left( {{A_1}} \right) } d{A_1} = \sqrt{\frac{\pi }{2}} \sigma , \end{aligned}$$

(20a)

$$\begin{aligned} E\left( {A_1^2} \right)= & {} \int _0^{ + \infty } {A_1^2 \cdot P\left( {{A_1}} \right) } d{A_1} = 2{\sigma ^2}. \end{aligned}$$

(20b)

Combining Eqs. (20a), (20b) and (13a), the mean-square response of pitch motion can be obtained

$$\begin{aligned} E\left( {{\alpha ^2}} \right)= & {} E{\left( {{\alpha _0} + {\alpha _1}} \right) ^2}\nonumber \\= & {} E{\left[ {{A_0}\cos \left( {{\varPhi _{{\alpha _0}}}} \right) + {A_1}\left( \tau \right) \cos \left( {{\varPhi _{{\alpha _1}}}} \right) } \right] ^2}\nonumber \\= & {} A_0^2{\cos ^2}\left( {\omega \tau + {\theta _{{\alpha _0}}}} \right) + {\sigma ^2}. \end{aligned}$$

(21)

It is seen from Eq. (21) that the mean-square response $E\left( {{\alpha ^2}} \right)$ is a periodic function of time $\tau$. Taking average with respect to time $\tau$, one can obtain the time-averaging mean-square response as Ref. [29]

$$\begin{aligned} {\left\langle {E\left( {{\alpha ^2}} \right) } \right\rangle _\tau }= & {} {\left\langle {A_0^2{{\cos }^2}\left( {\omega \tau + {\theta _{{\alpha _0}}}} \right) } \right\rangle _\tau } + {\sigma ^2} \nonumber \\= & {} \frac{{A_0^2}}{2} + {\sigma ^2}. \end{aligned}$$

(22)

where ${\left\langle \cdot \right\rangle _\tau } = \frac{1}{T}\int _0^T {\left( \cdot \right) } d\tau$ denotes the time-averaging operator with respect to time $\tau$ over one period T.

In order to verify the correctness of analytical solution, numerical results of original equations (3a), (3b) are presented to compare the differences between the numerical simulations and approximately analytical results in the next step. In this subsection, we choose the following parameters ${x_\alpha } = 0.1, {r_\alpha } = 1.0, {U^ * } = 1.0,\varpi = 1.0, {\zeta _\alpha } = {\zeta _\xi } = 0.1, {\beta _\alpha } = 0.25, {\beta _\xi } = 0, \varepsilon = \sqrt{0.1}, F = 1.5$. In Fig. 4, we first consider the deterministic case, namely $D = 0$ , and the approximately analytical results are in good agreement with the numerical simulation results. Subsequently, the stochastic case is considered in Fig. 5. It intuitively shows that the analytical time-averaging mean-square response coincide well with the numerical results.

For the deterministic case, we also consider the influence of the amplitude F of harmonic excitation on the system response. In Fig. 6, we obtain the amplitude–frequency response curves for different values of F. We find that the amplitude and multiple-value response area will become bigger with the increase in F.

Fig. 5

Time-averaging mean-square response of pitch motion. “Asterisks” numerical result, “solid line” analytical result ($D=0.01$)

4 Stochastic jump

In this section, the stochastic jump of TDOFA system is investigated by means of the changes in system responses. The values of system parameters are the same as the previous ones. In fact, stochastic jump phenomenon can be found from Figs. 4 and 5. As is shown in Fig. 4, we can find the amplitude of $\alpha$ and $\xi$ has a jump phenomenon with the increase in $\omega$, that is, from region 2 into region 3 for amplitude ${A_0}$, and from region 2 into region 3 for amplitude ${B_0}$; and vice versa. Moreover, similar result can be found from the mean-square response of $\alpha$ which is shown in Fig. 5. This phenomenon can be regarded as bifurcation.

In Figs. 7 and 8, we will verify the jump phenomenon through the response and the phase diagrams. Here we let $\omega = 1.15$, when the initial value is ${\alpha _0} = 3.0,{\alpha '_0} = 3.0,{\xi _0} = 0,$ and ${\xi '_0} = 0$, the system will stay at the upper branch of the multiple-value response area (region 2) in Fig. 4(a) (see Fig. 7); however, when the initial value is ${\alpha _0} = 0.5,{\alpha '_0} = 0.5,{\xi _0} = 0.5,$ and ${\xi '_0} = 0.5$, the system will stay at the lower branch (see Fig. 8).

Fig. 6

Amplitude–frequency response curves for different excitations: a pitch motion; b plunge motion. “Triangle symbol” $F=1.5$; “plus symbol” $F=3.0$; “circle” $F=6.0$

Fig. 7

Responses of the original systems (3a), (3b) with parameters: $\omega = 1.15, D = 0,{\alpha _0} = 3.0,{\alpha '_0} = 3.0,{\xi _0} = 0,{\xi '_0} = 0$

Fig. 8

Responses of the original systems (3a), (3b) with parameters: $\omega = 1.15, D = 0,{\alpha _0} = 0.5,{\alpha '_0} = 0.5,{\xi _0} = 0.5,{\xi '_0} = 0.5$

Fig. 9

Steady-state probability densities for amplitude A of pitch motion in original systems (3a), (3b) with the different noise intensities and initial values: a $D = 0.005,{\alpha _0} = 3.0,{\alpha '_0} = 3.0,{\xi _0} = 0,{\xi '_0} = 0$; b $D = 0.05,{\alpha _0} = 3.0,{\alpha '_0} = 3.0,{\xi _0} = 0,{\xi '_0} = 0$; c $D = 0.8,{\alpha _0} = 3.0,{\alpha '_0} = 3.0,{\xi _0} = 0,{\xi '_0} = 0$; d $D = 0.05,{\alpha _0} = 0.5,{\alpha '_0} = 0.5,{\xi _0} = 0.5,{\xi '_0} = 0.5$

Fig. 10

Responses of the original system (3a), (3b) for the same intensity of noise and the same initial values: $\omega = 1.15,D = 0.05,{\alpha _0} = 3.0,{\alpha '_0} = 3.0,{\xi _0} = 0,{\xi '_0} = 0$

Now the stochastic jump of TDOFA models subject to harmonic and random excitation is investigated to observe the effects of random noise. The Monte Carlo simulation will be used to demonstrate the steady-state probability density and the responses. Because the amplitude of pitch motion is $A\left( \tau \right) = \sqrt{{\alpha ^2}\left( \tau \right) + {{\left[ {{{\alpha '\left( \tau \right) } \big /\omega }} \right] }^2}}$, the steady-state probability density function $P\left( A \right)$ of $A\left( \tau \right)$ can be obtained by directly Monte Carlo simulation.

As shown in Fig. 9(a–c), we can see that the noise will induce the emergence of two peaks of the steady-state probability density, which means the stochastic jump occurs. And with the increase in noise intensity, the height of the small peak will increase gradually; meanwhile, the height of the large peak will reduce. In addition, by comparing Fig. 9(d) with Fig. 9(b), we can see that the steady-state probability density will not appear the two peaks in Fig. 9(d) under the same noise intensity, which means the stochastic jump not occurs. That means that the system responses will not jump to another state once it gets into a steady state. In the next part, we just consider that the initial value of system is taken as ${\alpha _0} = 3.0,{\alpha '_0} = 3.0,{\xi _0} = 0,$ and ${\xi '_0} = 0$.

Fig. 11

Responses of the original system (3a), (3b) in pitch motion for the parameters: $\omega = 1.15,{\alpha _0} = 3.0,{\alpha '_0} = 3.0,{\xi _0} = 0,{\xi '_0} = 0$, and with the different noise intensities: a $D=0.1$; b $D=0.3$; c $D=0.5$; d $D=0.8$

Now, the time history diagrams are plotted to further illustrate the stochastic jump phenomenon. As shown in Fig. 10, when the noise intensity is smaller relatively, the response of system changes from period motion of the deterministic case into random quasi-periodic motion, and it is relatively difficult to jump out of this stable region once it gets into a steady state. In other words, the stochastic jump phenomenon is not frequent. However, when the noise intensity is bigger (see Fig. 11), it intuitively shows the existence of stochastic jump. Meanwhile, with the increase in noise intensity gradually, the stochastic jump phenomenon will occur more and more frequently. Therefore, we can conclude that the noise can lead to a stochastic jump, which can be named as stochastic bifurcation due to the change in steady-state probability density.

5 Conclusion

In this paper, we investigate the nonlinear dynamical responses of a coupled cubic nonlinear TDOFA system under combined harmonic and Gaussian white noise excitation. In order to ascertain system response, the averaging method is used to drive the resultant equations of motion. It is shown that the numerical results obtained by the fourth-order Runge–Kutta simulation of original system (3a), (3b) coincide perfectly with the analytical solution obtained by the averaging method for both in deterministic and stochastic case. The stochastic jump phenomenon has been observed through the probability density figures and the time history diagrams with the changes in noise intensity. The results illustrate that the noise has an essential effect on the system response, which can induce the stochastic jump phenomenon. In addition, with the increase in noise intensity gradually, the stochastic jump phenomenon will occur more and more frequently. We also demonstrate the influences of the initial value and the noise intensity via the time history and the phase diagrams.