Nonlinear dynamics of an aeroelastic airfoil with free-play in transonic flow

Abstract

Nonlinear dynamic behaviors of an aeroelastic airfoil with free-play in transonic air flow are studied. The aeroelastic response is obtained by using time-marching approach with computational fluid dynamics (CFD) and reduced order model (ROM) techniques. Several standardized tests of transonic flutter are presented to validate numerical approaches. It is found that in time-marching approach with CFD technique, the time-step size has a significant effect on the calculated aeroelastic response, especially for cases considering both structural and aerodynamic nonlinearities. The nonlinear dynamic behavior for the present model in transonic air flow is greatly different from that in subsonic regime where only simple harmonic oscillations are observed. Major features of the responses in transonic air flow at different flow speeds can be summarized as follows. The aeroelastic responses with the amplitude near the free-play are dominated by single degree of freedom flutter mechanism, and snap-though phenomenon can be observed when the air speed is low. The bifurcation diagram can be captured by using ROM technique, and it is observed that the route to chaos for the present model is via period-doubling, which is essentially caused by the free-play nonlinearity. When the flow speed approaches the linear flutter speed, the aeroelastic system vibrates with large amplitude, which is dominated by the aerodynamic nonlinearity. Effects of boundary layer and airfoil profile on the nonlinear responses of the aeroelastic system are also discussed.

1 Introduction

The dynamic behavior of an aeroelastic airfoil, or typical wing section, with a free-play nonlinearity attracts interests of both aircraft engineers and dynamics researchers due to its substantial various nonlinear phenomenon. It is convenient to use either the Theodorson function [31] or the Wagner function [9] to calculate the unsteady aerodynamic loads in incompressible flow. And the piston theory [1] is suitable to obtain the unsteady loads in supersonic regime. Numerous investigations on such a nonlinear aeroelastic system are conducted in low subsonic or supersonic air flow. However, because of the challenging of modeling the transonic unsteady aerodynamics, only a few researches on nonlinear dynamic behavior of an aeroelastic airfoil with free-play in transonic air flow have been investigated before.

Generally speaking, the major feature of the transonic air flow is the mixed subsonic-supersonic flow and the appearance of shock wave, which may lead to aerodynamic nonlinearity in the aeroelastic system. As a high-fidelity technique to capture the shock wave in transonic air flow, the time-marching approach with computational fluid dynamics (CFD) technique is usually used to simulate the transonic limit cycle oscillation (LCO) considering structural nonlinearities. Kousen and Bendiksen [22] investigated the transonic LCO of an aeroelastic airfoil with a free-play nonlinearity in the pitching degree of freedom (DOF) and the bifurcation diagram was obtained by using time-marching approach. The transonic aeroelastic behavior of an airfoil with free-play nonlinearities in both of the pitching and plunging DOFs was analyzed by Kim and Lee [21], and LCOs and chaotic motions were observed in specific ranges of Mach numbers.

To reduce the computational costs in CFD simulations, the reduced order model (ROM) method based on CFD is also adopted in this problem. A three-DOF aeroelastic wing model with free-play in its control surface deflection was used to study the transonic LCO behavior by Dowell et al. [14] using ROM method, and the so-called chimney phenomenon was shown in their results. The LCOs for an aeroelastic airfoil with structural nonlinearity in subsonic and transonic air flow were obtained by Munteanu et al. [23] using ROM technique, and their results showed that the ROM approach can estimate the LCOs accurately and efficiently. An airfoil with piecewise nonlinearity was investigated by Jones et al. [19] in both low speed incompressible flow and transonic air flow, and the LCOs were rapidly identified with good accuracy in their study.

All of the research activities mentioned above focused on predicting the response of the nonlinear aeroelastic systems. However, the nonlinear dynamic behavior, e.g., LCO, bifurcation or chaos, in transonic air flow were not demonstrated systematically. In the current study, an aeroelastic airfoil with free-play in its pitching DOF is used to explore how the nonlinear system behaves in the transonic regime.

In this paper, the aeroelastic response is obtained by using time-marching approach with CFD and ROM techniques. For the present aeroelastic model, the nonlinear dynamic behavior in transonic air flow is greatly different from that in subsonic regime. In subsonic air flow, only simple harmonic oscillations are observed. However, in transonic air flow the aeroelastic system displays responses dominated by single degree of freedom (SDOF) flutter, simple LCO, complex LCO, nonperiodic motion or chaos motion at different dynamic pressures. These results demonstrate that our investigation considering the nonlinear effect of transonic aerodynamics may provide a new insight into the nonlinear dynamic behavior of a traditional aeroelastic airfoil model.

The paper is organized as follows. In Sect. 2, the governing equations and analytical method are formulated. Several standard transonic flutter problems are analyzed in Sect. 3 to verify the feasibility of numerical approaches used in the present study. To have a better understanding of the nonlinear dynamic behavior of the aeroelastic system, Sect. 4 presents preliminary analysis and shows the basic aeroelastic characteristics of the model. In Sect. 5, numerical results and discussions on the major features of the responses with different oscillation amplitudes are provided. Effects of boundary layer and airfoil profile on the nonlinear responses of the aeroelastic system are extendedly discussed in Sect. 6. Finally, the main conclusions are drawn in Sect. 7.

2 Theoretical analysis

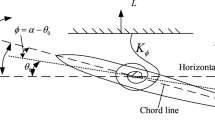
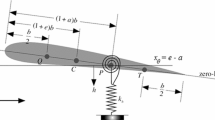
Figure 1 shows a sketch of a typical aeroelastic airfoil with plunging (h) and pitching ($\alpha$) DOFs. The elastic axis of the airfoil (E point) is located at a distance of ab after the mid-chord point, and the gravity center (G point) is located at $x_a b$ after the elastic axis, where b is the half-chord length. The mass per unit span is m, the first moment of inertia about the elastic axis is $S_\alpha = mx_\alpha b$, and the moment of inertia about the elastic axis is $I_\alpha =mr_\alpha ^2 b^2$. The bending stiffness and torsion stiffness are modeled by springs attached to the elastic axis, respectively. A linear spring is considered in plunging DOF, and the plunging stiffness coefficient is $K_h = m \omega _h^2$. While a free-play nonlinearity is assumed in the pitching DOF, and the nonlinear structural restoring moment can be described as

$$\begin{aligned} M(\alpha ) =\left\{ \begin{array}{l@{\qquad }l} K_\alpha (\alpha - \delta ) &{} \alpha \ge \delta \\ 0 &{} -\delta< \alpha < \delta \ \\ K_\alpha (\alpha + \delta ) &{} \alpha \le -\delta \end{array} \right. \end{aligned}$$

(1)

where $\delta$ denotes the measurement of free-play, $K_\alpha = I_\alpha \omega _\alpha ^2$ is the torsion stiffness coefficient. To express the equations in matrix form in the following parts of this section, Eq. (1) can also be rewritten as

$$\begin{aligned} M(\alpha ) =K_\alpha \alpha \cdot \left\{ \begin{array}{l@{\quad }l} 1 - \delta /\alpha &{} \alpha \ge \delta \\ 0 &{} -\delta< \alpha < \delta \ \\ 1 + \delta /\alpha &{} \alpha \le -\delta \end{array} \right. =K_\alpha \bar{M}(\alpha ) \alpha \end{aligned}$$

(2)

Note that when $\delta = 0$, the airfoil is degenerated to a linear structural model and consequently $\bar{M}(\alpha )=1$.

The governing equations of motion for linear springs have been derived from the Lagrange equations according to Dowell et al. [13]. In addition, the nonlinear structural restoring moment from the spring with free-play in pitching DOF has been considered in the present study. The nonlinear governing equations can be expressed as

$$\begin{aligned} \left\{ \begin{array}{l} m\ddot{h}+S_\alpha \ddot{\alpha }+K_hh=-L \\ S_\alpha \ddot{h}+I_\alpha \ddot{\alpha }+M(\alpha )= M_{e \alpha } \end{array} \right. \end{aligned}$$

(3)

where $L = \rho V^2 b c_l$ and $M_{e \alpha } = 2 \rho V^2 b^2 c_m$ are the aerodynamic lift and moment about the elastic axis, respectively. $c_l$ is the lift coefficient, $c_m$ is the aerodynamic moment coefficient, and $\rho$ is the air density.

Fig. 1

An aeroelastic airfoil in transonic air flow

Introducing nondimensional time $\tau =\omega _\alpha t$ and mass ratio $\mu = m/\pi \rho b^2$, Eq. (3) can be written as

$$\begin{aligned}&\left[ \begin{array}{ll} 1 &{} x_\alpha \\ x_\alpha &{} r_\alpha ^2 \end{array} \right] \left\{ \begin{array}{c} \frac{h''}{b}\\ \alpha '' \end{array} \right\} + \left[ \begin{array}{cc} \left( \frac{\omega _h}{\omega _\alpha }\right) ^2 &{} 0 \\ 0 &{} r_\alpha ^2 \bar{M}(\alpha ) \end{array} \right] \left\{ \begin{array}{c} \frac{h}{b}\\ \alpha \end{array} \right\} \nonumber \\&\quad =\frac{U^2}{\pi \mu } \left\{ \begin{array}{c} -c_l\\ 2c_m \end{array} \right\} \end{aligned}$$

(4)

or

$$\begin{aligned} \varvec{M}\varvec{\xi }''+\varvec{K_{non}}\varvec{\xi }=\frac{U^2}{\pi \mu }\varvec{f_a} \end{aligned}$$

(5)

where $()''=\hbox {d}^2()/\hbox {d}\tau ^2$, $U = V/b \omega _\alpha$, $\varvec{M}= \left[ \begin{array}{cc} 1 &{} x_\alpha \\ x_\alpha &{} r_\alpha ^2 \end{array} \right]$ and $\varvec{K_{non}} = \left[ \begin{array}{cc} (\frac{\omega _h}{\omega _\alpha })^2 &{} 0 \\ 0 &{} r_\alpha ^2 \bar{M}(\alpha ) \end{array} \right]$. $\varvec{M}$ is the mass matrix, $\varvec{K_{non}}$ is the nonlinear stiffness matrix, and U is the non-dimensional air speed. For this aeroelastic system, $\varvec{\xi } = \{h/b~~\alpha \}^T$ and $\varvec{f_a} = \{-c_l~~2c_m\}^T$ are served as the generalized displacements and the generalized aerodynamic forces, respectively.

By defining the structural state vector $\varvec{x_s} = \left\{ \xi ~~\xi '\right\} ^T$, the motion equation in state space can be written as

$$\begin{aligned} \left\{ \begin{array}{ll} \varvec{x_s}'(t) &{}=\varvec{A_s x_s}(t)+\frac{U^2}{\pi \mu } \varvec{B_s f_a}(t) \\ \varvec{\xi }(t) &{}=\varvec{C_s x_s}(t)+\varvec{D_s f_a}(t) \end{array} \right. \end{aligned}$$

(6)

where $()'=\hbox {d}()/\hbox {d}\tau$, $\varvec{A_s} = \left[ \begin{array}{cc} \varvec{0} &{} \varvec{I} \\ -\varvec{M}^{-1}\varvec{K_{non}} &{} \varvec{0} \end{array} \right]$, $\varvec{B_s} = \left[ \begin{array}{c} \varvec{0} \\ \varvec{M}^{-1} \end{array} \right]$, $\varvec{C_s} = \left[ \begin{array}{c} \varvec{I} \\ \varvec{0} \end{array} \right]$ and $\varvec{D_s} = \left[ \begin{array}{c} \varvec{0} \end{array} \right]$.

Before solving the above equations numerically, two important concepts dealing with the transonic unsteady aerodynamics should be summarized briefly. When the shock wave is generated in transonic air flow, the steady air flow parameters vary with spatial position in the flow field around the wing. So the behaviors of the unsteady aerodynamic forces induced by the airfoil motion will be nonlinear in the transonic region. Nevertheless, it can be assumed that the parameters of flow field and the motion of shock wave vary in a linear fashion with the wing motion when considering a small perturbation about the transonic steady air flow. And this is usually called dynamically linear, but statically nonlinear, aerodynamics according to Dowell et al. [13]. With the dynamically linear aerodynamics, the ROM aerodynamics can be used to replace the full-order model like CFD, and the computational cost can be significantly reduced. It should be noted that at some special conditions the dynamically linear aerodynamics will be accurate even though the airfoil oscillates with moderate amplitudes.

2.1 Time-marching approach with CFD

As mentioned in Sect. 1, the time-marching approach based on CFD technique is a high-fidelity tool to obtain the aeroelastic response in transonic air flow. And nowadays some commercial software packages are capable of running fluid-structure interaction simulations without much difficulty. In this study, we choose Ansys-CFX solver to obtain the aeroelastic response, which was also used by Cui and Han [8] to predict the flutter characteristics of a transport wing in transonic air flow.

CFX is a general purpose CFD program, which solves the Euler models by using a cell-vertex version of finite volume method [4]. The upwind scheme is provided to evaluate the advection fluxes in CFX. The transient term is discretized by implicit dual time-stepping method with a modified Second Order Backward Euler scheme for real time advancement. A multi-grid accelerated incomplete lower upper factorization technique is used to solve the discrete system of linearized equations in pseudo-time. Mesh deformation also plays an important rule in the present study. When the motion of nodes on boundary is specified, CFX uses a mesh model called Displacement Diffusion to determine the motion of all remaining nodes.

Ansys is a general purpose finite element analysis (FEA) program, which can be employed as a nonlinear structural solver. The nonlinear spring element (COMBIN 39) in Ansys is particular propitious to model the free-play nonlinearity. The nonlinear response is obtained by marching in time using an implicit Newmark integration scheme with Newton-Raphson procedure in this FEA program.

2.2 ARMA ROM for transonic aerodynamics

Among the numerous methods to build ROM aerodynamics, the system identification method is an effective and efficient technique. Here we choose the autoregressive moving average (ARMA) model [7, 33] to build the ROM of aerodynamics, which is described as

$$\begin{aligned} \varvec{f_a}(k) = \varSigma ^{na}_{i=1}\varvec{A_i f_a} (k-i)+\varSigma ^{nb-1}_{i = 0}\varvec{B_i \xi } (k-i) \end{aligned}$$

(7)

One advantage of ARMA model is that the system response at any time step $\varvec{f_a}(k)$ is a linear combination of past inputs $\varvec{\xi } (k-i)$ and outputs $\varvec{f_a} (k-i)$, so that this model is easy to employ to build the ROM mathematically. With an assumed model order consisting of na past outputs and nb inputs, the only task is to identify the constant coefficient matrices $\varvec{A_i}$ and $\varvec{B_i}$.

In the present study, a so-called 3211 signal developed by Cowan et al. [7] is employed as the input of the CFD solve due to its ease of implementation and broad frequency spectra. The least squares method is adopted to fit the time history of the output of the CFD solver, i.e., $\varvec{f_a}$, to estimate the unknown coefficient matrices.

A state vector $\varvec{x_a}(k)$ consisting of $(na+nb+1)$ vector states is defined as,

$$\begin{aligned} \varvec{x_a}(k)= & {} [\varvec{f_a}(k-1)~~\cdots ~~\varvec{f_a}(k-na)~~\varvec{\xi }(k-1)~~\cdots ~~ \nonumber \\&\varvec{\xi }(k-nb+1)]^T \end{aligned}$$

(8)

Then the discrete-time aerodynamic model in state-space form can be written as,

$$\begin{aligned} \left\{ \begin{array}{l} \varvec{x_a}(k+1)= \tilde{\varvec{A_a}}\varvec{x_a}(k)+\tilde{\varvec{B_a}}\varvec{\xi }(k)\\ \varvec{f_a}(k) = \tilde{\varvec{C_a}}\varvec{x_a}(k)+\tilde{\varvec{D_a}}\varvec{\xi }(k) \end{array} \right. \end{aligned}$$

(9)

where

$$\begin{aligned}&\tilde{\varvec{A_a}}\\&\quad = \left[ \begin{array}{cccccccccc} \varvec{A}_1&{}\varvec{A}_2&{}\cdots &{}\varvec{A}_{na-1}&{}\varvec{A}_{na}&{}\varvec{B}_1&{}\varvec{B}_2&{}\cdots &{}\varvec{B}_{nb-2}&{}\varvec{B}_{nb-1}\\ \varvec{I} &{}\varvec{0} &{}\cdots &{}\varvec{0} &{}\varvec{0} &{}\varvec{0} &{}\varvec{0} &{}\cdots &{}\varvec{0} &{}\varvec{0} \\ \vdots &{}\varvec{I} &{}\cdots &{}\varvec{0} &{}\varvec{0} &{}\varvec{0} &{}\varvec{0} &{}\cdots &{}\varvec{0} &{}\varvec{0} \\ \vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ \varvec{0} &{}\varvec{0} &{}\cdots &{}\varvec{I} &{}\varvec{0} &{}\varvec{0} &{}\varvec{0} &{}\cdots &{}\varvec{0} &{}\varvec{0} \\ \varvec{0} &{}\varvec{0} &{}\cdots &{}\varvec{0} &{}\varvec{0} &{}\varvec{0} &{}\varvec{0} &{}\cdots &{}\varvec{0} &{}\varvec{0} \\ \varvec{0} &{}\varvec{0} &{}\cdots &{}\varvec{0} &{}\varvec{0} &{}\varvec{I} &{}\varvec{0} &{}\cdots &{}\varvec{0} &{}\varvec{0} \\ \varvec{0} &{}\varvec{0} &{}\cdots &{}\varvec{0} &{}\varvec{0} &{}\varvec{0} &{}\varvec{I} &{}\cdots &{}\varvec{0} &{}\varvec{0} \\ \vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ \varvec{0} &{}\varvec{0} &{}\cdots &{}\varvec{0} &{}\varvec{0} &{}\varvec{0} &{}\varvec{0} &{}\cdots &{}\varvec{I} &{}\varvec{0} \\ \end{array} \right] \\&\tilde{\varvec{B_a}}= \left[ \begin{array}{cccccccccc} \varvec{B}_0&{}\varvec{0}&{}\varvec{0}&{}\cdots &{}\varvec{0}&{}\varvec{I}&{}\varvec{0}&{}\varvec{0}&{}\cdots &{}\varvec{0}\\ \end{array} \right] ^T \\&\tilde{\varvec{C_a}}= \left[ \begin{array}{cccccccc} \varvec{A}_1&{}\cdots &{}\varvec{A}_{na-1}&{}\varvec{A}_{na}&{}\varvec{B}_1&{}\cdots &{}\varvec{B}_{nb-2}&{}\varvec{B}_{nb-1}\\ \end{array} \right] ^T\\&\tilde{\varvec{D_a}}= \left[ \begin{array}{c} \varvec{B}_0 \end{array} \right] \end{aligned}$$

To couple the structural equations, the discrete-time state-space form of the aerodynamic ROM can be transformed into the continuous-time form, which can be written as

$$\begin{aligned} \left\{ \begin{array}{ll} \varvec{x_a}'(t) &{}= \varvec{A_a}\varvec{x_a}(t)+\varvec{B_a}\varvec{\xi }(t)\\ \varvec{f_a}(t) &{}= \varvec{C_a}\varvec{x_a}(t)+\varvec{D_a}\varvec{\xi }(t) \end{array} \right. \end{aligned}$$

(10)

Introducing $\varvec{x} = \left\{ \varvec{x_s}^T~~ \varvec{x_a}^T \right\} ^T$ and coupling the structural motion Eq. (6) and the aerodynamic ROM Eq. (10), the governing equation for the aeroelastic system in state-space form can be obtained,

$$\begin{aligned} \varvec{x}' = \varvec{A x} = \left[ \begin{array}{cc} \varvec{A_s}+\frac{U^2}{\pi \mu }\varvec{B_s D_a C_s} &{} \frac{U^2}{\pi \mu } \varvec{B_s C_a} \\ \varvec{B_a C_s} &{} \varvec{A_a} \end{array} \right] \varvec{x} \end{aligned}$$

(11)

Fig. 2

Computational grids for NACA 64A010 airfoil: a overall. b close-up

Fig. 3

Comparison of aerodynamic coefficients of NACA 64A010 airfoil for different meshes (Mach 0.8, $\alpha _0 = 1^\circ$, $k = 0.1$ and $a=-0.6$): a lift coefficient, b aerodynamic moment coefficient

It should be noted that the above equation is actually nonlinear, since $\bar{M}(\alpha )$ is included in the expression of $\varvec{A_s}$. However, if the linear structural model is adopted, i.e., $\bar{M}(\alpha ) = 1$, the linear flutter speed $U_l$ can be obtained by solving the eigenvalue of $\varvec{A}$ in Eq. (11).

2.3 RK4 with Henon’s method

Since the free-play nonlinearity is a type of discontinuous (or non-smooth) nonlinearity, the application of the classical fourth-order Runge–Kutta (RK4) method is limited due to the numerical inaccuracy induced by the crossover of the integration step according to Dai et al. [10]. Dai et al. [10] also pointed out that one effective method for accurately detecting the crossover is proposed by Henon [17], here called Henon’s method, originally applied to construct Poincaré maps.

The main idea of Henon’s method is described as follows [10, 17]. As shown in Eq. (1), the curve of elastic moment (M) and displacement ($\alpha$) for free-play nonlinearity can be divided into three linear sub-domains by $\pm \delta$ according to the location $\alpha (t_n)$. The classical RK4 is applied to integrate the system marching in time until a change in linear sub-domains is detected. At that time, the distance between previous location $\alpha (t_{n-1})$ and crossover ($\delta$ or $-\delta$) is known. By exchanging the dependent variable $\alpha$ and independent variable $\tau$, the response of the aeroelastic system can be integrated from its previous location forward to the exact point of discontinuity within one step with the initial conditions already known, which will be shown below in details. Then, time is reverted to $\tau$ and the classical RK4 is then adopted to integrate in the new linear sub-domain, until a next discontinuity is detected.

Fig. 4

Flutter characteristic of Isogai wing model: a flutter speed ($U/b \omega _\alpha \sqrt{\mu }$) versus Mach number from different methods, b root locus at Mach 0.85

Fig. 5

Comparison of LCO behavior of NACA 64A010 airfoil at Mach 0.8: a LCO amplitude of $\alpha$ versus non-dimensional speed, b LCO amplitude of h / b versus non-dimensional speed

The aeroelastic system of Eq. (11) can be rewritten as

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}\tau } \left\{ \begin{array}{c} x_1\\ x_2\\ \vdots \\ x_n \end{array} \right\} = \left\{ \begin{array}{c} f_1(\varvec{x})\\ f_2(\varvec{x})\\ \vdots \\ f_n(\varvec{x}) \end{array} \right\} \end{aligned}$$

(12)

where $x_1$ stands for the pitching motion $\alpha$. Henon’s method involves exchanging the dependent variable $\alpha$ and independent variable $\tau$ via first dividing each of the equation of Eq. (12) by $\hbox {d}x_1/\hbox {d}\tau = f_1(\varvec{x})$, and then replacing the first equation by $\hbox {d}\tau /\hbox {d}x_1 = 1/f_1(\varvec{x})$. Consequently, a new system with $x_1$ as the independent variable is

$$\begin{aligned} \frac{d}{dx_1} \left\{ \begin{array}{c} \tau \\ x_2\\ \vdots \\ x_n \end{array} \right\} = \left\{ \begin{array}{c} 1/f_1(\varvec{x})\\ f_2(\varvec{x})/f_1(\varvec{x})\\ \vdots \\ f_n(\varvec{x})/f_1(\varvec{x}) \end{array} \right\} \end{aligned}$$

(13)

Note that the new system is used only for one integration step immediately before $\alpha$ crosses $\delta$ or $-\delta$.

It should be mentioned that in the following sections, RK4 with Henon method is used to obtain the nonlinear aeroelastic response when considering the free-play nonlinearity.

Fig. 6

Root locus for linear flutter case at Mach 0.87

Fig. 7

Comparison of time history of pitching motion using different time-step sizes at $U = 4.2$ (Mach 0.87)

Fig. 8

Time histories of pitching and plunging at different non-dimensional speeds without free-play at Mach 0.87 at: a $U = 3.94$, b $U = 3.95$

2.4 Describing function method

In our previous study [31], the harmonic balance analysis, which can also be called describing function method, was used to examine the LCO behavior of an aeroelastic airfoil with nonlinear pitching stiffness.

According to Conner et al. [6], one advantage of using the describing function for aeroelastic analysis is that the magnitude of the LCO can be predicted well at least for the LCO motion is predominantly period-1. So the describing function method will be used to obtain the fundamental nonlinear characteristics for the present model in preliminary analysis section.

A fundamental harmonic solution for the pitching motion is firstly assumed as

$$\begin{aligned} \alpha (t) = \alpha _0\sin (\omega t) \end{aligned}$$

(14)

Then from Eq. (1) and the describing function approach, the linearized equivalent stiffness can be expressed as

$$\begin{aligned} K_\mathrm{eq}=f_\mathrm{eq}K_\alpha \end{aligned}$$

(15)

In this expression, $f_\mathrm{eq}$ is the so-called describing function, which depends on the amplitude of pitching oscillation. And according to Gelb and Vander Velde [16], the structural describing function for the free-play nonlinearity can be described as

$$\begin{aligned} f_\mathrm{eq} =\left\{ \begin{array}{ll} 0 &{} \alpha _0 < \delta \\ 1-\frac{2}{\pi } \left\{ \arcsin \left( \frac{\delta }{\alpha _0}\right) + \frac{\delta }{\alpha _0} \sqrt{1-\left( \frac{\delta }{\alpha _0}\right) ^2} \right\} &{} \alpha _0 \ge \delta \end{array} \right. \nonumber \\ \end{aligned}$$

(16)

So the equivalent structural restoring moment corresponding to the oscillation of airfoil is obtained,

$$\begin{aligned} M(\alpha ) = f_\mathrm{eq} K_\alpha \alpha \end{aligned}$$

(17)

For each prescribed LCO amplitude, $f_\mathrm{eq}$ is a constant, so the nonlinear aeroelastic system of Eq. (11) is reduced to an equivalent linear aeroelastic system. For such a linear aeroelastic system, the flutter speed and flutter frequency can be obtained straightforwardly from the eigenvalue analysis of matrix $\varvec{A}$ in Eq. (11), which is similar to the approach presented by Yang and Zhao [31].

Table 1 Comparison of linear flutter speed and flutter frequency at Mach 0.87

Fig. 9

LCO amplitude versus non-dimensional speed only considering aerodynamic nonlinearity at Mach 0.87

3 Validation and testing

3.1 Grid convergence study

Since a NACA 64A010 airfoil is used in the following numerical examples, firstly we conduct a grid convergence study for this airfoil. Three computational grids with different spatial resolutions (Mesh 1, Mesh 2 and Mesh 3) are generated to assess the mesh convergence, where the C-type structured mesh topology is adopted for each grid. All these three computational meshes are composed of 51 mesh points radially and the outer boundary for computational domain extends to a distance of 50 chord length from the airfoil, as shown in Fig. 2. However, the number of the mesh points surrounding the airfoil surface is different, for instance, 111 mesh points in Mesh 1, 221 in Mesh 2 and 331 in Mesh 3. So there are totally 211, 321 and 431 mesh points circumferentially in Mesh 1, Mesh 2 and Mesh 3, respectively.

CFD simulations of a NACA 64A010 airfoil with a sinusoid oscillating motion for $\alpha _0 = 1^\circ$ and $k = 0.1$ at Mach 0.8 are conducted, where $k=\omega b/V$ stands for the reduced frequency. The time histories of the unsteady aerodynamic coefficient for different meshes are shown in Fig. 3. It can be seen that the amplitude of $c_l$ obtained by using Mesh 1 is a little smaller than those obtained by using Mesh 2 and Mesh 3, respectively, and the amplitude of $c_m$ obtained by using Mesh 1 is a little larger than those obtained by using Mesh 2 and Mesh 3, respectively, but results obtained by using Mesh 2 and Mesh 3 are nearly the same. Thus both Mesh 2 and Mesh 3 are appropriate to calculate the unsteady aerodynamic forces. Considering the computational costs, Mesh 2 is adopted in the following sections.

Fig. 10

LCO amplitude versus non-dimensional speed for SDOF and two-DOF system at Mach 0.87

3.2 Tests for ARMA ROM

An aeroelastic airfoil model from Isogai [18] is a benchmark case for predicting transonic flutter. Its parameters are $a = -2.0$, $x_\alpha = 1.8$, $r_\alpha ^2 = 3.48$, $\omega _h/\omega _\alpha = 1.0$, $\mu = 60$.

Depicting the flutter speed versus Mach number, the flutter boundary is illustrated in Fig. 4a. These results obtained by using ARMA model are in good agreement with those obtained by using time-marching solutions with CFD technique [2, 30]. From Fig. 4a, it can be seen that flutter speed in the transonic regime is obviously lower than those in the subsonic regime, which is usually termed a “transonic dip”. Moreover, there are multiple values of flutter speed between Mach 0.85 and 0.9, which forms the so-called S shape flutter boundary [5].

It should be noted that the S shape flutter boundary was also seen in other literature for the Isogai wing. It is basically the result of a weakly amplified mode, which crosses zero damping twice in a row and hence gets damped again, and existence of a second mode instability, as shown in Fig. 4b. The weakly amplified mode is sometimes referred as “hump mode” behavior in aircraft applications.

Fig. 11

Comparison of phase plot from time-marching approach with CFD at U = 1.8 using different time-step sizes (Mach 0.87): a $\varDelta \tau$ = 0.2, b $\varDelta \tau$ = 0.1, c $\varDelta \tau$ = 0.02, d $\varDelta \tau$ = 0.01

3.3 Tests for time-marching approach with CFD

The aeroelastic system used to test the Ansys-CFX solver is from Thomas et al. [27], which is a well documented test case for aerodynamic nonlinear LCO analysis. In this case, the Mach number is 0.8, and the structural parameters are $a = -0.6$, $x_\alpha = 0.25$, $r_\alpha ^2 = 0.75$, $\omega _h/\omega _\alpha = 0.5$, $\mu = 75$.

Figure 5 shows the computed LCO amplitudes by using Ansys-CFX solver with successively smaller time-step sizes. It can be observed from Fig. 5, the time-step size will affect the computed linear flutter speed or the Hopf bifurcation point. These results are further compared with those obtained by harmonic balance method [27] and time-marching approach with CFD technique [32], demonstrating the feasibility of using the Ansys-CFX solver for a transonic LCO solution.

4 Preliminary analysis

The basic aeroelastic airfoil model studied in Sect. 4 and 5 is taken from the work of Kousen and Bendiksen [22], in which a free-play nonlinearity is assumed in the pitching DOF. The airfoil of this model is NACA 64A010, and the relevant parameters are $a = -0.2$, $x_\alpha = 0.2$, $r_\alpha ^2 = 0.29$, $\omega _h/\omega _\alpha = 0.34335$, $\mu = 60$, $\delta = 1^\circ$. The computed Mach number is 0.87 as a typical transonic Mach number. The Euler equations are employed to calculate the unsteady aerodynamic forces, which is also adopted by Kousen and Bendiksen [22]. It should be mentioned that the reduced velocity used in Ref. [22] is multiplied by 2 to obtain the non-dimensional air speed U defined in the present study.

Fig. 12

Nonlinear dynamic behavior at Mach 0.87: a evolution of the phase plot with increasing non-dimensional speed ratio, b LCO amplitude of pitching motion versus non-dimensional speed. Cycle (circle) stands for LCO amplitudes ($U > 2.2$) and maximal displacements of pitching ($U < 2.2$) from Ansys-CFX solver

4.1 Linear flutter analysis

To achieve the linear flutter characteristic, the free-play nonlinearity is removed from the aeroelastic model and the aeroelastic response with small amplitudes are considered in this section. The assumption of linear structure and dynamically linear aerodynamics means that the ARMA aerodynamic model can be used to predict the linear flutter speed.

Figure 6 shows the root loci computed by using the ARMA aerodynamic model. It can be seen that the real part of the root loci of the aeroelastic system transits from negative to positive as the air speed increases, indicating the occurrence of flutter.

Time-marching approach with CFD technique can also be used to obtain the linear flutter characteristic. As mentioned in Sect. 3.3, we are aware that the time-step size will affect the computations of linear flutter speed and LCO behavior remarkably. Thus, a time-step convergence study is carried out with a series of time-step sizes at $U = 4.2$ as shown in Fig. 7. As expected, the amplitude of pitching converges with the decreasing time-step size. Considering the computational cost, the time-step size of $\varDelta \tau = 0.02$ is adopted in the following calculations.

Figure 8 shows the transient response of plunging and pitching at different non-dimensional speed by using Ansys-CFX solver. It can be seen from Fig. 8 that, as the air speed increases, the response of the aeroelastic system shows damped motion at $U = 3.94$, and then neutrally stable motion at $U = 3.95$. So the non-dimensional linear flutter speed is about 3.95, which can also be inferred from the bifurcation diagram in the next section.

Fig. 13

Time histories and phase plots at different air speeds from time-marching approach with CFD at Mach 0.87: a time history and b phase plot at $U = 0.4$, c time history and d phase plot at $U = 0.8$, e time history and f phase plot at $U = 1$

Table 1 lists the non-dimensional flutter speed and flutter frequency ratio obtained by using different methods. The results from Ansys-CFX solver agree well with those obtained by Kousen and Bendiksen [22], also implying the feasibility of using the Ansys-CFX solver for transonic flutter analysis. There is a little difference of the non-dimensional flutter speed obtained by using ARMA ROM and the time-marching method with CFD technique, and the flutter frequency ratios obtained by using ARMA model and Ansys-CFX solver are almost the same.

Fig. 14

Time histories of displacement of SDOF system at Mach 0.87: plunging motion at a $U =0.4$ and b $U = 0.8$, pitching motion at c $U =0.4$ and d $U = 0.8$

4.2 LCOs without free-play

To assess the effect of the aerodynamic nonlinearity, we remove the free-play nonlinearity from the system. Figure 9 shows the calculated LCO amplitude versus the non-dimensional speed at Mach 0.87 using different time-step sizes. It is found that the time-step size has obvious effects on the computed linear flutter speed. But the bifurcation curve moves left along the speed axis with the decreasing of time-step size, which is different from the situation in Sect. 3.3. Furthermore, the curve of LCO amplitude versus air speed is nearly perpendicular to the air speed axis when the LCO amplitude of pitching is less than nearly 5$^\circ$, which can be regarded as a so-called linear LCO behavior trend as mentioned by Thomas et al. [28]. When the flow speed is increased further beyond the flutter speed, the LCO amplitude increases.

Our results demonstrate an important feature of the present aeroelastic system that the aerodynamic nonlinearity is weak ranging from very small amplitude to moderate amplitude. It means that the dynamically linear aerodynamics is feasible for time-domain simulation even if the free-play nonlinearity is included in the aeroelastic model.

In addition, the effect of aerodynamic nonlinearity on the aeroelastic system can also be assessed from Fig. 9. According to Kholodar et al. [20], the aerodynamic nonlinear effect can be either harmful or beneficial depending on the structural parameters of the model and Mach number. For the present model, the LCO appears when the flow speed is greater than the linear flutter speed, implying that the aerodynamic nonlinearity exhibits a (modest) beneficial effect.

4.3 Single degree of freedom flutter

In this section, the describing function method is used to deal with free-play nonlinearity, and the ARMA aerodynamics is adopted to model the transonic aerodynamics. Though the nonlinearity caused by the effect of motion amplitude is not taken into account in ARMA aerodynamics, the LCOs with small amplitude are still meaningful, and an interesting phenomenon related to SDOF flutter is discovered.

To show this phenomenon, we build a single equation of SDOF flutter system by retaining the pitching DOF in Eq. (4). Then the LCOs of the SDOF system only considering pitching DOF and the original two-DOF aeroelastic system considering both pitching and plunging DOFs are compared, as shown in Fig. 10. From this figure, we can see that when the LCO amplitude is around $1.1^\circ$, the SDOF system response is almost the same as to that of the two-DOFs aeroelastic system. Such results reveal that the LCO with small amplitude is dominated by the SDOF flutter mechanism.

Fig. 15

Comparison of phase plots from two-DOF and SDOF aeroelastic system at Mach 0.87 at: a $U =0.4$ and b $U = 0.8$

5 Results and discussions

In Sect. 3.3, it was noted that the time-step size has an important influence on the calculated aeroelastic response when using time-marching approach based on CFD technique. Figure 11 shows the comparison of calculated phase plots at U = 1.8 using successively time-step sizes. It is apparent that the calculated response behaves differently when using different time-step sizes, and the aeroelastic response converges to the same LCO with the decreasing of time-step size, as shown in Fig. 11. Thus, the time-step size of $\varDelta \tau =0.02$ is chosen to obtain the aeroelastic responses at different non-dimensional speeds in this section.

Figure 12a shows the evolution of the phase plot with increasing speed. In the work of Kousen and Bendiksen [22], only simple harmonic motions, i.e., the so-called simple LCOs, are reported. However, our results show that in the range of $U/U_l > 0.5528$ ($U > 2.2$) simple LCOs are observed, but the aeroelastic system displays simple LCOs, complex LCOs and non-periodic motions when $U/U_l < 0.5528$. In order to show the comparison of results from Ansys-CFX solver and Ref. [22], the LCO amplitudes ($U > 2.2$) and the maximal displacements of pitching ($U < 2.2$) from Ansys-CFX solver are plotted against the non-dimensional speed in Fig. 12b. From Fig. 12b, it is clear that the LCO amplitudes from Ansys-CFX solver agree very well with those from Ref. [22] based on the solution of Euler equations at large LCO amplitudes.

Fig. 16

Comparison of phase plots from time-marching approach with CFD and ARMA ROM at Mach 0.87 at: a $U/U_l = 0.3038$, b $U/U_l = 0.3544$, c $U/U_l = 0.4557$, d $U/U_l = 0.5570$

From the preliminary analysis in Sect. 4, it is found that the oscillation amplitude plays an important role in the nonlinear aeroelastic behavior. When the amplitude is near free-play angle $\delta$, e.g., around 1.1$^\circ$, aeroelastic response will be dominated by SDOF flutter. When the LCO amplitude is very large, greater than 5$^\circ$, the influence of aerodynamic nonlinearity is more significant. As for the moderate LCO amplitudes, e.g., $1.1^\circ<\alpha _0 < 5^\circ$, the free-play nonlinearity should dominate the behavior of the nonlinear aeroelastic system. Consequently, the bifurcation diagram can be divided into three regions according to the oscillation amplitude, i.e., small amplitude region, moderate amplitude region and large amplitude region, as discussed below.

5.1 Small amplitude region

From Sect. 4.3, we know that the flutter type of the aeroelastic system in this region should be SDOF flutter. Figure 13a, c show the time histories at $U = 0.4$ and 0.8, as representations in the small amplitude region. Figure 13e shows the time histories at $U = 1$ as a typical example in the moderate amplitude region. Figure 13b, d, f show the phase plot at $U = 0.4$, 0.8 and 1, respectively. Compared with the response in moderate amplitude region, it is found that the magnitude of plunging motion in the small amplitude region is very small, indicating SDOF flutter.

In addition, from Fig. 13a, c, as well as Fig. 12b, it is apparent that one of the features of the responses in this region is that the maximum value of pitching motion is near the free-play angle ($\delta = 1^\circ = 0.0175$). Fig. 13a, b show the aeroelastic response at $U = 0.4$, as a representation of cases at small non-dimensional speeds in this region, where a random-like phenomenon is observed. When the air speed is increased a little, the aeroelastic system settles into a LCO, as shown in Fig. 13c, d at $U = 0.8$.

Fig. 17

Bifurcation diagrams for pitching motion using ARMA ROM at Mach 0.87: a with initial condition of $\alpha '(0) = 0.001$ and the other initial states being zero ($0.2< U/U_l<0.8$ with $\triangle U/U_l = 0.002$), b applying parameter-marching procedure ($0.2< U/U_l<0.8$ with $\triangle U/U_l = 0.002$)

Fig. 18

Bifurcation diagram for pitching motion using ARMA ROM at Mach 0.87 ($\triangle U/U_l = 0.0001$): a upper branch, b middle branch and c lower branch

To understand the responses at $U = 0.4$ and 0.8, we first look into the response of SDOF aeroelastic system. Similar to the analysis in Sect. 4.3, we also retain single plunging or pitching DOF in the time-marching approach with CFD technique. When only considering plunging DOF, the aeroelastic system is stable as shown in Fig. 14a, b. But the SDOF system with pitching DOF displays LCOs as shown in Fig. 14c, d, since a free-play nonlinearity is included in the pitching DOF. These results demonstrate that the SDOF flutter governed by pitching motion can happen at $U = 0.4$ and $U = 0.8$.

The comparison of the phase plot of the two-DOF system with that of the SDOF system considering pitching DOF at $U = 0.8$ is shown in Fig. 15b. Good agreement of the amplitude for the pitching motion is observed, which is consistent with the conclusion drawn in Sect. 4.3.

Fig. 19

Nonlinear dynamics of pitching motion at $U/U_l$ = 0.39 using ARMA ROM (Mach 0.87): a time history, b phase plot, c Poincaré map, d power spectra

At $U = 0.4$, a non-symmetric phase plot from SDOF system is observed as shown in Fig. 15a. According to Fang and Dowell [15], a dual phase plot must exist symmetric to the original one, which can be obtained using different initial conditions, since the system is symmetric. With these two phase plots, the response of the two-DOF aeroelastic system at $U = 0.4$ can be easily understood. Similar to the analysis conducted by Dowell [11], the effect of plunging motion can be treated as a random perturbation to the SDOF system considering pitching motion. So the two-DOF aeroelastic system displays snap-though phenomenon, i.e., jumping from one LCO orbit to the other and then moving back randomly, as shown in Fig. 15a.

Fig. 20

Evolution of the phase portraits with increasing speed from: a time-marching approach with CFD at Mach 0.6, b ARMA ROM at Mach 0.6 and c Wagner’s function at Mach 0

Fig. 21

Comparison of LCO amplitude verses non-dimensional speed from different methods

5.2 Moderate amplitudes region

From Fig. 12a obtained by using time-marching approach with CFD technique, it can be speculated that bifurcation may occur in this region. However, there are some requirements to produce a bifurcation diagram: (1) The time history of the dynamic response at each air speed should be adequately long to identify the motion type. (2) The air speed increment should be sufficiently small to show details of the bifurcation process. Therefore, it is very difficult, if not impossible, to capture the bifurcation behavior by using the time-marching approach with CFD technique.

As we know from Sect. 4.2 the aerodynamic nonlinearity is weak for this model when the oscillation amplitude is less than $5^\circ$, so the ARMA aerodynamics can be used to obtain the unsteady aerodynamic forces in the transonic air flow. Several LCOs from the time-marching approach and the ARMA ROM are compared in Fig. 16 and a small difference is observed. It must be noted that the structure of the periodic orbit of the aeroelastic system is preserved when using ARMA aerodynamics, revealing that the ARMA ROM is able to capture the nonlinear dynamic properties. These good agreements also indicate that this bifurcation of the aeroelastic system is caused by the free-play nonlinearity rather than aerodynamic nonlinearity, because the aerodynamic dynamic nonlinearity is not taken into account in the ROM method, but only the static aerodynamic nonlinearity is considered.

Fig. 22

Phase plots from time-marching approach with CFD at Mach 0.87 at: a $U = 4.2$, b $U = 4.4$

Fig. 23

Time histories of pitching and plunging motions considering boundary layer effects at different non-dimensional speeds without free-play at Mach 0.87 at: a $U = 3.92$, b $U = 3.9382$, c $U = 3.944$

Since the ARMA ROM has the advantage of saving computational time, we can obtain the “entire” bifurcation diagram as shown in Fig. 17. Figure 17a shows the bifurcation diagrams of the pitching motion with a fixed initial condition, where the amplitude jumps in pitching DOF exist. The phenomenon of amplitude jumps in bifurcation diagram was also reported by Dai et al. [10] and Zhao and Hu [34], which is caused by the response duality for symmetric aeroelastic systems according to Xie et al. [29]. Figure 17b shows the bifurcation diagrams produced by applying a parameter-marching procedure, i.e., using the solution of the previous speed as the initial conditions for the next speed.

Figure 18 shows the upper, middle and lower branch of the bifurcation diagram in Fig. 17b with a smaller increment of $\triangle U/U_l = 0.0001$ to illustrate the bifurcation process more clearly. Period-1 LCOs are observed when $U/U_l < 0.3474$, and obviously the first bifurcation happens at $U/U_l = 0.3474$. Then period-2 oscillations occur between $0.3474<U/U_l< 0.3744$. A second bifurcation takes place at $U/U_l = 0.3744$, after which period-4 motions are found between $0.3744<U/U_l< 0.3816$. It can be seen that with the increasing of speed, the aeroelastic system oscillates in period-1, period-2, period-4 responses, etc, and finally goes to chaos. The time history, phase plot, Poincaré map and power spectra for pitching motion at $U/U_l = 0.39$, as a representation in chaos region, are used to identify chaotic motion, as shown in Fig. 19. Therefore, the route to chaos in the current study is via period-doubling.

Fig. 24

Root locus for linear flutter case considering boundary layer effects at Mach 0.87

At this stage, some important concerns arise, which include: Whether these complex dynamic responses are special phenomena occurring only in transonic air flow? And how does the aeroelastic system behave in subsonic air flow? Fig. 20a–c show the dynamic responses for aeroelastic airfoil using time-marching approach with CFD technique at Mach 0.6, ARMA ROM at Mach 0.6 and Wagner’s function for Mach 0, respectively. From the comparisons of the LCO amplitude against air speed obtained by using different methods as shown in Fig. 21, good agreements are observed. All those results demonstrate that only simple harmonic motions are observed in subsonic air flow, which is very different from the results found in transonic air flow.

As we all know, bifurcation is a typical feature for a nonlinear aeroelastic system. However, whether the bifurcation occurs or not depends on the parameters of the aeroelastic systems. Our results demonstrate that Mach number is one important parameter that can trigger the bifurcation of the aeroelastic system.

5.3 Large amplitude region

From Eq. (16), it can be seen that when LCO amplitude $\alpha _0$ is large enough, the describing function $f_\mathrm{eq}$ approaches to 1 leading to very large response as one approach the linear flutter speed. Moreover, from the experience of conventional numerical calculations without aerodynamic nonlinearity, we know that the LCO amplitude will be very large or nearly exhibit divergent oscillations when the speed approaches linear flutter speed.

In transonic air flow, the effect of aerodynamic nonlinearity becomes obvious when the oscillation amplitude is very large, and a supercritical bifurcation is observed without free-play nonlinearity for the present model as shown in Fig. 9. Therefore, when the flow speed nearly approaches the linear flutter speed, the effect of the aerodynamic nonlinearity emerges. As shown in Fig. 22, when the speed is greater than the linear flutter speed ($U_l = 3.95$), simple harmonic motions are observed as expected. There is no doubt that the aeroelastic response is dominated by the aerodynamic nonlinearity in this region.

Fig. 25

Time histories and phase plots at different air speeds from time-marching approach with CFD at Mach 0.87 in viscous air flow: a time history and b phase plot at $U = 0.7$, c time history and d phase plot at $U = 1.2$, e time history and f phase plot at $U = 2.4$

6 Extended discussions

In previous sections, several interesting nonlinear responses of an aeroelastic airfoil considering both structural and aerodynamic nonlinearities are presented, e.g., SDOF flutter, bifurcation and chaos. The aerodynamic nonlinearity is mainly caused by shock waves, viscous effects and separated flows. Another airfoil profile, which locates shock waves differently from NACA 64A010 airfoil, may lead to different aerodynamic nonlinear behaviors. We will extendedly discuss effects of boundary layer and airfoil profile on the nonlinear responses of the aeroelastic system in this section. It should be noted that structural parameters remain the same as those in Sect. 4 and 5.

6.1 Boundary layer effects

In order to take the effects of boundary layer into account, the shear stress transport (SST) turbulence model is adopted in the CFD solver, and a C-type mesh with fine grid resolution is generated. The first layer thickness of this grid is $1\times 10^{-5}$ chord length.

Removing the free-play nonlinearity from the aeroelastic model, linear flutter analysis is conducted by using time-marching approach with CFD and ARMA ROM. Figure 23 shows the transient response of plunging and pitching at different non-dimensional speeds by using Ansys-CFX solver considering viscous effects. It is clear that with the increasing of air speed, the response of the aeroelastic system shows damped motion at $U = 3.92$, neutrally stable motion at $U = 3.9382$, and divergent motion at $U = 3.944$. Thus, the non-dimensional linear flutter speed is 3.9382. Figure 24 shows the root loci of the aeroelastic system computed by using the ARMA aerodynamic model when considering boundary layer effects. It is observed that the real part of the root loci transits from negative to positive at $U = 3.9144$, implying the linear flutter speed. Good agreement of the linear flutter between time-marching approach with CFD and ARMA model is achieved in the present study. It is also found that the linear flutter speed considering boundary layer effects is a little different from that in inviscid air flow, which is consistent with the conclusion in [24].

Fig. 26

Bifurcation diagrams for pitching motion using ARMA ROM considering boundary layer effects at Mach 0.87: a $0.2< U/U_l<0.8$ with $\triangle U/U_l = 0.002$, b $0.25< U/U_l<0.35$ with $\triangle U/U_l = 0.0001$

Figure 25 shows the representative nonlinear response in viscous air flow at Mach 0.87 for NACA 64A010. From Fig. 25a, b, it can be seen that the flutter type of the aeroelastic system at $U = 0.7$ should be SDOF flutter, since the maximum value of pitching motion is near the free-play angle $\delta$. Figure 25c, d present complex nonlinear motion at $U = 1.2$, indicating that bifurcation may happen near this flow speed. And as the air speed increases further, Fig. 25e, f show single harmonic motions at $U = 2.4$.

Similar to Sect. 5.2, ARMA model is adopted again to capture the bifurcation process as shown in Fig. 26. It is clear that the aeroelastic system oscillates in period-1, period-2, period-4 responses, etc, and finally goes to chaos. To identify chaotic motion, the time history, phase plot, Poincaré map and power spectra for pitching motion at $U/U_l = 0.31$, as a representation in chaos region, are used as shown in Fig. 27. Similar to the inviscid case, the route to chaos considering viscous effects is via period-doubling. However, compared with trajectories in inviscid air flow, the motion considering boundary layer effects is more complex (see Figs. 19 and 27), and the bifurcation points differ greatly (see Figs. 18, 26).

Fig. 27

Nonlinear dynamics of pitching motion at $U/U_l = 0.31$ using ARMA ROM considering boundary layer effects (Mach 0.87): a time history, b phase plot, c Poincaré map, d power spectra

6.2 Airfoil profile effects

In this section, a cambered airfoil, NACA 64A109 airfoil, is used in the aeroelastic system to assess the effects of airfoil profile in inviscid air flow. This kind of airfoil was adopted by Gates Learjet 24D airplane according to [3]. It is obvious that the locations of shock wave on NACA 64A010 and NACA 64A109 would be different at the same Mach number and angle of attack. Furthermore, due to the existence of the camber, the lift and aerodynamic moment of NACA 64A109 at zero angle of attack will be nonzero, which is the main difference from a symmetric airfoil.

Fig. 28

Time histories of pitching and plunging motions for NACA 64A109 airfoil at different non-dimensional speeds without free-play at Mach 0.87 at: a $U = 3.6$, b $U = 4.04$

Fig. 29

Extrema of pitching motion versus non-dimensional speed for NACA 64A109 airfoil using time-marching approach with CFD at Mach 0.87

Fig. 30

Time history for NACA 64A109 airfoil at $U = 1.8$ from time-marching approach with CFD at Mach 0.87

Transient responses of plunging and pitching for NACA 64A109 airfoil at different non-dimensional speeds are shown in Fig. 28. The non-dimensional linear flutter speed for NACA 64A109 airfoil is 4.04 obtained by using time-marching approach with CFD. It should be noted that when the air speed is less than the linear flutter speed, taking $U = 3.6$ as an example, the pitching or plunging motion converges to a nonzero equilibrium point, which is conventionally called static aeroelastic equilibrium in aeroelastic analysis.

Figure 29 shows extrema of pitching motion versus non-dimensional speed for NACA 64A109 airfoil obtained by using time-marching approach with CFD. When U is less than 3.18, the transient responses converge to equilibriums as shown in Fig. 30. As the air speed increases, only simple LCOs vibrating around nonzero equilibriums are presented, taking $U = 3.3$ as a typical example shown in Fig. 31. To our surprise, no complex nonlinear response is detected after careful examinations of our calculations, where effects of the initial conditions are also considered.

Fig. 31

Nonlinear response for NACA 64A109 airfoil at $U = 3.3$ from time-marching approach with CFD at Mach 0.87: a time history, b phase plot

Fig. 32

Free-play with preload induced by a cambered airfoil

To address the nonlinear responses of NACA 64A109 airfoil, aerodynamic characters for a cambered airfoil and their effects are discussed firstly. Due to the nonzero aerodynamic moment at zero angle of attack, the static aeroelastic equilibrium of pitching motion would be nonzero. That is to say, the aeroelastic system with a cambered airfoil at zero angle of attack should oscillate around a nonzero angle. Though these deformations may have little influence on the linear flutter speed according to classical aeroelastic theory, the nonzero static aeroelastic equilibrium of pitching motion can turn the type of the structural nonlinearity to free-play with preload, as shown in Fig. 32.

The preload in free-play nonlinearity can be caused by unbalanced weight [31] or angle of attack [26], and in the current work it is induced by a cambered airfoil. According to experiments and calculations of Dowell [12], Tang and Dowell [26] and Price et al. [25], sufficient amount of loading could suppress flutter or LCOs. From Fig. 29, it is found that the preload $\alpha _f$ caused by the moment $M_0$ for the present model is about 0.3$^\circ$ at $U = 3.0$. It should be noted that the preload increases with the increasing of air speed. Consequently, only the motion type of simple LCOs at $U/U_l > 0.7871$ remains, but the types of bifurcation and chaos motions are eliminated by the preload.

7 Conclusions

Euler equations are employed to calculate the unsteady aerodynamic forces, and an aeroelastic airfoil with free-play in pitching DOF is investigated in the current study. A commercial software, Ansys-CFX solver, is adopted to obtain the aeroelastic response in time domain. To reduce the computational costs, the ARMA model is employed to build aerodynamic ROM, and then the RK4 with Henon method is used to obtain the nonlinear aeroelastic response.

In time-marching approach with CFD technique, the time-step size has an important influence on the calculated aeroelastic response. In particular, for the cases considering structural nonlinearity in transonic air flow, the computed topology of the aeroelastic response shows detectable differences using different time-step sizes.

For the present aeroelastic model, the nonlinear dynamic behavior in transonic air flow is greatly different from that in subsonic regime. In subsonic air flow, only simple harmonic oscillations are observed. However, in transonic air flow the aeroelastic system displays responses dominated by SDOF flutter, simple LCO, complex LCO, non-periodic motion or chaos at different air speeds. The major features of the responses for the aeroelastic airfoil at different air speeds can be summarized as follows:

• 1. For responses with small amplitudes, the flutter type of aeroelastic airfoil should be single degree of freedom flutter. Furthermore, snap-though phenomenon can be observed because of the existing of dual responses and SDOF flutter.

• 2. For responses with moderate amplitudes, the aeroelastic system is dominated by the free-play nonlinearity while the aerodynamic nonlinearity is weak. The “entire” bifurcation diagram are captured by using ARMA aerodynamics, and it is found that the route to chaos for the present model is via period-doubling.

• 3. For responses with large amplitudes, the aeroelastic response is dominated by the aerodynamic nonlinearity. The aeroelastic system displays simple harmonic motions when the air speed is greater than the linear flutter speed of the aeroelastic airfoil.

When considering boundary layer effects, SDOF flutter, bifurcation and chaos are also observed. However, the chaotic motion is more complex and the bifurcation points differ greatly, compared to those in inviscid flow. A cambered airfoil can turn the type of the structural nonlinearity to free-play with preload, which suppress bifurcation and chaotic motions in the present study.