1 Introduction

Aeroelasticity is the field of study that describes the response and stability characteristics of physical systems dealing with the interaction of structural, inertial, and aerodynamic forces. The airfoil flutter is an important phenomenon of self-excited vibration in aeroelasticity, which is caused by the coupling of structural nonlinearities and aerodynamic nonlinearities. Flutter instability may decrease the performance and life span of aircraft or even lead to a catastrophe in aircraft flight. Therefore, the airfoil flutter has attracted more and more attention, and so far, the phenomenon of which has been investigated greatly [1–6].

However, in most of the previous works, the random factors were seldom considered in the mathematical model of the flutter system. In recent years, along with the advance of the nonlinear random vibration theory, the almost analysis probability method which is based on the Fokker–Planck equation has been used more and more to deal with stochastic flutter. For example, Ibrahim and Orono [7, 8] studied the stochastic flutter of a panel subjected to random in-plane forces using the Fokker–Planck equation and cumulant-neglect closure approximation. The stochastic flutter of airfoil has been investigated by D. Poired and S.J. Price [9, 10], and they used a probabilistic and statistical approach to obtain the numerical results, which made the problem more realistic and more understanding in some ways. Recently, the Lyapunov exponent also has been used to research the stability of a stochastic flutter system in some works [11, 12] (If the maximal Lyapunov exponent is negative, the system is almost-sure stable; otherwise, it is almost-sure unstable.) Even for an almost-sure stable random system, the mean-square response of the system may still grow exponentially and exceed some threshold, which means that the mean-square response is unstable. Therefore, it is needed to study the moment Lyapunov exponent of the stochastic flutter system.

The pth moment Lyapunov exponent is defined as

where x(t;x 0) is the solution process of a linear random dynamical system. If Λ(p,x 0)<0, then E∥x(t;x 0)∥p→0 as t→∞ and it implies that the pth moment is stable.

The moment Lyapunov exponent is very significant in the research of the dynamic stability of the random system, but it is greatly difficult to determine the moment Lyapunov exponent. Among the researchers reported by now, there are only a few results on the moment Lyapunov exponent, and most of which were obtained based on the approximate analytical methods, such as the perturbation method and the stochastic averaging method. For a two-dimensional system driven by white or real noise, Arnold et al. [13] used a perturbation approach to construct an asymptotic expansion of the pth moment Lyapunov exponent. Utilizing a method similar to that in [13], Namachchivaya et al. [14] obtained an approximation for the moment Lyapunov exponent of two coupled oscillators under real noise. Furthermore, Namachchivaya et al. [15] determined the moment Lyapunov exponent and set up the eigenvalue problem of two coupled oscillators driven by real noise using the perturbation and stochastic averaging methods, respectively. For a limited value of p, Khasminskii and Moshchuk [16] proved that the moment Lyapunov exponent can be expanded to a series of low noise intensity via researching the two-dimensional system of two imaginary eigenvalues. Liu and Liew [17] examined the stability of a Van der Pol–Duffing oscillator that is excited parametrically by a small intensity real noise. Zhu et al. [18] studied the dynamic stability of two degrees-of-freedom under bounded noise excitation with a narrowband characteristic through the determination of moment Lyapunov exponents. Recently, Predrag Kozić et al. [19, 20] construct an approximation for the moment Lyapunov exponent of a two-dimensional system under white noise by applying the procedure employed in Khasminskii and Moshchuk [16].

In the present paper, the stochastic stability of binary airfoil under non-Gaussian colored noise is considered. The non-Gaussian colored noise, which can be simplified to an Ornstein–Uhlenbeck process by using a path-integral approach, has been applied in many physical systems [21–25]. Via the singular perturbation method, second-order asymptotic expansion of the moment Lyapunov exponent is obtained, and the eigenvalue problem governing the moment Lyapunov exponent is also established. Moreover, the Monte Carlo simulation results for the original system are given. The combined results from the perturbation method and numerical simulations may allow us to better understand the behavior of the original system. Finally, the effects of the non-Gaussian colored noise and the system parameters are investigated and discussed.

2 Mathematical model

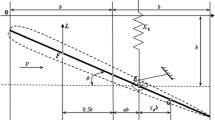
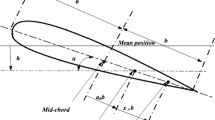
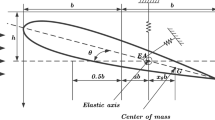
Considered the typical section, also known as the two-dimensional airfoil, with degrees of freedom in pitch and plunge is shown in Fig. 1. The non-dimensional equations of motion of the flutter system are given as (for the detailed derivation, see [26, 27])

(1)

where μ=m/(πρb 2),d=(2a+1)/μ, ϖ=ω h /ω θ , u=V/(bω θ ); h is the plunge displacement, θ is the pitching angle, ρ is the air density, m is the airfoil mass, b is the semi-chord length, ab is the distance of the elastic axis E from the mid-chord point, x θ b is the distance of the center of gravity G from E,r θ b is the radius of gyration of the airfoil with respect to the elastic axis, c h ,c θ are the nondimensional damping coefficients in plunge and pitch, respectively, k 3 is the nondimensional nonlinear pitching stiffness, ω h ,ω θ are the eigenfrequencies of the constrained one-degree-freedom system associated with the linear plunging and the pitching springs, respectively, and V is the mean of wind speed.

Fig. 1
figure 1

Sketch of the two-dimensional airfoil

Full size image

By linearizing the original system (1) and introducing a non-Gaussian colored noise ξ(t) in the nondimensional speed u, the governing equations are obtained as

(2)

where assuming the damping is a second-order small quantity of ε, and the random term is a small quantity of ε. The (εξ(t))2 term is neglected, and 0<ε≪1 is a small parameter.

Via a series of transformations and simplifications, the governing equations can be written as

(3)

where

(4)

3 Approximation to the Markov process

The process ξ(t) is a non-Gaussian colored noise given as

(5)
(6)

where r is the departure coefficient of non-Gaussian noise, denoting the departure from the Gaussian noise; D is the intensity of Gaussian noise; τ 0 is the noise correlation time; η(t) is a Gaussian white noise, and its statistical properties are

(7)

For r→1, the process ξ(t) is an Ornstein–Uhlenbeck process with correlation time τ 0. That is to say that it is an exponential Gaussian colored noise with correlation function given as \(\langle\xi(t)\xi(s) \rangle = (D / \tau_{0})e^{ - | t - s | / \tau _{0}}\); and when τ 0→0, the process ξ(t) is further reduced to a Gaussian white noise. As shown in [21, 28], the stationary probability density P s (ξ) can be normalizable if and only if r∈(−∞,3). The final expression for P s (ξ) of Eq. (5) is

(8)

where Z is a normalization constant. From Eq. (8), it is clear that the statistical properties of ξ(t) are

(9)

For |r−1|≪1, using a path-integral approach [21–23, 28], one has

(10)

with the effective noise correlation time

(11)

and the associated noise intensity

(12)

Therefore, Eq. (5) is simplified to an Ornstein–Uhlenbeck process with noise correlation time τ 1 and the associated noise intensity D 1.

(13)

where

(14)

W(t) is a Wiener process with unit intensity, and “∘” denotes a Stratonovitch stochastic integral. Both the \(\mathrm{It}\hat{o}\) form and the Stratonovitch form of the stochastic differential equation of the Ornstein–Uhlenbeck process are identical, because the diffusion coefficient of the Ornstein–Uhlenbeck process is constant i.e.,

(15)

with the power spectral density

(16)

4 Moment Lyapunov exponent

Applying the transformation q i =x 2i−1, \(\dot{q}_{i} = \omega_{i}x_{2i}\), i=1,2, Eq. (3) is written as

(17)

where

(18)

The following transformation from (x 1,x 2,x 3,x 4) to (ρ,ϕ 1,ϕ 2,ϑ)

(19)

yields a set of equations of the arguments of the amplitude ρ, phase variable (ϕ 1,ϕ 2,ϑ) and noise process ξ, i.e.,

(20)

where

and

(21)

Since the processes (ϕ 1,ϕ 2,ϑ,ξ) are independent of the variable ρ, the processes (ϕ 1,ϕ 2,ϑ,ξ) alone form a diffusive Markov process with the following generator:

(22)

where

(23)

The moment Lyapunov and Λ(p) is the principal simple eigenvalue for the operator L(p) [16, 29], i.e.,

(24)

4.1 Asymptotic analysis

In order to use the perturbation method, both the moment Lyapunov and Λ(p) and the eigenfunction ψ(p) are expanded in the power series of ε, respectively i.e.,

(25)

Insertion of Eq. (25) into Eq. (24) and equating terms of the equal power of ε, the following equations are obtained:

(26)
(27)
(28)

4.1.1 Zeroth-order perturbation

Since q 0(ϕ 1,ϕ 2,ϑ,ξ)≡0, the operator L 0(p) reduces to \(\mathcal{L}^{0}\). From the definition of Λ(p), we obtain that Λ 0(p)≡0 for all possible p. Thus, Eq. (26) reduces to

(29)

Applying the method of separation of variables and letting

Equation (29) becomes

(30)

One can easily obtain \(\varPhi_{1}(\phi_{1}) = C_{1}e^{a_{1}\phi _{1}}\) and \(\varPhi_{2}(\phi_{2}) = C_{2}e^{a_{2}\phi _{2}}\). Based on the periodic boundary conditions ψ 0(ϕ 1+2π,ϕ 2,ϑ,ξ)=ψ 0(ϕ 1,ϕ 2+2π,ϑ,ξ)=ψ 0(ϕ 1,ϕ 2,ϑ,ξ), we obtain a 1=a 2=0. So, Φ 1(ϕ 1)=C 1, Φ 2(ϕ 2)=C 2 and

(31)

The solution of Eq. (31) is \(Z(\xi) = C_{3} + C_{4}\times \operatorname{erf}(j\sqrt{\alpha_{0}} \xi / \sigma_{0})\), where \(\operatorname{erf}( \cdot)\) denotes the error function and j is the imaginary unit. For Z(ξ) to be a bounded function as ξ→±∞, it is required that C 4=0 i.e., Z(ξ)=C 3. Therefore, we obtain

(32)

where ψ 0(ϑ) is a function to be determined.

The adjoint equation of Eq. (29) is

(33)

Using the similar method of solving Eq. (29), we obtain

(34)

where \(\mathcal{F}(\vartheta)\) is an arbitrary function, and P s (ξ) is the stationary probability density of the process ξ(t).

4.1.2 First-order perturbation

Substituting Eq. (32) into Eq. (27) leads to

(35)

Applying the solvability condition to Eq. (35) yields

(36)

where

$$\bigl\langle( \cdot),( \cdot\cdot) \bigr\rangle = \int_{0}^{\pi / 2} \int_{M} \int_{0}^{2\pi} \int _{0}^{2\pi} ( \cdot) ( \cdot\cdot) d \phi_{1}\,d\phi_{2}\,d\xi \,d\vartheta. $$

The last equality in Eq. (36) results from the fact that R 1(ϕ 1,ϕ 2,ϑ;p) is periodic in ϕ 1 and ϕ 2, and ξ is a zero mean process. Hence, Eq. (35) reduces to

(37)

Introduce an auxiliary time t such that Eq. (37) becomes

(38)

where ψ 1t (0,ϕ 1,ϕ 2,ϑ,ξ;p)=0.

ψ 1(ϕ 1,ϕ 2,ϑ,ξ;p) is the stationary solution of Eq. (38) and solves Eq. (37) i.e.,

$$\psi_{1}(\phi_{1},\phi_{2},\vartheta,\xi ;p) = \lim_{t \to \infty} \bigl(\psi_{1t}(t,\phi_{1}, \phi_{2},\vartheta,\xi ;p) \bigr). $$

Applying the transformation \(\tilde{t} = t,\tilde{\phi}_{1} = \phi_{1} + \omega_{1}t\) and \(\tilde{\phi}_{2} = \phi_{2} + \omega_{2}t\) in Eq. (38) yields

(39)

where \(\tilde{\psi}_{1t}(\tilde{t},\tilde{\phi}_{1},\tilde{\phi}_{2},\vartheta,\xi ;p) = \psi_{1t}(t,\phi_{1},\phi_{2},\vartheta,\xi ;p)\) and \(\tilde{R}_{1}(\tilde{t},\tilde{\phi}_{1},\tilde{\phi}_{2},\vartheta ;p) = R_{1}(\phi_{1},\phi_{2},\vartheta ;p)\).

Using Duhamel’s principle (see, for example, [30]), we obtain the solution of Eq. (39) i.e.,

(40)

where P(η,τ;ξ,0) is the transient density which solves

The solution ψ 1(ϕ 1,ϕ 2,ϑ,ξ;p) to Eq. (37) is obtained by taking the limit as \(\tilde{t} \to\infty\):

(41)

4.1.3 Second-order perturbation

Applying the above results, Eq. (28) reduces to

(42)

The solvability condition is

(43)

Employing the correlation function of ξ and the power spectral density given, respectively, by

The solvability condition (43), via some calculations, becomes

(44)

where

for Eq. (44) must hold for arbitrary \(\mathcal{F}(\vartheta)\), and the bracketed quantity must vanish identically. This leads to

(45)

where

The boundary conditions of Eq. (45) are determined by considering the adjoint equation for the case p=0:

(46)

as [15] has shown that ϑ=0 and ϑ=π/2 are entrance boundaries. The eigenfunction ψ 0 satisfies the zero Neumann boundary condition, and Λ 2(p) is the largest eigenvalue of Eq. (45) with zeros Neumann boundary.

Since Λ 0(p)=0,Λ 1(p)=0, and ε is a small parameter, the second-order approximation of the moment Lyapunov exponent is given as

Hence, the approximate analytic expression of moment Lyapunov exponent can be obtained by solving the largest eigenvalue of Eq. (45).

4.2 Solution of the eigenvalue problem

According to Bolotin [31] and Wedig [32], the solution of Eq. (45) can be calculated by an orthogonal expansion. Since the zero Neumann boundary conditions, the eigenfunction ψ 0 is expressed as a Fourier cosine series i.e.,

(47)

Substituting Eq. (47) into Eq. (45) leads to the following set of equations:

(48)

where

Equation (48) can be written as

(49)

where M=RG −1,R=(r mn ), G=(G mn )=diag(2,1,1,…), z=(z 0,z 1,z 2,…)T, and y=Gz.

The existence of a nontrivial solution for z requires that the determinant of the coefficient matrix equals zero. Therefore, the problem of evaluating Λ 2(p) is converted to evaluate the leading eigenvalue of M. We construct a set of approximations by finding the eigenvalues of a set of submatrices:

The set of approximate eigenvalues obtained by this method converges to the associated true eigenvalues as n→∞. However, the amount of calculation increases rapidly with the increase of n. So, we obtain the approximate eigenvalues by the truncation of n. For example, \(\varLambda_{2}(p) \cong\frac{1}{2}r_{00}\) as n=0. Because of the complexity of expressions, we only present the elements of the second-order submatrix.

5 Numerical results and discussions

Monte Carlo simulation is used to determine the moment Lyapunov exponents of system (3) for the purpose of validating the accuracy of the approximate results obtained by the perturbation method. The algorithm presented in [33] is applied to simulate the moment Lyapunov exponents. For the simulation, the parameters are chosen as ε=0.1, ϖ 2=0.2, x θ =0.25, \(r_{\theta}^{2} = 0.5\), c h =0.1, c θ =0.1.

Letting \(y_{1} = q_{1},y_{2} = \dot{q}_{1},y_{3} = q_{2},y_{4} = \dot{q}_{2}\), Eq. (3) is presented as

(50)

where

The comparison of approximate analytical moment Lyapunov exponents obtained by perturbation and the Monte Carlo simulation results for different values of n and u are shown in Fig. 2. Based on the fact that is disclosed in Fig. 2, one easily finds that the approximate results agree well with the simulation results. And it also can be seen that the approximate results converge and the fourth-order approximations are sufficient. The two figures also indicate that the system may be almost-sure stable, as the slope of Λ′(0) (i.e., the maximal Lyapunov exponent) is negative, but unstable in pth moment sense for sufficiently large p in Fig. 2(a); and the system may be almost-sure unstable, as the slope of Λ′(0) is positive, but stable in pth moment sense for −2≤p≤0 in the Fig. 2(b).

Fig. 2
figure 2

Comparison of the perturbation results and numerical results of the moment Lyapunov exponent for the case r=0.95, D=0.5, τ 0=0.1; μ=20, d=0.05; (a) u=1.4; (b) u=1.7

Full size image

The effects of the noise and system parameters are discussed by using the fourth-order approximate analytical moment Lyapunov exponents.

The moment Lyapunov exponents for different parameters of the noise are plotted in Fig. 3. From Figs. 3(a) and 3(b), it is clear that both the noise parameters r and D can weaken the stability of the system along with the increase of them. But the effect of the noise parameters r on the stability of the system is very small as r→1, which can be neglected. Hence, we only need to notice the noise intensity D, trying to avoid the strong noise in actual engineering. The stability of the system can be strengthened by the noise correlation time τ 0, which is presented in Fig. 3(c). And in view of Fig. 3(c), it is seen that the moment Lyapunov exponents of the system are almost identical for the cases τ 0=0.00001 and τ 0=0.01, which implies when τ 0 is very small, the stochastic stability of the system is invariable along with the change of τ 0.

Fig. 3
figure 3

Effect of the noise on the moment Lyapunov exponent for the case u=1.5,μ=20,d=0.05; (a) D=0.5,τ 0=0.1; (b) r=0.95,τ 0=0.1; (c) r=0.95,D=0.5

Full size image

Figure 4 depicts the moment Lyapunov exponent for different values of u. It is clear that the stability of the system is weakened with the increase of the parameter u. And the maximal Lyapunov exponent of the system is changed from negative to positive, which implies that the stability of the system varies from almost-sure stable into almost-sure unstable. Based on the expression of parameter u, one easily finds that the system will come up flutter instability with probability 1 as the mean of wind speed V reaching the threshold, which expounds the mechanization of flutter from the view of stochastic theory.

Fig. 4
figure 4

Effect of the parameter u on the moment Lyapunov exponent for the case r=0.95, D=0.5, τ 0=0.1; μ=20, d=0.05

Full size image

Figure 5 gives the moment Lyapunov exponent with different values of parameter μ. Along with the increase of μ, the stochastic stability of the system is strengthened, as shown in Fig. 5. The parameter μ is mainly determined by the airfoil mass m, which can be seen from the expression of μ. However, in actual engineering, the airfoil mass is always limited and needed as small as possible. Therefore, we should choose the appropriate airfoil mass m to stabilize the system.

Fig. 5
figure 5

Effect of the parameter μ on the moment Lyapunov exponent for the case r=0.95, D=0.5, τ 0=0.1; u=1.5, d=0.05

Full size image

The moment Lyapunov exponent is depicted in Fig. 6 with different values of parameter d. In the view of Fig. 6, it is seen that the stochastic stability of the system weakens with the increase of d. From the expression of parameter d and the above discussion, it is clear that parameter d is determined by specific value (i.e., a) of the distance of the elastic axis E from the midchord point and the semichord length. So, the elastic axis of the airfoil should try to stay close to the midchord point in actual designing.

Fig. 6
figure 6

Effect of the parameter d on the moment Lyapunov exponent for the case r=0.95, D=0.5, τ 0=0.1; u=1.5, μ=20

Full size image

6 Conclusion

In the present paper, the stochastic stability of a binary airfoil system subjected to non-Gaussian colored noise is investigated by determining the moment Lyapunov exponents. The noise is simplified to an Ornstein–Uhlenbeck process by applying a path-integral approach. For weak noise excitations, the singular perturbation method is employed to obtain second-order expansions of the moment Lyapunov exponents. And the approximate analytic expression of the moment Lyapunov exponent is obtained by expanding the eigenfunction as a Fourier cosine series. Furthermore, the Monte Carlo simulation results are given to validate the accuracy of the approximate analytical results. It is seen that the analytical results fit rather well with the numerical results. Finally, the effects of the noise and the system parameters on the stochastic stability are discussed, and some results are presented.