Effects of nonlinear damping suspension on nonperiodic motions of a flexible rotor in journal bearings

Abstract

Nonlinear damping suspension is a promising method to be used in a rotor-bearing system for vibration isolation between the bearing and environment. However, the nonlinearity of the suspension may influence the stability of the rotor-bearing system. In this paper, the motions of a flexible rotor in short journal bearings with nonlinear damping suspension are studied. A computational method is used to solve the equations of motion, and the bifurcation diagrams, orbits, Poincaré maps, and amplitude spectra are used to display the motions. The results show that the effect of the nonlinear damping suspension on the motions of the rotor-bearing system depends on the speed of rotor: (a) For low speeds, the rotor- bearing system presents the same motion pattern under the nonlinear damping ($p=0.5, 2, 3$) suspension as for the linear damping ($p=1$) suspension; (b) For high speeds, the effect of nonlinear damping depends on a combination of the damping exponent and damping coefficient. The square root damping model ($p=0.5$) shows a wider stable speed range than the linear damping for large damping coefficients. The quadratic damping ($p=2$) shows similar results to linear damping with some special damping coefficients. The cubic damping ($p=3$) shows more stable response than the linear damping in general.

1 Introduction

Fluid film bearings are widely used in high speed rotating machinery owing to their high load-carrying capacity and long life. However, the inherent nonlinearity of hydrodynamic pressure may cause nonperiodic responses for rotors supported by fluid film bearings.

In 1978, the aperiodic behavior of a rigid shaft in journal bearings was first found by Holmes et al. [1] using numerical techniques, and this aperiodic motion was complex and did not settle to a limit cycle. Ehrich [2, 3] presented the chaotic motions of a Jeffcott rotor at high speeds. And the results showed that the low damping and extreme nonlinearity of the bearing system were the reasons for this high order subharmonic response. Zhao et al. [4] reported their observation of the quasi-periodic motions of a rigid rotor in journal bearings at speeds above twice the system critical speed. Brown et al. [5] studied a journal supported by short bearings using a numerical method, and the rotor showed chaotic motions when the rotating unbalance force exceeded the gravity force. In 1996, Adiletta et al. [6] presented a comprehensive study on the chaotic motions of a rotor in short journal bearings; the numerical and experimental results showed that the special values of unbalance and speed tend to cause chaos.

Besides the nonlinear hydrodynamic forces, there are some other nonlinear sources in the rotor-bearing system, such as the suspension between the bearing and foundation [9–24], the restoring forces of the shaft [7], the rub-impact effect [3, 8, 9], and high speed turbulent flow [10]. In this paper, we pay special attention to the nonlinear suspension.

In 1998, the role of nonlinear suspension in creating chaos of the rotor-bearing system was first studied by Chen and Yau [11]. In their study, a nonlinear elastic restoring force between the bearing and foundation was assumed. Numerical results showed that the rotor-bearing system experienced complicated nonperiodic motions at some speeds due to the nonlinear stiffness suspension. Then, the same authors [12, 13] discussed the chaos of a Jeffcott rotor in short journal bearings with the same nonlinear stiffness suspension model. Based on this nonlinear suspension model, different rotor-bearing systems were studied, such as rub-impact rotor, couple stress fluid lubricated bearings, and porous bearings [9, 10, 14–24]. The results showed that the dynamic responses of these systems with nonlinear suspension were entirely different from those with linear suspension. And the authors pointed out that the amplitudes of both the rotor and the bearing may have been underestimated based on the assumption of a linear suspension. However, the above nonlinear suspension model consisted of a linear damping force and a nonlinear elastic restoring force, which means that the nonlinearity of damping was ignored.

In recent years, researchers have demonstrated that the nonlinear (power law) damping is a useful method for vibration isolation [25–29]. In 2009, Lang et al. [25] theoretically proved that the nonlinear viscous damping could lead to an ideal vibration isolation of Single-Degree-Of-Freedom (SDOF) systems. Later, Laalej et al. [26] made an experimental verification of the above theoretical finding. In 2013, Lang et al. [29] reported the advantages of nonlinear viscous dampers over linear dampers for vibration control of Multi-Degree-Of-Freedom (MDOF) systems. Therefore, nonlinear damping suspension is a promising method to be used in the rotor-bearing system for vibration isolation between the bearing and environment.

However, the nonlinearity of damping may produce complicated nonlinear responses for the rotor-bearing system. The effect of nonlinear damping on the response and bifurcations of Duffing oscillators, the simplest nonlinear system, was considered by Ravindra and Mallik [30–32]. The Ref. [30] showed that the bifurcation structure and the structure of the chaotic attractor of soft Duffing oscillators were insensitive to the damping exponent, but the threshold values of the parameters depended both on the damping exponent and the damping coefficient. Sharma et al. [32] investigated the effects on the chaos in forced Duffing oscillator due to nonlinear damping, and the results suggested that the nonlinear damping increased the possibility of chaos in parameter space and affected the route to chaos in the system. Sanjuán [33] studied the effects of nonlinear damping on the dynamics of the universal escape oscillator and the result was similar to that of reference [30].

To investigate the effects of nonlinear damping suspension on nonperiodic motions of rotor-bearing system, a flexible rotor in short journal bearings with nonlinear damping suspension is studied in this paper. Computational methods are used to solve the nonlinear dynamic equations of the system. Dynamic trajectories, Poincaré maps, and bifurcation diagrams are applied to analyze the effects of damping exponent and the damping coefficient.

2 Mathematical modeling

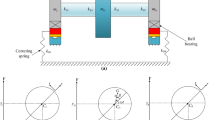
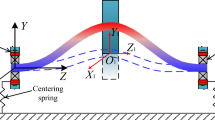
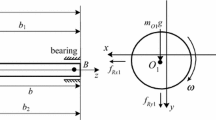
A flexible rotor, shown in Fig. 1, is supported by two journal bearings with nonlinear damping suspension. Figure 2 shows the positions of bearing, journal, and rotor. $O_0, O_1$, and $O_2$ are the geometric centers of bearing, journal, and rotor; $O_m$ is the gravity center of rotor; $X_i, Y_i$, and $Z_i$ (i = 0,1,2) are the coordinates of $O_0, O_1$, and $O_2; m_0$ and $m_2$ are the mass of bearing and rotor; $k_0$ and $c_0$ are the stiffness coefficient and damping coefficient of the supported structure; $k_2$ and $c_2$ are the stiffness coefficient and damping coefficient of shaft; $e$ is the dimensional eccentricity of journal; and $\varphi$ is the attitude angle of journal;

Fig. 1

Schematic diagram of a flexible rotor in journal bearings with nonlinear damping suspension

Fig. 2

Positions of bearing, journal, and rotor

Several assumptions are made to simplify the mathematical model [11]: the mass of shaft and the torque of rotor disk are negligible; the mass center of the bearing is at its geometric center; axial and torsional vibrations are negligible; the damping in the rotor disk due to aerodynamics is viscous; the lubricant is isothermal, laminar, and incompressible; the short bearing approximation is applicable.

2.1 Nonlinear dissipative force

Among the empirical mathematical models of nonlinear damping, the power law model is one of the simplest and most widely discussed [27, 28, 32, 34, 35]. This model is defined as follows:

$$\begin{aligned} F_d \left( v \right) =\hbox {sgn}\left( v \right) c\left| v \right| ^{p}, \end{aligned}$$

(1)

where $F_d$ is the damping force; $v$ is the relative velocity; sgn() is the signum function; $c$ is the damping coefficient; and $p$ is the damping exponent. The case $p=1$ retrieves the linear viscous damping model. The case $p<1$ can be found in civil engineering, where the damping is used as a vibration absorber [28, 36]. The case $p>1$ has been studied in some applied sciences, such as ship dynamics and vibration engineering [25, 26, 29, 33–35].

In this study, the effects of damping exponent ($p= 0.5, 1, 2$ and 3) and damping coefficient on the nonperiodic motions of a flexible rotor in short bearings are investigated.

2.2 Oil film force

In this study, the length–diameter ratio of the bearing is less than 0.25, so the short bearing approximation and the half Sommerfeld boundary condition are used to solve the Reynolds equation to compute the oil film force. Hence, a reasonable calculation accuracy can be ensured in a short computational time [37, 38]. Under the above approximations, the oil film forces on the journal center in the radial and tangential directions are [12, 21]

$$\begin{aligned} F_r&= -\mu RL\left( {\frac{L}{\delta }} \right) ^{2}\left[ \left( {\omega -2\dot{\varphi }} \right) \frac{\varepsilon ^{2}}{\left( {1-\varepsilon ^{2}} \right) ^{2}}\right. \nonumber \\&\left. +\,\frac{\pi }{2}\frac{\left( {1+2\varepsilon ^{2}} \right) \dot{\varepsilon }}{\left( {1-\varepsilon ^{2}} \right) ^{5/2}} \right] ,\end{aligned}$$

(2)

$$\begin{aligned} F_t&= \mu RL\left( {\frac{L}{\delta }} \right) ^{2}\left[ \left( {\omega -2\dot{\varphi }} \right) \frac{\pi \varepsilon }{4\left( {1-\varepsilon ^{2}} \right) ^{3/2}}\right. \nonumber \\&\left. +\,\frac{2\varepsilon \dot{\varepsilon }}{\left( {1-\varepsilon ^{2}} \right) ^{2}} \right] , \end{aligned}$$

(3)

where $F_r$ and $F_t$ are the oil film force in radial and tangential directions, $\mu$ is the dynamic viscosity of lubricant, $R$ is the radius of bearing, $L$ is the axial length of bearing, $\delta$ is the radial clearance of the bearing, $\omega$ is the angular speed of rotor, $\varphi$ is the attitude angle, $\dot{\varphi }={\mathrm{d}\varphi }/{\mathrm{d}t}, \varepsilon =e/\delta$ is the dimensionless eccentricity of journal, and $\dot{\varepsilon }={\mathrm{d}\varepsilon }/{\mathrm{d}t}$.

The oil film forces on the journal center in the X, Y directions can be given by

$$\begin{aligned} F_x&= F_r \sin \varphi +F_t \cos \varphi ,\end{aligned}$$

(4)

$$\begin{aligned} F_y&= -F_r \cos \varphi +F_t \sin \varphi , \end{aligned}$$

(5)

Knowing the eccentricity ($e)$ and the attitude angle ($\varphi$), the coordinates of journal center $O_1$ can be written as follows:

$$\begin{aligned} X_1&= X_0 +e\sin \varphi ,\end{aligned}$$

(6)

$$\begin{aligned} Y_1&= Y_0 -e\cos \varphi . \end{aligned}$$

(7)

2.3 Equations of motion

In this study, we assume that the bearing is supported with a nonlinear damping force and a linear elastic restoring force. The equations of motion of the center $O_0$ of the bearing in the Cartesian coordinates are

$$\begin{aligned}&m_0 \ddot{X}_0 =-F_x -\hbox {sgn}\left( {\dot{X}_0 } \right) c_0 \left| {\dot{X}_0 } \right| ^{p}-k_0 X_0,\end{aligned}$$

(8)

$$\begin{aligned}&m_0 \ddot{Y}_0 =-F_y -\hbox {sgn}\left( {\dot{Y}_0 } \right) c_0 \left| {\dot{Y}_0 } \right| ^{p}-k_0 Y_0 -m_0 g. \end{aligned}$$

(9)

Due to the mass of the shaft is negligible, the forces applied to the center $O_1$ of the journal are

$$\begin{aligned}&F_x \!=\!\frac{1}{2}k_2 \left( {X_1 \!-\!X_2 } \right) \!=\!\frac{1}{2}k_2 \left( {X_0 \!+\!e\sin \varphi \!-\!X_2 } \right) ,\quad \end{aligned}$$

(10)

$$\begin{aligned}&F_y \!=\!\frac{1}{2}k_2 \left( {Y_1 \!-\!Y_2 } \right) \!=\!\frac{1}{2}k_2 \left( {Y_0 \!-\!e\cos \varphi \!-\!Y_2 } \right) .\quad \end{aligned}$$

(11)

The equations of motion of the center $O_2$ of the rotor in the Cartesian coordinates are

$$\begin{aligned}&m_2 \ddot{X}_2 =-c_2 \dot{X}_2 -k_2 \left( {X_2 -X_1 } \right) +m_2 \rho \omega ^{2}\cos \phi \nonumber \\&\quad \!=\!-\!c_2 \dot{X}_2 \!-\!k_2 \left( {X_2 \!-\!X_0 \!-\!e\sin \varphi } \right) \!+\!m_2 \rho \omega ^{2}\cos \phi ,\end{aligned}$$

(12)

$$\begin{aligned}&m_2 \ddot{Y}_2 =-c_2 \dot{Y}_2 -k_2 \left( {Y_2 -Y_1 } \right) -m_2 g+m_2 \rho \omega ^{2}\sin \phi \nonumber \\&\quad \!=\!-\!c_2 \dot{Y}_2 \!-\!k_2 \left( {Y_2 \!-\!Y_0 \!+\!e\cos \varphi _1 } \right) \!-\!m_2 g\!+\!m_2 \rho \omega ^{2}\sin \phi .\nonumber \\ \end{aligned}$$

(13)

Substituting Eqs. (4) and (5) into Eqs. (10) and (11), we obtain

$$\begin{aligned}&F_r \sin \varphi \!+\!F_t \cos \varphi \!-\!\frac{1}{2}k_2 \left( {X_0 \!+\!e\sin \varphi -X_2 } \right) =0,\nonumber \\\end{aligned}$$

(14)

$$\begin{aligned}&-F_r \cos \varphi \!+\!F_t \sin \varphi \!-\!\frac{1}{2}k_2 \left( {Y_0 \!-\!e\cos \varphi _1 -Y_2 } \right) =0.\nonumber \\ \end{aligned}$$

(15)

Substituting Eqs. (2) and (3) into Eqs. (14) and (15), the $\dot{\varepsilon }$ and $\dot{\varphi }$ can be obtained as follows:

$$\begin{aligned}&\dot{\varepsilon }\!=\!\frac{\left\{ {\begin{array}{l} \pi k_2 \left( {1\!-\!\varepsilon ^{2}} \right) ^{5/2}\left[ \left( {X_2 \!-\!X_0 } \right) \sin \varphi \!-\!\left( {Y_2 \!-\!Y_0 } \right) \right. \\ \left. \cos \varphi \!-\!e \right] \!+\!4\varepsilon k_2 \left( {1\!-\!\varepsilon ^{2}} \right) ^{2}\left[ \left( {X_2 \!-\!X_0 } \right) \cos \varphi \right. \\ \left. \!+\!\left( {Y_2 \!-\!Y_0 } \right) \sin \varphi \right] \\ \end{array}} \right\} }{2\mu RL\left( {L/\delta } \right) ^{2}\left[ {{\pi ^{2}\left( {1+2\varepsilon ^{2}} \right) }/2-8\varepsilon ^{2}} \right] },\nonumber \\ \end{aligned}$$

(16)

$$\begin{aligned}&\dot{\varphi }=\frac{\omega }{2}-\nonumber \\&\,\,\frac{\left\{ {\begin{array}{l} 4k_2 \varepsilon \left( {1\!-\!\varepsilon ^{2}} \right) ^{2}\left[ \left( {X_2 \!-\!X_0 } \right) \sin \varphi \!-\!\left( {Y_2 \!-\!Y_0 } \right) \right. \\ \left. \cos \varphi \!-\!e \right] \!+\!\pi k_2 \left( {1\!+\!2\varepsilon ^{2}} \right) \left( {1\!-\!\varepsilon ^{2}} \right) ^{3/2}\left[ \left( {X_2 \!-\!X_0 } \right) \right. \\ \left. \cos \varphi \!+\!\left( {Y_2 \!-\!Y_0 } \right) \sin \varphi \right] \\ \end{array}} \right\} }{\mu RL\left( {L/\delta } \right) ^{2}\varepsilon \left[ {16\varepsilon ^{2}-\pi ^{2}\left( {1+2\varepsilon ^{2}} \right) } \right] }.\nonumber \\ \end{aligned}$$

(17)

2.4 Dimensionless equations of motion

With the following dimensionless substitutions

$$\begin{aligned}&x_i =\frac{X_i }{\delta },\, y_i =\frac{Y_i }{\delta },\, \phi =\omega t,\, \dot{x}_i =\frac{\mathrm{d}x_i }{\mathrm{d}\phi }\frac{\mathrm{d}\phi }{\mathrm{d}t}={x}'_i \omega ,\\&\dot{y}_i =\frac{\mathrm{d}y_i }{\mathrm{d}\phi }\frac{\mathrm{d}\phi }{\mathrm{d}t}={y}'_i \omega , \\&\omega _n =\sqrt{{k_2 }/{m_2 }},\, s=\sqrt{{\omega ^{2}}/{\omega _n^{2}}},\, P_k ={k_0 }/{k_2 },\\&P_m ={m_0 }/{m_2 },\, P_r =\frac{m_2 g}{k_2 \delta },\, \gamma =\frac{\delta \omega _n }{\beta } \\&\zeta _0 =\frac{c_0 \beta ^{p-1}}{2\sqrt{k_0 m_0 }},\, \zeta _2 =\frac{c_2 }{2\sqrt{k_2 m_2 }},\, b=\rho /\delta ,\,\\&\alpha =\frac{\delta ^{3}\sqrt{k_2 m_2 }}{\mu RL^{3}} \end{aligned}$$

Equations (8), (9), (12), (13), (16), and (17) can be put into a convenient nondimensional form:

$$\begin{aligned}&{x}_0'' =-\frac{2\zeta _0 }{s}\sqrt{\frac{P_k }{P_m }}\left( {\gamma s} \right) ^{p-1}\hbox {sgn}\left( {{x}'_0 } \right) \left| {{x}'_0 } \right| ^{p}-\frac{P_k }{P_m s^{2}}x_0 \nonumber \\&\qquad +\,\frac{x_2 -x_0 -\varepsilon \sin \varphi }{2P_m s^{2}},\end{aligned}$$

(18)

$$\begin{aligned}&{y}_0'' =-\frac{2\zeta _0 }{s}\sqrt{\frac{P_k }{P_m }}\left( {\gamma s} \right) ^{p-1}\hbox {sgn}\left( {{y}'_0 } \right) \left| {{y}'_0 } \right| ^{p}-\frac{P_k }{P_m s^{2}}y_0 \nonumber \\&\qquad +\,\frac{y_2 -y_0 +\varepsilon \cos \varphi }{2P_m s^{2}}-\frac{P_r }{s^{2}},\end{aligned}$$

(19)

$$\begin{aligned}&{x}_2'' =-\frac{2\zeta _2 }{s}{x}_2' -\frac{x_2 -x_0 -\varepsilon \sin \varphi }{s^{2}}+b\cos \phi ,\end{aligned}$$

(20)

$$\begin{aligned}&{y}_2'' \!=\!-\frac{2\zeta _2 }{s}{y}_2' \!-\!\frac{y_2 \!-\!y_0 \!+\!\varepsilon \cos \varphi }{s^{2}}\!+\!b\sin \phi -\frac{P_r }{s^{2}},\end{aligned}$$

(21)

$$\begin{aligned}&{\varepsilon }'=\frac{\left\{ \begin{array}{l} \alpha \pi \left( {1-\varepsilon ^{2}} \right) ^{5/2}\left[ \left( {x_2 -x_0 } \right) \sin \varphi -\left( {y_2 -y_0 } \right) \right. \\ \left. \cos \varphi -\varepsilon \right] +4\alpha \varepsilon \left( {1-\varepsilon ^{2}} \right) ^{2}\left[ \left( {x_2 -x_0 } \right) \right. \\ \left. \cos \varphi +\left( {y_2 -y_0 } \right) \sin \varphi \right] \end{array} \right\} }{s\left[ {\pi ^{2}\left( {1+2\varepsilon ^{2}} \right) -16\varepsilon ^{2}} \right] },\nonumber \\\end{aligned}$$

(22)

$$\begin{aligned}&{\varphi }'=\frac{1}{2}\nonumber \\&\quad +\frac{\left\{ {\begin{array}{l} 4\alpha \varepsilon \left( {1\!-\!\varepsilon ^{2}} \right) ^{2}\left[ \left( {x_2 \!-\!x_0 } \right) \sin \varphi \!-\!\left( {y_2 \!-\!y_0 } \right) \right. \\ \left. \quad \cos \varphi -\varepsilon \right] +\alpha \pi \left( {1+2\varepsilon ^{2}} \right) \left( {1-\varepsilon ^{2}} \right) ^{3/2}\\ \quad \left[ {\left( {x_2 -x_0 } \right) \cos \varphi +\left( {y_2 -y_0 } \right) \sin \varphi } \right] \\ \end{array}} \right\} }{s\varepsilon \left[ {\pi ^{2}\left( {1+2\varepsilon ^{2}} \right) -16\varepsilon ^{2}} \right] }.\nonumber \\ \end{aligned}$$

(23)

Hence, the motion of this rotor-bearing system is described by Eqs. (18)–(23).

3 Numerical studies

In order to solve the dimensionless equations of motion, a fourth order Runge–Kutta numerical method was used. In the solution procedure, the time step for the calculations was 1/600 of the nondimensional rotational period of the rotor, and the error tolerance was less than 0.0001. The integration results of the initial 1,000 revolutions were excluded to ensure that the analyzed data correspond to steady-state conditions.

In order to know the influence of nonlinear damping, the bifurcation diagrams were plotted from the integration results to check the dynamic motions of the rotor-bearing system. The bifurcation diagrams were obtained by increasing the rotational speed ratio, s, with a constant step size. It should be noted that the initial condition of the numerical integration was only set to the first speed ratio ($s=0$), the steady-state solution of the first speed then became the initial condition of the next speed ratio [11], and so on.

In the numerical integration, the following system parameters were used [12, 21]: $P_m =0.2, P_k =0.5, P_r =0.3, b=0.5, \alpha =0.735, \delta =0.025\,\mathrm{mm}, \beta$ $=1\,{\mathrm{m}/\mathrm{s}}, \omega _n =1,143.1\,{\mathrm{rad}/\mathrm{s}}, \zeta _2 =0.02$.

The rotor unbalance is one of the important factors influencing the responses of the rotor-bearing system. References [5, 6] presented the unbalanced rotor in journal bearings, and the results showed that the special values of unbalance tend to cause chaos. In this paper, we pay special attention to the nonlinear suspension. In the numerical integration of this study, the system parameters of Refs. [12, 21] were used, so only a single rotor unbalance value was assumed.

In nonlinear rotor-bearing system, possible co-existing stable and different periodic or nonperiodic motions may exist in the same intervals of speed. The initial condition may influence the numerical result, so different initial conditions were investigated: (a) The static state initial condition: $x_0 =0, x_0^{\prime }=0, y_0 =-0.42, y_0^{\prime }=0, x_2 =0, x_2^{\prime }=0, y_2 =-1.72, y_2^{\prime }=0$; (b) The “0” initial condition: $x_0 =0, x_0^{\prime }=0, y_0 =0, y_0^{\prime }=0, x_2 =0, x_2^{\prime }=0, y_2 =0, y_2^{\prime }=0$; (c) The initial condition of Ref. [15]: $x_0 =0.2, x_0 ^{\prime }=0.00000001, y_0 =0.4, y_0^{\prime }=0.00000001, x_2 =0.5,$ $x_2^{\prime }=0.00000001, y_2 =0.2, y_2^{\prime }=$ 0.00000001. However, the results of different initial conditions were almost the same. In this study, we chose the static state initial condition, which is most consistent with the experimental situation.

4 Results and discussion

From the results of numerical integration, we plotted bifurcation diagrams, orbits, Poincaré maps, and amplitude spectra, which could be used to check the effect of nonlinear damping suspension on the rotor-bearing system response.

A set of bifurcation diagrams is shown in Fig. 3a–d, which plots the dimensionless displacement of bearing and rotor center against the dimensionless rotational speed ratio s in the range (0, 6), with $\zeta _0 =0.05$ and $p=3$. The four bifurcation diagrams show that the motions of $x_0, y_0, x_2$, and $y_2$ are almost synchronous, which agrees with to the results of references [12, 15, 21]. To confirm the dynamic behaviors of the rotor- bearing system, the orbits, Poincaré map, and amplitude spectra of rotor center were used: Figs. 4a, 5a, 6a, 7a, and 8a are the orbits in ($x_2, y_2$) plane, Figs. 4b, 5b, 6b, 7b, and 8b are the orbits in ($x_2, x_2^{\prime }$) plane, Figs. 4c, 5c, 6c, 7c, and 8c are the orbits in ($y_2, y_2^{\prime }$) plane, Figs. 4d, 5d, 6d, 7d, and 8d are the Poincaré map in ($x_2, y_2$) plane; Figs. 4e, 5e, 6e, 7e, and 8e are the amplitude spectra of $x_2$, and Figs. 4f, 5f, 6f, 7f, and 8f are the amplitude spectra of $y_2$.

Fig. 3

Bifurcation diagrams of bearing center and rotor center: a ${x}_{0}$(nT), b ${y}_{0}$(nT), c ${x}_{2}$(nT), and d ${y}_{2}$(nT); function of the dimensionless rotational speed ratio s ($\zeta _0 =0.05,p=3$)

Fig. 4

Orbits, Poincaré map, and amplitude spectrum of rotor center at $s=0.5$ ($\zeta _0 =0.05,p=3)$

Fig. 5

Orbits, Poincaré map, and amplitude spectrum of rotor center at $s=0.55$ ($\zeta _0 =0.05,p=3$)

Fig. 6

Orbits, Poincaré map, and amplitude spectrum of rotor center at $s=1.2$ ($\zeta _0 =0.05,p=3$)

Fig. 7

Orbits, Poincaré map, and amplitude spectrum of rotor center at $s=2.35$ ($\zeta _0 =0.05,p=3$)

Fig. 8

Orbits, Poincaré map, and amplitude spectrum of rotor center at $s=4.6$ ($\zeta _0 =0.05,p=3$)

Form Fig. 3, the rotor-bearing system shows a $T$ periodic motion at low speed ($0<s\le 0.5$). This $T$ periodic motion corresponds to the orbits, Poincaré map, and amplitude spectra of rotor center in Fig. 4, which are plotted for $s=0.5$. Figure 4d displays a single return point.

For $s$ in the range (0.5, 1.2), $2T$ periodic motion occurs. This period doubling corresponds to orbits, Poincaré map, and amplitude spectrum of rotor center in Fig. 5, which are plotted for $s=0.55$.

When $s$ reaches to 1.2, the system shows a nonperiodic motion, which is illustrated by Fig. 6. The Poincaré map in Fig. 6d is a closed curve, which means the motion is quasi-periodic. And this nonperiodic motion is replaced by a $2T$ periodic motion from $s=2.35$ (Fig. 7). For $4.6\le s\le 6$ the rotor-bearing system returns to a quasi-periodic motion (Fig. 8).

In order to investigate the effects of nonlinear damping suspension on nonperiodic motions of the system, different damping coefficients ($\zeta _0 = 0.01, 0.02, 0.05, 0.1, 0.2$) and damping exponents ($p= 0.5, 1, 2, 3$) were used to plot the bifurcation diagrams. Figures 9, 10, 11, 12, and 13 are the bifurcation diagrams of rotor center in vertical direction.

Fig. 9

Bifurcation diagrams of rotor center in vertical direction when $\zeta _0 =0.01$: a $p=0.5$, b $p=1$, c $p=2$, and d $p=3$

Fig. 10

Bifurcation diagrams of rotor center in vertical direction when $\zeta _0 =0.02$: a $p=0.5$, b $p=1$, c $p=2$, and d $p=3$

Fig. 11

Bifurcation diagrams of rotor center in vertical direction when $\zeta _0 =0.05$: a $p=0.5$, b $p=1$, c $p=2$, and d $p=3$

Fig. 12

Bifurcation diagrams of rotor center in vertical direction when $\zeta _0 =0.1$: a $p=0.5$, b $p=1$, c $p=2$, and d $p=3$

Fig. 13

Bifurcation diagrams of rotor center in vertical direction when $\zeta _0 =0.2$: a $p=0.5$, b $p=1$, c $p=2$, and d $p=3$

The bifurcation diagrams are almost the same when $0<s<2.35$, which is a “$T$ periodic - 2$T$ periodic - nonperiodic” pattern. However, for $2.35\le s\le 6$, the motions of rotor-bearing system with a different damping are different, so we need to compare the results for $s$ in this range (2.35, 6). Table 1 is the ranges of the speed ratio $s$ (within (2.35, 6)) when the system shows periodic motions. Compared with the linear damping suspension ($p=1$), when the damping coefficients is large ($\zeta _0 =0.1$ and 0.2), the half nonlinear damping ($p=0.5$) shows a wider speed range for periodic motions, while when the damping coefficients is small ($\zeta _0 =0.02$ and 0.05) the speed range is more narrow. The difference between the linear damping ($p=1$) and the quadratic damping ($p=2$) is less apparent under some special damping coefficients. For the cubic damping suspension ($p=3$), the speed range for periodic motions is wider than that for linear damping ($p=1$) suspension in general, and the dynamic motions of the system are the same under different damping coefficients when $p=3$.

Table 1 Ranges of the speed ratio $s$ (within [2.35, 6]) when the system shows periodic motions

The above results show that for low speeds ($0<s<2.35$), the nonlinear damping suspension has no influence on the motion pattern of the rotor-bearing system. So for a low speed rotor-bearing system, if the nonlinear damping suspension damping is used for vibration isolation or other purpose, there is no need to worry about the nonlinear influence of damping on the motions of the system. The comparisons between the linear damping ($p=1$) and the nonlinear damping ($p=0.5, 2, 3$) show that for high speeds ($2.35\le s\le 6)$ the nonlinear damping has a complicated influence on the motion pattern of the system. If the half nonlinear damping ($p=0.5$) is used in a high speed system, higher damping coefficients may give rise to more stable 1-T or 2-T periodic motions. If the quadratic damping ($p=2$) is used, however, lower damping coefficients may give rise to more stable motions. If the cubic damping suspension ($p=3$) is used, the stability of motion is generally better than that for the linear damping suspension, and the damping coefficients have no effect on the motions.

The above bifurcation diagrams showed the speed ranges of periodic motions, but more quantitative analysis should be conducted to make clear the nature and character of these stable motions. Bearing transmitted forces and the rotor orbit amplitudes are often used to characterize the system during operation [39]. Figures 14, 15, 16, and 17 are the bearing transmitted forces (${F}_{{x}}, {F}_{{y}}$), the journal orbits (${x}_{1}, {y}_{1})$, and the rotor orbits (${x}_{2}, {y}_{2})$ when the rotor shows periodic motions, with $\zeta _0 =0.05$ and $s=4.4$. From the results of Fig. 14, the bearing forces, journal motion, and rotor motion are both T periodic when $p=0.5$. The peak–peak amplitude of the bearing force is about 600 N, the dimensionless peak–peak amplitude of the journal motion is about 0.25, and the dimensionless peak–peak amplitude of the rotor motion is about 1. With the same speed, the higher damping exponents ($p=1,2,3$) produce 2T periodic rotor motions and T periodic journal motions/bearing forces. The peak–peak amplitude of the bearing force is about 4,000 N, the dimensionless peak–peak amplitude of the journal motion is about 5, and the dimensionless peak–peak amplitude of the rotor motion is about 2.

Fig. 14

Bearing transmitted forces (a), journal orbit (b), and rotor orbit (c) with $\zeta _0 =0.05,p=0.5,s=4.4$

Fig. 15

Bearing transmitted forces (a), journal orbit (b), and rotor orbit (c) with $\zeta _0 =0.05,p=1,s=4.4$

Fig. 16

Bearing transmitted forces (a), journal orbit (b), and rotor orbit (c) with $\zeta _0 =0.05,p=2,s=4.4$

Fig. 17

Bearing transmitted forces (a), journal orbit (b), and rotor orbit (c) with $\zeta _0 =0.05,p=3,s=4.4$

References [1–7] presented the nonperiodic motions of a rotor, and the results showed that the extreme nonlinearity of the bearing system was the reason for this nonperiodic response. In the rotor-bearing system, the inherent nonlinearity of hydrodynamic pressure is the main source of nonlinearity which causes nonperiodic responses. In our study, the results at the top-right corner of Table 1 showed that, at high speeds, similar nonperiodic behaviors could be reached when the damping coefficient is small or the damping exponent is high. These results show that the introduction of nonlinear damping will not induce but just change the nonperiodic system responses.

References [9–24] discussed the effect of nonlinear stiffness suspension in rotor-bearing system, their nonlinear stiffness model included a simple linear stiffness term plus a cubic stiffness term. The results showed that the introduction of a cubic stiffness term changed the responses of the system, but a systematic research of the nonlinear stiffness in the rotor-bearing system has not been conducted as yet. For a nonlinear stiffness suspension, the rotor-bearing system of Ref. [13] showed similar bifurcation diagrams as that of our study. In our future work, the nonlinear damping and nonlinear stiffness will be studied further.

Nonlinear damping Duffing oscillator is a simple nonlinear system [30–32]; its equation of motion is $\ddot{X}+\hbox {sgn}\left( {\dot{X}} \right) {C}'\left| {\dot{X}} \right| ^{p}+X+X^{3}=F\cos \omega t$. The reference [30] showed that the bifurcation structure and the structure of the chaotic attractor of Duffing oscillators were insensitive to the damping exponent, but the threshold values of the parameters depended both on the damping exponent and the damping coefficient. Sanjuán [33] studied the effects of nonlinear damping on the dynamics of the universal escape oscillator, and the results suggest that increasing the power of the nonlinear damping has a similar effect as decreasing the damping coefficient for a linearly damped case. In our study, the rotor-bearing system with nonlinear damping showed insensitive characteristics at low speeds. At high speeds, the system with low damping coefficient or high damping exponent showed similar responses, which agrees with the results of Ref. [33].

When the nonlinear damping suspension is considered for vibration isolation between the bearing and environment in a flexible rotor- bearing system, the rotor speed should be taken into account in the first place. For low speed system, the nonlinear damping has no effect on the nonperiodic motions of the system, so the nonlinear damping can be used conveniently. For high speed system, however, the effect of nonlinear damping is due to a combination of the damping exponent and damping coefficient, which means the designers need to take everything into consideration.

5 Conclusions

A computational investigation of the effect of nonlinear damping suspension on the nonperiodic motions of a flexible rotor in journal bearings has been carried out. The results show that the effect of nonlinear damping is more complicated for the rotor- bearing system than for Duffing oscillators. Specifically, the effect depends on the speed of the rotor: (a) For low speeds, there is no difference in the motion patterns of the rotor-bearing system between the nonlinear damping suspension and the linear damping suspension; (b) For high speeds, the effect of nonlinear damping is due to a combination of the damping exponent and damping coefficient. The square root damping ($p=0.5$) shows wider stable speed ranges than linear damping with large damping coefficients. The quadratic damping ($p=2$) has similar results to most of linear damping under some special damping coefficients. The cubic damping ($p=3$) shows a more stable response than the linear damping.