Nonlinear dynamic modeling and response analysis of a rotor–blade system with whirling motion

Abstract

In this paper, we propose a new nonlinear dynamic model of a rotor–blade system with whirling motion, in which a rigid rotor and blades are modeled as a Jeffcott rotor and Euler–Bernoulli beams, respectively. The stiffening effects of the rotating blades are considered using a hybrid set of deformations, which consist of the stretch and chordwise deformations. After the nonlinear partial differential equations of motion are derived using Hamilton’s principle, they are discretized using the Galerkin method. From the discretized equations, the nonlinear dynamic responses are computed using the generalized-$\upalpha$ time integration method. Based on the dynamic responses and the frequency spectra, the proposed model is verified both for the case where the blade is considered to be a rigid body and for the case where there is no whirling motion of the rotor. In this study, the nonlinear dynamic responses of the rotor–blade system are analyzed in terms of the natural frequencies for whirling motion and the natural frequencies of the deformation of the rotating beam. In addition, the effects of the supporting stiffness, rotating speed and blade stiffness on the dynamic responses of the radial displacement and stretch/chordwise deformations are also analyzed.

1 Introduction

The dynamic analysis of a rotor–blade system is an important topic in mechanical engineering because rotor blades such as helicopter blades, turbine blades and wind turbines are widely used in many industry applications. Rotor–blade systems experience the elastic vibration of the blades as well as the rotating and whirling motions of the rotor, and the motions of the rotor and the blades affect each other. Since the rotor–blade system has very complex motions, a more reliable dynamic model is required for stable and accurate operation.

Many researchers have presented dynamic models of a rotating beam (or blade) attached to a rigid rotor, which rotates about its rotational axis. They focused on elastic vibrations of rotating beams, while they ignored the whirling motion of a rotor. One important feature in the dynamics of a rotating beam is the stiffening effect; that is, the natural frequencies of a beam increase as the rotating speed increases. The dynamic response of a rotating beam is generally analyzed by using three independent deformation variables. The most widely used deformations are the axial, chordwise and flapwise deformations. The axial deformation is in the radial direction of the rotating plane of a beam, the chordwise deformation is in the tangential direction of the rotating plane and the flapwise deformation is in the direction perpendicular to the rotating plane. Thus, the axial and chordwise deformations are in-plane deformations of a rotating beam, while the flapwise deformations is an out-of-plane deformation. These axial, chordwise and flapwise deformations are generally called Cartesian variables. In some studies, the stretch deformation, which is a deformation in the arc length of a rotating beam, is used instead of the axial deformation. To distinguish from the Cartesian variables, the variables consisting of the stretch, chordwise and flapwise transforms are called the non-Cartesian variables. The relations between the Cartesian and non-Cartesian variables are described by the von Karman strain theory [1].

The modeling methods for a rotating beam can be classified into three categories based on the method used to consider the stiffening effect. The first modeling method is to apply energy due to the centrifugal force along with the bending energy of the beam to the total potential energy [2,3,4]. This method has been widely used in previous studies because it can simplify the formulation and does not need to account for axial or stretch deformations. The second modeling method is based on nonlinear strain [5,6,7]. Here, the axial, chordwise and flapwise deformations are considered as the Cartesian variables. Finally, the third modeling method is to use a hybrid set of deformation variables, which are the stretch, chordwise, and flapwise deformations [8,9,10,11]. In this method, the stretch deformation of the non-Cartesian variable is adopted instead of the axial deformation of the Cartesian variable. In the second and third methods, the stiffening effect is expressed in a coupled term of axial (or stretch) and chordwise deformations. Researchers who used the second and third methods investigated the effect of the coupled term on the natural frequencies and dynamic responses of a rotating beam. Recently, Kim and Chung [11] showed that a modeling method using the hybrid set of deformation variables has high accuracy and good computation efficiency compared to the other modeling methods. In addition, some numerical methods were proposed to effectively solve problems described by complicated partial differential equations [12,13,14].

On the other hand, the dynamic modeling and analysis of a rotor–blade system with whirling motion were studied by some researchers [15,16,17,18,19,20]. They modeled a rotor as a Jeffcott rotor to account for whirling motion. Diken and Alnefaie [15] derived nonlinear equations for the whirling motion of a rotor and the chordwise motions of blades by using Lagrange’s equation. They analyzed the dynamic responses for the whirling motion and chordwise deformations when a rotor–blade system rotates at subcritical and supercritical speeds. Li et al. [16] established the dynamic model of a rotor–blade system with nonlinear supports. They investigated the effects of the friction, damping and stiffness coefficients on the dynamic response of the rotor–blade system. Thiery and Aidanpaa [17] performed the numerical and experimental studies for the nonlinear vibration of a rotor–blade system. Meanwhile, Crandall and Dugundji [18] introduced the interactions between the rotor and blade motions, which caused instability in a rotor–blade system. They found that the natural frequencies of the blade, which increase by the stiffening effect, may approach the natural frequency of the rotor. In addition, Najafi et al. [19, 20] derived the nonlinear equations of motion for a damped bladed rotor. They investigated the stability criteria and stability boundary from the eigenvalue analysis for the linear equations of an undamped bladed rotor. They obtained the bifurcation equations by using the multiple scales method around the stability boundary. The effects of the stiffness and damping of the bearing on the instability caused by the interaction of the rotor and blade were analyzed using the bifurcation equations.

Previous studies on the dynamic model of a rotor–blade system have considered only the whirling motion of the rotor and chordwise deformation of the blade, without considering the axial (or stretch) deformations of the blade. According to Refs. [7, 9, 10], the coupling effect between the axial (or stretch) and chordwise deformations of a rotating beam affects the dynamic characteristics such as the veering phenomenon and the divergence instability. That is, the coupling effect between the elastic deformations of the blade is very important when analyzing a rotating beam. To more accurately determine the dynamics of a rotor–blade system, it is necessary to consider the interaction between the rotor and blade motions along with the coupling effect between the elastic deformations of the blade. Therefore, in this paper, we propose a new model of a rotor–blade system considering the axial (or stretch) deformations.

In this study, a rigid rotor with flexible blades is modeled as a Jeffcott rotor with Euler–Bernoulli beams to establish a new nonlinear dynamic model of a rotor–blade system with whirling motion. During the modeling, the stiffening effects of the blades are considered with a hybrid set of deformations. After the nonlinear differential equations of motions for a rotor–blade system are derived by Hamilton’s principle, they are discretized by applying the Galerkin method. The generalized-$\alpha$ time integration method [21] is used to compute nonlinear dynamic responses from the discretized equations. Based on the computed responses, we analyze the effects of changes in the supporting stiffness, rotating speed and beam stiffness on the whirling motion of the rotor and the deformations of the blades. In addition, we investigate the frequency components of the nonlinear dynamic responses for the whirling motion and the deformations by using the fast Fourier transform (FFT).

2 Modeling and equations of motion

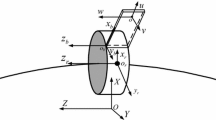
Consider a rotor–blade system consisting of two flexible blades and a rigid rotor, as shown in Fig. 1. The geometric center of the system is supported by a shaft and two bearings which have an equivalent radial spring constant k and an equivalent damping coefficient c. It is assumed that the rigid rotor with mass m, radius a and mass eccentricity e experiences a whirling motion with rotating speed $\Omega$. In Fig. 1, the OXY coordinate system is an inertia reference frame fixed in space, and the $O_{q}x_{q}y_{q}$ coordinate systems are the rotating reference frames fixed to the q-th blade ($q = 1, 2$). The geometric center C is defined by the polar coordinates r(t) and $\theta (t)$, while the mass center of the rotor, G, can be defined by the eccentricity e and the angle $\Omega t$. Since the angle of the blade axis from the X-axis is $\phi (t)$ and the angle of the mass center from the blade is $\phi _{0}$, the relationship between $\Omega t, \phi (t)$ and $\phi _{0}$ is given by

$$\begin{aligned} \Omega t=\phi (t)+\phi _0 . \end{aligned}$$

(1)

The blades, which are symmetrically clamped to the rotor, are regarded as Euler–Bernoulli beams, and they are uniform and homogeneous. The flexible cantilever beams have total length L, cross-sectional area A, Young’s modulus E and mass density $\rho$. In this figure, the blade has axial, stretch and chordwise deformations denoted by $u_{q}, s_{q}$ and $v_{q}$, respectively, when the point $P_{q}$ on the q-th blade moves to the point ${P}'_q$. In this study, only the force due to the rotation of the blade is considered, so that the deformation of the flapwise deformation in the z direction of the blade is neglected. The relationship between the axial deformation $u_{q}$ and the stretch deformation $s_{q}$ may be written as

$$\begin{aligned} u_q =s_q -h_q , \end{aligned}$$

(2)

where

$$\begin{aligned} h_q =\frac{1}{2}\int _0^{x_q } {\left( {\frac{\partial v_q }{\partial \eta }} \right) ^{2} \hbox {d}\eta }, \end{aligned}$$

(3)

and $\eta$ is a dummy variable. According to references [8,9,10,11], the use of the stretch deformation of the non-Cartesian variable is more advantageous than the use of the axial deformation of the Cartesian variable. Therefore, a hybrid set of deformation variables is used in this study.

Fig. 1

Dynamic model of a rotor–blade system with whirling motion

The kinetic energy, potential energy, and virtual work done by non-conservative forces are required to derive the equations of motion for the rotor–blade system. First, the position vector for the mass center of the rotor G is given by

$$\begin{aligned} \mathbf{r}_G =\left[ {r+e\cos \left( {\Omega t-\theta } \right) } \right] \mathbf{e}_r +\left[ {e\sin \left( {\Omega t-\theta } \right) } \right] \mathbf{e}_\theta ,\nonumber \\ \end{aligned}$$

(4)

where $\mathbf{e}_{r}$ and $\mathbf{e}_{\theta }$ are the unit vectors in the polar coordinates r and $\theta$, respectively. The position vector of an arbitrary point on the q-th blade, which is attached to the rotor, is given by

$$\begin{aligned} \mathbf{r}_q= & {} \left\{ r-(-1)^{q}\left[ (a+x_q +s_q -h_q )\cos (\phi -\theta )\right. \right. \nonumber \\&\quad \left. \left. -\,v_q \sin (\phi -\theta ) \right] \right\} \mathbf{e}_r\nonumber \\&\quad \,-\,\left( {-1} \right) ^{q}\left[ (a+x_q +s_q -h_q )\sin (\phi -\theta )\right. \nonumber \\&\quad \left. \,+\,v_q \cos (\phi -\theta ) \right] \mathbf{e}_\theta . \end{aligned}$$

(5)

The total kinetic energy is expressed as

$$\begin{aligned} T=\frac{1}{2}m{{\dot{\mathbf{r}}}}_G \cdot {{\dot{\mathbf{r}}}}_G +\frac{1}{2}I_G \Omega ^{2}+\sum _{q=1}^2 {\frac{1}{2}\rho A\int _0^L {{{\dot{\mathbf{r}}}}_q } \cdot {{\dot{\mathbf{r}}}}_q \hbox {d}x_q } ,\nonumber \\ \end{aligned}$$

(6)

where $I_{G}$ is the mass moment of inertia for the rotor mass center G; the superposed dot represents differentiation with respect to time. Neglecting gravity, the total potential energy is expressed as

$$\begin{aligned} U=\frac{1}{2}{{kr}}^{2}+\sum _{q=1}^2 {\frac{1}{2}\int _0^L {\left[ {{{EA}}\left( {\frac{\partial s_q }{\partial x_q }} \right) ^{2}+{{EI}}\left( {\frac{\partial ^{2}v_q }{\partial x_q^2 }} \right) ^{2}} \right] } \hbox {d}x_q },\nonumber \\ \end{aligned}$$

(7)

where I is the area moment of inertia of the blade. Note that the strain for the stretch deformation is nonlinear in terms of $u_{q}$ and $v_{q}$ because differentiation of Eq. (2) with respect to $x_{q}$ leads to the following nonlinear strain, called the von Karman strain:

$$\begin{aligned} \frac{\partial s_q }{\partial x_q }=\frac{\partial u_q }{\partial x_q }+\frac{1}{2}\left( {\frac{\partial v_q }{\partial x_q }} \right) ^{2}. \end{aligned}$$

(8)

On the other hand, the virtual work done by the damping force is written as

$$\begin{aligned} \delta W=-\,c\cdot \left( {{\dot{r}}{} \mathbf{e}_r +r{\dot{\theta }}\mathbf{e}_\theta } \right) \cdot \delta \left( {r\mathbf{e}_r } \right) , \end{aligned}$$

(9)

where $\delta$ is the variational notation.

The equations of motion are derived from Hamilton’s principle given by

$$\begin{aligned} \int _{t_1 }^{t_2 } {\left( {\delta T-\delta U+\delta W} \right) \hbox {d}t} =0, \end{aligned}$$

(10)

where $t_{1}$ and $t_{2}$ are any two instances. Substituting Eqs. (6), (7) and (9) into Eq. (10), the nonlinear equations of the radial, angular, stretch and chordwise motions can be obtained as follows:

$$\begin{aligned}&m\ddot{r}+c{\dot{r}}+kr-mr{\dot{\theta }}^{2}+2\rho AL(\ddot{r}-r{\dot{\theta }}^{2})\nonumber \\&\quad -\,me\left[ {\Omega ^{2}\cos (\Omega t-\theta )+{\dot{\Omega }}\sin (\Omega t-\theta )} \right] \nonumber \\&\quad -\,\sum _{q=1}^2 {\rho AL(-1)^{q}} \left\{ \left[ \ddot{s}_q -\ddot{h}_q -2\Omega {\dot{v}}_q \right. \right. \nonumber \\&\quad \left. -\,\Omega ^{2}(a+x_q +s_q -h_q )-\dot{\Omega }v_q \right] \cos (\phi -\theta )\nonumber \\&\quad - \left[ \ddot{v}_q +2\Omega ({\dot{s}}_q -\dot{h}_q )-\Omega ^{2}v_q \right. \nonumber \\&\quad \left. +\left. {\dot{\Omega }}(a+x_q +s_q -h_q ) \right] \sin (\phi -\theta ) \right\} =0, \end{aligned}$$

(11)

$$\begin{aligned}&mr\ddot{\theta }+cr{\dot{\theta }}+2m{\dot{r}}{\dot{\theta }}+2\rho AL(r\ddot{\theta }+2{\dot{r}}{\dot{\theta }})\nonumber \\&\quad -\,me\left[ {\Omega ^{2}\sin (\Omega t-\theta )-{\dot{\Omega }}\cos (\Omega t-\theta )} \right] \nonumber \\&\quad +\,\sum _{q=1}^2 {\rho AL(-1)^{q}} \left\{ \left[ \ddot{s}_q -\ddot{h}_q -2\Omega {\dot{v}}_q \right. \right. \nonumber \\&\quad -\left. \Omega ^{2}(a+x_q +s_q -h_q )-\dot{\Omega }v_q \right] \sin (\phi -\theta )\nonumber \\&\quad + \left[ \ddot{v}_q +2\Omega ({\dot{s}}_q -\dot{h}_q )-\Omega ^{2}v_q\right. \nonumber \\&\quad \left. \left. +{\dot{\Omega }}(a+x_q +s_q -h_q ) \right] \cos (\phi -\theta ) \right\} =0, \end{aligned}$$

(12)

$$\begin{aligned}&\rho A\left[ {\ddot{s}_q -\ddot{h}_q -2\Omega {\dot{v}}_q -\Omega ^{2}(s_q -h_q )-{\dot{\Omega }}v_q } \right] \nonumber \\&\quad -\,EA\frac{\partial ^{2}s_q }{\partial x_q^2 }\nonumber \\&\quad -\,\rho A\left( {-1} \right) ^{q}\left[ (\ddot{r}-r\dot{\theta }^{2})\cos (\phi -\theta )\right. \nonumber \\&\quad \left. +\,(r\ddot{\theta }+2\dot{r}{\dot{\theta }})\sin (\phi -\theta ) \right] =\rho A\Omega ^{2}(a+x_q )\hbox { for }q = 1, 2,\nonumber \\ \end{aligned}$$

(13)

$$\begin{aligned}&\rho A\left[ {\ddot{v}_q +2\Omega ({\dot{s}}_q -{\dot{h}}_q )-\Omega ^{2}v_q +{\dot{\Omega }}(s_q -h_q )} \right] \nonumber \\&\quad -EA\frac{\partial }{\partial x_q }\left( {\frac{\partial s_q }{\partial x_q }\frac{\partial v_q }{\partial x_q }} \right) \nonumber \\&\quad +EI\frac{\partial ^{4}v_q }{\partial x_q^4 }\nonumber \\&\quad +\rho A(-1)^{q}\left[ (\ddot{r}-r{\dot{\theta }}^{2})\sin (\phi -\theta )\right. \nonumber \\&\quad \left. -(r\ddot{\theta }+2{\dot{r}}{\dot{\theta }})\cos (\phi -\theta ) \right] =-\rho A{\dot{\Omega }}(a+x_q )\hbox { for }q = 1, 2.\nonumber \\ \end{aligned}$$

(14)

The associated boundary conditions are given by

$$\begin{aligned}&s_q =v_q =\frac{\partial v_q }{\partial x_q }=0\quad \hbox {at}\quad x_q =0\qquad (q =1, 2), \end{aligned}$$

(15)

$$\begin{aligned}&\frac{\partial s_q }{\partial x_q }=\frac{\partial ^{2}v_q }{\partial x_q^2 }=\frac{\partial ^{3}v_q }{\partial x_q^3 }=0 \quad \hbox {at}\quad x_q =L\qquad (q =1, 2).\nonumber \\ \end{aligned}$$

(16)

It is valuable to mention the sources of the nonlinear terms of the above equations of motion. The nonlinear terms related to r and $\theta$ are caused by the whirling motion, while the nonlinear terms related to $h_{q}$ are caused by the large transverse defections of blades.

Note that Eqs. (11) and (12) are the nonlinear equations for the whirling motion of the rotor–blade system, while Eqs. (13) and (14) are the nonlinear equations for the flexible motions of the q-th blade. These nonlinear equations are coupled with each other via the variables $r,\theta , s_{q}$ and $v_{q}$. If the blades are removed from this system, Eqs. (11) and (12) reduce to the equations of motion for the Jeffcott rotor. In contrast, if there are no radial and angular displacements of the rotor–blade system, the nonlinear equations for the stretch and chordwise deformations of the q-th blade are the same as the nonlinear equations of the rotating cantilever beam presented by Kim and Chung [11].

The equations of motion given by Eqs. (11)–(14) were transformed into autonomous form to perform an effective analysis. Since the angular displacement $\theta$ increases monotonically with time, the equations of the system are non-autonomous. Therefore, the non-autonomous equations need to be transformed into autonomous equations. For this reason, the phase angle $\psi$, which is the angle from the r-axis to the mass center, is used instead of $\theta$. The phase angle $\psi$ may be expressed by

$$\begin{aligned} \psi =\Omega t-\theta =\phi (t)+\phi _0 -\theta . \end{aligned}$$

(17)

The transformed equations can be derived by substituting Eq. (17) into Eqs. (11)–(14).

In addition, the equations for the radial and angular displacements must be modified for efficient numerical computations. The nonlinear terms, including $h_{q}$ in Eqs. (11) and (12), make numerical computations inaccurate and inefficient. These nonlinear terms can be removed from Eqs. (11) and (12) by using Eqs. (13) and (14). The modified equations of motion can be represented by

$$\begin{aligned}&m\ddot{r}+c{\dot{r}}+kr-mr(\Omega -{\dot{\psi }})^{2}\nonumber \\&\quad -\,me(\Omega ^{2}\cos \psi +{\dot{\Omega }}\sin \psi )\nonumber \\&\quad +\sum _{q=1}^2 \left( {-1} \right) ^{q}\left\{ -EAL\frac{\partial ^{2}s_q }{\partial x_q^2 }\cos (\psi -\phi _0 )\right. \nonumber \\&\quad +\left[ EAL\frac{\partial }{\partial x_q }\left( {\frac{\partial s_q }{\partial x_q }\frac{\partial v_q }{\partial x_q }} \right) \right. \nonumber \\&\quad \left. \left. -EIL\frac{\partial ^{4}v_q }{\partial x_q^4 } \right] \sin (\psi -\phi _0 ) \right\} =0, \end{aligned}$$

(18)

$$\begin{aligned}&mr({\dot{\Omega }}-\ddot{\psi })+cr(\Omega -{\dot{\psi }})+2m\dot{r}(\Omega -{\dot{\psi }})\nonumber \\&\quad -\,me(\Omega ^{2}\sin \psi -\dot{\Omega }\cos \psi )\nonumber \\&\quad +\sum _{q=1}^2 \left( {-1} \right) ^{q}\left\{ -EAL\frac{\partial ^{2}s_q }{\partial x_q^2 }\sin (\psi -\phi _0 )\right. \nonumber \\&\quad -\left[ EAL\frac{\partial }{\partial x_q }\left( {\frac{\partial s_q }{\partial x_q }\frac{\partial v_q }{\partial x_q }} \right) \right. \nonumber \\&\quad \left. \left. -\,EIL\frac{\partial ^{4}v_q }{\partial x_q^4 } \right] \cos (\psi -\phi _0 ) \right\} =0, \end{aligned}$$

(19)

$$\begin{aligned}&\rho A\left[ {\ddot{s}_q -\ddot{h}_q -2\Omega {\dot{v}}_q -\Omega ^{2}(s_q -h_q )-{\dot{\Omega }}v_q } \right] \nonumber \\&\quad -\,EA\frac{\partial ^{2}s_q }{\partial x_q^2 }\nonumber \\&\quad -\,\rho A(-1)^{q}\left\{ \left[ {\ddot{r}-r(\Omega -\dot{\psi })^{2}} \right] \cos (\psi -\phi _0 )\right. \nonumber \\&\quad \left. +\,\left[ {r(\dot{\Omega }-\ddot{\psi })+2{\dot{r}}(\Omega -{\dot{\psi }})} \right] \sin (\psi -\phi _0 ) \right\} \nonumber \\&=\rho A\Omega ^{2}(a+x_q )\quad \hbox {for }q = 1, 2, \end{aligned}$$

(20)

$$\begin{aligned}&\rho A\left[ {\ddot{v}_q +2\Omega ({\dot{s}}_q -{\dot{h}}_q )-\Omega ^{2}v_q +{\dot{\Omega }}(s_q -h_q )} \right] \nonumber \\&\quad -\,EA\frac{\partial }{\partial x_q }\left( {\frac{\partial s_q }{\partial x_q }\frac{\partial v_q }{\partial x_q }} \right) \nonumber \\&\quad +\,EI\frac{\partial ^{4}v_q }{\partial x_q^4 }\nonumber \\&\quad +\,\rho A(-1)^{q}\left\{ \left[ {\ddot{r}-r(\Omega -\dot{\psi })^{2}} \right] \sin (\psi -\phi _0 )\right. \nonumber \\&\quad \left. -\left[ {r(\dot{\Omega }-\ddot{\psi })+2{\dot{r}}(\Omega -{\dot{\psi }})} \right] \cos (\psi -\phi _0 ) \right\} \nonumber \\&=-\rho A{\dot{\Omega }}(a+x_q )\quad \hbox {for }q = 1, 2. \end{aligned}$$

(21)

3 Discretization and time integration

The Galerkin method was used to discretize the partial differential equations of motion given by Eqs. (18)–(21). Before using the Galerkin method, the variational equations need to be derived from the partial differential equations and boundary conditions. Trial and weighting functions are required to derive the variational equations. The trial functions are functions determined to satisfy the partial differential equation and the associated boundary conditions, while the weighting functions are arbitrary functions that have values of zero where the essential boundary conditions are prescribed. The trial functions for the stretch and chordwise deformations are denoted by $s_{q}$ and $v_{q}$, respectively, and the corresponding weighting functions are denoted by $\bar{{s}}_q$ and $\bar{{v}}_q$. The variational equations for r and $\psi$ are obtained by integrating both sides of Eqs. (18) and (19) over the blade domain. On the other hand, the variational equations for $s_{q}$ and $v_{q}$ can be derived by multiplying Eqs. (20) and (21) by $\bar{{s}}_q$ and $\bar{{v}}_q$, respectively, integrating the resulting equations over the blade domain, and applying integration by parts. The derived variational equations are expressed as

$$\begin{aligned}&m\ddot{r}+c{\dot{r}}+kr-mr(\Omega -{\dot{\psi }})^{2}\nonumber \\&\qquad -me(\Omega ^{2}\cos \psi +{\dot{\Omega }}\sin \psi )\nonumber \\&\qquad +\int _0^L \sum _{q=1}^2 (-1)^{q}\left\{ -EAL\frac{\partial ^{2}s_q }{\partial x_q^2 }\cos (\psi -\phi _0 )\right. \nonumber \\&\qquad +\left[ EAL\frac{\partial }{\partial x_q }\left( {\frac{\partial s_q }{\partial x_q }\frac{\partial v_q }{\partial x_q }} \right) \right. \nonumber \\&\qquad \left. \left. -EIL\frac{\partial ^{4}v_q }{\partial x_q^4 } \right] \sin (\psi -\phi _0 ) \right\} \hbox {d}x_q =0, \end{aligned}$$

(22)

$$\begin{aligned}&mr({\dot{\Omega }}-\ddot{\psi })+cr(\Omega -{\dot{\psi }})+2m\dot{r}(\Omega -{\dot{\psi }})\nonumber \\&\qquad -me(\Omega ^{2}\sin \psi -\dot{\Omega }\cos \psi )\nonumber \\&\qquad +\int _0^L \sum _{q=1}^2 (-1)^{q}\left\{ -EAL\frac{\partial ^{2}s_q }{\partial x_q^2 }\sin (\psi -\phi _0 )\right. \nonumber \\&\qquad -\left[ EAL\frac{\partial }{\partial x_q }\left( {\frac{\partial s_q }{\partial x_q }\frac{\partial v_q }{\partial x_q }} \right) \right. \nonumber \\&\qquad \left. \left. -EIL\frac{\partial ^{4}v_q }{\partial x_q^4 } \right] \cos (\psi -\phi _0 ) \right\} \hbox {d}x_q =0, \end{aligned}$$

(23)

$$\begin{aligned}&\rho A\int _0^L \left[ \bar{{s}}_q \ddot{s}_q -\bar{{s}}_q \ddot{h}_q -2\Omega \bar{{s}}_q {\dot{v}}_q \right. \nonumber \\&\qquad \left. -\Omega ^{2}\bar{{s}}_q (s_q -h_q )-{\dot{\Omega }}\bar{{s}}_q v_q \right] \hbox {d}x_q \nonumber \\&\qquad +EA\int _0^L {\frac{\partial \bar{{s}}_q }{\partial x_q }\frac{\partial s_q }{\partial x_q }} \hbox {d}x_q\nonumber \\&\qquad -\rho A\int _0^L (-1)^{q}\bar{{s}}_q \left\{ \left[ {\ddot{r}-r(\Omega -{\dot{\psi }})^{2}} \right] \cos (\psi -\phi _0 )\right. \nonumber \\&\qquad \left. +\left[ {r({\dot{\Omega }}-\ddot{\psi })+2{\dot{r}}(\Omega -\dot{\psi })} \right] \sin (\psi -\phi _0 ) \right\} \hbox {d}x_q\nonumber \\&\quad =\rho A\Omega ^{2}\int _0^L {\bar{{s}}_q (a+x_q )} \hbox {d}x_q \quad \hbox { for }q =1, 2, \end{aligned}$$

(24)

$$\begin{aligned}&\rho A\int _0^L \left[ \bar{{v}}_q \ddot{v}_q +2\Omega \bar{{v}}_q ({\dot{s}}_q -{\dot{h}}_q )-\Omega ^{2}\bar{{v}}_q v_q \right. \nonumber \\&\qquad \left. +\dot{\Omega }\bar{{v}}_q (s_q -h_q ) \right] \hbox {d}x_q \nonumber \\&\qquad +EA\int _0^L {\frac{\partial \bar{{v}}_q }{\partial x_q }\frac{\partial s_q }{\partial x_q }\frac{\partial v_q }{\partial x_q }} \hbox {d}x_q +EI\int _0^L {\frac{\partial ^{2}\bar{{v}}_q }{\partial x_q ^{2}}\frac{\partial ^{2}v_q }{\partial x_q ^{2}}} \hbox {d}x_q\nonumber \\&\qquad +\rho A\int _0^L (-1)^{q}\bar{{v}}_q \left\{ \left[ {\ddot{r}-r(\Omega -{\dot{\psi }})^{2}} \right] \sin (\psi -\phi _0 )\right. \nonumber \\&\qquad \left. -\left[ {r({\dot{\Omega }}-\ddot{\psi })+2{\dot{r}}(\Omega -\dot{\psi })} \right] \cos (\psi -\phi _0 ) \right\} \hbox {d}x_q\nonumber \\&\quad =-\rho A{\dot{\Omega }}\int _0^L {\bar{{v}}_q (a+x_q )} \hbox {d}x_q \quad \hbox { for }q =1, 2. \end{aligned}$$

(25)

The strong form consists of the partial differential equations of motion given by Eqs. (18)–(21) and the boundary conditions given by Eqs. (15) and (16). The above variational equations, which are often called the weak forms, are integral forms of the equations, which are needed to formulate the following approximation of solutions.

Using the Galerkin method, the trial and weighting functions for the stretch and chordwise deformations were approximated by linear combinations of basis functions as follows:

$$\begin{aligned} s_q (x_q ,t)= & {} \sum _{j=1}^N {S_j (x_q )T_j^{s_q } (t)} , \end{aligned}$$

(26)

$$\begin{aligned} v_q (x_q ,t)= & {} \sum _{n=1}^N {V_n (x_q )T_n^{v_q } (t)} , \end{aligned}$$

(27)

$$\begin{aligned} \bar{{s}}_q (x_q ,t)= & {} \sum _{i=1}^N {S_i (x_q )\bar{{T}}_i^{s_q } (t)} , \end{aligned}$$

(28)

$$\begin{aligned} \bar{{v}}_q (x_q ,t)= & {} \sum _{m=1}^N {V_m (x_q )\bar{{T}}_m^{v_q } (t)} , \end{aligned}$$

(29)

where N is the total number of basis functions, $S_{j}$ and $V_{n}$ are the basis functions for the stretch and chordwise deformations, $T_j^{s_q }$ and $T_n^{v_q}$ are unknown functions of time, and $\bar{{T}}_i^{s_q}$ and $\bar{{T}}_m^{v_q }$ are arbitrary functions of time. In this study, the basis functions $S_{j}$ and $V_{n}$ are selected as the eigenfunctions for the longitudinal and transverse vibrations of a stationary cantilever beam. These functions are comparison functions, which satisfy both essential and natural boundary conditions:

$$\begin{aligned} S_j (x_q )= & {} \sqrt{2}\sin \frac{\left( {2j-1} \right) \pi x_q }{2L}, \end{aligned}$$

(30)

$$\begin{aligned} V_n (x_q )= & {} \cosh \beta _n x_q -\cos \beta _n x_q \nonumber \\&-\frac{\sinh \beta _n L-\sin \beta _n L}{\cosh \beta _n L+\cos \beta _n L}\left( {\sinh \beta _n x_q -\sin \beta _n x_q } \right) .\nonumber \\ \end{aligned}$$

(31)

Here, $\beta _{n}$ is the n-th solution of the characteristic equation given by

$$\begin{aligned} \cos \beta _n L\cdot \cosh \beta _n L=-1. \end{aligned}$$

(32)

Table 1 Reference values of the physical parameters and dimensions used in computations

Table 2 Convergence characteristics of the RMS values for the stretch and chordwise deformations of the rotor–blade system

The discretized equations may be obtained by substituting Eqs. (26)–(29) into Eqs. (22)–(25), and they can be written in the following matrix-vector form:

$$\begin{aligned} \mathbf{M}{{\ddot{\mathbf{T}}}}+\left( {\mathbf{C}+\mathbf{G}} \right) {{\dot{\mathbf{T}}}}+\mathbf{KT}+\mathbf{N}\left( {\mathbf{T}, {{\dot{\mathbf{T}}}}, {{\ddot{\mathbf{T}}}}} \right) =\mathbf{F}, \end{aligned}$$

(33)

where M is the mass matrix, C is the damping matrix, G is the gyroscopic matrix, K is the stiffness matrix, N is the nonlinear internal force vector, F is the force vector, and T is the unknown vector to be determined, which is given by

$$\begin{aligned}&\mathbf{T}=\left\{ r, \theta , T_1^{s_1 } , T_2^{s_1 } , \ldots , T_N^{s_1 } , T_1^{v_1 } , T_2^{v_1 } , \right. \nonumber \\&\quad \left. \ldots , T_N^{v_1 } , T_1^{s_2 } , T_2^{s_2 } , \ldots , T_N^{s_2 } , T_1^{v_2 } , T_2^{v_2 } , \ldots , T_N^{v_2 } \right\} ^{\mathrm{T}}.\nonumber \\ \end{aligned}$$

(34)

4 Convergence and validation

Before analyzing the nonlinear dynamic responses, the convergence test for the dynamic responses was performed to determine the number of basis functions required to obtain reliable results. The following physical properties of the rotor–blade system were considered for the convergence test. The rotating blades have a total length of $L = 1\,\hbox {m}$, a cross-sectional area of $A = 5\times 10^{-3}\,\hbox {m}^{2}$, a Young’s modulus of $E = 7\times 10^{10}\,\hbox {N/m}^{2}$, a mass density of $\rho = 3000\, \hbox {kg/m}^{3}$ and an area moment of inertia of $I = 1.0204\times 10^{-6}\,\hbox {m}^{4}$. The blades are slim enough to be considered Euler–Bernoulli beams. The rotor has a mass of $m = 15$ kg, a radius of $a = 0.1\,\hbox {m}$, an eccentricity of $e = 0.01\,\hbox {m}$ and a maximum rotating speed of $\Omega _{m} = 200\,\hbox {rad/s}$. The equivalent supporting stiffness and damping coefficient for the shaft and bearings are given by $k = 1\times 10^{6}\,\hbox {N/m}$ and $c = 100\,\hbox {Ns/m}$. These values, which are listed in Table 1, were used for further computations unless otherwise noted. The rotating speed profile is given by

$$\begin{aligned} \Omega (t)=\left\{ {{\begin{array}{ll} \Omega _m \left( {t-\frac{1}{2\pi }\sin 2\pi t} \right) &{}\hbox { for }0 \le t\le t_m , \\ {\Omega _m }&{} \hbox { for }t_m \le t\le t_f . \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$

(35)

where $t_{m} = 1\,\hbox {s}$ and $t_{f} = 5\,\hbox {s}$. As shown in Fig. 2, the rotating speed smoothly increases to the maximum speed during time $t_{m}$. The initial conditions for the radial, stretch and chordwise deformations are zero, and the initial condition for the angular displacement is $\pi /2$. In this study, dynamic responses were computed by using dimensional parameters rather than dimensionless parameters because the dimensionless parameters make it difficult to independently evaluate the effects of the rotor and the blades.

Fig. 2

Rotating speed profile with a maximum speed of 200 rad/s

To investigate the convergence characteristics of dynamic responses, the stretch and chordwise deformations at the ends of two blades were computed as the number of basis functions, N, increased. For each N, the root-mean-square (RMS) values for the stretch and chordwise deformations of two blades were computed during the time interval from 0 to $t_{f}$, and these values are listed in Table 2. As shown in Table 2, the RMS values for the stretch and chordwise deformations of two blades converge sufficiently when $N = 10$. Therefore, the ten basis functions were used for further computations in this study.

First, the proposed model was validated with a rotor–blade system in which the blades can be treated as rigid bodies. After the Young’s modulus was selected to have a high value of $E = 7\times 10^{15}\,\hbox {N/m}^{2}$ to treat the blades as rigid bodies, the dynamic response for the radial displacement of the rotor–blade system was computed, and the frequency components of the response were investigated. If the Young’s modulus is very large, the deformations of the blades are negligible, and the rigid-body motion of the rotor–blade system becomes dominant compared to the flexible motions of the blades. In this case, the dynamic response of the radial displacement is displayed in Fig. 3, which shows that the radial displacement increases monotonically during the first second and then oscillates with decreasing vibration amplitude. To examine the frequency components of this dynamic response with damped magnitude, a frequency spectrum (Fig. 4) was obtained by applying FFT to the response. In this study, FFT was applied to dynamic responses during the time interval of 1–5 s in which the rotating speed is constant as shown in Fig. 2. Although one peak is observed in Fig. 4, another peak is found if the area within the ellipse is enlarged. The first and second peak frequencies are 46.0 and 354.7 rad/s, respectively.

Fig. 3

Dynamic response for the radial displacement of the rotor with $k = 1\times 10^{6}\,\hbox {N/m}$ when the blade stiffness is large ($E = 7\times 10^{15}\,\hbox {N/m}^{2}$)

If these frequencies are related to the natural frequencies for the whirling motion of the rotor–blade system, the proposed model is physically valid when the blades are stiff. For this purpose, it is necessary to check the natural frequencies of the rotor–blade system, assuming that the two blades are rigid without deformation. Although the mass moments of inertia for the blades should be considered, they are neglected when computing the natural frequencies for the whirling motion. Instead, the computation of the natural frequencies was carried out, assuming that the mass of the two blades is imposed on the rotor. In other words, the effective rotor mass is regarded as the total mass of the rotor and two blades, $m + 2\rho {\textit{AL}}$. Using the Jeffcott rotor model, the governing equations for the whirling motion of the equivalent rotor with mass $m + 2\rho {\textit{AL}}$ are obtained as follows.

$$\begin{aligned}&(m+2\rho AL)\ddot{r}+c{\dot{r}}+kr-(m+2\rho AL)r(\Omega -\dot{\psi })^{2}\nonumber \\&\quad =me\left( {\Omega ^{2}\cos \psi +{\dot{\Omega }}\sin \psi } \right) , \end{aligned}$$

(36)

$$\begin{aligned}&(m+2\rho AL)r({\dot{\Omega }}-\ddot{\psi })+cr(\Omega -\dot{\psi })\nonumber \\&\quad +\,2(m+2\rho AL){\dot{r}}(\Omega -{\dot{\psi }})=me\left( {\Omega ^{2}\sin \psi -{\dot{\Omega }}\cos \psi } \right) .\nonumber \\ \end{aligned}$$

(37)

Application of the perturbation method to Eqs. (36) and (37) leads to the equilibrium position, and equations that are linearized in the neighborhood of the equilibrium position can be obtained. Representing the equilibrium position by $r_{e}$ and $\varPsi _{e}$ and denoting the perturbed displacements by $\Delta r$ and $\Delta \varPsi$, the linearized equations can be expressed as

$$\begin{aligned}&(m+2\rho AL)\Delta \ddot{r}+c\Delta {\dot{r}}+2(m+2\rho AL)\Omega r_e \Delta {\dot{\psi }}\nonumber \\&\quad +\,[k-(m+2\rho AL)\Omega ^{2}]\Delta r+(me\Omega ^{2}\sin \psi _e )\Delta \psi =0,\nonumber \\ \end{aligned}$$

(38)

$$\begin{aligned}&(m+2\rho AL)r_e \Delta \ddot{\psi }-2(m+2\rho AL)\Omega \Delta {\dot{r}}\nonumber \\&\quad +\,cr_e \Delta {\dot{\psi }}-c\Omega \Delta r+(me\Omega ^{2}\cos \psi _e )\Delta \psi =0, \end{aligned}$$

(39)

where $r_{e}$ and $\varPsi _{e}$ are given by

$$\begin{aligned} r_e= & {} \frac{me\Omega ^{2}}{\sqrt{\left[ {k-(m+2\rho AL)\Omega ^{2}} \right] ^{2}+(c\Omega )^{2}}}, \end{aligned}$$

(40)

$$\begin{aligned} \psi _e= & {} \tan ^{-1}\frac{c\Omega }{\left[ {k-(m+2\rho AL)\Omega ^{2}} \right] }. \end{aligned}$$

(41)

The natural frequencies obtained from the eigenvalue problem for Eqs. (38) and (39) are 50.9 and 349.1 rad/s. These natural frequencies (50.9 and 349.1 rad/s) differ by 9.6 and 1.6%, respectively, from the peak frequencies in Fig. 4 (46.0 and 354.7 rad/s). These differences are caused by ignoring the mass moments of inertia and deformations of the blades from the above Jeffcott rotor model. Considering this point, it can be said that the equations of motion for the model presented in this paper provide a reasonable dynamic response when the blade stiffness is large.

Fig. 4

Frequency spectrum for the dynamic response during the time interval of 1–5 s shown in Fig. 3

Fig. 5

Waterfall plot of the frequency spectra for the radial displacements for various values of k when the blade stiffness is large ($E = 7\times 10^{15}\,\hbox {N/m}^{2}$)

Fig. 6

Natural frequencies of a Jeffcott rotor model and the peak frequencies in the frequency spectra when the blade stiffness is large ($E = 7\times 10^{15}\,\hbox {N/m}^{2}$)

Fig. 7

Dynamic responses of the first blade with $E = 7\times 10^{10}\,\hbox {N/m}^{2}$ when the spring constant is large ($k = 1\times 10^{9}\,\hbox {N/m}$): a stretch deformation and b chordwise deformation

Fig. 8

Frequency spectra for the dynamic responses shown in the dashed boxes of Fig. 7

To verify the proposed model more thoroughly, five frequency spectra for the radial displacements for the cases of $k = 2\times 10^{6}, 4\times 10^{6}, 6\times 10^{6}, 8\times 10^{6}$ and $1\times 10^{7}\,\hbox {N/m}$ are computed using Eq. (33) when the blade stiffness is large ($E = 7\times 10^{15}\,\hbox {N/m}^{2}$). The results are presented in Fig. 5 as a waterfall plot. The peak frequencies for the five spring constants shown in Fig. 5 are illustrated in Fig. 6. In this figure, the squares and triangles represent the first and second peak frequencies of the frequency spectra, and the solid lines represent the two natural frequencies of the Jeffcott rotor model, computed from Eqs. (38) and (39). As shown in Fig. 6, the dynamic responses of radial displacement have frequency components almost equal to the natural frequencies of the Jeffcott rotor model when the Young’s modulus is so high that the blades can be treated as rigid bodies. Therefore, the dynamic model presented in this study is valid when the stiffness of the blade is very large.

Next, we examined whether the dynamic responses for the blade deformations of the system with a high spring constant are the same as those of a rotating beam without the whirling motion presented in the previous research [10]. To minimize the whirling motion, i.e., the radial displacement, the supporting spring constant was chosen to be $k = 1\times 10^{9}\,\hbox {N/m}^{2}$, which is a very large value. The dynamic responses at the end of the first blade were computed with this large spring constant. These responses are presented in Fig. 7, where Fig. 7a is for the stretch deformation, and Fig. 7b is for the chordwise deformation. To better observe the dynamic responses at steady state, the responses of Fig. 7 are magnified for a time interval of 1 to 1.5 s and redrawn in the dashed boxes. The frequency components of the responses in the dashed boxes were identified by applying FFT to these responses. The frequency spectra obtained by FFT are shown in Fig. 8, where two peak frequencies of 268.4 and 1589.1 rad/s are observed. These frequencies are very close to the first and second natural frequencies of a rotating beam without whirling motion, 250.5 and 1543.3 rad/s, as calculated by Chung and Yoo [10] under the same conditions. In summary, the model proposed in this paper is valid because the dynamic response of a blade of the rotor–blade system with a very high supporting stiffness shows the characteristics of a rotating cantilever beam without whirling motion.

Fig. 9

Natural frequencies of a Jeffcott rotor model as a function of the spring constant corresponding to a rotor–blade system with $E=\infty$

5 Analysis of dynamic responses

In this section, we analyzed the effects of the supporting stiffness, the rotating speed and Young’s modulus on the dynamic responses of the rotor–blade system. Physical parameters such as the mass, eccentricity, radius, damping of the rotor and the mass, length, and area moment of inertia of the blade also affect the dynamic responses. However, only the three parameters mentioned above were considered in this study, because these parameters predominantly affect the natural frequencies of the rotor–blade system. Unless otherwise noted, the physical properties given in Table 1 were used in the following computations. In addition, the dynamic responses of the stretch and chordwise deformations were computed at the end of the first blade.

Fig. 10

Dynamic responses when $k = 5\times 10^{5}, 1\times 10^{6}$ and $1.5\times 10^{6}\,\hbox {N/m}$: a radial displacements, b stretch deformations and c chordwise deformations

First, we examined the influence of the supporting stiffness of the rotor on the dynamic responses of the rotor–blade system. The natural frequencies of the Jeffcott rotor considering the mass of the rotor and two blades were computed from the eigenvalue problem for Eqs. (38) and (39) for various supporting spring constants. The computed natural frequencies are plotted as solid lines in Fig. 9. For a given value of the spring constant, the Jeffcott rotor has two natural frequencies as shown in Fig. 9, where one monotonically increases with the spring constant and the other decreases to zero and then increases again. The reason for this phenomenon is that the motion of the Jeffcott rotor is described in terms of the Eulerian description [22]. When one of the natural frequencies is zero, the value of the spring constant is $1.8\times 10^{6}\,\hbox {N/m}$, at which the rotating speed of 200 rad/s becomes the critical speed of the rotor system. Denoting the spring constant corresponding to the critical speed by $k_{c}$, the value of $k_{c}$ is given by $k_{c} = 1.8\times 10^{6}\,\hbox {N/m}$. In other words, when $m + 2\rho {\textit{AL}} = 45\,\hbox {kg}$ and $k_{c} = 1.8\times 10^{6}\,\hbox {N/m}$, the critical speed of the Jeffcott rotor, $\Omega _{c}$, is calculated as 200 rad/s from the following equation

$$\begin{aligned} \Omega _c =\sqrt{{k_c }/{(m+2\rho AL)}}. \end{aligned}$$

(42)

Fig. 11

Frequency spectra when $k = 5\times 10^{5}, 1\times 10^{6}$ and $1.5\times 10^{6}\,\hbox {N/m}$: a radial displacements and b chordwise deformations

Fig. 12

Dynamic responses when $k= 2\times 10^{6}, 2.5\times 10^{6}$ and $3\times 10^{6}\,\hbox {N/m}$: a radial displacements, b stretch deformations and c chordwise deformations

Fig. 13

Frequency spectra when $k = 2\times 10^{6}, 2.5\times 10^{6}$ and $3\times 10^{6}\,\hbox {N/m}$: a radial displacements and b chordwise deformations

Fig. 14

Natural frequencies of a Jeffcott rotor model as a function of rotating speed corresponding to a rotor–blade system with $E=\infty$

Fig. 15

Dynamic responses when $\Omega = 80$, 110 and 140 rad/s: a radial displacements, b stretch deformations and c chordwise deformations

Fig. 16

Frequency spectra when $\Omega = 80$, 110 and 140 rad/s: a radial displacements and b chordwise deformations

Fig. 17

Dynamic responses when $\Omega = 170, 200$ and 230 rad/s: a radial displacements, b stretch deformations and c chordwise deformations

Fig. 18

Frequency spectra when $\Omega = 170, 200$ and 230 rad/s: a radial displacements and b chordwise deformations

Fig. 19

Dynamic responses when $E = 1\times 10^{10}, 4\times 10^{10}$ and $7\times 10^{10}\,\hbox {N/m}^{2}$: a radial displacements, b stretch deformations and c chordwise deformations

Fig. 20

Frequency spectra when $E = 1\times 10^{10}, 4\times 10^{10}$ and $7\times 10^{10}\,\hbox {N/m}^{2}$: a radial displacements and b chordwise deformations

To efficiently analyze the influence of the supporting stiffness, we selected three values of the spring constant less than $k_{c}$ and three values greater than $k_{c}$. The three values less than $k_{c}$ are $k = 5\times 10^{5}, 1\times 10^{6}$ and $1.5\times 10^{6}\,\hbox {N/m}$, and three values greater than $k_{c}$ are $k = 2\times 10^{6}, 2.5\times 10^{6}$ and $3\times 10^{6}$ N/m. The dynamic responses computed for three values smaller than $k_{c}$ are plotted in Fig. 10, in which Fig. 10a–c represents the radial displacement, stretch deformation and chordwise deformation, respectively. As shown in Fig. 10a, the vibration amplitude and period of the radial displacement increase with the spring constant. This phenomenon is also observed in the stretch deformation (Fig. 10b) and in the chordwise deformation (Fig. 10c). The reason for this phenomenon is that the critical speed approaches 200 rad/s as the spring constant increases when the spring constant is below $k_{c}$.

We determined how the change in the spring constant affects the frequency components of the dynamic responses. The frequency spectra obtained by applying FFT to the dynamic responses shown in Fig. 10 are presented in Fig. 11. The frequency spectra for the stretch deformation are very similar to the frequency spectra for the chordwise deformation; therefore, only the frequency spectra for the radial displacement and the chordwise deformation are illustrated in Fig. 11. The peak frequencies of 13.4, 44.1 and 88.2 rad/s shown in Fig. 11 are marked with small circles in Fig. 9, where it can be seen that these frequencies agree well with the first natural frequency of the Jeffcott rotor. However, the peak frequencies corresponding to the second natural frequency of the Jeffcott rotor are not observed in Fig. 11 because the contributions of the second natural frequency are too small. On the other hand, the peak frequency of 268.5 rad/s observed in Fig. 11b is very close to the first natural frequency (250.5 rad/s) for the chordwise deformation of the rotating cantilever beam without whirling motion [10]. Based on the above analysis, “(r)” is attached to the peak frequencies in Fig. 11a, meaning that the frequencies are caused by the whirling motion of the Jeffcott rotor, and “(b)” is attached to the peak frequency of 268.5 rad/s in Fig. 11b, meaning that it is caused by the deformation of the blade.

As shown in Fig. 11a, the peak frequency of the radial displacement changes significantly due to the supporting spring constant. In other words, the spring constant has a great influence on the natural frequencies of the whirling motion of the rotor–blade system. The peak frequencies shown in the frequency spectra of the radial displacement are also observed in the frequency spectra for the chordwise deformation, as shown in Fig. 11b. This means that the whirling motion of the rotor–blade system has a relatively large influence on the chordwise deformations of the blades. In contrast to the peak frequencies for the whirling motion, the peak frequencies for the blade deformation have the same value of 268.5 rad/s even though the spring constant changes (Fig. 11b). This implies that the spring constant has little influence on the natural frequencies for the blade deformation.

The effect of the spring constant change on the dynamic responses of the rotor–blade system was also investigated for spring constants larger than $k_{c}$. Three values of the spring constant that are greater than $k_{c} = 1.8\times 10^{6}\,\hbox {N/m}$ were considered: $k = 2\times 10^{6}, 2.5\times 10^{6}$ and $3\times 10^{6}$ N/m. The dynamic responses computed with these spring constant values are shown in Fig. 12. As shown in this figure, the vibration amplitude and period of the dynamic response decrease as the spring constant increases. This behavior is completely opposite to that when k is less than $k_{c}$. The critical speeds of the Jeffcott rotor when $k = 2\times 10^{6}, 2.5\times 10^{6}$ and $3\times 10^{6}$ N/m are calculated by Eq. (42) as 210.8, 235.7 and 258.2 rad/s, respectively. Thus, as the spring constant increases, the reference rotating speed of 200 rad/s is farther away from the critical speed, resulting in a decrease in the amplitude of the dynamic response.

To investigate the frequency components for the dynamic responses shown in Fig. 12, the frequency spectra were obtained in the same manner as before. The frequency spectra of the dynamic responses when $k = 2\times 10^{6}, 2.5\times 10^{6}$ and $3\times 10^{6}\,\hbox {N/m}$ are plotted in Fig. 13, where Fig. 13a, b is for the radial displacement and the chordwise deformation, respectively. As shown in Fig. 13a, the frequency spectra of the radial displacement when $k = 2\times 10^{6}, 2.5\times 10^{6}$ and $3\times 10^{6}\,\hbox {N/m}$ have peak frequencies of 13.4, 34.5 and 53.7 rad/s, respectively. These peak frequencies for the spring constant values are indicated as small squares in Fig. 9, which shows that the peak frequencies are in good agreement with the first natural frequencies of the Jeffcott rotor. Meanwhile, the peak frequency of 268.5 rad/s in Fig. 13 is very close to the natural frequency for the chordwise deformation of the blade, and it is the same as the peak frequency of 268.5 rad/s observed in Fig. 11b.

Next, we investigated the effect of the rotating speed on the dynamic responses of the rotor–blade system. The dynamic responses were computed for rotating speeds $\Omega = 80, 110, 140, 170, 200$ and 230 rad/s when all the physical properties (except the rotating speed) are the same as the values in Table 1. The natural frequencies of the Jeffcott rotor for various rotating speeds are shown in Fig. 14, where the natural frequencies versus rotating speed are drawn as straight lines. As the rotating speed increases, the first natural frequency linearly decreases to zero and then linearly increases. Meanwhile, the second natural frequency linearly increases with the rotating speed. The rotating speed of 149.1 rad/s is the critical speed at which the first natural frequency becomes zero. This speed coincides with the value calculated using Eq. (42). Since the dynamic responses when the rotating speed is lower than the critical speed are quite different from those when the rotating speed is larger than the critical speed, these two cases are analyzed separately.

The dynamic responses were analyzed first for cases when the rotating speed is lower than the critical speed, i.e., when $\Omega = 80, 110$ and 140 rad/s. The responses when $\Omega = 80, 110$ and 140 rad/s are shown in Fig. 15. As shown, the vibration amplitude and period for the radial displacement and the stretch/chordwise deformations increase with the rotating speed. These characteristics can be more clearly confirmed in frequency spectra. The dynamic responses in the time interval of 1–5 s are shown in Fig. 15a, c, while the associated frequency spectra are plotted in Fig. 16a, b, respectively. The peak frequencies with “(r)” in the frequency spectra of Fig. 16 are indicated as circles in Fig. 14. Since these circles are very close to a straight line, it can be said that these peak frequencies are due to the whirling motion of the system. On the other hand, the first natural frequencies of rotating cantilever beams without whirling motion when $\Omega = 80$, 110 and 140 rad/s were computed as 247.7, 250.5 and 257.0 rad/s, respectively [10]. These natural frequencies agree well with the peak frequencies of 247.4, 251.2 and 255.0 rad/s in Fig. 16. Therefore, these peak frequencies are caused by the natural frequencies of the blade deformation. This means that the rotating speed affects both the natural frequencies of the whirling motion of the system and the natural frequencies of the chordwise deformation of the blade.

The dynamic behavior when the rotating speed is larger than the critical speed is quite different from the behavior when the rotating speed is lower than the critical speed. The dynamic responses when the rotating speeds are larger than the critical speed (when $\Omega = 170, 200$ and 230 rad/s) are presented in Fig. 17. As shown, the vibration amplitude and period decrease as the rotating speed increases. This behavior is opposite to the behavior shown in Fig. 15, which shows the case when the rotating speeds are lower than the critical speed. Figure 18 illustrates the frequency spectra of the dynamic responses shown in Fig. 17. Like the previous analysis shown in Fig. 14, the peak frequencies indicated with “(r)” in Fig. 18 (which are presented as squares in Fig. 14) well match the natural frequencies of the Jeffcott rotor represented by straight lines in Fig. 14. Thus, it can be claimed that the peak frequencies of 17.3, 44.1, 72.9 and 389.3 rad/s in Fig. 18 are caused by the whirling motion of the rotor–blade system. The first peak frequency due to the whirling motion increases with the rotation speed. On the other hand, the first natural frequencies for the chordwise blade deformation without whirling motion were calculated as 260.8, 270.5 and 276.0 rad/s for rotating speeds of 170, 200 and 230 rad/s [10]. These natural frequencies are not significantly different from the peak frequencies marked by “(b),” i.e., 262.7, 268.5 and 276.1 rad/s, observed in Fig. 18b. Therefore, the peak frequencies with “(b)” are caused by the chordwise deformation of the blade.

Finally, we analyzed the effect of the blade stiffness, i.e., Young’s modulus, on the dynamic responses of the rotor–blade system. The dynamic responses were analyzed when all the physical properties except the Young’s modulus were the same as those shown in Table 1. Dynamic responses of the radial displacement and stretch/chordwise deformations were computed for three values of Young’s modulus ($E = 1\times 10^{10}, 4\times 10^{10}$ and $7\times 10^{10}\,\hbox {N/m}^{2}$), and the results are plotted in Fig. 19. As shown in Fig. 19a, the dynamic response of the radial displacement does not vary significantly with changes in Young’s modulus. This implies that the stiffness of the blades does not have a great influence on the whirling motion of the rotor–blade system. However, the stiffness of the blade has a great effect on the stretch and chordwise deformations. Figure 19b shows that the magnitude of the stretch deformation decreases with increasing stiffness of the blade. In Fig. 19c, the vibration amplitude of the chordwise deformation decreases as the stiffness of the blade increases. It is expected that the amplitudes of the stretch and chordwise deformations decrease as the stiffness of the blade increases.

To identify the frequency components of the dynamic responses shown in Fig. 19, the frequency spectra were obtained by applying FFT to the responses, and they are plotted in Fig. 20. The natural frequencies of the Jeffcott rotor based on the reference physical properties were 50.9 and 349.1 rad/s from Eqs. (38) and (39). These natural frequencies are close to the peak frequencies of 44.1 and 331.7 rad/s (Fig. 20a). Therefore, it can be said that these two peak frequencies are caused by the natural frequencies of the whirling motion of the rotor–blade system. It is shown in Fig. 20a that the magnitude and frequency of the most dominant peaks are independent of the change in the Young’s modulus of the blade. This again shows that the stiffness of the blade does not significantly affect the whirling motion of the system.

Unlike the frequency spectra for the radial displacement, the frequency spectra for the chordwise deformation have peak frequencies for blade deformation. The peak frequencies (141.9, 216.7 and 268.5 rad/s) shown in Fig. 20b are very close to the first natural frequencies (140.0, 217.3 and 270.5 rad/s) of the bending modes for the rotating blade without whirling motion. These first natural frequencies were obtained when the Young’s moduli are $E = 1\times 10^{10}, 4\times 10^{10}$ and $7\times 10^{10}\,\hbox {N/m}^{2}$. The peak frequency of 765.1 rad/s shown in Fig. 20b is close to the second natural frequency of 755.7 rad/s for the chordwise deformation of the rotating blade when $E = 1\times 10^{10}\,\hbox {N/m}^{2}$. Thus, this peak frequency is due to the second natural frequency of the rotating blade. Comparing Fig. 20a, b, we see that the whirling motion of the rotor–blade system has a great influence on the blade deformation, but the deformation of the blade does not greatly affect the whirling motion.

6 Conclusions

We proposed a new nonlinear dynamic model for a rotor–blade system with whirling motion and analyzed the dynamic responses of the system. The rigid rotor was modeled as a Jeffcott rotor, and the blades are regarded as Euler–Bernoulli beams. The nonlinear equations for the radial displacement, stretch deformation and chordwise deformation were derived by employing Hamilton’s principle. The nonlinear partial differential equations were discretized using the Galerkin method. The nonlinear dynamic responses were computed applying the generalized-$\upalpha$ time integration method to the discretized equations.

The proposed model was verified by separating the case where the Young’s modulus of the blade is very high and the case where the supporting stiffness of the rotor is very high. Assuming that the Young’s modulus of the blade is high in the proposed model, the results are similar to the radial displacement of the Jeffcott rotor. In contrast, if the rotor–blade system has high supporting stiffness, the stretch/chordwise deformations of the rotor–blade system match those of the rotating cantilever blade without the whirling motion. Thus, the proposed model is valid, and we showed that this model includes both characteristics of the Jeffcott rotor and the rotating beam without the whirling motion.

The analysis results obtained in this study are as follows.

• (1) If the supporting spring constant is less than the constant corresponding to the critical speed, the vibration amplitudes and periods of the radial displacement and the stretch/chordwise deformations increase with the spring constant. Otherwise, they decrease as the spring constant increases.

• (2) The supporting spring constant has a great influence on the natural frequencies of the whirling motion of the rotor–blade system. However, it has no influence on the natural frequencies associated with bending deformation of the blade.

• (3) If the rotating speed is lower than the critical speed, the vibration amplitude and period for both the radial displacement and the stretch/chordwise deformations increase with the rotating speed. Otherwise, they decrease as the speed increases.

• (4) The rotating speed affects both the natural frequencies of the whirling motion of the system and the natural frequencies of the chordwise deformation of the blade.

• (5) The blade stiffness does not have a significant effect on the whirling motion of the rotor–blade system, but it has a significant effect on the stretch and chordwise deformation of the blade.